数字信号处理 pdf (3)
数字信号处理第三版(姚天任、江太辉) 答案 第三章

3.1 图 P3.1 所示的序列 x(n) 是周期为 4 的周期性序列。请确定其傅里叶级数的系数 X (k) 。
∑ ∑ ∑ 解: X (k)
=
N −1
x(n)WNnk
=
N −1
x(−n)WNnk
=
−( N −1)
x(n)WN−nk
=
X (−k)
解:图 P3.5_1 所示的是计算这两个序列的周期卷积 x3 (n) 的过程,可以看出,x3 (n) 是 x1 (n) 延时 1 的结果, 即 x3(n) = x1(n −1) 。
3.6 计算下列序列的N点DFT:
(1) x(n) = δ (n)
(2) x(n) = δ [(n − n0 )]N * RN (n), 0 < n0 < N
总计需要时间: (105 + 21)s = 126s
用 FFT 计算 DFT:
复数乘法:
N 2
log2
N
=
5120次, 5120 ×100μ s
≈
0.512s
复数加法: N log2 N = 10240次,10240× 20μs ≈ 0.2048s
总计需要时间: (0.512 + 0.2048)s = 0.7168s
(2) x2 (n) = x ⎡⎣(2 − n)⎤⎦4 R4 (n)
解: x1(n) 和 x2 (n) 的图形如图 P3.7_1 所示:
3.8 图 P3.8 表示一个 4 点序列 x(n) 。 (1)绘出 x(n) 与 x(n) 的线性卷积结果的图形。 (2)绘出 x(n) 与 x(n) 的 4 点循环卷积结果的图形。 (3)绘出 x(n) 与 x(n) 的 8 点循环卷积结果的图形,并将结果与(1)比较,说明线性卷积与循环卷
数字信号处理(姚天任江太辉第三版)课后习题答案 清晰版

2 n+ ] 3 6
=ay1(n)+by2(n) 故该系统是线性系统。 由于
2 (n-k)+ ] 3 6 2 T[x(n-k)]=x(n-k)sin[ n+ ] 3 6
y(n-k)=x(n-k)sin[
因而有 T[x(n-k)]≠y(n-k) 帮该系统是移变系统。 设 |x(n)|≤M,则有 |y(n)|=|x(n)sin[
n
|h(n)|=
n
1
| a |=
n
n
a
n
,故该系统只有在|a|>1 时才是稳定系统。
(3) 因为在 n<O 时,h(n) ≠0,故该系统不是因果系统。 因为 S= |h(n)|= | (n+n 0 )|=1< ,故该系统是稳定系统。
sin(n ) sin
2 -2cos · +1=0
由特征方程求得特征根
1 =cos +jsin =e j , 2 =cos -jsin = e j
k
x(k ) =
n t
m
x(m t )
n
=T[x(n-t)] 所以该系统是非移变系统。 设 x(n)=M<∞ y(n)=
k
M =∞,所以该系统是不稳定系统。
n
n
因y(n)只取决于现在和过去的输入x(n),不取决于未来的输入,故该系统是因果系统。 (4)设 y1(n)=
n
u(-n),0<a<1 用直接计算线性卷积的方法,求
2.6 试证明线性卷积满足交换率、结合率和加法分配率。
数字信号处理 pdf

数字信号处理什么是数字信号处理?数字信号处理(Digital Signal Processing,简称DSP)是一种利用数字计算机进行信号处理的技术。
它将输入信号采样并转换成数字形式,在数字域上进行各种运算和处理,最后将处理后的数字信号转换回模拟信号输出。
数字信号处理在通信、音频、视频等领域都有广泛的应用。
数字信号处理的基本原理数字信号处理涉及许多基本原理和算法,其中包括信号采样、量化、离散化、频谱分析、滤波等。
信号采样信号采样是指将连续的模拟信号转换为离散的数字信号。
采样定理指出,为了能够准确地还原原始信号,采样频率必须大于信号中最高频率的两倍。
常用的采样方法有均匀采样和非均匀采样。
量化量化是将连续的模拟信号离散化为一组有限的量化值。
量化过程中,需要将连续信号的振幅映射为离散级别。
常见的量化方法有均匀量化和非均匀量化,其中均匀量化是最为常用的一种方法。
离散化在数字信号处理中,信号通常被表示为离散序列。
离散化是将连续的模拟信号转换为离散的数字信号的过程。
频谱分析频谱分析是一种用于研究信号频域特性的方法。
通过对信号的频谱进行分析,可以提取出其中的频率成分,了解信号的频率分布情况。
滤波滤波是数字信号处理中常用的一种方法,用于去除信号中的噪声或不需要的频率成分。
常见的滤波器有低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
数字信号处理的应用数字信号处理在许多领域都有广泛应用,下面列举了其中几个重要的应用领域:通信在通信领域,数字信号处理主要用于调制解调、信道编码、信号分析和滤波等方面。
数字信号处理的应用使得通信系统更加稳定和可靠,提高了通信质量和传输效率。
音频处理在音频处理领域,数字信号处理广泛应用于音频信号的录制、编码、解码、增强以及音频效果的处理等方面。
数字音乐、语音识别和语音合成等技术的发展离不开数字信号处理的支持。
视频处理数字信号处理在视频处理领域也发挥着重要作用。
视频压缩、图像增强、视频编码和解码等技术都离不开数字信号处理的支持。
数字信号处理英文版课后答案(3)
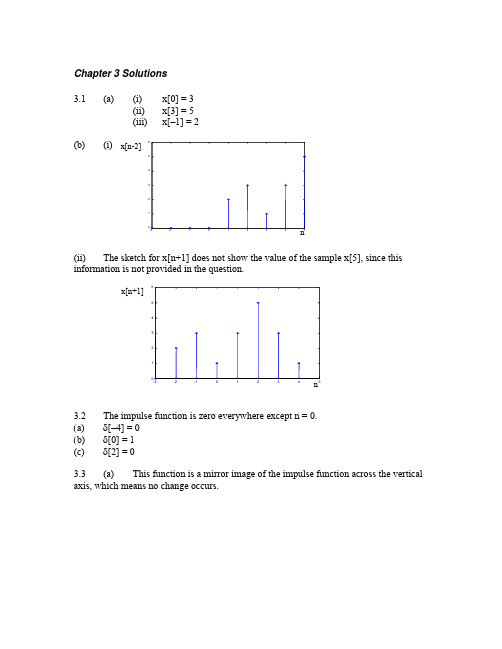
Chapter 3 Solutions3.1 (a) (i) x[0] = 3(ii) x[3] = 5(iii) x[–1] = 2(b) (i)(ii) The sketch for x[n+1] does not show the value of the sample x[5], since this information is not provided in the question.3.2 The impulse function is zero everywhere except n = 0.(a) δ[–4] = 0(b) δ[0] = 1(c) δ[2] = 03.3 (a) This function is a mirror image of the impulse function across the verticalaxis, which means no change occurs.(b) This function shifts the impulse two steps to the right and increases its amplitude to 2.(c) This function is the sum of two impulse functions.3.4 The step function is zero for n < 0 and one everywhere else.(a) u[–3] = 0(b) u[0] = 1(c) u[2] = 13.5 (a) x[n] = 4u[n–1](b) x[n] = –2u[n](c) x[n] = 2u[–n](d) x[n] = u[n–2](e) x[n] = u[2–n]3.6(a)(b)3.7 (a) This signal is a sum of shifted step functions, each with amplitude one. x[n] = 0.1u[n –1] + 0.1u[n –2] + 0.1u[n –3] + …(b) This signal is a sum of impulse functions with increasing amplitude. x[n] = 0.1δ[n –1] + 0.2δ[n –2] + 0.3δ[n –3] + …3.8 x[n] = (u[n] – u[n –2]) + (u[n –5] – u[n –7]) + (u[n –10] – u[n –12])3.9 x[n] = 2δ[n] – 3δ[n –1] + δ[n –2] – δ[n –3] + 3δ[n –4]3.10 (a)x[n] = δ[n –3] + δ[n –4] + δ[n –5] + δ[n –6] – δ[n –7] – δ[n –8] – δ[n –9] – δ[n –10] – δ[n –11] ∑∑==-δ--δ=117k 63k ]k n []k n [(b) x[n] = u[n –3] – 2u[n –7] + u[n –12] 3.11 x[n] = u[n] + 2u[n –4]3.123.13 The signal has values 1, 0.5, 0.25, 0.125, etc. These values can be generated from the function 0.5n , where each value is the amplitude of an impulse function. The signal may be expressed as ∑∞=-δ=0k k ]k n [)5.0(]n [x = δ[n] + 0.5δ[n –1] + 0.25δ[n –2] + 0.125δ[n –3] + …3.14 (a)By Euler’s identity, ⎪⎭⎫ ⎝⎛π-⎪⎭⎫ ⎝⎛π==π-4n sin j 4n cos e]n [x 4n j(b)From (a), 4π=Ω. Therefore, 18422=ππ=Ωπ. The digital period is 8 samples.3.15 (a)⎪⎭⎫⎝⎛π-⎪⎭⎫ ⎝⎛π==π-3n sin j 3n cos e ]n [x 3n j(b) The magnitude of any complex number is the square root of the sum of the squares of the real and imaginary parts. The magnitudes in the last column in (a) show that 3n j eπ- = 1. This equation is true for all n.3.16 The frequency of the analog signal is f = ω/2π = 200/2π Hz. The samplingfrequency f S = 1/T S = 1/(25x10–3) = 40 Hz. The digital frequency is Ω = 2πf/f S = 200/40 = 5 rads. The sampled signal is x[n] = 5sin(n Ω) = 5sin(5n).3.17 Check 2π/Ω for each function. The function is periodic if this ratio is rational. (a) 2π/Ω = 2π/(4/5) = 10π/4 = 5π/2This ratio is not rational, so the sinusoid is not periodic. (b) 2π/Ω = 2π/(6π/7) = 14/6 = 7/3This ratio is rational, and in lowest terms. The number in the numerator, 7, is the number of samples before the sequence repeats. (c) 2π/Ω = 2π/(2π/3) = 3This result may be seen as 3/1. Thus, the sinusoid is periodic with period 3.3.18 (a) From the equation for x(t), ω = 2πf = 1000π, so f = 500 Hz. Since seven samples are collected every three cycles, N = 7 and M = 3, so37M N 2==ΩπThis means SS f 5002f f 276π=π=π=Ω. Solving S f 500276π=π gives f S = 1167 Hz. (b) Since f S > 2f, the sampling rate is adequate to avoid aliasing.3.19 (a) The following samples are graphed below.(b) The ratio 2π/Ω is 2π/(4π/5)=10/4 = 5/2. The numerator, 5, indicates the sinusoidal sequence repeats every five samples. Because the denominator of the ratio is 2, these five samples are collected over two analog periods.(c) The analog signal is superimposed over the digital signal with a dashed line in the figure below.3.20 The analog frequency of x(t) is f = ω/(2π) = 2500π/(2π) = 1250 Hz. The digital frequency of x[n] is π/3 radians. These frequencies must be related through the equationSS f 12502f f 23π=π=π=ΩThe solution to this equation is f S = 7500 Hz. One other solution is possible, since⎪⎭⎫⎝⎛π=⎪⎭⎫ ⎝⎛π-π=⎪⎭⎫ ⎝⎛π3n 5cos 3n n 2cos 3n cos . This view givesSf 1250235π=π=Ωor f S = 1500 Hz. At this frequency, aliasing occurs. The signal appears at a frequency of 250 Hz. This explains why this second sampling rate works:315002502f f 2S π=π=π=Ω3.21 (a) From 052n 92=π+π, n = 59-. The shift moves the function left by 9/5samples. (b) The samples in the two signals do not match, because the shift is not an integer.(c) 951.052)0(92sin ]0[x 1=⎪⎭⎫ ⎝⎛π+π=927.052)1(92sin ]1[x 1=⎪⎭⎫ ⎝⎛π+π=(d) For a phase shift of two samples to the right,0)2(92n 92=θ+π=θ+π, so 94π-=θ. Thus, ⎪⎭⎫ ⎝⎛π-π=94n 92sin ]n [x 1. One period of this signal contains the same sample values as one period of x 2[n]. 3.22 (a)(b)(c)(d) 3.23(a)Since the digital sinusoid is periodic,M 10M N 2==Ωπ. Since Sf f 2π=Ω, M10f f S =. Therefore, 10Mf f S=. Possible frequencies f of the analog signal are defined by M = 1, 3, 7, 9, 11, …, that is, all integers that do not share any factors with 10. Other integers M result in a digital period less than 10. For 4 kHz sampling, the possible frequencies f are 400, 1200, 2800, 3600, 4400, … Hz. (b) The only two frequencies from (a) that lie within the Nyquist range are 400 Hz and 1200 Hz. All other frequencies f, when sampled at 4 kHz, produce aliases at 400 or 1200 Hz.3.24 A 16-bit image uses 16 bits to represent the gray scale level for each pixel in the image. A total of 65,536 gray scale values can be represented with 16 bits.3.25 Each square on the checkerboard is recorded by a 16 x 16 block of pixels. All pixels in the white squares have gray scale value 255. All pixels in the black squares have gray scale value 0.。
【免费下载】数字信号处理杨毅明习题答案

《数字信号处理》杨毅明,部分练习题参考答案1《数字信号处理》杨毅明,部分练习题参考答案第1章1.(1)模拟信号。
(2)模拟信号。
(3)数字信号。
2.(1)分时测量。
(2)数字信号。
3.(1)麦克风。
(2)模拟信号。
4. 数字信号。
5. 数字信号处理。
6. 数字信号处理的方法。
7. 模拟电路的功率放大器。
8. 光电信号转换、低通滤波、模数转换、数字信号处理、数模转换、低通滤波和电声信号转换。
12. 数字方式。
第2章1. x(n)=18δ(n-8)+20δ(n-10)+21δ(n-12)+21δ(n-14)+20δ(n-16)+17δ(n-18)。
2. x(n)=0.5δ(n)+0.866δ(n-1)+δ(n-2)+0.866δ(n-3)+0.5δ(n-4)。
4. x(n)=2R 5(n+5)+2R 5(n-10)。
5.(1)x(n)不是周期序列。
(2)y(n)是周期序列。
6. 自然频率f=10Hz 。
7.(1)根据标准的相关系数公式,v(n)的波形比w(n)的更像u(n);(2)根据简化的相关系数公式,不能确定v(n)和w(n)哪个最像u(n)。
9. 。
)2()1(2)(2)1()(-+-+++=n n n n n r xy δδδδ10. 卫星和地球表面的距离=1200km 。
11. 该系统没有线性性质,但有时不变性质。
12. 该系统不是线性时不变系统,但它是时不变系统。
13. 。
)3()2(2)1(2)()1()()(33-+-+-+=-+=n n n n n R n R n y δδδδ14. 将R 3(n+2)向右平移2点。
15.(1)不能绝对可和。
(2)乘上一个绝对值小于1的指数序列。
16. 。
)()5.0(2)(n u n h n-=17. 。
)1(6.0)(3)(-+=n y n x n y 18. 。
)1()()(-+=n ay n bx n y 20. 。
)()()(d n n As n s n x -+=21. 。
《数字信号处理》第三版课后习题答案

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n 及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n nn n n n nnn n 2. 给定信号:25,41()6,040,nnx n n其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列;(3)令1()2(2)x n x n ,试画出1()x n 波形;(4)令2()2(2)x n x n ,试画出2()x n 波形;(5)令3()2(2)x n x n ,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n nnnn n n n n n (3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n,A 是常数;(2)1()8()j n x n e 。
解:(1)3214,73w w ,这是有理数,因此是周期序列,周期是T=14;(2)12,168ww,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n;(3)0()()y n x n n ,0n 为整常数;(5)2()()y n x n ;(7)0()()n m y n x m 。
数字信号处理的一般过程及研究内容数字信号处理的特点及应用

2、可靠性高: 模拟系统信号容易受干扰,产生失真;
二进制的数字信号在传输、存储、处理中不容易丢失信息。
3、灵活性强: 模拟系统要改变系统特性一般要改变元件值、或改变电路连接,比较困难。 数字系统中,特别是计算机数字信号处理系统可以通过修改信号处理软件参
线性系统的输出 y(t) = h (t ) ∗ x (t )
Y( Ω ) = H (Ω ) X (Ω )
傅立叶反变换即可 得到输出响应
时域卷积特性从频域角度分析系统和求解系统响应。
傅立叶变换及性质
频域卷积特性:在时域中两信号相乘的频谱等于两信号频谱的卷 积乘以1/2π。
若 x1 (t ) ⎯⎯FT → X 1 (Ω ) x 2 (t ) ⎯⎯FT → X 2 (Ω )
则
x1 (t ) x 2 (t ) ⎯⎯FT →
1
2π
X (Ω ) ∗ X 2 (Ω )
频域卷积特性应用:
进行信号处理时,往往要将无限长的信号(数据)截短成有限 长,即进行“有限化”处理——相当于无限长的信号与一矩形脉冲 信号相乘;抽样信号——连续信号与周期冲激信号相乘,因此, 利用频域卷积特性可计算截短后的有限长信号的频谱和抽样信号 的频谱等。
)
频域卷积特性
理想采样信号的频谱是连续信号频谱的周期延拓, 重复周期为Ωs(采样频率)。
抽样技术
X(Ω)
理
原连续时间信号的频谱
想 抽
-
Ω
m
Ω
m
Ω
(带限信号)
样
Xδ(Ω)
信
号 的
周期冲激序列的频谱
频
谱
Xδ(Ω)
抽样信号的频谱
数字信号处理 刘顺兰第二章完整版习题解答

即 0 不在采样点上时,
X (k )
1 e
1 e
b 当 ○
j ( 0
1 e 1 e
j 0 N 2 k) N
j ( 0
sin[(
0
2
N
k)N ] e ) N
j(
0
2 N
k )( N 1)
sin(
0
2
k
0
X (1) 2 2 j
nk N
x(n)W
n 0
N 1
k 2k 3k 1 jW N WN jW N ,
可求得 X (0) 0,
N 1 n 0
X (1) 4, X (2) 0 , N ( k ) c 1 N 1 c c 1 k cW N
(3) x( n) c , 0 n N 1
n
解: (1) X ( k )
x(n)W
n 0
3
nk 4
1 W4k W42 k W43k , k 0,1,2,3 X (2) 0, X (3) 2 2 j N 4
可求得 X (0) 0, (2) X ( k )
1 N 1 j ( k ' k ) n N 1 j N ( k k ') n X ( k ) [ e N e ] 2 n 0 n 0 N , 2 0 ,
(3) X ( k )
N 1 N 1 n 0
2
2
k k ' 及k N k ' 其它
k N
1 k N 1
即
N ( N 1) , 2 X (k ) N k , W N 1
数字信号处理基础pdf

Sx ( f ) —双边谱 Gx ( f ) —单边谱
Gx
(
f
)
=
2S 0
x
(
f
)
f ≥0 f <0
P
=lim T →∞
1 T
T
∫2 −T 2
x2 (t )dt
= ∫∞ S ( f )df −∞
= ∫∞ G( f )df 0
上式称为 Perceval 定理。(单边谱与双边谱的关系同样适用于 ESD)
T
2 −T
x
cos
nω1
t
d
t
2
∫ bn
=
2 T
T
2 −T
x sin
nω1
t
d
t
2
( n = 1、2、3、…… )
7
傅里叶级数的复指数形式
Fourier series 缩写为 FS
( ) ∑[ ] ∞
x t = X0 +
X ne jnω1t + X −ne j(−nω1 )t
n=1
或
( ) ∑∞
x t = X n e jnω1t
( ) ∞ x t e− j2π f t d t
−∞
∫ x(t) = F [−1 X ( f )] =
( ) ∞
X
f
e j2π f t d f
−∞
FT
x(t )
X(f )
IFT
FT : Fourier Transform
傅里叶变换
IFT : Inverse Fourier Transform 傅里叶逆变换
13
矩形脉冲的傅里叶频谱
矩形脉冲
x(t) = A
dsp的原理及应用pdf

DSP的原理及应用1. 什么是DSP数字信号处理(Digital Signal Processing,简称DSP)是指通过对数字信号进行采集、转换、存储、处理和传输,以实现信号的各种处理功能的技术。
2. DSP的原理2.1 数字信号与模拟信号的区别•数字信号是以离散的方式表示的信号,而模拟信号是以连续的方式表示的信号。
•数字信号是由模拟信号经过采样、量化和编码得到的。
2.2 DSP的基本原理•采样:将模拟信号在时间上进行离散化,得到一系列的采样点。
•量化:对采样后的信号进行量化,将连续的信号值转换为离散的信号值。
•编码:将量化后的信号值用二进制表示。
•数字信号处理:通过各种数字信号处理算法对数字信号进行处理和分析。
•数字信号重构:将处理完的数字信号重新转换为模拟信号。
3. DSP的应用DSP技术在很多领域都有着广泛的应用。
3.1 通信领域•DSP技术在通信领域中被广泛应用,包括调制解调、信号传输、误码检测和校正等方面。
•移动通信、卫星通信、无线电通信等领域都离不开DSP技术的支持。
3.2 图像与视频处理•DSP技术在图像与视频处理中起着重要作用,如图像压缩、图像增强、图像识别等方面。
•视频编解码、视频压缩、视频传输等都离不开DSP技术的应用。
3.3 音频处理•DSP技术在音频处理中有着广泛的应用,如音频压缩、音频降噪、音频分析和合成等方面。
•数字音频处理的实时性和灵活性使得其在音频领域中得到了广泛的应用。
3.4 传感器信号处理•许多传感器产生的信号需要经过DSP处理才能得到有用的信息,如加速度计、陀螺仪、声纳等传感器。
•DSP技术能够对传感器产生的信号进行滤波、噪声消除、特征提取等处理,提高传感器信号的可靠性和准确性。
4. 总结DSP技术是数字信号处理的核心,通过对数字信号进行采集、转换、存储、处理和传输,实现了信号的各种处理功能。
在通信、图像与视频处理、音频处理以及传感器信号处理等领域都有着广泛的应用。
数字信号处理知识点汇总pdf

数字信号处理知识点汇总pdf1 概述数字信号处理(Digital Signal Processing,简称DSP)是一种用于处理、分析和转换数字信号的技术。
它利用各种算法和数字芯片,同时兼顾数字信号的时间和频率特性,将诸如声音、图像和视频等信号处理成有用的数字形式。
DSP技术被广泛应用在数字音频、自动控制、通信、信号分析、图像处理、视频处理等领域,对信号的采集、处理、变换、转换和分析,都能起到极大的作用。
2 基本概念数字信号处理一般包括一切关于用数字系统模拟或处理音频、图像或视频的研究方法。
DSP的基本概念包括:采样率、量化精度、编解码器、可编程处理器等;其中,采样率是指转换连续信号为数字信号所作记录时间间隔,量化精度是指记录信号时用来表述信号的位数;编解码器则是用来将信号进行编码和解码,使信号能由一种格式转换为另一种格式,而可编程处理器以及算法则是用来实现DSP处理的核心。
3 数字信号处理系统数字信号处理系统大致可以分为四大部分:数据采集、信号预处理、DSP处理和系统控制。
数据采集是指用于采集、存储、传输或必要话在实时和传统数字信号处理设备上经常使用的各种硬件设备。
信号预处理器主要用于对原始信号进行滤波、幅值检测、转换等预处理操作,以提高信号的品质。
DSP处理器一般是涵盖了原始信号的采样、量化、滤波处理等操作,用于获得有效的信号;而系统控制则是将处理后的信号传至后续处理系统,以及控制这些系统的运行状态。
4 应用数字信号处理技术在音频和视频领域的应用最为广泛,它可以实现信号的压缩、去噪、可视化和回放等功能。
在通信领域,它可以实现信号的激励、检测和序列处理。
在机器视觉方面,它可以实现图像处理,从而在机器中获取更多信息。
总之,数字信号处理技术为数字信号正确采集、表示、处理和转换提供了有效的技术手段,在日趋发达的信息社会中,已广泛应用于各行各业。
03数字信号处理_吴镇扬_习题解答

解答:
1
(1) 不能用令 x(n)=δ(n)来求 h(n),然后确定稳定性,因为该系统并非线性时不变系统。
实际上,因 g(n)有界,所以,当 x(n)有界时,y(n)= x(n) g(n)<= |x(n)| |g(n)|<∞, 所以系统稳定,y(n) 只与 x(n)的当前值有关,显然是因果的。 (2)
=
N −1
kn
x(n)WN2
+
(−1)k
N −1
kn
x(n)WN2
n=0
n=0
∑N −1
当k为偶数时,上式=2
n=0
kn
x(n)WN2
=
2X
( k ); 2
当k为奇数时,上式=0.
2-9 有限长为 N = 10 的两序列
x(n)
=
⎧1, 0 ≤ ⎨⎩0,5 ≤
n n
≤ ≤
4 9
y(n)
=
⎧1, 0 ⎨⎩−1,
DFS,试利用 X1(k ) 确定 X 2 (k) . 解答:
N −1
∑ X1(k) = x(n)WNkn n=0
2 N −1
N −1
N −1
∑ ∑ ∑ X 2 (k) = x(n)W2kNn = x(n)W2kNn + x(n + N )W2kN(n+N )
N =0
n=0
n=0
注:W2kNn
− j 2π kn
,式中 a 为实数
(1) 对于什么样的 a 值范围系统是稳定的? (2) 如果 0<a<1,画出零点-极点图,并标出收敛区域; (3) 在 z 平面上用图解证明该系统是一个全通系统,即频率响应的幅度为一常数. 解答:
数字信号处理(胡广书)

系统的能量累计情况 6.6 令 H1 ( z ) = 1 − 0.6 z −1 − 1.44 z −2 + 0.864 z −3
H 2 ( z ) = 1 − 0 . 98 z − 1 + 0 . 9 z − 2 − 0 . 8 z − 3
H 3 ( z ) = H1 ( z ) H 2 ( z )
相位,滤波器 系数的长度为 29 点,即 M/2=14 (1) 用矩形窗 (2) 利用 Hamming 窗 试计算并打印滤波器的系数,幅频响应及相频响应。滤波器系数 的计算先用手算,然后调用子程序 DEFIR1 来计算。 8.4 一滤波器的理想频率响应如图所示 (1)试用窗函数法设计该滤波器,要求具有线性相位,滤波器长 度为 33,用 Hamming 窗 (2)用频率抽样法设计,应要求具有线性相位,滤波器长度为 33,过度点自行设置。 注:先用手算出 h(n),然后上机求 H (e jω ) .
x(n)
y(n)
y(n) a
z
a
−1
x(n)
b
zb
−1
(a) x(n)
x(n)
y(n)
z
−1
z
b
−1
z
− a1
y(n)
−1
a (b)
− a2
z −1
b1 b2
− a3
2.9 (c)
2.10 题图 2.10 是一个三阶 FIR 系统,试写出该系统的差分方程及转 移函数。
x(n) -0.7026 -0.7026 0.7385 0.7385
1.4 给定下述系统:
1 (1)y(n)= N +1
∑
k =0
N
x(n-k),N 为大于零的整数。
数字信号处理习题答案及matlab实验详解.pdf

(2) 由 H(z)的表达式,不难求出, 当 w=0 时, H (e j0 ) 1/ 0.51 2;
当 w=π时, H (e j ) 1/ 2.77 0.36;
当
w=±π/4
时,
H
(e
j
4
)
1/ 0.256
4 ,峰值。
B=1; A=[1,-1.13,0.64]; [H,w]=freqz(B,A,256,'whole',1); figure(1); subplot(2,1,1); plot(w,abs(H)) subplot(2,1,2); plot(w,angle(H))
12
实验 2-3 离散系统的频率响应分析和零、极点分布 实验目的:加深对离散系统的频率响应分析和零、极点分布的概念理解。
在 MATLAB 中,可以用函数[z,p,K]=tf2zp(num,den)求得有理分式形式的 系统转移函数的零、极点,用函数 zplane(z,p)绘出零、极点分布图;也可以 用函数 zplane(num,den)直接绘出有理分式形式的系统转移函数的零、极点分 布图。
m
m0
即 y(0) 1, y(1) 0.75, y(2) 0.4375, y(3) 0.2344, y(4) 0.1211,......
利用函数 h=impz(b,a,N)和 y=filter(b,a,x)分别绘出冲激和阶跃响应: b=[1,-1]; a=[1,0.75,0.125]; x=ones(1,100); h=impz(b,a,100); y1=filter(b,a,x); figure(1) subplot(2,1,1); plot(h); subplot(2,1,2); plot(y1);
z 2
数字信号处理习题答案及matlab实验详解.pdf

2 已知用下列差分方程描述的一个线性移不变因果系统 y(n) y(n 1) y(n 2) x(n 1)
5
(a)
求这个系统的系统函数 H (z)
Y (z) X (z)
,画出
H
(
z)
的零-极点图并指出其
收敛区域; (b) 求此系统的单位抽样响应;
解:(a)
H (z)
Y (z) X (z)
1
z 1 z1
第一章
参考答案:
1
(1) 2
0
2 37
14 3
,有理数,所以周期为
14
(2)
2 0
2 16
12
,无理数,非周期
2 (1)[ 1 2 3 3 2 1]
(2) 当 n 0 时
y(n)
1
0.5n m 2 m
m
1 3
2n
当 n 1时
y(n)
n
0.5n m 2m
m
4 3
2n
3 线性,时变
4 (1)因果,不稳定 (2)非因果,稳定
j0.6286 z j / 4 1
9
y0s (n) 1.9608u(n) (0.4804 j0.6286)0.8n e jn / 4u(n) (0.4804 j0.6286)0.8n e jn / 4u(n) 系统输出: y(n) yos (n) y0i (n)
1.9608u(n) (0.2354 j0.308) 0.8n e jn /4u(n) (0.2354 j0.308)0.8n e jn /4u(n) >> y0=[1 1]; >> xic=filtic(b,a,y0); >> N=100;n=0:N-1;xn=ones(1,N); >> yn=filter(b,a,xn,xic); >> plot(n,yn);
数字信号处理-第二版-胡广书-习题解答

!!"#$%&’!"#$()*+,-./!!!"!!!"!""!!"#$!!""#!"$"#%$#"#%"%##"#$#"$%&%&’(!""9:!!""+;<&=>?@A+(%!!"BC !!""D&EF+GHIJ !!""%!&"K &"!""#!!!"%""&B9:&"!""+;<%!$"K &!!""#&!!"$!"&B9:&!!""+;<%!’"L !!""G H $M N O A P Q &R S T &U &&!""&B 9:&&!""+;<%!%"VL !!""ST &PGH $MNOAUW &$!""&B9:&$!""+;<%!’!""!!""+;<X;"’"’"YJ %;!"("("!!"!!""#%!!""$%!!"%""$%!!"%!"$%!!"%&"$%!!"%$"$)!!"$""$%!!"$!"$$!!"$&"$!!!"$$"!!"#$%&’()*+,-!!!!!&"&"!""#!!!"%""Z[4\!!""GH"MNO]^&P_Q‘-!UW+&&;<X;"’"’!YJ%;!"("(!!$"&!!""#&!!"$!"Z[4\!!""a7!MNO]^&=_Q‘-&UW+&;< X;"’"’&YJ%;!"("(&!’"L!!""GH$MNOAU!(!""#!!"%$"&PL!(!""Q&RSTU&&!""# !(!%""#!!%"%$"&&&!""+;<X;"’"’$YJ%;!"("($!%"&$!""bIc%’&$!""#!!%"$$"&&;<X;"’"’’YJ%!"#!!"#"!d"’"!:+!!""’!""9:!!%""+;<%"!./01#$2./01345’67(8"!;!"("(’!&"ef !+!""#"!(!!""%!!%"")&=9:!+!""+;<%!$"BC !*!""&!+!""IJ !!""&=ghLiM4\jk%iMldm4\niM odm4\+pq %!’!""!!%""+;<X;"’!’"YJ %;!"(!("!!"!*!""#"!(!!""$!!%"")#"$)%$#"#%"%"$)"#"#$%"###"$%&%&’(&;<X;"’!’!YJ %!!"#$%&’()*+,-#!!&"!+!""#"!(!!""%!!%"")#"$!%$#"#%""%!"#"#$#"$%&%&’(&;<X;"’!’&YJ %;!"(!(&!$"drstuvwx4\!!""&bQL&jk%iMldm4\!*!""yiMo dm4\!+!""zy &{Zuvwx#$jk+i|}~p & !!""#!*!""$!+!"" *!*!""#"!(!!""$!!%"")!+!""#"!(!!""%!!%"$%&") &!*!""y !+!""j !*!""#!*!%""&!+!""#%!+!%""+dm ‘%!"$!#"!"!!" ‘ ’!""&!""#!!""$!!"%""$!!"%!"%!!"&!""#&!%""%!&"&!""#!!"!"%!$"&!""#!!!""%!’"&!""#!!"",-.!"""%!%"&!""#)!!""$*&&*)&*% -%B iM‘ Z * += 0 %!’!""d‘ &!""#!!""$!!"%""$!!"%!"&!" !"!""y !!!""& Y! j p &"!./01#$2./01345’67(8$! K!!""##!"!""$$!!!""‘ d!!""+ F&!""#+(!!"")##!"!""$$!!!""$#!"!"%""$$!!!"%""$#!"!"%!"$$!!!"%!"##(!"!""$!"!"%""$!"!"%!")$$(!!!""$!!!"%""$!!!"%!")&!""##&"!""$$&!!""¡¢‘ !""Z +%r&!""#+(!!"")#!!""$!!"%""$!!"%!"£¤‘ d!!"%,"+ F&,!""Z&,!""#+(!!"%,")#!!"%,"$!!"%,%""$!!"%,%!"¥&!"%,"#!!"%,"$!!"%,%""$!!"%,%!"¦§&!"%,"#+(!!"%,")#&,!""¡¢‘ !"" %!!"d‘ &!""#&!%""&!" !"!""y!!!""& Y! jp &&"!""#+(!"!"")#!"!%""&!!""#+(!!!"")#!!!%""K!!""##!"!""$$!!!""£¤‘ d!!""+ F&!""#+(!!"")##!"!%""$$!!!%""##&"!""$$&!!"" ? +¨©ªZ&"!""y&!!""+«¬&‘ !!"Z +%r&!""#+(!!"")#!!%""£¤‘ d!!"%,"+ F&,!""Z&,!""#+(!!"%,")#!(%!"%,")¥&!"%,"#!(%!"%,")!!"#$%&’()*+,-%!YQ‘ !!" %!&"d‘ &!""#!!"!"&!" !"!""y !!!""& Y! jp & &"!""#+(!"!"")#!"!"!"&!!""#+(!!!"")#!!!"!"K!!""##!"!""$$!!!""£¤‘ d !!""+ F &!""#+(!!"")##!"!"!"$$!!!"!"##&"!""$$&!!""? +¨©ªZ &"!""y &!!""+«¬&‘ !&"Z +% r&!""#+(!!"")#!!"!"£¤‘ d !!"%,"+ F &,!""Z &,!""#+(!!"%,")#!(!"%,"!)¥&!"%,"#!(!"%,"!)¦§&!"%,"#+(!!"%,")#&,!""YQ‘ !&" %!$"d‘ &!""#!!!""&!" !"!""y !!!""& Y! jp & &"!""#+(!"!"")#!!"!""&!!""#+(!!!"")#!!!!""K!!""##!"!""$$!!!""£¤‘ d !!""+ F &!""#+(!!"")#(#!"!""$$!!!"")!’#&"!""$$&!!""¡¢&‘ !$"Z® +% r&!""#+(!!"")#!!!""£¤‘ d !!"%,"+ F &,!""Z &,!""#+(!!"%,")#!!!"%,"¥&!"%,"#!!!"%,""!./01#$2./01345’67(8&!YQ‘ !$" %!’"d‘ &!""#!!"",-.!"""&!" !"!""y !!!""& Y! jp & &"!""#+(!"!"")#!"!"",-.!"""&!!""#+(!!!"")#!!!"",-.!"""K!!""##!"!""$$!!!""£¤‘ d !!""+ F &!""#+(!!"")#(#!"!""$$!!!""),-.!"""##!"!"",-.!"""$$!!!"",-.!"""&!""##&"!""$$&!!""¡¢&‘ !’"Z +% r&!""#+(!!"")#!!"",-.!"""£¤‘ d !!"%,"+ F &,!""Z &,!""#+(!!"%,")#!!"%,",-.!"""¥&!"%,"#!!"%,",-.(!"%,"")¦§&!"%,"’+(!!"%,")#&,!""¡¢&‘ !’" %!%"d‘ &!""#)!!""$*&!" !"!""y !!!""& r )&*% -& Y! j p &&"!""#+(!"!"")#)!"!""$*&!!""#+(!!!"")#)!!!""$*K!!""##!"!""$$!!!""£¤‘ d !!""+ F &!""#+(!!"")#)(#!"!""$$!!!"")$*’#&"!""$$&!!""¡¢&‘ !%"Z® +% r!!"#$%&’()*+,-’!&,!""#+(!!"%,")#)!!"%,"$*¥&!"%,"#)!!"%,"$*¦§&!"%,"#+(!!"%,")#&,!""¡¢&‘ !%" %!"%!#"#"!!" ‘ ’!""&!""#"-$"(-,##!!"%,"&&*-%¯r°+±-%!!"&!""#)!!""$*%!&"&!""#!!""$.!!"$""&&*.% -%!$"&!""#!!"!"%!’"&!""#!!,""&&*,%¯r°+±-%!%"&!""#!!%""%B "²iMZ¡³‘ +²iMZ®¡³‘ += 0 %!’!""&!""#"-$"(-,##!!"%,"&&*-%¯r°+±-%¡%´‘ µs¶w·+ :¸¹"rºµw·y»¼+ !!""&!!"%""&,& !!"%-"&¥yL½+ ¾ &YQ&´‘ Z¡³‘ %!!"&!""#)!!""$*%¡%´‘ µs¶w·+ :¸¹"rºµw·+!!""&¥yL½+ ¾ &Y Q&´‘ Z¡³‘ %!&"&!""#!!""$.!!"$""&&*.% -%¡%´‘ µ¿7w·!""+ : ÀÁ¹r¿7w·!""+ !!""&¥ÂÃÁ¹rL½w·!"$""w+ !!"$""&YQ´‘ Z®¡³‘ %!$"&!""#!!"!"%µ")!w&´‘ ds¶w·"w+ :Ä L½w·"!+ Y¹"&¡¢´‘ %®¡³‘ %!’"&!""#!!,""&&*,%¯r°+±-%XÅÆ,!$"&¿"*#w&‘ + : L½w·,"+ Y¹"&¡¢‘ %®¡³‘ %"!./01#$2./01345’67(8(!¡³‘ %!"&!#"$"!X ÈM‘ ’!""&!""#(-%",###,!!"%,"&&*##&#"&,&#-%"% -%!!"&!""#!#/+,"#&!"%""%#!&!"%!"$!!""%#/+,"#!!"%""&&*#&"#% -%BÉ&ÊËNO F /!""&= ‘ Z Ì"+Ì"+ÍÎZϤ+!’!""ÊËNO FZ‘ µ %ÊËNO4\!!""w+ :%dr´‘ &&ÊËNO F/!""#(-%",###,!!"%,"!!ÐZi M ÑÒr "##&ÓÔ%-+ ÕÓ4\& Z i M 012‘ %Ö r ##&#"&,&#-%"Ä% Õ+ -&YQ´‘ gZÌ"+%!!"bCÈ|pqÉU´‘ +ÊËNO F %pqi ’K !!""#!!""& ‘ + :&!""#/!""& /!""#!#/+,"#/!"%""%#!/!"%!"$!!""%#/+,"#!!"%"""##!/!#"#""#"!/!""#!#/+,"#%#/+,"###/+,"#"#!!/!!"#!#/+,"#(#/+,"#)%#!##!/+,!"#"#&!/!&"#!#/+,"#(#!/+,!"#)%#!(#/+,"#)##&/+,&"#×¢ØÙ&/!""##"/+,""#0!""!!pqÚ’ÛÜbQÝCÞßà!á r 3 â+pqÉ:‘ +ÊËNO F %d‘ + jp ãä3 â&U !"%!#1%"/+,"#$#!1%!"2!1"#!"%#1%"/+,"#"3!1"ã¥UW´‘ T å-4!1"#2!1"3!1"#"%#1%"/+,"#"%!#1%"/+,"#$#!1%!ÊËNO F /!""ZT å-4!1"+æ3 â& Þß+I !’&’"!ç’d #-.#$/012$ZI !’’’""&U /!""#5%"(4!1")##"/+,""#0!""¿§&È|pq!:+h³ZiO+%!!"#$%&’()*+,-)*!8&!""8#8/!"""!!""8#($7,###,/+,"#,!!"%,"#($7,###,/+,"#,8!!"%,"8#6($7,###,/+,"#,#6($7,##8#,8#6($7,##8#8,¿#+"w &‘ + :&!""#/!"""!!""#6"%8#8ÇZ ë+&YQ‘ ZÌ"+%ìz &X³#)"& ‘ Ì"%?íYC+ pq ZÌ" +"î& ë+ ïð ë+ :!4145"%!"’!#"&"!K /!""#-/!#"&/!""&/!!".#-&&!&".&É!""&"!""#/!"""/!""!!"&!!""#/!"""/!"""/!""!’Ék´, È|p q &i Z ñò óô+"îÉ&ÚZ 678974*+:õÎ/+.;½É&ºj !:EF+h³%pqi ’dÆ,!""& &"!""#(79#%7/!"%9"/!9"&bÉ:&"!#"#/!#"/!#"#<&"!""#/!#"/!""$/!""/!#"#"!&"!!"#/!#"/!!"$/!""/!""$/!!"/!#"#"#&"!&"#/!""/!!"$/!!"/!""#$&"!$"#/!!"/!!"#"!!dÆ,!!"&ö÷?&!!""#&"!"""/!""&øùóô+"îbÉ:&!!""#-!=&’$&%&&$$&!"&%&". ú+Ékûüýþÿ!"!:%pqÚ’öºÆ,!""+678974 4Z *>/#"/#%/"(:&#ä´ 4+h³%<!!"!!!"#!!$!!"!!öºÆ,!!"+678974 4ýþÿ!"!:%!"(!/!""$ "’%,!:&K !!""#-!!#"&!!""&!!!"&!!&".#-"&!&&&$.%!""É/!""+!E å-:/!9"%!!"É/!""y !!""+%E å-:/!!9"&=9::/!9"&:/!!9"+;<%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理 PDF
1. 引言
数字信号处理是处理和分析数字信号的技术与方法的总称。
随着计算机和电子技术的发展,数字信号处理在多个领域中得到广泛应用,如通信、音频、图像等领域。
为了更好地理解和掌握数字信号处理的基本概念和技术,本文将介绍数字信号处理的基本原理,并提供一份数字信号处理的PDF文档供读者
参考学习。
2. 数字信号处理的基本概念
数字信号处理是用数值计算方法对信号进行处理和分析的
过程。
它包括信号采集、离散化、数字滤波、频谱分析、数据压缩等技术和方法。
数字信号处理的基本概念主要有以下几点:
•采样:将连续信号转换为离散信号的过程。
采样频
率决定了信号的频带宽度,低于采样定理要求的采样频率
可能导致采样信号中出现混叠现象。
•量化:将连续信号的幅度离散化为有限个数值的过程。
量化级数越大,表示幅度的精度越高,但也会增加数据存储和处理的复杂性。
•离散化:将连续信号的时间离散化为一系列离散时间点的过程。
离散信号的时间间隔决定了信号的频率分辨率。
•数字滤波:利用数字滤波器对离散信号进行滤波处理,包括滤波器设计、滤波器特性分析等。
常见的数字滤波器有低通滤波器、高通滤波器、带通滤波器等。
•频谱分析:对信号进行频域分析,得到信号的频谱特性,如功率谱密度、相位谱、幅度谱等。
频谱分析通常采用傅里叶变换或者快速傅里叶变换等算法。
•数据压缩:利用压缩算法对信号进行压缩,减少数据存储和传输的需求。
常用的压缩算法有无损压缩算法和有损压缩算法。
3. 数字信号处理的应用领域
数字信号处理在多个领域中得到广泛应用,例如:
•通信领域:数字信号处理在通信系统中起到重要的
作用,如信号调制、误码控制、信道编码等。
•音频处理:数字信号处理在音频处理中应用广泛,
如音频编解码、音频增强、音频合成等。
•图像处理:数字信号处理在图像处理中有很多应用,如图像压缩、图像增强、图像识别等。
•生物医学:数字信号处理在生物医学领域中有着重
要的应用,如生理信号处理、医学图像处理等。
•雷达与遥感:数字信号处理在雷达与遥感领域中有
广泛的应用,如目标检测与识别、图像重建与恢复等。
4. 数字信号处理的工具与软件
数字信号处理的学习与实践离不开一些常用的工具和软件。
以下是一些常用的数字信号处理工具和软件:
•MATLAB/Simulink:MATLAB是最常用的数字信号
处理工具之一,提供了丰富的数字信号处理函数和工具箱。
Simulink是MATLAB的拓展工具,用于系统建模和仿真。
•Python:Python是一种常用的编程语言,拥有丰富的数字信号处理库,如NumPy、SciPy等。
通过Python,可以进行数字信号处理的算法实现和应用开发。
•C/C++:C/C++是广泛应用于嵌入式系统和信号处理领域的编程语言,提供了底层的硬件接口和高效的算法实现能力。
•LabVIEW:LabVIEW是一种可视化程序设计语言,特别适用于仪器控制和数据采集,也可以用于数字信号处理的设计与实现。
5. 数字信号处理的学习资源
学习数字信号处理可以参考以下几种资源:
•书籍:有多本经典的数字信号处理教材可供选择,如《数字信号处理》(作者:陈世刚)、《数字信号处理导论》(作者:Orthogonal)等。
•在线课程:有许多优质的数字信号处理在线课程,如Coursera、edX等平台上的课程,可以根据自身情况选择适合的课程进行学习。
•博客与论坛:许多数字信号处理相关的博客和论坛
提供了丰富的学习资源和交流平台,可以通过阅读博客和
参与讨论来深入理解和掌握数字信号处理的知识。
6. 数字信号处理的发展趋势
随着计算机和通信技术的不断发展,数字信号处理领域也
在不断演进。
以下是数字信号处理的几个发展趋势:
•多媒体信号处理:随着多媒体技术的普及,数字信
号处理在音频、图像和视频处理方面得到广泛应用。
多媒
体信号处理领域的研究将更加关注人类感知和交互的特点。
•可嵌入式数字信号处理:随着嵌入式系统的广泛应
用,嵌入式数字信号处理的需求越来越大。
嵌入式数字信
号处理更加注重系统的实时性和资源的优化。
•智能信号处理:随着人工智能和机器学习的发展,
智能信号处理在数字信号处理中的应用越来越广泛。
智能
信号处理技术将进一步提高数字信号处理的自动化水平。
7. 结论
数字信号处理是处理和分析数字信号的技术与方法的总称。
本文介绍了数字信号处理的基本概念、应用领域、常用工具与软件、学习资源以及发展趋势。
希望读者能通过本文对数字信号处理有一个初步的了解,并能深入研究和应用数字信号处理的相关技术。
参考文献:
•陈世刚,《数字信号处理》,高等教育出版社,2017
•Orthogonal,《数字信号处理导论》,电子工业出
版社,2018。
