全等三角形及判定习题精选.doc
全等三角形判定练习题

全等三角形判定练习题一、选择题1. 在三角形ABC和三角形DEF中,若AB=DE,AC=DF,BC=EF,那么这两个三角形:A. 相似B. 全等C. 不全等D. 无法确定2. 若三角形ABC的角A等于角D,且AB=DE,AC=DF,但BC不等于EF,这两个三角形:A. 相似B. 全等C. 不相似D. 不全等3. 已知三角形ABC与三角形DEF全等,根据SAS(边-角-边)判定,下列选项正确的是:A. AB=DE,BC=EF,角A=角DB. AB=DE,AC=DF,角B=角EA. AB=DE,角A=角D,角B=角ED. AB=DE,角A=角D,角C=角F二、填空题4. 如果三角形ABC与三角形DEF全等,且角A等于角D,角B等于角E,那么角C等于______。
5. 在三角形ABC中,若AB=AC,角A等于角B,根据______判定,三角形ABC是等腰三角形。
6. 如果三角形ABC的边AB等于三角形DEF的边DE,且角A等于角D,角B等于角E,但角C不等于角F,根据______判定,这两个三角形不全等。
三、解答题7. 已知三角形ABC与三角形DEF全等,且AB=DE,角B=角E,求证AC=DF。
8. 在三角形ABC中,已知AB=AC,角A=角B,求证三角形ABC是等腰三角形。
9. 根据SSS(边-边-边)判定,如果三角形ABC的边AB、AC、BC分别等于三角形DEF的边DE、DF、EF,那么这两个三角形是______。
10. 如果三角形ABC的边AB、AC等于三角形DEF的边DE、DF,但角A不等于角D,角B不等于角E,求证这两个三角形不全等。
四、证明题11. 证明:如果三角形ABC的角A等于角D,角B等于角E,且AB+AC=DE+DF,那么三角形ABC与三角形DEF全等。
12. 已知三角形ABC与三角形DEF全等,且角A等于角D,角B等于角E,证明:角C等于角F。
13. 在三角形ABC中,如果角A等于角B,且AB+BC=AC+BC,证明:三角形ABC是等腰三角形。
(word完整版)全等三角形证明经典30题
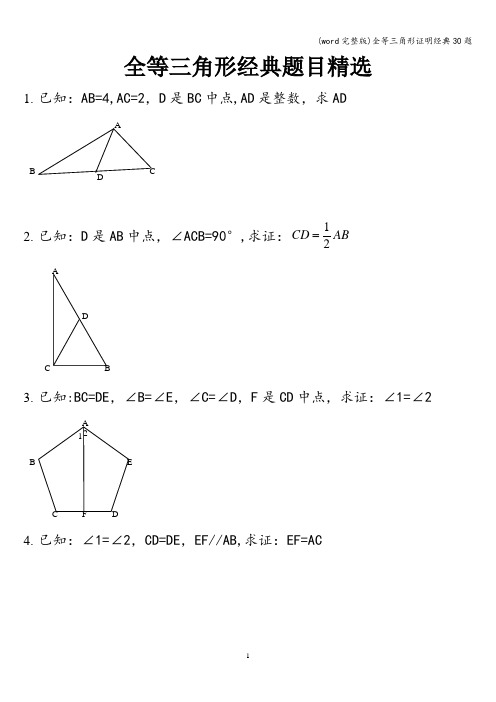
全等三角形经典题目精选1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB,求证:EF=ACAD BC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6. 已知:AC 平分∠BAD,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E在AD 上。
求证:BC=AB+DC 。
8.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CB ACDF21 ECD B A9。
已知:AB=CD ,∠A=∠D,求证:∠B=∠C10.P 是∠BAC 平分线AD 上一点,AC>AB,求证:PC-PB 〈AC-AB11。
已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC —AB=2BE12。
已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC13.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .DC B A F E A B C DPD A C B F AE DCB14.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA15.如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .PED CB A16.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠BD C B A17.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF (2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.18.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):O E DC B A19.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .FEDC B A20、如图:DF=CE ,AD=BC,∠D=∠C 。
全等三角形的判定练习题及答案

全等三角形的判定练习题及答案一、1. 如果D是△ABC中BC边上一点,并且△ADB≌△ADC,则△ABC是A.锐角三角形B.钝角三角形C.直角三角形D.等腰三角形2.如图,AO = BO,CO = DO,AD与BC交于E,∠O =0o,∠B =5o,则∠BED的度数是 A.60o B.90o C.75o D.85o 3.如图,已知△ABD和△ACE中,AB = AC,AD = AE,欲证△ABD≌△ACE,须补充的条件是第题第题A.∠B =∠CB.∠D =∠EC.∠DAE =∠BAC D.∠CAD =∠DAC4.在△ABC和△DEF中,下列各组条件中,不能判定两个三角形全等的是A.AB = DE,∠B =∠E,∠C =∠FB.AC = DF,BC = DE,∠C =∠DC.AB = EF,∠A =∠E,∠B =∠FD.∠A =∠F,∠B =∠E,AC = DE5.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是A.都全等 B.乙和丙C.只有乙D.只有丙6.下列判断正确的是A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等,且有一角为30°的两个等腰三角形全等C.有一角和一边对应相等的两个直角三角形全等D.有两角和一角的对边对应相等的两个三角形全等7.如图4所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①A S=AR;②QP∥AR;③△BRP≌△QSP中A.全部正确 B、仅①和②正确C.仅①正确D.仅①和③正确8.如图1所示,△ABC与△BDE都是等边三角形,AB A.AE=CD B.AE>CD C.AE 9.如图2所示,在等边△ABC 中,D、E、F,分别为AB、BC、CA上一点,且AD=BE=CF,图中全等的三角形组数为A.3组 B.4组 C.5组 D.6组10. 已知△ABC≌△MNP,?A?48?,?N?62?,则?B? 度数分别为,,.,?C,?M和?P的二、1、已知:如图12,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE?BF,AE=CF.求证:AF?CE;AB∥CD.A B C2.如图,已知AD = CB,AE = CF,DE = BF;求证:AB//CD 图.123.如图,已知AB = CD,AC = DB;求证:∠A =∠D.全等三角形的判定姓名1、已知AB=CD,BE=DF,AF=CE,则AB与CD有怎样的位置关系?2、已知O是AB中点,OC=OD,?AOD??BOC,求证:AC?BD3、已知:如图,?CAB??DBA,AC?BD。
(完整版)全等三角形的判定常考典型例题及练习

(完整版)全等三角形的判定常考典型例题及练习-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN全等三角形的判定一、知识点复习 ①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。
(SAS )图形分析:书写格式: 在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠=EFBC E B DEAB∴△ABC ≌△DEF (SAS )②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等。
(ASA)图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧∠=∠=∠=∠FC EF BC EB∴△ABC ≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS )图形分析:书写格式:在△ABC 和△DEF 中⎪⎩⎪⎨⎧=∠=∠∠=∠EFBC F C EB∴△ABC ≌△DEF(AAS)④“边边边”定理:三边对应相等的两个三角形全等。
(SSS )图形分析:书写格式: 在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===EF BC DF AC DE AB∴△ABC ≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。
(HL )图形分析:书写格式:在△ABC 和△DEF 中 ⎩⎨⎧==DF AC DE AB ∴△ABC ≌△DEF (HL )一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗比如说“SSA ”、“AAA ”能成为判定两个三角形全等的条件吗两个三角形中对应相等的元素 两个三角形是否全等反例 SSA⨯AAA⨯二、常考典型例题分析第一部分:基础巩固1.下列条件,不能使两个三角形全等的是( )A.两边一角对应相等 B.两角一边对应相等 C.直角边和一个锐角对应相等 D.三边对应相等2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙4.如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD6.如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线OC,作法用得的三角形全等的判定方法是()A.SAS B.SSS C.ASA D.HL第二部分:考点讲解考点1:利用“SAS ”判定两个三角形全等1.如图,A 、D 、F 、B 在同一直线上,AD=BF ,AE=BC ,且AE ∥BC .求证:△AEF ≌△BCD .2.如图,AB=AC ,AD=AE ,∠BAC=∠DAE .求证:△ABD ≌△ACE .考点2:利用“SAS ”的判定方法解与全等三角形性质有关的综合问题3.已知:如图,A 、F 、C 、D 四点在一直线上,AF=CD ,AB ∥DE ,且AB=DE ,求证:FEC CBF ∠=∠考点3:利用“SAS ”判定三角形全等解决实际问题 4.有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B 两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D ,使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?考点4:利用“ASA”判定两个三角形全等5.如图,已知AB=AD,∠B=∠D,∠1=∠2,求证:△AEC≌△ADE.6.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;考点6:利用“ASA”与全等三角形的性质解决问题:7.如图,已知EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC考点7:利用“SSS”证明两个三角形全等8.如图,A、D、B、E四点顺次在同一条直线上,AC=DF,BC=EF,AD=BE,求证:△ABC≌△EDF.考点8:利用全等三角形证明线段(或角)相等9.如图,AE=DF,AC=DB,CE=BF.求证:∠A=∠D.考点9:利用“AAS”证明两个三角形全等10.如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,求证:△ABD≌△ACE.考点10:利用“AAS”与全等三角形的性质求证边相等11.(2017秋?娄星区期末)已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.(1)求证:BM=AC;(2)求△ABC的面积.考点11:利用“HL”证明两三角形全等12.如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF。
全等三角形的判定练习题

全等三角形的判定练习题一、选择题1. 下列哪组条件可以判定两个三角形全等?A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等A. ∠A=∠DB. ∠B=∠EC. ∠C=∠FA. SAS(边角边)B. ASA(角边角)C. AAS(角角边)D. SSS(三边)二、填空题1. 若两个三角形的______相等,且它们的夹角相等,则这两个三角形全等。
2. 在全等三角形中,对应边______相等,对应角______相等。
3. 要判定两个三角形全等,至少需要知道它们的______个元素相等。
三、判断题1. 若两个三角形的两边和它们的夹角分别相等,则这两个三角形一定全等。
()2. 两个等腰三角形的底角相等,则这两个三角形全等。
()3. 两个等边三角形的边长相等,则这两个三角形全等。
()四、解答题1. 在△ABC中,AB=AC,∠B=∠C,求证:△ABC是等腰三角形。
2. 已知△ABC和△DEF,AB=DE,BC=EF,∠B=∠E,求证:△ABC≌△DEF。
3. 在△ABC中,AB=AC,∠A=40°,∠B=70°,求∠C的度数。
4. 已知△ABC和△DEF,AB=DE,BC=EF,AC=DF,求证:△ABC≌△DEF。
5. 在△ABC中,AB=8cm,AC=10cm,∠A=60°,求BC的长度。
五、作图题1. 请作出一个三角形,使其与给定三角形全等,已知条件是两边及其夹角。
2. 请作出一个三角形,使其与给定三角形全等,已知条件是两角及其夹边。
3. 请作出一个三角形,使其与给定三角形全等,已知条件是三边。
六、综合题1. 在平面直角坐标系中,点A(2, 3),点B(6, 3),点C和点D在x轴上,且△ABC≌△ABD,求点C和点D的坐标。
2. 在四边形ABCD中,AB=CD,AD=BC,且∠ABC=∠CDA=90°,证明:△ABC≌△CDA。
直角三角形全等的判定_习题精选

习题精选
直角三角形全等的判定
(一)习题精选
1、判断下列条件能否判断两直角三角形全等,并说明理由
(1)一个锐角和这个锐角的对边对应相等。
(2)一个锐角和这个锐角相邻的一条直角边对应相等。
(3)一锐角与斜边对应相等。
(4)两直角边对应相等。
(5)两边对应相等。
(6)两锐角对应相等。
(7)一锐角和一边对应相等
2、下面说法不正确的是()
A、有一角和一边对应相等的两个直角三角形全等
B、有两边对应相等的两个直角三角形全等
C、有两角对应相等的两个直角三角形全等
D、有两角和一边对应相等的两个直角三角形全等
提示:先作出距离,利用三角形全等得到所求距离与CM相等。
提示:欲证BE⊥AC,则证∠AEB=,而直接证∠AEB=不好证,转化为证∠AFE+∠DAC=
5、如图3,已知:AD=BC,BE⊥AC,DF⊥AC,且BE=DF.
求证:(1)△ABE≌△CDF,(2)AB∥CD
提示:(1)由已知得△ADF≌△CBE,即AF=CE也就得到AE=CF。
(2)利用内错角相等两直线平行。
6、如图4,已知:∠A=, AB=BD,ED⊥BC于 D
求证:AE=ED
提示:找两个全等三角形,需连结BE。
全等三角形证明经典40题含答案(供参考)

1.已知:AB=4, AC=2, D是BC中点,AD是整数,求AD的长.解:延长AD到E使AD=DEYD是BC中点ABD=DC^EAACD和厶BDE中AD=DEZBDE=ZADCBD=DCAAACD^ABDEAAC=BE=2•••在△ ABE 中AB-BE<AE<AB+BEVAB=4即4・2V2ADV4+21<AD<3AAD=22.已知:BC=ED, ZB二ZE, ZC=ZD, F 是CD 中点,求证:Z1 = Z2证明:连接BF和EF••• BC=ED.CF=DE ZBCF=ZEDF・•.三角形BCF全等于三角形EDF(边角边)••• BF=EEZCBF=ZDEF连接BE在三角形BEF中,BF=EF••• ZEBF=ZBEFo••• ZABC=ZAEDc••• ZABE=ZAEBo/. AB=AEo在三角形ABF和三角形AEF中AB=AE.BF=EEZABF=ZABE+ZEBF=ZAEB+ZBEF=ZAEF ・•.三角形ABF和三角形AEF全等。
••• ZBAF=ZEAF(Zl=Z2)o3.已知:Z1=Z2, CD=DE, EF//AB,求证:EF=AC过C作CG〃EF交AD的延长线于点GCG/7EF,可得,ZEFD=CGDDE=DCZFDE=ZGDC (对顶角)•••△ EFD^ACGDEF=CGZCGD=ZEFD又,EF〃AB•••, ZEFD=Z1Z1=Z2AZCGD=Z2・•・△ AGC为等腰三角形,AC=CG又EF=CG・・・EF=AC4.已知:AD 平分ZBAC, AC=AB+BD,求证:ZB=2ZC证明:延长AB取点E,使AE=AC,连接DE TAD 平分ZBAC •••ZEAD=ZCADVAE=AC, AD=ADAAAED^AACD (SAS)AZE=ZCVAC=AB+BDAAE = AB+BDVAE = AB+BE•••BD = BEAZBDE=ZEAZABC=2ZEAZABC=2ZC5.已知:AC 平分ZBAD, CE丄AB, ZB+ZD=180° ,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CFICE丄ABAZCEB = ZCEF=90°VEB=EF, CE=CE,AACEB^ACEF(SAS)AZB = ZCFEVZB4-ZD=180° , ZCFE+ZCFA=180°AZD=ZCFAVAC 平分ZBADAZDAC=ZFACVAC=ACAAADC^AAFC (SAS)•••AD = AF•••AE=AF+FE=AD+BE6.如图,四边形ABCD中,AB〃DC, BE、CE分别平分ZABC、ZBCD,且点E在AD 上。
(完整版)全等三角形基础练习及答案

全等三角形判断一一、选择题1. △ABC和△中,若AB=,BC=,AC=.则()A.△ABC≌△B. △ABC≌△C. △ABC≌△D. △ABC≌△2. 如图,已知AB=CD,AD=BC,则下列结论中错误的是()A.AB∥DCB.∠B=∠DC.∠A=∠CD.AB=BC3. 下列判断正确的是()A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4. 如图,AB、CD、EF相交于O,且被O点平分,DF=CE,BF=AE,则图中全等三角形的对数共有()A. 1对B. 2对C. 3对D. 4对5. 如图,将两根钢条,的中点O连在一起,使,可以绕着点O自由转动,就做成了一个测量工件,则的长等于内槽宽AB,那么判定△OAB≌△的理由是( )A.边角边B.角边角C.边边边D.角角边6. 如图,已知AB⊥BD于B,ED⊥BD于D,AB=CD,BC=ED,以下结论不正确的是()A.EC⊥ACB.EC=ACC.ED +AB =DBD.DC =CB二、填空题7. 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.8. 如图,在四边形ABCD中,对角线AC、BD互相平分,则图中全等三角形共有_____对.9. 如图,在△ABC和△EFD中,AD=FC,AB=FE,当添加条件_______时,就可得△ABC≌△EFD(SSS)10. 如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11. 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B =20°,则∠C=______.12. 已知,如图,AB=CD,AC=BD,则△ABC≌______,△ADC≌ ______.三、解答题13. 已知:如图,四边形ABCD中,对角线AC、BD相交于O,∠ADC=∠BCD,AD=BC,求证:CO=DO.14. 已知:如图,AB∥CD,AB=CD.求证:AD∥BC.分析:要证AD∥BC,只要证∠______=∠______,又需证______≌______.证明:∵ AB∥CD (),∴∠______=∠______ (),在△______和△______中,∴Δ______≌Δ______ ().∴∠______=∠______ ().∴ ______∥______().15. 如图,已知AB=DC,AC=DB,BE=CE求证:AE=DE.答案与解析一.选择题1. 【答案】B;【解析】注意对应顶点写在相应的位置.2. 【答案】D;【解析】连接AC或BD证全等.3. 【答案】D;4. 【答案】C;【解析】△DOF≌△COE,△BOF≌△AOE,△DOB≌△COA.5. 【答案】A;【解析】将两根钢条,的中点O连在一起,说明OA=,OB=,再由对顶角相等可证.6. 【答案】D;【解析】△ABC≌△EDC,∠ECD+∠ACB=∠CAB+∠ACB=90°,所以EC⊥AC,ED +AB =BC+CD=DB.二.填空题7. 【答案】66°;【解析】可由SSS证明△ABC≌△DCB,∠OBC=∠OCB=,所以∠DCB=∠ABC=25°+41°=66°.8. 【答案】4;【解析】△AOD≌△COB,△AOB≌△COD,△ABD≌△CDB,△ABC≌△CDA.9. 【答案】BC=ED;10.【答案】56°;【解析】∠CBE=26°+30°=56°.11.【答案】20°;【解析】△ABE≌△ACD(SAS)12.【答案】△DCB,△DAB;【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】证明:在△ADC与△BCD中,14. 【解析】3,4;ABD,CDB;已知;1,2;两直线平行,内错角相等;ABD,CDB;AB,CD,已知;∠1=∠2,已证;BD=DB,公共边;ABD,CDB,SAS;3,4,全等三角形对应角相等;AD,BC,内错角相等,两直线平行.15.【解析】证明:在△ABC和△DCB中∴△ABC≌△DCB(SSS)∴∠ABC=∠DCB,在△ABE和△DCE中∴△ABE≌△DCE(SAS)∴AE=DE.全等三角形判断二一、选择题1. 能确定△ABC≌△DEF的条件是()A.AB=DE,BC=EF,∠A=∠EB.AB=DE,BC=EF,∠C=∠EC.∠A=∠E,AB=EF,∠B=∠DD.∠A=∠D,AB=DE,∠B=∠E2.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中,和△ABC全等的图形是()图4-3A.甲和乙 B.乙和丙 C.只有乙 D.只有丙3.AD是△ABC的角平分线,作DE⊥AB于E,DF⊥AC于F,下列结论错误的是()A.DE=DF B.AE=AF C.BD=CD D.∠ADE=∠ADF4.如图,已知MB=ND,∠MBA=∠NDC,下列条件不能判定△ABM≌△CDN的是()A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN5. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是()A.带①去B.带②去C.带③去D.①②③都带去6.如图,∠1=∠2,∠3=∠4,下面结论中错误的是()A.△ADC≌△BCD B.△ABD≌△BACC.△ABO≌△CDO D.△AOD≌△BOC二、填空题7. 如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是_________.(填上你认为适当的一个条件即可).8. 在△ABC和△中,∠A=44°,∠B=67°,∠=69°,∠=44°,且AC=,则这两个三角形_________全等.(填“一定”或“不一定”)9. 已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.10. 如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.11. 如图, 已知:∠1 =∠2 , ∠3 =∠4 , 要证BD =CD , 需先证△AEB ≌△AEC , 根据是_________ ,再证△BDE ≌△_________,根据是_________.12. 已知:如图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“ASA”为依据,还缺条件_________(2)若以“AAS”为依据,还缺条件_________(3)若以“SAS”为依据,还缺条件_________三、解答题13.阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB 全等吗?若全等,试写出证明过程;若不全等,请说明理由.答:△AOD≌△COB.证明:在△AOD和△COB中,∴△AOD≌△COB (ASA).问:这位同学的回答及证明过程正确吗?为什么?14. 已知如图,E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分.15. 已知:如图, AB∥CD,OA = OD, BC过O点, 点E、F在直线AOD上, 且AE = DF.求证:EB∥CF.答案与解析【答案与解析】一.选择题1. 【答案】D;【解析】A、B选项是SSA,没有这种判定,C选项字母不对应.2. 【答案】B;【解析】乙可由SAS证明,丙可由ASA证明.3. 【答案】C;【解析】可由AAS证全等,得到A、B、D三个选项是正确的.4. 【答案】C;【解析】没有SSA定理判定全等.5. 【答案】C;【解析】由ASA定理,可以确定△ABC.6. 【答案】C;【解析】△ABO与△CDO中,只能找出三对角相等,不能判定全等.二、填空题7. 【答案】∠B=∠C;【解析】可由AAS来证明三角形全等.8. 【答案】一定;【解析】由题意,△ABC≌△,注意对应角和对应边.9. 【答案】6;【解析】△ABF≌△CDE,BE=CF=2,EF=10-2-2=6.10.【答案】5;【解析】△ABO≌△CDO,△AFO≌△CEO,△DFO≌△BEO,△AOD≌△COB,△ABD≌△CDB.11.【答案】ASA,CDE,SAS;【解析】△AEB ≌△AEC后可得BE=CE.12.【答案】(1)∠A=∠D;(2)∠ACB=∠F;(3) BC=EF.三、解答题13. 【解析】解:这位同学的回答及证明过程不正确.因为∠D所对的是AO,∠C所对的是OB,证明中用到了OA=OB,这不是一组对应边,所以不能由ASA去证明全等.14.【解析】证明:∵BF=DE,∴BF-EF=DE-EF,即BE=DF在△ABE和△CDF中,∴△ABE≌△CDF(SSS)∴∠B=∠D,在△ABO和△CDO中∴△ABO≌△CDO(AAS)∴AO=OC,BO=DO,AC与BD互相平分.15.【解析】证明:∵AB∥CD,∴∠CDO=∠BAO在△OAB和△ODC中,∴△OAB≌△ODC(ASA)∴OC=OB又∵AE = DF,∴AE+OA=DF+OD,即OE=OF在△OCF和△OBE中∴△OCF≌△OBE(SAS)∴∠F=∠E,∴CF∥EB.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形(1)
—.知识点:
1.能够完全重合的两个三角形叫做全等三角形含义:形状相同,大小相等.
2.符号:“丝”
3.对应(边、角、顶点):重合的边、重合的角,重合的顶点
4.全等三角形的性质:
⑴全等三角形的对应边相等.⑵全等三角形的对应角相等.⑶全等三角形的周长、面积相等. 二、基础习题
1如图,AABC竺AA庞,ZE4C=3(P ,求ZBAD的度数. /
2、如图,ADEF,且A、。
、B、 E在同一条直线上,试找出图中互相平行的线段,并说明理由.
3、如图,A4CD, Z1 = Z2 , ZB = ZC.求证:ZBAD= Z.CAE
4.如图,瑟BC# 通FC, B、C、E 在同一条直线上,旦CE = 4cm, ZEFC=5T.
求AF的长和ZA的度数
5.如图,长方形ABCD沿AE折叠,使得点。
落在边上的点F处,且 .
ZBAF=5(f.
求的度数.
6、如图,点A、E、B、F在同一条直线上,MBC竺"ED.
⑴判断AC与。
尸的位置关系,并说明理由;
⑵判断AE与”的数量关系,并说明理由.
2、如图,点 A 、
C 、F 、。
在同一直线上,AF=DC, AB=DE, 求证:AB H DE
3、如图,在四边形ABCD 中,AB=CD, 求证:①AB H CD ;②AD H BC .
4、如图,AC 与8D 交于点O, AD=CB, E 、 求证:(l)ZD = Zfi ; (2) AEII CF
F 是 80上两点,HAE=CF, DE=BF.
全等三角形⑵
—.全等三角形的判定1:三边对应相等的两个三角形全等.简写成“边边边”或“SSS”
二、基础习题
1 如图,点 B 、E 、C 、F 在同一直线上,BE=CF, AB=DE, AC=DF .求证:ZEGC=ZD
全等三角形⑶
—.全等三角形的判定2:两边和它们的夹角对应相等的两个三角形全等.筒写为“边角边”或“SAS” 二、基础习题
1、如图,。
是 A43C 中边 的中点,ZABD=ZACD, ^AB=AC.
求证:(1) MCD (2) EB= EC
2、点A 、D 、F 、B 在同一直线上,AD=BF, AE/! BC .
求证:(1) ABCD (2) EF // CD
3、 如图,CDLDE 于 O, ABYDB 于/? , CD=BE, AB=DE.
求证:CE±AE
4、如图,AABCff AECD都是等边三角形,连接HE
、A£)交于O.
求证:⑴ AD= BE(2)ZAOB=6(T
全等三角形⑷
全等三角形的判定3:有两角和其夹边对应相等的两个三角形全等.简写成“角边角”或“ASA” 全等三角形的判定4:有两角和其一角对边对应相等的两个三角形全等.简写成“角角边”或“4AS”
二、基础习题
1.已知AB=A!B\ ZA = ZA r, ZB = ZB',则 AABC竺 AA'&C'的根据是()
A. SAS
B. SSA
C. ASA
D. AAS
2. AABC和ADE尸中,AB=DE, ZB = ZE,要使^DEF ,则下列补充的条件中错误的是()
A. AC=DF
B. BC=EF
C. ZA = ZD
D. ZC=ZF
3.如图,人。
平分ZBAC, AB=AC,则图中全等三角形的对数是()
A. 2对
B. 3对
C. 4对
D. 5对
4.如图,己知ABH CD ,欲证明ACOD,可补充条件.(填写一个适合的条件即可)
5.如图,ABA-AC, BDA-CD, Z1=Z2,欲得到BE=CE,可先利用
/\DCB,得到=,再根据证明至
BE=CE.
6.如图,AC平分ZDAB和欲证明ZAEB=ZAED,可先利用—
竺庄4。
,得到____ = ______ ,再根据 ________ ,证明竺
ZAEB= ZAED.
7.如图,AC=AE, NC = ZE, Z1 = Z2. 求证:MDE.
8.如图,己知BD=CE, ZI = Z2 ,那么AB= AC,你知道这是为什么吗?
全等三角形⑸
—.全等三角形的判定5:斜边和一条直角边对应相等的两个直角三角形全等.
简写为“斜边、直角边”或“ HL"
,即可得到
—\基础习题
1.如图,AB=AC, AD±13C于。
. 求证:川。
平分ZBAC, BD=CD
2.如图,AB=AC, AE=AF, AE_LEC于 8, AFJ.FB于F. 求证:Z1 = Z2
3.在 MBC 中,ZBAC=9(T , AB=AC, AE 是过点 A 的一条直线,且BD±AE于。
,
CELAE^E.
⑴当直线AE处于如图1的位置口寸,猜想BD、DE、CE之间的数量关系,并证明.
⑵请你在图2选择与⑴不同位置进行操作,并猜想⑴中的结论是否还成立?加以证明;
⑶归纳⑴、⑵,请你用简洁的语言表达位)、DE、CE1之间的数量关系.
4.如图,在AABC和AD以中,B、E、C、F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明. • •
®AB=DE, ®AC=DF,③ ZABC=ZDEF, ® BE=CF .
5.如图,OA=OB, OC=OD, ZAOB=ZCOD=9(T.
猜想线段AC、BO的关系,并说明理由.
A0
D。
