有限差分法求解偏微分方程复习进程
有限差分法的步骤

有限差分法的步骤嘿,朋友们!今天咱来聊聊有限差分法的那些事儿。
有限差分法啊,就像是搭积木一样,一步步地构建出我们想要的结果。
首先呢,要确定问题的定义域,这就好比是给搭积木找个合适的场地。
你得清楚知道在哪个范围里玩这个游戏。
然后就是划分网格啦,这就像是把场地划分成一格一格的,让每个部分都有自己的位置。
网格分得越细,就好像积木的格子越小,能呈现的细节就越多,但也别太细啦,不然可就复杂得让人头疼咯。
接下来,要对微分方程进行离散化。
啥叫离散化呢?就好比把连续的东西切成一段一段的,这样就好处理啦。
把那些复杂的微分方程转化成一个个可以计算的小式子,这可不简单呐!再之后呢,就是建立差分格式啦。
这就像是给每个小格子都定好规则,让它们知道该怎么表现。
不同的差分格式就像是不同的玩法,各有各的特点。
建立好差分格式后,就得开始计算啦!把各种数值代进去,就像摆弄那些积木一样,看看能得出啥结果。
这计算的过程可不能马虎,一个小错误可能就会让整个结果都不对啦。
计算出结果后,还得检查检查呢,看看合不合理,就像检查搭好的积木稳不稳一样。
要是有问题,还得重新调整,重新再来一遍。
你说这有限差分法是不是挺有意思的?虽然过程有点复杂,但只要一步一步慢慢来,总能搞明白的呀。
它就像是一个神秘的魔法,能把那些看似无解的问题给解开。
咱想想啊,要是没有有限差分法,那好多科学问题可咋解决呀?那些复杂的物理现象、工程问题,不都得靠它来帮忙嘛。
所以说呀,学会有限差分法,那可真是太有用啦!咱可得好好研究研究,把这个厉害的工具掌握好,让它为我们服务呀!这有限差分法的步骤,咱可不能小瞧咯,每个步骤都得认真对待,这样才能得出准确的结果呀,你们说是不是呢?。
有限差分法推导

有限差分法推导有限差分法是一种常用的数值分析方法,用于近似求解偏微分方程。
它的主要思想是将连续的空间域或时间域离散化,通过有限差分逼近来计算偏微分方程的解。
本文将对有限差分法的推导过程进行详细讲解。
在使用有限差分法求解偏微分方程时,我们首先需要将空间或时间的连续域划分成离散的网格点。
设定网格点的步长为Δx或Δt,其中Δx表示空间步长,Δt表示时间步长。
然后,我们利用有限差分近似替代原始的偏微分方程,得到一个离散的数值方程。
有限差分法的推导有以下几个基本步骤:第一步是建立离散的网格。
我们将空间或时间的连续域划分成网格点,并标记每个网格点的位置。
第二步是对原始的偏微分方程进行泰勒级数展开。
我们以空间变量为例,对偏微分方程中的函数进行泰勒级数展开,并截取到一阶或二阶导数的项。
第三步是利用差分逼近代替泰勒级数展开中的导数项。
根据差分逼近的精确度要求和稳定性要求,我们可以选择合适的差分格式来近似代替导数项。
第四步是将差分格式代入偏微分方程中,得到一个离散的数值方程。
通过有限差分逼近替代原始的偏微分方程,我们可以得到一个离散的方程组。
第五步是求解离散的方程组。
我们可以利用数值方法,如迭代法或直接法,求解离散的方程组,得到偏微分方程的数值解。
有限差分法推导的关键在于差分逼近的选择和方程离散化的建立。
不同的差分格式和离散化方法会导致不同的数值精度和稳定性。
因此,在实际应用中,需要根据具体问题来选择合适的差分格式和离散化方法。
总之,有限差分法是一种常用的数值分析方法,用于近似求解偏微分方程。
通过将连续的空间或时间离散化,并利用差分逼近替代原始方程中的导数项,可以得到一个离散的数值方程,然后通过求解离散的方程组来得到偏微分方程的数值解。
在实际应用中,需要根据具体问题选择合适的差分格式和离散化方法,以提高数值解的精度和稳定性。
差分法求解偏微分方程MAAB

南京理工大学课程考核论文课程名称:高等数值分析论文题目:有限差分法求解偏微分方程姓名:罗晨学号:成绩:有限差分法求解偏微分方程一、主要内容1.有限差分法求解偏微分方程,偏微分方程如一般形式的一维抛物线型方程:具体求解的偏微分方程如下:2.推导五种差分格式、截断误差并分析其稳定性;3.编写MATLAB程序实现五种差分格式对偏微分方程的求解及误差分析;4.结论及完成本次实验报告的感想。
二、推导几种差分格式的过程:有限差分法(finite-differencemethods )是一种数值方法通过有限个微分方程近似求导从而寻求微分方程的近似解。
有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。
推导差分方程的过程中需要用到的泰勒展开公式如下:()2100000000()()()()()()()......()(())1!2!!n n n f x f x f x f x f x x x x x x x o x x n +'''=+-+-++-+-(2-1)求解区域的网格划分步长参数如下:11k k k kt t x x h τ++-=⎧⎨-=⎩(2-2) 2.1古典显格式2.1.1古典显格式的推导由泰勒展开公式将(,)u x t 对时间展开得2,(,)(,)()()(())i i k i k k k uu x t u x t t t o t t t∂=+-+-∂(2-3) 当1k t t +=时有21,112,(,)(,)()()(())(,)()()i k i k i k k k k k i k i k uu x t u x t t t o t t tuu x t o tττ+++∂=+-+-∂∂=+⋅+∂(2-4)得到对时间的一阶偏导数1,(,)(,)()=()i k i k i k u x t u x t uo t ττ+-∂+∂(2-5) 由泰勒展开公式将(,)u x t 对位置展开得223,,21(,)(,)()()()()(())2!k i k i k i i k i i u uu x t u x t x x x x o x x x x∂∂=+-+-+-∂∂(2-6)当11i i x x x x +-==和时,代入式(2-6)得2231,1,1122231,1,1121(,)(,)()()()()(())2!1(,)(,)()()()()(())2!i k i k i k i i i k i i i i i k i k i k i i i k i i i iu u u x t u x t x x x x o x x x xu u u x t u x t x x x x o x x x x ++++----⎧∂∂=+-+-+-⎪⎪∂∂⎨∂∂⎪=+-+-+-⎪∂∂⎩(2-7) 因为1k k x x h +-=,代入上式得2231,,22231,,21(,)(,)()()()2!1(,)(,)()()()2!i k i k i k i k i k i k i k i ku u u x t u x t h h o h x xu u u x t u x t h h o h x x +-⎧∂∂=+⋅+⋅+⎪⎪∂∂⎨∂∂⎪=-⋅+⋅+⎪∂∂⎩(2-8) 得到对位置的二阶偏导数2211,22(,)2(,)(,)()()i k i k i k i k u x t u x t u x t uo h x h+--+∂=+∂(2-9) 将式(2-5)、(2-9)代入一般形式的抛物线型偏微分方程得(2-10)为了方便我们可以将式(2-10)写成11122k kk k k k i i i i i i u u u u u f h ατ++-⎡⎤--+-=⎢⎥⎣⎦(2-11) ()11122k k k k k k i i i i i i u u uu u f hτατ++----+=(2-12)最后得到古典显格式的差分格式为()111(12)k k k k k i i i i i u ra u r u u f ατ++-=-+++(2-13)2r hτ=其中,古典显格式的差分格式的截断误差是2()o h τ+。
PDE 有限差分法

������������+1,������ −
{
������
������������,������ + ������ ������|������=0 =
������������,������+1 − ������������,������−1
2ℎ exp(������������������������)
������������采用中心差分
������������
������������ (������������)������,������
=
������������,������+1 − ������������,������−1 2ℎ
������������采用这三种都不行,因为:中心差分将依赖前两层,而初值仅仅给出一层;向前或向后差
=
������2������2
[������������,������+1
−
2������������,������ ℎ2
+
������������,������−1
+
������������,������ ]
+
2������������,������
−
������������−1,������
������������,0 = ������������
������������+1,������ − 2������������,������ + ������������−1,������ ������2
=
1 2
[������������+1,������+1
−
2������������+1,������ ℎ2
微分方程数值求解——有限差分法
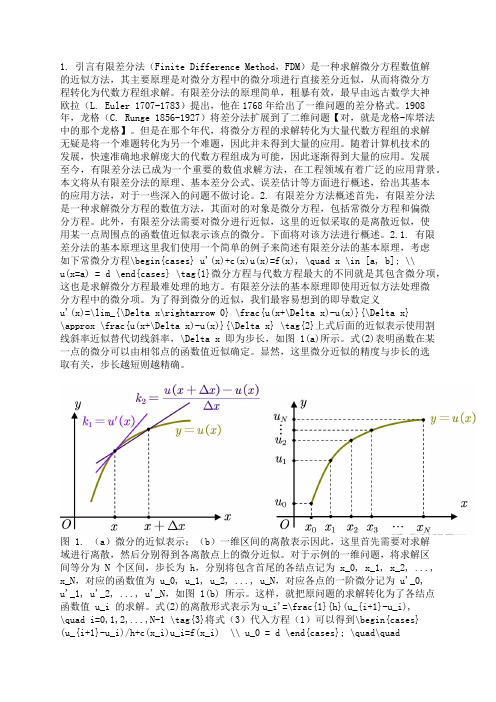
1. 引言有限差分法(Finite Difference Method,FDM)是一种求解微分方程数值解的近似方法,其主要原理是对微分方程中的微分项进行直接差分近似,从而将微分方程转化为代数方程组求解。
有限差分法的原理简单,粗暴有效,最早由远古数学大神欧拉(L. Euler 1707-1783)提出,他在1768年给出了一维问题的差分格式。
1908年,龙格(C. Runge 1856-1927)将差分法扩展到了二维问题【对,就是龙格-库塔法中的那个龙格】。
但是在那个年代,将微分方程的求解转化为大量代数方程组的求解无疑是将一个难题转化为另一个难题,因此并未得到大量的应用。
随着计算机技术的发展,快速准确地求解庞大的代数方程组成为可能,因此逐渐得到大量的应用。
发展至今,有限差分法已成为一个重要的数值求解方法,在工程领域有着广泛的应用背景。
本文将从有限差分法的原理、基本差分公式、误差估计等方面进行概述,给出其基本的应用方法,对于一些深入的问题不做讨论。
2. 有限差分方法概述首先,有限差分法是一种求解微分方程的数值方法,其面对的对象是微分方程,包括常微分方程和偏微分方程。
此外,有限差分法需要对微分进行近似,这里的近似采取的是离散近似,使用某一点周围点的函数值近似表示该点的微分。
下面将对该方法进行概述。
2.1. 有限差分法的基本原理这里我们使用一个简单的例子来简述有限差分法的基本原理,考虑如下常微分方程\begin{cases} u'(x)+c(x)u(x)=f(x), \quad x \in [a, b]; \\u(x=a) = d \end{cases} \tag{1}微分方程与代数方程最大的不同就是其包含微分项,这也是求解微分方程最难处理的地方。
有限差分法的基本原理即使用近似方法处理微分方程中的微分项。
为了得到微分的近似,我们最容易想到的即导数定义u'(x)=\lim_{\Delta x\rightarrow 0} \frac{u(x+\Delta x)-u(x)}{\Delta x}\approx \frac{u(x+\Delta x)-u(x)}{\Delta x} \tag{2}上式后面的近似表示使用割线斜率近似替代切线斜率,\Delta x 即为步长,如图 1(a)所示。
二阶偏微分方程组的有限差分解法

二阶偏微分方程组的有限差分解法下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!二阶偏微分方程组的有限差分解法引言在科学与工程领域中,二阶偏微分方程组的求解是一项重要而又具有挑战性的任务。
有限差分法求解偏微分方程MATLAB79516复习课程

南京理工大学课程考核论文课程名称:高等数值分析论文题目:有限差分法求解偏微分方程姓名:罗晨学号:115104000545成绩:有限差分法求解偏微分方程一、主要内容1.有限差分法求解偏微分方程,偏微分方程如一般形式的一维抛物线型方程:22(,)()u uf x t t xαα∂∂-=∂∂其中为常数具体求解的偏微分方程如下:22001(,0)sin()(0,)(1,)00u u x t x u x x u t u t t π⎧∂∂-=≤≤⎪∂∂⎪⎪⎪=⎨⎪⎪==≥⎪⎪⎩2.推导五种差分格式、截断误差并分析其稳定性;3.编写MATLAB 程序实现五种差分格式对偏微分方程的求解及误差分析;4.结论及完成本次实验报告的感想。
二、推导几种差分格式的过程:有限差分法(finite-difference methods )是一种数值方法通过有限个微分方程近似求导从而寻求微分方程的近似解。
有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。
推导差分方程的过程中需要用到的泰勒展开公式如下:()2100000000()()()()()()()......()(())1!2!!n n n f x f x f x f x f x x x x x x x o x x n +'''=+-+-++-+- (2-1)求解区域的网格划分步长参数如下:11k k k k t t x x hτ++-=⎧⎨-=⎩ (2-2)2.1 古典显格式2.1.1 古典显格式的推导由泰勒展开公式将(,)u x t 对时间展开得 2,(,)(,)()()(())i i k i k k k uu x t u x t t t o t t t∂=+-+-∂ (2-3) 当1k t t +=时有21,112,(,)(,)()()(())(,)()()i k i k i k k k k k i k i k uu x t u x t t t o t t tuu x t o tττ+++∂=+-+-∂∂=+⋅+∂ (2-4)得到对时间的一阶偏导数1,(,)(,)()=()i k i k i k u x t u x t uo t ττ+-∂+∂ (2-5) 由泰勒展开公式将(,)u x t 对位置展开得223,,21(,)(,)()()()()(())2!k i k i k i i k i i u uu x t u x t x x x x o x x x x∂∂=+-+-+-∂∂ (2-6)当11i i x x x x +-==和时,代入式(2-6)得2231,1,1122231,1,1121(,)(,)()()()()(())2!1(,)(,)()()()()(())2!i k i k i k i i i k i i i i i k i k i k i i i k i i i iu u u x t u x t x x x x o x x x x u u u x t u x t x x x x o x x x x ++++----⎧∂∂=+-+-+-⎪⎪∂∂⎨∂∂⎪=+-+-+-⎪∂∂⎩(2-7) 因为1k k x x h +-=,代入上式得2231,,22231,,21(,)(,)()()()2!1(,)(,)()()()2!i k i k i k i k i k i k i k i ku u u x t u x t h h o h x xu u u x t u x t h h o h x x +-⎧∂∂=+⋅+⋅+⎪⎪∂∂⎨∂∂⎪=-⋅+⋅+⎪∂∂⎩ (2-8) 得到对位置的二阶偏导数2211,22(,)2(,)(,)()()i k i k i k i k u x t u x t u x t uo h x h+--+∂=+∂ (2-9) 将式(2-5)、(2-9)代入一般形式的抛物线型偏微分方程得21112(,)(,)(,)2(,)(,)(,)()i k i k i k i k i k i k u x t u x t u x t u x t u x t f x t o h h αττ++---+⎡⎤-=++⎢⎥⎣⎦(2-10)为了方便我们可以将式(2-10)写成11122k kk k k ki i i i i i u u u u u f h ατ++-⎡⎤--+-=⎢⎥⎣⎦(2-11) ()11122k k k k k k i i i i i i u u uu u f h τατ++----+= (2-12)最后得到古典显格式的差分格式为()111(12)k k k k k i i i i i u ra u r u u f ατ++-=-+++ (2-13)2r h τ=其中,古典显格式的差分格式的截断误差是2()o h τ+。
有限差分法解偏微分方程

有限差分法解偏微分方程综述绪论有限元方法最早应用于结构力学,后来随着计算机的发展慢慢用于流体力学的数值模拟。
在有限元方法中,把计算域离散剖分为有限个互不重叠且相互连接的单元,在每个单元内选择基函数,用单元基函数的线形组合来逼近单元中的真解,整个计算域上总体的基函数可以看为由每个单元基函数组成的,则整个计算域内的解可以看作是由所有单元上的近似解构成。
有限差分方法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。
该方法将求解域划分为差分网格,用有限个网格节点代替连续的求解域。
有限差分法以Taylor 级数展开等方法,把控制方程中的导数用网格节点上的函数值的差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。
该方法是一种直接将微分问题变为代数问题的近似数值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。
对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。
从差分的空间形式来考虑,可分为中心格式和逆风格式。
考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。
目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。
差分方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。
构造差分的方法有多种形式,目前主要采用的是泰勒级数展开方法。
其基本的差分表达式主要有三种形式:一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等,其中前两种格式为一阶计算精度,后两种格式为二阶计算精度。
通过对时间和空间这几种不同差分格式的组合,可以组合成不同的差分计算格式。
有限元方法的基础是变分原理和加权余量法,其基本求解思想是把计算域划分为有限个互不重叠的单元,在每个单元内,选择一些合适的节点作为求解函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解。
有限差分法解偏微分方程式

有限差分法解偏微分方程式第一節偏微分方程已知二階偏微分方程0,,,,22222=⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂+∂∂∂+∂∂t u x u u t x f t u C t x u B x u A 若042=-AC B ,則稱上式為拋物線型偏微分方程。
若042>-AC B ,則稱上式為雙曲線型偏微分方程。
若042<-AC B ,則稱上式為橢圓型偏微分方程。
第二節Heat conduction 偏微分方程之數值解Heat Conduction Equation :t u x u ∂∂=∂∂2221α,L x <<0,0>t 邊界條件與初始條件必須給定。
將x 分成n 段n L h x ==∆,並取t 方向增量tk ∆=【方法一】顯性近似法:考慮節點()j i ,處之差分公式:grid points:()j i t x ,,()ji ij t x u u ,=二階偏微分為中央差分近似2,1,,12,1,,12222h u u u x u u u x u j i j i j i j i j i j i +-+-+-≈∆+-≈∂∂一階偏微分為前向差分近似ku u t u u t u j i j i j i j i ,1,,1,-≈∆-≈∂∂++代入熱傳方程t u x u ∂∂=∂∂2221α,得k u u h u u u j i j i j i j i j i ,1,22,1,,112-=+-++-α移項整理得()j i j i j i j i j i u u u u u hk ,1,,1,,1222-=+-++-α令22*hk αα=代入,得節點()j i ,之有限差分近似公式()j i j i j i j i j i u u u u u ,1,,1,1,2*+-++-+=α,n i ,,2,1,0 =, ,2,1,0=j 其中0=j 為初始條件,0,i u 為給定。
移項得PDE finite difference formula for the heat equation:()ji j i j i j i u u u u ,1,,11,**21*+-++-+=ααα0=i 及n i =為邊界條件,j u ,0,j n u ,為給定。
偏微分方程求解-有限差分法解析

--以有限差分法为例偏微分方程数值求解1. 偏微分方程求解问题的描述教材P653[12.1.1]椭圆型教材P653[12.1.2]教材P664[12.2.1]双曲型教材P665[12.2.4]拉普拉斯泊松对流波动教材P684[12.3.1]抛物型教材P685[12.3.6]扩散对流扩散教材P686[12.3.8]二维扩散教材P678[12.2.23]二维对流⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≤≤==≥≤≤==≤≤=>≥≤≤≤≤⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂0,0, ),(),,(),(),0,(0,0,),(),,(),(),,0(,0,),()0,,(0,0 , 0 , 0 21212222t L x t x v t L x u t x v t x u t L y t y t y L u t y t y u L y x y x y x u b t L y L x y u x u b t u μμϕΩ求解域初值条件边值条件),,(t y x u 未知函数⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥<<-==≥<<==≥≤≤-==≥≤≤==≤≤==≤≤≤≤≤≤⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂0 , 50 , sin 255sin ),(),5,(0 , 50 , 0),(),0,(0 , 50 , 5sin sin 25),(),,5(0 , 50 , 0),(),,0(5,0,0),()0,,( 10000 , 50 , 50 001.022********t x x x t x v t x u t x t x v t x u t y y y t y t y u t y t y t y u y x y x y x u t y x y u x u t u μμϕΩ求解域初值条件边值条件以具体问题为例演示具体的求解过程),,(t y x u 未知函数0x 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t x j jh x =y k kh y =τn t n =xh x 区间的剖分步长τ区间的剖分步长t y h y 区间的剖分步长y x h h h ==0x 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t jh x j =khy k =τn t n =xh x 区间的剖分步长τ区间的剖分步长t y h y 区间的剖分步长y x h h h ==1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x),,(n k j t y x ⎩⎨⎧===4..0 , 4..04..0j k n 0x 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t ),,(211t y x ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤≤≤≤≤≤=Ω100005050),,(t y x t y x ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧====Ω4..04..04..0),,(j k n t y x n k j n kj0x 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤≤≤≤≤≤=Ω100005050),,(t y x t y x ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧====Ω4..04..04..0),,(j k n t y x n k j n kj ?),,(),,(=Ω∈t y x t y x u ?),,(),,(=Ω∈nkjn k j t y x n k j t y x u 求解目标求解目标离散化n kju4040====k k j j 或或或边界点:1x 2x 3x 4x 0y 1y 2y 3y4y 0t 1t 2t 3t 4t 0x4040≠≠≠≠k k j j 且且且内点:1x 2x 3x 4x 0y 1y 2y 3y4y 0t 1t 2t 3t 4t 0x1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 5,0,0)0,,(≤≤=y x y x u 初值条件0),,(04..04..00====t y x u uk j k j kj 0kju000u001u002u003u004u1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x000u001u002u003u004u1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 010u011u012u013u014u000u 001u002u003u 004u1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 010u011u 012u 013u014u 020u021u022u023u024u000u 001u 002u 003u 004u 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 010u 011u 012u 013u 014u 020u 021u 022u 023u 024u 030u031u032u033u034u000u 001u 002u 003u 004u 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 010u 011u 012u 013u 014u 020u 021u 022u 023u 024u 030u 031u 032u033u 034u040u041u042u043u044u的存储设计计算数据0kju 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 000u 001u 002u 003u 004u 010u 011u 012u 013u 014u 020u 021u 022u 023u 024u 030u 031u 032u033u 034u040u041u042u043u044u1234512345行号列号MATLAB矩阵U0的存储设计计算数据0kju 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 000u 001u 002u 003u 004u 010u 011u 012u 013u 014u 020u 021u 022u 023u 024u 030u 031u 032u033u 034u040u041u042u043u044u012341234行号列号C 语言矩阵U0的图像计算结果可视化)0,,( :y x u 1x 2x 3x 4x 0y 1y 2y 3y 4y 0t 1t 2t 3t 4t 0x 000u 001u 002u 003u 004u 010u 011u 012u 013u 014u 020u 021u 022u 023u 024u 030u031u 032u 033u034u 040u041u042u043u044u1234512345行号列号MATLAB 矩阵U00kju),,()0,,(0kjk j u y x y x u 上的点4..0,4..0 ),,( :211===k j t y x u u k j kj求步第边值条件11104t x 103t x y 102t x y 101t x y 100t x y 0,50 , 0),,0(≥≤≤=t y t y u 0),,(104..00===t y x u uk k k边值条件1104tx 103t x y 102tx y 101tx y 10t x y 140u 130u 120u 110u 100u 0),,(104..010===t y x u uk k k 0,50 , 0),,0(≥≤≤=t y t y u边值条件25sin )()sin(25),,(2144..014k k k k k y y t y x u u-===14t 14t 14t x 141t x 140t x y 0,50 , 5sin sin 25),,5(2≥≤≤-=t y y y t y u边值条件25sin )()sin(25),,(2144..014k k k k k y y t y x u u-===14t 14t 14tx 141t x 14t x y 144u134u124u 114u104u 0,50 , 5sin sin 25),,5(2≥≤≤-=t y y y t y u边值条件3),,(103..110===t y x u uj j j 0,50 , 0),0,(≥<<=t x t x u 110t x y 120t x y 130t x y边值条件3),,(103..110===t y x u uj j j 110t x y 120tx y 130t x y 101u102u 103u 0,50 , 0),0,(≥<<=t x t x u边值条件411t x 12t x 13t x )sin(255sin )(),,(2143..114j j j j j x x t y x u u-===0,50 , sin 255sin ),5,(2≥<<-=t x x x t x u边值条件411t x 12t x 13t x )sin(255sin )(),,(2143..114j j j j j x x t y x u u-===0,50 , sin 255sin ),5,(2≥<<-=t x x x t x u 141u 142u143u141u 142u 143u 101u 102u 103u 144u 134u 124u 114u 104u 140u 130u 120u 110u 100u1,,+n j k t x y nj k t x y ,,1+nj k t x y ,,1-nj k t x y ,,1-nj k t x y ,,1+nj k t x y ,,策略”1,,+n jk t x y nj k t xy ,,1+n j k tx y ,,1-njk t x y ,,1-nj k t x y,,1+nj kt x y ,,2,1,121,1,22hu u ubhu u ubuujk kj jk j k kj j k kjkj-+-++-++-=-τ策略”1+n kj u nkj u nj k u 1,-nj k u 1,+nj u ,njk u ,1+策略”1+n kjun kjun j k u1,-n j k u 1,+n jk u,1-n jk u,1+2,1,121,1,22hu u ubhu u ubuujk kj jk j k kj j k kjkj-+-++-++-=-τ策略”1+n kjun kjun j k u1,-n j k u 1,+n jk u,1-n jk u,1+2,1,121,1,22hu u ubhu u ubuujk kj jk j k kj j k kjkj-+-++-++-=-τ策略”1+n kjun kjun j k u1,-n j k u 1,+n jk u,1-n jk u,1+2,1,121,1,22hu u ubhu u ubuujk kj jk j k kj j k kjkj-+-++-++-=-τ)(, 22.3.12,41:22h PDE h b +O =−−−→−≤ττ误差估计的解原偏微分方程求出的近似解按显式差分格式当可证收敛并稳定{}1..1,1-=+M j k n kj u {}Mj k nkj u ..0,=目标{}Mj M k n kju 或或或001==+“隐式差1,,+n j k t x y 11,,++n j k t x y 11,,+-n j k t x y 11,,+-n j k t x y 11,,++n j k t x y nj k t x y ,,“隐式差1,,+n jk t x y 11,,++n j k t xy 11,,+-n j k t x y 11,,+-n j k t x y 11,,++n j k t x yn j k t x y ,,“隐式差11,+-n j k u11,++n j k u 1,1++n jk u 1,1+-n jk unjk u ,1+n kj u“隐式差11,+-n j k u11,++n j k u 1,1++n jk u 1,1+-n jk unjk u,1+n kjuτn kjn kjuu-+1=211,1,11,2h uuub n j k n j k n j k +-++++-21,11,1,12h uuub n j k n j k n jk +-++++-+2hbc τ=标准化nj k n j k n j k n j k n j k n j k u u c u c u c u c u c ,1,111,1,11,1,1)41(=•-•-++•-•-++++++-+-“隐式差11,+-n j k u11,++n j k u 1,1++n jk u 1,1+-n jk un jk u,1+n kjun jk n jk n j k n jk n j k n jk uuc uc uc uc uc ,1,111,1,11,1,1)41(=•-•-++•-•-++++++-+-2hbc τ=“隐式差11,+-n j k u11,++n j k u 1,1++n jk u 1,1+-n jk un jk u,1+n kjun jk n jk n j k n jk n j k n jk uuc uc uc uc uc ,1,111,1,11,1,1)41(=•-•-++•-•-++++++-+-2hbc τ=+1kjn“隐式差+1kjn n n n n n n uuc uc uc uc uc 11111)41(=•-•-++•-•-+++++111+n u110+n u112+n u 121+n u 101+n unu11列差分方程层的内点值基于例如111:+n u t n n n n n n uuc uc uc uc uc 11121112111110101)41(=•-•-++•-•-+++++列差分方程基于内点值111+n u “隐式差n n n n n n uuc uc uc uc uc 11111)41(=•-•-++•-•-+++++112+n u 111+n u113+n u122+n u102+n u n u 12列差分方程层的内点值基于例如121:+n u t n n n n n n uuc uc uc uc uc 12122113112111102)41(=•-•-++•-•-+++++列差分方程基于内点值112+n u “隐式差n n n n n n uuc uc uc uc uc 11111)41(=•-•-++•-•-+++++112+n u111+n u113+n u 122+n u 132+n u 121+n u131+n u123+n u133+n un 12un 11un 13un 22un 32u n 21un 31un 23un 33u线性方程组“隐式差n n n n n n uuc uc uc uc uc 11111)41(=•-•-++•-•-+++++红色标志方程组的未知量绿色标志方程组的已知量个差分方程列出个内点值层的基于9)3..1,3..1(911==++j k ut n kjn112+n u111+n u113+n u 122+n u 132+n u 121+n u131+n u123+n u133+n un12u n 11u n 13u n 22u n 32un 21u n 31u n 23u n 33u线性方程组“隐式差n n n n n n uuc uc uc uc uc 11111)41(=•-•-++•-•-+++++红色标志方程组的未知量绿色标志方程组的已知量个差分方程列出个内点值层的基于9)3..1,3..1(911==++j k ut n kjn )( 32.3.12:2h PDE +O =−−−−→−τ误差估计的解原偏微分方程求出的近似解按隐式差分格式可证收敛并绝对稳定。
有限差分法解方程

有限差分法(Finite Difference Method)是一种数值方法,用于求解偏微分方程(PDEs)的近似解。
这种方法通过将连续的微分方程离散化,将其转化为一系列代数方程,从而在计算机上进行求解。
有限差分法特别适用于求解具有固定边界条件和初始条件的偏微分方程。
以下是有限差分法求解偏微分方程的基本步骤:1. 网格划分:首先,将问题的连续域划分为离散的网格点。
对于二维问题,这通常涉及到在空间和时间上进行网格划分,形成网格点的集合。
2. 离散化:使用差分公式将微分方程中的导数替换为差分。
例如,一阶导数可以用前向差分或后向差分近似,而二阶导数可以用中心差分近似。
3. 构建差分方程:在每个网格点上应用差分公式,将微分方程转化为代数方程。
对于边界条件,也需要进行相应的离散化处理。
4. 求解线性方程组:差分方程通常会导致一个线性方程组。
对于大型问题,这可能需要使用迭代方法或直接求解器来找到解。
5. 稳定性分析:在求解过程中,需要确保数值解的稳定性。
这涉及到对时间步长和空间步长的选择,以满足CFL(Courant-Friedrichs-Lewy)条件。
6. 迭代求解:对于时间依赖的问题,如热传导或波传播,可以通过时间步进方法(如显式或隐式方法)来迭代求解。
7. 结果分析:最后,分析数值解以验证其准确性,并与解析解(如果存在)进行比较。
有限差分法在处理规则区域和简单边界条件的问题时非常有效。
然而,对于具有复杂几何形状或边界条件的问题,可能需要更高级的数值方法,如有限元方法(FEM)或边界元方法(BEM)。
在实际应用中,有限差分法通常与计算机软件结合使用,如MATLAB、Python的SciPy库等,以便于高效地处理大规模问题。
有限差分法

u xxx
xr
+
(1.5a) (1.5b)
进而,在点 xr 处的一阶导数的两个近似公式可由(1.5)给出
ux
xr
= (ux )r
≈
u ( xr
+ h) − u(xr ) h
=
ur+1 − ur h
ux
xr
= (ux )r
≈
u(xr ) − u(xr h
− h)
=
ur
− ur−1 h
(1.6a) (1.6b)
有限差分法的基本思想是用离散的、只含有限个未知数的差分方程去代替连续变量的微 分方程和定解条件。对于求解的偏微分方程定解问题,有限差分方法的主要步骤如下:利用 网格线将定解区域化为离散点集;在此基础上,通过适当的途径将微分方程离散化为差分方 程,并将定解条件离散化,这一过程叫做构造差分格式,不同的离散化途径一般会得到不同 的差分格式;建立差分格式后,就把原来的偏微分方程定解问题化为代数方程组,通过解代 数方程组,得到出定解问题的解在离散点上的近似值组成的离散解,应用插值方法可从离散 解得到定解问题在整个定解区域上的近似解。由此可见,有限差分方法有大体固定的模式, 它有较强的通用性。但是,不能误认为不去了解这种逼近方法的基本知识,只是单纯模仿, 便能轻易获得满意的结果。因为在应用这种逼近方法时会发生许多重要的但有时还是相当困 难的数学问题,包括精度、稳定性与收敛性等。
− hD exp( 2 )ur
由(*1)式与(*2)相减得到
ur+1/ 2
− ur−1/ 2
=
exp(
hD 2
)ur
−
exp(
−
hD 2
)ur
= δur
偏微分方程数值解法的计算方法

偏微分方程数值解法的计算方法偏微分方程(Partial Differential Equations, PDEs)是描述物理现象的一个有力工具,它可以描述复杂系统中物质、能量和动量的行为。
由于解析解十分困难或者甚至不存在,数值模拟是解决PDE问题的重要方法之一。
现今,许多物理和生物学领域的实际应用中,PDE的数值解法已经发挥了重要作用。
本文将介绍PDE的数值解法计算方法。
1.有限差分法(Finite Difference Method)有限差分法是PDE数值解法中最广泛应用的一种方法,其基本思想是用离散网格来逼近连续的PDE问题。
用有限差分法求解PDE问题可以分为以下几步:首先,将求解区域离散化,建立一个离散网格;然后,在网格上构造符合原始问题条件的差分方程;最后,将差分方程解出来,得到离散的数值解。
有限差分法的优点是简单易行,对于解决一些简单问题非常有效。
但由于精度受限,难以处理复杂问题,例如边界条件比较复杂、域的形状不规则等问题,效果不是很理想。
此外,如果PDE包含时间变量,用有限差分法求解的效果也不是很好,容易产生数值震荡现象。
2.有限体积法(Finite Volume Method)有限体积法是一种在控制体上积分求解PDE的方法。
所谓的控制体是指PDE求解区域的一个子集。
有限体积法与有限差分法的思想是相似的,它们都是将求解域分成若干个小的控制体,然后在每个控制体上构造差分方程来近似PDE。
和有限差分法相比,有限体积法的主要优势在于能够更好的处理不规则域和复杂边界条件,并且数值解更为准确。
3.有限元法(Finite Element Method)有限元法是PDE数值解法中的一种重要方法,其基本思想是通过将求解域分成若干个小三角形、四边形等有限元来逼近实际域。
有限元法与有限差分法和有限体积法的不同之处在于,它使用基函数来逼近原始问题中的未知函数。
在求解过程中,有限元法需要对基函数进行插值,从而方便地求出未知函数在任意点的近似值。
详细版第四章偏微分方程的有限差分法.ppt

算
物 理
ui,k1 ui1,k (1 2 )ui,k ui1,k
学 ui,0 (ih)
u0,k g1(k ) ul,k g2 (k )
i=0,1, ,N k=0,1, ,M
.精品课件.
4.2 热传导方程的差分解法
计 显示差分递推公式的稳定性:
算
物 理
ui,k ui',k i,k k i,k
计
算 一维各向同性、均匀介质,且无热源的热传导方程:
物 理 学
u 2u
t x2
0t T 0 xl
为了求解u(x,t),还必须利用边界条件和初 始条件。
定解条件:边界条件和初始条件。
定解问题:解存在、唯一并且连续依赖初始条件。
.精品课件.
4.2 热传导方程的差分解法
计 对于一维热传导问题(第一类边界条件)
计 同样,在节点(xi,tk)上
算
物
理 学
( x, t )
u xi ,tk u xi ,tk
t xxi
t tk
ui,k 1 ui,k
一阶向前差商O(h)
.精品课件.
4.2 热传导方程的差分解法
计 一维热传导方程可以近似为
算 物 理 学
ui,k 1 ui,k ui1,k 2ui,k ui1,k
理
学
u t0
f1(x, y, z)
u t
t0
f2 (x, y, z)
边界条件:边界受到外界的影响
常见的物理问题可以归结为三大类边界条件
.精品课件.
4.1 有限差分法原理
1 第一类边界条件(狄利克雷Dirichlet)
计
算
u u0(r,t)
偏微分方程的有限差分方法

二阶线性偏微分方程的一般形式为:
A 2 u B 2 u C 2 u D u E u F G u 0 x 1 2 x 1 x 2 x 2 2 x 1 x 2
对于变量 x1 和 x 2 给定的值 xˆ1 和 xˆ 2 若 4 A (x ˆ 1 ,x ˆ 2 ) C (x ˆ 1 ,x ˆ 2 ) B 2 (x ˆ 1 ,x ˆ 2 )
这里,[ u ] ij 表示 u(xi, yj )。上两式分别简记为
x p u x ijh 1 1 2x(pijx[u]i)jO (h1 2)
yp u yijh 12 2y(pij y[u]ij)O (h2 2)
则 L u x p u x y p u y q u f (x ,y ) 在 (i, j) 点被表示为
余弦是 (co,scos)。
由
u nij
u xijc
os u yijc
os
用单侧差商逼近 x方向和 y方向的导数,然后列
出边界网点上的差分方程。
(2)邻近边界的网格点 (xi , yj ) 不在上 可以采用直接转移法近似处理,即将边界
条件用于邻近边界的网格点,然后再在该点列 出差分方程。
2 用积分插值法构造差分格式 3 差分格式的稳定性和收敛性 4 差分方程求解的一些方法
— 数值积分 有限元法
— 函数插值
不同的数值微分和数值积分方法、不同的函数插值方 法,就产生了不同的有限差分法与不同的有限元法。
其它数学基础:
数理方程、数值代数、最优化理论与方法等
偏微分方程的有限差分方法
基本思想:使用离散的、只含有限个未知 数的差分方程去近似代替连续变量的微分方程 及边值条件,并将相应的差分方程解作为(初)边 值问题的近似解。
17 偏微分方程的有限差分法

ti ti t i , k
k
k 1
(Backward difference)
k k k 2t t i 1 2 t i t i 1 2 (Central difference) 2 x x i ,k
代入微分方程得,
偏微分方程有限差分法 简介
1
一 建立离散方程的方法 (Discretization of the heat equation)
1. 有限差分法(finite-difference methods)
1)、网格划分(Nodal network/grid/mesh )
把物体分割为有限数目的网格单元,将微分方程变换为差 分方程,通过数值计算直接求取各网格单元节点的温度。
Diffusion set to zero k=0
Hot fluid T = 100º C
Cold fluid T = 0º C
Accuracy and false diffusion
First-order Upwind
Second-order UpwindBiblioteka 8x864 x 64
17
Seismogram Dispersion
10
整理得
ti
或
k 1
a a k k k ( ti 1 ti 1 ) (1 2 2 )ti 2 x x
ti
k 1
Fo( ti 1 ti 1 ) (1 2Fo)ti
k k
k
上式称为显式差分格式。
11
2). 稳定性条件(Stability Criterion)
x
2
t i , j 1 2 t i , j t i , j 1 y
非线性偏微分方程数值解法

非线性偏微分方程数值解法非线性偏微分方程是研究自然界中许多现象的重要数学模型,其解析解往往难以获得。
因此,数值解法成为解决非线性偏微分方程问题的一种有效手段。
本文将介绍几种常用的非线性偏微分方程的数值解法。
一、有限差分法有限差分法是求解偏微分方程的一种常见数值方法。
其核心思想是将求解区域离散化为有限个网格点,并利用中心差分公式来近似替代微分运算。
对于非线性偏微分方程,可以采用迭代的方法进行求解。
具体步骤如下:1. 将求解区域离散化为有限个网格点,确定网格的步长。
2. 利用中心差分公式将偏微分方程离散化为差分方程。
3. 将差分方程转化为非线性代数方程组,采用迭代方法求解。
二、有限元法有限元法是求解偏微分方程的一种重要数值方法。
其核心思想是将求解区域划分为无重叠的小单元,通过在每个单元内构造适当的试探函数和加权函数,将问题转化为求解代数方程组。
对于非线性偏微分方程,可以采用Newton-Raphson迭代方法进行求解。
具体步骤如下:1. 将求解区域进行网格剖分,确定单元的形状和大小。
2. 构造试探函数和加权函数,并利用加权残差法将偏微分方程离散化为代数方程组。
3. 对于非线性方程组,采用Newton-Raphson迭代方法求解。
三、有限体积法有限体积法是求解偏微分方程的一种常用数值方法。
其核心思想是将求解区域划分为有限个体积单元,通过对单元内偏微分方程进行积分,将方程转化为守恒形式。
对于非线性偏微分方程,可以采用显式或隐式方法进行求解。
具体步骤如下:1. 将求解区域进行网格剖分,确定体积单元的大小和形状。
2. 对体积单元内的偏微分方程进行积分,建立守恒形式的方程。
3. 将方程离散化为代数方程组,采用显式或隐式方法进行时间步进求解。
四、谱方法谱方法是求解偏微分方程的一种高效数值方法。
其核心思想是采用特定的基函数展开待求解的函数,通过选取合适的基函数,可以有效地提高求解效率。
对于非线性偏微分方程,可以采用谱方法进行求解。
有限差分法求解偏微分方程

有限差分法求解偏微分方程摘要:本文主要使用有限差分法求解计算力学中的系统数学模型,推导了有限差分法的理论基础,并在此基础上给出了部分有限差分法求解偏微分方程的算例验证了推导的正确性及操作可行性。
关键词:计算力学,偏微分方程,有限差分法Abstract:This dissertation mainly focuses on solving the mathematic model of computation mechanics with finite-difference method. The theoretical basis of finite-difference is derived in the second part of the dissertation, and then I use MATLAB to program the algorithms to solve some partial differential equations to confirm the correctness of the derivation and the feasibility of the method.Key words:Computation Mechanics, Partial Differential Equations, Finite-Difference Method1 引言机械系统设计常常需要从力学观点进行结构设计以及结构分析,而这些分析的前提就是建立工程问题的数学模型。
通过对机械系统应用自然的基本定律和原理得到带有相关边界条件和初始条件的微分积分方程,这些微分积分方程构成了系统的数学模型。
求解这些数学模型的方法大致分为解析法和数值法两种,而解析法的局限性众所周知,当系统的边界条件和受载情况复杂一点,往往求不出问题的解析解或近似解。
另一方面,计算机技术的发展使得计算更精确、更迅速。
求解偏微分方程三种数值方法

求解偏微分方程三种数值方法偏微分方程是数学中研究包含多个变量及其偏导数的方程。
解决偏微分方程的数值方法有很多,但本文将重点介绍三种常用的数值方法,分别是有限差分法、有限元法和谱方法。
一、有限差分法:有限差分法是一种常用的数值方法,用于求解偏微分方程的数值解。
其基本思想是通过建立网格来离散化偏微分方程中的空间变量,并近似替代导数,将偏微分方程转化为代数方程组,进而求解。
常见的有限差分格式有向前差分、向后差分和中心差分。
有限差分法主要包括以下步骤:1.空间离散化:将区域划分为网格点,在每个网格点上计算方程中的函数值。
2.近似代替导数:使用差分公式,将导数近似替代为函数在相邻网格点上的差分。
3.建立代数方程组:根据近似的导数和偏微分方程的形式,可以建立相应的代数方程组。
4.求解方程组:使用求解线性方程组的方法,如高斯消元法或迭代法,求解代数方程组。
5.恢复连续解:通过插值或者其他方法,将离散解恢复为连续解。
二、有限元法:有限元法是一种广泛应用的数值方法,用于求解偏微分方程的数值解。
其基本思想是将区域划分为有限个小区域,称为单元,通过求解单元上的局部方程,最终得到整个区域上的数值解。
有限元法主要包括以下步骤:1.离散化:将区域划分为单元,并选择适当的有限元空间。
2.建立局部方程:在每个单元上,根据选择的有限元空间和边界条件,建立局部方程。
3.组装全局方程:将所有单元上的局部方程组装成整个区域上的全局方程。
4.施加边界条件:根据问题的边界条件,施加适当的边界条件。
5.求解方程组:使用求解线性方程组的方法,求解全局方程组,得到数值解。
6.后处理:通过插值等方法,将离散解恢复为连续解,并进行后续的分析。
三、谱方法:谱方法是一种高精度的数值方法,适用于求解偏微分方程的数值解。
其基本思想是将区域上的函数展开为一组基函数的线性组合,通过选取适当的基函数和系数,来逼近求解方程。
谱方法主要包括以下步骤:1. 选择基函数:根据问题的性质,选择合适的基函数,如Legendre多项式、Chebyshev多项式等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限差分法求解偏微分方程有限差分法求解偏微分方程摘要:本文主要使用有限差分法求解计算力学中的系统数学模型,推导了有限差分法的理论基础,并在此基础上给出了部分有限差分法求解偏微分方程的算例验证了推导的正确性及操作可行性。
关键词:计算力学,偏微分方程,有限差分法Abstract:This dissertation mainly focuses on solving the mathematic model of computationmechanics with finite-difference method. The theoretical basis of finite-difference is derived in the second part of the dissertation, and then I use MATLAB to program the algorithms to solve some partial differential equations to confirm the correctness of the derivation and the feasibility of the method.Key words:Computation Mechanics, Partial Differential Equations, Finite-Difference Method1 引言机械系统设计常常需要从力学观点进行结构设计以及结构分析,而这些分析的前提就是建立工程问题的数学模型。
通过对机械系统应用自然的基本定律和原理得到带有相关边界条件和初始条件的微分积分方程,这些微分积分方程构成了系统的数学模型。
求解这些数学模型的方法大致分为解析法和数值法两种,而解析法的局限性众所周知,当系统的边界条件和受载情况复杂一点,往往求不出问题的解析解或近似解。
另一方面,计算机技术的发展使得计算更精确、更迅速。
因此,对于绝大多数工程问题,研究其数值解法更具有实用价值。
对于微分方程而言,主要分为差分法和积分法两种,本论文主要讨论差分法。
2 有限差分法理论基础2.1 有限差分法的基本思想当系统的数学模型建立后,我们面对的主要问题就是微分积分方程的求解。
基本思想是用离散的只含有限个未知量的差分方程组去近似地代替连续变量的微分方程和定解条件,并把差分方程组的解作为微分方程定解问题的近似解。
将原方程及边界条件中的微分用差分来近似,对于方程中的积分用求和或及机械求积公式来近似代替,从而把原微分积分方程和边界条件转化成差分方程组。
有限差分法求解偏微分方程的步骤主要有以下几步:区域离散,即把所给偏微分方程的求解区域细分成由有限个格点组成的网格,这些离散点称作网格的节点;⏹近似替代,即采用有限差分公式替代每一个格点的导数;⏹逼近求解,换而言之,这一过程可以看作是用一个插值多项式及其微分来代替偏微分方程的解的过程。
从原则上说,这种方法仍然可以达到任意满意的计算精度。
因为方程的连续数值解可以通过减小独立变量离散取值的间格,或者通过离散点上的函数值进行插值计算来近似得到。
理论上,当网格步长趋近于零时,差分方程组的解应该收敛于精确解,但由于机器字节的限制,网格步长不可能也没有必要取得无限小,那么差分法的收敛性或者说算法的稳定性就显得至关重要。
因此,在运用有限差分法时,除了要保证精度外,还必须要保证其收敛性。
2.2 系统微分方程的一般形式由于大多数工程问题都是二维问题,所以得到的微分方程一般都是偏微分方程,对于一维问题得到的是常微分方程,解法与偏微分方程类似,故为了不是一般性,这里只讨论偏微分方程。
由于工程中高阶偏微分较少出现,所以本文仅仅给出二阶偏微分方程的一般形式,对于高阶的偏微分,可进行类似地推广。
二阶偏微分方程的一般形式如下:其中,为弹性体上的某一特征物理量(连续函数)。
当A、B、C都是常数时,(1)式称为准线性,有三种准线性方程形式:⏹如果,则称为椭圆型方程;⏹如果,则称为抛物型方程;⏹如果,则称为双曲型方程。
(1)椭圆型方程主要用来处理稳态或静态问题,如热传导等问题;抛物线方程主要用来处理瞬态问题,如渗透、扩散等问题;双曲型方程主要用来处理振动问题,如玄震动、薄膜震动等问题。
除了上述微分方程外,必须给出定解条件,通常有如下三类:⏹第一类边界条件(Dirichlet 条件):;⏹第二类边界条件(Neumann 条件):;⏹第三类边界条件(Robin条件):;其中,为求解域的边界,为的单位外法矢,。
第二类和第三类边界条件统称为导数边界条件。
2.3 有限差分方程的数学基础2.3.1 一元函数导数的差分公式一个函数在x 点上的导数,可以近似地用它所临近的两点上的函数值的差分来表示。
函数在处的泰勒展式如下:对一个单变量函数,以步长将区间等距划分,我们得到一系列节点:,,,(),然后求出在这些节点上的近似值。
与节点相邻的节点有和,因此在点处可以构造如下形式的展开式:(2(3)由式(3)和式(4)可得到:⏹ 一阶向前差分: ⏹⏹ 一阶向后差分: ⏹⏹ 一阶中心差分: ⏹不妨,记,则式(5)、(6)、(7)分别简写为:⏹ 一阶向前差分: ⏹⏹ 一阶向后差分: ⏹⏹ 一阶中心差分: ⏹根据式(8)、式(9)和式(10),可得二阶差分: ⏹ 二阶向前差分: ⏹⏹ 二阶向后差分: ⏹⏹ 二阶中心差分: ⏹差分公式(13)是以相隔2h 的两结点处的函数值来表示中间结点处的一阶导数值,可称为中点导数公式。
式(11)和式(12)是以相邻三结点处的函数(5)(6)(7)(8)(9)(10)(11)(12)(13)值来表示一个端点处的一阶导数值,可称为端点导数公式。
应当指出:中点导数公式与端点导数公式相比,精度较高。
因为前者反映了结点两边的函数变化,而后者却只反映了结点一边的函数变化。
因此,我们总是尽可能应用前者,而只有在无法应用前者时才不得不应用后者。
但是,由于式(11)中的各阶导数均使用的是向前差分,导致用到的节点不相邻,同时为了均衡误差,将节点处用到的一阶差分换成向后差分,则式(11)修正为:同理,根据上述推导过程,可得到任意阶的差分公式: ⏹ n 阶向前差分: ⏹⏹ n 阶向后差分: ⏹⏹ n 阶中心差分: ⏹说明,上述公式中各节点处前一阶导数的代入可能存在不一致,可能是向前差分、向后差分或者中心差分,从而使最终的公式在系数上存在差别。
当然,也可以对各相邻节点进行需要阶数的泰勒展开,从而建立方程组直接求各阶导数。
2.3.2 微分方程转化为线性方程由于三种类型的微分方程解法类似,故这里仅以椭圆型微分方程为例,将微分方程转化为代数方程,对于双曲型和抛物型方程依次类推即可。
不妨记:(15) (16)(17)(14)(称为拉普拉斯算子),和是求解域上的连续函数。
假设求解区域为:,将求解区域划分成个网格,其中:,如图1所示。
记,则根据式(14)可得到:图1 五点差分公式式(18)也称为五点差分公式,同理根据式(12)和式(13)可分别得到向前差分公式(19)和向后差分公式(20),如图(2所示)。
⏹向前差分⏹⏹向后差分⏹(19)(20)图2向前差分(左)和向后差分(右)图3 中心差分、向前差分和向后差分的拉普拉斯算子表示利用中心差分公式(18),由于式(18)在点处具有二阶精度(),所以式(18)可近似改写成下式:根据椭圆方程的具体形式可以将其分为以下三种形式:⏹拉普拉斯(Laplace)方程:⏹泊松(Poison)方程:⏹赫耳墨次(Helmholtz)方程:根据式(21),可建立三种不同形式椭圆方程的代数方程如下:⏹拉普拉斯方程:化简后得到拉普拉斯方程的计算公式:(21)(22)⏹ 泊松方程:⏹⏹ 赫耳墨次方程:2.3.3 建立有限差分方程组根据式(22)~(24)建立方程组,但是需要知道对应的边界条件才能使方程组存在定解,根据2.2中可知,边界条件一般分为狄利克雷边界条件和导数边界条件两种,下面分别给出这两种边界条件的有限差分方程组的建立过程: ⏹ 狄利克雷边界条件:对于狄氏条件而言,给出了边界上各节点出的函数计算公式,直接代入节点值计算即可,如下所示为矩形区域的边界点计算:(左边界) (右边界)(下边界) (上边界)⏹ 导数边界条件:以右边界点为例,对于右边界点,根据Neumann 条件可得下式:对于拉普拉斯方程,根据计算公式(22),对于边界上的点可得:显然,上式中的在求解域外,是未知量。
根据中心差分公式(10)可得到:(23)(24) (25)(26) (27)(28)根据式(28)可得到逼近表示:,并且具有2阶逼近精度,代入式(27)可得下式:同理,对于其它边界可获得如下边界方程:(下边界)(上边界)(左边界)图4 Neumann条件算子对于泊松方程和赫耳墨次方程同样根据上述方法,获得边界条件的线性方程,然后将这些方程添加到式(22)~(24)所建立的方程组中,从而建立起个元的线性方程组,解该方程组即可获得各节点的函数值。
对于上述过程建立的线性方程组的求解,可采用多种方法,比如Jacob 迭代法、Gauss-Seidel迭代法、超松弛迭代法(SOR法)、高斯消元法等方法求解。
(29)(30)2.4 有限差分法的收敛性和稳定性由于迭代法必须保证收敛性,所以在解有限差分方程组时还应保证其收敛性,也就是通常所说的算法稳定性。
有限差分法的算法稳定性可以通过特征值方法、傅里叶变换(冯诺依曼条件)以及能量估计等方法来判断,下面给出常用的冯诺依曼条件: ⏹ 向前差分:,绝对收敛; ⏹ 向后差分:,绝对收敛;⏹ 中心差分:对任何的对不收敛;假设求解域内方向网格划分的步长为,方向网格划分的步长为,将偏微分方程化为标准形式,具体来说标准形式如下: ⏹ 双曲方程: ⏹对于式(31)所示的双曲方程,冯诺依曼条件为:. ⏹ 抛物方程: ⏹对于式(32)所示的抛物方程,冯诺依曼条件为:. ⏹ 椭圆方程: ⏹对于式(33)所示的椭圆方程,冯诺依曼条件为:.为了使算法在任何情况下都能保持稳定性,去掉对网格划分的冯诺依曼条件,通常采用隐式方案,对五点差分公式中的节点所在的行做差分,然后把这些差分的加权作为中心点的差分值,则拉普拉斯算子可修正为:(31)(33) (32)(34)利用式(34)进行计算时,稳定性没有任何限制。
取不同的值得到不同的差分公式,通常取.为了提高计算精度,很明显的一个措施就是网格细分,但是由于随着网格步长的减小,未知量的数目将会呈指数增长,网格划分太细会导致计算量过于庞大而无法计算。
通常,我们可以通过提高逼近的精度,采用更高精度的差分公式,例如对公式(21)进行修改,可得到九点差分公式:图5 九点差分公式3有限差分法求解实例根据上述推导有限差分法理论,对于不同类型的偏微分方程建立有限差分方程组,采用mat lab编程给出一些计算实例如下:1.椭圆型方程拉普拉斯方程:;求解域:(35)下面分别给出拉普拉斯方程在不同的边界条件下的解。
