双层玻璃隔音效果(数学建模)
双层玻璃隔音效果

一、 问题重述
噪声不但可以引起人听力的衰退、多种疾病的发作;同时,还影响人们的日常工作 与学习,降低劳动生产率。引起噪声的原因有很多种,其中临街的住房公路交通噪声是 我们要面对的主要噪声污染源。 面对城市环境中持续增高的交通噪音,双层玻璃窗户是一种有效的对应方式,它能 提供比单层更加优越的隔声效果。 双层玻璃窗户可以显著的改善建筑的隔声性能。其外层玻璃相当于一面玻璃声障, 安装于建筑外层。当声波遇到建筑物时,其绝大部分都被外层玻璃所反射,从而使进入 到内层空间的噪声降低。 事实上, 相当一部分双层玻璃窗户的最主要的功能就在于隔声。 通过所学的知识和查资料, 可以知道声音在传播过程中的变化与声音的频率、 声强、 声压、以及传播介质的吸收率有关,还与介质的密度和声音在介质中的传播速度有关。 声音在穿透玻璃时,在空气与玻璃接触的界面,声音会被反射一部分,还会被玻璃吸收 一部分(此部分能量被转化成玻璃的内能),剩下的声音才是穿透玻璃的声音。 查找相关数据,解决以下问题: 问题一:计算频率为 500 赫兹 75 分贝的噪音,经过厚度为 4mm 间隔为 1cm 的钢化 双层玻璃后,在玻璃的另一侧声音是多少分贝。 问题二:针对玻璃窗户的规格(大小、厚度等),不同楼层分布(喇叭效应导致的声 音影响等),建立双层玻璃隔音效果模型,并计算临街 1-35 层高楼的隔音效果。
K
(3)
I
1 K 1 2 2 2 A 2 A K 2 2
(4)
随着波的传播,波的能量会逐渐衰减,伴随着能量的衰减,波的振幅也逐渐减小。
4
振幅 A 与传播距离 x 对应的图像如下(图 4):
图 4
在同一介质中,设声波沿着 x 轴(对于此问题我们设垂直玻璃窗从外界指向室内为 其在 x 处的振幅为 A , 当传到 x dx 处时的振幅为 A dA , x 轴的正方向)的正方向传播, 即通过厚度 dx 的介质后振幅的减小量为 dA ,根据物理知识, dA 与振幅 A 和传播距 离 dx 成正比,即 dA Adx 这里的 称为吸声系数(或衰减系数),可对上式变形为 dA dx A 再对其进行求积分 A dA x dA A0 A 0 A 则可得
数学建模实例-双层玻璃的功效教学提纲

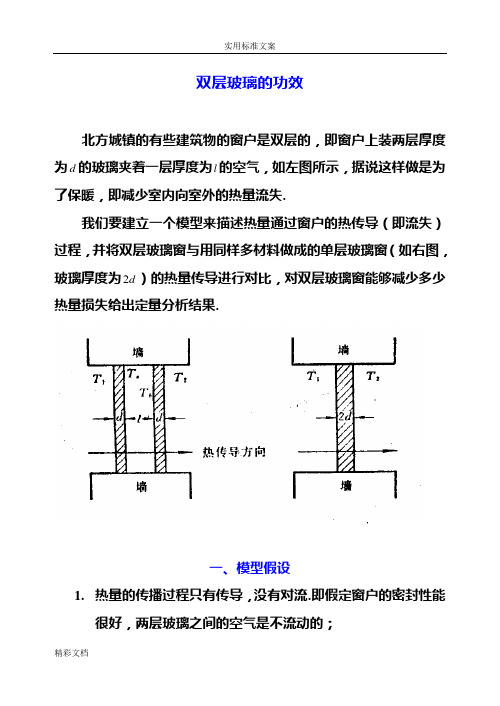
数学建模实例-双层玻璃的功效双层玻璃的功效北方城镇的有些建筑物的窗户是双层的,即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气,如下左图所示,据说这样做是为了保暖,即减少室内向室外的热量流失。
我们要建立一个模型来描述热量通过窗户的热传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如下右图,玻璃厚度为d2)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果。
一、模型假设1、热量的传播过程只有传导,没有对流。
即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的;2、室内温度T和室外温度2T保持不变,热传导过程已处于稳定1状态,即沿热传导方向,单位时间通过单位面积的热量是常数;3、 玻璃材料均匀,热传导系数是常数。
二、 符号说明1T ——室内温度2T ——室外温度d ——单层玻璃厚度l ——两层玻璃之间的空气厚度a T ——内层玻璃的外侧温度b T ——外层玻璃的内侧温度k ——热传导系数Q ——热量损失三、 模型建立与求解由物理学知道,在上述假设下,热传导过程遵从下面的物理规律:厚度为d 的均匀介质,两侧温度差为T ∆,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量Q ,与T ∆成正比,与d 成反比,即dT k Q ∆= (1) 其中k 为热传导系数。
1、双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ,外层玻璃的内侧温度为b T ,玻璃的热传导系数为1k ,空气的热传导系数为2k ,由(1)式单位时间单位面积的热量传导(热量流失)为: dT T k d T T k d T T k Q b b a a 21211-=-=-= (2)由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=- 再代入d T T k Q b a -=2就将(2)中a T 、b T 消去,变形可得: ()dl h k k h s s d T T k Q ==+-= , , 2)(21211 (3)2、单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户,容易写出热量流失为: dT T k Q 2211-=' (4)3、 单层玻璃窗和双层玻璃窗热量流失比较比较(3)(4)有:22+='s Q Q (5) 显然,Q Q '<。
数学建模案例分析报告报告材料2.双层玻璃地功效
双层玻璃的功效北方城镇的有些建筑物的窗户是双层的,即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气,如左图所示,据说这样做是为了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如右图,玻璃厚度为d2)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的;2.室内温度T和室外温度2T保持不变,热传导过程已处于稳定1状态,即沿热传导方向,单位时间通过单位面积的热量是常数;3.玻璃材料均匀,热传导系数是常数.二、符号说明T——室内温度1T——室外温度2d——单层玻璃厚度l——两层玻璃之间的空气厚度T——内层玻璃的外侧温度aT——外层玻璃的内侧温度bk——热传导系数Q——热量损失三、模型建立与求解由物理学知道,在上述假设下,热传导过程遵从下面的物理规律:厚度为d的均匀介质,两侧温度差为T∆,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q,与T∆成正比,与d成反比,即dT k Q ∆= (1) 其中k 为热传导系数.1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ,外层玻璃的内侧温度为b T ,玻璃的热传导系数为1k ,空气的热传导系数为2k ,由(1)式单位时间单位面积的热量传导(热量流失)为:d T T k d T T k d T T k Q b b a a 21211-=-=-= (2) 由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=- 再代入d T T k Q b a -=2就将(2)中a T 、b T 消去,变形可得: ()dl h k k h s s d T T k Q ==+-=, , 2)(21211 (3) 2. 单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户,容易写出热量流失为: d T T k Q 2211-=' (4)3. 单层玻璃窗和双层玻璃窗热量流失比较比较(3)(4)有:22+='s Q Q (5) 显然,Q Q '<.为了获得更具体的结果,我们需要21,k k 的数据,从有关资料可知,不流通、干燥空气的热传导系数42105.2-⨯=k (J/cm.s.ºC ),常用玻璃的热传导系数331108~104--⨯⨯=k (J/cm.s.ºC ),于是32~1621=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时,我们作最保守的估计,即取1621=k k ,由(3)(5)可得:d l h h Q Q =+=' 181 (6) 4. 模型讨论 比值Q Q '反映了双层玻璃窗在减少热量损失上的功效,它只与d l h =有关,下图给出了h Q Q ~'的曲线,当h 由0增加时,Q Q '迅速下降,而当h 超过一定值(比如4>h )后Q Q '下降缓慢,可见h 不宜选得过大.四、模型的应用这个模型具有一定的应用价值.制作双层玻璃窗虽然工艺复杂会增加一些费用,但它减少的热量损失却是相当可观的.通常,建筑规范要求4≈h.按照这个模型,%3≈'QQ,即双层玻璃窗比用同=d l样多的玻璃材料制成的单层窗节约热量97%左右.不难发现,之所以有如此高的功效主要是由于层间空气的极低的热传导系数k,而2这要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下当然不可能完全满足,所以实际上双层玻璃窗的功效会比上述结果差一些.。
数学建模双层玻璃的功效模型评价

数学建模双层玻璃的功效模型评价
双层玻璃是一种常见的建筑材料,具有一些独特的功效。
本文将基于数学建模方法,对双层玻璃的功效进行评价。
首先,我们可以通过数学模型评估双层玻璃的保温性能。
双层玻璃的两层之间通常会填充一种叫做气体的绝热材料,如氩气或氪气。
这些气体具有较低的热传导性,可以减少室内与室外的热量传递。
我们可以利用传热学中的热传导理论,建立数学模型来计算双层玻璃的热传导系数。
通过对比单层玻璃和双层玻璃的热传导系数,我们可以评估双层玻璃在保温方面的功效。
其次,我们可以利用数学模型来研究双层玻璃的隔音效果。
双层玻璃通过夹层的气体和两层之间的距离,可以有效吸收声波的能量,减少声音的传播。
我们可以运用声学原理,建立声波传播的数学模型,计算双层玻璃的声学性能指标,如声传递系数和噪音减少量。
通过与单层玻璃进行对比,我们可以评估双层玻璃在隔音方面的功效。
此外,数学建模还可以应用于评估双层玻璃的安全性能。
双层玻璃的两层之间可以夹入一层薄膜,以增强玻璃的抗冲击能力和防护性能。
我们可以运用力学原理建立数学模型,评估双层玻璃在受力情况下的强度和稳定性。
通过计算双层玻璃的抗压强度和抗张强度,我们可以对其安全性能进行评价。
总之,数学建模是评价双层玻璃功效的有效工具。
通过建立合适的数学模型,我们可以准确评估双层玻璃在保温、隔音和安全性能方面的优势,为建筑设计和使用提供科学依据。
数学建模-双层玻璃窗、隔热效果、隔音效果

数学建模-双层玻璃窗、隔热效果、隔音效果摘要:中国仍处于工业化初期,节能减排具有较大空间。
通过对问题一的数学模型进行分析后得到:一般情况下,建筑标准要求d l /≈4。
据此模型可得12/Q Q ≈3.03%,即双层玻璃窗比同样多的玻璃材料制成的单层玻璃窗节约热量约为96.97%; 双层玻璃的隔声优势为 :lge ,根据以上推导的结果,当空气的吸收系数与两片玻璃的距离越大时,双层玻璃窗的隔音效果就越好。
游客节能低碳的交通出行工具安排:〔1〕长途参观者建议直接或间接购买碳信用额度;〔2〕对中短途参观者,建议优先选择火车、轮船和长途客车等公共交通方式;〔3〕对于长三角等周边地区自驾车出行的参观者,建议采用停车换乘〔P+R 〕方式;〔4〕对上海城区内的参观者,建议优先选择轨交、公共汽车等公共交通,减少私人汽车的使用;〔5〕对距世博园区较近的参观者,建议步行或自行车出行。
最后,我们计算了各种出行方式的二氧化碳的排放量后,据此代表上海世博会组委会给游客写了一份建议书。
关键字:双层玻璃窗 隔热效果 隔音效果 碳足迹目录1、问题重述与分析 (3)1.1、问题重述 (4)1.2、问题分析 (4)2、条件假设 (4)3、符号说明 (4)4、模型的建立及求解 (5)双层玻璃隔热效果探究 (5)模型建立 (5)4.1.2、模型的应用 (8)4.2、双层玻璃隔音效果探究 (9)4.2.1、模型建立 (9) (11) (11) (11) (15)参考文献 (16)1、问题重述与分析中国仍处于工业化初期,节能减排具有较大空间。
中国现在是工业排放量占大头,交通和建筑类排放较小。
随着生活水平的提高,建筑节能的比重将逐步上升,有很大发展潜力。
据研究报告称,相关交通工具所使用燃料释放的气体是目前造成全球变暖的主要原因之一。
为此请考虑以下几个问题:1、请用数学模型说明双层〔中间有密封空气层〕玻璃窗户对单层玻璃窗户的优势以及双层玻璃窗户的隔音效果如何?2、请你为参观上海世博会的各种游客分别设计节能低碳的交通出行工具安排,计算相应二氧化碳的排放量,并据此代表上海世博会组委会给游客一份建议书。
双层玻璃隔音计算书

中德工程有限公司
工程名稱 : 澳門理工學院氹仔新校區珍禧樓及研發大樓裝修工程
計算項目: WR22雙層玻璃夾百葉隔音效能計算
本工程研發樓GF層文化創意中心設置有WR22雙層玻璃夾百葉隔斷,玻璃隔斷總厚度85mm,內外兩側玻璃厚度各8mm,按《建築隔聲評價標準》、《民用建築隔聲設計規範》及《建築門窗空氣聲隔聲性能分級及檢測方法》有關規定複核其隔音效能。
隔斷總厚度T=85mm
內側玻璃厚度t1=8mm
外側玻璃厚度t2=8mm
空氣層厚度t3=69mm
鋼化玻璃密度ρ=2560kg/m3
內側玻璃面密度m1=20.48kg/m2
外側玻璃面密度m2=20.48kg/m2
玻璃隔斷隔音量R=13.5lg(m1+m2)+13+ΔR
其中附加隔音量ΔR=0.1*t3
=6.9dB
玻璃隔斷總隔音量R=41.7dB
page 1。
双层玻璃隔音效果(数学建模)

双层玻璃隔音问题班级:2012级软件4班小组成员:周冀浩(12101020427)游清文(12101020424)2013-10-22摘要社会现代化进程的快速发展,各种机械设备的创造和使用,给人类带来了繁荣和进步,但同时也产生了越来越多而且越来越强的噪音。
噪音严重影响人的生活、学习以及工作,对人的身体健康也有极大的影响。
因此,怎样减少噪音成了重要的研究课题。
本文通过对双层玻璃与单层玻璃隔音量的比较研究双层玻璃的隔音效果,建立了在不同介质中声音的衰减模型。
考虑到声音在介质中衰减的不好计算,通过微积分的方法处理得到声音强度级I0的一声波,通过为吸收系数为k厚度为d的介质的后声波所剩下的强度I,一、问题重述临街的房屋通常都安装双层玻璃,目的就是为了减少噪声。
试建立模型分析一下双层玻璃的隔音效果,并且进一步分析对于一栋临街的楼房不同楼层隔音效果的变化。
(考虑11层的正规楼房,噪声源离房屋20米,噪声90分贝)二、问题分析本问题的关键在于寻找声音在穿越玻璃的过程中能量的变化规律,即找到声波在穿过玻璃后的隔声量。
此变化规律不仅与声音的自身属性(频率、声压、声强等)有关,还会受到外部因素(例如介质的吸收率、介质的密度等)的影响。
因此,对本问题的考虑会涉及到这两个主要方面。
本题难点在于不同频率不同方向的噪音传播效果不同,即难精确计算声音损失量。
而且双层玻璃间的空气会对声音产生共振减弱等作用削弱声音的传播,这也增大了对问题求解的难度。
因此,课一考虑对模型作一定的理想化,忽略一些难度大影响又小的因素,而只考虑主要因素。
一定程度上保证了所用方法的科学性和计算结果的合理性。
三、模型假设1.因为阻碍物远大于噪音波长,衍射现象不明显,所以不考虑衍射现象带来的影响。
2.不考虑钢化玻璃的弹性,即忽略声波入射到钢化玻璃上时激起的弯曲振动。
3.双层玻璃材质均匀,厚度相同,声传导系数为常数。
4.假定窗户的密闭性能很好,两层玻璃之间的空气是不流动的。
最新数学建模案例分析2双层玻璃的功效

精品文档双层玻璃的功效北方城镇的有些建筑物的窗户是双层的,即窗户上装两层厚度为的玻璃夹着一层厚度为的空气,如左图所示,据说这样做是为dl了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如右图,玻璃厚度为)的热量传导进行对比,对双层玻璃窗能够减少多少d2热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的;2.室内温度和室外温度保持不变,热传导过程已处于稳定TT12状态,即沿热传导方向,单位时间通过单位面积的热量是常数;3.玻璃材料均匀,热传导系数是常数.精品文档.精品文档二、符号说明——室内温度T1——室外温度T2——单层玻璃厚度d——两层玻璃之间的空气厚度l——内层玻璃的外侧温度T a——外层玻璃的内侧温度T b——热传导系数k ——热量损失Q三、模型建立与求解由物理学知道,在上述假设下,热传导过程遵从下面的物理规律:厚度为的均匀介质,两侧温度差为,则单位时间由温度高dT?的一侧向温度低的一侧通过单位面积的热量为,与成正比,与Q T?成反比,即d?T(1)k?Q d其中为热传导系数. k 1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为,外层玻璃的内侧温度为,TT ba玻璃的热传导系数为,空气的热传导系数为,由(1)式单位时kk12间单位面积的热量传导(热量流失)为:T?TT?TT?T(2)ba1b2a k?k??Qk及可得由b12a kk?Q?Q2??(TT)?T?T112a1b kdd1 112dddT?TT?TQd精品文档.精品文档T?T就将(2)中再代入、消去,变形可得:ba k?QTT ba2d k)?Tk(Tl)(3 1211?, , s?hQ?h ??d2kds?2单层玻璃的热量流失2.的单层玻璃窗户,容易写出热量流失为:对于厚度为d2TT? 4)(?21kQ?1d2单层玻璃窗和双层玻璃窗热量流失比较3.2Q)(5 )有:比较(3)(4??2?Qs.显然,?Q?Q的数据,从有关资料可为了获得更具体的结果,我们需要k,k21,常).oC (J/cm.s知,不流通、干燥空气的热传导系数4?10?2k?.52(J/cm.s.用玻璃的热传导系数,于是C)o33??10k~?10?4?81k13216?~k2在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时,我们k,由(3)(5)可得:作最保守的估计,即取116?k2Q1l(6)?h??d1?h8Q精品文档.精品文档4. 模型讨论反映了双层玻璃窗在减少热量损失上的功效,它只与比值?QQ迅的曲线,当有关,下图给出了由0增加时,??Q~QQh?ldhQ h不下降缓慢,可见速下降,而当超过一定值(比如)后?QQ4?hhh.宜选得过大四、模型的应用制作双层玻璃窗虽然工艺复杂这个模型具有一定的应用价值.通常,建筑会增加一些费用,但它减少的热量损失却是相当可观的.按照这个模型,,即双层玻璃窗比用同.规范要求?%??ld4?3Qh样多的玻璃材料制成的单层窗节约热量97%左右.不难发现,之所以有如此高的功效主要是由于层间空气的极低的热传导系数,而这k2要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下精品文档.精品文档当然不可能完全满足,所以实际上双层玻璃窗的功效会比上述结果差一些.精品文档.。
【数学建模实例】双层玻璃的功效

双层玻璃的功效北方城镇的有些建筑物的窗户是双层的,即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气,如左图所示,据说这样做是为了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如右图,玻璃厚度为d2)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的;2.室内温度T和室外温度2T保持不变,热传导过程已处于稳定1状态,即沿热传导方向,单位时间通过单位面积的热量是常数;3.玻璃材料均匀,热传导系数是常数.二、 符号说明1T ——室内温度 2T ——室外温度 d ——单层玻璃厚度l ——两层玻璃之间的空气厚度 a T ——内层玻璃的外侧温度 b T ——外层玻璃的内侧温度 k ——热传导系数 Q ——热量损失三、 模型建立与求解由物理学知道,在上述假设下,热传导过程遵从下面的物理规律:厚度为d 的均匀介质,两侧温度差为T ∆,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q ,与T ∆成正比,与d 成反比,即dTkQ ∆= (1) 其中k 为热传导系数. 1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ,外层玻璃的内侧温度为b T ,玻璃的热传导系数为1k ,空气的热传导系数为2k ,由(1)式单位时间单位面积的热量传导(热量流失)为:dT T k d T T k d T T k Q b b a a 21211-=-=-= (2) 由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=-再代入dT T k Q ba -=2就将(2)中a T 、b T 消去,变形可得: ()dlh k k h s s d T T k Q ==+-=, , 2)(21211 (3)2. 单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户,容易写出热量流失为: dT T k Q 2211-=' (4)3. 单层玻璃窗和双层玻璃窗热量流失比较 比较(3)(4)有: 22+='s Q Q (5) 显然,Q Q '<.为了获得更具体的结果,我们需要21,k k 的数据,从有关资料可知,不流通、干燥空气的热传导系数42105.2-⨯=k (J/cm.s .ºC ),常用玻璃的热传导系数331108~104--⨯⨯=k (J/cm.s .ºC ),于是32~1621=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时,我们作最保守的估计,即取1621=k k ,由(3)(5)可得: dlh h Q Q =+=' 181 (6) 4. 模型讨论比值Q Q '反映了双层玻璃窗在减少热量损失上的功效,它只与d l h =有关,下图给出了h Q Q ~'的曲线,当h 由0增加时,Q Q '迅速下降,而当h 超过一定值(比如4>h )后Q Q '下降缓慢,可见h 不宜选得过大.四、模型的应用这个模型具有一定的应用价值.制作双层玻璃窗虽然工艺复杂会增加一些费用,但它减少的热量损失却是相当可观的.通常,建筑规范要求4≈=d l h .按照这个模型,%3≈'Q ,即双层玻璃窗比用同样多的玻璃材料制成的单层窗节约热量97%左右.不难发现,之所以有如此高的功效主要是由于层间空气的极低的热传导系数2k ,而这要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下当然不可能完全满足,所以实际上双层玻璃窗的功效会比上述结果差一些.。
双层玻璃窗功效、汽车刹车距离、划艇比赛成绩—数学建模初等模型的应用

Q1 Q2
l d
k1=410-3 ~8 10-3, k2=2.510-4, k1/k2=16 ~32 对Q1比Q2的减少量 Q1 1 , h 作最保守的估计,
取k1/k2 =16
Q2
8h 1
模型应用
Q1 1 l , h Q2 8h 1 d
Q1/Q2 0.06 0.03 0.02 0
模型 np fv f 建立 s1/2 A1/3 A W(=w0+nw) n sv2
pw
v (n/s)1/3 s n2/3
v n1/9
比赛成绩 t n – 1/9
模型检验
n 1 2 4 8 t 7.21 6.88 6.32 5.84
利用4次国际大赛冠军的平均 成绩对模型 t n – 1/ 9 进行检验
常识:刹车距离与车速有关
问 题 分 析
10英里/小时(16公里/小时)车速下2秒钟行驶 29英尺( 9米) >>车身的平均长度15英尺(=4.6米) “2秒准则”与“10英里/小时加一车身”规则 不同 反 司机 制动系统 反应时间 应 状况 灵活性 距 车速 离 常数
制 制动器作用力、车重、车速、道路、气候… … 动 最大制动力与车质量成正比, 常数 距 离 使汽车作匀减速运动。
Q1
墙 室 内 T1 室 外 T2
2d
热传导定律
T Qk d
Q2
墙
建模 记双层玻璃窗传导的热量Q1
Ta~内层玻璃的外侧温度
Tb~外层玻璃的内侧温度
k1~玻璃的热传导系数
室 内 T1
Ta T b d l d
室 外 T2
Q1
墙
k2~空气的热传导系数
双层玻璃的功效建模

第3章 微分方程模型3.1 微分方程模型的建模步骤在自然科学以及工程、经济、医学、体育、生物、社会等学科中的许多系统,有时很难找到该系统有关变量之间的直接关系——函数表达式,但却容易找到这些变量和它们的微小增量或变化率之间的关系式,这时往往采用微分关系式来描述该系统——即建立微分方程模型。
我们以一个例子来说明建立微分方程模型的基本步骤。
例1 某人的食量是10467(焦/天),其中5038(焦/天)用于基本的新陈代谢(即自动消耗)。
在健身训练中,他所消耗的热量大约是69(焦/公斤•天)乘以他的体重(公斤)。
假设以脂肪形式贮藏的热量100%地有效,而1公斤脂肪含热量41868(焦)。
试研究此人的体重随时间变化的规律。
模型分析在问题中并未出现“变化率”、“导数”这样的关键词,但要寻找的是体重(记为W )关于时间t 的函数。
如果我们把体重W 看作是时间t 的连续可微函数,我们就能找到一个含有的dtdW 微分方程。
模型假设1.以)(t W 表示t 时刻某人的体重,并设一天开始时人的体重为0W 。
2.体重的变化是一个渐变的过程。
因此可认为)(t W 是关于t 连续而且充分光滑的。
3.体重的变化等于输入与输出之差,其中输入是指扣除了基本新陈代谢之后的净食量吸收;输出就是进行健身训练时的消耗。
模型建立问题中所涉及的时间仅仅是“每天”,由此,对于“每天”体重的变化=输入-输出。
由于考虑的是体重随时间的变化情况,因此,可得体重的变化/天=输入/天—输出/天。
代入具体的数值,得输入/天 = 10467(焦/天)—5038(焦/天)=5429(焦/天), 输出/天 = 69(焦/公斤•天)×W (公斤)= 69W (焦/天)。
体重的变化/天=tW ∆∆(公斤/天)dtdW t =→∆0考虑单位的匹配,利用 “公斤/天=公斤焦天焦/41868/”, 可建立如下微分方程模型⎪⎩⎪⎨⎧=-≈-==001000016129641868695429W WW W dtdWt 。
双层玻璃问题求解

双层玻璃的功效双层玻璃问题在数学建模中非常易见,在这类我做一些说明: 北方城镇的有些建筑物的窗户是双层的,即窗户上装两层厚度 为d 的玻璃夹着一层厚度为l 的空气,如左图所示,据说这样做是为 了保暖,即减少室内向室外的热量流失。
我们要建立一个模型来描述热量通过窗户的热传导(即流失) 过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗 (如右图, 玻璃厚度为2d )的热量传导进行对比,对双层玻璃窗能够减少多少 热量损失给出定量分析结果。
一、模型假设1、 热量的传播过程只有传导,没有对流。
即假定窗户的密封性 能很好,两层玻璃之间的空气是不流动的;2、 室内温度T i 和室外温度T 2保持不变,热传导过程已处于稳定 状态,即沿热传导方向,单位时间通过单位面积的热量是常数;3、 玻璃材料均匀,热传导系数是常数。
、符号说明T i ——室内温度 T 2 ――室外温度墙热传导方向d――单层玻璃厚度l ――两层玻璃之间的空气厚度T a ――内层玻璃的外侧温度T b ――外层玻璃的内侧温度k 热传导系数Q 热量损失三、模型建立与求解由物理学知道,在上述假设下,热传导过程遵从下面的物理规律:厚度为d的均匀介质,两侧温度差为•汀,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q,与订成正比,与d成反比,即Q = k 红(1)d其中k为热传导系数。
1、双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为T a,外层玻璃的内侧温度为T b,玻璃的热传导系数为k i,空气的热传导系数为k2,由(1)式单位时间单位面积的热量传导(热量流失)为:(2)d d d由Q =ki T1及Q 二k』空可得T a -几=(% -T2)-2Qdd d k1再代入Q =k2Ta Tb就将(2)中T a、T b消去,变形可得:d2、单层玻璃的热量流失对于厚度为2d 的单层玻璃窗户,容易写出热量流失为:3、 单层玻璃窗和双层玻璃窗热量流失比较 比较(3)(4)有: -(5)Q s + 2显然,Q : Q 。
双层玻璃的隔音效果

( ) Aa
20 o C,φ
= 7.4 f 2r ×10−8 φ
不同温度、不同湿度时候的每百米声音衰减分贝数:
Aa
(T
0
c,φ
)
=
1
Aa (200 C,φ ) + ∆Tf 4 ×10−6
5
对于不同温度,可以修正成如下公式,以便于计算:
( ) I0
=
I
r −×
100
Aa
T OC,φ
根据第一问可以得出以下结论:
声音波经过外层玻璃后:
- I0 × ρ 声音波经过外层玻璃和中间空气层后 :
I 2 = I1e−∂2l 声音波经过双层玻璃窗后 :
I 3 = I 2e−∂2d - I 2 × ρ
为了方便计算我们假设声源距离高楼的垂直为 35m,声源频率为 250Hz, 60 分 贝的一声波,高楼的每层楼高 3.5m,通过查资料得在这种情况下大气对声音的衰 减为 0.14db/100m,我们算得 60db 的声音经过双层玻璃后: 第一层楼为 43.4817db; 底 35 层楼为 43.3635db。 ∆I =43.4817-43.3635 =0.1182
r
马路 S
声源
4
窗户 楼层高度 h
图(二)
声源到楼层的实际距离为:
图(三)
r= S 0 2 + h 2
楼层里地面的高度: h=n × H
0
我们查资料可知玻璃的声音反射率为:
(N12 − N 2)2 ρ = (NI 2 + N 2)2
我们可知道,温度为 20℃,湿度为 30 的时候每百米距离声音的衰减的分贝数:
1
四、符号定义及说明
1.I 声强级; 2.D 玻璃厚度; 3.L 双层玻璃中空气层厚度; 4.B 加权声; 5.Gs 玻璃窗户的整体隔声量; 6.Gs1 单层玻璃窗户封闭部分的隔声量; 7.U 玻璃窗户上开口面隔声材料单位面积的质量; 8.M 隔声材料单位面积的质量; 9. ∂ 为介质的吸收系数; 10.△L 声能的衰减; 11.r 声源到玻璃的距离; 12.f 波的频率; 13 H0 每层楼的高度; 14 n 楼层数 ; 15 S0 声源到楼层的垂直距离; 15 Aa 每一百米声音的衰减量; 16 T 空气的温度; 17 Φ 空气的湿度; 18 N1 玻璃的折射率; 19 N2 空气的折射率; 20 ρ 声音反射率。
多层玻璃隔音效果数学建模

多层玻璃隔音效果数学建模在现代社会中,噪音污染日益成为影响人们生活质量和健康的重要问题。
为了有效地减少噪音的传播,提高室内环境的安静程度,多层玻璃的应用越来越广泛。
多层玻璃的隔音效果受到多种因素的影响,如玻璃的层数、厚度、间距以及玻璃的材质等。
为了更好地理解和优化多层玻璃的隔音性能,建立数学模型来定量描述其隔音效果是非常有必要的。
首先,我们需要了解声音传播的基本原理。
声音是一种机械波,通过介质的振动来传播。
当声音遇到障碍物时,一部分会被反射,一部分会被吸收,还有一部分会穿透障碍物继续传播。
多层玻璃就相当于声音传播路径上的障碍物,其隔音效果主要取决于对声音的反射、吸收和穿透的综合作用。
在建立数学模型时,我们可以将多层玻璃系统看作一系列串联的声学单元。
每个声学单元由一层玻璃和其两侧的空气层组成。
对于每一层玻璃,我们可以用其质量、弹性模量和阻尼系数来描述其声学特性。
而对于空气层,我们可以用其声阻抗来表示。
假设我们有 n 层玻璃,第 i 层玻璃的厚度为 di,密度为ρi,声速为ci,其两侧空气层的厚度分别为 li 和 ri。
声音在玻璃中的传播速度可以表示为:vi =√(Ei/ρi)其中 Ei 是第 i 层玻璃的弹性模量。
声音在玻璃和空气界面上的反射系数和透射系数可以通过声学阻抗匹配原理来计算。
反射系数 Ri 表示为:Ri =(Zi Z(i-1))/(Zi + Z(i-1))其中 Zi 是第 i 层的声阻抗,Z(i-1) 是第 i 1 层的声阻抗。
透射系数 Ti 则为:Ti = 1 Ri声音在通过每一层玻璃和空气层时都会有能量的损失。
对于第 i 层玻璃,其能量损失可以表示为:αi =-20 log10(Ti)整个多层玻璃系统的总隔音量可以通过将各层的隔音量相加得到:总隔音量=∑αi为了更准确地描述隔音效果,我们还需要考虑玻璃之间的耦合作用以及声波的频率特性。
一般来说,声音的频率越高,多层玻璃的隔音效果越好。
【数学建模学习】双层玻璃的功效

双层玻璃的功效北方城镇的有些建筑物的窗户是双层的,即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气,如左图所示,据说这样做是为了保暖,即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导(即流失)过程,并将双层玻璃窗与用同样多材料做成的单层玻璃窗(如右图,玻璃厚度为d2)的热量传导进行对比,对双层玻璃窗能够减少多少热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导,没有对流.即假定窗户的密封性能很好,两层玻璃之间的空气是不流动的;2.室内温度T和室外温度2T保持不变,热传导过程已处于稳定1状态,即沿热传导方向,单位时间通过单位面积的热量是常数;3.玻璃材料均匀,热传导系数是常数.二、 符号说明1T ——室内温度 2T ——室外温度 d ——单层玻璃厚度l ——两层玻璃之间的空气厚度 a T ——内层玻璃的外侧温度 b T ——外层玻璃的内侧温度 k ——热传导系数 Q ——热量损失三、 模型建立与求解由物理学知道,在上述假设下,热传导过程遵从下面的物理规律:厚度为d 的均匀介质,两侧温度差为T ∆,则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q ,与T ∆成正比,与d 成反比,即dTkQ ∆= (1) 其中k 为热传导系数. 1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ,外层玻璃的内侧温度为b T ,玻璃的热传导系数为1k ,空气的热传导系数为2k ,由(1)式单位时间单位面积的热量传导(热量流失)为:dT T k d T T k d T T k Q b b a a 21211-=-=-= (2) 由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=-再代入dT T k Q ba -=2就将(2)中a T 、b T 消去,变形可得: ()dlh k k h s s d T T k Q ==+-=, , 2)(21211 (3)2. 单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户,容易写出热量流失为: dT T k Q 2211-=' (4)3. 单层玻璃窗和双层玻璃窗热量流失比较 比较(3)(4)有: 22+='s Q Q (5) 显然,Q Q '<.为了获得更具体的结果,我们需要21,k k 的数据,从有关资料可知,不流通、干燥空气的热传导系数42105.2-⨯=k (J/cm.s .ºC ),常用玻璃的热传导系数331108~104--⨯⨯=k (J/cm.s .ºC ),于是32~1621=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时,我们作最保守的估计,即取1621=k k ,由(3)(5)可得: dlh h Q Q =+=' 181 (6) 4. 模型讨论比值Q Q '反映了双层玻璃窗在减少热量损失上的功效,它只与d l h =有关,下图给出了h Q Q ~'的曲线,当h 由0增加时,Q Q '迅速下降,而当h 超过一定值(比如4>h )后Q Q '下降缓慢,可见h 不宜选得过大.四、模型的应用这个模型具有一定的应用价值.制作双层玻璃窗虽然工艺复杂会增加一些费用,但它减少的热量损失却是相当可观的.通常,建筑规范要求4≈=d l h .按照这个模型,%3≈'Q ,即双层玻璃窗比用同样多的玻璃材料制成的单层窗节约热量97%左右.不难发现,之所以有如此高的功效主要是由于层间空气的极低的热传导系数2k ,而这要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下当然不可能完全满足,所以实际上双层玻璃窗的功效会比上述结果差一些.。
初等数学建模论文常见的题目和要求

将
,得
于是当 一定时,有不等式最值定理得
可使 最小
设
4, m
代入上式得 =5 ~6
一般情况下,人的步行速度不可能每秒五步,所以这个结果不合理。
3.3 模型修改
将( 3 )的假设修改为: 腿的质量集中在脚部,行走看作脚的直线运动时,动能将变为
= 当 v 一定, W 最小时有
4 , m 时,
此结果较合适,所以此模型成立。
设腿长 ,步长 s (s< ):
( 2 )人行走时人体重心升高 ,腿的质量 m ,行走速度 v; ( 3 )人体质量 M ,每秒行走步 n 。
3.模型的建立与求解
如图,通过近似图形分析和直角三角形性质易知人重心在行走时升高。 所以,动能增加的同时也重力势能会增加。以下对此求解:
3.1. 人行走时的动能
a) 、现因学生转系,三系人数为 103, 63, 34, 问 20 席如何分配? b) 、若增加为 21 席,又如何分配?
四、汽车刹车距离
•
美国的某些司机培训课程中的驾驶规则:正常驾驶条件下 , 车速每增 10 英里
/ 小时,
后面与前车的距离应增一个车身的长度。
•
实现这个规则的简便办法是 “2 秒准则 ” :
车距离。5. 人行走最省力模型。 论文的要求。论文的关键环节。 论文正题。 初等模型题目
一、贷款购房方案的选择 贷款买房这一消费方式已被越来越多的市民接受,但是在“花明天的钱,享受今天的幸福” 的同时,许多购房者希望能有一个较好的理财方案。中国人民银行 1998 年 5 月出台了《个 人住房贷款管理办法》中明确规定,住房贷款主要有两种不同的还款方式:等额本息和、等 额本金,并允许借款人和贷款人在双方协商基础上进行选择,但一笔借款合同只能选择一种 还款方式,而合同签订后,不得更改。对一位购房者来说,最终选择哪一种还款方式,而合 同签订后,不得更改。对一位购房者来说,最终选择哪一种还款方式呢?哪一种还款方式更 有利于自己呢?为了寻根究底,我们开始探索研究——贷款者在每期偿还相等的款额情况 下,如何选择还款方式?
19067-数学建模-2.2

§2.2双层玻璃的功效
在寒冷的北方,许多住房的玻璃窗都是双层玻璃的,现在我们来建立一个简单的数学模
型,研究一下双层玻璃到底有多大的功效。
比较两座其他条件完全相同的房屋,它们的差异仅仅在窗户不同。
不妨可以提出以下假设:1、设室内热量的流失是热传导引起的,不存在户内外的空气对流。
2、室内温度T 1与户外温度T 2均
为常数。
3、玻璃是均匀的,热传导系数
为常数。
设玻璃的热传导系数为k 1,空气的热传导系数为k 2,单位时间通过单位面积由温度高的一侧流向温度低的一侧的热量为θd d
l
室
外
T 2室内T 1T a T b 由热传导公式θ=k ΔT /d
d
T T k l T T k d T T k b b a a 21211--=-=θ())/()(21212
121d k l k T T d k l k T a +++=解得:()
d k l k d T T k d d k l k T T d k l k T k 212112*********)1(+-=+++-=θ
此函数的图形为d d 室外T 2室内T 1d T T k 2211-='θ)/()(2221d k l k +='θθ类似有32~1621=k k 一般d l /811+≤'θθ故记h=l/d 并令f(h)=181+h 012345678910
00.10.20.30.40.50.6
0.70.80.91
h f (h )考虑到美观和使用上的方便,h 不必取得过大,例如,可取h=3,即l=3d ,此时房屋热量的损失不超过单层玻璃窗时的3%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于单层玻璃:
根据(3)(4)两式有:
通过资料可计算出 <0恒成立,所以I2/I3<0,即I2<I3。所以双层玻璃的隔音效果强于单层玻璃。
五、模型推广
对于11层高的楼房,声源距楼房20米,声源强度90分贝的模型。
图2楼层示意图
设声源到楼层实际距离为R,楼层高为H,声源到一层的距离为S=20m,根据实际情况,每层楼的高度为h=3m,楼层数为b。
1.因为阻碍物远大于噪音波长,衍射现象不明显,所以不考虑衍射现象带来的影响。
2.不考虑钢化玻璃的弹性,即忽略声波入射到钢化玻璃上时激起的弯曲振动。
3.双层玻璃材质均匀,厚度相同,声传导系数为常数。
4.假定窗户的密闭性能很好,两层玻璃之间的空气是不流动的。
5.假设玻璃内外两侧所处环境的温度不变。
四、模型建立与求解
一、问题重述
临街的房屋通常都安装双层玻璃,目的就是为了减少噪声。试建立模型分析一下双层玻璃的隔音效果,并且进一步分析对于一栋临街的楼房不同楼层隔音效果的变化。(考虑11层的正规楼房,噪声源离房屋20米,噪声90分贝)
二、问题分析
本问题的关键在于寻找声音在穿越玻璃的过程中能量的变化规律,即找到声波在穿过玻璃后的隔声量。此变化规律不仅与声音的自身属性(频率、声压、声强等)有关,还会受到外部因素(例如介质的吸收率、介质的密度等)的影响。因此,对本问题的考虑会涉及到这两个主要方面。
图1双层玻璃窗与单层玻璃窗
根据物理学知识可知,沿x轴正方向的平面波通过均匀介质,则波的强度级是波面位置x的函数,即I=I(x)。设I(0)=I0,波经过x
与x+dx两平面所夹的一层薄介质后,波的强度减少了dI,即有-dI=kIdx,其中k为介质的吸收系数。
对上式两边同时进行积分可得:
即得到:
设k1为玻璃的吸收系数,k2为空气的吸收系数;n1为玻璃折射率,n2为空气折射率。对于双层玻璃窗(如图1):声音反射率 ,由于双层玻璃间距离很小,对声音的衰减量很小,所以忽略不计,由此可得到
双层玻璃隔音问题
班级:2012级 软件4班
小组成员:周冀浩(12101020427)
游清文(12101020424)
2013-10-22
摘要
社会现代化进程的快速发展,各种机械设备的创造和使用,给人类带来了繁荣和进步,但同时也产生了越来越多而且越来越强的噪音。噪音严重影响人的生活、学习以及工作,对人的身体健康也有极大的影响。因此,怎样减少噪音成了重要的研究课题。
本题难点在于不同频率不同方向的噪音传播效果不同,即难精确计算声音损失量。而且双层玻璃间的空气会对声音产生共振减弱等作用削弱声音的传播,这也增大了对问题求解的难度。因此,课一考虑对模型作一定的理想化,忽略一些难度大影响又小的因素,而只考虑主要因素。一定程度上保证了所用方法的科学性和计算结果的合理性。
三、模型假设
,可知其差距ΔI较小,所以楼层高度对噪音的传播几乎无影响。
六、参考文献
[1]姜启元 谢金星 叶俊 《数学模型》 高等教育出版社 2011
[2]史君林涂学海吴松双层玻璃隔音效果分析模型 /view/e9b13034ee06eff9aef8077f.html
七、附录
声源到楼层的实际距离为: ,
由于声强级在空气中的衰减量公式为:
由(6)(7)式有
为方便计算,假设噪声的频率பைடு நூலகம்500Hz,则k1=0.18,玻璃厚度d为4mm,玻璃的折射率n1=1.5,空气近似真空,折射率n2=1。
于是,
穿过第一层的声强为:Ia=59.8404dB
穿过第十一层的声强为:Ib=55.1505dB
本文通过对双层玻璃与单层玻璃隔音量的比较研究双层玻璃的隔音效果,建立了在不同介质中声音的衰减模型。考虑到声音在介质中衰减的不好计算,通过微积分的方法处理得到声音强度级I0的一声波,通过为吸收系数为k厚度为d的介质的后声波所剩下的强度I,他们的关系为 ;声波传到玻璃会有一定量的反射,反射率的计算公式为 。点声源在空气中的声强级衰减公式为 。
表1 普通玻璃对几种不同频率声音的吸收系数
声音频率
125Hz
250Hz
500Hz
1000Hz
2000Hz
4000Hz
普通玻璃声音吸收系数
0.35
0.25
0.18
0.12
0.07
0.04
