11级离散数学试题(A)参考答案
离散数学试题(A卷答案)

离散数学试题(A 卷答案)一、(10分)求(P ↓Q )→(P ∧⌝(Q ∨⌝R ))的主析取范式 解:(P ↓Q )→(P ∧⌝(Q ∨⌝R ))⇔⌝(⌝( P ∨Q ))∨(P ∧⌝Q ∧R ))⇔(P ∨Q )∨(P ∧⌝Q ∧R ))⇔(P ∨Q ∨P )∧(P ∨Q ∨⌝Q )∧(P ∨Q ∨R ) ⇔(P ∨Q )∧(P ∨Q ∨R )⇔(P ∨Q ∨(R ∧⌝R ))∧(P ∨Q ∨R ) ⇔(P ∨Q ∨R )∧(P ∨Q ∨⌝R )∧(P ∨Q ∨R ) ⇔0M ∧1M⇔2m ∨3m ∨4m ∨5m ∨6m ∨7m二、(10分)在某次研讨会的休息时间,3名与会者根据王教授的口音分别作出下述判断: 甲说:王教授不是苏州人,是上海人。
乙说:王教授不是上海人,是苏州人。
丙说:王教授既不是上海人,也不是杭州人。
王教授听后说:你们3人中有一个全说对了,有一人全说错了,还有一个人对错各一半。
试判断王教授是哪里人?解 设设P :王教授是苏州人;Q :王教授是上海人;R :王教授是杭州人。
则根据题意应有: 甲:⌝P ∧Q 乙:⌝Q ∧P 丙:⌝Q ∧⌝R王教授只可能是其中一个城市的人或者3个城市都不是。
所以,丙至少说对了一半。
因此,可得甲或乙必有一人全错了。
又因为,若甲全错了,则有⌝Q ∧P ,因此,乙全对。
同理,乙全错则甲全对。
所以丙必是一对一错。
故王教授的话符号化为:((⌝P ∧Q )∧((Q ∧⌝R )∨(⌝Q ∧R )))∨((⌝Q ∧P )∧(⌝Q ∧R ))⇔(⌝P ∧Q ∧Q ∧⌝R )∨(⌝P ∧Q ∧⌝Q ∧R )∨(⌝Q ∧P ∧⌝Q ∧R ) ⇔(⌝P ∧Q ∧⌝R )∨(P ∧⌝Q ∧R ) ⇔⌝P ∧Q ∧⌝R ⇔T因此,王教授是上海人。
三、(10分)证明tsr (R )是包含R 的且具有自反性、对称性和传递性的最小关系。
证明 设R 是非空集合A 上的二元关系,则由定理4.19知,tsr (R )是包含R 的且具有自反性、对称性和传递性的关系。
(完整版)离散数学题目及答案

数理逻辑习题判断题1.任何命题公式存在惟一的特异析取范式 ( √ ) 2. 公式)(q p p →⌝→是永真式 ( √ ) 3.命题公式p q p →∧)(是永真式 ( √ ) 4.命题公式r q p ∧⌝∧的成真赋值为010 ( × ) 5.))(()(B x A x B x xA →∃=→∀ ( √ )6.命题“如果1+2=3,则雪是黑的”是真命题 ( × ) 7.p q p p =∧∨)( ( √ )8.))()((x G x F x →∀是永真式 ( × ) 9.“我正在撒谎”是命题 ( × ) 10. )()(x xG x xF ∃→∀是永真式( √ )11.命题“如果1+2=0,则雪是黑的”是假命题 ( × ) 12.p q p p =∨∧)( ( √ )13.))()((x G x F x →∀是永假式 ( × )14.每个命题公式都有唯一的特异(主)合取范式 ( √ ) 15.若雪是黑色的:p ,则q →p 公式是永真式 ( √ ) 16.每个逻辑公式都有唯一的前束范式 ( × ) 17.q →p 公式的特异(主)析取式为q p ∨⌝ ( × ) 18.命题公式 )(r q p →∨⌝的成假赋值是110 ( √ ) 19.一阶逻辑公式)),()((y x G x F x →∀是闭式( × )单项选择题1. 下述不是命题的是( A )A.花儿真美啊! B.明天是阴天。
C.2是偶数。
D.铅球是方的。
2.谓词公式(∀y)(∀x)(P(x)→R(x,y))∧∃yQ(x,y)中变元y (B)A.是自由变元但不是约束变元B.是约束变元但不是自由变元C.既是自由变元又是约束变元D.既不是自由变元又不是约束变元3.下列命题公式为重言式的是( A )A.p→ (p∨q)B.(p∨┐p)→qC.q∧┐q D.p→┐q4.下列语句中不是..命题的只有(A )A.花儿为什么这样红?B.2+2=0C.飞碟来自地球外的星球。
离散数学期末试题A答案及评分标准

--北京工商大学离散数学试卷(A)答案及评分标准题号 一 二三 四 五 六 七总分得分一、(30分)设A ={1,2,3,4},给定A 上二元关系R 如下:R ={<1,1>, <1,2>, <2,3>, <3,3>, <4,4>}请回答以下各问题:1.写出R 的关系矩阵. (3分)2.画出R 的关系图. (3分)3.求包含R 的最小的等价关系,并写出由其确定的划分. (6分)4.分别用关系矩阵表示出R 的自反闭包r (R )、对称闭包s (R ). (6分)5.求传递闭包t (R ).(写出计算步骤)(6分)6.求R 2的关系矩阵. (3分)7.集合A 上最多可以确定多少个不同的二元关系?说明理由。
(3分)[解] (1)⎪⎪⎪⎪⎪⎭⎫⎝⎛=1000010001000011R M 。
……(3分)(2) ……(3分)(3)法一:直接由等价关系与划分之间的一一对应可知,包含R 的最小等价关系为: {<1, 2>, <1, 3>, <2, 1>,<2, 3>, <3, 1> <3, 2>}∪I A , ……(3分) 对应的划分为{{1, 2, 3},{4}}. ……(6分) 法二:包含R 的最小的等价关系就是tsr (R ), 计算过程如下:⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=100001000110001110000100001000011000010001000011)(E M M R R r,100001100111001110000110001100011000010001100011][)()()(⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+=T R r R r R sr M M M ,3,10001110111011110000110011100111000011001110011)]([)()()]([2≥=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯=k M M M M k R sr R sr R sr R sr 从而,10000111011101111000011101110111100001110111011110000111011101111000011001110011432)]([)]([)]([)()(⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+++=R sr R sr R sr R sr R tsr M M M M M即}2,3,1,3,3,2,1,2,3,1,2,1{)(><><><><><><⋃=A I R tsr =包含R 的最小的等价关系, ……(3分) 故其对应的划分为{{1, 2, 3},{4}}. ……(6分) 法三:由于4=A ,包含R 的最小的等价关系就是4131211)()()()()()(----⋃⋃⋃⋃⋃⋃⋃⋃==R R R R R R R R I R rts R tsr A ,计算过程如下:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=-⋃100001100101001110000110000100011000010001000011][1TR R R R M M M ⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=-⋃10000111011101111000011001010011)][(22)(21T R R R R M M M412131)()(33)(10000111011101111000011001010011)][(---⋃⋃⋃==⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=R R R R T R R R R M M M M M 考试纪律承诺本人自愿遵守学校考试纪律,保证以诚信认真的态度作答试卷。
11级离散数学试题(A)参考答案

2011级离散数学(A)参考答案一、填空题(每小题2分,共30分)1. 设():M x x 为人, ():F x x 不吃饭。
将命题“没有不吃饭的人”符号化为:))()((x F x M x ⌝→∀ 或 ))()(((x F x m x ∧∃⌝ 。
2. 设A={1, 2, 3, 4} ,则 A 的全部2元子集共有 6 个。
3. 设p :明天是周一,q :明天是周三,r :我有课。
则命题“如果明天是周一或周三,我就有课”的符号化形式为 r q p →∨)( 。
4. 已知命题公式A 含有2个命题变项,其成真赋值为00、10、11,则其主析取范式为 320m m m ∨∨ 。
5. 设p :北京比大连人口多,q :2+2=4,r :乌鸦是白色的。
则命题公式)()(r p r q ⌝→→∨的真值为 1 。
6. 集合}3,2,1{=A 上的关系}3,2,3,1,2,1{><><><=R ,则=-1R { <2,1>,<3,1>,<3,2> }。
7. 画出下图的补图 。
8.设A={1,2,3},B={a,b,c},A 1={1},f={<1,a>,<2,a>,<3,b>},则=-))((11A f f { 1,2 }。
9. 设无向图的度数序列为:1,2,2,3,4。
则该无向图的边数m= 6 。
10. 3阶有向完全图的2条边的非同构的生成子图有 4 个。
11. 设〈≤,A 〉为偏序集,A B ⊆。
若y x B y x 与,,∈∀都是可比的,则称B是A 中的一条链,B 中的元素个数称为链的长度。
在偏序集〈{1,2,…,9},整除〉中,{1,2,4,8}是长为 4 的链。
12. 下面运算表中的单位元是 b 。
13. 写出模4加法群G=<Z 4,⊕ >的运算表14. 模4加法群中, 2-3= 2 。
离散数学试卷及答案

离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:A BC* a b c d a b c da b c d b c d a c d a b d a b c那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有( )个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是( ) A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
资料:离散数学试题 (1)

离散数学考试题库(A卷及答案)一、(10分)证明⌝(A∨B)→⌝(P∨Q),P,(B→A)∨⌝P A。
证明:(1)⌝(A∨B)→⌝(P∨Q)P(2)(P∨Q)→(A∨B) T(1),E(3)P P(4)A∨B T(2)(3),I(5)(B→A)∨⌝P P(6)B→A T(3)(5),I(7)A∨⌝B T(6),E(8)(A∨B)∧(A∨⌝B) T(4)(7),I(9)A∧(B∨⌝B) T(8),E(10)A T(9),E二、(10分)甲、乙、丙、丁4个人有且仅有2个人参加围棋优胜比赛。
关于谁参加竞赛,下列4种判断都是正确的:(1)甲和乙只有一人参加;(2)丙参加,丁必参加;(3)乙或丁至多参加一人;(4)丁不参加,甲也不会参加。
请推出哪两个人参加了围棋比赛。
解符号化命题,设A:甲参加了比赛;B:乙参加了比赛;C:丙参加了比赛;D:丁参加了比赛。
依题意有,(1)甲和乙只有一人参加,符号化为A⊕B⇔(⌝A∧B)∨(A∧⌝B);(2)丙参加,丁必参加,符号化为C→D;(3)乙或丁至多参加一人,符号化为⌝(B∧D);(4)丁不参加,甲也不会参加,符号化为⌝D→⌝A。
所以原命题为:(A⊕B)∧(C→D)∧(⌝(B∧D))∧(⌝D→⌝A)⇔((⌝A∧B)∨(A∧⌝B))∧(⌝C∨D)∧(⌝B∨⌝D)∧(D∨⌝A)⇔((⌝A∧B∧⌝C)∨(A∧⌝B∧⌝C)∨(⌝A∧B∧D)∨(A∧⌝B∧D))∧((⌝B∧D)∨(⌝B∧⌝A)∨(⌝D∧⌝A))⇔(A∧⌝B∧⌝C∧D)∨(A∧⌝B∧D)∨(⌝A∧B∧⌝C∧⌝D)⇔T但依据题意条件,有且仅有两人参加竞赛,故⌝A∧B∧⌝C∧⌝D为F。
所以只有:(A∧⌝B∧⌝C∧D)∨(A∧⌝B∧D)⇔T,即甲、丁参加了围棋比赛。
三、(10分)指出下列推理中,在哪些步骤上有错误?为什么?给出正确的推理形式。
(1)∀x(P(x)→Q(x)) P(2)P(y)→Q(y) T(1),US(3)∃xP(x) P(4)P(y) T(3),ES(5)Q(y) T(2)(4),I(6)∃xQ(x) T(5),EG解(4)中ES错,因为对存在量词限制的变元x引用ES规则,只能将x换成某个个体常元c,而不能将其改为自由变元。
离散数学期末试题及答案A

学年第二学期期末考试《离散数学》试卷( A )使用班级:命题教师:主任签字:一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1.一个连通的无向图G,如果它的所有结点的度数都是偶数,那么它具有一条( )A.汉密尔顿回路B.欧拉回路C.汉密尔顿通路D.初级回路2.设G是连通简单平面图,G中有11个顶点5个面,则G中的边是( )A.10B.12C.16D.143.在布尔代数L中,表达式(a∧b)∨(a∧b∧c)∨(b∧c)的等价式是( )A.b∧(a∨c)B.(a∧b)∨(a’∧b)C.(a∨b)∧(a∨b∨c)∧(b∨c)D.(b∨c)∧(a∨c)4.设i是虚数,·是复数乘法运算,则G=<{1,-1,i,-i},·>是群,下列是G的子群是( )A.<{1},·>B.〈{-1},·〉C.〈{i},·〉D.〈{-i},·〉5.设Z为整数集,A为集合,A的幂集为P(A),+、-、/为数的加、减、除运算,∩为集合的交运算,下列系统中是代数系统的有( )A.〈Z,+,/〉B.〈Z,/〉C.〈Z,-,/〉D.〈P(A),∩〉6.下列各代数系统中不含有零元素的是( )A.〈Q,*〉Q是全体有理数集,*是数的乘法运算B.〈Mn(R),*〉,Mn(R)是全体n阶实矩阵集合,*是矩阵乘法运算C.〈Z,ο〉,Z是整数集,ο定义为xοxy=xy,∀x,y∈ZD.〈Z,+〉,Z是整数集,+是数的加法运算7.设A={1,2,3},A上二元关系R的关系图如下:R具有的性质是A.自反性B.对称性C.传递性D.反自反性8.设A={a,b,c},A上二元关系R={〈a,a〉,〈b,b〉,〈a,c〉},则关系R的对称闭包S(R)是( )A.R∪I AB.RC.R∪{〈c,a〉}D.R∩I A9.设X={a,b,c},Ix是X上恒等关系,要使Ix∪{〈a,b〉,〈b,c〉,〈c,a〉,〈b,a〉}∪R为X上的等价关系,R应取( )A.{〈c,a〉,〈a,c〉}B.{〈c,b〉,〈b,a〉}C.{〈c,a〉,〈b,a〉}D.{〈a,c〉,〈c,b〉}10.下列式子正确的是( )A. ∅∈∅B.∅⊆∅C.{∅}⊆∅D.{∅}∈∅11.设解释R如下:论域D为实数集,a=0,f(x,y)=x-y,A(x,y):x<y.下列公式在R下为真的是( )A.( ∀x)( ∀y)( ∀z)(A(x,y))→A(f(x,z),f(y,z))B.( ∀x)A(f(a,x),a)C.(∀x)(∀y)(A(f(x,y),x))D.(∀x)(∀y)(A(x,y)→A(f(x,a),a))12.设B是不含变元x的公式,谓词公式(∀x)(A(x)→B)等价于( )A.(∃x)A(x)→BB.(∀x)A(x)→BC.A(x)→BD.(∀x)A(x)→(∀x)B13.谓词公式(∀x)(P(x,y))→(∃z)Q(x,z)∧(∀y)R(x,y)中变元x( )A.是自由变元但不是约束变元B.既不是自由变元又不是约束变元C.既是自由变元又是约束变元D.是约束变元但不是自由变元14.若P:他聪明;Q:他用功;则“他虽聪明,但不用功”,可符号化为( )A.P∨QB.P∧┐QC.P→┐QD.P∨┐Q15.以下命题公式中,为永假式的是( )A.p→(p∨q∨r)B.(p→┐p)→┐pC.┐(q→q)∧pD.┐(q∨┐p)→(p∧┐p)二、填空题(每空1分,共20分)16.在一棵根树中,仅有一个结点的入度为______,称为树根,其余结点的入度均为______。
离散数学试题及答案

离散数学考试试题(A卷及答案)一、(10分)某项工作需要派A、B、C和D 4个人中的2个人去完成,按下面3个条件,有几种派法?如何派?(1)若A去,则C和D中要去1个人;(2)B和C不能都去;(3)若C去,则D留下。
解设A:A去工作;B:B去工作;C:C去工作;D:D去工作。
则根据题意应有:A→C⊕D,⌝(B ∧C),C→⌝D必须同时成立。
因此(A→C⊕D)∧⌝(B∧C)∧(C→⌝D)⇔(⌝A∨(C∧⌝ D)∨(⌝C∧D))∧(⌝B∨⌝C)∧(⌝C∨⌝D)⇔(⌝A∨(C∧⌝ D)∨(⌝C∧D))∧((⌝B∧⌝C)∨(⌝B∧⌝D)∨⌝C∨(⌝C∧⌝D))⇔(⌝A∧⌝B∧⌝C)∨(⌝A∧⌝B∧⌝D)∨(⌝A∧⌝C)∨(⌝A∧⌝C∧⌝D)∨(C∧⌝ D∧⌝B∧⌝C)∨(C∧⌝ D∧⌝B∧⌝D)∨(C∧⌝ D∧⌝C)∨(C∧⌝ D∧⌝C∧⌝D)∨(⌝C∧D∧⌝B∧⌝C)∨(⌝C∧D∧⌝B∧⌝D)∨(⌝C∧D∧⌝C)∨(⌝C∧D∧⌝C∧⌝D)⇔F∨F∨(⌝A∧⌝C)∨F∨F∨(C∧⌝ D∧⌝B)∨F∨F∨(⌝C∧D∧⌝B)∨F∨(⌝C∧D)∨F⇔(⌝A∧⌝C)∨(⌝B∧C∧⌝ D)∨(⌝C∧D∧⌝B)∨(⌝C∧D)⇔(⌝A∧⌝C)∨(⌝B∧C∧⌝ D)∨(⌝C∧D)⇔T故有三种派法:B∧D,A∧C,A∧D。
二、(15分)在谓词逻辑中构造下面推理的证明:某学术会议的每个成员都是专家并且是工人,有些成员是青年人,所以,有些成员是青年专家。
解:论域:所有人的集合。
S(x):x是专家;W(x):x是工人;Y(x):x是青年人;则推理化形式为:∀x(S(x)∧W(x)),∃x Y(x)∃x(S(x)∧Y(x))下面给出证明:(1)∃x Y(x) P(2)Y(c) T(1),ES(3)∀x(S(x)∧W(x)) P(4)S( c)∧W( c) T(3),US(5)S( c) T(4),I(6)S( c)∧Y(c) T(2)(5),I(7)∃x S((x)∧Y(x)) T(6) ,EG三、(10分)设A、B和C是三个集合,则A⊂B⇒⌝(B⊂A)。
11-12-2离散数学A卷试题

共 3 页 第 3 页 总印
份 (附卷纸 1 页)
七、(11 分)设 Q 是有理数集合,在 Q 上定义二元运算 如下:对任意 a,b Q , ab abab,
1.证明 0 是幺元且 Q, 是独异点; 2. Q, 是否有零元?若有零元,找出其零元; 3.任意 a Q ,若 a 有逆元,找出其逆元。
C. (P Q) R D. (P R) Q
3. 设集合 A {2, 3} , B {3,4} ,下列命题_______不正确。
课程名称:离散数学 试卷类型:A 卷
考试专业、年级:计科、软件 11 级
A. K[A] K[B] B.| P( A B) | 4 C. A B {2,4} D. A B {2} 4. 设 A={1, 2, 3},R 是集合 A 上的关系, R { 1,1 , 1, 2 , 2, 3 } ,则 R 是_______。
线
学号
线
共 3 页 第 1 页 总印
份 (附卷纸 1 页)
2012 年 7 月 4 日 西安邮电大学课程考试试题(A 卷)
考试用
(2011 —— 2012 学年度第 2 学期)
2. 设 P:2 是素数,Q:3 是素数,R: 2 是有理数。下列复合命题中_______是假命题。
A. (P Q) P B. R (P Q)
eabc
e
eabc
a
abce
b
bcea
c
ceab
则在 G, 中,c 为_______阶元, G, 的生成元总共有_______个。
6. 若图 G V , E 是自对偶的,且|V | n ,则| E | _____________。
离散数学考试试题(A卷及答案)

离散数学考试试题(A 卷及答案)一、 (10 分)判断下列公式的类型(永真式、永假式、可满足式)?1)((P Q)∧Q)一 ((Q∨R)∧Q) 2)((Q P)∨P)∧ (P∨R)3)((P∨Q)R)((P∧Q)∨R)解: 1)永真式; 2) 永假式; 3)可满足式。
二、 (8 分) 个体域为{1, 2},求x3y (x+y=4)的真值。
解:x3y (x+y=4) 一 x ((x+1=4)∨(x+2=4))一((1+1=4)∨(1+2=4))∧((2+1=4)∨(2+1=4))一(0∨0)∧(0∨1)一1∧1一0三、 (8 分) 已知集合 A 和 B 且|A|=n, |B|=m,求 A 到 B 的二元关系数是多少? A 到 B 的函数数是多少?解:因为|P(A×B) |=2|A×B|=2|A| |B|=2mn,所以 A 到 B 的二元关系有 2mn 个。
因为|BA|= |B| |A|=mn,所以 A 到 B 的函数 mn 个。
四、 (10 分) 已知 A={1,2,3,4,5}和 R={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>},求 r(R) 、s(R)和 t(R)。
解: r(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<2,2>,<3,3>,<4,4>,<5,5>} s(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<3,2>,<4,3>,<4,5>}t(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<1,3>,<2,2>,<2,4>,<1,4>}五、 (10 分) 75 个儿童到公园游乐场,他们在那里可以骑旋转木马,坐滑行铁道,乘宇宙飞船,已知其中20 人这三种东西都乘过,其中 55 人至少乘坐过其中的两种。
《离散数学》2011试题及答案

解答:用Huffman算法求频率(乘以100)为权的最优2元树,其中w1=5,w2=5,w3=10,w4=10,w5=15,w6=20,w7=35;最优2元树如图所示:
故,可采取如下编码:A---11 B---01 C---101 D---100 E---001
F---0001 G---0000
传输100个按比例出现的7个字母所需二进制数字的个数为w(T)=255个,故传输10000个所用二进制数字的个数为25500个。
1.求命题公式:(PQ)(QP)的主析取范式和主合取范式。
答案:用等值演算法、真值表法均可,根据解题过程及答案正确与否酌情给分。
主吸取范式为:(PQ)(PQ)(PQ)=(0,2,3)
主合取范式为:PQ
2.设A={a,b,c,d},1、2、3是A上的划分,1={{a,b},{c,d}},2={{a},{b},{c},{d}},3={{a,b,c,d}},试求:
⑩x(F(x)R(x)G(x)) T,⑨,EG
(2)设7个字母在通信中出现的频率如下:
A:35% B:20% C:15% D:10%
E:10% F:5% G:5%
采用2元前缀码,求传输数字最少的2元码(即最小前缀码),并求传输10000个按上述比例出现的八进制数字需要多少个二进制数字?若用长为3的等长码字传输需要多少个二进制数字?
答案:QP
2.对命题公式:P(QR)PQ化为仅含和的等价表达式。
答案:(PQ)
3.设S(x):x是火车,L(x):x是卡车,F(x,y):x比y快。在谓词逻辑中符号化命题“所有火车都比所有卡车快”。
答案: x(S(x)→y(L(y) ∧F(x , y))
离散数学考试试题(A、B卷及答案)

离散数学考试试题(A卷及答案)一、证明题(10分)1) (P∧Q∧A→C)∧(A→P∨Q∨C)⇔ (A∧(P↔Q))→C。
P<->Q=(p->Q)合取(Q->p)证明: (P∧Q∧A→C)∧(A→P∨Q∨C)⇔(⌝P∨⌝Q∨⌝A∨C)∧(⌝A∨P∨Q∨C)⇔((⌝P∨⌝Q∨⌝A)∧(⌝A∨P∨Q))∨C反用分配律⇔⌝((P∧Q∧A)∨(A∧⌝P∧⌝Q))∨C⇔⌝( A∧((P∧Q)∨(⌝P∧⌝Q)))∨C再反用分配律⇔⌝( A∧(P↔Q))∨C⇔(A∧(P↔Q))→C2) ⌝(P↑Q)⇔⌝P↓⌝Q。
证明:⌝(P↑Q)⇔⌝(⌝(P∧Q))⇔⌝(⌝P∨⌝Q))⇔⌝P↓⌝Q。
二、分别用真值表法和公式法求(P→(Q∨R))∧(⌝P∨(Q↔R))的主析取范式与主合取范式,并写出其相应的成真赋值和成假赋值(15分)。
主析取范式与析取范式的区别:主析取范式里每个括号里都必须有全部的变元。
主析取范式可由析取范式经等值演算法算得。
证明:公式法:因为(P→(Q∨R))∧(⌝P∨(Q↔R))⇔(⌝P∨Q∨R)∧(⌝P∨(Q∧R)∨(⌝Q∧⌝R))⇔(⌝P∨Q∨R)∧(((⌝P∨Q)∧(⌝P∨R))∨(⌝Q∧⌝R))分配律⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝Q)∧(⌝P∨Q∨⌝R)∧(⌝P∨R∨⌝Q)∧(⌝P ∨R∨⌝R)⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝R)∧(⌝P∨⌝Q∨R)⇔4M∧5M使(非P析取Q析取R)为0所赋真值,即100,二进制M∧6为4⇔0m∨1m∨2m∨3m∨7m所以,公式(P→(Q∨R))∧(⌝P∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
真值表法:P Q R Q↔R P→(Q∨R)⌝P∨(Q↔R) (P→(Q∨R))∧(⌝P∨(Q↔R))0 0 0 0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1 1111111111111111111111由真值表可知,公式(P→(Q∨R))∧(⌝P∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
(完整版)《离散数学》试题及答案解析,推荐文档

4. 设 I 是如下一个解释:D = {2, 3},
a
b
f (2) f (3)
3
2
3
2
试求 (1) P(a, f (a))∧P(b, f (b));
WORD 整理版
一、填空题 1 设集合 A,B,其中 A={1,2,3}, B= {1,2}, 则 A - B=____________________;
(A)
- (B)= __________________________ . 2. 设有限集合 A, |A| = n, 则 |(A×A)| = __________________________. 3. 设集合 A = {a, b}, B = {1, 2}, 则从 A 到 B 的所有映射是 __________________________ _____________, 其中双射的是
专业资料学习参考
WORD 整理版
0 1 1 1 1
15. 设图 G 的相邻矩阵为 1 0 1 0 0 ,则 G 的顶点数与边数分别为(
).
1 1 0 1 1
1 0 1 0 1
1 0 1 1 0
(A)4, 5 (B)5, 6 三、计算证明题
(C)4, 10
(D)5, 8.
1.设集合 A={1, 2, 3, 4, 6, 8, 9, 12},R 为整除关系。
则在解释 I 下取真值为 1 的公式是( ).
(A)xyP(x,y) (B)xyP(x,y) (C)xP(x,x) (D)xyP(x,y). 6. 若供选择答案中的数值表示一个简单图中各个顶点的度,能画出图的是( ).
离散数学参考答案

1.(单选题)A.明年“五一”是晴天。
B.这朵花多好看呀!。
C.这个男孩真勇敢啊! D.明天下午有会吗?答题: A. B. C. D. (已提交)参考答案:A问题解析:2.(单选题) 在上面句子中,是命题的是( )A.1+101=110 B.中国人民是伟大的。
C.这朵花多好看呀! D.计算机机房有空位吗?答题: A. B. C. D. (已提交)参考答案:B问题解析:3.(单选题) 在上面句子中,是命题的是( )A.如果天气好,那么我去散步。
B.天气多好呀!C.x=3。
D.明天下午有会吗?答题: A. B. C. D. (已提交)参考答案:A问题解析:4.(单选题) 在上面句子中( )是命题下面的命题不是简单命题的是( )A.3 是素数或4 是素数B.2018 年元旦下大雪C.刘宏与魏新是同学 D.圆的面积等于半径的平方与π之积答题: A. B. C. D. (已提交)参考答案:A问题解析:5.(单选题) 下面的表述与众不一致的一个是( )A.P :广州是一个大城市 B.ØP :广州是一个不大的城市C.ØP :广州是一个很不小的城市 D.ØP :广州不是一个大城市答题: A. B. C. D. (已提交)参考答案:C问题解析:6.(单选题) 设,P:他聪明;Q:他用功。
在命题逻辑中,命题:“他既聪明又用功。
”可符号化为:()A.PÙQ B.P®QC.PÚØQ D.PÙØQ答题: A. B. C. D. (已提交)参考答案:A问题解析:7.(单选题) 设:P :刘平聪明。
Q:刘平用功。
在命题逻辑中,命题:“刘平不但聪明,而且用功”可符号化为:()A.PÙQ B.ØPÚQC.PÚØQ D.PÙØQ答题: A. B. C. D. (已提交)参考答案:A问题解析:8.(单选题)设:P:他聪明;Q:他用功。
离散数学11-12A(信管、电商)试题及答案
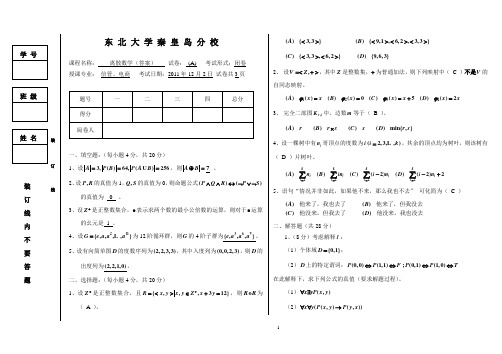
东 北 大 学 秦 皇 岛 分 校课程名称: 离散数学(答案) 试卷: (A) 考试形式:闭卷 授课专业: 信管、电商 考试日期:2011年12月2日 试卷共3页一、填空题:(每小题4分,共20分)1、设3,()64,()256 A P B P A B ===,则A B ⊕=7 。
2、设,P R 的真值为1,,Q S 的真值为0,则命题公式()()P Q R P S ∧∧↔⌝∨⌝的真值为 0 。
3、设Z +是正整数集合,*表示求两个数的最小公倍数的运算,则对于*运算的幺元是 1 。
4、设211{,,,,}G e a a a = 为12阶循环群,则G 的4阶子群为369{,,,}e a a a 。
5、设有向简单图D 的度数序列为(2,2,3,3),其中入度列为(0,0,2,3),则D 的出度列为(2,2,1,0)。
二、选择题:(每小题4分,共20分)1、设Z +是正整数集合,且{,,,312}R x y x y Z x y +=<>∈+=,则 R R 为( A )。
(){3,3}(){9,1,6,2,3,3}A B <><><><> (){3,3,6,2}(){9,6,3}C D <><>2、 设,V Z =<+>,其中Z 是整数集,+为普通加法,则下列映射中( C )不是V 的自同态映射。
1234()()()()0()()5()()2A x x B x C x x D x x ϕϕϕϕ===+= 3、 完全二部图,r s K 中,边数m 等于( B )。
()()()()min{,}A rB r sC sD r s ⨯4、设一棵树中有i n 哥顶点的度数为(2,3,,) i i k =,其余的顶点均为树叶,则该树有( D )片树叶。
2222()()()(2)()(2)2kkkkiiiii i i i A nB inC i nD i n ====--+∑∑∑∑5、语句“情况并非如此,如果他不来,那么我也不去” 可化简为( C )()()()()A B C D 他来了,我也去了他来了,但我没去他没来,但我去了他没来,我也没去二、解答题(共28分)1、(8分)考虑解释I : (1)个体域{0,1}D =;(2)D 上的特定谓词:(0,0)(1,1);(0,1)(1,0)P P F P P T ⇔⇔⇔⇔ 在此解释下,求下列公式的真值(要求解题过程)。
离散数学试题A卷及答案

离散数学试题A卷及答案一、单项选择题(每题2分,共10分)1. 在集合{1,2,3}中,子集的个数是多少?A. 3B. 7C. 8D. 9答案:C2. 以下哪个命题是真命题?A. ∃x∈R, x^2 = -1B. ∀x∈R, x^2 ≥ 0C. ∀x∈R, x^2 = 1D. ∃x∈R, x^2 = 2答案:B3. 函数f: N → N定义为f(x) = 2x,该函数是:A. 单射B. 满射C. 双射D. 非函数答案:A4. 以下哪个逻辑表达式等价于p∧(q∨¬p)?A. p∧qB. p∨qC. ¬p∨qD. p∧¬p答案:A5. 以下哪个图是二分图?A. 完全图K5B. 完全二分图K3,3C. 环图C5D. 星形图K1,4答案:B二、填空题(每题3分,共15分)1. 若A={1,2,3},B={2,3,4},则A∩B=______。
答案:{2,3}2. 命题“若x>0,则x^2>0”的逆否命题是:若x^2≤0,则______。
答案:x≤03. 在一个有向图中,若存在从顶点u到顶点v的有向路径,则称v可到达u,若图中每个顶点都可到达其他所有顶点,则称该有向图是______。
答案:强连通的4. 一个集合的幂集包含该集合的所有______。
答案:子集5. 在逻辑中,合取(AND)操作符用符号______表示。
答案:∧三、解答题(每题10分,共20分)1. 证明:若A⊆B且B⊆C,则A⊆C。
证明:设x∈A,则由A⊆B,可得x∈B。
又由B⊆C,可得x∈C。
因此,A⊆C。
2. 给定一个图G,包含顶点集V={v1, v2, v3, v4}和边集E={(v1,v2), (v2, v3), (v3, v4), (v4, v1), (v1, v3), (v2, v4)},请判断该图是否是欧拉图,并说明理由。
答案:该图是欧拉图。
因为该图是连通的,且每个顶点的度都是偶数。
结束语:本试题涵盖了离散数学中的基本概念和原理,通过这些题目的练习,可以加深对离散数学知识的理解。
离散数学试题与参考答案

《离散数学》试题及答案一、选择题:本题共5小题,每小题3分,共15分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 命题公式Q Q P →∨)(为 ( )(A) 矛盾式 (B) 可满足式 (C) 重言式 (D) 合取范式2.设P 表示“天下大雨”, Q 表示“他在室内运动”,则命题“除非天下大雨,否则他不在室内运动”符号化为( )。
(A). P Q →; (B).P Q ∧; (C).P Q ⌝→⌝; (D).P Q ⌝∨.3.设集合A ={{1,2,3}, {4,5}, {6,7,8}},则下式为真的是( )(A) 1∈A (B) {1,2, 3}⊆A(C) {{4,5}}⊂A (D) ∅∈A4. 设A ={1,2},B ={a ,b ,c },C ={c ,d }, 则A ×(B ⋂C )= ( )(A) {<1,c >,<2,c >} (B) {<c ,1>,<2,c >} (C) {<c ,1><c ,2>,} (D) {<1,c >,<c ,2>}5. 设G 如右图:那么G 不是( ). (A)哈密顿图; (B)完全图;(C)欧拉图; (D) 平面图.二、填空题:本大题共5小题,每小题4分,共206. 设集合A ={∅,{a }},则A 的幂集P (A )=7. 设集合A ={1,2,3,4 }, B ={6,8,12}, A 到B 的关系R =},,2,{B y A x x y y x ∈∈=><,那么R -1=8. 在“同学,老乡,亲戚,朋友”四个关系中_______是等价关系.9. 写出一个不含“→”的逻辑联结词的完备集 .10.设X ={a ,b ,c },R 是X 上的二元关系,其关系矩阵为 M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001001101,那么R 的关系图为三、证明题(共30分)11. (10分)已知A 、B 、C 是三个集合,证明A ∩(B ∪C)=(A ∩B)∪(A ∩C)12. (10分)构造证明:(P →(Q →S))∧(⌝R ∨P)∧Q ⇒R →S13.(10分)证明(0,1)与[0,1),[0,1)与[0,1]等势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011级离散数学(A)参考答案一、填空题(每小题2分,共30分)1. 设():M x x 为人, ():F x x 不吃饭。
将命题“没有不吃饭的人”符号化为:))()((x F x M x ⌝→∀ 或 ))()(((x F x m x ∧∃⌝ 。
2. 设A={1, 2, 3, 4} ,则 A 的全部2元子集共有 6 个。
3. 设p :明天是周一,q :明天是周三,r :我有课。
则命题“如果明天是周一或周三,我就有课”的符号化形式为 r q p →∨)( 。
4. 已知命题公式A 含有2个命题变项,其成真赋值为00、10、11,则其主析取范式为 320m m m ∨∨ 。
5. 设p :北京比大连人口多,q :2+2=4,r :乌鸦是白色的。
则命题公式)()(r p r q ⌝→→∨的真值为 1 。
6. 集合}3,2,1{=A 上的关系}3,2,3,1,2,1{><><><=R ,则=-1R { <2,1>,<3,1>,<3,2> }。
7. 画出下图的补图 。
8.设A={1,2,3},B={a,b,c},A 1={1},f={<1,a>,<2,a>,<3,b>},则=-))((11A f f { 1,2 }。
9. 设无向图的度数序列为:1,2,2,3,4。
则该无向图的边数m= 6 。
10. 3阶有向完全图的2条边的非同构的生成子图有 4 个。
11. 设〈≤,A 〉为偏序集,A B ⊆。
若y x B y x 与,,∈∀都是可比的,则称B是A 中的一条链,B 中的元素个数称为链的长度。
在偏序集〈{1,2,…,9},整除〉中,{1,2,4,8}是长为 4 的链。
12. 下面运算表中的单位元是 b 。
13. 写出模4加法群G=<Z 4,⊕ >的运算表14. 模4加法群中, 2-3= 2 。
15. 设群>⊕=<}),.({b a P G ,其中⊕为对称差。
群方程 {a }⊕X =∅ 的解X = {a} 。
二、试解下列各题(每小题5分,共25分)1. 给定解释I 如下:(a )个体域D={1,2}.(b )(,)F x y -为(1,1)(2,2)0,(1,2)(2,1)1F F F F ----====.试求公式:(,)(,)x yF x y x yF x y ∃∀∨∀∃在I 下的真值。
解:)01()10())2,2()1,2(())2,1()1,1((),2(),1(),(⇔∧∨∧⇔∧∨∧⇔∀∨∀⇔∀∃F F F F y yF y yF y x yF x(2分)1)01()10())2,2()1,2(())2,1()1,1((),2(),1(),(⇔∨∧∨⇔∨∧∨⇔∃∧∃⇔∃∀F F F F y yF y yF y x yF x(2分)所以:(,)(,)x yF x y x yF x y ∃∀∨∀∃=1 (1分)2. 用等值演算法求公式 (⌝p →q ) →(⌝ q ∨ p )的主析取范式,并求成真赋值。
解:320)()()()()()()()()()()()(m m m q p q p q p q p q p pq q p p q q p p q q p p q q p ∨∨⇔⌝∧∨∧∨⌝∧⌝∨⌝∧∨⌝∧⌝⇔∨⌝∨⌝∧⌝⇔∨⌝∨∨⌝⇔∨⌝→∨⇔∨⌝→→⌝(4分)成真赋值为:00,10,11 (1分)3. 无向图G 有11条边,2,3,4,5,6度顶点各1个,其余顶点均为悬挂顶点,求G 中悬挂顶点的个数。
解:总度数=2+3+4+5+6+x=x+20=2*11=22; (4分) 所以:x=2,即悬挂顶点个数为2。
(1分)4. 设A={1,2,3,4,5,6,7,8,9,10,11,12,24},偏序集≤>=<,A S ,其中≤为整除关系。
画出哈斯图并找出子集{4,6}的上界、下界、最小上界和最大下界。
(3分)上界:12,24;下界:2,1;最小上界:12;最大下界:2。
(2分)5. 设A={1,2},B 是A 上的等价关系的集合。
列出B 的元素并给出代数系统>⋂=<,B V 的运算表。
集合:},{A A E I B = (1分)(4分)三、计算题(每小题5分,共20分)1. 2)(,323)(,:,:2+=⎩⎨⎧<-≥=→→x x g x x x x f R R g R R f 设,求g f 。
解:R R g f →: ⎩⎨⎧<≥+=332)(2x x x x g f (5分)2. 设},,,,,{f e d c b a A =,R 是A 上的二元关系,且},,,,,{><><><=f e c a b a R 。
设)(*R t s r R =(R 的自反对称传递闭包),则*R 是A 上的等价关系。
试画出*R 的关系图并求商集*/R A 。
(3分)商集*/R A ={{a,b,c},{d},{e,f}} (2分)3. 设有向图>=<E V D ,,其中},,,{4321v v v v V =,其邻接矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0100100001000121A 试求D 中各顶点的入度和出度,并求出D 中1v 到4v 长度为3的通路有多少条。
解:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0121A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10000100100013212A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=01001000010034213A (3分) 出度列:4,1,1,1。
入度列:1,2,3,1。
(1分)1v 到4v 长度为3的通路有3条。
(1分)4. 求下面所示图中的最小生成树并给出最小生成树的权。
并说明该图中有欧拉通路和欧拉回路吗?(3分)权重W=12, 有欧拉通路,没有欧拉回路。
(2分)四、证明题(本题共25分) 1. 在自然推理系统中,构造下面推理的证明。
(10分)如果我的程序通过,那么我很快乐。
如果我快乐,那么阳光很好。
现在阳光不好,所以,我的程序没有通过。
符号化:p :我的程序通过;q :我很快乐;r :阳光很好。
(2分) 前提:r r q q p ⌝→→,,结论:p ⌝ (2分) 证明: ○1 r q → 前提引入○2 r ⌝ 前提引入 ○3 q ⌝ ○1○2拒取式 ○4 q p → 前提引入○5 p ⌝ ○3○4拒取式 (6分) 2. 设++⨯=Z Z A ,在A 上定义二元关系如下:R v u y x >>∈<><<,,, 当且仅当yu xv =,证明R 是一等价关系。
(10分) 证明:自反性:任取><y x ,,则R y x y x yx xy Z Z y x >>∈<>⇒<<=⇒⨯>∈<++,,,, (3分)对称性:任取++⨯>∈<><Z Z v u y x ,,,,则R y x v u vx uy yu xv R v u y x >>∈<>⇒<<=⇒=⇒>>∈<><<,,,,,, (3分)传递性:任取++⨯>∈<><><Z Z t w v u y x ,,,,,,则R t w y x yw xt twy x t w v u v u y x vw ut yu xv Rt w v u R v u y x >>∈<>⇒<<=⇔=⇒=∧=⇒=∧=⇒>>∈<><<∧>>∈<><<,,,,,,,,, (4分)3. 某二进制码的码字7654321x x x x x x x x =由7位构成,其中4321,,x x x x 和为数据位,765,x x x 和为校验位,并且满足3215x x x x ⊕⊕=,4216x x x x ⊕⊕=,4317x x x x ⊕⊕=,这里⊕是模2加法。
设G 为所有码字构成的集合,在G上定义二元运算如下:7,...,2,1,,,,7654321=⊕==∈∀i y x z z z z z z z z y x G y x i i i o证明><o ,G 构成半群。
(5分)证明:任取721721,y y y y x x x x ==,721z z z y x =。
首先验证 3215z z z z ⊕⊕=555321321332211321)()()()()(z y x y y y x x x y x y x y x z z z =⊕=⊕⊕⊕⊕⊕=⊕⊕⊕⊕⊕=⊕⊕从而验证了封闭性。
(3分) 任取G z y x ∈,,,令721,721)()(b b b z y x a a a z y x ==由于⊕运算满足结合律,因此有i i i i i i i i b z y x z y x a =⊕⊕=⊕⊕=)()( (2分)从而证明了G 中运算满足结合律。
