计量经济学 第二版 庞皓 第九章 设定误差与测量误差
(完整word版)《计量经济学》第二版-庞皓-试卷2

2009第一学期《计量经济学》试卷一、填空题(20%, 每空1分)1.计量经济学是以 为指导, 以 为依据, 以 为方法, 以计算机专用软件为手段, 研究经济关系和经济活动的 规律及其应用, 并以建立和应用经济数学模型为核心的一门经济学学科。
2、对于计量经济模型的检验的内容, 一般分为四种形式的检验: 、 、 和 。
3.在计量经济学中线性模型的“线性”有两种解释: 一是模型就 而言是线性的, 二是模型就 而言是线性的。
在计量经济学中, 从回归理论的发展和参数的估计方法考虑, 通常是就 而言来判断是否线性回归模型。
4.简单线性回归模型的五条基本假定是: (1) ;(2) ; (3) ;(4) ;(5) 。
5.根据高斯-马尔可夫定理, 最小二乘估计具有四个性质: (1) 、(2) 、(3) 、(4) 。
二、判断题(10%, 每题1分, 请将×或√写在表格中, 否则该题不得分。
) 1.( )经典线性回归模型 的零均值假设是指 。
2.( )对经济计量模型进行的各种检验中, 经济准则检验是第一位的, 如果经济准则检验无效, 则只能放弃模型。
3.( )如果可决系数r2等于0.8, 说明在总变差中有80%是可以由所拟合的回归直线作出解释的。
4.( )当估计标准误差s =0时, 说明被解释变量的观测值Yi 与回归估计值Ŷi 完全一致。
5.( )若X 与Y 为函数关系, 则相关系数| r|=1。
6、( )对于单个回归系数进行t -检验, 目的在于检验参数的估计量是否等于参数真值。
7、( )描述产品平均成本(Y )依存产品产量(X )而变动的关系, 适宜配合倒数变换模型 。
8、( )依据样本资料计算的相关系数r 是一个随机变量。
9、( )在使用横截面数据进行经济计量分析时, 要求指标统计的对象及其范围必须相同。
10、( )在经济计量研究中, 有时引入滞后内生变量作为解释变量, 作为解释变量的滞后内生变量是非随机变量。
计量经济学(庞皓_第二版)课后习题及答案(1)
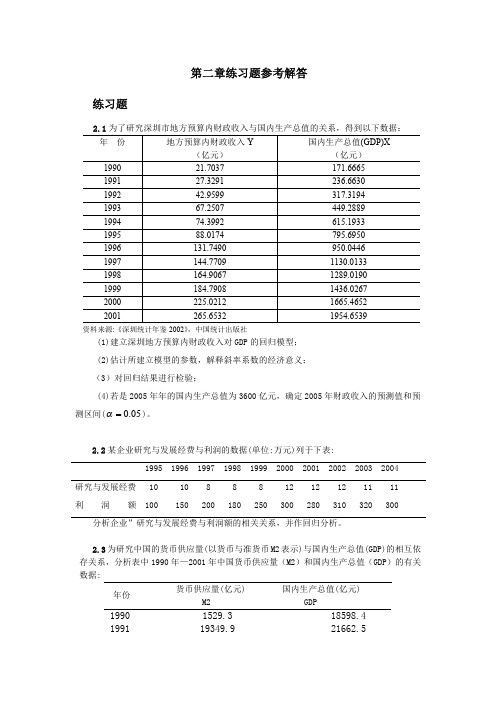
Yf 个别值置信度 95%的预测区间为:
∑ ^
^
Yf m tα 2 σ
1+ 1 + (X f − X )2
n
xi2
即
480.884 m 2.228× 7.5325× 1+ 1 + 7195337.357
12 3293728.494
= 480.884 m 30.3381 (亿元)
练习题 2.3 参考解答 计算中国货币供应量(以货币与准货币 M2 表示)与国内生产总值(GDP)的相关系数为
Yˆ2005 = −3.611151 + 0.134582 × 3600 = 480.884 (亿元)
区间预测:
∑ 平均值为:
xi2
=
σ
2 x
(n
−1)
=
587.26862
× (12
−1)
=
3793728.494
( X f 1 − X )2 = (3600 − 917.5874)2 = 7195337.357
测区间(α = 0.05 )。
2.2 某企业研究与发展经费与利润的数据(单位:万元)列于下表: 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
研究与发展经费 10 10 8 8 8 12 12 12 11 11 利 润 额 100 150 200 180 250 300 280 310 320 300
Yˆi = 6.017832 − 0.070414 × 80 = 0.384712 (次)
练习题 2.7 参考解答
美国软饮料公司的广告费用 X 与销售数量 Y 的散点图为
说明美国软饮料公司的广告费用 X 与销售数量 Y 正线性相关,可建立线性回归模型
计量经济学复习提纲—庞皓版

第一章1.计量分析的四个步骤:模型设定——参数估计——模型检验——模型应用2.计量模型检验:经济意义检验——统计推断检验——计量经济学检验——模型预测检验3.计量模型的应用:结构分析——经济预测——政策评价——检验与发展经济理论4.正确选择解释变量的原则:符合理论、规律——忽略众多次要因素,突出主要经济变量——数据可得性——每个解释变量之间是独立的5.参数的数据类型:时间序列数据——截面数据——面板数据——虚拟变量数据第二章1.总体相关系数:ρ=Cov(X,Y)/√Var(X)√Var(Y)2.样本相关系数:rxy=Σ(Xi-X_)(Yi-Y_)/√Σ(Xi-X_)^2√Σ(Yi-Y_)^23.总体回归函数中引入随机扰动项的原因:作为未知影响因素的代表——作为无法取得数据的已知因素代表——作为众多细小影响因素的综合代表——模型的设定误差——变量的观测误差——经济现象的内在随机性4.简单线性回归模型的基本假定:1、对变量和模型的假定;2、对随机扰动项ui统计分布的假定(古典假定):零均值假定——同方差假定——无自相关假定——随机扰动项ui与解释变量Xi不相关——正态性假定5.违反零均值假定:影响截距上的估计(影响小)6.违反正态性假定:不影响OLS估计是最佳无偏性,但会使t检验F检验失真(影响大)7.样本回归函数的离差形式:yi^=β2^*xi8.OLS估计值的离差表达式:β2^=Σ(Xi-X_)(Yi-Y_)/Σ(Xi-X_)^2=Σxiyi/Σxi^2β1^=Y_-β2^*X_9.OLS回归线的性质:样本回归线过(X_,Y_)——估计值均值等于实际值均值——剩余项ei的均值为零——Cov(Yi^,ei)=0——Cov(Xi,ei)=010.β^的评价标准:无偏性——有效性——一致性11.β^的统计性质:线性——无偏性——有效性12.Var(^β1)=Ơ^2/Σxi^2——Var(^β2)=ΣXi^2/n*Ơ^2/Σxi^213.^Ơ^2=Σei^2/(n-2)14.总变差平方和:Σ(Yi-Y_)^2=Σyi^2……TSS……n-1回归平方和:Σ(Yi^-Y_)^2=Σ^yi^2……ESS……k-1残差平方和:Σ(Yi-Yi^)^2=Σei^2……RSS……n-k15.可决系数:R^2=ESS/TSS16.SE(^β1)=√(Ơ^2ΣXi^2)/(nΣxi^2)SE(^β2)=√Ơ^2/Σxi^217.t=(^β1-β1)/^SE(^β1)~t(n-2)t=(^β2-β2)/^SE(^β2)~t(n-2)18.区间估计:1.当总体方差Ơ^2已知,α=0.1—±1.645,α=0.05—±1.96,α=0.01—±2.33,P[-tα<z=(^β2-β2)/^SE(^β2)<tα]=1-α2.当总体方差Ơ^2未知,样本容量大,可用^Ơ^2=Σei^2/(n-2)代替Ơ^2,z=(^β2-β2)/(^Ơ/√Σxi^2)3.当总体方差Ơ^2未知,样本容量小,P[-tα/2<t=(^β2-β2)/^SE(^β2)<tα/2]=1-α19.对Y平均值的区间预测:SE(^Yf)=Ơ√{1/n+[(Xf-X_)^2/Σxi^2]},置信度1-α的预测区间[^Yf-tα/2*SE(^Yf),^Yf+tα/2*SE(^Yf)]20.对Y个别值预测区间:Yf=^Yf±tα/2*^Ơ√{1+1/n+[(Xf-X_)^2/Σxi^2]}第三章1.多元线性回归模型的古典假定:零均值假定——同方差和无自相关假定——随机扰动项与解释变量不相关——无多重共线性假定——正态性假定2.修正的可决系数:_R^2=1-(1-R^2)(n-1)/(n-k)……k是待估参数个数,R^2必定为正,但修正的可决系数可能为负,这是规定其为0,随着k的增加,_R^2越来越小于R^23.F=ESS(k-1)/RSS(n-k)=R^2/(1-R^2)*(n-k)/(k-1)4.S.E.of regression:Ơ^2=Σei^2/(n-k)——Ơ=5.t-statistic=coefficient/std.error6.TSS=(n-1)*(S.D.dependent var)^2第四章1.多重共线性产生的原因:经济变量之间具有共同变化趋势——模型中包含滞后变量——利用截面数据建立模型也可能出现多重共线性——样本数据自身的原因2.完全多重共线性产生的后果:参数的估计值不确定——参数估计值得方差无限大3.不完全多重共线性后果:参数估计值的方差和协方差增大——对参数区间估计时,置信区间趋于变大——严重多重共线性时,假设检验容易作出错误判断——参数估计经济含义不合理。
计量经济学课件(庞浩版)

劳动经济学中经常运用联立方程模型来研究劳动力市场中 的各种问题,如工资决定、就业与失业、劳动力流动等。 例如,可以构建一个包含工资方程和就业方程的联立方程 模型,以分析最低工资制度对就业和工资水平的影响。
06
CATALOGUE
面板数据计量经济学模型
面板数据基本概念与特点
面板数据定义
面板数据是指在时间序列上取多个截面,在这些截面上同时选取样本观测值所构成的样 本数据。
面板数据模型估计方法及应用举例
估计方法
面板数据模型的估计方法主要有最小二乘法 、广义最小二乘法和极大似然法等。
应用举例
面板数据模型在经济学、金融学、社会学等 领域有广泛的应用,如经济增长、劳动力市 场、金融市场、环境经济学等问题的研究。 例如,可以利用面板数据模型研究不同国家 经济增长的影响因素,或者分析某个政策对 不同地区或不同群体的影响效果。
模型设定
多元线性回归模型是描述多个自变量与一 个因变量之间线性关系的模型,形式为 Y=β0+β1X1+β2X2+...+βkXk+u。
假设ห้องสมุดไป่ตู้验
对各个自变量的回归系数进行假设检验, 判断其是否显著不为零。
参数估计
通过最小二乘法等方法对模型中的参数进 行估计,得到各个自变量的回归系数估计 值。
多重共线性问题
采用逐步回归法、岭回归法、主成分分析法等方法对多重 共线性进行修正,同时也可以通过增加样本容量或收集更 多信息来缓解多重共线性的影响。
04
CATALOGUE
时间序列计量经济学模型
时间序列基本概念与性质
时间序列定义
按时间顺序排列的一组数据,反映现象随时间 变化的发展过程。
计量经济学-(西南财大)庞皓-博导

●计量经济学对经济关系要作出定量的估计,
对经济理论提出经验的内容
18
2、计量经济学与经济统计学的关系
联系:
●经济统计侧重于对社会经济现象的描述性计量
●经济统计提供的数据是计量经济学据以估计参
数、验证经济理论的基本依据
●经济现象不能作实验,只能被动地观测客观经 济现象变动的既成事实,只能依赖于经济统计 数据
假定条件经常不能满足,需要建立一些专门的
经济计量方法
21
第二节 计量经济学的研究方法
需要做的工作
选择变量和数学关系式 —— 模型设定
确定变量间的数量关系 —— 估计参数
检验所得结论的可靠性 —— 模型检验
作经济分析和经济预测 —— 模型应用
22
一、模型设定
经济模型及设定
模型:对经济现象或过程的一种数学模拟 设定(Specification):
数据的要求:
真实性、完整性、可比性
37
四、计量经济模型的建立
经济模型是对实际经济现象或过程的一种数学模
拟,是对复杂经济现象的简化与抽象 特点:只能在一定假定前提下 忽略次要因素,突出主要因素
38
可利用来建立计量经济模型的关系:
行为关系(如生产、投资、消费)
生产技术关系 (如投入产出关系)
制度关系(如税率) 定义关系 计量经济模型的数学形式: 线性模型:如 非线性模型:如
8
特点
计量经济学的重要特点是它自身并没有固定的 经济理论,计量经济学中的各种计量方法和技 术,大多来自数学和统计学。
计量经济学产生的意义
从定性研究到定量分析的发展,是经济学更精 密、更科学的表现,是现代经济学的重要特征
计量经济学西南财大庞皓博导

●理论与方法的新突破
除了经典线性计量经济学模型以外,出现 非线 性模型、合理预期模型、非参数、半参数模型、 动态模型、时间序列模型、协整理论、Panel Data数据模型、贝叶斯方法、小样本理论等 新的研究领域
11
二、计量经济学的性质
若干代表性表述:
●“计量经济学是统计学、经济学和数学的结合。” (弗瑞希)
13
注意:计量经济研究的三个方面
理论:即说明所研究对象经济行为的经济理论 ——计量经济研究的基础
数据:对所研究对象经济行为观测所得到的信息 ——计量经济研究的原料或依据
方法:模型的方法与估计、检验、分析的方法 ——计量经济研究的工具与手段
三者缺一不可
14
计量经济学研究的基本概述:
经济 数量化 经济
表现经济变量相互依存程度的、决定经济结 构和特征的、相对稳定的因素,通常不能直 接观测。
24
设定计量经济模型的基本要求
●要有科学的理论依据 ●选择适当的数学形式
类型: 单一方程、联立方程 线性形式、非线性形式
● 模型要兼顾真实性和实用性
两种不好的模型: 太过复杂—真实但不实用 过分简单—不真实
● 包含随机误差项
●“计量经济学是用数学语言来表达经济理论,以便通 过统计方法来论述这些理论的一门经济学分支。” (美国现代经济词典)
●“计量经济学可定义为:根据理论和观测的事实,运 用合适的推理方法使之联系起来同时推导,对实际经 济现象进行的数量分析。” (萨谬尔逊等)
各种表述的共性:
计量经济学与经济理论、统计学、数学都有关系
43
第二章 简单线性回归模型
本章主要讨论:
●回归分析与回归函数 ●简单线性回归模型参数的估计 ●拟合优度的度量 ●回归系数的区间估计和假设检验 ●回归模型预测
计量经济学-设定误差与测量误差

设正确的模型为:
Yi 1 2 X 2i 3i X 3i ui
正确模型离差形式为:
yi 2 x2i 2 x3i (ui - u )
15
却对方程 Yi 1 2 X 2i i 进行回归,得: 取期望
计量经济学
第 九 章 设定误差与测量误差
1
引子:简单一定胜于复杂吗?
西方国家盛行奥卡姆剃刀(Occam`s razor)原则,威廉修士称原理为“如 无必要,勿增实体”(意思是“简单优于复杂”的节约性原则)。这一原 理最常见的形式是:如果你有两个原理,它们都能解释观测到的事实, 那么你应该使用简单的那个,直到发现更多的证据。(经济原理、吝啬 定律、朴素原则)。经济模型永远无法完全把握现实,在建立模型中一 定的抽象和简化是不可避免的。 在研究进口与国内生产总值的关系时,考虑到时间趋势,建立并估计了 以下模型
对模型的设定是计量经济研究的重要环节。 前面各章除了对随机扰动项 ui 分布的基本假定以 外,还强调:
假定设定的模型对变量和函数形式的设定是
正确地描述被解释变量与解释变量之间的真实关
系,假定模型中的变量没有测量误差。
但是在实际的建模实践中,对模型的设定不一定
能够完全满足这样的要求,从而会使模型出现设
10
1. 相关变量的遗漏
(Omitting Relevant Variables)
例如,如果“正确”的模型为
Yi 1 2 X 2i 3 X 3i i
而我们将模型设定为
Yi 1 2 X 2i i
即设定模型时漏掉了一个相关的解释变量。 这类错误称为遗漏相关变量(“欠拟合”)。
第九章_设定误差

DW检验步骤如下: 1、对设定的回归模型运用OLS估计得残差序列 ei ; 2、假设 H0:未遗漏相关变量,H1:遗漏相关变量 ; 3、计算DW统计量: n 2 ( e e ) i i 1 DW i 2 n 2 e i
i 1
4、查DW表,得临界值dL和dU,进行判断,如 果DW值显著,则拒绝原假设,表明遗漏了 重要的解释变量,否则,表明没有遗漏。
变量设定误差主要有两类: 相关变量的遗漏(欠拟合) 无关变量的误选(过拟合)
9
1、遗漏相关变量(欠拟合)的后果
把采用遗漏了重要解释变量的模型进行估计而带 来的偏误,称为遗漏相关变量误差。
假定真实模型为: Yi =β1 +β2 X2i +β3X3i + ui 但因某种原因遗漏了解释变量 X3,而将模型设为:
Yi X i ei ui X i vi
为使问题简化,假定
2 e ~ N ( 0 , ui ~ N (0, ), i e )
(2)
2 u
且 ui 和 ei 是不相关的,于是
var( ui ei )
2 v 2 u
2 e
因此,如果用OLS分别估计(1)和(2)式,得
25
一、测量误差的后果
1、被解释变量的测量误差 设真实的模型为
Yi X i u i
*
(1)
其中Yi* 为被解释变量的理论值,Xi为解释变量的理 论值。 假设由于某种原因,被解释变量的观测值 Yi 与理论 值之间存在一个测量误差 ei ,即
Yi Yi* ei
26
于是上述模型相应变为
Yi =α1 +α2X2i + vi
庞皓《计量经济学》(第4版)配套题库(考研真题精选+章节题库)

三、简答题 1计量经济学中常用的样本数据有哪几种?请分别举例说明。 答:常用的样本数据有三类:时间序列数据、截面数据和面板数据。 (1)时间序列数据是一个或多个变量按照时间先后排列的统计数据,例如近20年全国的GDP、各年的 商品零售总额、年进出口总额等; (2)截面数据是一个或多个变量发生在同一时间截面上的调查数据,例如2000年人口普查数据、 2008年的经济普查数据等; (3)面板数据指在时间序列上取多个截面,在这些不同截面上同时选取样本观测值所构成的样本数 据,反映了空间和时间两个维度的经验信息。例如,我国1000个上市公司2000年至2014年的市值,共 15000个数据构成的样本数据。
内容简介
本书是庞皓《计量经济学》(第4版)教材的配套题库,主要包括以下内容: 第一部分为考研真题精选。本部分精选了名校的考研真题,按照题型分类,并提供了详解。通过本部 分,可以熟悉考研真题的命题风格和难易程度。 第二部分为章节题库。结合国内多所知名院校的考研真题和考查重点,根据该教材的章目进行编排 ,精选典型习题并提供详细答案解析,供考生强化练习。
二、判断题 1计量经济学是一门应用数学学科。( ) 【答案】× 【解析】计量经济学是经济学的一个分支学科,即它是一门经济学科,而不是应用数学或其他学科。
2人口普查数据属于时间序列数据。( )
【答案】× 【解析】时间序列数据是一个或多个变量按照时间先后排列的统计数据,而“人口普查数据”是一个 或多个变量发生在同一时间截面上的调查数据,即属于截面数据。
2由间接最小二乘法与两阶段最小二乘法得到的估计量都是无偏估计量。( )[北航2010研] 【答案】× 【解析】对于简化式模型应用普通最小二乘法得到的参数估计量具有线性、无偏性、有效性。通过参 数关系体系计算得到结构方程参数估计量在小样本下是有偏的,在大样本下是无偏的。采用两阶段最 小二乘法得到结构方程的参数估计量在小样本下是有偏的,在大样本下是渐近无偏的。
计量经济学(庞皓)课后思考题规范标准答案

2.4为什么在对参数作最小二乘估计之前,要对模型提出古典假设?
答:在对参数作最小二乘估计之前,要对模型提出古典假设。因为模型中有随机扰动,估计的参数是随机变量,只有对随机扰动的分布作出假定,才能确定所估计参数的分布性质,也才可能进行假设检验和区间估计。只有具备一定的假定条件,所作出的估计才具有较好的统计性质。
在简单线性回归中,可决系数越大,说明在总变差中由模型作出了解释的部分占的比重越大,X对Y的解释能力越强,模型拟合优度越好。对参数的t检验是判断解释变量X是否是被解释变量Y的显著影响因素。二者的目的作用是一致的。
2.7有人说:“得到参数区间估计的上下限后,说明参数的真实值落入这个区间的概率为 。”如何评论这种说法?
一般来说参数是未知的,又是不可直接观测的。由于随机误差项的存在,参数也不能通过变量值去精确计算。只能通过变量样本观测值选择适当方法去估计。
1.10你能分别举出三个时间序列数据、截面数据、面板数据、虚拟变量数据的实际例子,并分别说明这些数据的来源吗?
答:时间序列数据:中国1981年至2010年国内生产总值,可从中国统计年鉴查得数据。
庞皓计量经济学课后答案第九章
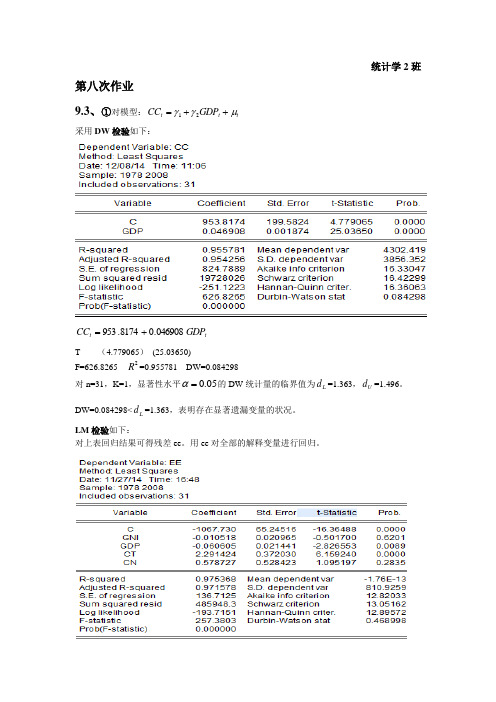
统计学2班第八次作业9.3、①对模型:t t t GDP CC μγγ++=21采用DW 检验如下:t t GDP CC 046908.08174.953+=T (4.779065) (25.03650)F=626.8265 2R =0.955781 DW=0.084298对n=31,K=1,显著性水平05.0=α的DW 统计量的临界值为L d =1.363,U d =1.496。
DW=0.084298<L d =1.363,表明存在显著遗漏变量的状况。
LM 检验如下:对上表回归结果可得残差ee 。
用ee 对全部的解释变量进行回归。
得2R =0.975368,n 2R =31*0.975368=30.236408>)3(205.0χ,所以拒绝原假设,认为受约束模型不成立。
②i i i GDP GNI ω+=*,对实证分析模型t t t GDPCC εγγ++=21进行误差检验。
将GDP 对GNI 进行回归将所得到的残差带入t t t GDP CC εγγ++=21再回归,得到以下结果i t t GDP CC ωˆ181633.0046864.09648.956++= T (4.908136)(25.60231) (1.545974)从表中可以看出,i ωˆ的系数t 值多对应的P 值为0.1333大于显著性水平0.05,所以应该接受原假设,认为不存在测量误差。
10.1、①利润(profit)散点图:红利(bonus)散点图:直观地从图中看出这两个时间序列为非平稳序列②对利润(profit)的单位根检验:从检验结果看,在1%,5%,10%三个显著水平下,单位根检验的临界值非别为:-4.066981,-3.462292,-3.157475,t检验统计量值为-1.797079,大于相应临界值,从而不能拒绝原假设,表明利润(profit)序列存在单位根,是非平稳序列。
对红利(bonus)作单位根检验从检验结果看,在1%,5%,10%三个显著水平下,单位根检验的临界值非别为:-4.068290,-3.462912,-3.157836,t检验统计量值为-2.893559,大于相应临界值,从而不能拒绝原假设,表明红利(bonus)序列存在单位根,是非平稳序列。
庞皓《计量经济学》(第4版)章节题库-第9章 设定误差与测量误差【圣才出品】

2 / 13
圣才电子书
严重的影响。
十万种考研考证电子书、题库视频学习平 台
(1)如果模型中遗漏变量,需要分成两种情况讨论:①遗漏变量与模型中的解释变
量相关。这种情况是最常见的,此时参数的估计是有偏且不一致的,并且参数估计也不满
圣才电子书
十万种考研考证电子书、题库视频学习平 台
第 9 章 设定误差与测量误差
一、选择题 1.若真实模型是解释变量为 X1 的一元线性回归模型,但在建模时将与 X1 无关的变量 X2 包含在模型中,则斜率参数的最小二乘估计量( )。 A.仍具有无偏性、一致性和最小方差性 B.不具有无偏性、一致性和最小方差性 C.仍具有无偏性、一致性,但不具有最小方差性 D.不具有无偏性、一致性,但仍具有最小方差性 【答案】C 【解析】在包含无关变量的模型中,最小二乘估计量是无偏且一致的,随机干扰项的 方差也能被正确估计,但 OLS 估计量不具有最小方差性。该类错误的后果通常体现为,包 含无关变量的偏误主要表现为“错误”模型的普通最小二乘估计量的方差一般会大于“正 确”模型相应参数估计量的方差。
程的自由度降低,从而扰动项的方差估计变小,模型中参数的标准误增大,从而影响参数
的假设检验,置信区间的计算。
都很严重。
3.“好的”经济计量模型有哪些性质? 答:一个好的模型应具备以下条件: (1)模型应尽可能简洁; (2)模型中系数的估计值应唯一; (3)对样本数据的拟合程度较好; (4)模型中估计系数的符号同相关经济理论相符; (5)具有良好的预测力。
料限制等问题,忽略某些重要变量而造成的模型设定偏误。
b.误选无关变量:在回归模型引入了一些无关紧要的自变量,从而造成模型设定偏
课程教纲(金融工程XXXX级XXXX0906)

一、滞后效应与滞后变量模型(经济活动中的滞后现象、滞后效应产生的原因、滞后变量模型)
二、分布滞后模型的估计(分布滞后模型估计的困难、经验加权估计法、阿尔蒙法)
三、自回归模型的构建(库伊克模型、自适应预期模型、局部调整模型)
四、自回归模型的估计(自回归模型估计的困难、工具变量法、德宾h-检验)
四、异方差性的补救措施(对模型变换、加权最小二乘法、模型的对数变换)
五、案例分析
本章重点和难点分析:重点掌握异方差性检验及修正,难点是对异方差性产生原因理解。
第六章自相关
本章学习目的和要求:通过本章学习,掌握自相关产生原因、检验及修正方法。
本章知识要点:
一、什么是自相关(自相关的概念、自相关产生的原因、自相关的表现形式)
四、计量经济模型的建立
本章重点和难点分析:重点是对模型设定、估计参数、模型检验、模型应用的理解,变量类型和数据类型的划分。难点在于变量内生性与外生性的理解。
第二章简单线性回归模型
本章学习目的与要求:通过本章学习,掌握经典计量经济学模型基本原理与思想,掌握一元线性模型设定、估计、检验和应用,理解基本假定。
二、自相关的后果(自相关对参数估计、模型检验、模型预测的影响)
三、自相关的检验(图示检验法、DW检验法)
四、自相关的补救(广义差分法、科克伦—奥克特迭代法)
五、案例分析
本章重点和难点分析:自相关的后果、DW检验和广义差分法、科克伦—奥克特迭代法
第七章分布滞后模型与自回归模型
本章学习目的和要求:通过本章学习,掌握分布滞后模型估计,熟悉自回归模型构建。
四、案例分析
本章重点和难点分析:重点掌握联立方程模型概念、识别阶条件、秩条件、联立偏倚问题,联立方程模型估计(间接最小二乘法、两阶段最小二乘)。难点是对联立方程模型识别的理解,联立性偏倚的理解。
庞浩计量经济学复习重点整理版

计量经济学复习重点总结任课老师:姜婷By fantasy题型:单选20*2 多选5*3 判断5*3 计算3*10第一章导论计量经济学数据类型:时间序列数据:把反映某一总体特征的同一指标的数据,按照一定的时间顺序和时间间隔(如月度.季度.年度)排列起来,这样的统计数据称为时间序列数据。
时间序列数据可以是时期数据,也可以是时点数据。
如逐年的GDP CPI截面数据:同一时间(时期或时点)某个指标在不同空间的观测数据。
如某一年各省GDP 面板数据:指时间序列数据和截面数据相结合的数据。
如在居民收支调查中收集的对各个固定调查户在不同时期的调查数据。
虚拟变量数据:某些客观存在的定性现象,如政策、自然灾害、战争等等第二章简单线性回归模型总体回归函数的表示形式:条件期望形式:个别值形式:样本回归函数的表示形式:条件均值形式个别值形式随机扰动项和残差项的区别和联系:区别:随机扰动项代表总体的误差,反应了未知因素、模型设定误差、变量观测误差;残差代表样本的误差,残差=随机误差项+参数估计误差。
随机扰动项无法直接观测;残差的数值可以求出。
联系:残差概念上类似于随机扰动项,将残差引入样本回归函数和随机引入总体回归函数的理由是相同的。
简单线性回归的基本假定:P31随机扰动项和解释变量不相关假定,零均值假定:同方差假定:正态性假定:无自相关假定:采用普通最小二乘法拟合的样本回归线的性质:P34回归线通过样本均值:Yi估计值的均值等于实际值的均值:剩余项的均值为零:被解释变量估计值与剩余项不相关:解释变量与剩余项不相关:OLS估计式的统计性质:P36(BLUE最佳线性无偏估计量)线性特性:无偏性:最小方差性:可决系数:R 2=ESS/TSS=1-RSS/TSS回归系数的假设检验:t 检验选取的统计量及其服从的分布 P48回归模型结果的经济含义分析: 练习题:2.7和2.92.7 设销售收入X 为解释变量,销售成本Y 为被解释变量。
计量经济学-庞皓-第二版-思考题-答案

第一章 绪论 思考题1.1答:计量经济学的产生源于对经济问题的定量研究,这是社会经济发展到一定阶段的客观需要。
计量经济学的发展是与现代科学技术成就结合在一起的,它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。
经济学从定性研究向定量分析的发展,是经济学逐步向更加精密、更加科学发展的表现。
1.2答:理论计量经济学是以计量经济学理论与方法技术为研究内容,目的在于为应用计量经济学提供方法论。
所谓计量经济学理论与方法技术的研究,实质上是指研究如何运用、改造和发展数理统计方法,使之成为适合测定随机经济关系的特殊方法。
应用计量经济学是在一定的经济理论的指导下,以反映经济事实的统计数据为依据,用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。
1.3答:1、计量经济学与经济学的关系。
联系:计量经济学研究的主体—经济现象和经济关系的数量规律;计量经济学必须以经济学提供的理论原则和经济运行规律为依据;经济计量分析的结果:对经济理论确定的原则加以验证、充实、完善。
区别:经济理论重在定性分析,并不对经济关系提供数量上的具体度量;计量经济学对经济关系要作出定量的估计,对经济理论提出经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
区别:经济统计学主要用统计指标和统计分析方法对经济现象进行描述和计量;计量经济学主要利用数理统计方法对经济变量间的关系进行计量。
1.4答:解释变量是变动的原因,被解释变量是变动的结果。
被解释变量是模型要分析研究的对象。
解释变量是说明被解释变量变动主要原因的变量。
1.5一个完整的计量经济模型应包括哪些基本要素?你能举一个例子吗?答:一个完整的计量经济模型应包括三个基本要素:经济变量、参数和随机误差项。
1-庞皓《计量经济学(科学出版社(2010年6月第2版))》实验数据
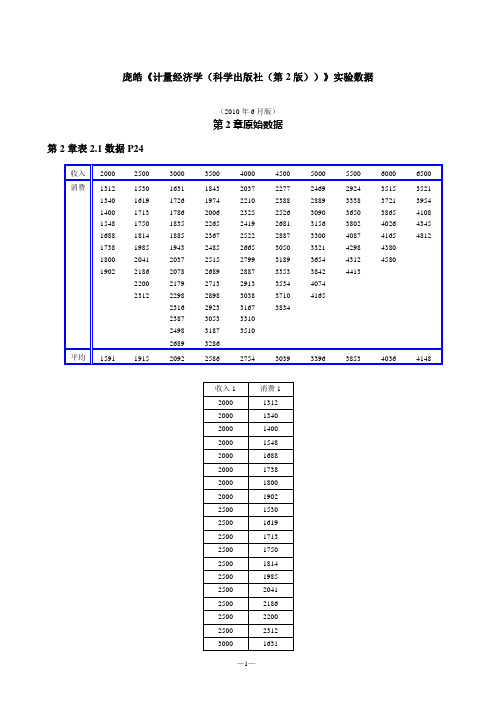
庞皓《计量经济学(科学出版社(第2版))》实验数据(2010年6月版)第2章原始数据第2章表2.1数据P24第2章表2.2-2.3数据P28两个随机样本收入消费1 消费22000 1548 1688 2500 1814 1750 3000 2179 2079 3500 2485 23674000 2665 26654500 3050 31895000 3321 33215500 3650 38026000 4087 41656500 4265 4345第2章表2.4数据P33序号可支配收入Xi 消费支出Yi xi=Xi-X yi=Yi-Y xiyi xi21 2000 1548 -2250 -1358.4 3056400 50625002 2500 1814 -1750 -1092.4 1911700 30625003 3000 2179 -1250 -727.4 909250 15625004 3500 2485 -750 -421.4 316050 5625005 4000 2665 -250 -241.4 60350 625006 4500 3050 250 143.6 35900 625007 5000 3321 750 414.6 310950 5625008 5500 3650 1250 743.6 929500 15625009 6000 4087 1750 1180.6 2066050 306250010 6500 4265 2250 1358.6 3056850 5062500 合计42500 29064 12653000 20625000 平均4250 2906.4第2章表2.5数据P55第2章表2.9 P63习题2.1数据表2.11 1990-2007年中国货币供应量(M2)和国内生产总值(GDP)的有关数据年份货币供应量M2/亿元国内生产总值GDP/亿元1990 15293.4 18718.31991 19349.9 21826.21992 25402.2 26937.31993 34879.8 35260.01994 46923.5 48108.51995 60750.5 59810.51996 76094.9 70142.51997 90995.3 78060.81998 104498.5 83024.31999 119897.9 88479.22000 134610.4 98000.52001 158301.9 108068.22002 185007.0 119095.72003 221222.8 135174.02004 254107.0 159586.72005 298755.7 184088.62006 345603.6 213131.72007 403442.2 251483.2第2章表2.10P64习题2.2数据美国软饮料公司广告费用于销售数量品牌名称广告费用X/10E6美元销售数量Y/10E6箱Coca-Cola Classic 131.3 1929.2 Pepsi-Cola 92.4 1384.6 Diet-Coke 60.4 811.4 Sprite 55.7 541.5 Dr.Pepper 40.2 546.9 Moutain Dew 29.0 535.6 7-Up 11.6 219.5第2章表2.11P64习题2.3数据深圳市地方政府预算内财政收入与国内生产总值的关系(单位:万元)年份地方预算内财政收入Y 国内生产总值(GDP) X 1990 21.70 171.671991 27.33 236.661992 42.96 317.321993 67.25 453.141994 74.40 634.671995 88.02 842.481996 131.75 1048.441997 142.06 1297.421998 164.39 1534.731999 184.21 1804.022000 221.92 2187.452001 262.49 2482.492002 265.93 2969.522003 290.84 3585.722004 321.47 4282.142005 421.38 4950.912006 500.88 5813.562007 658.06 6801.57第2章表2.12P65习题2.4数据中国国民总收入与最终消费(单位:亿元)年份国民总收入X 最终消费Y1978 3,645.217 2239.11979 4,062.579 2633.71980 4,545.624 300.71981 4,889.461 3361.51982 5,330.451 3714.81983 5,985.552 4126.41984 7,243.752 4846.31985 9040.737 5986.31986 10,274.38 6821.81987 12050.62 7804.61988 15036.82 9839.51989 17000.92 11164.21990 18,718.32 12090.51991 21,826.2 14091.91992 26,937.28 17203.31993 35260.02 21899.91994 48108.46 29242.21995 59810.53 36748.21996 70142.49 43919.51997 78060.83 48140.61998 83024.28 51588.21999 88479.15 55636.92000 98000.45 615162001 108068.2 66878.32002 119095.7 71691.22003 135174 77449.52004 159586.7 87032.92005 184088.6 97822.72006 213131.7 110595.32007 251483.2 128444.6第2章表2.13P66习题2.5数据表2.13 美国各航空公司航班正点到达比率和每10万名乘客投诉的次数航空公司名称航班正点率/% 投诉率/(次/10名乘客)西南(Southwest)航空公司81.8 0.21大陆(Continental)航空公司76.6 0.58西北(Northwest)航空公司76.6 0.85美国(US Airways)航空公司75.7 0.68 联合(United)航空公司73.8 0.74美洲(American)航空公司72.2 0.93德尔塔(Delta)航空公司71.2 0.72 美国西部(Americawest)航空公司70.8 1.22 环球(TWA)航空公司68.5 1.25第2章表2.14P66习题2.6数据表2.12 某年16种公益股票每股账面价值和当年红利公司序号账面价值/元红利/元1 22.44 2.42 20.89 2.983 22.09 2.064 14.48 1.095 20.73 1.966 19.25 1.557 20.37 2.168 26.43 1.609 12.14 0.8010 23.31 1.9411 16.23 3.0012 0.56 0.2813 0.84 0.8414 18.05 1.8015 12.45 1.2116 11.33 1.07第2章表2.15 P67数据P67表2.151992年亚洲各国人均寿命等数据序号国家和地区人均寿命人均GDPX1/100美元成人识字率X2/% 一岁儿童疫苗X3/%1 日本79 194 99 992 中国香港77 185 90 793 韩国70 83 97 834 新加坡74 147 92 905 泰国69 53 94 866 马来西亚70 74 80 907 斯里兰卡71 27 89 888 中国内地70 29 80 949 菲律宾65 24 90 9210 朝鲜71 18 95 9611 蒙古63 23 95 8512 印度尼西亚62 27 84 9213 越南63 13 89 9014 缅甸57 7 81 7415 巴基斯坦58 20 36 8116 老挝50 18 55 3617 印度60 12 50 9018 孟加拉国52 12 37 6919 柬埔寨50 13 38 3720 尼泊尔53 11 27 7321 不丹48 6 41 8522 阿富汗43 7 32 35第3章原始数据第3章表3.1数据P792002年西部各地区电力消费等数据地区电力消费量Y(亿kw·h) 国内生产总值X2(亿元)水电燃料价格指数X3(%)内蒙古320.43 1734.31 104.7广西356.95 2455.36 101.7重庆248.01 1971.3 109四川660.51 4875.12 103.4贵州366.63 1185.04 99.3云南353.2 2232.32 102.9陕西355.97 2035.96 103.2甘肃339.66 1161.43 102.6青海125.51 341.11 107.3宁夏178.76 329.28 105.2新疆214.6 1598.28 109.6第3章表3.3数据P93表3.3 中国税收收入及相关数据年份税收收入国内生产总值财政支出商品零售价格指数1978 519.28 3624.1 1122.09 100.71979 537.82 4038.2 1281.79 1021980 571.7 4517.8 1228.83 1061981 629.89 4862.4 1138.41 102.41982 700.02 5294.7 1229.98 101.91983 775.59 5934.5 1409.52 101.51984 947.35 7171 1701.02 102.81985 2040.79 8964.4 2004.25 108.81986 2090.73 10202.2 2204.91 1061987 2140.36 11962.5 2262.18 107.31988 2390.47 14928.3 2491.21 118.51989 2727.4 16909.2 2823.78 117.81990 2821.86 18547.9 3083.59 102.11991 2990.17 21617.8 3386.62 102.91992 3296.91 26638.1 3742.2 105.41993 4255.3 34634.4 4642.3 113.21994 5126.88 46759.4 5792.62 121.71995 6038.04 58478.1 6823.72 114.81996 6909.82 67884.6 7937.55 106.11997 8234.04 74462.6 9233.56 100.81998 9262.8 78345.2 10798.18 97.41999 10682.58 82067.5 13187.67 972000 12581.51 89468.1 15886.5 98.52001 15301.38 97314.8 18902.58 99.22002 17636.45 104790.6 22053.15 98.72003 20017.31 135822.8 24649.95 99.92004 24165.68 159878.3 28486.89 102.82005 28778.54 183217.4 33930.28 100.82006 34804.35 211923.5 40422.73 1012007 45621.97 249529.9 49781.35 103.8第3章表3.7数据P99表3.7 某地区部分家庭书刊消费抽样调查的样本数据家庭书刊年消费支出Y/元家庭月平均收入x /元户主受教育年数T/a家庭书刊年消费支出Y/元家庭月平均收入X/元户主受教育年数T/a450 1027.2 8 793.2 1998.6 14 507.7 1045.2 9 660.8 2196 10 613.9 1225.8 12 792.7 2105.4 12 563.4 1312.2 9 580.8 2147.4 8501.5 1316.4 7 612.7 2154 10 781.5 1442.4 15 890.8 2231.4 14 541.8 1641 9 1121 2611.8 18 611.1 1768.8 10 1094.2 3143.4 16 1222.1 1981.2 18 1253 3624.6 20第3章表3.8数据P99表3.7 1970-1982年某国实际通货膨胀率、失业率和预期通货膨胀率年份实际通货膨胀率Y/% 失业率X2/% 预期通货膨胀率X3/% 1970 5.92 4.9 4.781971 4.3 5.9 3.841972 3.3 5.6 3.311973 6.23 4.9 3.441974 10.97 5.6 6.841975 9.14 8.5 9.471976 5.77 7.7 6.511977 6.45 7.1 5.921978 7.6 6.1 6.081979 11.47 5.8 8.091980 13.46 7.1 10.011981 10.24 7.6 10.811982 5.99 9.7 8第3章表3.9数据P100表3.8 某地区城镇居民人均全年耐用消费品支出、人均年可支配收入及耐用消费品价格指数的统计资料(单位:元)年份人均耐用消费品支出Y 人均年可支配收入X1 耐用消费品价格指数X2(1990年为100)1991 137.16 1181.4 115.96 1992 124.56 1375.7 133.35 1993 107.91 1501.2 128.21 1994 102.96 1700.6 124.85 1995 125.24 2026.6 122.49 1996 162.45 2577.4 129.86 1997 217.43 3496.2 139.52 1998 253.42 4283 140.44 1999 251.07 4838.9 139.12 2000 285.85 5160.3 133.35 2001 327.26 5425.1 126.39第3章表3.10数据P100表3.9 1960-1982年7个OECD国家的能源需求指数(Y)、实际GDP指数(X1)、能源价格指数(X2)年份能源需求指数Y实际GDP指数X1能源价格指数X2 年份能源需求指数Y实际GDP指数X1能源价格指数X21960 54.1 54.1 111.9 1972 97.2 94.3 98.6 1961 55.4 56.4 112.4 1973 100 100 100 1962 58.5 59.4 111.1 1974 97.3 101.4 120.1 1963 61.7 62.1 110.2 1975 93.5 100.5 131 1964 63.6 65.9 109 1976 99.1 105.3 129.6 1965 66.8 69.5 108.3 1977 100.9 109.9 137.7 1966 70.3 73.2 105.3 1978 103.9 114.4 133.7 1967 73.5 75.7 105.4 1979 106.9 118.3 144.5 1968 78.3 79.9 104.3 1980 101.2 119.6 179 1969 83.3 83.8 101.7 1981 98.1 121.1 189.4 1970 88.9 86.2 97.7 1982 95.6 120.6 190.9 1971 91.8 89.8 100.3第3章表3.11数据P101表3.11某市粮食年销售量、常住人口、人均收入、肉、蛋、鱼的销售数据P101年份粮食年销售量Y/万吨常住人口X2/万人人均收入X3/元肉销售量X4/万吨蛋销售量X5/万吨鱼虾销售量X6/万吨1974 98.45 560.20 153.20 6.53 1.23 1.89 1975 100.70 603.11 190.00 9.12 1.30 2.03 1976 102.80 668.05 240.30 8.10 1.80 2.71 1977 133.95 715.47 301.12 10.10 2.09 3.00 1978 140.13 724.27 361.00 10.93 2.39 3.29 1979 143.11 736.13 420.00 11.85 3.90 5.24 1980 146.15 748.91 491.76 12.28 5.13 6.83 1981 144.60 760.32 501.00 13.50 5.41 8.36 1982 148.94 774.92 529.20 15.29 6.09 10.07 1983 158.55 785.30 552.72 18.10 7.97 12.57 1984 169.68 795.50 771.16 19.61 10.18 15.121985 162.14 804.80 811.80 17.22 11.79 18.25 1986 170.09 814.94 988.43 18.60 11.54 20.59 1987 178.69 828.73 1094.65 23.53 11.68 23.37第4章原始数据第4章表4.3数据P119第4章表4.11数据P125表4.11 中国商品进口额、国内生产总值、消费价格指数年份商品进口额/亿元国内生产总值/亿元居民消费价格指数(1985年为100)/%1985 1257.8 9016.0 100.0 1986 1498.3 10275.2 106.5 1987 1614.2 12058.6 114.3 1988 2055.1 15042.8 135.8 1989 2199.9 16992.3 160.2 1990 2574.3 18667.8 165.2 1991 3398.7 21781.5 170.8 1992 4443.3 26923.5 181.7 1993 5986.2 35333.9 208.4 1994 9960.1 48197.9 258.6 1995 11048.1 60793.7 302.8 1996 11557.4 71176.6 327.9 1997 11806.5 78973.0 337.1 1998 11626.1 84402.3 334.4 1999 13736.4 89677.1 329.7 2000 18638.8 99214.6 331.0 2001 20159.2 109655.2 333.3 2002 24430.3 120332.7 330.6 2003 34195.6 135822.8 334.6 2004 46435.8 159878.3 347.72005 54273.7 183084.8 353.9 2006 63376.9 211923.5 359.2 2007 73284.6 249529.9 376.5第4章表4.12数据P126表4.12 1985-2002年统计数据年份能源消费标准煤总量Y/万t国民总收入X1/亿元GDPX2/亿元工业增加值X3/亿元建筑业增加值X4/亿元交通运输邮电业增加值X5/亿元人均生活电力消费X6/(kW.h)能源加工转换效率X7/%1985 76682 9040.7 9016 3448.7 417.9 406.9 21.3 68.29 1986 80850 10274.4 10275.2 3967 525.7 475.6 23.2 68.32 1987 86632 12050.6 12058.6 4585.8 665.8 544.9 26.4 67.48 1988 92997 15036.8 15042.8 5777.2 810 661 31.2 66.54 1989 96934 17000.9 16992.3 6484 794 786 35.3 66.51 1990 98703 18718.3 18667.8 6858 859.4 1147.5 42.4 67.2 1991 103783 21826.2 21781.5 8087.1 1015.1 1409.7 46.9 65.9 1992 109170 26937.3 26923.5 10284.5 1415 1681.8 54.6 66.00 1993 115993 35260 35333.9 14188 2266.5 2205.6 61.2 67.32 1994 122737 48108.5 48197.9 19480.7 2964.7 2898.3 72.7 65.2 1995 131176 59810.5 60793.7 24950.6 3728.8 3424.1 83.5 71.05 1996 138948 70142.5 71176.6 29447.6 4387.4 4068.5 93.1 71.5 1997 137798 77653.1 78973 32921.4 4621.6 4593 101.8 69.23 1998 132214 83024.3 84402.3 34018.4 4985.8 5178.4 106.6 69.44 1999 133831 88189 89677.1 35861.5 5172.1 5821.8 118.2 69.19 2000 138553 98000.5 99214.6 4003.6 5522.3 7333.4 132.4 69.04 2001 143119 108068.2 109655.2 43580.6 5931.7 8406.1 144.6 69.03 2002 151797 19095.7 120332.7 47431.3 6465.5 9393.4 156.3 69.04 2003 174990 135174 135822.8 54945.5 7490.8 10098.4 173.7 69.4 2004 203227 159586.7 159878.3 65210 8694.3 12147.6 190.2 70.71 2005 223319 183956.1 183084.8 76912.9 10133.8 10526.1 216.7 71.08 2006 246270 213131.7 211923.5 91310.9 11851.1 12481.1 249.4 71.24 2007 265583 251483.2 249529.9 107317.2 14014.1 14604.1 274.9 71.25第4章表4.13P127(本章引言部分的例题数据)表4.13 1978-2007年财政收入及其影响因素数据年份CS NZ GZ JZZ TPOP CUM SZM1978 1132.3 1027.5 1607 138.2 96259 2239.1 507901979 1146.4 1270.2 1769.7 143.8 97542 2633.7 393701980 1159.9 1371.6 1996.5 195.5 98705 3007.9 445261981 1175.8 1559.5 2048.4 207.1 100072 3361.5 397901982 1212.3 1777.4 2162.3 220.7 101654 3714.8 331301983 1367 1978.4 2375.6 270.6 103008 4126.4 347101984 1642.9 2316.1 2789 316.7 104357 4846.3 318901985 2004.8 2564.4 3448.7 417.9 105851 5986.3 443651986 2122 2788.71 3967 525.7 107507 6821.8 471401987 2199.4 3233.0 4585.8 665.8 109300 7804.6 420901988 2357.2 3865.4 5777.2 810 111026 9839.5 508701989 2664.9 4265.9 6484 794 112704 11164.2 469911990 2937.1 5062.0 6858 859.4 114333 12090.5 384741991 3149.48 5342.2 8087.1 1015.1 115823 14091.9 554721992 3483.37 5866.6 10284.5 1415 117171 17203.3 51333 1993 4348.95 6963.8 14188 2266.5 118517 21899.9 48829 1994 5218.1 9572.7 19480.7 2964.7 119850 29242.2 55043 1995 6242.2 12135.8 24950.6 3728.8 121121 36748.2 45821 1996 7407.99 14015.4 29447.6 4387.4 122389 43919.5 46989 1997 8651.14 14441.9 32921.4 4621.6 123626 48140.6 53429 1998 9875.95 14817.6 34018.4 4985.8 124761 51588.2 50145 1999 11444.08 14770.0 35861.5 5172.1 125786 55636.9 49981 2000 13395.23 14944.7 40036 5522.3 126743 61516 54688 2001 16386.04 15781.3 43580.6 5931.7 127627 66878.3 52215 2002 18903.64 16537.0 47431.3 6465.5 128453 71691.2 47119 2003 21715.25 17381.7 54945.5 7290.8 129227 77449.5 54506 2004 26396.47 21412.7 65210 8694.3 129988 87032.9 37106 2005 31649.29 22420.0 76912.9 10133.8 130756 98918.1 38818 2006 38760.20 24040.0 91310.9 11851.1 131448 110595.3 41091 2007 51321.78 28095.0 107367.2 14014.1 132129 128444.6 48992第4章表4.13数据P128表4.13 1978-2003年财政收入及其影响因素数据年份财政收入CS/亿元农业增加值NZ/亿元工业增加值GZ/亿元建筑业增加值JZZ/亿元总人口TPOP/万人最终消费CUM/亿元受灾面积SZM/万hm21978 1132.3 1018.4 1607 138.2 96259 2239.1 50760 1979 1146.4 1258.9 1769.7 143.8 97542 2619.4 39370 1980 1159.9 1359.4 1996.5 195.5 98705 2976.1 44530 1981 1175.8 1545.6 2048.4 207.1 100072 3309.1 39790 1982 1212.3 1761.6 2162.3 220.7 101654 3637.9 33130 1983 1367 1960.8 2375.6 270.6 103008 4020.5 34710 1984 1642.9 2295.5 2789 316.7 104357 4694.5 31890 1985 2004.8 2541.6 3448.7 417.9 105851 5773 44370 1986 2122 2763.9 3967 525.7 107507 6542 47140 1987 2199.4 3204.3 4585.8 665.8 109300 7451.2 42090 1988 2357.2 3831 5777.2 810 111026 9360.1 50870 1989 2664.9 4228 6484 794 112704 10556.5 46991 1990 2937.1 5017 6858 859.4 114333 11365.2 38474 1991 3149.48 5288.6 8087.1 1015.1 115823 13145.9 55472 1992 3483.37 5800 10284.5 1415 117171 15952.1 51333 1993 4348.95 6882.1 14143.8 2284.7 118517 20182.1 48829 1994 5218.1 9457.2 19359.6 3012.6 119850 26796 55043 1995 6242.2 11993 24718.3 3819.6 121121 33635 45821 1996 7407.99 13844.2 29082.6 4530.5 122389 40003.9 46989 1997 8651.14 14211.2 32412.1 4810.6 123626 43579.4 53429 1998 9875.95 14552.4 33387.9 5231.4 124761 46405.9 50145 1999 11444.08 14472 35087.2 5470.6 125786 49722.7 49981 2000 13395.23 14628.2 39047.3 5888 126743 54600.9 54688 2001 16386.04 15411.8 42374.6 6375.4 127627 58927.4 52215 2002 18903.64 16117.3 45975.2 7005 128453 62798.5 47119 2003 21715.25 17092.1 53092.9 8181.3 129227 67442.5 54506第5章原始数据第5章表5.1数据P142表5.1 四川省2000年各地区医疗机构数与人口数地区人口数X/万人医疗机构数Y/个地区人口数X/万人医疗机构数Y/个成都1013.3 6304 眉山339.9 827 自贡315 911 宜宾508.5 1530 攀枝花103 934 广安438.6 1589 泸洲463.7 1297 达州620.1 2403 德阳379.3 1085 雅安149.8 866 锦阳518.4 1616 巴中346.7 1223 广元302.6 1021 资阳488.4 1361 遂宁371 1375 阿坝82.9 536 内江419.9 1212 甘孜88.9 594 乐山345.9 1132 凉山402.4 1471 南充709.2 4064第5章表5.8数据P149表5.8 消费Y与收入X的数据Y X Y X Y X55 80 84 115 74 10565 100 98 130 110 16070 85 95 140 113 15080 110 90 125 125 16579 120 75 90 108 145115 180 55 80 115 180140 225 70 85 130 185120 200 75 90 135 190145 240 65 100 120 200130 185 74 105 140 205152 220 80 110 140 210144 210 84 115 152 220175 245 79 120 140 225180 260 90 125 137 230135 190 98 130 145 240140 205 95 140 175 245178 265 108 145 189 250191 270 113 150 180 260137 230 110 160 178 265189 250 125 165 191 270第5章表5.9数据P150P150页表5.9各地区农村居民家庭人均收入与家庭人均生活消费支出的数据(单位:亿元)地区家庭人均纯收入家庭消费支出北京9439.63 6399.27天津7010.06 3538.31河北4293.43 2786.77山西3665.66 2682.57内蒙古3953.1 3256.15辽宁4773.43 3368.16吉林4191.34 3065.14黑龙江4132.29 3117.44上海10144.62 8844.88江苏6561.01 4786.15浙江8265.15 6801.6安徽3556.27 2754.04福建5467.08 4053.47江西4044.7 2994.49山东4985.34 3621.57河南3851.6 2676.41湖北3997.48 3090湖南3904.2 3377.38广东5624.04 4202.32广西3224.05 2747.47海南3791.37 2556.56重庆3509.29 2526.7四川3546.69 2747.27贵州2373.99 1913.71云南2634.09 2637.18西藏2788.2 2217.62陕西2644.69 2559.59甘肃2328.92 2017.21青海2683.78 2446.5宁夏3180.84 2528.76新疆3182.97 2350.58第5章表5.11数据P151P151表5.11各地区建筑业总产值和建筑业企业利润总额(单位:万元)地区建筑业总产值X 建筑业企业总利润Y 北京25767692 960256.4天津12219419 379211.6河北16146909 446520.8山西10607041 194565.9内蒙古6811038.3 353362.6辽宁21000402 836846.6吉林7383390.8 102742黑龙江8758777.8 98028.5上海25241801 794136.5江苏70105724 2368711.7浙江69717052 1887291.7安徽15169772 378252.8福建15441660 375531.9江西7861403.8 188502.4山东32890450 1190084.1河南21517230 574938.7湖北21108043 698837.4湖南18288148 545655.7广东29995140 1388554.6广西6127370 126343.1海南821834 14615.7重庆11287118 386177.5四川21099834 466176贵州3487908.1 41893.1云南7566795.1 266333.1西藏602940.7 52895.2陕西11730972 224646.6甘肃4369038.8 152143.1青海1254431.1 24468.3宁夏1549486.5 25224.6新疆4508313.7 68276.6第5章表5.10数据P151表5.10个人储蓄和个人收入数据资料(单位:元)P151 时期储蓄额Y 收入额X 时期储蓄额Y 收入额X1 264 8777 17 1578 241272 105 9210 18 1654 256043 90 9954 19 1400 265004 131 10508 20 1829 276705 122 10979 21 2200 283006 107 11912 22 2017 274307 406 12747 23 2105 295608 503 13499 24 1600 281509 431 14269 25 2250 3210010 588 15522 26 2420 3250011 898 16730 27 2570 3525012 950 17662 28 1720 3350013 779 18575 29 1900 3600014 819 19635 30 2100 3620015 1222 21163 31 2300 3820016 1702 22880第5章表5.12数据P152表5.14 1978~2008年四川省农村人均纯收入和人均生活费支出(单位:元)时间农村人均村收入X农村人均生活费支出Y商品零售价格指数时间农村人均村收入X农村人均生活费支出Y商品零售价格指数1978 127.1 120.3 100 1994 946.33 904.28 310.2 1979 155.9 142.1 102 1995 1158.29 1092.91 356.1 1980 187.9 159.5 108.1 1996 1453.42 1349.88 377.8 1981 221 184 110.7 1997 1680.69 1440.48 380.8 1982 256 208.23 112.8 1998 1731.76 1440.77 370.9 1983 258.4 231.12 114.5 1999 1843.47 1426.06 359.8 1984 286.8 251.83 117.7 2000 1903.60 1485.34 354.4 1985 315.07 276.25 128.1 2001 1886.99 1497.52 351.6 1986 337.9 310.92 135.8 2002 2107.64 1591.99 3471987 369.46 348.32 145.7 2003 2229.86 1747.02 346.7 1988 448.85 426.47 172.7 2004 2580.28 2010.88 356.4 1989 494.07 473.59 203.4 2005 2802.78 2274.17 359.3 1990 557.76 509.16 207.7 2006 3002.38 2395.04 362.9 1991 590.21 552.39 213.7 2007 3546.69 2747.27 376.7 1992 634.31 569.46 225.2 2008 4121.2 3127.9 398.9 1993 698.27 647.43 254.9第6章原始数据第6章表6.3数据P167表6.3 1985-2007年农村居民人均收入和消费年份全年人均纯收入(现价)全年人均消费性支出(现价)消费价格指数(1985年为100)人均实际纯收入(1985年可比价)人均实际消费性支出(1985年可比价)1985 397.60 317.42 100.0 397.60 317.40 1986 423.80 357.00 106.1 399.43 336.48 1987 462.60 398.30 112.7 410.47 353.42 1988 544.90 476.70 132.4 411.56 360.05 1989 601.50 535.40 157.9 380.94 339.08 1990 686.30 584.63 165.1 415.69 354.11 1991 708.60 619.80 168.9 419.54 366.96 1992 784.00 659.80 176.8 443.44 373.19 1993 921.60 769.70 201.0 458.51 382.94 1994 1221.00 1016.81 148.0 492.34 410.00 1995 1577.70 1310.36 291.4 541.42 449.69 1996 1923.10 1572.10 314.4 611.67 500.03 1997 2090.10 1617.15 322.3 648.50 501.77 1998 2162.00 1590.33 319.1 677.53 498.28 1999 2214.30 1577.42 314.3 704.52 501.75 2000 2253.40 1670.00 314.0 415.69 531.85 2001 2366.40 1741.00 316.5 747.68 550.08 2002 2475.60 1834.00 315.2 785.41 581.85 2003 2622.24 1943.30 320.2 818.86 606.81 2004 2936.40 2185.00 335.6 874.97 651.07 2005 3254.93 2555.00 343 948.96 744.90 2006 3587.00 2829.00 348.1 1030.45 812.70 2007 4140.00 3224.00 366.9 1128.37 878.70第6章表6.6数据P172表6.6 1960~1995美国个人实际可支配收入和个人实际消费收入(单位:1010美元)年份个人实际可支配收入X个人实际消费支出Y 年份个人实际可支配收入X 个人实际消费支出Y1960 157 143 1978 326 295 1961 162 146 1979 335 302 1962 169 153 1980 337 301 1963 176 160 1981 345 305 1964 188 169 1982 348 308 1965 200 180 1983 358 324 1966 211 190 1984 384 3411967 220 196 1985 396 357 1968 230 207 1986 409 371 1969 237 215 1987 415 382 1970 247 220 1988 432 397 1971 256 228 1989 440 406 1972 268 242 1990 448 413 1973 287 253 1991 449 411 1974 285 251 1992 461 422 1975 290 257 1993 467 434 1976 301 271 1994 478 447 1977 311 283 1995 493 458第6章表6.7数据P173表6.7 北京市连续19年城镇居民家庭人均收入与支出数据表(单位:元)年份顺序人均收入/元人均生活消费支出/元商品零售物价指数/%人均实际收入/元人均实际支出/元1 450.18 359.86 100.00 450.18 359.862 491.54 408.66 101.50 484.28 402.623 599.4 490.44 108.60 551.93 451.604 619.57 511.43 110.20 562.22 464.095 668.06 534.82 112.30 594.89 476.246 716.60 574.06 113.00 634.16 508.027 837.65 666.75 115.40 725.87 577.778 1158.84 923.32 136.80 847.11 674.949 1317.33 1067.38 145.90 902.90 731.5810 1413.24 1147.60 158.60 891.07 723.5811 1767.67 1455.55 193.30 914.47 753.0012 1899.57 1520.41 229.10 829.14 663.6413 2067.33 1646.05 238.50 866.81 690.1714 2359.88 1860.17 258.80 911.85 718.7715 2813.10 2134.65 280.30 1003.60 761.5616 3935.39 2939.60 327.70 1200.91 897.0417 5585.88 4134.12 386.40 1445.62 1069.9118 6748.68 5019.76 435.10 1551.06 1153.7019 7945.78 5729.45 466.90 1701.82 1227.13第6章表6.8数据P174表6.8 日本工薪家庭实际消费支出与实际可支配收入(单位:103日元)年份个人实际可支配收入X个人实际消费支出Y 年份个人实际可支配收入X个人实际消费支出Y1970 239 300 1983 304 384 1971 248 311 1984 308 392 1972 258 329 1985 310 400 1973 272 351 1986 312 403 1974 268 354 1987 314 411 1975 280 364 1988 324 428 1976 279 360 1989 326 434 1977 282 366 1990 332 441 1978 285 370 1991 334 4491979 293 378 1992 336 451 1980 291 374 1993 334 449 1981 294 371 1994 330 449 1982 302 381第6章表6.09数据P175表6.10 地区生产总值(Y)与固定资产投资额(X)(单位:亿元)年份地区生产总值(Y)固定资产投资额(X)年份地区生产总值(Y)固定资产投资额(X)1980 1402 216 1991 3158 523 1981 1624 254 1992 3578 548 1982 1382 187 **** **** 668 1983 1285 151 **** **** 699 1984 1665 246 1995 4897 745 1985 2080 368 1996 5120 667 1986 2375 417 1997 5506 845 1987 2517 412 1998 6088 951 1988 2741 438 1999 7042 1185 1989 2730 436 2000 8756 1180 1990 3124 544第7章原始数据第7章表7.1数据P183表7.1 1955—1974年美国制造业库存量Y和销售额X的统计资料(单位:亿美元)年份Y X 年份Y X1955 450.69 264.80 1965 682.21 410.031956 506.42 277.40 1966 779.65 448.691957 518.70 287.36 1967 846.55 464.491958 500.70 272.80 1968 908.75 502.821959 527.07 302.19 1969 970.74 535.551960 538.14 307.96 1970 1016.45 528.591961 549.39 308.96 1971 1024.45 559.171962 582.13 331.13 1972 1077.19 620.171963 600.43 350.32 1973 1208.70 713.981964 633.83 373.35 1974 1471.35 820.78第7章表7.4数据P1971996-2005年全国广义货币供应量及物价指数月度数据时间广义货币M2/1011元广义货币增长量M2Z/1011元居民消费价格同比指数TBZS1996年1月58.401 109 1996年2月63.778 5.377 109.3 1996年3月64.511 0.733 109.8 1996年4月65.723 1.212 109.7 1996年5月66.88 1.157 108.9 1996年6月68.132 1.252 108.6 1996年7月69.346 1.214 108.31996年8月72.309 2.963 108.1 1996年9月69.643 -2.666 107.4 1996年10月73.1522 3.5092 107 1996年11月74.142 0.9898 106.9 1996年12月76.0949 1.9529 107 1997年1月78.648 2.5531 105.9 1997年2月78.998 0.35 105.6 1997年3月79.889 0.891 104 1997年4月80.818 0.929 103.2 1997年5月81.151 0.333 102.8 1997年6月82.789 1.638 102.8 1997年7月83.46 0.671 102.7 1997年8月84.746 1.286 101.9 1997年9月85.892 1.146 101.8 1997年10月86.644 0.752 101.5 1997年11月87.59 0.946 101.1 1997年12月90.9953 3.4053 100.4 1998年1月92.2114 1.2161 100.3 1998年2月92.024 -0.1874 99.9 1998年3月92.015 -0.009 100.7 1998年4月92.662 0.647 99.7 1998年5月93.936 1.274 99 1998年6月94.658 0.722 98.7 1998年7月96.314 1.656 98.6 1998年8月97.299 0.985 98.6 1998年9月99.795 2.496 98.5 1998年10月100.8752 1.0802 98.9 1998年11月102.229 1.3538 98.8 1998年12月104.4985 2.2695 99 1999年1月105.5 1.0015 98.8 1999年2月107.778 2.278 98.7 1999年3月108.438 0.66 98.2 1999年4月109.218 0.78 97.8 1999年5月110.061 0.843 97.8 1999年6月111.363 1.302 97.9 1999年7月111.414 0.051 98.6 1999年8月112.827 1.413 98.7 1999年9月115.079 2.252 99.2 1999年10月115.39 0.311 99.4 1999年11月116.559 1.169 99.1 1999年12月119.898 3.339 99 2000年1月121.22 1.322 99.8 2000年2月121.5834 0.3634 100.7 2000年3月122.5807 0.9973 99.8 2000年4月124.1219 1.5412 99.7 2000年5月124.0533 -0.0686 100.1 2000年6月126.6053 2.552 100.5 2000年7月126.3239 -0.2814 100.5 2000年8月127.79 1.4661 100.3 2000年9月130.4738 2.6838 1002000年10月129.522 -0.9518 100 2000年11月130.9941 1.4721 101.3 2000年12月134.6103 3.6162 101.5 2001年1月137.5436 2.9333 101.2 2001年2月136.2102 -1.3334 100 2001年3月138.7445 2.5343 100.8 2001年4月139.9499 1.2054 101.6 2001年5月139.0158 -0.9341 101.7 2001年6月147.8097 8.7939 101.4 2001年7月149.2287 1.419 101.5 2001年8月149.9418 0.7131 101 2001年9月151.8226 1.8808 99.9 2001年10月151.4973 -0.3253 100.2 2001年11月154.0883 2.591 99.7 2001年12月158.3019 4.2136 99.7 2002年1月159.6393 1.3374 99 2002年2月160.9356 1.2963 100 2002年3月164.0646 3.129 99.2 2002年4月164.5706 0.506 98.7 2002年5月166.061 1.4904 98.9 2002年6月169.6012 3.5402 99.2 2002年7月170.8511 1.2499 99.1 2002年8月173.2509 2.3998 99.3 2002年9月176.9824 3.7315 99.3 2002年10月177.2942 0.3118 99.2 2002年11月179.7363 2.4421 99.3 2002年12月185.0073 5.271 99.6 2003年1月190.4883 5.481 100.4 2003年2月190.1084 -0.3799 100.2 2003年3月194.4873 4.3789 100.9 2003年4月196.1301 1.6428 101 2003年5月199.5052 3.3751 100.7 2003年6月204.9314 5.4262 100.3 2003年7月206.1931 1.2617 100.5 2003年8月210.5919 4.3988 100.9 2003年9月213.5671 2.9752 101.1 2003年10月214.4694 0.9023 101.8 2003年11月216.3517 1.8823 103 2003年12月221.2228 4.8711 103.2 2004年1月225.1019 3.8791 103.2 2004年2月227.0507 1.9488 102.1 2004年3月231.6546 4.6039 103 2004年4月233.6279 1.9733 103.8 2004年5月234.8424 1.2145 104.4 2004年6月238.4275 3.5851 105 2004年7月234.127 -0.3005 105.3 2004年8月239.7292 1-6002 105.3 2004年9月243.7569 4.0277 105.2 2004年10月243.7403 -0.0166 104.3 2004年11月247.1356 3.3953 102.82004年12月254.107 6.9714 102.42005年1月257.7085 4.6015 101.92005年2月259.3573 1.6488 103.92005年3月264.5889 5.2316 102.72005年4月266.9927 2.4038 101.82005年5月269.2405 2.2478 101.82005年6月275.7855 6.545 101.62005年7月276.9663 1.1808 101.82005年8月281.2882 4.3219 101.32005年9月287.4383 6.1501 100.92005年10月287.5916 0.1533 101.22005年11月292.3504 4.7588 101.32005年12月298.7557 6.4053 101.62006年1月303.5717 4.816 101.92006年2月304.5163 0.9446 100.92006年3月310.4907 5.9744 100.82006年4月313.7023 3.2116 101.22006年5月316.7098 3.0075 101.42006年6月322.7564 6.0466 101.52006年7月324.0108 1.2544 1012006年8月327.8867 3.8759 101.32006年9月331.8654 3.9787 101.52006年10月332.7472 0.8818 101.42006年11月337.5042 4.757 101.92006年12月345.6036 8.0994 102.82007年1月351.4988 5.8952 102.22007年2月358.6593 7.1605 102.72007年3月364.0937 5.4344 103.32007年4月367.4256 3.33187 1032007年5月369.7182 2.29258 103.42007年6月377.8322 8.114 104.42007年7月383.8849 6.05273 105.62007年8月387.205 3.32016 106.52007年9月393.0989 5.89387 106.22007年10月394.2042 1.10526 106.52007年11月399.7579 5.55374 106.92007年12月403.4013 3.64339 106.52008年1月417.8462 14.44487 107.12008年2月421.0378 3.19167 108.72008年3月423.0545 2.01669 108.32008年4月429.2409 6.18638 108.52008年5月436.2216 6.98069 107.72008年6月443.141 6.91942 107.12008年7月446.3622 3.22115 106.32008年8月448.8467 2.48451 104.92008年9月452.8987 4.05203 104.62008年10月453.1333 0.23461 1042008年11月458.6447 5.51134 102.4第7章表7.11数据P205表7.11 1970—1987年美国个人消费支出(PCE)和个人可支配收入(PDI)数据年份PCE PDI 年份PCE PDI 年份PCE PDI 1970 1492.0 1668.1 1976 1803.9 2001.0 1982 2050.7 2261.5 1971 1538.8 1728.4 1977 1883.8 2066.6 1983 2146.0 2331.9 1972 1621.9 1797.4 1978 1961.0 2167.4 1984 2249.3 2469.8 1973 1689.6 1916.3 1979 2004.4 2212.6 1985 2354.8 2542.8 1974 1674 1896.6 1980 2000.4 2214.3 1986 2455.2 2640.9 1975 1711.9 1931.7 1981 2042.2 2248.6 1987 2521.0 2686.3第7章表7.12数据P205表7.12 某地区1980—2001年固定资产投资Y与销售额X的资料(单位:亿元)年份Y X 年份Y X1980 36.99 52.805 1992 128.68 168.1291981 33.60 55.906 1992 123.97 163.3511982 35.42 63.027 1993 117.35 172.5471983 42.35 72.931 1994 139.61 190.6821984 52.48 84.790 1995 152.88 194.5381985 53.66 86.589 1996 137.95 194.6571986 58.53 98.797 1997 141.06 206.3261987 67.48 113.201 1998 163.45 223.5411988 78.13 126.905 1999 183.80 232.7241989 95.13 143.936 2000 192.61 239.4591990 112.60 154.391 2001 182.81 235.142第7章表7.13数据P206表7.13 1962—1995年某地区基本建设新增固定资产Y和全省工业总产值X(单位:亿元)年份Y X 年份Y X1962 0.94 4.95 1979 2.06 42.691963 1.69 6.63 1980 7.93 51.611964 1.78 8.51 1981 8.01 61.51965 1.84 9.37 1982 6.64 60.731966 4.36 11.23 1983 16 64.641967 7.02 11.34 1984 8.81 66.671968 5.55 19.9 1985 10.38 73.781969 6.93 29.49 1986 6.2 69.521970 7.17 36.83 1987 7.97 79.641971 2.33 21.19 1988 27.33 92.451972 2.18 18.14 1989 12.58 102.941973 2.39 19.69 1990 12.47 105.621974 3.3 23.88 1991 10.88 104.881975 5.24 29.65 1992 17.7 113.31976 5.39 40.94 1993 14.72 127.131977 1.78 33.08 1994 13.76 141.441978 0.73 20.3 1995 14.42 173.75第7章表7.14数据P207。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设定误差的原因
●数据来源渠道可能不畅。例如,数据很难取得被 数据来源渠道可能不畅。例如, 迫将具有重要的经济意义变量排斥在模型之外。 迫将具有重要的经济意义变量排斥在模型之外。 ●不知道变量应当以什么确切的函数形式出现在回 归模型中。 归模型中。 ●事先并不知道所研究的实证数据中所隐含的真实 模型究竟是什么。 模型究竟是什么。 设定误差在建模中较容易出现。 设定误差在建模中较容易出现。设定误差的存在 可能会对模型形成不良的后果。 可能会对模型形成不良的后果。
σ2
ˆ Var(β2 ) =
∑ x2i x3i ) 2 ∑ x2i (1- x2 x2 ∑ 2i ∑ 3i
σ2
=
2 2 x2i (1- r23 ) ∑
σ2
17
ˆ 相关, ˆ 如果 X 3 与 X 2 相关,显然有 Var(α 2 ) ≠ Var( β 2 )
ˆ 不相关, 如果 X 3与 X 2不相关,也有 Var(α2 ) ≠ Var(β2 ) ˆ
yi = β2 x2i + β2 x3i + (ui - u )
13
却对方程 Y i = α 1 + α 2 X 进行回归, 进行回归,得:
ˆ α 2 = β 2 + β3
2i
+ν i
取期望
∑x x ∑x
2 i 3i 2 2i
∑ x (u - u ) + ∑x
2i i 2 2i
∑ x2i x3i + ∑ x2i (ui - u ) ˆ E (α 2 ) = E β 2 + β 3 2 2 ∑ x2i ∑ x2i
本下有偏,在大样本下非一致。 本下有偏,在大样本下非一致。
的估计却是有偏的。 性;但这时α2 的估计却是有偏的。 即OLS估计量在小样 估计量在小样
16
ˆ 方差的有偏估计: 3. α 2 的方差是 β 2 方差的有偏估计: ˆ
由Y
ˆ = β1 + β2X2 + β3X3 +u 得 Var(α2 ) = x2 ∑ 2i 由Y = α + α x + v 得 1 2 2
4
第九章 设定误差与测量误差
本章主要讨论: 本章主要讨论:
●设定误差 ●设定误差的检验 ●测量误差
5
第一节 设定误差
本节基本内容: 本节基本内容:
●设定误差及类型 ●变量设定误差的后果
6
一、设定误差及类型
计量经济模型是对变量间经济关系因果性的设想, 计量经济模型是对变量间经济关系因果性的设想, 若所设定的回归模型是“正确” 若所设定的回归模型是“正确”的,主要任务是所 选模型参数的估计和假设检验。 选模型参数的估计和假设检验。但是如果对计量模 型的各种诊断或检验总不能令人满意, 型的各种诊断或检验总不能令人满意,这时应把注 意力集中到模型的设定方面: 意力集中到模型的设定方面: 考虑所建模型是否遗漏了重要的变量? 考虑所建模型是否遗漏了重要的变量? 是否包含了多余的变量? 是否包含了多余的变量? 所选模型的函数形式是否正确? 所选模型的函数形式是否正确? 随机扰动项的设定是否合理? 随机扰动项的设定是否合理? 变量的数据收集是否有误差? 变量的数据收集是否有误差? 所有这些,计量经济学中被统称为设定误差。 所有这些,计量经济学中被统称为设定误差。 7
而我们将模型设定为
Y =α +α2 X2i +νi i 1
即设定模型时漏掉了一个相关的解释变量。 即设定模型时漏掉了一个相关的解释变量。 这类错误称为遗漏相关变量 遗漏相关变量( 欠拟合” 这类错误称为遗漏相关变量(“欠拟合”)。
9
2. 无关变量的误选
(Including Irrevelant Variables)
设定误差的类型
从误差来源看,设定误差主要包括: 从误差来源看,设定误差主要包括: (1)变量的设定误差,包括相关变量的遗漏 )变量的设定误差, 欠拟合)、无关变量的误选(过拟合); )、无关变量的误选 (欠拟合)、无关变量的误选(过拟合); (2)变量数据的测量误差; )变量数据的测量误差; (3)模型函数形式的设定误差; )模型函数形式的设定误差; (4)随机扰动项设定误差。 )随机扰动项设定误差。 本章主要讨论的两类变量设定误差: 本章主要讨论的两类变量设定误差
IM = -172.42 + 0.271 D - 949.12 + 160.73 2 - 10.18T3 G P T T
t = (-0.177) (5.67) (-2.22) (2.20) (-2.74)
R2 = 0.991 F = 272.95 D = 1.97 W
2
有人根据“简单优于复杂”原则,得到以下方程: 有人根据“简单优于复杂”原则,得到以下方程:
4. 遗漏变量 X 3 ,式中的随机扰动项 v i的方差估计 量将是有偏的, 量将是有偏的,即: ˆ σ v2 = RSSv ( n - 2)
ˆ E (σ v2 ) ≠ σ u2
5. 与方差相关的检验,包括假设检验、区间估计, 与方差相关的检验,包括假设检验、区间估计, 在关于参数的统计显著性方面, 在关于参数的统计显著性方面,都容易导出错误的 结论。 结论。
21
2. 包含无关变量偏误
定义:模型中包括了不重要的解释变量, 定义 模型中包括了不重要的解释变量,即采用误 模型中包括了不重要的解释变量 选了无关解释变量的模型进行估计而带来的偏误, 选了无关解释变量的模型进行估计而带来的偏误, 称为包含无关变量偏误 设正确模型 Y = β + β X + µ (1) 1 2 2 但却估计了 Y = α + α X + α X + v (2) 1 2 2 3 3 相同, 如果 α3 = 0 则(2)与(1)相同,因此,可将 式 , 与 相同 因此,可将(1)式 为约束的(2)式的特殊形式。 视为以 α3 = 0 为约束的 式的特殊形式。 采用OLS 法对(2)进行估计,有: 法对( )进行估计, 采用
18
ˆ ˆ (1) 若 X3与 2相关, 23 ≠ 0,显然,Var (α2 ) ≠ Var β2 X r2
ˆ ˆ 似乎有:Var (α2 ) < Var β2 ;
但实际情形并不完全如此。 但实际情形并不完全如此。 可以注意到残差平方和 可以注意到残差平方和RSS的计算 的计算
( )
( )
ˆ ˆ σν2 = RSSv (n − 2) ≠ RSSu (n − 3) = σu2 ;
例如,如果“真实模型” 例如,如果“真实模型”为:
Y = β1 + β2 X2i + β3X3i + µi i
但我们却将模型设定为
Y =α1 +α2 X2i +α3X3i +α4 X4i +νi i
即设定模型时,多选了一个无关解释变量。 即设定模型时,多选了一个无关解释变量。这类 错误称为无关变量的误选( 过拟合” 错误称为无关变量的误选(“过拟合”)。
11
二、变量设定误差的后果
当模型设定出现误差时, 当模型设定出现误差时,模型估计结果也会与 “实际”有偏误; 实际”有偏误; 偏误的性质与程度与模型设定误差的类型密切相 关。 从实质上看,变量设定误差的主要后果, 从实质上看,变量设定误差的主要后果,是一个 或多个解释变量与随机扰动项之间存在着相关性, 或多个解释变量与随机扰动项之间存在着相关性, 进而影响参数估计的统计特性。 进而影响参数估计的统计特性。
因此,有可能: 因此,有可能:
RSSv (n − 2) > RSSu (n − 3);
19
不相关, (2)若 X 3与X 2 不相关,有 )
2 r23 = 0和 ∑ x2i x3i 2 x2i = 0; ∑
似乎分别有: 似乎分别有: ˆ E (α2 ) = β2
ˆ ˆ Var(β2 ) = Var(α2 );
IM = -217.186 + 0.173G P D
t = (-0.5) ( 16.94)
(2)
R2 = 0.960 F = 286.95
D = 0.735 W
进行比较: 进行比较:
两个方程的检验结果都较理想; 两个方程的检验结果都较理想; 方程( ) 检验值似乎优于方程( ); 方程(2)GDP的t检验值似乎优于方程(1); 的 检验值似乎优于方程 方程( )函数形式也更为简单; 方程(2)函数形式也更为简单; 然而,能否根据“ 原则, 然而,能否根据“Occam’s razor”原则,判断方程(2)比 原则 判断方程( ) 方程( ) 方程(1)好?
3
对模型的设定是计量经济研究的重要环节。 对模型的设定是计量经济研究的重要环节。 前面各章除了对随机扰动项 还强调: 外,还强调 分布的基本假定以 ui
假定设定的模型对变量和函数形式的设定是 正确地描述被解释变量与解释变量之间的真实关 假定模型中的变量没有测量误差。 系,假定模型中的变量没有测量误差。 但是在实际的建模实践中, 但是在实际的建模实践中,对模型的设定不一定 能够完全满足这样的要求, 能够完全满足这样的要求,从而会使模型出现设 定误差。 定误差。
14
遗漏变量设定误差的后果
由此可以看出, 的遗漏将产生如下后果。 由此可以看出,X3的遗漏将产生如下后果。 两边取概率极限, 两边取概率极限,有:
Cov ( X 2i , X3i ) Cov ( X 2i , ui ) ˆ p limα2 = β2 + β3 + Var ( X 2i ) Var ( X 2i ) n→∞
(1)相关变量的遗漏(欠拟合); )相关变量的遗漏(欠拟合); (2)无关变量的误选(过拟合)。 )无关变量的误选(过拟合)。
8
1. 相关变量的遗漏
(Omitting Relevant Variables) )
