多组分系统热力学及其在溶液中的应用 概念及公式总结
大学物理化学 第三章 多组分系统热力学习指导及习题解答

RT Vm p A Bp
积分区间为 0 到 p,
RT
p
d ln
f=
(p RT
A Bp)dp
0
0p
RT p d ln( f )= (p A Bp)dp Ap 1 Bp2
0
p0
2
因为
lim ln( f ) 0 p0 p
则有
RT ln( f )=Ap 1 Bp2
为两相中物质的量浓度,K 为分配系数。
萃取量
W萃取
=W
1
KV1 KV2 V2
n
二、 疑难解析
1. 证明在很稀的稀溶液中,物质的量分数 xB 、质量摩尔浓度 mB 、物质的量浓度 cB 、质量分数 wB
之间的关系: xB
mBM A
MA
cB
MA MB
wB 。
证明:
xB
nA
nB nB
nB nA
)pdT
-S
l A,m
dT
RT xA
dxA
-S(mg A)dT
-
RT xA
dxA =
S(mg A)-S
l A,m
dT
Δvap Hm (A) T
dT
-
xA 1
dxA = xA
Tb Tb*
Δvap Hm (A) R
dT T2
若温度变化不大, ΔvapHm 可视为常数
- ln
xA =
Δvap Hm (A) R
真实溶液中溶剂的化学势 μA μ*A(T, p) RT ln γx xA =μ*A(T, p) RT ln aA,x
真实溶液中溶质 B μB μB* (T, p) RT ln γx xB =μ*A(T, p) RT ln aB,x
物理化学:第4章_多组分系统热力学_
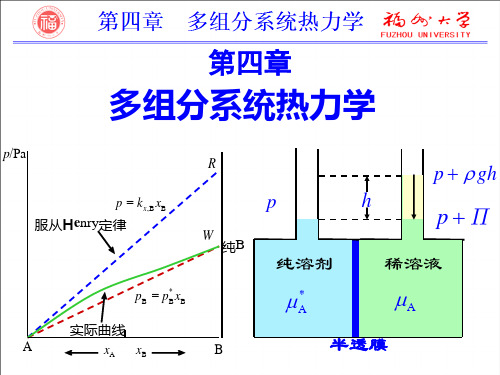
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
傅献彩《物理化学》第5版笔记和课后习题含考研真题详解(多组分系统热力学及其在溶液中的应用)【圣才出品

令 kb
R(Tb* )2MA
Δ
fus
Hห้องสมุดไป่ตู้
θ m,A
,则有
Tb kbmB
式中,kb 称为沸点升高系数,只与溶剂的性质有关。
3.渗透压 渗透压Π求解公式为
cBRT
式中,cB 为溶质的浓度,该式仅适用于稀溶液。
六、活度与活度因子(见表 4-1-2) 表 4-1-2 活度与活度因子
5 / 39
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:(1)质量摩尔浓度
mB
nH2SO4 W水
0.0947 0.1/ 0.09808 molkg1 (1 0.0947) 0.1
1.067molkg1
(2)物质的量浓度
cB
nB V
mB / M B m溶液 / B
0.0947 0.1kg / 0.09808kgmol-1 0.1kg /1.0603103 kgm3
2 / 39
圣才电子书 十万种考研考证电子书、题库视频学习平台
三、稀溶液中的两个经验定律
1.Raoult 定律
pA
p
A
x
A
2.Henry 定律
pB kx,B xB
3 / 39
圣才电子书 十万种考研考证电子书、题库视频学习平台
四、理想液态混合物的通性
(1)应加入水的体积; (2)加水后,能得到含乙醇的质量分数为 0.56 的酒的体积。
8 / 39
圣才电子书 十万种考研考证电子书、题库视频学习平台
已知该条件下,纯水的密度为 999.1 kg·m-3,水和乙醇的偏摩尔体积为 表 3-2-1
解:(1)先计算 10.0m3 的含乙醇 0.96 的酒中水和乙醇的物质的量。
多组分系统热力学及其在溶液中的应用

第四章多组分系统热力学及其在溶液中的应用教材分析:本章介绍了溶液组成的表示方法,讲述了化学势和偏摩尔量两个重要概念,将多组分系统的热力学理论应用于溶液中各组分的化学势的表示,从而为研究溶液的各种性质奠定了基础,在此基础上,讨论了稀溶液的最基本的性质——依数性。
它是热力学理论对于溶液系统的应用。
教学目的和要求:通过本章的教学使学生了解和掌握溶液的浓度的各种表示方法,拉乌尔定律及亨利定律,稀溶液、理想溶液的意义;实际溶液与理想溶液的区别;活度的概念及意义,标准态的选用。
化学势及偏摩尔量的定义及相关公式。
掌握稀溶液与理想溶液、非理想溶液三者的区别、关系及各自性质。
加深对拉乌尔定律及亨利定律的理解并熟悉其应用。
活度的概念及标准态的选用及溶液中各组分化学势的表示,是本章的一个难点,必须使学生理解这些概念及其意义。
重点和难点:拉乌尔定律和亨利定律;偏摩尔量和化学势概念;由两个经验定律导出溶液中各组分的化学势的过程和思路;稀溶液、理想溶液的意义;活度的概念与意义;标准态的选用。
教学内容与过程:溶液组成的表示法,偏摩尔量和化学势的概念,溶液的基本性质和两个经验定律,混合气体中各组分的化学势,稀溶液(组分的化学势与标准态,依数性),理想溶液(理想溶液的定义,化学势,通性等)。
思考题、作业:1.课后全部复习题2.作业题:6,8,10,11,12,15,17,18,20,23,25,26,27。
参考资料:1.胡英主编,《物理化学》2.天津大学主编,《物理化学》3.万洪文主编,《物理化学》4.各种习题解题辅导书5.课后所列各种参考读物。
第三节 多组分系统中物质的偏摩尔量与化学势在这以前人们所讨论的热力学体系都是纯组分的体系或者是组分不变的单相体系。
因此,所有的热力学函数U m 、H m 、S m 、G m 、F m 在体系的T 、p 一定的条件下有确定值。
即在这种情况下,要描述体系的状态只要两个状态性质(如T 、p )就行了。
多组分系统

第四章 多组分系统热力学及其在溶液中的应用§4.1 引 言1.基本概念1)多组分系统:由两种或两种以上物质所组成的系统。
(多组分系统可以是单相的也可以是多相的。
)2)混合物:由两种或两种相互均匀混合而构成的系统。
(可以是气相、液相或固相) 3)溶 液(1)定义:由两种或两种以上物质在分子级别呈均匀混合而成的系统。
(2)溶液组分命名:溶质,溶剂。
(3)分类:(1)固态溶液、液态溶液。
(2)电解质溶液、非电解质溶液。
(4)应注意问题:形成溶液后,一般溶质、溶剂受力 情况与纯组分受力情况不同,所以对它们研究方法是不同的。
2.溶液中物质受力情况溶剂-溶剂 f 11 ,溶质-溶质 f 22 ,溶剂-溶质 f 12。
1) 纯态: 溶质 f 22 溶剂 f 11 2) 稀溶液: 溶质 f 22 溶剂 f 11 3) 中等浓度: 溶质 f 22,f 12 溶剂 f 12, f 11 4) 高浓度: 溶质 f 22 溶剂 f 12 3.受力变化同热效应关系1) 放热2) 吸热3) 不吸热不放热§4.2 多组分系统的组成表示法1.组成表示法1)B 的质量浓度:单位体积混合物中所含B 的质量。
1211,22f f f >121122,f f f <121122f f f ==()B B m Vρ=单位 与T 有关2)B 的质量分数:单位质量混合物中所含B 的质量。
单位为1,与T 无关3)B 的浓度:单位体积混合物中所含B 的物质的量。
单位 或 同T 有关。
4)B 的摩尔分数( 或):组分B 的物质的量与混合物中总物质的量的比值。
单位为1,与T 无关液体用 ,气体用5)溶质B 的质量摩尔浓度:每千克溶剂中所含溶质的物质的量。
单位 与T 无关。
6)溶质B 的摩尔比:单位物质的量的溶剂中所含溶质的物质的量。
单位为1,与T 无关。
2.常用的浓度表示法之间的关系 1) 与 的关系:若取1000 g 溶剂对稀溶液 2) 与 关系:-3kg m ⋅B B W w W =B Bn c V =-3mol m ⋅-3mol dm ⋅B x B y B B n x n=B x By ()BB A n m m =⋅-1mol kg BB A n r n =B x B m B BB A B n n x n n n ==+∑AB B A B BB A10001000m x m m M M m M ==++∑∑A B 1000M m <<∑B AB 1000m M x =B x BC A B B BW W c M ρρ=-=-∑∑AB B B B A AB B B B B BB A A c c c M x W c M c M c M c c M M ρρ===--+++∑∑∑∑∑()B AB A B Bc M x c M M ρ=+-∑若溶液很稀则3) 同 的关系: 取 取若溶液很稀则 若 取 对水§4.3 偏摩尔量1.偏摩尔量的定义 1. 问题的引出对简单均相系统 ,要描述其状态,只需要两个状态性质(T 、p )就可以了。
第四章 多组分系统热力学及其在溶液中的应用

第四章 多组分系统热力学及其在溶液中的应用1.在298K 时,有0.10kg 质量分数为0.0947的硫酸H 2SO 4水溶液,试分别用(1)质量摩尔浓度B m ;(2)物质的量浓度和B c (3)摩尔分数B x 来表示硫酸的含量。
已知在该条件下,硫酸溶液的密度为331.060310kg m -⨯⋅ ,纯水的浓度为3997.1kg m -⋅ 。
解:质量摩尔浓度:()2410.19.47%/1009.47%0.1981.067mol H SO B n m W kg -⨯==-⨯=⋅水物质量浓度:()24331009.47%0.10.19.47%/98997.11.02310mol H SO B n c V m --⨯⨯===⨯g 水 摩尔分数:242420.0189H SO B H SO H On x n n ==+2、在K 298和大气压力下,含甲醇()B 的摩尔分数B x 为0.458的水溶液密度为30.8946kg dm -⋅,甲醇的偏摩尔体积313()39.80V CH OH cm mol -=⋅,试求该水溶液中水的摩尔体积2()V H O 。
解:3322CH OH CH OH H O H O V n V n V =+3322CH OH CH OHH O H OV n V V n -=以1mol 甲醇水溶液为基准,则330.45832(10.458)180.027290.894610m V dm ρ⨯+-⨯===⨯ ∴23310.027290.45839.801016.7210.458H OV cm mol ---⨯⨯==⋅-3.在298K 和大气压下,某酒窖中存在酒10.0m3,其中含乙醇的质量分数为0.96。
今欲加水调制含乙醇的质量分数为0.56的酒,试计算(1)应加入水的体积;(2)加水后,能得到含乙醇的质量分数为0.56的酒的体积已知该条件下,纯水的密度为3997.1kg m -⋅,水和乙醇的偏摩尔体积为()25C H OH ω()()6312/10V H O m mol --⋅()()63125/10V C H OH m mol --⋅0.96 14.61 58.0 0.5617.1156.58解:设加入水的物质的量为O H n 2',根据题意,未加水时,2520.9610.96::9.3914618C H OH H O n n -== 2525221C H OHC H OH H O H O V n V n V =⋅+⋅ 即 661001.581061.1410522--⨯⨯+⨯⨯=OH H C O H n n解出:25167882C H OH n mol =217877H O n mol = 加入水后,25220.5610.56:():0.4984618C H OH H O H O n n n -'+== 20.5610.56167882:(17877):0.4984618H O n -'+==2'317887H On mol = 加入水的物质的体积为23331788718105.727()999.1H O V m -⨯⨯'== 2525222252'26'6()56.5810(17877)17.1110C H OH C H OH H O H OH OC H OH H OV n V n n V n n --=++=⨯⨯++⨯⨯329.4984495 5.76753115.266V m =+=4.在K 298和kPa 100下,甲醇)(B 的摩尔分数B x 为30.0的水溶液中,水)(A 和甲醇)(B 的偏摩尔体积分别为:132765.17)(-⋅=mol cm O H V ,133632.38)(-⋅=mol cm OH CH V 。
物理化学答案――第三章_多组分系统热力学及其在溶液中的应用习.

第三章多组分系统热力学及其在溶液中的应用一、基本公式和内容提要1. 偏摩尔量定义:其中X为多组分系统的任一种容量性质,如V﹑U﹑S......全微分式:总和:偏摩尔量的集合公式:2. 化学势定义物质的化学势是决定物质传递方向和限度的强度因素,是决定物质变化方向和限度的函数的总称,偏摩尔吉布斯函数只是其中的一种形式。
3. 单相多组分系统的热力学公式4. 化学势判据等温等压、只做体积功的条件下将化学势判据用于多相平衡和化学平衡中,得多组分系统多相平衡的条件为:化学平衡的条件为:5.化学势与温度、压力的关系(1)化学势与压力的关系(2)化学势与温度的关系6.气体的化学势(1)纯组分理想气体的化学势理想气体压力为(标准压力)时的状态称为标准态,称为标准态化学势,它仅是温度的函数。
(2)混合理想气体的化学势式中:为物质B的分压;为物质B的标准态化学势;是理想气体混合物中B组分的摩尔分数;是B纯气体在指定T,p时的化学势,p是总压。
(3)实际气体的化学势式中:为实际气体或其混合物中物质B的化学势;为B的标准态化学势,其对应状态是B在温度T、压力、且假想具有理想气体行为时的状态,这个状态称为实际气体B的标准态;分别为物质B的逸度系数和逸度。
7. 稀溶液中的两个经验定律(1)拉乌尔定律一定温度时,溶液中溶剂的蒸气压与溶剂在溶液中的物质的量分数成正比,其比例系数是纯溶剂在该温度时的蒸气压。
用公式表示为。
对二组分溶液来说,,故拉乌尔定律又可表示为即溶剂蒸气压的降低值与纯溶剂蒸气压之比等于溶质的摩尔分数。
(2)亨利定律一定温度时,稀溶液中挥发性溶质的平衡分压与溶质在溶液中的物质的量分数成正比。
用公式表示。
式中:为溶质的浓度分别为摩尔分数、质量摩尔浓度和物质的量浓度表示时的亨利系数,单位分别为Pa、和。
使用亨利定律时应注意:①是溶质在液面上的分压;②溶质在气体和在溶液中的状态必须是相同的。
8.溶液的化学势(1)理想液态混合物中物质的化学势①定义:在一定的温度和压力下,液态混合物中任意一种物质在任意浓度均遵守拉乌尔定律的液态混合物称为理想液态混合物。
物理化学主要公式及使用条件(第四、五章)

第四章 多组分系统热力学 主要公式及其适用条件1. 偏摩尔量:定义: C n p,T,n X X ⎪⎪⎭⎫⎝⎛∂∂=B B (1)其中X 为广延量,如V ﹑U ﹑S ......全微分式:d ⎛⎫∂∂⎛⎫=++ ⎪ ⎪∂∂⎝⎭⎝⎭∑B B B B Bd d d p,n T,n X X X T p X n T p (2)总和: ∑=BB B X n X (3)2. 吉布斯-杜亥姆方程在T ﹑p 一定条件下,0d BB B =∑X n , 或0d BBB =∑Xx 。
此处,x B 指B 的摩尔分数,X B 指B 的偏摩尔量。
3. 偏摩尔量间的关系广延热力学量间原有的关系,在它们取了偏摩尔量后,依然存在。
例:H = U + PV ⇒ H B = U B + PV B ; A = U - TS ⇒ A B = U B - TS B ; G = H – TS ⇒ G B = H B - TS B ;…...S T G ;S T G ;V p G V p Gn p,p n T,TB B B B BB -=⎪⎭⎫ ⎝⎛∂∂⇒-=⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂⇒=⎪⎪⎭⎫ ⎝⎛∂∂4. 化学势定义 Cn p,T,n G G μB B ⎪⎪⎭⎫⎝⎛∂∂==B5. 单相多组分系统的热力学公式∑+-=BBB d d d d n μV p S T U∑++=BBB d d d d n μp V S T H ∑+-=BBB d d d d n μV p T S -A∑++=BBB d d d d n μp V T S -GCCCCB B B B B n p,T,n V,T,n p,S,n V,S,n G n A n H n U μ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂====但按定义,只有 CB n p,T,n G ⎪⎪⎭⎫ ⎝⎛∂∂才是偏摩尔量,其余3个均不是偏摩尔量。
6. 化学势判据在d T = 0 , d p = 0 δW ’= 0 的条件下,⎪⎭⎫⎝⎛≤α=<∑∑平衡自发,,00α0 )()d (αBB B n μ 其中,∑α指有多相共存,)(αB μ指 α相内的B 物质。
04章 多组分系统热力学及其在溶液中的应用

在溶液中,表示溶质浓度的方法有:
(4)溶质B的当量浓度
组分 B的当量浓度:NB(N),每升溶液含B
的当量数(在分析化学中常用)。
• 物理化学中最常用的溶液浓度表示法为: – 摩尔分数(xB); – 质量摩尔浓度(mB); – 质量分数 ( WB) ;重量百分数( WB )。
§4.1 引言
多组分系统 两种或两种以上的物质(或称为组分)所形 成的系统称为多组分系统。 多组分系统可以是均相的,也可以是多相的。
混合物(mixture) 多组分均匀系统中,各组分均可选用相同的方 法处理,有相同的标准态,遵守相同的经验定律, 这种系统称为混合物。
混合物有气态、液态和固态之分。
溶体
若固体的晶型在温度变化范围内不变,则 溶解度-温度变化曲线是光滑连续的;
若在某温度点发生晶型转变,则在该温度 处其溶解度会突变,溶解度-温度曲线不连 续。
注意:
• 溶液中的所谓溶质和溶剂也是相对的。习 惯上: – 气体或固体溶于液体中时,后者称为溶 剂,前者称为溶质; – 如果是液体溶于液体时,量多者为溶剂, 量少者为溶质。
• 要确定该体系的强度性质(如密度),也 须规定各组分的浓度。
• 由此需要引入一个新的概念 —— 偏摩尔量
§4.3 偏摩尔量
多组分系统与单组分系统的差别
单组分系统的广度性质具有加和性
若1 mol单组分B物质的体积为
V* m,B
则2 mol单组分B物质的体积为
2
V* m,B
而1 mol单组分B物质和1 mol单组分C物质混合,
系统中任一容量性质Z(代表V,U,H,S, A,G等)除了与温度、压力有关外,还与各
第四章 多组分系统热力学及其在溶液中的应用

第四章 多组分系统热力学及其在溶液中的应用1.在298K 时,有0.10kg 质量分数为0.0947的硫酸H 2SO 4水溶液,试分别用(1)质量摩尔浓度B m ;(2)物质的量浓度和B c (3)摩尔分数B x 来表示硫酸的含量。
已知在该条件下,硫酸溶液的密度为331.060310kg m -⨯⋅ ,纯水的浓度为3997.1kg m -⋅ 。
解:质量摩尔浓度:()2410.19.47%/1009.47%0.1981.067mol H SO B n m W kg -⨯==-⨯=⋅水物质量浓度:()24331009.47%0.10.19.47%/98997.11.02310mol H SO B n c V m --⨯⨯===⨯g 水 摩尔分数:242420.0189H SO B H SO H On x n n ==+2、在K 298和大气压力下,含甲醇()B 的摩尔分数B x 为0.458的水溶液密度为30.8946kg dm -⋅,甲醇的偏摩尔体积313()39.80V CH OH cm mol -=⋅,试求该水溶液中水的摩尔体积2()V H O 。
解:3322CH OH CH OH H O H O V n V n V =+3322CH OH CH OHH O H OV n V V n -=以1mol 甲醇水溶液为基准,则330.45832(10.458)180.027290.894610m V dm ρ⨯+-⨯===⨯ ∴23310.027290.45839.801016.7210.458H OV cm mol ---⨯⨯==⋅-3.在298K 和大气压下,某酒窖中存在酒10.0m3,其中含乙醇的质量分数为0.96。
今欲加水调制含乙醇的质量分数为0.56的酒,试计算(1)应加入水的体积;(2)加水后,能得到含乙醇的质量分数为0.56的酒的体积已知该条件下,纯水的密度为3997.1kg m -⋅,水和乙醇的偏摩尔体积为()25C H OH ω()()6312/10V H O m mol --⋅ ()()63125/10V C H OH m mol --⋅0.96 14.61 58.0 0.5617.11 56.58解:设加入水的物质的量为O H n 2',根据题意,未加水时,2520.9610.96::9.3914618C H OH H O n n -== 2525221C H O H C H O H H O H OV n V n V =⋅+⋅ 即 661001.581061.1410522--⨯⨯+⨯⨯=O H H C O H n n 解出:25167882C H OH n mol =217877H O n mol = 加入水后,25220.5610.56:():0.4984618C H O HH O H On n n -'+== 20.5610.56167882:(17877):0.4984618H O n -'+== 2'317887H O n mol = 加入水的物质的体积为23331788718105.727()999.1H O V m -⨯⨯'== 2525222252'26'6()56.5810(17877)17.1110C H OH C H OH H O H OH OC H OH H OV n V n n V n n--=++=⨯⨯++⨯⨯329.4984495 5.76753115.266V m =+=4.在K 298和kPa 100下,甲醇)(B 的摩尔分数B x 为30.0的水溶液中,水)(A 和甲醇)(B 的偏摩尔体积分别为:132765.17)(-⋅=mol cm O H V ,133632.38)(-⋅=mol cm OH CH V 。
第四章多组分系统热力学2

物化习题第四章多组分系统热力学一判断题1、在101.3Kpa下,往纯水中加入少量NaCl,与纯水比较,此稀溶液沸点升高。
()2、偏摩尔量集合公式Z=∑nBzB,m适用条件是恒温过程。
()恒温恒压过程3、Henry系数Kx,B只与溶剂溶质性质有关,而与温度无关。
()温度不同,亨利系数不同。
温度升高,系数升高。
4、沸点升高系数Kb的数值与溶剂、溶质的性质有关,且与温度有关。
()Kb的量仅与溶剂的性质有关5.、若A分子和B分子之间的相互作用力,与A,B各自处于纯态时分子之间的相处作用力相同,混合后,则有⊿Hmin=0.( )6、标准就态是认为规定的某些特定状态。
()7、理想溶液中,各种微粒间的相互作用力可忽略不计。
()处于凝聚态的分子,其分子间的距离很小,分子间的相互作用力和分子的体积均不能忽略。
8、一切纯物质的凝固点都随外压的增大而上升。
()9、稀溶液的非典一定比纯溶剂的沸点高。
()在同一外压条件下10、在相同温度和压力下,相同质量摩尔浓度的葡萄糖和食盐水的渗透压不相同。
()Ⅱ=CbRT,溶液的渗透压的大小只由溶液中的溶质的浓度决定,而与溶质的本性无关。
11、摩尔分数和质量摩尔浓度与温度无关,而物质的量浓度与温度有关()12、在相平衡中,若各相中均有组分B,则组分B在个相中的化学势一定相等。
()系统处于相平衡,由于系统任一组分B在其存在的每个相中的化学势相等。
13、溶剂中融入挥发性溶质,肯定会引起溶液的蒸汽压升高。
()14、二组分理想液态混合物的总蒸汽压大于任一组分的蒸汽压。
()处于中间态。
15、只有广度性质才有偏摩尔量。
( )16、凡是自由能降低的过程一定都是自发过程。
()17、拉乌尔定律和亨利定律既适合于理想溶液,也适合于稀溶液。
()18、偏摩尔量因为与浓度有关,因此它不是一个强度性质。
()19、某一体系达平衡时,熵最大,自由能最小。
()20、在一个多组分溶液中,只有溶质才有偏摩尔量。
()21、封闭系统中,由状态1经定温、定压过程变化到状态2,非体积功W′>△G和△G﹤0,则此过程一定能发生。
多组分系统热力学及其在溶液中的应用2

多组分系统热力学及其在溶液中的应用2在前面的讨论中,我们所涉及到的系统均为纯物质系统或组成恒定的系统。
但在实际上常见的却是多组分系统或变速成系统。
本章将就多组分系统的热力学问题进行讨论。
在正式讨论之前,先将多组分系统进行分类:①按研究的方法分:多组分系统可有单相和多相之分。
本章将讨论多组分系统单相系统。
多组分单相系统由两种或两种以上的物质以分子大小相互均匀混合而成的均匀系统当对均匀系统中各组分现用相同的标准和同样方法研究时,称之为混合物;当对均匀系统中各组分加以区别,选用不同的标准和不同的方法(例如:将系统中的组分分为溶剂(A)和溶质(B))研究时,称之为溶液。
②按聚集状态分:分为气态溶液或混合物、液态溶液或混合物、固态溶液或混合物本章讨论的对象主要是液态系统,包括液态溶液和液态混合物。
③按导电性能分:对于溶液中溶质,按其导电性能可分为电解质溶液和非电解质溶液,本能力讨论非电解质溶液。
④按规律性分:理想混合物理想稀溶液混合物{溶液{真实混合物真实溶液本章讨论的主要对象为混合物和稀溶液,适当介绍一些真实溶液。
1.物质B的物质的量分数(物质B的摩尔分数):某BnB某B=────∑B某B=1∑BnB2.物质B的物质的质量分数:WBmBWB=────∑BWB=1∑BmB3.物质B的量浓度:CB/mol·m-3nBcB=───V4.物质B的质量摩尔浓度:mB/mol·kg-1nBmB=───W剂1.拉乌尔定律在一定温度下,纯液体A有一定的蒸汽压p某A,若向液体A加入溶质B,实验表明这是溶剂A的蒸汽压会下降。
法国化学家拉乌尔归纳多次的实验结果得出如下结论:“定温下稀溶液内溶剂的蒸汽压等于同温度下纯溶剂的蒸汽压乘它在溶液内的摩尔分数”。
即pA=p某A某A推导:设溶液由二个组分构成:A-溶剂B-溶质向溶剂A加入溶质B由实验知pA<p某A即Δp=(p某A-pA)>0且某B↑→Δp↑所以Δp∝某B由于构成稀溶液,加入的溶质较少,溶剂A分子电动势受力环境没有什么改变,只是单位体积溶液中A分子的数量减少了,使气相中ρA下降,而导致pA亦下降,也就是说加入B的数量越多,ρA下降越多,pA的下降也越大,这样,Δp仅与加入溶质B的数量有关,而与其本性无关了。
71-88 第四章多组分系统热力学及其在溶液中的应用

= −SB
4.(1)理想气体中组分 B 的化学势
B = B (T , p) + RT ln xB
式中,xB 是气体 B 在理想气体混合物中的摩尔分数
( ) B = B (T ) + RT ln p / p ,p 是总压
(2)非理想气体混合物化学势
= (T ) + RT ln ( f / p )
p = f ,f 称为逸度
K
=
mB mB
( (
) )
=
cB cB
( (
) )
K
(T
,
p)
=
aB aB
( (
) )
典型例题讲解 例 1 在 60℃,把水和有机物(B)混合,形成两个液层。一层(a)为水中质量分数B=0.17 的有机物的稀溶液;另一层(B)为有机物液体中质量分数A=0.045 的水的稀溶液。若两液 层 均 可 看 作 理 想 溶 液 , 求 此 混 合 系 统 的 气 相 总 压 及 气 相 组 成 。 已 知 在 60 ℃ 时 ,
非理想溶液中: mixV 0 , mix H 0
mixG = nBRTlnxB + nBRln B
B
B
7.活度和活度因子求法 (1)蒸气压法
溶剂: aA = A xA = pA / pA
溶质: aB = C,BcA = pB / kC,B
(2)凝固点降低法
( ) ln aA
=
fus
H
m
(2)土壤溶液的渗透压大,水由庄稼向土壤渗透,造成失水过多,而影响作物生长,甚 至导致作物死亡。
(3)海水中盐分很大,海水的渗透压大于液体,口渴时,喝海水会感觉渴得更厉害; (4)由于渗透压的存在,使味觉器官两侧的浓度差越来越小,所以感觉甜味越来越淡; (5)溶液的依数性,砂锅中肉汤的沸点高于开水的沸点,所以肉汤烫伤的程度要比开水
热力学公式总结

物理化学主要公式及使用条件第一章 气体的pVT 关系 主要公式及使用条件1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1。
R =8.314510 J · mol -1 · K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2. 气体混合物 (1) 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AV y A m ,A式中∑AA n 为混合气体总的物质的量。
Am,*V表示在一定T ,p 下纯气体A 的摩尔体积。
∑*AA m ,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2) 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3)V V p p n n y ///B B B B *=== 式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B的分压力。
*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
3. 道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体。
对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。
第二章 热力学第一定律 主要公式及使用条件1. 热力学第一定律的数学表示式W Q U +=∆或 'amb δδδd δdU Q W Q p V W =+=-+规定系统吸热为正,放热为负。
系统得功为正,对环境作功为负。
南京大学物理化学 第四章 多组分均相系统热力学及其在溶液中的应用

大能力(可逆时系统对外所做功最大) ② 当W’=0时,:反应永远向着化学势降低的方向进行,可用来判断
反应进行的情况(=0可逆,<0不可逆) 该判据也可推广到多组分多相系统:和 2. 判据的应用 (1) 相变
广义的相变是物质由一个相迁往另一个相的过程,是一个物质流动的 过程。
第15次课
3. 理想溶液的化学势
化学势是物质迁移的推动力,不论物质是否混合,只要气液两相平 衡,则气液两相的化学势相等。 混合前:纯组分 混合后:溶液组分
是纯液体A在温度为T、压力为溶液上方总压时的化学势。
4. 理想溶液的热力学性质 (1) 蒸气压与液相组成的关系
,故 (2) 蒸气压与气相组成的关系
等温等压条件下,非挥发性溶质形成的溶液中,溶剂的蒸气压等于 纯溶剂的蒸汽压乘以溶液中溶剂的摩尔分数(或:溶剂蒸气压的降低值 与纯溶剂的蒸气压之比等于溶质的摩尔分数) 说明:公式只适用于溶液中只有A、B两个组分的系统(),而则具有 普适性。
2. 亨利定律(Henry) 一定温度、压力下,稀溶液中某挥发性物质的平衡分压与该溶质的
① ∵∴压力p升高,化学势μB也随之增加 ② 若已知,则可求出 说明:实际上,在与吉布斯自由能有关的关系式中,如果把G换成μ, 并将公式中其它广度量换成相应的偏摩尔量,则公式仍然成立。 例:
第14次课
(四)化学势判据
1. 判据推导 组成可变的封闭系统,发生广义化学变化时(可逆取等号) 将上述四式与⑤-⑧式对比,得到
可称为定浓物理量
2 偏摩尔量的集合公式(加和定理) 等温等压条件下,
在任一系统中,将各组分的物质的量增加一倍,其各组分浓度仍不 变,广度量Z则相应增加一倍。 注:在所有偏摩尔量中,只有偏摩尔体积可测,可由求出溶液的总体 积。
第四章_多组分系统热力学及其在溶液中的应用习题课

66.66 kPa,101.325kPa。设A和B构成理想溶液。则当
A 在溶液中的物质的量分数为 0.5 时,气相中 A 的物质 的量分数为( C ) (A) 0.200 (B) 0.300 (C) 0.397 (D) 0.603
解:根据拉乌尔定律 pi=pi*xi pA = pA*xA=66.66×0.5 pB = pB*xB =101.325×0.5 p = pA+pB=(66.66+101.325) ×0.5 yA(g)= pA /p=66.66/(66.66+101.325)= 0.397
解:混合成理想溶液时,无热效应,故H=0,
SB S R ln xB
* B
SB R ln xB
mixS RnB ln xB
S = – R ln x苯= 7.617 J ·K-1 , G = RT ln x苯= - 2270 J ·mol-1
10.
已知在 373K 时液体 A 、 B 的饱和蒸气压分别为
11、 在25℃时,纯水的蒸气压为3167.7Pa。某溶液 x(水) =0.98,与溶液成平衡的气相中,水的分压为 3066Pa。以298K, p为纯水的标准态,则该溶液中 水的活度系数( B ) (A)大于1 解: (B)小于1 (C)等于1 (D)不确定
p p * ax
p p * x x
一、偏摩尔量及化学势的概念
为了确定组成可变的多组分系统的热力学性质,引入了 偏摩尔量的概念;为了判定组成可变的多组分系统中过程 的自发变化的方向和限度,引入了化学势的概念。
1. 偏摩尔量 (1) 定义
Z ZB n B T , p ,nC
(2) 基本公式 标准态时的化学势,均是T,p的函数,它们 分别为:当xB=1,mB=1molkg-1,cB=1moldm-3 时且服从亨利定律的那个假想态的化学势。
物理化学04多组分系统热力学

dG=dG( ) +dG()
当恒温恒压,W’=0 时
β相
dG() ()dn()
dG( ) ( )dn( )
dn( ) dn()
dX
X T
p,nB ,nc ,nD
X
dT
p
T ,nB ,nc ,nD
X
dp
nB
T , p,nc ,nD
dnB
X
X
nC
T , p,nB p,nB ,nc
dnD
2021/1/6
偏摩尔量XB的定义为: X B def
X ( nB )T , p,nc
2021/1/6
解:取1kg溶液
nH2O
mH2O M H2O
(1 0.12)1 18.015 103
mol
48.85mol
nAgNO3
mAgNO3 M AgNO3
0.12 1 169.89 103
mol
0.7064mol
xAgNO3
nAgNO3
n n AgNO3
H2O
0.01425
cAgNO3
2021/1/6
由题意:
VA 17.35cm3 / mol
VB 39.01cm3 / mol
由集合公式,混合后:
V nAVA nBVB {0.617.35 0.4 39.01}cm3 26.01cm3
混合前:
VA '
nAM A A
10.84cm3
VB'
nB M B B
16.19cm3
dA SdT pdV BdnB
dA
B
BdnB 0
自发 =平衡
B
(dT 0,dV 0, W ' 0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章多组分系统热力学及其在溶液中的应用
一、多组分系统的组成表示法
1、混合物中任一组分B的表示法:
(1)B的质量浓度:B的质量浓度=B密度
(2)B的质量分数:
(3)B的浓度:
(4)B的摩尔分数:(单位为1)
2、溶液中任一组分B的表示法:
(1)溶质B的质量摩尔浓度或:
(2)溶质B的摩尔比:(单位为1)
二、偏摩尔量
1、系统的任一种容量性质Z除了与温度、压力有关外,还与系统中各组分的数量即物质的量有关。
2、偏摩尔量的Gibbs自由能:
【只有广度性质才有偏摩尔量,偏微商外的下角标均为,,即只有在等温等压,除B以外的其她组分的量保持不变时,某广度性质对组分B的物质的量的偏微分才称为偏摩尔量又称为化学势】
3、偏摩尔量的加与公式:
例:在298K与大气压力下,含甲醇(B)的摩尔分数X B 为0、458的水溶液的密度为0、8946Kg/dm3 ,甲醇的偏摩尔体积,试求该溶液中水的偏摩尔体积:
三、化学势(化学势就是状态函数,就是强度量,绝对值不可知,因此不同物质的化学势大小不能进行比较)
1、热力学能:
狭义化学势就是指偏摩尔Gibbs自由能:
2、化学势在相平衡中的应用:
化学式与温度、压力的关系:
化学式与压力的关系:
化学式与温度的关系:
四、气体混合物中各组分的化学式:
对于理想气体混合物的分子模型与纯理想气体就是相同的,即分子自身的体积相对容器体积而言可以忽略不计,分子间的相互作用能极小也可以忽略不计。
因此,把几组纯组分的理想气体混合变成混合气体时,混合热等于零,并在宏观上遵守如下的状态方程:也满足道尔顿分压定律:混合气体平衡后有:
混合气体的化学势:
五、稀溶液中的两个经验定律
1、拉乌尔定律:(溶剂)
(如果溶剂与溶质分子间的相互作用的差异可以忽略不计,而且当溶质与溶剂形成溶液时,,相当于形成了液体混合物,则由于在纯溶剂中加入溶质后减少了溶液单位体积与单位表面上溶剂分子的数目,因而也减少了单位时间内可能离开液相表面而进入气相的溶剂分子数目,以致溶剂与其蒸汽在较低的蒸汽压力下即可达到平衡,所以溶液中溶剂的蒸气压较纯溶剂的蒸气压较低)
2、亨利定律:(溶质)
、、
六、理想液态混合物:
(当各组分混合时,没有焓变与体积的变化,即、) 1理想液态混合物中任一组分的化学势:
设温度T时,当理想液态混合物与其蒸汽达平衡时,理想液态混合物中任一组分B与气相中该组分的化学势相等,即、
对于纯的液相B,X B=1 , 故在温度T,压力P时,
七、稀溶液的依数性:(取决于所含溶质分子的数目,而与溶质本性无关)
1、凝固点降低:
固态纯溶剂与溶液成平衡时的温度称为溶液的凝固点。
(固液两相平衡时共存的温度称为凝固点)
凝固点降低常数:
2、沸点升高:
沸点就是指液体的蒸气压等于外压时的温度。
根据拉乌尔定律,在定温时当溶
液中含有不挥发性溶质时,溶液的蒸气压总就是比纯溶剂低,所以溶液的沸点比纯溶剂高。
