振动单位换算表
振动单位换算表
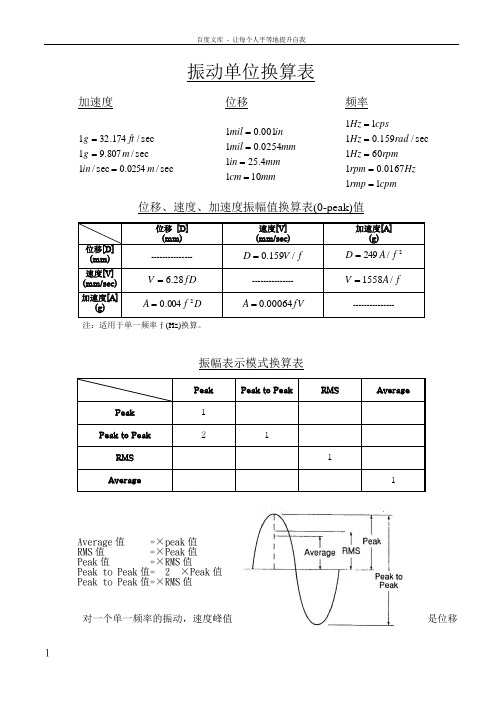
振动单位换算表加速度位移频率sec/0254.0sec /1sec /807.91sec /174.321m in m g ft g ===mmcm mm in mm mil inmil 1014.2510254.01001.01==== cpmrmp Hz rpm rpm Hz rad Hz cpsHz 110167.01601sec/159.0111=====位移、速度、加速度振幅值换算表(0-peak)值位移 [D] (mm) 速度[V] (mm/sec)加速度[A](g)位移[D] (mm) ---------------fV D /159.0=2/249f A D =速度[V] (mm/sec) fD V 28.6= ---------------f A V /1558=加速度[A](g)D f A 2004.0=fV A 00064.0=---------------注:适用于单一频率f (Hz)换算。
振幅表示模式换算表Peak Peak to PeakRMS AveragePeak 1 Peak to Peak2 1 RMS 1 Average1Average 值 =×peak 值 RMS 值 =×Peak 值 Peak 值 =×RMS 值Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=×RMS 值对一个单一频率的振动,速度峰值是位移峰值的2πf倍,加速度峰值又是速度峰值的2πf倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
赫兹单位换算

赫兹单位换算单位换算,是学生常见而又容易忽视的问题。
尤其是在物理科目里,一些看似简单的问题却很容易被忽略掉,导致实际解决问题的时候困难重重。
我们今天来讲讲赫兹与其他的物理单位之间的转换关系。
在生活中有许多地方都要用到赫兹这个物理单位,但是由于不同领域的人往往对它们的概念有些模糊不清,如果不了解这些知识,就会影响到学习。
将一秒钟分为一百万份的话,那么一份等于一个赫兹。
我们的时钟滴答作响,每敲响一下就是一个周期。
一天等于24个小时,一年等于365天。
每天的中午12点和下午12点都相当于我们所说的1小时,每一小时为60分钟,每一分钟也就是1000赫兹。
其他的还有:1赫兹=1次方秒= 1/3600秒;秒针走一圈= 60秒,也就是360赫兹。
1米=3尺= 3/4英寸;波长=1/*1*pi* 6,约为1/*1*pi*10^-12。
毫米= 10微米;英尺=12英寸= 1/2英里。
电流的速度每秒大约为*1*4.18*1**2,即(*1*1*pi*6*1**2)/*4.18=2.55*10^-15m/s。
这是因为:当光线通过介质时,传播速度会减慢,光在真空中的传播速度最大,约为* 1**2。
当传播介质的厚度增加时,光的传播速度就会降低。
当电磁波的频率与赫兹相同或者更高时,我们说该电磁波的频率是多少赫兹。
频率越高,该物体发出的波的波长就越短,频率越低,波长就越长。
赫兹可以被用来表示光的强度。
一般来说,光是指频率在3~300 THz的电磁波。
我们通常说的光,实际上就是指这种波长范围的电磁波。
赫兹也可以用来表示光的颜色,比如我们通常说的红光、绿光、蓝光。
5秒,被称为光的1秒,指的是一次电磁辐射在真空中1秒内走完的距离。
10,被称为光的10秒,指的是一次电磁辐射在真空中10秒内走完的距离。
光波的周期取决于光子的数量。
在常温下,光的周期与温度成正比,这意味着当温度升高时,光的周期也将缩短。
但并非所有的电磁波都是这样。
例如,在0 ℃的时候,水银蒸汽几乎没有振动,也就无法产生光;氦氖激光器在-269 ℃仍然能够工作。
振动单位换算表
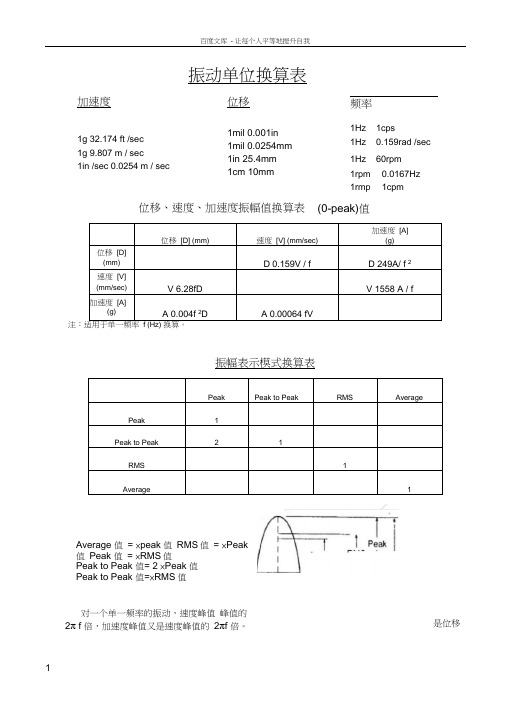
振动单位换算表位移 [D] (mm)速度 [V] (mm/sec) 加速度 [A](g)位移 [D](mm)D 0.159V / fD 249A/ f 2 速度 [V](mm/sec)V 6.28fDV 1558 A / f加速度 [A](g)A 0.004f 2D A 0.00064 fVf (Hz) 振幅表示模式换算表PeakPeak to PeakRMSAveragePeak 1Peak to Peak21RMS1Average1Average 值 = ×peak 值 RMS 值 = ×Peak值 Peak 值 = ×RMS 值Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=×RMS 值对一个单一频率的振动,速度峰值 峰值的 2π f 倍,加速度峰值又是速度峰值的 2πf 倍。
加速度1g 32.174 ft /sec 1g 9.807 m / sec1in /sec 0.0254 m / sec位移1mil 0.001in 1mil 0.0254mm 1in 25.4mm 1cm 10mm频率1Hz 1cps 1Hz 0.159rad /sec 1Hz 60rpm 1rpm 0.0167Hz 1rmp 1cpm位移、速度、加速度振幅值换算表 (0-peak)值是位移当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
但使用范围也有重叠。
位移值体现的是设备在空间上的振动范围,因此取其峰峰值,电力行业一般以位移为评判标准。
速度的有效值和振动的能量是成比例的,其大小代表了振动能量的大小,现在出了电力行业基本上都是以速度有效值为标准的。
振动的基础知识

频率
频率f是物体每秒钟振动循环的次数,单位是 赫兹[Hz]。 频率是一种振动特性,是分析振动故障原因 的主要依据。机器发生故障,一般只是某个 或某些部件出了故障并产生异常振动,异常 振动的频率是由此故障自身机理特性所决定 的,也就是说故障与频率存在着对应关系, 即“问题严重程度看振幅,什么问题看频 率”。
FFT
时间域 IFFT 频率域
之间的相位差,单位是度°。(也是就是转频分量从键相信 号起到振动最高峰值之间的时间计算值) (正峰值计算法:第一个正峰值与固定参考点的角位置)无 论采取何种相位取值方法,基频信号的相位都是值落后角度。 是振动在时间先后关系上或空间位置关系上相互差异的标志。 确定相位标记 在工程上指转轴上所做的键相谱(光电标)位置。 相位主要用于比较不同振动运动之间的关系(时间差及方位 差),或确定一个部件相对于另一个部件的振动状况,在区 别相同故障频率的不同故障类型时(特别是不平衡)往往起 关键作用。
速度振幅反映了分析频段内时间历程的振动能量即 振动烈度 振动烈度是描述机器振动状态的特征量。 通常在各个测量位置的水平、垂直和轴向上都进行 测量,得到一组不同的振幅值,所测的宽带最大振 幅值定义为振动烈度。 由于振动烈度可参照振动标准,评价机器振动状态 优劣;因此,在机器壳体上测量振动时要求在靠近 轴承位置处的三个方向上都进行测量,最后取最大 值作为振动烈度。
机械的支承分类
测量方向上,机器-基础组合分为柔性支承和 刚性支承。 柔性支承:系统自振转速低于工作转速。 刚性支承:系统自振转速高于工作转速。 对应基础组合系统的自振转速都有180°的相 位变化。 其中刚性基础不能承受系统的剪切力;柔性 基础能承受系统的剪切力
谢谢大家
振动一般可以用以下三个单位表示

振动一般可以用以下三个单位表示:mm、mm/s、mm/(s^2)。
mm振动位移:一般用于低转速机械的振动评定; mm/s振动速度:一般用于中速转动机械的振动评定; mm/(s^2)振动加速度:一般用于高速转动机械的振动评定。
现在的测振仪一般都采用压电式的,结构形式大致有二种:① 压缩式;② 剪切式,其原理是利用石英晶体和人工极化陶瓷(PZT)的压电效应设计而成。
当石英晶体或人工极化陶瓷受到机械应力作用时,其表面就产生电荷,所形成的电荷密度的大小与所施加的机械应力的大小成严格的线性关系。
同时,所受的机械应力在敏感质量一定的情况下与加速度值成正比。
在一定的条件下,压电晶体受力后产生的电荷与所感受的加速度值成正比。
产生的电荷经过电荷放大器及其它运算处理后输出就是我们所需要的数据了Q=dij·F=dij·m a式中:Q ── 压电晶体输出的电荷dij ── 压电晶体的二阶压电张量m ── 加速度的敏感质量a ── 所受的振动加速度值'. 压电加速度计承受单位振动加速度值输出电荷量的多少,称其电荷灵敏度,单位为pC/ms-2或pC/g(1g = 9.8ms-2)。
压电加速度计实质上相当于一个电荷源和一只电容器,通过等效电路简化以后,则可换算出加速度计的电压灵敏度为Sv = SQ/CaSv ── 加速度计的电压灵敏度 mV/ms-2SQ ── 加速度计的电荷灵敏度 pC/ms-2Ca ── 加速度计的电容量压电式速度传感器,它是通过在压电式加速度传感器上加一个积分电路,通过将加速度信号积一次分,可以得到振动的速度值!在振动测量时,应合理选择测量参数,如振动位移是研究强度和变形的重要依据;振动加速度与作用力或载荷成正比,是研究动力强度和疲劳的重要依据;振动速度决定了噪声的高低,人对机械振动的敏感程度在很大频率范围内是由速度决定的。
速度又与能量和功率有关,并决定动量的大小。
振动单位换算表.docx
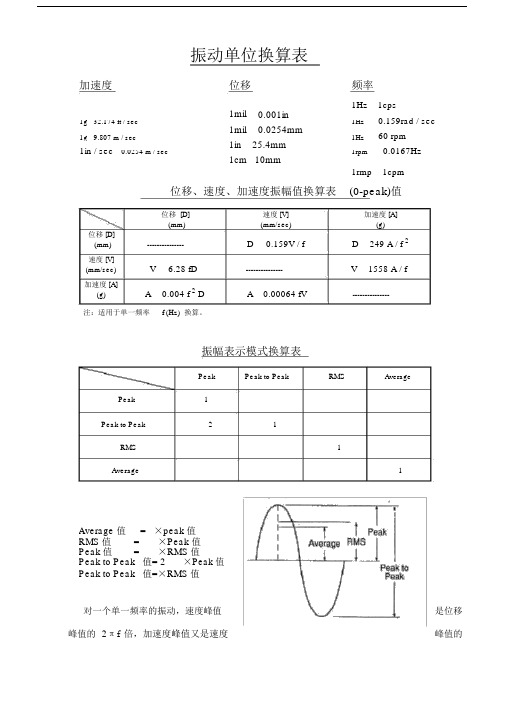
振动单位换算表加速度位移频率1mil 1Hz1cps 0.001in 0.159rad / sec1g 32.174 ft / sec 1Hz1mil0.0254mm60 rpm 1g 9.807 m / sec1Hz 1in / sec1in 25.4mm 0.0167Hz 0.0254 m / sec1rpm1cm 10mm1cpm1rmp位移、速度、加速度振幅值换算表(0-peak)值位移 [D] 速度 [V] 加速度 [A](mm)(mm/sec)(g)位移 [D] ---------------D 0.159V / f D 249 A / f2(mm) 速度 [V] V 6.28 fD ---------------V1558 A / f(mm/sec) 加速度 [A]A0.004 f 2DA0.00064 fV---------------(g)注:适用于单一频率f (Hz) 换算。
振幅表示模式换算表PeakPeak to Peak RMS AveragePeak1Peak to Peak21RMS1Average1Average 值 = ×peak 值 RMS 值 = ×Peak 值 Peak 值 = ×RMS 值 Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=×RMS 值对一个单一频率的振动,速度峰值是位移峰值的2πf 倍,加速度峰值又是速度峰值的2πf倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
但使用范围也有重叠。
振动一般可以用以下三个单位表示

振动一般可以用以下三个单位表示:mm、mm/s、mm/(s^2)。
mm振动位移:一般用于低转速机械的振动评定; mm/s振动速度:一般用于中速转动机械的振动评定; mm/(s^2)振动加速度:一般用于高速转动机械的振动评定。
现在的测振仪一般都采用压电式的,结构形式大致有二种:① 压缩式;② 剪切式,其原理是利用石英晶体和人工极化陶瓷(PZT)的压电效应设计而成。
当石英晶体或人工极化陶瓷受到机械应力作用时,其表面就产生电荷,所形成的电荷密度的大小与所施加的机械应力的大小成严格的线性关系。
同时,所受的机械应力在敏感质量一定的情况下与加速度值成正比。
在一定的条件下,压电晶体受力后产生的电荷与所感受的加速度值成正比。
产生的电荷经过电荷放大器及其它运算处理后输出就是我们所需要的数据了Q=dij·F=dij·m a式中:Q ── 压电晶体输出的电荷dij ── 压电晶体的二阶压电张量m ── 加速度的敏感质量a ── 所受的振动加速度值'. 压电加速度计承受单位振动加速度值输出电荷量的多少,称其电荷灵敏度,单位为pC/ms-2或pC/g(1g = 9.8ms-2)。
压电加速度计实质上相当于一个电荷源和一只电容器,通过等效电路简化以后,则可换算出加速度计的电压灵敏度为Sv = SQ/CaSv ── 加速度计的电压灵敏度 mV/ms-2SQ ── 加速度计的电荷灵敏度 pC/ms-2Ca ── 加速度计的电容量压电式速度传感器,它是通过在压电式加速度传感器上加一个积分电路,通过将加速度信号积一次分,可以得到振动的速度值!在振动测量时,应合理选择测量参数,如振动位移是研究强度和变形的重要依据;振动加速度与作用力或载荷成正比,是研究动力强度和疲劳的重要依据;振动速度决定了噪声的高低,人对机械振动的敏感程度在很大频率范围内是由速度决定的。
速度又与能量和功率有关,并决定动量的大小。
振动分析中常用的计算公式

振动分析中常用的计算公式在振动分析中,有许多常用的计算公式,以下是一些常见的计算公式和它们的应用。
1. 频率(Frequency)计算公式:频率是指振动系统中单位时间内的往复运动次数。
频率的计算公式为:f=1/T其中,f为频率,T为周期,频率的单位是赫兹(Hz)。
2. 周期(Period)计算公式:周期是指振动系统中一个完整循环所需的时间。
周期的计算公式为:T=1/f其中,T为周期,f为频率,周期的单位是秒(s)。
3. 振幅(Amplitude)计算公式:振幅是指振动系统中最大偏离平衡位置的距离。
振幅的计算公式为:A = (x1 + x2 + ... + xn) / n其中,A为振幅,xi为第i个测量值,n为测量次数。
4. 谐振频率(Resonant Frequency)计算公式:谐振频率是指在没有外力作用下,振动系统自然地振动的频率。
谐振频率的计算公式为:f=√(k/m)/(2π)其中,f为谐振频率,k为系统的弹性系数(刚度),m为系统的质量,谐振频率的单位是赫兹(Hz)。
5.等效刚度(Equivalent Stiffness)计算公式:等效刚度是指在多个弹簧(或多个质量)连接的振动系统中,与整个系统的振动特性相同的单个刚度。
等效刚度的计算公式为:keq = k1 + k2 + ... + kn其中,keq为等效刚度,ki为第i个弹簧(或质量)的刚度。
6.等效质量(Equivalent Mass)计算公式:等效质量是指在多个质量连接的振动系统中,与整个系统的振动特性相同的单个质量。
等效质量的计算公式为:meq = m1 + m2 + ... + mn其中,meq为等效质量,mi为第i个质量。
7. 阻尼比(Damping Ratio)计算公式:阻尼比是指振动系统中阻尼力与临界阻尼力之比。
阻尼比的计算公式为:ζ = c / (2√(mk))其中,ζ为阻尼比,c为阻尼系数,m为质量,k为刚度。
8. 动力响应(Dynamic Response)计算公式:动力响应是指系统在受到外界力作用时的振动响应。
振动单位换算表(完整资料).doc
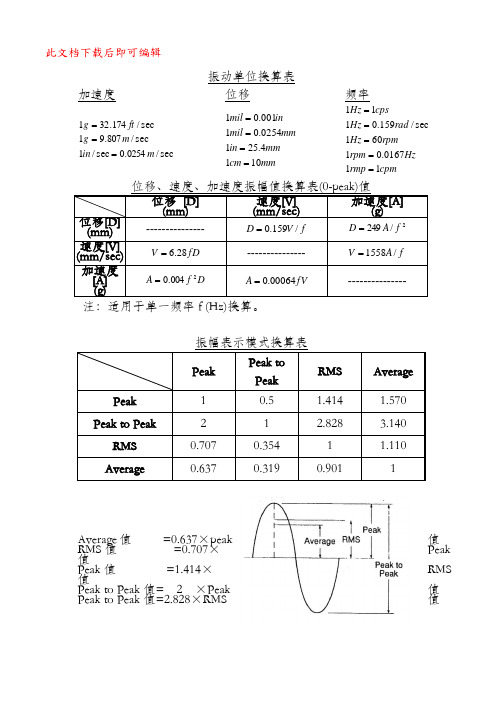
此文档下载后即可编辑 振动单位换算表 加速度位移 频率 sec /0254.0sec /1sec/807.91sec/174.321m in m g ft g === mm cm mmin mm mil in mil 1014.2510254.01001.01==== cpm rmp Hzrpm rpm Hz rad Hz cps Hz 110167.01601sec /159.0111=====位移、速度、加速度振幅值换算表(0-peak)值 位移 [D] (mm) 速度[V] (mm/sec) 加速度[A] (g) 位移[D] (mm) --------------- f V D /159.0= 2/249f A D = 速度[V] (mm/sec) fD V 28.6= --------------- f A V /1558= 加速度[A] (g)D f A 2004.0= fV A 00064.0= ---------------振幅表示模式换算表Peak Peak to Peak RMS Average Peak1 0.5 1.414 1.570 Peak to Peak2 1 2.828 3.140 RMS0.707 0.354 1 1.110 Average0.637 0.319 0.901 1Average 值 =0.637×peak 值 RMS 值 =0.707×Peak 值 Peak 值 =1.414×RMS 值 Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=2.828×RMS 值对一个单一频率的振动,速度峰值是位移峰值的2πf倍,加速度峰值又是速度峰值的2πf倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
振动单位换算表
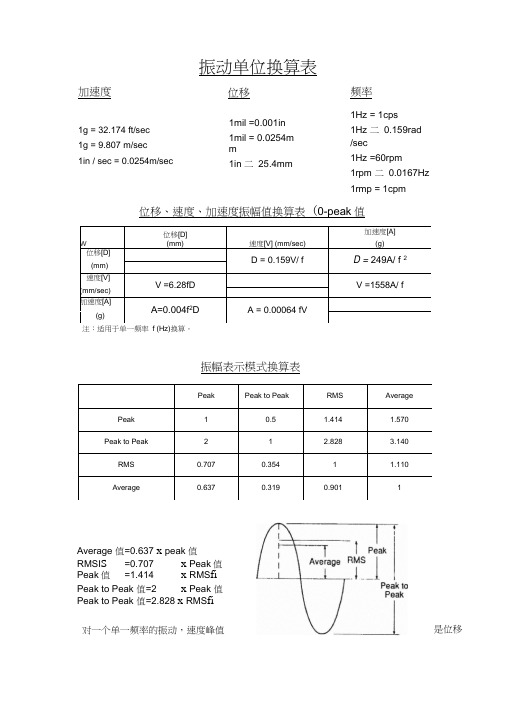
振动单位换算表加速度 1g = 32.174 ft/sec 1g = 9.807 m/sec 1in / sec = 0.0254m/sec频率1Hz = 1cps 1Hz 二 0.159rad /sec 1Hz =60rpm 1rpm 二 0.0167Hz 1rmp = 1cpm位移、速度、加速度振幅值换算表 (0-peak 值w 位移[D] (mm)速度[V] (mm/sec)加速度[A](g)位移[D]D = 0.159V/ fD = 249A/ f 2(mm)速度[V] V =6.28fDV =1558A/ f(mm/sec)加速度[A] A=0.004f 2DA = 0.00064 fV(g)注:适用于单一频率 f (Hz)换算。
振幅表示模式换算表Peak Peak to PeakRMS Average Peak 1 0.5 1.414 1.570 Peak to Peak 2 1 2.828 3.140 RMS 0.707 0.354 1 1.110 Average 0.6370.3190.9011Average 值=0.637 x peak 值RMSI S =0.707 x Peak 值 Peak 值 =1.414 x RMS fi Peak to Peak 值=2 x Peak 值 Peak to Peak 值=2.828 x RMS fi 对一个单一频率的振动,速度峰值 是位移1mil =0.001in 1mil = 0.0254m m1in 二 25.4mm 1cm = 10mm位移峰值的2n f倍,加速度峰值又是速度峰值的2n f倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
随机振动名称解释

加速度頻譜密度(Acceleration Spectral Density, ASD)就是隨機振動的功率頻譜密度(Power Spectral Density, PSD),隨機振動只能用能量表示,單位為g^2(加速度g平方),密度是指單位頻寬。
取窄頻帶振動時域訊號的傅立葉轉換值平方後除以頻帶寬,即可計算得到該頻帶對應的加速度頻譜密度值。
ASD:加速度谱密度常用单位:(m/s2)2 /Hz,m2/s3PSD:功率谱密度常用单位:g2/Hz (一般是根据实测数据(一般是测加速度),简化处理得到振动台所需要的PSD,或是根据相关标准直接得到。
)加速度谱密度就是(功率谱密度)它是指每个单位频率的能量。
换算公式:1g2/Hz=96.04(m/s2)2 /Hz=96.04m2/s3g — 加速度(acceleration)的单位,每秒增加9.81公尺称为一个加速度.1 g = 9.81 m/s2lg2/Hz — 功率频谱密度(P.S.D)的单位,每单位时间内所做的功率.lG rms — 指将各频率点之功率频谱密度进行积分后的总能量,为有效值.我们平常所说的g‘值是一个重力加速度值,就是1G=9.8m/s2, 而Grms是个积累的物理量,类似于能量一样,在一定的频率范围内对PSD积分(近似的算法就是求面积,在将面积开方就是你所需要的了),然后将积分的结果开方,也叫加速度总均方根值。
在物理学中,信号通常是波的形式,例如电磁波、随机振动或者声波。
当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率,这被称为信号的功率谱密度(power spectral density, PSD)或者谱功率分布(spectral power distribution, SPD)。
功率谱密度的单位通常用每赫兹的瓦特数(W/Hz)表示,或者使用波长而不是频率,即每纳米的瓦特数(W/nm)来表示。
因为运动的质点处于不规则的运动状态,永远不会精确地重复,对其进行一系列的测量各次记录也不一样,所以没有固定的周期。
db与hz的换算关系

db与hz的换算关系在音乐领域,我们常常会涉及到频率的概念,而说到频率,不可避免地就要提到hz和db两个单位。
这两个单位的换算关系,在音乐学习和实践中是非常必要的。
本文将重点介绍hz和db的换算关系,并讨论它们在音乐中的实际应用。
1. hz的概念和基本认识首先,我们来认识一下hz这个单位。
Hz全称为赫兹(Hertz),是电磁波、声波振动等频率的单位。
hz是一种表示每秒钟振动次数的单位,换句话说,hz是时间单位中的一种。
通常,我们用hz来表示声音的频率,即指每秒钟振动的声波次数。
例如,“1000Hz”意味着每秒钟有1000个声波震动。
音频文件的采样率也是以hz为单位来表示的。
其次,让我们来了解一下db这个单位。
db全称为分贝(decibel),是一种无量纲单位。
它用来表示声音、光线等在传播过程中强度的比值。
分贝的定义是10倍对数的比值。
例如,某声音的强度是另一声音的10倍,则它的分贝数为10dB。
在音乐中,我们通常使用分贝来描述音量和音色。
音量越大,分贝数就越高,而音色则与分贝没有直接的关系。
通常,我们使用分贝来进行音量调节,如在现场演出中调节音响的输出音量。
hz和db这两个单位没有直接的换算公式,因为它们表示的是不同的物理量,不能互相转换。
然而,在实际的音乐学习和实践中,我们经常需要将它们进行关联,以便更好地理解和应用。
在音乐中,我们通常使用一种名为“等响曲线”的概念来描述不同频率下的“响度”(即人能感受到的声音强度)。
等响曲线是一种图表,用来表示不同频率下人类耳朵对声音强度的感知程度。
在这个图表中,响度单位是分贝,频率单位是hz。
通过对不同频率下的等响曲线的测量和研究,我们可以推断出不同频率下的声音强度与分贝的大致关系。
例如,根据常见的等响曲线,对于人类耳朵来说,1000Hz左右的频率下的声音强度为60dB。
因此,在音乐实践中,我们可以将音乐设备的输出音量控制在60dB左右,以保证听众能够舒适地聆听音乐。
振动单位换算表

振动单位换算表振动单位换算表:1 Hz = 1 cps1 Hz = 0.159 rad/sec1 g = 32.174 ft/sec1 g = 9.807 m/sec1 in/sec = 0.0254 m/sec1 mil = 0.001 in1 mil = 0.0254 mm1 in = 25.4 mm1 cm = 10 mm1 Hz = 60 rpm1 rpm = 0.0167 Hz1 rpm = 1 cpm位移、速度、加速度振幅值换算表(0-peak)值:位移[D] (mm) 速度[V] (mm/sec) 加速度[A] (g)位移[D] (mm) --------------- 速度[V] (mm/sec) 加速度[A] (g) D = 0.159V/f --------------- D = 249A/f^2V = 6.28fDA = 0.004f^2DV = 1558A/f --------------- A = 0.fV注:适用于单一频率f(Hz)换算。
振幅表示模式换算表:Peak Peak to Peak RMS AveragePeak 1 2 0.707 0.637Peak to Peak 0.5 1 0.354 0.319 RMS 1.414 2.828 1 0.901 Average 1.570 3.140 1.110 1其中。
Average值 = 0.637 × peak值RMS值 = 0.707 × Peak值Peak值 = 1.414 × RMS值Peak to Peak值 = 2 × Peak值Peak to Peak值 = 2.828 × RMS值对于单一频率的振动,速度峰值是位移峰值的2πf倍,而加速度峰值是速度峰值的2πf倍。
需要注意的是,位移一般使用峰峰值,速度使用有效值,加速度使用峰值。
此外,现场测量的位移是轴和轴瓦的相对振动,而速度和加速度测量的是轴瓦的绝对振动。
振动单位换算表精编版
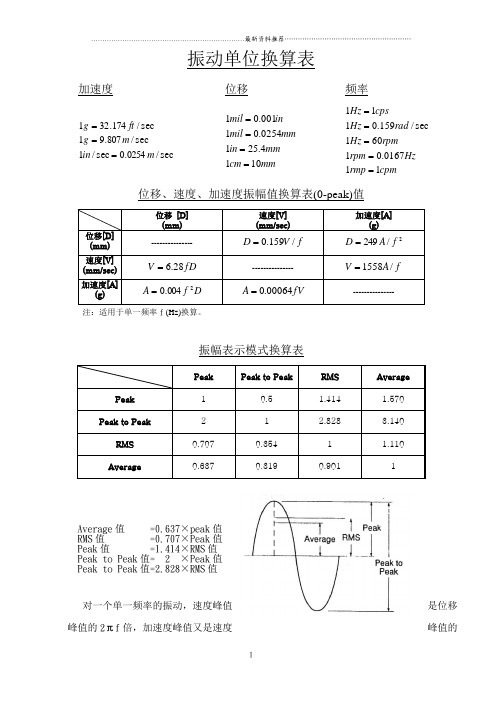
振动单位换算表 加速度 位移 频率sec /0254.0sec /1sec/807.91sec/174.321m in m g ft g === mm cm mmin mm mil in mil 1014.2510254.01001.01==== cpm rmp Hzrpm rpm Hz rad Hz cpsHz 110167.01601sec /159.0111=====位移、速度、加速度振幅值换算表(0-peak)值注:适用于单一频率f (Hz)换算。
振幅表示模式换算表Average 值 =0.637×peak 值RMS 值 =0.707×Peak 值Peak 值 =1.414×RMS 值Peak to Peak 值= 2 ×Peak 值Peak to Peak 值=2.828×RMS 值对一个单一频率的振动,速度峰值是位移峰值的峰值的2πf 倍,加速度峰值又是速度2πf倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
但使用范围也有重叠。
位移值体现的是设备在空间上的振动范围,因此取其峰峰值,电力行业一般以位移为评判标准。
速度的有效值和振动的能量是成比例的,其大小代表了振动能量的大小,现在出了电力行业基本上都是以速度有效值为标准的。
加速度和力成正比,一般用其峰值,其大小表示了振动中最大的冲击力,冲击力大设备更容易疲劳损坏,现在没有加速度的标准。
振动幅值的表达式是正弦函数形式的,位移微分得到速度,速度微分得到加速度。
则:振动位移方程式: Y=Asinωt振动速度方程式: V= -Aωcosωt振动速度方程式: G= -Aωωsinωt如果振动频率为f的话,那么ω=2πf 其中π=3.1415926如果是单频率f的振动,位移的幅值为A,则速度幅值为2πfA,加速度幅值为2πf*2πfA。
振动单位换算
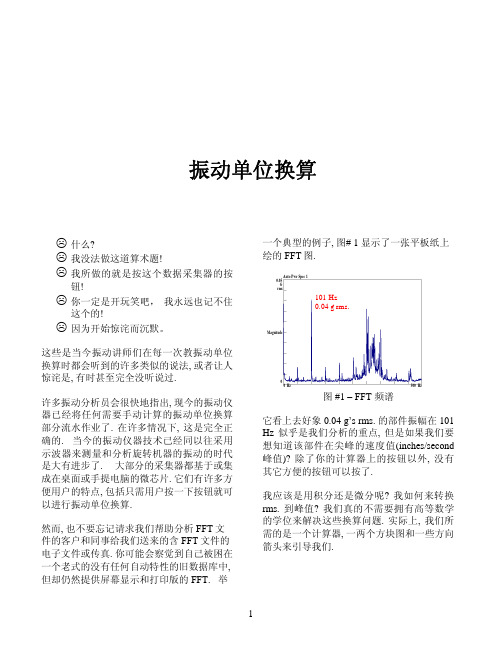
在图 #4 中, “Pi”的值大约是 3.14, “f” 的值是 要被转换的振幅组成部分的频率. 在图#1 的 例子中, 0.04 g’s rms.振幅组成部分的频率的 值是 101 Hz. 因此, 如果我们采用图#1 的数 据和图#4 的方块图的话, “f” 的值将等于 101 Hz .
让我们试试采用图#4 的方块图将图#1 的数据 (0.04 g’s rms. 在 101 Hz) 转换(积分)为速度. 从图#4 方块图的顶端开始按照箭头方向向右 移动到显示乘数为 9807 的数学方块处, 我们 可 以 将 用 g’s 表 示 的 加 速 度 值 转 换 成 以 mm/second2 表示的加速度值
要将换峰值转换到峰-峰值, 必须连续向方块
图的左上方移动. 在左上方角的数学方块表 示我们必须用 2 乘以峰值来得到峰-峰值.
0.057 g’s 峰 值 x 2 = 0.114 g’s 峰-峰值
同样, 我们如果要转换 0.114 g’s 峰-峰值到峰 值, 我们会从方块图的上方向右边箭头移动. 数学方块表示我们必须用 2 来除以峰-峰值来 得到峰值.
我应该是用积分还是微分呢? 我如何来转换 rms. 到峰值? 我们真的不需要拥有高等数学 的学位来解决这些换算问题. 实际上, 我们所 需的是一个计算器, 一两个方块图和一些方向 箭头来引导我们.
1
振动单位换算
转换单位后缀:
在我们开始进行加速度, 速度和位移单位换算 前, 让我们先来学习如何将单位从 rms 转换成 峰值再到峰-峰值. 峰值和 rms 通常被用在 FFT 图中, 表示一个频率组成的幅度. 峰值通 常和测得的最大幅值相关, 而 rms. (均方根) 经常和能量或幅度功率相联. 这两个单位都被 用于测量加速度和速度. 位移的测量是使用 峰-峰值单位后缀来表示振动所导致的总移动 或动作. 在所有单位之间进行换算是可能的, 现在就让我们用图#2 的带箭头的方块图来作 例子讲解.
振动值mm与um的换算关系

振动值mm与um的换算关系
互联网是一个充满活力的现代社会信息终端,也是在众多行业中开创着无限可
能性的多元空间之一。
其中,振动涉及到衡量质量标准、设备操作参数设定、机器检测等方面,是科学实验中极为重要的一个概念。
以mm和um振动数值来评估振动,也是我们日常实验工作中常用的一个参数。
振动值的换算关系显然是mm的毫米和um的微米之间的关系。
一般来说。
一毫
米(mm)有一千微米(um),或者反过来也可以说一微米就有一千分之一毫米。
也就是说,如果要把mm的振动值转换成UM的振动值,我们只需要把mm的振动值乘
以一千就可以了。
所以,要想准确测量振动,无论是用mm还是UM来衡量,我们都需要知道他们
之间的换算关系。
只有通过转换,才能准确把振动值衡量出来,从而确保检测结果的准确性。
另外,为了提高精度,也可以在换算时使用其他精度度量来换算。
比如在换算时,可以采用”千分之一mm“的精度来更加准确的测量mm的振动值,也可以采用”千万分之一um“精度度量来更加准确的测量um的振动值。
总之,我们在实验工作或设备检测等时,会遇到mm和um的振动值的折衷,所
以我们需要正确掌握他们之间的换算关系,努力去提高精度,以提供准确的振动值评价。
振动测量标准

振幅的定义是:物体离开平衡位置的最大位移,叫振动的振幅.它是表示振动的强弱的物理量.振速:是指波动中各质点都在平衡位置附近做周期性振动,是变加速运动。
质点并没有沿波的传播方向随波迁移。
加速度的定义是速度的变化量和所用时间的比值叫做物体运动的加速度.振动,指的是振幅,既振动的幅度,单位是mm,% x) I& @3 H4 a振速,是说振动的速度,单位是mm/s,1、mm是振幅值,mm/s是振速,也叫振动烈度。
不同的转机可能按照制造厂的出厂说明采取不同的单位来考核。
换算公式可以用:A=V×1000×60×2^(0.5)/(pi×w)A是振动位移峰峰值,单位um。
V是振动烈度,w是转速(r/min)。
2、风机运行工况一般通过测量其轴承温度和振动来判定。
振动大小可通过测量振动位移、振动速度、振动加速度的方式来判定。
太仓港环保发电有限公司送风机和一次风机测量的是振动速度(单位为mm/s),引风机测量的是振动位移(单位为um)。
通常大家习惯于测量振动位移(即振幅),这就存在振动位移和振动速度二者相互换算,其换算公式为:V eff=7.4×10-5nsV eff---振动速度,单位为mm/ss------振动位移, 单位为umn------风机转速, 单位为r/min3、mm/s指振速,mm指振幅,因为不能输入公式编辑器,简单地说二者换算关系为:Sf≈0.225vf/f,式中Sf 为振动的位移幅值,vf 为主频率为f的振动速度的均方根值。
一般f值均为10Hz,所以Sf≈0.0225vf 。
举例说如果vf =1.00m m/s,那么换算成振幅则为Sf≈0.0225mm。
《中华人民共和国机械行业标准(JB/T 10490-2004)·振动。
hz之间的换算单位

hz之间的换算单位
在物理学和工程学中,频率的单位是赫兹(Hz)。
赫兹是每秒
一个周期的频率单位。
换句话说,1赫兹等于每秒1个周期。
赫兹
通常用于描述声音、电磁波、振动等周期性现象的频率。
除了赫兹,还有一些其他常用的频率单位,例如千赫兹(kHz)、兆赫兹(MHz)和吉赫兹(GHz)。
这些单位用于描述高频率的现象,比如无线电通信和计算机处理器的时钟速度。
在实际应用中,频率的换算单位非常简单。
例如,1千赫兹等
于1000赫兹,1兆赫兹等于1000千赫兹,1吉赫兹等于1000兆赫兹。
因此,如果需要在赫兹和其他单位之间进行换算,只需要简单
地进行乘法或除法运算即可。
除了赫兹以外,有时候也会用角频率来描述周期性现象的频率。
角频率的单位是弧度每秒(rad/s),它与赫兹之间的换算可以通过
2π的关系进行转换。
具体而言,1赫兹等于2π弧度每秒。
总之,频率的单位换算涉及到赫兹、千赫兹、兆赫兹、吉赫兹
以及弧度每秒等单位,它们之间的换算可以通过简单的乘除法或者
2π的关系来实现。
这些单位在不同领域的应用中都具有重要的意义,了解它们的换算关系可以帮助我们更好地理解和应用频率概念。
API标准振动值计算公式
API标准振动值计算公式常用的振动测量参数有振幅、振动速度(振速)、振动加速度。
对应单位表示为:mm、mm/s、mm/s²。
振幅是表象,定义为在波动或振动中距离平衡位置或静止位置的最大位移。
振幅在数值上等于最大位移的大小。
振幅是标量,单位用米或厘米表示。
它描述了物体振动幅度的大小和振动的强弱。
系统振动中最大动态位移,称为振幅。
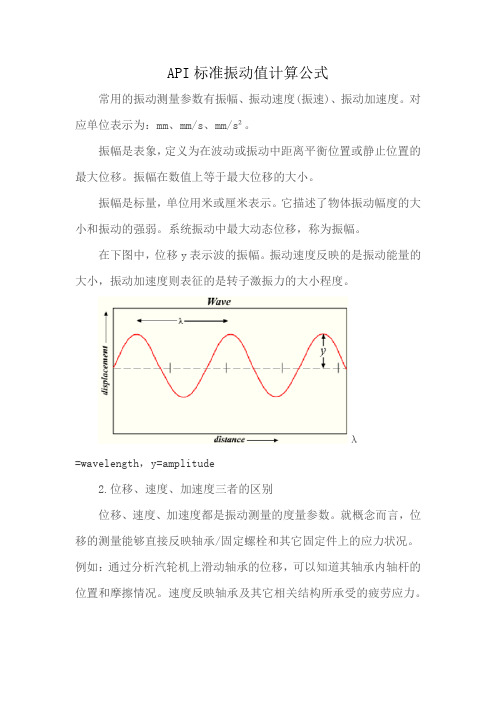
在下图中,位移y表示波的振幅。
振动速度反映的是振动能量的大小,振动加速度则表征的是转子激振力的大小程度。
λ=wavelength,y=amplitude2.位移、速度、加速度三者的区别位移、速度、加速度都是振动测量的度量参数。
就概念而言,位移的测量能够直接反映轴承/固定螺栓和其它固定件上的应力状况。
例如:通过分析汽轮机上滑动轴承的位移,可以知道其轴承内轴杆的位置和摩擦情况。
速度反映轴承及其它相关结构所承受的疲劳应力。
而这正是导致旋转设备故障的重要原因。
加速度则反映设备内部各种力的综合作用。
表达上三者均为正弦曲线,分别有90度,180度的相位差。
现场应用上,对于低速设备(转速小于1000rpm)来说,位移是最好的测量方法。
而那些加速度很小,其位移较大的设备,一般采用折衷的方法,即采用速度测量,对于高速度或高频设备,有时尽管位移很小,速度也适中,但其加速度却可能很高的设备采用加速度测量是非常重要的手段。
3.现场的一般选用原则振动位移:与频率f无关,特别适合低频振动(<10Hz))选用,一般用于低转速机械的振动评定。
振动速度:速度V=Xω,与频率f成正比,通常推荐选用,一般用于中速转动机械(或中频振动(10~1000Hz))的振动评定。
振动加速度:A=Vω=Xω²,与频率f²成正比,特别适合高频振动选用,一般用于高速转动机械(或高频振动(>1000Hz))的振动评定。
其中:工程上对于大多数机器来说,最佳诊断参数是速度(速度的有效值),因为它是反映诊断强度的理想参数,表征的是振动的能量;所以国际上许多振动诊断标准都是采用速度有效值作为判别参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振动单位换算表
振动单位换算表
加速度位移
位移、速度、加速度振幅值换算表(0巾eakWi
注:适用于单•频率换算•
振幅表示模式换算表
Average 值=X peak 值
RMSfil =XPeak 值
Peak 值=XRMS 值
Peak to Peak 值=2 X Peak 值
Peak to Peak fi=XRMSfi
对一个单一频率的据动,速度峰值是位移峰值的2Jtf倍,加速度峰值乂是速度峰值的
2兀f倍。
当然要注童位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频掘动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
但使用范M也有重叠。
位移值体现的是设备在空间上的掘动范因此取其峰峰值,电力行业一般以位移
为评判标准。
速度的有效值和摭动的能量是成比例的,其大小代表了振动能量的大小,现在
出了电力行业基本上都是以速度有效值为标准的。
加速度和力成正比,一般用其峰值, 其大小表示了振动中最大的冲击力,冲击力大设备更容易疲劳损坏,现在没有加速度的标
振动幅值的表达式是正弦函数形式的,位移微分得到速度,速度微分得到加速度。
则:
振动位移方程式J Y=Asin cot
摭动速度方程式J V= -ACDCOSCDt
振动速度方程式:G= -Ao) CDsincot
如果摭动频率为f的话,那么3=2兀f其中打= 如果是单频率f的振动,位移的幅值为A,则速度幅值为2兀fA,加速度幅值为
2兀f*2兀fA。
但是工程中读取的振动值,位移用峰峰值,速度用有效值,加速度用峰
值。
所以一个单频率的振动,位移读数是A的话,速度应该是KfA,加速度是
2兀f*兀fA。
但是因为现场是复杂的,不是单一频率的振动,所以位移,速度和加速度读数间通常没有确定的换算关系。
但是振动频率比较单一,以一个频率为主时可以利用上述关系近似计算。
计算方法举例:
S =峰值偏移振幅,* m
N =频率min-1 f =频率Hz
Veff =有效振动速率mm/s
sN Veff = 1•机械振动物体相对于平衡位置所作的的往复运动称为机械振动。
简称振动。
“振动三
要素"-振幅、频率、相位。
2.振幅摭幅是物体动态运动或振动的幅度。
振幅是振动强度和能量水平的标志,是评
判机器运转状态优劣的主要指标。
峰峰值、单峰值、有效值振幅的量值可以表示为峰峰值(PP)、单峰值(P)(也称为最大值)、有效值(nns)或平均值(叩)。
峰峰值是整个振动历程的最大值,即正峰与负峰之间的差值;单峰值是正峰或负峰的最大值;有效值即均方根值。
只有在纯正弦波(如简谐振动)的情况下,单峰值等于峰峰值的1/2,有效值等于单峰值的倍,平均值等于单峰值的倍;平均值在振动测量中很少使用。
它们之间的换算关系是:峰峰值=2X单峰值=2X (2X有效值)
摭动位移、振动速度、振动加速度振幅分别釆用振动的位移、速度或加速度值加以描述、度量,三者可以通过微分或积分进行换算。
在振动测量中,除特别注明外,振动位移的量值为峰峰值,单位是微米[pmj毫米=100线=1000微米]或密耳[mil];摭动速度的量值为有效值,单位是毫米/秒[mm/s]或英寸/秒[ips];振动加速度的量值是单峰值,单位是重力加速度[g]。
可以认为,振动位移具体地反映了间隙的大小,振动速度反映了能量的大小,振动加速度
反映了冲击力的大小。
也可以认为,在低频范M内,振动强度与位移成正比;在中频范囤内,振动强度与速度成正比;在高频范B内,振动强度与加速度成正比。
正是山于上述原因,在工厂的实际应用中,在通常悄况下,大机组转子的振动用振动位移
的峰峰值[pm]表示,用装在轴承上的非接触式电涡流位移传感器来测量转子轴颈的摭
动;大机组轴承箱及缸体、中小型机泵的振动用振动速度的有效值[mm/s]表示,用装在机器壳体上的磁电式速度传感器或压电式加速度传感器来测量;
齿轮的振动用振动加速度的单峰值[g]表示,用加速度传感器来测量。
振动烈度、振动标准振动烈度是掘动标准中的通用术语,是描述一台机器振动状态的特征
量(大机组不完全如此)。
可以认为,振动烈度就是振动速度的有效值。
在国际及我国振动标准中,儿乎都规定用振动速度的有效值来作为振动烈度的度量值。
此外,还要求在壽近轴承位置处的水平、垂直、轴向三个方向上进行测量。
所以,对一般的转动设备进行振动监测时,应测量振动速度的有效值。
因为只有振动烈度才有振动标准可以参照,评定机器运转状态的优劣才能有据可依。
右图为中石化旋转机械振动标准SHS 01003-2004关于机器振动烈度的评定等级表。
我
国及国际其它振动标准关于机器振动烈度的评定等级也大致如此。
其中,根据输出功率、机器一支承系统的刚性等将旋转机械分为如下4类:
I〜小型转机,如15 kW以下的电机;
II〜安装在刚性S础上的中型转机,功率在300 kW以下;
1【1〜大型转机,机器一支承系统为刚性支承状态:
W〜大型转机,机器一支承系统为挠性支承状态。
当支座的固有频率大于转子轴承系统的固有频率时,机器一支承系统为刚性支承状态;
当支座的固有频率小于转子轴承系统的固有频率时,机器一支承系统为挠性支承状态。
对大型旋转机组转子振动的评定标准,我国及国际振动标准儿乎都规定用在爲近轴承处轴颈振动位移的峰峰值进行度量,但评定标准的具体数值不够统一。
对石油化工用离心式压缩机及汽轮机,API617、API612标准规定,在制造厂进行机械运转试验时,转子振动位移的峰峰值不应超过A值或pm中的较小值,A= (12000/n) 1/2, n为最大连续丄作
转速。
对石化大机组,转子实际运行中振幅的许可值应该遵照制造商的规定。
在无制造商规定时,也可以认为:
小于A值时为优良状态,A为(12000/n) 1/2或Rm中的较小值;
大于A值、小于B值时为合格状态,B = 〜A,转速较低时取大值,转速高时取小值,
B值可设为低报警值;
大于B值、小于C值时为不合格状态,C=, C为高报警值或连锁值;大于C值为不
允许状态。
另外,当振动值变化的增量超过报警值(B值)的25%时,应受到关注。
振动烈度与振动位移的转换
S ====== 25gin (: 个丝)
pm
S ===== 63 P m
100 gin
2 J2X振动烈度/2rif二振动位移其中f取50hz
大家习惯说位移叫振幅,其实位移,速度,加速度都叫振幅,是振动幅度的三种表述方式。
下边是我在其他论坛发过的三个量的换算关系:
关于摭幅换算:
旋转机械的振动方程是正弦函数形式的,位移微分得到速度,速度微分得到加速度。
所以三个参数的幅值间就有如下关系:
必须是单频率f的振动,如果位移的幅值为A,则速度幅值为2兀fA,加速度幅值为
2兀f*2兀fA。
但是工程中读取的振动值,位移用峰峰值,速度用有效值,加速度用峰
值。
所以一个单频率的振动,位移读数是A的话,速度应该是兀fA,加速度是
2兀f*兀fA。
因为现场是复杂的,不是单一频率的振动,所以位移,速度和加速度读数间通常没有确定的换算关系。
但是振动频率比较单一,以一个频率为主时可以利用上述关系近似讣算, 比如通常振动都是一倍频的振动,所以公式中的频率f就是设备的转速。
