数字逻辑课后习题答案
数字逻辑第二版毛法尧课后题答案

(2)F ( A, B, C, D) AB ACD AC BC
AB 00
01 11
10
CD
00 1
1
1
0
1
1
01
1
0
11 1
0
10 1
0
1
1
1
1
(2)F ( A, B,C, D) AB AC BC
最简或与表达式: F ABC ABC F F (A B C)(A B C)
(3)F ( A, B,C, D) BC D D(B C)( AD B) BC D AD B
AB AC D m(0,1,2,3,4,8,12)
2.8
(1)F ( A, B,C) m(0,1,2,4) (2)F ( A, B,C, ) m(0,3,5,6) (3)F ( A, B,C) m(3,5,6,7)
2.9)F f1 f2 (BCD BC C D)( ABC AD CD) BCD ABC D ABC D AC D BCD AC D ABC D BCD AC D BC D
2.7(1)F ( A, B,C) ( AB AC)
( A B)(A C) A BC m(3,4,5,6,7)
(2)F ( A, B,C, D) AB ABCD BC BC D
m(4,5,6,7,8,9,12,13)
(3)F ( A, B,C, D) ( A BC)(B C D)
2.2 用逻辑代数的公理、定理和规则证明下列表达式
(1)(AB AC) AB AC
证明:( AB AC) (A B)(A C)AB 1
证明:AB AB AB AB A A 1
(3) AABC ABC ABC ABC
(2)F ( A B AB)( A B) AB D
数字逻辑课后习题答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制491100016153110101651271111111177635100111101111737.493111.11117.7479.4310011001.0110111231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010101211110161751011100921340.100110.593750.4610111147570110113153.将下列十进制数转换成8421BCD码1997=000110011001011165.312=01100101.0011000100103.1416=0011.00010100000101100.9475=0.10010100011101014.列出真值表,写出X的真值表达式A B C X00000010010001111000101111011111X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1)(A⊕B)⊕C=A⊕(B⊕C)A B C(A⊕B)⊕C A⊕(B⊕C)0000000111010110110010011101001100011111所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C00011001000100001111100001011111011111007.证明下列等式(1)A+A B=A+B 证明:左边=A+A B=A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2)ABC+A B C+AB C =AB+AC 证明:左边=ABC+A B C+AB C=ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C )=AB+AC =右边(3)E D C CD A C B A A )(++++=A+CD+E证明:左边=ED C CD A C B A A )(++++=A+CD+A B C +CDE =A+CD+CD E =A+CD+E =右边(4)C B A C B A B A ++=CB C A B A ++证明:左边=CB AC B A B A ++=C B A C AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1)F=A+ABC+A C B +CB+C B =A+BC+C B (2)F=(A+B+C )(A+B+C)=(A+B)+C C =A+B (3)F=ABC D +ABD+BC D +ABCD+B C =AB+BC+BD (4)F=C AB C B BC A AC +++=BC(5)F=)()()()(B A B A B A B A ++++=B A 9.将下列函数展开为最小项表达式(1)F(A,B,C)=Σ(1,4,5,6,7)(2)F(A,B,C,D)=Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式(1)CAB C B BC A AC F +++=0 ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111AB CD 00 01 11 1000011110化简得F=DA B A +(3)F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111ABCD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4)F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑第四版课后练习题含答案

数字逻辑第四版课后练习题含答案1. 第一章1.1 课后习题1. 将十进制数22转换为二进制数。
答:22 = 101102. 将二进制数1101.11转换为十进制数。
答:1101.11 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 1 x 2^(-1) + 1 x 2^(-2) = 13.753. 将二进制数1101.01101转换为十进制数。
答:1101.01101 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 0 x 2^(-1)+ 1 x 2^(-2) + 1 x 2^(-4) + 0 x 2^(-5) + 1 x 2^(-6) = 13.406251.2 实验习题1. 合成与门电路设计一个合成与门电路,使得它的输入A,B和C,只有当A=B=C=1时输出为1,其他情况输出为0。
答:下面是一个合成与门电路的示意图。
合成与门电路示意图其中,S1和S2是两个开关,当它们都被打开时,电路才会输出1。
2. 第二章2.1 课后习题1. 将十进制数168转换为八进制数和二进制数。
答:168 = 2 x 8^3 + 1 x 8^2 + 0 x 8^1 + 0 x 8^0 = 250(八进制)。
168 = 10101000(二进制)。
2. 将八进制数237转换为十进制数和二进制数。
答:237 = 2 x 8^2 + 3 x 8^1 + 7 x 8^0 = 159(十进制)。
237 = 010111111(二进制)。
2.2 实验习题1. 全加器电路设计一个全加器电路,它有三个输入A,B和C_in,两个输出S和C_out。
答:下面是一个全加器电路的示意图。
C_in|/ \\/ \\/ \\/ \\/ \\A|________ \\| | AND Gate______| |B|__| XOR |_| S\\\\ /\\ /\\ /\\ /| | OR Gate| ||_| C_out其中,AND Gate表示与门,XOR Gate表示异或门,OR Gate表示或门。
数字逻辑课后习题答案(科学出版社_第五版)

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边(3)EDCCDACBAA)(++++=A+CD+E 证明:左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑课本习题答案
习 题 五1. 简述时序逻辑电路与组合逻辑电路的主要区别。
解答组合逻辑电路:若逻辑电路在任何时刻产生的稳定输出值仅仅取决于该时刻各输入值的组合,而与过去的输入值无关,则称为组合逻辑电路。
组合电路具有如下特征:②信号是单向传输的,不存在任何反馈回路。
时序逻辑电路:若逻辑电路在任何时刻产生的稳定输出信号不仅与电路该时刻的输入信号有关,还与电路过去的输入信号有关,则称为时序逻辑电路。
时序逻辑○1○2 电路中包含反馈回路,通过反馈使电路功能与“时序”○3 电路的输出由电路当时的输入和状态(过去的输入)共同决定。
2. 作出与表1所示状态表对应的状态图。
表 1解答根据表1所示状态表可作出对应的状态图如图1所示。
图13.已知状态图如图2所示,输入序列为x=11010010,设初始状态为A,求状态和输出响应序列。
图 2解答状态响应序列:A A B C B B C B输出响应序列:0 0 0 0 1 0 0 14. 分析图3所示逻辑电路。
假定电路初始状态为“00”,说明该电路逻辑功能。
图 3 解答○1根据电路图可写出输出函数和激励函数表达式为 xK x,J ,x K ,xy J y xy Z 1111212=====○2 根据输出函数、激励函数表达式和JK 触发器功能表可作出状态表如表2所示,状态图如图4所示。
表2图4○3由状态图可知,该电路为“111…”序列检测器。
5. 分析图5所示同步时序逻辑电路,说明该电路功能。
图5解答○1根据电路图可写出输出函数和激励函数表达式为 )(D ,x y x D y y x Z 21112121212y x y y y y y x ⊕=+=+=○2 根据输出函数、激励函数表达式和D 触发器功能表可作出状态表如表3所示,状态图如图6所示。
表3图6○3由状态图可知,该电路是一个三进制可逆计数器(又称模3可逆计数器),当x=0时实现加1计数,当x=1时实现减1计数。
6.分析图7所示逻辑电路,说明该电路功能。
第四章1 《数字逻辑》(第二版)习题答案

第四章1.分析图1所示的组合逻辑电路,说明电路功能,并画出其简化逻辑电路图。
图1 组合逻辑电路解答○1根据给定逻辑电路图写出输出函数表达式CA B CBA B CAA B CF⋅+⋅+⋅=○2用代数法简化输出函数表达式CBA ABC CBA ABC C)B(A ABCCABCBABCAABCF+ =+ ++ =+ +=⋅+⋅+⋅=○3由简化后的输出函数表达式可知,当ABC取值相同时,即为000或111时,输出函数F的值为1,否则F的值为0。
故该电路为“一致性电路”。
○4实现该电路功能的简化电路如图2所示。
图24.设计一个组合电路,该电路输入端接收两个2位二进制数A=A2A1,B=B2B1。
当A>B时,输出Z=1,否则Z=0。
解答○1根据比较两数大小的法则,可写出输出函数表达式为○2根据所得输出函数表达式,可画出逻辑电路图如图6所示。
图66.假定X=AB代表一个2位二进制数,试设计满足如下要求 (2) Y=X3(Y也用二进制数表示。
)○1假定AB表示一个两位二进制数,设计一个两位二进制数立方器。
由题意可知,电路输入、输出均为二进制数,输出二进制数的值是输入二进制数AB的立方。
由于两位二进制数能表示的最大十进制数为3,3的立方等于27,表示十进制数27需要5位二进制数,所以该电路应有5个输出。
假定用TWXYZ表示输出的5位二进制数,根据电路输入、输出取值关系可列出真值表如表4所示。
由真值表可写出电路的输出函数表达式为T=AB,====BWAB,ZA,Y0,X根据所得输出函数表达式,可画出用与非门实现给定功能的逻辑电路图如图9所示。
图98.设计一个“四舍五入”电路。
该电路输入为1位十进制数的8421码,当其值大于或等于5时,输出F 的值为1,否则F 的值为0。
解答○1 根据题意,可列出真值表如表5所示。
表5○2 由真值表可写出输出函数表达式为 F(A,B,C,D)=∑m(5~9)+∑d(10~15)经化简变换后,可得到最简与非表达式为○3逻辑电路图如图11所示。
数字逻辑课后习题答案(华中科技大学出版社,欧阳星明主编)

习题课
1.4 最简电路是否一定最佳?为什么? 解答: 最简电路并不一定是最佳电路。最佳电路应满足全面的 性能指标和实际应用要求。
4
习题课
1.5 把下列不同进制数写成按权展开形式。 (1)(4517.293)10 (3)(325.744)8 (2)(10110.0101)2 (4)(785.4AF)16 解答: (1)(4517.293)10=4×103+5×102+1×101+ 7 × 1 0 0 + 2× 1 0 - 1 +9 × 1 0 - 2 + 3×10-3 (2)(10110.0101)2=1×24+0×23+1×22+1×21+0×20+ 0×2-1+1×2-2 +0×2-3+1×2-4 (3)(325.744)8=3×82+2×81+5×80+7×8-1+4×8-2+ 4×8-3 (4)(785.4AF)16=7×162+8×161+5×160+4×16-1+ 10×8-2 +15×16-3
(3) A ABC ABC ABC ABC
(4) ABC ABC ( AB BC AC )
解答: (1) 左边= ( AB AC)= AB AC (定理6)= ( A B)(A C) (定理6)= AB AC BC (分配率)= AB AC (定理8)=右边
解答: (1)不正确。如当X、Y、Z取值为1,0,1时。 (2)不正确。如当X、Y、Z取值为0,1,0时。 (3)正确。Y=(Y X )(Y X )= (Z X )(Y X ) = XY YZ X Z Z YZ XZ = X Z YZ = =Z。 (4)正确。X= XY X Y = X Y X Y = X Y , Y= XY XY = X Y XY= X Y , 所以,X=Y。
(完整版)数字逻辑课后习题答案
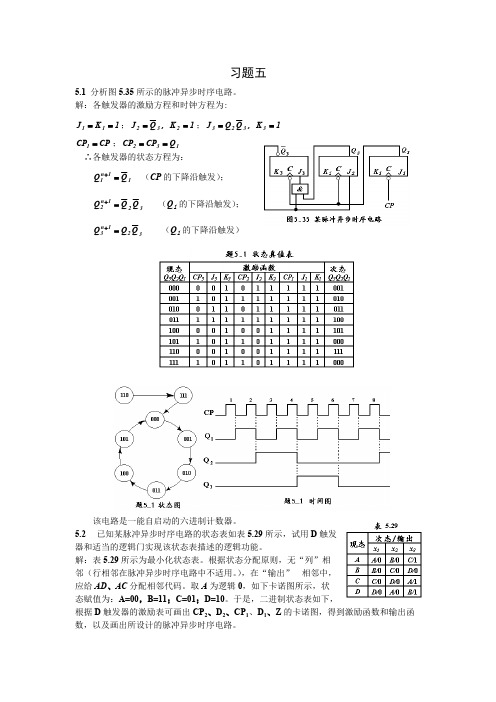
习题五5.1 分析图5.35所示的脉冲异步时序电路。
解:各触发器的激励方程和时钟方程为:;;1K J 11==1K ,Q J 232==1K ,Q Q J 3323==;CP CP 1=132Q CP CP == ∴各触发器的状态方程为:(CP 的下降沿触发);11n 1Q Q =+ (Q 1的下降沿触发);321n 2Q Q Q =+ (Q 1的下降沿触发)321n 3Q Q Q =+该电路是一能自启动的六进制计数器。
5.2 已知某脉冲异步时序电路的状态表如表5.29所示,试用D 触发器和适当的逻辑门实现该状态表描述的逻辑功能。
解:表5.29所示为最小化状态表。
根据状态分配原则,无“列”相邻(行相邻在脉冲异步时序电路中不适用。
),在“输出” 相邻中,应给AD 、AC 分配相邻代码。
取A 为逻辑0,如下卡诺图所示,状态赋值为:A=00,B=11;C=01;D=10。
于是,二进制状态表如下,根据D 触发器的激励表可画出CP 2、D 2、CP 1、D 1、Z 的卡诺图,得到激励函数和输出函数,以及画出所设计的脉冲异步时序电路。
得激励方程和输出方程:;22x CP =;32212x x Q x D ++=;3221x x Q CP +=;31211x Q x Q D +=。
)Q Q (x Q x Q x Z 2132313+=+=5.3 设计一个脉冲异步时序电路,该电路有三个输入端x 1、x 2和x 3,一个输出端Z 。
仅当输入序列x 1-x 2-x 3出现时,输出Z 产输出脉冲,并且与输入序列的最后一个脉冲重叠。
试作出该电路的原始状态图和状态表。
解:5.4 分析图5.36所示的电平异步时序电路。
解:(一)写出激励函数和输出函数表达式:;1112122y x y y x x Y ++=;1221121y x y x x x Y ++=12y x Z = (二)作状态流程表。
(三) 作时间图。
设输入状态的变化序列为00→01→11→10→00→10→11→01,初始总态为(12x x 12x x ,12y y )=(00,00)。
《数字逻辑》(第二版)习题答案

第一章1. 什么是模拟信号?什么是数字信号?试举出实例。
模拟信号-----指在时间上和数值上均作连续变化的信号。
例如,温度、压力、交流电压等信号。
数字信号-----指信号的变化在时间上和数值上都是断续的,阶跃式的,或者说是离散的,这类信号有时又称为离散信号。
例如,在数字系统中的脉冲信号、开关状态等。
2. 数字逻辑电路具有哪些主要特点?数字逻辑电路具有如下主要特点:●电路的基本工作信号是二值信号。
●电路中的半导体器件一般都工作在开、关状态。
●电路结构简单、功耗低、便于集成制造和系列化生产。
产品价格低廉、使用方便、通用性好。
●由数字逻辑电路构成的数字系统工作速度快、精度高、功能强、可靠性好。
3. 数字逻辑电路按功能可分为哪两种类型?主要区别是什么?根据数字逻辑电路有无记忆功能,可分为组合逻辑电路和时序逻辑电路两类。
组合逻辑电路:电路在任意时刻产生的稳定输出值仅取决于该时刻电路输入值的组合,而与电路过去的输入值无关。
组合逻辑电路又可根据输出端个数的多少进一步分为单输出和多输出组合逻辑电路。
时序逻辑电路:电路在任意时刻产生的稳定输出值不仅与该时刻电路的输入值有关,而且与电路过去的输入值有关。
时序逻辑电路又可根据电路中有无统一的定时信号进一步分为同步时序逻辑电路和异步时序逻辑电路。
4. 最简电路是否一定最佳?为什么?一个最简的方案并不等于一个最佳的方案。
最佳方案应满足全面的性能指标和实际应用要求。
所以,在求出一个实现预定功能的最简电路之后,往往要根据实际情况进行相应调整。
5. 把下列不同进制数写成按权展开形式。
(1) (4517.239)10 (3) (325.744)8(2) (10110.0101)2 (4) (785.4AF)16解答(1)(4517.239)10= 4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3(2)(10110.0101)2= 1×24+1×22+1×21+1×2-2+1×2-4(3)(325.744)8= 3×82+2×81+5×80+7×8-1+4×8-2+4×8-3 (4) (785.4AF)16= 7×162+8×161+5×160+4×16-1+10×16-2+15×16-36.将下列二进制数转换成十进制数、八进制数和十六进制数。
数字逻辑课后习题答案(科学出版社_第五版)

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边(3)EDCCDACBAA)(++++=A+CD+E证明:左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边(4)C B A C B A B A ++=CB C A B A ++证明:左边=CB AC B A B A ++=CB AC AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1) F=A+ABC+A C B +CB+C B = A+BC+C B(2) F =(A+B+C )(A+B+C) = (A+B)+C C = A+B(3) F =ABC D +ABD+BC D +ABCD+B C = AB+BC+BD(4) F=C AB C B BC A AC +++= BC(5) F=)()()()(B A B A B A B A ++++=BA 9.将下列函数展开为最小项表达式(1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式(1)CAB C B BC A AC F +++=0ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111ABCD 00 01 11 1000011110化简得F=DA B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111AB CD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑课后答案

F = ABC + ABC
= (A + B + C)(A + B + C )
10
1
0
1
1
F的卡诺图 的卡诺图 ABC
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题 章习题 2.8用卡诺图化简法求出最简与-或表达式和最简或-与表达式。 ⑵ F(A, B, C, D ) = BC + D + D(B + C )⋅ (AD + B) 解: 画出逻辑函数的卡诺图。 先转换成与或表达式
Y2 = B Y2 = A
EN = 1 门2、4打开 Y1 = B
A B EN Y1 Y2
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题 章习题 3.13 在图3.65(a)所示的D触发器电 路中,若输入端D的波形如图 3.66(b) 所示,试画出输出端Q的波 形(设触发器初态为0)。 解: 触发器初态为0 在CP=1期间, Qn+1=D Q CP D
F = (A + B)(A + C)(C + D )(B + D )
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题 章习题 2.9用卡诺图判断函数F(A,B,C,D)和G(A,B,C,D) 之间的关系。
F(A, B, C, D ) = BD + A D + CD + ACD G (A, B, C, D ) = BD + CD + ACD + ABD
⊕ ⊕⊕⊕ ⊕
⊕ ⊕⊕⊕ ⊕⊕
⑵ (1100110)2 = 64+32+4+2 = (102)10 = (0001 0000 0010)8421码 (1100110)2 =( 1010101 )格雷码 ?
数字逻辑 课后习题答案

1. 什么是模拟信号?什么是数字信号?试举出实例。
解答 模拟信号-----指在时间上和数值上均作连续变化的信号。例如,温度、压
力、交流电压等信号。 数字信号-----指信号的变化在时间上和数值上都是断续的,阶跃式的,或
者说是离散的,这类信号有时又称为离散信号。例如,在数 字系统中的脉冲信号、开关状态等。
第二章
1 假定一个电路中,指示灯 F 和开关 A、B、C 的关系为 F=(A+B)C
试画出相应电路图。 解答
电路图如图 1 所示。
图1
2 用逻辑代数的公理、定理和规则证明下列表达式:
(1) AB + AC = AB + AC (2) AB + AB + AB + AB = 1 (3) AABC = ABC + ABC + ABC
= (A + B) ⋅ (A + B) =B
( ) F = BC + D + D ⋅ B + C ⋅ (AC + B)
= BC + D + (B + C)(AC + B) = BC + D + BC(AC + B) = BC + D + AC + B = B + D + AC
(3) (33.33)10 =(?)2 =(?)8 =(?)16
23
3
21
6………… .1
2
8…………..0
2
4…………..0
2 2…………..0
2 1 ………. 0
0…………1
0.3 3
×
2
0.6 6
数字逻辑课后习题答案(华中科技大学出版社,欧阳星明主编)

F ( A B)( A C)(C DE) E
反函数: F ( AB AC C(D E))E ABE ACE C DE
对偶函数:F ' ( AB AC C(D E))E ABE AC E CDE
16
习题课
解答: F [ AB (C D) AC] (3) 反函数: F AB AC AD DC 对偶函数:F ' A B (C D) ( A C )
7
习题课
1.8 如何判断一个二进制数B=b6b5b4b3b2b1b0能否被(4)整除? 解答: 因 为 B= b6b5b4b3b2b1b0 , 所 以 ( B)2= b6×26+ b5×25 +b4×24+b3×23+b2×22+b1×21+b0×20, 很 显 然 , b6×26 +b5×25+b4×24+b3×23+b2×22可以被4即2整除,所以 当 b1×21+b0×20 能被2整除时,B可以被4整除。因为b1 、 b0 只能取0和1,所以,当b1= b0=0时,B可以被4整除。
A B AC A D C D A B AC C D
(4)
F A[B (C D E )G]
反函数:
F A BCE BDE BG 对偶函数:F ' A BC E B D E BG
17
习题课
2.5 回答下列问题: (1)如果已知X+Y=X+Z,那么Y=Z。正确吗?为什么? (2)如果已知XY=XZ,那么Y=Z。正确吗?为什么? (3)如果已知X+Y=X+Z,且XY=XZ,那么Y=Z。正确吗? 为什么? (4)如果已知X+Y=XY,那么X=Y。正确吗?为什么?
20
数字逻辑(第二版)毛法尧课后题答案(1-6章)

习题一1.1 把下列不同进制数写成按权展开式:⑴(4517.239)10= 4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3⑵(10110.0101)2=1×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+0×2-3+1×2-4⑶(325.744)8=3×82+2×81+5×80+7×8-1+4×8-2+4×8-3⑷(785.4AF)16=7×162+8×161+5×160+4×16-1+A×16-2+F×16-31.2 完成下列二进制表达式的运算:1.3 将下列二进制数转换成十进制数、八进制数和十六进制数:⑴(1110101)2=(165)8=(75)16=7×16+5=(117)10⑵(0.110101)2=(0.65)8=(0.D4)16=13×16-1+4×16-2=(0.828125)10⑶(10111.01)2=(27.2)8=(17.4)16=1×16+7+4×16-1=(23.25)101.4 将下列十进制数转换成二进制数、八进制数和十六进制数,精确到小数点后5位:⑴(29)10=(1D)16=(11101)2=(35)8⑵(0.207)10=(0.34FDF)16=(0.001101)2=(0.15176)8⑶(33.333)10=(21.553F7)16=(100001.010101)2=(41.25237)81.5 如何判断一个二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除?解: 一个二进制正整数被(2)10除时,小数点向左移动一位, 被(4)10除时,小数点向左移动两位,能被整除时,应无余数,故当b1=0和b0=0时, 二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除.1.6 写出下列各数的原码、反码和补码:⑴0.1011[0.1011]原=0.1011; [0.1011]反=0.1011; [0.1011]补=0.1011⑵0.0000[0.000]原=0.0000; [0.0000]反=0.0000; [0.0000]补=0.0000⑶-10110[-10110]原=110110; [-10110]反=101001; [-10110]补=1010101.7 已知[N]补=1.0110,求[N]原,[N]反和N.解:由[N]补=1.0110得: [N]反=[N]补-1=1.0101, [N]原=1.1010,N=-0.10101.8 用原码、反码和补码完成如下运算:⑴0000101-0011010[0000101-0011010]原=10010101;∴0000101-0011010=-0010101。
第四章 《数字逻辑》(第二版)习题答案
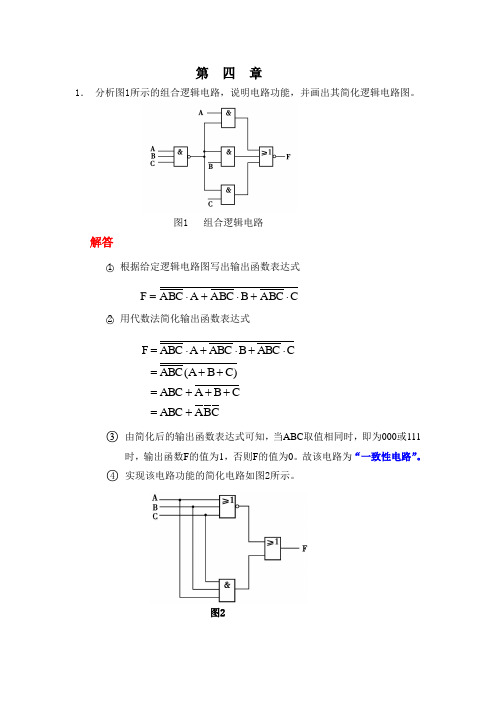
第四章1.分析图1所示的组合逻辑电路,说明电路功能,并画出其简化逻辑电路图。
图1 组合逻辑电路解答○1根据给定逻辑电路图写出输出函数表达式CABCBABCAABCF⋅+⋅+⋅=○2用代数法简化输出函数表达式CBA ABC CBA ABC C)B(A ABCCABCBABCAABCF+ =+ ++ =+ +=⋅+⋅+⋅=○3由简化后的输出函数表达式可知,当ABC取值相同时,即为000或111时,输出函数F的值为1,否则F的值为0。
故该电路为“一致性电路”。
○4实现该电路功能的简化电路如图2所示。
图22. 分析图3所示的逻辑电路,要求:(1) 指出在哪些输入取值下,输出F 的值为1。
(2) 改用异或门实现该电路的逻辑功能。
图3 组合逻辑电路解答分析给定逻辑电路,可求出输出函数最简表达式为 C B A C B A F ⊕⊕=⊕⊕=○1 当ABC 取值000、011、101、110时,输出函数F 的值为1; ○2 用异或门实现该电路功能的逻辑电路图如图4所示。
图43.析图5所示组合逻辑电路,列出真值表,并说明该电路的逻辑功能。
图5 组合逻辑电路= 1 = 1 = 1 A W B C D X Y Z . . .解答○1 写出电路输出函数表达式如下: D C Z C,B Y B,A X A,W ⊕=⊕=⊕==○2 列出真值表如表1所示。
表1ABCD WXYZ ABCD WXYZ 0000 0001 0010 0011 0100 0101 0110 0111 0000 0001 0011 0010 0110 0111 0101 0100 1000 1001 1010 1011 1100 1101 1110 1111 1100 1101 1111 1110 1010 1011 1001 1000○3 由真值表可知,该电路的功能是将四位二进制码转换成Gray 码。
4.设计一个组合电路,该电路输入端接收两个2位二进制数A=A 2A 1,B=B 2B 1。
(完整word版)《数字逻辑》(第二版)习题答案-第六章

习 题 六1 分析图1所示脉冲异步时序逻辑电路。
(1) 作出状态表和状态图; (2) 说明电路功能。
图1解答(1)该电路是一个Mealy 型脉冲异步时序逻辑电路。
其输出函数和激励函数表达式为211221212Q D x C Q D x Q CQ x Q Z =====(2)电路的状态表如表1所示,状态图如图2所示。
现 态 Q 2 Q 1次态/输出ZX=10 0 0 1 1 0 1 1 01/0 11/0 10/0 00/1图2(3) 由状态图可知,该电路是一个三进制计数器。
电路中有一个多余状态10,且存在“挂起”现象。
2 分析图3所示脉冲异步时序逻辑电路。
(1) 作出状态表和时间图; (2) 说明电路逻辑功能。
图3解答○1 该电路是一个Moore 型脉冲异步时序逻辑电路,其输出即电路状 态。
激励函数表达式为 1321123132233Q C C CP;C 1;K K K 1J ; Q J ; Q Q J =========○2 电路状态表如表2所示,时间图如图4所示。
表2图4○3 由状态表和时间图可知,该电路是一个模6计数器。
3 分析图5所示脉冲异步时序逻辑电路。
(1) 作出状态表和状态图; (2) 说明电路逻辑功能。
图5时 钟CP 现 态 Q 3 Q 2 Q 1 次 态 Q 3(n+1)Q 2(n+1)Q 1(n+1)11111111000 001 010 011 100 101 110 111 001 010 011 100 101 000 111 000解答○1 该电路是一个Moore 型脉冲异步时序逻辑电路,其输出函数和激励函数表达式为322111132212122212x y x R ; x S y x y x x R ; y y x S y y Z +==++===○2该电路的状态表如表3所示,状态图如图6所示。
表3现态 y 2y 1次态y 2(n+1)y 1(n+1)输出 Zx 1 x 2 x 3 0001 11 1001 01 01 0100 11 00 0000 00 10 000 0 0 1图6○3 该电路是一个“x 1—x 2—x 3”序列检测器。
数字逻辑习题(含部分答案)

一、用代数化简法求逻辑函数的最简与—或表达式。
(14分)( 1 )F=AC+BD+AD+AD+AB+BE+DEF=AC+BD+A(D+D)+AB+BE+DEF=AC+A+BD+AB+BE+DEF=A+C+AB+BD+BE+DE(C+C)F=A+C+BD+BE( 2 ) F=A B C+ABCD+ACDF=A C(B+BD)+ACDF=A B C+A CD+ACDF=A B C+CD(A+A)F=A B C+CD二、用卡诺图化简法求出逻辑函数的最简与—或表达式。
(14分)( 1 )F(A,B,C,D)=AC+BC+A B+A CD解:卡诺图如图所示由卡诺图得F(A,B,C,D)=A B+BC+AC( 2 )F(A,B,C,D)=BCD+ABC+ABC D+A CD+AB CD+ABCD解:卡诺图如图所示由卡诺图得F=CD+BD三、组合逻辑电路的设计。
(12分)设计一个四变量“多数表决”组合逻辑电路,求出逻辑函数的最简与—或表达式并并画出逻辑电路图。
解:分别设四变量为A,B,C,D,其真值表如下得F=ABCD+ABCD+ABCD+ABCD+ABCD化简得F=ABC+ABD+ACD+BCD逻辑电路图如下图所示四、组合逻辑电路的分析。
(12分)分析下图所示组合逻辑电路的功能。
要求:写出每个或非门的输出函数,根据F表达式列出真值表,最后分析电路的功能。
解:P1=A+B=A∙B P2=A+P1=A+(A∙B)=A∙(A+B)=A BP3=B+P1=B+(A∙B)=B∙(A+B)=ABP4=C+P2+P3=C+(P2+P3)=C+(A⊕B)=(A⊕B)∙CP5=P2+P3+P4=(A⊕B)+(A⊕B)∙C=(A⊕B)+C=(A⊕B)∙CP6=C+P4=(A⊕B)+C=(A⊕B)∙C综上得F=P5+P6=(A⊕B)∙C∙(A⊕B)∙C=(A⊕B)∙C+(A⊕B)∙C=(A⊕B)⊙C 真值表如下图所示由真值表知仅当A,B,C中0的个数为一个或三个时,F的值才为1,故该电路的功能为检测A,B,C中0的个数为奇书还是偶数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制491100016153110101651271111111177635100111101111737.493111.11117.7479.4310011001.0110111231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010101211110161751011100921340.100110.593750.4610111147570110113153.将下列十进制数转换成8421BCD码1997=000110011001011165.312=01100101.0011000100103.1416=0011.00010100000101100.9475=0.10010100011101014.列出真值表,写出X的真值表达式A B C X00000010010001111000101111011111X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1)(A⊕B)⊕C=A⊕(B⊕C)A B C(A⊕B)⊕C A⊕(B⊕C)0000000111010110110010011101001100011111所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C00011001000100001111100001011111011111007.证明下列等式(1)A+A B=A+B 证明:左边=A+A B=A(B+B )+A B =AB+A B +A B =AB+A B +AB+A B =A+B =右边(2)ABC+A B C+AB C =AB+AC 证明:左边=ABC+A B C+AB C=ABC+A B C+AB C +ABC =AC(B+B )+AB(C+C )=AB+AC =右边(3)E D C CD A C B A A )(++++=A+CD+E证明:左边=ED C CD A C B A A )(++++=A+CD+A B C +CDE =A+CD+CD E =A+CD+E =右边(4)C B A C B A B A ++=CB C A B A ++证明:左边=CB AC B A B A ++=C B A C AB C B A B A +++)(=C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式(1)F=A+ABC+A C B +CB+C B =A+BC+C B (2)F=(A+B+C )(A+B+C)=(A+B)+C C =A+B (3)F=ABC D +ABD+BC D +ABCD+B C =AB+BC+BD (4)F=C AB C B BC A AC +++=BC(5)F=)()()()(B A B A B A B A ++++=B A 9.将下列函数展开为最小项表达式(1)F(A,B,C)=Σ(1,4,5,6,7)(2)F(A,B,C,D)=Σ(4,5,6,7,9,12,14)10.用卡诺图化简下列各式(1)CAB C B BC A AC F +++=0 ABC00 01 11 1011111化简得F=C(2)CB A D A B A DC AB CD B A F++++=111111AB CD 00 01 11 1000011110化简得F=DA B A +(3)F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)1111111111ABCD 00 01 11 1000011110化简得F=DBC D C A BC A C B D C ++++(4)F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)Φ1ΦΦ1ΦΦ1Φ1AB CD 00 01 11 1000011110化简得F=ACAD B A ++11.利用与非门实现下列函数,并画出逻辑图。
(1)F=C B A C AB +=1∙C AF<=(A nand (not C))nand 1(2)F=))((D C B A ++=))((D C B A (3)F(A,B,C,D)=∑m(0,1,2,4,6,10,14,15)=))()(()(ABC C B A D A D C A D A B C CB AC A1C D12.已知逻辑函数A C C B B A X ++=,试用以下方法表示该函数真值表:A B C X 00000011010101111001101111011110卡诺图:逻辑图:波形图VHDL 语言X<=(A and not B)or (B and not C)or (c and not A)13.根据要求画出所需的逻辑电路图。
(a )(b )14..画出F1,F2的波形解A B B A CF2F1F1 = A ⊕B F2 = F1⊕C:C A B F1F2第二章组合逻辑1.分析图中所示的逻辑电路,写出表达式并进行化简A BFF = AB + B = ABA B CFF = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC2.分析下图所示逻辑电路,其中S3、S2、S1、S0为控制输入端,列出真值表,说明F 与A、B 的关系。
F1=1SB BS A ++F2=32SB A ABS +F=F 1F 2=1SB BS A ++A 0 0 AB A B 00 11 01 1F 1S 1 S 010 0A+B A+B A0 11 01 1F 2S 3 S 2F 0 0 ××1F 1F 1F 10 1 ××1 0 ××1 1 ××F=F 1F 2S 3 S 2 S 1 S 0A ××0 0 A B A B 0××0 1×× 1 0×× 1 1F=F 1F 2S 3 S 2 S 1 S 03.分析下图所示逻辑电路,列出真值表,说明其逻辑功能。
解:F1=C B BC A C AB C B A +++=ABCC B A C B A ++真值表如下:当B ≠C 时,F1=A 当B=C=1时,F1=A 当B=C=0时,F1=0F2=ACBC AB C A C B B A ++=++真值表如下:当A 、B 、C 三个变量中有两个及两个以上同时为“1”时,F2=1。
4.图所示为数据总线上的一种判零电路,写出F 的逻辑表达式,说明该电路的逻辑功能。
解:F=1514131211109876543210A A A A A A A A A A A A A A A A +++只有当变量A0~A15全为0时,F =1;否则,F =0。
因此,电路的功能是判断变量是否全部为逻辑“0”。
5.分析下图所示逻辑电路,列出真值表,说明其逻辑功能解:301201101001X A A X A A X A A X A A F +++=真值表如下:F A X 0 X 1X 2X 30 00 11 01 11 A 0因此,这是一个四选一的选择器。
6.下图所示为两种十进制数代码转换器,输入为余三码,输出为什么代码?解:W= AB+ACDX = BC+BD+BCD Y = CD+CDZ = DW X Y ZA B C D0 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 1 0 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 11 0 1 01 0 1 11 1 0 0这是一个余三码至8421BCD码转换的电路7.下图是一个受M控制的4位二进制码和格雷码的相互转换电路。
M=1时,完成自然二进制码至格雷码转换;M=0时,完成相反转换。
请说明之解:Y3=X3322XXY⊕=)22(11YMMXXY+⊕=)11(0YMMXXY+⊕=当M=1时Y3=X3Y2=X2⊕X3Y1=X1⊕X2Y0=X0⊕X1当M=0时Y3=X3Y2=X2⊕X3Y1=X1⊕Y2=X1⊕X2⊕X3Y0=X0⊕Y1=X0⊕X1⊕X2⊕X30 0 0 0X 0 0 0 10 0 1 10 0 1 00 1 1 00 1 1 10 1 0 10 1 0 01 1 0 01 1 0 11 1 1 11 1 1 01 0 1 01 0 1 11 0 0 11 0 0 00 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 11 0 1 01 0 1 11 1 0 01 1 0 11 1 1 01 1 1 1Y 3Y 2Y 1Y 03X 2X 1X 0M= 1 的真值表Y X 0 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 11 0 1 01 0 1 11 1 0 01 1 0 11 1 1 01 1 1 10 0 0 00 0 0 10 0 1 10 0 1 00 1 1 00 1 1 10 1 0 10 1 0 01 1 0 01 1 0 11 1 1 11 1 1 01 0 1 01 0 1 11 0 0 11 0 0 03Y 2Y 1Y 03X 2X 1X 0M= 0 的真值表由真值表可知:M=1时,完成8421BCD 码到格雷码的转换;M=0时,完成格雷码到8421BCD 码的转换。
8.已知输入信号A,B,C,D 的波形如下图所示,选择适当的集成逻辑门电路,设计产生输出F 波形的组合电路(输入无反变量)解:列出真值表如下:F A B C D 01011100111110000 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 11 0 1 01 0 1 11 1 0 01 1 0 11 1 1 01 1 1 1AB111111111CD 00 01 11 1000011110)(D C A C B A D C B D B B A F 或+++=9.用红、黄、绿三个指示灯表示三台设备的工作情况:绿灯亮表示全部正常;红灯亮表示有一台不正常;黄灯亮表示有两台不正常;红、黄灯全亮表示三台都不正常。
