(完整版)等差数列基础练习题.docx

合集下载

等差数列练习题(有答案)百度文库

一、等差数列选择题1．设等差数列{}n a 的前n 项和为n S ，若2938a a a +=+，则15S =（） A ．60B ．120C ．160D ．2402．中国古代数学著作《九章算术》中有如下问题：“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，重二斤.问次一尺各重几何?” 意思是:“现有一根金锤，长五尺，一头粗一头细.在粗的一端截下一尺，重四斤;在细的一端截下一尺，重二斤.问依次每一尺各重几斤?”根据已知条件，若金箠由粗到细是均匀变化的，中间三尺的重量为（） A ．3斤B ．6斤C ．9斤D ．12斤3．在巴比伦晚期的《泥板文书》中，有按级递减分物的等差数列问题，其中有一个问题大意是：10个兄弟分100两银子，长兄最多，依次减少相同数目，现知第8兄弟分得6两，则长兄可分得银子的数目为（） A ．825两 B ．845两 C ．865两 D ．885两 4．已知数列{}n a 是等差数列，其前n 项和为n S ，若454a a +=，则8S =（） A ．16 B ．-16 C ．4D ．-45．设数列{}n a 的前n 项和21n S n =+. 则8a 的值为（）．A ．65B ．16C ．15D ．14 6．在等差数列{a n }中，a 3+a 7＝4，则必有（）A ．a 5＝4B ．a 6＝4C ．a 5＝2D ．a 6＝27．已知等差数列{}n a 前n 项和为n S ，且351024a a a ++=，则13S 的值为（） A ．8B ．13C ．26D ．1628．《周髀算经》是中国最古老的天文学和数学著作，它揭示日月星辰的运行规律.其记载“阴阳之数，日月之法，十九岁为一章，四章为一部，部七十六岁，二十部为一遂，遂千百五二十岁”.现恰有30人，他们的年龄(都为正整数)之和恰好为一遂(即1520)，其中年长者年龄介于90至100，其余29人的年龄依次相差一岁，则最年轻者的年龄为（） A ．32B ．33C ．34D ．359．等差数列{}n a 的公差为2，若248,,a a a 成等比数列，则9S =（） A ．72B ．90C ．36D ．4510．设n S 是等差数列{}n a （*n N ∈）的前n 项和，且141,16a S ==，则7a =（） A ．7B ．10C ．13D ．1611．在函数()y f x =的图像上有点列{},n n x y ，若数列{}n x 是等比数列，数列{}n y 是等差数列，则函数()y f x =的解析式可能是（） A ．3(4)f x x =+B ．2()4f x x =C ．3()4xf x ⎛⎫= ⎪⎝⎭D ．4()log f x x =12．已知等差数列{}n a 的前n 项和n S 满足：21<<m m m S S S ++，若0n S >，则n 的最大值为（） A ．2mB ．21m +C ．22m +D ．23m +13．《张丘建算经》是我国北魏时期大数学家张丘建所著，约成书于公元466-485年间.其中记载着这么一道“女子织布”问题：某女子善于织布，一天比一天织得快，且每日增加的数量相同.已知第一日织布4尺，20日共织布232尺，则该女子织布每日增加（）尺 A ．47B ．1629C ．815D ．4514．在数列{}n a 中，129a =-，()*13n n a a n +=+∈N ，则1220a a a +++=（）A ．10B ．145C ．300D ．32015．设等差数列{}n a 的前n 项之和为n S ，已知10100S =，则47a a +=（） A ．12B ．20C ．40D ．10016．已知等差数列{}n a 的前n 项和为n S ，且2n S n =.定义数列{}n b 如下：()*1m m b m m+∈N 是使不等式()*n a m m ≥∈N 成立的所有n 中的最小值，则13519 b b b b ++++=（）A ．25B ．50C ．75D ．100 17．设等差数列{}n a 的公差d ≠0，前n 项和为n S ，若425S a =，则99S a =（） A ．9B ．5C ．1D ．5918．已知数列{}n a 的前n 项和()2*n S n n N =∈，则{}na 的通项公式为（）A ．2n a n =B ．21n a n =-C ．32n a n =-D ．1,12,2n n a n n =⎧=⎨≥⎩19．设等差数列{}n a 的前n 项和为n S ，若7916+=a a ，则15S =（） A ．60B ．120C ．160D ．24020．已知等差数列{}n a 的前n 项和为n S ，31567a a a +=+，则23S =（） A ．121B ．161C ．141D ．151二、多选题21．题目文件丢失！22．已知数列{}n a 的前4项为2，0，2，0，则该数列的通项公式可能为（）A ．0,2,n n a n ⎧=⎨⎩为奇数为偶数B ．1(1)1n n a -=-+C ．2sin2n n a π= D ．cos(1)1n a n π=-+23．已知等差数列{}n a 的前n 项和为,n S 且15110,20,a a a 则（）A ．80a <B ．当且仅当n = 7时，n S 取得最大值C ．49S S =D ．满足0n S >的n 的最大值为1224．已知数列{}n a ：1，1，2，3，5，…其中从第三项起，每个数等于它前面两个数的和，记n S 为数列{}n a 的前n 项和，则下列结论正确的是（） A ．68S a = B ．733S =C ．135********a a a a a ++++= D ．2222123202020202021a a a a a a ++++=25．已知数列0,2,0,2,0,2,，则前六项适合的通项公式为（）A ．1(1)nn a =+-B ．2cos2n n a π= C ．(1)2sin2n n a π+= D ．1cos(1)(1)(2)n a n n n π=--+--26．记n S 为等差数列{}n a 的前n 项和.已知450,5S a ==，则（） A ．25n a n =-B ．310na nC ．228n S n n =- D ．24n S n n =-27．（多选题）在数列{}n a 中，若221n n a a p --=，（2n ≥，*n N ∈，p 为常数），则称{}n a 为“等方差数列”．下列对“等方差数列”的判断正确的是（）A ．若{}n a 是等差数列，则{}2n a 是等方差数列B ．(){}1n-是等方差数列C ．若{}n a 是等方差数列，则{}kn a （*k N ∈，k 为常数）也是等方差数列D ．若{}n a 既是等方差数列，又是等差数列，则该数列为常数列 28．已知数列{}n a 为等差数列，则下列说法正确的是（） A ．1n n a a d +=+（d 为常数）B ．数列{}n a -是等差数列C ．数列1n a ⎧⎫⎨⎬⎩⎭是等差数列D ．1n a +是n a 与2n a +的等差中项29．记n S 为等差数列{}n a 的前n 项和.已知535S =，411a =，则（）A ．45n a n =-B ．23n a n =+C ．223n S n n =-D ．24n S n n =+30．设公差不为0的等差数列{}n a 的前n 项和为n S ，若1718S S =，则下列各式的值为0的是（）A ．17aB ．35SC ．1719a a -D ．1916S S -【参考答案】***试卷处理标记，请不要删除一、等差数列选择题 1．B 【分析】根据等差数列的性质可知2938a a a a +=+，结合题意，可得出88a =，最后根据等差数列的前n 项和公式和等差数列的性质，得出()11515815152a a S a +==，从而可得出结果.【详解】解：由题可知，2938a a a +=+，由等差数列的性质可知2938a a a a +=+，则88a =，故()1158158151521515812022a a a S a +⨯====⨯=. 故选：B. 2．C 【分析】根据题意转化成等差数列问题，再根据等差数列下标的性质求234a a a ++. 【详解】由题意可知金锤每尺的重量成等差数列，设细的一端的重量为1a ，粗的一端的重量为5a ，可知12a =，54a =，根据等差数列的性质可知1533263a a a a +==⇒=，中间三尺为234339a a a a ++==. 故选：C 【点睛】本题考查数列新文化，等差数列的性质，重点考查理解题意，属于基础题型. 3．C 【分析】设10个兄弟由大到小依次分得()1,2,,10n a n =⋅⋅⋅两银子，数列{}n a 是等差数列，8106100a S =⎧⎨=⎩利用等差数列的通项公式和前n 项和公式转化为关于1a 和d 的方程，即可求得长兄可分得银子的数目1a . 【详解】设10个兄弟由大到小依次分得()1,2,,10n a n =⋅⋅⋅两银子，由题意可得设数列{}n a 的公差为d ，其前n 项和为n S ，则由题意得8106100a S =⎧⎨=⎩，即1176109101002a d a d +=⎧⎪⎨⨯+=⎪⎩，解得186585a d ⎧=⎪⎪⎨⎪=-⎪⎩. 所以长兄分得865两银子. 故选：C. 【点睛】关键点点睛：本题的关键点是能够读懂题意10个兄弟由大到小依次分得()1,2,,10n a n =⋅⋅⋅两银子构成公差0d <的等差数列，要熟练掌握等差数列的通项公式和前n 项和公式. 4．A 【详解】由()()18458884816222a a a a S +⨯+⨯⨯====.故选A.5．C 【分析】利用()12n n n a S S n -=-≥得出数列{}n a 的通项公差，然后求解8a . 【详解】由21n S n =+得，12a =，()2111n S n -=-+，所以()221121n n n a S S n n n -=-=--=-，所以2,121,2n n a n n =⎧=⎨-≥⎩，故828115a =⨯-=.故选：C. 【点睛】本题考查数列的通项公式求解，较简单，利用()12n n n a S S n -=-≥求解即可. 6．C 【分析】利用等差数列的性质直接计算求解【详解】因为a 3+a 7＝2a 5＝4，所以a 5＝2. 故选：C 7．B 【分析】先利用等差数列的下标和性质将35102a a a ++转化为()410724a a a +=，再根据()11313713132a a S a +==求解出结果.【详解】因为()351041072244a a a a a a ++=+==，所以71a =，又()1131371313131132a a S a +===⨯=，故选：B. 【点睛】结论点睛：等差、等比数列的下标和性质：若()*2,,,,m n p q t m n p q t N +=+=∈，（1）当{}n a 为等差数列，则有2m n p q t a a a a a +=+=；（2）当{}n a 为等比数列，则有2m n p q t a a a a a ⋅=⋅=.8．D 【分析】设年纪最小者年龄为n ，年纪最大者为m ,由他们年龄依次相差一岁得出(1)(2)(28)1520n n n n m ++++++++=，结合等差数列的求和公式得出111429m n =-，再由[]90,100m ∈求出n 的值.【详解】根据题意可知，这30个老人年龄之和为1520，设年纪最小者年龄为n ，年纪最大者为m ，[]90,100m ∈，则有(1)(2)(28)294061520n n n n m n m ++++++++=++=则有291114n m +=，则111429m n =-，所以90111429100m ≤-≤ 解得34.96635.31n ≤≤，因为年龄为整数，所以35n =. 故选：D 9．B 【分析】由题意结合248,,a a a 成等比数列，有2444(4)(8)a a a =-+即可得4a ，进而得到1a 、n a ，即可求9S . 【详解】由题意知：244a a =-，848a a =+，又248,,a a a 成等比数列，∴2444(4)(8)a a a =-+，解之得48a =，∴143862a a d =-=-=，则1(1)2n a a n d n =+-=，∴99(229)902S ⨯+⨯==，故选：B思路点睛：由其中三项成等比数列，利用等比中项性质求项，进而得到等差数列的基本量 1、由,,m k n a a a 成等比，即2k m n a a a =； 2、等差数列前n 项和公式1()2n n n a a S +=的应用. 10．C 【分析】由题建立关系求出公差，即可求解. 【详解】设等差数列{}n a 的公差为d ，141,16a S ==，41464616S a d d ∴=+=+=，2d ∴=， 71613a a d ∴=+=.故选：C 11．D 【分析】把点列代入函数解析式，根据{x n }是等比数列，可知1n nx x +为常数进而可求得1n n y y +-的结果为一个与n 无关的常数，可判断出{y n }是等差数列．【详解】对于A ，函数3(4)f x x =+上的点列{x n ，y n }，有y n ＝43n x +，由于{x n }是等比数列，所以1n nx x +为常数，因此1n n y y +-＝()()()()114343441n n n n n x x x x x q +++-+=-=-这是一个与n 有关的数，故{y n }不是等差数列；对于B ，函数2()4f x x =上的点列{x n ，y n }，有y n ＝24n x ，由于{x n }是等比数列，所以1n nx x +为常数，因此1n n y y +-＝()222214441n n n x x x q +-=-这是一个与n 有关的数，故{y n }不是等差数列；对于C ，函数3()4xf x ⎛⎫= ⎪⎝⎭上的点列{x n ，y n }，有y n ＝3()4n x ，由于{x n }是等比数列，所以1n nx x +为常数，因此1n n y y +-＝133()()44n n x x+-＝33()()144n qx⎡⎤-⎢⎥⎣⎦，这是一个与n 有关的数，故{y n }不是等对于D ，函数4()log f x x =上的点列{x n ，y n }，有y n ＝4log n x，由于{x n }是等比数列，所以1n nx x +为常数，因此1n n y y +-＝114444log log log log n n n nx x x x q ++-==为常数，故{y n }是等差数列；故选：D ．【点睛】方法点睛：判断数列是不是等差数列的方法：定义法，等差中项法. 12．C 【分析】首先根据数列的通项n a 与n S 的关系，得到10m a +>，2<0m a +，12+>0m m a a ++，再根据选项，代入前n 项和公式，计算结果. 【详解】由21<<m m m S S S ++得，10m a +>，2<0m a +，12+>0m m a a ++. 又()()()1212112121>02m m m m a a S m a +++++==+，()()()1232322323<02m m m m a a S m a +++++==+， ()()()()1222212211>02m m m m m a a S m a a ++++++==++.故选:C.【点睛】关键点睛：本题的第一个关键是根据公式11,2,1n n n S S n a S n --≥⎧=⎨=⎩，判断数列的项的正负，第二个关键能利用等差数列的性质和公式，将判断和的正负转化为项的正负. 13．D 【分析】设该妇子织布每天增加d 尺，由等差数列的前n 项和公式即可求出结果【详解】设该妇子织布每天增加d 尺，由题意知2020192042322S d ⨯=⨯+=，解得45d =．故该女子织布每天增加45尺．14．C 【分析】由等差数列的性质可得332n a n =-，结合分组求和法即可得解。

等差数列练习题(有答案)百度文库(1)

一、等差数列选择题1．已知数列{}n a ，{}n b 都是等差数列，记n S ，n T 分别为{}n a ，{}n b 的前n 项和，且713n n S n T n -=，则55a b =（） A ．3415B ．2310C ．317D ．62272．等差数列{a n }的前n 项和为S n ，若a 1＝2，S 3＝12，则a 6等于（） A ．8B ．10C ．12D ．143．设n S 是等差数列{}n a 的前n 项和.若1476a a a ++=，则7S =（） A ．10-B ．8C ．12D ．144．在等差数列{}n a 中，3914a a +=，23a =，则10a =（） A ．11B ．10C ．6D ．35．为了参加学校的长跑比赛，省锡中高二年级小李同学制定了一个为期15天的训练计划.已知后一天的跑步距离都是在前一天的基础上增加相同距离.若小李同学前三天共跑了3600米，最后三天共跑了10800米，则这15天小李同学总共跑的路程为（） A ．34000米 B ．36000米 C ．38000米 D ．40000米 6．在等差数列{a n }中，a 3+a 7＝4，则必有（） A ．a 5＝4 B ．a 6＝4 C ．a 5＝2 D ．a 6＝27．已知等差数列{}n a 的前n 项和为n S ，且110a =，56S S ≥，下列四个命题：①公差d 的最大值为2-；②70S <；③记n S 的最大值为M ，则M 的最大值为30；④20192020a a >.其真命题的个数是（） A ．4个B ．3个C ．2个D ．1个 8．等差数列{}n a 的前n 项和为n S ，若12a =，315S =，则8a =（） A ．11B ．12C ．23D ．249．等差数列{}n a 中，22a =，公差2d =，则10S =（） A ．200B ．100C ．90D ．8010．已知等差数列{}n a 中，5470,0a a a >+<，则{}n a 的前n 项和n S 的最大值为（） A ．4SB ．5SC ． 6SD ． 7S11．已知正项数列{}n a 满足11a =，1111114n n n n a a a a ++⎛⎫⎛⎫+-=⎪⎪⎝⎭⎝⎭，数列{}n b 满足1111n n nb a a +=+，记{}n b 的前n 项和为n T ，则20T 的值为（） A ．1B ．2C ．3D ．412．已知等差数列{}n a 的前n 项和为n S ，若936S S =，则612SS =（） A ．177B ．83 C ．143D ．10313．已知数列{}n a 中，132a =，且满足()*1112,22n n n a a n n N -=+≥∈，若对于任意*n N ∈，都有n a nλ≥成立，则实数λ的最小值是（） A ．2B ．4C ．8D ．1614．已知等差数列{}n a 的前n 项和n S 满足：21<<m m m S S S ++，若0n S >，则n 的最大值为（） A ．2mB ．21m +C ．22m +D ．23m +15．记n S 为等差数列{}n a 的前n 项和．若5620a a +=，11132S =，则{}n a 的公差为（） A ．2B ．43C ．4D ．4-16．设等差数列{}n a 、{}n b 的前n 项和分别是n S 、n T .若237n n S n T n =+，则63a b 的值为（） A ．511B ．38C ．1D ．217．设等差数列{}n a 的前n 项和为n S ，且71124a a -=，则5S =（） A ．15B ．20C ．25D ．3018．已知数列{}n a 的前n 项和()2*n S n n N =∈，则{}na 的通项公式为（）A ．2n a n =B ．21n a n =-C ．32n a n =-D ．1,12,2n n a n n =⎧=⎨≥⎩19．已知数列{}n a 的前n 项和为n S ，且()11213n n n n S S a n +++=+-+，现有如下说法：①541a a =；②222121n n a a n ++=-；③401220S =. 则正确的个数为（） A ．0B ．1C ．2D ．320．设a ，0b ≠，数列{}n a 的前n 项和(21)[(2)22]n nn S a b n =---⨯+，*n N ∈，则存在数列{}n b 和{}n c 使得（）A ．n n n a b c =+，其中{}n b 和{}n c 都为等比数列B ．n n n a b c =+，其中{}n b 为等差数列，{}n c 为等比数列C ．·n n n a b c =，其中{}n b 和{}n c 都为等比数列D ．·n n n a b c =，其中{}n b 为等差数列，{}n c 为等比数列二、多选题21．已知等差数列{}n a 的公差0d ≠，前n 项和为n S ，若612S S =，则下列结论中正确的有（） A ．1:17:2a d =-B ．180S =C ．当0d >时，6140a a +>D ．当0d <时，614a a >22．题目文件丢失！23．(多选题)已知数列{}n a 中，前n 项和为n S ，且23n n n S a +=，则1n n a a -的值不可能为（） A ．2B ．5C ．3D ．424．朱世杰是元代著名数学家，他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中涉及一些“堆垛”问题，主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔，小明模仿“堆垛”问题，将它们全部堆放成纵断面为等腰梯形的“垛”，要求层数不小于2，且从最下面一层开始，每一层比上一层多1根，则该“等腰梯形垛”应堆放的层数可以是（） A ．4B ．5C ．7D ．825．无穷等差数列{}n a 的前n 项和为S n ，若a 1＞0，d ＜0，则下列结论正确的是（） A ．数列{}n a 单调递减 B ．数列{}n a 有最大值 C ．数列{}n S 单调递减D ．数列{}n S 有最大值26．已知等差数列{}n a 的公差不为0，其前n 项和为n S ，且12a 、8S 、9S 成等差数列，则下列四个选项中正确的有（） A ．59823a a S +=B ．27S S =C ．5S 最小D ．50a =27．设等差数列{}n a 的前n 项和为n S ，公差为d .已知312a =，120S >，70a <则（） A ．60a > B ．数列1n a ⎧⎫⎨⎬⎩⎭是递增数列C ．0nS <时，n 的最小值为13D ．数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项 28．等差数列{}n a 的前n 项和为n S ，1385a a S +=，则下列结论一定正确的是（） A ．100a = B ．当9n =或10时，n S 取最大值 C ．911a a <D ．613S S =29．已知{}n a 为等差数列，其前n 项和为n S ，且13623a a S +=，则以下结论正确的是（）. A ．10a =0B ．10S 最小C ．712S S =D ．190S =30．设等差数列{}n a 的前n 项和为n S ，公差为d ，且满足10a >，1118S S =，则对n S 描述正确的有（） A ．14S 是唯一最小值 B ．15S 是最小值 C ．290S =D ．15S 是最大值【参考答案】***试卷处理标记，请不要删除一、等差数列选择题 1．D 【分析】利用等差数列的性质以及前n 项和公式即可求解. 【详解】由713n n S n T n-=， ()()19551991955199927916229239272a a a a a a Sb b b b b b T ++⨯-======++⨯. 故选：D 2．C 【分析】利用等差数列的通项公式即可求解. 【详解】 {a n }为等差数列，S 3＝12，即1232312a a a a ++==，解得24a =. 由12a =，所以数列的公差21422d a a =-=-=，所以()()112212n a a n d n n =+-=+-=，所以62612a =⨯=. 故选：C 3．D 【分析】利用等差数列下标性质求得4a ，再利用求和公式求解即可【详解】147446=32a a a a a ++=∴=，则()177477142a a S a +=== 故选：D 4．A 【分析】利用等差数列的通项公式求解1,a d ，代入即可得出结论. 【详解】由3914a a +=，23a =，又{}n a 为等差数列，得39121014a a a d +=+=，213a a d =+=，解得12,1a d ==，则101+92911a a d ==+=；故选：A. 5．B 【分析】利用等差数列性质得到21200a =，143600a =，再利用等差数列求和公式得到答案. 【详解】根据题意：小李同学每天跑步距离为等差数列，设为n a ，则123233600a a a a ++==，故21200a =，13141514310800a a a a ++==，故143600a =，则()()11521411151********n S a a a a =+⨯=+⨯=. 故选：B. 6．C 【分析】利用等差数列的性质直接计算求解【详解】因为a 3+a 7＝2a 5＝4，所以a 5＝2. 故选：C 7．B 【分析】设公差为d ，利用等差数列的前n 项和公式，56S S ≥，得2d ≤-，由前n 项和公式，得728S ≤，同时可得n S 的最大值，2d =-，5n =或6n =时取得，结合递减数列判断D ．【详解】设公差为d ，由已知110a =，56S S ≥，得5101061015d d ⨯+≥⨯+，所以2d ≤-，A 正确；所以7710217022128S d =⨯+≤-⨯=，B 错误；1(1)10(1)0n a a n d n d =+-=+-≥，解得101n d≤-+，11100n a a nd nd +=+=+≤，解得10n d≥-，所以10101n d d-≤≤-+，当2d =-时，56n ≤≤，当5n =时，有最大值，此时51010(2)30M =⨯+⨯-=，当6n =时，有最大值，此时61015(2)30M =⨯+⨯-=，C 正确．又该数列为递减数列，所以20192020a a >，D 正确．故选：B ．【点睛】关键点点睛：本题考查等差数列的前n 项和，掌握等差数列的前n 和公式与性质是解题关键．等差数列前n 项和n S 的最大值除可利用二次函数性质求解外还可由10n n a a +≥⎧⎨≤⎩求得．8．C 【分析】由题设求得等差数列{}n a 的公差d ，即可求得结果. 【详解】32153S a ==，25a ∴=， 12a =，∴公差213d a a =-=， 81727323a a d ∴=+=+⨯=，故选：C. 9．C 【分析】先求得1a ，然后求得10S . 【详解】依题意120a a d =-=，所以101104545290S a d =+=⨯=. 故选：C 10．B 【分析】根据已知条件判断0n a >时对应的n 的范围，由此求得n S 的最大值. 【详解】依题意556475600000a a a a a a a d >⎧>⎧⎪⇒<⎨⎨+=+<⎩⎪<⎩，所以015n a n >⇒≤≤，所以{}n a 的前n 项和n S 的最大值为5S . 11．B 【分析】由题意可得221114n n a a +-=，运用等差数列的通项公式可得2143n n a =-，求得14n b =，然后利用裂项相消求和法可求得结果【详解】解：由11a =，1111114n n n n a a a a ++⎛⎫⎛⎫+-=⎪⎪⎝⎭⎝⎭，得221114n n a a +-=，所以数列21n a ⎧⎫⎨⎬⎩⎭是以4为公差，以1为首项的等差数列，所以2114(1)43n n n a =+-=-，因为0n a >，所以n a =，所以1111n n nb a a +=+=所以14n b ==，所以201220T b b b =++⋅⋅⋅+111339(91)244=++⋅⋅⋅+=⨯-=，故选：B 【点睛】关键点点睛：此题考查由数列的递推式求数列的前n 项和，解题的关键是由已知条件得221114n n a a +-=，从而数列21n a ⎧⎫⎨⎬⎩⎭是以4为公差，以1为首项的等差数列，进而可求n a =，14nb ==，然后利用裂项相消法可求得结果，考查计算能力和转化思想，属于中档题【分析】由等差数列前n 项和性质得3S ，63S S -，96S S -，129S S -构成等差数列，结合已知条件得633S S =和31210S S =计算得结果. 【详解】已知等差数列{}n a 的前项和为n S ，∴3S ，63S S -，96S S -，129S S -构成等差数列，所以()()633962S S S S S ⋅-=+-，且936S S =，化简解得633S S =. 又()()()96631292S S S S S S ⋅-=-+-，∴31210S S =，从而126103S S =. 故选：D 【点睛】思路点睛：（1）利用等差数列前n 项和性质得3S ，63S S -，96S S -，129S S -构成等差数列，（2）()()633962S S S S S ⋅-=+-，且936S S =，化简解得633S S =，（3）()()()96631292S S S S S S ⋅-=-+-，化简解得31210S S =. 13．A 【分析】将11122n n n a a -=+变形为11221n n n n a a --=+，由等差数列的定义得出22n n n a +=，从而得出()22nn n λ+≥，求出()max22n n n +⎡⎤⎢⎥⎣⎦的最值，即可得出答案. 【详解】因为2n ≥时，11122n n n a a -=+，所以11221n n n n a a --=+，而1123a = 所以数列{}2nn a 是首项为3公差为1的等差数列，故22nn a n =+，从而22n nn a +=. 又因为n a n λ≥恒成立，即()22nn n λ+≥恒成立，所以()max22n n n λ+⎡⎤≥⎢⎥⎣⎦. 由()()()()()()()1*121322,221122n n nn n n n n n n n n n n +-⎧+++≥⎪⎪∈≥⎨+-+⎪≥⎪⎩N 得2n = 所以()()2max2222222n n n +⨯+⎡⎤==⎢⎥⎣⎦，所以2λ≥，即实数λ的最小值是214．C 【分析】首先根据数列的通项n a 与n S 的关系，得到10m a +>，2<0m a +，12+>0m m a a ++，再根据选项，代入前n 项和公式，计算结果. 【详解】由21<<m m m S S S ++得，10m a +>，2<0m a +，12+>0m m a a ++. 又()()()1212112121>02m m m m a a S m a +++++==+，()()()1232322323<02m m m m a a S m a +++++==+， ()()()()1222212211>02m m m m m a a S m a a ++++++==++.故选:C.【点睛】关键点睛：本题的第一个关键是根据公式11,2,1n n n S S n a S n --≥⎧=⎨=⎩，判断数列的项的正负，第二个关键能利用等差数列的性质和公式，将判断和的正负转化为项的正负. 15．C 【分析】由等差数列前n 项和公式以及等差数列的性质可求得6a ，再由等差数列的公式即可求得公差. 【详解】解：()11111611111322a a S a+⨯===，612a ∴=，又5620a a +=，58a ∴=，654d a a ∴=-=.故选：C ． 16．C 【分析】令22n S n λ=，()37n T n n λ=+，求出n a ，n b ，进而求出6a ，3b ，则63a b 可得．【详解】令22n S n λ=，()37n T n n λ=+，可得当2n ≥时，()()221221221n n n a S S n n n λλλ-=-=--=-，()()()()137134232n n n b T T n n n n n λλλ-=-=+--+=+，当1n =，()11112,3710a S b T λλλ====+=，符合()221n a n λ=-，()232n b n λ=+故622a λ=，322b λ=，故631a b =. 【点睛】由n S 求n a 时，11,1,2n nn S n a S S n -=⎧=⎨-≥⎩，注意验证a 1是否包含在后面a n 的公式中，若不符合要单独列出，一般已知条件含a n 与S n 的关系的数列题均可考虑上述公式求解． 17．B 【分析】设出数列{}n a 的公差，利用等差数列的通项公式及已知条件，得到124a d +=，然后代入求和公式即可求解【详解】设等差数列{}n a 的公差为d ，则由已知可得()()111261024a d a d a d +-+=+=，所以()5115455254202S a d a d ⨯=+=+=⨯= 故选：B 18．B 【分析】利用1n n n a S S -=-求出2n ≥时n a 的表达式，然后验证1a 的值是否适合，最后写出n a 的式子即可. 【详解】2n S n =，∴当2n ≥时，221(1)21n n n a S S n n n -=-=--=-，当1n =时，111a S ==，上式也成立，()*21n a n n N ∴=-∈，故选：B. 【点睛】易错点睛：本题考查数列通项公式的求解，涉及到的知识点有数列的项与和的关系，即11,1,2n nn S n a S S n -=⎧=⎨-≥⎩，算出之后一定要判断1n =时对应的式子是否成立，最后求得结果，考查学生的分类思想与运算求解能力，属于基础题.19．D 【分析】由()11213n n n n S S a n +++=+-+得到()11132n n n a a n ++=-+-，再分n 为奇数和偶数得到21262k k a a k +=-+-，22165k k a a k -=+-，然后再联立递推逐项判断. 【详解】因为()11213n n n n S S a n +++=+-+，所以()11132n n n a a n ++=-+-，所以()212621k k a a k +=-+-，()221652k k a a k -=+-，联立得：()212133k k a a +-+=，所以()232134k k a a +++=，故2321k k a a +-=，从而15941a a a a ===⋅⋅⋅=，22162k k a a k ++=-，222161k k a a k ++=++，则222121k k a a k ++=-，故()()()4012345383940...S a a a a a a a a =++++++++，()()()()234538394041...a a a a a a a a =++++++++，()()201411820622k k =+⨯=-==∑1220，故①②③正确. 故选：D 20．D 【分析】由题设求出数列{}n a 的通项公式，再根据等差数列与等比数列的通项公式的特征，逐项判断，即可得出正确选项. 【详解】解：(21)[(2)22](2)2(2)n n n n S a b n a b bn a b =---⨯+=+-⋅-+，∴当1n =时，有110S a a ==≠；当2n ≥时，有11()2n n n n a S S a bn b --=-=-+⋅，又当1n =时，01()2a a b b a =-+⋅=也适合上式，1()2n n a a bn b -∴=-+⋅，令n b a b bn =+-，12n n c -=，则数列{}n b 为等差数列，{}n c 为等比数列，故n n n a b c =，其中数列{}n b 为等差数列，{}n c 为等比数列；故C 错，D 正确；因为11()22n n n a a b bn --+=-⋅⋅，0b ≠，所以{}12n bn -⋅即不是等差数列，也不是等比数列，故AB 错. 故选：D. 【点睛】方法点睛：由数列前n 项和求通项公式时，一般根据11,2,1n n n S S n a a n --≥⎧=⎨=⎩求解，考查学生的计算能力.二、多选题21．ABC 【分析】因为{}n a 是等差数列，由612S S =可得9100a a +=，利用通项转化为1a 和d 即可判断选项A ；利用前n 项和公式以及等差数列的性质即可判断选项B ；利用等差数列的性质961014a d a a d a =++=+即可判断选项C ；由0d <可得6140a a d +=<且60a >，140a <即可判断选项D ，进而得出正确选项.【详解】因为{}n a 是等差数列，前n 项和为n S ，由612S S =得：1267891011120S S a a a a a a -=+++++=，即()91030a a +=，即9100a a +=，对于选项A ：由9100a a +=得12170a d +=，可得1:17:2a d =-，故选项A 正确；对于选项B ：()()118910181818022a a a a S ++===，故选项B 正确；对于选项C ：911691014a a a a a a d d =+=++=+，若0d >，则6140a a d +=>，故选项C 正确；对于选项D ：当0d <时，6140a a d +=<，则614a a <-，因为0d <，所以60a >，140a <，所以614a a <，故选项D 不正确，故选：ABC 【点睛】关键点点睛：本题的关键点是由612S S =得出9100a a +=，熟记等差数列的前n 项和公式和通项公式，灵活运用等差数列的性质即可.22．无23．BD 【分析】利用递推关系可得1211n n a a n -=+-，再利用数列的单调性即可得出答案．【详解】解：∵23n n n S a +=， ∴2n ≥时，112133n n n n n n n a S S a a --++=-=-，化为：112111n n a n a n n -+==+--，由于数列21n ⎧⎫⎨⎬-⎩⎭单调递减，可得：2n =时，21n -取得最大值2． ∴1nn a a -的最大值为3．故选：BD ．【点睛】本题考查了数列递推关系、数列的单调性，考查了推理能力与计算能力，属于中档题． 24．BD 【分析】依据题意，根数从上至下构成等差数列，设首项即第一层的根数为1a ，公差即每一层比上一层多的根数为1d =，设一共放()2n n ≥层，利用等差数列求和公式，分析即可得解. 【详解】依据题意，根数从上至下构成等差数列，设首项即第一层的根数为1a ，公差为1d =，设一共放()2n n ≥层，则总得根数为：()()111110022n n n d n n S na na --=+=+=整理得120021a n n=+-，因为1a *∈N ，所以n 为200的因数，()20012n n+-≥且为偶数，验证可知5,8n =满足题意. 故选：BD. 【点睛】关键点睛：本题考查等差数列的求和公式，解题的关键是分析题意，把题目信息转化为等差数列，考查学生的逻辑推理能力与运算求解能力，属于基础题. 25．ABD由10n n a a d +-=<可判断AB ，再由a 1＞0，d ＜0，可知等差数列数列{}n a 先正后负，可判断CD. 【详解】根据等差数列定义可得10n n a a d +-=<，所以数列{}n a 单调递减，A 正确；由数列{}n a 单调递减，可知数列{}n a 有最大值a 1，故B 正确；由a 1＞0，d ＜0，可知等差数列数列{}n a 先正后负，所以数列{}n S 先增再减，有最大值，C 不正确，D 正确. 故选：ABD. 26．BD 【分析】设等差数列{}n a 的公差为d ，根据条件12a 、8S 、9S 成等差数列可求得1a 与d 的等量关系，可得出n a 、n S 的表达式，进而可判断各选项的正误. 【详解】设等差数列{}n a 的公差为d ，则8118788282S a d a d ⨯=+=+，9119899362S a d a d ⨯=+=+，因为12a 、8S 、9S 成等差数列，则81922S a S =+，即11116562936a d a a d +=++，解得14a d =-，()()115n a a n d n d ∴=+-=-，()()219122n n n d n n d S na --=+=. 对于A 选项，59233412a a d d +=⨯=，()2888942d S d -⨯==-，A 选项错误；对于B 选项，()2229272d Sd -⨯==-，()2779772d Sd -⨯==-，B 选项正确；对于C 选项，()2298192224n d d S n n n ⎡⎤⎛⎫=-=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.若0d >，则4S 或5S 最小；若0d <，则4S 或5S 最大.C 选项错误；对于D 选项，50a =，D 选项正确. 故选：BD. 【点睛】在解有关等差数列的问题时可以考虑化归为a 1和d 等基本量，通过建立方程（组）获得解，另外在求解等差数列前n 项和n S 的最值时，一般利用二次函数的基本性质或者数列的单调性来求解.【分析】由已知得()()612112712+12+220a a a a S ==>，又70a <，所以6>0a ，可判断A ；由已知得出2437d -<<-，且()12+3n a n d =-，得出[]1,6n ∈时，>0n a ，7n ≥时，0n a <，又()1112+3n a n d =-，可得出1na 在1,6n n N上单调递增，1na 在7n nN ，上单调递增，可判断B ；由()313117713+12203213a a a S a ⨯==<=，可判断C ；判断 n a ，n S 的符号， n a 的单调性可判断D ；【详解】由已知得311+212,122d a a a d ===-，()()612112712+12+220a a a a S ==>，又70a <，所以6>0a ，故A 正确；由7161671+612+40+512+3>0+2+1124+7>0a a d d a a d d a a a d d ==<⎧⎪==⎨⎪==⎩，解得2437d -<<-，又()()3+312+3n a n d n d a =-=-，当[]1,6n ∈时，>0n a ，7n ≥时，0n a <，又()1112+3n a n d=-，所以[]1,6n ∈时，1>0na ，7n ≥时，10n a <，所以1na 在1,6nn N上单调递增，1na 在7nn N ，上单调递增，所以数列1n a ⎧⎫⎨⎬⎩⎭不是递增数列，故B 不正确；由于()313117713+12203213a a a S a ⨯==<=，而120S >，所以0n S <时，n 的最小值为13，故C 选项正确；当[]1,6n ∈时，>0n a ，7n ≥时，0n a <，当[]1,12n ∈时，>0n S ，13n ≥时，0nS <，所以当[]7,12n ∈时，0n a <，>0n S ，0nnS a <，[]712n ∈，时，n a 为递增数列，n S 为正数且为递减数列，所以数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项，故D 正确；【点睛】本题考查等差数列的公差，项的符号，数列的单调性，数列的最值项，属于较难题. 28．AD 【分析】由1385a a S +=求出100a =，即19a d =-，由此表示出9a 、11a 、6S 、13S ，可判断C 、D 两选项；当0d >时，10a <，n S 有最小值，故B 错误. 【详解】解：1385a a S +=，111110875108,90,02da a d a a d a ⨯++=++==，故正确A. 由190a d +=，当0d >时，10a <，n S 有最小值，故B 错误.9101110,a a d d a a d d =-==+=，所以911a a =，故C 错误.61656+5415392dS a d d d ⨯==-+=-， 131131213+11778392dS a d d d ⨯==-+=-，故D 正确. 故选：AD 【点睛】考查等差数列的有关量的计算以及性质，基础题. 29．ACD 【分析】由13623a a S +=得100a =，故A 正确；当0d <时，根据二次函数知识可知n S 无最小值，故B 错误；根据等差数列的性质计算可知127S S =，故C 正确；根据等差数列前n 项和公式以及等差数列的性质可得190S =，故D 正确. 【详解】因为13623a a S +=，所以111236615a a d a d ++=+，所以190a d +=，即100a =，故A 正确；当0d <时，1(1)(1)922n n n n n S na d dn d --=+=-+2(19)2dn n =-无最小值，故B 错误；因为127891*********S S a a a a a a -=++++==，所以127S S =，故C 正确；因为()1191910191902a a S a+⨯===，故D 正确.故选：ACD. 【点睛】本题考查了等差数列的通项公式、前n 项和公式，考查了等差数列的性质，属于中档题. 30．CD 【分析】根据等差数列中1118S S =可得数列的公差0d <，再根据二次函数的性质可知15S 是最大值，同时可得150a =，进而得到290S =，即可得答案；【详解】1118S S =，∴0d <，设2n S An Bn =+，则点(,)n n S 在抛物线2y Ax Bx =+上，抛物线的开口向下，对称轴为14.5x =，∴1514S S =且为n S 的最大值，1118S S =12131815070a a a a ⇒+++=⇒=，∴129291529()2902a a S a +===，故选：CD. 【点睛】本题考查利用二次函数的性质研究等差数列的前n 项和的性质，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力.。

等差数列练习题及答案详解.docx

等差数列练习题及答案详解等差数列一、选择题1、等差数列a n中，A. 12B. 48S10120，那么a1a10（）24 C.36 D.2、已知等差数列a n，a n2n19 ，那么这个数列的前n项和 s n（）A. 有最小值且是整数B. 有最小值且是分数C. 有最大值且是整数D. 有最大值且是分数3、已知等差数列a n的公差d1， a2a4a10080，2那么 S100A．80B．120 C．135D．160．4、已知等差数列a n中，a2a5a9 a1260，那么 S13 A．390B． 195C．180D．120 5、从前180个正偶数的和中减去前180 个正奇数的和，其差为（）A. 0B. 90C. 180D. 3606、等差数列a n的前m项的和为30，前2m项的和为100，则它的前3m 项的和为()A. 130B. 170C. 210D. 2607、在等差数列a n中，a2 6 ， a8 6 ，若数列a n的前 n 项和为 S n，则（）A. S4S5B. S4S5C. S6S5D. S6S58、一个等差数列前3项和为34，后3项和为146，所有项和为 390 ，则这个数列的项数为（）A. 13B.12C.11D.109、已知某数列前n项之和n3为，且前n个偶数项的和为 n2 ( 4n 3) ，则前 n 个奇数项的和为（）A．D．3n 2 ( n 1)B．n2(4n 3)C．3n2 1n 3210若一个凸多边形的内角度数成等差数列，最小角为 100°，最大角为 140°，这个凸多边形的边比为（）A．6B．8C．10D．12一．选择题（ 10×5 分）题12345678910号答案二．填空题1、等差数列a n中，若a6a3a8，则s922 、等差数列a n中，若S n3n2n.，则公差d.3、在小于100的正整数中，被3除余2的数的和是.4 、已知等差数列{ a n}的公差是正整数，且a3a712, a4a64 ，则前10项的和S10=5、一个等差数列共有10 项，其中奇数项的和为25，偶数项的和为 15，则这个数列的第 6 项是2*6 、两个等差数列a n 和b n 的前n项和分别为S n 和S n7n 3，则a8.Tn ，若T n n 3b8三．解答题1、在等差数列a n中，a40.8 ， a11 2.2 ，求a 51a52L a80.2、等差数列a n的前n和S n，已知a312，S12 >0，S 13 <0，①求公差 d 的取范；②S1 , S2,L, S12中哪一个最大？并明理由.3、己知{ a n}等差数列，a12, a23，若在每相两之插入三个数，使它和原数列的数构成一个新的等差数列，求：（1）原数列的第 12 是新数列的第几？（2）新数列的第 29 是原数列的第几？4、等差数列{ a n}的前ｎ的和S n ,且 S 4 =－62,S 6 =－75,求：（1）{ a n}的通公式 a n及前ｎ的和 Sn；（2）|a 1 |+|a 2 |+|a 3 |+⋯⋯ +|a 14 |.5、某渔业公司年初用98 万元购买一艘捕鱼船，第一年各种费用 12 万元，以后每年都增加 4 万元，每年捕鱼收益 50 万元，（Ⅰ）问第几年开始获利？（Ⅱ）若干年后，有两种处理方案：（ 1）年平均获利最大时，以 26 万元出售该渔船；（ 2）总纯收入获利最大时，以 8 万元出售该渔船 .问哪种方案合算 .参考答案一、选择题1-5 B A C B C 6-10 C B A B A二、填空题1、 02、63、16504、-105、36、6三．解答题1、 an0.2n ， a51a 52a 80 393．S 1212 (a 1 a 12 ) 6( a 6 a 7 ) 0a 6 a 7 2a 1 11d2、 ①∵26d 0 S1313(a 1 a 13 ) 13ga 70 a 7 0, ∴a 1a 12d 12224 a 6 a 7 0 a 6 024 a n 是减数列 ,解得 ,d3, ②由a 7 0a 7, 又∵d3 ∴77∴S 1 , S 2 ,L , S 12 中 S 6 最大 .3、解：新数列b n , 则 b 1 a 1 2,b 51即 3=2+4d ，∴ d4a 2 3,根据b n b 1 (n 1) d, 有b 5 b 1 4d,1 n 7 ，∴b n2 ( n 1)44又Q a n a 1 (n 1) 1n 1(4 n 3) 7，∴ a n b 4 n 34即原数列的第 n 新数列的第 4n －3 ．（ 1 ）当 n=12 ， 4n －3=4×12－3=45，故原数列的第 12 新数列的第 45 ；（ 2 ）由 4n －3=29,得 n=8 ，故新数列的第 29 是原数列的第 8 。

等差数列求和及练习题(整理).doc

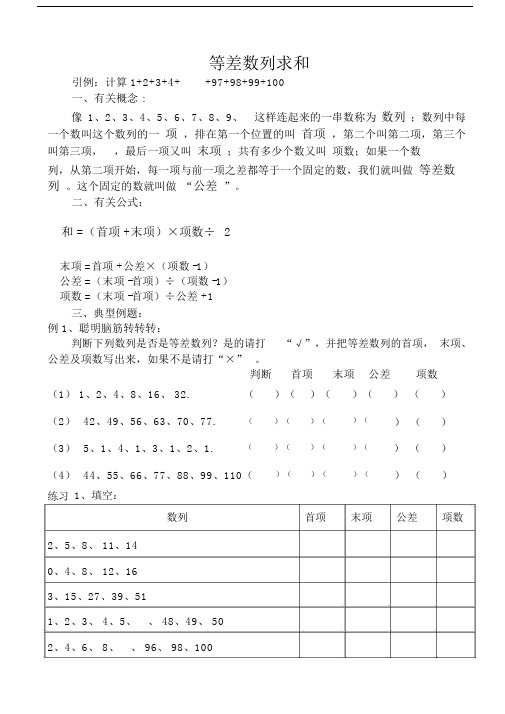
等差数列求和引例：计算 1+2+3+4++97+98+99+100一、有关概念 :像1、2、3、4、5、6、7、8、9、这样连起来的一串数称为数列；数列中每一个数叫这个数列的一项，排在第一个位置的叫首项，第二个叫第二项，第三个叫第三项，，最后一项又叫末项；共有多少个数又叫项数；如果一个数列，从第二项开始，每一项与前一项之差都等于一个固定的数，我们就叫做等差数列。

这个固定的数就叫做“公差”。

二、有关公式：和 =（首项 +末项）×项数÷ 2末项 =首项 +公差×（项数 -1）公差 =（末项 -首项）÷（项数 -1）项数 =（末项 -首项）÷公差 +1三、典型例题：例 1、聪明脑筋转转转：判断下列数列是否是等差数列？是的请打“√”，并把等差数列的首项，末项、公差及项数写出来，如果不是请打“×”。

判断首项末项公差项数（1） 1、2、4、8、16、 32.（）（）（）（）（）（2）42、49、56、63、70、77. （）（）（）（）（）（3）5、1、4、1、3、1、2、1. （）（）（）（）（）（4）44、55、66、77、88、99、110（）（）（）（）（）练习1、填空：数列首项末项公差项数2、5、8、 11、140、4、8、 12、163、15、27、39、511、2、3、 4、5、、 48、49、 502、4、6、 8、、 96、 98、100例 2、已知等差数列 1,8,15, , 78.共 12 项，和是多少？（博易 P27例 2）（看 ppt,推出公式）例 3、计算 1+3+5+7++35+37+39练习 2：计算下列各题（1）6+10+14+18+22+26+30 （3）1+3+5+7++95+97+99（2）3+15+27+39+51+63（4）2+4+6+8++96+98+100（3）已知一列数 4,6,8,10 ，，64，共有 31 个数，这个数列的和是多少？例 5、有一堆圆木堆成一堆，从上到下，上面一层有 10 根，每向下一层增加一根，共堆了 10 层。

等差数列通项公式基础训练题(含详解)

等差数列通项公式基础训练题（含详解)
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．等差数列中，已知，，则（）
A．16B．17C．18D．19
2．设为等差数列，若，则
A．4B．5C．6D．7
3．设数列是公差为的等差数列，若，则（）
A．4B．3C．2D．1
4．已知数列满足，且，那么（）
A．8B．9C．10D．11
5．在数列{an}中，若，a1＝8，则数列{an}的通项公式为（）
A．an＝2（n+1）2B．an＝4（n+1）C．an＝8n2D．an＝4n（n+1）
6．在数列中， =1，，则的值为（）
A．99B．49C．101D．102
7．在数列中，，，，则（）
A．6B．7C．8D．9
8．等差数列中，，则 ( ).
A．110B．120C．130D．140
9．已知数列是等差数列，，则 ( )
A．36B．30C．24 D．1
10．在等差数列中，若，则（）
A．10B．5C． D．
11．等差数列满足，则其前10项之和为（）
【详解】
根据题意，设，数列是等差数列，
则，，
则，
即；
解可得；
故答案为：
【点睛】
本题考查等差数列的性质，关键是求出数列的通项公式．
19．
【解析】
【分析】
本次考察的是等差数列通项公式的求法。
【详解】
，
【点睛】
等差数列通项公式除了掌握，考生还应掌握

(完整版)等差数列基础习题选(附详细答案)-答案

参考答案与试题解析一．选择题（共26小题）1．已知等差数列{a n}中，a3=9，a9=3，则公差d的值为（）A．B．1C．D．﹣1考点：等差数列．专题：计算题．分析：本题可由题意，构造方程组，解出该方程组即可得到答案．解答：解：等差数列{a n}中，a3=9，a9=3，由等差数列的通项公式，可得解得，即等差数列的公差d=﹣1．故选D点评：本题为等差数列的基本运算，只需构造方程组即可解决，数基础题．2．已知数列{a n}的通项公式是a n=2n+5，则此数列是（）A．以7为首项，公差为2的等差数列B．以7为首项，公差为5的等差数列C．以5为首项，公差为2的等差数列D．不是等差数列考点：等差数列．专题：计算题．分析：直接根据数列{a n}的通项公式是a n=2n+5求出首项，再把相邻两项作差求出公差即可得出结论．解答：解：因为a n=2n+5，所以a1=2×1+5=7；a n+1﹣a n=2（n+1）+5﹣（2n+5）=2．故此数列是以7为首项，公差为2的等差数列．故选A．点评：本题主要考查等差数列的通项公式的应用．如果已知数列的通项公式，可以求出数列中的任意一项．3．在等差数列{a n}中，a1=13，a3=12，若a n=2，则n等于（）A．23 B．24 C．25 D．26考点：等差数列．专题：综合题．分析：根据a1=13，a3=12，利用等差数列的通项公式求得d的值，然后根据首项和公差写出数列的通项公式，让其等于2得到关于n的方程，求出方程的解即可得到n的值．解答：解：由题意得a3=a1+2d=12，把a1=13代入求得d=﹣，则a n=13﹣（n﹣1）=﹣n+=2，解得n=23故选A点评：此题考查学生灵活运用等差数列的通项公式化简求值，是一道基础题．4．等差数列{a n}的前n项和为S n，已知S3=6，a4=8，则公差d=（）A．一1 B．2C．3D．一2考点：等差数列．专题：计算题．分析：根据等差数列的前三项之和是6，得到这个数列的第二项是2，这样已知等差数列的；两项，根据等差数列的通项公式，得到数列的公差．解答：解：∵等差数列{a n}的前n项和为S n，S3=6，∴a2=2∵a4=8，∴8=2+2d∴d=3，故选C．点评：本题考查等差数列的通项，这是一个基础题，解题时注意应用数列的性质，即前三项的和等于第二项的三倍，这样可以简化题目的运算．5．两个数1与5的等差中项是（）A．1B．3C．2D．考点：等差数列．专题：计算题．分析：由于a，b的等差中项为，由此可求出1与5的等差中项．解答：解：1与5的等差中项为：=3，故选B．点评：本题考查两个数的等差中项，牢记公式a，b的等差中项为：是解题的关键，属基础题．6．一个首项为23，公差为整数的等差数列，如果前六项均为正数，第七项起为负数，则它的公差是（）A．﹣2 B．﹣3 C．﹣4 D．﹣5考点：等差数列．专题：计算题．分析：设等差数列{a n}的公差为d，因为数列前六项均为正数，第七项起为负数，所以，结合公差为整数进而求出数列的公差．解答：解：设等差数列{a n}的公差为d，所以a6=23+5d，a7=23+6d，又因为数列前六项均为正数，第七项起为负数，所以，因为数列是公差为整数的等差数列，所以d=﹣4．故选C．点评：解决此类问题的关键是熟练掌握等差数列的通项公式，并且结合正确的运算．7．（2012•福建）等差数列{a n}中，a1+a5=10，a4=7，则数列{a n}的公差为（）A．1B．2C．3D．4考点：等差数列的通项公式．专题：计算题．分析：设数列{a n}的公差为d，则由题意可得2a1+4d=10，a1+3d=7，由此解得d的值．解答：解：设数列{a n}的公差为d，则由a1+a5=10，a4=7，可得2a1+4d=10，a1+3d=7，解得d=2，故选B．点评：本题主要考查等差数列的通项公式的应用，属于基础题．8．数列的首项为3，为等差数列且，若，，则=（）A．0B．8C．3D．11考点：等差数列的通项公式．专题：计算题．分析：先确定等差数列的通项，再利用，我们可以求得的值．解答：解：∵为等差数列，，，∴∴b n=b3+（n﹣3）×2=2n﹣8∵∴b8=a8﹣a1∵数列的首项为3∴2×8﹣8=a8﹣3，∴a8=11．故选D点评：本题考查等差数列的通项公式的应用，由等差数列的任意两项，我们可以求出数列的通项，是基础题．9．已知两个等差数列5，8，11，…和3，7，11，…都有100项，则它们的公共项的个数为（）A．25 B．24 C．20 D．19考点：等差数列的通项公式．专题：计算题．分析：（法一）：根据两个等差数列的相同的项按原来的先后次序组成一个等差数列，且公差为原来两个公差的最小公倍数求解，（法二）由条件可知两个等差数列的通项公式，可用不定方程的求解方法来求解．解答：解法一：设两个数列相同的项按原来的前后次序组成的新数列为{a n}，则a1=11∵数列5，8，11，…与3，7，11，…公差分别为3与4，∴{a n}的公差d=3×4=12，∴a n=11+12（n﹣1）=12n﹣1．又∵5，8，11，…与3，7，11，…的第100项分别是302与399，∴a n=12n﹣1≤302，即n≤25.5．又∵n∈N*，∴两个数列有25个相同的项．故选A解法二：设5，8，11，与3，7，11，分别为{a n}与{b n}，则a n=3n+2，b n=4n﹣1．设{a n}中的第n项与{b n}中的第m项相同，即3n+2=4m﹣1，∴n=m﹣1．又m、n∈N*，可设m=3r（r∈N*），得n=4r﹣1．根据题意得1≤3r≤100 1≤4r﹣1≤100 解得≤r≤∵r∈N*从而有25个相同的项故选A点评：解法一利用了等差数列的性质，解法二利用了不定方程的求解方法，对学生的运算能力及逻辑思维能力的要求较高．10．设S n为等差数列{a n}的前n项和，若满足a n=a n﹣1+2（n≥2），且S3=9，则a1=（）A．5B．3C．﹣1 D．1考点：等差数列的通项公式．专题：计算题．分析：根据递推公式求出公差为2，再由S3=9以及前n项和公式求出a1的值．解答：解：∵a n=a n﹣1+2（n≥2），∴a n﹣a n﹣1=2（n≥2），∴等差数列{a n}的公差是2，由S3=3a1+=9解得，a1=1．故选D．点评：本题考查了等差数列的定义，以及前n项和公式的应用，即根据代入公式进行求解．11．（2005•黑龙江）如果数列{a n}是等差数列，则（）A．a1+a8＞a4+a5B．a1+a8=a4+a5C．a1+a8＜a4+a5D．a1a8=a4a5考点：等差数列的性质．分析：用通项公式来寻求a1+a8与a4+a5的关系．解答：解：∵a1+a8﹣（a4+a5）=2a1+7d﹣（2a1+7d）=0∴a1+a8=a4+a5∴故选B点评：本题主要考查等差数列通项公式，来证明等差数列的性质．12．（2004•福建）设S n是等差数列{a n}的前n项和，若=（）A．1B．﹣1 C．2D．考点：等差数列的性质．专题：计算题．分析：充分利用等差数列前n项和与某些特殊项之间的关系解题．解答：解：设等差数列{a n}的首项为a1，由等差数列的性质可得a1+a9=2a5，a1+a5=2a3，∴====1，故选A．点评：本题主要考查等差数列的性质、等差数列的前n项和公式以及等差中项的综合应用，已知等差数列{a n}的前n项和为S n，则有如下关系S2n﹣1=（2n﹣1）a n．13．（2009•安徽）已知{a n}为等差数列，a1+a3+a5=105，a2+a4+a6=99，则a20等于（）A．﹣1 B．1C．3D．7考点：等差数列的性质．专题：计算题．分析：根据已知条件和等差中项的性质可分别求得a3和a4的值，进而求得数列的公差，最后利用等差数列的通项公式求得答案．解答：解：由已知得a1+a3+a5=3a3=105，a2+a4+a6=3a4=99，∴a3=35，a4=33，∴d=a4﹣a3=﹣2．∴a20=a3+17d=35+（﹣2）×17=1．故选B点评：本题主要考查了等差数列的性质和等差数列的通项公式的应用．解题的关键是利用等差数列中等差中项的性质求得a3和a4．14．在等差数列{a n}中，a2=4，a6=12，，那么数列{}的前n项和等于（）A．B．C．D．考点：数列的求和；等差数列的性质．专题：计算题．分析：求出等差数列的通项，要求的和是一个等差数列与一个等比数列的积构成的数列，利用错位相减法求出数列的前n项的和．解答：解：∵等差数列{a n}中，a2=4，a6=12；∴公差d=；∴a n=a2+（n﹣2）×2=2n；∴；∴的前n项和，=两式相减得=∴故选B点评：求数列的前n项的和，先判断通项的特点，据通项的特点选择合适的求和方法．15．已知S n为等差数列{a n}的前n项的和，a2+a5=4，S7=21，则a7的值为（）A．6B．7C．8D．9考点：等差数列的性质．专题：计算题．分析：由a2+a5=4，S7=21根据等差数列的性质可得a3+a4=a1+a6=4①，根据等差数列的前n项和公式可得，，联立可求d，a1，代入等差数列的通项公式可求解答：解：等差数列{a n}中，a2+a5=4，S7=21根据等差数列的性质可得a3+a4=a1+a6=4①根据等差数列的前n项和公式可得，所以a1+a7=6②②﹣①可得d=2，a1=﹣3所以a7=9故选D点评：本题主要考查了等差数列的前n项和公式及等差数列的性质的综合应用，属于基础试题．16．已知数列{a n}为等差数列，a1+a3+a5=15，a4=7，则s6的值为（）A．30 B．35 C．36 D．24考点：等差数列的性质．专题：计算题．分析：利用等差中项的性质求得a3的值，进而利用a1+a6=a3+a4求得a1+a6的值，代入等差数列的求和公式中求得答案．解答：解：a1+a3+a5=3a3=15，∴a3=5∴a1+a6=a3+a4=12∴s6=×6=36故选C点评：本题主要考查了等差数列的性质．特别是等差中项的性质．17．（2012•营口）等差数列{a n}的公差d＜0，且，则数列{a n}的前n项和S n取得最大值时的项数n是（）A．5B．6C．5或6 D．6或7考点：等差数列的前n项和；等差数列的通项公式．专题：计算题．分析：由，知a1+a11=0．由此能求出数列{a n}的前n项和S n取得最大值时的项数n．解答：解：由，知a1+a11=0．∴a6=0，故选C．点评：本题主要考查等差数列的性质，求和公式．要求学生能够运用性质简化计算．18．（2012•辽宁）在等差数列{a n}中，已知a4+a8=16，则该数列前11项和S11=（）A．58 B．88 C．143 D．176考点：等差数列的性质；等差数列的前n项和．专题：计算题．分析：根据等差数列的定义和性质得a1+a11=a4+a8=16，再由S11=运算求得结果．解答：解：∵在等差数列{a n}中，已知a4+a8=16，∴a1+a11=a4+a8=16，∴S11==88，故选B．点评：本题主要考查等差数列的定义和性质，等差数列的前n项和公式的应用，属于中档题．19．已知数列{a n}等差数列，且a1+a3+a5+a7+a9=10，a2+a4+a6+a8+a10=20，则a4=（）A．﹣1 B．0C．1D．2考点：等差数列的通项公式；等差数列的前n项和．专题：计算题．分析：由等差数列得性质可得：5a5=10，即a5=2．同理可得5a6=20，a6=4，再由等差中项可知：a4=2a5﹣a6=0解答：解：由等差数列得性质可得：a1+a9=a3+a7=2a5，又a1+a3+a5+a7+a9=10，故5a5=10，即a5=2．同理可得5a6=20，a6=4．再由等差中项可知：a4=2a5﹣a6=0故选B点评：本题考查等差数列的性质及等差中项，熟练利用性质是解决问题的关键，属基础题．20．（理）已知数列{a n}的前n项和S n=n2﹣8n，第k项满足4＜a k＜7，则k=（）A．6B．7C．8D．9考点：等差数列的通项公式；等差数列的前n项和．专题：计算题．分析：先利用公式a n=求出a n，再由第k项满足4＜a k＜7，建立不等式，求出k的值．解答：解：a n==∵n=1时适合a n=2n﹣9，∴a n=2n﹣9．∵4＜a k＜7，∴4＜2k﹣9＜7，∴＜k＜8，又∵k∈N+，∴k=7，故选B．点评：本题考查数列的通项公式的求法，解题时要注意公式a n=的合理运用，属于基础题．21．数列a n的前n项和为S n，若S n=2n2﹣17n，则当S n取得最小值时n的值为（）A．4或5 B．5或6 C．4D．5考点：等差数列的前n项和．专题：计算题．分析：把数列的前n项的和S n看作是关于n的二次函数，把关系式配方后，又根据n为正整数，即可得到S n取得最小值时n的值．解答：解：因为S n=2n2﹣17n=2﹣，又n为正整数，所以当n=4时，S n取得最小值．故选C点评：此题考查学生利用函数思想解决实际问题的能力，是一道基础题．22．等差数列{a n}中，a n=2n﹣4，则S4等于（）A．12 B．10 C．8D．4考点：等差数列的前n项和．专题：计算题．分析：利用等差数列{a n}中，a n=2n﹣4，先求出a1，d，再由等差数列的前n项和公式求S4．解答：解：∵等差数列{a n}中，a n=2n﹣4，∴a1=2﹣4=﹣2，a2=4﹣4=0，d=0﹣（﹣2）=2，∴S4=4a1+=4×（﹣2）+4×3=4．故选D．点评：本题考查等差数列的前n项和公式的应用，是基础题．解题时要认真审题，注意先由通项公式求出首项和公差，再求前四项和．23．若{a n}为等差数列，a3=4，a8=19，则数列{a n}的前10项和为（）A．230 B．140 C．115 D．95考点：等差数列的前n项和．专题：综合题．分析：分别利用等差数列的通项公式化简已知的两个等式，得到①和②，联立即可求出首项和公差，然后利用求出的首项和公差，根据公差数列的前n项和的公式即可求出数列前10项的和．解答：解：a3=a1+2d=4①，a8=a1+7d=19②，②﹣①得5d=15，解得d=3，把d=3代入①求得a1=﹣2，所以S10=10×（﹣2）+×3=115故选C．点评：此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值，是一道基础题．26．设a n=﹣2n+21，则数列{a n}从首项到第几项的和最大（）A．第10项B．第11项C．第10项或11项D．第12项考点：等差数列的前n项和；二次函数的性质．专题：转化思想．分析：方法一：由a n，令n=1求出数列的首项，利用a n﹣a n﹣1等于一个常数，得到此数列为等差数列，然后根据求出的首项和公差写出等差数列的前n项和的公式，得到前n项的和与n成二次函数关系，其图象为开口向下的抛物线，当n=﹣时，前n项的和有最大值，即可得到正确答案；方法二：令a n大于等于0，列出关于n的不等式，求出不等式的解集即可得到n的范围，在n的范围中找出最大的正整数解，从这项以后的各项都为负数，即可得到正确答案．解答：解：方法一：由a n=﹣2n+21，得到首项a1=﹣2+21=19，a n﹣1=﹣2（n﹣1）+21=﹣2n+23，则a n﹣a n﹣1=（﹣2n+21）﹣（﹣2n+23）=﹣2，（n＞1，n∈N+），所以此数列是首项为19，公差为﹣2的等差数列，则S n=19n+•（﹣2）=﹣n2+20n，为开口向下的抛物线，当n=﹣=10时，S n最大．所以数列{a n}从首项到第10项和最大．方法二：令a n=﹣2n+21≥0，解得n≤，因为n取正整数，所以n的最大值为10，所以此数列从首项到第10项的和都为正数，从第11项开始为负数，则数列{a n}从首项到第10项的和最大．故选A点评：此题的思路可以先确定此数列为等差数列，根据等差数列的前n项和的公式及二次函数求最值的方法得到n 的值；也可以直接令a n≥0，求出解集中的最大正整数解，要求学生一题多解．二．填空题（共4小题）27．如果数列{a n}满足：=．考点：数列递推式；等差数列的通项公式．专题：计算题．分析：根据所给的数列的递推式，看出数列是一个等差数列，根据所给的原来数列的首项看出等差数列的首项，根据等差数列的通项公式写出数列，进一步得到结果．解答：解：∵根据所给的数列的递推式∴数列{}是一个公差是5的等差数列，∵a1=3，∴=，∴数列的通项是∴故答案为：点评：本题看出数列的递推式和数列的通项公式，本题解题的关键是确定数列是一个等差数列，利用等差数列的通项公式写出通项，本题是一个中档题目．28．如果f（n+1）=f（n）+1（n=1，2，3…），且f（1）=2，则f（100）=101．考点：数列递推式；等差数列的通项公式．专题：计算题．分析：由f（n+1）=f（n）+1，x∈N+，f（1）=2，依次令n=1，2，3，…，总结规律得到f（n）=n+1，由此能够求出f（100）．解答：解：∵f（n+1）=f（n）+1，x∈N+，f（1）=2，∴f（2）=f（1）+1=2+1=3，f（3）=f（2）+1=3+1=4，f（4）=f（3）+1=4+1=5，…∴f（n）=n+1，∴f（100）=100+1=101．故答案为：101．点评：本题考查数列的递推公式的应用，是基础题．解题时要认真审题，仔细解答．29．等差数列{a n}的前n项的和，则数列{|a n|}的前10项之和为58．考点：数列的求和；等差数列的通项公式．专题：计算题．分析：先求出等差数列的前两项，可得通项公式为a n=7﹣2n，从而得到n≤3时，|a n|=7﹣2n，当n＞3时，|a n|= 2n﹣7．分别求出前3项的和、第4项到第10项的和，相加即得所求．解答：解：由于等差数列{an}的前n项的和，故a1=s1=5，∴a2=s2﹣s1=8﹣5=3，故公差d=﹣2，故a n=5+（n﹣1）（﹣2）=7﹣2n．当n≤3时，|a n|=7﹣2n，当n＞3时，|a n|=2n﹣7．故前10项之和为a1+a2+a3﹣a4﹣a5﹣…﹣a10=+=9+49=58，故答案为58．点评：本题主要考查等差数列的通项公式，前n项和公式及其应用，体现了分类讨论的数学思想，属于中档题．11。

等差数列知识点总结及考点练习.docx

等差数列知识点总结一、等差数列知识点回顾与技巧点拨1．等差数列的定义一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母d 表示．2．等差数列的通项公式若等差数列{a n }的首项是a 1，公差是d ，则其通项公式为a n ＝a 1＋(n －1)d ＝(n －m )d＝p .3．等差中项如果三个数x ，A ，y 组成等差数列，那么A 叫做x 和y 的等差中项，如果A 是x 和y 的等差中项，则A ＝x ＋y2.4．等差数列的常用性质(1)通项公式的推广：a n ＝a m ＋(n －m )d (n ，m ∈N *)． (2)若{a n }为等差数列，且m ＋n ＝p ＋q ，则a m ＋a n ＝a p ＋a q (m ，n ，p ，q ∈N *)．(3)若{a n }是等差数列，公差为d ，则a k ，a k ＋m ，a k ＋2m ，…(k ，m ∈N *)是公差为md 的等差数列．(4)数列S m ，S 2m －S m ，S 3m －S 2m ，…也是等差数列． (5)S 2n －1＝(2n －1)a n .(6)若n 为偶数，则S 偶－S 奇＝nd2；若n 为奇数，则S 奇－S 偶＝a 中(中间项)． 5．等差数列的前n 项和公式若已知首项a 1和末项a n ，则S n ＝n a 1＋a n2，或等差数列{a n }的首项是a 1，公差是d ，则其前n 项和公式为S n ＝na 1＋n n －12d .6．等差数列的前n 项和公式与函数的关系S n ＝d 2n 2＋⎝⎛⎭⎪⎫a 1－d 2n ，数列{a n }是等差数列的充要条件是S n ＝An 2＋Bn (A ，B 为常数)．7．最值问题在等差数列{a n }中，a 1＞0，d ＜0，则S n 存在最大值，若a 1＜0，d ＞0，则S n 存在最小值．一个推导利用倒序相加法推导等差数列的前n 项和公式： S n ＝a 1＋a 2＋a 3＋…＋a n ，① S n ＝a n ＋a n －1＋…＋a 1，②①＋②得：S n ＝n a 1＋a n2.两个技巧已知三个或四个数组成等差数列的一类问题，要善于设元． (1)若奇数个数成等差数列且和为定值时，可设为…，a －2d ，a －d ，a ，a ＋d ，a ＋2d ，…. (2)若偶数个数成等差数列且和为定值时，可设为…，a －3d ，a －d ，a ＋d ，a ＋3d ，…，其余各项再依据等差数列的定义进行对称设元．四种方法等差数列的判断方法(1)定义法：对于n ≥2的任意自然数，验证a n －a n －1为同一常数；(2)等差中项法：验证2a n －1＝a n ＋a n －2(n ≥3，n ∈N *)都成立； (3)通项公式法：验证a n ＝pn ＋q ；(4)前n 项和公式法：验证S n ＝An 2＋Bn .注：后两种方法只能用来判断是否为等差数列，而不能用来证明等差数列．回顾：1．已知等差数列{a n }中，a 3=9，a 9=3，则公差d 的值为（） A ．B ． 1C ．D ． ﹣12．已知数列{a n }的通项公式是a n =2n+5，则此数列是（） A ．以7为首项，公差为2的等差数列 B ．以7为首项，公差为5的等差数列 C ．以5为首项，公差为2的等差数列 D ．不是等差数列 3．在等差数列{a n }中，a 1=13，a 3=12，若a n =2，则n 等于（） A ． 23 B ． 24 C ． 25 D ． 26 4．两个数1与5的等差中项是（） A ． 1 B ． 3 C ． 2 D ． 5．（2005•黑龙江）如果数列{a n }是等差数列，则（） A ． a 1+a 8＞a 4+a 5 B ． a 1+a 8=a 4+a 5 C ． a 1+a 8＜a 4+a 5 D ． a 1a 8=a 4a 5考点1:等差数列的通项与前n 项和题型1：已知等差数列的某些项，求某项【解题思路】给项求项问题，先考虑利用等差数列的性质，再考虑基本量法【例1】已知{}n a 为等差数列，，则解：方法1：方法2：，方法3：令，则方法4：{}n a 为等差数列，也成等差数列，设其公差为，则为首项，20,86015==a a =75a 154,156420598141160115==⇒⎩⎨⎧=+==+=d a d a a d a a ∴2415474156474175=⨯+=+=d a a 1544582015601560=-=--=a a d ∴241541520)6075(6075=⨯+=-+=d a a b an a n +=38,45162060815==⇒⎩⎨⎧=+=+b a b a b a ∴24384516757575=+⨯=+=b a a ∴7560453015,,,,a a a a a 1d 15a 60a为第4项.方法5：{}n a 为等差数列，三点共线对应练习：1、已知{}n a 为等差数列，（互不相等），求.2、已知个数成等差数列，它们的和为，平方和为，求这个数.题型2：已知前项和及其某项，求项数.【解题思路】⑴利用等差数列的通项公式求出及，代入可求项数；⑵利用等差数列的前4项和及后4项和求出，代入可求项数.【例2】已知为等差数列{}n a 的前项和，，求解：设等差数列的首项为，公差为，则对应练习：3、若一个等差数列的前4项和为36，后4项和为124，且所有项的和为780，求这个数列的项数.4.已知为等差数列{}n a 的前项和，，则.题型3：求等差数列的前n 项和【解题思路】（1）利用求出，把绝对值符号去掉转化为等差数列的求和问题.∴438203111560=⇒+=⇒+=d d d a a ∴2442016075=+=+=d a a ∴),75(),,60(),,15(756015a a a 2415204582060751560757560751560=⇒-=-⇒--=--a a a a a a q a p a n m ==,k n m ,,k a 551655n n S d n a a n )1(1-+=1a dn S n n a a +1n S n n S n 63,6,994=-==n S a a n 1a d3,186893111-==⇒⎩⎨⎧-=+=+d a d a d a ∴7,663)1(231821==⇒=--=n n n n n S n n n S n 100,7,141===n S a a =n n S n a（2）含绝对值符号的数列求和问题，要注意分类讨论.【例3】已知为等差数列{}n a 的前项和，.（1）；⑵求； ⑶求.解：，当时，，当时，，当时，， .由，得，当时，；当时，.（1）；⑵；（3）时，，当时，对应练习：5、已知为等差数列{}n a 的前项和，，求.n S n 212n n S n -=321a a a ++10321a a a a ++++ n a a a a ++++ 321212n n S n -=∴1=n 1111211=-==S a 2≥n n n n n n S S a n n n 213)1()1(12)12(221-=-+---=-=-1=n 1111213a ==⨯-∴n a n 213-=0213≥-=n a n 213≤n ∴61≤≤n 0>n a 7≥n 0<n a 27331223321321=-⨯==++=++S a a a a a a )(10987632110321a a a a a a a a a a a a +++-++++=++++ 52)101012()6612(2222106=-⨯--⨯=-=S S 61≤≤n 232132112n n a a a a a a a a n n -=++++=++++ 7≥n )(876321321n n a a a a a a a a a a a +++-++++=++++ .7212)12()6612(222226+-=---⨯=-=n n n n S S n n S n 10,10010010==S S 110S考点2 ：证明数列是等差数列【名师指引】判断或证明数列是等差数列的方法有：1、定义法：（，是常数）{}n a 是等差数列；2、中项法：(){}n a 是等差数列；3、通项公式法：（是常数）{}n a 是等差数列； 4、项和公式法：（是常数，）{}n a 是等差数列.【例4】已知为等差数列{}n a 的前项和，. 求证：数列是等差数列.解：方法1：设等差数列{}n a 的公差为，，（常数）数列是等差数列.方法2：，，，数列是等差数列.对应练习：6、设为数列{}n a 的前项和，，（1）常数的值；（2）证：数列是等差数列.d a a n n =-+1+∈N n d⇔212+++=n n n a a a +∈N n ⇔b kn a n +=b k ,⇔Bn An S n +=2B A ,0≠A ⇔n S n )(+∈=N n nS b nn {}n b d d n n na S n )1(211-+=∴d n a n S b n n )1(211-+==∴2)1(2121111dd n a nd a b b n n =---+=-+∴{}n bd n a n S b n n )1(211-+==∴nd a b n 2111+=+d n a b n )1(2112++=+∴1111222)1(21)1(21++=+=-++++=+n n n b nd a d n a d n a b b ∴{}n b n S n )(+∈=N n pna S n n .21a a =p{}n a考点3 :等差数列的性质【解题思路】利用等差数列的有关性质求解.【例5】1、已知为等差数列{}n a 的前项和，，则；2、知为等差数列{}n a 的前项和，，则.解：1、；2、方法1：令，则. ，，；方法2：不妨设.，；方法3：{}n a 是等差数列，为等差数列三点共线..对应练习：7、含个项的等差数列其奇数项的和与偶数项的和之比为（）8.设、分别是等差数列{}n a 、{}n a 的前项和，，则n S n 1006=a =11S nS n)(,m n n S m S m n ≠===+n m S 11001122112)(116611111==⨯=+=a a a a S Bn An S n +=2n m m n B m n A nBm Am mBn An -=-+-⇒⎩⎨⎧=+=+)()(2222 m n ≠∴1)(-=++B m n A ∴)()()(2n m n m B n m A S n m +-=+++=+n m >mn a a n m a a a a a S S m n m m n n n n m -=+-=+++++=-+-+++2))((11321 ∴211-=+=+++m n n m a a a a ∴)(2))((1n m a a n m S n m n m +-=++=++∴⎭⎬⎫⎩⎨⎧n S n ∴⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+n m S n m m S m n S n n m m n ,,,,,∴)(n m S nm nn m S n m n m m n n m n m +-=⇒-+=--++12+n .A n n 12+.B n n 1+.C n n 1-.D nn 21+n S nT n 327++=n n T S nn. 考点4：等差数列与其它知识的综合【解题思路】1、利用与的关系式及等差数列的通项公式可求；2、求出后，判断的单调性.【例6】已知为数列{}n a 的前项和，；数列满足：，，其前项和为⑴ 数列{}n a 、的通项公式；⑵设为数列的前项和，，求使不等式对都成立的最大正整数的值. 解：⑴，当时，；当时，当时，，；，是等差数列，设其公差为.则，.⑵=55b a n a n S n T n T n S n n n S n 211212+={}n b 113=b n n n b b b -=++1229.153{}n b nT {}n c n )12)(112(6--=n n n b a c 57kT n >+∈∀N n k n n S n 211212+=∴1=n 611==S a 2≥n 5)1(211)1(2121121221+=----+=-=-n n n n n S S a n n n 1=n 1651a ==+∴5+=n a n 222112+++++=⇒-=n n n n n n b b b b b b ∴{}n b d3,5153369112111==⇒⎩⎨⎧=+=+d b d b d b ∴23)1(35+=-+=n n b n [][]1)23(211)5(26)12)(112(6-+-+=--=n n b a c n n n 121121)12)(12(2+--=+-=n n n n，是单调递增数列. 当时，对都成立所求最大正整数的值为.对应练习：9.已知为数列{}n a 的前项和，，.⑴ 数列{}n a 的通项公式；⑵数列{}n a 中是否存在正整数，使得不等式对任意不小于的正整数都成立？若存在，求最小的正整数，若不存在，说明理由.课后练习：1.(2010广雅中学)设数列是等差数列，且，，是数列的前项和，则A ．B ．C ．D ．2.在等差数列{}n a 中，，则 .3.数列{}n a 中，，当数列{}n a 的前项和取得最小值时，.4.已知等差数列{}n a 共有项，其奇数项之和为，偶数项之和为，则其公差是 .5.设数列中，，则通项 .6.从正整数数列中删去所有的平方数，得到一个新数列，则这个新数列的第项是 .答案与解析：对应练习：1、【解析】2、【解析】设这个数分别为则∴1211)121121()7151()5131()311(+-=+--++-+-+-=n n n T n +∈N n ∴n T ∴1=n ()323111min =-==T T n ∴57k T n >+∈∀N n ()38573257min <⇔>⇔>⇔k kk T n ∴k 37n S n 31=a )2(21≥=-n a S S n n n k 1+>k k a a k k {}n a 28a =-155a =n S {}n a n 1011S S =1011S S >910S S =910S S <1205=a =+++8642a a a a 492-=n a n nnS =n 101030{}n a 112,1n n a a a n +==++n a = ,5,4,3,2,11964n m k m q n k p a n k q a n m q p n k a a n m a a k k n k n m --+-=⇒--=--⇒--=--)()(5.2,,,,2d a d a a d a d a ++--⎩⎨⎧=+=⇒⎩⎨⎧=+++++-+-=+++++-+-1651051165)2()()()2(5)2()()()2(2222222d a a d a d a a d a d a d a d a a d a d a解得当时，这个数分别为：；当时，这个数分别为：3、【解析】4、【解析】设等差数列的公差为，则 .5、【解析】方法1：设等差数列的公差为，则；方法2：6、【解析】⑴，，⑵由⑴知：，当时，，，数列是等差数列.7、【解析】（本两小题有多种解法），.选B. 8、【解析】填4,1±==d a 4,1==d a 59,5,1,3,7--4,1-==d a 5.7,3,1,5,9--124,363214321=+++=+++---n n n n a a a a a a a a 3423121---+=+=+=+n n n n a a a a a a a a ∴40160)(411=+⇒=+n n a a a a ∴39780207802)(1=⇒=⇒=+=n n a a n S n n d 23171414=-=--=a a d 101002)1(21=⇒=⨯-+=n n n n S n d ⎪⎩⎪⎨⎧=-=⇒⎩⎨⎧=+=+100109950111049501001004510111d a d a d a ∴110109110211101110-=⨯⨯+=d a S 2902)(90100111001110100-=+⇒-=+=-a a a a S S 1102)(1102)(110100*********-=+=+=a a a a Sn n pna S =21a a =∴111=⇒=p pa a n n na S =2≥n 0))(1()1(111=--⇒--=-=---n n n n n n n a a n a n na S S a ∴)2(01≥=--n a a n n ∴{}n a2))(1(12112531++++=++++=n n a a n a a a a S 奇2)(222642n n a a n a a a a S +=++++= 偶nn a a a a 22121+=++∴nn S S 1+=偶奇∴12652525514225143)12(2)12(7551212=+⨯-⨯=⇒+-=+-+-==--b a n n n n T S b a n n n n ∴. 9、【解析】⑴当时，，且，{}n a 是以为公差的等差数列，其首项为.当时，当时，，；⑵，得或，当时，恒成立，所求最小的正整数课后练习：1、【解析】C ．另法：由，，得，，计算知2、【解析】3、【解析】由知{}n a 是等差数列，4、【解析】已知两式相减，得5、【解析】利用迭加法（或迭代法），也可以用归纳—猜想—证明的方法.6、【解析】12652≥n )(22111----=⇒=n n n n n n n S S S S a S S ∴21111-=--n n S S 3111=S ∴21-31∴nS n n S S n n 356635)1(21111-=⇒-=--=∴2≥n )53)(83(18211--==-n n S S a n n n 1=n 11018)53)(83(18a ≠=--∴⎪⎩⎪⎨⎧≥--=)2()53)(83(18)1(3n n n n 0)23)(53)(83(181>---=-+k k k a a k k 3532<<k 38>k ∴3≥k 1+>k k a a .3=k 1091521015216292)(,22S S a d a S d a a a a S =⇒++=++=+=28a =-155a =713815)8(5=---=d 76921=-=d a a 910S S =480.480458642==+++a a a a a 24492-=n a n .250>⇒>n a n ∴.24=n 4.4205=⇒=d d 1)1(21++n n 2008。

等差数列知识点+基础练习题

n-m（1）如果a，A，b成等差数列，那么A叫做a与b的等差中项．即：A=或S=n(a+a)2222n+1是项数为2n+1的等差数列的中间项==(2n+1)an+1（项数为奇数的等差数列的各项和等于项数2{a}是等n差数列n+2．{a}是等差数列⇔a n+=1kn+n b（其中k,b是常数）。

（4）数列{a}是等差数列⇔S=An2+Bn,（其中A、B是常数）。

aaa等差数列知识点1.等差数列的定义：a-an 2．等差数列通项公式：n-1=d（d为常数）（n≥2）；a=a+(n-1)d=dn+a-d(n∈N*)，首项:a，公差:d，末项:an111a-a推广：a=a+(n-m)d．从而d=n m；n mn3．等差中项a+b22A=a+b（2）等差中项：数列{}是等差数列n⇔2a=a+a(n≥2)⇔2a=a+an n-1n+1n+1n n+24．等差数列的前n项和公式：n(n-1)d11n=na+d=n2+(a-d)n=An2+Bn n11（其中A、B是常数，所以当d≠0时，Sn是关于n的二次式且常数项为0）特别地，当项数为奇数2n+1时，a(2n+1)(a+a)S12n+12n+1乘以中间项）5．等差数列的判定方法（1）定义法：若a-a=d或a-a=d(常数n∈N*)⇔{}是等差数列．n n-1n+1n（2）等差中项：数列n ⇔2a=a+a(n≥2)⇔2a=a+an n-1n+1⑶数列n nn n6．等差数列的证明方法定义法：若a-a=d或an n-1n+1-a=d(常数n∈N*)⇔{}是等差数列．n n7.提醒：（1）等差数列的通项公式及前n和公式中，涉及到5个元素：a、d、n、a及S，1n n 其中a、d称作为基本元素。

只要已知这5个元素中的任意3个，便可求出其余2个，即1知3求2。

（2）设项技巧：①一般可设通项a=a+(n-1)dn1②奇数个数成等差，可设为…，a-2d,a-d,a,a+d,a+2d…（公差为d）；③偶数个数成等差，可设为…，a-3d,a-d,a+d,a+3d,…（注意；公差为2d）8..等差数列的性质：2 2 2{ a(2222nn+1 ⇒ ⎨ ⎨⎪⎩⎪⎩ ⎪ n+1是项数为 2n+1 的等差数列的中间项）．（1）当公差 d ≠ 0 时，等差数列的通项公式 a = a + (n - 1)d = dn + a - d 是关于 n 的一次函数，且斜 n11率为公差 d ；前 n 和 S = na + n 1 n (n - 1) d dd = n 2 + (a - )n 是关于 n 的二次函数且常数项1为 0.（2）若公差 d > 0 ，则为递增等差数列，若公差 d < 0 ，则为递减等差数列，若公差 d = 0 ，则为常数列。

等差数列基础测试题(附详细答案)

等差数列：1、已知等差数列{a n }的首项a 1＝1，公差d ＝2，则a 4等于( )A ．5B ．6C ．7D ．92、已知{a n }为等差数列，a 2＋a 8＝12，则a 5等于( )A ．4B ．5C ．6D ．73、在数列{a n }中，若a 1＝1，a n ＋1＝a n ＋2(n ≥1)，则该数列的通项公式a n ＝( )A ．2n ＋1B ．2n －1C ．2nD ．2(n －1)4、等差数列{a n }的公差为d ，则数列{ca n }(c 为常数且c ≠0)( )A ．是公差为d 的等差数列B ．是公差为cd 的等差数列C ．不是等差数列D ．以上都不对5、在等差数列{a n }中，a 1＝21，a 7＝18，则公差d ＝( )A.12B.13C ．－12D ．－136、在等差数列{a n }中，a 2＝5，a 6＝17，则a 14＝( )A ．45B ．41C ．39D ．377、若数列{a n }是等差数列，且a 1＋a 4＝45，a 2＋a 5＝39，则a 3＋a 6＝( )A ．24B ．27C ．30D ．338、下面数列中，是等差数列的有( )①4,5,6,7,8，… ②3,0，－3,0，－6，… ③0,0,0,0，…④110，210，310，410，… A ．1个 B ．2个C ．3个D ．4个二、填空题（共20，每小题5分）9、在等差数列{a n }中，a 10＝10，a 20＝20，则a 30＝________.10、△ABC 三个内角A 、B 、C 成等差数列，则B ＝__________.11、在等差数列{a n }中，若a 7＝m ，a 14＝n ，则a 21＝________.三、解答题（共70分）12、在等差数列{a n }中，已知a 5＝10，a 12＝31，求它的通项公式．（10分）13、在等差数列{a n }中，(1)已知a 5＝－1，a 8＝2，求a 1与d ；(2)已知a 1＋a 6＝12，a 4＝7，求a 9.14、已知{a n }是等差数列，且a 1＋a 2＋a 3＝12，a 8＝16.（12分）(1)求数列{a n }的通项公式；答案：一、选择题1-5 CCBBC 6-8BDB二、填空题13、解析：法一：d ＝a 20－a 1020－10＝20－1020－10＝1，a 30＝a 20＋10d ＝20＋10＝30. 法二：由题意可知，a 10、a 20、a 30成等差数列，所以a 30＝2a 20－a 10＝2×20－10＝30. 答案：3014、解析：∵A 、B 、C 成等差数列，∴2B ＝A ＋C . 又A ＋B ＋C ＝180°，∴3B ＝180°，∴B ＝60°. 答案：60°15、解析：∵a 7、a 14、a 21成等差数列，∴a 7＋a 21＝2a 14，a 21＝2a 14－a 7＝2n －m . 答案：2n －m三、解答题17、解：由a n ＝a 1＋(n －1)d 得⎩⎪⎨⎪⎧ 10＝a 1＋4d 31＝a 1＋11d ，解得⎩⎪⎨⎪⎧a 1＝－2d ＝3. ∴等差数列的通项公式为a n ＝3n －5.18、解：(1)由题意，知⎩⎪⎨⎪⎧ a 1＋(5－1)d ＝－1，a 1＋(8－1)d ＝2. 解得⎩⎪⎨⎪⎧ a 1＝－5，d ＝1. (2)由题意，知⎩⎪⎨⎪⎧ a 1＋a 1＋(6－1)d ＝12，a 1＋(4－1)d ＝7. 解得⎩⎪⎨⎪⎧a 1＝1，d ＝2. ∴a 9＝a 1＋(9－1)d ＝1＋8×2＝17.19、解：(1)∵a 1＋a 2＋a 3＝12，∴a 2＝4，∵a 8＝a 2＋(8－2)d ，∴16＝4＋6d ，∴d ＝2， ∴a n ＝a 2＋(n －2)d ＝4＋(n －2)×2＝2n .(2)a 2＝4，a 4＝8，a 8＝16，…，a 2n ＝2×2n ＝4n . 当n ＞1时，a 2n －a 2(n －1)＝4n －4(n －1)＝4.∴{b n }是以4为首项，4为公差的等差数列． ∴b n ＝b 1＋(n －1)d ＝4＋4(n －1)＝4n .。

等差数列基础练习题doc

一、等差数列选择题1．已知数列{}n a 的前n 项和为n S ，112a =，2n ≥且*n ∈N ，满足120n n n a S S -+=，数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，则下列说法中错误的是（）A ．214a =-B ．648211S S S =+ C ．数列{}12n n n S S S +++-的最大项为712D ．1121n n n n nT T T n n +-=++ 2．设n S 是等差数列{}n a 的前n 项和.若1476a a a ++=，则7S =（） A ．10-B ．8C ．12D ．143．已知数列{}n a 的前n 项和为n S ，15a =，且满足122527n na a n n +-=--，若p ，*q ∈N ，p q >，则p q S S -的最小值为（）A ．6-B ．2-C ．1-D ．04．已知数列{}n a 是等差数列，其前n 项和为n S ，若454a a +=，则8S =（） A ．16 B ．-16 C ．4D ．-45．设数列{}n a 的前n 项和21n S n =+. 则8a 的值为（）．A ．65B ．16C ．15D ．14 6．在等差数列{a n }中，a 3+a 7＝4，则必有（）A ．a 5＝4B ．a 6＝4C ．a 5＝2D ．a 6＝27．《周髀算经》是中国最古老的天文学和数学著作，它揭示日月星辰的运行规律.其记载“阴阳之数，日月之法，十九岁为一章，四章为一部，部七十六岁，二十部为一遂，遂千百五二十岁”.现恰有30人，他们的年龄(都为正整数)之和恰好为一遂(即1520)，其中年长者年龄介于90至100，其余29人的年龄依次相差一岁，则最年轻者的年龄为（） A ．32B ．33C ．34D ．358．已知数列{}n a 的前n 项和n S 满足()12n n n S +=，则数列11n n a a +⎧⎫⎨⎬⎩⎭的前10项的和为（） A ．89B ．910C ．1011D ．11129．等差数列{}n a 中，22a =，公差2d =，则10S =（） A ．200B ．100C ．90D ．8010．若两个等差数列{}n a ，{}n b 的前n 项和分别为n S 和n T ，且3221n n S n T n +=+，则1215a b =（） A ．32B ．7059C ．7159D ．8511．已知{}n a 为等差数列，n S 是其前n 项和，且100S =，下列式子正确的是（） A ．450a a +=B ．560a a +=C ．670a a +=D ．890a a +=12．在等差数列{}n a 中，若n S 为其前n 项和，65a =，则11S 的值是（） A ．60 B ．11 C ．50 D ．55 13．在等差数列{a n }中，已知a 5=3，a 9=6，则a 13=（）A ．9B ．12C ．15D ．1814．设等差数列{}n a 的前n 项之和为n S ，已知10100S =，则47a a +=（） A ．12B ．20C ．40D ．10015．在等差数列{}n a 中，已知前21项和2163S =，则25820a a a a ++++的值为（）A ．7B ．9C ．21D ．4216．设等差数列{}n a 的前n 项和为n S ，若718a a a -<<-，则必定有（） A ．70S >，且80S < B ．70S <，且80S > C ．70S >，且80S >D ．70S <，且80S <17．已知数列{x n }满足x 1＝1，x 2＝23，且11112n n n x x x -++=(n ≥2)，则x n 等于（） A ．(23)n －1B ．(23)n C ．21n + D ．12n + 18．在等差数列{}n a 中，520164a a +=，S ，是数列{}n a 的前n 项和，则S 2020=（） A ．2019B ．4040C ．2020D ．403819．数学著作《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二(除以3余2)，五五数之剩三(除以5余3)，问物几何？”现将1到2020共2020个整数中，同时满足“三三数之剩二，五五数之剩三”的数按从小到大的顺序排成一列，构成数列{},n a 则该数列共有（） A ．132项B ．133项C ．134项D ．135项20．设等差数列{}n a 的前n 项和为n S ，10a <且11101921a a =，则当n S 取最小值时，n 的值为（） A ．21B ．20C ．19D ．19或20二、多选题21．题目文件丢失！ 22．题目文件丢失！23．(多选题)已知数列{}n a 中，前n 项和为n S ，且23n n n S a +=，则1n n a a -的值不可能为（） A ．2B ．5C ．3D ．424．已知递减的等差数列{}n a 的前n 项和为n S ，57S S =，则（） A ．60a > B ．6S 最大 C ．130S >D ．110S >25．已知正项数列{}n a 的前n 项和为n S ，若对于任意的m ，*n N ∈，都有m n m n a a a +=+，则下列结论正确的是（）A ．11285a a a a +=+B ．56110a a a a <C ．若该数列的前三项依次为x ，1x -，3x ，则10103a = D ．数列n S n ⎧⎫⎨⎬⎩⎭为递减的等差数列 26．意大利人斐波那契于1202年从兔子繁殖问题中发现了这样的一列数：1,1,2,3,5,8,13,….即从第三项开始，每一项都是它前两项的和.后人为了纪念他，就把这列数称为斐波那契数列.下面关于斐波那契数列{}n a 说法正确的是（） A ．1055a = B ．2020a 是偶数C ．2020201820223a a a =+D ．123a a a +++…20202022a a +=27．记n S 为等差数列{}n a 的前n 项和.已知450,5S a ==，则（） A ．25n a n =-B ．310na nC ．228n S n n =- D ．24n S n n =-28．已知数列{}n a 的前n 项和为n S ，前n 项积为n T ，且3201911111a a e e +≤++，则（） A ．当数列{}n a 为等差数列时，20210S ≥ B ．当数列{}n a 为等差数列时，20210S ≤ C ．当数列{}n a 为等比数列时，20210T > D ．当数列{}n a 为等比数列时，20210T <29．等差数列{}n a 的首项10a >，设其前n 项和为{}n S ，且611S S =，则（） A ．0d > B ．0d <C ．80a =D ．n S 的最大值是8S 或者9S30．设等差数列{}n a 的前n 项和为n S ，公差为d .已知312a =，120S >，70a <则（） A ．60a >B ．数列1n a ⎧⎫⎨⎬⎩⎭是递增数列C ．0n S <时，n 的最小值为13D ．数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项【参考答案】***试卷处理标记，请不要删除一、等差数列选择题 1．D 【分析】当2n ≥且*n ∈N 时，由1n n n a S S -=-代入120n n n a S S -+=可推导出数列1n S ⎧⎫⎨⎬⎩⎭为等差数列，确定该数列的首项和公差，可求得数列1n S ⎧⎫⎨⎬⎩⎭的通项公式，由221a S S =-可判断A 选项的正误；利用n S 的表达式可判断BC 选项的正误；求出n T ，可判断D 选项的正误. 【详解】当2n ≥且*n ∈N 时，由1n n n a S S -=-，由120n n n a S S -+=可得111112020n n n n n nS S S S S S ----+=⇒-+=，整理得1112n n S S --=（2n ≥且n +∈N ）. 则1n S ⎧⎫⎨⎬⎩⎭为以2为首项，以2为公差的等差数列()12122n n n S ⇒=+-⋅=，12n S n ∴=. A 中，当2n =时，221111424a S S =-=-=-，A 选项正确； B 中，1n S ⎧⎫⎨⎬⎩⎭为等差数列，显然有648211S S S =+，B 选项正确； C 中，记()()1212211221n n n n b S S n n n S ++=+-=+-++， ()()()1123111212223n n n n b S S S n n n ++++=+-=+-+++，()()()1111602223223n n n b b n n n n n n ++∴-=--=-<++++，故{}n b 为递减数列， ()1123max 111724612n b b S S S ∴==+-=+-=，C 选项正确； D 中，12n n S =，()()2212n n n T n n +∴==+，()()112n T n n +∴=++. ()()()()()()11112112111n n n n T T n n n n n n n n n n n n n n +-=⋅++⋅++=+--+++++222122212n n n n n n T =-++=+-≠，D 选项错误.故选：D ．【点睛】关键点点睛：利用n S 与n a 的关系求通项，一般利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩来求解，在变形过程中要注意1a 是否适用，当利用作差法求解不方便时，应利用1n n n a S S -=-将递推关系转化为有关n S 的递推数列来求解. 2．D 【分析】利用等差数列下标性质求得4a ，再利用求和公式求解即可【详解】147446=32a a a a a ++=∴=，则()177477142a a S a +=== 故选：D 3．A 【分析】转化条件为122527n na a n n +-=--，由等差数列的定义及通项公式可得()()2327n a n n =--，求得满足0n a ≤的项后即可得解.【详解】因为122527n n a a n n +-=--，所以122527n na a n n +-=--，又1127a =--，所以数列27n a n ⎧⎫⎨⎬-⎩⎭是以1-为首项，公差为2的等差数列，所以()1212327na n n n =-+-=--，所以()()2327n a n n =--，令()()23270n a n n =--≤，解得3722n ≤≤，所以230,0a a <<，其余各项均大于0，所以()()()3123min13316p q S S a a S S =-=+=⨯-+--⨯=-.故选：A. 【点睛】解决本题的关键是构造新数列求数列通项，再将问题转化为求数列中满足0n a ≤的项，即可得解. 4．A 【详解】由()()18458884816222a a a a S +⨯+⨯⨯====.故选A.5．C 【分析】利用()12n n n a S S n -=-≥得出数列{}n a 的通项公差，然后求解8a . 【详解】由21n S n =+得，12a =，()2111n S n -=-+，所以()221121n n n a S S n n n -=-=--=-，所以2,121,2n n a n n =⎧=⎨-≥⎩，故828115a =⨯-=.故选：C. 【点睛】本题考查数列的通项公式求解，较简单，利用()12n n n a S S n -=-≥求解即可. 6．C 【分析】利用等差数列的性质直接计算求解【详解】因为a 3+a 7＝2a 5＝4，所以a 5＝2. 故选：C 7．D 【分析】设年纪最小者年龄为n ，年纪最大者为m ,由他们年龄依次相差一岁得出(1)(2)(28)1520n n n n m ++++++++=，结合等差数列的求和公式得出111429m n =-，再由[]90,100m ∈求出n 的值.【详解】根据题意可知，这30个老人年龄之和为1520，设年纪最小者年龄为n ，年纪最大者为m ，[]90,100m ∈，则有(1)(2)(28)294061520n n n n m n m ++++++++=++=则有291114n m +=，则111429m n =-，所以90111429100m ≤-≤解得34.96635.31n ≤≤，因为年龄为整数，所以35n =. 故选：D 8．C 【分析】首先根据()12n n n S +=得到n a n =，设11111n n n b a a n n +==-+，再利用裂项求和即可得到答案. 【详解】当1n =时，111a S ==，当2n ≥时，()()11122n n n n n n n a S S n -+-=-=-=. 检验111a S ==，所以n a n =. 设()1111111n n n b a a n n n n +===-++，前n 项和为n T ，则10111111101122310111111T ⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭…. 故选：C 9．C 【分析】先求得1a ，然后求得10S . 【详解】依题意120a a d =-=，所以101104545290S a d =+=⨯=. 故选：C 10．C 【分析】可设(32)n S kn n =+，(21)n T kn n =+，进而求得n a 与n b 的关系式，即可求得结果．【详解】因为{}n a ，{}n b 是等差数列，且3221n n S n T n +=+，所以可设(32)n S kn n =+，(21)n T kn n =+，又当2n 时，有1(61)n n n a S S k n -=-=-，1(41)n n n b T T k n -=-=-， ∴1215(6121)71(4151)59a kb k ⨯-==⨯-，故选：C ． 11．B 【分析】由100S =可计算出1100a a +=，再利用等差数列下标和的性质可得出合适的选项.【详解】由等差数列的求和公式可得()110101002a a S +==，1100a a ∴+=，由等差数列的基本性质可得561100a a a a +=+=. 故选：B. 12．D 【分析】根据题中条件，由等差数列的性质，以及等差数列的求和公式，即可求出结果. 【详解】因为在等差数列{}n a 中，若n S 为其前n 项和，65a =，所以()1111161111552a a S a +===.故选：D. 13．A 【分析】在等差数列{a n }中，利用等差中项由95132a a a =+求解. 【详解】在等差数列{a n }中，a 5=3，a 9=6，所以95132a a a =+，所以139522639a a a =-=⨯-=，故选：A 14．B 【分析】由等差数列的通项公式可得47129a a a d +=+，再由1011045100S a d =+=，从而可得结果. 【详解】解：1011045100S a d =+=，12920a d ∴+=， 4712920a a a d ∴+=+=.故选：B. 15．C 【分析】利用等差数列的前n 项和公式可得1216a a +=，即可得113a =，再利用等差数列的性质即可求解. 【详解】设等差数列{}n a 的公差为d ，则()1212121632a a S +==，所以1216a a +=，即1126a =，所以113a =，所以()()()2582022051781411a a a a a a a a a a a ++++=++++++111111111122277321a a a a a =+++==⨯=，故选：C 【点睛】关键点点睛：本题的关键点是求出1216a a +=，进而得出113a =，()()()2582022051781411117a a a a a a a a a a a a ++++=++++++=即可求解.16．A 【分析】根据已知条件，结合等差数列前n 项和公式，即可容易判断. 【详解】依题意，有170a a +>，180a a +< 则()177702a a S +⋅=>()()188188402a a S a a +⋅==+<故选：A . 17．C 【分析】由已知可得数列1n x ⎧⎫⎨⎬⎩⎭是等差数列，求出数列1n x ⎧⎫⎨⎬⎩⎭的通项公式，进而得出答案．【详解】由已知可得数列1n x ⎧⎫⎨⎬⎩⎭是等差数列，且121131,2x x ==，故公差12d = 则()1111122n n n x +=+-⨯=，故21n x n =+故选：C 18．B 【分析】由等差数列的性质可得52012016024a a a a +==+，则()15202020202016202010102a a a a S +=⨯=⨯+可得答案. 【详解】等差数列{}n a 中, 52012016024a a a a +==+()12020202052016202010104101040402a a a a S +===⨯=+⨯⨯ 故选：B 19．D 【分析】由题意抽象出数列是等差数列，再根据通项公式计算项数. 【详解】被3除余2且被5除余3的数构成首项为8，公差为15的等差数列，记为{}n a ，则()8151157n a n n =+-=-，令1572020n a n =-≤，解得：213515n ≤，所以该数列的项数共有135项. 故选：D 【点睛】关键点点睛：本题以数学文化为背景，考查等差数列，本题的关键是读懂题意，并能抽象出等差数列. 20．B 【分析】由题得出1392a d =-，则2202n dS n dn =-，利用二次函数的性质即可求解.【详解】设等差数列{}n a 的公差为d ，由11101921a a =得11102119a a =，则()()112110199a d a d +=+，解得1392a d =-，10a <，0d ∴>，()211+2022n n n dS na d n dn -∴==-，对称轴为20n =，开口向上， ∴当20n =时，n S 最小.故选：B. 【点睛】方法点睛：求等差数列前n 项和最值，由于等差数列()2111+222n n n d d S na d n a n -⎛⎫==+- ⎪⎝⎭是关于n 的二次函数，当1a 与d 异号时，n S 在对称轴或离对称轴最近的正整数时取最值；当1a 与d 同号时，n S 在1n =取最值.二、多选题 21．无22．无23．BD 【分析】利用递推关系可得1211n n a a n -=+-，再利用数列的单调性即可得出答案．【详解】解：∵23n n n S a +=， ∴2n ≥时，112133n n n n n n n a S S a a --++=-=-，化为：112111n n a n a n n -+==+--，由于数列21n ⎧⎫⎨⎬-⎩⎭单调递减，可得：2n =时，21n -取得最大值2． ∴1n n a a -的最大值为3．故选：BD ．【点睛】本题考查了数列递推关系、数列的单调性，考查了推理能力与计算能力，属于中档题． 24．ABD 【分析】转化条件为670a a +=，进而可得60a >，70a <，再结合等差数列的性质及前n 项和公式逐项判断即可得解. 【详解】因为57S S =，所以750S S -=，即670a a +=，因为数列{}n a 递减，所以67a a >，则60a >，70a <，故A 正确；所以6S 最大，故B 正确；所以()113137131302a a S a+⨯==<，故C 错误；所以()111116111102a a S a+⨯==>，故D 正确.故选：ABD. 25．AC令1m =，则11n n a a a +-=，根据10a >，可判定A 正确；由256110200a a a a d -=>，可判定B 错误；根据等差数列的性质，可判定C 正确；122n d d n a n S ⎛⎫=+- ⎪⎝⎭，根据02>d ，可判定D 错误. 【详解】令1m =，则11n n a a a +-=，因为10a >，所以{}n a 为等差数列且公差0d >，故A 正确；由()()22225611011119209200a a a a a a d daa d d -=++-+=>，所以56110a a a a >，故B错误；根据等差数列的性质，可得()213x x x -=+，所以13x =，213x -=，故1011109333a =+⨯=，故C 正确；由()111222n n n na dS d d n a n n -+⎛⎫==+- ⎪⎝⎭，因为02>d ，所以n S n ⎧⎫⎨⎬⎩⎭是递增的等差数列，故D 错误. 故选：AC . 【点睛】解决数列的单调性问题的三种方法；1、作差比较法：根据1n n a a +-的符号，判断数列{}n a 是递增数列、递减数列或是常数列；2、作商比较法：根据1(0n n na a a +>或0)n a <与1的大小关系，进行判定； 3、数形结合法：结合相应的函数的图象直观判断. 26．AC 【分析】由该数列的性质，逐项判断即可得解. 【详解】对于A ，821a =，9211334a =+=，10213455a =+=，故A 正确；对于B ，由该数列的性质可得只有3的倍数项是偶数，故B 错误；对于C ，20182022201820212020201820192020202020203a a a a a a a a a a +=++=+++=，故C 正确；对于D ，202220212020a a a =+，202120202019a a a =+，202020192018a a a =+，32121,a a a a a ⋅⋅⋅=+=，各式相加得()2022202120202021202020192012182a a a a a a a a a ++⋅⋅⋅+=+++⋅⋅⋅++，所以202220202019201811a a a a a a =++⋅⋅⋅+++，故D 错误.【点睛】关键点点睛：解决本题的关键是合理利用该数列的性质去证明选项. 27．AD 【分析】设等差数列{}n a 的公差为d ，根据已知得1145460a d a d +=⎧⎨+=⎩，进而得13,2a d =-=，故25n a n =-，24n S n n =-.【详解】解：设等差数列{}n a 的公差为d ，因为450,5S a ==所以根据等差数列前n 项和公式和通项公式得：1145460a d a d +=⎧⎨+=⎩，解方程组得：13,2a d =-=，所以()31225n a n n =-+-⨯=-，24n S n n =-.故选：AD. 28．AC 【分析】将3201911111a a e e +≤++变形为32019111101212a a e e -+-≤++，构造函数()1112xf x e =-+，利用函数单调性可得320190a a +≥，再结合等差数列与等比数列性质即可判断正确选项【详解】由3201911111a a e e +≤++，可得32019111101212a a e e -+-≤++，令()1112x f x e =-+， ()()1111101111x x x x x e f x f x e e e e --+=+-=+-=++++，所以()1112xf x e =-+是奇函数，且在R 上单调递减，所以320190a a +≥，所以当数列{}n a 为等差数列时，()320192*********a a S +=≥；当数列{}n a 为等比数列时，且3a ，1011a ，2019a 同号，所以3a ，1011a ，2019a 均大于零，故()2021202110110T a =>.故选：AC 【点睛】本题考查等差数列与等比数列，考查逻辑推理能力，转化与化归的数学思想，属于中档题【分析】由6111160S S S S =⇒-=，即950a =，进而可得答案．【详解】解：1167891011950S S a a a a a a -=++++==，因为10a >所以90a =，0d <，89S S =最大，故选：BD ．【点睛】本题考查等差数列的性质，解题关键是等差数列性质的应用，属于中档题． 30．ACD 【分析】由已知得()()612112712+12+220a a a a S ==>，又70a <，所以6>0a ，可判断A ；由已知得出2437d -<<-，且()12+3n a n d =-，得出[]1,6n ∈时，>0n a ，7n ≥时，0n a <，又()1112+3n a n d =-，可得出1n a 在1,6n n N上单调递增，1na 在7nn N ，上单调递增，可判断B ；由()313117713+12203213a a a S a ⨯==<=，可判断C ；判断 n a ，n S 的符号， n a 的单调性可判断D ；【详解】由已知得311+212,122d a a a d ===-，()()612112712+12+220a a a a S ==>，又70a <，所以6>0a ，故A 正确；由7161671+612+40+512+3>0+2+1124+7>0a a d d a a d d a a a d d ==<⎧⎪==⎨⎪==⎩，解得2437d -<<-，又()()3+312+3n a n d n d a =-=-，当[]1,6n ∈时，>0n a ，7n ≥时，0n a <，又()1112+3n a n d=-，所以[]1,6n ∈时，1>0na ，7n ≥时，10n a <，所以1na 在1,6n n N上单调递增，1na 在7n n N ，上单调递增，所以数列1n a ⎧⎫⎨⎬⎩⎭不是递增数列，故B 不正确；由于()313117713+12203213a a a S a ⨯==<=，而120S >，所以0n S <时，n 的最小值为13，故C 选项正确；当[]1,6n ∈时，>0n a ，7n ≥时，0n a <，当[]1,12n ∈时，>0n S ，13n ≥时，0nS <，所以当[]7,12n ∈时，0n a <，>0n S ，0nnS a <，[]712n ∈，时，n a 为递增数列，n S 为正数且为递减数列，所以数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项，故D 正确；【点睛】本题考查等差数列的公差，项的符号，数列的单调性，数列的最值项，属于较难题.。

等差数列基础习题选（附有详细解答）

等差数列基础习题选（附有详细解答）一．选择题（共26小题）1．已知等差数列{a n}中，a3=9，a9=3，则公差d的值为（的值为（）A．B．1C．D．﹣12．已知数列{a n}的通项公式是a n=2n+5，则此数列是（，则此数列是（）A．以7为首项，公差为2的等差数列的等差数列的等差数列 B．以7为首项，公差为5的等差数列C．以5为首项，公差为2的等差数列的等差数列 D．不是等差数列3．在等差数列{a n}中，a1=13，a3=12，若a n=2，则n等于（等于（）A．23B．24C．25D．264．等差数列{a n}的前n项和为S n，已知S3=6，a4=8，则公差d=（）A．一1B．2C．3D．一25．两个数1与5的等差中项是（的等差中项是（）A．1B．3C．2D．6．一个首项为23，公差为整数的等差数列，如果前六项均为正数，第七项起为负数，则它的公差是（，公差为整数的等差数列，如果前六项均为正数，第七项起为负数，则它的公差是（）A．﹣2B．﹣3C．﹣4D．﹣57．（2012•福建）等差数列{a n}中，a1+a5=10，a4=7，则数列{a n}的公差为（的公差为（）A．1B．2C．3D．48．数列的首项为3，为等差数列且，若，，则=（）A．0B．8C．3D．119．已知两个等差数列5，8，11，…和3，7，11，…都有100项，则它们的公共项的个数为（项，则它们的公共项的个数为（）A．25B．24C．20D．1910．设S n为等差数列{a n}的前n项和，若满足a n=a n﹣1+2（n≥2），且S3=9，则a1=（）A．5B．3C．﹣1D．111．（2005•黑龙江）如果数列{a n}是等差数列，则（是等差数列，则（）A．a1+a8＞a4+a5 B．a1+a8=a4+a5C．a1+a8＜a4+a5D．a1a8=a4a5 12．（2004•福建）设S n是等差数列{a n}的前n项和，若=（）A．1B．﹣1C．2D．13．（2009•安徽）已知{a n}为等差数列，a1+a3+a5=105，a2+a4+a6=99，则a20等于（等于（）A．﹣1B．1C．3D．714．在等差数列{a n}中，a2=4，a6=12，，那么数列{}的前n项和等于（项和等于（）A．B．C．D．15．已知S n为等差数列{a n}的前n项的和，a2+a5=4，S7=21，则a7的值为（的值为（）A．6B．7C．8D．916．已知数列{a n}为等差数列，a1+a3+a5=15，a4=7，则s6的值为（的值为（）A．30B．35C．36D．2417．（2012•营口）等差数列{a n}的公差d＜0，且，则数列{a n}的前n项和S n取得最大值时的项数n是（）A．5B．6C．5或6D．6或718．（2012•辽宁）在等差数列{a n}中，已知a4+a8=16，则该数列前11项和S11=（）A．58B．88C．143D．17619．已知数列{a n}等差数列，且a1+a3+a5+a7+a9=10，a2+a4+a6+a8+a10=20，则a4=（）A．﹣1B．0C．1D．220．（理）已知数列{a n}的前n项和S n=n2﹣8n，第k项满足4＜a k＜7，则k=（）A．6B．7C．8D．921．数列a n的前n项和为S n，若S n=2n2﹣17n，则当S n取得最小值时n的值为（的值为（）A．4或5B．5或6C．4D．522．等差数列{a n}中，a n=2n﹣4，则S4等于（等于（）A．12B．10C．8D．423．若{a n}为等差数列，a3=4，a8=19，则数列{a n}的前10项和为（项和为（）A．230B．140C．115D．9524．等差数列{a n}中，a3+a8=5，则前10项和S10=（）A．5B．25C．50D．10025．设S n是公差不为0的等差数列{a n}的前n项和，且S1，S2，S4成等比数列，则等于（等于（）A．1B．2C．3D．426．设a n=﹣2n+21，则数列{a n}从首项到第几项的和最大（从首项到第几项的和最大（）A．第10项B．第11项C．第10项或11项D．第12项二．填空题（共4小题）27．如果数列{a n}满足：=_________．28．如果f（n+1）=f（n）+1（n=1，2，3…），且f（1）=2，则f（100）=_________．29．等差数列{a n}的前n项的和，则数列{|a n|}的前10项之和为项之和为 _________．30．已知{a n}是一个公差大于0的等差数列，且满足a3a6=55，a2+a7=16．（Ⅰ）求数列{a n}的通项公式：的通项公式：（Ⅱ）若数列{a n}和数列{b n}满足等式：a n==（n为正整数），求数列{b n}的前n项和S n．参考答案与试题解析一．选择题（共26小题）1．已知等差数列{a n}中，a3=9，a9=3，则公差d的值为（的值为（）A．B．1C．D．﹣1考点：等差数列．计算题．专题：计算题．分析：，解出该方程组即可得到答案．本题可由题意，构造方程组，解出该方程组即可得到答案．解答：解：等差数列{a n}中，a3=9，a9=3，由等差数列的通项公式，可得解得，即等差数列的公差d=﹣1．故选D点评：本题为等差数列的基本运算，只需构造方程组即可解决，数基础题．本题为等差数列的基本运算，只需构造方程组即可解决，数基础题．2．已知数列{a n}的通项公式是a n=2n+5，则此数列是（，则此数列是（）A．以7为首项，公差为2的等差数列的等差数列的等差数列 B．以7为首项，公差为5的等差数列C．以5为首项，公差为2的等差数列是等差数列的等差数列 D．不是等差数列考点：等差数列．专题：计算题．分析：直接根据数列{a n}的通项公式是a n=2n+5求出首项，再把相邻两项作差求出公差即可得出结论．解答：解：因为a n=2n+5，所以 a1=2×1+5=7；所以a n+1﹣a n=2（n+1）+5﹣（2n+5）=2．的等差数列．故此数列是以7为首项，公差为2的等差数列．故选A．本题主要考查等差数列的通项公式的应用．如果已知数列的通项公式，可以求出数列中的任意一项．点评：本题主要考查等差数列的通项公式的应用．如果已知数列的通项公式，可以求出数列中的任意一项．3．在等差数列{a n}中，a1=13，a3=12，若a n=2，则n等于（等于（）A．23B．24C．25D．26考点：等差数列．专题：综合题．分析：根据a1=13，a3=12，利用等差数列的通项公式求得d的值，然后根据首项和公差写出数列的通项公式，让其等于2得到关于n的方程，求出方程的解即可得到n的值．解答：解：由题意得a3=a1+2d=12，把a1=13代入求得d=﹣，则a n=13﹣（n﹣1）=﹣n+=2，解得n=23故选A此题考查学生灵活运用等差数列的通项公式化简求值，是一道基础题．点评：此题考查学生灵活运用等差数列的通项公式化简求值，是一道基础题．4．等差数列{a n}的前n项和为S n，已知S3=6，a4=8，则公差d=（）A．一1B．2C．3D．一2考点：等差数列．专题：计算题．分析：根据等差数列的前三项之和是6，得到这个数列的第二项是2，这样已知等差数列的；两项，根据等差数列的通项公式，得到数列的公差．的通项公式，得到数列的公差．解答：解：∵等差数列{a n}的前n项和为S n，S3=6，∴a2=2∵a4=8，∴8=2+2d∴d=3，故选C．点评：本题考查等差数列的通项，这是一个基础题，解题时注意应用数列的性质，即前三项的和等于第二项的三倍，这样可以简化题目的运算．5．两个数1与5的等差中项是（的等差中项是（）A．1B．3C．2D．考点：等差数列．计算题．专题：计算题．分析：的等差中项．由于a，b的等差中项为，由此可求出1与5的等差中项．解答：解：1与5的等差中项为：=3，故选B．点评：是解题的关键，属基础题．本题考查两个数的等差中项，牢记公式a，b的等差中项为：是解题的关键，属基础题．6．一个首项为23，公差为整数的等差数列，如果前六项均为正数，第七项起为负数，则它的公差是（，公差为整数的等差数列，如果前六项均为正数，第七项起为负数，则它的公差是（）A．﹣2B．﹣3C．﹣4D．﹣5考点：等差数列．专题：计算题．计算题．分析：设等差数列{a n}的公差为d，因为数列前六项均为正数，第七项起为负数，所以，结合公差为整数进而求出数列的公差．差为整数进而求出数列的公差．解答：解：设等差数列{a n}的公差为d，所以a6=23+5d，a7=23+6d，又因为数列前六项均为正数，第七项起为负数，又因为数列前六项均为正数，第七项起为负数，所以，因为数列是公差为整数的等差数列，因为数列是公差为整数的等差数列，所以d=﹣4．故选C．解决此类问题的关键是熟练掌握等差数列的通项公式，并且结合正确的运算．点评：解决此类问题的关键是熟练掌握等差数列的通项公式，并且结合正确的运算．7．（2012•福建）等差数列{a n}中，a1+a5=10，a4=7，则数列{a n}的公差为（的公差为（）A．1B．2C．3D．4考点：等差数列的通项公式．计算题．专题：计算题．分析：设数列{a n}的公差为d，则由题意可得的值．，则由题意可得 2a1+4d=10，a1+3d=7，由此解得d的值．解答：解：设数列{a n}的公差为d，则由a1+a5=10，a4=7，可得，解得 d=2，，可得 2a1+4d=10，a1+3d=7，解得故选B．本题主要考查等差数列的通项公式的应用，属于基础题．点评：本题主要考查等差数列的通项公式的应用，属于基础题．8．数列的首项为3，为等差数列且，若，，则=（）A．0B．8C．3D．11考点：等差数列的通项公式．专题：计算题．计算题．分析：先确定等差数列的通项，再利用，我们可以求得的值．的值．解答：解：∵为等差数列，，，∴∴b n=b3+（n﹣3）×2=2n﹣8∵∴b8=a8﹣a1∵数列的首项为3∴2×8﹣8=a8﹣3，∴a8=11．故选D点评：本题考查等差数列的通项公式的应用，由等差数列的任意两项，我们可以求出数列的通项，是基础题．9．已知两个等差数列5，8，11，…和3，7，11，…都有100项，则它们的公共项的个数为（项，则它们的公共项的个数为（）A．25B．24C．20D．19考点：等差数列的通项公式．计算题．专题：计算题．分析：（法一）：根据两个等差数列的相同的项按原来的先后次序组成一个等差数列，且公差为原来两个公差的最小公倍数求解，小公倍数求解，（法二）由条件可知两个等差数列的通项公式，可用不定方程的求解方法来求解．（法二）由条件可知两个等差数列的通项公式，可用不定方程的求解方法来求解．解答：解法一：设两个数列相同的项按原来的前后次序组成的新数列为{a n}，则a1=11∵数列5，8，11，…与3，7，11，…公差分别为3与4，∴{a n}的公差d=3×4=12，∴a n=11+12（n﹣1）=12n﹣1．又∵5，8，11，…与3，7，11，…的第100项分别是302与399，∴a n=12n﹣1≤302，即n≤25.5．又∵n∈N*，个相同的项．∴两个数列有25个相同的项．故选A解法二：设5，8，11，与3，7，11，分别为{a n}与{b n}，则a n=3n+2，b n=4n﹣1．设{a n}中的第n项与{b n}中的第m项相同，项相同，即3n+2=4m﹣1，∴n=m﹣1．又m、n∈N*，可设m=3r（r∈N*），得n=4r﹣1．根据题意得 1≤3r≤100 1≤4r﹣1≤100 解得≤r≤根据题意得∵r∈N*个相同的项从而有25个相同的项故选A点评：解法一利用了等差数列的性质，解法二利用了不定方程的求解方法，对学生的运算能力及逻辑思维能力的要求较高．要求较高．10．设S n为等差数列{a n}的前n项和，若满足a n=a n﹣1+2（n≥2），且S3=9，则a1=（）A．5B．3C．﹣1D．1考点：等差数列的通项公式．专题：计算题．分析：根据递推公式求出公差为2，再由S3=9以及前n项和公式求出a1的值．的值．解答：解：∵a n=a n﹣1+2（n≥2），∴a n﹣a n﹣1=2（n≥2），∴等差数列{a n}的公差是2，由S3=3a1+=9解得，a1=1．故选D．项和公式的应用，即根据代入公式进行求解．点评：本题考查了等差数列的定义，以及前n项和公式的应用，即根据代入公式进行求解．11．（2005•黑龙江）如果数列{a n}是等差数列，则（是等差数列，则（）A．a1+a8＞a4+a5B．a1+a8=a4+a5C．a1+a8＜a4+a5D．a1a8=a4a5考点：等差数列的性质．分析：用通项公式来寻求a1+a8与a4+a5的关系．的关系．解答：解：∵a1+a8﹣（a4+a5）=2a1+7d﹣（2a1+7d）=0∴a1+a8=a4+a5∴故选B点评：本题主要考查等差数列通项公式，来证明等差数列的性质．本题主要考查等差数列通项公式，来证明等差数列的性质．12．（2004•福建）设S n 是等差数列{an}的前n项和，若=（）A．1B．﹣1C．2D．考点：等差数列的性质．专题：计算题．计算题．分析：充分利用等差数列前n项和与某些特殊项之间的关系解题．项和与某些特殊项之间的关系解题．解答：解：设等差数列{a n}的首项为a1，由等差数列的性质可得，由等差数列的性质可得a1+a9=2a5，a1+a5=2a3，∴====1，故选A．点评：本题主要考查等差数列的性质、等差数列的前n项和公式以及等差中项的综合应用，项和公式以及等差中项的综合应用，已知等差数列{a n}的前n项和为S n，则有如下关系S2n﹣1=（2n﹣1）a n．13．（2009•安徽）已知{a n}为等差数列，a1+a3+a5=105，a2+a4+a6=99，则a20等于（等于（）A．﹣1B．1C．3D．7考点：等差数列的性质．专题：计算题．计算题．分析：根据已知条件和等差中项的性质可分别求得a3和a4的值，进而求得数列的公差，最后利用等差数列的通项公式求得答案．公式求得答案．解答：解：由已知得a1+a3+a5=3a3=105，a2+a4+a6=3a4=99，∴a3=35，a4=33，∴d=a4﹣a3=﹣2．∴a20=a3+17d=35+（﹣2）×17=1．故选B点评：本题主要考查了等差数列的性质和等差数列的通项公式的应用．解题的关键是利用等差数列中等差中项的性质求得a3和a4．14．在等差数列{a n}中，a2=4，a6=12，，那么数列{}的前n项和等于（项和等于（）A．B．C．D．考点：数列的求和；等差数列的性质．专题：计算题．计算题．分析：求出等差数列的通项，要求的和是一个等差数列与一个等比数列的积构成的数列，利用错位相减法求出数列的前n项的和．项的和．解答：解：∵等差数列{a n}中，a2=4，a6=12；∴公差d=；∴a n=a2+（n﹣2）×2=2n；∴；∴的前n项和，=两式相减得=∴故选B点评：求数列的前n项的和，先判断通项的特点，据通项的特点选择合适的求和方法．15．已知S n为等差数列{a n}的前n项的和，a2+a5=4，S7=21，则a7的值为（的值为（）A．6B．7C．8D．9考点：等差数列的性质．计算题．专题：计算题．分析：由a2+a5=4，S7=21根据等差数列的性质可得a3+a4=a1+a6=4①，根据等差数列的前n项和公式可得，，代入等差数列的通项公式可求，联立可求d，a1，代入等差数列的通项公式可求解答：解：等差数列{a n}中，a2+a5=4，S7=21根据等差数列的性质可得a3+a4=a1+a6=4①根据等差数列的前n项和公式可得，所以 a1+a7=6②所以②﹣①可得d=2，a1=﹣3所以a7=9故选D项和公式及等差数列的性质的综合应用，属于基础试题．点评：本题主要考查了等差数列的前n项和公式及等差数列的性质的综合应用，属于基础试题．16．已知数列{a n}为等差数列，a1+a3+a5=15，a4=7，则s6的值为（的值为（）A．30B．35C．36D．24考点：等差数列的性质．专题：计算题．分析：利用等差中项的性质求得a3的值，进而利用a1+a6=a3+a4求得a1+a6的值，代入等差数列的求和公式中求得答案．答案．解答：解：a1+a3+a5=3a3=15，∴a3=5∴a1+a6=a3+a4=12∴s6=×6=36故选C点评：本题主要考查了等差数列的性质．特别是等差中项的性质．17．（2012•营口）等差数列{a n}的公差d＜0，且，则数列{a n}的前n项和S n取得最大值时的项数n是（）A．5B．6C．5或6D．6或7考点：等差数列的前n项和；等差数列的通项公式．专题：计算题．分析：由，知a1+a11=0．由此能求出数列{a n}的前n项和S n取得最大值时的项数n．解答：解：由，知a1+a11=0．∴a6=0，故选C．点评：本题主要考查等差数列的性质，求和公式．要求学生能够运用性质简化计算．18．（2012•辽宁）在等差数列{a n}中，已知a4+a8=16，则该数列前11项和S11=（）A．58B．88C．143D．176考点：等差数列的性质；等差数列的前n项和．计算题．专题：计算题．分析：根据等差数列的定义和性质得 a1+a11=a4+a8=16，再由S11=运算求得结果．根据等差数列的定义和性质得解答：解：∵在等差数列{a n}中，已知a4+a8=16，∴a1+a11=a4+a8=16，∴S11==88，故选B．点评：本题主要考查等差数列的定义和性质，等差数列的前n项和公式的应用，属于中档题．项和公式的应用，属于中档题．19．已知数列{a n}等差数列，且a1+a3+a5+a7+a9=10，a2+a4+a6+a8+a10=20，则a4=（）A．﹣1B．0C．1D．2考点：等差数列的通项公式；等差数列的前n项和．计算题．专题：计算题．分析：由等差数列得性质可得：5a5=10，即a5=2．同理可得5a6=20，a6=4，再由等差中项可知：a4=2a5﹣a6=0解答：解：由等差数列得性质可得：a1+a9=a3+a7=2a5，又a1+a3+a5+a7+a9=10，故5a5=10，即a5=2．同理可得5a6=20，a6=4．再由等差中项可知：a 4=2a 5﹣a 6=0故选B点评：本题考查等差数列的性质及等差中项，熟练利用性质是解决问题的关键，属基础题．20．（理）已知数列{a n }的前n 项和S n =n 2﹣8n ，第k 项满足4＜a k ＜7，则k=（） A ． 6 B ．7 C ． 8 D ． 9考点：等差数列的通项公式；等差数列的前n 项和．专题：计算题．计算题．分析：先利用公式a n =求出a n ，再由第k 项满足4＜a k ＜7，建立不等式，求出k 的值．的值．解答：解：a n ==∵n=1时适合a n =2n ﹣9，∴a n =2n ﹣9．∵4＜a k ＜7，∴4＜2k ﹣9＜7， ∴＜k ＜8，又∵k ∈N +，∴k=7，故选B ．点评：本题考查数列的通项公式的求法，解题时要注意公式a n =的合理运用，属于基础题．21．数列a n 的前n 项和为S n ，若S n =2n 2﹣17n ，则当S n 取得最小值时n 的值为（的值为（）A ． 4或5B ． 5或6C ．4 D ． 5考点：等差数列的前n 项和．专题：计算题．分析：把数列的前n 项的和S n 看作是关于n 的二次函数，把关系式配方后，把关系式配方后，又根据又根据n 为正整数，为正整数，即可得到即可得到S n 取得最小值时n 的值．解答：解：因为S n =2n 2﹣17n=2﹣，又n 为正整数，为正整数，所以当n=4时，S n 取得最小值．取得最小值．故选C点评：此题考查学生利用函数思想解决实际问题的能力，是一道基础题．22．等差数列{a n }中，a n =2n ﹣4，则S 4等于（等于（）A ． 12B ．10 C ． 8 D ． 4考点：等差数列的前n 项和．专题：计算题．计算题．分析：利用等差数列{a n }中，a n =2n ﹣4，先求出a 1，d ，再由等差数列的前n 项和公式求S 4．解答：解：∵等差数列{a n }中，a n =2n ﹣4，∴a 1=2﹣4=﹣2，a2=4﹣4=0，d=0﹣（﹣2）=2，∴S4=4a1+=4×（﹣2）+4×3=4．故选D．点评：本题考查等差数列的前n项和公式的应用，是基础题．解题时要认真审题，注意先由通项公式求出首项和公差，再求前四项和．公差，再求前四项和．23．若{a n}为等差数列，a3=4，a8=19，则数列{a n}的前10项和为（项和为（）A．230B．140C．115D．95考点：等差数列的前n项和．综合题．专题：综合题．分析：分别利用等差数列的通项公式化简已知的两个等式，得到①和②，联立即可求出首项和公差，然后利用求出的首项和公差，根据公差数列的前n项和的公式即可求出数列前10项的和．解答：解：a3=a1+2d=4①，a8=a1+7d=19②，②﹣①得5d=15，解得d=3，把d=3代入①求得a1=﹣2，所以S10=10×（﹣2）+×3=115故选C．项和的公式化简求值，是一道基础题．点评：此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值，是一道基础题．24．等差数列{a n}中，a3+a8=5，则前10项和S10=（）A．5B．25C．50D．100考点：等差数列的前n项和；等差数列的性质．计算题．专题：计算题．分析：根据条件并利用等差数列的定义和性质可得 a1+a10=5，代入前10项和S10 =运算求得结根据条件并利用等差数列的定义和性质可得果．解答：解：等差数列{a n}中，a3+a8=5，∴a1+a10=5，∴前10项和S10 ==25，故选B．点评：本题主要考查等差数列的定义和性质，以及前n项和公式的应用，求得a1+a10=5，是解题的关键，属于基础题．25．设S n是公差不为0的等差数列{a n}的前n项和，且S1，S2，S4成等比数列，则等于（等于（）A．1B．2C．3D．4考点：等差数列的前n项和．专题：计算题．计算题．分析：由S1，S2，S4成等比数列，根据等比数列的性质得到S22=S1S4，然后利用等差数列的前n项和的公式分别代入即可得到首项和公差的关系式，根据公差不为根据公差不为0，即可求出公差与首项的关系并解出公表示出各项后，代入即可得到首项和公差的关系式，的关系式代入即可求出比值．差d，然后把所求的式子利用等差数列的通项公式化简后，把公差d的关系式代入即可求出比值．解答：解：由S1，S2，S4成等比数列，∴（2a1+d）2=a1（4a1+6d）．∵d≠0，∴d=2a1．∴===3．故选C点评：此题考查学生掌握等比数列的性质，灵活运用等差数列的通项公式及前n项和的公式化简求值，是一道综合题．n nA．第10项B．第11项C．第10项或11项D．第12项考点：等差数列的前n项和；二次函数的性质．转化思想．专题：转化思想．分析：方法一：由a n，令n=1求出数列的首项，利用a n﹣a n﹣1等于一个常数，得到此数列为等差数列，然后根据求出的首项和公差写出等差数列的前n项和的公式，得到前n项的和与n成二次函数关系，其图象为开口项的和有最大值，即可得到正确答案；向下的抛物线，当n=﹣时，前n项的和有最大值，即可得到正确答案；方法二：令a n大于等于0，列出关于n的不等式，求出不等式的解集即可得到n的范围，在n的范围中找出最大的正整数解，从这项以后的各项都为负数，即可得到正确答案．出最大的正整数解，从这项以后的各项都为负数，即可得到正确答案．解答：解：方法一：由a n=﹣2n+21，得到首项a1=﹣2+21=19，a n﹣1=﹣2（n﹣1）+21=﹣2n+23，则a n﹣a n﹣1=（﹣2n+21）﹣（﹣2n+23）=﹣2，（n＞1，n∈N+），的等差数列，所以此数列是首项为19，公差为﹣2的等差数列，则S n=19n+•（﹣2）=﹣n2+20n，为开口向下的抛物线，，为开口向下的抛物线，当n=﹣=10时，S n最大．所以数列{a n}从首项到第10项和最大．方法二：令a n=﹣2n+21≥0，解得n≤，因为n取正整数，所以n的最大值为10，项开始为负数，所以此数列从首项到第10项的和都为正数，从第11项开始为负数，则数列{a n}从首项到第10项的和最大．项的和最大．故选A点评：此题的思路可以先确定此数列为等差数列，根据等差数列的前n项和的公式及二次函数求最值的方法得到n 的值；也可以直接令a n≥0，求出解集中的最大正整数解，要求学生一题多解．满足：=．考点：数列递推式；等差数列的通项公式．专题：计算题．计算题．分析：根据所给的数列的递推式，看出数列是一个等差数列，根据所给的原来数列的首项看出等差数列的首项，根据等差数列的通项公式写出数列，进一步得到结果．根据等差数列的通项公式写出数列，进一步得到结果．解答：解：∵根据所给的数列的递推式∴数列{}是一个公差是5的等差数列，∵a1=3，∴=，∴数列的通项是∴故答案为：点评：本题看出数列的递推式和数列的通项公式，本题解题的关键是确定数列是一个等差数列，利用等差数列的通项公式写出通项，本题是一个中档题目．通项公式写出通项，本题是一个中档题目．28．如果f（n+1）=f（n）+1（n=1，2，3…），且f（1）=2，则f（100）=101．考点：数列递推式；等差数列的通项公式．计算题．专题：计算题．分析：由f（n+1）=f（n）+1，x∈N+，f（1）=2，依次令n=1，2，3，…，总结规律得到f（n）=n+1，由此能够求出f（100）．解答：解：∵f（n+1）=f（n）+1，x∈N+，f（1）=2，∴f（2）=f（1）+1=2+1=3，f（3）=f（2）+1=3+1=4，f（4）=f（3）+1=4+1=5，…∴f（n）=n+1，∴f（100）=100+1=101．故答案为：101．本题考查数列的递推公式的应用，是基础题．解题时要认真审题，仔细解答．点评：本题考查数列的递推公式的应用，是基础题．解题时要认真审题，仔细解答．29．等差数列{a n}的前n项的和，则数列{|a n|}的前10项之和为项之和为 58．考点：数列的求和；等差数列的通项公式．专题：计算题．分析：先求出等差数列的前两项，可得通项公式为a n=7﹣2n，从而得到n≤3时，|a n|=7﹣2n，当n＞3时，|a n|= 2n﹣7．分别求出前3项的和、第4项到第10项的和，相加即得所求．项的和，相加即得所求．解答：解：由于等差数列{an}的前n项的和，故a1=s1=5，∴a2=s2﹣s1=8﹣5=3，故公差d=﹣2，故a n=5+（n﹣1）（﹣2）=7﹣2n．当n≤3时，|a n|=7﹣2n，当n＞3时，|a n|=2n﹣7．项之和为 a1+a2+a3﹣a4﹣a5﹣…﹣a10=+=9+49=58，故前10项之和为故答案为 58．故答案为项和公式及其应用，体现了分类讨论的数学思想，属于中档题．点评：本题主要考查等差数列的通项公式，前n项和公式及其应用，体现了分类讨论的数学思想，属于中档题．（考点：数列的求和；等差数列的通项公式．计算题．专题：计算题．分析：（1）将已知条件a3a6=55，a2+a7=16，利用等差数列的通项公式用首项与公差表示，列出方程组，求出首项与公差，进一步求出数列{a n}的通项公式的通项公式（2）将已知等式仿写出一个新等式，两个式子相减求出数列{bn}的通项，利用等比数列的前n项和公式求出数列{b n}的前n项和S n．解答：解（1）解：设等差数列{a n} 的公差为d，则依题设d＞0 由a2+a7=16．得2a1+7d=16 ①由a3•a6=55，得（a1+2d）（a1+5d）=55 ②由①得2a1=16﹣7d 将其代入②得（16﹣3d）（16+3d）=220．即256﹣9d2=220∴d2=4，又d＞0，∴d=2，代入①得a1=1∴a n=1+（n﹣1）•2=2n﹣1 所以a n=2n﹣1（2）令c n=，则有a n=c1+c2+…+c n，a n+1=c1+c2+…+c n﹣1两式相减得a n+1﹣a n=c n+1，由（1）得a1=1，a n+1﹣a n=2∴c n+1=2，c n=2（n≥2），即当n≥2时，b n=2n+1又当n=1时，b1=2a1=2∴b n=＜BR＞于是S n=b1+b2+b3…+b n=2+23+24+…+2n+1=2+22+23+24+…+2n+1﹣4=﹣6，即S n=2n+2﹣6项和应该先求出数列的通项，利用通项的特点，然后选择合适的求和的方法．点评：求一个数列的前n项和应该先求出数列的通项，利用通项的特点，然后选择合适的求和的方法．。

(完整版)等差数列练习题及答案.doc

等差数列1、已知等差数列a n满足 a1 a2 a101 0 ，则有（）A 、a1 a101 0 B 、a2a100 0 C、a3a990 D 、a51 512、等差数列a n 的前 n 项和记为 S n，若 a2 a4 a15得值是一个确定的常数,则数列S n 中也为常数的值为( )A 、S7 B、S8 C、S13 D 、S153、在等差数列a n 中 , a3 a9 ,公差d 0 ,则前n项和S n 取得最大值的 n 为( )A 、 4 或 5B 、 5 或 6 C、6 或 7 D、不存在4、等差数列a n 前 m 项和为30,前2m 项和为 100,则它的前 3 m项的和为( )A 、 130 B、 170 C、 210 D 、 2605、等差数列a n 的公差为 2 ，且 a1 a4 a7 a97 50，那么a3a6a9 a99_____.6、等差数列a n , a n=q， a m p ( m n) ，则 a k=________7、在－ 1 与 7 之间顺次插入三个数a, b, c ，使这五个数成等差数列，则这五个数为______8、已知数列a n 的前 n 项和为 S n= n2 2n 3 ,求数列 a n 的通项公式 ,并判断a n 是否为等差数列 ?9、若 x y, 两个数列 : x, a1 , a 2 , a 3 , y 和 x, b1 , b2 , b3 , b4 , y 都是等差数列 ,求a2 a1 的值b4 b310、已知公差大于0 的等差数列a n 的前n 项和为S n ,且满足a3 a4 117, a 2 a5 22.(1)求通项a n ; (2) 若数列 { b n } 是等差数列,且 b n =S n求非零常数 c n c答案1【答案】 C2【答案】 C【分析】设首项 a1 , 公差 da2 a4 a15 3(a1 6d )为定值,a713(a1 a13 )a1 6d 为定值,S13 13a7为定值23【答案】 B【分析】设首项 a1 , 公差 da3 a9a1 2d a1 8d ,即a1 5dS n na1 n(n 1)1 (n2 11n)d2d2当n5或6 时 , S n最大4. 【答案】 C【分析】S m , S2 m S m , S3m S2m成等差数列S3m S2m 110S3m 2105【答案】82【分析】 a3 a6 a9 a99a1 a4 a7a97 66d826、【解】从 a n与n的函数关系看,可以看作 a n是n的一次函数 ,因此 ,函数 a n的图象是共线离散的点.已知条件表明 , 点 (m, p), (n, q) 在 a n的图象上 , 问题是求与这两个点共线的点(k, x) 的纵坐标, 由共线条件知p q x q , x p(k n) q(m k) .m n k n m n7【解】设这几个数组成的等差数列为 a n ,知 a11, a5 7 .解得 d 2, 所求数列为1，1，3，5，78【解】解 :当 n 1时 , a1 2;当 n 2 时 , a n S n S n 1 2n 32(n1)a n2n 3(n2)显然 a n 1 a n2(n 2) 但 a2a1 1 21 2a n不是等差数列.9【解】设两个等差数列的公差分别为d1 , d2 即求 d1 ,由已知得d2y x 4d1 4d1 y x即y x 5d 2 5d2 y x解 d1 5 即 a2 a1 54 4d 2 b4 b310【解】 (1) a n 为等差数列 , a 3 a4 a2 a5 22, 又 a3 a4 117,a ,a4 是方程 x 2 22x 117 0 的两实根 .3又公差 d 0 a3 a4 a3 9, a 4 13 a1 2d 9 a1 1a n 4n 3a1 3d 13 d 4(2)、 (1)知S n n 1 n( n 1) 4 2n 2 n2b nS n 2n 2 nb11 6 15n c n c, b22, b33,1 c c cb n 为等差数列2b2 b1621 15b3 ,即1 c 3 c2 c2c2 c 0 , c1( c 0 舍去 ),故c 1 .2 2。

等差数列练习试题及包括答案.docx

等差数列练习题及答案等差数列练习一、选择题1、等差数列a n中，S10120 ，那么 a1a10A. 12B.24C.36 48（）D.2、已知等差数列a n ，a n2n 19 ，那么这个数列的前n项和 s n（）A. 有最小值且是整数B.有最小值且是分数C. 有最大值且是整数D.有最大值且是分数3、已知等差数列a n的公差d1，a2a4a10080 ，2那么 S100A ．80B ．120C ．135 D．160．4、已知等差数列a n中，a2a5 a9a1260 ，那么S13A．390B．195 C．180D．1205、从前180个正偶数的和中减去前180 个正奇数的和，其差为（）A. 0B.90C.180D.3606、等差数列a n的前m项的和为30，前2m项的和为100，则它的前3m 项的和为()A. 130B.170C.210D.2607、在等差数列a n中，a2 6 ， a86，若数列a n的前 n 项和为 S n，则（）A. S4S5B. S4S5C.S6S5D.S6 S58、一个等差数列前3项和为 34，后 3项和为146 ，所有项和为 390 ，则这个数列的项数为（）A. 13B.12C.11D.109、已知某数列前n项之和n3为，且前n个偶数项的和为 n2 ( 4n 3) ，则前 n 个奇数项的和为（）A ．3n2(n 1)B．n2(4n 3)C．3n2 D．1n32 10若一个凸多边形的内角度数成等差数列，最小角为 100°，最大角为 140°，这个凸多边形的边比为（）A．6B．8C．10D．12二．填空题1、等差数列a n中，若a6a3a8，则s9.2 、等差数列a n中，若S n3n22n，则公差d.3、在小于100的正整数中，被3除余2的数的和是4 、已知等差数列{ a n}的公差是正整数，且a3a712, a4a64，则前 10 项的和 S10 =5、一个等差数列共有10 项，其中奇数项的和为25 ，偶数项的和为15，则这个数列的第6 项是2*6 、两个等差数列a n和 b n的前n项和分别为S n和S n7n 3，则a8.Tn ，若T n n 3b8三．解答题1、在等差数列a n中，a40.8 ， a11 2.2 ，求a 51a52L a80 .2、设等差数列a n的前n项和为S n，已知a312，S12 >0，S13<0，①求公差 d 的取值范围；② S1 , S2,L , S12中哪一个值最大？并说明理由.3、己知{a n}为等差数列，a12, a23，若在每相邻两项之间插入三个数，使它和原数列的数构成一个新的等差数列，求：（1）原数列的第12 项是新数列的第几项？（2）新数列的第 29 项是原数列的第几项？4、设等差数列{ a n}的前ｎ项的和为 S n , 且 S 4 =的通项公式 a n及－62, S 6 = －75, 求：（1）{ an}前ｎ的和 S n；（2）|a 1 |+|a 2 |+|a 3 |+ ⋯⋯ +|a 14 |.5、某公司年初用98 万元一艘捕船，第一年各种用12 万元，以后每年都增加4 万元，每年捕收益 50 万元，（Ⅰ）第几年开始利？（Ⅱ）若干年后，有两种理方案：（1）年平均利最大，以 26 万元出售船；（2）收入利最大，以 8 万元出售船 .哪种方案合算 .参考答案一、 1-5 B A C B C 6-10 C B A B A二、1 、0 2、63 、16504 、-105、3 6、6三． 1、 an0.2n， a 51a 52 a 80393．S1212(a 1 a 12 ) 6(a 6 a 7 ) 0a 6 a 7 02a 1 11d2、①∵2, ∴ a 16d 0 S1313ga 7a 1 2d 12(a 1 a 13 ) 13 a 72解得 ,24a 6 a 7 0a 6 0247d3 , ②由 a 7a 70 ,又∵7d3∴ a n是递减数列 ,∴ S 1 , S 2 ,L, S 12中 S 6最大 .3、解：设新数列为b n , 则b 1 a 1 2, b 5 a 2 3,根据 b n b 1 (n 1)d ,有 b 5 b 1 4d ,即 3=2+4d ，∴ d，∴ b n2 (n 1)n 7 11444又Q a n a 1(n 1) 1 n 1(4 n 3)7，∴ a n b 4n 34即原数列的第 n 项为新数列的第 4n －3项．（ 1）当 n=12 时， 4n －3=4×12－ 3=45，故原数列的第 12 项为新数列的第 45 项；（2）由 4n－3=29, 得 n=8，故新数列的第 29是原数列的第8 。

(完整word版)等差数列基础练习题

等差数列·基础练习题一、填空题1. 等差数列8，5，2，…的第20项为___________.2. 在等差数列中已知a 1=12, a 6=27，则d=___________3. 在等差数列中已知13d =-，a 7=8,则a 1=_______________ 4. 2()a b +与2()a b -的等差中项是________________— 5. 等差数列—10,—6,-2,2,…前___项的和是54 6. 正整数前n 个数的和是___________7. 数列{}n a 的前n 项和23n S n n -＝,则n a ＝___________二、选择题8. 若lg2,lg(21),lg(23)x x -+成等差数列，则x 的值等于（）A.0B. 2log 5 C 。

32 D.0或329。

在等差数列{}n a 中31140a a +=,则45678910a a a a a a a -+++-+的值为（）A 。

84B 。

72 C.60 . D.4810. 在等差数列{}n a 中，前15项的和1590S = ，8a 为（）A.6 B 。

3 C 。

12 D.411。

等差数列{}n a 中， 12318192024,78a a a a a a ++=-++=,则此数列前20下昂的和等于A 。

160 B.180 C.200 D 。

22012。

在等差数列{}n a 中，若34567450a a a a a ++++=，则28a a +的值等于( ）A 。

45B 。

75 C.180 D.30013. 设n S 是数列{}n a 的前n 项的和,且2n S n =，则{}n a 是（ )A 。

等比数列,但不是等差数列 B.等差数列，但不是等比数列C 。

等差数列，且是等比数列D 。

既不是等差数列也不是等比数列 14. 数列3，7，13，21，31，…的通项公式是（） A 。

41n a n =- B. 322n a n n n =-++ C. 21n a n n =++ D.不存在三、计算题15。

(完整)小学五年级等差数列练习.docx

等差数列1、6＋7＋8＋9＋⋯⋯＋ 74＋ 75＝2、2＋6＋10＋ 14＋⋯⋯＋ 122＋126＝3、已知数列 2、5、8、 11、14⋯⋯， 47是其中的第几？4、有一个数列： 6、10、 14、18、22⋯⋯，个数列前 100的和是多少？5、在等差数列 1、 5、 9、 13、17⋯⋯ 401中， 401是第几？第 50是多少？6、1＋2＋3＋4＋⋯⋯＋ 2007＋2008＝7、（ 2＋ 4＋ 6＋⋯⋯＋ 2000）－（ 1＋3＋5＋⋯⋯＋ 1999）＝8、1＋2－3＋4＋5－6＋ 7＋8－9＋⋯⋯＋ 58＋59－60＝9、有从小到大排列的一列数，共有100，末 2003，公差 3，求个数列的和。

10、求 1—— 99个自然数的所有数字的和。

2：1、在等差数列 1， 5， 9， 13，17，⋯， 401中 401是第几？2、100个小朋友排成一排数，每后一个同学的数都比前一个同学的数多3，小明站在第一个位置，小宏站在最后一个位置。

已知小宏的数是300，小明的数是几？3、有一堆粗均匀的木，堆成梯形，最上面的一有 5 根木，每向下一增加一根，一共堆了 28 。

最下面一有多少根？4、1+2+3+4+5+6+⋯+97+98+99+100=？5、求 100 以内所有被 5 除余 0 的自然数的和。

6、小王和小胡两个人跑，限定10 秒，跑的距离就。

小王第一秒跑1 米，以后每秒都比以前一秒多跑0.1 米，小胡自始至每秒跑 1.5 米，能取？3：1.数列 4，7，10，⋯⋯ 295， 298 中 298 是第几？2.牛每小都比前一小多爬 0.1 米，第 10 小牛爬了 1.9 米，第一小牛爬多少米？3.求自然数中所有三位数的和。

4.求所有除以4余1的两位数的和。

5.有12个数成等差数列，第六与第七的和是12，求 12 个数的和。

728.一个物体从高空落下，已知第一秒下落距离是 4.9 米，以后每秒落下的距离是都比前一秒多 9.8 米 50 秒后物体落地。

(完整word版)等差数列基础题训练

基础题训练11. 等差数列{}n a 中,已知,2,101-==d a 则=6a ——。

2. 等差数列{}n a 中，已知=++==76593,9,1a a a a a 则_______。

3. 等差数列{}n a 中,==-=982,6,6s a a 则_______.4. 等差数列{}n a 中，===n a a a 则,21,952_________. 5. 等差数列{}n a 中，_____,7,118452=-=-=+a a a a 则。

6. 在等差数列{}n a 中,33,39852741=++=++a a a a a a 则=++963a a a 则____7．在等差数列{}n a 中，若34567a +a +a +a +a =450，则28a +a =_______。

8.已知等差数列{}n a 中，26a a 与的等差中项为5，37a a 与的等差中项为7,则n a = 。

9．等差数列{}n a 中，n S =40，1a =13，d = -2 时，n =______________. 10．已知等差数列{}n a 的前n 项和为__,,80,35,1107===a s s s n 则d=____. 11。

已知等差数列{}n a 的前m 项和为30, 前2m 项和为100, 则前3m 项和为____. 12.在等差数列{}n a 中,3,15654321=++=++a a a a a a =12s 则____ 13. 等差数列{}n a 中,._____,10,10011010010===a a a 那么若 14.等差数列{}n a 中， 1a 〈0, 最小，若n s s s ,4525=则n=______15．已知等差数列{n a ｝中，,0,166473=+-=a a a a 求{n a ｝前n 项和n s . 16.等差数列{}n a 的前n 项和记为n S ,已知102020,410a S ==,（1)求数列{}n a 的通项公式; (2）若S n =135，求以n ．基础题训练21。

等差数列基础题训练

等差数列基础题训练基础题训练11.等差数列a n中，已知a i 10,d 2,则――.2.等差数列a n中，已知a3 1,a9 9,则a§ a6 a? ______________ .3.等差数列a n中,a2 6,兎6,则S9 _________ .4.等差数列a n中，a? 9,a5 21,则a n___________ .5.等差数列a n中，a2 a s 11, a4 7,则a s _________ .6.在等差数列a n中a1 a4 a739,则a2 a5 a833,则a3 a6 a9 ______7.________________________________________________ 在等差数列a n中，若a3+a4+a s+a6+a7=450 ,则 a2+a s= ______________ .8.已知等差数列an中，a2与a6的等差中项为5 , a3与a?的等差中项为7 , 则a n _________________________ . ___________9.等差数列a n 中，S n =40，a1 =13，d= -2 时，n= ________________ .10 . 已知等差数列a n 的前n 项和为S n ,S7 35,Se 80,则a〔__, d= ____ .11.已知等差数列a n的前m项和为30,前2m项和为100,则前3m项和为 ___ .12.在等差数列a n中a i a2 a315,84 a5a6 3,则卷______13.等差数列 a n 中，若8io 100,8100 10,那么an o ________________ .14.等差数列a n中，81 <0, S25 S45,若S n最小，则n= _______15.已知等差数列｛a n｝中，a3a716,a4 a6 0,求｛a.｝前n项和s n .16.等差数列｛a n｝的前n项和记为S n，已知a10 20$0 410 ,(1)求数列｛a n｝的通项公式；(2)若S = 135，求以n .基础题训练21.｛a n｝为等差数列，且a7-2a4=- 1, a3= 0,则公差d= ( )1A.—2B.—2 D. 22.在等差数列｛a n｝中，已知a3 2，贝卩该数列的前5项之和为( )(A) 10 ( B) 16 (C 20 (D) 323.设等差数列｛a n｝的前n项和为S n，若S3 9 , S6 36，则a? a* a93(A ) 63 (B ) 45(C 36(D ) 27那么a g a 6 a ?川a ?9的值是 ((A )- 78 (B )— 82 (Q- 148 (D )— 1825.设S n 是等差数列｛a n ｝的前n 项和.已知a 2 = 3, a 6 = 11,则S ?等于 ( ) A. 13B. 35C. 49D. 636. 设数列｛a n ｝的前n 项和S n n 2，则a 8的值为()(A ) 15(B) 16 (C) 49 (D ) 647.设等差数列a n 的前n 项和为S n ,若a 111, a 4比6,则当S n 取最小值时,n 等于( )A . 6B . 7C. 8 D . 98. 等差数列｛a .｝中，a 1 3a 8亦120，则3a ? a^的值为______________9. 等差数列｛a n ｝中，a 1 - , a 2 a § 4 , a . 3，则 n4.已知等差数列｛%｝的公差d2, aia4 a 7|卄 a9750 ,解答题3。