定积分计算的新公式及其应用
定积分的计算方法总结

定积分的计算方法总结引言定积分是微积分中重要的概念之一,它可以用于求取曲线下的面积、求解物理问题中的积分以及解决各种与变化量有关的问题。
本文将总结定积分计算的常用方法,包括基本定积分公式、换元积分法和分部积分法。
基本定积分公式基本定积分公式是计算定积分时最基础也是最常用的方法之一。
以下为常见的基本定积分公式:1.$\\int x^m dx = \\frac{1}{m+1}x^{m+1}$,其中m为常数,m eq−1。
2.$\\int \\frac{1}{x} dx = \\ln|x|$,其中x为正实数。
3.$\\int e^x dx = e^x$。
4.$\\int \\sin x dx = -\\cos x$。
5.$\\int \\cos x dx = \\sin x$。
6.$\\int \\tan x dx = -\\ln|\\cos x|$。
换元积分法换元积分法是一种常用的定积分计算方法,它通过引入一个新的变量来简化被积函数的形式。
具体步骤如下:1.选择一个适当的变量代换,通常选择与题目给定的被积函数中具有根号、三角函数等特殊形式相关的变量。
2.根据选择的变量代换,将被积函数中的所有变量都用新的变量表示。
3.计算新的被积函数的导数,并将被积函数转换为对新变量的积分。
4.计算新的积分。
以下是换元积分法的一个例子:求解定积分$\\int 2x(x^2+1)^3 dx$。
解:设u=x2+1,则du=2xdx。
将被积函数中的所有x用u表示,则原积分变为$\\int u^3 du$。
计算新的积分得$\\frac{1}{4}u^4 + C$,其中C为常数。
最后,将u替换回x得到最终结果$\\frac{1}{4}(x^2+1)^4 + C$。
分部积分法分部积分法是解决定积分问题中的另一种常用方法,它是利用乘积的导数公式来简化积分计算的步骤。
具体步骤如下:1.选择一个适当的分部积分公式。
分部积分公式为$\\int u dv = uv -\\int v du$。
定积分应用

(1) 总量在区间上具有可加性,即把区间 分成几个小区间时总量就等于各个小区间上 的局部量之和,
(2)局部量可用 f (i )xi 近似表示
它们之间只相差一个xi 的高阶无穷小
不均匀量U就可以用定积分来求得
这是建立所求量的积分式的基本方法 分析其实质,不难将四步简化为两步 第一步 “分割取近似 ” 含“分”、“粗”两步即将区间分成子区间
的值与 xi 之积代替 Ui f (i )xi
和 把局部量的近似值累加得到总量
的近似值 即
n
n
U Ui f (i )xi
i 1
i 1
精 max xi
n 1in
b
U
lim
0
i 1
f (i )xi
a
f ( x)dx
由此可知,若某个非均匀量U在区间[a,b]上 满足两个条件:
y2 2 x 解得交点为(2,-2)和(8,4) y x4
若取 x 为积分变量 在 [x,x+dx] 上取部分量
则对于 x 的不同值 局部量的位置不同 其 上、下曲边有多种情况运用上述公式计算 较为复杂
如下图
但若将这一面积看作是分布在区间 [ -2,4] 上 以 y 为变量计算将会简单
在[-2,4] 上任取一小区间 [ y, y dy]
设量U非均匀地分布 [ a ,b ]上 求U的步骤
分 用分点 a x0 x1 xn1 xn b 将
区间分成n个小区间 [xi1, xi ], xi xi xi1
粗 把U在小区间上的局部量 Ui
用某个函数 f ( x) 在 i (i [xi1, xi ])
2 sin
定积分计算公式大全

定积分计算公式大全一、定积分的基本公式。
1. 牛顿 - 莱布尼茨公式(Fundamental Theorem of Calculus)- 如果函数f(x)在区间[a,b]上连续,并且F(x)是f(x)的一个原函数,即F^′(x) = f(x),那么∫_a^bf(x)dx=F(b)-F(a)。
- 例如:计算∫_1^2x^2dx,因为F(x)=(1)/(3)x^3是f(x) = x^2的一个原函数,所以∫_1^2x^2dx=(1)/(3)x^3big_1^2=(1)/(3)×2^3-(1)/(3)×1^3=(8)/(3)-(1)/(3)=(7)/(3)。
2. 定积分的线性性质。
- ∫_a^b[k_1f(x)+k_2g(x)]dx = k_1∫_a^bf(x)dx + k_2∫_a^bg(x)dx,其中k_1,k_2为常数。
- 例如:计算∫_0^1(2x + 3x^2)dx,根据线性性质∫_0^1(2x+3x^2)dx =2∫_0^1xdx+3∫_0^1x^2dx。
- 因为∫_0^1xdx=(1)/(2)x^2big_0^1=(1)/(2),∫_0^1x^2dx=(1)/(3)x^3big_0^1=(1)/(3),所以∫_0^1(2x + 3x^2)dx=2×(1)/(2)+3×(1)/(3)=1 + 1=2。
二、定积分的换元积分法。
设函数f(x)在区间[a,b]上连续,函数x = φ(t)满足条件:1. φ(α)=a,φ(β)=b;2. φ(t)在[α,β](或[β,α])上具有连续导数,且其值域R_φ⊆[a,b],则∫_a^bf(x)dx=∫_α^βf[φ(t)]φ^′(t)dt。
例如:计算∫_0^4(dx)/(1 + √(x))。
令t=√(x),则x = t^2,dx = 2tdt。
当x = 0时,t = 0;当x = 4时,t=2。
所以∫_0^4(dx)/(1+√(x))=∫_0^2(2t)/(1 + t)dt=2∫_0^2(t + 1-1)/(1 + t)dt=2∫_0^2(1-(1)/(1 + t))dt=2<=ft[t-ln(1 + t)]big_0^2=2(2-ln3)三、定积分的分部积分法。
定积分替换公式

定积分替换公式
摘要:
1.定积分替换公式的概念
2.定积分替换公式的例子
3.定积分替换公式的应用
4.定积分替换公式的注意事项
正文:
一、定积分替换公式的概念
在数学中,定积分替换公式是一种求解定积分的技巧,主要用于将较难求解的定积分问题转换为容易求解的问题。
替换公式可以帮助我们简化积分过程,提高求解效率。
二、定积分替换公式的例子
以下是一个使用定积分替换公式的例子:
求解积分:∫(x^2 + 3x - 2) dx
通过观察,我们可以将这个积分式替换为:∫(x^2 + 3x - 2) dx = ∫(x^2 + 2x + x - 2) dx
然后,我们可以将这个替换后的积分式分解为两个简单的积分:∫(x^2 + 2x) dx - ∫(2) dx
继续简化,我们得到:[x^3 / 3 + x^2 / 2] - 2
最后,我们可以得到积分的结果:(x^3 / 3 + x^2 / 2) - 2
通过这个例子,我们可以看到定积分替换公式可以帮助我们简化积分过程,提高求解效率。
三、定积分替换公式的应用
定积分替换公式在实际应用中有广泛的应用,例如在物理、工程等领域。
通过使用定积分替换公式,我们可以更快地求解定积分,从而为实际问题提供解决方案。
四、定积分替换公式的注意事项
在使用定积分替换公式时,我们需要注意以下几点:
1.替换公式应根据积分式的特点进行,不能盲目替换。
2.在替换后,需要对积分式进行适当的简化和求解。
3.替换公式并不是适用于所有积分问题,需要根据具体情况选择合适的方法。
总之,定积分替换公式是一种求解定积分的有效方法,可以帮助我们简化积分过程,提高求解效率。
用定积分求面积的两个重要公式
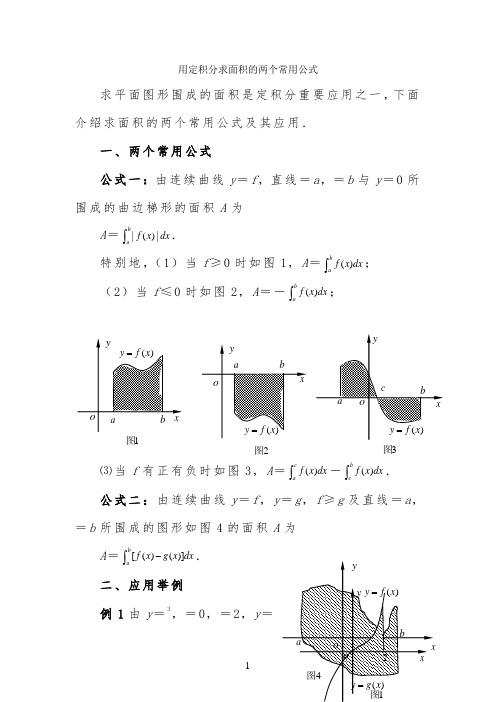
用定积分求面积的两个常用公式求平面图形围成的面积是定积分重要应用之一,下面介绍求面积的两个常用公式及其应用.一、两个常用公式公式一:由连续曲线y =f ,直线=a ,=b 与y =0所围成的曲边梯形的面积A 为A =|()|ba f x dx ⎰.特别地,(1)当f ≥0时如图1,A =()ba f x dx ⎰;(2)当f ≤0时如图2,A =-()baf x dx ⎰;⑶当f 有正有负时如图3,A =()caf x dx ⎰-()bcf x dx ⎰.公式二:由连续曲线y =f ,y =g ,f ≥g 及直线=a ,=b 所围成的图形如图4的面积A 为A =[()()]ba f x g x dx -⎰.二、应用举例例1由y =3,=0,=2,y =1图2图3图0围成的图形面积.分析:先画出图象,利用公式1转化为定积分问题即可解决.解:(1)如图1,由公式1,得S =230x dx ⎰=42440111|204444x =⨯-⨯=.评注:注意定积分与利用定积分计算曲线围成图形的面积区别.定积分是一种积分和的极限,可为正,也可为负或零,而平面图形的面积在一般意义上总为正.一般情况下,借助定积分分别求出每一部分曲边梯形的面积,然后将它们加在一起.例2(1)由曲线y =2,y 2=所围成图形的面积. (2)由y =142-1,y =12,y =34x 在第一象限所围成图形的面积.分析:先画图象找出范围,利用公式2,用积分表示,再求积分.解:(1)如图2,所求面积为阴影部分. 解方程组22y xy x⎧=⎪⎨=⎪⎩,得交点0,0,1,1,由公式2,得S =120)x dx ⎰=331202211()|33333x x -=-=.(2)如图3,解方程组211412y x y x ⎧=-⎪⎪⎨⎪=⎪⎩和211434y x y x ⎧=-⎪⎪⎨⎪=⎪⎩,得=0,=1+的舍去,=4.由公式2,得图形面积S=1031()42x dx -⎰+42111[(1)]42x x dx --⎰216-=.3图。
定积分公式大全24个

定积分公式大全24个在微积分中,定积分是一个非常重要的概念,它在数学和物理学等领域有着广泛的应用。
定积分公式作为定积分的重要工具,可以帮助我们解决各种复杂的问题。
在本文中,我们将介绍24个常见的定积分公式,希望对大家的学习和工作有所帮助。
1. 基本积分公式。
定积分的基本公式是。
\[ \int_{a}^{b} f(x)dx=F(b)-F(a) \]其中,\(F(x)\)是\(f(x)\)的不定积分。
这个公式是定积分的基础,我们可以通过它来求解更复杂的积分问题。
2. 定积分的线性性质。
如果\(f(x)\)和\(g(x)\)在区间\([a,b]\)上可积,\(k\)是任意常数,那么有。
\[ \int_{a}^{b} [kf(x)+g(x)]dx=k\int_{a}^{b} f(x)dx+\int_{a}^{b} g(x)dx \]这个公式可以帮助我们简化定积分的计算过程,尤其是在处理复杂的函数时非常有用。
3. 定积分的换元积分法。
如果\(u=g(x)\)在\([a,b]\)上具有连续导数,\(f(u)\)在对应区间上可积,那么有。
\[ \int_{a}^{b} f(g(x))g'(x)dx=\int_{g(a)}^{g(b)} f(u)du \]这个公式可以帮助我们将原来的积分转化为更容易处理的形式,从而简化计算。
4. 定积分的分部积分法。
如果\(u=f(x)\)和\(v=g(x)\)都在\([a,b]\)上具有连续导数,那么有。
\[ \int_{a}^{b} u dv=uv|_{a}^{b}-\int_{a}^{b} v du \]这个公式可以帮助我们将原来的积分转化为更容易处理的形式,从而简化计算。
5. 定积分的换限积分法。
如果\(f(x)\)在\([a,b]\)上可积,\(F(x)\)是\(f(x)\)的一个原函数,那么有。
\[ \int_{a}^{b} f(x)dx=-\int_{b}^{a} f(x)dx \]这个公式可以帮助我们简化定积分的计算过程,尤其是在处理对称函数时非常有用。
高等数学第六章《定积分的应用》

第六章 定积分的应用一、内容提要(一)主要定义【定义】 定积分的元素法 如果(1)所求量U 是与一个变量x 的变化区间[]b a ,有关的一个整体量; (2)U 对区间[]b a ,具有可加性; (3)部分量i U ∆可表示为()i i i U f x ξ∆≈∆.则可按以下步骤计算定积分(1)选取一个变量x 或y ,并确定它的变化区间[]b a ,;(2)把区间[]b a ,分成n 个小区间, 求任一小区间[],x x dx +的部分量U ∆的近似dU .()U dU f x dx ∆≈=; (3)计算()U=baf x dx ⎰.(二)主要定理与公式根据定积分的元素法可建立一些几何和物理方面的定积分表达式. 1.平面图形面积 (1)直角坐标情形①由()(),(0),,y f x f x x a x b =≥==所围图形的面积()bas f x dx =⎰.②由()()12,,,y f x y f x x a x b ====所围图形的面积()()12 bas f x f x dx =-⎰.③由()()12,,,x y x y y c y d ϕϕ====所围图形的面积()()12dcs y y dy ϕϕ=-⎰(2)参数方程情形 由曲线l :()()x t y t ϕψ=⎧⎪⎨=⎪⎩,12t t t ≤≤,x 轴及,x a x b ==所围图形的面积 ()()21t t s t t dt ψϕ'=⎰(3)极坐标情形① 由(),,ρϕθθαθβ===所围图形的面积()212s d βαϕθθ=⎰ ② 由()()12,,,ρϕθρϕθθαθβ====所围图形的面积()()222112s d βαϕθϕθθ⎡⎤=-⎣⎦⎰ 2.体积(1)旋转体的体积① 由()0,,,y y f x x a x b ====所围图形绕x 轴旋转所得旋转体体积:()2b a V f x dx π=⎡⎤⎣⎦⎰. 当0a b ≤<时,上述曲边梯形绕y 轴旋转所得旋转体的体积: ()22bbaaV x y dx x f x dx ππ==⎰⎰.② 由(),0,,x y x y c y d ϕ====所围图形绕y 轴旋转一周形成的立体体积:()2d c V y dy πϕ=⎡⎤⎣⎦⎰ (2)平行截面面积为已知的立体的体积设以()[],A x C a b ∈表示立体Ω的过点x 且垂直于x 轴的截面面积,且立体Ω夹在平面x a x b ==与之间,则立体Ω的体积:()baV A x dx =⎰.3.平面曲线的弧长(1)光滑曲线():,l y f x a x b =≤≤的弧长为as =⎰.(2)光滑曲线()(),: ,x x t l t y y t αβ=⎧⎪≤≤⎨=⎪⎩的弧长为s βα=⎰.(3)光滑曲线():, l ρϕθαθβ=≤≤的弧长为s βαθ=⎰4.变力沿直线做功、水压力 (1)变力沿直线做功设物体在变力()F x 的作用下,沿变力的方向由x a =移到x b =,在物体的位移区间[],a b 内任一子区间[],x x dx +上功的元素为 ()dW F x dx =,全部功()baW F x dx =⎰.(2)水压力设平板铅直地放入液体中,液体的密度为ρ,平板位于液面下的深度在区间[]0,b 内任一子区间[],x x dx +上,液体深x 处的压强为p gx ρ=,压力元素()dp gx f x dx ρ=⋅. 全部压力为 ()0bp gx f x dx ρ=⋅⎰.二、典型题解析(一)填空题【例6.1】 由曲线,xxy e y e -==及直线1x =所围成图形的面积是 . 解 所求面积 ()()1112xx x x S ee dx e e e e ---=-=+=+-⎰.故应填12e e -+-. 【例6.2】 由222,82x y x y =+=所围成图形(见图6.1)面积A (上半平面部分),则A = .解 两曲线22228x y x y ⎧=⎪⎨⎪+=⎩的交点为()()2,2,2,2-.所求的面积为222)2x A dx -=⎰328226x ⎫=-⎪⎭423π=+. 故应填423π+. 【例6.3】 曲线sin 02y x x π⎛⎫=≤≤⎪⎝⎭与直线,02x y π==围成一个平面图形,此平面图形绕x 轴旋转产生的旋转体的体积 .解 2220s i n 4V x d x πππ==⎰. 故应填24π.【例6.4】 阿基米德螺线()0aeλθρλ=>从0θ=到θα=一段弧长s = .解 0s αθ=⎰ ()01eλαθλ==-⎰.)1eλα-.【例6.5】 曲线322y x x x =-++与x 轴所围成的图形的面积A = . 解 函数322(2)(1)y x x x x x x =-++=--+与x 轴的交点为()()()1,0,0,02,0-.()()023232122A x x x dx x x x dx -=--+++-++⎰⎰3712=. (二)选择题图6.122x y =228x y +=【例6.6】 曲线x y e =与其过原点的切线及y 轴所围成的图形(见图6.2)面积为[ ](A ) ()1x e ex dx -⎰; (B )()1ln ln ey y y dy -⎰;(C )()1e x x e xe dx -⎰; (D )()1ln ln y y y dy -⎰.解 曲线x y e =在任意点(),x y 的切线方程为()x x Y e e X x -=-,由于切线过原点,可以求出1x =,于是过原点的切线方程为Y eX =.所求平面图形的面积等于()1xeex dx -⎰. 故选择A.【例6.7】 由曲线()()12y x x x =--与x 轴围成的平面图形的面积为 [ ]. (A )()()()()12011212x x x dx x x x dx -----⎰⎰;(B )()()212x x x dx ---⎰;(C )()()()()12011212x x x dx x x x dx ---+--⎰⎰;(D )()()212x x x dx --⎰.解 在区间[]0,1,0y <,在区间[]1,2,0y >, 所以 ()()112S x x x dx =---⎰()()2112x x x dx +--⎰.故选择C.【例 6.8】 曲线cos 22y x x ππ⎛⎫=-≤≤ ⎪⎝⎭与x 轴围成的平面图形绕x 轴旋转一周而成的旋转体体积为 [ ](A )2π (B )π (C )212π (D )2π. 解 2222cos2V xdx ππππ-==⎰.故选择C.图6.2【例6.9】 双纽线()22222x yx y +=-围成的平面图形的面积为 [ ](A )402cos 2d πθθ⎰; (B )404cos 2d πθθ⎰;(C)2θ; (D )()2401cos 22d πθθ⎰.解 双纽线的极坐标方程为2cos 2 r θ=,(,44ππθ-≤≤35)44ππθ≤≤由对称性 2244001422S r d r d ππθθ=⨯=⎰⎰402cos 2d πθθ=⎰. 故选择A.【例6.10】 曲线()2ln 1y x =-上102x ≤≤的一段弧长l = [ ].(A); (B )1222011x dx x +-⎰; (C); (D ). 解 曲线是直角坐标表示的曲线,采用公式al =⎰.由曲线方程()2ln 1y x =-可得210x ->,221x y x -'=-,则1222011x l dx x +==-⎰. 故选择B .(三)非客观题 1. 平面图形的面积解题方法 (1)先画出草图;(2)求出交点;(3)选取积分变量、区间,找出面积元素,然后积分. (1)直角坐标情形【例6.11】求曲线22,ax y ay x ==所围(见图6.3)的面积. 解 如图所示,交点为()(),00,0A a O 及.图6.32ax y =2y ax =所围的面积()23232002)333aax x aS dx ax a aa ⎡⎤==-=⎢⎥⎣⎦⎰. 【例6.12】 求介于由曲线2121,2+==x y x y 和x 轴围成的平面图形(见图6.4)的面积.解 (法一)设此面积为S ,有12101111()d ()d 2222S x x x x x -=+++-⎰⎰0122310()()42423x x x x x -=+++-23=(法二)13122002(21)]d ()3S y y y y y =-=-+⎰23=.【例6.12】 求0,2x x π==之间由曲线sin y x =和cos y x =所围成的图形(见图6.5)的面积. 解 20sin cos A x x dx π=-⎰()40cos sin x x dx π=-⎰()544sin cos x x dx ππ+-⎰()254cos sin x x dx ππ+-⎰=【例6.13】 求抛物线243y x x =-+-及其在点()0,3-和()3,0处的切线所围成的图形(见图6.6)的面积.解 由24y x '=-+得过点()0,3-和()3,0的切线方程为1:43l y x =-和2:26l y x =-+,图 6.4图 6.24π54π2π图 6.5图 6.6且可得12,l l 交点坐标为3,32⎛⎫⎪⎝⎭,则所围图形的面积为()32204343A x x x dx ⎡⎤=---+-⎣⎦⎰()32322643x x x dx ⎡⎤+-+--+-⎣⎦⎰94=. 【例6.14】求由曲线322,0a y y a x==+所围的面积. 解 所求面积为33222202lim b b a dx S dx a dx a x a x+∞-∞→+∞==++⎰⎰ 3212limarctan b a b a aπ→+∞==. 【例6.15】确定常数k ,使曲线2y x =与直线,2,0x k x k y ==+=所围成图形的面积最小. 解 选x 为积分变量,变化区间为[],2k k +,面积元素2dA x dx =,所求面积为()()22 k kA k x dx k +=-∞<<+∞⎰,要求k 使()A k 取最小值,()A k 是积分上(下)限函数,故()()22241dA k k k dk=+-=+, 令0dA dk =,解得驻点1k =-,因为2240d Adk=>,则1k =-为()A k 在(),-∞+∞内唯一极小值点,即当1k =-时,所围成图形的面积最小. (2)参数方程情形【例6.16】求摆线()()sin ,1cos x a t t y a t =-=-()020t y π≤≤=及所围的面积. 解 所求面积为20(1cos )(1cos )S a t a t dt π=-⋅-⎰图 6.72220(12cos cos )a t t dt π=-+⎰221cos 2(12cos )2tat dt π+=-+⎰20312sin sin 224t t t π⎡⎤=-+⎢⎥⎣⎦23a π=【例6.17】求椭圆渐趋线()2233222cos ,sin c c x t y t c a b a b===-所围面积. 解 所求面积为223324sin cos c c S t t dt b a π'⎛⎫= ⎪⎝⎭⎰22322034sin cos sin c c t t tdt b aπ=⎰4422012sin (1sin )c t t dt abπ=--⎰438c abπ=.(3)极坐标情形【例6.18】求曲线2(2cos )r a θ=+所围成图形(见图6.7)的面积. 解 所求面积为()201222cos 2S a d πθθ=⋅+⎡⎤⎣⎦⎰ ()220444cos cos a d πθθθ=++⎰201cos 2444cos 2a d πθθθ+⎛⎫=++ ⎪⎝⎭⎰209sin 244sin 24a πθθθ⎡⎤=++⎢⎥⎣⎦ 218a π=【例6.19】 求心脏线1cos r θ=+与圆3cos r θ=公共部分(见图6.8)的面积. 解 由3cos 1cos θθ=+得交点坐标为3,23π⎛⎫± ⎪⎝⎭,()2232031121cos (3cos )22S d d πππθθθθ⎡⎤=++⎢⎥⎣⎦⎰⎰54π=. 【例6.20】 求由双纽线()()222222x ya x y +=-所围成且在圆周22212x y a +=内部的图形(见图6.9)的面积.解将r =代入方程22cos2r a θ=中得6πθ=.令0r =代入22cos 2r a θ=中得4πθ=,故 226410611cos 222A d a d πππθθθ=+⎰⎰ 224611sin 22264a a πππθ=⋅⋅+2(633)24a π=+-, 214(66a A A π∴==+-.【例6.21】求由曲线2cos2r r θθ==及所围成的图形的公共部分(见图6.10)的面积.解 解方程组2cos 2r r θθ⎧=⎪⎨=⎪⎩,得两曲线的交点坐标为26π⎛⎫ ⎪ ⎪⎝⎭. 所求的面积为1r =+图 6.9)2646112cos222S d dπππθθθθ=+⎰⎰[]64061112sin2sin2242πππθθθ⎡⎤=-+⎢⎥⎣⎦1626ππ=+=.2.体积的计算(1)旋转体的体积【例6.22】将抛物线24y ax=及直线x x=()x>所围成的图形绕x轴旋转,计算所得的旋转抛物体的体积.解()2,dV f x dxπ=其中()f x=所求体积()00222002x xV f x dx dx axπππ===⎰⎰.【例6.23】求曲线22,0y x x y=-=所围图形分别绕ox轴,oy轴旋转所成旋转体的体积.解所求体积为()22216215xV x x dxππ=-=⎰;()228223yV x x x dxππ=-=⎰。
3.4定积分的计算(二)、应用

简证: F ( x )是 f ( x )的一个原函数,则 设
b
a
f ( x )dx F (b) F (a )
又 F ( ( t )) f ( (t )) (t )
( t )dt F ( ( t )) F ( ( )) F ( ( )) f ( ( t ))
3,
1
令 若作如下运算: x t , 2xdx dt , dx
2
1 2 t
dt ,
于是
2
1
x dx 1
2
4
1 tdt 1 4 tdt t 3 2 t 2 1
2
3 4 2 1
7 . 3
这显然是错误的,原因在于 x t不是单值的.
3.4.3 定积分的分部积分法
a a
0 f ( x )dx a 2 0 f ( x )dx
当 f ( x ) 为奇函数 当 f ( x ) 为偶函数
例4 解
计算
I
2 x 2
2
4 x 2 dx.
x 2 2
2 2 2
4 x 2 dx
2 2
x 4 x dx 2
a
udv vdu
b b a a
b
a
udv uv vdu 分部积分公式
a a
b
b
例5 解
计算
2
1
x ln xdx .
2
1
1 2 x ln xdx ln xd ( x 2 ) 2 1
1 2 1 2 2 1 x ln x x dx 2 2 1 x 1
定积分的四则运算公式

定积分的四则运算公式定积分是微积分中的一个重要概念,而定积分的四则运算公式则像是我们在数学海洋中航行的有力工具。
先来说说定积分的加法运算公式。
假设函数 f(x) 和 g(x) 在区间 [a, b] 上可积,那么它们的定积分之和就等于这两个函数相加之后的定积分,即∫(a 到b) [f(x) + g(x)]dx = ∫(a 到b) f(x)dx + ∫(a 到 b) g(x)dx 。
就像上次我给学生们讲这个知识点的时候,我拿了一个装着不同颜色糖果的盒子举例。
假设盒子里红色糖果的数量与位置可以用函数 f(x) 表示,蓝色糖果的数量与位置用函数 g(x) 表示。
那么整个盒子里糖果的总数,就相当于把红色糖果和蓝色糖果分别计算数量然后加起来,这就和定积分的加法运算一个道理。
再看定积分的减法运算公式。
同样地,如果函数 f(x) 和 g(x) 在区间[a, b] 上可积,那么它们的定积分之差就等于这两个函数相减之后的定积分,即∫(a 到 b) [f(x) - g(x)]dx = ∫(a 到 b) f(x)dx - ∫(a 到 b) g(x)dx 。
这就好比是两个班的同学参加考试,一班同学的平均成绩用 f(x) 表示,二班同学的平均成绩用 g(x) ,那么一班比二班平均成绩高多少,就是用一班的平均成绩减去二班的平均成绩,和定积分的减法运算如出一辙。
接着是定积分的数乘运算公式。
若函数 f(x) 在区间 [a, b] 上可积,k 为常数,那么 k 乘以 f(x) 的定积分就等于 k 乘以 f(x) 的定积分,即∫(a到b) kf(x)dx = k∫(a 到 b) f(x)dx 。
比如说,一个工人每天能生产 f(x) 个零件,工资按件计算,某天老板决定给他的工资加倍,那这天他的总收入就是原来的两倍,这就类似于定积分的数乘运算。
最后是定积分的乘法运算公式。
这个相对复杂一些,但我们可以通过具体的例子来理解。
假设函数 f(x) 和 g(x) 在区间 [a, b] 上可积,那么它们的乘积的定积分一般不能简单地表示为两个定积分的乘积。
定积分公式大全24个

定积分公式大全24个1.基本积分公式:∫ x^n dx = (x^(n+1))/(n+1) + C, 其中n≠-1∫ 1/x dx = ln,x, + C∫ e^x dx = e^x + C∫ a^x dx = (a^x)/ln(a) + C,其中a为正实数且不等于1∫ sin(x) dx = -cos(x) + C∫ cos(x) dx = sin(x) + C∫ sec^2(x) dx = tan(x) + C∫ csc^2(x) dx = -cot(x) + C∫ sec(x)tan(x) dx = sec(x) + C∫ csc(x)cot(x) dx = -csc(x) + C2.反常积分公式:∫ 1/x dx = ln,x, + C, 其中x取区间(-∞, 0)或(0, +∞)∫ e^x dx = e^x + C, 区间为(-∞, +∞)∫ a^x dx = (a^x)/ln(a) + C,其中a为正实数且不等于1,区间为(-∞, +∞)∫ sin(x) dx = -cos(x) + C, 区间为(-∞, +∞)∫ cos(x) dx = sin(x) + C,区间为(-∞, +∞)3.分部积分法公式:∫ u dv = uv - ∫ v du,其中u, v是关于x的函数4.和差积分公式:∫ (f(x) ± g(x)) dx = ∫ f(x) dx ± ∫ g(x) dx5.一些特殊函数的积分:∫ e^(x^2) dx = √π*erf(x)/2 + C∫ ln(x) dx = x(ln(x) - 1) + C∫ sin^2(x) dx = (x - sin(x)cos(x))/2 + C6.换元法公式:∫ f(g(x))g'(x) dx = ∫ f(u) du,其中u=g(x)7.可以通过递推关系求解的积分:∫ sin^n(x) dx = -1/n * sin^(n-1)(x) * cos(x) + (n-1)/n * ∫ sin^(n-2)(x) dx∫ cos^n(x) dx = 1/n * cos^(n-1)(x) * sin(x) + (n-1)/n * ∫ cos^(n-2)(x) dx8.积分的对称性:∫ f(x) dx = ∫ f(a+b-x) dx,其中a和b为常数以上是定积分的一些基本公式。
定积分的应用(10

定积分的应用(10定积分是微积分中的一个重要概念。
它表示在一定区间内,函数曲线与 x 轴之间的面积,也可以理解为变化率的累加。
定积分的应用非常广泛,下文将介绍其中的十个应用。
一、求物体在一定时间内的位移我们知道,物体在做匀加速运动时,其位移可以用位移公式S=vt+1/2at² 来计算。
如果物体的运动速度是变化的,我们可以将其速度函数 v(t) 求出,然后将其积分得到位移函数 S(t),再在一定时间段内求出 S(t) 的定积分即可得到物体在该时间段内的位移。
二、计算概率密度函数下的概率概率密度函数也是一个函数,其定义为:在一个无限小区间内,事件发生的概率与该区间长度的比值。
在一定范围内,概率密度函数曲线下的面积等于该范围内事件发生的概率。
因此,我们可以通过计算概率密度函数的定积分来获得某个事件发生的概率。
三、计算质心位置质心是物体的一个重要物理概念,其位置定义为将物体划分成若干小的无限小质量体积元,在这些质量体积元上求平均位置所得的点。
计算出物体每个质量体积元的质心位置,然后按质量将它们加权平均,就可以得到整个物体的质心位置。
计算质心位置的过程实质上就是对质量体积元的轴心距进行加权平均,这就是定积分的应用。
四、计算曲线长度我们可以用定积分来计算一个曲线的长度。
将曲线划分成许多小段,每个小段都近似为一条直线段,利用勾股定理计算它们的长度之和,然后取极限即可得到曲线的长度。
五、计算旋转体积旋转体积的计算方法就是将一个平面图形绕某个轴线旋转所形成的体积。
可以用定积分来计算旋转体积,其基本思想就是把旋转体积看作是由许多小的圆柱体构成的,计算出每个小圆柱的体积之和即可得到整个旋转体积。
六、计算弧度在物理学和天文学中,我们往往需要计算弧度。
弧度是一个角度的度量方式,它表示弧长与半径之比。
对于一个圆,一周的弧长就是圆的周长,因此圆的一周弧度为2π 弧度。
如果我们知道了一个圆弧所对应的角度度数,就可以通过简单的定积分计算出它的弧度。
2021考研高等数学重点公式详解-定积分及其应用

f 此时也称反常积分J:J(x灿收敛,否则称反常积分 J(x讪发散
J: 3)设函数 f(x) 在[a,小 (c,b] 上连续,出 f(x) =oo,如果反常积分 J(x'ylx 和
I: J: f(x灿都收敛,则称f:J<抽+ f(树为函数/(x)刮风b] 上的反常积分,即
= (3)曲线方程为极坐标方程r =r(θ),α豆θ β,则
J:2 S倒 = 矿(O)sin o.Jr2 (的+r'2
4.平丽曲线的弧长 〈数学-,二〉
r: F+λ (1)曲线方程 y = f(x) , aSxSb ,则S=
ι°? d
(2)曲线方程 x=x(y), c 豆 y!::d ,则s= L
dx.
r 2)类似地,设函数f(x) 定义在(咽,b]上连续,取 t<b ,如果但 f(x讪存在,则
称此极限为函数f(x) 在(-oo,b]上的反常积分,即
f (!(抽 . = 坐立 1c抽1
( ( 此时也称反常积分 f(x灿收敛,否则称反常积分 f(x)dx发散
i- ( 叫函数/(机义在(-oo,+oo)上连续,如果反常积分 f(树和 f(x)dx都收敛,
豆豆?一一一 称为函数 f(x) 在区间 [a,b]上的平均值. a
性服6如果 f(x) 为奇函数时,汇/(柏=0;
如果f(均为奇函数时,巳 f(对此= 2J:f(x)耐
性质7如果f(x) 是以T为周期的周期函数,则有
J: T
r /(X)命= f(x)dx.
nT
r f(x)由=nJ: /(x)
三、积分上限函数 (1)积分上限函数定义
I 则有 J:1<抽 =
更广泛的定积分公式计算及其应用

更广泛的定积分公式计算及其应用
定积分是一类数学运算,用于求解函数的积分。
它最常见的形式为:∫f(x)dx 其中,f(x)表示需要积分的函数,x表示变量,dx表示对x的微小增量。
定积分的计算方法是将x从a到b之间的连续区间离散成多个部分,然后逐步计算每个部分的积分和,最后得到定积分的值。
定积分可以用于计算一类特殊形式的函数,如曲线面积、体积和动能等,还可以应用于不同科学领域,如物理、经济学等。
例如: 1. 动能定律:K = 1/2mv2 = ∫Fdx 2. 电场力定律:F = qE =
∫E·dl 3. 经济学中的边际成本:MC = dC/dQ = ∫CdQ。
定积分的计算与应用

奇偶性:如果f(x)是偶函数,那么∫(-a,a)f(x)dx=2∫(0,a)f(x)dx;如果f(x) 是奇函数,那么∫(-a,a)f(x)dx=0。
定积分的几何意义
定积分表示曲线与x轴所夹的面积 定积分表示函数图像在某一区间上的高度 定积分的值与被积函数和积分的区间有关 定积分的值可以通过微积分基本定理计算
应用:用于求解复杂的定积分问 题,特别是被积函数为幂函数与 三角函数或指数函数的乘积时
注意事项:选择适当的u和v以简 化计算
有理函数的积分
定义:有理函数是指多项式之比,其积分是有理函数的线性组合
计算方法:通过部分分式分解,将有理函数分解为简单分式之和,再分别积分
注意事项:在计算过程中需要注意分母的零点,避免出现无穷大或未定义的积分结果
应用:有理函数的积分在数学、物理等领域有着广泛的应用,如求解微分方程、计算面 积和体积等
03 定积分的应用
面积与体积的计算
计算平面图形的面积
计算立体的体积
计算旋转体的体积
计算曲线的长度
物理应用:引力、力矩、线密度
计算天体之间的引力 分析旋转体的角动量 计算细杆的线密度 确定物体的重心位置
经济学应用:成本、收益、利润
定义:将积分区间分成若干小区间,在每个小区间上取一个代表点,再求和近似计算定积分 公式:∫(0,1)f(x)dx≈∑(i=0,n-1)Δxi·f(xi) 应用:适用于被积函数在积分区间上变化不大的情况,可以提高计算精度 注意事项:选取代表点时要尽量均匀分布,且小区间的长度要足够小
自适应积分方法
定义:根据积分区间的大小和函数的变化情况,自动选择合适的积分方法进行计算的方 法。
法
适用范围:被 积函数具有无
一换元积分法二常用的定积分公式及应用

1ex1dx 21dx
0
1x
01ex1dx1121xdx
ex 11 0ln x1 211 eln 2
二、常用的定积分公式及应用
1.设 fx 在 a,a上连续,则
a afx d x 0 afx fx dx………①
(1)若 fx为偶函数,fx f x ,
a fxdx 2afxdx
a
0
………②
x1, t , 2
1
0
1 x2d x 0 2
1 s2 itn ctodst
2
0
cos2
tdt
12021co2stdt
1 20 2d t0 2co2ts1 2d2t
12t
12sin2t02
4
注 第一步是采用的换元(不定积分第二类换
元法),换元的同时必须换限。在计算 2 0
cos2tdt
时,我们采用了凑微分法,没有写出新变量,
解 0 sx i s n 3 i x d n 0 x sx ic n 2 x o ds x
0 sixncoxsdx
2 0
sixc no xd s xsix n co x dsx
2
2 0
sixd nsixn
sixd nsixn
2
32sin23x02
32sin23x
4 3
2
例4
设
f x 11x, x 0,
第三节 定积分的换元积分
一、换元积分法 二、常用的定积分公式及应用
一、换元积分法
1.定理 设函数 fx在 a,b上连续;函数 t在 ,(或 ,)上有连续导数; 当 t在 t在 ,(或 ,)上变化时, x在a,b上变化,且 a,b,
则有
定积分求导计算公式

定积分求导计算公式定积分求导是微积分中的重要概念,它是求取函数导数的一种方法。
在本文中,我们将介绍定积分求导的计算公式及其应用。
定积分求导的计算公式可以通过积分定义和导数的定义相结合得到。
首先,我们回顾一下导数的定义:对于函数f(x),如果存在极限lim(h→0) [f(x+h)-f(x)]/h,则称该极限为f(x)在点x处的导数,记作f'(x)。
现在,我们考虑定积分的定义:对于函数f(x),如果存在极限lim(n→∞) Σ[f(xi*)Δxi],其中Δxi是区间[xi-1, xi]的长度,xi*是该区间上的某个点,则称该极限为函数f(x)在区间[a,b]上的定积分,记作∫[a,b] f(x)dx。
根据导数的定义,我们可以得到定积分求导的计算公式。
设函数F(x)是f(x)的一个原函数,即F'(x)=f(x)。
根据导数的链式法则,我们有:d/dx ∫[a,x] f(t)dt = d/dx [F(x) - F(a)]= F'(x) - F'(a)= f(x) - f(a)这就是定积分求导的基本公式。
根据这个公式,我们可以通过已知的定积分来计算函数的导数。
接下来,我们将通过一个具体的例子来说明定积分求导的应用。
考虑函数f(x) = ∫[0,x] e^t dt,我们要求函数f(x)的导数。
根据定积分求导的公式,我们有:f'(x) = d/dx ∫[0,x] e^t dt= e^x - e^0= e^x - 1因此,函数f(x)的导数为f'(x) = e^x - 1。
这个结果可以通过直接对函数f(x)求导得到的结果验证。
我们知道,e^x的导数为e^x,常数函数1的导数为0,因此e^x - 1是f(x)的导数。
定积分求导的计算公式在实际问题中有着广泛的应用。
例如,在物理学中,速度是位移对时间的导数,而位移又可以通过速度的定积分来计算。
因此,通过定积分求导的方法,我们可以得到物体的速度。
定积分的计算方法与技巧的扩展和深化

定积分的计算方法与技巧的扩展和深化在数学中,定积分是一种非常重要的概念,它在各个领域都有广泛的应用。
对于定积分的计算,有许多方法和技巧可以帮助我们简化运算并且准确求解。
本文将介绍一些常用的计算方法,并探讨如何扩展和深化这些技巧。
一、基本的计算方法定积分的计算可以通过积分区间的划分和求和来实现。
我们可以将积分区间划分为若干小区间,然后在每个小区间内选取一个代表点进行函数值的求解。
接着,我们将每个小区间内的函数值与区间长度相乘,并将这些乘积相加,就可以得到定积分的近似值。
当然,为了得到更精确的结果,我们可以将积分区间划分得更细,并选取更多的代表点进行计算。
这样,通过逐步增加代表点的数量,我们可以逼近定积分的真实值。
当划分的小区间数量足够多时,我们可以得到一个非常接近定积分的近似值。
二、常见的计算技巧1. 基本函数的积分公式对于一些常见的函数,它们的积分有一些已知的公式,可以帮助我们快速计算定积分。
例如,对于多项式函数、指数函数、三角函数和对数函数等,它们的积分公式都是已知的,可以直接使用。
2. 替代变量法有时候,我们可以通过进行变量替换,将原有的积分问题转化为一个更简单的积分问题。
例如,当我们面对根号下存在二次项的函数时,我们可以通过令变量等于二次项的系数与根号外的部分,从而将问题转化为一个更简单的形式。
3. 分部积分法对于一些复杂的函数积分,我们可以使用分部积分法来简化计算。
分部积分法是积分学中的一种重要技巧,它可以将积分问题转化为一个更易求解的问题。
4. 奇偶函数的性质对于一些具有奇偶性质的函数,我们可以利用这些性质来简化定积分的计算。
例如,奇函数的积分在对称轴两侧的面积相等,而偶函数的积分在对称轴两侧的面积正好抵消,因此我们可以根据函数的奇偶性来减少计算量。
三、方法的扩展和深化除了上述常用的技巧和方法之外,我们还可以进一步扩展和深化这些计算方法,以应对更加复杂的积分计算问题。
1. 数值积分方法数值积分方法是一种通过数值计算的方式来求解定积分的方法。
2023年最新的定积分公式6篇

2023年最新的定积分公式6篇一、变上限函数设函数在区间上连续,并且设x为上的任一点,于是,在区间上的定积分为这里x既是积分上限,又是积分变量,由于定积分与积分变量无关,故可将此改为如果上限x在区间上任意变动,则对于每一个取定的x值,定积分有一个确定值与之对应,所以定积分在上定义了一个以x为自变量的函数,我们把称为函数在区间上变上限函数记为从几何上看,也很显然。
因为X是上一个动点,从而以线段为底的曲边梯形的面积,必然随着底数端点的变化而变化,所以阴影部分的面积是端点x的函数(见图5-10)定积分计算公式利用定义计算定积分的值是十分麻烦的,有时甚至无法计算。
因此,必须寻求计算定积分的简便方法。
我们知道:如果物体以速度作直线运动,那么在时间区间上所经过的路程s 为另一方面,如果物体经过的路程s是时间t的函数,那么物体从t=a到t=b 所经过的路程应该是(见图5-11)即由导数的物理意义可知:即是一个原函数,因此,为了求出定积分,应先求出被积函数的原函数,再求在区间上的增量即可。
如果抛开上面物理意义,便可得出计算定积分的一般方法:设函数在闭区间上连续,是的一个原函数,即,则这个公式叫做牛顿-莱布尼兹公式。
为了使用方便,将公式写成牛顿-莱布尼兹公式通常也叫做微积分基本公式。
它表示一个函数定积分等于这个函数的原函数在积分上、下限处函数值之差。
它揭示了定积分和不定积分的内在联系,提供了计算定积分有效而简便的方法,从而使定积分得到了广泛的应用。
例1 计算因为是的一个原函数所以例 2 求曲线和直线x=0、x= 及y=0所围成图形面积A(5-12)解这个图形的面积为二、定积分的性质设、在相应区间上连续,利用前面学过的知识,可以得到定积分以下几个简单性质:性质1 被积函数的常数因子可以提到定积分符号前面,即(A为常数)性质2 函数的代数和的定积分等于它们的定积分的代数和,即这个性质对有限个函数代数和也成立。
性质3 积分的上、下限对换则定积分变号,即以上性质用定积分的定义及牛顿-莱布尼兹公式均可证明,此处证明从略。
定积分的计算方法

则F[ (t )] 是 f [ (t )] (t )的一个原函数, 从而
f [ ( t )] ( t )dt F [ ( t )]
由此可得
F [ ( )] F [ ( )] F (b) F (a )
b
a
f ( x )dx f [ (t )] (t )dt
证
b
a
f ( x )dx f [ (t )] (t )dt
设F(x)是ƒ(x)的一个原函数, 则
b
a
f ( x )dx F (b) F (a )
因为当 x ( t ) 时, 有 F ( x) F (t ) , 则有复合函数求导法 则, 有
d F [ ( t )] F [ ( t )] ( t ) f [ ( t )] ( t ) dt
§ 定积分的计算方法
一. 换元积分法 二. 分部积分法
由牛顿—莱布尼茨公式知: 计算定积分
b
a
f ( x )dx 的关键在
于求出ƒ(x)在[a, b]上的一个原函数F(x); 从而不定积分的换元 积分法和分部积分法在求定积分时仍适用. 本节讨论在一定 条件下, 如何利用换元积分法和分部积分法计算定积分.
1 2
2
1
1 ln 2 2
注 如果不明确写出新的变量, 则定积分的上、下限就不需要 变更. 如
1 x 1 1 2 2 ln 1 x dx d( x 1) 2 0 1 x2 0 2 2 1 x
1
1
1
0
1 ln 2 2
例4
计算 I 0 sin3 x sin5 xdx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d i f f e r s f r o m Ne wt o n - Le i b n i z f o r mu l a , a n d i l l us t r a t e s he t f o mu r l a me ho t d o f us e .
Ke y wo r ds:La p l a c e t r a n s f o m r wi h t p a r a me t e r s ;d e ini f t e i n t e g r a l ;n e w f o m u r l a
函 数, F ( s , ) 称为象函 数, 并记为
( 1 )
( f ) 在( — o o , + o 。 ) 内有定义 ,并 且可 定理 1 设 函数 厂
.
为 函数 , ( f ) 的含参变量 的拉普 拉斯变换 。, ( f ) 称为原
积 ,则有
厂 ( f ) , 】 = F ( s , ) ,
第 4期
符 云锦
定积分计算的新公式及其应用
1 3
s i nAn
广
e 。
f e o ( ) d 卜f 『 e ) f ( t ) d t =
注意
F ( O , 口 ) 一 F( O , 6 ) 。 定理 1 的公式 ( 2)表 明: , ( f ) 在 区间 , b 】
l F ( s , ) l : / ( f ) 。
注意 式 ( 1 )中,参数 和变量 均可为复数 。
文献 【 1 】 中还给 出了含参 变量 的拉 普拉斯 变换 的
存 在性 和基本性 质 ;还利 用含参 变量 的拉 普拉斯 变
f f ( t ) d t — l f ( t ) d t
第2 8 卷第4 期
2 0 1 4年 7月
湖
南
工
业
大
学 学
报
VO 1 . 2 8 No . 4 J u l y 2 0 1 4
J o u ma l o f Hu n a n Un i v e r s i t y o f T e c h n o l o g y
其逆 变换 记作
f ] f ( t ) d t = =( F ( 0 , ) 一 F ( O , 6 ) ,
象 函数 的 函数值 。
证 根据 定积 分性质 ,有 ) ) d , + 厂 ( f )
( 2 )
其中F ( O , 日 ) 和F ( 0 , 6 ) 是取 s = 0 ,参变量2 = a 与2 = b 时的
 ̄ l J F( O , ) :— x c — o s _பைடு நூலகம்A n
-
—
l +丁 c 。
再 由公 式 ( 2)得
上的定积分l f ( t ) d t , 等于s = 0 , A = a 与 = b 时, , ( f ) 的
定义 1 设函数 在区间【 , + o o ) 上有定义,如果
含 参变 量 , 的 无穷积分I e - S ( t - x ) f ( t ) d t 对 的 某一取
值范 围是 收敛 的 ,则称 无穷 积分
1 计算 定 积分 的新公 式
F ( s , ) = f _ e - S ( f _ ) f ( t ) d t
F u Y u n j i n
( L i a n g l i n S c h o o l Di s t r i c t ,F e n g h u a n g Hu n a n 4 1 6 2 1 1 ,C h i n a )
Abs t r a c t :By u s i n g La p l a c e t r a ns f o r m wi t h pa r a me t e r s , d e r i v e s a n e w f o m u r l a f o r d e in f i t e i n t e g r a l c lc a u l a t i o n wh i c h
收稿 日期 :2 0 1 4 - 0 3 - 1 7 作者简介 :符云锦 ( 1 9 8 4 一 ) ,男 ,湖南泸溪人 ,湖南凤凰县两林学 区教师 ,主要研究方 向为初 等数学 ,分析学及其应用 ,微
分方程 ,教育理论及其应用 ,E . ma i l :w s a s w4 2 6 4 7 3 1 1 2 3 @1 6 3 . c o m
并举例 说 明该公 式使 用方 法 。
关键 词 :合 参 变量的拉 普拉 斯 变换 ;定积 分 ;新公 式 中图分类号 : O1 7 2 . 2 文献标志码 : A 文章编号 :1 6 7 3 - 9 8 3 3 ( 2 0 1 4 ) 0 4 — 0 0 1 2 — 0 2
A Ne w F o r mu l a f o r De i f n i t e I n t e g r a l Ca lc u l a t i o n a n d I t s Ap p l i c a t i o n
0 引 言
文 献[ 1 】 给 出了如下含 参变量 的拉普拉 斯变换 的
定义 :
换 ,推 导出了一些常用 的含参 变量 的拉普 拉斯变换
的公式 。 本文 利用 含参 变量 的拉普 拉斯 变换 ,推导 出计
算定 积分 的 1 个 新公 式 ,并 举例 说 明如何 用该公 式 来计 算 定积 分 。
d o i : 1 0 . 3 9 6 9  ̄ . i s s n . 1 6 7 3 - 9 8 3 3 . 2 0 1 4 . 0 4 . 0 0 3
定积分计算的新公 式及其应用
符 云 锦
( 凤凰县 两林学 区,湖南 凤凰 4 1 6 2 1 1 )
摘
要 :利 用合参 变量的拉 普拉斯 变换 ,推 导 出不 同于牛顿 一莱布尼 茨公 式的计 算定积分 的 1 个新公 式 ,
