重庆大学结构力学(二)资料
结构力学2ppt课件

G G
E
F
E
F
C
C
D
D
A
B
A
B
注:二元体遇到,可以先去掉。
例2:分析图示体系
解:
固定一个刚片的 装配方式。
AB部分与基础固 结在一起,可视为一
扩大的刚片Ⅰ。CD视 为刚片Ⅱ,Ⅰ、Ⅱ用 链杆1,2,3联结。
A
B 1C
ⅡD
Ⅰ
2
3
结论:几何不变,无多 余约束。
.
例3:分析图示体系
•
不变。如有多余约束,体系几何可变。
• ③ 、W<0,或V<0,体系有多余约束,是否
•
几何不变则需分析。
说明:
W≤0,是体系几何不变的必要条件,非充分条件。
体系的几何组成,不仅与约束的数量有关,而且与 约束的布置有关。
.
•说明:
• (1)、W≤0
是体系几何不变的 必要条件,非充分 条件。 • (2)、体系的 几何组成(是否几 何不变)不仅与约 束的数量有关,而 且与约束布置有关。
与地面相连接只限制了两个自由度有一根链杆是多余约束多余联如果在一个体系中增加一个约束体系的自由度因此减少此约束称为必要约束或非多余约束
第二章
结构的几何构造分析
(机动分析) ( 组成分析)
.
§2-1几何构造分析的几个概念
• 一.体系——杆件+ 约束(联系)
• 杆件:不考虑材料应 变,视作刚体,平面刚 体称为“刚片”。
.
W=2×6-9-3=0
体系几何不变
W=2×6-9-3=0
体系几何可变
习题课I:平面杆件体系的几何构造分析
• 重点:掌握用基本规律分析体系几 何组成的方法。 • 要求: • 1、明确几何构造分析的目的和计算 步骤。 • 2、掌握用基本规律分析体系的几何 构成。 • 3、了解结构的组成顺序和特点。
结构力学课后习题答案重庆大学
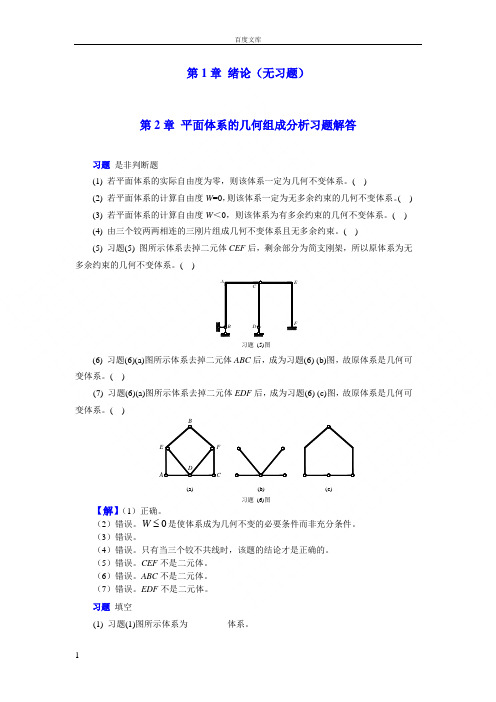
第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 (5)图(6) 习题(6)(a)图所示体系去掉二元体ABC 后,成为习题(6) (b)图,故原体系是几何可变体系。
( )(7) 习题(6)(a)图所示体系去掉二元体EDF 后,成为习题(6) (c)图,故原体系是几何可变体系。
( )(a)(b)(c)D习题 (6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题 填空(1) 习题(1)图所示体系为_________体系。
习题(1)图(2) 习题(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题(3)图(4) 习题(4)图所示体系的多余约束个数为___________。
习题(4)图(5) 习题(5)图所示体系的多余约束个数为___________。
习题(5)图(6) 习题(6)图所示体系为_________体系,有_________个多余约束。
习题(6)图(7) 习题(7)图所示体系为_________体系,有_________个多余约束。
《结构力学》课后习题答案__重庆大学出版社

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
重庆大学 工程力学2

例2
在刚体上作用着四个汇交力,它们在坐标轴 上的投影如下表所示,试求这四个力的合力的大 小和方向。
F1 Fx Fy 1 10 F2 2 15 F3 0 -5 F4 2 10 单位 kN kN
Fz
3
4
1
-2
kN
解: 由上表得
Fx 1 kN 2 kN 0 kN 2 kN 5 kN, Fy 10 kN 15 kN 5 kN 10 kN 30 kN, Fz 3 kN 4 kN 1 kN 2 kN 6 kN
力系可合成一个合力偶,其矩等于原力系对于简化中心 的主矩MO 。此时主矩与简化中心O的位置无关。
0, (2) FR 0, (3) FR
MO 0 MO 0 MO (a) FR
力系可合成为一个合力,合力的作用线过简化中心O,大小 和方向与主矢相同。
此时分三种情况讨论。
可进一步简化成一合力
i 1
n
力多边形
力多边形规则
各力矢与合力矢构成的多边形称为力多边形。 用力多边形求合力的作图规则称为力的多边形规则。 力多边形中表示合力矢量的边称为力多边形的封闭边。
结论:平面汇交力系可简化为一合力,其合力的 大小与方向等于各分力的矢量和(几何和),合力的 作用线通过汇交点。 用矢量式表示为:
F R F 1 F 2 ...F n
n
合力矢FR的大小和方向余弦为
大小
FR Fx2 Fy2 Fz2 ( Fxi ) ( Fyi ) ( Fzi )
2 2 2
方向余弦
Fx Fxi cos( FR , i ) FR FR Fy Fyi cos( FR , j ) FR FR Fz Fzi cos( FR , k ) FR FR
结构力学2_张金生教材配套课件(精品教程)

方法1: 若基础与其它部分三杆相连,去掉基础只分析其它彭部怀分林-2
方法2: 利用规则将小刚片变成大刚片. 方法3: 将只有两个铰与其它部分相连的刚片看成链杆. 方法4: 去掉二元体.
例6: 对图示体系作几何组成分析
解: 该体系为无多余约束的几何不变体系. 方法2: 利用规则将小刚片变成大刚片.
§1. 几何组成分析
作业: 1-2 (d)试分析图示体系的几何组成 依次去掉二元体. 几何常变体系
§1. 几何组成分析
作业: 1-1 (b)试计算图示体系的计算自由度
解: W =8×3−11×2−3= −1 或: W =1×3+5×2−2×2−10= −1
由结果不能判定其是否能作为结构
§1. 几何组成分析
一. 三刚片规则 三刚片以不在一条直线上的三铰两两相联,构
成无多余约束的几何不变体系.
瞬变体系
N
=
P 2 Sin α
§1. 几何组成分析
§1-1 基本概念 §1-2 无多余约束的几何不变体系的组成规则 §1-3 几何组成分析举例
例1: 对图示体系作几何组成分析
解: 三刚片三铰相连,三铰不共线,所以该体系为无多余约束 的几何不变体系.
在一个体系上加减二元体不影响原体系的机动性质.
§1. 几何组成分析
§1-1 基本概念
一. 几何不变体系 几何可变体系 二. 刚片 几何形状不能变化的平面物体
三. 自由度 确定体系位置所需的独立坐标数
点
刚
的 自
几何不变体系的自由片 自度一定等于零
由 几何可变体系的自由由度一定大于零
度
度
§1. 几何组成分析
§1-2 无多余约束的几何不变体系的组成规则
结构力学(二) ( 复习资料汇总 )

第1次作业(结构力学二)一、单项选择题(本大题共40分,共 20 小题,每小题 2 分)1. 位移法的基本结构是( )A. 静定刚架;B. 单跨静定梁的组合体;C. 单跨超静定梁的组合体D. 铰结体系2. :以下关于影响线的说法不正确的一项为( )A. 影响线指的是单位力在结构上移动时所引起的结构的某一内力(或反力)变化规律的图形B. 利用影响线可以求结构在固定荷载作用下某个截面的内力C. 利用影响线可以求结构某个截面内力的最不利荷载位置D. 影响线的横坐标是截面位置,纵坐标为此截面位置处的截面内力值3.A. B. C. D. 仅由平衡条件不能确定4. 不计杆的分布质量,图示体系的动力自由度为( )A. 1;B. 2;C. 3;D. 45. 用力法计算超静定结构时,其基本未知量为A. 杆端弯矩;B. 结构角位移;C. 结点线位移;D. 多余未知力6. 单元坐标转换矩阵是() A. 奇异矩阵 B. 对称三对角矩阵 C. 对称非奇异矩阵 D. 正交矩阵7. 位移法的基本未知量包括()A. 独立的角位移B. 独立的线位移C. 独立未知的结点角位移和线位移D. 结点位移8. 图乘法计算位移的公式中( )A. A和yC 可取自任何图形B. A和yC必须取自直线图形C. 仅要求A必须取自直线图形D. 仅要求yC必须取自直线图形9. 已知材料屈服极限 =300MPa,结构截面形状如图所示,则极限弯矩Mu=()A. 20kN•mB. 25kN•mC. 30kN•mD. 35kN•m.10. 整体坐标系下单元刚度矩阵与下面的哪一个因素无关A. 局部坐标与整体坐标的选取B. 结构的约束信息C. 单元的几何参数D. 杆端位移与杆端力之间的变换关系11. 欲减小图示结构的自振频率,可采取的措施有()A. 减小质量mB. 增大刚度EIC. 将B支座改为固定端D. 去掉B支座12. 图(b)为图(a)所示结构MK影响线,利用该影响线求得图(a)所示固定荷载作用下的MK值为()A. 4kN•mB. 2kN•mC. -2kN•mD. -4kN•m13. 图示为三自由度体系的振型,其相应的频率是ωa 、ωb、ωc,它们之间的大小关系应是( )A. B. C. D.14. 图(a)所示一组移动荷载作用在图(b)所示的梁上,则C截面弯矩的最不利位置为()A. P1作用在C点上 B. P2作用在C点上 C. P3作用在C点上 D. P3作用在B点上15. 平面杆件自由单元(一般单元)的单元刚(劲)度矩阵是( )A. 非对称、奇异矩阵B. 对称、奇异矩阵C. 对称、非奇异矩阵D. 非对称、非奇异矩阵16. 对称结构在反对称荷载作用下,内力图中为正对称的是( )A. 弯矩图B. 剪力图C. 轴力图D. 弯矩图、剪力图和轴力图17. 由于温度改变,静定结构() A. 会产生内力,也会产生位移; B. 不产生内力,会产生位移; C. 会产生内力,不产生位移; D. 不产生内力,也不产生位移。
工程力学(二)重庆大学 练习题库及答案

1、图示体系是()。
•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系•
2、图示体系为()。
•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系•
•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系•
4、图示体系为()。
•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系
•
5、
图示结构的超静定次数为()。
•A、1
•B、2
•C、3
•
6、
设水平简支梁跨度为l,横截面C位于距左支座l/3处,则M C和F QC影响线在跨中的值分别为()。
•A、
l/9,1/3
•B、
l/6,1/2
•C、
l/9,1/2
•
7、(),都相当于解除了结构中的1个约束。
•A、去掉一根支杆或将固定支座变成活动铰支座
•B、断开一根链杆或去掉一个单铰结点
•C、将固定支座变成固定铰支座或者将固定支座变成定向支座
•
8、
力法步骤前四步的顺序是()。
设①代表步骤“列写基本方程”、②代表“确定基本体系”、③代表“确定超静定次数”、④代表“求解系数和自由项”。
•A、
①④②③
•B、
②①③④
•C、
③②①④
•
9、一个体系的计算自由度为-3,已知其有3个多余约束。
()
•A、该体系为几何可变体系
•B、该体系为无多余约束的几何不变体系
•C、该体系为有3个多余约束的几何不变体系
•
•A、常变体系。
1绪论,重庆大学,文国治版结构力学课件

11
土木工程专业系列教材—结构力学
出版社 科技分社 出版社 科技分社
2)计算简图的简化要点 ——应从以下几方面进行简化
(1) 结构体系的简化 ——如平面杆件结构 。 (2) 杆件的简化——不论是直杆或曲杆均可用其轴线(截面 形心的连线)表示。 (3) 结点的简化 ①刚结点:刚结点的特点是汇交于结点的各杆端之间不能 发生相对转动,各杆间可相互传递力和力矩。
29
土木工程专业系列教材
出版社 科技分社 出版社 科技分社
再见
30
3
土木工程指导性专业规范系列教材—结构力学
出版社 科技分社出版社 科
第1章 绪论
1.1 结构力学的研究对象和任务 1) 结构及其分类
建筑物或构筑物中承担荷载而起骨架作用的部分,或 其中的某些承重构件,都可称为结构。
南京长江大桥
上海金茂大厦(右)和国际金融中心(左)
4
土木工程专业系列教材—结构力学
18
土木工程专业系列教材—结构力学
出版社 科技分社 出版社 科技分社
4)结构计算简图举例
例1.1 图示为一根两端 搁在墙上的梁,其上 放一重物,现确定梁 的计算简图。
b /2 b l0 (a)
b /2 b
FP g
l (b)
19
土木工程专业系列教材—结构力学
出版社 科技分社 出版社 科技分社
例2:单层厂房的计算简图
屋架
柱
吊车梁 牛腿
基础
(c)
EA→∞
20
(d)
土木工程专业系列教材—结构力学
出版社 科技分社 出版社 科技分社
1.3
平面杆件结构的分类
结构的分类,实际上是指结构计算简图的分类。 1)按受力和变形特性分
结构力学2复习资料 重难点习题

2
y st
2 1 2 4 2
2
2
2
,
振幅:yp,最大静力位移 yst=F/k=F/mω2
3.形成结构的荷载列阵 { P }
(1)将各原始结点荷载集合进结构的荷载列阵 { P } ; (2)将各杆上荷载转化后,集合叠加进结构荷载列阵 { P } 。
4.解方程 [ K ]{ } P ,求出结点位移{Δ}(整体坐标系); (局部坐标系) 5.求杆端内力
(1)由定位向量确定各单元 ,并转换为
(5)弹簧和桁架杆不影响体系的自由度。
(4)单自由度体系的频率、周期的计算公式;振幅、相 位的算式和各种力的平衡关系;简谐荷载下纯受迫振动的 动力放大系数与频率比、阻尼比间的关系等等。这些基本 概念必须深刻理解、熟练掌握。 (5) 由于阻尼比一般很小,它对频率、周期的影响一般 可忽略。 (6)在共振区,阻尼的作用是不可忽略的。从能量角度 看,阻尼使能量耗散,当不希望有能量耗散时应减少阻尼, 而当希望尽可能使输入结构的能量减少时,应增大阻尼。
1
有阻尼的自由振动
k m
.. . 2 y 2 y y 0
,
c
2m
( 阻尼比damping
ratio )
y 设解为: (t ) Ce
i r
t
1)ξ<1(低阻尼)情况
特征方程为: 2 2 2 0 (characteristic ( ± 2 1 ) equation)
总
结
矩阵位移法的基本思路是:
(1) 先把结构离散成单元,进行单元分析,建立单元杆 端力与杆端位移之间的关系; (2)在单元分析的基础上,考虑结构的几何条件和平衡 条件,将这些离散单元组合成原来的结构,进行整体分析, 建立结构的结点力与结点位移之间的关系,即结构的总刚 度方程,进而求解结构的结点位移和单元杆端力。 在从单元分析到整体分析的计算过程中,全部采用矩 阵运算。
《结构力学(二)》复习题

一. 判断(每题2分, 共20分) 1. 图示杆AB 与CD 的EI ,l 相等,但A 端的劲度系数(转动刚度)AB S 大于C 端的劲度系数(转动刚度)CD S 。
( )2. 图示刚架可利用力矩分配法求解。
( )3. 梁的绝对最大弯矩表示在一定移动荷载作用下梁某一截面的最大弯矩( )4. 图示结构E Q 影响线的AC 段纵标不为零。
()5. 静定结构及超静定结构的内力影响线都是由直线组成。
()6. 图示梁的绝对最大弯矩发生在距支座A 6.625m 处。
( )7. 图示体系设为自振频率)可如下计算稳态动位移。
33max 27175,6961(/)st st y Pl Pl y y EI EI θω===-8. 体系的动力自由度与质点的个数不一定相等。
9. 单自由度体系如图,,欲使顶端产生水平位移,需加水平力,则体系的自振频率。
10. 结构刚度矩阵是对称矩阵,即有i j ji K K ,这可由位移互等定理得到证明。
11. 图a 对称结构可简化为图b 来计算。
( )12. 图示结构横梁无弯曲变形,故其上无弯矩。
( )13. 位移法未知量的数目与结构的超静定次数有关。
( )14. 位移法的典型方程与力法的典型方程一样,都是变形谐调方程。
( ) 15. 用位移法可以计算超静定结构,也可以计算静定结构。
( ) 16. 图b 为图a 用位移法求解时的基本体系和基本未知量,其位移法典型方程中的自由项,。
( )Z为水平横梁的水平位移,则图应如图b形状。
17.图示结构a用位移法求解时,基本未知量3()18.图示结构在荷载作用下的弯矩图形状是正确的。
( )19.力矩分配法中的分配系数、传递系数与外来因素(荷载、温度变化等)有关。
()20.力矩分配法仅适用于解无线位移结构。
()21.图示体系是几何不变体系。
22.图示体系是几何不变体系。
N为30kN。
()23.图示拱在荷载作用下,DE24.图示结构中的反力2H kN。
结构力学_张来仪_结构力学Ⅱ试卷及答案

重庆大学 结构力学Ⅱ 课程试卷2005 ~2006 学年 第 2 学期开课学院: 土木工程考试日期: 2006.4.23考试方式:考试时间: 120 分钟注:1.大标题用四号宋体、小标题及正文用小四号宋体;2.按A4纸缩小打印一、 是非判断题(每小题3分,共9分)1.图a 所示体系的自振周期大于图b 体系的自振周期。
( )2.用能量法计算无限自由度体系的临界荷载,所得计算结果均不小于精确解。
( ) 3.当温度升高时,连续梁的极限弯矩值将降低。
( )二、 填空题(共14分)1.(本小题6分)受到简谐荷载作用的单自由度体系,为减小质点的振幅,当自振频率ω 小于荷载频率θ 时,应______体系的刚度;当自振频率ω 大于荷载频率θ 时,应______体系的刚度。
2.(本小题4分)图示结构的极限荷载为F Pu =____。
P(第2小题图)(第3小题图)3.(本小题4分)图示体系的动力自由度数为____。
三、 计算题(共77分)1.(本小题8分)将图示结构简化为单根压杆,并计算相应的弹簧刚度k 。
(已知13EIk l =)1k2.(本小题10分)不考虑阻尼,试列出图示体系的运动方程,并求出相应的柔度系数。
命题人:文国治组题人:文国治审题人: 张来仪命题时间:学院 专业 年级 学号 姓名封线密3.(本小题12分)求图示连续梁的极限荷载F Pu,并绘出极限状态下的弯矩图。
4.(本小题8分)计算图示体系的临界荷载F Pcr。
5.(本小题14分)求图示体系的自振频率和主振型,并绘出主振型图。
(已知层间侧移刚度k1 = 2k,k2 = k,m1 = m2 = m)6.(本小题12分)求图示刚架稳态振动时质点的振幅,并绘出最大动力弯矩图。
(已知F P = 8kN,θ=EI = 2.5×104kN·m 2,不考虑阻尼)F重庆大学 结构力学(1) 课程试卷2005 ~2006 学年 第 2 学期开课学院: 土木工程考试日期: 06.4.23考试方式:考试时间: 120 分钟 注:1.大标题用四号宋体、小标题及正文用小四号宋体;2.按A4纸缩小打印四、 是非判断题(每小题3分,共9分)1.图a 所示体系的自振周期大于图b 体系的自振周期。
《结构力学》课后习题答案__重庆大学出版社

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
[课程]结构力学2课后概念题答案
![[课程]结构力学2课后概念题答案](https://img.taocdn.com/s3/m/948cd1ee760bf78a6529647d27284b73f24236ec.png)
[课程]结构力学2课后概念题答案(龙驭球) 概念题于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
1.1 结构动力计算与静力计算的主要区别是什么,粘滞阻尼理论的优点是便于求解,但其缺点是与往往实际不符,为扬长避短,按能量等答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时假设称为等效粘滞阻尼。
间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法一般与荷载类型无关。
1.6 采用集中质量法、广义位移法(坐标法)和有限元法都可使无限自由度体系简化为有限自由度体系,它们采用的手法有何不同,1.2 什么是动力自由度,确定体系动力自由度的目的是什么,答:确定体系在振动过程中任一时刻体系全部质量位置或变形形态所答:集中质量法:将结构的分布质量按一定规则集中到结构的某个或需要的独立参数的个某些位置上,认为其他数,称为体系的动力自由度(质点处的基本位移未知量)。
地方没有质量。
质量集中后,结构杆件仍具有可变形性质,称为“无重杆”。
广义坐标法:在数学中常采用级数展开法求解微分方程,在结构动力确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程分析中,也可采用相同的方法求解,这就是广义坐标法的理论依据。
所假设的形状曲线数=自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和数目代表在这个理想化动位移)与结构的动力特性有密切关系,而动力特性又与质量的可能形式中所考虑的自由度个数。
考虑了质点间均匀分布质量的影响(形位置有关。
状函数),一般来说,对于一个给定自由度数目的动力分析,用理想化的形状函数法比用集1.3 结构动力自由度与体系几何分析中的自由度有何区别,中质量法更为精确。
答:二者的区别是:几何组成分析中的自由度是确定刚体系位置所需有限元法:有限元法可以看成是广义坐标法的一种特殊的应用。
