初中经典几何证明练习题(含答案)
初中经典几何证明练习题(含答案)

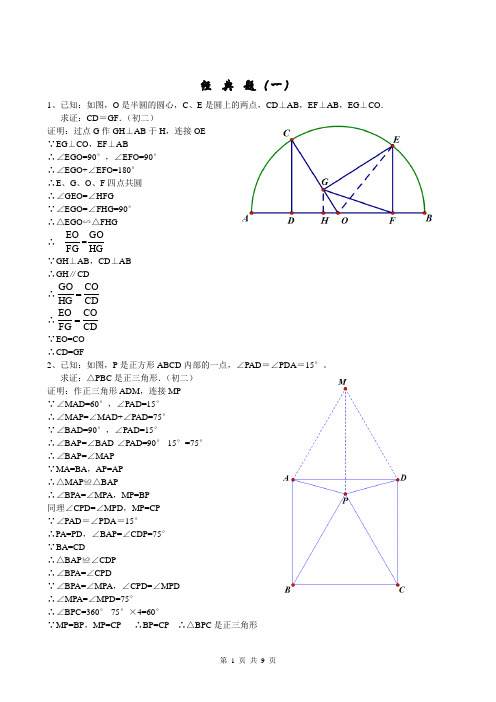
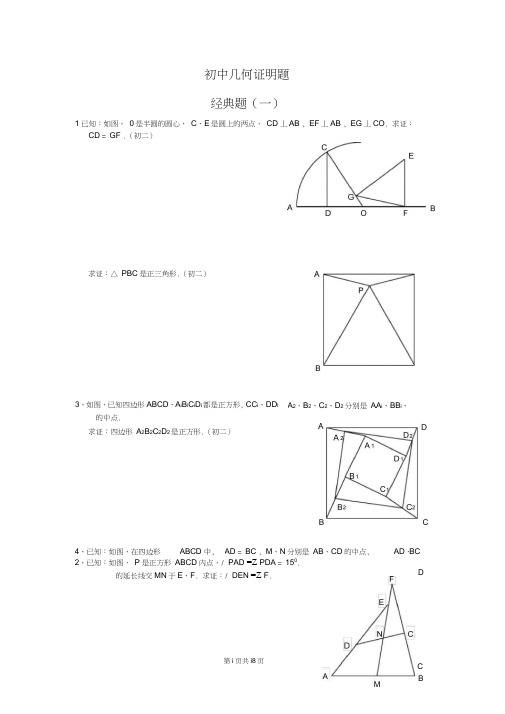
初中几何证明题经典题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90°∴∠EGO+∠EFO=180°∴E 、G 、O 、F 四点共圆∴∠GEO=∠HFG∵∠EGO=∠FHG=90°∴△EGO ∽△FHG ∴FG EO =HGGO ∵GH ⊥AB ,CD ⊥AB∴GH ∥CD ∴CDCO HG GO = ∴CD CO FG EO =∵EO=CO∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二)证明:作正三角形ADM ,连接MP∵∠MAD=60°,∠PAD=15°∴∠MAP=∠MAD+∠PAD=75°∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75°∴∠BAP=∠MAP∵MA=BA ,AP=AP∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP同理∠CPD=∠MPD ,MP=CP∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75°∵BA=CD∴△BAP ≌∠CDP∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG∵CN=DN ,CG=DG∴GN ∥AD ,GN=21AD∴∠DEN=∠GNM∵AM=BM ,AG=CG∴GM ∥BC ,GM=21BC ∴∠F=∠GMN∵AD=BC∴GN=GM∴∠GMN=∠GNM∴∠DEN=∠F 经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G∵OG ⊥AF∴AG=FG∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC∴∠BHD+∠DBH=90°∠ACB+∠DBH=90°∴∠ACB=∠BHD∴∠F=∠BHD∴BH=BF 又AD ⊥BC∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD又AD ⊥BC ,OM ⊥BC ,OG ⊥AD∴四边形OMDG 是矩形∴OM=GD ∴AH=2OM(2)连接OB 、OC∵∠BAC=60∴∠BOC=120°∵OB=OC ,OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P .求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆∴∠AEF+∠FCQ=180°∵EF ⊥AG ,PQ ⊥AG∴EF ∥PQ∴∠PAF=∠AFE∴∠AFE=∠AEF∴∠AEF=∠PAF∵∠PAF+∠QAF=180°∴∠FCQ=∠QAF∴F 、C 、A 、Q 四点共圆∴∠AFQ=∠ACQ又∠AEP=∠ACQ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG∵C 、D 、B 、E 四点共圆∴∠B=∠D ,∠E=∠C∴△ABE ∽△ADC ∴DFBG FD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF∴∠AGB=∠AFD∴∠AGE=∠AFC∵AM=AN ,∴OA ⊥MN又OG ⊥BE ,∴∠OAQ+∠OGQ=180°在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ∴O、A、Q、E四点共圆∴∠AOQ=∠AGE同理∠AOP=∠AFC∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA∴△OAQ≌△OAP∴AP=AQ4、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,OP⊥BC求证:BC=2OP(初二)证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N∵OF=OD,DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.BF求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初三几何证明练习题含答案

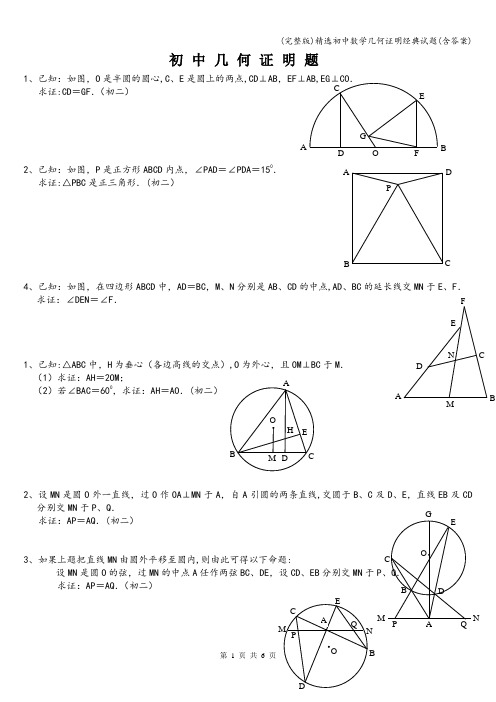
初三几何证明题经典题一1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.2、已知:如图,P是正方形ABCD内部的一点,∠PAD=∠PDA=15°;求证:△PBC是正三角形.初二3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题二1、已知:△ABC中,H为垂心各边高线的交点,O为外心,且OM⊥BC于M.1求证:AH=2OM;2若∠BAC=600,求证:AH=AO.2、设MN是圆O外一条直线,过O作OA⊥MN于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP=AQ.3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF 的中点,OP⊥BC求证:BC=2OP证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N∵OF=OD,DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题三1、如图,四边形ABCD 为正方形,DE ∥AC,AE =AC,AE 与CD 相交于F . 求证:CE =CF .证明:连接BD 交AC 于O;过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30° ∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°-15°=75° ∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA,直线EC 交DA 延长线于F . 求证:AE =AF .证明:连接BD,过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC,又EG ⊥AC∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG =OD =21BD=21AC=21CE ∴∠GCE=30° ∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP,CF 平分∠DCE . 求证:PA =PF .初二证明:过点F 作FG ⊥CE 于G,FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF ∵AP ⊥FP∴∠APB+∠FPG=90° ∵∠APB+∠BAP=90° ∴∠FPG=∠BAP 又∠FGP=∠PBA ∴△FGP ∽△PBA ∴FG :PB=PG :AB4、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D . 求证:AB =DC,BC =AD .初三证明:过点E 作EK ∥BD,分别交AC 、AF 于M 、K,取EF 的中点H, 连接OH 、MH 、EC设AB=x ,BP=y ,CG=zz :y=x-y+z :x化简得x-y ·y =x-y ·z ∵x-y ≠0 ∴y=z 即BP=FG ∴△ABP ≌△PGF∴∠CAE=∠CEA=21∠GCE=15° 在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE=180°-135°-30°=15°∵EH=FH∴OH ⊥EF,∴∠PHO=90° 又PC ⊥OC,∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO又EK ∥BD,∴∠HPO=∠HEK ∴∠HCM=∠HEM ∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题四1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =求∠APB 的度数.初二解:将△ABP 绕点B 顺时针方向旋转60°得△BCQ,连接PQ 则△BPQ 是正三角形 ∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .初二∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO∴四边形ABCD 的对角证明:过点P 作AD 的平行线,过点A 作PD 的平行线, 两平行线相交于点E,连接BE ∵PE ∥AD,AE ∥PD ∴ADPE 是平行四边形 ∴PE=AD,又ABCD 是平行四边形 ∴AD=BC ∴PE=BC又PE ∥AD,AD ∥BC ∴PE ∥BC∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .初三 证明:在BD 上去一点E,使∠BCE=∠ACD ∵错误!=错误!∴∠CAD=∠CBD ∴△BEC ∽△ADC ∴ACBCAD BE∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD∵错误!=错误!,∴∠BAC=∠BDC △BAC ∽△EDC又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB∴CDACDE AB∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .初二证明:过点D 作DG ⊥AE 于G,作DH ⊥FC 于H,连接DF 、∴S △ADE =错误!AE ·DG,S △FDC =错误!FC ·DH 又S △ADE =S △FDC =错误!S □ABCD ∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA =∠DPC经典题五1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,求证:3≤L <2. 证明:1将△BPC 绕B 点顺时针旋转60°的△BEF,连接PE,∵BP=BE,∠PBE=60° ∴△PBE 是正三角形; ∴PE=PB 又EF=PC ∴L=PA+PB+PC=PA+PE+EF当PA 、PE 、EF 在一条直线上的时候,L=PA+PE+EF 的值最小如图在△ABF 中,∠ABP=120°∴AF=3BGB∴L=PA+PB+PC ≤32过点P 作BC 的平行线分别交AB 、AC 于D 、G 则△ADG 是正三角形 ∴∠ADP=∠AGP,AG=DG ∵∠APD >∠AGP ∴∠APD >∠ADP∴AD >PA …………………………① 又BD+PD >PB ……………………② CG+PG >PC ……………………③①+②+③得AD+BD+CG+PD+PG >PA+PB+PC ∴AB+CG+DG=AB+CG+AG=AB+AC >PA+PB+PC=L ∵AB=AC=1∴L <2 由12可知:3≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.解:将△BCP 绕点B 顺时针旋转60°得△BEF,连接PE, 则△BPE 是正三角形 ∴PE=PB∴PA +PB +PC=PA+PE+EF∴要使PA +PB +PC 最小,则PA 、PE 、EF 应该在一条直线上如图此时AF=PA+PE+EF过点F 作FG ⊥AB 的延长线于G则∠GBF=180°-∠ABF=180°-150°=30° ∴GF=错误!,BG=23∴AF=22AG GF +=2212321⎪⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛=32+∴PA +PB +PC 的最小值是32+3、P 为正方形ABCD 内的一点,并且PA =a,PB =2a,PC =3a,求正方形的边长. 证明:将△ABP 绕点B 顺时针旋转90°得△BCQ,连接PQ 则△BPQ 是等腰直角三角形, ∴PQ=2PB=2×2a=22a 又QC=AP=a∴QP 2+QC 2=22a 2+a 2=9a 2=PC 2∴△PQC 是直角三角形 ∴∠BQC=135°∵BC 2=BQ 2+CQ 2-2BQ ·CQ ·cos ∠BQC=PB 2+PA 2-2PB ·PAcos135°=4a 2+a 2-2×2a ×a ×-22解得BC=a 225+∴正方形的边长为a 225+4、如图,△ABC 中,∠ABC =∠ACB =80°,D 、E 分别是AB 、AC 上的点,∠DCA =30°,∠EBA =20°,求∠BED 的度数.解:在AB 上取一点F,使∠BCF=60°,CF 交BE 于G,连接EF 、DG ∵∠ABC=80°,∠ABE=20°,∴∠EBC=60°,又∠BCG=60° ∴△BCG 是正三角形∴BG=BC∵∠ACB=80°,∠BCG=60°∴∠FCA=20°∴∠EBA=∠FCA 又∵∠A=∠A,AB=AC ∴△ABE ≌ACF ∴AE=AF ∴∠AFE=∠AEF=错误!180°-∠A=80°又∵∠ABC=80°=∠AFE ∴EF ∥BC ∴∠EFG=∠BCG=60° ∴△EFG 是等边三角形∴EF=EG,∠FEG=∠EGF=∠EFG=60°∵ACB=80°,∠DCA=30°∴∠BCD=50°∴∠BDC=180°-∠BCD-∠ABC=180°-50°-80°=50° ∴∠BCD=∠BDC ∴BC=BD 前已证BG=BC ∴BD=BG ∠BGD=∠BDG=错误!180°-∠ABE=80°∴∠FGD=180°-∠BGD-∠EGF=180°-80°-60°=40° 又∠DFG=180°-∠AFE-∠EFG=180°-80°-60°=40°∴∠FGD=∠DFG ∴DF=DG 又EF=EG,DE=DE ∴△EFD ≌△EGD ∴∠BED=∠FED=错误!∠FEG=错误!×60°=30°5、如图,△ABC 内接于⊙O,且AB 为⊙O 的直径,∠ACB 的平分线交⊙O 于点D,过点D 作⊙O 的切线PD 交CA 的延长线于点P,过点A 作AE ⊥CD 于点E,过点B 作BF ⊥CD 于点F,若AC=6,BC=8,求线段PD 的长; 解:∵∠ACD=∠BCD ∴错误!=错误!∴AD=BD ∵AB 为⊙O 的直径∴∠ADB=90° ∴△ABD 是等腰直角三角形∵∠ACB=90°,AC=6,BC=8 ∴AB=10∴AD=AB ·cos ∠DAB=10×22=52 又AE ⊥CD,∠ACD=45°∴△ACE 是等腰直角三角形∴CE=AE=AC ·cos ∠CAE=6×22=32 在△ADE 中,DE 2=AD 2-AE 2∴DE 2=32232522=)()(-∴DE=24 ∴CD=CE+DE=32+24=27∵∠PDA=∠PCD,∠P=∠P ∴△PDA ∽△PCD ∴752725====CD AD PD PA PC PD ∴PC=57PD,PA=75PD ∵PC=PA+AC ∴57PD=75PD+6解得PD=435 1证明:过点G 作GH ⊥AB 于H,连接OE ∵EG ⊥CO,EF ⊥AB ∴∠EGO=90°,∠EFO=90°∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG ∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB,CD ⊥AB ∴GH ∥CD ∴CD COHG GO =∴CDCOFG EO =∵EO=CO ∴CD=GF2证明:作正三角形ADM,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA,AP=AP ∴△MAP ≌△BAP ∴∠BPA=∠MPA,MP=BP 同理∠CPD=∠MPD,MP=CP ∵∠PAD =∠PDA =15° ∴PA=PD,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA,∠CPD=∠MPD ∴∠MPA=∠MPD=75° ∴∠BPC=360°-75°×4=60°∵MP=BP,MP=CP ∴BP=CP ∴△BPC 是正三角形3证明:连接AC,取AC 的中点G,连接NG 、MG ∵CN=DN,CG=DG ∴GN ∥AD,GN=21AD ∴∠DEN=∠GNM ∵AM=BM,AG=CG ∴GM ∥BC,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM ∴∠GMN=∠GNM ∴∠DEN=∠F1证明:1延长AD 交圆于F,连接BF,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵错误!=错误! ∴∠F=∠ACB 又AD ⊥BC,BE ⊥AC ∴∠BHD+∠DBH=90°∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD ∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2GH+DH=2GD 又AD ⊥BC,OM ⊥BC,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM 2连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由1知AH=2OM ∴AH=BO=AO2证明:作点E 关于AG 的对称点F,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF ∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG,PQ ⊥AG ∴EF ∥PQ ∴∠PAF=∠AFE ∵AF=AE ∴∠AFE=∠AEF∴∠AEF=∠PAF∵∠PAF+∠QAF=180°∴∠FCQ=∠QAF∴F、C、A、Q四点共圆∴∠AFQ=∠ACQ又∠AEP=∠ACQ∴∠AFQ=∠AEP在△AEP和△AFQ中∠AFQ=∠AEPAF=AE∠QAF=∠PAE∴△AEP≌△AFQ∴AP=AQ。
(完整版)初中几何证明题五大经典(含答案)
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
(完整版)精选初中数学几何证明经典试题(含答案)
初中几何证明题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 求证:AP =AQ .(初二)APCDB AFGCEB O D NF 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA,直线EC求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 求证:PA =PF .(初二)4、如图,PC 切圆O于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D经典题(一)1。
初中数学几何证明试题(含答案)
第 6 页 共 15 页
4.如下图连接 AC 并取其中点 Q,连接 QN 和 QM,所以可得∠QMF=∠F,∠QNM=∠
DEN 和∠QMN=∠QNM,从而得出∠DEN=∠F。
经 典 题(二)
1.(1)延长 AD 到 F 连 BF,做 OG⊥AF,
又∠F=∠ACB=∠BHD, 可得 BH=BF,从而可得 HD=DF, 又 AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
BE AD
= ,即 AD•BC=BE•AC,
①
BC AC
又∠ACB=∠DCE,可得△ABC∽△DEC,既得
AB = DE ,即 AB•CD=DE•AC,
②
AC DC
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
第 11 页 共 15 页
4.过 D 作 AQ⊥AE
(2)连接 OB,OC,既得∠BOC=1200,
从而可得∠BOM=600, 所以可得 OB=2OM=AH=AO, 得证。
第 7 页 共 15 页
3.作 OF⊥CD,OG⊥BE,连接 OP,OA,OF,AF,OG,AG,OQ。 由于 AD = AC = CD = 2FD = FD , AB AE BE 2BG BG
(2)过 P 点作 BC 的平行线交 AB,AC 与点 D,F。
由于∠APD>∠ATP=∠ADP,
推出 AD>AP
①
又 BP+DP>BP
②
和 PF+FC>PC
③
又 DF=AF
④
由①②③④可得:最大 L< 2 ;
几何证明题(含答案)
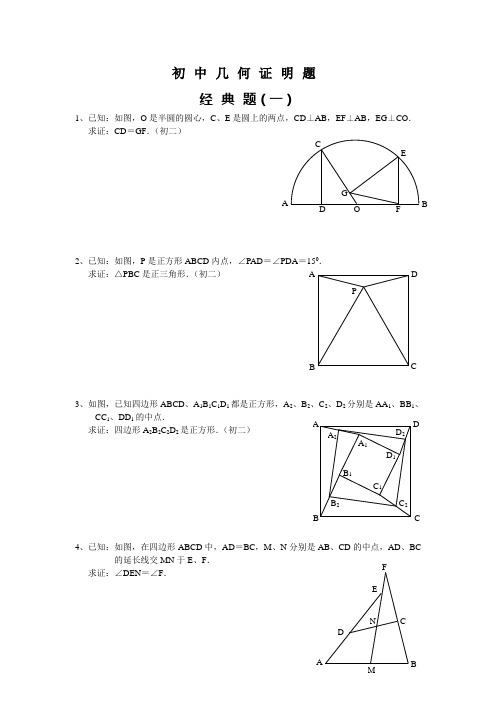
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)E经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
(完整版)初中数学几何证明经典试题(含答案)
初中几何证明题 经典题(一)1 已知:如图, 0是半圆的圆心, C 、E 是圆上的两点, CD 丄AB , EF 丄AB , EG 丄CO . 求证:CD = GF .(初二)2、已知:如图, P 是正方形 ABCD 内点,/ PAD =Z PDA = 150.的延长线交MN 于E 、F . 求证:/ DEN =Z F .求证:△ PBC 是正三角形.(初二)3、如图,已知四边形 ABCD 、A i B i C i D i 都是正方形, CC i 、DD i的中点.求证:四边形 A 2B 2C 2D 2是正方形.(初二)A 2、B 2、C 2、D 2 分别是 AA i 、BB i 、4、已知:如图,在四边形 ABCD 中, AD = BC , M 、N 分别是 AB 、CD 的中点, AD 、BCD经典题(二)及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP = AQ .(初二) 3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆0的弦,过MN 的中点A 任作两弦BC 、DE , 于 P 、Q .求证:AP = AQ .(初二)4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于1已知:△ ABC 中,H 为垂心(各边高线的交点)(1) 求证:AH = 2OM ;(2) 若/ BAC = 600,求证:AH = AO .(初二),O 为外心,且0M 丄BC 于M .2、设MN 是圆0外一直线,过0作0A 丄MN 于A ,自A 引圆的两条直线,交圆于AB 的一半.(初二)HEBCM DG N BF经典题(二)1 如图,四边形 ABCD 为正方形,DE // AC , AE = AC , AE 与CD 相交于F .求证:CE = CF .(初二)4、如图,PC 切圆0于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB = DC , BC = AD .(初三)F .E2、如图,四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于 求证:AE = AF .(初二)3、设ABCD 为圆内接凸四边形,求证: AB • CD + AD • BC = AC • BD .(初三)4、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证:/ DPA =Z DPC .(初二)经典题(四)1已知:△ ABC 是正三角形,P 是三角形内一点 求:/ APB的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/求证:/ PAB = Z PCB .(初二)C经典难题(五)1、设P是边长为1的正△ ABC内任一点,求证:一:<L V 2.B C2、已知:P是边长为1的正方形ABCD内的一点,求PA + PB + PC的最小值.3、P为正方形ABCD内的一点,并且PA= a, PB= 2a, PC= 3a,求正方形的边长.4、如图,△ ABC 中,/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点,/ DCA = 30°, / EBA = 20°,求/ BED 的度数.经典题(一)1•如下图做GH丄AB,连接E0。
初中经典几何证明练习题(含答案)
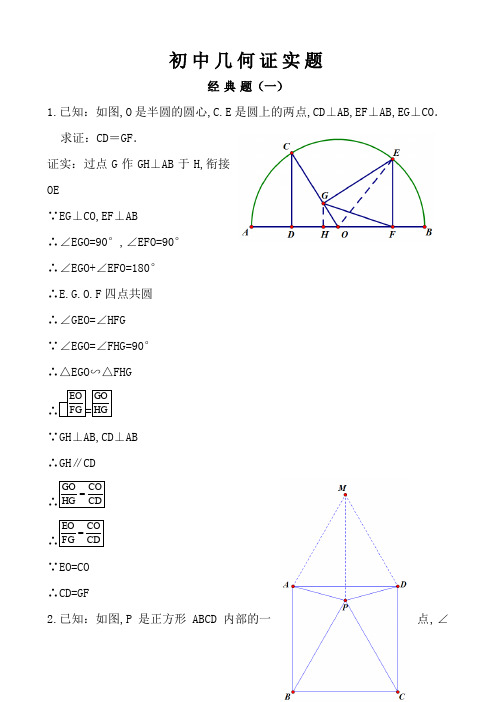
初中几何证实题经典题(一)1.已知:如图,O 是半圆的圆心,C.E 是圆上的两点,CD ⊥AB,EF ⊥AB,EG ⊥CO . 求证:CD =GF .证实:过点G 作GH ⊥AB 于H,衔接OE∵EG ⊥CO,EF ⊥AB∴∠EGO=90°,∠EFO=90°∴∠EGO+∠EFO=180°∴E.G.O.F 四点共圆∴∠GEO=∠HFG∵∠EGO=∠FHG=90°∴△EGO ∽△FHG ∴FG EO =HG GO∵GH ⊥AB,CD ⊥AB∴GH ∥CD∴CD CO HG GO = ∴CD CO FG EO = ∵EO=CO∴CD=GF2.已知:如图,P 是正方形ABCD 内部的一点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)证实:作正三角形ADM,衔接MP∵∠MAD=60°,∠PAD=15°∴∠MAP=∠MAD+∠PAD=75°∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75°∴∠BAP=∠MAP∵MA=BA,AP=AP∴△MAP≌△BAP∴∠BPA=∠MPA,MP=BP同理∠CPD=∠MPD,MP=CP∵∠PAD=∠PDA=15°∴PA=PD,∠BAP=∠CDP=75°∵BA=CD∴△BAP≌∠CDP∴∠BPA=∠CPD∵∠BPA=∠MPA,∠CPD=∠MPD∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP,MP=CP ∴BP=CP ∴△BPC是正三角形3.已知:如图,在四边形ABCD中,AD=BC,M.N分离是AB.CD的中点,AD.BC的延伸线交MN于E.F.求证:∠DEN =∠F .证实:衔接AC,取AC 的中点G,衔接NG.MG∵CN=DN,CG=DG∴GN ∥AD,GN=21AD∴∠DEN=∠GNM∵AM=BM,AG=CG∴GM ∥BC,GM=21BC∴∠F=∠GMN∵AD=BC∴GN=GM∴∠GMN=∠GNM∴∠DEN=∠F经典题(二)1.已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM;(2)若∠BAC =600,求证:AH =AO .(初二)证实:(1)延伸AD 交圆于F,衔接BF,过点O作OG ⊥AD 于G∵OG ⊥AF∴AG=FG∵AB ⌒ =AB ⌒∴∠F=∠ACB又AD ⊥BC,BE ⊥AC∴∠BHD+∠DBH=90°∠ACB+∠DBH=90°∴∠ACB=∠BHD∴∠F=∠BHD∴BH=BF 又AD ⊥BC∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD又AD ⊥BC,OM ⊥BC,OG ⊥AD∴四边形OMDG 是矩形∴OM=GD ∴AH=2OM(2)衔接OB.OC∵∠BAC=60∴∠BOC=120°∵OB=OC,OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30°∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2.设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A,自A 引圆的两条割线交圆O 于B.C 及D.E,衔接CD 并延伸交MN 于Q,衔接EB 并延伸交MN 于P. 求证:AP =AQ .证实:作点E 关于AG 的对称点F,衔接AF.CF.QF∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF即∠PAE=∠QAF∵E.F.C.D 四点共圆∴∠AEF+∠FCQ=180°∵EF ⊥AG,PQ ⊥AG∴EF ∥PQ∴∠PAF=∠AFE∵AF=AE∴∠AFE=∠AEF∴∠AEF=∠PAF∵∠PAF+∠QAF=180°∴∠FCQ=∠QAF∴F.C.A.Q 四点共圆∴∠AFQ=∠ACQ又∠AEP=∠ACQ∴∠AFQ=∠AEP3.设MN 是圆O 的弦,过MN 的中点A 任作两弦BC.DE,设CD.EB 分离交MN 于P.Q .求证:AP =AQ .(初二)证实:作OF ⊥CD 于F,OG ⊥BE 于G,衔接OP.OQ.OA.AF.AG∵C.D.B.E 四点共圆∴∠B=∠D,∠E=∠C∴△ABE ∽△ADC 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ∴DF BG FD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF∴∠AGB=∠AFD∴∠AGE=∠AFC∵AM=AN,∴OA ⊥MN又OG ⊥BE,∴∠OAQ+∠OGQ=180°∴O.A.Q.E 四点共圆∴∠AOQ=∠AGE同理∠AOP=∠AFC∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA∴△OAQ ≌△OAP∴AP=AQ4.如图,分离以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证实:分离过F.A.D 作直线BC 的垂线,垂足分离是L.M.N∵OF=OD,DN ∥OP ∥FL∴PN=PL∴OP 是梯形DFLN 的中位线∴DN+FL=2OP∵ABFG 是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL ≌△ABM∴FL=BM同理△AMC ≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1.如图,四边形ABCD 为正方形,DE ∥AC,AE =AC,AE 与CD 订交于F . 求证:CE =CF .(初二)证实:衔接BD 交AC 于O.过点E 作EG ⊥AC于G∵ABCD 是正方形∴BD ⊥AC 又EG ⊥AC∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90°∴ODEG 是矩形∴EG=OD=21BD=21AC=21AE∴∠EAG=30°∵AC=AE∴∠ACE=∠AEC=75°又∠AFD=90°-15°=75°∴∠CFE=∠AFD=75°=∠AEC∴CE=CF2.如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA,直线EC 交DA 延伸线于F .求证:AE =AF .(初二)证实:衔接BD,过点E 作EG ⊥AC 于G∵ABCD 是正方形∴BD ⊥AC,又EG ⊥AC∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90°∴ODEG 是矩形∴EG =OD =21BD=21AC=21CE∴∠GCE=30°∵AC=EC3.设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP,CF 等分∠DCE . 求证:PA =PF .(初二)证实:过点F 作FG ⊥CE 于G,FH ⊥CD 于H∵CD ⊥CG ∴HCGF 是矩形∴∠CAE=∠CEA=21∠GCE=15° 在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AF∵∠HCF=∠GCF ∴FH=FG∴HCGF 是正方形∴CG=GF∵AP ⊥FP∴∠APB+∠FPG=90°∵∠APB+∠BAP=90°∴∠FPG=∠BAP又∠FGP=∠PBA∴△FGP ∽△PBA∴FG :PB=PG :AB4.如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE.AF 与直线PO 订交于B.D .求证:AB =DC,BC =AD .(初三)证实:过点E 作EK ∥BD,分离交AC.AF 于M.K,取EF 的中点H,衔接OH.MH.EC∵EH=FH∴OH ⊥EF,∴∠PHO=90°又PC ⊥OC,∴∠POC=90°∴P.C.H.O 四点共圆∴∠HCO=∠HPO又EK ∥BD,∴∠HPO=∠HEK∴∠HCM=∠HEM∴H.C.E.M 四点共圆 设AB=x ,BP=y ,CG=z z :y=(x-y+z ):x 化简得(x-y )·y =(x-y )·z ∵x-y ≠0 ∴y=z 即BP=FG ∴△ABP ≌△PGF ∴EM=KM ∵EK ∥BD ∴KM OD AM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相等分 ∴ABCD 是平行四边形B ∴∠ECM=∠EHM又∠ECM=∠EFA∴∠EHM=∠EFA∴HM ∥AC∵EH=FH经典题(四)1.已知:△ABC 是正三角形,P 是三角形内一点求∠APB 的度数.(初二)解:将△ABP 绕点B 顺时针偏向扭转60°得△则△BPQ 是正三角形∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5∴△PQC 是直角三角形∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150°∴∠APB=∠BQC=150°2.设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二) 证实:过点P 作AD 的平行线,两平行线订交于点E,衔接BE∵PE ∥AD,AE ∥PD∴ADPE 是平行四边形∴PE=AD,又ABCD 是平行四边形 ∴AD=BC ∴PE=BC又PE ∥AD,AD ∥BC ∴PE ∥BC∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP3.设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三) 证实:在BD 上去一点E,使∠BCE=∠ACD ∵CD ⌒ =CD⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD∵BC ⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC∴AB ·CD=DE ·AC ……………………②又∠ADP=∠ABP∴∠AEP=∠ABP ∴A.E.B.P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB①+②得AB ·CD+ AD ·BC =DE ·AC+ BE ·AC=(DE+BE )·AC =BD ·AC4.平行四边形ABCD 中,设E.F 分离是BC.AB 上的一点,AE 与CF 订交于P,且AE =CF .求证:∠DPA =∠DPC .(初二)证实:过点D 作DG ⊥AE 于G,作DH ⊥FC 于∴S △ADE =12AE ·DG,S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角等分线上 ∴∠DPA =∠DPC经典题(五)1.设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,L <2. 证实:(1)将△BPC 绕B 点顺时针扭转60°的△BEF,衔接PE,∵BP=BE,∠PBE=60° ∴△PBE 是正三角形.∴PE=PB 又EF=PC ∴L=PA+PB+PC=PA+PE+EF当PA.PE.EF 在一条直线上的时刻,L=PA+PE+EF 在△ABF 中,∠ABP=120°∴∴L=PA+PB+PC (2)过点P 作BC 的平行线分离交AB.AC 于D.G 则△ADG 是正三角形BGB∴∠ADP=∠AGP,AG=DG ∵∠APD >∠AGP ∴∠APD >∠ADP∴AD >PA …………………………① 又BD+PD >PB ……………………② CG+PG >PC ……………………③ ①+②+③得AD+BD+CG+PD+PG >PA+PB+PC ∴AB+CG+DG=AB+CG+AG=AB+AC >PA+PB+PC=L ∵AB=AC=1∴L <2由(1)(2L <2.2.已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB 解:将△BCP 绕点B 顺时针扭转60°得△BEF,衔接PE, 则△BPE 是正三角形 ∴PE=PB∴PA +PB +PC=PA+PE+EF∴要使PA +PB +PC 最小,则PA.PE.EF 此时AF=PA+PE+EF过点F 作FG ⊥AB 的延伸线于G则∠GBF=180°-∠ABF=180°-150°=30° ∴GF=12,BG=∴C∴PA +PB +PC3.P 为正方形ABCD 内的一点,并且PA =a,PB =2a,PC =3a,求正方形的边长.证实:将△ABP 绕点B 顺时针扭转90°得△BCQ,则△BPQ 是等腰直角三角形, ∴又QC=AP=a∴QP 2+QC 22+a 2=9a 2=PC 2∴△PQC 是直角三角形 ∴∠BQC=135°∵BC 2=BQ 2+CQ 2-2BQ ·CQ ·cos ∠BQC =PB 2+PA 2-2PB ·PAcos135° =4a 2+a 2-2×2a ×a ×解得4.如图,△ABC 中,∠ABC =∠ACB =80°,D.E 分离是AB.AC 上的点,∠DCA =30°,∠EBA =20°,求∠BED 的度数.解:在AB 上取一点F,使∠BCF=60°,CF 交BE 于G,衔接∵∠ABC=80°,∠ABE=20°,∴∠EBC=60°,又∠BCG=60° ∴△BCG 是正三角形∴BG=BC∵∠ACB=80°,∠BCG=60°∴∠FCA=20°∴∠EBA=∠FCA 又∵∠A=∠A,AB=AC ∴△ABE ≌ACF ∴AE=AF ∴∠AFE=∠AEF=12(180°-∠A )=80°又∵∠ABC=80°=∠AFE ∴EF ∥BC ∴∠EFG=∠BCG=60° ∴△EFG 是等边三角形∴EF=EG,∠FEG=∠EGF=∠EFG=60° ∵ACB=80°,∠DCA=30°∴∠BCD=50°∴∠BDC=180°-∠BCD-∠ABC=180°-50°-80°=50° ∴∠BCD=∠BDC ∴BC=BD 前已证BG=BC ∴BD=BG ∠BGD=∠BDG=12(180°-∠ABE )=80°∴∠FGD=180°-∠BGD-∠EGF=180°-80°-60°=40° 又∠DFG=180°-∠AFE-∠EFG=180°-80°-60°=40° ∴∠FGD=∠DFG ∴DF=DG 又EF=EG,DE=DE ∴△EFD ≌△EGD ∴∠BED=∠FED=12∠FEG=12×60°=30°5.如图,△ABC 内接于⊙O,且AB 为⊙O 的直径,∠ACB 的等分线交⊙O 于点D,过点D 作⊙O 的切线PD 交CA 的延伸线于点P,过点A 作AE ⊥CD 于点E,过点B 作BF ⊥CD 于点F,若AC=6,BC=8,求线段PD 的长. 解:∵∠ACD=∠BCD ∴AD ⌒=BD ⌒∴AD=BD ∵AB 为⊙O 的直径∴∠ADB=90° ∴△ABD 是等腰直角三角形∵∠ACB=90°,AC=6,BC=8 ∴AB=10 ∴AD=AB ·cos ∠DAB=10×22=52又AE ⊥CD,∠ACD=45°∴△ACE 是等腰直角三角形∴CE=AE=AC ·cos ∠CAE=6×22=32在△ADE 中,DE 2=AD 2-AE 2∴DE2=32232522 )()(-∴DE=24∴∵∠PDA=∠PCD,∠P=∠P ∴△PDA∽△PCD∴∵PC=PA+AC解得。
初中经典几何证明练习题(含答案)
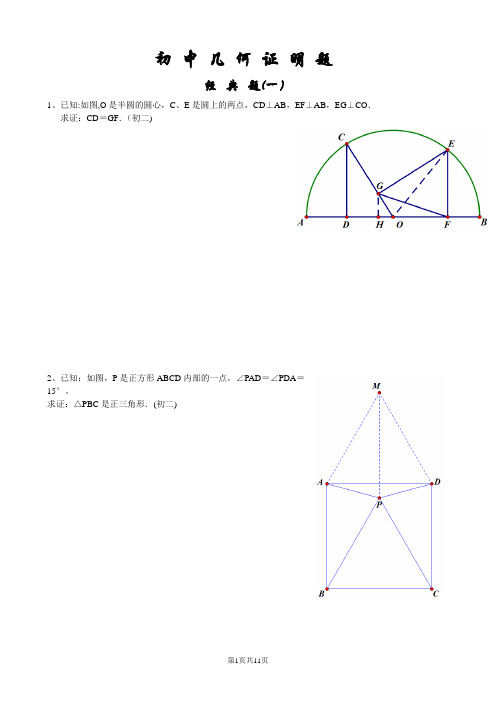
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二)2、已知:如图,P是正方形ABCD内部的一点,∠PAD=∠PDA=15°。
求证:△PBC是正三角形.(初二)3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一条直线,过O作OA⊥MN于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P。
求证:AP=AQ.3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,OP⊥BC求证:BC=2OP(初二)证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N∵OF=OD,DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30°∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°—15°=75° ∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)证明:连接BD ,过点E 作EG ⊥AC 于G ∵ABCD 是正方形∴BD ⊥AC ,又EG ⊥AC ∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形∴EG =OD =21BD=21AC=21CE∴∠GCE=30°∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)证明:过点F 作FG ⊥CE 于G,FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF ∵AP ⊥FP ∴∠APB+∠FPG=90° ∵∠APB+∠BAP=90° ∴∠FPG=∠BAP 设AB=x ,BP=y ,CG=z z :y=(x-y+z ):x 化简得(x-y )·y =(x-y )·z ∵x-y ≠0 ∴∠CAE=∠CEA=21∠GCE=15°在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AFP E PB AC∴△FGP ∽△PBA ∴FG :PB=PG :AB4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D . 求证:AB =DC ,BC =AD .(初三)证明:过点E 作EK ∥BD ,分别交AC 、AF 于M 、K ,取EF 的中点H , 连接OH 、MH 、EC ∵EH=FH∴OH ⊥EF,∴∠PHO=90° 又PC ⊥OC ,∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO 又EK ∥BD,∴∠HPO=∠HEK ∴∠HCM=∠HEM ∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求∠APB 的度数.(初二)解:将△ABP 绕点B 顺时针方向旋转60°得△BCQ ,连接PQ 则△BPQ 是正三角形∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)证明:过点P 作AD 的平行线,过点A 作PD 的平行线, 两平行线相交于点E ,连接BE ∵PE ∥AD,AE ∥PD∴ADPE 是平行四边形∴PE=AD,又ABCD 是平行四边形∴AD=BC∴PE=BC又PE ∥AD ,AD ∥BC ∴PE ∥BC ∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相平分 ∴ABCD 是平行四边形 ∴AB=DC ,BC=AD 又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB∴∠ADP=∠AEP3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三) 证明:在BD 上去一点E ,使∠BCE=∠∵错误!=错误!∴∠CAD=∠CBD ∴△BEC ∽△ADC ∴ACBCAD BE =∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD∵错误!=错误!,∴∠BAC=∠BDC △BAC ∽△EDC ∴CDACDE AB =∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)证明:过点D 作DG ⊥AE 于G ,作DH ⊥FC 于H ,连接DF ∴S △ADE =错误!AE ·DG,S △FDC =错误!FC ·DH 又S △ADE =S △FDC =错误!S □ABCD ∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA =∠DPC经典题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:3≤L <2. 证明:(1)将△BPC 绕B 点顺时针旋转60°的△BEF ,连接PE , ∵BP=BE ,∠PBE=60° ∴△PBE 是正三角形。
初中经典几何证明练习题(含答案).doc
又∠OAQ=∠OAP=90°,OA=OA
∴△OAQ≌△OAP
∴AP=AQ
4、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,
OP⊥BC
求证:BC=2OP(初二)
证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N
初中几何证明题
经典题(一)
1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.
求证:CD=GF.
证明:过点G作GH⊥AB于H,连接OE
∵EG⊥CO,EF⊥AB
∴∠EGO=90°,∠EFO=90°
∴∠EGO+∠EFO=180°
∴E、G、O、F四点共圆∴∠GEO=∠HFG
∴CG=GF
设AB=x,BP=y,CG=z
∵AP⊥FP
z:y=(x-y+z):x
∴∠APB+∠FPG=90°
化简得(x-y)·y=(x-y)·z
∵∠APB+∠BAP=90°
∵x-y≠0
∴∠FPG=∠BAP
∴y=z
又∠FGP=∠PBA
即BP=FG
∴△FGP∽△PBA
∴△ABP≌△PGF
∴FG:PB=PG:AB
4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.
求证:AB=DC,BC=AD.(初三)
证明:过点E作EK∥BD,分别交
连接OH、MH、EC
∵EH=FH
∴OH⊥EF,∴∠PHO=90°
又PC⊥OC,∴∠POC=90°
AC、AF于M、K,取EF的中点H,
∴EM=KM
初中经典几何证明练习题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD ∴CD CO HG GO = ∴CD CO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG∴GN ∥AD ,GN=21AD∴∠DEN=∠GNM ∵AM=BM ,AG=CG∴GM ∥BC ,GM=21BC∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30°∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC∴DF BG FD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC 求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中经典几何证明练习题(含答案)

初中几何证明题经典题(一)1已知:如图,O是半圆的圆心,求证:CD = GF.(初二)CD 丄AB , EF⊥ AB ,EG 丄CO。
2、已知:如图,P是正方形ABCD内部的一点,∠ PAD = ∠ PDA =15°。
求证:△ PBC是正三角形.(初二)C、E是圆上的两点,3、已知:如图,在四边形ABCD中,AD = BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F。
求证:∠ DEN = ∠ F.M M B经典题(二)1已知:△ ABC中,H为垂心(各边高线的交点),O为外心,且OM丄BC于M .(1)求证:AH = 2OM ;(2)若∠ BAC = 600,求证:AH = AO .(初二)2、设MN是圆O外一条直线,过O作OA丄MN于A ,自A引圆的两条割线交圆0于B、C及D、E, 连接CD并延长交MN于Q,连接EB并延长交MN于P。
求证:AP = AQ 。
3、如图,分别以△ ABC的AB和AC为一边,在△ ABC的外侧作正方形ABFG和正方形ACDE ,点0是DF 的中点,OP丄BC求证:BC=2OP (初二)证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N ∙∙∙OF=OD , DN // OP // FL∙∙∙ PN=PL∙∙∙ OP是梯形DFLN的中位线∙DN+FL=2OPT ABFG是正方形∙∠ABM+ ∠ FBL=90 °又∠ BFL+ ∠ FBL=90 °∙∠ABM= ∠ BFL又∠ FLB= ∠ BMA=90 ° , BF=AB•••△ BFL ◎△ ABM•FL=BM同理△ AMC ◎△ CND•CM=DN•BM+CN=FL+DN•BC=FL+DN=2OP经典题(二)1 如图,四边形ABCD为正方形,DE // AC ,AE = AC ,AE与CD相交于F。
求证:CE = CF.(初二)证明:连接BD交AC于0。
初中经典几何证明练习题集(含答案解析)
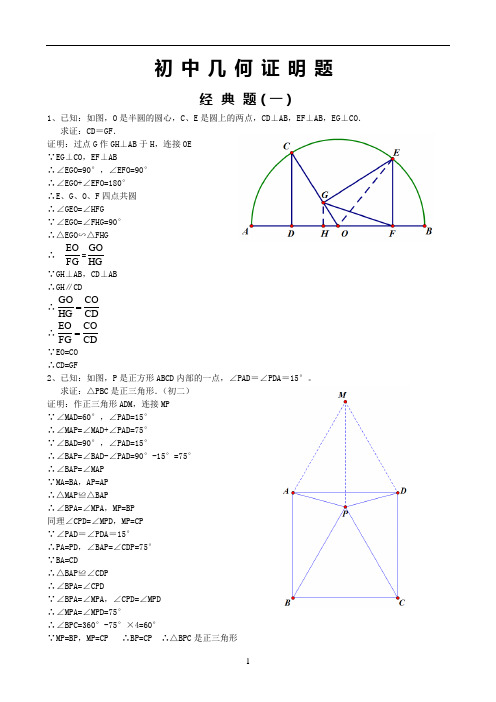
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB,E F⊥AB ,E G⊥C O. 求证:CD =G F.证明:过点G 作GH ⊥AB 于H,连接OE ∵E G⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO +∠EFO=180° ∴E 、G、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠E GO =∠FHG =90° ∴△EGO ∽△F HG ∴FG EO =HGGO∵GH ⊥A B,CD ⊥AB ∴GH∥CD∴CD COHG GO =∴CDCO FG EO = ∵E O=C O ∴CD =GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD=∠PDA=15°。
求证:△PB C是正三角形.(初二) 证明:作正三角形ADM,连接MP ∵∠MA D=60°,∠PAD =15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PA D=15°∴∠BAP=∠BAD -∠PAD=90°-15°=75° ∴∠B AP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=B P 同理∠CPD=∠MP D,MP =C P ∵∠PAD=∠PDA =15°∴PA=P D,∠BA P=∠CDP=75° ∵BA=CD∴△BAP ≌∠C DP ∴∠BP A=∠CPD∵∠B PA =∠MPA ,∠CPD=∠MPD ∴∠MP A=∠M PD=75°∴∠BPC=360°-75°×4=60°∵M P=BP,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形A BCD中,AD=BC ,M 、N 分别是AB、CD 的中点,A D、B C的延长线交MN于E 、F . 求证:∠DEN=∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN =DN,CG=DG ∴GN ∥AD ,GN =21AD ∴∠DE N=∠GN M ∵AM=BM,AG=C G ∴G M∥BC ,GM=21BC ∴∠F =∠GM N ∵AD=B C ∴GN=GM∴∠GMN=∠GNM ∴∠DE N=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH=2OM ;(2)若∠BAC=600,求证:AH=AO.(初二)证明:(1)延长A D交圆于F,连接BF,过点O 作OG ⊥AD 于G ∵OG ⊥A F ∴AG=FG ∵AB ,⌒ =错误!∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠A CB+∠DBH=90° ∴∠A CB=∠B HD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+G H=G H+DH+DF+GH=2GH+2D H=2(GH +DH)=2G D 又AD ⊥BC ,OM ⊥BC ,OG⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH =2O M (2)连接OB 、OC∵∠B AC =60∴∠BOC=120° ∵O B=OC,O M⊥BC ∴∠BOM=21∠BOC =60°∴∠O BM=30° ∴BO=2OM由(1)知AH =2O M∴AH=BO=AO2、设MN 是圆O 外一条直线,过O作OA ⊥MN 于A ,自A 引圆的两条割线交圆O于B 、C 及D、E,连接CD 并延长交MN 于Q,连接EB 并延长交MN 于P. 求证:AP=AQ .证明:作点E关于AG 的对称点F ,连接A F、CF 、QF ∵AG ⊥PQ ∴∠PA G=∠QAG=90°又∠GAE =∠GAF ∴∠PAG +∠GAE =∠QA G+∠GAF 即∠PAE=∠QAF∵E、F 、C 、D 四点共圆 ∴∠AEF+∠FC Q=180° ∵EF ⊥AG ,PQ⊥AG ∴EF ∥P Q∴∠PA F=∠AFE ∵A F=AE∴∠AFE =∠A EF ∴∠AEF=∠P AF ∵∠PA F+∠Q AF=180° ∴∠F CQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP =∠ACQ ∴∠A FQ =∠AEP3、设MN 是圆O的弦,过MN 的中点A 任作两弦BC 、DE,设C D、E B分别交MN 于P 、Q. 求证:AP=AQ .(初二)证明:作OF ⊥CD 于F,OG ⊥BE 于G ,连接OP 、OQ 、O A、AF 、AG ∵C 、D、B 、E 四点共圆 ∴∠B=∠D,∠E=∠C ∴△ABE ∽△A DC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵A M=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OA Q+∠OGQ =180° ∴O 、A、Q、E四点共圆 ∴∠AOQ=∠A GE 同理∠AOP=∠AFC ∴∠AOQ=∠AO P又∠OAQ=∠OAP=90°,OA =OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△A BC 的AB 和AC为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE,点O 是DF 的中点,OP ⊥B C 求证:BC =2O P(初二)证明:分别过F、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF =OD,D N∥OP ∥FL ∴PN =P L∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵AB FG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL +∠FBL =90° ∴∠A BM =∠B FL又∠FLB=∠BMA =90°,BF=AB ∴△BF L≌△ABM ∴FL=BM同理△AMC ≌△CND ∴C M=DN∴BM+CN=FL+DN ∴BC=FL +DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE=AC,AE 与CD相交于F . 求证:CE=C F.(初二)证明:连接B D交AC 于O 。
过点E 作EG ⊥A C于G ∵ABCD 是正方形∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG=O D=21BD =21A C=21A E ∴∠EAG=30°∵AC=AE∴∠ACE=∠A EC=75°又∠AFD=90°-15°=75° ∴∠C FE=∠AF D=75°=∠A EC ∴CE=CF2、如图,四边形A BCD 为正方形,DE ∥AC,且CE =CA ,直线EC 交D A延长线于F. 求证:AE=AF.(初二)证明:连接BD ,过点E 作EG ⊥AC 于G ∵ABCD 是正方形∴BD⊥AC,又EG ⊥AC ∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形∴EG = O D =21BD =21AC=21CE∴∠GCE=30°∵AC=E C3、设P 是正方形AB CD 一边B C上的任一点,PF ⊥A P,CF 平分∠DCE . 求证:PA =PF .(初二)证明:过点F 作FG ⊥C E于G ,F H⊥C D于H ∵CD ⊥CG ∴HCG F是矩形 ∵∠H CF =∠G CF ∴FH=FG ∴HCG F是正方形 ∴CG=GF ∵AP⊥FP ∴∠APB +∠FPG=90° ∵∠APB+∠BAP=90° ∴∠FPG=∠BA P 又∠FGP=∠P BA ∴△FG P∽△PB A ∴F G:P B=PG:AB 4、如图,P C切圆O 于C ,AC 为圆的直径,PE F为圆的割线,AE 、AF 与直线PO 相交于B、D . 求证:A B=DC ,BC =A D.(初三)证明:过点E 作EK ∥BD,分别交AC 、AF 于M 、K,取EF 的中点H, 连接O H、MH 、EC ∵EH=FH∴OH ⊥EF,∴∠PH O=90° 又PC ⊥OC,∴∠P OC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO 又EK ∥BD ,∴∠HPO =∠HEK ∴∠HCM=∠HEM ∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EH M 又∠EC M=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH设AB=x ,BP=y ,CG=z z :y=(x-y+z ):x 化简得(x-y )·y =(x-y )·z ∵x-y ≠0 ∴y=z 即BP=FG ∴△ABP ≌△PGF∴∠CAE=∠CEA=21∠GCE=15°在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AF ∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相平分 ∴ABCD 是平行四边形 ∴AB=DC ,BC=ADB经典题(四)1、已知:△AB C是正三角形,P 是三角形内一点,P A=3,PB =4,P C=5. 求∠AP B的度数.(初二)解:将△ABP 绕点B 顺时针方向旋转60°得△BC Q,连接PQ 则△BPQ是正三角形∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ =AP=3,PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQ C=60°+90°=150° ∴∠APB=∠BQC=150° 2、设P 是平行四边形A BCD 内部的一点,且∠PBA=∠PDA . 求证:∠PAB=∠PC B.(初二)证明:过点P 作A D的平行线,过点A作PD 两平行线相交于点E ,连接BE ∵PE ∥AD ,AE ∥PD∴AD PE 是平行四边形∴PE=AD,又AB CD 是平行四边形∴A D=BC ∴PE=BC又PE∥AD,AD ∥BC ∴P E∥B C ∴BCPE 是平行四边形 ∴∠BEP=∠P CB ∵AD PE是平行四边形 ∴∠AD P=∠AEP3、设ABCD 为圆内接凸四边形,求证:AB ·CD+AD ·BC =AC ·BD.(初三) 证明:在BD 上去一点E,使∠B CE=∠A∵错误!=错误!∴∠CA D=∠CBD ∴△BE C∽△ADC ∴ACBCAD BE =∴AD ·B C=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BC A=∠ECD∵错误!=错误!,∴∠BA C=∠BDC △B AC ∽△EDC ∴CDACDE AB = ∴AB ·C D=DE ·AC ……………………②4、平行四边形AB CD 中,设E 、F 分别是BC 、AB 上的一点,AE 与C F相交于P ,且 又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB证明:过点D 作DG ⊥AE 于G,作D H⊥F C于H,连接DF、DE ∴S△AD E=12 AE ·DG ,S△FDC =错误!F C·DH又S △ADE = S △FDC =\F(1,2) S □ABC D ∴AE ·DG=FC ·DH 又A E=CF ∴DG=DH∴点D 在∠AP C的角平分线上 ∴∠DPA=∠DPC经典题(五)1、设P 是边长为1的正△ABC 内任一点,L=PA +PB +PC , 求证:3≤L<2. 证明:(1)将△BP C绕B 点顺时针旋转60°的△BEF,连接PE, ∵B P=BE,∠PBE=60° ∴△PBE 是正三角形。
