七年级下几何证明题精华版
七年级数学典型几何证明50题
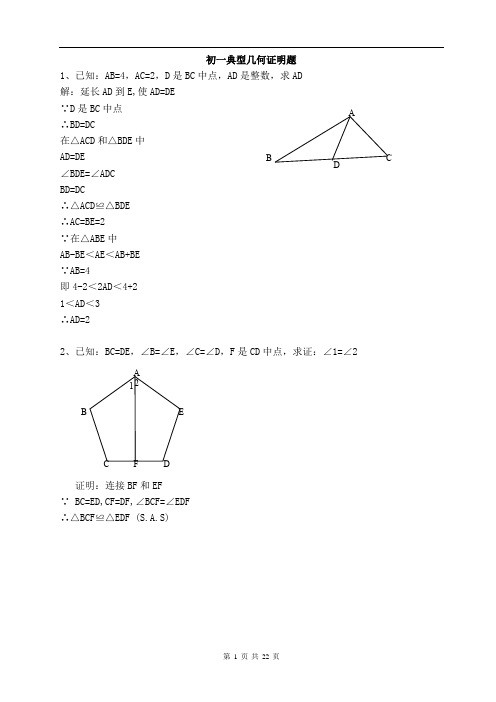
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
七年级下册数学期末考试几何大题证明必考题精选
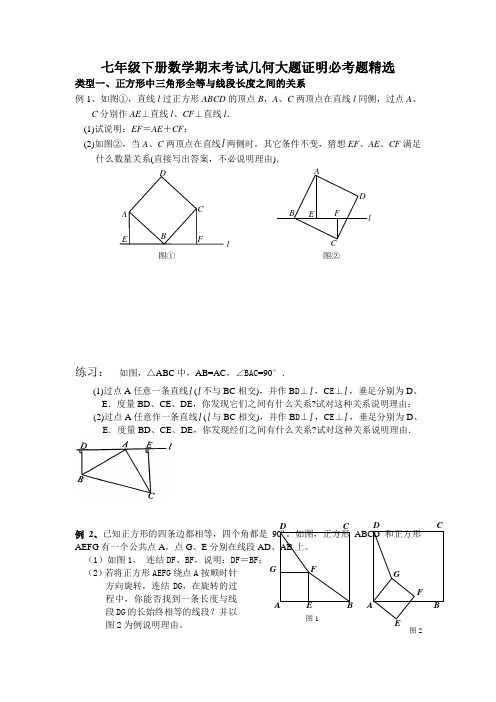
图①DA EC B Fl图②ABEF C lD 七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
(1)如图1, 连结DF 、BF ,说明:DF =BF ;(2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
A EB 图1D CG FA BD C GFE 图2练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上(1)BD 与CE 相等吗?请说明理由.(2)你能求出BD 与CE 的夹角∠BFC 的度数吗?(3)若将已知条件改为:四边形ABCD 与四边形AEFG 都是正方形,例3、正方形四边条边都相等,四个角都是90.如图,已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,点E 是直线MN 上一点,以AE 为边在直线MN 的上方作正方形AEFG .(1)如图1,当点E 在线段BC 上(不与点B 、C 重合)时: ①判断△ADG 与△ABE 是否全等,并说明理由;②过点F 作FH ⊥MN ,垂足为点H ,观察并猜测线段BE 与线段CH 的数量关系,并说明理由;(2)如图2,当点E 在射线CN 上(不与点C 重合)时: ①判断△ADG 与△ABE 是否全等,不需说明理由;F B②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度α,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C图 2FG D A 图 1F D A外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论. (4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o , R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21A B C D EP A B C DE P M(3) A B C D EP M (2) A B C D EM (P ) (1) A B C D E P M(5)C B APDEFC B E 又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中,h 1、h 2、h 3、h 之间的关系;⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的;例2、已知△ABC 是等边三角形,将一块含30角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存在,请指出这条线段,并证明;如果不存在,请说明理由.(B)CE F图1ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P ) (1)练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
(完整版)七年级几何证明题训练(含答案),推荐文档

1. 已知:如图11所示,∆ABC 中,∠=C 90于E ,且有AC AD CE ==。
求证:DE =122. 已知:如图 求证:BC =3. 已知:如图13所示,过∆ABC 的顶点A ,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ 。
设M 为BC 的中点。
求证:MP =MQ4. ∆ABC 中,∠=︒⊥BAC AD BC 90,于D ,求证:()AD AB AC BC <++14【试题答案】1. 证明:取ΘAC ADAF CDAFC =∴⊥∴∠= 又∠+∠=︒∠+∠=︒14901390,∴∠=∠=∴≅∴=∴=4312ΘAC CEACF CED ASA CF EDDE CD∆∆()2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截ΘΘCB CE BCD ECD CD CD CBD CEDB EBAC B BAC E=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22又∠=∠+∠BAC ADE E∴∠=∠∴=∴==ADE E AD AEBC CE ,3. 证明:延长PM ΘCQ AP BP BP CQ PBM ⊥∴∴∠=∠,// 又BM CM =,∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线ΘAD BC AD AEBC AE AD⊥∴<∴=>,22()ΘAB AC BCBC AB AC BC AD AB AC BC AD AB AC BC +>∴<++∴<++∴<++2414。
七年级数学典型几何证明50题

七年级数学典型几何证明50题初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)A BC DEF 21 ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF =CG ∠CGD=∠EFD又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE6、如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
版七年级几何证明题训练含答案,文档

七年级下几何证明题训练1.已知:如图11所示,ABC中,C 90,D是AB上一点,DE⊥CD于D,交BC12CEA D B图112.已知:如图12所示,在ABC中,A 2 B,CD是∠C的均分线。
求证:BC=AC+ADADB C图12-1-3.已知:如图13所示,过ABC的极点A,在∠A内任引一射线,过B、C作此射线的垂线BP和CQ。
设M为BC的中点。
求证:MP=MQAQBP图134. ABC中,BAC 90,AD BC于D,求证:AD 1ABACBC4-2-【试题答案】1.证明:取CD的中点F,连接AFC4 1F3 EA D BAC ADAF CDAFC CDE 90又 1 4 90, 1 3 9043ACCEACFCED(ASA)CFED1DE CD2剖析:此题从已知和图形上看好象比较简单,但一时又不知怎样下手,那么在证明一条线段等于两条线段之和时,我们常常采纳“截长补短”的手法。
“截长”马上长的线段截成两部分,证明这两部分分别和两条短线段相等;“补短”马上一条短线段延伸出另一条短线段之长,证明其和等于长的线段。
EADB C证明:延伸CA至E,使CE=CB,连接ED在CBD和CED中,-3-CB CEBCD ECDCD CDCBD CEDBEBAC2BBAC2EBACADEEADEE,ADAEBC CE AC AE AC AD3.证明:延伸PM交CQ于RAQ RB CMPCQ AP,BP APBP//CQPBM RCMBMCM,BMPCMRBPM CRMPM RMQM是RtQPR斜边上的中线MP MQ4.取BC中点E,连接AEAB D E CBAC 902AE BC-4-A D,ADAEBCBC2AE2ADA BACBC2 BCABACBC4 ADABACBCA D 1BCABAC4-5-。
初一下册几何证明题(完整版)

初一下册几何证明题初一下册几何证明题第一篇:初一下册几何证明题初一下册几何证明题1.已知在三角形ab中,be,f分别是角平分线,d是ef中点,若d到三角形三边b,ab,a的距离分别为x,,z,求证:x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fq,do,en都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,=h,z=dj.所以x=+z。
在正五边形abde中,m、n分别是de、ea上的点,bm与n相交于点o,若∠bon=108°,请问结论bm=n是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中,ab=a,角a=58°,ab的垂直平分线交a与n,则角nb=3°因为ab=a,∠a=58°,所以∠b=61°,∠=61°。
初一下册几何证明题(完整版)

初一下册几何证明题初一下册几何证明题第一篇:初一下册几何证明题初一下册几何证明题1.已知在三角形ab中,be,f分别是角平分线,d是ef中点,若d到三角形三边b,ab,a的距离分别为x,,z,求证:x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fq,do,en都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,=h,z=dj.所以x=+z。
在正五边形abde中,m、n分别是de、ea上的点,bm与n相交于点o,若∠bon=108°,请问结论bm=n是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中,ab=a,角a=58°,ab的垂直平分线交a与n,则角nb=3°因为ab=a,∠a=58°,所以∠b=61°,∠=61°。
七年级下几何证明题

第4题H2DC 几何说理题1、填空完成推理过程: 如图,∵AB ∥EF (已知)∴∠A+=1800() ∵DE ∥BC (已知) ∴∠DEF=() ∠ADE=()2.如图,EF ∥AD ,∠1=∠2,∠BAC=70°.将求∠AGD 的过程填写完整.因为EF ∥AD ,所以∠2=. 又因为∠1=∠2,所以∠1=∠3. 所以AB ∥. 所以∠BAC+=180°. 又因为∠BAC=70°, 所以∠AGD=.3.已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.4.已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.5.已知:如图,AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数 6、直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.49、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37o ,求∠D 的度数.50、如图,已知:21∠∠=,50=D ∠,求B ∠的度数。
51、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.52、AB//CD,EF ⊥AB 于点E ,EF 交CD 于点F ,已知∠1=600.求∠2的度数.53、如图,AB∥CD,BF∥CE,则∠B 与∠C 有什么关系?请说明理由.54.如图,已知:DE∥BC,CD 是∠ACB 的平分线,∠B=70°,∠ACB =50°,求∠EDC 和∠BDC 的度数.55.如图AB∥CD,∠NCM=90°,∠NCB=30°,CM 平分∠BCE,求∠B 的大小.56、如图,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?DEB CAENMCD BANMFDCBA57、如图,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.58、如图,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .59、如图所示,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.60、如图,在△ABC 中,∠ABC =80°,∠ACB =50°,BP 平分∠ABC ,CP 平分∠ACB ,求∠BPC 的度数.61、如图,点D 是△ABC 内一点,∠A =65°,∠1=20°,∠2=25°,求∠BDC 的度数。
初一下数学证明经典例题及答案

如图,已知D是△ABC内一点,试说明AB+AC>BD+CD 证明:延长BD交AC于E在△ABC中,AB+AE>BE,即AB+AE>BD+DE……①在△DEC中,DE+EC>DC……②①+②,得(AB+AE)+(DE+EC)>(BD+DE)+CD 即AB+(AE+EC)+DE>(BD+DE)+CD即AB+AC+DE>BD+DE+CD∴AB+AC>BD+CD如图,△ABC中,D是BC的中点,求证:(1)AB+AC>2AD(2)若AB=5,AC=3,求AD的范围。
(1)延长AD到点G,使DG=AD.连接BG在△CDA和△BDE中AD=GD,∠ADC=∠GDB∵D是BC的中点∴CD=BD∴△CDA≌△BDG.∴BG=AC在△ABG中,AB+BG=AB+BCAG=2AD因为三角形两边和大于第三边,所以AB+BE>AG ∴AB+BC>2AD(2)AB-AC<2AD<AB+ACDC BAEAB CDG2<2AD <8 1<AD <4如图,AB=AD,AC=AE,∠BAD=∠CAE=90°,点F 为DE 的中点,求证:BC=2AF. 延长AF 到点G,使AF=DF.连接GD 在△AFE 和△DFG 中 AF=GF,∠AFE=∠DFG ∵点F 为DE 的中点 ∴DF=EF所以△AFE ≌△DFG. (SAS) GD=AE=AC;∠G=∠FAE.∴DG ∥AE.(内错角相等,两直线平行)则∠GDA+∠DAE=180°.(两直线平行,同旁内角互补) 又∵∠BAC+∠DAE=180°.∴∠GDA=∠BAC.(同角的补角相等). 又∵AD=AB.∴⊿ADG ≌⊿BAC(SAS) ∴AG=BC,即2AF=BC. ∴BC=2AF.如图,AD 是△ABC 的中线,点E 在BC 的延长线上,CE=AB, ∠BAC=∠BCA 求证:AE=2AD证明:在AD 的延长线上取点F,使AD =FD,连接CF ∵AD 是中线∴BD =CD,AD =FD,∠ADB =∠FDCECDBA∴△ABD≌△FCD (SAS)∴CF=AB,∠B=∠FCD∵∠ACF=∠BCA+∠BCE,∠ACE=∠BAC+∠B,∠BAC=∠BCA∴∠ACF=∠ACE∵CE=AB∴CE=CF∴△ACE≌△ACF (SAS)∴AE=AF∵AF=AD+FD=2AD∴AE=2AD如图,△ABC中,∠ABC=90°,AC=CE,BC=CD,∠ACE=∠BCD=90°,BC的延长线交DE于F。
七年级下几何证明题

第4题H2DC 几何说理题1、填空完成推理过程: 如图,∵AB ∥EF (已知)∴∠A+=1800() ∵DE ∥BC (已知) ∴∠DEF=() ∠ADE=()2.如图,EF ∥AD ,∠1=∠2,∠BAC=70°.将求∠AGD 的过程填写完整.因为EF ∥AD ,所以∠2=. 又因为∠1=∠2,所以∠1=∠3. 所以AB ∥. 所以∠BAC+=180°. 又因为∠BAC=70°, 所以∠AGD=.3.已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.4.已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.5.已知:如图,AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数 6、直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.49、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37o ,求∠D 的度数.50、如图,已知:21∠∠=,50=D ∠,求B ∠的度数。
51、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.52、AB//CD,EF ⊥AB 于点E ,EF 交CD 于点F ,已知∠1=600.求∠2的度数.53、如图,AB∥CD,BF∥CE,则∠B 与∠C 有什么关系?请说明理由.54.如图,已知:DE∥BC,CD 是∠ACB 的平分线,∠B=70°,∠ACB =50°,求∠EDC 和∠BDC 的度数.55.如图AB∥CD,∠NCM=90°,∠NCB=30°,CM 平分∠BCE,求∠B 的大小.56、如图,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?DEB CAENMCD BANMFDCBA57、如图,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.58、如图,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .59、如图所示,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.60、如图,在△ABC 中,∠ABC =80°,∠ACB =50°,BP 平分∠ABC ,CP 平分∠ACB ,求∠BPC 的度数.61、如图,点D 是△ABC 内一点,∠A =65°,∠1=20°,∠2=25°,求∠BDC 的度数。
七年级下册数学几何证明题

七年级下册数学几何证明题七年级下册数学几何证明题一、直线平分角在平面几何中,对于给定的角,如果有一条直线能够将这个角划分成两个相等的小角,我们称这条直线是该角的平分线。
接下来我们将证明两个定理和一个引理。
定理1:如果直线ab平分角BAC,则直线ab与弧BCB′的切点C相同。
引理:如果点D在圆弧BCB′上,且点D在角BAC的平分线ab上,则BD=DC。
定理2:如果点E在角BAC的平分线ab上,且BE=CE,则直线ab平分角BAC。
证明:首先,我们先证明引理。
根据圆的性质,半径与弦垂直且平分弦。
又因为BD=DC,所以BD和DC分别是圆弧BCB′的半径,从而BD⊥BC,DC⊥BC。
又因为点D在角BAC的平分线ab上,所以BD⊥BA,DC⊥CA。
综上所述,BD⊥BA,BD⊥BC,BD是角BAC的平分线上任意一点至圆弧BCB′的切线。
同理,DC是角BAC的平分线上任意一点至圆弧BCB′的切线。
这样,我们就证明了引理。
接下来,我们证明定理1。
假设直线ab平分角BAC,且ab与弧BCB′的切点为C′。
根据引理,如果D是角BAC的平分线上的一点,且D在圆弧BCB′上,则BD=DC。
所以,当切点C与切点C′不同时,就会导致BD≠DC,与引理矛盾。
所以,点C和点C′必须是同一个点,即直线ab与弧BCB′的切点C唯一。
综上所述,我们证明了定理1。
最后,我们证明定理2。
假设点E在角BAC的平分线ab上,且BE=CE。
根据定理1,直线ab与弧BCB′的切点C唯一。
假设BE和CE分别与圆弧BCB′交于点F和G。
根据弧与切线的性质,∠BCF≤90°,∠BCG≤90°。
又因为BE=CE,所以∠BEF=∠CEG。
综上所述,∠BCF=∠BEF=∠BAC,∠BCG=∠CEG=∠BAC。
所以,直线ab平分角BAC。
综上所述,我们证明了定理2。
二、垂直平分线在平面几何中,对于给定的线段,如果有一条直线能够将这个线段划分成两个相等的小线段,并且与这个线段垂直相交,我们称这条直线是该线段的垂直平分线。
证明题七年级下册

证明题七年级下册一、相交线与平行线证明题。
1. 如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠2 : ∠1 = 4:1,求∠AOF的度数。
证明:设∠1 = x,因为∠2:∠1 = 4:1,则∠2 = 4x。
因为OE平分∠BOD,所以∠DOE=∠1 = x。
又因为∠2+∠DOE = 180°(邻补角之和为180°),即4x + x=180°,5x = 180°,解得x = 36°。
所以∠COE=180° - ∠1=180° - 36° = 144°。
因为OF平分∠COE,所以∠COF=(1)/(2)∠COE=(1)/(2)×144° = 72°。
∠AOC = ∠1 = 36°(对顶角相等)所以∠AOF=∠AOC + ∠COF = 36°+72° = 108°。
2. 已知:如图,AB∥CD,∠1 = ∠2,求证:AM∥CN。
证明:因为AB∥CD,所以∠EAB = ∠ACD(两直线平行,同位角相等)。
又因为∠1 = ∠2,所以∠EAB - ∠1=∠ACD - ∠2,即∠MAC = ∠NCA。
所以AM∥CN(内错角相等,两直线平行)3. 如图,已知∠1 = ∠2,∠C = ∠D,求证:∠A = ∠F。
证明:因为∠1 = ∠2,∠1 = ∠3(对顶角相等),所以∠2 = ∠3。
所以DB∥EC(同位角相等,两直线平行)。
所以∠D = ∠4(两直线平行,同位角相等)。
又因为∠C = ∠D,所以∠C = ∠4。
所以DF∥AC(内错角相等,两直线平行)。
所以∠A = ∠F(两直线平行,内错角相等)二、三角形证明题。
4. 在△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于F。
求证:AF=(1)/(3)AC。
证明:过点D作DG∥BF交AC于G。
七年级下几何证明题

七年级下几何证明题正文第一篇:七年级下几何证明题七年级下几何证明题学了三角形的外角吗?(三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于和它不相邻的任何一个内角)角acd>角bac>角afe角acd+角acb=180度角bac+角abc+角acb=180度所以角acd=角bac+角abc所以角角acd>角bac同理:角bac>角afe所以角acd>角bac>角afe2解∶﹙1﹚连接ac∴五边形acdeb的内角和为540°又∵∠abe+∠bed+∠cde=360°∴∠a+∠c=180°∴ab∥cd﹙2﹚过点d作ab的垂线de∵∠cad=∠bad,∠c=∠aedad为公共边∴rt△acd≌rt△aed∴ac=ae,cd=de∵∠b=45°∠deb=90°∴∠edb=45°∴de=beab=ae+be=ac+cd﹙3﹚∵腰相等,顶角为120°∴两个底角为30°根据直角三角形中30°的角所对的边为斜边的一半∴腰长=2高=16﹙4﹚根据一条线段垂直平分线上的点到线段两个端点的距离相等∴该交点到三角形三个顶点的距离相等3解∶﹙1﹚先连接ac∴五边形acdeb的内角和为540°∵∠abe+∠bed+∠cde=360°∴∠a+∠c=180°∴就证明ab∥cd♂等鴏♀栐薳20XX-05-3017:334(1)解:过e作fg∥ab∵fg∥ab∴∠abe+∠feb=180°又∵∠abe+∠cde+∠bed=360°∴∠fed+∠cde=180°∴fg∥cd∴ab∥cd(2)解:作de⊥ab于e∵ad平分∠cab,cd垂直ac,de垂直ab∴cd=de,ac=ae又∵ac=cb,de=eb,ac⊥cb,de⊥eb∴∠abc=∠edb=45°∴de=eb∴ab=ae+eb=ac+cd(3)16cm(4)3个顶点5如图已知在四边形abcd中,∠bad为直角,ab=ad,g为ad上一点,de⊥bg 交bg的延长线于e,de的延长线与ba的延长线相交于点f。
初一下几何证明题
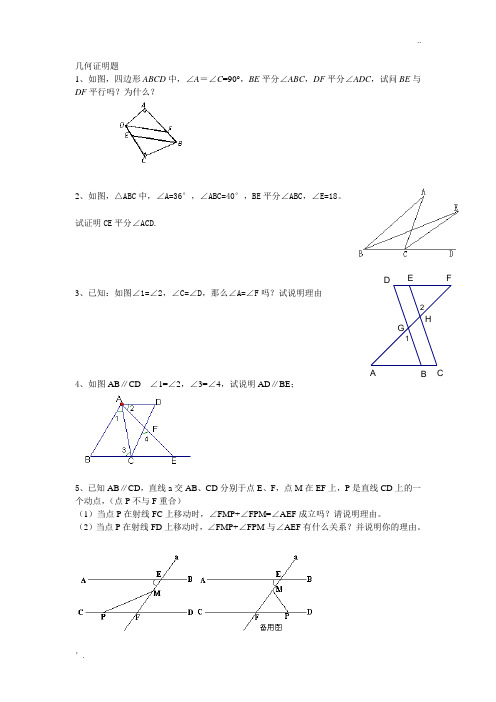
几何证明题1、如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,试问BE与DF平行吗?为什么?2、如图,△ABC中,∠A=36°,∠ABC=40°,BE平分∠ABC,∠E=18。
试证明CE平分∠ACD.3、已知:如图∠1=∠2,∠C=∠D,那么∠A=∠F吗?试说明理由4、如图AB∥CD ∠1=∠2,∠3=∠4,试说明AD∥BE;5、已知AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,P是直线CD上的一个动点,(点P不与F重合)(1)当点P在射线FC上移动时,∠FMP+∠FPM=∠AEF成立吗?请说明理由。
(2)当点P在射线FD上移动时,∠FMP+∠FPM与∠AEF有什么关系?并说明你的理由。
H G2 1FEDCBA6、如图,E 、F 分别是AB 、CD 上一点,D ∠=∠2,1∠与C ∠互余, AF EC ⊥. 试说明CD AB //7、如图,已知ABC ∆,AD BC ⊥于D ,E 为AB 上一点,EF BC ⊥于F ,//DG BA 交CA 于G .求证12∠=∠.8、如图5-29,已知:AB //CD ,求证:∠B +∠D +∠BED =360︒(至少用三种方法)EABCD9、如图,已知AB ∥CD ,∠1:∠2:∠3=1:2:3,求证:BA 平分∠EBF10、已知,如图,AB ∥CD ∥GH ,EG 平分∠BEF ,FG 平分∠EFD 求证:∠EGF=90°1AE 2 3 FCDDG A E B H CF 1 23 4。
七年级下几何证明题(精华版)
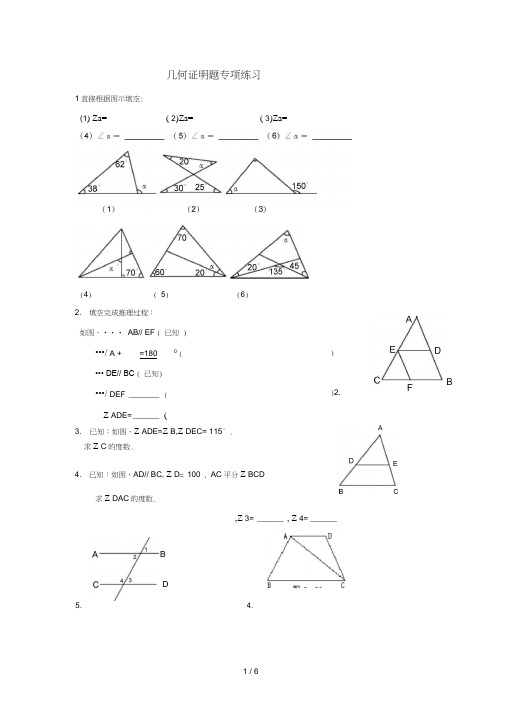
几何证明题专项练习1直接根据图示填空:(1) Za= ___________ ( 2)Za= _____________ ( 3)Za= _____________2. 填空完成推理过程:如图,••• AB// EF ( 已知 )•••/ A +=180(••• DE// BC ( 已知)•••/ DEF _______ ( Z ADE= ______ (3. 已知:如图,Z ADE=Z B,Z DEC= 115° .求Z C 的度数.4. 已知:如图,AD// BC, Z D = 100°, AC 平分Z BCD求Z DAC 的度数.))2.,Z 3= ______ , Z 4= ______5.4.(4)( 5) (6)FB D5. _________________________________ 已知AB// CD Z 1=70° 则Z 2= _________________________________& 如图,AE//CD,EF 分别交AE、CD 于M、N,/EME =MF,MG交CD于G,求/I的度数10. 如图,已知:仁2 , D =50,求B的度数。
11. 已知:如图,AB/CD,/B=4O°,/E=3O O,求/ D的度数12. 如图所示,/仁72 ° , / 2=72°,/3=60°,求/ 4的度数.13. 如图,AB//CD , AE交CD于点C, DE I AE,垂足为E,/ A=37°,14. A B//CD,EF 丄AB于点E,已知/ 1=600.求/ 2的度数.50° ,MG平分/E 求/D的度数.15.6.已知:如图4, AB// CD 直线EF分别交AB CD于点E、F,Z BEF的平分线与/ DEF的平分线相交于点P.求/ P的度数八7•直线AB、CD相交于O, OE 平分/ AOC / EOA / AOD=1 4,求/ EOB的度数.EF交CD于点F,13.L D15. 如图所示,把一张长方形纸片ABCD沿EF折叠,若/ EFG=50 ,求/ DEG的度数.个关系中任选一个加以说明17•如图,AB // CD ,19. 如图AE//CD,/ NCM = 90° / NCB = 30° CM 平分/ BCE ,求/ B 的大小. 20. 如图 5-24, AB 丄BD , CD 丄 MN ,垂足分别是 B 、D 点,/ FDC= / EBA .(1) 判断CD 与AB 的位置关系; (2) BE 与DE 平行吗?为什么?20.图 5-25BF // CE ,则/ B 与/ C 有什么关系?请说明理由./ BDC 的度数.18.N图 5-24 A21. 如图5-25,/ 1+ / 2=180 ° / DAE= / BCF , DA 平分/ BDF .(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分/ DBE吗?为什么.22. 如图5-28,已知:E 、F 分别是 AB 和CD 上的点,DE 、AF 分别交BC 于G 、H , A= D ,2,求证:0 0 023 如图,CD 是/ ACB 的平分线,/ EDC= 25,/ DCE= 25 ,/ B= 7°证:DE//BC ②求/ BDC 的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
34ﻩ33ﻩ32
33.如图,AB//CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=370,
求∠D的度数.
34.如图,AB//CD,EF⊥AB于点E,EF交CD于点F,
已知∠1=600.求∠2的度数.
35.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=500,∠C=600,
29.如图所示,AB∥ED,∠B=48°,∠D=42°,BC垂直于CD吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.
30.如图,已知:DE∥BC,CD是∠ACB的平分线,∠B=70°,
∠ACB=50°,求∠EDC和∠BDC的度数.
31.AD∥BC,AB∥DC,∠1=100º,求∠2,∠3的度数
ﻩ14.13.
14.AB//CD,EF⊥AB于点E,EF交CD于点F,
已知∠1=600.求∠2的度数.
15.如图所示,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,求∠DEG的度数.
15.
16. 如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系, 请你从所得的四个关系中任选一个加以说明.
38.如图,∠1=20°,∠2=25°,∠A=35°,求∠BDC的度数。38
39.如图,∠C=48°,∠E=25°,∠BDF=140°,求∠A与∠EFD的度数。
40.如图△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠EDF=________。
40
41.如图所示,已知∠A=∠1,∠E=∠2,且AC⊥EC,试证明:AB∥DE.
25、如图5,AO⊥CO,BO⊥DO,且∠AOB= ,求∠COD的度数。
ﻩ26
26.如图,已知:AB//CD,求证: B+ D+ BED= (至少用三种方法)
27.直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.
28、如图,已知OB平分∠AOC,且∠2:∠3:∠4=2:5:3,求∠1,∠2,∠3,∠4的度数.
(4)∠α=_________(5)∠α=_________(6)∠α=_________
(1) (2) (3)
(4) (5) (6)
2、填空完成推理过程:
如图,∵AB∥EF( 已知 )
∴∠A +=1800( )
∵DE∥BC( 已知 )
∴∠DEF=( )2.
∠ADE=()
3.已知:如图,∠ADE=∠B,∠DEC=115°.
求∠C的度数.
4.已知:如图,AD∥BC,∠D=100°,AC平分∠BCD,
求∠DAC的度数.3.
5.已知AB∥CD,∠1=70°则∠2=_______,∠3=______,∠4=______
5. ﻩ4.
6. 已知:如图4, AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求∠P的度数
ﻩ12.
9.
ﻩ10.ﻩ11.
10.如图,已知: , ,求 的度数。
11.已知:如图,AB∥CD,∠B=400,∠E=300,求∠D的度数
12.如图所示,∠1=ቤተ መጻሕፍቲ ባይዱ2°,∠2=72°,∠3=60°,求∠4的度数.
13,如图,AB//CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=370,ﻩ
求∠D的度数.
6.7.ﻩ8.
7.直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.
8.如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
9.如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,求∠D的度数.
七年级下几何证明题(精华版)
———————————————————————————————— 作者:
———————————————————————————————— 日期:
几何证明题专项练习
1、直接根据图示填空:
(1)∠α=_________(2)∠α=_________(3)∠α=_________
20.如图5-24,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DE平行吗?为什么?
21.如图5-25,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
20.ﻩ
22.如图5-28,已知:E、F分别是AB和CD上的点,DE、AF分别交BC于G、H, A= D, 1= 2,求证: B= C.
ﻫ23.22.24.
.
23如图,CD是∠ACB的平分线,∠EDC= ,∠DCE= ,∠B=
证:DE//BC②求∠BDC的度数。
24、如图,AB、CD相交于点O,∠DOE= ,∠AOC= ,求∠BOC,∠BOE的度数。
(1) (2) (3) (4)
17.如图,AB∥CD,BF∥CE,则∠B与∠C有什么关系?请说明理由.
18.如图,已知:DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.
19.如图AB∥CD,∠NCM=90°,∠NCB=30°,CM平分∠BCE,求∠B的大小.
42、如图,已知∠A=∠F,∠C=∠D.试问BD是否与CE平行?为什么?
求∠DAC及∠BOA
36
ﻩ
37
36.如图,A岛在B岛的北偏东52°方向,A岛在C岛北偏西31°方向,从A岛看B、C两岛的视角∠BAC是多少度?(提示:过A点作AD∥BE)
37.如图7-37,在△ABC中,已知AD是△ABC角平分线,DE是△ADC的高线,∠B=600,
∠C=450, 求∠ADB和∠ADE的度数.
