最优化问题的数学模型及其分类
多目标最优化数学模型

第六章 最优化数学模型§1 最优化问题1.1 最优化问题概念 1.2 最优化问题分类1.3 最优化问题数学模型 §2 经典最优化方法 2.1 无约束条件极值 2.2 等式约束条件极值 2.3 不等式约束条件极值 §3 线性规划 3.1 线性规划 3.2 整数规划§4 最优化问题数值算法 4.1 直接搜索法 4.2 梯度法 4.3 罚函数法§5 多目标优化问题 5.1 多目标优化问题 5.2 单目标化解法 5.3 多重优化解法 5.4 目标关联函数解法 5.5 投资收益风险问题第六章 最优化问题数学模型 §1 最优化问题1.1 最优化问题概念 (1)最优化问题在工业、农业、交通运输、商业、国防、建筑、通信、政府机关等各部门各领域的实际工作中,我们经常会遇到求函数的极值或最大值最小值问题,这一类问题我们称之为最优化问题。
而求解最优化问题的数学方法被称为最优化方法。
它主要解决最优生产计划、最优分配、最佳设计、最优决策、最优管理等求函数最大值最小值问题。
最优化问题的目的有两个:①求出满足一定条件下,函数的极值或最大值最小值;②求出取得极值时变量的取值。
最优化问题所涉及的内容种类繁多,有的十分复杂,但是它们都有共同的关键因素:变量,约束条件和目标函数。
(2)变量变量是指最优化问题中所涉及的与约束条件和目标函数有关的待确定的量。
一般来说,它们都有一些限制条件(约束条件),与目标函数紧密关联。
设问题中涉及的变量为n x x x ,,,21 ;我们常常也用),,,(21n x x x X 表示。
(3)约束条件在最优化问题中,求目标函数的极值时,变量必须满足的限制称为约束条件。
例如,许多实际问题变量要求必须非负,这是一种限制;在研究电路优化设计问题时,变量必须服从电路基本定律,这也是一种限制等等。
在研究问题时,这些限制我们必须用数学表达式准确地描述它们。
最优化方法第一章最优化问题与凸分析基础

4.2 凸函数
定义: 设集合 S Rn 为凸集,函数 f :SR, 若 x(1), x(2) S, ( 0 , 1 ) ,均有
f( x(1)+(1- ) x(2) ) ≤f(x(1))+(1- )f(x(2)) , 则称 f(x) 为凸集 S 上的凸函数。
hi x 0 等式约束
称满足所有约束条件的向量 x为可行解,或可行点,全体
可行点的集合称为可行集,记为D 。
D {x | hi x 0, i 1, 2, m, g j x 0,
j 1, 2, p, x Rn } 若 hi ( x), g j ( x) 是连续函数,则D 是闭集。
2.3 Hesse矩阵
Hesse 矩阵:多元函数 f (x) 关于 x 的二阶偏导
数矩阵
2
f
X
x12
2
f
X
f
X
2 f X
x1 x2
2
f
X
x1xn
2 f X
x2x1
2 f X
x22
2 f X
x2 xn
2
f
X
xnx1
2
f
X
xnx2
2
f
X
xn2
例:求目标函数 f (x) x12 x22 x32 2x1x2 2x2x3 3x3 的梯度和Hesse矩阵。
若进一步有上面不等式以严格不等式成立,则称
f(x) 为凸集 S 上的严格凸函数。 当- f(x) 为凸函数(严格凸函数)时,则称 f(x) 为
凹函数(严格凹函数)。
严格凸函数
最优化问题数学模型

• 进入该区域的飞机在到达区域边缘时,与区域内 飞机的距离应在60km以上;
根据当年竞赛题目给出的数据,可以验证 新进入的飞机与区域内的飞机的距离超过 60公里。
• 最多需考虑六架飞机;
cij xij 表示该队员的成 目标函数:当队员i入选泳姿j时, 绩,否则 cij xij 0 。于是接力队的成绩可表示为
f cij xij .
j 1 i 1
4
5
约束条件:根据接力队要求, xij 满足约束条件
a. 每人最多只能入选4种泳姿之一,即
x
j 1
4
ij
1.
b. 每种泳姿必须有1人而且只能有一人入选,即
分析,对实际问题进行合理的假设、简化,首先考虑用
线性规划模型,若线性近似误差较大时,则考虑用非线 性规划.
例题讲解
例1 1995年全国数学建模A题:飞行管理问题 在约1万米的高空的某边长为160km的正方 形区域内,经常有若干架飞机作水平飞行,区 域内每架飞机的位置和速度向量均由计算机记 录其数据,以便进行飞行管理。当一架欲进入 该区域的飞机到达区域边缘时,计算机记录其 数据后,要立即计算并判断是否会发生碰撞。 若会发生碰撞,则应计算如何调整各架飞机 (包括新进入的飞机)飞行的方向角,以避免 碰撞,且使飞机的调整的幅度尽量小,
目标:求函数极值或最值,求取得极值时变量的取值。
x
1.线性规划
问题:某工厂在计划期内要安排生产I、II两种产品,已 知生产单位产品所需的设备台时及A、B两种原材料的消 耗,如下表所示
I 设备 1 II 2 8台时
第一章 最优化问题概述

43
黄金分割法
若第一次选取的试点为x1<x2,则下一步保留的 区间为[a,x2]或[x1,b],两者的机会是均等的. 因此我们选取试点时希望x2-a=b-x1. 设x1=a+p(b-a),则x2=a+(1-p)(b-a). x2 x1 a
26
可行方向
定义1.2.2(可行方向) 已知区域 , x k∈ D , 对于向量pk≠0,若存在实数b >0, 使得对任意的 a∈(0,b ),有:xk+apk∈D, 则称pk为点xk处关于区域D的可行方向. 对于D的内点(存在邻域包含于D),任意方向可 行,对于边界点(任意邻域既有D的点也有不在D 中的点),则有些方向可行,有些方向不可行. 若下降方向关于域D可行,则称为可行下降方向.
29
收敛速度
定义1.2.3 设序列{xk}收敛于x*,而且
若0<b<1,则称{xk}为线性收敛的,称b为收敛比;
若b=0,则称{xk}为超线性收敛的.
定义1.2.4 设序列{xk}收敛于x*,而且
则称{xk}为p阶收敛.
30
终止准则
对于一种算法,应该有某种终止准则,当某次迭代 满足终止准则时,就停止迭代.常用的终止准则有:
21
最优化问题的分类
根据数学模型中有无约束函数分为有约束的 最优化问题和无约束的最优化问题. 根据目标函数和约束函数的函数类型分类:线 性最优化问题,非线性最优化问题,二次规划, 多目标规划,动态规划,整数规划,0-1规划.
22
§1.2 最优化问题的一般算法
23
迭代算法
迭代算法 选取一个初始可行点x0∈D,由这个 初始可行点出发,依次产生一个可行点列: x1,x2,· · · ,xk,· · · , 记为{xk},使得某个xk恰好是问题的一个最优解, 或者该点列收敛到问题的一个最优解x*. 下降算法 在迭代算法中一般要求 f(xk+1)≤f(xk).
最优化问题的数学模型
为凸集.
1,
0 证明: x , y 为超球中的任意两点, 设
则有:
x 1 y
r ???
x 1 y
r r r 1
即点 x 1 y 属于超球
所以超球为凸集.
注: 常见的凸集:空集,整个欧氏空间 超平面: H
T
aR
n
和实数
,
使得: T x a
a y , x D ,
xR a x
n T
即存在超平面 H y 与凸集 D .
严格分离点
注: 点与闭凸集的分离定理。
y.
D
定理
(点与凸集的分离定理)
是非空凸集,x D, 则存在 非零向量 a R n 使成立
DR
n
目标函数
R ( i 1, 2 , , p )
1
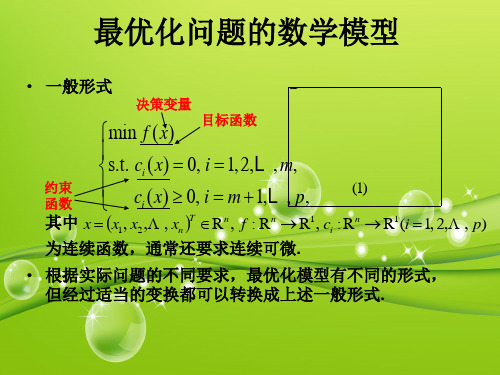
• 根据实际问题的不同要求,最优化模型有不同的形式, 但经过适当的变换都可以转换成上述一般形式.
最优化问题的分类
最优化问题
根据约束条件 分类
m in f ( x ), x R .
n
无约束最优化问题 约束最优化问题 等式约束最优化问题 不等式约束最优化问题 混合约束优化问题
设
a xa x
T T
x D . ( D代 表 D 的 闭 包 )
_ _
定理
(两个凸集的分离定理)
n
x
x
设 D1 , D2 是
且 R 的两个非空凸集, D1 D2 ,
则存在超平面分离 D1 和 D2 , 即存在非零向量 n a R 使得 aT x aT y , x D , y D . 1 2
最优化问题数学模型

最优化问题数学模型在我们的日常生活和各种实际应用中,最优化问题无处不在。
从生产线上的资源分配,到物流运输中的路径规划,从金融投资中的资产配置,到工程设计中的参数选择,都需要找到最优的解决方案,以实现效率最高、成本最低、效益最大等目标。
而数学模型就是帮助我们解决这些最优化问题的有力工具。
那么,什么是最优化问题数学模型呢?简单来说,它是将实际问题转化为数学语言和表达式的一种方式,通过建立数学关系式,来描述问题中的各种约束条件和目标函数,然后运用数学方法和算法求解,找到最优的决策变量取值。
举个简单的例子,假设一家工厂要生产两种产品 A 和 B,生产 A 产品每件需要消耗 2 个单位的原材料和 3 个小时的工时,生产 B 产品每件需要消耗 3 个单位的原材料和 2 个小时的工时。
工厂共有 100 个单位的原材料和 80 个小时的工时可用,每件 A 产品的利润是 5 元,每件 B 产品的利润是 4 元。
那么,如何安排生产才能使工厂的总利润最大呢?为了建立这个问题的数学模型,我们首先定义决策变量:设生产 A 产品的数量为 x 件,生产 B 产品的数量为 y 件。
然后,我们确定目标函数,即要最大化的总利润:Z = 5x + 4y 。
接下来,考虑约束条件。
原材料的限制可以表示为:2x +3y ≤ 100 ;工时的限制可以表示为:3x +2y ≤ 80 ;还有非负约束:x ≥ 0 ,y ≥ 0 。
这样,我们就建立了一个简单的最优化问题数学模型。
通过求解这个模型,就可以得到最优的生产方案,即 x 和 y 的取值,使得总利润Z 最大。
最优化问题数学模型的类型多种多样,常见的有线性规划、非线性规划、整数规划、动态规划等。
线性规划是最简单也是应用最广泛的一种模型。
它的目标函数和约束条件都是线性的,就像我们上面的例子。
线性规划问题可以通过单纯形法等有效的算法在较短的时间内求解。
非线性规划则是目标函数或约束条件中至少有一个是非线性的。
优化问题中的数学规划模型

优化问题中的数学规划模型优化问题中的数学规划模型1.优化问题及其一般模型优化问题是人们在工程技术、经济管理和科学研究等领域中最常遇到的问题之一。
例如:设计师要在满足强度要求等条件下选择材料的尺寸,使结构总重量最轻;公司经理要根据生产成本和市场需求确定产品价格,使所获利润最高;调度人员要在满足物质需求和装载条件下安排从各供应点到需求点的运量和路线,使运输总费用最低;投资者要选择一些股票、债券下注,使收益最大,而风险最小等等。
一般地,优化模型可以表述如下:minz?f(x)s.t.gi(x)?0,i=1,2,?,m (1.1)这是一个多元函数的条件极值问题,但是许多实际问题归结出的这种优化模型,其决策变量个数n和约束条件个数m一般较大,并且最优解往往在可行域的边界上取得,这样就不能简单地用微分法求解,数学规划就是解决这类问题的有效方法。
2.数学规划模型分类“数学规划是运筹学和管理科学中应用及其广泛的分支。
在许多情况下,应用数学规划取得的如此成功,以致它的用途已超出了运筹学的范畴,成为人们日常的规划工具。
”[H.P.Williams.数学规划模型的建立]。
数学规划包括线性规划、非线性规划、整数规划、几何规划、多目标规划等,用数学规划方法解决实际问题,就要将实际问题经过抽象、简化、假设,确定变量与参数,建立适当层次上的数学模型,并求解。
3.建立数学规划模型的步骤当你打算用数学建模的方法来处理一个优化问题的时候,首先要确定寻求的决策是什么,优化的目标是什么,决策受到那些条件的限制(如果有限制的话),然后用数学工具(变量、常数、函数等)表示它们,最后用合适的方法求解它们并对结果作出一些定性、定量的分析和必要的检验。
Step 1. 寻求决策,即回答什么?必须清楚,无歧义。
阅读完题目的第一步不是寻找答案或者解法,而是…… Step 2. 确定决策变量第一来源:Step 1的结果,用变量固定需要回答的决策第二来源:由决策导出的变量(具有派生结构)其它来源:辅助变量(联合完成更清楚的回答) Step 3. 确定优化目标用决策变量表示的利润、成本等。
数学建模第三章

数学建模第三章第三章⾮线性最优化⽅法§3.1 最优化问题与建模⼀. 基本概念:因为⼈类所从事的⼀切⽣产或社会活动均是有⽬的的,其⾏为总是在特定的价值观念或审美取向的⽀配下进⾏的,经常⾯临求解⼀个可⾏的甚⾄是最优的⽅案的决策问题。
可以说,最优化思想是数学建模的灵魂。
⽽最优化⽅法作为⼀门特殊的数学学科分⽀有着⼴泛的实际应⽤背景。
典型的最优化模型可以被描述为如下形式:其中表⽰⼀组决策变量,通常在实数域内取值,称决策变量的函数为该最优化模型的⽬标函数;为维欧⽒空间的某个⼦集,通常由⼀组关于决策变量的等式或不等式刻画,形如:这时,称模型中关于决策变量的等式或不等式、为约束条件,⽽称满⾜全部约束条件的空间中的点为该模型的可⾏解,称,即由所有可⾏解构成的集合为该模型的可⾏域。
称为最优化模型的(全局)最优解,若满⾜:对均有,这时称处的⽬标函数值的为最优化模型的(全局)最优值;称为最优化模型的局部最优解,若存在,对,均有。
(全局)最优解⼀定是局部最优解,但反之不然,其关系可由下图得到反映:上图为函数在区间上的⼀段函数曲线(由Mathematica绘制),如果考察最优化问题,从图中发现它有三个局部最优解、、,其中是全局最优解,最优值为“”。
⼆. 最优化问题的⼀些典型的分类:优化⽅法涉及的应⽤领域很⼴,问题种类与性质繁多,根据不同的原则可以给出不同的分类。
从数学建模的⾓度,对最优化问题的⼀些典型分类及相关概念的了解是有益的。
根据决策变量的取值类型,可分为函数优化问题与组合优化问题,称决策变量均为连续变量的最优化问题为函数优化问题;若⼀个最优化问题的全部决策变量均离散取值,则称之为组合优化问题。
⽐⽅⼀些最优化问题的决策变量被限定只能取整数值,即为组合最优化问题,这类优化问题通常被称为整数规划问题,另外⼤多⽹络规划问题属于组合最优化问题。
当然,也有许多应⽤问题的数学模型表现为混合类型的,即模型的部分决策变量为连续型的,部分决策变量为离散型的;另外当谈论⼀个最优化问题是函数优化问题还是组合优化问题时,还需结合我们对这⼀问题的思考⽅式来进⾏确定,⽐⽅后⾯介绍的线性规划问题的求解,既有将其作为⼀个组合优化问题⽽开发的算法,也有将其作为⼀个函数优化问题⽽开发的算法;另外的⼀种分类⽅式是根据问题中⽬标、约束条件函数的形式或性质来加以划分的:若⼀个最优化问题的⽬标、约束条件函数均为决策变量的线性函数,则称之为线性规划问题,否则称之为⾮线性最优化问题。
最优化方法试卷与答案5套

《最优化方法》1一、填空题:1 •最优化问题的数学模型一般为:_____________________________ ,其中___________ 为目标函数, _____________ 为约束函数,可行域D可以表示为 _______________________________ ,若 _______________________________ ,称x*为问题的局部最优解,若 _________________________________________ 称X*为问题的全局最优解。
2 •设f(x)= 2x1 2x1X2 X i 5X2 ,则其梯度为_______________________ ,海色矩阵___________ ,令x (1,2)T,d (1,0)T,则f(x)在x处沿方向d的一阶方向导数为___________ 几何意义为________________________________________ 二阶方向导数为 ____________________ ,几何意义为_____________________________3 •设严格凸二次规划形式为:min f (x) 2x; 2x| 2x1x2s.t. 2x1x21x10x20则其对偶规划为4•求解无约束最优化问题:min f(x), x R n,设x k是不满足最优性条件的第k 步迭代点,则:用最速下降法求解时,搜索方向d k= ___________用Newton法求解时,搜索方向d k= ____________用共轭梯度法求解时,搜索方向 d k= ________________二.(10分)简答题:试设计求解无约束优化问题的一般下降算法。
三.(25分)计算题1. (10分)用一阶必要和充分条件求解如下无约束优化问题的最优解:3 2min f (x) 2x! 3为6x^2(^ x21).2. ( 15分)用约束问题局部解的一阶必要条件和二阶充分条件求约束问题:min f (x) x1x22 2s.t. c(x) % X2 1 0的最优解和相应的乘子。
数学建模 最优化方法建模及实现

max Z 400 x1 900 x2 500 x3 200 x4 40 x1 75 x2 30 x3 15 x4 800 300 x 400 x 200 x 100 x 2000 1 2 3 4 s.t. 40 x1 75 x2 500 x1 3, x2 2, 5 x3 10, 5 x4 10
实际问题中的优化模型maxminx决策变量fx目标函数x0约束条件数学规划线性规划lp二次规划qp非线性规划nlp纯整数规划pip混合整数规划mip整数规划ip01整数规划一般整数规划连续规划优化模型的分类线性规划问题的求解在理论上有单纯形法在实际建模中常用以下解法
实验07 最优化方法建模及实现
实验目的
优化模型的分类
实际问题中 Min(或Max) z f ( x), x ( x1 , x n )T 的优化模型 s.t. g i ( x) 0, i 1,2, m x~决策变量 线性规划(LP) 二次规划(QP) 非线性规划(NLP) f(x)~目标函数 数学规划 0-1整数规划 一般整数规划 纯整数规划(PIP) 混合整数规划(MIP) gi(x)0~约束条件
例3: 任务分配问题:某车间有甲、乙两台机床,可用于加 工三种工件。假定这两台车床的可用台时数分别为800和900, 三种工件的数量分别为400、600和500,且已知用三种不同车 床加工单位数量不同工件所需的台时数和加工费用如下表。 问怎样分配车床的加工任务,才能既满足加工工件的要求, 又使加工费用最低?
1、了解最优化问题的基本内容。
2、掌握线性规划及非线性规划建模及其MATLAB实现。 3、基于最优化方法建模及实现、论文写作。
实验内容
1、基础知识、例子。
最优化方法教案

第一章最优化问题及数学预备知识最优化分支:线性规划,整数规划,几何规划,非线性规划,动态规划。
又称规划论。
应用最优化方法解决问题时一般有以下几个特点:1. 实用性强2. 采用定量分析的科学手段3. 计算量大,必须借助于计算机4. 理论涉及面广应用领域:工业,农业,交通运输,能源开发,经济计划,企业管理,军事作战……。
§1.1 最优化问题实例最优化问题:追求最优目标的数学问题。
经典最优化理论:(1) 无约束极值问题:),,,(opt 21n x x x f(),,,(m in 21n x x x f 或),,,(m ax 21n x x x f )其中,),,,(21n x x x f 是定义在n 维空间上的可微函数。
解法(求极值点):求驻点,即满足⎪⎪⎩⎪⎪⎨⎧='='='0),,(0),,(0),,(11121n x n x n x x x f x x f x x f n并验证这些驻点是否极值点。
(2) 约束极值问题:),,,(opt 21n x x x fs.t. )(,,2,1,0),,,(21n l l j x x x h n j <==解法:采用Lagrange 乘子法,即将问题转化为求Lagrange 函数),,(),,,(),,;,,,(1121121n j j lj n l n x x h x x x f x x x L λλλ∑=+=的无约束极值问题。
近代最优化理论的实例:例1 (生产计划问题) 设某工厂有3种资源B 1,B 2,B 3,数量各为b 1,b 2,b 3,要生产10种产品A 1,…,A 10 。
每生产一个单位的A j 需要消耗B i 的量为a ij ,根据合同规定,产品A j 的量不少于d j ,再设A j 的单价为c j 。
问如何安排生产计划,才能既完成合同,又使总收入最多?(线性规划问题)数学模型:设A j 的计划产量为 j x ,z 为总产值。
最优化问题的数学模型

最优化问题的数学模型《最优化问题的数学模型》嘿,同学们!你们知道什么是最优化问题的数学模型吗?这可真是个超级有趣又有点复杂的东西呢!就好像我们玩游戏,想要用最少的时间通过最多的关卡,这就是在找一种最优的方法,对吧?那最优化问题的数学模型就像是我们玩游戏时的攻略秘籍!有一次,我们数学老师在课堂上给我们出了一道题。
她说:“假如你要去商店买东西,手里只有20 块钱,商店里有铅笔1 块钱一支,笔记本3 块钱一本,橡皮5 毛钱一块,那怎么买才能让这20 块钱花得最值?” 这就是一个小小的最优化问题呀!我当时就想,哎呀,这可咋办?要是都买铅笔,能买20 支,可要是都买笔记本,只能买6 本还多2 块钱。
这就好像是在选择走不同的路,哪条路能让我们到达更好的地方呢?同桌小明凑过来跟我说:“我觉得多买点笔记本好,能记好多笔记呢!” 我摇摇头说:“可是铅笔也很有用呀,能写好多字。
” 这时候,学习委员小红发言了:“咱们得算算,怎么搭配才能让买的东西又多又有用。
” 我们大家都纷纷点头,觉得她说得有道理。
然后我们就开始算呀算,就像一群小数学家。
最后发现,如果买5 本笔记本,5 支铅笔,20 块橡皮,这样就能把20 块钱花得刚刚好,而且东西也都很实用。
这只是一个小小的例子,其实在生活中,最优化问题的数学模型无处不在呢!比如说,工厂生产东西,怎么安排生产计划能让成本最低、产量最高?物流公司送货,怎么规划路线能最快最省钱地把货物送到目的地?这难道不像我们在玩拼图游戏,要找到最合适的那块拼图,才能拼出最完美的图案吗?再想想,如果没有最优化问题的数学模型,那得多乱呀!就像做饭没有菜谱,不知道放多少盐多少油,做出来的饭能好吃吗?所以呀,最优化问题的数学模型真的超级重要!它能帮助我们在各种各样的情况中找到最好的解决办法,让我们的生活变得更有条理,更有效率。
我觉得,我们一定要好好学数学,掌握这个神奇的工具,这样才能在生活这个大舞台上,跳出最精彩的舞步!。
最优化设计:第1章 最优化基本要素

1.4 最优化问题的数学模型及分类
根据以上讨论,由优化变量、目标函
数和约束条件三要素所组成的最优化问题 的数学模型可表述为:在满足约束条件的 前提下,寻求一组优化变量,使目标函数 达到最优值。一般约束优化问题数学模型 的基本表达方式为
min f ( x)
s.t. hl ( x) 0
gm(x) 0
目标函数的极小化可表示为
f (x) min 或 min f (x) 目标函数的极大化可表示为
f (x) max 或 max f (x)
求目标函数的极大化等效于求目标函
数的极小化,为规范起见,将求目标函数 的极值统一表示为求其极小值。
在优化问题中,如只有一个目标函数,
则其为单目标函数优化问题;如有两个或 两个以上目标函数,则其为多目标函数优 化问题。目标函数越多,对优化的评价越 周全,综合效果也越好,但是问题的求解 也越复杂。
度分类,以下是一些常见的分类和名称。
(1)按照约束的有无可分为无约束优化 问题和有约束优化问题。
(2)按照优化变量的个数可分为一维优 化问题和多维优化问题。
(3)按照目标函数的数目可分为单目标优 化问题和多目标优化问题。 (4)按照目标函数与约束条件线性与否可 分为线性规划问题和非线性规划问题。当 目标函数是优化变量的线性函数,且约束 条件也是优化变量的线性等式或不等式时, 称该优化问题为线性规划问题;当目标函 数和约束条件中至少有一个是非线性时, 称该优化问题为非线性规划问题。 (5)当目标函数为优化变量的二次函数, 和均为线性函数时,称该优化问题称为二 次规划问题。
对同一优化目标来说,约束条件越多, 可行域就越小,可供选择的方案也就越少, 计算求解的工作量也随之增大。所以,在 确定约束条件时,应在满足要求的前提下, 尽可能减少约束条件的数量。同时也要注 意避免出现重复的约束,互相矛盾的约束 和线性相关的约束。 例1-1 分析以下约束优化问题的可行和非 可行区域。
数学建模-最优化模型共48页

1、无约束极值问题的求解
例1:求函数y=2x3+3x2-12x+14在区间[-3,4]上的最 大值与最小值。
解:令f(x)=y=2x3+3x2-12x+14
f’(x)=6x2+6x-12=6(x+2)(x-1) 解方程f’(x)=0,得到x1= -2,x2=1,又 由于f(-3)=23,f(-2)=34,f(1)=7,f(4)=142, 综上得, 函数f(x)在x=4取得在[-3,4]上得最大值f(4)=142,在 x=1处取得在[-3,4]上取得最小值f(1)=7
xmax=x fmax=-fval
MATLAB(wliti2)
运算结果为: xmax = 0.5000,fmax =2.0000.即剪掉的正方形的边 长为0.5m时水槽的容积最大,最大容积为2m3.
2.多元函数无约束优化问题
标准型为:min F ( X )
命令格式为: (1)x= fminunc(fun,X0 );或x=fminsearch(fun,X0 ) (2)x= fminunc(fun,X0 ,options);
或x=fminsearch(fun,X0 ,options) (3)[x,fval]= fminunc(...);
或[x,fval]= fminsearch(...) (4)[x,fval,exitflag]= fminunc(...);
或[x,fval,exitflag]= fminsearch (5)[x,fval,exitflag,output]= fminunc(...);
解 设剪去的正方形的边长为 x ,则水槽的容积为: (3 2x)2 x
建立无约束优化模型为:min y =- (3 2x)2 x , 0< x <1.5
最优化理论:理解最优解和最优化算法

局部最优解和全局最优解
全局最优解:在整个解空间中 的最优解,是真正的最优解
局部最优解和全局最优解的 区别与联系
局部最优解:在一定范围内的 最优解,不一定是全局最优
如何从局部最优解过渡到全 局最优解
最优解的性质
唯一性:在一定条件下,最优解是唯一的 存在性:在一定条件下,一定存在最优解 稳定性:在一定条件下,最优解是稳定的 可行性:在一定条件下,最优解是可行的
求解方法:常见的求 解线性规划的方法有 单纯形法、椭球法等。
优缺点:线性规划具有 简单易行、计算量小等 优点,但也可能存在无 解或无穷多解的情况。
非线性规划
定义:求解非线性 函数的最优解的问 题
特点:约束条件和 目标函数都是非线 性的
应用领域:经济、 金融、工程、运筹 等领域
最优化算法:梯度 下降法、牛顿法、 拟牛顿法等
最优化理论
汇报人:XX
目录
最优化问题的定义
01
最优解的概念
02
最优化算法的概述
03
最优化算法的应用
04
最优化算法的局限性和未 来发展
05
最优化问题的定 义
什么是最优化问题
分类:线性规划、非线性规 划、动态规划、整数规划等
最优化问题的定义:在所有可 行方案中选择最优方案,使得 目标函数达到最优值
应用领域:经济、 金融、工程、物 流等
算法类型:进化算 法、粒子群算法、 模拟退火算法等
案例分析:以实际 案例说明多目标规 划的应用和效果
最优化算法的局 限性和未来发展
最优化算法的局限性
计算复杂度高: 最优化算法通常 需要大量的计算 资源,对于大规 模问题,计算时 间较长。
对初始解敏感: 最优化算法的初 始解对最终结果 有很大影响,有 时会陷入局部最 优解而非全局最 优解。
数学建模常用算法模型

数学建模常用算法模型在数学建模中,常用的算法模型包括线性规划、整数规划、非线性规划、动态规划、图论算法以及遗传算法等。
下面将对这些算法模型进行详细介绍。
1.线性规划:线性规划是一种用于求解最优化问题的数学模型和解法。
它的目标是找到一组线性约束条件下使目标函数取得最大(小)值的变量取值。
线性规划的常用求解方法有单纯形法、内点法和对偶理论等。
2.整数规划:整数规划是一种求解含有整数变量的优化问题的方法。
在实际问题中,有时变量只能取整数值,例如物流路径问题中的仓库位置、设备配置问题中的设备数量等。
整数规划常用的求解方法有分支界定法和割平面法等。
3.非线性规划:非线性规划是一种求解非线性函数优化问题的方法,它在实际问题中非常常见。
与线性规划不同,非线性规划的目标函数和约束函数可以是非线性的。
非线性规划的求解方法包括牛顿法、拟牛顿法和全局优化方法等。
4.动态规划:动态规划是一种用于解决决策过程的优化方法。
它的特点是将问题划分为一系列阶段,然后依次求解每个阶段的最优决策。
动态规划常用于具有重叠子问题和最优子结构性质的问题,例如背包问题和旅行商问题等。
5.图论算法:图论算法是一类用于解决图相关问题的算法。
图论算法包括最短路径算法、最小生成树算法、网络流算法等。
最短路径算法主要用于求解两点之间的最短路径,常用的算法有Dijkstra算法和Floyd-Warshall算法。
最小生成树算法用于求解一张图中连接所有节点的最小代价树,常用的算法有Prim算法和Kruskal算法。
网络流算法主要用于流量分配和问题匹配,例如最大流算法和最小费用最大流算法。
6.遗传算法:遗传算法是一种借鉴生物进化原理的优化算法。
它通过模拟生物的遗传、变异和选择过程,不断优化问题的解空间。
遗传算法适用于对问题解空间有一定了解但难以确定最优解的情况,常用于求解复杂的组合优化问题。
总结起来,数学建模中常用的算法模型包括线性规划、整数规划、非线性规划、动态规划、图论算法以及遗传算法等。
工程优化第1章

历史与现状
• 公元前500年,古希腊在讨论建筑美学中就已发 现了长方形长与宽的最佳比例为1.618,称为黄金 分割比。其倒数至今在优选法中仍得到广泛应用。
• 在微积分出现以前,已有许多学者开始研究用数 学方法解决最优化问题。阿基米德证明:给定周 长,圆所包围的面积为最大。这就是欧洲古代城 堡几乎都建成圆形的原因。但是最优化方法真正 形成为科学方法则在17世纪以后。
为什么要学习工程优化
• 最优化技术与数学模型是工程类研究生应掌握的 数学基础课,是从事相应学科理论研究的前提。
• 工程中许多实际问题都可以抽象为数学建模问题, 数学模型其中包括最优化模型。了解最优化技术 的基本原理、相关算法是分析问题、解决问题的 一种技能,同时也是写出高水平学术论文的关键 素材。
• 最优化技术与数学模型所包括的知识点很多,选 取了一些实用的方法。
题
Lr.h. 2 rh
2 r 2
r
2h
4 3
分别对r, h,λ求偏导数,并令其等于零.有:
L r
2
h
4 r
2rh 0
L 2 r r 2 0
h
h
2r
L r 2h 4 0
3
r 3 2/3
h 23 2/3
2
所以,圆柱体的表面积为:
S
6
2 3
3
例2:多参数曲线拟合问题 已知两个物理量x和y之间的依赖关系为:
此外有:
x1≤2; x2≤1.4
• 化简有:
min z=1000x1+800x2
x1
≥1
0.8x1 + x2 ≥1.6
x1 ≤2
x2 ≤1.4
x1、x2 ≥0
例5:(混合饲料配合)以最低成本确定满足动物所需营养的 最优混合饲料。设每天需要混合饲料的批量为100磅,这份饲 料必须含:至少0.8%而不超过1.2%的钙;至少22%的蛋白质; 至多5%的粗纤维。假定主要配料包括石灰石、谷物、大豆粉。 这些配料的主要营养成分为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最优化问题的数学模型及其分类
例1.1.1 产品组合问题
某公司现有三条生产线用来生产两种新产品,其主要数据如表1-1所示。
请问如何生产可以让公司每周利润最大? 表1-1
设每周生产的产品一和产品二 的产量分别为1x 和2x ,则每周的生产利润为:2153x x z +=。
由于每周的产品生产受到三条生产线的可用时间的限制,因此1x ,2x 应满足以下条件:
⎪⎪⎩⎪⎪⎨
⎧≥≤+≤≤0,
18231224212121
x x x x x x 故上述问题的数学模型为
2153max
x x z +=
.
.t s ⎪⎪⎩⎪⎪⎨
⎧≥≤+≤≤0,
18231224212121
x x x x x x 其中max 是最大化(maximize )的英文简称,⋅⋅t s 是受约束于(subject to )的简写。
例1.1.2 把一个半径为1的实心金属球熔化后,铸成一个 实心圆柱体,问圆柱体取什么尺寸才能使它的表面积最小? 设圆柱体的底面半径为r ,高为h ,则该问题的数学模型为:
⎪⎩⎪
⎨⎧=⋅
⋅+=ππππ3
422min
22
h r t s r rh S 其中min 是最小化(minimize )的简写。
通过以上二例,可以看出最优化问题的数学模型具有如下结构:
(1) 决策变量(decision variable ):即所考虑问题
可归结为优选若干个被称为参数或变量的量
n x x x ,,,21 ,它们都取实数值,它们的一组值构
成了一个方案。
(2) 约束条件(constraint condition ):即对决策
变量n x x x ,,,21 所加的限制条件,通常用不等式或等式表示为: ()(),,,2,1,
0,,,,,2,1,
0,,,2121l j x x x h m i x x x g n
j n i ===≥
(3) 目标函数(objective function )和目标:如使
利润达到最大或使面积达到最小,通常刻划为极大化(maximize )或极小化(minimize )一个实值函数()n x x x f ,,21
因此,最优化问题可理解为确定一组决策变量在满足约束条件下,寻求目标函数的最优。
注意到极大化目标函数()n x x x f ,,21相当于极小化
()n x x x f ,,21-,因此,约束最优化问题的数学模型一般可
表示为:
()
()()()⎪⎩
⎪
⎨⎧===≥⋅⋅l
j x x x h m i x x x g t s x x x f n j n i n ,,2,1,0,,,1.1.1,,2,1,0,,,,,min 212121
若记()T
n x x x x
,,21=,则(1.1.1)又可写成:
()()()
()⎪⎪⎩
⎪
⎪⎨⎧=='
=≥⋅⋅l
j x h m i x g t s x f j i ,,2,1,01.1.1,,2,1,0min
其中
()()
m i x g i ,2,10
=≥称为不等式约束;
()()l j x h j ,,2,10 ==称为等式约束。
()()m i x g i ,,2,1 =与
()()l j x h j ,,2,10 ==称约束函数(constraint function )。
* 当目标函数和约束函数均为变量x 的线性函数时,问题(1.1.1)称为线性规划问题(linear programming problem )。
* 当目标函数和约束函数中至少有一个函数是x 的非线性函数时。
问题(1.1.1)称为非线性规划问题(nonlinear programming problem )
* 当目标函数为x 的二次函数,约束函数均为x 的线性函数时,问题(1.1.1)称为二次规划问题(guadratic programming problem )
* 如果要求某些决策变量或全部决策变量取非负整数值时,问题(1.1.1)称为整数规划问题(integer programming problem ) * 若目标函数不止一个,即
()()()()()2,,,21≥=p x f x f x f x f T
p ,
* 则问题()'1.1.1为多目标规划问题(multiobjective
programming problem )
*此外,根据决策变量、目标函数和约束函数的不同特点,最优化问题还可以划分为许多其它分支。
例如:动态规划(dynamical programming)
网络规划(network programming)
几何规划(geometric programming)
非光滑优化 (non-smooth optimization )
随机规划(stochastic programming)
目标规划(goal programming)
模糊规划(fuzzy programming)。
