常用概率函数在EXCEL中的实现

合集下载

excel表格计算概率的教程

excel表格计算概率的教程
Excel中经常需要使用到函数计算概率，概率具体该如何计算呢?下面是由店铺分享的excel表格计算概率的教程，以供大家阅读和学习。

excel表格计算概率的教程：
计算概率步骤1：FACT函数求组合
FACT函数是求组合的函数。

例1、1至9中组成不包含重复数的9位数，有几种组合方式呢，可以用下列公式 =FACT(9)。

计算概率步骤2：PERMUT求排列计算11选5的概率
例2，11选5共有多少种排列方式呢，一个公式就可以求出=PERMUT(11,5)。

计算概率步骤3：也可以用FACT函数求得这个结果，公式为=FACT(11)/FACT(11-5)。

三、COMBIN函数计算福彩双色球中头奖概率
计算概率步骤4：福彩双色球当中有33个红球，16个蓝球，要在红球中选择6个，蓝球中选择1个，因此中头奖的概率用公式表示就是=1/COMBIN(33，6)/COMBIN(16，1)。

要在单元格中设置一下小数点的显示数。

计算概率步骤5：结果就出来了。

计算概率步骤6：那么要中头奖要花多少钱呢，用公式表示就是=COMBIN(33，6)*COMBIN(16，1)*2,结果需要花费35442176 元才能中头奖。

excel概率函数

excel概率函数Excel提供了多种概率函数，用于计算和分析统计数据的概率分布。

在Excel中，可以使用以下概率函数：1. NORM.DIST：用于计算正态分布的概率密度函数。

该函数有四个参数：x（要计算概率的数值），mean（正态分布的平均值），stdev（正态分布的标准差），cumulative（一个逻辑值，用于指定是否计算累积概率）。

例如：=NORM.DIST(A2,B2,C2,TRUE)可以计算数值A2的正态分布累积概率。

2. NORM.INV：用于计算正态分布的逆函数，即给定概率，计算对应的数值。

该函数有三个参数：probability（给定的概率），mean（正态分布的平均值），stdev（正态分布的标准差）。

例如：=NORM.INV(A2,B2,C2)可以计算给定概率A2对应的数值。

3. BINOM.DIST：用于计算二项分布的累积概率。

该函数有四个参数：x（进行成功次数），n（重复试验的总次数），p（每次试验成功的概率），cumulative（一个逻辑值，用于指定是否计算累积概率）。

例如：=BINOM.DIST(A2,B2,C2,TRUE)可以计算进行了A2次成功的重复试验的累积概率。

4. POISSON.DIST：用于计算泊松分布的概率密度函数。

该函数有三个参数：x（进行事件次数），mean（事件的平均发生率），cumulative （一个逻辑值，用于指定是否计算累积概率）。

例如：=POISSON.DIST(A2,B2,TRUE)可以计算进行A2次事件的泊松分布累积概率。

5. WEIBULL.DIST：用于计算Weibull分布的概率密度函数。

该函数有四个参数：x（要计算概率的数值），alpha（Weibull分布的形状参数），beta（Weibull分布的尺度参数），cumulative（一个逻辑值，用于指定是否计算累积概率）。

例如：=WEIBULL.DIST(A2,B2,C2,TRUE)可以计算数值A2的Weibull分布累积概率。

excel随机概率公式

excel随机概率公式在Excel中，随机概率公式是一种用于生成随机数并分配概率的功能。

通过使用Excel的内置函数，您可以轻松地创建这些公式，并以各种方式应用。

一种常用的随机概率公式是RAND函数。

该函数会在0到1之间生成一个随机数。

通过与其他函数结合使用，可以将此随机数映射为符合特定概率分布的值。

例如，要创建一个返回1或0的公式，使1以70%的概率出现，而0以30%的概率出现，您可以使用如下公式：=IF(RAND()<=0.7,1,0)在这个公式中，RAND()函数生成0到1之间的随机数。

IF函数则会检查该随机数是否小于等于0.7，如果是，则返回1；否则，返回0。

由于RAND函数的随机性，该公式将以接近70%的概率返回1，以接近30%的概率返回0。

除了使用IF函数外，您还可以使用其他函数来创建更复杂的随机概率公式。

例如，使用CHOOSE函数可以根据随机数的范围分配不同的值。

以下是一个例子：=CHOOSE(CEILING(RAND()*5,1), "A", "B", "C", "D", "E")在这个公式中，RAND函数生成0到1之间的随机数，并使用CEILING函数将其乘以5并取最小整数。

CHOOSE函数将根据结果的整数值返回对应的字母。

因此，A、B、C、D和E将以近似相等的概率返回。

通过灵活运用这些函数和其他Excel功能，您可以根据自己的需求创建各种随机概率公式。

这些公式可以应用于数据分析、模拟实验、抽样等各种场景，为您带来更高效和准确的工作效果。

几种假设检验的Excel实现

三、差异显著性检验之一：单侧检验
0.05
三、差异显著性检验之一：单侧检验
0.01
四、差异显著性检验之二：双侧检验
1. 2. 3. 4.
1. 假设检验的基本原理零假设（虚无假设）：是关于当前样本所属的总体（指参数）与假设总体（指参数）无区别的假设，一般H0表示。备择假设（研究假设）：是关于当前样本所属的总体（指参数）与假设总体（指参数）相反的假设，一般用H1表示。由于直接检验备择假设的真实性困难，假设检验一般都是从零假设出发，通过零假设的不真实性来证明备假设的真实性。
累积概率为“=BINOMDIST(6, 10, 0.5, TRUE)”，计算的结果等于0.828125。
一、常见的概率分布
（二）在Excel软件中的实现 2. NORMDIST(x,µ ,σ,0) ：计算正态分布N(µ,σ2)的概率密度函数 f(x) 在 x 处的函数值； NORMDIST(x,µ ,σ,1) ：计算正态分布N(µ , σ2) 累积分布函数 F(x) 在 x 的函数值。【NORMDIST函数详解】：用途：返回给定平均值和标准差的正态分布的概率密度函数/分布函数的值。
一、常见的概率分布
（一）教育统计理论基础 1. 二项分布：是一种离散型随机变量的概率分布
一、常见的概率分布
（一）教育统计理论基础 2. 正态分布：是一种连续型随机变量的概率分布
一、常见的概率分布
（二）在Excel软件中的实现
1. BINOMDIST(k,n,p,0)：计算二项分布的分布律； BINOMDIST(k,n,p,1)：计算二项分布的累积分布。【BINOMDIST函数详解】：用途：返回一元二项式分布的概率分布律/累积分布。BINOMDIST函数适用于固定次数的独立实验，实验的结果只包含成功或失败二种情况，且成功的概率在实验期间固定不变。

t分布函数的应用及在excel软件中的实现

t分布函数的应用及在excel软件中的实现t分布函数是一种统计学中常用的概率分布函数，通常用于小样本量的数据。

它可以在一些情况下用于代替正态分布函数。

t分布函数在贝叶斯统计学、假设检验、回归分析等领域具有广泛的应用。

在Excel软件中，可以使用函数TDIST()来计算t分布函数的值。

TDIST()函数有三个参数：x值（统计值），自由度（样本量减1）以及尾数（单尾或双尾检验）。

例如，要计算在一个双尾检验中一个t分布函数值为0.05的x值，当样本量为20时，可使用以下公式：
=TDIST(0.05,19,2)。

在使用Excel进行t分布函数计算时，需要注意自由度的设定。

如果输入的自由度过大或过小，可能会导致计算结果的误差。

因此，使用时需要根据具体情况合理选择自由度。

excel正态分布随机数

excel正态分布随机数正态分布随机数是统计抽样中常用的概率论算法，用它可以生成一系列随机数，其特点是遵循正态分布规律。

一、定义：正态分布随机数是指服从正态分布概率密度函数的随机变量，其标准正态分布概率密度函数形如：f(x)=(1/σ√2π)exp(-(x-μ)2/2σ^2)其中μ代表均值，σ代表标准差。

二、应用：1、模拟蒙特卡洛法蒙特卡罗法是采用正太分布的随机数来模拟复杂的系统的行为，以此获得可行的解答，用计算机来计算出一系列个体在指定的条件下的表现情况，以此来进行分析和研究。

2、期望收益率计算正态分布随机数常用于计算一定投资组合的期望收益率，通过把投资组合的不同资产回报率的分布图拟合成一个正态分布，找出均值和标准差，生成正态分布的随机数，计算投资组合收益率的分布。

3、实验设计优化实验设计分析应用正态分布随机数的一个重要场景就是对实验设计进行优化，首先要运用数学统计决定实验任务的参数，接着利用正态分布随机数生成实验任务，观察实验任务完成情况，并做出必要的优化调整，反复调整实现实验任务最佳优化。

三、优势：1、正态分布随机数对社会经济等具有广泛适应性，它能够在复杂的现实社会环境中模拟出一个比较真实的概率分布结果，比较符合客观实际；2、正态分布随机数的计算和提取都比较容易实现；3、可以实现更准确有效的随身和经济方面的决定；4、正态分布模型的灵巧性更好，有效避免反弹的情况。

四、缺点：1、正态分布随机数仅仅能够模拟最简单的概率场景，并不能模拟变化多样且不同类型的变量；2、正态分布随机数模型参数具有一定的敏感性，小的变动可能会引起较大的改变；3、在非常小的概率场景下，正态分布随机数的计算可能不太准确。

常用概率函数在EXCEL中实现

常用概率函数在EXCEL中实现在Excel中，常用的概率函数可以使用内置函数进行实现。

下面将介绍四个常用的概率函数以及它们在Excel中的实现方法。

1.正态分布函数（NORM.DIST）正态分布函数可以用于计算一个随机变量处于指定范围内的概率。

在Excel中，可以使用NORM.DIST函数来计算正态分布的概率。

语法：NORM.DIST(x,mean,standard_dev,cumulative)-x：要计算概率的数值。

- mean：正态分布函数的均值。

- standard_dev：正态分布函数的标准差。

- cumulative：一个逻辑值，指定概率函数是累积函数（TRUE）还是密度函数（FALSE）。

例如，要计算一个随机变量X的值小于等于5的概率，该随机变量服从均值为10，标准差为2的正态分布，可以使用以下公式：=NORM.DIST(5,10,2,TRUE)2.标准正态分布函数（NORM.S.DIST）标准正态分布函数可以用于计算一个随机变量在标准正态分布中的概率。

在Excel中，可以使用NORM.S.DIST函数来计算标准正态分布的概率。

语法：NORM.S.DIST(z,cumulative)-z：要计算概率的数值。

- cumulative：一个逻辑值，指定概率函数是累积函数（TRUE）还是密度函数（FALSE）。

例如，要计算一个随机变量Z的值小于等于1的概率，可以使用以下公式：=NORM.S.DIST(1,TRUE)3.卡方分布函数（CHISQ.DIST）卡方分布函数可以用于计算一个随机变量处于指定范围内的概率。

在Excel中，可以使用CHISQ.DIST函数来计算卡方分布的概率。

语法：CHISQ.DIST(x,deg_freedom,cumulative)-x：要计算概率的数值。

- deg_freedom：卡方分布的自由度。

- cumulative：一个逻辑值，指定概率函数是累积函数（TRUE）还是密度函数（FALSE）。

常用概率函数在EXCEL中的实现

常用概率函数在EXCEL中的实现在Excel中，我们可以使用各种常见的概率函数来解决与概率相关的问题。

以下是一些常见的概率函数及其在Excel中的实现方法：1.累积分布函数（CDF）：CDF函数用于计算随机变量小于或等于给定值的概率。

在Excel中，我们可以使用NORM.DIST函数来计算正态分布的累积分布函数。

该函数的语法如下：NORM.DIST(x, mean, standard_dev, cumulative)其中，x是随机变量的值，mean是正态分布的均值，standard_dev 是标准差，cumulative是一个布尔值，如果为TRUE，则计算累积分布函数；如果为FALSE，则计算概率密度函数。

2.概率密度函数（PDF）：PDF函数用于计算给定随机变量取一些值的概率。

在Excel中，我们可以使用NORM.DIST函数来计算正态分布的概率密度函数。

该函数的语法与累积分布函数一样。

3.百分位数函数：百分位数函数用于计算给定分布中的一些数值的百分位数。

在Excel 中，我们可以使用PERCENTILE函数来计算一些数据集的一些百分位数。

该函数的语法如下：PERCENTILE(array, k)其中，array是数据集，k是一个介于0和1之间的小数，表示所需的百分位数。

4.期望值（均值）：期望值是随机变量的平均值。

在Excel中，我们可以使用AVERAGE函数来计算一个数据集的期望值。

该函数的语法如下：AVERAGE(number1, number2, ...)其中，number1、number2等是数据集中的数值。

5.方差：方差是随机变量的离散程度的度量。

在Excel中，我们可以使用VAR函数来计算一个数据集的方差。

该函数的语法如下：VAR(number1, number2, ...)其中，number1、number2等是数据集中的数值。

6.标准差：标准差是方差的平方根，用于衡量随机变量的离散程度。

概率函数在EXCEL中的使用方法

概率函数在EXCEL中的使用方法在Excel中，概率函数被称为统计函数，用于计算概率分布函数（Probability Distribution Function，简称PDF）和累积分布函数（Cumulative Distribution Function，简称CDF）的值。

概率函数在统计分析和数据建模中非常有用，可以帮助我们计算出特定事件发生的可能性。

下面将介绍Excel中一些常用的概率函数的使用方法。

1.概率密度函数（PDF）：在Excel中，我们可以使用函数DENSITY函数来计算概率密度函数的值。

这个函数的语法如下：DENSITY(x, mean, standard_dev, cumulative)其中，x是要计算PDF的数值；mean是概率分布的平均值；standard_dev是概率分布的标准偏差；cumulative是一个逻辑值，用于指示是否计算累积分布函数（CDF）的值。

如果cumulative为TRUE（默认值），则计算CDF的值；如果为FALSE，则计算PDF的值。

2.累积分布函数（CDF）：在Excel中，我们可以使用函数NORM.DIST来计算累积分布函数的值。

这个函数的语法如下：NORM.DIST(x, mean, standard_dev, cumulative)其中，x是要计算CDF的数值；mean是概率分布的平均值；standard_dev是概率分布的标准偏差；cumulative是一个逻辑值，指示是否计算累积分布函数（CDF）的值。

如果cumulative为TRUE（默认值），则计算CDF的值；如果为FALSE，则计算PDF的值。

3.正态分布：在Excel中，正态分布是一种非常常见的概率分布，可以使用NORM.DIST函数来计算正态分布的概率密度函数（PDF）和累积分布函数（CDF）的值。

4.t-分布：在Excel中，t-分布是一种常用的概率分布，用于小样本的假设检验。

高中数学第三章概率随机数的含义与应用EXCEL随机数据生成方法素材

3。

3 随机数的含义与应用EXCEL随机数据生成方法求教:我的电子表格中rand()函数的取值范围是-1到1，如何改回1到0回答：有两种修改办法：是[1－rand（)]/2,或[1＋rand()]/2。

效果是一样的，都可生成0到1之间的随机数电子表格中RAND（）函数的取值范围是0到1，公式如下：=RAND()如果取值范围是1到2，公式如下：=RAND（)*（2—1）+1RAND( ）注解：若要生成a 与b 之间的随机实数：=RAND（)＊（b-a）+a如果要使用函数RAND 生成一随机数，并且使之不随单元格计算而改变，可以在编辑栏中输入“=RAND（)”,保持编辑状态，然后按F9,将公式永久性地改为随机数。

示例RAND（）介于0 到1 之间的一个随机数（变量）=RAND(）*100 大于等于0 但小于100 的一个随机数（变量）excel产生60—70随机数公式=RAND()＊10+60要取整可以用=int(RAND()*10+60）我想用excel在B1单元个里创建一个50-80的随机数且这个随机数要大于A1单元个里的数值，请教大家如何编写公式!整数：=ROUND（RAND(）*（80-MAX（50,A1+1)）+MAX(50,A1+1），0）无需取整数：=RAND()*（80—MAX（50，A1))+MAX（50，A1)要求：1，小数保留0。

12，1000-1100范围3,不要出现重复=LEFT(RAND()*100+1000，6)至于不许重复你可以设置数据有效性在数据—有效性设=countif(a:a，a1)=1选中a列设有效性就好了其他列耶可以急求excel随机生成数字的公式，取值要在38.90-44。

03之间，不允许重复出现，保留两位小数，不允许变藏=round（RAND（)＊5+38.9,2)公式下拉Excel随机数Excel具有强大的函数功能，使用Excel函数,可以轻松在Excel表格产生一系列随机数。

excel表格随机生成区间小数的函数

Excel表格随机生成区间小数的函数在Excel中，我们经常需要使用到随机生成区间小数的函数，这在统计分析、数据模拟等领域都是非常常见的需求。

今天，我就来和大家共享一下我对于在Excel中随机生成区间小数的函数的理解和使用技巧。

1. 随机函数的基本介绍在Excel中，我们可以利用内置的随机函数来实现随机生成区间小数的需求。

常见的随机函数包括RANDBETWEEN、RAND、RANDARRAY等。

其中，RANDBETWEEN函数可以随机生成指定范围内的整数，而RAND函数则可以随机生成0到1之间的小数。

2. RANDBETWEEN函数的应用如果我们需要随机生成一个区间内的小数，可以先利用RANDBETWEEN函数随机生成一个整数，然后再除以一个较大的数，从而得到区间内的小数。

如果我们需要随机生成0到1之间的小数，可以使用=RANDBETWEEN(0,1000)/1000的方式来实现。

3. RAND函数的应用另外，我们也可以直接利用RAND函数来实现随机生成区间内的小数。

如果我们需要在0.5到1之间随机生成小数，可以直接使用=0.5+0.5*RAND的方式来实现。

4. RANDARRAY函数的应用除了上述两种方法，Excel 365还提供了RANDARRAY函数，可以一次性生成多个随机数。

通过RANDARRAY函数，我们可以很方便地指定需要生成的随机数数量和区间范围，从而快速得到多个区间内的随机小数。

总结通过上面的介绍，我们可以看到，在Excel中实现随机生成区间小数的函数有多种方法。

无论是利用RANDBETWEEN函数、RAND函数，还是采用新的RANDARRAY函数，都可以轻松地实现这一需求。

在日常的数据处理和分析中，灵活运用这些函数，可以为我们节省大量时间，提高工作效率。

个人观点作为一个热爱数据分析的人，我深深体会到随机生成区间小数在模拟实验、抽样调查等方面的重要性。

掌握好这些随机函数的使用技巧，不仅可以帮助我们更好地理解和分析数据，还可以为我们的工作带来更多的可能性。

常用概率函数在EXCEL中实现

常用概率函数在EXCEL中实现在Excel中实现常用概率函数非常简单，Excel提供了一系列内置的概率函数，可以帮助我们计算概率、分布函数以及反函数。

下面将介绍常用的概率函数和它们在Excel中的实现。

1.正态分布函数(NORM.DIST)正态分布函数用于计算给定均值和标准差的随机变量的概率。

可以使用Excel的NORM.DIST函数来计算正态分布。

语法：NORM.DIST(x,mean,standard_dev,cumulative)其中，x是要计算概率的随机变量的值，mean是均值，standard_dev 是标准差，cumulative是一个逻辑值，用于指定计算概率密度函数(FALSE) 还是累积分布函数 (TRUE)。

例子：假设一个随机变量的均值为5，标准差为2、我们想要计算随机变量取值为6的概率密度函数和累积分布函数。

使用Excel的NORM.DIST函数，可以在单元格中输入以下公式：```=NORM.DIST(6,5,2,FALSE)=NORM.DIST(6,5,2,TRUE)```第一个公式计算概率密度函数，第二个公式计算累积分布函数。

2.标准正态分布函数(NORM.S.DIST)标准正态分布函数是一种特殊的正态分布函数，其均值为0，标准差为1、在Excel中，可以使用NORM.S.DIST函数来计算标准正态分布。

语法：NORM.S.DIST(x,cumulative)其中，x是要计算概率的随机变量的值，cumulative是一个逻辑值，用于指定计算概率密度函数 (FALSE) 还是累积分布函数 (TRUE)。

例子：假设想要计算标准正态分布的概率密度函数和累积分布函数，可以在单元格中输入以下公式：```=NORM.S.DIST(1,FALSE)=NORM.S.DIST(1,TRUE)```第一个公式计算概率密度函数，第二个公式计算累积分布函数。

3.反正态分布函数(NORM.INV)反正态分布函数是正态分布函数的反函数。

常用概率函数在EXCEL中的实现

Poisson distribution (POISSON)
statement： POISSON(x, mean, cumulative)
options：
X:事件数 Mean:期望值
introductions：
如果 x 不为整数，将被截尾Fra bibliotek整如果 x 或 mean 为非数值型，函数返回错误值
Normal distribution (NORMDIST)
statement：
NORMDIST( x, mean, standard_dev, cumulative)
options：
X:需要计算其分布的数值。 Mean:分布的算术平均值。 Standard_dev:分布的标准偏差。
Normal distribution (NORMDIST)
#VALUE!。如果 x < 0，函数返回错误值 #NUM!。如果 mean ≤ 0，函数返回错误值 #NUM!。
Poisson distribution (POISSON)
例3：
实验显示某100cm2的培养皿中平均菌落数为 6个，试估计该培养皿菌落数等于3个的概率。
Poisson distribution (POISSON)
Normal Distribution Binomial Distribution Poisson Distribution
Binomial distribution (BINOMDIST)
statement：
BINOMDIST(number_s,trials,probability_s,cumulative)
P( X
10)
150！ 10！(150 10)!
0.1310

excel随机函数概率

excel随机函数概率
Excel中的随机函数包括RAND、RANDBETWEEN和RANDARRAY。

这
些函数可以用于生成随机数，用于模拟概率分布、抽样和随机实验等。

首先，我们来看一下RAND函数。

这个函数返回一个0到1之间
的随机数，可以用来模拟均匀分布的概率。

例如，如果你想模拟抛
硬币的概率，你可以使用RAND函数生成一个0到1之间的随机数，
然后根据这个随机数的大小来判断是正面还是反面。

其次，RANDBETWEEN函数可以生成指定范围内的随机整数。

这
个函数可以用来模拟离散型随机变量的概率分布，比如投掷骰子的
结果或者抽奖的中奖号码等。

你可以设置RANDBETWEEN函数的参数
来指定随机数的范围，然后根据生成的随机数来进行相应的模拟实验。

另外，Excel 365中新增了RANDARRAY函数，可以一次性生成
多个随机数，这样可以更方便地进行大量的模拟实验或者抽样操作。

除了这些内置的随机函数，Excel还可以通过组合其他函数来
模拟各种概率分布，比如正态分布、泊松分布、指数分布等。

你可
以使用Excel的函数库来实现这些复杂的模拟操作。

总的来说，Excel中的随机函数可以帮助我们模拟各种概率事
件和随机实验，从而更好地理解和分析随机现象的规律和特性。

当然，在使用随机函数时，我们也需要注意控制随机数的范围和分布，以确保模拟结果的准确性和可靠性。

正态分布的概率计算实验报告参考模板

实验项
目
名称
利用Excel进行区间估计
实验目的及要求
要求学生熟练利用Excel进行统计推断，通过实例分析，培养学生的动手操作能力，达到理论知识与实践相结合的目的。

要求利用计算机软件进行Excel进行统计推断，提高实际应用能力。

实验内容利用Excel进行正态分布的概率计算利用Excel进行区间估计
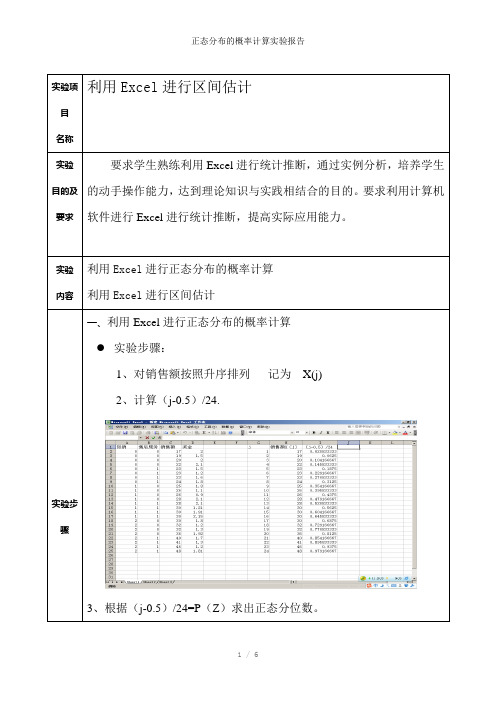
实验步骤一、利用Excel进行正态分布的概率计算
实验步骤：
1、对销售额按照升序排列记为X(j)
2、计算（j-0.5）/24.
3、根据（j-0.5）/24=P（Z）求出正态分位数。

单击I2选择“插入”然后选择函数对话框”统计”，“NORMSINV”然后确定
4、选择工具的数据分析，在选择“回归”然后确定，以P（Z）为纵轴X（j）为横轴
绘出正态图
正态分布图
正态分布图
二、利用Excel进行区间估计
实验步骤：
一大分布样本
1、在EXCEl工作表中，依次点击：工具一数据分析一描述统计
实验环境
电脑操作系统为Windows XP或更高版本，所需软件为Excel 2003或更高版本。

注：可根据实际情况加页
友情提示：范文可能无法思考和涵盖全面，供参考!最好找专业人士起草或审核后使用，感谢您的下载！。

excel表格一定范围内的随机数值

Excel表格中的随机数生成在Excel表格中，我们经常需要使用随机数来进行模拟、抽样或者其他一些计算。

Excel本身提供了多种方式来生成随机数，包括函数和工具，下面我将从简单到复杂逐一介绍。

在文章中，我将会指导你如何在Excel表格中生成指定范围内的随机数，并通过实例展示其应用。

1. 使用RAND()函数生成随机数在Excel中，我们最简单的方式是使用RAND()函数来生成0到1之间的随机数。

其公式为=RAND()，每次编辑表格时都会重新生成一个随机数。

然而，如果我们需要生成指定范围内的随机数，比如在1到100之间，就需要进行一些计算。

我们可以使用以下公式来实现：=1+INT(RAND()*100)这个公式中，RAND()函数生成的随机数乘以100，再通过INT函数取整，最后再加1，就可以生成1到100之间的随机数。

2. 使用RANDBETWEEN(min, max)函数生成指定范围内的随机数为了更加方便地生成指定范围内的随机数，Excel还提供了RANDBETWEEN函数。

其公式为=RANDBETWEEN(min, max)，其中min和max分别为所需随机数的范围。

要生成1到100之间的随机数，可以使用=RANDBETWEEN(1, 100)。

值得注意的是，RANDBETWEEN函数生成的随机数是包括边界值的，即1和100都有可能被选中。

3. 高级的随机数生成方法除了上述两种方法外，还可以通过自定义宏或者安装插件来实现更加复杂的随机数生成，比如正态分布随机数、指数分布随机数等。

这些方法通常需要一定的编程知识和Excel技巧，但可以提供更加丰富和灵活的随机数生成功能。

总结回顾通过本文的介绍，我们了解了在Excel表格中生成随机数的几种常见方法。

无论是简单的0到1之间的随机数，还是指定范围内的随机数，Excel都提供了相应的函数和工具来满足我们的需求。

当然，如果需要更加复杂和灵活的随机数生成，还可以通过自定义宏或者插件来实现。

excel 标准正态分布的累积分布函数

excel 标准正态分布的累积分布函数标准正态分布是一种特殊的正态分布，其均值为0，标准差为1。

累积分布函数（Cumulative Distribution Function，简称CDF）是描述随机变量X的取值小于或等于某个给定值x的概率的函数。

标准正态分布的累积分布函数通常用符号Φ(x)表示，为了计算Φ(x)，我们需要使用统计表或者软件来查找或计算。

下面是一张标准正态分布的累积分布函数的部分统计表，它给出了标准正态分布的累积概率值。

Z Φ(Z)-3.0 0.0013-2.9 0.0019-2.8 0.0026-2.7 0.0035-2.6 0.0047-2.5 0.0062-2.4 0.0082-2.3 0.0107-2.2 0.0139-2.1 0.0179-2.0 0.0228-1.9 0.0287-1.8 0.0359-1.7 0.0446-1.6 0.0548-1.5 0.0668-1.3 0.0968 -1.2 0.1151 -1.1 0.1357 -1.0 0.1587 -0.9 0.1841 -0.8 0.2119 -0.7 0.2420 -0.6 0.2743 -0.5 0.3085 -0.4 0.3446 -0.3 0.3821 -0.2 0.4207 -0.1 0.4602 0.0 0.5000 0.1 0.5398 0.2 0.5793 0.3 0.6179 0.4 0.6554 0.5 0.6915 0.6 0.7257 0.7 0.7580 0.8 0.78810.9 0.81591.0 0.8413 1.1 0.8643 1.2 0.8849 1.3 0.9032 1.4 0.9192 1.5 0.93321.7 0.95541.8 0.96411.9 0.97132.0 0.97722.1 0.98212.2 0.98612.3 0.98932.4 0.99182.5 0.99382.6 0.99532.7 0.99652.8 0.99742.9 0.99813.0 0.9987从上表可以看出，标准正态分布的累积分布函数Φ(Z)是一个对称函数，其取值范围在0到1之间。

常用概率函数在EXCEL中的实现

常用概率函数在EXCEL中的实现在Excel中，有多种常用的概率函数可以进行实现。

这些函数可以帮助我们计算和分析随机事件的概率。

下面是一些常用的概率函数及其在Excel中的实现方式：1.NORM.DIST函数-正态分布函数NORM.DIST函数可用于计算给定值的正态分布的概率密度函数值。

该函数有四个参数：x（要计算其概率密度函数值的值）、mean（正态分布的平均值）、standard_dev（正态分布的标准差）和cumulative（一个逻辑值，表示是否计算累积分布函数）。

以下是一个示例：=NORM.DIST(A2,B2,C2,TRUE)其中，A2为要计算概率密度函数值的数值，B2为正态分布的平均值，C2为正态分布的标准差，TRUE表示计算累积分布函数值。

2.BINOM.DIST函数-二项分布函数BINOM.DIST函数可用于计算二项分布的概率密度函数值。

该函数有四个参数：x（要计算其概率密度函数值的值）、n（试验的次数）、p（每次试验成功的概率）和cumulative（一个逻辑值，表示是否计算累积分布函数）。

以下是一个示例：=BINOM.DIST(A2,B2,C2,TRUE)其中，A2为要计算概率密度函数值的数值，B2为试验的次数，C2为每次试验成功的概率，TRUE表示计算累积分布函数值。

3.POISSON.DIST函数-泊松分布函数POISSON.DIST函数可用于计算泊松分布的概率密度函数值。

该函数有三个参数：x（要计算其概率密度函数值的值）、mean（平均发生率）和cumulative（一个逻辑值，表示是否计算累积分布函数）。

以下是一个示例：=POISSON.DIST(A2,B2,TRUE)其中，A2为要计算概率密度函数值的数值，B2为平均发生率，TRUE 表示计算累积分布函数值。

4.GEOMEAN函数-几何平均数GEOMEAN函数可用于计算一组数的几何平均数。

以下是一个示例：=GEOMEAN(A2:A5)其中，A2:A5为要计算几何平均数的数据范围。

excel 对数分布区间概率

excel 对数分布区间概率摘要：1.引言2.Excel 对数分布的概念3.区间概率的计算方法4.用Excel 绘制对数分布的概率密度曲线5.结论正文：1.引言在统计学中，对数分布是一种重要的概率分布，它在许多实际应用场景中都有广泛的应用。

而在Excel 中，我们可以通过一些方法来计算和对数分布相关的区间概率。

本文将介绍如何在Excel 中实现对数分布的区间概率计算以及如何绘制对数分布的概率密度曲线。

2.Excel 对数分布的概念对数分布是一种以对数为自变量的概率分布，其概率密度函数为f(x)=1/(x(1+e^(-rx)))，其中x 为对数，r 为尺度参数，e 为自然对数的底数。

对数分布的性质使得它在处理一些具有对数特性的数据时具有很好的适用性。

3.区间概率的计算方法在Excel 中，我们可以使用内置的函数来计算对数分布的区间概率。

例如，我们可以使用POISSON.DIST() 函数来计算泊松分布的概率密度，使用NORM.DIST() 函数来计算正态分布的概率密度。

通过将这些函数与Excel 的数据分析工具结合，我们可以轻松地计算出给定区间内的概率。

4.用Excel 绘制对数分布的概率密度曲线要绘制对数分布的概率密度曲线，我们可以使用Excel 的散点图功能。

首先，我们需要在Excel 中输入对数分布的累积分布值。

然后，通过将这些值作为散点图的Y 轴值，并将对数作为X 轴值，我们可以得到对数分布的概率密度曲线。

5.结论Excel 在对数分布的计算和绘图方面具有很好的功能。

通过使用内置的函数和数据分析工具，我们可以轻松地计算出给定区间内的概率，并绘制出对数分布的概率密度曲线。

excel极小值概率分布函数

Excel极小值概率分布函数：深度与广度兼具的探讨在统计学和概率论中，极小值概率分布函数是一种用来描述随机变量中的最小值的概率分布函数。

在实际应用中，我们经常会遇到需要分析最小值的情况，比如在工程、金融和自然科学领域。

而Excel作为一款强大的数据分析工具，也提供了一些函数来帮助我们计算极小值的概率分布。

在本文中，我将从简到繁地向你介绍Excel中极小值概率分布函数的计算方法，并共享一些个人的理解和观点。

1. 极小值概率分布函数的基本概念让我们来了解一下什么是极小值概率分布函数。

在统计学中，我们常常会遇到一组随机变量，我们希望知道其中的最小值落在某个区间的概率是多少。

这时，就可以使用极小值概率分布函数来进行计算。

在Excel中，我们可以通过一些内置的函数来实现这一目的。

2. Excel中的极小值概率分布函数在Excel中，有几个与极小值概率分布函数相关的函数可以帮助我们进行计算，其中最常用的是MINVERSE函数和MIN函数。

MINVERSE函数用于计算矩阵的逆矩阵，而MIN函数则用于计算一组数值中的最小值。

举个例子，假设我们有一组数据存储在A1:A10的单元格中，我们可以使用=MIN(A1:A10)来计算这组数据中的最小值。

而如果我们想要计算最小值落在某个区间的概率，就可以借助MINVERSE函数来实现。

3. 如何在Excel中计算极小值概率分布函数在Excel中，我们可以通过以下步骤来计算极小值概率分布函数：a. 将需要计算的数据存储在一个单元格区域中。

b. 使用MIN函数来计算这组数据的最小值，比如=MIN(A1:A10)。

c. 接下来，根据最小值的范围，使用MINVERSE函数来计算最小值落在该范围的概率。

4. 个人观点和理解极小值概率分布函数在实际应用中有着广泛的用途，特别是在风险管理和可靠性分析领域。

通过计算最小值的概率分布，我们可以更好地理解系统或过程的稳定性和可靠性。

而在Excel中，通过MINVERSE和MIN函数的结合，我们可以快速、准确地进行这样的计算，为决策提供有力的支持。

常用概率函数在EXCEL中的实现

excel表格计算概率的教程

excel概率函数

excel随机概率公式

几种假设检验的Excel实现

t分布函数的应用及在excel软件中的实现

excel正态分布随机数

常用概率函数在EXCEL中实现

常用概率函数在EXCEL中的实现

概率函数在EXCEL中的使用方法

高中数学第三章概率随机数的含义与应用EXCEL随机数据生成方法素材

excel表格随机生成区间小数的函数

常用概率函数在EXCEL中实现

常用概率函数在EXCEL中的实现

excel随机函数概率

正态分布的概率计算实验报告参考模板

excel表格一定范围内的随机数值

excel 标准正态分布的累积分布函数

常用概率函数在EXCEL中的实现

excel 对数分布 区间概率

excel极小值概率分布函数

excel 对数分布区间概率