桁架优化 - 360文档中心

基于满应力法的平面桁架优化

（ＧｕａｎｇｄｏｎｇＵｎｉｖｅｒｓｉｔｙｏｆＰｅｔｒｏｃｈｅｍｉｃａｌＴｅｃｈｎｏｌｏｇｙ，Ｍａｏｍｉｎｇ５２５０００，Ｃｈｉｎａ）
ＡＢＳＴＲＡＣＴ：ＴｈｅｐｕｒｐｏｓｅｏｆｏｐｔｉｍｉｚａｔｉｏｎｄｅｓｉｇｎｉｓｔＯｒｅｄｕｃｅｍａｔｅｒｉａｌｃｏｎｓｕｍｐｔｉｏｎａｎｄｃｏｓｔｓ．Ｉｎｔｈｉｓｐａｐｅｒ，ｔｈｅｆｕｌｌ
ＤＯＩ：１０．１３２０６／Ｊ．￣ｇ２０１５０３００４
ｏＰＴＩＭＩＺＡＴＩｏＮＯＦＰＬＡＮＥＴＲＵＳＳＢＡＳＥＤｏＮＦＵＬＬＳＴＲＥＳＳＭＥＴＨｏＤ
ＹａｎｇＢｏＪｉｎＲｅｎｈｅ
并在迭代计算过程中创造性地提出了中间值法，大大减少了迭代计算量，提高了计算效率，得到结构最优截面尺
寸，用钢量减少４Ｏ，经济效益显著，该方法值得推广。
关键词：结构优化；满应力法；平面桁架；中间值法
ＫＥＹＷＯＲＤＳ：ｓｔｒｕｃｔｕｒｅｏｐｔｉｍｉｚａｔｉｏｎ；ｆｕｌｌｓｔｒｅｓｓｍｅｔｈｏｄ；ｐｌａｎｅｔｒｕｓｓ；ｍｅｄｉａｎｍｅｔｈｏｄ
１概述
２满应力法数学模型

桁架优化的改进粒子群算法

学规划（Ｐ法等传统的算法已经广泛应用于Ｍ）求解简单优化问题，并取得了较好的效果．但这些传统优化算法在进行大型复杂的结构系统的优化时，则通常会出现通用性差、算量大等缺点．计随着计算技术的发展，如遗传算法（Ａ）粒子群算法Ｇ、（ｓ）微分演化算法（Ｅ、ＰＯ、Ｄ）免疫克隆选择算法（ＣＡ、ＩＳ）蚁群算法（Ｃ）ＡＯ等一仿生智能优化算法逐渐应用于工程优化领域．这些仿生智能优化，算法较之于传统的优化算法，不需要变量的梯度信息，不要求函数的连续性和可微性，因此更适合于求解结构优化问题．但仿生智能算法也存在共同的缺点，即参数不易确定，参数的设置通常会影响算法收敛的效果．在上述仿生智能计算技术中，子群优化粒
ＰＯ算法是受鸟群等群体的社会性行为启Ｓ
发，模拟它们在觅食时群体协作，此信息共享等彼
机制的行为发展起来的启发式的仿生智能算法．算法中，群体中的每一个粒子代表一个备选解，粒子
在每一代的更新过程中通过和其周边的粒子共享
Ｊｎａ．
２１０２
文章编号：０８—１０（０２Ｏ００ —０１０４２２１）１— ０１５
桁架优化的改进粒子群算法①
许锐王泽兴罗，，雪２
（．１同济大学结构工程与防灾研究所。上海２０９；．同济大学浙江学院。００２２浙江嘉兴３４５）１１０

桁架结构优化设计

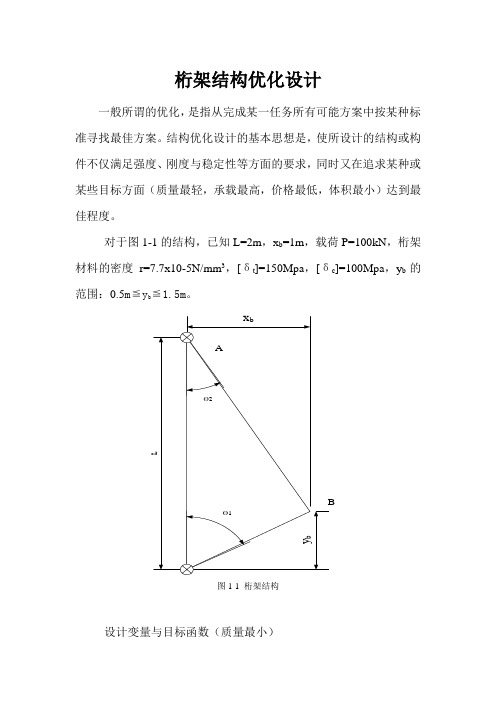
桁架结构优化设计一般所谓的优化，是指从完成某一任务所有可能方案中按某种标准寻找最佳方案。

结构优化设计的基本思想是，使所设计的结构或构件不仅满足强度、刚度与稳定性等方面的要求，同时又在追求某种或某些目标方面（质量最轻，承载最高，价格最低，体积最小）达到最佳程度。

对于图1-1的结构，已知L=2m，x b=1m，载荷P=100kN，桁架材料的密度r=7.7x10-5N/mm3，[δt]=150Mpa，[δc]=100Mpa，y b的范围：0.5m≦y b≦1.5m。

图1-1 桁架结构设计变量与目标函数（质量最小）预定参数（设计中已确定，设计者不能任意修改的量）：L ， x b ，P ，r ，[δt ] ，[δc ]设计变量（可由设计者调整的量）y b ，A 1，A 2 约束条件（对设计变量的约束条件）（1）强度条件约束（截面、杆件的强度）（2）几何条件约束（B 点的高度范围）目标函数：桁架的质量W （最小）解：1. 应力分析0sin sin 02112=--=∑θθN N F x0cos cos 02112=---=∑P N N Fyθθ由此得：)sin(sin 2111θθθ+=p N )sin(sin 2122θθθ+-=p N由正弦定理得：ly l x pN B B 21)(2-+=ly x pN BB 222+=由此得杆1和2横截面上的正应力121)(2lA y l x pB B -+=σ2222lA y x pB B +=σ2.最轻质量设计目标函数（桁架的质量）))((222122B B y x A y l x A W B B ++-+=γ（1-1）约束条件[][]⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤+≤-+c B t B lA y x p lA y l x p B B σσ221222)( （1-2）0.5≦y b ≦1.5（m ）（1-3）（于是问题归结为：在满足上述约束条件下，确定设计变量y b ，A 1，A 2，使目标函数W 最小。

钢桁架桥的设计与优化

钢桁架桥的设计与优化钢桁架桥是一种常见且重要的桥梁结构形式，其以其高度的强度和耐久性而被广泛应用于现代交通建设。

设计和优化钢桁架桥的过程是一个综合性的工程，需要考虑多种因素并做出合理权衡。

本文将探讨钢桁架桥的设计和优化过程，并介绍一些相关的技术和方法。

首先，设计钢桁架桥时需要考虑的一个重要因素是桥梁的结构强度。

钢桁架桥需要能够承受车辆和行人的荷载，并保证桥梁的稳定和安全运行。

设计师通常会使用结构力学和有限元分析等方法来计算和评估桥梁的结构强度，并确保其满足工程要求。

同时，设计师还应考虑桥梁在不同环境条件下的稳定性和可靠性，如地震和风荷载等。

其次，钢桁架桥的设计过程还需要考虑到桥梁的美观性和可持续性。

作为城市交通建设的重要组成部分，钢桁架桥的外观设计应与周围环境相协调，并具备一定的艺术价值。

同时，设计师还应采用可持续材料和技术来减少桥梁的环境影响，如使用高强度钢材和节能设计等。

此外，钢桁架桥的优化也是设计过程中的一个重要环节。

通过优化设计，可以改善桥梁的结构性能、减少材料的使用量和降低工程成本。

一种常见的优化方法是拟合和调整钢桁架的形状和尺寸，以实现最佳的结构效果。

此外，优化还可以通过改进桥梁的抗震性能和减少桥梁的自重来提高桥梁的性能。

在设计和优化钢桁架桥时，还需要考虑到桥梁施工和维护的可行性。

设计师应该选择合适的施工方法和工艺，以确保桥梁能够按照设计要求安全、高效地建设。

此外，桥梁的维护和保养也是一个重要的方面，设计师应考虑到桥梁的维修和检查的便利性，并采用合理的方法和技术来延长桥梁的使用寿命。

总结来说，钢桁架桥的设计和优化是一个复杂且综合性的工程，需要考虑多个因素并做出合理的决策。

设计师应该熟悉相关的技术和方法，并具备一定的工程实践经验。

通过合理的设计和优化，可以创建出结构稳定、美观实用且具备可持续性的钢桁架桥，为城市交通建设提供有效的支持。

大跨度钢桁架施工方案优化与经济论证比选

大跨度钢桁架施工方案优化与经济论证比选
大跨度钢桁架结构应用范围广泛，如机场航站楼、体育场馆、展览馆、桥梁等。

在其
施工方案优化和经济论证比选中，应考虑以下几个方面：
1. 结构设计方案优化：大跨度钢桁架结构需要满足强度、刚度、稳定性等多重要求，同时也需要考虑到施工难度和成本等因素。

因此，在结构设计方案上，应从多方面出发，
通过合理的布局和优化的节点连接设计等方式，实现轻量化、刚度、稳定性和施工方便等
优点。

2. 施工工艺方案优化：大跨度钢桁架结构在施工时面临的诸多挑战，如高空操作、
安全保障、设备和物料运输等。

因此，在施工工艺方案上，应通过合理的选材、建立安全
管理体系、装备先进的运输和吊装设备等方式，实现高效、安全、无事故的施工过程。

3. 经济性比选：在施工中，成本是一个至关重要的指标。

因此，应通过综合分析多
个方案，如材料成本、施工工资、工程周期等多个维度，进行经济性比选，选择最合适的
方案。

4. 工期进度控制：钢桁架结构施工周期长，需要在施工前制定详细的工期计划，及
时控制施工进度，缩短工期，确保工程顺利进行。

综上所述，大跨度钢桁架施工方案的优化与经济论证比选，需要从结构设计方案、施
工工艺方案、经济性比选和工期进度控制四个方面进行分析，以实现施工效果的最大化。

桁架结构布局优化的并行子空间方法

桁架结构布局优化的并行子空间方法王毅;姚卫星【摘要】由于结构布局优化存在设计变量类型众多和变量耦合等问题，采取合适的优化方法获得满足结构设计要求的最小质量的结构具有重要的工程意义．基于多学科设计优化方法中的并行子空间优化法，提出一种桁架结构布局优化的并行子空间优化方法．将结构布局设计问题按设计变量类型分为布局、形状和尺寸三个并行的子空间，设计变量在各自的子空间内单独优化，各子空间优化结束后，在系统级中协调3类设计变量，保持最小质量的子空间的优化设计变量不变，采用近似一维搜索的方法协调其他子空间的设计变量，然后进行下一次迭代直至收敛．2个算例表明该方法能够取得较好的优化结果，具有实际工程应用价值．%Structural layout design exists some problems ,such as complexity of variable types and existence of variables coupling .It is of important engineering significance to design the lightest structure ,w hich meets the specific constraints .Based on the concurrent subspace optimization method in multidisciplinary design optimization ,a structural concurrent subspace optimization method was developed for the layout design of trusses .In terms of the type of variables ,the de‐sign problem of structures was decomposed into three concurrent subspaces as layout ,shape andsize .And the optimization in each subspace was carried out separately to avoid the coupling of de‐sign variables .By remaining the design variables in the lightest subspace unchanged and altering two other types of variables with approximate one‐dimensional search algorithm ,the coordination was achieved in system level to ensure the convergence ofthe analysis problem .Then next iterate was executed untiltermination .Two examples were solved successfully to demonstrate practical engineering value of the proposed method .【期刊名称】《工程设计学报》【年(卷),期】2015(000)003【总页数】7页(P256-261,268)【关键词】桁架;并行子空间优化方法;布局优化;形状优化;尺寸优化【作者】王毅;姚卫星【作者单位】南京航空航天大学飞行器先进设计技术国防重点学科实验室，江苏南京210016;南京航空航天大学飞行器先进设计技术国防重点学科实验室，江苏南京210016【正文语种】中文【中图分类】O224结构优化设计的目的在于寻求既轻又能满足设计要求的结构.一个复杂的结构设计问题通常包括尺寸、形状和布局三类变量，它们属于不同层次，在结构设计中相互耦合，传统的优化方法常常难以求解.通过有效的结构优化方法解耦3类设计变量，提高设计效率，得到既满足设计需求又质量较小的结构，具有重要的工程意义.按设计变量的层次，结构优化可分为尺寸优化、形状优化和布局优化，设计难度随着设计变量层次增加而增加.目前，对于结构布局优化问题，多采用分层分级的优化方法，将不同类型的设计变量分为2级或多级进行逐层分步求解［1－6］.虽然分级优化方法解除了各类变量之间的耦合关系，但并不一定能找到最优解.因此有研究者将不同层次的设计变量耦合成一类变量统一进行优化，并得到了较好的优化结果［7－9］.并行子空间优化方法（concurrent subspace optimization，CSSO）是由Sobieski于1988年提出的一种多学科优化设计方法，早期的并行子空间优化方法是基于灵敏度分析的［10］，后来Sellar等人［11］发展了基于响应面的并行子空间优化方法（CSSO－RS），该方法收敛性高，实用性更强.目前，将多学科优化设计方法应用到结构优化设计中的研究较少.张振伟等［12］提出一种桁架结构的尺寸和形状协同优化的方法，冯玉龙等［13］给出复合材料加筋板的布局优化子空间协同方法.本文针对结构布局优化问题，提出一种桁架结构布局的并行优化子空间方法，通过2个算例验证得到了较好的设计结果.1 结构布局优化子空间方法1.1 优化问题的数学模型对于桁架结构布局优化问题，设计变量通常包括尺寸、形状和布局三类变量.设计目标为结构质量最小，约束条件包括静强度、刚度和稳定性等约束.优化模型如下：式中：W为结构质量；X1，X2，X3分别为尺寸、形状和布局三类变量；［σ］和［ε］分别为结构的许用应力和许用应变；δmax为结构变形允许值；XiL和XiU为设计变量Xi的上下限.1.2 并行子空间优化将优化问题分为尺寸优化、形状优化和布局优化三个并行的子空间，相应的设计变量为尺寸、形状和布局变量.在每个子空间内，只优化自身设计变量，其他类型变量作为状态变量保持不变，这样解除了不同类型变量之间的耦合，降低了问题的复杂程度.3个子空间优化过程同时进行，在得到各自最优的新的设计变量和最小目标值后，计算3个子空间的最优质量的方差，如果小于收敛精度e，整个优化结束，此时取尺寸优化子空间得到的各个设计变量的值作为整个优化问题的最优解，否则进行系统级设计变量协调.在系统级内，选取3个子空间中最小质量的子空间作为该次设计的最优值，该空间的设计变量在下一次优化时保持不变，而对其他空间的设计变量进行协调处理.在变量协调时，采用类似一维搜索中的进退法对优化变量进行调整，其基本思想是从初始点开始以初始步长向前或向后探索目标函数的变化趋势，若减小，向前搜索，若增大，向后搜索，从而找到包含目标函数最小值的闭区间.在本文中，搜索步长为α（k），搜索方向为X（k）others，opti－X（k）others.变量协调结束后，进行下一次迭代，直至整个优化过程收敛.整个优化流程如图1所示.需要说明的是，该设计流程并非只适用布局优化，若针对形状优化问题，优化流程与图1相同，而并行的子空间只有形状和尺寸优化.图1中μ1和μ2为布局和形状优化时引入的约束松弛变量，μ1和μ2均大于1.μ1和μ2的表达式为其中k为迭代次数，μ0为一个给定的正数（本文中布局优化时取1，形状优化时取0.5）.随着迭代次数k增加，松弛变量μ逐渐变小.s2为各子空间优化质量的方差.e为收敛精度（本文取结构质量的3%）.表示3个子空间优化结果最小的A空间的质量.ΔW为与A空间的质量差.步长α（k）对形状和尺寸变量取，对布局优化取－1，即在形状和布局子空间内部优化时，引入约束松弛变量的目的是扩大可行域范围，防止由于尺寸优化后下一次迭代的形状和布局优化的可行域缩小，难以找到最优解.而在尺寸优化中不设置松弛变量是为了协调形状和布局最优解落在可行域外的情况.针对布局优化变量离散的问题，调整α（k）表达式的值，以保证布局变量满足实际要求.由于每轮优化过程选取质量最小的子空间的设计变量作为下一轮优化的状态值，因而下一轮优化的最优解必定小于上一轮优化的最优解，优化收敛性能够得到保证.图1 布局优化流程图Fig.1 The flow chart of layout optimization1.3 优化流程实施整个计算流程借助ISIGHT多学科优化平台搭建而成，该软件不仅集成了多种优化算法，能够求解各类优化问题，而且还能实现不同程序的调用执行以及相关文件的修改.在尺寸优化子空间内，设计变量为杆件的截面积，变量连续，本文采用Nastran 软件集成的序列二次规划算法（SQP）求解.Nastran软件是一款广泛应用于机械设计、航空航天等领域的有限元分析软件，其对结构的尺寸优化分析结果已经得到广泛认可.该优化求解器内部集成了诸如序列二次规划法（SQP）、修正可行方向法（MMFD）和序列无约束极小化法（SUMT）等优化算法，结构设计者可直接借助该软件优化得到满意的结果.在形状优化子空间内，设计变量为节点坐标，由于变量是连续的，本文采用ISIGHT软件中集成的可行方向法（MFD），借助该软件不断地修改节点坐标并调用Nastran计算分析找到满足设计要求的最优解.在布局优化子空间内，设计变量取0和1，分别代表杆件的删除与增加，并将初始结构设定为整个优化的基结构.设计变量不连续，且只有0和1两种情况，因此本文在优化时借助ISIGHT软件中集成的遗传算法进行求解，通过基因交叉、变异等手段不断地调整编码序列，以实现不同结构布局形式.在优化过程中，对于几何可变结构采取自动删除的方式，其计算结果不放入优化取值中.2 算例2.1 15杆平面桁架结构布局优化如图2所示为一15杆桁架［2］.杆件E＝6.897×106 N／cm2，ρ＝0.002 768 kg／cm3，＝17 243.5 N／cm2＝－17 243.5N／cm2.工况有2个，工况1：P3y＝P5y＝P7y＝－4.45×105 N；工况2：P4y＝P6y＝P8y＝－4.45×105 N.位移约束是节点5在Y向的位移不超过2.032cm，坐标设计变量为X3，X4，Y4，Y6.杆截面积下限为6.452cm2.桁架结构对称，外载荷对称，因此将尺寸设计变量（即15个杆件面积）按对称性分为8组，见表1.同样按照对称性，将形状设计变量（即6个节点的坐标）进行了变量链接，见表2.图2 15杆平面桁架结构图Fig.2 Initial 15－bar truss structure表1 杆件截面变量Table 1 Size variables of bars设计变量杆件编号设计变量杆件编号A1 1－4，2－8 A5 4－5，5－8 A2 4－6，6－8 A6 1－3，2－7 A3 3－4，7－8 A7 3－5，5－7 A4 3－6，6－7 A8 5－6表2 坐标链接情况Table 2 Link of coordinates3 X3 Y3（≡0）4 X4 Y4 6 X6（≡0） Y6 7－X3 Y3（≡0）8－X4 Y 4经过6次迭代优化，4－5和5－8杆件被删除，得到桁架结构质量为283.52kg，该结果比文献［2］减轻65.87kg，见表3.结构质量优化历程和优化后的结构图如图3和图4所示.表3 15杆桁架优化结果Table 3 Optimization results of 15－bar trussA1／cm2129.032 70.968 78.448 A2／cm2 129.032 45.161 75.321 A3／cm2 129.032 32.258 23.45 A4／cm2 129.032 0.000 6.619 A5／cm2 129.0326.452 0.000 A6／cm2 129.032 6.452 6.452 A7／cm2 129.032 6.452 6.452 A8／cm2 129.032 32.258 36.74 X3／cm －254.0 －189.99 －314.76 X4／cm －254.0 －228.22 －340.44 Y4／cm 381.0 310.64 96.05 Y6／cm 508.0 401.87 170.32质量／kg 2 028.13 349.39 283.52图3 15杆桁架结构质量变化历程Fig.3 History of 15－bar truss structure weight图4 本文布局优化结果图Fig.4 The best truss diagram by our method图5为文献［2］的布局优化结果，与图4相比较可以看到，经过本文方法优化后的桁架高度变小了，高度变小的原因可能是载荷工况不够大造成的.如果将桁架结构看作一个两支点的工程梁，在外载不变的情况下，梁的高度降低了，必然导致上下缘条的载荷变大，相应桁架结构杆的截面积也会变大，质量会有所增加.然而高度变小的另一个好处是杆的长度变小了，相反会带来结构质量的减小，权衡两者给结构质量带来的影响，从优化结果看，高度变小带来的质量减小效果更明显.如果外载荷足够大，可能会有不一样的优化结果.图5 文献［2］优化结果图Fig.5 The best truss diagram of reference［2］2.2 25杆桁架结构布局优化结构模型如图6所示，共包含10个节点和25根杆［2］，其中底部4个节点固定.各杆弹性模量E＝6.8974×106 N／cm2，密度ρ＝0.002 768kg／cm3.不考虑结构稳定性.桁架结构受到2个载荷工况作用，具体载荷值见表4所示.杆截面积不得小于0.064 5 cm2，节点1和节点2的最大位移不超过0.889cm，整个桁架高度不得低于355.6cm.图6 25杆桁架结构图Fig.6 25－bar space truss structure with initial dimensions表4 25杆桁架载荷工况Table 4 Load cases of 25－bar truss1 1 4.45 44.5 －22.25 2 0 44.5 －22.25 3 2.225 0 0 6 2.225 0 0 2 1 0 89 －22.5 2 0 －89 －22.5根据结构对称性将25根杆分为8组，每组截面积相同，使用同一设计变量.分组情况和各组许用应力见表5所示.6个节点共18个坐标采用6个坐标变量X2，Y2，Z2，X4，Y4和Z4描述，节点坐标链接如表6所示.表5 25杆桁架尺寸变量与应力约束Table 5 Size variables and stress constraints of 25－bar truss设计变量杆件编号限制应力／（N／cm2）下限值上限值A11－2 －24 204.4 27 589.6 A2 1－4，2－3，1－5，2－6 －7 994.1 27 589.6 A3 2－5，2－4，1－3，1－6 －11 936.0 27 589.6 A4 3－6，4－5 －24 204.4 27 589.6 A5 3－4，5－6 －24 204.4 27 589.6 A6 3－10，6－7，4－9，5－8 －4 661.9 27 589.6 A7 3－8，4－7，6－9，5－10 －4 661.9 27 589.6 A8 3－7，4－8，5－9，6－10 －7 643.7 27 589.6表6 节点坐标链接Table 6 Link of coordinates节点号X Y Z 1－X2 Y2 Z 2 2 X2 Y2 Z2 3－X4 Y4 Z4 4 X4 Y4 Z4 5 X4 －Y4 Z4 6－X4 －Y4 Z 4最终优化结果列在表7，同时表7还列出了文献［5］和文献［2］的优化结果，其中文献［5］只优化了形状和尺寸变量，并未作布局变量优化，文献［2］截面尺寸为离散变量.经过10次迭代优化，1，4，5三根杆件被删除，桁架变为22杆结构.最终优化质量为41.7kg，比文献［5］和文献［2］分别减轻19.8kg和21.1kg.结构质量优化历程和优化后的结构图如图7和图8所示.表7 25杆优化结果Table 7 Optimization results of 25－bar trussA1／cm20.064 5 0 0 A2／cm2 5.458 6.542 5.893 A3／cm2 3.961 4.065 3.364 A4／cm2 0.064 5 0 0 A5／cm2 0.064 5 0 0 A6／cm2 0.658 1.355 0.130 A7／cm2 3.187 0.774 2.74 A8／cm2 6.781 7.742 1.84 X2／cm 25.4 6.45 18.76 Y2／cm 0 －0.39 0 Z2／cm 355.6 355.6 355.6 X4／cm 52.07 124.48 52.7 Y4／cm 88.65 161.63 141.85 Z4／cm 247.4 174.94 180.96质量／kg 61.5 62.8 41.73 结论图7 25杆桁架结构质量优化历程图Fig.7 History of 25－bar truss structureweight图8 25杆桁架布局优化结果图Fig.8 The best 25－bar truss diagram by our method将一个复杂的结构设计问题分解为布局、形状和尺寸优化3个子空间，在独立的子空间内并行优化，然后在系统级协调3个子空间的设计结果，降低了分析和计算的难度.通过15杆和25杆桁架算例表明，该方法是可行的，能够得到较好的优化结果.同时该方法迭代次数较少，框架简单，易于在ISIGHT平台上实现.该方法不仅适用于桁架结构的优化问题，也适用于其他结构的优化设计，后续也将会将该方法推广到更多的优化设计实例中.参考文献：［1］张广圣，王其祚.机械结构多级优化的问题与对策［J］.合肥工业大学学报：自然科学版，1990，13（1）：52－58.ZHANG Guang－sheng，WANG Qi－zuo.Multilevel mechanical structure optimization difficulties and strategies ［J］.Journal of Hefei University of Technology：Natural Science，1990，13（1）：52－58.［2］王跃方，孙焕纯.离散变量桁架结构的布局优化设计［J］.大连理工大学学报，1995，35（5）：458－462.WANG Yue－fang，SUN Huan－chun.On layout optimization of truss structures with discrete sizing variables［J］.Journalof Dalian University of Technology，1995，35（5）：458－462.［3］刘福江.复合材料翼面结构多级优化设计方法［J］.中国民航学院学报：综合版，1997，15（1）：15－21.LIU Fu－jiang.A multi－level optimization procedure of the composite wing structure［J］.Journal of Civil Aviation Institute of China，1997，15（1）：15－21.［4］常楠，刘江，赵美英.复合材料蒙皮／长桁壁板结构优化设计［J］.飞机设计，2007，27（6）：28－32.CHANG Nan，LIU Jiang，ZHAO Mei－ying.Design optimization for composite skin／stringer panel［J］.Aircraft Design，2007，27（6）：28－32.［5］隋允康，由衷.具有两类变量的空间桁架分层优化方法［J］.计算机结构力学及应用，1990，7（4）：82－91.SUI Yun－kang，YOU Zhong.A mulit－level optimization method for space trusses with combining sectional area and coordinate variables［J］.Computational Structural Mechanics and Applications，1990，7（4）：82－91.［6］刘涛，邓子辰.桁架结构尺寸和形状、拓扑的渐进优化方法［J］.西北工业大学学报，2004，22（6）：739－743.LIU Tao，DENG Zi－bined sizing，shaping and topology optimization of truss structure using evolutionary structure optimization［J］.Journal of Northwestern Polytechnical University，2004，22（6）：739－743.［7］AZID I A，KWAN A S K，SEETHARAMU K N.An evolutionary approach for layout optimization of a threedimensional truss［J］.Struct Multidisc Optim，2002，24（4）：333－337.［8］王勇.基于微粒群算法的桁架结构优化设计［D］.上海：同济大学土木工程学院，2008：32－46.WANG Yong.Particle swarm optimization for truss structure optimal design［D］.Shanghai：Tongji University，College of Civil Engineering，2008：32－46.［9］刘军伟，姜节胜.桁架动力学形状优化的统一设计变量方法［J］.振动工程学报，2000，13（1）：84－88.LIU Jun－wei，JIANG Jie－sheng.Shape optimization for truss dynamics with unified design variables［J］.Journalof Vibration Engineering，2000，13（1）：84－88.［10］SOBIESZCZANSKI－SOBIESKI J.A step from hierarchic to non－hierarchic systems［R］.NASA CP－3031，Hampton：Langley Research Center，1988.［11］SELLAR R S，BATILL S M，RENAUD J E.Response surface based，concurrent subspace optimization for multidisciplinary system design ［C］.AIAA 34th Aerospace Sciences Meeting and Exhibit.Reno，NV，Jan 15－18，1996.［12］张振伟，姚卫星，周琳，等.桁架结构尺寸和形状协同优化方法研究［J］.航空工程进展，2012，3（2）：138－143.ZHANG Zhen－wei，YAO Wei－xing，ZHOU Lin，et al.Study on size and shape collaborative optimization method of truss structure［J］.Advances in Aeronautical Science and Engineering，2012，3（2）：138－143.［13］冯玉龙，程家林，姚卫星.复合材料加筋板结构的并行空间协同优化设计方法［J］.南京航空航天大学学报，2013，45（3）：360－366.FENG Yu－long，CHENG Jia－lin，YAO Wei－xing.Concurrent subspace optimum design method for composite stiffened panel［J］.Journal of Nanjing University of Aeronautics ＆Astronautics，2013，45（3）：360－366.。

谈大跨度桁架通廊的优化设计

谈大跨度桁架通廊的优化设计摘要：桁架在工业设计中较为普遍，但对于大跨度的桁架通廊一般较少接触，笔者结合2500m3高炉工程上料主胶带机通廊的设计过程，通过电算分析桁架弦杆、腹杆计算长度系数确定，节点板设计、施工时的注意事项，介绍在设计过程中的一些经验。

关键词：大跨度桁架计算长度系数节点板设计中图分类号：tu7文献标识码：a文章编号：2095-2104（2012）1 引言桁架主要是轴心受力构件(拉杆和压杆)组成的的格构式扩大构件，用以承受横向荷载和跨越较大的空间，当跨度较大采用实腹式受弯构件将造成多费钢材时，就需采用桁架。

目前工业项目自动化程度逐步提高，工程项目规模越来越大，尤其是工业项目中，为满足工艺及空间利用的要求，桁架的使用较为普遍，笔者结合2500m3高炉工程上料主胶带机通廊钢桁架工程，对大跨度桁架的优化设计，介绍自己的处理方法。

2 工程概况本工程为2500m3高炉工程上料主胶带机通廊，通廊总长度(平面尺寸252.8米)，通廊爬升角度约为10.863º，通廊支座最高点距地面53.42米，支座最低点距地面6.52米，通廊支座高差47.8米。

由于通廊需穿越多条铁路、公路及部分高炉附属设备构筑物，共有支架 5个，包括1个固定支架、4个活动支架。

通廊最高点支承于高炉42.3米钢平台上，通廊最大跨度66.720米(斜长)。

通廊断面为4.8×5m(宽×高)，通廊维护结构采用100厚彩色岩棉复合夹芯板。

本工程地处八钢，实际计算时，荷载取值如下(均为标准值)：屋面积灰荷载：1.0kn/m2(高炉中心≤50米范围内)；通廊内平台灰荷载：0.5kn/m2；屋面雪荷载：0.8kn/m2；风荷载(距地面h=10米)：0.8kn/m2，按距地面55米高计算，风荷载取1.35 kn/m2；通廊内平台检修荷载：4kn/m2，屋面按不上人屋面考虑活荷载0.5 kn/m2；通廊内平台恒荷载：1.5kn/m2；屋面恒荷载：1.0kn/m2；墙体恒荷载：0.35kn/m。

基于满应力法的平面桁架优化

基于满应力法的平面桁架优化摘要：优化设计的目的是减少材料用量，使成本造价降低。

采用满应力法对典型的平面桁架结构进行截面优化，并在迭代计算过程中创造性地提出了中间值法，大大减少了迭代计算量，提高了计算效率，得到结构最优截面尺寸，用钢量减少40%，经济效益显著，该方法值得推广。

关键词：结构优化; 满应力法; 平面桁架; 中间值法1 概述结构优化研究主要集中在两个方面，一种是结构形状优化，它是将结构边界形状参数化，通过改变边界控制点来改变结构形状[1]，达到最优边界形状，这其中包括著名的拓扑优化法[2]；另一种是结构尺寸优化，通过优化算法或灵敏度分析[3]来获得最优结构尺寸。

由于尺寸优化较为直接，将结构截面尺寸作为变量，通过优化截面尺寸，使结构重量最轻，以达到优化的目的，而尺寸优化中最常用的方法则是满应力法。

满应力法是以充分发挥结构材料特性为目的，即在结构设计过程中，从结构力学原理出发，以满应力设计为准则，充分达到其设计强度。

对于桁架结构，给定设计荷载工况，首先利用结构力学原理进行受力分析，其次通过对桁架杆件的截面尺寸进行调整，使每个杆件充分发挥其承载能力，此时即为满应力状态，其所对应的杆件截面即为最优截面，满足桁架重量最轻的要求，达到了优化的目的。

本文利用满应力法在满足杆件应力、稳定性、位移及最小截面尺寸的约束条件下，通过建立数学模型，利用循环迭代调整来确定桁架杆件截面的最小尺寸，最终使结构得到优化。

2 满应力法数学模型桁架结构尺寸优化最终目的就是使其重量最轻，即可建立目标函数为：(1)式中:W为结构的重量;li、ρi和Ai分别为杆件的长度、材料密度和截面面积。

其次还需满足以下条件[4]。

应力约束：(2)式中分别为i号杆单元的允许拉、压应力值。

位移约束：ui≤[ui](3)式中：[ui]为杆件位移限值。

最小截面约束：Ai>Amin(4)压杆局部稳定性约束：对于桁架结构中的细长杆件，可能会产生失稳现象，在本文中通过限制杆件长细比来控制其稳定性,其中临界失稳应力[5]σcri=π2E/λ2。

桁架结构拓扑及截面尺寸优化设计方法

桁架结构拓扑及截面尺寸优化设计方法周奇才;吴青龙;熊肖磊;王璐【摘要】为克服传统基结构设计方法对最优解的束缚,实现桁架结构的拓扑布局及尺寸优化,提出了将连续体与离散杆系相结合的桁架结构优化设计方法.从连续体出发,基于SKO连续体拓扑优化方法得到了最优拓扑布局;以二值图像细化算法为基础,提出了基于有限单元8邻域网格模型的骨架提取算法,通过剥离冗余单元,得到了连续体拓扑优化结果的中心传力骨架;以单元主应力为判据,精确找到骨架中的关键点,并连接关键点形成了初始桁架结构;基于拉格朗日乘数法和Kuhn-Tucker条件,以初始桁架中杆件的内外半径为设计变量,结构体积为约束条件,结构柔度为目标函数,建立了桁架结构杆件尺寸优化的数学模型,并推导出其优化迭代准则.最后,以一悬臂结构为例对该优化方法的应用进行了说明,并使用一经典算例与其他文献中的方法进行了对比,结果表明:该优化方法得到的桁架结构具有优化的拓扑构型和力学特性,杆件布局、尺寸合理,应力均匀.【期刊名称】《西安交通大学学报》【年(卷),期】2016(050)009【总页数】9页(P1-9)【关键词】桁架;连续体;拓扑优化;骨架提取;尺寸优化【作者】周奇才;吴青龙;熊肖磊;王璐【作者单位】同济大学机械与能源工程学院,201804,上海;同济大学机械与能源工程学院,201804,上海;同济大学机械与能源工程学院,201804,上海;同济大学机械与能源工程学院,201804,上海【正文语种】中文【中图分类】TH11桁架结构因具有造价低、重量轻、施工简便的特点而在工程领域中得到了广泛应用。

桁架结构的优化设计包扩结构的拓扑和布局优化及杆件的尺寸优化。

在桁架拓扑和布局优化方面,Michell于1904年提出的Michell桁架理论以及Prager于1977年建立的经典布局理论为其奠定了理论基础,而Dorn等提出的基结构法则标志着桁架拓扑优化工作的真正开始[1-2]。

基于CAE分析的桁架优化设计

Ｉ
ｍｌｉ
一
Ｉ｝
开县
— — ・
一
，
０ … 川 ¨ 川 … … … 川 …川 … … 川 … 川 … … … Ｊ … … ｝至｝』… … 川｝
地面线
Ｉ
＝＝— — ＝ ——
—
１０３０
—
—
一
Ｉ／／瓮ｆ
【常水位３５５Ｉ９
机械结构设计的传统方法是以经验、性、感静态和手工劳动为基础的一种设计方法，括类比设包计法、算法、格法、算法等ｌｊ工程中的试表图１。
的桁架拓扑结构。
结构不但受到静载荷作用，而且许多工程结构在使用中都会受到强烈的振动与冲击。结构优化的目
梁的安全，要对桥梁进行加固。图１示的石拱需所

现结构的最优性能，括强度、包刚度、定性等目稳标。依靠传统的设计方法实现工程结构的优化设
计难度较大＿Ｊ４。
桥，能承受重型载重汽车运输石油钻井设备，不利用传统加固桥梁的方法实施非常困难，程部门通工过对各种加固方案进行比较，出在桥墩上制造一提
作者简介：桂Ｊｌ１６胡ｉ９４一）男，（，四川泸州人，庆科技学院副教授，士，重硕主要研究方向为计算机辅助工程分析、算流体力学。计

综述拱桁架结构优化设计

综述拱桁架结构优化设计【摘要】拱桁架结构是当前大跨度建筑结构设计中经常应用到的一种设计方式，这种结构方式不但能够很好的满足大跨度的屋盖设计需求，而且可以通过合理的设计来降低工程的施工总成本，因而极受设计人员的青睐。

本文结合实际工程案例，对优化拱桁架结构的设计方法进行了讨论分析，指出了在本工程的拱桁架设计中，采用拉杆拱桁架可有效降低工程施工难度，并且能够实现更好的经济效益。

【关键词】钢结构；拱桁架；拉杆型；优化设计随着社会发展的需求不断增多，建筑结构的设计形式也发生了很大的改革，由传统的较为单一的建筑结构设计形式逐渐转变为多样化、现代化的结构设计。

其中钢结构就是这样一种在新的社会需求下发展而来的建筑结构形式，而且就钢结构而言，在材料和技术不断改进的情况下，也有了很多不同结构形式的发展。

拱桁架结构作为钢结构设计形式中较为常见的一种结构设计方法，是相对来讲受力最合理、施工最经济的一种结构形式。

1、拱桁架结构的概述就目前我国的拱桁架结构设计发展现状来讲，拱桁架按照支座的不同可以分为不拉索和杆、拉索以及拉杆等三种不同的结构设计方式。

这是因为在拱桁架的结构中，拱所承受的荷载是通过曲杆来抗衡，并将去传递到支座而实现整体受力的。

也就是说，拱桁架结构的支座在承受荷载时，不但需要受结构上部对其的竖向压力，而且还要承受因拱结构传递而来的水平推力。

为了平衡这两种应力，处理好支座的结构是关键。

一般来讲，支座化解水平推力的处理方法有两种形式，其一是将推力完全由支撑结构来承受，其二是在拱桁架下部设置一定的下弦单拉杆，通过拉杆来承受推力。

第一种方案中，由于支座要承受所有的推力，因此负荷很大，对其构件质量也提出更高的要求，施工所用材料较多，而第二种则是将推力通过杆件分散出去，对于支座的构件要求不是太高，施工用料则较为节省。

为此，一般在采用拱桁架结构进行施工时，大都会采用拉杆的方式来进行结构设计。

2、工程实例概况在某地区的一个生态园区的发展建设中，为了满足生产的需要，要在园区内建造一个钢屋盖结构的大空间、大跨度建筑。

基于ANSYS的桁架结构优化

基于ANSYS的桁架结构优化【摘要】空间桁架结构广泛应用于工程各种领域，其结构的力学分析及优化，是桁架结构设计中的关键技术难题。

本文利用ansys 软件，采用apdl语言编制用户程序，对混凝土运输系统的桁架结构进行在四种不同设计方案进行优化比选，最终选择既满足工程实际又经济的桁架结构。

【关键词】 ansys 桁架结构优化选型1 工程概况混凝土运输系统是大体积混凝土工程顺利实施的关键。

混凝土熟料从拌和系统出来后经水平运输和垂直运输到浇筑作业面，施工中，根据地形、工程量、混凝土性质和企业能力等采用不同的运输方式。

对于水平运输，中小型工程一般采用斗车或罐车，大型工程一般采用罐车、自卸汽车或皮带机运输；对于垂直运输，中小型工程一般采用溜槽、人工翻仓、汽车吊、输送泵等，大型工程一般采用塔式起重机、门式起重机、塔带机和缆机等。

某水库是一座大（2）型水库，其进水塔为2级建筑物，相邻的两个进水塔高度分别为102m和86m，均为岸坡式建筑物，混凝土工程量13.2万m3，塔体采用限裂设计。

[1]结合两个进水塔均为岸坡式建筑物，根据现场地形确定了以下运输方案。

在施工道路旁架设皮带机（简称1#机）进行水平运输，通过铅直布设的box管进行垂直运输，box管的下端再架设一条皮带机（简称2#机）把混凝土输送给仓面布料机，360°旋转的仓面布料机两端挂直径420mm的象鼻溜管进行仓面布料，当完成2～3个浇筑层（一般每层3m）需要上升布料机时，用900tm塔式起重机把2#皮带机和布料机提升布设，进行下一循环的作业。

该方案虽然能够满足施工强度要求，资金投入相对较少，但亟待解决混凝土输送桁架结构选型这一技术问题。

2 桁架结构的有限元模型有限元模型建立是否恰当会直接影响到工程计算结果的可靠性。

所谓建立模型，就是结构的离散化，对结构施加约束条件和荷载，然后进行计算分析。

因此，选择合适的计算模型和单元模型是十分重要的。

本文中，在建立ansys模型时采用杆单元link8来模拟二力杆，可用梁单元beam4来模拟可承受拉、压、弯、扭的受力单元。

大跨度钢结构桁架优化措施

大跨度钢结构桁架优化措施嘿，咱今儿就来聊聊大跨度钢结构桁架优化措施这档子事儿！你想想啊，那大跨度钢结构桁架，就像是建筑界的大力士，撑起了一片片广阔的空间。

可要是没弄好，那可不行呀！咱先说说设计这块儿。

这设计就好比是给桁架规划路线，得精心琢磨。

你不能随随便便就画个图，那可不行！得考虑各种因素，比如受力情况，就像人得知道自己能扛多重的东西，桁架也得清楚自己能承受多大的力呀。

还有啊，节点的设计也很关键，这就好比是人的关节，得灵活又牢固，不然怎么能活动自如呢？再讲讲材料的选择。

这材料就像是桁架的血肉呀，得挑好的。

不能贪便宜用那些质量不靠谱的，不然到时候出问题可就麻烦大了。

好的材料能让桁架更结实，更耐用，就像好马配好鞍一样。

然后呢，施工过程也不能马虎。

工人师傅们得像对待艺术品一样对待桁架的安装。

焊接得严丝合缝，安装得稳稳当当，这可不是闹着玩的。

要是这里歪一点，那里斜一点，那整个桁架不就变形了吗？还有啊，咱得注意后期的维护。

别以为建好就完事大吉了，还得时不时去看看，有没有生锈啊，有没有松动啊。

就像人要定期体检一样，桁架也需要我们的关心和照顾。

优化大跨度钢结构桁架，不就是为了让它更好地为我们服务吗？让那些大空间变得更加安全可靠，更加美观实用。

这可不是一件简单的事儿，但只要我们用心去做，肯定能做好呀！你想想看，如果一个大跨度钢结构桁架设计不合理，那会怎么样？肯定会存在安全隐患呀！那要是材料不好呢？说不定用不了多久就出问题了。

施工不仔细，后期不维护，那后果简直不堪设想！所以说呀，这些优化措施一个都不能少，都得认真对待。

咱们可不能小瞧了这大跨度钢结构桁架，它可是建筑领域的重要组成部分。

通过优化措施，让它发挥出更大的作用，这难道不是一件很有意义的事情吗？咱得把这事儿做好，让每一个大跨度钢结构桁架都能成为建筑中的亮点，成为我们生活中的可靠支撑！这就是咱对待大跨度钢结构桁架优化措施该有的态度，你说是不是呢？。

基于遗传算法的桁架形状优化及最小质量设计

向为建筑结构优化设计， 2MJNE9 ： FIBCOPQCR %!# : F8J
"ห้องสมุดไป่ตู้第K期
陈芸：基于遗传算法的桁架形状优化及最小质量设计
<<
数为 !，对每个个体进行评价，按适应度高低，依此每两个个体作为一对母体进行交叉、繁殖，每对母体产生两个子体，这时有 ! = 9 个以每组母、子 > 个个体的组合，对每个组合再进行评价，适应度高的两个个体生存下来，其余两个被淘汰。生存下来的个体作为下一代的母体，再进行评价、交叉、繁殖。家族内淘汰模型见图 9，图 9 中 ? 表示母体， @ 表示子体。
’()*+,- (. +,+’/+0 )+/12*3/45 (. 4267+(-(05
189: !" +8: # +8;: !$$#
基于遗传算法的桁架形状优化及最小质量设计
陈& 芸
（南京工业大学建筑与城市规划学院，江苏南京 !%$$$< ）
摘& 要：在工程结构的优化设计中，应用遗传算法的基本原理，研究了离散设计变量全局寻优等传统优化方法难于解决的特殊问题。以平面桁架梁作为解析例，选取桁架的节点坐标和杆件的截面特征为设计参数，模拟遗传操作过程中的生物进化机制，对桁架的构成和形状的优化问题进行了解析。得到桁架在不同情况下的形状优化解，并使桁架质量趋于最小。研究结果验证了遗传算法在桁架的形状最优化和最小质量设计中应用的可行性。关键词：遗传算法；桁架；优化；最小质量! 中图分类号：4)%!& & & 文献标识码： ,& & & 文章编号： %#=% > =#?@ （ !$$#） $# > $$@! > $A

最小位移类桁架连续体拓扑设计优化

● ● ｌ－ｌ・
ＡｂｔａｔＴｘａｄｆｘｂｌｙｍｉｉｚｔｎｐｏｌｍｎｔｐｌｇｐｉｚｔｎｔｅｅａｉｌｃｍｅｔｓｒｃ：ｏｅｐｎｅｉｉｔｎｍｉａｉｒｂｅｉｏｏｏｙｏｔｌｉｏｍｉａｉｏｇｎｒｌｄｓａｅｎｏｐ
用类桁架连续体材料模型，并假设杆件在设计域内连续分布．将杆件在节点位置的密度和方向作为
设计变量，指定位置和方向的位移作为目标函数，用基于目标函数梯度的优化准则法，将采通过优
化杆件的连续分布场形成拓扑优化的类桁架连续体．方法可结合结构力学的基本概念，该选择部分
最小位移类桁架连续体拓扑设计优化
李宝龙，周克民
（华侨大学土木工程学院，福建厦门３１２）６０１
摘
要：为将拓扑优化中的柔度最小化问题拓展到一般位移最小化问题，有限元划分设计域，用采
杆件形成拓扑优化刚架．
关键词：结构优化；扑优化；类桁架连续体；最小位移；限元法拓有
中图分类号：Ｕ２Ｔ３文献标志码：Ａ
Ｔｏｏｏｙｄｅｉｎｏｉｉａｉｎ０ｔｕｓ —ｉｅｃｎｔｎｕｍｔｐｌｇｓｇｐｔｍｚｔｏｎｒｓｌｏｉｕｋｗｉｈ
ｄｎｓｔｎｒｅｔｔｏｆｒｄａｏｓｔｎａｅｓｌｃｅｓｇｅｉｙａｄｏｎａｉｎｏｏｔｎｄｅｐｏｉｉｒｅｅｔｄａｅｉｎｖｒａｌｓｉｏｅｄｓｌｃｍｎｌｎ

大跨度钢桁架施工方案优化与经济论证比选

大跨度钢桁架施工方案优化与经济论证比选大跨度钢桁架是一种常见的结构形式，用于桥梁、体育场、展馆等大空间覆盖结构中，具有跨度大、自重轻、刚度高、施工速度快等优点。

钢桁架的施工方案优化与经济论证比选是在施工前必不可少的一项工作，通过科学合理的施工方案和经济性的比选，可以确保工程的质量和安全，同时降低工程造价，提高工程效益。

本文将重点探讨大跨度钢桁架施工方案的优化和经济性的比选。

一、施工方案优化1. 结构形式选择大跨度钢桁架的结构形式多样，包括平行桁架、转换桁架、曲线桁架等。

在选择结构形式时，需要考虑框架的受力性能、构件的制作和安装工艺、工程的运输和施工条件等因素。

比如在桥梁工程中，如果跨度较大且要求空间通行性好，可以选择平行桁架；如果需要考虑桥梁的美观性和风荷载，可以选择曲线桁架。

2. 施工工艺优化钢桁架的制作和安装是整个施工工艺的关键环节。

在施工前需要对每一个环节进行科学合理的规划和优化，避免出现不必要的工期拖延和安全隐患。

比如在制作工艺上，可以采用现代化的数字化加工设备，提高构件的加工精度和效率；在安装过程中，可以采用模块化组装的方法，减少现场焊接和钻孔工作，提高工程的安全性和质量。

3. 材料选择和利用大跨度钢桁架的材料选择和利用也是施工方案优化的重要内容。

在材料选择上，可以根据工程的实际情况和经济性，选择合适的钢材规格和型号；在材料利用上，可以采用预制装配的方法，减少现场焊接和切割工作，提高材料的利用率和减少浪费。

二、经济性比选1. 成本估算在大跨度钢桁架工程的施工中，成本是一个非常重要的考量因素。

施工前需要对各种施工方案进行成本估算，包括材料成本、人工成本、设备成本、施工工期等。

只有对各种施工方案的成本有一个清晰的认识，才能进行经济性的比选。

2. 施工进度施工进度是另一个重要的经济性考量因素。

在选择施工方案时，需要考虑每种方案的施工周期和工期计划，以及对工期的风险分析。

比如在选择工艺优化方案时，需要考虑到施工周期的缩短和进度的加快，从而降低施工期间的资金成本和风险。

三杆桁架的优化设计

三杆桁架的优化设计本文旨在介绍三杆桁架优化设计的背景和目的。

三杆桁架是一种常用的结构形式，具有高强度、轻量化和刚性好的特点，广泛应用于建筑、航空航天等领域。

然而，在实际应用中，三杆桁架结构的设计效果往往会受到诸多因素的制约，包括材料选择、结构形式、荷载条件等。

因此，对三杆桁架进行优化设计，不仅可以提高结构的性能和稳定性，还可以降低材料的使用量，减少成本。

本文将分析三杆桁架优化设计的背景和目的，探讨优化设计的方法和策略，以期为相关领域的研究者和设计师提供参考和指导。

三杆桁架的结构分析三杆桁架是一种常见的结构形式，由三根杆件和若干个节点组成。

它具有简单的结构和良好的稳定性，在工程领域得到广泛应用。

三杆桁架的基本结构是由三根杆件连接而成的三角形，每个顶点都是一个节点，杆件在节点处连接。

三杆桁架的性质取决于杆件的材料特性和连接方式。

三杆桁架的优化设计在设计三杆桁架时，可以采用优化设计的方法来提高其性能和效率。

优化设计的目标是使得三杆桁架在给定约束条件下，达到最佳的结构性能。

优化设计中的关键是确定合适的优化目标和设计变量。

优化目标可以包括最小化杆件的重量、最大化桁架的刚度或最小化应力集中等。

而设计变量可以包括杆件的截面积、材料的选择等。

进行三杆桁架的优化设计时，可以采用数值计算方法，如有限元分析和遗传算法等。

通过建立数学模型和进行参数优化，可以找到最优的设计方案。

总之，三杆桁架的优化设计是一项复杂而重要的工作。

通过合理的优化设计，可以提升三杆桁架的性能，实现结构的优化和效率的提高。

本文将介绍三杆桁架的优化设计方法，包括有限元分析等相关内容。

通过优化设计，我们可以改善三杆桁架的性能和结构强度，以满足特定的工程需求。

三杆桁架的优化设计可以采用以下方法：1.确定设计目标在开始优化设计之前，需要明确设计目标。

这可以包括改善结构强度、减小重量、降低成本等方面。

明确设计目标可以帮助我们选择适当的优化方法和评估指标。

2.建立数学模型根据设计目标，我们需要建立三杆桁架的数学模型。

基于满应力法的平面桁架优化

基于满应力法的平面桁架优化满应力法是一种常见的工程优化方法，经常用于平面桁架的设计和优化。

平面桁架是由杆件和节点组成的结构，在工程领域中被广泛应用于桥梁、建筑和机械设备等领域。

满应力法的主要思想是将结构中的每个杆件看作是单轴张力或压缩状态，并使得每个杆件满足其允许的最大应力。

通过找到这样的结构布局和杆件尺寸，可以得到最优的平面桁架设计。

平面桁架的设计优化通常包括以下几个步骤：1.定义设计目标：首先需要明确设计目标，例如最小重量、最小体积、最小应力等。

根据具体应用需求确定设计目标，并进行量化。

2.约束条件的建立：根据平面桁架的使用要求和性能要求，建立适当的约束条件。

这些约束条件可以包括结构稳定性、几何约束、最大应力限制等。

约束条件的建立需要根据具体问题进行合理的假设和分析。

3.结构模型的建立：根据设计要求和约束条件，建立平面桁架的结构模型。

结构模型包括杆件和节点的连接关系、材料性质和荷载情况等。

根据模型进行初步的计算和分析。

4.杆件尺寸的选择：根据满应力法的原则，选择合适的杆件截面尺寸。

首先需要确定每个杆件的最大应力，并根据材料的强度特性和安全系数进行计算。

然后从预先设定的杆件截面库中选择合适的截面尺寸。

5.结构优化：通过迭代计算和分析，不断优化平面桁架的结构布局和杆件尺寸。

可以使用合适的优化算法，如遗传算法、粒子群算法等，来寻找最优解。

优化过程中需要考虑设计目标和约束条件，以及结构的可行性和性能。

6.结果评估和验证：得到优化结果后，需要对结果进行评估和验证。

评估可以通过计算和分析得到最优解的性能和效果。

验证可以通过实验或数值模拟来验证最优解的可行性和可靠性。

7.结果分析和优化调整：根据评估和验证的结果，分析最优解的优点和不足之处。

如果需要，可以对优化结果进行调整和改进，以达到更好的设计效果。

通过以上的步骤，基于满应力法的平面桁架优化可以得到最优的设计方案。

这种方法能够充分考虑结构的受力性能和优化目标，有效提高平面桁架的结构性能和设计效率。

基于强度和变形约束的钢桁架优化

ｖｒａｌ，ｔｅｍｉｉｍｆｈｔｕｔｒｉｈｓｔｅｏｊｃｉｅｆｎｔｎａｄｔｅｍｅｅｔｅｇｈａｄｄｓｌｃｍｅｔａａｉｂｅｈｎｍｕｏｅｓｒｃｕｅｗｅｇｔｈｂｔｖｕｃｉｎｈｍｂｒｓｒｎｔｎｉｐａｅｎｓｔａｅｏ
ＺｕｄｅｉｎＬｏＦｎｈｉｊｇａｕｅｇ
ｎａｉｅｓｔＤｅａｔｎｔｏｖｌｇｉｅｒｎｈａｇｈｉＵｎｖｒｉｙ，Ｓａｇｉ２０７ｈｎｈａ００２，Ｃｈｉａｎ）
朱杰江，：于强度和变形约束的钢桁架优化等基
基于强度和变形约束的钢桁架优化
朱杰江罗峰
２０７）００２（ｚ大学土木工程系，海Ｊ海上
摘要：结合序列线性规划方法和对偶仿射尺度算法对钢桁架进行优化，且通过ｃ＋和ＪＡ两种编程语言并＋Ａｖ实现模型计算的程序化。Ｃ＋主要用于对优化算法的实现和迭代文件的生成，ＡＶ主要用于对桁架模型的可＋ＪＡ视化的实现以及显示模型的一些信息。以桁架的杆件面积为设计变量、结构的最小质量为目标函数、以以杆件的强度和变形为约束条件进行优化，过两个算例的计算分析，实所编程序可行并且结构模型的质量优化效果显通证
则应用满应力设计理论与有限元法相结合，制了编桁架优化设计通用程序，是该文献的程序同样也但没有考虑位移约束而且也没有进行相关的可视化工作，能够直观地了解其优化结果。不由于桁架结构中各杆件的受力情况不同，力应