阶段滚动月考卷(二)
中考数学复习滚动检测卷(二)试题(2021年整理)

2018届中考数学复习滚动检测卷(二)试题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018届中考数学复习滚动检测卷(二)试题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018届中考数学复习滚动检测卷(二)试题的全部内容。
单元滚动检测卷(二)【测试范围:第三单元及第四单元时间:100分钟分值:100分】一、选择题(每题5分,共30分)1.解分式方程错误!+错误!=3时,去分母后变形正确的是( D )A.3x+(x+2)=3(x-3)B.3x-x+2=3(x-3)C.3x-(x+2)=3D.3x-(x+2)=3(x-3)2.已知等腰三角形两边长分别为3和5,第三边是方程x2-5x+6=0的解,则这个三角形的周长是( C )A.9 B.10C.11 D.143.[2017·临沂]不等式组错误!中,不等式①和②的解集在数轴上表示正确的是( B )【解析】解不等式①,得x<1,解不等式②,得x≥-3。
∴原不等式组的解集为-3≤x<1,而x≥-3在数轴上表示应该从-3向右画,并且用实心圆点,x<1在数轴上表示应该从1向左画,并且用空心圆圈,∴其解集在数轴上表示正确的应为选项B.4.[2017·安徽]一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x,则x满足( D )A.16(1+2x)=25 B.25(1-2x)=16C.16(1+x)2=25 D.25(1-x)2=165.关于x的方程kx2+2x-1=0有实数根,则k的取值范围是( A ) A.k≥-1 B.k≥-1且k≠0C.k≤-1 D.k≤1且k≠0【解析】当k=0时,2x-1=0,解得x=错误!;当k≠0时,此方程是一元二次方程,∵关于x的方程kx2+2x-1=0有实数根,∴Δ=22-4k×(-1)≥0,解得k≥-1,综上所述,k 的取值范围是k≥-1。
江西省校永修县第三中学2023-2024学年八年级上学期第二次月考数学试题(含解析)

2023-2024学年度上学期阶段(二)质量检测试卷八年级数学考生须知:1、全卷满分120分,考试时间120分钟;2、试卷和答题卡都要写上班级、姓名;3、请将答案写在答题卡上的相应位置上,否则不给分.一、选择题(本大题共6个小题,每小题3分,共18分)每小题只有一个正确选项.1中,无理数有()A.2个B.3个C.4个D.5个2.已知△ABC的三条边分别为a,b,c,下列条件不能判断是直角三角形的是()A.a2=b2-c2B.a=6,b=8,c=10C.∠A=∠B+∠C D.∠A:∠B:∠C=5:12:133.《九章算术》中第七章《盈不足》记载了一个问题:“今有共买物,人出八,赢三;人出七,不足四.问人数、物价各几何?”译文:“现有一些人合伙购买物品,若每人出8钱,则多出3钱;若每人出7钱,则还差4钱,问人数、物品价格各是多少?”设有x个人,物品价格为y钱,则下列方程组中正确的是()A.B.C.D.4.直线y=kx+3与y=3x+k在同一坐标系内,其位置可能是()A.B.C.D.5.一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),s与t之间的函数关系如图所示,下列说法中正确的有()①A、B两地相距120千米;②出发1小时,货车与小汽车相遇;③出发1.5小时,小汽车比货车多行驶了60千米;④小汽车的速度是货车速度的2倍.A.1个B.2个C.3个D.4个220.10100100017π8374x yx y=--=⎧⎨⎩8374x yx y=+-=⎧⎨⎩8374x yx y=++=⎧⎨⎩8374x yx y=-+=⎧⎨⎩6.如图,在平面直角坐标系中,(图中的三角形都是等边三角形),一个点从原点O 出发,沿折线移动,每次移动1个单位长度,则点的坐标为()A .B .C .D .二、填空题(本大题共6小题,每小题3分,共18分)7______.8.点A (-2,3)关于x 轴的对称点的坐标为______.9.已知点都在直线上,则大小关系是______.10.如图,Rt △ABC 的周长为24,∠C =90°,且AB :AC =5:4,则BC 的长为______.第10题11.如图,直线y =-x +3与y =mx +n 交点的横坐标为1,则关于x 、y 的二元一次方程组的解为______.第11题12.如图,直线y =2x -4与x 轴和y 轴分别交与A ,B 两点,射线AP ⊥AB 于点A ,若点C 是射线AP 上的一11223341O A AA A A A A ===== 1234n O AA A A A 2023A ()1348,0113482⎛ ⎝11348,2⎛ ⎝()1349,0A '()()124,,2,y y -122y x =-+12,y y3x y mx y n+=-+=⎧⎨⎩个动点,点D是x轴上的一个动点,且以A,C,D为顶点的三角形与△AOB全等,则OD的长为______.第12题三、(本大题共5小题,每小题6分,共30分)13.(1(2)解方程组:14.已知2a-7和a+4是某正数的两个不同的平方根,b-11的立方根是-2.(1)求a、b的值.(2)求a+b的平方根.15.如图,一只小鸟旋停在空中4点,A点到地面的高度AB=20米,A点到地面C点(B、C两点处于同一水平面)的距离AC=25米.若小鸟竖直下降12米到达D点(D点在线段AB上),求此时小鸟到地面C点的距离.16.图(1)、图(2)均是5×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作△ABC,点C在格点上.图(1)图(2)(1)在图(1)中,△ABC的面积为5;(2)在图(2)中,△ABC是面积为的钝角三角形.)22+-23451x yx y-=+=-⎧⎨⎩5217.若的值.四、(本大题共3小题,每小题8分,共24分)18.某中学八(1)共有45人,该班计划为每名学生购买一套学具,超市现有A 、B 两种品牌学具可供选择.已知1套A 学具和1套B 学具的售价为45元;2套A 学具和5套B 学具的售价为150元.(1)A 、B 两种学具每套的售价分别是多少元?(2)现在商店规定,若一次性购买A 型学具超过20套,则超出部分按原价的6折出售.设购买A 型学具a 套(a >20)且不超过30套,购买A 、B 两种型号的学具共花费w 元.①请写出w 与a 的函数关系式;②请帮忙设计最省钱的购买方案,并求出所需费用.19.先阅读,再解方程组.解方程组时,设a =x +y ,b =x -y ,则原方程组变为,整理,得,解这个方程组,得,即,解得.请用这种方法解下面的方程组:.20.甲、乙两车间一起加工一批零件,同时开始加工,10个小时完成任务.在这个过程中,甲车间的工作效率不变,乙车间在中间停工一段时间维修设备,然后按停工前的工作效率继续加工.设甲、乙两车间各自加工零件的数量为y (个),甲车间加工的时间为x (时),y 与x 之间的函数图象如图所示.(1)甲车间每小时加工零件的个数为______个,这批零件的总个数为______个;(2)求乙车间维护设备后,乙车间加工零件的数量y 与x 之间的函数关系式;(3)在加工这批零件的过程中,当甲、乙两车间共同加工完930个零件时,求甲车间加工的时间.五、(本大题共2小题,每小题9分,共18分)21.如图,已知△ABC 中,∠B =90°,AB =16cm ,BC =12cm ,P 、Q 是△ABC 边上的两个动点,其中点Px y ==22x xy y -+()()623452x y x yx y x y +-⎧-=⎪⎨⎪+--=⎩623452a ba b ⎧+=⎪⎨⎪-=⎩3236452a b a b +=⎧⎨-=⎩86a b =⎧⎨=⎩86x y x y +=⎧⎨-=⎩71x y =⎧⎨=⎩()()()()5316350x y x y x y x y +--=⎧⎪⎨+--=⎪⎩从点A 开始沿A →B 方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B →C →A 方向运动,且速度为每秒2cm ,它们同时出发,同时停止.备用图(1)P 、Q 出发4秒后,求PQ 的长;(2)当点Q 在边CA 上运动时,出发几秒钟后,△CQB 能形成直角三角形?22.如图,已知A (3,0),B (0,4),点D 在y 轴的负半轴上,若将△DAB 沿直线AD 折叠,点B 恰好落在x 轴正半轴上的点C 处.(1)求直线AB 的表达式;(2)求C 、D 的坐标;(3)在直线DA 上是否存在一点P ,使得?若存在,直接写出点P 的坐标;若不存在,请说明理由.六、(本大题共1小题,共12分)我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.特例感知①等腰直角三角形______勾股高三角形(请填写“是”或者“不是”);②如图,已知△ABC 为勾股高三角形,其中C 为勾股顶点,CD 是AB 边上的高.若BD =1,AD =2,试求线段CD的长度.10P A B S △深入探究如图,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明:推广应用如图,等腰△ABC为勾股高三角形,其中AB=AC>BC,CD为AB边上的高,过点D向BC边引平行线与AC 边交于点E.若CE=a,直接写出线段DE的长度(用含a的代数式表示).八年级阶段二数学答案1.【答案】C【分析】根据无理数的定义,即可求解.,,4个.故选:C2.【答案】D.3.【答案】C4.【答案】A【分析】根据一次函数的性质分k>0,k<0两种情形分别分析即可.【详解】解:当时,两条直线都经过第一,二,三象限,四个选项都不符合题意;当时,经过第一,二,四象限,的图象经过第一,三,四象限,只有选项A正确,故选:A.5.【答案】D6.【答案】B【分析】过作轴,垂足为B,求出,,求出前若干个点的坐标,找到规律点的每运动6次循环一次,每循环一次向右移动4个单位,每个周期内点的横坐标变化为:,,计算出2023与6的商和余数,据此得到结果.【详解】解:∵图中的三角形都是等边三角形,边长为1,如图,过作轴,垂足为B,则,∴,3=-k>k<3y kx=+3y x k=+1A1AB x⊥OB1AB A1111,,1,,,12222++++++ 1A1AB x⊥212OB A B==1A B==∴点的坐标为:;点的坐标为:;点的坐标为:;点的坐标为:;点的坐标为:;点的坐标为:;…分析图象可以发现,点的每运动6次循环一次,每循环一次向右移动4个单位,每个周期内点的横坐标变化为:,,,∴点的坐标为,即,故选B .7.【答案】±28.【答案】9.【答案】10.【答案】611.【答案】12.【答案】6或13.(1)1A 12⎛⎝2A ()1,03A ()2,04A 5,2⎛ ⎝5A ()3,06A ()4,0A 1111,,1,,,12222++++++20236337......1÷=2023A 133742⎛⨯+ ⎝113482⎛ ⎝()23-,-12yy >12x y =⎧⎨=⎩2+)22++-.(2)【答案】14.【详解】(1)由题意得:2a -7+a +4=0,b -11=-8,解得:a =1,b =3;(2)∵a =1,b =3,∴a +b =4,4的平方根为±2.【答案】17米【详解】解:由勾股定理得;,∴(米),∵(米),∴在中,由勾股定理得,∴此时小鸟到地面C 点的距离17米.答;此时小鸟到地面C 点的距离为17米.16.点C 到AB,进而可找到点C 所在的直线,与网格的交点即为点C 的位置).(2)如图(3)所示(点拨:由,可知点C 的距离为,进而可找到点C 所在的直线,再结合△ABC 角三角形,且点C在格点处,即可找到点C 的位置)17.【答案】13∵x y,∴x =2,y =,∴x 2-xy ﹢y 2=(x -y )2﹢xy =+1=1318.【详解】解:设A 种品牌的学具售价为x 元,B 种品牌的学具售价为y 元,根据题意有,,解之可得,222=+-34=-1=11x y =⎧⎨=-⎩222222520225BC AC AB =-=-=15BC =20128BD AB AD =-=-=Rt BCD 17CD ==52ABC AB S ==△(2()14525150x y x y +=⎧⎨+=⎩{2520x y ==所以A 、B 两种学具每套的售价分别是25和20元;因为,其中购买A 型学具的数量为a ,则购买费用,即函数关系式为:,;符合题意的还有以下情况:Ⅰ、以的方案购买,因为-5<0,所以时,w 为最小值,即元;Ⅱ、由于受到购买A 型学具数量的限制,购买A 型学具30套w 已是最小,所以全部购买B 型学具45套,此时元元,综上所述,购买45套B 型学具所需费用最省钱,所需费用为:900元.故答案为(1)A 、B 两种学具每套的售价分别是25和20元;(2)①w =-5a +1100,(20<a ≤30);②购买45套B 型学具所需费用最省钱,所需费用为900元.19.【答案】【分析】根据举例,结合换元法a =x +y ,b =x -y ,可得方程组;解方程,可以得到a ,b 的值,代入所设,组成关于x ,y 的方程组,解方程组即可.【详解】解:设,,则原方程组变为,解得,所以,解得.20.【答案】(1)75,1110(2)(3)8.5小时【详解】(1)甲车间每小时加工零件的个数为个;这批零件的总个数为个,故答案为:75,1110;(2)设乙车间维护设备后,y 与x 之间的函数关系式为,()2①2030a <≤()()2025202560%4520w a a =⨯+-⨯⨯+-⨯500153009002051100a a a =+-+-=-+51100w a =-+(2030)a <≤②①30a =5301100950(w =-⨯+=4520900(w =⨯=)950<41x y =⎧⎨=⎩5316350a b a b -=⎧⎨-=⎩a x y =+b x y =-5316350a b a b -=⎧⎨-=⎩53a b =⎧⎨=⎩53x y x y +=⎧⎨-=⎩41x y =⎧⎨=⎩4590y x =-750=7510750360=1110+y kx b =+将点代入,得,解得,∴设乙车间维护设备后,y 与x 之间的函数关系式为;(3)乙车间每小时加工零件的个数为个,设甲车间加工x 小时,则解得,∴甲车间加工8.5小时.21.【详解】(1)解:由题意可得,BQ =2×4=8(cm ),BP =ABAP =161×4=12(cm ),∵∠B =90°,∴PQcm ),即PQ 的长为cm ;(2)解:当BQ ⊥AC 时,∠BQC =90°,∵∠B =90°,AB =16cm ,BC =12cm ,∴AC (cm ),∵,∴,解得cm ,∴CQ(cm ),∴当△CQB 是直角三角形时,经过的时间为:(12+)÷2=9.6(秒);当∠CBQ =90°时,点Q 运动到点A ,此时运动的时间为:(12+20)÷2=16(秒);由上可得,当点Q 在边CA 上运动时,出发9.6秒或16秒后,△CQB 能形成直角三角形.22.【答案】(1)(2),(3)存在,或()()4,90,10,75049010360k b k b +=⎧⎨+=⎩4590k b =⎧⎨=-⎩4590y x =-90245÷=()75452930x x +-=8.5x ===20=22AB BC AC BQ = 16122022BQ ⨯=485BQ =365==365443y x =-+()80C ,()06D -,()14-,()54,【详解】(1)解:设一次函数表达式:,将点的坐标代入得:,解得:,故直线的表达式为:;(2)解:,,由题意得:,,,故点,设点D 的坐标为:,,解得:,故点;(3)解:存在,理由如下:设直线的表达式为,由点、的坐标代入得:,解得:,直线的表达式为:,,,,,,点P 在直线上,设,,解得:或5,y kx b =+()()3004A B ,,,034k b b =+⎧⎨=⎩434k b ⎧=-⎪⎨⎪=⎩AB 443y x =-+()()3004A B ,,,5AB ∴=CD BD =5AC AB ==358OC OA AC ∴=+=+=()80C ,()0m ,CD BD =4m =-6m =-()06D -,AD 11y k x b =+()30A ,()06D -,111036k b b =+⎧⎨=-⎩1126k b =⎧⎨=-⎩AD 26y x =-()04B ,()06D -,10BD ∴=1103152ABD S ∴=⨯⨯= 10P A B S =DA (),26P a a -13102PAB BDP BDA S S S BD a ∴=-=⨯⨯-= 1a =即点P 的坐标为:或.23.【详解】解:特例感知:①等腰直角三角形是勾股高三角形.,∵,∵等腰直角三角形的一条直角边可以看作另一条直角边上的高,∴等腰直角三角形是勾股高三角形,故答案为:是;②∵是边上的高,,,∴,,∵为勾股高三角形,为勾股顶点,是边上的高,∴,∴,解得:或(负值不符合题意,舍去),∴线段;深入探究:.证明:∵为勾股高三角形,为勾股顶点且,是边上的高,∴,∴,∵,∴,∴;推广应用:过点作于,∴,∵等腰为勾股高三角形,且,为边上的高,∴,,由上问可知:,∵,∴,,∵,∴,∴,∴,()14-,()54,=)222a a -=CD AB 1BD =2AD =22221CB CD BD CD =+=+22224CA CD AD CD =+=+ABC C CD AB 222CD CA CB =-()()22241CD CD CD =+-+CD CD =CD AD CB =ABC C CA CB >CD AB 222CA CB CD -=222CA CD CB -=222CA CD AD -=22AD CB =AD CB =A AG ED ⊥G 90AGD ∠=︒ABC AB AC BC =>CD AB 222AC BC CD -=90CDB ∠=︒AD BC =ED BC ∥ADE B ∠=∠AED ACB ∠=∠AB AC =ACB B =∠∠ADE AED ∠=∠AE AD =∵,在和中,,∴,∴,∵为等腰三角形,∴,∵,,,∴,∴,∴线段的长度为.90AGD CDB ∠=∠=︒AGD △CDB △AGD CDB ADG CBD AD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS AGD CDB △≌△DG BD =ADE 22ED DG BD ==AB AC =AE AD =CE a =BD CE a ==2ED a =DE 2a。
八年级数学上册 滚动周练卷(二)同步训练 (新版)新人教版

滚动周练卷(二)[时间:45分钟测试范围:12.1~12.2 分值:100分]一、选择题(每题5分,共30分)1.[2016·天津期末]下列说法正确的是( )A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等2.[2016·寿光期末]如图1,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中错误的是( )图1A.BE=EC B.BC=EFC.AC=DF D.△ABC≌△DEF3.[2016·金堂期末]如图2,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还需添加一个条件才能使△ABC≌△DEF,下列条件不能添加的是( )图2A.∠B=∠E B.BC=EFC.∠C=∠F D.AC=DF4.[2016·永登期末]如图3,AB∥DE,CD=BF,若要使△ABC≌△EDF,还需补充的条件可以是( )图3A.∠B=∠E B.AC=EFC.AB=ED D.不用补充条件5.[2016·西藏期末]如图4,CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )图4A.SSS B.AAS C.SAS D.HL6.[2016·山亭期末]如图5,已知线段AB=18 m,MA⊥AB于点A,MA=6 m,射线BD⊥AB 于点B,P点从B点沿BA向A点运动,每秒走1 m,Q点从B点沿BD向D运动,每秒走2 m,P,Q同时从B出发,则出发x s后,在线段MA上有一点C,使得△CAP与△PBQ全等,则x 的值为( )图5A.4 B.6 C.4或9 D.6或9二、填空题(每题4分,共24分)7.[2016·宜兴月考]已知△ABC≌△DEF,点A与点D,点B与点E分别是对应顶点.(1)若△ABC的周长为32,AB=10,BC=14,则AC=__ __,EF=__ __;(2)若∠A=48°,∠B=53°,则∠D=__ __,∠F=__ __.8.[2016·萧山期中]如图6所示,∠C=∠D=90°,若使用“HL”判定Rt△ABC与Rt△ABD全等,则应添加一个条件是____(填写一个即可).图69.[2016·灵石期末]如图7,黄芳不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带第__ __块去配,其依据是三角形全等判定定理__ __.图710.[2016·普宁期末]如图8,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是___.图811.[2016·荣成期中]如图9所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=__ _.图912.[2016·西城期中]如图10,已知△ABC中,AB=5,AC=3,则中线AD的取值范围是__ _.图10三、解答题(共46分)13.(8分)[2016·江汉区一模]如图11,已知EF∥MN,EG∥HN,且FH=MG,求证:△EFG≌△NMH.图1114.(8分)[2016·永登期末]如图12,某湖的湖岸在A,B之间呈一段圆弧状,A,B之间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A,B之间的距离吗?图12第14题答图15.(10分)[2016·沛县期中]如图13,已知∠1=∠2,∠3=∠4,点E在BD上,连接AE,CE,求证:AE=CE.图1316.(10分)[2016·陕西一模]如图14,在△ABC中,AB=CB,∠ABC=90°,D为AB 延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.图14(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求∠CDB的度数.17.(10分)[2016·罗平一模]在数学实践课上,老师在黑板上画出如图15的图形,其中点B,F,C,E在同一条直线上,并写出四个条件:①AB=DE;②∠1=∠2;③BF=EC;④∠B=∠E.交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.(1)请你写出所有的真命题;(2)任选一个真命题给予证明.图15参考答案1.C 2.A 3.B 4.C 5.B 6.B7.8 14 48°79° 8.AC=AD或BC=BD 9.③ ASA 10.AC=DE 11.55° 12.1<AD<413.证明:∵EF∥MN,EG∥HN,∴∠F=∠M,∠EGF=∠NHM,∵FH=MG,∴FH+HG=MG+HG,∴GF =HM ,在△EFG 和△NMH 中, ⎩⎪⎨⎪⎧∠F =∠M ,GF =HM ,∠EGF =∠NHM , ∴△EFG ≌△NMH (ASA).14.解:要测量A ,B 之间的距离,可用如下方法:如答图,过点B 作AB 的垂线BF ,在BF 上取两点C ,D ,使CD =BC ,再过点D 作BF 的垂线DE ,使A ,C ,E 在同一条直线上.∵∠ACB =∠ECD ,CB =CD ,∠ABC =∠EDC , ∴△ABC ≌△EDC (ASA). ∴BA =DE .∴测出DE 的长就等于A ,B 之间的距离. 15.证明:在△ABD 和△CBD 中, ⎩⎪⎨⎪⎧∠1=∠2,BD =BD ,∠3=∠4,∴△ABD ≌△CBD (ASA), ∴AD =CD ;在△AED 和△CED 中,⎩⎪⎨⎪⎧AD =CD ,∠3=∠4,ED =ED ,∴△AED ≌△CED (SAS), ∴AE =CE .16.(1)证明:在△ABE 和△CBD 中,⎩⎪⎨⎪⎧AB =CB ,∠ABE =∠CBD =90°,BE =BD ,∴△ABE ≌△CBD (SAS);(2)解:∵在△ABC 中,AB =CB ,∠ABC =90°,∴∠BAC =∠ACB =45°, 又∵△ABE ≌△CBD , ∴∠AEB =∠CDB , ∵∠AEB 为△AEC 的外角,∴∠AEB =∠ACB +∠CAE =45°+30°=75°, ∴∠CDB =75°.17.解:(1)情况一:题设为①②④;结论为③; 情况二:题设为①③④;结论为②; 情况三:题设为②③④;结论为①.(2)(答案不唯一)如选题设为①③④,结论为②. 证明:∵BF =EC ,∴BF +CF =EC +CF ,即BC =EF , 在△ABC 和△DEF 中,⎩⎪⎨⎪⎧AB =DE ,∠B =∠E ,BC =EF ,∴△ABC ≌△DEF (SAS), ∴∠1=∠2.。
2021届高三人教版物理一轮复习全程考卷:阶段评估月考卷(二) Word版含答案

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调整合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
阶段评估月考卷(二)曲线运动与机械能(90分钟100分)第Ⅰ卷(选择题共50分)一、选择题(本题共10小题,每小题5分,共50分。
1~6题为单选题,7~10题为多选题)1.(2022·江门模拟)汽车沿平直的大路以恒定功率P从静止开头启动,经过一段时间t达到最大速度v,若所受阻力始终不变,则在t这段时间内( )A.汽车牵引力恒定B.汽车牵引力做的功为PtC.汽车加速度不断增大D.汽车牵引力做的功为12mv22.(滚动单独考查)质量均为1kg的木块M和N叠放在水平地面上,用一根细线分别拴接在M和N右侧,在细线中点用水平向右的力F=5N拉动M和N一起沿水平面匀速滑动,细线与竖直方向夹角θ=60°,g取10m/s2,则下列说法正确的是( )A.木块N和地面之间的动摩擦因数μ=0.35B.木块M和N之间的摩擦力F f=2.5NC.木块M对木块N的压力大小为10ND.若θ变小,拉动M、N一起匀速运动所需拉力应大于5N3.质量为M的皮带轮工件放置在水平桌面上。
一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上。
如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽视不计,则重物下落过程中,工件的加速度为( )A.mg2MB.mgM+mC.2mgM+4mD.2mgM+2m4.(滚动单独考查)(2022·南昌模拟)图甲中的塔吊是现代工地必不行少的建筑设备,图乙为150kg的建筑材料被吊车竖直向上提升过程的简化运动图象,g取10m/s2,下列推断正确的是( )A.前10 s悬线的拉力恒为1 500 NB.46 s末材料离地面的距离为22 mC.0~10 s材料处于失重状态D.在30~36 s钢索最简洁发生断裂5.(2022·益阳模拟)一物体在粗糙的水平面上受到水平拉力作用,在一段时间内的速度随时间变化状况如图所示。
滚动测试卷二

滚动测试卷二(第一~四单元)(时间:90分钟满分:100分)滚动测试卷第5页一、选择题(本题共18小题,每小题3分,共54分,每小题只有一个选项符合题目要求)1.(2015江西上饶二模)化学与社会、科学、技术、环境等有密切联系。
下列有关说法不正确的是()A.PM2.5是指氮、硫的氧化物溶于水形成的酸性液体造成的空气污染B.氯气是塑料、合成橡胶、合成纤维、农药、染料及药品的重要原料C.硅陶瓷和碳纤维复合制成的材料是一种新型无机非金属材料D.用浸泡过溴的四氯化碳溶液的硅藻土吸收水果产生的乙烯以达到保鲜目的〚导学号25730491〛答案:A解析:PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,不是氮、硫的氧化物溶于水形成的酸性液体造成的空气污染,A错误;Cl2用途广泛,是重要的化工原料,B正确;硅陶瓷和碳纤维复合而成的陶瓷碳纤维是一种新型无机非金属材料,C正确;溴与乙烯发生加成反应而消耗了乙烯,从而达到保鲜效果,D正确。
2.(2015北京西城一模)V L 0.5 mol·L-1盐酸,欲使其浓度增大1倍,下列采取的措施合理的是()A.标准状况下通入11.2V L HCl气体B.加入10 mol·L-1盐酸0.1V L,再稀释至1.5V LC.将溶液加热浓缩到0.5V LD.加入V L 1.5 mol·L-1盐酸后混合均匀答案:B解析:A项,通入HCl气体后溶液的体积会发生变化,该项措施不合理;C项,盐酸具有挥发性,加热浓缩会导致HCl挥发,该项措施不合理;D项,不同浓度的盐酸混合时,混合后溶液的体积不能用两溶液的体积相加,该项措施不合理。
3.(2015湖南益阳一模)设N A表示阿伏加德罗常数的数值,下列叙述正确的是()A.标准状况下,22.4 L H2O含有的分子数为N AB.常温常压下,1.06 g Na2CO3含有的Na+数目为0.02N AC.通常状况下,N A个CO2分子占有的体积为22.4 LD.物质的量浓度为0.5 mol·L-1 MgCl2溶液中,含有Cl-个数为N A答案:B解析:标准状况下,H2O为液体,A错误;常温常压下,1.06 g Na2CO3的物质的量为0.01 mol,所以含有的Na+数为0.02N A,B正确;标准状况下,N A个CO2分子占有的体积为22.4 L,C错误;题目未告诉溶液体积,不能确定含有Cl-个数,D错误。
2022-2023学年八年级数学上学期第一次阶段性检测卷二原卷

2022-2023学年八年级阶段性检测卷数学(考试时间:120分钟试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:第一章、第二章。
5.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本题共12小题,每小题3分,共36分)。
1.下列长度的各组线段中,能组成三角形的是()A.3cm,12cm,8cm B.6cm,8cm,15cmC.2.5cm,3cm,5cm D.6.3cm,6.3cm,12.6cm2.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是()A.两点之间的线段最短B.两点确定一条直线C.三角形具有稳定性D.长方形的四个角都是直角4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A .B .C .D .5.一个三角形的三个内角度数之比为4:5:9,则这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.斜三角形6.根据下列已知条件,能唯一画出△ABC的是()A.AB=3,BC=4,AC=8B.AB=4,BC=3,∠A=30°C.∠A=60°,∠B=45°,AB=4D.∠C=90°,AB=67.如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是()A.SAS B.ASA C.SSS D.AAS8.用一批完全相同的正多边形能镶嵌成一个平面图案的是()A.正五边形B.正六边形C.正七边形D.正八边形9.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°10.如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组11.如图,将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A的度数等于()A.70°B.60°C.50°D.40°12.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①AD=BE;②PQ∥AE;③AP=BQ;④∠AOB=60°.其中正确的结论个数是()A.1个B.2个C.3个D.4个第Ⅱ卷二、填空题(本题共6题,每小题3分,共18分)。
2020—2021年高考总复习数学(理)阶段滚动月考卷(二)及参考答案(精品试题).docx

阶段滚动月考卷(二)三角函数、解三角形、平面向量、复数(时间:120分钟 分值:150分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.i 是虚数单位,则复数z=(1+i 1−i)2+i 的共轭复数为( ) A.2+i B.2-iC.-1+iD.-1-i2.(滚动单独考查)已知集合A={1,3,x},B={1,√x },若A ∩B=B,则x= ( ) A.0或3 B.0或9 C.1或9D.3或93.(滚动单独考查)(2016·杭州模拟)函数y=√x 2−2x −3+log 3(x+2)的定义域为 ( ) A.(-∞,-1)∪(3,+∞) B.(-∞,-1]∪[3,+∞) C.(-2,-1]D.(-2,-1]∪[3,+∞)4.已知向量a,b 满足|a|=2,|b|=1,且5()2a b ⊥(a+b),则a 与b 的夹角θ为( )A.π6B.π3C.23πD.56π5.(2016·济宁模拟)如图所示,非零向量OA →=a,OB →=b,且BC ⊥OA,点C 为垂足,若OC →=λa(λ≠0),则λ= ( )6.(2016·石家庄模拟)已知ω>0,0<φ<π,直线x=π4和x=5π4是函数f(x)=sin(ωx+φ)的图象上两条相邻的对称轴,则φ= ( ) A.π4B.π3C.π2D.3π47.已知a=(cos θ2,sin θ2),b=(cos θ,sin θ),θ∈(0,π),则|a-b|的取值范围是( )A.(0,1)B.(0,1]C.(0,√2)D.(0,√2]8.(2016·洛阳模拟)在△ABC 中,角A,B,C 的对边分别为a,b,c, cosC=14,AC →·CB →=-2且a+b=5,则c 等于 ( )A.√B.√C.4D.√9.(滚动交汇考查)(2016·泰安模拟)已知f(x)=sin 2(x +π4),若a=f(lg5), b=f (lg 15),则 ( ) A.a+b=0 B.a-b=0 C.a+b=1D.a-b=110.(滚动单独考查)已知x 0是函数f(x)=2x+11−x的一个零点.若x 1∈(1,x 0),x 2∈(x 0,+∞),则 ( )A.f(x 1)<0,f(x 2)<0B.f(x 1)<0,f(x 2)>0C.f(x 1)>0,f(x 2)<0D.f(x 1)>0,f(x 2)>0二、填空题(本大题共5小题,每小题5分,共25分.请把正确答案填在题中横线上)11.(滚动交汇考查)计算:log 2sin π12+log 2cos π12= .12.(2016·枣庄模拟)已知|a|=2,|b|=4,a 和b 的夹角为π3,以a,b 为邻边作平行四边形,则该四边形的面积为 .13.在△ABC 中,若sin 2B=sinAsinC,则角B 的最大值为 . 14.在△ABC 中,角A,B,C 的对边分别为a,b,c,且2cos2A−B2cosB-sin(A-B)sinB+cos(A+C)=-35,若a=4√2,b=5,则BA →在BC →方向上的投影为 . 15.已知函数f(x)=-x 2-2x,g(x)={x +14x ,x >0,x +1,x ≤0.若方程g(f(x))-a=0有4个实数根,则实数a 的取值范围为 .三、解答题(本大题共6小题,共75分.解答时应写出必要的文字说明、证明过程或演算步骤)16.(12分)(2016·杭州模拟)在△ABC 中,角A,B,C 的对边分别为a,b,c,且b=3.已知向量m=(cos 2B2,sinB),n=(√3,2),且m ∥n.(1)若A=5π12,求c 的值.(2)求AC 边上的高的最大值.17.(12分)(2016·临沂模拟)已知函数f(x)=√3sinxcosx-cos 2x-12,x ∈R.(1)求函数f(x)的最小值和最小正周期.(2)已知△ABC 内角A,B,C 的对边分别为a,b,c,且c=3,f(C)=0,若向量m=(1,sinA)与n=(2,sinB)共线,求a,b 的值.18.(12分)(2016·黄山模拟)已知向量a=(sin(ωx+φ),2),b=(1,cos(ωx+φ))(ω>0,0<φ<π4),函数f(x)=(a+b)·(a-b),y=f(x)图象的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点M (1,72).(1)求函数f(x)的解析式.(2)当-1≤x ≤1时,求函数f(x)的单调区间.19.(12分)(2016·郑州模拟)在△ABC 中,a,b,c 分别是A,B,C 的对边.若向量m=(2,0)与n=(sinB,1-cosB)所成的角为π3.(1)求角B 的大小.(2)若b=√3,求a+c 的最大值.20.(13分)(滚动单独考查)根据统计资料,某工厂的日产量不超过20万件,每日次品率p 与日产量x(万件)之间近似地满足关系式p={x 2+60540,0<x ≤12,12,12<x ≤20.已知每生产1件正品可盈利2元,而生产1件次品亏损1元.(该工厂的日利润y=日正品盈利额-日次品亏损额)(1)将该工厂日利润y(万元)表示为日产量x(万件)的函数.(2)当该工厂日产量为多少万件时日利润最大?最大日利润是多少万元? 21.(14分)(滚动单独考查)(2016·太原模拟)已知函数f(x)=2lnx-ax. (1)若曲线f(x)在点(1,f(1))处的切线过点(2,0),求a 的值. (2)求f(x)的单调区间.(3)如果x 1,x 2(x 1<x 2)是函数f(x)的两个零点,f ′(x)为f(x)的导数,证明: f ′(x 1+2x 23)<0.答案解析1.D z=(1+i)2(1−i)+i=2i−2i+i=-1+i,所以其共轭复数为-1-i. 2.B 因为A ∩B=B,所以B A,验证易知x=0满足,x=9满足.3.D 由{x 2−2x −3≥0,x +2>0得-2<x ≤-1或x ≥3. 4.B 由题意,得·(a+b)=a 2-32a ·b-52b 2=4-32a ·b-52=0.所以a ·b=1, 所以cos θ==12,因为θ∈[0,π],所以θ=π3. 5.A BC →⊥OA →,即BC →⊥OC →, 所以(OC →-OB →)·OC →=0,所以|OC →|2-OB →·OC →=0,即λ2|a|2-λa ·b=0,又λ≠0,解得λ=6.A2πω=2(5π4−π4),得ω=1,所以f(x)=sin(x+φ),故f (π4)=sin (π4+φ)=±1.因为0<φ<π,所以π4<φ+π4<5π4,所以φ+π4=π2,即φ=π4. 7.C 因为a-b=(cos θ2−cosθ,sin θ2−sinθ),所以|a-b|=√(cos θ2−cosθ)+(sin θ2−sinθ)=√2−2(cos θ2cosθ+sin θ2sinθ)=√2−2cos (θ2−θ)=√2−2cos θ2,因为θ∈(0,π),所以θ2∈(0,π2),cos θ2∈(0,1).故|a-b|∈(0,√2).8.【解题提示】由已知cosC=14,AC →·CB →=-2,利用数量积公式得到ab=8,再利用余弦定理c 2=a 2+b 2-2abcosC 可求c. A 由已知cosC=14,AC →·CB →=-2,得b ·a ·cos(π-C)=-2⇒b ·a ·cosC=2, 所以ab=8,利用余弦定理可得,c 2=a 2+b 2-2abcosC=(a+b)2-2ab-2abcosC=52-2×8-4=5. 所以c=√5.【加固训练】在△ABC 中,内角A,B,C 所对边分别为a,b,c,已知m=(1,2),n=(ccosA,b),p=(c,-bcosA),若m ∥n,m ⊥p,则△ABC 的形状是 .【解析】由m ∥n 可得,b=2ccosA. 由正弦定理可得sinB=2sinCcosA, 即sin(A+C)=2sinCcosA.从而sinAcosC+cosAsinC=2sinCcosA, 故sinAcosC-cosAsinC=0. 即sin(A-C)=0,又-π<A-C<π, 所以A-C=0,即A=C. 由m ⊥p 可得c-2bcosA=0, 从而sinC-2sinBcosA=0, 故sin(A+B)-2sinBcosA=0. 即sinAcosB-cosAsinB=0, 即sin(A-B)=0,故A-B=0,A=B. 所以A=B=C.故三角形为等边三角形. 答案:等边三角形9.C a=f(lg5)=sin 2(lg5+π4)=1−cos(2lg5+π2)2=1+sin(2lg5)2,b=f (lg 15)=sin 2(lg 15+π4)=1−cos(2lg 15+π2)2=1−sin(2lg5)2,则可得a+b=1.10.B 设g(x)=11−x,由于函数g(x)=11−x=-1x−1在(1,+∞)上单调递增,函数h(x)=2x在(1,+∞)上单调递增,故函数f(x)=h(x)+g(x)在(1,+∞)上单调递增,所以函数f(x)在(1,+∞)上只有唯一的零点x 0,且在(1,x 0)上f(x 1)<0,在(x 0,+∞)上f(x 2)>0. 11.【解析】原式=log 2(sin π12cosπ12)=log 2(12sin π6)=log 214=-2.答案:-212.【解析】S=2×12|a||b|sin π3=2×4×√32=4√.答案:4√13.【解题提示】化角为边,利用基本不等式求解. 【解析】由正弦定理,得b 2=ac, 由余弦定理,得cosB=a 2+c 2−b 22ac=a 2+c 2−ac2ac≥2ac−ac 2ac=12.因为B ∈(0,π),y=cosx 在(0,π)上单调递减, 所以B 的最大值为π3.答案:π314.【解题提示】利用已知条件先转化求得cosA,再利用正余弦定理可解. 【解析】由2cos2A−B2cosB-sin(A-B)·sinB+cos(A+C)=-35,得[cos(A-B)+1]cosB-sin(A-B)sinB-cosB=-35,即cos(A-B)cosB-sin(A-B)sinB=-35.则cos(A-B+B)=-35,即cosA=-35.由0<A<π,得sinA=45,由正弦定理,有asinA =bsinB,所以,sinB=bsinA a=√22.由题知a>b,则A>B,故B=π4,根据余弦定理,有(4√2)2=52+c 2-2×5c ×(−35),解得c=1或c=-7(舍去).故向量BA →在BC →方向上的投影为|BA →|cosB=√22.答案:√2215.【解题提示】利用数形结合法求解.【解析】令f(x)=t,则原方程化为g(t)=a,易知方程f(x)=t 在t ∈(-∞,1)内有2个不同的解,则原方程有4个解等价于函数y=g(t)(t<1)与y=a 的图象有2个不同的交点,作出函数y=g(t)(t<1)的图象,如图所示,由图象可知,当1≤a<54时,函数y=g(t)(t<1)与y=a 有2个不同的交点, 即所求a 的取值范围是[1,54).答案:[1,54)16.【解析】(1)方法一:由m ∥n,得2cos 2B2=√3sinB,即1+cosB=√得sin (B −π6)=12.又0<B<π,所以-π6<B-π6<5π6,故B-π6=π6,即B=π3.结合A=5π12,可得C=π4.由正弦定理bsinB =csinC,得c=√方法二:由m ∥n,得2cos 2B2=√3sinB,则2cos 2B 2=2√3sin B 2cos B 2,又cos B 2≠0,故cos B 2=√3sin B2,即tan B 2=√33,又0<B<π,所以0<B 2<π2,故B 2=π6,即B=π3.结合A=5π12,可得C=π4.由正弦定理bsinB =csinC,得c=√(2)设AC 边上的高为h,则S △ABC =12bh=32h=12acsinB=√34ac,即h=2√3ac.而b 2=a 2+c 2-2accosB=a 2+c 2-ac ≥ac(当且仅当a=c 时,等号成立),所以ac ≤9,因此h=2√3ac ≤3√32.所以AC 边上的高的最大值为3√32.17.【解析】(1)f(x)=√3sinxcosx-cos 2x-12=√32sin2x-12cos2x-1=sin (2x −π6)-1.所以f(x)的最小值为-2,最小正周期为π. (2)因为f(C)=sin (2C −π6)-1=0,即sin (2C −π6)=1,又因为0<C<π,-π6<2C-π6<11π6,所以2C-π6=π2,故C=π3.因为m 与n 共线,所以sinB-2sinA=0. 由正弦定理a sinA =bsinB,得b=2a.①因为c=3,由余弦定理,得9=a 2+b 2-2abcos π3,即a 2+b 2-ab=9,② 联立①②,解得{a =√3.b =2√3.【加固训练】(2015·洛阳模拟)在△ABC 中,角A,B,C 所对的边分别为a,b,c, cos2C+2√cosC+2=0.(1)求角C 的大小.(2)若b=√2a,△ABC 的面积为√22sinAsinB,求sinA 及c 的值. 【解析】(1)因为cos2C+2√2cosC+2=0,所以2cos 2C+2√2cosC+1=0,即(√2cosC+1)2=0,所以cosC=-√22. 又C ∈(0,π),所以C=3π4. (2)因为c 2=a 2+b 2-2abcosC=3a 2+2a 2=5a 2,所以c=√5a,即sinC=√5sinA,sinA =√5sinC=√1010, 因为S △ABC =12absinC,且S △ABC =√22sinAsinB, 所以12absinC=√22sinAsinB, 即ab sinAsinB sinC=√2, 由正弦定理得:(csinC )2sinC=√, 解得c=1. 18.【解析】(1)f(x)=(a+b)·(a-b)=a 2-b 2=|a|2-|b|2=sin 2(ωx+φ)+3-cos 2(ωx+φ)=-cos(2ωx+2φ)+3,由题意得周期T=2π2ω=4, 故ω=π4,又图象过点M (1,72),所以72=3-cos (π2+2φ), 即sin2φ=12,而0<φ<π4,故2φ=π6, 则f(x)=3-cos (π2x +π6). (2)当-1≤x ≤1时,-π3≤π2x+π6≤2π3. 所以当-π3≤π2x+π6≤0时, 即x ∈[−1,−13]时,f(x)是减函数. 当0≤π2x+π6≤2π3时, 即x ∈[−13,1]时,f(x)是增函数. 则函数f(x)的单调递减区间是[−1,−13],单调递增区间是[−13,1]. 19.【解析】(1)由题意得cos π3= =2√sin 2B+(1−cosB)2=12, 即√2−2cosB =12, 所以2sin 2B=1-cosB,2cos 2B-cosB-1=0,所以cosB=-12或cosB=1(舍去), 因为0<B<π,所以B=2π3. (2)由(1)知A+C=π3, 而a sinA =c sinC =b sinB =√3sin 2π3=2, 所以a+c=2sinA+2sinC=2[sinA +sin (π3−A)]=2(sinA +√32cosA −12sinA) =2sin (A +π3), 因为0<A<π3,所以π3<A+π3<2π3. 所以√32<sin (A +π3)≤1, 所以a+c=2sin (A +π3)∈(√3,2], 故a+c 的最大值为2.20.【解析】(1)由题意知,当0<x ≤12时,y=2x(1-p)-px,所以y=2x (1−x 2+60540)-x 3+60x 540=53x-x 3180,当12<x ≤20时,y=2x(1-p)-px=2x (1−12)-12x=12x, 即y={53x −x 3180,x ∈(0,12],12x,x ∈(12,20]. (2)当x ∈(0,12]时,y ′=53-x 260=100−x 260,令y ′=0,得x=10, 当0<x<10时,y ′>0;当10<x ≤12时,y ′<0,所以,当x=10时,y max =1009, 当x ∈(12,20]时,y=12x 在(12,20]上单调递增,当x=20时,y max =10,由于1009>10,所以当该工厂的日产量为10万件时,日利润最大,最大日利润为1009万元.21.【解题提示】(1)由导数的几何意义求解.(2)分类讨论.(3)构造函数证明不等式.【解析】(1)因为f′(x)=2x-a(x>0),所以f′(1)=2-a,又f(1)=-a,所以切线方程为y+a=(2-a)(x-1).又切线过点(2,0),所以0+a=(2-a)(2-1),解得a=1.(2)由(1)知f′(x)=2x-a(x>0),①当a≤0时,f′(x)>0恒成立,函数f(x)在(0,+∞)上单调递增;②当a>0时,令f′(x)>0,有x∈(0,2a),f(x)在(0,2a )上单调递增;令f′(x)<0,有x∈(2a,+∞),f(x)在(2a,+∞)上单调递减.故当a≤0时,f(x)的单调增区间为(0,+∞),当a>0时,f(x)的单调增区间为(0,2a ),单调减区间为(2a,+∞).(3)由题意知f(x1)=0,f(x2)=0. 即2lnx1-ax1=0,2lnx2-ax2=0,则2lnx2-2lnx1=a(x2-x1),a=2ln x2x1 x2−x1.因为f′(x)=2x-a,所以f′(x1+2x23)=6x1+2x2-a=6x1+2x2-2ln x2x1x2−x1,要证f′(x1+2x23)<0,只需证6x1+2x2-2ln x2x1x2−x1<0,①因为x2>x1>0,所以x2-x1>0,x1+2x2>0,故①式可化为3(x 2−x 1)x 1+2x 2-ln x 2x 1<0,即3(x 2x 1−1)2·x 2x 1+1-ln x 2x 1<0, 令t=x 2x 1,则t>1,构造函数h(t)=3(t−1)2t+1-lnt,则h ′(t)=9(2t+1)2-1t =-(4t−1)(t−1)t(2t+1)2.显然t>1时,h ′(t)<0,即h(t)在[1,+∞)上单调递减,所以h(t)<h(1)=0. 即证得f ′(x 1+2x 23)<0.关闭Word 文档返回原板块。
滚动周练卷2-2020秋人教版九年级数学上册

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
滚动周练卷(二)[测试时间:45分钟测试范围:22.1.1~22.1.3分值:100分]一、选择题(每题5分,共30分)1.[2019秋·翁牛特旗期中]二次函数y=12(x-4)2+5的图象的开口方向、对称轴、顶点坐标分别是()A.向上,直线x=4,(4,5)B.向上,直线x=-4,(-4,5)C.向上,直线x=4,(4,-5)D.向下,直线x=-4,(-4,5)2.[2018秋·汝阳县期末]在同一直角坐标系中,函数y=ax2+b 与y=ax+b(a,b都不为0)的图象的相对位置可以是()3.关于二次函数y=-12(x-3)2-2的图象与性质,下列结论错误的是()A.抛物线的开口向下B.当x=3时,函数有最大值-2C.当x>3时,y随x的增大而减小D.抛物线可由y=12x2的图象经过平移得到4.已知二次函数y=a(x-1)2+3,当x<1时,y随x的增大而增大,则a的取值范围是()A.a≥0 B.a≤0C.a>0 D.a<05.[2019秋·睢宁县期中]将二次函数y=2x2的图象先向左平移4个单位长度,再向下平移1个单位长度,所得新的图象的函数表达式为()A.y=2(x-4)2-1 B.y=2(x+4)2-1C.y=2(x-4)2+1 D.y=2(x+4)2+16.[2019·丰台区模拟]如图1,排球运动员站在点O处练习发球,将球从点O正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-k)2+h.已知球与点O的水平距离为6 m时,达到最高2.6 m,球网BC与点O的水平距离为9 m,高度为2.43 m,球场的边界N距点O的水平距离为18 m.下列判断正确的是()图1A.球不会过球网B.球会过球网但不会出界C.球会过球网并会出界D.无法确定二、填空题(每题4分,共24分)7.二次函数y=-(x-3)2+2的图象的顶点坐标是________,对称轴是____________.8.[2019·闵行区一模]已知二次函数y=-12x2-3,若x>0,则函数值y随着自变量x的增大而________(填“增大”或“减小”).9.隧道的截面是抛物线形,以水平面为x轴,隧道中线为y轴,则抛物线的解析式为y=-19x2+3.25,一辆车高3 m、宽4 m,该车________通过该隧道(填“能”或“不能”).10.[2019·杨浦区一模]如果抛物线C1的顶点在抛物线C2上,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2是“互为关联”的抛物线.与抛物线y=2x2是“互为关联”且顶点不同的抛物线的解析式可以是____________(只需写出一个).11.[2018秋·富阳区期中]某游乐园要建一个圆形喷水池,在喷水池的中心安装一个大的喷水头,高度为103m,喷出的水柱沿抛物线轨迹运动(如图2),在离中心水平距离4 m处达到最高,高度为6 m,之后落在水池边缘,那么这个喷水池的直径为________m.图212.如图3,抛物线y=ax2+c(a<0)交x轴于点G,F,交y轴于点D,在x轴上方的抛物线上有两点B,E,它们关于y轴对称,点G,B在y轴左侧,BA⊥OG于点A,BC⊥OD于点C,四边形OABC 与四边形ODEF的面积分别为6和10,则△ABG与△BCD的面积之和为____________.图3三、解答题(共46分)13.(8分)已知抛物线如图4,根据图象可得:图4(1)抛物线的顶点坐标为________;(2)对称轴为____________;(3)当x=________时,y有最大值,最大值是________;(4)当________时,y随着x的增大而增大;(5)当____________时,y>0.14.(8分)[2019秋·思明区校级期中]如图5,在平面直角坐标系中,若抛物线y=2x2与直线y=x+1交于点A(a,b)和点B(c,d),其中a>c,点O为原点,求△ABO的面积.图515.(10分)[2019秋·南关区校级月考]如图6是一个抛物线形拱桥的示意图,桥的跨度AB为100 m,支撑桥的是一些等距的立柱(未全部画出),正中间的立柱OC的高为10 m(不考虑立柱的粗细),相邻立柱间的水平距离为10 m.建立如图6所示的坐标系,求距点A 最近处的立柱EF的高度.图616.(10分)[2019·金华节选]如图7,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴、y轴的正半轴上,把正方形OABC的内部及边上横、纵坐标均为整数的点称为“好点”.点P为抛物线y=-(x-m)2+m+2的顶点.(1)当m=0时,求该抛物线下方(包括边界)的“好点”个数;(2)当m=3时,求该抛物线上的“好点”坐标.图717.(10分)[2018秋·青山区校级月考]如图8,抛物线的顶点为(1,-4),与x轴交于A,B两点,与y轴负半轴交于点C(0,-3).(1)求抛物线的解析式;(2)点P为对称轴右侧抛物线上一点,以BP为斜边作等腰直角三角形,直角顶点M落在对称轴上,求点P的坐标.图8参考答案1.A 2.A 3.D 4.D 5.B 6.C7.(3,2)直线x=38.减小9.不能10.y=-2(x-1)2+2(答案不唯一)11.2012.413.(1)(-3,2)(2)直线x=-3(3)-32(4)x<-3(5)-5<x<-114.S△ABO=34.15.立柱EF的高度为3.6 m.16.(1)“好点”有(0,0),(0,1),(0,2),(1,0),(1,1),共5个.(2)坐标分别为(1,1),(2,4),(4,4).17.(1)y=x2-2x-3.(2)点P的坐标为(2,-3)或(4,5).关闭Word文档返回原板块。
人教A版高三数学文科一轮复习滚动检测试卷(二)含答案

高三单元滚动检测卷·数学考生注意:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.2.答卷前,考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上.3.本次考试时间120分钟,满分150分.4.请在密封线内作答,保持试卷清洁完整.滚动检测二第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(·浏阳联考)设全集U =R ,A ={x |2x (x-2)<1},B ={x |y =ln(1-x )},则图中阴影部分表示的集合为( )A .{x |x ≥1}B .{x |x ≤1}C .{x |0<x ≤1}D .{x |1≤x <2}2.已知f (x )=⎩⎪⎨⎪⎧cos πx ,x ≤0,f (x -1)+1,x >0,则f (43)+f (-43)的值为( ) A.12 B .-12C .-1D .1 3.(·湖北荆州中学模拟)已知函数f (x )=⎩⎪⎨⎪⎧x 2+ax +1,x ≥1,ax 2+x +1,x <1,则-2≤a ≤1是f (x )在R 上单调递增的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.(·山东枣庄八中阶段检测)若方程|x 2+4x |=m 有实数根,则所有实数根的和可能是( )A .-2,-4,-6B .-4,-5,-6C .-3,-4,-5D .-4,-6,-85.已知函数f (x )是定义在R 上的偶函数,且当x ≥0时,f (x )=ln(x +1),则函数f (x )的大致图象为( )6.若函数f (x )=cos x +2xf ′⎝⎛⎭⎫π6,则f ⎝⎛⎭⎫π3与f ⎝⎛⎭⎫-π3的大小关系是( ) A .f ⎝⎛⎭⎫-π3=f ⎝⎛⎭⎫π3 B .f ⎝⎛⎭⎫-π3>f ⎝⎛⎭⎫π3 C .f ⎝⎛⎭⎫-π3<f ⎝⎛⎭⎫π3 D .不确定7.(·渭南质检一)已知函数f (x )满足f (-x )=f (x )和f (x +2)=f (x ),且当x ∈[0,1]时,f (x )=1-x ,则关于x 的方程f (x )=(13)x 在x ∈[0,4]上解的个数是( ) A .5B .4C .3D .28.若函数f (x )=kx -ln x 在区间(1,+∞)上单调递增,则k 的取值范围是( )A .(-∞,-2]B .(-∞,-1]C .[2,+∞)D .[1,+∞)9.已知函数f (x )=⎩⎪⎨⎪⎧x 2+2x -1,x ≥0,x 2-2x -1,x <0,则对任意x 1,x 2∈R ,若0<|x 1|<|x 2|,下列不等式成立的是( )A .f (x 1)+f (x 2)<0B .f (x 1)+f (x 2)>0C .f (x 1)-f (x 2)>0D .f (x 1)-f (x 2)<010.当x ∈[-2,1]时,不等式ax 3-x 2+4x +3≥0恒成立,则实数a 的取值范围是( )A .[-5,-3]B .[-6,-98]C .[-6,-2]D .[-4,-3]11.已知定义在R 上的函数f (x )满足f (x )=-f (x +32),且f (1)=2,则f (2 017)等于( ) A .-1B .2C .-2 D.312.(·济源模拟)函数f (x )的定义域为A ,若当x 1,x 2∈A 且f (x 1)=f (x 2)时,总有x 1=x 2,则称f (x )为单函数.例如:函数f (x )=2x +1 (x ∈R )是单函数.给出下列结论:①函数f (x )=x 2(x ∈R )是单函数;②指数函数f (x )=2x (x ∈R )是单函数;③若f (x )为单函数,x 1,x 2∈A 且x 1≠x 2,则f (x 1)≠f (x 2);④在定义域上具有单调性的函数一定是单函数.其中正确结论的个数是( )A .3B .2C .1D .0第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.设函数f (x )=1+(-1)x 2(x ∈Z ),给出以下三个结论:①f (x )为偶函数;②f (x )为周期函数;③f (x +1)+f (x )=1,其中正确结论的序号是________.14.关于函数f (x )=lg x 2+1|x |(x ≠0),有下列命题: ①其图象关于y 轴对称;②当x >0时,f (x )是增函数;当x <0时,f (x )是减函数;③f (x )的最小值是lg 2;④f (x )在区间(-1,0),(2,+∞)上是增函数;⑤f (x )无最大值,也无最小值.其中所有正确结论的序号是________.15.(·江西省五校协作体高三期中)下列四个命题:①∃x ∈(0,+∞),(12)x >(13)x ; ②∃x ∈(0,+∞),log 2x <log 3x ;③∀x ∈(0,+∞),(12)x >log 12x ; ④∀x ∈(0,13),(12)x <log 13x . 其中正确命题的序号是________.16.给出定义:若函数f (x )在D 上可导,即f ′(x )存在,且导函数f ′(x )在D 上也可导,则称f (x )在D 上存在二阶导函数,记f ″(x )=(f ′(x ))′.若f ″(x )<0在D 上恒成立,则称f (x )在D上为凸函数.以下四个函数在⎝⎛⎭⎫0,π2上是凸函数的是________(把你认为正确的序号都填上). ①f (x )=sin x +cos x ;②f (x )=ln x -2x ;③f (x )=-x 3+2x -1;④f (x )=x e x .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)(·黄冈中学月考)若二次函数f (x )=ax 2+bx +c (a ,b ,c ∈R )满足f (x +1)-f (x )=4x +1,且f (0)=3.(1)求f (x )的解析式;(2)若在区间[-1,1]上,不等式f (x )>6x +m 恒成立,求实数m 的取值范围.18.(12分)定义在[-1,1]上的奇函数f (x ),已知当x ∈[-1,0]时的解析式为f (x )=14x -a 2x (a ∈R ). (1)写出f (x )在(0,1]上的解析式;(2)求f (x )在(0,1]上的最大值.19.(12分)(·哈尔滨三中第一次测试)已知定义在(0,+∞)上的函数f (x )对任意正数m ,n 都有f (mn )=f (m )+f (n )-12,当x >1时,f (x )>12,且f ⎝⎛⎭⎫12=0. (1)求f (2)的值;(2)解关于x 的不等式f (x )+f (x +3)>2.20.(12分)经市场调查,某商品在过去100天内的销售量和价格均为时间t (天)的函数,且日销售量近似地满足g (t )=-13t +1123(1≤t ≤100,t ∈N ),前40天价格为f (t )=14t +22(1≤t ≤40,t ∈N ),后60天价格为f (t )=-12t +52(41≤t ≤100,t ∈N ),试求该商品的日销售额s (t )的最大值和最小值.21.(12分)(·广东阳东一中模拟)已知函数f (x )=ax +x ln|x +b |是奇函数,且图象在点(e ,f (e))处的切线斜率为3(e 为自然对数的底数).(1)求实数a 、b 的值;(2)若k ∈Z ,且k <f (x )x -1对任意x >1恒成立,求k 的最大值.22.(12分)(·沈阳质检)设函数f (x )=ln x ,g (x )=f (x )+f ′(x ).(1)求g (x )的单调区间和最小值;(2)讨论g (x )与g ⎝⎛⎭⎫1x 的大小关系;(3)令h (x )=g (x )-g ⎝⎛⎭⎫1x ,若对任意x ∈⎣⎡⎦⎤1e ,1,存在a ∈[1,e],使h (x )>m -f (a )成立,求实数m 的取值范围.答案解析1.D 2.D 3.B4.D [若方程|x 2+4x |=m 有实数根,先讨论根的个数,可能为2个,3个,4个.易求所有实数根的和可能为-4,-6,-8.故选D.]5.C [∵当x ≥0时,f (x )=ln(x +1),∴设x ≤0,得-x ≥0,f (-x )=ln(-x +1),又∵函数f (x )是定义在R 上的偶函数,∴f (-x )=f (x ),即当x ≤0时,f (x )=ln(-x +1).当x ≥0时,原函数由对数函数y =ln x 图象左移一个单位而得,当x ≥0时函数为增函数,函数图象是上凸的,故选C.]6.C [依题意得f ′(x )=-sin x +2f ′⎝⎛⎭⎫π6, ∴f ′⎝⎛⎭⎫π6=-sin π6+2f ′⎝⎛⎭⎫π6,∴f ′⎝⎛⎭⎫π6=12. ∴f (x )=cos x +x ,则f ⎝⎛⎭⎫π3=cos π3+π3=12+π3, f ⎝⎛⎭⎫-π3=cos ⎝⎛⎭⎫-π3-π3=12-π3, ∴f ⎝⎛⎭⎫π3>f ⎝⎛⎭⎫-π3.]7.A [因为f (-x )=f (x ),故f (x )为偶函数;因为f (x +2)=f (x ),故T =2.作出f (x )在[0,4]上的图象如图所示,再作出g (x )=(13)x 的图象,可知f (x )和g (x )在[0,4]上有5个交点,即方程f (x )=(13)x 在[0,4]上解的个数为5,故选A.]8.D [f ′(x )=k -1x ,由已知得f ′(x )≥0在x ∈(1,+∞)上恒成立,故k ≥1x在(1,+∞)上恒成立.因为x >1,所以0<1x<1, 故k 的取值范围是[1,+∞).]9.D [函数f (x )的图象如图所示:且f (-x )=f (x ),从而函数f (x )是偶函数且在[0,+∞)上是增函数.又0<|x 1|<|x 2|,∴f (x 2)>f (x 1),即f (x 1)-f (x 2)<0.]10.C [不等式ax 3-x 2+4x +3≥0变形为ax 3≥x 2-4x -3.当x =0时,0≥-3恒成立,故实数a 的取值范围是R .当x ∈(0,1]时,a ≥x 2-4x -3x 3恒成立,记f (x )=x 2-4x -3x 3, f ′(x )=-x 2+8x +9x 4=-(x -9)(x +1)x 4>0,故函数f (x )单调递增,则f (x )max =f (1)=-6,故a ≥-6.当x ∈[-2,0)时,a ≤x 2-4x -3x 3恒成立, 记f (x )=x 2-4x -3x 3, 令f ′(x )=0,得x =-1或x =9(舍去),当x ∈[-2,-1)时,f ′(x )<0;当x ∈(-1,0)时,f ′(x )>0,故f (x )min =f (-1)=-2,则a ≤-2.综上所述,实数a 的取值范围是[-6,-2].]11.B [∵f (x )=-f (x +32), ∴f (x +3)=f [(x +32)+32]=-f (x +32)=f (x ). ∴f (x )是以3为周期的周期函数,则f (2 017)=f (672×3+1)=f (1)=2.]12.A [由单函数的定义可知,函数值相同则自变量也必须相同.依题意可得①不正确,②正确,③正确,④正确.]13.①②③解析 对于x ∈Z ,f (x )的图象为离散的点,关于y 轴对称,①正确;f (x )为周期函数,T =2,②正确;f (x +1)+f (x )=1+(-1)x +12+1+(-1)x 2=1+(-1)x +1+(-1)x 2=1,③正确. 14.①③④解析 根据已知条件可知f (x )=lg x 2+1|x |(x ≠0)为偶函数,显然利用偶函数的性质可知命题①正确;对真数部分分析可知最小值为2,因此命题③成立;利用复合函数的性质可知命题④成立;命题②,单调性不符合复合函数的性质,因此错误;命题⑤,函数有最小值,因此错误,故填写①③④.15.①②④解析 ①∃x ∈(0,+∞),(12)x >(13)x 是真命题,如x =2,14>19成立; ②∃x ∈(0,+∞),log 2x <log 3x 是真命题,如x =12, log 212=-1,log 312>log 313=-1, 即∃x ∈(0,+∞),log 2x <log 3x ;③∀x ∈(0,+∞),(12)x >log 12x 是假命题, 如x =12,log 1212=1>(12)12; ④∀x ∈(0,13),(12)x <log 13x 是真命题,因为∀x ∈(0,13),(12)13<(12)x <1,log 13x >1. 16.①②③解析 ①中,f ′(x )=cos x -sin x ,f ″(x )=-sin x -cos x =-sin ⎝⎛⎭⎫x +π4<0在区间⎝⎛⎭⎫0,π2上恒成立;②中,f ′(x )=1x -2(x >0),f ″(x )=-1x 2<0在区间⎝⎛⎭⎫0,π2上恒成立;③中,f ′(x )=-3x 2+2,f ″(x )=-6x 在区间⎝⎛⎭⎫0,π2上恒小于0.故①②③为凸函数.④中,f ′(x )=e x +x e x ,f ″(x )=2e x +x e x =e x (x +2)>0在区间⎝⎛⎭⎫0,π2上恒成立,故④中函数不是凸函数. 17.解 (1)由f (0)=3,得c =3.∴f (x )=ax 2+bx +3.又f (x +1)-f (x )=4x +1,∴a (x +1)2+b (x +1)+3-(ax 2+bx +3)=4x +1, 即2ax +a +b =4x +1,∴⎩⎪⎨⎪⎧ 2a =4,a +b =1,∴⎩⎪⎨⎪⎧a =2,b =-1.∴f (x )=2x 2-x +3.(2)f (x )>6x +m 等价于2x 2-x +3>6x +m ,即2x 2-7x +3>m 在[-1,1]上恒成立,令g (x )=2x 2-7x +3,x ∈[-1,1],则g (x )min =g (1)=-2,∴m <-2.18.解 (1)设x ∈(0,1],则-x ∈[-1,0),f (-x )=14-x -a 2-x =4x -a ·2x , 又因为函数f (x )为奇函数,所以f (x )=-f (-x )=a ·2x -4x ,x ∈(0,1].(2)因为f (x )=a ·2x -4x ,x ∈(0,1],令t =2x ,t ∈(1,2],所以g (t )=at -t 2=-(t -a 2)2+a 24, 当a 2≤1,即a ≤2时,g (t )<g (1)=a -1,此时f (x )无最大值;当1<a 2<2,即2<a <4时,g (t )max =g (a 2)=a 24; 当a 2≥2,即a ≥4时,g (t )max =g (2)=2a -4. 综上所述,当a ≤2时,f (x )无最大值,当2<a <4时,f (x )的最大值为a 24, 当a ≥4时,f (x )的最大值为2a -4.19.解 (1)f (1)=f (1)+f (1)-12,解得f (1)=12. f ⎝⎛⎭⎫2×12=f (2)+f ⎝⎛⎭⎫12-12,解得f (2)=1. (2)任取x 1,x 2∈(0,+∞),且x 1<x 2,则f (x 2)-f (x 1)=f ⎝⎛⎭⎫x 2x 1-12.因为x 1<x 2,所以x 2x 1>1,则f ⎝⎛⎭⎫x 2x 1>12,f (x 2)-f (x 1)>0, 所以f (x )在(0,+∞)上是增函数.因为f (4)=f (2)+f (2)-12=32, 所以f (x )+f (x +3)=f (x 2+3x )+12>2, 即f (x 2+3x )>32=f (4). 所以⎩⎪⎨⎪⎧ x >0,x +3>0,x 2+3x >4,解得x ∈(1,+∞).20.解 当1≤t ≤40,t ∈N 时,s (t )=g (t )f (t )=(-13t +1123)(14t +22) =-112t 2+2t +112×223=-112(t -12)2+2 5003, 所以768=s (40)≤s (t )≤s (12)=112×223+12=2 5003. 当41≤t ≤100,t ∈N 时,s (t )=g (t )f (t )=(-13t +1123)(-12t +52) =16t 2-36t +112×523=16(t -108)2-83, 所以8=s (100)≤s (t )≤s (41)=1 4912. 所以s (t )的最大值为2 5003,最小值为8. 21.解 (1)由f (x )=ax +x ln|x +b |=x (a +ln|x +b |)是奇函数,则y =a +ln|x +b |为偶函数,∴b =0.又x >0时,f (x )=ax +x ln x ,∴f ′(x )=a +1+ln x ,∵f ′(e)=3,∴a =1.(2)当x >1时,令g (x )=f (x )x -1=x +x ln x x -1, ∴g ′(x )=x -2-ln x (x -1)2,令h (x )=x -2-ln x , ∴h ′(x )=1-1x =x -1x>0, ∴y =h (x )在(1,+∞)上是增函数,∴h (1)=-1<0,h (3)=1-ln 3<0,h (4)=2-ln 4>0,∴存在x 0∈(3,4),使得h (x 0)=0,则x ∈(1,x 0),h (x )<0,g ′(x )<0,y =g (x )为减函数.x ∈(x 0,+∞),h (x )>0,g ′(x )>0,y =g (x )为增函数.∴g (x )min =g (x 0)=x 0+x 0ln x 0x 0-1=x 0. ∴k <x 0,又x 0∈(3,4),k ∈Z ,∴k max =3.22.解 (1)由题设知f (x )=ln x ,g (x )=ln x +1x,定义域为(0,+∞). 所以g ′(x )=x -1x 2,令g ′(x )=0得x =1, 当x ∈(0,1)时,g ′(x )<0,故(0,1)是g (x )的单调递减区间.当x ∈(1,+∞)时,g ′(x )>0,故(1,+∞)是g (x )的单调增区间. 所以g (x )最小值=g (1)=1.综上,g (x )的单调递增区间为(1,+∞),单调递减区间为(0,1),最小值为1.(2)g ⎝⎛⎭⎫1x =-ln x +x .设h (x )=g (x )-g ⎝⎛⎭⎫1x =2ln x -x +1x, 则h ′(x )=-(x -1)2x 2≤0, 因此,h (x )在(0,+∞)内单调递减.又h (1)=0,当x =1时,h (1)=0,即g (x )=g ⎝⎛⎭⎫1x ;当0<x <1时,h (x )>h (1)=0,即g (x )>g ⎝⎛⎭⎫1x ;当x >1时,h (x )<h (1)=0,即g (x )<g ⎝⎛⎭⎫1x .(3)由(2)知h (x )在x ∈⎣⎡⎦⎤1e ,1上单调递减,∴h (x )在x ∈⎣⎡⎦⎤1e ,1上的最小值为h (1)=0,又对任意x ∈⎣⎡⎦⎤1e ,1,使h (x )>m -f (a )成立,则m -f (a )<h (x )最小值=h (1)=0,即m <f (a ). 又存在a ∈[1,e],使m <f (a )成立, 又f (x )=ln x 是增函数, 所以m <f (a )最大值=f (e)=1. 所以m <1.。
阶段滚动检测卷2
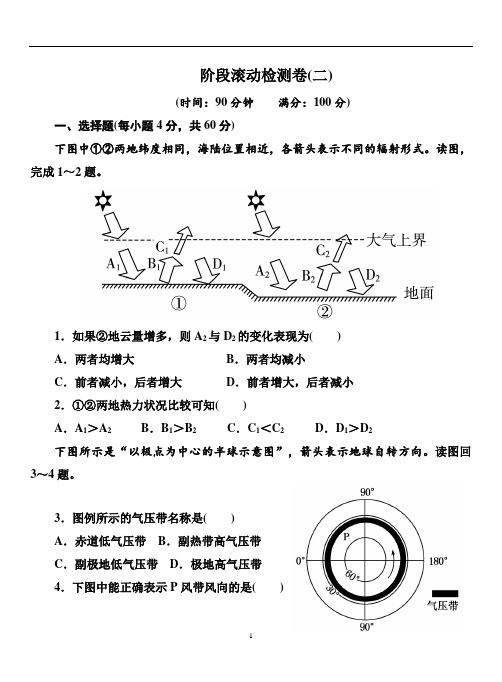
阶段滚动检测卷(二)(时间:90分钟满分:100分)一、选择题(每小题4分,共60分)下图中①②两地纬度相同,海陆位置相近,各箭头表示不同的辐射形式。
读图,完成1~2题。
1.如果②地云量增多,则A2与D2的变化表现为()A.两者均增大B.两者均减小C.前者减小,后者增大D.前者增大,后者减小2.①②两地热力状况比较可知()A.A1>A2B.B1>B2 C.C1<C2D.D1>D2下图所示是“以极点为中心的半球示意图”,箭头表示地球自转方向。
读图回3~4题。
3.图例所示的气压带名称是()A.赤道低气压带B.副热带高气压带C.副极地低气压带D.极地高气压带4.下图中能正确表示P风带风向的是()据此回答5~6题。
5.甲乙两图中,受锋面影响可能产生的天气现象是()A.甲图中暖空气被迫抬升,形成降雨天气B.甲图中锋过境后出现升温、降压、晴朗天气C.乙图中暖空气主动爬升,形成阵性降水D.乙图中锋过境后狂风大作,出现短时雷暴天气6.我国东部受甲图中锋面影响时,会出现的天气现象是()A.长江下游伏旱B.华北平原春旱C.北方寒潮D.江淮梅雨(2014·衢州模拟)下图为我国2013年1月11日近地面等压线图(单位:百帕)和雾的空间分布图,据此回答7~8题。
7.下列有关城市天气状况的叙述,正确的是()A.西安有轻雾,盛行东北风B.重庆有大雾,气压值可能为1 0233百帕C.南京有大雾,日平均气温比北京高D.杭州有轻雾,天气晴朗8.有关雾的形成,下列说法正确的有()①处在低压区,大部分地区吹偏南风,带来较为丰富的水汽②风力小,有利于雾的形成③处在经济发达地区,凝结核多④冬季北方气温低,燃煤量大,凝结核多A.①②③B.②③④C.①③④D.①②③④读西北地区气候从暖干向暖湿转型范围和程度示意图,完成9~10题。
9.据图可知()A.该地降水量由东南向西北递增B.天山及其以北显著趋于暖湿C.伊宁增加的蒸发量小于兰州D.陕西降水量趋于减少10.图中气候显著转型区环境要素变化最不可信的是()A.冰川退缩将会停止B.洪涝灾害将会严重C.湖泊水位将会上升D.沙尘暴日数将会减少下图为沿某经线圈部分陆地气候类型分布示意图(阴影部分表示陆地),O为极点,点A、B均位于赤道上。
2023-2024学年广东省深圳市高级中学初中部(北校区)九年级上学期物理滚动测试二

2023-2024学年广东省深圳市高级中学初中部(北校区)九年级上学期物理滚动测试二1.用分子动理论观点对下列现象的解释不正确的是()A.氧气被压缩装入钢瓶——分子间有空隙B.破碎的玻璃无法复原——分子间存在排斥力C.挂在室外的湿衣服变干了——分子不停地无规则运动D.两块表面平滑的铅块挤压后会粘在一起——分子间存在吸引力2.春节期间,学校开展了“寻根同源,记住年味”的活动,下列描述正确的是()A.饺子香气四溢,说明分子只在高温下运动B.年粽入嘴时很烫,说明粽子含有的热量高C.写春联时闻到墨香,说明墨香分子在运动D.煮汤圆时温度升高,汤圆的内能不一定增加3.暑假期间,小宇一家去海边游玩。
小宇发现烈日下海滩上的沙子热得烫脚,而海水却很清凉;傍晚,沙子凉了,海水却依然温暖。
这主要是因为()A.沙子吸收的热量较多B.海水吸收的热量较少C.沙子的比热容较大D.海水的比热容较大4.下列对图中热现象分析正确的是()A.图甲中塞子冲出的过程中管内水蒸气的内能增加B.图乙中迅速压下活塞硝化棉燃烧是利用做功改变物体的内能C.图丙中的汽油机正处于吸气冲程D.图丁中碘升华时是由做功的方式改变碘的内能5.下列说法正确的是()A.热值大的燃料完全燃烧,放出的热量一定多B.燃料完全燃烧放出的热量越多,热值一定越大C.热值由燃料本身决定,与燃烧质量和燃烧状态无关D.燃料燃烧时温度越高,热值越大6.如图所示,是“风光互补”景观照明灯,它“头顶”小风扇,“肩扛”电池板,“脚踩”蓄电池,“腰”挎照明灯,下列解释合理的是()A.小风扇是风力发电机,将电能转化为机械能B.照明灯是将光能转化电能C.光电池板是将光能转化为电能D.蓄电池在夜晚放电时,将电能转化为化学能7.如图所示下列关于静电现象,说法正确的是()A.甲图:摩擦后的气球能够吸引头发,是因为带电体具有吸引轻小物体的性质B.乙图:细绳悬挂的轻质泡沫塑料小球相互吸引,则两小球一定带有异种电荷C.丙图:丝绸摩擦过的玻璃棒会带上正电荷,在这个过程中丝绸会失去电子D.丁图:验电器是利用了异种电荷相互吸引的原理制成的8.如图所示,小亮将两只相同的气球在自己的头发上摩擦后,就可以让一只气球在另一只气球上方“跳舞”,以下判断正确的是()A.摩擦时,电子在头发与气球之间发生了转移B.上方的气球可能不带电C.若把气球靠近头发,气球与头发将互相排斥D.两个气球带的是异种电荷9.小林同学的父亲是一名电力工人,如图所示为他随身携带的电工箱,箱内的下列物品中属于导体的是()A.金属刀片B.塑料空心手柄C.橡胶保护套D.电工胶带10.生活中的静电,有的可以利用,有的需要防止,下列选项属于利用静电的是()A.油罐车的尾部通常拖一条铁链B.地毯中编织了一些细小的钢丝C.复印时,让硒鼓带电吸引墨粉D.高层楼房顶部都安装上避雷针11.下列日常生活的电路中,说法正确的是()①节日的夜晚,装扮用的小彩灯是并联的②教室的灯管之间是并联的③一般家庭的卫生间都要安装照明灯和换气扇,它们是并联的④道路两旁的路灯晚上同时亮,早上同时灭,它们是串联的⑤楼道中的电灯是由声控开关和光控开关共同控制的,只有在天暗并且有声音时才能亮,所以声控开关、光控开关并联,而后与灯是串联的A.①②③④⑤B.②③④⑤C.②③⑤D.②③12.在如图所示的电路中,闭合开关后,有一只灯泡被短接的是()A.B.C.D.13.在如图所示的各电路中,开关闭合后,两盏小灯泡都能发光的是()A.B.C.D.14.某学校保密室有两道门,只有当两道门都关上时(关上一道门相当于闭合一个开关),值班室内的指示灯才会亮,表明门都关上了.下图中符合要求的电路图是()A.B.C.D.15.如图所示,取两个相同的不带电的验电器A和B,用丝绸摩擦过的玻璃棒接触验电器A 的金属球使之带电,再用带有绝缘手柄的金属棒把A和B的金属球连接起来,下列说法正确的是()A.A中正电荷通过金属棒流向B,A金属箔的张角减小B.B中的自由电子通过金属棒流向A,A金属箔的张角增大C.A中正电荷通过金属棒流向B,B中负电荷通过金属棒流向AD.金属棒中瞬间电流的方向从A流向B,B金属箔的张角增大16.根据实物图,画出相应的电路图。
阶段滚动月考卷(二)

阶段滚动月考卷(二)一、选择题(每题2分,共20分)A. 火药B. 指南针C. 造纸术D. 印刷术2. 在下列生物中,属于单细胞生物的是()A. 草履虫B. 青蛙C. 蚂蚁D. 狮子A. 唐朝B. 宋朝C. 元朝D. 明朝A. 《红楼梦》B. 《西游记》C. 《水浒传》D. 《三国演义》5. 下列哪个科学家提出了相对论?()A. 牛顿B. 爱因斯坦C. 伽利略D. 达尔文A. 台湾岛B. 海南岛C. 崇明岛D. 舟山群岛7. 下列哪个是我国的国粹?()A. 京剧B. 越剧C. 评剧D. 黄梅戏A. 字节B. 千克C. 米D. 秒9. 下列哪个是太阳系中的八大行星之一?()A. 水星B. 冥王星C. 天王星D. 地球A. 郦道元B. 徐霞客C. 司马迁D. 王安石二、填空题(每题2分,共20分)1. 我国古代的“文房四宝”是指笔、墨、纸、______。
2. 《论语》是______的弟子及其再传弟子编撰的一部语录体散文集。
3. 地球上最大的一片沙漠是______沙漠。
4. 人体内最长的神经是______神经。
5. 世界上面积最大的国家是______。
6. 我国历史上著名的“焚书坑儒”事件发生在______朝。
7. 世界上第一台电子计算机诞生于______年。
8. 在化学元素周期表中,原子序数为1的元素是______。
9. 世界上最早的纸币是我国的______。
10. “山重水复疑无路,柳暗花明又一村”这句诗出自______的作品。
三、判断题(每题2分,共20分)1. 《孙子兵法》是我国古代著名的兵书,其作者是孙武。
()2. 地球自转的方向是自西向东。
()3. 世界上最长的河流是尼罗河。
()4. 诺贝尔奖最初设立时只有物理、化学、生理学或医学三个奖项。
()5. 人类最早使用的金属是铜。
()6. “草船借箭”故事的主人公是诸葛亮。
()7. 现代奥运会每四年举办一次。
()8. DNA是生物体内的一种蛋白质。
2021届河北省初中毕业生升学文化课考试 滚动检测卷(二)

2021年河北省初中毕业生升学文化课考试滚动检测卷(二)(时间:100分钟满分:100分)一、选择题(本大题共15小题,共33分,1~12小题为单选题,每小题的四个选项中,只有一个选项符合题意,每小题2分;13~15小题为多选题,每小题的四个选项中,有两个或两个以上选项符合题意,每小题3分,全选对的得3分,选对但不全的得2分,有错选或不选的不得分)1.如图所示的工具中属于费力杠杆的是( )2.用1 m的玻璃管做托里拆利实验,下面几种情况中对管内水银柱竖直高度有影响的是( )A.玻璃管的粗细B.玻璃管的长短C.实验所在的高度D.玻璃管插入水银槽的深度3.如图所示的三只相同的烧杯分别放有质量相等的煤油、水、硫酸,根据液面高度判断盛硫酸的是( )A.甲杯B.乙杯C.丙杯D.无法判断4.三个分别用铜、铁、铝制成的正立方体,它们的质量相等,把它们放在水平桌面上,则对桌面压强大的是( )A.铜立方体B.铁立方体C.铝立方体D.三个一样大5.有一人用一滑轮组分别将1 000 N和2 000 N的物体匀速提高相同的高度,动滑轮重200 N,绳重及摩擦都不计,则在上述两种情况中( )A.人做的额外功相等B.滑轮组的机械效率相等C.人做的总功相等D.人做功的功率相等6.下列各现象中不属于惯性现象的是( )A.刹车时,人的身体向前倾B.放入水中的铁球很快沉入水底C.汽车关闭发动机后,车还会向前运动一段距离D.锤头松了,用力将锤柄撞击固定物,使锤头紧套在柄上7.用手握住汽水瓶,汽水瓶并不滑落,这是因为( )A.手的握力大于汽水瓶的重力B.手的握力等于汽水瓶的重力C.手给汽水瓶的摩擦力大于瓶的重力D.手给汽水瓶的摩擦力等于瓶的重力8.如图所示,原来静止的物体A在水平拉力F作用下沿水平面做直线运动,速度逐渐增大,则拉力F( )A.一定大于阻力F f B.一定等于阻力F fC.可能等于阻力F f D.可能小于阻力F f9.如图所示,小明遛狗时,用力拉住拴狗的绳子,正僵持不动,如果绳子的质量不计。
沪粤版八年级上学期物理 滚动训练(二)

沪粤版八上物理滚动训练(二)1.下列关于温度的描述中符合实际的是A.人体感觉舒适的环境温度约为25∘CB.洗澡时,淋浴水温约为70∘CC.饺子煮熟即将出锅时的温度约为40∘CD.冰镇橙汁饮料的温度约为−20∘C2.我国劳动人民在生产生活中创造性运用物理知识。
对图中所蕴含物理知识的解说错误的是A.自制简易冰箱利用蒸发吸热来保存食物B.把鱼埋在冰粒中利用了冰温度较低且熔化吸热来保鲜鱼C.北方冬天在菜窖里放几桶水是利用水凝固吸热来保存蔬菜的D.新疆坎儿井利用地下水管引水,减少水在输送过程中的蒸发3.下列做法中,利用物态变化放热的是A.运输食品时,为了防止食品腐烂变质,常放些干冰B.北方的冬天,常在保存蔬菜的菜窖里放几桶水C.夏天,为了凉快,常在地面上洒水D.夏天,为了喝到冰凉的饮料,常在饮料中加冰块4.我国是一个缺水的国家,因而污水净化具有重要的意义。
如图所示是江涛发明的太阳能净水器,在污水净化过程中该净水器内发生的物态变化是A.先熔化,后液化B.先升华,后凝华C.先汽化,后液化D.先汽化,后凝固5.下列场景与所蕴含的物理知识对应完全正确的是A.春季,小会体育训练后满头大汗,回到教室不停扇风——提高液体温度加快蒸发B.夏季,小会手拿着一瓶冰冻矿泉水,一段时间后冰减少,手感到凉——熔化吸热C.秋季,小会发现清晨操场边的双杠上铺满了一层霜——霜是水蒸气凝固形成的D.冬季,戴眼镜的小会从教室外走进温暖的教室内,眼镜镜片模糊不清——液化吸热6.如图所示,水的三态在物态变化过程中的指向对应的名称都正确的是A.B.C.D.7.如图甲、乙所示,分别是酒精在1个标准大气压下熔化和沸腾时温度随时间变化的图象,下列说法中正确的是A.固态酒精是非晶体B.在−117∘C时,酒精处于液态C.酒精温度计可以用来测量沸水的温度D.酒精在沸腾过程中吸热但温度不变8.如图所示,温度计显示的温度是∘C。
9.医学上针对外伤的疼痛常用“冷疗法”治疗,其原理是医生用一种叫做氯乙烷的气态有机物,先用压缩体积的方法使它,然后喷在伤口处时又在皮肤上迅速(前两空均填物态变化名称),同时大量的热,使人体受伤部位的温度降低,皮肤血管收缩,神经纤维传导速度变慢,类似局部麻醉,人的伤痛很快消失,同时防止伤口处形成瘀血。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
阶段滚动月考卷(二)古今中外的政治文明(90分钟100分)一、选择题(本大题共25小题,每小题2分,共50分)1.“春秋争霸”的“霸”是“伯”的通假字,“伯”是一方诸侯首领的意思。
可见,春秋时期的争霸战争( )A.推动社会结构转型B.以维持秩序为目的C.强化了周王的权威D.本质上是爵位之争2.(2016·晋中模拟)战国时期,郡制设立多在边远之地近敌之处,如魏文侯“以吴起善用兵……乃以为西河(郡)守,以拒秦、韩”。
朝廷往往授予这些“郡守”节制周边县域文武官员,统一调度县域人、财、物以应对紧急突发事件的权力。
这反映出当时( )A.郡的设置具有巩固国防的意图B.吴起变法加强了魏国集权体制C.魏国地方管理实行郡守负责制D.负责地方管理的郡守都是武将3.唐代的三省六部制完善了专制主义中央集权制度,主要体现在( )A.使中央与地方官员相互制约B.地方权力逐渐被削弱C.有利于皇帝集权和政令的贯彻执行D.中央各部门职责分明,效率提高4.(2016·沈阳模拟)我国古代中央机构不断变革,曾出现三公九卿、三省六部、内阁、军机处等制度。
这些变革反映的趋势是不断强化( )A.专制皇权B.中央集权C.监察权力D.对农民的控制5.克利斯提尼时期,五百人议事会的职责是向公民大会提供法案,后者每年约集结四十次以履行其职责。
被提议的法案可能被通过、驳回或者发回“议事会”进行修订。
这表明( )A.五百人议事会的职责尚不明确B.政治决策先有民主再有集中C.公民大会实为国家权力机关D.希腊奴隶制度逐步确立起来6.下框是古罗马法官判决的一个案例,该案例主要说明了罗马法( )A.重视维护平民的利益B.司法审判程序严格完备C.确保私有财产不受侵犯D.理性、公平、证据的精神7.“英国‘光荣革命’在一个有长期专制传统的国家找到了一个摆脱革命与专制的循环,能有效地控制‘控制者’的办法。
”这里的“办法”是指( ) A.恢复“王在议会” B.确立议会主权C.建立责任内阁制D.发动宫廷政变8.“美国政治意在使候选人代表主流思想,远离边缘化集团利益。
‘赢家通吃’的方法就是迫使候选人转向主流路线,以便获得最多的政治支持。
”这种现象根源于( )A.两党政策大同小异B.两党轮流执政的安排C.总统制共和制政体的特点D.联邦权力高于各州权力9.(2016·广州模拟)随着工业革命的进展,经济的飞速发展及社会结构的急剧变化,“光荣革命”的遗产渐次落伍了。
由此,英国( )A.颁布了《航海条例》B.确立了责任内阁制C.进行了1832年议会改革D.组建了垄断性贸易公司10.“虽然搞现代化比较早和比较晚的国家的前提有很大的不同,但是参加现代化行列比较晚的各国的前提都是十分相似的。
”文中所说的如中国等参加现代化行列比较晚的各国“十分相似”的“前提”是指( )A.近代工业的起步B.资本主义制度的建立C.自给自足的自然经济的解体D.受到外来文明的冲击、影响11.古代中国历史撰写有为尊者讳的传统,如以“狩猎”来指代君王出逃。
据此推断,与近代著作《庚子西狩丛谈》记载的内容紧密相关的历史事件是( ) A.鸦片战争 B.中日甲午战争C.八国联军侵华战争D.辛亥革命12.《庚子诗鉴》记载,拳民搜索教堂,“见蜡人不能辨,以为人腊”。
“遇粤之荔枝干,又以为人眼,相与痛詈西人,暴其惨酷”。
以上材料反映出( )A.洋教势力对中国民众的毒害B.东西文化碰撞中产生的误解C.义和团拳民深受传统文化影响D.义和团运动中的盲目排外13.某学者指出:“武昌起义后,一个月之内……十三省相继宣布独立,并且没有一个地方发生激烈的战争。
满清的灭亡,不是革命军以军力打倒的,是清朝自己瓦解的。
”这一材料( )A.说明了革命势力的强大B.揭示了清朝灭亡的内在原因C.否定了武昌起义的重要作用D.说明了资产阶级革命派的软弱性14.毛泽东曾经指出:“没有五四运动,第一次大革命是没有可能的。
五四运动的的确确给第一次大革命准备了舆论,准备了人心,准备了思想,准备了干部。
”毛泽东突出评价的是五四运动( )A.在政党政治方面的作用B.在民主革命中的作用C.在文化系统重建中的地位D.对中国社会主义运动的意义15.(2016·洛阳模拟)19世纪末20世纪初的中国,外国传教士、资产阶级、先进知识分子、无政府主义者都在积极宣传各种社会主义思潮,其中包括马克思主义。
这种现象的出现表明( )A.马克思主义适合中国的国情B.中国亟需改造社会的良方C.社会主义已经成为时代潮流D.中国共产党的政治影响不断扩大16.“她像一声惊雷震撼着沉睡的大地,以磅礴的气势向世界宣告:资本主义必然灭亡,无产阶级将是未来世界的主人!”从此,工人运动开创了一个新纪元。
这里的“新”的含义是( )A.推翻资产阶级的条件已经具备B.工人运动有了科学理论指导C.无产阶级开始尝试夺取政权D.开创了世界现代化的新模式17.美国记者约翰·里德在《震撼世界的十天》一书中写道:“革命把俄国从底层翻腾出来。
现在是底层人跃升到上层来了。
”这主要表明俄国十月革命( )A.推翻了统治俄国的罗曼诺夫王朝B.走的是从城市到农村的革命道路C.开创了国际社会主义运动新局面D.使工农群众掌握了国家政权18.(2016·清远模拟)1930年6月,共产国际断定“最近将来革命形势即使不能够包括整个中国,但至少也要包括几个有决定意义的省份,在这一种情况下,中国共产党应该为迫在眉睫的解放战争做好准备”。
这反映出( )A.中国共产党对革命目标做出了调整B.共产国际可以指挥中国革命C.中国共产党革命受共产国际的影响D.中国共产党认识到夺取大城市的重要性19.邮票是“国家的名片”,中华人民共和国与中华民国分别于2015年和1939年发行了纪念邮票,前者是《中国人民抗日战争暨世界反法西斯战争胜利七十周年》纪念邮票,后者是右图的邮票。
中华民国邮政发行此邮票的主要意图是( )A.纪念美国成立一百五十年B.希望和美国建立外交关系C.鼓动美国开辟太平洋战场D.争取美国支持中国的抗战20.天津的解放桥最初建于1902年,原名“万国桥”,抗日战争胜利后国民政府将“万国桥”改为“中正桥”。
1949年,天津解放后此桥正式更名为“解放桥”,并沿用至今。
透过解放桥名称的变更历程,我们可以了解近代天津( ) A.反侵略求民主的历史 B.经济的近代化C.半殖民地化加深D.文化的平民化21.阅读下图所示中国外交活动。
下列解读最准确的是( )A.推动建立国际政治新秩序B.加强与第三世界国家合作C.积极推进新型区域合作D.参与以联合国为中心的多边外交活动22.1965年,中央人民政府正式设立西藏自治区。
这一举措对形成中国特色的民主政治的意义在于( )A.实现了自治区人民自己当家作主的愿望B.开创了民族区域自治的先例C.促进了自治区社会经济的发展D.实现了祖国统一和民族团结23.有人认为,目前的欧洲有两种东扩,一种是制度性的,一种是战略性的。
这两种东扩是指下列哪两者的东扩( )A.北约与华约B.北约与欧盟C.欧盟与北约D.恐怖与流感24.1946年9月19日,丘吉尔在苏黎世大学发表的题为《欧洲的悲剧》的演说中指出:“摧毁了纳粹政权之时……我向欧洲提出的建议可以概括为一句话:联合起来!”欧洲国家为此进行最初的实践是( )A.建立北约B.建立欧洲煤钢共同体C.组建欧洲联盟D.成立欧共体25.“我们亚非国家所需要的是和平和独立,我们并无意于使亚非国家同其他地区的国家对立,我们同样需要同其他地区的国家建立和平合作的关系。
”这段话的目的在于( )A.强调亚非国家具有共同的利益B.突出了新中国的领导地位C.体现了摆脱美苏两极格局的要求D.世界多极化趋势加强二、非选择题(本大题共4小题,第26题13分,第27题13分,第28题12分,第29题12分,共50分)26.阅读材料,完成下列各题。
材料一公选制——两汉开国之初,尚有不少武力功臣。
可是一旦百废俱兴,尤其是建国十年、二十年之后,旧臣凋零,就需要大量补充吏员,察举、征辟之事应时而兴。
察举征辟就是从民间访求有才有德而又未仕之人,由于征诸乡里,因有“乡举里选”之说。
我称此制为“公选”。
公选的名目很多,有贤良、方正、孝廉、秀才等科。
——张传玺《秦汉中央集权制的“公天下”因素》材料二显而易见的是,科举制改变了传统选官制度中自下而上、权力下移的性质。
再同以往的察举、九品中正制相比,科举是一种由中央确定标准、决定取舍的自上而下的选官方式。
比如说,唐代的“乡贡”,已经完全不同于察举制下的推荐,更不同于征辟除制下的自行任免,地方官不再掌握推荐的权力,只不过是奉命行事,按照中央规定的具体选官标准进行资格审查和预选而已。
明清的“乡试”,实际上已经成为全部由中央操办的全国统一的分区考试。
这种统一的选官标准和方式,排除了地方长官对政策的解释权力,即自行解释人才标准和按个人好恶取舍人才的因素。
——刘文瑞杨柯《试论科举制对中央集权体制的历史作用》(1)依据材料一及所学知识,说明汉朝推行察举制、征辟制的原因。
材料一作者为什么称察举制为“公选”制?(4分)(2)依据材料二说明,相对于察举制,科举制的变化是什么。
以察举制发展的事实说明这一变化的作用。
(6分)(3)根据上述材料,谈谈你对人才选拔制度的认识。
(3分)27.阅读下列材料,完成问题。
材料一纵览英国民主革命史,还有一层也是我们应该认识到的:这里,我是指着它的合理的协商精神而言的,不通过流血的手段而达到理想的目标正是民主的最高境界。
虽然英国革命之初也曾有过内战,但比较起来,它依然算是流血最少的一个。
此后,代议制既经奠定,英国的政治革命便一直循着和平协商的方式进行了。
——余英时《民主制度与近代文明》材料二我对许多问题的看法,一如所有此类看法一样,得益于民主历史中以后这个特别的立场,亦即这样一种信念:民主的思想和实践只有最终得到保护,才能在我们的政治、社会和经济生活中得到扩展和深化。
——赫尔德《民主的模式》材料三在某种意义上,民主的不同形式的发展历史正是一定政治观念和政治实践形成的历史,而这一历史在西方的具体体现最为明显。
——赫尔德《民主的模式》(1)通过对材料一中“合理的协商精神”的理解,请你举出英国民主实践中符合这一“精神”的两个事例,并分别指出其能够通过协商方式解决的主要原因。
(5分)(2)根据材料二和所学知识,概括指出民主的思想和实践最终得到“保护”的主要原因。
(2分)(3)通过对材料三的理解,请指出近代西方有哪两种不同形式的民主制度。
以英国和美国为例,其政治理念和实践方式有何不同?(6分)28.(2016·晋中模拟)阅读材料,完成下列要求。
