管理运筹学lindo案例分析
天大运筹学相关软件lindo案例-13页文档资料

(a)Lindo的数据分析及习题(a)灵敏性分析(Range,Ctrl+R)用该命令产生当前模型的灵敏性分析报告:研究当目标函数的费用系数和约束右端项在什么范围(此时假定其它系数不变)时,最优基保持不变。
灵敏性分析是在求解模型时作出的,因此在求解模型时灵敏性分析是激活状态,但是默认是不激活的。
为了激活灵敏性分析,运行LINGO|Op tions…,选择General Solver Tab,在Dual Computations列表框中,选择Prices and Ranges选项。
灵敏性分析耗费相当多的求解时间,因此当速度很关键时,就没有必要激活它。
下面我们看一个简单的具体例子。
例5.1某家具公司制造书桌、餐桌和椅子,所用的资源有三种:木料、木工和漆工。
生产数据如下表所示:每个书桌每个餐桌每个椅子现有资源总数木料8单位6单位1单位48单位漆工4单位2单位 1.5单位20单位木工2单位 1.5单位0.5单位8单位成品单价60单位30单位20单位若要求桌子的生产量不超过5件,如何安排三种产品的生产可使利润最大?用DESKS、TABLES和CHAIRS分别表示三种产品的生产量,建立LP模型。
max=60*desks+30*tables+20*chairs;8*desks+6*tables+chairs<=48;4*desks+2*tables+1.5*chairs<=20;2*desks+1.5*tables+.5*chairs<=8;tables<=5;求解这个模型,并激活灵敏性分析。
这时,查看报告窗口(Reports Window),可以看到如下结果。
Global optimal solution found at iteration: 3Objective value: 280.0000Variable Value Reduced CostDESKS 2.000000 0.000000TABLES 0.000000 5.000000CHAIRS 8.000000 0.000000Row Slack or Surplus Dual Price1 280.0000 1.0000002 24.00000 0.0000003 0.000000 10.000004 0.000000 10.000005 5.000000 0.000000“Global optimal solution found at iteration: 3”表示3次迭代后得到全局最优解。
管理运筹学-用LINDO验证目标规划模型并求解

实验报告实验课程名称运筹学
实验项目名称用LINDO验证目标规划
模型并求解
年级
专业
学生姓名
学号
实验时间:年月日
原问题为课本p119面的例3。
一、建立原问题的目标规划模型:
利用LINDO 求解出一个满意解:
从求解结果来看:
满足要求的一个生产计划是:1x (彩色电视机)生产24台;2x (黑白电视机)生产26台。
其中:D12=10,D41=4,表示:每周装配线多开机了10个小时,黑白电视机与30台的目标相比少成产了4台。
而 D22=D21=D31=D32=0,表示每周装配线刚好加班10个小时,彩色电视机的生产量刚好为目标值。
二、调整期望值,再求解:
如果每周开机计划开动可以增加10个小时,那么:
模型的表示形式为:
利用LINDO求解出一个满意解:
从求解结果来看:
满足生产目标的生产计划没有发生改变。
但是,D12=D11=D22=D21=D31=D32=0,说明如果每周的计划开机时间定为50个小时的话,不用加班就能满足其他生产计划。
三、改变优先级
1)让黑白电视的生产量尽可能达到生产计划:
利用LINDO求解出一个满意解:
从求解结果来看:
如果想在扩大黑白电视的生产使其尽可能达到生产目,那么就必须要以牺牲工人的加班时间为代价了,装配线的工作时间就要再超出4个小时。
2)如果员工不满加班:
利用LINGO求解出一个满意解:
从结果来看,
即使增大加班时间不超过10个小时的优先级,工人还需要加班10个小时。
这说明如果工人做出让步,同意加班,那么他们的工作时间就会达到他们心中的底线,尽管他们不满意加班。
优化软件LINDO在运筹学中的应用

案例分析
案例分析
以下是一个应用案例,通过使用软件,学生对某物流公司的运输网络进行了 优化。
1、问题描述:该物流公司拥有多个仓库和配送中心,货物的运输和配送由多 个车辆完成。由于公司业务量的增长,原有的运输网络已经不能满足需求,因此 需要优化车辆路径以提高运输效率。
案例分析
2、软件应用:学生使用MATLAB和Simulation Builder来建立并求解该优化 问题。首先,使用MATLAB建立一个车辆路径优化模型;然后,使用Simulation Builder对该模型进行模拟和测试;最后,通过MATLAB进行结果分析和可视化。
软件应用
软件应用
1、建模:在物流运筹学教学中,软件可以帮助学生轻松建立各种数学模型, 如线性规划模型、整数规划模型等。这些模型可以准确地描述物流系统的实际情 况,为进一步的分析和优化奠定基础。
软件应用
2、分析:软件集成了大量的数据分析工具和算法,可以帮助学生深入分析物 流系统中的各种数据,如成本数据、时间数据等。通过这些分析,学生可以更好 地理解物流系统的性能瓶颈和优化潜力。
应用实践
1、需求分析
1、需求分析
在物流工程运筹学中,需求分析是解决问题的第一步。教师可引导学生使用 LINGO软件进行问题定义和场景模拟,以便更好地理解问题背景和需求。例如, 在解决车辆路径问题(VRP)时,可以通过LINGO软件对客户需求、车辆容量等进 行分析,为后续建模优化做好准备。
案例分析
3、结果分析:经过优化,车辆路径长度减少了20%,运输时间减少了15%,从 而大幅提高了运输效率。但是,由于仓库和配送中心的布局以及货物的特性限制, 部分优化目标的改善幅度较小。
案例分析
4、不足与挑战:在这个案例中,虽然软件的应用取得了显著的效果,但仍存 在一些不足之处。例如,模型假设较为简化,忽略了一些现实中的影响因素,如 交通状况、天气等。此外,优化过程中只考虑了运输成本和时间,而未考虑到其 他潜在的成本和利益相关者需求。未来,学生需要对模型进行进一步的改进和完 善,以更好地应对现实中的复杂问题。
(典型例题)《运筹学》运输问题

xj0,yij0,zij0,(i=1,┈,4;j=1,┈,5)
2008/11
--22--
--《Ⅵ 产量
新购 1 第一天 M 第二天 M 第三天 M
第四天 M
1 1 1 1 0 5200
0.2 0.1 0.1 0.1 0 1000
2008/11
--21--
建立模型:
--《运筹学》 运输问题--
设 xj—第j天使用新毛巾的数量;yij—第i天送第j天使用快洗 餐巾的数量;zij—第i天送第j天使用慢洗餐巾的数量;
Min z=∑xj+∑∑0.2yij+∑∑0.1zij
第一天:x1=1000
需 第二天:x2+y12=700
求 约
m1
xij b j (j 1,2,...,n)
i1
x 0 (i 1,...,m,m 1; j 1,...,n) ij
2008/11
--16--
--《运筹学》 运输问题--
销>产问题单位运价表
产地销地 B1 B2 ┈
A1
C11 C12 ┈
A2
C21 C22 ┈
┊ ┆┊┈
Am Cm1 Cm2 ┈
2008/11
--8--
产销平衡表
--《运筹学》 运输问题--
单位运价表
B1 B2 B3 B4 产量
A1 (1) (2) 4 3 7 A2 3 (1) 1 (-1) 4 A3 (10) 6 (12) 3 9 销量 3 6 5 6
B1 B2 B3 B4 A1 3 11 3 10 A2 1 9 2 8 A3 7 4 10 5
Ⅰ Ⅱ
示。又如果生产出来的柴
Ⅲ
运筹学实例分析及lingo求解讲解

运筹学实例分析及lingo 求解一、线性规划某公司有6个仓库,库存货物总数分别为60、55、51、43、41、52,现有8个客户各要一批货,数量分别为35,37,22,32,41,32,43,38。
各供货仓库到8个客户处的单位货物运输价见表试确定各仓库到各客户处的货物调运数量,使总的运输费用最小。
解:设ijx 表示从第i 个仓库到第j 个客户的货物运量。
ij c表示从第i 个仓库到第j 个客户的单位货物运价,i a 表示第i 个仓库的最大供货量,j d 表示第j 个客户的订货量。
目标函数是使总运输费用最少,约束条件有三个:1、各仓库运出的货物总量不超过其库存数2、各客户收到的货物总量等于其订货数量3、非负约束数学模型为:∑∑===6181)(min i j ijij x c x f⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥===≤∑∑==08,,2,1,6,2,1,,..6181ij j i ij i j ij x j d x i a x t s 编程如下:model : Sets :Wh/w1..w6/:ai; Vd/v1..v8/:dj;links(wh,vd):c,x;endsetsData:ai=60,55,51,43,41,52;dj=35,37,22,32,41,32,43,38;c=6,2,6,7,4,2,5,94,9,5,3,8,5,8,25,2,1,9,7,4,3,37,6,7,3,9,2,7,12,3,9,5,7,2,6,55,5,2,2,8,1,4,3;EnddataMin=@sum(links(i,j):c(i,j)*x(i,j));@for(wh(i):@sum(vd(j):x(i,j))<=ai(i));@for(vd(j):@sum(wh(i):x(i,j))=dj(j));endGlobal optimal solution found.Objective value: 664.0000Total solver iterations: 0Variable Value Reduced Cost AI( W1) 60.00000 0.000000 AI( W2) 55.00000 0.000000 AI( W3) 51.00000 0.000000 AI( W4) 43.00000 0.000000 AI( W5) 41.00000 0.000000 AI( W6) 52.00000 0.000000 DJ( V1) 35.00000 0.000000 DJ( V2) 37.00000 0.000000 DJ( V3) 22.00000 0.000000 DJ( V4) 32.00000 0.000000 DJ( V5) 41.00000 0.000000 DJ( V6) 32.00000 0.000000 DJ( V7) 43.00000 0.000000 DJ( V8) 38.00000 0.000000 C( W1, V1) 6.000000 0.000000 C( W1, V2) 2.000000 0.000000 C( W1, V3) 6.000000 0.000000 C( W1, V4) 7.000000 0.000000 C( W1, V5) 4.000000 0.000000 C( W1, V6) 2.000000 0.000000 C( W1, V7) 5.000000 0.000000C( W2, V1) 4.000000 0.000000 C( W2, V2) 9.000000 0.000000 C( W2, V3) 5.000000 0.000000 C( W2, V4) 3.000000 0.000000 C( W2, V5) 8.000000 0.000000 C( W2, V6) 5.000000 0.000000 C( W2, V7) 8.000000 0.000000 C( W2, V8) 2.000000 0.000000 C( W3, V1) 5.000000 0.000000 C( W3, V2) 2.000000 0.000000 C( W3, V3) 1.000000 0.000000 C( W3, V4) 9.000000 0.000000 C( W3, V5) 7.000000 0.000000 C( W3, V6) 4.000000 0.000000 C( W3, V7) 3.000000 0.000000 C( W3, V8) 3.000000 0.000000 C( W4, V1) 7.000000 0.000000 C( W4, V2) 6.000000 0.000000 C( W4, V3) 7.000000 0.000000 C( W4, V4) 3.000000 0.000000 C( W4, V5) 9.000000 0.000000 C( W4, V6) 2.000000 0.000000 C( W4, V7) 7.000000 0.000000 C( W4, V8) 1.000000 0.000000 C( W5, V1) 2.000000 0.000000 C( W5, V2) 3.000000 0.000000 C( W5, V3) 9.000000 0.000000 C( W5, V4) 5.000000 0.000000 C( W5, V5) 7.000000 0.000000 C( W5, V6) 2.000000 0.000000 C( W5, V7) 6.000000 0.000000 C( W5, V8) 5.000000 0.000000 C( W6, V1) 5.000000 0.000000 C( W6, V2) 5.000000 0.000000 C( W6, V3) 2.000000 0.000000 C( W6, V4) 2.000000 0.000000 C( W6, V5) 8.000000 0.000000 C( W6, V6) 1.000000 0.000000 C( W6, V7) 4.000000 0.000000 C( W6, V8) 3.000000 0.000000 X( W1, V1) 0.000000 5.000000 X( W1, V2) 19.00000 0.000000 X( W1, V3) 0.000000 5.000000X( W1, V5) 41.00000 0.000000 X( W1, V6) 0.000000 2.000000 X( W1, V7) 0.000000 2.000000 X( W1, V8) 0.000000 10.00000 X( W2, V1) 1.000000 0.000000 X( W2, V2) 0.000000 4.000000 X( W2, V3) 0.000000 1.000000 X( W2, V4) 32.00000 0.000000 X( W2, V5) 0.000000 1.000000 X( W2, V6) 0.000000 2.000000 X( W2, V7) 0.000000 2.000000 X( W2, V8) 0.000000 0.000000 X( W3, V1) 0.000000 4.000000 X( W3, V2) 11.00000 0.000000 X( W3, V3) 0.000000 0.000000 X( W3, V4) 0.000000 9.000000 X( W3, V5) 0.000000 3.000000 X( W3, V6) 0.000000 4.000000 X( W3, V7) 40.00000 0.000000 X( W3, V8) 0.000000 4.000000 X( W4, V1) 0.000000 4.000000 X( W4, V2) 0.000000 2.000000 X( W4, V3) 0.000000 4.000000 X( W4, V4) 0.000000 1.000000 X( W4, V5) 0.000000 3.000000 X( W4, V6) 5.000000 0.000000 X( W4, V7) 0.000000 2.000000 X( W4, V8) 38.00000 0.000000 X( W5, V1) 34.00000 0.000000 X( W5, V2) 7.000000 0.000000 X( W5, V3) 0.000000 7.000000 X( W5, V4) 0.000000 4.000000 X( W5, V5) 0.000000 2.000000 X( W5, V6) 0.000000 1.000000 X( W5, V7) 0.000000 2.000000 X( W5, V8) 0.000000 5.000000 X( W6, V1) 0.000000 3.000000 X( W6, V2) 0.000000 2.000000 X( W6, V3) 22.00000 0.000000 X( W6, V4) 0.000000 1.000000 X( W6, V5) 0.000000 3.000000 X( W6, V6) 27.00000 0.000000 X( W6, V7) 3.000000 0.000000Row Slack or Surplus Dual Price 1 664.0000 -1.000000 2 0.000000 3.000000 3 22.00000 0.000000 4 0.000000 3.000000 5 0.000000 1.000000 6 0.000000 2.000000 7 0.000000 2.000000 8 0.000000 -4.000000 9 0.000000 -5.000000 10 0.000000 -4.000000 11 0.000000 -3.000000 12 0.000000 -7.000000 13 0.000000 -3.000000 14 0.000000 -6.000000 15 0.000000 -2.000000由以上结果可以清楚的看到由各仓库到各客户处的货物调运数量,由此得出的符合条件的最佳运货方案,而使运费最低,最低为664。
lindo软件求解管理领域中的各种问题实验总结

lindo软件求解管理领域中的各种问题实验总结Lindo软件是一款用于线性规划、整数规划、非线性规划、动态规划等问题求解的工具软件。
在管理领域中,Lindo软件被广泛应用于生产调度、库存管理、物流运输等方面。
本文将对Lindo软件在管理领域中的应用进行总结,并探讨其中存在的问题和解决方法。
一、Lindo软件在生产调度中的应用1.1 生产调度模型生产调度是制造企业中非常重要的一个环节,它涉及到生产计划的制定和实施。
通过使用Lindo软件,可以建立一个生产调度模型,根据不同的约束条件和目标函数,求解出最优的生产计划。
1.2 生产调度问题在实际应用中,生产调度问题常常涉及到多个工序之间的协调与配合。
例如,在汽车制造过程中,需要对钣金、喷漆、装配等多个工序进行协调和安排。
这就需要建立一个复杂的数学模型,并通过Lindo软件来求解。
1.3 生产调度案例分析以某汽车厂为例,该厂需要安排钣金、喷漆、装配三个工序之间的关系。
通过使用Lindo软件,可以得出最优的生产计划,并实现生产调度的优化。
二、Lindo软件在库存管理中的应用2.1 库存管理模型库存管理是企业中非常重要的一个环节,它涉及到物料采购、仓储管理、销售预测等方面。
通过使用Lindo软件,可以建立一个库存管理模型,根据不同的约束条件和目标函数,求解出最优的物料采购计划和销售预测。
2.2 库存管理问题在实际应用中,库存管理问题常常涉及到多个因素之间的协调与平衡。
例如,在零售业中,需要根据销售预测和季节变化等因素来制定物料采购计划。
这就需要建立一个复杂的数学模型,并通过Lindo软件来求解。
2.3 库存管理案例分析以某零售企业为例,该企业需要根据销售预测和季节变化等因素来制定物料采购计划。
通过使用Lindo软件,可以得出最优的物料采购计划,并实现库存管理的优化。
三、Lindo软件在物流运输中的应用3.1 物流运输模型物流运输是企业中非常重要的一个环节,它涉及到货物运输、仓储管理、配送等方面。
运筹学的应用简介及实例(lindo,lingo,ahp)

运筹学的应用简介及实例(lindo,lingo,ahp)一.运筹学可以用于物流中心选址:配送中心合理选址的目的是为了提高物流企业的服务质量,最大限度地增加物流企业的经济效益。
科学合理的选址不仅能够减少货物运输费用,大幅度地降低运营成本,而且能为客户带来方便快捷的服务。
二.运筹学可以用于路线选择:利用运筹学中的图论和线性规划方法,对已有的空运、水运、公路运输、管道运输、铁路运输组成的交通网,根据不同的决策目标制定不同的调运方案,可以是最短时间的运输路线、最少费用的运输路线或是最大运输量最低运费的运输线路等,从而达到降低物流成本的目的。
三.运筹学中排队论在物流中应用:排队论主要研究具有随机性的拥挤现象,在物流中有许多问题涉及,诸如机场跑道设计和机场设施数量问题, 如何才能既保证飞机起降的使用要求, 又不浪费机场资源又如码头的泊位设计和装卸设备的购置问题, 如何达到既能满足船舶到港的装卸要求, 而又不浪费港口资源等等。
四.运筹学中库存论在物流中应用:库存论主要是研究物资库存策略的理论, 即确定物资库存量、补货频率和一次补货量。
合理的库存是生产和生活顺利进行的必要保障, 可以减少资金的占用, 减少费用支出和不必要的周转环节, 缩短物资流通周期, 加速再生产的过程等。
在物流领域中的各节点如工厂、港口、配送中心、物流中心、仓库、零售店等都或多或少地保有库存。
五.运筹学中对策论在物流中应用:对策论研究有利害冲突的双方在竞争性的活动中是否存在自己制胜对方的最优策略, 以及如何找出这些策略等问题。
在这些问题中, 把双方的损耗用数量来描述, 并找出双方最优策略。
对策论的发展, 考虑有多方参加的竞争活动, 在这些活动中, 竞争策略要通过参加者多次的决策才能确定。
参考文献:[1] 左元斌.运筹学在物流配送中心的应用研究[J].商场现代化,2006(458):125-127.[2] 李宇鸣.浅谈运筹学在物流管理中应用与发展[J].吉林工商学报,2007(4):55-56.[3] 田进波.运筹学在管理物流管理中的应用[J].石油工程建设,2010(36):153-155.LINDO 求解目标规划:题目:一个小型的无线电广播台考虑如何最好地来安排音乐、新闻和商业节目时间。
用LINDO解运筹学问题

输入语句: 输入语句:
max(不区分大小写 不区分大小写) 不区分大小写 x1+x2+x3+x4 ST(大写或写 大写或写subject to) 大写或写 x5+x6+x7+x8>=250000 x1+x5<=380000 x2+x6<=265200 x3+x7<=408100 x4+x8<=130100 2.85x1-1.42x2+4.27x318.49x4>=0 2.85x5-1.42x6+4.27x718.49x8>=0 16.5x1+2.0x2-4.0x3+17x4>=0 7.5x5-7.0x6-13.0x7+8.0x8>=0 end
例 加工奶制品的生产计划
输入窗中输入如下代码 max 72 x+64 y st 2) x+y<50 3) 12x+8y<480 4) 3x<100 end 再点按求解命令即可得到优化结果(含灵敏度分析 再点按求解命令即可得到优化结果 含灵敏度分析 信息) 信息
使用LINDO的一些注意事项 的一些注意事项 使用 1.目标函数所在行是第一行,第二行起为约束条件 目标函数所在行是第一行, 目标函数所在行是第一行 2.目标函数及各约束条件之间一定要有“Subject to (ST) ”分 目标函数及各约束条件之间一定要有“ 目标函数及各约束条件之间一定要有 分 开。 3.变量与系数间可有空格 甚至回车 但无运算符 变量与系数间可有空格(甚至回车 变量与系数间可有空格 甚至回车), (如乘号“*”等) 如乘号“ 4.变量名以字母开头,不能超过8个字符 变量名以字母开头,不能超过 个字符 变量名以字母开头 5.变量名不区分大小写(包括LINDO中的关键字) 变量名不区分大小写(包括 中的关键字) 变量名不区分大小写 中的关键字 6. “>”(或“<”)号与“>=”(或“<=”)功能相同 ( )号与“ ( ) 7.行号 行名 自动产生或人为定义。行名以“)”结束 行号(行名 自动产生或人为定义。行名以“ 行号 行名)自动产生或人为定义 8.行中注有“!”符号的后面部分为注释。如: 行中注有“ 符号的后面部分为注释 符号的后面部分为注释。 行中注有 ! It’s Comment.
运筹学经典案例 --农场管理

农场管理背景介绍:普拉夫家族拥有一个大农场,场主普拉夫家族世代经营着农场,主要从事种植农作物和饲养牲畜的工作。
但是农场的设备及相关科学技术没有及时更新。
现在,这个家族正经历了一次大丰收,场主面临着在现有条件下,如何分配有限的现金和劳动力使明年年底能够拥有最多的现金的问题。
劳动力提供冬春两季可提供4000个人工;秋夏两季可提供4500个人工。
鸡:3美元一只现有2000 价值$5000 牛:1500美元一头现有30 价值$35000一年之后,每头牛会增值10%,而鸡由于老化会贬值25%。
每头牛需要有两亩地的草,以及每月10个人工,每年可净收入现金850美元。
一只鸡每月0.05个人工,每年净收入4.25美元。
最多可饲养5000只鸡和42头牛。
另外为了给牲畜提供足够的饲料,约翰决定下一年为每头牛种植至少一亩的玉米,而为每只鸡种植至少0.05亩的小麦。
——最多可以饲养42头牛和5000只鸡问题:现在,这个家族正经历了一次大丰收,拥有了20000美元可用于购买更多的牲畜(其他的一些现金将会用于将来的开支,包括农作物的种植;约翰、尤妮斯和父亲现在正在讨论每年应该种植多少农作物以及饲养多少头牛和多少只鸡。
他们讨论的目的是为了明年年底能够拥有最多的现金(牲畜的收入加上农作物的收入加上原有的货币资产加上年底所拥有的牲畜的价值减去明年40000美元的生活费)。
1.要如何分配有限的现金和劳动力使明年年底能够拥有最多的现金上面每年农作物的净值是在假设气候良好的条件下得出的。
如果气候不好的话,会严重影响农作物的收成。
他们最担心的自然灾害是旱、涝、早霜及干旱和早霜、涝灾和早霜一起来。
在这2.针对上面每种情况估计明年年底该家族拥有的货币资产。
如果同时有两种情况发生,该家族的货币资产会有何种变化?该家族应如何决定才能最有效的平衡气候良好条件下的好收成和气候不好条件下的坏收成。
3.基于这些数据,该家族决定作出如下的牲畜和种植决策。
LINDO软件求解线性规划的应用案例

问题3:若可以聘用临时工人以增加劳动时间,付给临时工人 的工资最多是每小时几元?
劳动时间的影子价格为2元,含义 是增加1小时劳动,利润增加2元。 所以,答案是:最多每小时2元
问题4:由于市场需求变化,每公斤A1的获利增加到30元,应 否改变生产计划?
X1的价值系数变化范围为(64,96) Z=30*3x1+16*4x2 =90x1+64x2
西安邮电大学 现代邮政学院
Xi'an post and telecommunications university modern post College
LINDO软件求解线性规划的应用案例
例题
一奶制品加工厂用牛奶生产A1、A2两种奶制品,1桶牛奶可 以在设备甲上用12小时加工成3公斤A1,或者在设备乙上用8小 时加工成4公斤A2。根据市场需求,生产的A1、A2能全部售出, 且每公斤A1获利24元,每公斤A2获利16元。现在加工厂每天能 得到50桶牛奶的供应,每天正式工人总的劳动时间为480小时, 并且设备甲每天至多能加工100公斤A1,设备乙的加工能力没有 限制。
(1)请为该厂制定一个生产计划,使每天获利最大。
(2)若用35元可以购买到1桶牛奶,应否作这项投资?
(3)若可以聘用临时工人以增加劳动时间,付给临时工人的工 资最多是每小时几元?
(4)由于市场需求变化,每公斤A1的获利增加到30元,应否改 变生产计划?
决策变量
设用X1桶牛奶生产A1,用X2桶牛奶生产A2
运 筹 学
劳动时间 加工能力
132xx1 1180x02 480
非负约束
x1 ,x2 0
问题1:请为该厂制定一个生产计划,使每天获利最大。
20桶牛奶生产A1,30桶牛奶生产 A2,利润3360元。
lindo软件求解管理领域中的各种问题实验总结

Lindo软件求解管理领域中的各种问题实验总结一、引言Lindo软件是一款经典的数学规划软件,广泛应用于管理领域中的各种问题的求解。
本文将以Lindo软件为工具,对管理领域中的各种问题进行实验,并总结实验结果和经验教训。
二、线性规划问题求解2.1 问题描述线性规划是管理领域中常见的一种问题求解方法,其目标是寻找一组决策变量的最优值,使得目标函数达到最大或最小值,同时满足一系列线性约束条件。
2.2 实验步骤1.定义决策变量:根据问题的需求和约束条件,定义相关的决策变量。
2.构建目标函数和约束条件:根据问题的目标和约束条件,构建数学模型。
3.输入模型:使用Lindo软件将模型输入到软件中进行求解。
4.分析结果:分析Lindo软件求解的结果,得出最优解和相应的决策变量取值。
5.可行性分析:对结果进行可行性分析,判断解的合理性和可行性。
2.3 实验总结•Lindo软件可以高效地求解线性规划问题,快速得出最优解。
•在构建模型时,需要确保目标函数和约束条件的准确性和合理性。
•对结果进行可行性分析时,需要结合实际情况进行合理判断。
三、整数规划问题求解3.1 问题描述整数规划是线性规划的一种扩展,其决策变量取值限定为整数。
在管理领域中,很多问题需要求解整数规划模型,例如生产调度问题、旅行商问题等。
3.2 实验步骤1.定义决策变量:根据问题的需求和约束条件,定义相关的决策变量,并确定变量的取值范围为整数。
2.构建目标函数和约束条件:根据问题的目标和约束条件,构建整数规划模型。
3.输入模型:使用Lindo软件将整数规划模型输入到软件中进行求解。
4.分析结果:分析Lindo软件求解的结果,得出最优解和相应的决策变量取值。
5.灵敏度分析:对结果进行灵敏度分析,了解目标函数系数和约束条件的变化对结果的影响。
3.3 实验总结•在求解整数规划问题时,需要确定决策变量的取值范围为整数,以确保结果的可行性和合理性。
•Lindo软件在求解整数规划问题时需要更多的计算资源和时间,但仍能得到较好的求解效果。
运筹学与最优化方法线性规划案例分析报告

案例:连续投资的优化问题一、题目:某企业在今后五年内考虑对下列项目投资,已知:项目A,从第一年到第四年每年年初需要投资,并于次年末收回本利115%。
项目B,第三年年初需要投资,到第五年末能收回本利125%,但规定最大投资额不超过40万元。
项目C,第二年年初需要投资,到第五年末能收回本利140%,但规定最大投资额不超过30万元。
项目D,五年内每年年初可购买公债,于当年末归还,并加利息6%。
该企业5年内可用于投资的资金总额为100万元,问它应如何确定给这些项目的每年投资使得到第五年末获得的投资本利总额为最大?二、建立上述问题的数学模型设X1A,X iB , X iC, X iD(i=1.2.3.4.5)为第i年初给项目A,B,C,D的投资额,它们都是待定的未知量。
由于项目D每年年初均可投资,年末收回本利,固每年的投资额应该等于手中拥有的资金额。
建立该问题的线性规划模型如下:Max Z=1.15X4A+1.40X2C+1.25X3B+1.06X5DX1A+X1D=1000000 (1)X2A+X2C+X2D=1.06X1D(2)X3A+X3B+X3D=1.15X1A+1.06X2D (3)s.t. X4A+X4D=1.15X2A+1.06X3D (4)X5D=1.15X3A+1.06X4D (5)X3B<=400000 (6)X2C<=300000 (7)X1A , X iB , X iC, X iD>=0 i=1,2,3,4,5经过整理后如下:Max Z=1.15X4A+1.40X2C+1.25X3B+1.06X5DX1A+X1D=1000000-1.06X1D+ X2A+X2C+X2D =0-1.15X1A-1.06X2D+ X3A+X3B+X3D=0s.t. -1.15X2A-1.06X3D +X4A+X4D=0-1.15X3A-1.06X4D+ X5D=0X3B<=400000X2C<=300000X1A , X iB , X iC, X iD>=0 i=1,2,3,4,5三、Excel求解过程以及相应的结果(1)在Excel中进行布局并输入相应的公式相应公式说明:其中目标函数单元格B16中公式为:=G3*E11+G4*D12+G5*C13+G6*F14 约束条件为投资额的限制以及每年资金分配部分:每年资金分配部分为原模型中约束(1)~(5):J11 =SUMPRODUCT(B11:B14,J3:J6);K11 =SUMPRODUCT(C11:C14,K3:K6);L11 =SUMPRODUCT(D11:D14,L3:L6);M11 =SUMPRODUCT(E11:E14,M3:M6);N11 =SUMPRODUCT(F11:F14,N3:N6);投资额约束:原模型中约束(6)~(7)D12<=P4;C13<=P5;(2)设置规划求解参数并进行求解如右图所示:另外单击选项-采用线性模型,假定非负(3)规划求解结果与分析实验数据分析:线性模型的优化的结果将显示在Excel的界面中,决策变量及目标函数的位置就会出现相应的优化结果值,目标函数的优化结果值是143.75。
管理运筹学-用LINDO、TORA求解整数规划

实验内容(包括实验具体内容、算法分析、源代码等等) : 1.用 lindo 求一般的解整数规划模型:
2
2.用 lindo 求 0-1 规划模型:
3
3.用 tora 求一般的解整数规划模型:
4
第一步:求出一个最优解
第二步,对 x1 进行分支 对于 x1 4 的问题 N20
5
对于 x1 5 的问题 N21
实 验 报 告
实验课程名称 运筹学 实验项目名称用 LINDO、TORA 求解整数规划 年 专 级 业
学 生 姓 名 学 号
实验时间:
年
月
日
学生所在学院: 姓 名 学
专业: 号
班级: 实验组 成 绩
实验时间 实验项目名称
指导教师 用 LINDO、TORA 求解整数规划
实验目的及要求: 1.掌握 lindo 整数规划模型的输入并求解。 2.用 tora 软件验证分支定界法。
无整数解! 3.用 tor意见:
签名:
年
月
日
8
实验(或算法)原理:
《运筹学》课本 p134-p138
实验硬件及软件平台: LINDO TORA PC
win xp
1
实验步骤: 1.用 lindo 求一般的解整数规划模型; 2.用 lindo 求 0-1 规划模型; 3.用 tora 求一般的解整数规划模型; 4.用 tora 求 0-1 规划模型.
第三步:将问题 N20 的 x 2 进行分支定界 对于 N20 问题加上 x2 2 的问题 N30
得到最优解: x1 4, x2 2, zmax 340 对于 N21 问题加上 x2 3 的问题 N31
6
没有整数解! 第四步:对 N21 的 x2 进行分支定界 对于 x2 1 的问题 N32
用LINDO、LINGO 解运筹学问题

用LINDO、LINGO 解运筹学问题一、 软件简介LINDO是一种专门用于求解数学规划问题的软件包。
由于LINDO执行速度很快、易于方便输入、求解和分析数学规划问题。
因此在数学、科研和工业界得到广泛应用。
LINDO主要用于解线性规划、非线性规划、二次规划和整数规划等问题。
也可以用于一些非线性和线性方程组的求解以及代数方程求根等。
LINDO中包含了一种建模语言和许多常用的数学函数(包括大量概论函数),可供使用者建立规划问题时调用。
一般用LINDO(Linear Interactive and Discrete Optimizer)解决线性规划(LP—Linear Programming)。
整数规划(IP—Integer Programming)问题。
其中LINDO 6 .1 学生版至多可求解多达300个变量和150个约束的规划问题。
其正式版(标准版)则可求解的变量和约束在1量级以上。
LINGO则用于求解非线性规划(NLP—NON—LINEAR PROGRAMMING)和二次规则(QP—QUARATIC PROGRAMING)其中LINGO 6.0学生版最多可版最多达300个变量和150个约束的规则问题,其标准版的求解能力亦再10^4量级以上。
虽然LINDO和LINGO不能直接求解目标规划问题,但用序贯式算法可分解成一个个LINDO和LINGO能解决的规划问题。
要学好用这两个软件最好的办法就是学习他们自带的HELP文件。
二、下面拟举数例以说明这两个软件的最基本用法。
(例子均选自张莹《运筹学基础》)例1.(选自《运筹学基础》P54.汽油混合问题,线性规划问题)一种汽油的特性可用两个指标描述:其点火性用“辛烷数”描述,其挥发性用“蒸汽压力”描述。
某炼油厂有四种标准汽油,设其标号分别为1,2,3,4,其特性及库存量列于下表1中,将上述标准汽油适量混合,可得两种飞机汽油,某标号为1,2,这两种飞机汽油的性能指标及产量需求列于表2中。
运筹学实验二灵敏度分析

实验概述:实验二、灵敏度分析(操作型)【实验目的及要求】1、进一步掌握管理运筹学、LINDO和LINGO软件的基本入门知识,学习使用管理运筹学、LINDO和LINGO软件对线性规划问题进行灵敏度分析。
2、熟练掌握用单纯形法求解线性规划问题。
【实验原理】单纯形法迭代原理及其基本步骤【实验环境】(使用的软件)管理运筹学软件、LINDO软件,信息中心6机房计算机实验内容:【实验方案设计】1、分别打开管理运筹学、LIND软件;2、在打开的软件中输入课本例题和习题数据,对线性规划问题进行灵敏度分析;3、运行实验并保存实验结果。
【实验过程】使用管理运筹学、LINDO软件分别对线性规划问题进行灵敏度分析。
1、使用管理运筹学软件对线性规划问题进行灵敏度分析:(1)打开管理运筹学软件,选择“线性规划”,单击“新建”菜单,输入P59-例题2.6.1的变量个数、约束条件个数并选择目标函数,点击“确定”。
在目标函数中输入价值系数,再输入变量的约束条件数据,然后选择变量的正、负、无。
选择“解决”得到线性规划结果,保存文件于指定文件夹。
(2)将例2.6.1中的右端向量b=(2 1)T变为b1=(-2 1)T,其他数据不变。
(3)在“线性规划”界面中,单击“新建”菜单,输入P77-习题20的变量个数、约束条件个数并选择目标函数,点击“确定”。
在目标函数中输入价值系数,再输入变量的约束条件数据,然后选择变量的正、负、无。
选择“解决”得到线性规划结果,保存文件于指定文件夹。
(4)将P77-习题20中的价值系数C1由1变为(-5/4);C1由1变为(-5/4),C3由1变为2;b由(5 3)T变为b1=(-2 1)T;b=(5 3)T变为b1=(2 3)T。
2、使用LINDU软件对线性规划问题进行灵敏度分析:(1)打开LINDU软件,在空白框中输入P79-习题B(1)的目标函数和约束条件,点击靶形工具,是否进行灵敏度分析选择“是”,得到线性规划及灵敏度分析结果,保存文件到LINDO文件夹。
管理运筹学lindo案例分析报告

管理运筹学lindo案例分析⑻Lindo的数据分析及习题用该命令产生当前模型的灵敏性分析报告:研究当目标函数的费用系数和约束右端项在什么围(此时假定其它系数不变)时,最优基保持不变。
灵敏性分析是在求解模型时作出的,因此在求解模型时灵敏性分析是激活状态,但是默认是不激活的。
为了激活灵敏性分析,运行LINGO|Options…,选择General Solver Tab , 在Dual Computations 列表框中,选择Prices and Ranges 选项。
灵敏性分析耗费相当多的求解时间,因此当速度很关键时,就没有必要激活它。
下面我们看一个简单的具体例子。
例5.1某家具公司制造书桌、餐桌和椅子,所用的资源有三种:木料、木工和漆工。
生产数据如下表所示:用DESKS TABLES和CHAIRS分别表示三种产品的生产量,建立LP模型。
max=60*desks+30*tables+20*chairs;8*desks+6*tables+chairs<=48;4*desks+2*tables+1.5*chairs<=20;2*desks+1.5*tables+.5*chairs<=8;tables<=5;求解这个模型,并激活灵敏性分析。
这时,查看报告窗口(Reports Window),可以看到如下结果。
Global optimal solution found at iteration:3Objective value:280.0000Variable Value Reduced CostDESKS 2.0000000.000000TABLES0.000000 5.000000CHAIRS8.0000000.000000Row Slack or Surplus Dual Price1280.0000 1.000000224.000000.00000030.00000010.0000040.00000010.000005 5.0000000.000000“ Global optimal solution found at iteration: 3 ”表示 3 次迭代后得到全局最优解。
管理运筹学实验报告

实验题目线性规划建模应用一、实验目的1、掌握线性规划问题的建模与解决。
2、学会使用LINDO软件,并在线性规划的求解中的应用。
二、实验内容假定某医院院周会上正在研究制定一昼夜护士值班安排计划。
在会议上,护理部主任提交了一份全院24小时各时段内需要在岗护士的数量报告,见下表。
如果按照每人每天两小班轮换,中间间隔休息时间8小时,这样安排岗位不但会造成人员冗余,同时护理人员上下班不是很方便。
由于医院护理工作的特殊性,又要求尽量保证护理人员工作的连续性,最终确定每名护士连续工作两个小班次,即24小时内一个大班8小时,即连续上满两个小班。
为了合理的压缩编制,医务部提出一个合理化建议:允许不同护士的大班之间可以合理相互重叠小班,即分成六组轮班开展全天的护理值班(每一个小班时段实际上由两个交替的大班的前段和后段共同承担)。
现在人力部门面临的问题是:如何合理安排岗位,才能满足值班的需要?正在会议结束之前,护理部又提出一个问题:目前全院在编的正式护士只有50人,工资定额为10元/小时;如果人力部门提供的定编超过50人,那么必须以15元/小时的薪酬外聘合同护士。
一但出现这种情况又如何安排上述班次?保卫处后来又补充到,最好在深夜2点的时候避免交班,这样又如何安排班次?三、实验分析报告根据各部门提出的意见,预备提出四种备选方案,各方案分析如下:1、没考虑定编上限和保卫处的建议令2:00-6:00-10:00,6:00-10:00-14:00,10:00-14:00-18:00,14:00-18:00-22:00,18:00-22:00-2:00,22:00-2:00-6:00时段的大班开始上班的人数分别为X1, X2, X3, X4, X5, X6. 由此可得的2:00-6:00,6:00-10:00,10:00-14:00,14:00-18:00,18:00-22:00,22:00-2:00各小班人数为X1+X6, X1+X2 , X2+X3, X3+X4, X4+X5, X5+X6.可得线性规划问题如下:目标函数为要求所需开始上班的人数最小,约束条件为由各大班开始上班人数所得的各小班人数必须大于规定的小班需要护士量.MinZ=X1+X2+X3+X4+X5+X6X1+X6>=10 ,X1+X2>=15X2+X3>=25 ,X3+X4>=20X4+X5>=18 ,X5+X6>=12X1~X6>=0,且X1~X6为整数在不考虑定编上限和保卫处的建议的情况下,在满足正常需要的情况下医院最少需要53名护士。
运筹学案例分析
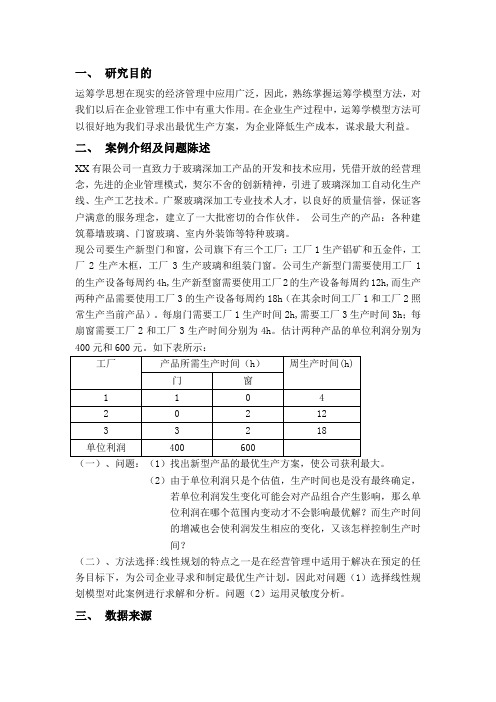
一、研究目的运筹学思想在现实的经济管理中应用广泛,因此,熟练掌握运筹学模型方法,对我们以后在企业管理工作中有重大作用。
在企业生产过程中,运筹学模型方法可以很好地为我们寻求出最优生产方案,为企业降低生产成本,谋求最大利益。
二、案例介绍及问题陈述XX有限公司一直致力于玻璃深加工产品的开发和技术应用,凭借开放的经营理念,先进的企业管理模式,契尔不舍的创新精神,引进了玻璃深加工自动化生产线、生产工艺技术。
广聚玻璃深加工专业技术人才,以良好的质量信誉,保证客户满意的服务理念,建立了一大批密切的合作伙伴。
公司生产的产品:各种建筑幕墙玻璃、门窗玻璃、室内外装饰等特种玻璃。
现公司要生产新型门和窗,公司旗下有三个工厂:工厂1生产铝矿和五金件,工厂2生产木框,工厂3生产玻璃和组装门窗。
公司生产新型门需要使用工厂1的生产设备每周约4h,生产新型窗需要使用工厂2的生产设备每周约12h,而生产两种产品需要使用工厂3的生产设备每周约18h(在其余时间工厂1和工厂2照常生产当前产品)。
每扇门需要工厂1生产时间2h,需要工厂3生产时间3h;每扇窗需要工厂2和工厂3生产时间分别为4h。
估计两种产品的单位利润分别为400元和600元。
如下表所示:(一)、问题:(1)找出新型产品的最优生产方案,使公司获利最大。
(2)由于单位利润只是个估值,生产时间也是没有最终确定,若单位利润发生变化可能会对产品组合产生影响,那么单位利润在哪个范围内变动才不会影响最优解?而生产时间的增减也会使利润发生相应的变化,又该怎样控制生产时间?(二)、方法选择:线性规划的特点之一是在经营管理中适用于解决在预定的任务目标下,为公司企业寻求和制定最优生产计划。
因此对问题(1)选择线性规划模型对此案例进行求解和分析。
问题(2)运用灵敏度分析。
三、数据来源公司介绍及生产产品来自网络,但是由于公司很多信息数据是保密的,无法获取,因此我根据所学知识及与实际进行了对比,其余数据是我个人进行设置,以达到研究的目的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
管理运筹学lindo案例分析(a)Lindo的数据分析及习题(a)灵敏性分析(Range,Ctrl+R)用该命令产生当前模型的灵敏性分析报告:研究当目标函数的费用系数和约束右端项在什么围(此时假定其它系数不变)时,最优基保持不变。
灵敏性分析是在求解模型时作出的,因此在求解模型时灵敏性分析是激活状态,但是默认是不激活的。
为了激活灵敏性分析,运行LINGO|Options…,选择General Solver Tab,在Dual Computations列表框中,选择Prices and Ranges选项。
灵敏性分析耗费相当多的求解时间,因此当速度很关键时,就没有必要激活它。
下面我们看一个简单的具体例子。
例5.1某家具公司制造书桌、餐桌和椅子,所用的资源有三种:木料、木工和漆工。
生产数据如下表所示:用DESKS、TABLES和CHAIRS分别表示三种产品的生产量,建立LP模型。
max=60*desks+30*tables+20*chairs;8*desks+6*tables+chairs<=48;4*desks+2*tables+1.5*chairs<=20;2*desks+1.5*tables+.5*chairs<=8;tables<=5;求解这个模型,并激活灵敏性分析。
这时,查看报告窗口(Reports Window),可以看到如下结果。
Global optimal solution found at iteration: 3Objective value: 280.0000Variable Value Reduced CostDESKS 2.000000 0.000000TABLES 0.000000 5.000000CHAIRS 8.000000 0.000000Row Slack or Surplus Dual Price1 280.0000 1.0000002 24.00000 0.0000003 0.000000 10.000004 0.000000 10.000005 5.000000 0.000000“Global optimal solution found at iteration: 3”表示3次迭代后得到全局最优解。
“Objective value:280.0000”表示最优目标值为280。
“Value”给出最优解中各变量的值:造2个书桌(desks), 0个餐桌(tables), 8个椅子(chairs)。
所以desks、chairs是基变量(非0),tables 是非基变量(0)。
“Slack or Surplus”给出松驰变量的值:第1行松驰变量=280(模型第一行表示目标函数,所以第二行对应第一个约束)第2行松驰变量=24第3行松驰变量=0第4行松驰变量=0第5行松驰变量=5“Reduced Cost”列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时, 目标函数的变化率。
其中基变量的reduced cost值应为0,对于非基变量X j, 相应的reduced cost 值表示当某个变量X j 增加一个单位时目标函数减少的量( max型问题)。
本例中:变量tables对应的reduced cost值为5,表示当非基变量tables的值从0变为1时(此时假定其他非基变量保持不变,但为了满足约束条件,基变量显然会发生变化),最优的目标函数值= 280 - 5 = 275。
“DUAL PRICE”(对偶价格)表示当对应约束有微小变动时, 目标函数的变化率。
输出结果中对应于每一个约束有一个对偶价格。
若其数值为p,表示对应约束中不等式右端项若增加1 个单位,目标函数将增加p个单位(max型问题)。
显然,如果在最优解处约束正好取等号(也就是“紧约束”,也称为有效约束或起作用约束),对偶价格值才可能不是0。
本例中:第3、4行是紧约束,对应的对偶价格值为10,表示当紧约束3) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 20变为3) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 21时,目标函数值= 280 +10 = 290。
对第4行也类似。
对于非紧约束(如本例中第2、5行是非紧约束),DUAL PRICE 的值为0, 表示对应约束中不等式右端项的微小扰动不影响目标函数。
有时, 通过分析DUAL PRICE, 也可对产生不可行问题的原因有所了解。
灵敏度分析的结果是Ranges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable AllowableVariable Coefficient Increase DecreaseDESKS 60.00000 0.0 0.0TABLES 30.00000 0.0 0.0CHAIRS 20.00000 0.0 0.0Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 48.00000 0.0 0.03 20.00000 0.0 0.04 8.000000 0.0 0.05 5.000000 0.0 0.0目标函数中DESKS变量原来的费用系数为60,允增加(Allowable Increase)=4、允减少(Allowable Decrease)=2,说明当它在[60-4,60+20] = [56,80]围变化时,最优基保持不变。
对TABLES、CHAIRS变量,可以类似解释。
由于此时约束没有变化(只是目标函数中某个费用系数发生变化),所以最优基保持不变的意思也就是最优解不变(当然,由于目标函数中费用系数发生了变化,所以最优值会变化)。
第2行约束中右端项(Right Hand Side,简写为RHS)原来为48,当它在[48-24,48+∞] = [24,∞]围变化时,最优基保持不变。
第3、4、5行可以类似解释。
不过由于此时约束发生变化,最优基即使不变,最优解、最优值也会发生变化。
灵敏性分析结果表示的是最优基保持不变的系数围。
由此,也可以进一步确定当目标函数的费用系数和约束右端项发生小的变化时,最优基和最优解、最优值如变化。
下面我们通过求解一个实际问题来进行说明。
例5.2一奶制品加工厂用牛奶生产A1,A2两种奶制品,1桶牛奶可以在甲车间用12小时加工成3公斤A1,或者在乙车间用8小时加工成4公斤A2。
根据市场需求,生产的A1,A2全部能售出,且每公斤A1获利24元,每公斤A2获利16元。
现在加工厂每天能得到50桶牛奶的供应,每天正式工人总的劳动时间480小时,并且甲车间每天至多能加工100公斤A1,乙车间的加工能力没有限制。
试为该厂制订一个生产计划,使每天获利最大,并进一步讨论以下3个附加问题:1)若用35元可以买到1桶牛奶,应否作这项投资?若投资,每天最多购买多少桶牛奶?2)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元?3)由于市场需求变化,每公斤A1的获利增加到30元,应否改变生产计划?模型代码如下:max=72*x1+64*x2;x1+x2<=50;12*x1+8*x2<=480;3*x1<=100;求解这个模型并做灵敏性分析,结果如下。
Global optimal solution found at iteration: 0Objective value: 3360.000Variable Value Reduced CostX1 20.00000 0.000000X2 30.00000 0.000000Row Slack or Surplus Dual Price1 3360.000 1.0000002 0.000000 48.000003 0.000000 2.0000004 40.00000 0.000000Ranges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable AllowableVariable Coefficient Increase DecreaseX1 72.00000 24.00000 8.000000X2 64.00000 8.000000 16.00000Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 50.00000 10.00000 6.6666673 480.0000 53.33333 80.000004 100.0000 INFINITY 40.00000结果告诉我们:这个线性规划的最优解为x1=20,x2=30,最优值为z=3360,即用20桶牛奶生产A1, 30桶牛奶生产A2,可获最大利润3360元。
输出中除了告诉我们问题的最优解和最优值以外,还有多对分析结果有用的信息,下面结合题目中提出的3个附加问题给予说明。
3个约束条件的右端不妨看作3种“资源”:原料、劳动时间、车间甲的加工能力。
输出中Slack or Surplus给出这3种资源在最优解下是否有剩余:原料、劳动时间的剩余均为零,车间甲尚余40(公斤)加工能力。
目标函数可以看作“效益”,成为紧约束的“资源”一旦增加,“效益”必然跟着增长。
输出中DUAL PRICES 给出这3种资源在最优解下“资源”增加1个单位时“效益”的增量:原料增加1个单位(1桶牛奶)时利润增长48(元),劳动时间增加1个单位(1小时)时利润增长2(元),而增加非紧约束车间甲的能力显然不会使利润增长。
这里,“效益”的增量可以看作“资源”的潜在价值,经济学上称为影子价格,即1桶牛奶的影子价格为48元,1小时劳动的影子价格为2元,车间甲的影子价格为零。
读者可以用直接求解的办法验证上面的结论,即将输入文件中原料约束milk)右端的50改为51,看看得到的最优值(利润)是否恰好增长48(元)。
用影子价格的概念很容易回答附加问题1):用35元可以买到1桶牛奶,低于1桶牛奶的影子价格48,当然应该作这项投资。
回答附加问题2):聘用临时工人以增加劳动时间,付给的工资低于劳动时间的影子价格才可以增加利润,所以工资最多是每小时2元。
目标函数的系数发生变化时(假定约束条件不变),最优解和最优值会改变吗?这个问题不能简单地回答。
上面输出给出了最优基不变条件下目标函数系数的允变化围:x1的系数为(72-8,72+24)=(64,96);x2的系数为(64-16,64+8)=(48,72)。
