第25届全国中学生物理竞赛复赛试卷(含答案)
第二十五届初中物理竞赛(大同中杯)复赛试题及答案

初中物理竞赛试题说明:1.本试卷共有五大题,答题时间为120分钟,试题满分为150分2.答案及解答过程均写在答卷纸上。
其中第一、第二大题只要写出答案,不写解答过程;第三至第五大题按题型要求写出完整的解答过程。
解答过程中可以使用计算器。
3.本试卷中常数g取10N/kg,水的比热容4.2×103J/kg·℃,水的密度1.0×103 kg/m3,冰的密度0.9×103 kg/m3,冰的熔化热3.33×105J/kg 。
一、选择题(以下每题只有一个选项符合题意,每小题4分,共32分)1.潜泳的人,从水下向上看,会看到一彩色镶边、内有图像的圆面,那么 ( )A.圆面内只能呈现水面上的部分景物B.彩色镶边是由于水面四周各种物体的颜色所引起的C.彩色镶边是由于不同颜色的光折射程度略有不同所致D.圆面中图像呈现的是水面外的景物,且看到景物的高度比实际景物要低2.磁带录放机可高速播放正常录制的声音,在高速播放时最有可能听不到的声音是正常录音时 ( )A.音调较低的声音B.音调较高的声音C.响度较小的声音D.响度较大的声音3.两个人共同搬一个50千克质量分布均匀的木箱上楼梯,如图所示。
木箱长1.25米,高0.5米;楼梯和地面成45o,而且木箱与楼梯平行。
如果两人手的用力方向都是竖直向上的,那么在下面的人对木箱施加的力与上面的人对木箱施加的力的比值是( )A.8/3 B.7/3 C.5/3 D.5/44.月球是地球的卫星,在地球上我们总是只能看到月球的一面,是因为月球绕地球公转的周期与自转的周期相等,请问登上月球的航天员在月球上看地球,将看到地球( )A.既有绕月球的转动,又有自转B.只有绕月球的转动,没有自转C.只有自转,没有绕月球的转动D.既没有绕月球的转动,也没有自转5.在如图所示的电路中,当电键S闭合后,电压表有示数,调节可变电阻R的阻值,电压表的示数增大了△U。
2023年全国中学生物理竞赛复赛试题及答案

全国中学生物理竞赛复赛试卷姓名()总分()本卷共九题,满分160 分.计算题的解答应写出必要的文字说明、方程式和重要的演算环节.只写出最后结果的不能得分.有数字计算的题.答案中必须明确写出数值和单位.填空题把答案填在题中的横线上,只要给出结果,不需写出求解的过程.一、(15 分)蛇形摆是一个用于演示单摆周期与摆长关系的实验仪器(见图).若干个摆球位于同一高度并等间距地排成一条直线,它们的悬挂点在不同的高度上,摆长依次减小.设重力加速度g = 9 . 80 m/ s2 ,1 .试设计一个包含十个单摆的蛇形摆(即求出每个摆的摆长),规定满足:( a )每个摆的摆长不小于0 . 450m ,不大于1.00m ; ( b )初始时将所有摆球由平衡点沿x 轴正方向移动相同的一个小位移xo ( xo <<0.45m ) ,然后同时释放,通过40s 后,所有的摆可以同时回到初始状态.2 .在上述情形中,从所有的摆球开始摆动起,到它们的速率初次所有为零所通过的时间为________________________________________.二、(20 分)距离我们为L 处有一恒星,其质量为M ,观测发现其位置呈周期性摆动,周期为T ,摆动范围的最大张角为△θ.假设该星体的周期性摆动是由于有一颗围绕它作圆周运动的行星引起的,试给出这颗行星的质量m所满足的方程.若L=10 光年,T =10 年,△θ= 3 毫角秒,M = Ms (Ms为太阳质量),则此行星的质量和它运动的轨道半径r各为多少?分别用太阳质量Ms 和国际单位AU (平均日地距离)作为单位,只保存一位有效数字.已知1 毫角秒=11000角秒,1角秒=13600度,1AU=1.5×108km,光速 c = 3.0×105km/s.三、(22 分)如图,一质量均匀分布的刚性螺旋环质量为m,半径为R ,螺距H =πR ,可绕竖直的对称轴OO′,无摩擦地转动,连接螺旋环与转轴的两支撑杆的质量可忽略不计.一质量也为m 的小球穿在螺旋环上并可沿螺旋环无摩擦地滑动,一方面扶住小球使其静止于螺旋环上的某一点A ,这时螺旋环也处在静止状态.然后放开小球,让小球沿螺旋环下滑,螺旋环便绕转轴O O′,转动.求当小球下滑到离其初始位置沿竖直方向的距离为h 时,螺旋环转动的角速度和小球对螺旋环作用力的大小.四、( 12 分)如图所示,一质量为m、电荷量为 q ( q > 0 )的粒子作角速度为ω、半径为 R 的匀速圆周运动.一长直细导线位于圆周所在的平面内,离圆心的距离为d ( d > R ) ,在导线上通有随时间变化的电流I, t= 0 时刻,粒子速度的方向与导线平行,离导线的距离为d+ R .若粒子做圆周运动的向心力等于电流 i ,的磁场对粒子的作用力,试求出电流 i 随时间的变化规律.不考虑变化的磁场产生的感生电场及重力的影响.长直导线电流产生的磁感应强度表达式中的比例系数 k 已知.五、(20分)如图所示,两个固定的均匀带电球面,所带电荷量分别为+Q和-Q (Q >0) ,半径分别为R和R/2,小球面与大球面内切于C点,两球面球心O和O’的连线MN沿竖直方在MN与两球面的交点B、0和C 处各开有足够小的孔因小孔损失的电荷量忽略不计,有一质量为m,带电荷为q(q>0的质点自MN线上离B点距离为R的A点竖直上抛。
第25届全国高中生物理竞赛答案(复赛)

第25届全国中学生物理竞赛复赛理论试题参考解答一、答案1. 14103.1⨯ 2. 31122kg m s -⋅⋅ 51.0610-⨯(答51.0510-⨯也给分)3.34T T 二、参考解答:1. 椭圆半长轴a 等于近地点和远地点之间距离的一半,亦即近地点与远地点矢径长度(皆指卫星到地心的距离)n r 与f r 的算术平均值,即有 ()()()()n f n f n f111222a r r H R H R H H R =+=+++=++⎡⎤⎣⎦ (1) 代入数据得43.194610a =⨯km (2) 椭圆半短轴b 等于近地点与远地点矢径长度的几何平均值,即有b = (3)代入数据得41.94210km b =⨯ (4) 椭圆的偏心率ab a e 22-=(5) 代入数据即得0.7941e = (6)2. 当卫星在16小时轨道上运行时,以n v 和f v 分别表示它在近地点和远地点的速度,根据能量守恒,卫星在近地点和远地点能量相等,有22n f n f1122GMm GMmm m r r -=-v v (7) 式中M 是地球质量,G 是万有引力常量. 因卫星在近地点和远地点的速度都与卫星到地心的连线垂直,根据角动量守恒,有n n f f m r m r =v v (8) 注意到g RGM=2(9)由(7)、(8)、(9)式可得n =v (10)n f n f r r ==v v (11) 当卫星沿16小时轨道运行时,根据题给的数据有n n r R H =+ f f r R H =+ 由(11)式并代入有关数据得f 1.198=v km/s (12)依题意,在远地点星载发动机点火,对卫星作短时间加速,加速度的方向与卫星速度方向相同,加速后长轴方向没有改变,故加速结束时,卫星的速度与新轨道的长轴垂直,卫星所在处将是新轨道的远地点.所以新轨道远地点高度4f f 5.093010H H '==⨯km ,但新轨道近地点高度2n6.0010H '=⨯km .由(11)式,可求得卫星在新轨道远地点处的速度为 f 1.230'=v km/s (13) 卫星动量的增加量等于卫星所受推力F 的冲量,设发动机点火时间为∆t ,有()f f m F t '-=∆v v (14) 由(12)、(13)、(14)式并代入有关数据得∆t=21.510s ⨯ (约2.5分) (15) 这比运行周期小得多.3. 当卫星沿椭圆轨道运行时,以r 表示它所在处矢径的大小,v 表示其速度的大小,θ表示矢径与速度的夹角,则卫星的角动量的大小sin 2L rm m θσ==v (16 ) 其中1sin 2r σθ=v (17)是卫星矢径在单位时间内扫过的面积,即卫星的面积速度.由于角动量是守恒的,故σ是恒量.利用远地点处的角动量,得f f 12r σ=v (18)又因为卫星运行一周扫过的椭圆的面积为πS ab = (19) 所以卫星沿轨道运动的周期σST =(20)由(18)、(19)、(20) 式得f f2πabT r =v (21) 代入有关数据得45.67810T =⨯s (约15小时46分) (22)注:本小题有多种解法.例如,由开普勒第三定律,绕地球运行的两亇卫星的周期T 与T 0之比的平方等于它们的轨道半长轴a 与a 0之比的立方,即2300T a T a ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭若0a 是卫星绕地球沿圆轨道运动的轨道半径,则有202002πGMmma a T ⎛⎫= ⎪⎝⎭得22203204π4πT a GM gR ==从而得T =代入有关数据便可求得(22)式.4. 在绕月圆形轨道上,根据万有引力定律和牛顿定律有2m m 2m m2π()GM m mr r T = (23) 这里m m r r H =+是卫星绕月轨道半径,m M 是月球质量. 由(23)式和(9)式,可得23mm 22m4πr M M gR T = (24) 代入有关数据得m0.0124M M= (25)三、参考解答:足球射到球门横梁上的情况如图所示(图所在的平面垂直于横梁轴线).图中B 表示横梁的横截面,O 1为横梁的轴线;11O O '为过横梁轴线并垂直于轴线的水平线;A 表示足球,O 2为其球心;O 点为足球与横梁的碰撞点,碰撞点O 的位置由直线O 1OO 2与水平线11O O '的夹角θ 表示.设足球射到横梁上时球心速度的大小为v 0,方向垂直于横梁沿水平方向,与横梁碰撞后球心速度的大小为v ,方向用它与水平方向的夹角ϕ表示(如图).以碰撞点O 为原点作直角坐标系Oxy ,y 轴与O 2OO 1重合.以α0表示碰前速度的方向与y 轴的夹角,以α表示碰后速度的方向与y 轴(负方向)的夹角,足球被横梁反弹后落在何处取决于反弹后的速度方向,即角α的大小.以F x 表示横梁作用于足球的力在x 方向的分量的大小,F y 表示横梁作用于足球的力在y 方向的分量的大小,∆t 表示横梁与足球相互作用的时间,m 表示足球的质量,有x 0x x F t m m ∆=-v v (1) y y 0y F t m m ∆=+v v (2) 式中0x v 、0y v 、x v 和y v 分别是碰前和碰后球心速度在坐标系Oxy 中的分量的大小.根据摩擦定律有x y F F μ= (3) 由(1)、(2)、(3)式得 0x xy 0yμ-=+v v v v (4)根据恢复系数的定义有y 0y e =v v (5) 因0x00ytan α=v v (6) xytan α=v v (7) 由(4)、(5)、(6)、(7)各式得⎪⎭⎫⎝⎛+-=e e 11tan 1tan 0μαα (8) 由图可知αθϕ+= (9)若足球被球门横梁反弹后落在球门线内,则应有90ϕ≥ (10) 在临界情况下,若足球被反弹后刚好落在球门线上,这时90ϕ= .由(9)式得()tan 90tan θα-=(11)因足球是沿水平方向射到横梁上的,故θα=0,有⎪⎭⎫⎝⎛+-=e e 11tan 1tan 1μθθ (12) 这就是足球反弹后落在球门线上时入射点位置θ所满足的方程.解(12)式得tan θ=13)代入有关数据得tan 1.6θ= (14) 即58θ=(15)现要求球落在球门线内,故要求58θ≥ (16)四、参考解答:1. 当阀门F 关闭时,设封闭在M 和B 中的氢气的摩尔数为n 1,当B 处的温度为T 时,压力表显示的压强为 p ,由理想气体状态方程,可知B 和M 中氢气的摩尔数分别为 RTpV n BB 1=(1) 0MM 1RT pV n = (2) 式中R 为普适气体恒量.因1M 1B 1n n n =+ (3) 解(1)、(2)、(3)式得 1MB B 011n R V T V p V T =- (4) 或1MB B 0p T n R V p V V T =- (5) (4)式表明,T 1与p1成线性关系,式中的系数与仪器结构有关.在理论上至少要测得两个已知温度下的压强,作T 1对p1的图线,就可求出系数. 由于题中己给出室温T 0时的压强p 0,故至少还要测定另一己知温度下的压强,才能定量确定T 与p 之间的关系式.2. 若蒸气压温度计测量上限温度v T 时有氢气液化,则当B 处的温度v T T ≤时,B 、M 和E 中气态氢的总摩尔数应小于充入氢气的摩尔数.由理想气体状态方程可知充入氢气的总摩尔数 ()0B M E 20p V V V n RT ++=(6)假定液态氢上方的气态氢仍可视为理想气体,则B 中气态氢的摩尔数为 v B2B vp V n RT =(7) 在(7)式中,已忽略了B 中液态氢所占的微小体积.由于蒸气压温度计的其它都分仍处在室温中,其中氢气的摩尔数为()νM E 2M 2Ep V V n n RT ++= (8)根据要求有2B 2M 2E 2n n n n ++≤ (9) 解(6)、(7)、(8)、(9)各式得 ()B vv 0v00v E M V T p p T p T p V V --≥+ (10)代入有关数据得M E B 18V V V +≥ (11)五、答案与评分标准:1.59.022122=-=+(3分) 2 (2分)2.如图(15分.代表电流的每一线段3分,其中线段端点的横坐标占1分,线段的长度占1分,线段的纵坐标占1分)六、参考解答:如果电流有衰减,意味着线圈有电阻,设其电阻为R ,则在一年时间t 内电流通过线圈因发热而损失的能量为Rt I E 2=∆ (1) 以ρ 表示铅的电阻率,S 表示铅丝的横截面积,l 表示铅丝的长度,则有 SlR ρ= (2) 电流是铅丝中导电电子定向运动形成的,设导电电子的平均速率为v ,根据电流的定义有 I S ne =v (3) 所谓在持续一年的时间内没有观测到电流的变化,并不等于电流一定没有变化,但这变化不会超过电流检测仪器的精度∆I ,即电流变化的上限为mA 0.1=∆I .由于导电电子的数密度n 是不变的,电流的变小是电子平均速率变小的结果,一年内平均速率由v 变为 v -∆v ,对应的电流变化I neS ∆=∆v (4) 导电电子平均速率的变小,使导电电子的平均动能减少,铅丝中所有导电电子减少的平均动能为()221122k E lSn m m ⎡⎤∆=--∆⎢⎥⎣⎦v v v l S n m ≈∆v v (5) 由于∆I<<I ,所以∆v <<v ,式中∆v 的平方项已被略去.由(3)式解出 v ,(4)式解出 ∆v ,代入(5)式得2k lmI IE ne S∆∆=(6) 铅丝中所有导电电子减少的平均动能就是一年内因发热而损失的能量,即E E k ∆=∆ (7) 由(1)、(2)、(6)、(7)式解得2Δm I ne Itρ= (8)式中7365243600s =3.1510s t =⨯⨯⨯ (9)在(8)式中代入有关数据得261.410Ωm ρ-=⨯⋅ (10)所以电阻率为0的结论在这一实验中只能认定到m Ω104.126⋅⨯≤-ρ (11)七、参考解答:按照斯特藩-玻尔兹曼定律,在单位时间内太阳表面单位面积向外发射的能量为 4s s W T σ=(1)其中σ为斯特藩-玻尔兹曼常量,T s 为太阳表面的绝对温度.若太阳的半径为R s ,则单位时间内整个太阳表面向外辐射的能量为2s s s 4πP R W= (2) 单位时间内通过以太阳为中心的任意一个球面的能量都是s P .设太阳到地球的距离为r se ,考虑到地球周围大气的吸收,地面附近半径为R 的透镜接收到的太阳辐射的能量为 ()2s 2seπ14πP P R r α=- (3)薄凸透镜将把这些能量会聚到置于其后焦面上的薄圆盘上,并被薄圆盘全部吸收.另一方面,因为薄圆盘也向外辐射能量.设圆盘的半径为D R ,温度为D T ,注意到簿圆盘有两亇表面,故圆盘在单位时间内辐射的能量为24D D D 2πP R T σ=⋅⋅ (4)显然,当D P P = (5) 即圆盘单位时间内接收到的能量与单位时间内辐射的能量相等时,圆盘达到稳定状态,其温度达到最高.由(1)、(2)、(3)、(4)、(5)各式得 ()1224s D s 22se D12R R T T r R α⎡⎤=-⎢⎥⎣⎦(6) 依题意,薄圆盘半径为太阳的像的半径s R '的2倍,即D 2s R R '=.由透镜成像公式知s sseR R f r '= (7) 于是有sD se2R R f r = (8) 把(8)式代入(6)式得()124D s 218R T T f α⎡⎤=-⎢⎥⎣⎦(9) 代入已知数据,注意到s s (273.15)T t =+K , T D =1.4×103K (10)即有3o D D 273.15 1.110C t T =-=⨯ (11) 八、参考解答:1.根据爱因斯坦质能关系,3H 和3He 的结合能差为()332n p H He B m m m m c ∆=--+ (1)代入数据,可得763.0=∆B MeV (2) 2.3He 的两个质子之间有库仑排斥能,而3H 没有.所以3H 与3He 的结合能差主要来自它们的库仑能差.依题意,质子的半径为N r ,则3He 核中两个质子间的库仑排斥能为2C N2e E k r = (3)若这个库仑能等于上述结合能差,C E B =∆,则有2N 2Δke r B= (4)代入数据,可得N 0.944r =fm (5)3.粗略地说,原子核中每个核子占据的空间体积是 3N (2)r .根据这个简单的模型,核子数为A 的原子核的体积近似为33N N (2)8V A r Ar == (6)另一方面,当A 较大时,有 343V R π=(7) 由(6)式和(7)式可得R 和A 的关系为1/31/31/3N 06πR r A r A ⎛⎫== ⎪⎝⎭(8)其中系数1/30N 6πr r ⎛⎫= ⎪⎝⎭(9)把(5)式代入(9)式得17.10=r fm (10) 由(8)式和(10)式可以算出Pb 208的半径Pb 6.93fm R =。
全国中学生物理竞赛复赛试卷及参考解答
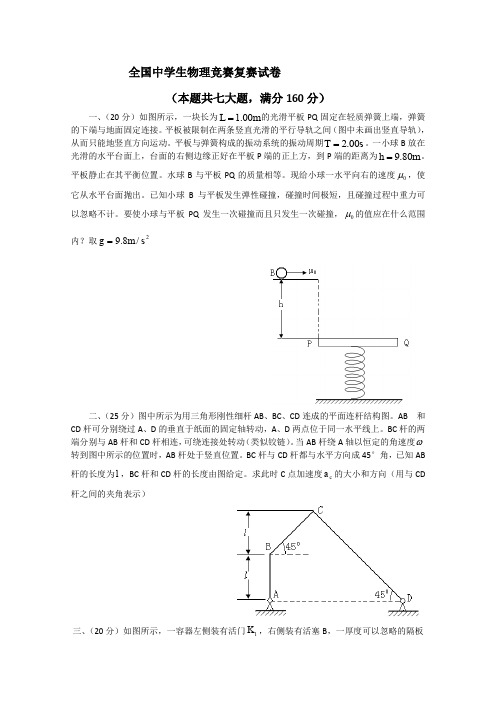
全国中学生物理竞赛复赛试卷(本题共七大题,满分160分)一、(20分)如图所示,一块长为m L 00.1=的光滑平板PQ 固定在轻质弹簧上端,弹簧的下端与地面固定连接。
平板被限制在两条竖直光滑的平行导轨之间(图中未画出竖直导轨),从而只能地竖直方向运动。
平板与弹簧构成的振动系统的振动周期s T 00.2=。
一小球B 放在光滑的水平台面上,台面的右侧边缘正好在平板P 端的正上方,到P 端的距离为m h 80.9=。
平板静止在其平衡位置。
水球B 与平板PQ 的质量相等。
现给小球一水平向右的速度0μ,使它从水平台面抛出。
已知小球B 与平板发生弹性碰撞,碰撞时间极短,且碰撞过程中重力可以忽略不计。
要使小球与平板PQ 发生一次碰撞而且只发生一次碰撞,0μ的值应在什么范围内?取2/8.9s m g =二、(25分)图中所示为用三角形刚性细杆AB 、BC 、CD 连成的平面连杆结构图。
AB 和CD 杆可分别绕过A 、D 的垂直于纸面的固定轴转动,A 、D 两点位于同一水平线上。
BC 杆的两端分别与AB 杆和CD 杆相连,可绕连接处转动(类似铰链)。
当AB 杆绕A 轴以恒定的角速度ω转到图中所示的位置时,AB 杆处于竖直位置。
BC 杆与CD 杆都与水平方向成45°角,已知AB 杆的长度为l ,BC 杆和CD 杆的长度由图给定。
求此时C 点加速度c a 的大小和方向(用与CD 杆之间的夹角表示)三、(20分)如图所示,一容器左侧装有活门1K ,右侧装有活塞B ,一厚度可以忽略的隔板M 将容器隔成a 、b 两室,M 上装有活门2K 。
容器、隔板、活塞及活门都是绝热的。
隔板和活塞可用销钉固定,拔掉销钉即可在容器内左右平移,移动时不受摩擦作用且不漏气。
整个容器置于压强为P 0、温度为T 0的大气中。
初始时将活塞B 用销钉固定在图示的位置,隔板M 固定在容器PQ 处,使a 、b 两室体积都等于V 0;1K 、2K 关闭。
第25届全国中学生物理竞赛决赛试题及详细解答

第25届全国中学生物理竞赛决赛试题2008年10月 北京★ 理论部分一、足球比赛,一攻方队员在图中所示的 A 处沿 Ax 方向传球,球在草地上以速度 v 匀速滚动,守方有一队员在图中 B 处,以 d 表示 A ,B 间的距离,以 θ 表示 AB 与Ax 之间的夹角,已知 θ <90° .设在球离开 A 处的同时,位于 B 处的守方队员开始沿一直线在匀速运动中去抢球,以 v p 表示他的速率.在不考虑场地边界限制的条件下,求解以下问题(要求用题中给出的有关参量间的关系式表示所求得的结果):1.求出守方队员可以抢到球的必要条件.2.如果攻方有一接球队员处在 Ax 线上等球,以 l r 表示他到 A 点的距离,求出球不被原在 B 处的守方队员抢断的条件.3.如果攻方有一接球队员处在 Ax 线上,以L 表示他离开 A 点的距离.在球离开 A 处的同时,他开始匀速跑动去接球,以 v r 表示其速率,求在这种情况下球不被原在 B 处的守方队员抢断的条件. 二、卫星的运动可由地面观测来确定;而知道了卫星的运动,又可以用它来确定空间飞行体或地面上物体的运动.这都涉及时间和空间坐标的测定.为简化分析和计算,不考虑地球的自转和公转,把它当做惯性系.1.先来考虑卫星运动的测定.设不考虑相对论效应.在卫星上装有发射电波的装置和高精度的原子钟.假设从卫星上每次发出的电波信号,都包含该信号发出的时刻这一信息. (I )地面观测系统(包含若干个观测站)可利用从电波中接收到的这一信息,并根据自己所处的已知位置和自己的时钟来确定卫星每一时刻的位置,从而测定卫星的运动.这种测量系统至少需要包含几个地面观测站?列出可以确定卫星位置的方程.(II )设有两个观测站 D 1 ,D 2 ,分别位于同一经线上北纬 θ 和南纬 θ(单位:(°))处.若它们同时收到时间 之前卫星发出的电波信号.(i )试求出发出电波时刻卫星距地面的最大高度 H ;(ii )当 D 1 ,D 2 处观测站位置的纬度有很小的误差△θ 时,试求H的误A差;(iii)如果上述的时间τ有很小的误差τ△,试求H 的误差.2.在第1(II)小题中,若θ= 45°,τ= 0.10 s .(i)试问卫星发出电波时刻卫星距地面最大高度H 是多少千米?(ii)若△θ= ±1.0′′ ,定出的H 有多大误差?(iii)若τ△= ±0.010 μs ,定出的H 有多大误差?假设地球为半径R = 6.38 × 103 km 的球体,光速c = 2.998 ×108 m / s ,地面处的重力加速度g = 9.81 m / s2.3.再来考虑根据参照卫星的运动来测定一个物体的运动.设不考虑相对论效应.假设从卫星持续发出的电波信号包含卫星运动状态的信息,即每个信号发出的时刻及该时刻卫星所处的位置.再假设被观测物体上有一台卫星信号接收器(设其上没有时钟),从而可获知这些信息.为了利用这种信息来确定物体的运动状态,即物体接收到卫星信号时物体当时所处的位置以及当时的时刻,一般来说物体至少需要同时接收到几个不同卫星发来的信号电波?列出确定当时物体的位置和该时刻的方程.4.根据狭义相对论,运动的钟比静止的钟慢.根据广义相对论,钟在引力场中变慢.现在来考虑在上述测量中相对论的这两种效应.已知天上卫星的钟与地面观测站的钟零点已经对准.假设卫星在离地面h = 2.00 ×104 km 的圆形轨道上运行,地球半径R、光速c 和地面重力加速度g 取第2小题中给的值.(I)根据狭义相对论,试估算地上的钟经过24h 后它的示数与卫星上的钟的示数差多少?设在处理这一问题时,可以把匀速直线运动中时钟走慢的公式用于匀速圆周运动.(II)根据广义相对论,钟在引力场中变慢的因子是(1-2φ/ c2 )1 / 2 ,φ是钟所在位置的引力势(即引力势能与受引力作用的物体质量之比;取无限远处引力势为零)的大小.试问地上的钟24 h 后,卫星上的钟的示数与地上的钟的示数差多少?三、致冷机是通过外界对机器做功,把从低温处吸取的热量连同外界对机器做功所得到的能量一起送到高温处的机器;它能使低温处的温度降低,高温处的温度升高.已知当致冷机工作在绝对温度为T1 的高温处和绝对温度为T2 的低温处之间时,若致冷机从低温处吸取的热量为Q,外界对致冷机做的功为W,则有QW≤T2T1-T2,式中“=”对应于理论上的理想情况.某致冷机在冬天作为热泵使用(即取暖空调机),在室外温度为-5.00℃的情况下,使某房间内的温度保持在20.00℃.由于室内温度高于室外,故将有热量从室内传递到室外.本题只考虑传导方式的传热,它服从以下的规律:设一块导热层,其厚度为 l ,面积为 S ,两侧温度差的大小为 T ,则单位时间内通过导热层由高温处传导到低温处的热量为H = k △T lS , 其中 k 称为热导率,取决于导热层材料的性质.1.假设该房间向外散热是由面向室外的面积 S = 5.00 m 2 、厚度 l = 2.00 mm 的玻璃板引起的.已知该玻璃的热导率 k = 0.75 W / ( m ? K ),电费为每度0.50元.试求在理想情况下该热泵工作12 h 需要多少电费?2.若将上述玻璃板换为“双层玻璃板”,两层玻璃的厚度均为2.00mm ,玻璃板之间夹有厚度 l 0 = 0.50 mm 的空气层,假设空气的热导率 k 0 = 0.025 W / ( m ? K ),电费仍为每度0.50元.若该热泵仍然工作12 h ,问这时的电费比上一问单层玻璃情形节省多少?四、如图1所示,器件由相互紧密接触的金属层( M )、薄绝缘层( I )和金属层( M )构成.按照经典物理的观点,在I 层绝缘性能理想的情况下,电子不可能从一个金属层穿过绝缘层到达另一个金属层.但是,按照量子物理的原理,在一定的条件下,这种渡越是可能的,习惯上将这一过程称为隧穿,它是电子具有波动性的结果.隧穿是单个电子的过程,是分立的事件,通过绝缘层转移的电荷量只能是电子电荷量-e ( e = 1.60 ×10-19 C )的整数倍,因此也称为单电子隧穿,MIM 器件亦称为隧穿结或单电子隧穿结.本题涉及对单电子隧穿过程控制的库仑阻塞原理,由于据此可望制成尺寸很小的单电子器件,这是目前研究得很多、有应用前景的领域.1.显示库仑阻塞原理的最简单的做法是将图1的器件看成一个电容为C 的电容器,如图2所示.电容器极板上的电荷来源于金属极板上导电电子云相对于正电荷背景的很小位移,可以连续变化.如前所述,以隧穿方式通过绝缘层的只能是分立的单电子电荷.如果隧穿过程会导致体系静电能量上升,则此过程不能发生,这种现象称为库仑阻塞.试求出发生库仑阻塞的条件即电容器极板间的电势差V AB = V A -V B 在什么范围内单电子隧穿过程被禁止.2.假定 V AB = 0.10 mV 是刚能发生隧穿的电压.试估算电容 C 的大小.3.将图1的器件与电压为 V 的恒压源相接时,通常采用图2所示的双结构器件来观图1察单电子隧穿,避免杂散电容的影响.中间的金属块层称为单电子岛.作为电极的左、右金属块层分别记为 S ,D .若已知岛中有净电荷量-ne ,其中净电子数 n 可为正、负整数或零,e 为电子电荷量的大小,两个 MIM 结的电容分别为 C S 和 C D .试证明双结结构器件的静电能中与岛上净电荷量相关的静电能(简称单电子岛的静电能)为U n = (-ne )22( C S +C D ). 4.在图3给出的具有源( S )、漏( D )电极双结结构的基础上,通过和岛连接的电容 C G 添加门电极( G )构成如图4给出的单电子三极管结构,门电极和岛间没有单电子隧穿事件发生.在V 较小且固定的情况下,通过门电压 V G 可控制岛中的净电子数 n .对于 V G 如何控制 n ,简单的模型是将 V G 的作用视为岛中附加了等效电荷q 0 = C G V G .这时,单电子岛的静电能可近似为 U n = (-ne+ q 0 )2 / 2C ∑,式中C ∑= C S +C D +C G .利用方格图(图5),考虑库仑阻塞效应,用粗线画出岛中净电子数从 n = 0开始,C G V G / e 由0增大到3的过程中,单电子岛的静电能 U n 随 C G V G 变化的图线(纵坐标表示 U n ,取 U n 的单位为 e 2 / 2C ∑;横坐标表示 C G V G ,取 C G V G 的单位为 e ).要求标出关键点的坐标,并把 n = 0 ,1 ,2 ,3时 C G V G / e 的变化范围填在表格中.(此小题只按作图及所填表格(表1)评分).表1图3 图4图5五、折射率n = 1.50 、半径为R的透明半圆柱体放在空气中,其垂直于柱体轴线的横截面如图所示,图中O 点为横截面与轴线的交点.光仅允许从半圆柱体的平面AB 进入,一束足够宽的平行单色光沿垂直于圆柱轴的方向以入射角i射至AB 整个平面上,其中有一部分入射光束能通过半圆柱体从圆柱面射出.这部分光束在入射到AB 面上时沿y 轴方向的长度用 d 表示.本题不考虑光线在透明圆柱体内经一次或多次反射后再射出柱体的复杂情形.1.当平行入射光的入射角i 在0°~90°变化时,试求 d 的最小值d min 和最大值d max.2.在如图所示的平面内,求出射光束与柱面相交的圆弧对O 点的张角与入射角i 的关系.并求在掠入射时上述圆弧的位置.六、根据广义相对论,光线在星体的引力场中会发生弯曲,在包含引力中心的平面内是一条在引力中心附近微弯的曲线.它距离引力中心最近的点称为光线的近星点.通过近星点与引力中心的直线是光线的对称轴.若在光线所在平面内选择引力中心为平面极坐标(r ,φ)的原点,选取光线的对称轴为坐标极轴,则光线方程(光子的轨迹方程)为r =GM / c2a cosφ+a2 ( 1 + sin2φ),G 是万有引力恒量,M 是星体质量,c 是光速,a 是绝对值远小于1的参数.现在假设离地球80.0光年处有一星体,在它与地球连线的中点处有一白矮星.如果经过该白矮星两侧的星光对地球上的观测者所张的视角是1.80×10-7rad ,试问此白矮星的质量是多少千克?已知G = 6.673 ×10-11 m3 / ( kg ?s2 )七、1.假设对氦原子基态采用玻尔模型,认为每个电子都在以氦核为中心的圆周上运动,半径相同,角动量均为:= h / 2π,其中h 是普朗克常量.(I)如果忽略电子间的相互作用,氦原子的一级电离能是多少电子伏?一级电离能是指把其中一个电子移到无限远所需要的能量.(II)实验测得的氦原子一级电离能是24.6 eV .若在上述玻尔模型的基础上来考虑电子之间的相互作用,进一步假设两个电子总处于通过氦核的一条直径的两端.试用此模型和z假设,求出电子运动轨道的半径 r 0 、基态能量 E 0 以及一级电离能 E + ,并与实验测得的氦原子一级电离能相比较.已知电子质量 m = 0.511 MeV / c 2 ,c 是光速,组合常量c =197.3 MeV ? fm = 197.3 eV ? nm ,ke 2 = 1.44 MeV ? fm = 1.44 eV ? nm ,k 是静电力常量,e 是基本电荷量.2.右图是某种粒子穿过云室留下的径迹的照片.径迹在纸面内,图的中间是一块与纸面垂直的铅板,外加恒定匀强磁场的方向垂直纸面向里.假设粒子电荷的大小是一个基本电荷量 e :e = 1.60×10-19 C ,铅板下部径迹的曲率半径 r d = 210 mm ,铅板上部径迹的曲率半径 r u = 76.0 mm ,铅板内的径迹与铅板法线成 θ = 15.0° ,铅板厚度 d = 6.00 mm ,磁感应强度 B = 1.00 T ,粒子质量 m = 9.11 ×10-31 kg = 0.511MeV / c 2.不考虑云室中气体对粒子的阻力.(I )写出粒子运动的方向和电荷的正负.(II )试问铅板在粒子穿过期间所受的力平均为多少牛?(III )假设射向铅板的不是一个粒子,而是从加速器引出的流量为 j = 5.00 ×1018 / s 的脉冲粒子束,一个脉冲持续时间为 =2.50 ns .试问铅板在此脉冲粒子束穿过期间所受的力平均为多少牛?铅板在此期间吸收的热量又是多少焦?第25届全国中学生物理竞赛决赛参考解答一、1 .解法一:设守方队员经过时间 t 在 Ax 上的 C点抢到球,用 l 表示 A 与C 之间的距离,l p 表示 B 与C 之间的距离(如图1所示),则有l = vt ,l p = v p t (1)和 l 2p = d 2 + l 2 -2dl cos θ. (2) 解式(1),(2)可得l = d 1-( v p / v )2 {cos θ ± [ ( v p v )2 -sin 2θ ]1 / 2 }. (3) 由式(3)可知,球被抢到的必要条件是该式有实数解,即v p ≥ v sin θ . (4)解法二:设 BA 与 BC 的夹角为 φ(如图1).按正弦定理有图1l p sinθ=lsinφ.利用式(1)有v pv= sinθsinφ.从sinφ≤1可得必要条件(4).2.用l min 表示守方队员能抢断球的地方与 A 点间的最小距离.由式(3)知l min =d1-( v p / v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }.(5)若攻方接球队员到 A 点的距离小于l min ,则他将先控制球而不被守方队员抢断.故球不被抢断的条件是l r <l min .(6)由(5),(6)两式得l r <d1-( v p / v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }(7)由式(7)可知,若位于Ax 轴上等球的攻方球员到A 点的距离l r 满足该式,则球不被原位于B 处的守方球员抢断.3.解法一:如果在位于B 处的守方球员到达Ax 上距离A 点l min 的C1 点之前,攻方接球队员能够到达距 A 点小于l min 处,球就不会被原位于 B 处的守方队员抢断(如图2所示).若L≤l min 就相当于第2小题.若L>l min ,设攻方接球员位于Ax 方向上某点 E 处,则他跑到C1 点所需时间t rm = ( L-l min ) / v r ;(8)守方队员到达C1 处所需时间t pm = ( d2+ l2min-2dl min cosθ)1 / 2/v p.球不被守方抢断的条件是t rm <t pm .(9)即L<v rv p( d2 + l2min-2dl min cosθ)1 / 2 + l min ,(10)式中l min 由式(5)给出.解法二:守方队员到达C1 点的时间和球到达该点的时间相同,因此有t pm = l min / v .从球不被守方队员抢断的条件(9)以及式(8)可得到图2L<( 1 + v r / v ) l min(11)式中l min也由式(5)给出.易证明式(11)与(10)相同.二、1.(I)选择一个坐标系来测定卫星的运动,就是测定每一时刻卫星的位置坐标x,y,z.设卫星在t时刻发出的信号电波到达第i 个地面站的时刻为t i.因为卫星信号电波以光速c 传播,于是可以写出(x-x i )2 + (y-y i )2 + (z -z i )2 = c2 (t-t i )2( i = 1 ,2 ,3 ),(1)式中x i,y i,z i是第i个地面站的位置坐标,可以预先测定,是已知的;t i 也可以由地面站的时钟来测定;t 由卫星信号电波给出,也是已知的.所以,方程(1)中有三个未知数x,y,z,要有三个互相独立的方程,也就是说,至少需要包含三个地面站,三个方程对应于式(1)中i = 1 ,2 ,3 的情况.(II)(i)如图所示,以地心O和两个观测站D1,D2的位置为顶点所构成的三角形是等腰三角形,腰长为R .根据题意,可知卫星发出信号电波时距离两个观测站的距离相等,都是L = cτ.(2)当卫星P 处于上述三角形所在的平面内时,距离地面的高度最大,即H.以θ表示D1,D2 所处的纬度,由余弦定理可知L2 = R2 + ( H + R )2 -2R ( H + R ) cosθ.(3)由(2),(3)两式得H = (cτ)2 -(R sinθ)2 -R ( 1-cosθ) .(4)式(4)也可据图直接写出.(ii)按题意,如果纬度有很小的误差△θ,则由式(3)可知,将引起H发生误差△H .这时有L2 = R2 + ( H +△H + R )2 -2R ( H +△H + R ) cos ( θ+△θ).(5)将式(5)展开,因△θ很小,从而△H也很小,可略去高次项,再与式(3)相减,得△H = -R ( R +H ) sin θ△θH + ( 1-cos θ ) R, (6) 其中 H 由(4)式给出.(iii )如果时间τ有τ△的误差,则 L 有误差△L = c τ△ . (7)由式(3)可知,这将引起 H 产生误差△H .这时有( L +△L )2 = R 2 + ( H +△H + R )2 -2R ( H +△H + R ) cos θ. (8)由式(7),(8)和(3),略去高次项,可得△H = c 2ττ△H + R ( 1-cos θ ), (9) 其中 H 由式(4)给出.2.(i )在式(4)中代入数据,算得 H = 2.8 ×104 km .(ii )在式(6)中代入数据,算得△H =25m .(iii )在式(9)中代入数据,算得△H = ±3.0 m .3.选择一个坐标系,设被测物体待定位置的坐标为 x ,y ,z ,待定时刻为 t ,第 i 个卫星在 t i 时刻的坐标为 x i ,y i ,z i .卫星信号电波以光速传播,可以写出(x -x i )2 + (y -y i )2 + (z -z i )2 = c 2 (t -t i )2 ( i = 1 ,2 ,3 ,4 ), (10) 由于方程(1)有四个未知数 t ,x ,y ,z ,需要四个独立方程才有确定的解,故需同时接收至少四个不同卫星的信号.确定当时物体的位置和该时刻所需要的是式(10)中 i = 1 ,2 ,3 ,4 所对应的四个独立方程.4.(I )由于卫星上钟的变慢因子为[ 1-( v / c )2] 1 / 2 ,地上的钟的示数 T 与卫星上的钟的示数 t 之差为T -t = T -1-(v c )2 T = [ 1-1-(v c)2 ] T , (11) 这里 v 是卫星相对地面的速度,可由下列方程定出:v 2r = GM r2 , (12) 其中 G 是万有引力常量,M 是地球质量,r 是轨道半径.式(11)给出v = GM r = g r R = g R + hR , 其中 R 是地球半径,h 是卫星离地面的高度,g = GM / R 2 是地面重力加速度;代入数值有 v = 3.89 km / s .于是 ( v / c )2 ≈1.68 ×10-10 ,这是很小的数.所以 [ 1- (v c )2 ]1 / 2 ≈1- 12 (v c)2 . 最后,可以算出 24 h 的时差T -t ≈12 (v c )2T = 12 gR 2c 2 ( R + h )T = 7.3 μs . (13) (II )卫星上的钟的示数t 与无限远惯性系中的钟的示数T 0之差t -T 0 = 1-2φ c 2 T 0-T 0 = ( 1-2φc 2 -1 )T 0 . (14) 卫星上的钟所处的重力势能的大小为φ= GM R + h = R 2R + h g . (15)所以 φ c 2 = gR 2c 2 ( R + h ); 代入数值有φ/ c 2 = 1.68 ×10-10 ,这是很小的数.式(14)近似为 t -T 0 ≈- φ c 2T 0 . (16) 类似地,地面上的钟的示数 T 与无限远惯性系的钟的示数之差T -T 0 = 1-2E φ c 2 T 0-T 0 = ( 1-2Eφ c 2 -1 )T 0 . (17) 地面上的钟所处的重力势能的大小为E φ= GM R =gR . (18) 所以 E φ c 2 = gR c 2 ;代入数值有E φ/ c 2 = 6.96 ×10-10 ,这是很小的数.与上面的情形类似,式(17)近似为 T -T 0 ≈- E φ c 2T 0 . (19) (16),(19)两式相减,即得卫星上的钟的示数与地面上的钟的示数之差t -T ≈- Eφφ- c 2 T 0 . (20)从式(19)中解出 T 0 ,并代入式(20)得t -T ≈- E φφ- c 2 / (1- Eφ c 2 )T ≈- Eφφ- c 2 T = gR c 2 h R + hT . (21) 注意,题目中的 24 h 是指地面的钟走过的时间 T .最后,算出 24 h 卫星上的钟的示数与地面上的钟的示数之差t -T = 46 μs . (22)三、1.依题意,为使室内温度保持不变,热泵向室内放热的功率应与房间向室外散热的功率相等.设热泵在室内放热的功率为q,需要消耗的电功率为P,则它从室外(低温处)吸收热量的功率为q-P.根据题意有q-PP≤T2T1-T2,(1)式中T1 为室内(高温处)的绝对温度,T2 为室外的绝对温度.由(1)式得P≥T1-T2T1q .(2)显然,为使电费最少,P 应取最小值;即式(2)中的“≥”号应取等号,对应于理想情况下P 最小.故最小电功率P min =T1-T2T1q .(3)又依题意,房间由玻璃板通过热传导方式向外散热,散热的功率H =k T1-T2l S .(4)要保持室内温度恒定,应有q = H .(5)由(3)~(5)三式得P min =k S ( T1-T2 )2lT1.(6)设热泵工作时间为t,每度电的电费为c,则热泵工作需花费的最少电费C min = P min tc .(7)注意到T1 = 20.00 K + 273.15 K = 293.15 K ,T2 = -5.00 K + 273.15 K = 268.15 K ,1度电= 1 kW ? h .由(6),(7)两式,并代入有关数据得C min = ( T1-T2 )2T1l Sktc = 23.99 元.(8)所以,在理想情况下,该热泵工作12 h 需约24元电费.2.设中间空气层内表面的温度为T i,外表面的温度为T0 ,则单位时间内通过内层玻璃、中间空气层和外层玻璃传导的热量分别为H1=k T1-T il S ,(9)H2=k0T i-T0l0S ,(10)H3=k T0-T2l S .(11)在稳定传热的情况下,有H1= H2= H3 .(12)由(9)~(12)四式得k T1-T il= k0T i-T0l0和T1-T i = T0-T2.(13)解式(13)得T i = l0k + lk0l0k + 2lk0T1 +lk0l0k + 2lk0T2.(14)将(14)式代入(9)式得H1 =kk0l0k + 2lk0( T1-T2 )S .(15)要保持室内温度恒定,应有q =H1.由式(3)知,在双层玻璃情况下热泵消耗的最小电功率P′min =kk0l0k + 2lk0( T1-T2 )2T1S .(16)在理想情况下,热泵工作时间t需要的电费C ′min = P′min tc ;(17)代入有关数据得C′min = 2.52 元.(18)所以,改用所选的双层玻璃板后,该热泵工作12 h 可以节约的电费△C min = C min -C′min = 21.47 元.(19)四、1.先假设由于隧穿效应,单电子能从电容器的极板A 隧穿到极板B.以Q 表示单电子隧穿前极板A 所带的电荷量,V AB 表示两极板间的电压(如题目中图3所示),则有V AB = Q / C .(1)这时电容器储能U= 12CV2AB.(2)当单电子隧穿到极板B后,极板A所带的电荷量为Q′ = Q + e ,(3)式中 e 为电子电荷量的大小.这时,电容器两极板间的电压和电容器分别储能为V′AB = Q + eC,U′ =12CV ′2AB.(4)若发生库仑阻塞,即隧穿过程被禁止,则要求U′-U >0 .(5)由(1)~(5)五式得V AB >- 12 eC. (6)再假设单电子能从电容器的极板 B 隧穿到极板 A .仍以 Q 表示单电子隧穿前极板A 所带的电荷量,V AB 表示两极板间的电压.当单电子从极板 B 隧穿到极板 A 时,极板A 所带的电荷量为 Q ′ = Q -e .经过类似的计算,可得单电子从极板 B 到极板 A 的隧穿不能发生的条件是V AB < 12 eC. (7)由(6),(7)两式知,当电压 V AB 在-e / 2C ~ e / 2C 之间时,单电子隧穿受到库仑阻塞,即库仑阻塞的条件为- 12 e C < V AB < 12 eC. (8) 2.依题意和式(8)可知,恰好能发生隧穿时有V AB = 12 e C= 0.10 mV . (9)由式(9),并代入有关数据得C = 8.0 ×10-16F . (10)3.设题目中图3中左边的 MIM 结的电容为 C S ,右边的 MIM 结的电容为 C D .双结结构体系如图a 所示,以 Q 1 ,Q 2 分别表示电容 C S ,C D 所带的电荷量.根据题意,中间单电子岛上的电荷量为-ne = Q 2-Q 1 . (11)体系的静电能为 C S 和 C D 中静电能的总和,即U = Q 212C S + Q 222C D; (12)电压V =Q 1C S + Q 2C D. (13) 由(11)~(13)三式解得U = 12CV 2 + (Q 2-Q 1)22 ( C S + C D ). (14)由于 V 为恒量,从式(13)可知体系的静电能中与岛上净电荷相关的静电能 U n = (-ne )2 / 2 (C S + C D ).图a4.U n 随 C G V G 变化的图线如图b ;C G V G / e 的变化范围如表2.表2五、1.在图1中,z 轴垂直于 AB 面.考察平行光束中两条光线分别在 AB 面上 C 与 C ′ 点以入射角 i 射入透明圆柱时的情况,r 为折射角,在圆柱体中两折射光线分别射达圆柱面的 D 和 D ′ ,对圆柱面其入射角分别为 i 2 与 i ′2 .在△OCD 中,O 点与入射点 C 的距离 y c 由正弦定理得y c sin i 2 = R sin ( 90° + r ) ,即 y c = sin i 2cos r R . (1) 同理在△OC ′D ′ 中,O 点与入射点 C ′ 的距离有y c ′sin i ′2 = R sin ( 90°-r ),即 y c ′ = sin i ′2cos r R . (2) 当改变入射角 i 时,折射角 r 与柱面上的入射角 i 2 与 i ′2 亦随之变化.在柱面上的入射角满足临界角i 20 = arcsin ( 1 / n ) ≈ 41.8° (3)时,发生全反射.将 i 2 = i ′2 = i 20 分别代入式(1),(2)得y o c = y o c ′ =sin i 20cos rR , (4) 即 d = 2y o c = 2sin i 20cos rR .(5)当 y c > y o c 和 y c ′ > y o c ′ 时,入射光线进入柱体,经过折射后射达柱面时的入射角大于临界角 i 20 ,由于发生全反射不能射出柱体.因折射角 r 随入射角 i 增大而增大.由式(4)图b图1知,当r = 0 ,即i = 0(垂直入射)时,d 取最小值d min = 2R sin i20 = 1.33 R .(6)当i →90°(掠入射)时,r→41.8°.将r =41.8°代入式(4)得d max = 1.79 R.(7)2.由图2可见,φ是Oz 轴与线段OD 的夹角,φ′是Oz 轴与线段OD′的夹角.发生全反射时,有φ= i20 + r ,(8)φ′= i20-r ,(9)和θ= φ+φ′=2i20≈83.6°.(10)由此可见,θ与i 无关,即θ独立于i .在掠入射时,i ≈90°,r =41.8°,由式(8),(9)两式得φ= 83.6°,φ′= 0°.(11)六、由于方程r =GM / c2a cosφ + a2 ( 1 + sin2φ)(1)是φ的偶函数,光线关于极轴对称.光线在坐标原点左侧的情形对应于a<0 ;光线在坐标原点右侧的情形对应a>0 .右图是a<0的情形,图中极轴为Ox,白矮星在原点O处.在式(1)中代入近星点坐标r = r m,φ= π,并注意到a 2| a | ,有a≈-GM / c2r m .(2)经过白矮星两侧的星光对观测者所张的视角θS 可以有不同的表达方式,相应的问题有不同的解法.解法一:若从白矮星到地球的距离为d,则可近似地写出θS≈2r m / d.(3)在式(1)中代入观测者的坐标r = d,φ= -π/ 2,有a2≈GM / 2c2d.(4)由(2)与(4)两式消去a,可以解出r m = 2GMd / c2 .(5)把式(5)代入式(3)得ySrxOEr mφ图2θS≈8GM / c2d;(6)即M≈θ2Sc2d / 8G ,(7)其中d = 3.787 ×1017 m ;代入数值就可算出M≈2.07 ×1030 kg .(8)解法二:光线射向无限远处的坐标可以写成r→∞,φ= -π2+θ2.(9)近似地取θS≈θ,把式(9)代入式(1),要求式(1)分母为零,并注意到θ1,有aθ / 2 + 2a2= 0 .所以θS≈θ=-4a = 8GM / c2d,(10)其中用到式(4),并注意到a<0 .式(10)与式(6)相同,从而也有式(8).解法三:星光对观测者所张的视角θS 应等于两条光线在观测者处切线的夹角,有sin θS2=△( r cosφ)△r= cosφ-r sinφ△φ△r.(11)由光线方程(1)算出△φ/△r ,有sin θS2= cosφ-r sinφGM / c2r2a sinφ= cosφ-GMc2ra;代入观测者的坐标r = d, = -π/ 2以及a的表达式(4),并注意到θS很小,就有θS≈2GMc2d2c2dGM=8GMc2d,与式(6)相同.所以,也得到了式(8).解法四:用式(2)把方程(1)改写成-r m = r cosφ-GMc2r m r[ (r cosφ )2 + 2 (r sinφ)2 ] ,即x = -r m + GMc2r m r( x2 +2y2 ) .(12)当y→-∞时,式(12)的渐近式为x = -r m-2GMc2r m y.这是直线方程,它在x轴上的截距为-r m ,斜率为1-2GM/ c2r m ≈1-tan ( θS / 2 )≈-1θS / 2 .于是有θS ≈4GM/ c2r m.r m用式(5)代入后,得到式(6),从而也有式(8).七、1.(I)氦原子中有两个电子,一级电离能E+ 是把其中一个电子移到无限远处所需要的能量满足He + E+ →He+ + e-.为了得到氦原子的一级电离能E+ ,需要求出一个电子电离以后氦离子体系的能量E*.这是一个电子围绕氦核运动的体系,下面给出两种解法.解法一:在力学方程2ke2r2= mv2 r中,r 是轨道半径,v 是电子速度.对基态,用玻尔量子化条件(角动量为)可以解出r0 =2/ 2ke2m .(1)于是氦离子能量E* = p22m-2ke2r0= -2k2e4m2,(2)其中p0 为基态电子动量的大小;代入数值得E* = -2( ke2 )2mc2(c )2≈-54.4 eV .(3)由于不计电子间的相互作用,氦原子基态的能量E0 是该值的2倍,即E0 =2E* ≈-108.8 eV .(4)氦离子能量E*与氦原子基态能量E0之差就是氦原子的一级电离能E+ =E*-E0 = -E*≈ 54.4 eV .(5)解法二:氦离子能量E*= p22m-2ke2r.把基态的角动量关系rp =代入,式(3)可以改写成E* =22mr2-2ke2r=22m(1r-2ke2m2)2-2k2e4m2.因基态的能量最小,式(4)等号右边的第一项为零,所以半径和能量r 0 =22ke2m,E*= -2k2e4m2分别与(1),(2)两式相同.(II)下面,同样给出求氦原子基态能量E0和半径r0的两种解法.解法一:利用力学方程mv2r= 2ke2r2-ke2( 2r )2=7ke24r2和基态量子化条件rmv =,可以解出半径r0 = 42/ 7ke2m,(6)于是氦原子基态能量E0 = 2 ( p22m-2ke2r0) +ke22r0= -49k2e4m162;(7)代入数值算得E0 = -49( ke2 )2mc216(c )2≈-83.4 eV ,(8)r0 = 4 (c)27ke2mc2≈ 0.0302 nm .所以,氦原子的一级电离能E+ =E*-E0≈ 29.0 eV .(9)这仍比实验测得的氦原子一级电离能24.6 eV 高出4.4 eV .解法二:氦原子能量E = 2 (p22m-2ke2r) +ke22r=2mr2-7ke22r可以化成E =2m(1r-7ke2m42)2-49k2e4m162.当上式等号右边第一项为零时,能量最小.由此可知,基态能量与半径E0 =-49k2e4m162,r0=427ke2m分别与(7),(6)两式相同.2.(I)粒子从下部射向并穿过铅板向上运动,其电荷为正.(II)如题图所示,粒子的运动速度v 与磁场方向垂直,洛伦兹力在纸面内;磁力不改变荷电粒子动量的大小,只改变其方向.若不考虑云室中气体对粒子的阻力,荷电粒子在恒定磁场作用下的运动轨迹就是曲率半径为一定值的圆弧;可以写出其运动方程qBv=|△p△t| =p△φ△t=pvr,(1)其中q 是粒子电荷,v 是粒子速度的大小,p 是粒子动量的大小,△φ是粒子在△t时间内转过的角度,r是轨迹曲率半径.于是有p= qBr .(2)按题意,q=e .用p d 和p u 分别表示粒子射入铅板和自铅板射出时动量的大小,并在式(1)中代入有关数据,可以算得p d = 63.0 MeV / c , p u = 22.8 MeV / c . (3)注意到当 pcmc 2 时应使用狭义相对论,从p =mv1-( v / c )2. (4)中可以得到v =c1 +( mc / p )2. (5)用 v d 和 v u 分别表示粒子进入和离开铅板时的速度大小.把式(2)以及 m = 0.511 MeV / c 2 代入式(3),可得v d ≈ c , v u ≈ c . (6)于是,粒子穿过铅板的平均速度 v = ( 1 / 2 ) ( v d + v u ) ≈c .用△t 表示粒子穿过铅板的时间,则有v cos θ△t = d . (7)再用△p du 表示粒子穿过铅板动量改变量的大小,铅板所受到的平均力的大小f =△p du △t = p d -p u d / (v cos θ )≈ ( p d -p u ) c cos θd ; (8)代入有关数值得f ≈1.04 ×10-9 N . (9)(III )一个粒子穿过铅板的时间△t =dv cos θ≈d c cos θ≈2.07 ×10-11 s = 0.0207 ns , (10)比粒子束流的脉冲周期 = 2.50 ns 小得多.铅板在此脉冲粒子束穿过期间所受的力的平均大小F ≈( p d -p u ) j ; (11)代入数据得F = 0.107 N . (12)运用式(4),可把粒子能量写成E = p 2c 2 + m 2c 4 , (13)所以粒子穿过铅板前后的能量分别为 E d =p 2d c 2 + m 2c 4= 63.0 MeV ,E u =p 2u c 2 + m 2c 4= 22.8 MeV . (14)。
2023年全国中学生物理竞赛复赛试题参考解答

全国中学生物理竞赛复赛试题参考解答、评分标准一、参考解答令 表达质子的质量, 和 分别表达质子的初速度和到达a 球球面处的速度, 表达元电荷, 由能量守恒可知2201122mv mv eU =+ (1)由于a 不动, 可取其球心 为原点, 由于质子所受的a 球对它的静电库仑力总是通过a 球的球心, 所以此力对原点的力矩始终为零, 质子对 点的角动量守恒。
所求 的最大值相应于质子到达a 球表面处时其速度方向刚好与该处球面相切(见复解20-1-1)。
以 表达 的最大值, 由角动量守恒有 max 0mv l mvR = (2)由式(1)、(2)可得20max 1/2eU l R mv =- (3) 代入数据, 可得max 22l R = (4) 若把质子换成电子, 则如图复解20-1-2所示, 此时式(1)中 改为 。
同理可求得 max 62l R =(5)评分标准: 本题15分。
式(1)、(2)各4分, 式(4)2分, 式(5)5分。
二、参考解答在温度为 时, 气柱中的空气的压强和体积分别为, (1)1C V lS = (2)当气柱中空气的温度升高时, 气柱两侧的水银将被缓慢压入A 管和B 管。
设温度升高届时 , 气柱右侧水银刚好所有压到B 管中, 使管中水银高度增大C BbS h S ∆= (3) 由此导致气柱中空气体积的增大量为C V bS '∆= (4)与此同时, 气柱左侧的水银也有一部分进入A 管, 进入A 管的水银使A 管中的水银高度也应增大 , 使两支管的压强平衡, 由此导致气柱空气体积增大量为A V hS ''∆=∆ (5)所以, 当温度为 时空气的体积和压强分别为21V V V V '''=+∆+∆ (6)21p p h =+∆ (7)由状态方程知112212p V p V T T = (8) 由以上各式, 代入数据可得2347.7T =K (9)此值小于题给的最终温度 K, 所以温度将继续升高。
第25届全国中学生物理竞赛决赛试题及详细解答

第25届全国中学生物理竞赛决赛试题★ 理论部分一、足球比赛,一攻方队员在图中所示的 A 处沿 Ax 方向传球,球在草地上以速度 v 匀速滚动,守方有一队员在图中 B 处,以 d 表示 A ,B 间的距离,以 θ 表示 AB 与Ax 之间的夹角,已知 θ <90° .设在球离开 A 处的同时,位于 B 处的守方队员开始沿一直线在匀速运动中去抢球,以 v p 表示他的速率.在不考虑场地边界限制的条件下,求解以下问题(要求用题中给出的有关参量间的关系式表示所求得的结果):1.求出守方队员可以抢到球的必要条件.2.如果攻方有一接球队员处在 Ax 线上等球,以 l r 表示他到 A 点的距离,求出球不被原在 B 处的守方队员抢断的条件.3.如果攻方有一接球队员处在 Ax 线上,以L 表示他离开 A 点的距离.在球离开 A 处的同时,他开始匀速跑动去接球,以 v r 表示其速率,求在这种情况下球不被原在 B 处的守方队员抢断的条件.二、卫星的运动可由地面观测来确定;而知道了卫星的运动,又可以用它来确定空间飞行体或地面上物体的运动.这都涉及时间和空间坐标的测定.为简化分析和计算,不考虑地球的自转和公转,把它当做惯性系.1.先来考虑卫星运动的测定.设不考虑相对论效应.在卫星上装有发射电波的装置和高精度的原子钟.假设从卫星上每次发出的电波信号,都包含该信号发出的时刻这一信息. (I )地面观测系统(包含若干个观测站)可利用从电波中接收到的这一信息,并根据自己所处的已知位置和自己的时钟来确定卫星每一时刻的位置,从而测定卫星的运动.这种测量系统至少需要包含几个地面观测站?列出可以确定卫星位置的方程.(II )设有两个观测站 D 1 ,D 2 ,分别位于同一经线上北纬 θ 和南纬 θ(单位:(°))处.若它们同时收到时间 之前卫星发出的电波信号.(i )试求出发出电波时刻卫星距地面的最大高度 H ;(ii )当 D 1 ,D 2 处观测站位置的纬度有很小的误差△θ 时,试求H的误A差;(iii)如果上述的时间τ有很小的误差τ△,试求H 的误差.2.在第1(II)小题中,若θ= 45°,τ= 0.10 s .(i)试问卫星发出电波时刻卫星距地面最大高度H 是多少千米?(ii)若△θ= ±1.0′′ ,定出的H 有多大误差?(iii)若τ△= ±0.010 μs ,定出的H 有多大误差?假设地球为半径R = 6.38 × 103 km 的球体,光速c = 2.998 ×108 m / s ,地面处的重力加速度g = 9.81 m / s2.3.再来考虑根据参照卫星的运动来测定一个物体的运动.设不考虑相对论效应.假设从卫星持续发出的电波信号包含卫星运动状态的信息,即每个信号发出的时刻及该时刻卫星所处的位置.再假设被观测物体上有一台卫星信号接收器(设其上没有时钟),从而可获知这些信息.为了利用这种信息来确定物体的运动状态,即物体接收到卫星信号时物体当时所处的位置以及当时的时刻,一般来说物体至少需要同时接收到几个不同卫星发来的信号电波?列出确定当时物体的位置和该时刻的方程.4.根据狭义相对论,运动的钟比静止的钟慢.根据广义相对论,钟在引力场中变慢.现在来考虑在上述测量中相对论的这两种效应.已知天上卫星的钟与地面观测站的钟零点已经对准.假设卫星在离地面h = 2.00 ×104 km 的圆形轨道上运行,地球半径R、光速c 和地面重力加速度g 取第2小题中给的值.(I)根据狭义相对论,试估算地上的钟经过24h 后它的示数与卫星上的钟的示数差多少?设在处理这一问题时,可以把匀速直线运动中时钟走慢的公式用于匀速圆周运动.(II)根据广义相对论,钟在引力场中变慢的因子是(1-2φ/ c2 )1 / 2 ,φ是钟所在位置的引力势(即引力势能与受引力作用的物体质量之比;取无限远处引力势为零)的大小.试问地上的钟24 h 后,卫星上的钟的示数与地上的钟的示数差多少?三、致冷机是通过外界对机器做功,把从低温处吸取的热量连同外界对机器做功所得到的能量一起送到高温处的机器;它能使低温处的温度降低,高温处的温度升高.已知当致冷机工作在绝对温度为T1 的高温处和绝对温度为T2 的低温处之间时,若致冷机从低温处吸取的热量为Q,外界对致冷机做的功为W,则有QW≤T2T1-T2,式中“=”对应于理论上的理想情况.某致冷机在冬天作为热泵使用(即取暖空调机),在室外温度为-5.00℃的情况下,使某房间内的温度保持在20.00℃.由于室内温度高于室外,故将有热量从室内传递到室外.本题只考虑传导方式的传热,它服从以下的规律:设一块导热层,其厚度为 l ,面积为 S ,两侧温度差的大小为 T ,则单位时间内通过导热层由高温处传导到低温处的热量为H = k △T lS , 其中 k 称为热导率,取决于导热层材料的性质.1.假设该房间向外散热是由面向室外的面积 S = 5.00 m 2 、厚度 l = 2.00 mm 的玻璃板引起的.已知该玻璃的热导率 k = 0.75 W / ( m • K ),电费为每度0.50元.试求在理想情况下该热泵工作12 h 需要多少电费?2.若将上述玻璃板换为“双层玻璃板”,两层玻璃的厚度均为2.00mm ,玻璃板之间夹有厚度 l 0 = 0.50 mm 的空气层,假设空气的热导率 k 0 = 0.025 W / ( m • K ),电费仍为每度0.50元.若该热泵仍然工作12 h ,问这时的电费比上一问单层玻璃情形节省多少?四、如图1所示,器件由相互紧密接触的金属层( M )、薄绝缘层( I )和金属层( M )构成.按照经典物理的观点,在I 层绝缘性能理想的情况下,电子不可能从一个金属层穿过绝缘层到达另一个金属层.但是,按照量子物理的原理,在一定的条件下,这种渡越是可能的,习惯上将这一过程称为隧穿,它是电子具有波动性的结果.隧穿是单个电子的过程,是分立的事件,通过绝缘层转移的电荷量只能是电子电荷量-e ( e = 1.60 ×10-19 C )的整数倍,因此也称为单电子隧穿,MIM 器件亦称为隧穿结或单电子隧穿结.本题涉及对单电子隧穿过程控制的库仑阻塞原理,由于据此可望制成尺寸很小的单电子器件,这是目前研究得很多、有应用前景的领域.1.显示库仑阻塞原理的最简单的做法是将图1的器件看成一个电容为C 的电容器,如图2所示.电容器极板上的电荷来源于金属极板上导电电子云相对于正电荷背景的很小位移,可以连续变化.如前所述,以隧穿方式通过绝缘层的只能是分立的单电子电荷.如果隧穿过程会导致体系静电能量上升,则此过程不能发生,这种现象称为库仑阻塞.试求出发生库仑阻塞的条件即电容器极板间的电势差V AB = V A -V B 在什么范围内单电子隧穿过程被禁止.图12.假定 V AB = 0.10 mV 是刚能发生隧穿的电压.试估算电容 C 的大小.3.将图1的器件与电压为 V 的恒压源相接时,通常采用图2所示的双结构器件来观察单电子隧穿,避免杂散电容的影响.中间的金属块层称为单电子岛.作为电极的左、右金属块层分别记为 S ,D .若已知岛中有净电荷量-ne ,其中净电子数 n 可为正、负整数或零,e 为电子电荷量的大小,两个 MIM 结的电容分别为 C S 和 C D .试证明双结结构器件的静电能中与岛上净电荷量相关的静电能(简称单电子岛的静电能)为U n = (-ne )22( C S +C D ). 4.在图3给出的具有源( S )、漏( D )电极双结结构的基础上,通过和岛连接的电容 C G 添加门电极( G )构成如图4给出的单电子三极管结构,门电极和岛间没有单电子隧穿事件发生.在 V 较小且固定的情况下,通过门电压 V G 可控制岛中的净电子数 n .对于 V G 如何控制 n ,简单的模型是将 V G 的作用视为岛中附加了等效电荷 q 0 = C G V G .这时,单电子岛的静电能可近似为 U n = (-ne + q 0 )2 / 2C∑,式中C ∑= C S +C D +C G .利用方格图(图5),考虑库仑阻塞效应,用粗线画出岛中净电子数从 n = 0开始,C G V G / e 由0增大到3的过程中,单电子岛的静电能U n 随 C G V G 变化的图线(纵坐标表示 U n ,取 U n 的单位为e 2 / 2C ∑;横坐标表示C G V G ,取 C G V G 的单位为e ).要求标出关键点的坐标,并把 n = 0 ,1 ,2 ,3时 C G V G / e 的变化范围填在表格中.(此小题只按作图及所填表格(表1)评分).图3 图 4图5 U n ( e 2 / 2C ∑) C G V G e表1五、折射率n = 1.50 、半径为R的透明半圆柱体放在空气中,其垂直于柱体轴线的横截面如图所示,图中O 点为横截面与轴线的交点.光仅允许从半圆柱体的平面AB 进入,一束足够宽的平行单色光沿垂直于圆柱轴的方向以入射角i射至AB 整个平面上,其中有一部分入射光束能通过半圆柱体从圆柱面射出.这部分光束在入射到AB 面上时沿y 轴方向的长度用 d 表示.本题不考虑光线在透明圆柱体内经一次或多次反射后再射出柱体的复杂情形.1.当平行入射光的入射角i 在0°~90°变化时,试求 d 的最小值d min 和最大值d max.2.在如图所示的平面内,求出射光束与柱面相交的圆弧对O 点的张角与入射角i 的关系.并求在掠入射时上述圆弧的位置.六、根据广义相对论,光线在星体的引力场中会发生弯曲,在包含引力中心的平面内是一条在引力中心附近微弯的曲线.它距离引力中心最近的点称为光线的近星点.通过近星点与引力中心的直线是光线的对称轴.若在光线所在平面内选择引力中心为平面极坐标(r ,φ)的原点,选取光线的对称轴为坐标极轴,则光线方程(光子的轨迹方程)为r =GM / c2a cosφ+a2 ( 1 + sin2φ),G 是万有引力恒量,M 是星体质量,c 是光速,a 是绝对值远小于1的参数.现在假设离地球80.0光年处有一星体,在它与地球连线的中点处有一白矮星.如果经过该白矮星两侧的星光对地球上的观测者所张的视角是1.80×10-7rad ,试问此白矮星的质量是多少千克?已知G = 6.673 ×10-11 m3 / ( kg •s2 )七、z1.假设对氦原子基态采用玻尔模型,认为每个电子都在以氦核为中心的圆周上运动,半径相同,角动量均为:= h / 2π,其中h 是普朗克常量.(I)如果忽略电子间的相互作用,氦原子的一级电离能是多少电子伏?一级电离能是指把其中一个电子移到无限远所需要的能量.(II)实验测得的氦原子一级电离能是24.6 eV .若在上述玻尔模型的基础上来考虑电子之间的相互作用,进一步假设两个电子总处于通过氦核的一条直径的两端.试用此模型和假设,求出电子运动轨道的半径r0、基态能量E0以及一级电离能E+,并与实验测得的氦原子一级电离能相比较.已知电子质量m = 0.511 MeV / c2,c是光速,组合常量c =197.3 MeV • fm = 197.3 eV • nm ,ke2 = 1.44 MeV • fm = 1.44 eV • nm ,k是静电力常量,e 是基本电荷量.2.右图是某种粒子穿过云室留下的径迹的照片.径迹在纸面内,图的中间是一块与纸面垂直的铅板,外加恒定匀强磁场的方向垂直纸面向里.假设粒子电荷的大小是一个基本电荷量e:e = 1.60×10-19 C ,铅板下部径迹的曲率半径r d= 210 mm ,铅板上部径迹的曲率半径r u= 76.0 mm ,铅板内的径迹与铅板法线成θ= 15.0°,铅板厚度d = 6.00 mm ,磁感应强度B = 1.00 T ,粒子质量m = 9.11 ×10-31 kg = 0.511MeV / c2.不考虑云室中气体对粒子的阻力.(I)写出粒子运动的方向和电荷的正负.(II)试问铅板在粒子穿过期间所受的力平均为多少牛?(III)假设射向铅板的不是一个粒子,而是从加速器引出的流量为j = 5.00 ×1018 / s 的脉冲粒子束,一个脉冲持续时间为 =2.50 ns .试问铅板在此脉冲粒子束穿过期间所受的力平均为多少牛?铅板在此期间吸收的热量又是多少焦?第25届全国中学生物理竞赛决赛参考解答一、1 .解法一:设守方队员经过时间 t 在 Ax 上的 C点抢到球,用 l 表示 A 与C 之间的距离,l p 表示 B 与C 之间的距离(如图1所示),则有l = vt ,l p = v p t (1)和 l 2p = d 2 + l 2 -2dl cos θ. (2) 解式(1),(2)可得l = d 1-( v p / v )2 {cos θ ± [ ( v p v )2 -sin 2θ ]1 / 2 }. (3) 由式(3)可知,球被抢到的必要条件是该式有实数解,即v p ≥ v sin θ . (4)解法二:设 BA 与 BC 的夹角为 φ(如图1).按正弦定理有l p sin θ = l sin φ. 利用式(1)有v p v = sin θsin φ. 从 sin φ ≤1可得必要条件(4).2.用 l min 表示守方队员能抢断球的地方与 A 点间的最小距离.由式(3)知l min = d 1-( v p / v )2 {cos θ ± [ ( v p v )2 -sin 2θ ]1 / 2 }. (5) 若攻方接球队员到 A 点的距离小于 l min ,则他将先控制球而不被守方队员抢断.故球不被抢断的条件是l r < l min . (6)由(5),(6)两式得l r <d 1-( v p / v )2 {cos θ ± [ ( v p v )2 -sin 2θ ]1 / 2 } (7) 由式(7)可知,若位于 Ax 轴上等球的攻方球员到 A 点的距离 l r 满足该式,则球不被原位于 B 处的守方球员抢断.3.解法一:如果在位于 B 处的守方球员到达 Ax 上距离 A 点 l min 的 C 1 点之前,攻方接球队员能够到达距 A 点小于 l min 处,球就不会被原位于 B 处的守方队员抢断(如图2所示).若 L ≤l min 就相当于第2小题.若 L >l min ,设攻方接球员位于 Ax 方向上某点 E 处,则他跑到 C 1 点所需时间图1t rm = ( L -l min ) / v r ; (8)守方队员到达 C 1 处所需时间 t pm = ( d 2 + l 2min-2dl min cos θ )1 / 2 / v p .球不被守方抢断的条件是 t rm < t pm . (9)即 L < v r v p( d 2 + l 2min -2dl min cos θ )1 / 2 + l min , (10) 式中 l min 由式(5)给出.解法二:守方队员到达 C 1 点的时间和球到达该点的时间相同,因此有t pm = l min / v .从球不被守方队员抢断的条件(9)以及式(8)可得到L < ( 1 + v r / v ) l min (11)式中l min 也由式(5)给出.易证明式(11)与(10)相同.二、1.(I )选择一个坐标系来测定卫星的运动,就是测定每一时刻卫星的位置坐标x ,y ,z .设卫星在t 时刻发出的信号电波到达第 i 个地面站的时刻为t i .因为卫星信号电波以光速 c 传播,于是可以写出(x -x i )2 + (y -y i )2 + (z -z i )2 = c 2 (t -t i )2 ( i = 1 ,2 ,3 ), (1)式中 x i ,y i ,z i 是第i 个地面站的位置坐标,可以预先测定,是已知的;t i 也可以由地面站的时钟来测定;t 由卫星信号电波给出,也是已知的.所以,方程(1)中有三个未知数 x ,y ,z ,要有三个互相独立的方程,也就是说,至少需要包含三个地面站,三个方程对应于式(1)中 i = 1 ,2 ,3 的情况.(II )(i )如图所示,以地心 O和两个观测站 D 1 ,D 2 的位置为顶点所构成的三角形是等腰三角形,腰长为 R .根据题意,可知卫星发出信号电波时距离两个观测站的距离相等,都是L = c . (2)当卫星 P 处于上述三角形所在的平面内时,距离地面的高度最大,即 H .以 θ 表示图2D 1 ,D 2 所处的纬度,由余弦定理可知L 2 = R 2 + ( H + R )2 -2R ( H + R ) cos θ . (3)由(2),(3)两式得H = (c τ)2 -(R sin θ )2 -R ( 1-cos θ ) . (4)式(4)也可据图直接写出.(ii )按题意,如果纬度有很小的误差△θ ,则由式(3)可知,将引起H 发生误差△H .这时有L 2 = R 2 + ( H +△H + R )2 -2R ( H +△H + R ) cos ( θ +△θ ) . (5)将式(5)展开,因△θ很小,从而△H 也很小,可略去高次项,再与式(3)相减,得△H = -R ( R +H ) sin θ△θH + ( 1-cos θ ) R, (6) 其中 H 由(4)式给出.(iii )如果时间τ有τ△的误差,则 L 有误差△L = c τ△ . (7)由式(3)可知,这将引起 H 产生误差△H .这时有( L +△L )2 = R 2 + ( H +△H + R )2 -2R ( H +△H + R ) cos θ. (8)由式(7),(8)和(3),略去高次项,可得△H = c 2ττ△H + R ( 1-cos θ ), (9) 其中 H 由式(4)给出.2.(i )在式(4)中代入数据,算得 H = 2.8 ×104 km .(ii )在式(6)中代入数据,算得△H =25m .(iii )在式(9)中代入数据,算得△H = ±3.0 m .3.选择一个坐标系,设被测物体待定位置的坐标为 x ,y ,z ,待定时刻为 t ,第 i 个卫星在 t i 时刻的坐标为 x i ,y i ,z i .卫星信号电波以光速传播,可以写出(x -x i )2 + (y -y i )2 + (z -z i )2 = c 2 (t -t i )2 ( i = 1 ,2 ,3 ,4 ), (10) 由于方程(1)有四个未知数 t ,x ,y ,z ,需要四个独立方程才有确定的解,故需同时接收至少四个不同卫星的信号.确定当时物体的位置和该时刻所需要的是式(10)中 i = 1 ,2 ,3 ,4 所对应的四个独立方程.4.(I )由于卫星上钟的变慢因子为[ 1-( v / c )2] 1 / 2 ,地上的钟的示数 T 与卫星上的钟的示数 t 之差为T -t = T -1-(v c )2 T = [ 1-1-(v c)2 ] T , (11) 这里 v 是卫星相对地面的速度,可由下列方程定出:v 2r = GM r2 , (12) 其中 G 是万有引力常量,M 是地球质量,r 是轨道半径.式(11)给出v = GM r = g r R = g R + hR , 其中 R 是地球半径,h 是卫星离地面的高度,g = GM / R 2 是地面重力加速度;代入数值有 v = 3.89 km / s .于是 ( v / c )2 ≈1.68 ×10-10 ,这是很小的数.所以 [ 1- (v c )2 ]1 / 2 ≈1- 12 (v c)2 . 最后,可以算出 24 h 的时差T -t ≈12 (v c )2T = 12 gR 2c 2 ( R + h )T = 7.3 μs . (13) (II )卫星上的钟的示数t 与无限远惯性系中的钟的示数T 0之差t -T 0 = 1-2φ c 2 T 0-T 0 = ( 1-2φ c 2 -1 )T 0 . (14)卫星上的钟所处的重力势能的大小为φ= GM R + h = R 2R + h g . (15)所以 φ c 2 = gR 2c 2 ( R + h ); 代入数值有φ/ c 2 = 1.68 ×10-10 ,这是很小的数.式(14)近似为t -T 0 ≈- φ c 2T 0 . (16) 类似地,地面上的钟的示数 T 与无限远惯性系的钟的示数之差T -T 0 = 1-2E φ c 2 T 0-T 0 = ( 1-2Eφ c 2 -1 )T 0 . (17) 地面上的钟所处的重力势能的大小为E φ= GM R =gR . (18) 所以 E φ c 2 = gR c 2 ;代入数值有E φ/ c 2 = 6.96 ×10-10 ,这是很小的数.与上面的情形类似,式(17)近似为T-T 0 ≈- Eφ c 2T 0 . (19)(16),(19)两式相减,即得卫星上的钟的示数与地面上的钟的示数之差t -T ≈-Eφφ- c 2T 0 . (20)从式(19)中解出 T 0 ,并代入式(20)得t-T ≈-E φφ- c 2/ (1-Eφ c 2)T ≈-Eφφ- c 2T =gR c 2 hR + hT . (21) 注意,题目中的 24 h 是指地面的钟走过的时间 T .最后,算出 24 h 卫星上的钟的示数与地面上的钟的示数之差t -T = 46 μs . (22)三、1.依题意,为使室内温度保持不变,热泵向室内放热的功率应与房间向室外散热的功率相等.设热泵在室内放热的功率为 q ,需要消耗的电功率为 P ,则它从室外(低温处)吸收热量的功率为 q -P .根据题意有q -P P ≤ T 2T 1-T 2, (1) 式中 T 1 为室内(高温处)的绝对温度,T 2 为室外的绝对温度.由(1)式得P ≥ T 1-T 2T 1q . (2)显然,为使电费最少,P 应取最小值;即式(2)中的“≥”号应取等号,对应于理想情况下 P 最小.故最小电功率P min =T 1-T 2T 1q . (3) 又依题意,房间由玻璃板通过热传导方式向外散热,散热的功率H = kT 1-T 2lS . (4) 要保持室内温度恒定,应有q = H . (5)由(3)~(5)三式得Pmin = k S ( T 1-T 2 )2lT 1. (6)设热泵工作时间为 t ,每度电的电费为 c ,则热泵工作需花费的最少电费C min = P min tc . (7)注意到 T 1 = 20.00 K + 273.15 K = 293.15 K ,T 2 = -5.00 K + 273.15 K = 268.15 K ,1度电= 1 kW • h .由(6),(7)两式,并代入有关数据得C min = ( T1-T2 )2T1l Sktc = 23.99 元.(8)所以,在理想情况下,该热泵工作12 h 需约24元电费.2.设中间空气层内表面的温度为T i,外表面的温度为T0 ,则单位时间内通过内层玻璃、中间空气层和外层玻璃传导的热量分别为H1=k T1-T il S ,(9)H2=k0T i-T0l0S ,(10)H3=k T0-T2l S .(11)在稳定传热的情况下,有H1= H2= H3 .(12)由(9)~(12)四式得k T1-T il= k0T i-T0l0和T1-T i = T0-T2.(13)解式(13)得T i = l0k + lk0l0k + 2lk0T1 +lk0l0k + 2lk0T2.(14)将(14)式代入(9)式得H1 =kk0l0k + 2lk0( T1-T2 )S .(15)要保持室内温度恒定,应有q =H1.由式(3)知,在双层玻璃情况下热泵消耗的最小电功率P′min =kk0l0k + 2lk0( T1-T2 )2T1S .(16)在理想情况下,热泵工作时间t需要的电费C ′min = P′min tc ;(17)代入有关数据得C′min = 2.52 元.(18)所以,改用所选的双层玻璃板后,该热泵工作12 h 可以节约的电费△C min = C min -C′min = 21.47 元.(19)四、1.先假设由于隧穿效应,单电子能从电容器的极板A 隧穿到极板B.以Q 表示单电子隧穿前极板A 所带的电荷量,V AB 表示两极板间的电压(如题目中图3所示),则有V AB = Q / C .(1)这时电容器储能U= 12CV2AB.(2)当单电子隧穿到极板B后,极板A所带的电荷量为Q′ = Q + e ,(3)式中 e 为电子电荷量的大小.这时,电容器两极板间的电压和电容器分别储能为V′AB = Q + eC,U′ =12CV ′2AB.(4)若发生库仑阻塞,即隧穿过程被禁止,则要求U′-U >0 .(5)由(1)~(5)五式得V AB >-12eC .(6)再假设单电子能从电容器的极板B隧穿到极板A.仍以Q表示单电子隧穿前极板A 所带的电荷量,V AB 表示两极板间的电压.当单电子从极板B隧穿到极板A时,极板A所带的电荷量为Q′ = Q-e .经过类似的计算,可得单电子从极板B 到极板A的隧穿不能发生的条件是V AB <12eC .(7)由(6),(7)两式知,当电压V AB 在-e / 2C~e / 2C 之间时,单电子隧穿受到库仑阻塞,即库仑阻塞的条件为-12eC <V AB <12eC .(8)2.依题意和式(8)可知,恰好能发生隧穿时有V AB =12eC = 0.10 mV .(9)由式(9),并代入有关数据得C =8.0 ×10-16 F .(10)3.设题目中图3中左边的MIM 结的电容为C S,右边的MIM 结的电容为CD .双结结构体系如图a所示,以Q1 ,Q2 分别表示电容C S ,C D 所带的电荷量.根据题意,中间单电子岛上的电荷量为-ne = Q 2-Q 1 . (11)体系的静电能为 C S 和 C D 中静电能的总和,即U = Q 212C S + Q 222C D; (12)电压V =Q 1C S + Q 2C D. (13) 由(11)~(13)三式解得U = 12CV 2 + (Q 2-Q 1)22 ( C S + C D ). (14)由于 V 为恒量,从式(13)可知体系的静电能中与岛上净电荷相关的静电能 U n = (-ne )2 / 2 (C S + C D ).4.U n 随 C G V G 变化的图线如图b ;C G V G / e 的变化范围如表2.表2五、1.在图1中,z 轴垂直于 AB 面.考察平行光束中两条光线分别在 AB 面上 C 与 C ′ 点以入射角 i 射入透明圆柱时的情况,r 为折射角,在圆柱体中两折U n( e 2 / 2C)图b射光线分别射达圆柱面的 D 和 D ′ ,对圆柱面其入射角分别为 i 2 与 i ′2 .在△OCD 中,O 点与入射点 C 的距离 y c 由正弦定理得y c sin i 2 = R sin ( 90° + r ) ,即 y c = sin i 2cos r R . (1) 同理在△OC ′D ′ 中,O 点与入射点 C ′ 的距离有y c ′sin i ′2 = R sin ( 90°-r ),即 y c ′ = sin i ′2cos r R . (2) 当改变入射角 i 时,折射角 r 与柱面上的入射角 i 2 与 i ′2 亦随之变化.在柱面上的入射角满足临界角i 20 = arcsin ( 1 / n ) ≈ 41.8° (3)时,发生全反射.将 i 2 = i ′2 = i 20 分别代入式(1),(2)得y o c = y o c ′ =sin i 20cos rR , (4) 即 d = 2y o c = 2sin i 20cos rR . (5)当 y c > y o c 和 y c ′ > y o c ′ 时,入射光线进入柱体,经过折射后射达柱面时的入射角大于临界角 i 20 ,由于发生全反射不能射出柱体.因折射角 r 随入射角 i 增大而增大.由式(4)知,当 r = 0 ,即 i = 0(垂直入射)时,d 取最小值d min = 2R sin i 20 = 1.33 R . (6)当 i →90°(掠入射)时,r → 41.8° .将 r = 41.8° 代入式(4)得 d max = 1.79 R .(7)2.由图2可见,φ 是 Oz 轴与线段 OD 的夹角,φ′ 是 Oz 轴与线段 OD ′ 的夹角.发生全反射时,有φ = i 20 + r , (8) φ′ = i 20- r , (9)和 θ = φ + φ′ = 2i 20≈83.6° . (10) 由此可见,θ 与 i 无关,即 θ 独立于 i .在掠入射时,i ≈90° ,r = 41.8° ,由式(8),(9)两式得φ = 83.6° ,φ′ = 0°. (11)六、由于方程r = GM / c 2a cos φ + a 2 ( 1 + sin 2φ)(1)图2是φ的偶函数,光线关于极轴对称.光线在坐标原点左侧的情形对应于a<0 ;光线在坐标原点右侧的情形对应a>0 .右图是a<0的情形,图中极轴为Ox,白矮星在原点O处.在式(1)中代入近星点坐标r = r m,φ= π,并注意到a 2| a | ,有a≈-GM / c2r m .(2)经过白矮星两侧的星光对观测者所张的视角θS 可以有不同的表达方式,相应的问题有不同的解法.解法一:若从白矮星到地球的距离为d,则可近似地写出θS≈2r m / d.(3)在式(1)中代入观测者的坐标r = d,φ= -π/ 2,有a2≈GM / 2c2d.(4)由(2)与(4)两式消去a,可以解出r m = 2GMd / c2 .(5)把式(5)代入式(3)得θS≈8GM / c2d;(6)即M≈θ2Sc2d / 8G ,(7)其中d = 3.787 ×1017 m ;代入数值就可算出M≈2.07 ×1030 kg .(8)解法二:光线射向无限远处的坐标可以写成r→∞,φ= -π2+θ2.(9)近似地取θS≈θ,把式(9)代入式(1),要求式(1)分母为零,并注意到θ1,有aθ / 2 + 2a2= 0 .所以θS≈θ=-4a = 8GM / c2d,(10)其中用到式(4),并注意到a<0 .式(10)与式(6)相同,从而也有式(8).解法三:星光对观测者所张的视角θS 应等于两条光线在观测者处切线的夹角,有sin θS2=△( r cosφ)△r= cosφ-r sinφ△φ△r.(11)由光线方程(1)算出△φ/△r ,有sin θS2= cosφ-r sinφGM / c2r2a sinφ= cosφ-GMc2ra;ySrxOEr mφ代入观测者的坐标r = d, = -π/ 2以及a的表达式(4),并注意到θS很小,就有θS≈2GMc2d2c2dGM=8GMc2d,与式(6)相同.所以,也得到了式(8).解法四:用式(2)把方程(1)改写成-r m = r cosφ-GMc2r m r[ (r cosφ )2 + 2 (r sinφ)2 ] ,即x = -r m + GMc2r m r( x2 +2y2 ) .(12)当y→-∞时,式(12)的渐近式为x = -r m-2GMc2r m y.这是直线方程,它在x轴上的截距为-r m ,斜率为1-2GM/ c2r m ≈1-tan ( θS / 2 )≈-1θS / 2 .于是有θS ≈4GM/ c2r m.r m用式(5)代入后,得到式(6),从而也有式(8).七、1.(I)氦原子中有两个电子,一级电离能E+ 是把其中一个电子移到无限远处所需要的能量满足He + E+ →He+ + e-.为了得到氦原子的一级电离能E+ ,需要求出一个电子电离以后氦离子体系的能量E*.这是一个电子围绕氦核运动的体系,下面给出两种解法.解法一:在力学方程2ke2r2= mv2 r中,r 是轨道半径,v 是电子速度.对基态,用玻尔量子化条件(角动量为)可以解出r0 =2/ 2ke2m .(1)于是氦离子能量E* = p22m-2ke2r0= -2k2e4m2,(2)其中p0 为基态电子动量的大小;代入数值得E* = -2( ke2 )2mc2(c )2≈-54.4 eV .(3)由于不计电子间的相互作用,氦原子基态的能量E0 是该值的2倍,即E0 =2E* ≈-108.8 eV .(4)氦离子能量E*与氦原子基态能量E0之差就是氦原子的一级电离能E+ =E*-E0 = -E*≈ 54.4 eV .(5)解法二:氦离子能量E*= p22m-2ke2r.把基态的角动量关系rp =代入,式(3)可以改写成E* =22mr2-2ke2r=22m(1r-2ke2m2)2-2k2e4m2.因基态的能量最小,式(4)等号右边的第一项为零,所以半径和能量r 0 =22ke2m,E*= -2k2e4m2分别与(1),(2)两式相同.(II)下面,同样给出求氦原子基态能量E0和半径r0的两种解法.解法一:利用力学方程mv2r= 2ke2r2-ke2( 2r )2=7ke24r2和基态量子化条件rmv =,可以解出半径r0 = 42/ 7ke2m,(6)于是氦原子基态能量E0 = 2 ( p22m-2ke2r0) +ke22r0= -49k2e4m162;(7)代入数值算得E0 = -49( ke2 )2mc216(c )2≈-83.4 eV ,(8)r0 = 4 (c)27ke2mc2≈ 0.0302 nm .所以,氦原子的一级电离能E+ =E*-E0≈ 29.0 eV .(9)这仍比实验测得的氦原子一级电离能24.6 eV 高出4.4 eV .解法二:氦原子能量E = 2 (p22m-2ke2r) +ke22r=2mr2-7ke22r可以化成E =2m(1r-7ke2m42)2-49k2e4m162.当上式等号右边第一项为零时,能量最小.由此可知,基态能量与半径E0 =-49k2e4m162,r0=427ke2m分别与(7),(6)两式相同.2.(I)粒子从下部射向并穿过铅板向上运动,其电荷为正.(II)如题图所示,粒子的运动速度v 与磁场方向垂直,洛伦兹力在纸面内;磁力不改变荷电粒子动量的大小,只改变其方向.若不考虑云室中气体对粒子的阻力,荷电粒子在恒定磁场作用下的运动轨迹就是曲率半径为一定值的圆弧;可以写出其运动方程qBv=|△p△t| =p△φ△t=pvr,(1)其中q 是粒子电荷,v 是粒子速度的大小,p 是粒子动量的大小,△φ是粒子在△t时间内转过的角度,r是轨迹曲率半径.于是有p= qBr .(2)按题意,q=e .用p d 和p u 分别表示粒子射入铅板和自铅板射出时动量的大小,并在式(1)中代入有关数据,可以算得p d =63.0 MeV / c ,p u= 22.8 MeV / c .(3)注意到当pc mc2 时应使用狭义相对论,从p=mv1-(v / c)2.(4)中可以得到v=c1+(mc / p)2.(5)用v d 和v u 分别表示粒子进入和离开铅板时的速度大小.把式(2)以及m = 0.511 MeV / c2代入式(3),可得v d ≈c,v u≈c.(6)于是,粒子穿过铅板的平均速度v= ( 1 / 2 ) ( v d + v u )≈c.用△t表示粒子穿过铅板的时间,则有v cosθ△t = d.(7)再用△p du表示粒子穿过铅板动量改变量的大小,铅板所受到的平均力的大小f = △p du△t=p d-p ud / (v cosθ)≈( p d-p u ) c cosθd;(8)。
第二十五届物理竞赛试题

第二十五届物理竞赛试题一、选择题(每题3分,共30分)1. 一个物体在水平面上做匀速直线运动,其速度为v,质量为m。
如果物体的质量增加到2m,而速度减半,那么物体的动能将如何变化? - A. 保持不变- B. 减半- C. 增加到原来的两倍- D. 变为原来的四分之一2. 两个完全相同的金属球,分别放在两个不同的电场中,如果它们的电荷量相同,那么它们的电势能将:- A. 相等- B. 取决于金属球的半径- C. 取决于电场的强度- D. 无法确定3. 一个物体从静止开始自由下落,忽略空气阻力。
在落地时,它的动能和势能之和将:- A. 保持不变- B. 增加- C. 减少- D. 变为零4. 一个理想的气体在等压过程中膨胀,其内能将:- A. 增加- B. 减少- C. 保持不变- D. 无法确定5. 根据热力学第二定律,不可能从单一热源吸热并将其完全转化为功,而不产生其他效果。
这表明:- A. 热机的效率可以无限接近100%- B. 热机的效率不能达到100%- C. 热机的效率必须为0%- D. 热机的效率必须小于100%6. 一个物体在斜面上下滑,如果斜面的角度增加,而物体的质量不变,那么物体下滑的加速度将:- A. 增加- B. 减少- C. 保持不变- D. 无法确定7. 一个光子的能量E与它的频率ν之间的关系为E=hν,其中h是普朗克常数。
如果光子的频率增加,那么它的能量将:- A. 增加- B. 减少- C. 保持不变- D. 无法确定8. 一个电路中的电流I与电压V之间的关系由欧姆定律V=IR描述。
如果电路中的电阻R增加,而电压V保持不变,那么电流I将:- A. 增加- B. 减少- C. 保持不变- D. 变为零9. 根据狭义相对论,一个物体的质量m随速度v的增加而增加,其关系为m=m0/√(1-v²/c²),其中m0是静止质量,c是光速。
当速度v接近光速c时,物体的质量将:- A. 保持不变- B. 增加- C. 减少- D. 变为无穷大10. 一个物体在受到一个恒定的力F作用下做匀加速直线运动,如果力F增加,那么物体的加速度a将:- A. 增加- B. 减少- C. 保持不变- D. 变为零二、计算题(每题15分,共45分)1. 一个质量为2kg的物体从静止开始在水平面上受到一个恒定的力10N作用,求物体在前5秒内移动的距离。
上海市2011年第25届初中物理竞赛(大同杯)复赛试题参考答案

上海市第二十五届初中物理竞赛(大同中学杯)复赛参考答案一、选择题(每小题4分,共32分)二、填空题(每题6分,共30分)9、 虚 , 凸 。
10、 p 0 , h 。
11、 圆弧 , 932Lπ 。
12、 1062 。
13、 下降 , 600 。
三、计算题(本题共36分) 14、(本题共9分)解:由投入含有石块的冰块可知,F 浮=G (冰+石块)ρ水gS Δh =(m 冰+m 石)gm 冰+m 石=ρ水S Δh =1.0×103×100×10-4×6×10-2kg =0.6kg 冰熔化后,水位下降的高度: m g p h 3310528.510100.128.55-⨯=⨯⨯=∆='∆水ρ 水位下降就是由于冰化成水体积减小引起的,即 V 冰-V 水=S Δh ’S h m m ρρ'-=∆冰冰冰水kg kg h S m 498.010528.510100109.0100.1109.0100.1343333=⨯⨯⨯⨯⨯-⨯⨯⨯⨯='∆-=--冰水冰水冰ρρρρ 石块的质量m 石=0.6kg -0.498kg =0.102kg石块的体积35333241067.4109.0498.010610100S m m m m h V ---⨯=⨯-⨯⨯⨯=-∆=冰冰石ρ 石块的密度335/1018.21067.4102.0m kg V m ⨯=⨯==-石石石ρ15、(本题共8分)设v 1=4km/s ,v 2=2km/s ,O 点为震中地点,t 和t ´分别为纵向地震波传至甲处(A 点)和(B 点)乙处的时间; 则km s km OA s v v t t v t v OA 164/4414)4(2121=⨯=⇒=-=⇒+==同理可得:km OB 40= O 点位置如图,由余弦定理可得:5.0401628.3440162cos 222222≈⨯⨯-+=⋅-+=OBOA ABOB OA θ,060≈⇒θ 16.(本题共9分)解答:加热器在2分钟内所供应的总热量,等于水温升高所吸收的热量,加上散失到周围环境的热量,即 21()Pt cm T T Q =-+若水温变化不大,则散失到周围环境的热量与时间成正比。
2008年第25届CPhO复赛试题+答案

2008年第25届全国中学生物理竞赛复赛试卷本卷共八题,满分160分 一、(15分) 1、(5分)蟹状星云脉冲星的辐射脉冲周期是0.033s 。
假设它是由均匀分布的物质构成的球体,脉冲周期是它的旋转周期,万有引力是唯一能阻止它离心分解的力,已知万有引力常量113126.6710G m kg s ---=⨯⋅⋅,由于脉冲星表面的物质未分离,故可估算出此脉冲星密度的下限是 3kg m -⋅。
2、(5分)在国际单位制中,库仑定律写成122q q F kr =,式中静电力常量9228.9810k N m C -=⨯⋅⋅,电荷量q 1和q 2的单位都是库仑,距离r 的单位是米,作用力F 的单位是牛顿。
若把库仑定律写成更简洁的形式122q q F r =,式中距离r 的单位是米,作用力F 的单位是牛顿。
若把库仑定律写成更简洁的形式122q qF r=,式中距离r 的单位是米,作用力F 的单位是牛顿,由此式可这义一种电荷量q 的新单位。
当用米、千克、秒表示此新单位时,电荷新单位= ;新单位与库仑的关系为1新单位= C 。
3、(5分)电子感应加速器(betatron )的基本原理如下:一个圆环真空室处于分布在圆柱形体积内的磁场中,磁场方向沿圆柱的轴线,圆柱的轴线过圆环的圆心并与环面垂直。
圆中两个同心的实线圆代表圆环的边界,与实线圆同心的虚线圆为电子在加速过程中运行的轨道。
已知磁场的磁感应强度B 随时间t 的变化规律为0cos(2/)B B t T π=,其中T 为磁场变化的周期。
B 0为大于0的常量。
当B 为正时,磁场的方向垂直于纸面指向纸外。
若持续地将初速度为v 0的电子沿虚线圆的切线方向注入到环内(如图),则电子在该磁场变化的一个周期内可能被加速的时间是从t= 到t= 。
二、(21分)嫦娥1号奔月卫星与长征3号火箭分离后,进入绕地运行的椭圆轨道,近地点离地面高22.0510n H km =⨯,远地点离地面高45.093010f H km =⨯,周期约为16小时,称为16小时轨道(如图中曲线1所示)。
第25届全国中学生物理竞赛决赛试题及详细解答

第25届全国中学生物理竞赛决赛试题2008年10月 北京★理论部分一、足球比赛,一攻方队员在图中所示的A 处沿Ax 方向传球,球在草地上以速度v 匀速滚动,守方有一队员在图中B 处,以d 表示A ,B 间的距离,以θ表示AB 与Ax 之间的夹角,已知θ<90°.设在球离开A 处的同时,位于B 处的守方队员开始沿一直线在匀速运动中去抢球,以v p 表示他的速率.在不考虑场地边界限制的条件下,求解以下问题(要求用题中给出的有关参量间的关系式表示所求得的结果):1.求出守方队员可以抢到球的必要条件.2.如果攻方有一接球队员处在Ax 线上等球,以l r 表示他到A 点的距离,求出球不被原在B 处的守方队员抢断的条件.3.如果攻方有一接球队员处在Ax 线上,以L 表示他离开A 点的距离.在球离开A 处的同时,他开始匀速跑动去接球,以v r 表示其速率,求在这种情况下球不被原在B 处的守方队员抢断的条件.二、卫星的运动可由地面观测来确定;而知道了卫星的运动,又可以用它来确定空间飞行体或地面上物体的运动.这都涉及时间和空间坐标的测定.为简化分析和计算,不考虑地球的自转和公转,把它当做惯性系.1.先来考虑卫星运动的测定.设不考虑相对论效应.在卫星上装有发射电波的装置和高精度的原子钟.假设从卫星上每次发出的电波信号,都包含该信号发出的时刻这一信息.(I )地面观测系统(包含若干个观测站)可利用从电波中接收到的这一信息,并根据自己所处的已知位置和自己的时钟来确定卫星每一时刻的位置,从而测定卫星的运动.这种测量系统至少需要包含几个地面观测站?列出可以确定卫星位置的方程.(II )设有两个观测站D 1 ,D 2 ,分别位于同一经线上北纬θ和南纬θ(单位:(°))处.若它们同时收到时间 之前卫星发出的电波信号.(i)试求出发出电波时刻卫星距地面A的最大高度H;(ii)当D1,D2处观测站位置的纬度有很小的误差△θ时,试求H的误差;(iii)如果上述的时间τ有很小的误差τ△,试求H的误差.2.在第1(II)小题中,若θ= 45°,τ= 0.10 s .(i)试问卫星发出电波时刻卫星距地面最大高度H是多少千米?(ii)若△θ= ±1.0′′ ,定出的H有多大误差?(iii)若τ△= ±0.010 μs ,定出的H有多大误差?假设地球为半径R= 6.38×103km 的球体,光速c = 2.998×108 m / s ,地面处的重力加速度g = 9.81 m / s2.3.再来考虑根据参照卫星的运动来测定一个物体的运动.设不考虑相对论效应.假设从卫星持续发出的电波信号包含卫星运动状态的信息,即每个信号发出的时刻及该时刻卫星所处的位置.再假设被观测物体上有一台卫星信号接收器(设其上没有时钟),从而可获知这些信息.为了利用这种信息来确定物体的运动状态,即物体接收到卫星信号时物体当时所处的位置以及当时的时刻,一般来说物体至少需要同时接收到几个不同卫星发来的信号电波?列出确定当时物体的位置和该时刻的方程.4.根据狭义相对论,运动的钟比静止的钟慢.根据广义相对论,钟在引力场中变慢.现在来考虑在上述测量中相对论的这两种效应.已知天上卫星的钟与地面观测站的钟零点已经对准.假设卫星在离地面h = 2.00×104 km的圆形轨道上运行,地球半径R、光速c和地面重力加速度g取第2小题中给的值.(I)根据狭义相对论,试估算地上的钟经过24h后它的示数与卫星上的钟的示数差多少?设在处理这一问题时,可以把匀速直线运动中时钟走慢的公式用于匀速圆周运动.(II)根据广义相对论,钟在引力场中变慢的因子是(1-2φ/ c2 )1 / 2 ,φ是钟所在位置的引力势(即引力势能与受引力作用的物体质量之比;取无限远处引力势为零)的大小.试问地上的钟24 h后,卫星上的钟的示数与地上的钟的示数差多少?三、致冷机是通过外界对机器做功,把从低温处吸取的热量连同外界对机器做功所得到的能量一起送到高温处的机器;它能使低温处的温度降低,高温处的温度升高.已知当致冷机工作在绝对温度为T1的高温处和绝对温度为T2的低温处之间时,若致冷机从低温处吸取的热量为Q,外界对致冷机做的功为W,则有Q W≤T2T1-T2,式中“=”对应于理论上的理想情况.某致冷机在冬天作为热泵使用(即取暖空调机),在室外温度为-5.00℃的情况下,使某房间内的温度保持在20.00℃.由于室内温度高于室外,故将有热量从室内传递到室外.本题只考虑传导方式的传热,它服从以下的规律:设一块导热层,其厚度为l ,面积为S ,两侧温度差的大小为T ,则单位时间内通过导热层由高温处传导到低温处的热量为H = k △T lS , 其中k 称为热导率,取决于导热层材料的性质.1.假设该房间向外散热是由面向室外的面积S = 5.00 m 2 、厚度l = 2.00 mm 的玻璃板引起的.已知该玻璃的热导率k = 0.75 W / ( m • K ),电费为每度0.50元.试求在理想情况下该热泵工作12 h 需要多少电费?2.若将上述玻璃板换为“双层玻璃板”,两层玻璃的厚度均为2.00mm ,玻璃板之间夹有厚度l 0= 0.50 mm 的空气层,假设空气的热导率k 0= 0.025 W / ( m • K ),电费仍为每度0.50元.若该热泵仍然工作12 h ,问这时的电费比上一问单层玻璃情形节省多少?四、如图1所示,器件由相互紧密接触的金属层( M )、薄绝缘层( I )和金属层( M )构成.按照经典物理的观点,在I 层绝缘性能理想的情况下,电子不可能从一个金属层穿过绝缘层到达另一个金属层.但是,按照量子物理的原理,在一定的条件下,这种渡越是可能的,习惯上将这一过程称为隧穿,它是电子具有波动性的结果.隧穿是单个电子的过程,是分立的事件,通过绝缘层转移的电荷量只能是电子电荷量-e ( e = 1.60×10-19 C )的整数倍,因此也称为单电子隧穿,MIM 器件亦称为隧穿结或单电子隧穿结.本题涉及对单电子隧穿过程控制的库仑阻塞原理,由于据此可望制成尺寸很小的单电子器件,这是目前研究得很多、有应用前景的领域.1.显示库仑阻塞原理的最简单的做法是将图1的器件看成一个电容为C 的电容器,如图2所示.电容器极板上的电荷来源于金属极板上导电电子云相对于正电荷背景的很小位移,可以连续变化.如前所述,以隧穿方式通过绝缘层的只能是分立的单电子电荷.如果隧穿过程会导致体系静电能量上升,则此过程不能发生,这种现象称为库仑阻塞.试求出发生库仑阻塞的条件即电容器极板间的电势差V AB = V A -V B在什么范围图1内单电子隧穿过程被禁止.2.假定V AB = 0.10 mV 是刚能发生隧穿的电压.试估算电容C 的大小.3.将图1的器件与电压为V 的恒压源相接时,通常采用图2所示的双结构器件来观察单电子隧穿,避免杂散电容的影响.中间的金属块层称为单电子岛.作为电极的左、右金属块层分别记为S ,D .若已知岛中有净电荷量-ne ,其中净电子数n 可为正、负整数或零,e 为电子电荷量的大小,两个MIM 结的电容分别为C S 和C D .试证明双结结构器件的静电能中与岛上净电荷量相关的静电能(简称单电子岛的静电能)为U n =(-ne )22( C S +C D ). 4.在图3给出的具有源( S )、漏( D )电极双结结构的基础上,通过和岛连接的电容C G 添加门电极( G )构成如图4给出的单电子三极管结构,门电极和岛间没有单电子隧穿事件发生.在V 较小且固定的情况下,通过门电压V G 可控制岛中的净电子数n .对于V G 如何控制n ,简单的模型是将V G 的作用视为岛中附加了等效电荷q 0= C G V G .这时,单电子岛的静电能可近似为U n =(-ne +q 0)2 / 2C ∑,式中C ∑=C S +C D +C G .利用方格图(图5),考虑库仑阻塞效应,用粗线画出岛中净电子数从n = 0开始,C G V G / e 由0增大到3的过程中,单电子岛的静电能U n 随C G V G 变化的图线(纵坐标表示U n ,取U n 的单位为e 2 / 2C ∑;横坐标表示C G V G ,取C G V G 的单位为e ).要求标出关键点的坐标,并把n = 0 ,1 ,2 ,3时C G V G / e 的变化范围填在表格中.(此小题只按作图及所填表格(表1)评分).图3 图 4图5表1五、折射率n = 1.50 、半径为R的透明半圆柱体放在空气中,其垂直于柱体轴线的横截面如图所示,图中O点为横截面与轴线的交点.光仅允许从半圆柱体的平面AB进入,一束足够宽的平行单色光沿垂直于圆柱轴的方向以入射角i射至AB整个平面上,其中有一部分入射光束能通过半圆柱体从圆柱面射出.这部分光束在入射到AB面上时沿y轴方向的长度用d表示.本题不考虑光线在透明圆柱体内经一次或多次反射后再射出柱体的复杂情形.1.当平行入射光的入射角i在0°~90°变化时,试求d的最小值d min和最大值d max.2.在如图所示的平面内,求出射光束与柱面相交的圆弧对O点的张角与入射角i的关系.并求在掠入射时上述圆弧的位置.六、根据广义相对论,光线在星体的引力场中会发生弯曲,在包含引力中心的平面内是一条在引力中心附近微弯的曲线.它距离引力中心最近的点称为光线的近星点.通过近星点与引力中心的直线是光线的对称轴.若在光线所在平面内选择引力中心为平面极坐标(r ,φ)的原点,选取光线的对称轴为坐标极轴,则光线方程(光子的轨迹方程)为r =GM / c2a cosφ+a2 ( 1 + sin2φ),G是万有引力恒量,M是星体质量,c是光速,a是绝对值远小于1的参数.现在假设离地球80.0光年处有一星体,在它与地球连线的中点处有一白矮星.如果经过该白矮星两侧的星光对地球上的观测者所张的视角是1.80×10-7rad ,试问此白矮星的质量是多少千克?已知G = 6.673 ×10-11m3 / ( kg •s2 )七、1.假设对氦原子基态采用玻尔模型,认为每个电子都在以氦核为中心的圆周上运动,半径相同,角动量均为:= h / 2π,其中h是普朗克常量.(I)如果忽略电子间的相互作用,氦原子的一级电离能是多少电子伏?一级电离能是指把其中一个电子移到无限远所需要的能量.z(II )实验测得的氦原子一级电离能是24.6 eV .若在上述玻尔模型的基础上来考虑电子之间的相互作用,进一步假设两个电子总处于通过氦核的一条直径的两端.试用此模型和假设,求出电子运动轨道的半径r 0 、基态能量E 0 以及一级电离能E + ,并与实验测得的氦原子一级电离能相比较.已知电子质量m = 0.511 MeV / c 2 ,c 是光速,组合常量c =197.3 MeV • fm =197.3 eV • nm ,ke 2= 1.44 MeV • fm =1.44 eV • nm ,k 是静电力常量,e 是基本电荷量.2.右图是某种粒子穿过云室留下的径迹的照片.径迹在纸面内,图的中间是一块与纸面垂直的铅板,外加恒定匀强磁场的方向垂直纸面向里.假设粒子电荷的大小是一个基本电荷量e :e =1.60×10-19 C ,铅板下部径迹的曲率半径r d = 210 mm ,铅板上部径迹的曲率半径r u = 76.0 mm ,铅板内的径迹与铅板法线成θ= 15.0° ,铅板厚度d = 6.00 mm ,磁感应强度B = 1.00 T ,粒子质量 m = 9.11×10-31kg =0.511MeV/ c 2.不考虑云室中气体对粒子的阻力.(I )写出粒子运动的方向和电荷的正负.(II )试问铅板在粒子穿过期间所受的力平均为多少牛?(III )假设射向铅板的不是一个粒子,而是从加速器引出的流量为j = 5.00 ×1018 / s 的脉冲粒子束,一个脉冲持续时间为 =2.50 ns .试问铅板在此脉冲粒子束穿过期间所受的力平均为多少牛?铅板在此期间吸收的热量又是多少焦?第25届全国中学生物理竞赛决赛参考解答一、1 .解法一:设守方队员经过时间t 在Ax 上的C点抢到球,用l 表示A 与C 之间的距离,l p 表示B 与C之间的距离(如图1所示),则有l = vt ,l p = v p t (1)和 l 2p = d 2 + l 2-2dl cos θ.(2)解式(1),(2)可得图1l=d1-(v p/ v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }.(3)由式(3)可知,球被抢到的必要条件是该式有实数解,即v p≥v sinθ.(4)解法二:设BA与BC的夹角为φ(如图1).按正弦定理有l psinθ=lsinφ.利用式(1)有v p v= sinθsinφ.从sinφ≤1可得必要条件(4).2.用l min表示守方队员能抢断球的地方与A点间的最小距离.由式(3)知l min=d1-( v p/ v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }.(5)若攻方接球队员到A点的距离小于l min,则他将先控制球而不被守方队员抢断.故球不被抢断的条件是l r <l min.(6)由(5),(6)两式得l r <d1-( v p/ v)2{cosθ±[ (v pv)2 -sin2θ]1 / 2 }(7)由式(7)可知,若位于Ax轴上等球的攻方球员到A点的距离l r满足该式,则球不被原位于B处的守方球员抢断.3.解法一:如果在位于B处的守方球员到达Ax上距离A点l min的C1点之前,攻方接球队员能够到达距A点小于l min处,球就不会被原位于B处的守方队员抢断(如图2所示).若L≤l min 就相当于第2小题.若L>l min ,设攻方接球员位于Ax方向上某点E处,则他跑到C1点所需时间t rm = ( L-l min) / v r ;(8)守方队员到达C1处所需时间t pm = ( d2+ l2min-2dl min cosθ)1 / 2/v p.球不被守方抢断的条件是t rm <t pm .(9)图2即 L <v r v p( d 2 + l 2min -2dl min cos θ)1 / 2 + l min ,(10)式中l min 由式(5)给出.解法二:守方队员到达C 1点的时间和球到达该点的时间相同,因此有t pm = l min / v .从球不被守方队员抢断的条件(9)以及式(8)可得到L < ( 1 + v r / v )l min (11)式中l min 也由式(5)给出.易证明式(11)与(10)相同.二、1.(I )选择一个坐标系来测定卫星的运动,就是测定每一时刻卫星的位置坐标x ,y ,z .设卫星在t 时刻发出的信号电波到达第i 个地面站的时刻为t i .因为卫星信号电波以光速c 传播,于是可以写出(x -x i )2 + (y -y i )2 + (z -z i )2 = c 2 (t -t i )2 ( i = 1 ,2 ,3 ), (1)式中x i ,y i ,z i 是第i 个地面站的位置坐标,可以预先测定,是已知的;t i 也可以由地面站的时钟来测定;t 由卫星信号电波给出,也是已知的.所以,方程(1)中有三个未知数x ,y ,z ,要有三个互相独立的方程,也就是说,至少需要包含三个地面站,三个方程对应于式(1)中i = 1 ,2 ,3 的情况.(II )(i )如图所示,以地心O 和两个观测站D 1 ,D 2 的位置为顶点所构成的三角形是等腰三角形,腰长为R .根据题意,可知卫星发出信号电波时距离两个观测站的距离相等,都是L = c . (2)当卫星P 处于上述三角形所在的平面内时,距离地面的高度最大,即H .以θ表示D 1 ,D 2所处的纬度,由余弦定理可知L 2 = R 2 + ( H +R )2-2R ( H +R )cos θ. (3)由(2),(3)两式得H =(c τ)2 -(R sin θ)2 -R ( 1-cos θ). (4)式(4)也可据图直接写出.(ii )按题意,如果纬度有很小的误差△θ,则由式(3)可知,将引起H 发生误差△H .这时有L 2 = R 2 + ( H +△H + R )2 -2R ( H +△H +R )cos ( θ+△θ).(5)将式(5)展开,因△θ很小,从而△H 也很小,可略去高次项,再与式(3)相减,得△H = -R ( R +H )sin θ△θH +( 1-cos θ)R,(6) 其中H 由(4)式给出.(iii )如果时间τ有τ△的误差,则L 有误差△L = c τ△ . (7)由式(3)可知,这将引起H 产生误差△H .这时有( L +△L )2 = R 2 + ( H +△H + R )2 -2R ( H +△H +R )cos θ.(8)由式(7),(8)和(3),略去高次项,可得△H = c 2ττ△H +R ( 1-cos θ), (9) 其中H 由式(4)给出.2.(i )在式(4)中代入数据,算得H = 2.8×104 km .(ii )在式(6)中代入数据,算得△H =25m .(iii )在式(9)中代入数据,算得△H = ±3.0 m .3.选择一个坐标系,设被测物体待定位置的坐标为x ,y ,z ,待定时刻为t ,第i 个卫星在t i 时刻的坐标为x i ,y i ,z i .卫星信号电波以光速传播,可以写出(x -x i )2 + (y -y i )2 + (z -z i )2 = c 2 (t -t i )2 ( i = 1 ,2 ,3 ,4 ), (10)由于方程(1)有四个未知数t ,x ,y ,z ,需要四个独立方程才有确定的解,故需同时接收至少四个不同卫星的信号.确定当时物体的位置和该时刻所需要的是式(10)中i = 1 ,2 ,3 ,4所对应的四个独立方程.4.(I )由于卫星上钟的变慢因子为[ 1-( v / c )2]1 / 2 ,地上的钟的示数T 与卫星上的钟的示数t 之差为T -t = T -1-(v c )2T = [ 1-1-(v c)2 ]T , (11)这里v 是卫星相对地面的速度,可由下列方程定出:v 2r = GM r2 , (12)其中G 是万有引力常量,M 是地球质量,r 是轨道半径.式(11)给出 v = GM r = g r R =g R + hR ,其中R 是地球半径,h 是卫星离地面的高度,g = GM / R 2是地面重力加速度;代入数值有v = 3.89 km / s .于是 ( v / c )2≈1.68×10-10 ,这是很小的数.所以[ 1-(v c )2]1 / 2≈1-12(v c)2.最后,可以算出24 h 的时差 T -t ≈12(v c )2T = 12gR 2c 2 ( R + h )T = 7.3μs .(13)(II )卫星上的钟的示数t 与无限远惯性系中的钟的示数T 0之差t -T 0= 1-2φc 2T 0-T 0=( 1-2φc 2-1 )T 0 .(14)卫星上的钟所处的重力势能的大小为φ= GM R + h = R 2R + h g . (15)所以 φc 2 = gR 2c 2 ( R + h );代入数值有φ/ c 2 = 1.68×10-10,这是很小的数.式(14)近似为t -T 0 ≈- φc2T 0 . (16)类似地,地面上的钟的示数T 与无限远惯性系的钟的示数之差T -T 0 =1-2E φc 2T 0-T 0=(1-2E φc 2-1 )T 0 . (17)地面上的钟所处的重力势能的大小为E φ=GMR =gR . (18)所以Eφc2=gR c 2; 代入数值有E φ/ c 2 =6.96 ×10-10,这是很小的数.与上面的情形类似,式(17)近似为T -T 0 ≈-Eφc 2T 0 . (19)(16),(19)两式相减,即得卫星上的钟的示数与地面上的钟的示数之差t -T ≈-Eφφ-c 2T 0 .(20)从式(19)中解出T 0 ,并代入式(20)得t -T ≈-Eφφ-c2/ (1-Eφc2)T ≈-Eφφ-c2T =gR c 2hR + hT .(21)注意,题目中的24 h 是指地面的钟走过的时间T .最后,算出24 h 卫星上的钟的示数与地面上的钟的示数之差t -T = 46 μs . (22)三、1.依题意,为使室内温度保持不变,热泵向室内放热的功率应与房间向室外散热的功率相等.设热泵在室内放热的功率为q ,需要消耗的电功率为P ,则它从室外(低温处)吸收热量的功率为q -P .根据题意有q -P P ≤T 2T 1-T 2, (1)式中T 1为室内(高温处)的绝对温度,T 2为室外的绝对温度.由(1)式得P ≥T 1-T 2T 1q . (2)显然,为使电费最少,P 应取最小值;即式(2)中的“≥”号应取等号,对应于理想情况下 P 最小.故最小电功率P min =T 1-T 2T 1q .(3) 又依题意,房间由玻璃板通过热传导方式向外散热,散热的功率H =k T 1-T 2lS . (4)要保持室内温度恒定,应有q =H . (5)由(3)~(5)三式得P min =k S ( T 1-T 2 )2lT 1. (6)设热泵工作时间为t ,每度电的电费为c ,则热泵工作需花费的最少电费C min =P min tc . (7)注意到 T 1= 20.00 K + 273.15 K = 293.15 K ,T 2 = -5.00 K + 273.15 K = 268.15 K ,1度电 = 1 kW • h .由(6),(7)两式,并代入有关数据得C min =( T 1-T 2 )2T 1lSktc = 23.99 元.(8)所以,在理想情况下,该热泵工作12 h 需约24元电费.2.设中间空气层内表面的温度为 T i ,外表面的温度为 T 0,则单位时间内通过内层玻璃、中间空气层和外层玻璃传导的热量分别为H 1=k T 1-T ilS , (9)H 2=k 0T i -T 0l 0S , (10)H 3=k T 0-T 2lS . (11)在稳定传热的情况下,有H 1=H 2=H 3 . (12)由(9)~(12)四式得k T 1-T i l = k 0T i -T 0l 0和T 1-T i =T 0-T 2.(13)解式(13)得T i =l 0k + lk 0l 0k + 2lk 0T 1 +lk 0l 0k + 2lk 0T 2. (14)将(14)式代入(9)式得H 1 =kk 0l 0k + 2lk 0( T 1-T 2 )S . (15)要保持室内温度恒定,应有q =H 1.由式(3)知,在双层玻璃情况下热泵消耗的最小电功率P ′min =kk 0l 0k + 2lk 0( T 1-T 2 )2T 1S .(16)在理想情况下,热泵工作时间t 需要的电费C ′min =P ′min tc ; (17)代入有关数据得C ′min =2.52 元. (18)所以,改用所选的双层玻璃板后,该热泵工作12 h 可以节约的电费△C min =C min -C′min=21.47 元.(19)四、1.先假设由于隧穿效应,单电子能从电容器的极板A隧穿到极板B.以Q 表示单电子隧穿前极板A所带的电荷量,V AB表示两极板间的电压(如题目中图3所示),则有V AB= Q / C .(1)这时电容器储能U= 12CV2AB.(2)当单电子隧穿到极板B后,极板A所带的电荷量为Q′ = Q + e ,(3)式中e 为电子电荷量的大小.这时,电容器两极板间的电压和电容器分别储能为V′AB= Q + eC,U′ =12CV′2AB.(4)若发生库仑阻塞,即隧穿过程被禁止,则要求U′-U >0 .(5)由(1)~(5)五式得V AB>-12eC .(6)再假设单电子能从电容器的极板B隧穿到极板A.仍以Q表示单电子隧穿前极板A 所带的电荷量,V AB表示两极板间的电压.当单电子从极板B隧穿到极板A时,极板A所带的电荷量为Q′ = Q-e.经过类似的计算,可得单电子从极板B到极板A的隧穿不能发生的条件是V AB<12eC .(7)由(6),(7)两式知,当电压V AB在-e / 2C~e / 2C 之间时,单电子隧穿受到库仑阻塞,即库仑阻塞的条件为-12eC <V AB<12eC .(8)2.依题意和式(8)可知,恰好能发生隧穿时有V AB =12eC= 0.10 mV . (9)由式(9),并代入有关数据得C =8.0×10-16F . (10)3.设题目中图3中左边的MIM 结的电容为 C S ,右边的MIM 结的电容为 C D .双结结构体系如图a 所示,以Q 1 ,Q 2 分别表示电容C S ,C D 所带的电荷量.根据题意,中间单电子岛上的电荷量为-ne = Q 2-Q 1 .(11)体系的静电能为 C S 和 C D 中静电能的总和,即U =Q 212C S + Q 222C D; (12)电压V =Q 1C S + Q 2C D. (13) 由(11)~(13)三式解得U =12CV 2 +(Q 2-Q 1)22 (C S + C D ). (14)由于V 为恒量,从式(13)可知体系的静电能中与岛上净电荷相关的静电能U n = (-ne )2 / 2 (C S + C D ).4.U n 随 C G V G 变化的图线如图b ;C G V G / e 的变化范围如表2.表2五、1.在图1中,z 轴垂直于AB 面.考察平行光图a束中两条光线分别在AB 面上C 与C ′点以入射角i 射入透明圆柱时的情况,r 为折射角,在圆柱体中两折射光线分别射达圆柱面的 D 和D ′,对圆柱面其入射角分别为i 2与i ′2.在△OCD 中,O 点与入射点C 的距离y c 由正弦定理得y c sin i 2 = R sin ( 90° + r ),即 y c = sin i 2cos r R .(1)同理在△OC ′D ′中,O 点与入射点C ′的距离有y c ′sin i ′2 = R sin ( 90°-r ),即 y c ′= sin i ′2cos r R . (2)当改变入射角 i 时,折射角 r 与柱面上的入射角i 2与 i ′2亦随之变化.在柱面上的入射角满足临界角i 20 = arcsin ( 1 / n )≈41.8° (3)时,发生全反射.将i 2= i ′2=i 20 分别代入式(1),(2)得y o c =y o c ′=sin i 20cos rR , (4)即d = 2y o c = 2sin i 20cos rR . (5)当y c >y o c 和y c ′>y o c ′时,入射光线进入柱体,经过折射后射达柱面时的入射角大于临界角i 20 ,由于发生全反射不能射出柱体.因折射角 r 随入射角 i 增大而增大.由式(4)知,当 r = 0 ,即 i = 0(垂直入射)时,d 取最小值d min = 2R sin i 20 = 1.33R . (6)当 i →90°(掠入射)时,r →41.8° .将 r =41.8°代入式(4)得 d max = 1.79 R .(7)2.由图2可见,φ是 Oz 轴与线段 OD 的夹角,φ′是Oz 轴与线段OD ′的夹角.发生全反射时,有φ=i 20 + r ,(8) φ′=i 20-r , (9)和 θ=φ+φ′=2i 20≈83.6° .(10)由此可见,θ与i 无关,即θ独立于i .在掠入射时,i ≈90°,r =41.8°,由式(8),(9)两式得φ= 83.6° ,φ′= 0°.(11)六、图2由于方程r =GM / c 2a cos φ + a 2 ( 1 + sin 2φ)(1) 是φ的偶函数,光线关于极轴对称.光线在坐标原点左侧的情形对应于a <0 ;光线在坐标原点右侧的情形对应a >0 .右图是a <0的情形,图中极轴为 Ox ,白矮星在原点O 处.在式(1)中代入近星点坐标r =r m ,φ= π,并注意到a 2| a | ,有a ≈-GM / c 2r m .(2)经过白矮星两侧的星光对观测者所张的视角θS 可以有不同的表达方式,相应的问题有不同的解法.解法一:若从白矮星到地球的距离为 d ,则可近似地写出θS ≈2r m / d . (3)在式(1)中代入观测者的坐标 r =d ,φ= -π/ 2,有a 2≈GM / 2c 2d .(4)由(2)与(4)两式消去 a ,可以解出r m =2GMd / c 2.(5)把式(5)代入式(3)得θS ≈8GM / c 2d ; (6)即 M ≈θ2S c 2d / 8G , (7)其中d = 3.787×1017 m ;代入数值就可算出M ≈2.07 ×1030kg .(8)解法二:光线射向无限远处的坐标可以写成r →∞,φ= -π2 + θ2.(9)近似地取θS ≈θ,把式(9)代入式(1),要求式(1)分母为零,并注意到θ1,有a θ / 2 + 2a 2= 0 .所以 θS ≈θ=-4a = 8GM / c 2d ,(10)其中用到式(4),并注意到a <0 .式(10)与式(6)相同,从而也有式(8).解法三:星光对观测者所张的视角 θS 应等于两条光线在观测者处切线的夹角,有sin θS 2=△(r cos φ)△r = cos φ-r sin φ△φ△r.(11)ySr xOEr mφ由光线方程(1)算出△φ/△r,有sin θS2=cosφ-r sinφGM / c2r2a sinφ= cosφ-GMc2ra;代入观测者的坐标r =d, = -π/ 2以及a的表达式(4),并注意到θS很小,就有θS≈2GMc2d2c2dGM=8GMc2d,与式(6)相同.所以,也得到了式(8).解法四:用式(2)把方程(1)改写成-r m = r cosφ-GMc2r m r[ (r cosφ )2 + 2 (r sinφ)2 ] ,即x = -r m+ GMc2r m r( x2 +2y2 ).(12)当y→-∞时,式(12)的渐近式为x = -r m-2GMc2r m y.这是直线方程,它在x轴上的截距为-r m,斜率为1-2GM/c2r m ≈1-tan ( θS / 2 )≈-1θS / 2 .于是有θS ≈4GM/c2r m.r m用式(5)代入后,得到式(6),从而也有式(8).七、1.(I)氦原子中有两个电子,一级电离能E+是把其中一个电子移到无限远处所需要的能量满足He + E+→He++ e-.为了得到氦原子的一级电离能E+,需要求出一个电子电离以后氦离子体系的能量E*.这是一个电子围绕氦核运动的体系,下面给出两种解法.解法一:在力学方程=中,r 是轨道半径,v 是电子速度.对基态,用玻尔量子化条件(角动量为)可以解出r0 =2/ 2ke2m.(1)于是氦离子能量E* =2,2m)-= -2),(2)其中p0为基态电子动量的大小;代入数值得E* = -ke2 )2mc2,(c)2)≈-54.4 eV .(3)由于不计电子间的相互作用,氦原子基态的能量E0 是该值的2倍,即E0 =2E*≈-108.8 eV .(4)氦离子能量E*与氦原子基态能量E0之差就是氦原子的一级电离能E+ =E*-E0= -E*≈ 54.4 eV .(5)解法二:氦离子能量E*= -.把基态的角动量关系rp=代入,式(3)可以改写成E* = 2,2mr2)-= 2,2m) ( -2))2-2).因基态的能量最小,式(4)等号右边的第一项为零,所以半径和能量r0 = 2,2ke2m) ,E*=-2)分别与(1),(2)两式相同.(II)下面,同样给出求氦原子基态能量E0和半径r0的两种解法.解法一:利用力学方程= -2r )2) =和基态量子化条件rmv =,可以解出半径r0 = 42/7ke2m,(6)于是氦原子基态能量,2m)-) + = -2);(7)E0 = 2 (2代入数值算得E 0 =-ke2 )2mc2,16(c)2)≈-83.4 eV ,(8)r 0 = (c)2,7ke2mc2)≈0.0302 nm .所以,氦原子的一级电离能E+ =E*-E0≈ 29.0 eV .(9)这仍比实验测得的氦原子一级电离能24.6 eV 高出4.4 eV .解法二:氦原子能量E = 2 ( -) + = 2,mr2)-可以化成E = 2,m)( -2))2-2) .当上式等号右边第一项为零时,能量最小.由此可知,基态能量与半径E0 =-2) ,r0= 2,7ke2m)分别与(7),(6)两式相同.2.(I)粒子从下部射向并穿过铅板向上运动,其电荷为正.(II)如题图所示,粒子的运动速度v 与磁场方向垂直,洛伦兹力在纸面内;磁力不改变荷电粒子动量的大小,只改变其方向.若不考虑云室中气体对粒子的阻力,荷电粒子在恒定磁场作用下的运动轨迹就是曲率半径为一定值的圆弧;可以写出其运动方程qBv=||= φ,△t)= ,(1)其中q 是粒子电荷,v是粒子速度的大小,p是粒子动量的大小,△φ是粒子在△t时间内转过的角度,r是轨迹曲率半径.于是有p=qBr .(2)按题意,q=e .用p d 和p u 分别表示粒子射入铅板和自铅板射出时动量的大小,并在式(1)中代入有关数据,可以算得p d=63.0MeV / c ,p u= 22.8MeV / c.(3)注意到当pc mc2 时应使用狭义相对论,从p=/ c)2)).(4)中可以得到v=/ p)2 )).(5)用v d 和v u分别表示粒子进入和离开铅板时的速度大小.把式(2)以及m = 0.511 MeV / c2代入式(3),可得v d ≈c,v u≈c.(6)于是,粒子穿过铅板的平均速度v= ( 1 / 2 ) ( v d+v u)≈c.用△t表示粒子穿过铅板的时间,则有v cosθ△t = d.(7)再用△p du表示粒子穿过铅板动量改变量的大小,铅板所受到的平均力的大小f= = / (v cosθ))≈p d-p u)c cosθ,d);(8)代入有关数值得f ≈1.04×10-9N .(9)。
第25届全国中学生物理竞赛复赛试题(含答案)

第25届全国中学生物理竞赛复赛试卷本卷共八题,满分160分 一、(15分) 1.(5分)蟹状星云脉冲星的辐射脉冲周期是0.033s 。
假设它是由均匀分布的物质构成的球体,脉冲周期是它的旋转周期,万有引力是唯一能阻止它离心分解的力,已知万有引力常量113126.6710G m kg s ---=⨯⋅⋅,由于脉冲星表面的物质未分离,故可估算出此脉冲星密度的下限是 3kg m -⋅。
2.(5分)在国际单位制中,库仑定律写成122q q F kr =,式中静电力常量9228.9810k N m C -=⨯⋅⋅,电荷量q 1和q 2的单位都是库仑,距离r 的单位是米,作用力F 的单位是牛顿。
若把库仑定律写成更简洁的形式122q q F r=,式中距离r 的单位是米,作用力F 的单位是牛顿。
若把库仑定律写成更简洁的形式122q qF r=,式中距离r 的单位是米,作用力F 的单位是牛顿,由此式可这义一种电荷量q 的新单位。
当用米、千克、秒表示此新单位时,电荷新单位= ;新单位与库仑的关系为1新单位= C 。
3.(5分)电子感应加速器(betatron )的基本原理如下:一个圆环真空室处于分布在圆柱形体积内的磁场中,磁场方向沿圆柱的轴线,圆柱的轴线过圆环的圆心并与环面垂直。
圆中两个同心的实线圆代表圆环的边界,与实线圆同心的虚线圆为电子在加速过程中运行的轨道。
已知磁场的磁感应强度B 随时间t 的变化规律为0cos(2/)B B t T π=,其中T 为磁场变化的周期。
B 0为大于0的常量。
当B 为正时,磁场的方向垂直于纸面指向纸外。
若持续地将初速度为v 0的电子沿虚线圆的切线方向注入到环内(如图),则电子在该磁场变化的一个周期内可能被加速的时间是从t= 到t= 。
二、(21分)嫦娥1号奔月卫星与长征3号火箭分离后,进入绕地运行的椭圆轨道,近地点离地面高22.0510n H km =⨯,远地点离地面高45.093010f H km =⨯,周期约为16小时,称为16小时轨道(如图中曲线1所示)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年第25届全国中学生物理竞赛复赛试卷本卷共八题,满分160分 一、(15分) 1、(5分)蟹状星云脉冲星的辐射脉冲周期是0.033s 。
假设它是由均匀分布的物质构成的球体,脉冲周期是它的旋转周期,万有引力是唯一能阻止它离心分解的力,已知万有引力常量113126.6710G m kg s ---=⨯⋅⋅,由于脉冲星表面的物质未分离,故可估算出此脉冲星密度的下限是3kg m -⋅。
2、(5分)在国际单位制中,库仑定律写成122q q F kr=,式中静电力常量9228.9810k N m C -=⨯⋅⋅,电荷量q 1和q 2的单位都是库仑,距离r 的单位是米,作用力F 的单位是牛顿。
若把库仑定律写成更简洁的形式122q q F r =,式中距离r 的单位是米,作用力F 的单位是牛顿。
若把库仑定律写成更简洁的形式122q q F r=,式中距离r 的单位是米,作用力F 的单位是牛顿,由此式可这义一种电荷量q 的新单位。
当用米、千克、秒表示此新单位时,电荷新单位= ;新单位与库仑的关系为1新单位= C 。
3、(5分)电子感应加速器(betatron )的基本原理如下:一个圆环真空室处于分布在圆柱形体积内的磁场中,磁场方向沿圆柱的轴线,圆柱的轴线过圆环的圆心并与环面垂直。
圆中两个同心的实线圆代表圆环的边界,与实线圆同心的虚线圆为电子在加速过程中运行的轨道。
已知磁场的磁感应强度B 随时间t 的变化规律为0cos(2/)B B t T π=,其中T为磁场变化的周期。
B 0为大于0的常量。
当B 为正时,磁场的方向垂直于纸面指向纸外。
若持续地将初速度为v 0的电子沿虚线圆的切线方向注入到环内(如图),则电子在该磁场变化的一个周期内可能被加速的时间是从t= 到t= 。
二、(21分)嫦娥1号奔月卫星与长征3号火箭分离后,进入绕地运行的椭圆轨道,近地点离地面高22.0510n H km =⨯,远地点离地面高45.093010f H km =⨯,周期约为16小时,称为16小时轨道(如图中曲线1所示)。
随后,为了使卫星离地越来越远,星载发动机先在远地点点火,使卫星进入新轨道(如图中曲线2所示),以抬高近地点。
后来又连续三次在抬高以后的近地点点火,使卫星加速和变轨,抬高远地点,相继进入24小时轨道、48小时轨道和地月转移轨道(分别如图中曲线3、4、5所示)。
已知卫星质量32.35010m kg =⨯,地球半径36.37810R km =⨯,地面重力加速度29.81/g m s =,月球半径31.73810r km =⨯。
1、试计算16小时轨道的半长轴a 和半短轴b 的长度,以及椭圆偏心率e 。
2、在16小时轨道的远地点点火时,假设卫星所受推力的方向与卫星速度方向相同,而且点火时间很短,可以认为椭圆轨道长轴方向不变。
设推力大小F=490N ,要把近地点抬高到600km ,问点火时间应持续多长?3、试根据题给数据计算卫星在16小时轨道的实际运行周期。
4、卫星最后进入绕月圆形轨道,距月面高度H m 约为200km ,周期T m =127分钟,试据此估算月球质量与地球质量之比值。
三、(22分)足球射到球门横梁上时,因速度方向不同、射在横梁上的位置有别,其落地点也是不同的。
已知球门的横梁为圆柱形,设足球以水平方向的速度沿垂直于横梁的方向射到横梁上,球与横梁间的滑动摩擦系数0.70μ=,球与横梁碰撞时的恢复系数e=0.70。
试问足球应射在横梁上什么位置才能使球心落在球门线内(含球门上)?足球射在横梁上的位置用球与横梁的撞击点到横梁轴线的垂线与水平方向(垂直于横梁的轴线)的夹角θ(小于90)来表示。
不计空气及重力的影响。
四、(20分)图示为低温工程中常用的一种气体、蒸气压联合温度计的原理示意图,M 为指针压力表,以V M 表示其中可以容纳气体的容积;B 为测温饱,处在待测温度的环境中,以V B 表示其体积;E 为贮气容器,以V E 表示其体积;F 为阀门。
M 、E 、B 由体积可忽略的毛细血管连接。
在M 、E 、B 均处在室温T 0=300K 时充以压强50 5.210p Pa =⨯的氢气。
假设氢的饱和蒸气仍遵从理想气体状态方程。
现考察以下各问题:1、关闭阀门F ,使E 与温度计的其他部分隔断,于是M 、B 构成一简易的气体温度计,用它可测量25K 以上的温度, 这时B 中的氢气始终处在气态,M 处在室温中。
试导出B 处的温度T 和压力表显示的压强p 的关系。
除题中给出的室温T 0时B 中氢气的压强P 0外,理论上至少还需要测量几个已知温度下的压强才能定量确定T 与p 之间的关系?2、开启阀门F ,使M 、E 、B 连通,构成一用于测量20~25K 温度区间的低温的蒸气压温度计,此时压力表M 测出的是液态氢的饱和蒸气压。
由于饱和蒸气压与温度有灵敏的依赖关系,知道了氢的饱和蒸气压与温度的关系,通过测量氢的饱和蒸气压,就可相当准确地确定这一温区的温度。
在设计温度计时,要保证当B 处于温度低于25V T K =时,B 中一定要有液态氢存在,而当温度高于25V T K =时,B 中无液态氢。
到达到这一目的,M E V V +与V B 间应满足怎样的关系?已知25V T K =时,液态氢的饱和蒸气压53.310V p Pa =⨯。
3、已知室温下压强51 1.0410p Pa =⨯的氢气体积是同质量的液态氢体积的800倍,试论证蒸气压温度计中的液态气不会溢出测温泡B 。
五、(20分)一很长、很细的圆柱形的电子束由速度为v 的匀速运动的低速电子组成,电子在电子束中均匀分布,沿电子束轴线每单位长度包含n 个电子,每个电子的电荷量为(0)e e ->,质量为m 。
该电子束从远处沿垂直于平行板电容器极板的方向射向电容器,其前端(即图中的右端)于t=0时刻刚好到达电容器的左极板。
电容器的两个极板上各开一个小孔,使电子束可以不受阻碍地穿过电容器。
两极板A 、B 之间加上了如图所示的周期性变化的电压AB V (AB A B V V V =-,图中只画出了一个周期的图线),电压的最大值和最小值分别为V 0和-V 0,周期为T 。
若以τ表示每个周期中电压处于最大值的时间间隔,则电压处于最小值的时间间隔为T -τ。
已知τ的值恰好使在V AB 变化的第一个周期内通过电容器到达电容器右边的所有的电子,能在某一时刻t b 形成均匀分布的一段电子束。
设电容器两极板间的距离很小,电子穿过电容器所需要的时间可以忽略,且206mv eV =,不计电子之间的相互作用及重力作用。
1、满足题给条件的τ和t b 的值分别为τ= T ,t b = T 。
2、试在下图中画出t=2T 那一时刻,在0-2T 时间内通过电容器的电子在电容器右侧空间形成的电流I ,随离开右极板距离x 的变化图线,并在图上标出图线特征点的纵、横坐标(坐标的数字保留到小数点后第二位)。
取x 正向为电流正方向。
图中x=0处为电容器的右极板B 的小孔所在的位置,横坐标的单位0eV s m=。
(本题按画出的图评分,不须给出计算过程)六、(22分)零电阻是超导体的一个基本特征,但在确认这一事实时受到实验测量精确度的限制。
为克服这一困难,最著名的实验是长时间监测浸泡在液态氦(温度T=4.2K )中处于超导态的用铅丝做成的单匝线圈(超导转换温度T C =7.19K )中电流的变化。
设铅丝粗细均匀,初始时通有I=100A 的电流,电流检测仪器的精度为 1.0I mA ∆=,在持续一年的时间内电流检测仪器没有测量到电流的变化。
根据这个实验,试估算对超导态铅的电阻率为零的结论认定的上限为多大。
设铅中参与导电的电子数密度2038.0010n m =⨯,已知电子质量319.1110m kg -=⨯,基本电荷191.6010e C -=⨯。
(采用的估算方法必须利用本题所给出的有关数据)七、(20分)在地面上方垂直于太阳光的入射方向,放置一半径R=0.10m 、焦距f=0.50m 的薄凸透镜,在薄透镜下方的焦面上放置一黑色薄圆盘(圆盘中心与透镜焦点重合),于是可以在黑色圆盘上形成太阳的像。
已知黑色圆盘的半径是太阳像的半径的两倍。
圆盘的导热性极好,圆盘与地面之间的距离较大。
设太阳向外辐射的能量遵从斯特藩—玻尔兹曼定律:在单位时间内在其单位表面积上向外辐射的能量为4W T σ=,式中σ为斯特藩—玻尔兹曼常量,T 为辐射体表面的的绝对温度。
对太而言,取其温度35.5010s t C =⨯。
大气对太阳能的吸收率为0.40α=。
又设黑色圆盘对射到其上的太阳能全部吸收,同时圆盘也按斯特藩—玻尔兹曼定律向外辐射能量。
如果不考虑空气的对流,也不考虑杂散光的影响,试问薄圆盘到达稳定状态时可能达到的最高温度为多少摄氏度?八、(20分)质子数与中子数互换的核互为镜像核,例如3He 是3H 的镜像核,同样3H 是3He 的镜像核。
已知3H 和3He 原子的质量分别是3 3.016050H m u =和3 3.016029He m u =,中子和质子质量分别是 1.008665n m u =和 1.007825p m u =,2931.51u MeV c =,式中c 为光速,静电力常量21.44k MeV fm e=⋅,式中e 为电子的电荷量。
1、试计算3H 和3He 的结合能之差为多少MeV 。
2、已知核子间相互作用的“核力”与电荷几乎没有关系,又知质子和中子的半径近似相等,试说明上面所求的结合能差主要是由什么原因造成的。
并由此结合能之差来估计核子半径r N 。
3、实验表明,核子可以被近似地看成是半径r N 恒定的球体;核子数A 较大的原子核可以近似地被看成是半径为R 的球体。
根据这两点,试用一个简单模型找出R 与A 的关系式;利用本题第2问所求得的r N 的估计值求出此关系式中的系数;用所求得的关系式计算208Pb 核的半径pb R 。
第25届全国中学生物理竞赛复赛理论试题参考解答一、答案1. 14103.1⨯ 2. 31122kg m s -⋅⋅ 51.0610-⨯(答51.0510-⨯也给)3.34T T 二、参考解答:1. 椭圆半长轴a 等于近地点和远地点之间距离的一半,亦即近地点与远地点矢径长度(皆指卫星到地心的距离)n r 与f r 的算术平均值,即有 ()()()()n f n f n f 111222a r r H R H R H H R =+=+++=++⎡⎤⎣⎦ (1) 代入数据得43.194610a =⨯km (2) 椭圆半短轴b 等于近地点与远地点矢径长度的几何平均值,即有b = (3)代入数据得41.94210km b =⨯ (4) 椭圆的偏心率ab a e 22-= (5)代入数据即得0.7941e = (6)2. 当卫星在16小时轨道上运行时,以n v 和f v 分别表示它在近地点和远地点的速度,根据能量守恒,卫星在近地点和远地点能量相等,有22n f n f1122GMm GMm m m r r -=-v v (7) 式中M 是地球质量,G 是万有引力常量. 因卫星在近地点和远地点的速度都与卫星到地心的连线垂直,根据角动量守恒,有n n f f m r m r =v v (8) 注意到g RGM=2 (9)由(7)、(8)、(9)式可得n =v (10)n f n f r r ==v v (11) 当卫星沿16小时轨道运行时,根据题给的数据有n n r R H =+ f f r R H =+ 由(11)式并代入有关数据得f 1.198=v km/s (12)依题意,在远地点星载发动机点火,对卫星作短时间加速,加速度的方向与卫星速度方向相同,加速后长轴方向没有改变,故加速结束时,卫星的速度与新轨道的长轴垂直,卫星所在处将是新轨道的远地点.所以新轨道远地点高度4f f 5.093010H H '==⨯km ,但新轨道近地点高度2n6.0010H '=⨯km .由(11)式,可求得卫星在新轨道远地点处的速度为 f 1.230'=v km/s (13) 卫星动量的增加量等于卫星所受推力F 的冲量,设发动机点火时间为∆t ,有()f f m F t '-=∆v v (14) 由(12)、(13)、(14)式并代入有关数据得∆t=21.510s ⨯ (约2.5分) (15) 这比运行周期小得多.3. 当卫星沿椭圆轨道运行时,以r 表示它所在处矢径的大小,v 表示其速度的大小,θ表示矢径与速度的夹角,则卫星的角动量的大小sin 2L rm m θσ==v (16 ) 其中1sin 2r σθ=v (17)是卫星矢径在单位时间内扫过的面积,即卫星的面积速度.由于角动量是守恒的,故σ是恒量.利用远地点处的角动量,得f f 12r σ=v (18)又因为卫星运行一周扫过的椭圆的面积为πS ab = (19) 所以卫星沿轨道运动的周期σST =(20)由(18)、(19)、(20) 式得f f2πabT r =v (21) 代入有关数据得45.67810T =⨯s (约15小时46分) (22)注:本小题有多种解法.例如,由开普勒第三定律,绕地球运行的两亇卫星的周期T 与T 0之比的平方等于它们的轨道半长轴a 与a 0之比的立方,即2300T a T a ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭若0a 是卫星绕地球沿圆轨道运动的轨道半径,则有202002πGMm ma a T ⎛⎫= ⎪⎝⎭得 22203204π4πT a GM gR ==从而得2πaa T R g=代入有关数据便可求得(22)式.4. 在绕月圆形轨道上,根据万有引力定律和牛顿定律有2m m 2m m2π()GM m mr r T = (23) 这里m m r r H =+是卫星绕月轨道半径,m M 是月球质量. 由(23)式和(9)式,可得23mm 22m4πr M M gR T = (24) 代入有关数据得m0.0124M M= (25)三、参考解答:足球射到球门横梁上的情况如图所示(图所在的平面垂直于横梁轴线).图中B 表示横梁的横截面,O 1为横梁的轴线;11O O '为过横梁轴线并垂直于轴线的水平线;A 表示足球,O 2为其球心;O 点为足球与横梁的碰撞点,碰撞点O 的位置由直线O 1OO 2与水平线11O O '的夹角θ 表示.设足球射到横梁上时球心速度的大小为v 0,方向垂直于横梁沿水平方向,与横梁碰撞后球心速度的大小为v ,方向用它与水平方向的夹角ϕ表示(如图).以碰撞点O 为原点作直角坐标系Oxy ,y 轴与O 2OO 1重合.以α0表示碰前速度的方向与y 轴的夹角,以α表示碰后速度的方向与y 轴(负方向)的夹角,足球被横梁反弹后落在何处取决于反弹后的速度方向,即角α的大小.以F x 表示横梁作用于足球的力在x 方向的分量的大小,F y 表示横梁作用于足球的力在y 方向的分量的大小,∆t 表示横梁与足球相互作用的时间,m 表示足球的质量,有x 0x x F t m m ∆=-v v (1) y y 0y F t m m ∆=+v v (2)式中0x v 、0y v 、x v 和y v 分别是碰前和碰后球心速度在坐标系Oxy 中的分量的大小.根据摩擦定律有 x y F F μ= (3) 由(1)、(2)、(3)式得 0x xy 0yμ-=+v v v v (4)根据恢复系数的定义有y 0y e =v v (5) 因0x00ytan α=v v (6) xytan α=v v (7) 由(4)、(5)、(6)、(7)各式得⎪⎭⎫⎝⎛+-=e e 11tan 1tan 0μαα (8) 由图可知αθϕ+= (9) 若足球被球门横梁反弹后落在球门线内,则应有90ϕ≥ (10) 在临界情况下,若足球被反弹后刚好落在球门线上,这时90ϕ=.由(9)式得()tan 90tan θα-= (11) 因足球是沿水平方向射到横梁上的,故θα=0,有⎪⎭⎫⎝⎛+-=e e 11tan 1tan 1μθθ (12) 这就是足球反弹后落在球门线上时入射点位置θ所满足的方程.解(12)式得tan θ= (13)代入有关数据得tan 1.6θ= (14) 即58θ= (15) 现要求球落在球门线内,故要求58θ≥ (16)四、参考解答:1. 当阀门F 关闭时,设封闭在M 和B 中的氢气的摩尔数为n 1,当B 处的温度为T 时,压力表显示的压强为 p ,由理想气体状态方程,可知B 和M 中氢气的摩尔数分别为 RTpV n BB 1=(1) 0MM 1RT pV n = (2) 式中R 为普适气体恒量.因1M 1B 1n n n =+ (3) 解(1)、(2)、(3)式得 1MB B 011n R V T V p V T =- (4) 或1MB B 0p T n R V p V V T =- (5)(4)式表明,T 1与p1成线性关系,式中的系数与仪器结构有关.在理论上至少要测得两个已知温度下的压强,作T1对p 1的图线,就可求出系数. 由于题中己给出室温T 0时的压强p 0,故至少还要测定另一己知温度下的压强,才能定量确定T 与p 之间的关系式.2. 若蒸气压温度计测量上限温度v T 时有氢气液化,则当B 处的温度v T T ≤时,B 、M 和E 中气态氢的总摩尔数应小于充入氢气的摩尔数.由理想气体状态方程可知充入氢气的总摩尔数 ()0B M E 20p V V V n RT ++=(6)假定液态氢上方的气态氢仍可视为理想气体,则B 中气态氢的摩尔数为 v B2B vp V n RT =(7) 在(7)式中,已忽略了B 中液态氢所占的微小体积.由于蒸气压温度计的其它都分仍处在室温中,其中氢气的摩尔数为()νM E 2M 2E 0p V V n n RT ++= (8)根据要求有2B 2M 2E 2n n n n ++≤ (9) 解(6)、(7)、(8)、(9)各式得()B vv 0v00v E M V T p p T p T p V V --≥+ (10)代入有关数据得M E B 18V V V +≥ (11)五、答案与评分标准:1.59.022122=-=+(3分) 2 (2分)2.如图(15分.代表电流的每一线段3分,其中线段端点的横坐标占1分,线段的长度占1分,线段的纵坐标占1分)六、参考解答:如果电流有衰减,意味着线圈有电阻,设其电阻为R ,则在一年时间t 内电流通过线圈因发热而损失的能量为Rt I E 2=∆ (1) 以ρ 表示铅的电阻率,S 表示铅丝的横截面积,l 表示铅丝的长度,则有 SlR ρ= (2) 电流是铅丝中导电电子定向运动形成的,设导电电子的平均速率为v ,根据电流的定义有 I S ne =v (3) 所谓在持续一年的时间内没有观测到电流的变化,并不等于电流一定没有变化,但这变化不会超过电流检测仪器的精度∆I ,即电流变化的上限为mA 0.1=∆I .由于导电电子的数密度n 是不变的,电流的变小是电子平均速率变小的结果,一年内平均速率由v 变为 v -∆v ,对应的电流变化 I neS ∆=∆v (4) 导电电子平均速率的变小,使导电电子的平均动能减少,铅丝中所有导电电子减少的平均动能为 ()221122k E lSn m m ⎡⎤∆=--∆⎢⎥⎣⎦v v v lSnm ≈∆v v (5)由于∆I<<I ,所以∆v <<v ,式中∆v 的平方项已被略去.由(3)式解出 v ,(4)式解出 ∆v ,代入(5)式得2k lmI IE ne S∆∆=(6) 铅丝中所有导电电子减少的平均动能就是一年内因发热而损失的能量,即E E k ∆=∆ (7)由(1)、(2)、(6)、(7)式解得 2Δm I ne Itρ=(8) 式中7365243600s=3.1510s t =⨯⨯⨯ (9) 在(8)式中代入有关数据得261.410Ωm ρ-=⨯⋅ (10)所以电阻率为0的结论在这一实验中只能认定到m Ω104.126⋅⨯≤-ρ (11)七、参考解答:按照斯特藩-玻尔兹曼定律,在单位时间内太阳表面单位面积向外发射的能量为4s sW T σ=(1)其中σ为斯特藩-玻尔兹曼常量,T s 为太阳表面的绝对温度.若太阳的半径为R s ,则单位时间内整个太阳表面向外辐射的能量为2s s s 4πP R W = (2)单位时间内通过以太阳为中心的任意一个球面的能量都是s P .设太阳到地球的距离为r se ,考虑到地球周围大气的吸收,地面附近半径为R 的透镜接收到的太阳辐射的能量为 ()2s 2seπ14πP P R r α=- (3) 薄凸透镜将把这些能量会聚到置于其后焦面上的薄圆盘上,并被薄圆盘全部吸收.另一方面,因为薄圆盘也向外辐射能量.设圆盘的半径为D R ,温度为D T ,注意到簿圆盘有两亇表面,故圆盘在单位时间内辐射的能量为24D D D 2πP R T σ=⋅⋅ (4)显然,当D P P = (5) 即圆盘单位时间内接收到的能量与单位时间内辐射的能量相等时,圆盘达到稳定状态,其温度达到最高.由(1)、(2)、(3)、(4)、(5)各式得()1224s D s 22se D12R R T T r R α⎡⎤=-⎢⎥⎣⎦(6) 依题意,薄圆盘半径为太阳的像的半径s R '的2倍,即D 2s R R '=.由透镜成像公式知s sseR R f r '= (7) 于是有sD se2R R f r = (8) 把(8)式代入(6)式得()124D s 218R T T f α⎡⎤=-⎢⎥⎣⎦(9) 代入已知数据,注意到s s (273.15)T t =+K , T D =1.4×103K (10)即有3oD D 273.15 1.110C t T =-=⨯ (11)八、参考解答:1.根据爱因斯坦质能关系,3H 和3He 的结合能差为()332n p H He B m m m m c ∆=--+ (1) 代入数据,可得763.0=∆B MeV (2)2.3He 的两个质子之间有库仑排斥能,而3H 没有.所以3H 与3He 的结合能差主要来自它们的库仑能差.依题意,质子的半径为N r ,则3He 核中两个质子间的库仑排斥能为2C N2e E k r = (3)若这个库仑能等于上述结合能差,C E B =∆,则有2N 2Δke r B= (4)代入数据,可得N 0.944r =fm (5)3.粗略地说,原子核中每个核子占据的空间体积是 3N (2)r .根据这个简单的模型,核子数为A的原子核的体积近似为33N N (2)8V A r Ar == (6)另一方面,当A 较大时,有 343V R π=(7) 由(6)式和(7)式可得R 和A 的关系为1/31/31/3N 06πR r A r A ⎛⎫== ⎪⎝⎭(8)其中系数1/30N 6πr r ⎛⎫= ⎪⎝⎭(9)把(5)式代入(9)式得17.10=r fm (10) 由(8)式和(10)式可以算出Pb 208的半径Pb 6.93fm R = (11)。
