考点27 空间向量求空间距离(练习) (原卷版)
用空间向量求距离

计算点到直线距离
利用向量数量积的性质,有$vec{PQ} cdot vec{n} = 0$,进而求得点
$P$到直线的距离$d = frac{|Ax_0 + By_0 + C|}{sqrt{A^2 + B^2}}$。
公式在实际问题中应用场景
几何问题
01
在平面几何中,点到直线的距离公式可用于求解点到直线的最
计算向量$vec{AB}$
$vec{AB} = (x_2 - x_1, y_2 - y_1, z_2 z_1)$。
计算向量$vec{AB}$的模
得出两点间距离公式
$|vec{AB}| = sqrt{(x_2 - x_1)^2 + (y_2 y_1)^2 + (z_2 - z_1)^2}$。
$d = sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$。
公式在实际问题中应用场景
1 2 3
空间几何问题
在解决涉及三维空间中点、线、面等几何元素的 问题时,两点间距离公式可用于计算两点之间的 距离。
物理问题
在物理学中,两点间距离公式可用于计算质点之 间的距离,进而解决与距离相关的物理问题,如 万有引力、电场强度等。
工程测量
在土木工程、水利工程等领域,两点间距离公式 可用于测量地面上两点之间的水平距离或空间中 两点之间的直线距离。
短距离、判断点与直线的位置关系等问题。
物理问题
02
在物理学中,点到直线的距离公式可用于计算电场强度、磁场
强度等物理量在空间中的分布情况。
工程问题
03
在工程领域中,点到直线的距离公式可用于计算建筑物之间的
空间向量求空间距离2023年高考数学一轮复习(基础版)(新高考地区专用)
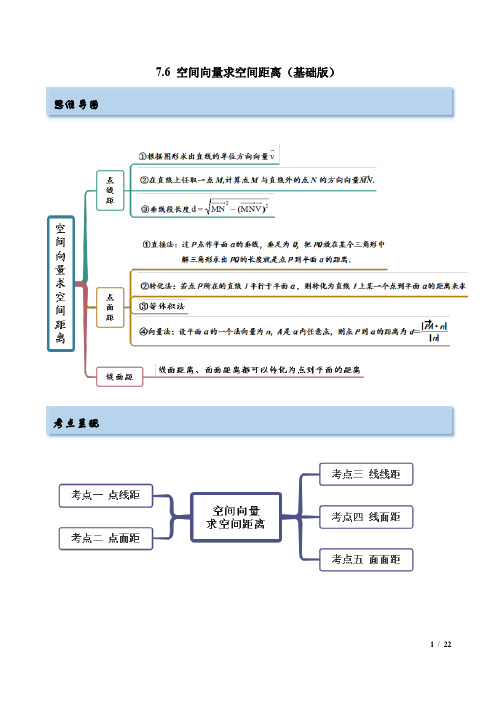
7.6 空间向量求空间距离(基础版)思维导图考点呈现考点一 点线距【例1】(2022·福建)在空间直角坐标系中,点()()()1,2,0,0,1,0,2,2,2A B P ,则P 到直线AB 的距离为___.【答案】322【解析】依题意得()1,1,0AB =--,()1,0,2AP =则P 到直线AB 的距离为22132522AP AB d AP AB ⎛⎫⋅ ⎪=-=-= ⎪⎝⎭故答案为:322【一隅三反】1(2022·北京·二模)如图,已知正方体1111ABCD A B C D -的棱长为1,则线段1AD 上的动点P 到直线11A C 的距离的最小值为( )A .1B .22C .64D .33【答案】D【解析】如图建立空间直角坐标系,则()()111,0,1,0,1,1A C ,例题剖析设(),0,1,01P x x x -≤≤,则()()1111,0,,1,1,0A P x x AC =--=-, ∴动点P 到直线11A C 的距离为()()22222111111112A P AC xd A P x x AC ⋅-=-=-+--2231311322233x x x ⎛⎫-+-+ ⎪⎝⎭13x =时取等号, 即线段1AD 上的动点P 到直线11A C 3故选:D.2.(2022·浙江绍兴)如图,在正三棱柱111ABC A B C -中,若122AB BB ==,则C 到直线1AB 的距离为( )A 15B 10C 15D30【答案】D【解析】由题意知,122AC AB BB ==, 取AC 的中点O ,则3BO AC BO ⊥=,建立如图所示的空间直角坐标系O xyz -, 则1(0,1,0)(3,0,2)(0,1,0)A B C -,,, 所以1(3,1,2)(0,2,0)AB CA ==-,, 所以CA 在1AB 上的投影的长度为11266CA AB AB ⋅== 故点C 到直线1AB 的距离为:22630()3d AC =- 故选:D3.(2022·广东)如图,在棱长为4的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在线段1D E 上,点Р到直线1CC 的距离的最小值为_______.45【解析】在正方体1111ABCD A B C D -中,建立如图所示的空间直角坐标系,则11(0,4,0),(0,0,4),(2,4,0),(0,4,4)C D E C ,11(2,0,0),(0,0,4),(2,4,4)CE CC ED ===--, 因点P 在线段1D E 上,则[0,1]λ∈,1(2,4,4)EP ED λλλλ==--,(22,4,4)CP CE EP λλλ=+=--,向量CP 在向量1CC 上投影长为11||4||CP CC d CC λ⋅==,而222||(22)(4)(4)CP λλλ=-+-+Р到直线1CC 的距离22221445||25215()55h CP d λλλ=-=-+=-+15λ=时取“=”,所以点Р到直线1CC 4545考点二 点面距【例2】(2022·江苏常州)已知正方体1111ABCDA B C D -的棱长为2,E ,F 分别为上底面1111D C B A 和侧面11CDD C 的中心,则点C 到平面AEF 的距离为( )A 411B 11C 11D 211【答案】A【解析】如图,以A 为原点,1,,AB AD AA 所在直线为,,x y z 轴建立空间直角坐标系,易知(0,0,0),(1,1,2),(1,2,1),(2,2,0)A E F C ,设平面AEF 的法向量(,,)n x y z =,则2020n AE x y z n AF x y z ⎧⋅=++=⎨⋅=++=⎩,令1y =-,解得(3,1,1)n =--,故点C 到平面AEF 的距离为6411911n AC n⋅-==++. 故选:A. 【一隅三反】1.(2022·哈尔滨)在长方体1111ABCD A B C D -中,2AB AD ==,11AA =,则点B 到平面1D AC 的距离等于_____. 6【解析】如图,以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴, 建立空间直角坐标系,则()220B ,,,()200A ,,,()020C ,,,()1001D ,,, ()020AB =,,,()220AC =-,,,()1201AD =-,,,设平面1D AC 的法向量()n x y z =,,,则122020n AC x y n AD x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩,取1x =,得()112n =,,, ∴点B 到平面1D AC 的距离:266AB n d n⋅=== 62.(2022·江苏)2的正方形ABCD 沿对角线BD 折成直二面角,则点D 到平面ABC 的距离为___. 23【解析】记AC 与BD 的交点为O ,图1中,由正方形性质可知AC BD ⊥, 所以在图2中,,OB AC OD AC ⊥⊥,所以2BOD π∠=,即OB OD ⊥如图建立空间直角坐标系,易知1OA OB OC OD ==== 则(0,0,1),(0,1,0),(1,0,0),(0,1,0)A B C D - 则(0,1,1),(1,0,1),(0,2,0)AB AC BD =--=-= 设(,,)n x y z =为平面ABC 的法向量,则00AB n y z AC n x z ⎧⋅=--=⎨⋅=-=⎩,取1x =,得(1,1,1)n =-所以点D 到平面ABC 的距离2233BD n d n⋅=== 233.(2022·福建福州)如图,在正四棱柱1111ABCD A B C D -中,已知2AB AD ==,15AA =,E ,F 分别为1DD ,1BB 上的点,且11DE B F ==.(1)求证:BE ⊥平面ACF : (2)求点B 到平面ACF 的距离.【答案】(1)证明见详解.(2)43.【解析】(1)以D 为坐标原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴建立空间直角坐标系,如下图所示:则()()()()()2,0,0,2,2,0,0,2,0,0,0,1,2,2,4A B C E F ,设面ACF 的一个法向量为()=,,n x y z ,()()=2,2,0,0,2,4AC AF -=,可得00n AC n AF ⎧⋅=⎪⎨⋅=⎪⎩,即220240x y y z -+=⎧⎨+=⎩,不妨令1z =则()=2,2,1n BE --=,BE ∴⊥平面ACF .(2)()=0,2,0AB ,则点B 到平面ACF 的距离为43AB n n⋅=. 考点三 线线距【例3】(2022·全国·高三专题练习)在长方体1111ABCD A B C D -中,1AB =,2BC =,13AA =,则异面直线AC 与1BC 之间的距离是( )A 5B 7C 6D .67【答案】D【解析】如图所示,以D 为原点,1,,DA DC DD 所在直线为,,x y z 轴如图建立空间直角坐标系 则1(2,0,0),(0,1,0),(2,1,0),(0,1,3)A C B C 1(2,1,0),(2,0,3)CA BC ∴=-=-设直线AC 与1BC 的公垂线的方向向量为(,,)n x y z =则12002300x y n CA x z n BC ⎧-=⋅=⎧⎪∴⎨⎨-+=⋅=⎪⎩⎩不妨令23,6(3,6,2)z x y n =∴==∴=又(0,1,0)AB =则异面直线AC 与1BC 之间的距离2226||7||362AB n d n ⋅===++故选:D【一隅三反】1.(2022·山东)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在长方体1111ABCD A B C D -中,1AB =,2BC =,13AA =,则异面直线AC 与1BC 之间的距离是( ) A 5B 7C 6D .67【答案】D【解析】如图,以D 为坐标原点建立空间直角坐标系,则()()()()12,0,0,0,1,0,2,1,0,0,1,3A C B C ,则()2,1,0AC =-,()12,0,3BC =-, 设AC 和1BC 的公垂线的方向向量(),,n x y z =,则100n AC n BC ⎧⋅=⎪⎨⋅=⎪⎩,即20230x y x z -+=⎧⎨-+=⎩,令3x =,则()3,6,2n =,()0,1,0AB =,67AB n d n⋅∴==.故选:D.【点睛】2.(2022·江苏)长方体1111ABCD A B C D -中,12AB AA ==,1AD =,E 为1CC 的中点,则异面直线1BC 与AE 之间的距离是( )A .13B 21C .23D 221【答案】D【解析】建立如图所示的空间直角坐标系,则(1,0,0)A ,(1,2,0)B ,(0,2,0)C ,1(0,2,2)C ,(0,2,1)E , (1,2,1)AE =-,1(1,0,2)BC =-,设1BC 与AE 的公垂线的一个方向向量为(,,)n x y z =,则12020n AE x y z n BC x z ⎧⋅=-++=⎪⎨⋅=-+=⎪⎩,取1z =,得2x =,12y =,即1(2,,1)2n =,又(0,2,0)AB =,所以异面直线1BC 与AE 之间的距离为22212221212()12AB n d n⨯⋅===++D .3.(2022·全国·高三专题练习)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在棱长为1的正方体1111ABCD A B C D -中,直线AC 与1BC 之间的距离是( )A 2B 3C .12D .13【答案】B【解析】设M 为直线AC 上任意一点, 过M 作1MN BC ⊥,垂足为N ,可知此时M 到直线1BC 距离最短 设AM AC AB AD λλλ==+,11BN BC AD AA μμμ==+,则1(1)()MN AN AM AB BN AM AB AD AA λμλμ=-=+-=-+-+,11BC AA AD =+,1MN BC ⊥,∴1·0MN BC =,即11[(1)()]()0AB AD AA AD AA λμλμ-+-+⋅+=,221()0AD AA μλμ∴-+=,即0μλμ-+=, 2λμ∴=,∴1(12)MN AB AD AA μμμ=--+,()()()2112222212121112641633MN AB AD AA AB AD AA μμμμμμμμμμμμ⎡⎤∴=--+=--+⎣⎦⎛⎫-++-+-+⎪⎝⎭∴当13μ=时,||MN 133=故直线AC 与1BC 3故选:B.考点四 线面距【例4】(2022广西)如图,已知斜三棱柱1111902ABC A B C BCA AC BC A ∠-=︒==,,,在底面ABC 上的射影恰为AC 的中点D ,又知11BA AC ⊥.(1)求证:1AC ⊥平面1A BC ; (2)求1CC 到平面1A AB 的距离. 【答案】(1)证明见解析221【解析】(1)证明:∴1A 在底面ABC 上的射影为AC 的中点D ,∴平面11A ACC ⊥平面ABC ,∴BC AC ⊥,且平面11A ACC ⋂平面ABC AC =,BC ⊂平面ABC ,∴BC ⊥平面11A ACC ,∴1AC ⊂平面11A ACC ,∴1BC AC ⊥,∴11AC BA ⊥,且1BC BA B ⋂=,1,BC BA ⊂平面1A BC ,∴1AC ⊥平面1A BC .(2)解:取11A C 的中点1D ,以C 为坐标原点,CA ,CB ,1CD 分别为x 轴,y 轴,z 轴建立空间直角坐标系,∴1AC ⊥平面1A BC ,1AC ⊂平面1A BC ,∴11AC A C ⊥,∴四边形11A ACC 是菱形,∴D 是AC 的中点,∴160A AD ∠=︒,∴()2,0,0A ,(13A ,()0,2,0B ,(13C -,∴(111,0,3B B A A ==-,()112,2,0A B AB ==-,设平面1A AB 的法向量(),,n x y z =,则100n A A n AB ⎧⋅=⎨⋅=⎩,30220x z x y ⎧=⎪∴⎨-+=⎪⎩,取()3,3,1n =,()12,0,0CA =,1C ∴到平面1A AB 的距离12217CA n d n⋅==.11//CC AA ,1AA ⊂平面1A AB ,1CC ⊄平面1 A AB 1//CC ∴平面1A AB ,1CC ∴到平面1A AB 的距离等于1C 到平面1A AB 的距离217.【一隅三反】1.(2022·山西)如图,在正方体1111ABCD A B C D -中,E 为1BB 的中点.(1)证明:1//BC 平面AD 1E (2)求直线1BC 到平面1AD E 的距离; 【答案】(1)证明见解析(2)23【解析】(1)11//D C AB ,11D C AB =,∴四边形11D ABC 为平行四边形,11//D A C B ∴,1D A ⊂面1AD E ,1C B ⊄面1AD E ,1//BC ∴平面1AD E .(2)如图建立空间直角坐标系A xyz -,设正方体的棱长为2,则()000A ,,,()020B ,,,()1202D ,,,()1222C ,,,()021E ,,,1//BC 平面1AD E ,∴直线1BC 到平面1AD E 的距离即为点B 到平面1AD E 的距离,所以()020AB =,,,()1202AD =,,,()021AE =,,,设平面1AD E 的一个法向量为()n x y z =,,,则122020n AD x z n AE y z ⎧⋅=+=⎨⋅=+=⎩,取1z =-,得1112n ⎛⎫=- ⎪⎝⎭,,,()1020112123311124AB n d n⎛⎫⋅- ⎪⋅⎝⎭∴====++,,,,,∴直线1BC 到平面1AD E 的距离为23.2.(2022·海南)如图,在正方体1111ABCD A B C D -中,棱长为2,E 为1BB 的中点.(1)求1BC 到平面1AD E 的距离. (2)若1A C面1AED M =,求1A MCM. 【答案】(1)23(2)23【解析】(1)如图,以A 为坐标原点,1,,AD AB AA 分别为x ,y,z 轴建立空间直角坐标系,则111(0,0,0),(0,2,0),(2,2,2),(2,0,2),(0,2,1),(0,0,2)A B C D E A , 因为正方体1111ABCD A B C D -中,111//,AD B AD C ⊂平面1AD E ,所以1//BC 平面1AD E ,则1BC 到平面1AD E 的距离即为1C 到平面1AD E 的距离, 而111(0,2,0),(2,0,2),(0,2,1)DC AD AE === ,设平面1AD E 的法向量为(,,n x y z =),则100n AD n AE ⎧⋅=⎨⋅=⎩, 即22020x z y z +=⎧⎨+=⎩ ,令1y = ,则2,2x z ==- , 故(2,1,2n =-),故1C 到平面1AD E 的距离1122||3||9n D C d n ⋅=== , 即1BC 到平面1AD E 的距离为23; (2)111(2,0,0),(0,2,2)A D CD ==- ,由题意可得1111111||||42||63||||||n A D A M n A D n CM n CD n CD n ⋅⋅====⋅⋅.3.(2022·北京)图1是直角梯形,,90ABCD AB CD D ∠=∥,四边形ABCE 是边长为2的菱形,并且60BCE ∠=,以BE 为折痕将BCE 折起,使点C 到达1C 的位置,且16AC 2.(1)求证:平面1BC E ⊥平面ABED ;(2)在棱1DC 上是否存在点P ,使得P 到平面1ABC 15?若存在,求出直线EP 与平面1ABC 所成角的正弦值.【答案】(1)详见解析;(2)存在点P 且为1DC 15 【解析】(1)证明:如图所示:在图1中连接AC ,交BE 于O ,因为四边形ABCE 是边长为2的菱形,并且60BCE ∠=, 所以AC BE ⊥,且3OA OC == 在图2中,相交直线1,OA OC 均与BE 垂直, 所以1AOC ∠是二面角1A BE C --的平面角,因为16AC =222111,OA OC AC OA OC +=⊥,所以平面1BC E ⊥平面ABED ; (2)由(1)分别以1,,OA OB OC 为x ,y ,z 建立如图所示空间直角坐标系, 则()()()133,0,3,3,0,0,0,1,0,0,1,02D C AB E ⎫--⎪⎪⎝⎭,所以()13333,,3,,,0,3,1,0,2222DC AD AB ⎛⎫⎛⎫=-=--=- ⎪ ⎪ ⎪ ⎪⎝⎝⎭()()13,0,3,3,1,0,AC AE =-=--, 设[]1,0,1DP DC λλ=∈,则13333,322AP AD DP AD DC λλλ⎛⎫=+=+=-+ ⎪ ⎪⎝⎭, 设平面1ABC 的一个法向量为(),,n x y z =,则100AB AC n n ⎧⋅=⎪⎨⋅=⎪⎩,即30330x y x z ⎧+=⎪⎨=⎪⎩,取()1,3,1n =, 因为P 到平面1ABC 15所以2323155AP n d nλ-+⋅===,解得12λ=,则33334AP ⎛=- ⎝⎭,所以31344EP AP AE ⎛=-= ⎝⎭, 设直线EP 与平面1ABC 所成的角为θ,所以直线EP 与平面1ABC 所成角的正弦值为:15sin cos ,5EP n EP n EP nθ⋅===⋅.考点五 面面距【例5】(2022·全国·高三专题练习)已知正方体1111ABCD A B C D -的棱长为a ,则平面11AB D 与平面1BDC 的距离为( ) A 2a B 3a C 2 D 3 【答案】D【解析】由正方体的性质,1AB ∴1DC ,11D B ∴DB ,1111AB D B B =,1DC DB D =,易得平面11AB D ∥平面1BDC ,则两平面间的距离可转化为点B 到平面11AB D 的距离.以D 为坐标原点,DA ,DC ,1DD 所在的直线分别为x 轴、y 轴、z 轴 建立空间直角坐标系,则(),0,0A a ,(),,0B a a ,()1,0,A a a ,()0,,0C a ,()1,,B a a a ,()10,0,D a 所以()1,,CA a a a =-,()0,,0BA a =-,()10,,AB a a =,()11,,0a D B a =--.连接1A C ,由()()11,,0,,0AB A a a a a C a ⋅=⋅=-,()()111,,00,,CA D B a a a a a ⋅=--=-⋅,且1111AB B D B =,可知1A C ⊥平面11AB D ,得平面11AB D 的一个法向量为()1,1,1n =-,则两平面间的距离33BA n a d n ⋅===. 故选:D 【一隅三反】1.(2022·全国·高三专题练习)在棱长为1的正方体1111ABCD A B C D -中,则平面1AB C 与平面11AC D 之间的距离为 A 3B 3C 23D 3【答案】B【解析】建立如图所示的直角坐标系,则1(1,0,0)A ,1(0,1,0)C ,(0,0,1)D ,(1,0,1)A ,所以1(1,0,1)DA =-,1(0,1,1)DC =-,(1,0,0)AD =-, 设平面11AC D 的一个法向量(,,1)x y =m ,则11m DA m DC ⎧⊥⎪⎨⊥⎪⎩, 即111010m DA x m DC y ⎧⋅=-=⎪⎨⋅=-=⎪⎩,解得11x y =⎧⎨=⎩,故(1,1,1)=m ,显然平面1AB C ∥平面11AC D ,所以平面1AB C 与平面11AC D 之间的距离||3||3AD d ⋅===m m2.(2022山西)两平行平面 α,β 分别经过坐标原点 O 和点 ()2,1,1A ,且两平面的一个法向量()1,0,1n =-,则两平面间的距离是 ( )A .32B 2C 3D .32【答案】B【解析】两平行平面 α,β 分别经过坐标原点 O 和点 ()2,1,1A ,()2,1,1OA =,且两平面的一个法向量()1,0,1,n =-∴两平面间的距离20122n OA n⋅-++===B.3.(2022·青海西宁)底面为菱形的直棱柱1111ABCD A B C D -中,E F 、分别为棱1111A B A D 、的中点. (1)在图中作一个平面α,使得BD α⊂,且平面//AEF α.(不必给出证明过程,只要求作出α与直棱柱1111ABCD A B C D -的截面).(2)若012,60AB AA BAD ==∠=,求平面AEF 与平面α的距离d .【答案】(1)见解析;(2)457d =【解析】【详解】 (1)如图,取1111,B C D C 的中点,M N ,连接,,BM MN ND ,则平面BMND 即为所求平面α. (2)如图,连接,AC AC 交BD 于O ,∴在直棱柱1111ABCD A B C D -中,底面为菱形, ∴AC BD ⊥,∴分别以,DB AC 为,x y 轴,O 为原点建立如图所示空间直角坐标系, 又∴所有棱长为2,060BAD ∠=, ∴()()()0,3,0,1,0,0,3,0A B C ,()()()111,0,0,0,3,2,1,0,2D A B --,()11,0,2D -, ∴1313,2,,222E F ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, ∴1313,,2,2222AE AF ⎛⎫⎛⎫==-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,()1,3,0AB =,设(),,n x y z =是平面AEF 的一个法向量,则·0{·0n AE n AF ==,即13202{13202x y z x y z +=-+=, 令43y =()0,43,3n =-,57n , ∴点B 到平面AEF 的距离·1245757AB n h n === ∴平面AEF 与平面α的距离457d =.。
2024-2025学年高二数学上学期期中必刷题精选(压轴6类考点专练)(原卷版)

高二上学期期中必刷题精选(压轴6类考点专练)一、单选题1.(24-25高三上·云南玉溪·阶段练习)在下图所示直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,π1,3AB DAB =Ð=,12AA =,动点P 在体对角线1BD 上,则顶点B 到平面APC 距离的最大值为( )A .12BCD2.(24-25高二上·广东东莞·阶段练习)在正方体1111ABCD A B C D -中,平面a 经过点B ,D ,平面b 经过点A ,1D ,当平面a ,b 分别截正方体所得截面面积最大时,平面a 与平面b 的夹角的余弦值为( )ABC .12D .133.(24-25高二上·河北·在正三棱柱111ABC A B C -中,2AB =,1AA =2BC BO =uuu r uuu r ,M 为棱11B C 上的动点,N 为线段AM 上的动点,且MN MOMOMA=,则线段MN 长度的最小值为( )A .2BC D 4.(24-25高二上·云南大理·阶段练习)在长方体1111ABCD A B C D -中,2AB AD ==,11AA =,O 是AC 的中点,点P 在线段11A C上,若直线OP 与平面1ACD 所成的角为q ,则sin q 的取值范围是( )A.B.C.D .5.(24-25高二上·重庆·阶段练习)长方体11ABCD ABC D -,1AB BC ==,12BB =,动点P 满足1(,[0,1])BP BC BBl m l m =+Îuuu r uuur uuur,1AP BD ^,则二面角P AD B --的正切值的取值范围是( )A .10,4éùêúëûB .10,2éùêúëûC .11,42éùêúëûD .1,12éùêúëû二、多选题6.(24-25高二上·江西南昌·阶段练习)在长方体1111ABCD A B C D -中,12,4AB BC CC ===,点E 在棱1AA 上,且13AE EA =.点M 为线段11B D 上动点(包括端点),则下列结论正确的是( )A .当点M 为11B D 中点时,1C M ^平面11BB D DB .过E 点作与直线1BD 垂直的截面a ,则直线AD 与截面aC .三棱锥E BDM -的体积是定值D .点M 到直线1BC 7.(24-25高二上·吉林·阶段练习)在棱长为1的正方体1111ABCD A B C D -中,P 为棱1BB 上一点,且12B P PB =,Q 为正方形11BB C C 内一动点(含边界),则下列说法中正确的是( )A .若1D Q ∥平面1A PD ,则动点Q 的线段B .存在点Q ,使得1D Q ⊥平面1A PDC .三棱锥1Q A PD -的最大体积为518D .若1D Q ,且1D Q 与平面1A PD 所成的角为q ,则sin q 三、填空题8.(24-25高二上·北京·阶段练习)如图,在四棱锥P ABCD -中,PA ^底面ABCD ,DAB Ð为直角,//AB CD ,AD CD ==2AB ,E ,F 分别为PC ,CD 的中点,(0)PA kAB k =>,且二面角E BD C --的平面角大于30°,则k 的取值范围是 .9.(湖北省问津教育联合体2024-2025学年高二上学期10月联考数学试卷)正方体1111ABCD A B C D -中,点E 是1AA 的中点,点F 为正方形11AA B B 内一动点,且//CF 平面1DEC ,若异面直线CF 与11A D 所成角为q ,则cos q 的最小值为 .一、单选题1.(24-25高二上·江西·阶段练习)点()2,3-关于直线2230x y +-=对称的点的坐标为( )A .37,22æö-ç÷èøB .73,22æö-ç÷èøC .53,22æö-ç÷èøD .35,22æö-ç÷èø2.(24-25高二上·全国·课后作业)已知直线1l 过点()2,4A ,与x 轴交于点()3,0B ,直线1l 与2l 关于y 轴对称,则直线2l 的方程为( )A .4120x y +-=B .4120x y -+=C .45120x y +-=D .45120x y -+=3.(2025高三·全国·专题练习)已知0x y +=)AB .CD .4.(24-25高二上·天津·开学考试)已知点()3,6A -和()1,2B ,在x 轴上求一点M ,使AM BM +最小,那么点M 的坐标为( )A .()2,0-B .()1,0C .()4.4,0D .()0,05.(24-25高二上·云南玉溪·期中)一光线过点(2,4),经倾斜角为3π4的且过(0,1)的直线l 反射后过点(5,0),则反射后的光线不会经过下列哪个点( )A .11,2æö-ç÷èøB .32,8æö-ç÷èøC .13,4æö-ç÷èøD .14,4æö-ç÷èø6.(24-25高二上·全国·课后作业)若点M 在直线:1l y x =--上,则点M 到点()()2,1,3,4A B 的距离之和的最小值为( )A .BC .D .7.(24-25高二上·辽宁沈阳·阶段练习)直线1(1):220l x m y m ++--=与直线2:(1)220l m x y m +---=相交于点P ,对任意实数m ,直线12,l l 分别恒过定点,A B ,则||||PA PB +的最大值为( )A .2B .C .D .48.(24-25高二上·江苏南通·阶段练习)已知P ,Q 是直线:10l x y -+=上两动点,且||PQ (4,6)A -,(0,6)B ,则||||||AP PQ QB ++的最小值为( )A.10B.10C.D .12一、单选题1.(24-25高二上·重庆·阶段练习)已知点A 、B 在圆22:16O x y +=上,且AB 的中点M 在圆22:(2)1C x y -+=上,则弦长AB 的最小值为( )A.B.C.D.2.(24-25高二上·辽宁沈阳·阶段练习)若经过点()1,2且半径大于1的圆与两坐标轴都相切,若该圆上至少有三个不同的点到直线0x y c -+=的距离等于52,则实数c 的取值范围是( )A.æçèB .55,22æö-ç÷èøC.éêëD .55,22éù-êúëû3.(24-25高二上·山东菏泽·阶段练习)已知直线1:310(R)l mx y m m --+=Î与直线2:310(R)l x my m m +--=Î相交于点P ,则P 到直线0x y +=的距离d 的取值范围是( )A.B.C.D.4.(24-25高二上·四川自贡·阶段练习).已知点(,)P x y 为直线240l x y ++=:上的动点,过P 点作圆22:(1)1C x y +-=的切线PA ,PB ,切点为,A B ,则PAB V 周长的最小值为()A.4B.5C.4D.4+5.(24-25高二上·湖南长沙·阶段练习)已知,A B 两点的坐标分别为()()0,1,1,0A B ,两条直线1:10l mx y -+=和()2:10l x my m +-=ÎR 的交点为P ,则AP BP +的最大值为( )ABC .1D .26.(24-25高二上·江苏徐州·阶段练习)已知圆()22:11C x y -+=,直线:(1)l y k x =+,若直线与x 轴交于点A ,过直线l 上一点P 作圆C 的切线,切点为T,且PA =,则k 的取值范围是( ).A.éêëB .11,33éù-êúëûC.13éùêúëûD.13é-êë7.(24-25高二上·黑龙江鹤岗·阶段练习)设m ÎR ,22:260M x y x y +--=e .若动直线1:20l x my m +--=与M e 交于点A ,C ,动直线2210:mx y l m --+=与M e 交于点B ,D ,则AC BD +的最大值是( )A.B.C.D.8.(24-25高二上·安徽阜阳·阶段练习)已知圆()()221122:(4)4,,,,C x y A x y B x y -+=是圆上的两个动点,且AB =,则112211x y x y -++-+的最大值为( )A.10-B1+C.5D.10+一、单选题1.(23-24高二上·湖南常德·阶段练习)如图,已知12F F 、分别是双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点,现以2F 为圆心作一个通过双曲线中心的圆并且交双曲线C 于M N 、两点.若直线1MF 是圆2F 的切线,则该双曲线的离心率为( )A1BC.D22.(24-25高三上·浙江·阶段练习)已知双曲线2222:1(0,0)x y C a b a b -=>>的左焦点为1F ,O 为坐标原点,若在C 的右支上存在关于x 轴对称的两点,P Q ,使得1PF Q △为正三角形,且1OQ F P ^,则C 的离心率为()A B .1C D .13.(2022·陕西榆林·模拟预测)已知双曲线2222:1(0,0)x y C a b a b -=>>的左,右焦点分别为1F ,2F ,点P 在双曲线C 的右支上,直线1PF 与双曲线C 的一条渐近线垂直,垂足为H ,若114PF HF =,则双曲线C 的离心率为( )A .73B .53C D 4.(24-25高二上·全国·课后作业)已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点为12,,,F F P Q 为C 在第一象限的两个动点,且1212π,6PF QF PF F l =Ð=uuu r uuuu r ,若123PF QF =,则C 的离心率为( )A B .12C D 5.(24-25高三上·海南海口·阶段练习)已知椭圆C :22221(0)x y a b a b+=>>的左、右焦点分别为1F ,2F ,P是C 上一点,且212PF F F ^,H 是线段1PF 上靠近1F 的四等分点,且10OH PF ×=uuur uuu r,则C 的离心率为( )A B 1C 1D 6.(2025·四川巴中·模拟预测)已知12,F F 是椭圆2222:1(0)x yC a b a b+=>>的左,右焦点,A ,B 是椭圆C 上的两点.若122F A F B =uuu r uuu u r ,且1π4AF F Ð=,则椭圆C 的离心率为( )A .13BCD .237.(24-25高二上·浙江温州·阶段练习)已知椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别为12,F F ,过1F 的直线与椭圆C 交于,M N 两点,若21225MNF MF F S S =V V 且2121F F N F NF ÐÐ=,则椭圆C 的离心率为( )A .35B C .13D 8.(24-25高二上·全国·课后作业)已知椭圆()22112211:10x yE a b a b +=>>与双曲线()22222222:10,0x y C a b a b -=>>共焦点,12,F F 分别为左、右焦点,点P 为E 与C 的一个交点,且12120F PF Ð=°,设E 与C 的离心率分别为12,e e ,则2212e e +的取值范围是( )A .)+¥B .)+¥C .()2,+¥D .()3,+¥一、单选题1.(24-25高二上·全国·课后作业)已知抛物线2:24C y x =的焦点为F ,定点()6,3,Q P 为C 上一动点,则PF PQ +的最小值为( )A .12B .14C .16D .182.(23-24高三上·广东广州·期中)直线l 经过抛物线24y x =的焦点F ,且与抛物线交于A ,B 两点.若3AF BF =,则AB =( )A .83B .3C .163D .323.(24-25高二上·全国·课后作业)已知点,A B 为抛物线22y x =上异于原点的两个动点,若AB 4=,则线段AB 中点的横坐标的最小值为( )A .1B .32C .53D .24.(2024·辽宁锦州·模拟预测)抛物线2:4C y x =的焦点为F ,准线为l ,A 为C 上一点,以点F 为圆心,以AF 为半径的圆与l 交于点B ,D ,与x 轴交于点M ,N ,若AB FM =uuu r uuuu r,则AM =uuuu r ( )A.B.C.D.5.(23-24高二下·浙江·2:4C x y =,过抛物线C 焦点的直线交抛物线C 于A B 、两点,交圆22:20E x y y +-=于M N 、两点,其中A M 、位于第一象限,则14AM BN+的最小值为( )A .2B .3C .4D .56.(23-24高二下·山东烟台·阶段练习)已知,A B 为抛物线()220y px p =>上的两个动点,以AB 为直径的圆C 经过抛物线的焦点F ,且面积为4π,若过圆心C 作该抛物线准线l 的垂线,垂足为D ,则CD 的最大值为( ).A .4B.C.D .67.(2024·西藏林芝·模拟预测)已知抛物线28y x =上一点P 到准线的距离为1d ,到直线:43120l x y -+=的距离为2d ,则12d d +的最小值为( )A .1B .2C .3D .48.(24-25高三上·内蒙古赤峰·阶段练习)已知抛物线2:2(0)C y px p =>的焦点为F ,过点F 的直线l 与抛物线C 交于(,A B A 在第一象限)两点,O 为坐标原点,若39AB BF ==,则OAB △的面积是( )A.B .6C.D .12一、解答题1.(24-25高二上·陕西西安·阶段练习)已知椭圆()2222:10x y C a b a b +=>>的左焦点为,F P 是椭圆上任意一点,PF 的最大值为3,最小值为1.(1)求椭圆的标准方程;(2)已知1,12M æöç÷èø是椭圆内一点,过点M 任做一条直线与椭圆交于B C 、两点,求以M 为中点的弦所在的直线方程.2.(24-25高三上·福建泉州·阶段练习)已知双曲线2222:1(0,0)x y C a b a b -=>>,右焦点到双曲线C 的一条渐近线的距离为1A ,B 在双曲线C 上,线段AB 的中点为(2,)(0)M m m m ≠.(1)求双曲线C 的标准方程;(2)O 为坐标原点,若OAB △的面积为23,求直线AB 的方程.3.(24-25高三上·云南大理·开学考试)已知椭圆2222:1(0)x y C a b a b+=>>过点()3,1P ,焦距为,斜率为13-的直线l 与椭圆C 相交于异于点P 的,M N 两点,且直线,PM PN 均不与x 轴垂直.(1)求椭圆C 的方程.(2)记直线PM 的斜率为1k ,直线PN 的斜率为2k ,证明:12k k 为定值.(3)若MN A =为椭圆C 的上顶点,求AMN V 的面积.4.(23-24高二上·江苏南通·2:2(0)y px p =>的焦点为F ,O 为坐标原点,M 为抛物线上一点,且3MF OF =,MFO △(1)求E 的方程;(2)若不过点F 的直线l 与E 交于A ,B 两点,ABF △的重心在直线2y =上,且13.AF BF +=则满足条件的直线l 是否存在,若存在求出直线l 的方程;若不存在,请说明理由.5.(24-25高三上·黑龙江大庆·阶段练习)已知双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为12,F F ,点(A 在C 上,且离心率e =(1)求双曲线C 的方程;(2)记点A 在x 轴上的射影为点B ,过点B 的直线l 与C 交于M ,N 两点.探究:2211||||BM BN +是否为定值,若是,求出该定值;若不是,请说明理由.6.(24-25高二上·江苏连云港·阶段练习)如图,已知椭圆2222:1(0)x y C a b a b+=>>过点()3,1P ,焦距为13-的直线l 与椭圆C 相交于异于点P 的,M N 两点,且直线,PM PN 均不与x 轴垂直.(1)求椭圆C 的方程;(2)若MN =MN 的方程;(3)记直线PM 的斜率为1k ,直线PN 的斜率为2k ,证明:12k k 为定值.7.(24-25高二上·黑龙江·期中)已知动点(,)P x y 到定点(2,0)F 的距离与动点P 到定直线2x =-的距离相等,若动点P 的轨迹记为曲线C .(1)求C 的方程;(2)不过点F 的直线与C 交于横坐标不相等的A ,B 两点,且6AF BF +=,若AB 的垂直平分线交x 轴于点N ,证明:N 为定点.8.(24-25高三上·江苏南通·阶段练习)设抛物线2:4C y x =的焦点为F ,点(2,0)D ,过F 的直线交C 于,M N 两点,直线,MD ND 与C 的另一个交点分别为,A B ,记直线,MN AB 的斜率分别为12,k k .(1)求证:12k k 为定值;(2)直线AB 是否过定点?若过定点,求出定点坐标.9.(2024高三下·河南·专题练习)动点(),P x y 与定点()2,0F 的距离和它到定直线1:2l x =的距离的比是2,记动点P 的轨迹为曲线C .(1)求C 的方程;(2)过()2,0R -的直线l 与C 交于,A B 两点,且(0)RA aRB a =>uuu r uuu r ,若点M 满足AM aMB =uuuu r uuu r ,证明:点M 在一条定直线上.10.(2024·青海海南·二模)已知双曲线2222:1(0,0)x y C a b a b-=>>的虚轴长为(3,2)P -在C 上.设直线l 与C 交于A ,B 两点(异于点P ),直线AP 与BP 的斜率之积为13.(1)求C 的方程;(2)证明:直线l 的斜率存在,且直线l 过定点.11.(24-25高二上·广西梧州·阶段练习)已知O 为坐标原点,动点P 到x 轴的距离为d ,且22||OP d l m =+,其中,l m 均为常数,动点P 的轨迹称为(),l m 曲线.(1)若1,2m æöç÷èø曲线为焦点在y 轴上的椭圆,求m 的取值范围.(2)设曲线Ω为19,8æö-ç÷èø曲线,斜率为()0k k ≠的直线l 过Ω的右焦点,且与Ω交于,A B 两个不同的点.(i )若2k =,求AB ;(ii )若点B 关于x 轴的对称点为点D ,证明:直线AD 过定点.12.(23-24高二下·广东惠州·阶段练习)已知抛物线2:2(0)C x py p =>的焦点F 关于直线2y =-的对称点为()0,5-.(1)求C 的方程;(2)若O 为坐标原点,过焦点F 且斜率为1的直线l 交C 于A B 、两点,求|AB |;(3)过点()4,1M 的动直线l 交C 于不同的,A B 两点,N 为线段AB 上一点,且满足AM BN AN BM ×=×,证明:点N 在某定直线上,并求出该定直线的方程.。
2020高考提分秘笈:利用空间向量求夹角与距离(距离供选用)(原卷版+解析版)

【训练 2】 (2019·郑州测试)在如图所示的多面体中,四边形 ABCD 是平行四边形,四边形 BDEF 是矩形, π
ED⊥平面 ABCD,∠ABD=6,AB=2AD.
(1)求证:平面 BDEF⊥平面 ADE; (2)若 ED=BD,求直线 AF 与平面 AEC 所成角的正弦值.
6 千里之行 始于足下
9 千里之行 始于足下
=2CD,E 为线段 AB 的中点,F 是线段 DD1 上的动点.
实用文档 用心整理
(1)求证:EF∥平面 BCC1B1;
(2)(一题多解)若∠BCD=∠C1CD=60°,且平面 D1C1CD⊥平面 ABCD,求平面 BCC1B1 与平面 DC1B1 所成 角(锐角)的余弦值.
1 千里之行 始于足下
实用文档 用心整理
【规律方法】 1.利用向量法求异面直线所成角的一般步骤是:(1)选好基底或建立空间直角坐标系;(2)求出两直线的方向
|v1·v2| 向量 v1,v2;(3)代入公式|cos〈v1,v2〉|=|v1||v2|求解.
2 千里之行 始于足下
实用文档 用心整理
π 2.两异面直线所成角的范围是 θ∈0,2,两向量的夹角 α 的范围是[0,π],当异面直线的方向向量的夹
14 千里之行 始于足下
实用文档 用心整理
和计算程序化、简单化.主要是建系、设点、计算向量的坐标、利用数量积的夹角公式计算. 2.利用法向量求距离问题的程序思想方法 第一步,确定法向量; 第二步,选择参考向量; 第三步,确定参考向量到法向量的投影向量; 第四步,求投影向量的长度.
角为锐角或直角时,就是该异面直线的夹角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直 线的夹角.
【训练 1】(一题多解)如图,在正三棱柱 ABC-A1B1C1 中,AA1= 2AB,E,F 分别为 BC,BB1 的中点, M,N 分别为 AA1,A1C1 的中点,则直线 MN 与 EF 所成角的余弦值为( )
专题27 空间向量求空间距离-2021年高考数学一轮复习专题讲义附真题及解析
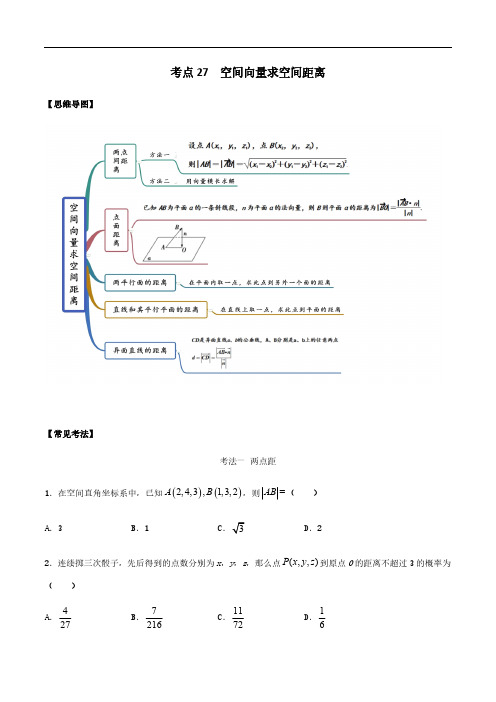
其中 (1,1,1), (1,1, 2), (1, 2,1), (1, 2, 2), (2,1,1), (2, 2,1), (2,1, 2) 满足条件
则点 P(x, y, z) 到原点 O 的距离不超过 3 的概率为 P 7 故选:B 216
考法二 点线距
1.【答案】A
【解析】 ∵ A(0,0,2),B(1,0,2),C(0,2,0),AB = (1,0,0),BC = ( - 1,2, -2),
A. 3 6
B. 3 3
C. 2 3 3
D. 3 2
解析:
【常见考法】 1.【答案】C
考法一 两点距
【解析】 AB = (2 1)2 (4 3)2 (3 2)2 3 故选:C
2.【答案】B
【解析】点 P(x, y, z) 到原点 O 的距离不超过 3,则 x2 y2 z2 3 ,即 x2 y2 z2 9 连续掷三次骰子,得到的点的坐标共有 6 6 6 216 个
(2)求点 E 到平面 PAB 的距离.
3.如图,在正四棱柱 ABCD A1B1C1D1 中,已知 AB 1, BB1 2 .
(1)求异面直线 A1C 与直线 AD1 所成的角的大小; (2)求点 C 到平面 AB1D1 的距离.
4.如图,在四棱锥 P ABCD 中,底面 ABCD 是菱形, BAD 120 ,且 PA 平面 ABCD , PA AB 2 ,M,N 分别为 PB , PD 的中点.
(1)记平面 CMN 与底面 ABCD 的交线为 l,试判断直线 l 与平面 PBD 的位置关系,并证明. (2)点 Q 在棱 PC 上,若 Q 到平面 CMN 的距离为 13 ,求线段 CQ 的长.
13
考法四 线面距
1.已知斜三棱柱 ABC A1B1C1 , BCA 90 , AC BC 2 , 在底面 ABC 上的射影恰为 AC 的中点 D ,又知 BA1 AC1 .
向量与空间距离(有答案)

年级
性 别
学 校
学 科ห้องสมุดไป่ตู้
教师
上课日期
上课时间
课题
18向量与空间距离
类型一 点到直线的距离
例1、 在正方体ABCD-A1B1C1D1中棱长为1,利用向量法求点C1到A1C的距离.
(1)计算直线A1C的方向向量 =(1,1,-1).
(2)找到直线A1C上一点C(1,1,0).
(3)求点C1与直线A1C上一点C(1,1,0)的向量 =(0,0,1).
∴ =(0,1,0), =(-1,0,1).设n=(1,y,z)是平面ABC1D1的一个法向量,则
解得y=0,z=1,
∴n=(1,0,1).又 =( ,- ,-1),∴点O到平面ABC1D1的距离为 = = .
类型三 直线到平面与平面到平面的距离
例3、 正方体ABCD-A1B1C1D1的棱长为1,求平面A1BD与平面B1CD1间的距离.
由题意,得A(2,0,0),C(0,4,0),E(2,4,1),F(0,0,z),C1(0,4,3),
∵四边形AEC1F为平行四边形,∴ = .
∴(-2,0,z)=(-2,0,2).∴z=2.∴F(0,0,2).则 =(0,4,1), =(-2,0,2).
设平面AEC1F的法向量为n=(x,y,z),则 ⇒
设面ABD的法向量为n=(x,y,z),则 ∴x=y=z.∴可取n=(1,1,1).
又 =( ,0,0),∴由公式得 = = a.答案: a
取z=1,则n=(1,- ,1).又∵ =(0,0,3),∴d= = = .
变式:正方体ABCD-A1B1C1D1的棱长为1,O是面A1B1C1D1的中心,则O到平面ABC1D1的距离是()A. B. C. D.
空间向量求距离

B
b
na
A
例4
. 已 知 直 三 棱 柱 ABC─A1B1C1 的 侧 棱 AA1 4 , 底 面 △ABC 中, AC BC 2, BCA 90 , E 是 AB 的中点, 求异面直线CE 与 AB1 的距离.
z
C1
A1
B1
C
A
B
xE
y
例4
. 已 知 直 三 棱 柱 ABC ─A1B1C1 的 侧 棱 AA1 4 , 底 面
|n|
这个结论说明,平面外一点到平面的距离等于连结此点与平面 上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的 绝对值.
一、求点到平面的距离
PA n d
n
P M
O
n
N
A
方法指导:若点P为平面α外一点,点A为平面α内任 一点,平面的法向量为n,则点P到平面α的距离公式 为
例1、已知正方形ABCD的边长为4,
n2
2
二、求直线与平面间距离
例2、已知正方形ABCD的边长为4,CG⊥平面ABCD,
CG=2,E、F分别是AB、AD的中点,求直线BD到平面
GEF的距离。
z
G
d | n BE| 2 11 .n11源自xDCFA
E
B
y
练习3:
正方体AC1棱长为1,求BD与平面GB1D1的
距离
Z D1
DD1 n C1 d
两条平行线间的公垂线段的长,叫做两条平行线间 的距离。
(4)两条异面直线间的距离
和两条异面直线分别垂直相交的直线,叫两条异面直线 的公垂线;公垂线上夹在两异面直线间的线段的长度,叫两 异面直线的距离。
考点37 空间向量在空间几何中的运用(原卷版)
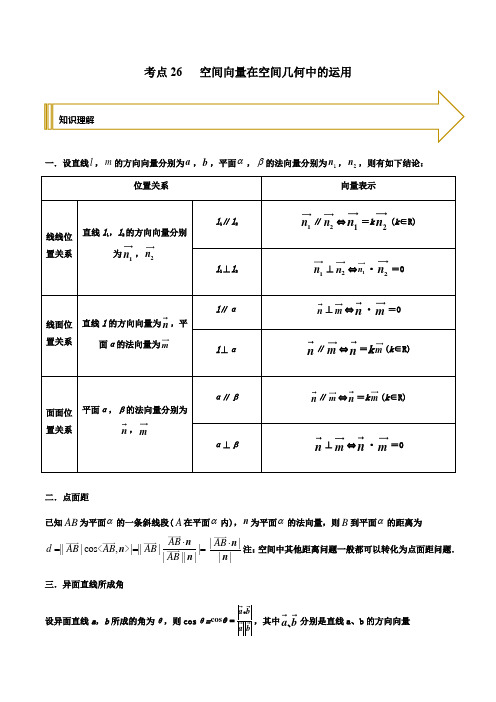
考点26 空间向量在空间几何中的运用一.设直线l ,m 的方向向量分别为a ,b ,平面α,β的法向量分别为1n ,2n ,则有如下结论:2的方向向量分别1n ,2n 1n ∥2n ⇔1n =k 2n (k ∈R)1n ⊥2n ⇔1n ·2n =0的方向向量为n ,平mn ⊥m ⇔n ·m =0n ∥m ⇔n =k m (k ∈R)β的法向量分别为n ,mn ∥m ⇔n =k m (k ∈R)n ⊥m ⇔n ·m =0二.点面距已知AB 为平面α的一条斜线段(A 在平面α内),n 为平面α的法向量,则B 到平面α的距离为|||cos ,|||||||||AB d AB AB AB AB ⋅===<>n n n ||||AB ⋅n n 注:空间中其他距离问题一般都可以转化为点面距问题.三.异面直线所成角设异面直线a ,b 所成的角为θ,则cos θ=cos a b a bθ=,其中a b 、分别是直线a 、b 的方向向量知识理解四.直线与平面所成角l 为平面α的斜线,a 为l 的方向向量,n 为平面α的法向量,φ为l 与α所成的角,则||a n sin cos a n a nϕ=〈,〉=(直线与平面所成角的范围为⎣⎢⎡⎦⎥⎤0,π2)五.二面角 平面α的法向量为1n ,平面β的法向量为2n ,〈1n ,2n 〉=θ,设二面角大小为φ,则1212||cos =|cos |=||||n n n n ϕθ考向一 空间向量证平行垂直【例1】(2020·全国高三专题练习)如图所示,平面PAD ⊥平面ABCD ,ABCD 为正方形,△PAD 是直角三角形,且PA =AD =2,E ,F ,G 分别是线段PA ,PD ,CD 的中点.求证:(1)PB //平面EFG ; (2)平面EFG //平面PBC . 【举一反三】1.(2020·全国高三专题练习)如图所示,在直二面角D ABE--中,四边形ABCD 是边长为2的正方形,AE EB =,F 为CE 上的点,且BF ⊥平面ACE .考向分析(1)求证:AE⊥平面BCE;(2)求证:平面BDF平面ABCD.2.(2020·全国高三专题练习)如图,在多面体ABC—A1B1C1中,四边形A1ABB1是正方形,AB=AC,BCAB,B1C1=12BC,二面角A1ABC是直二面角.求证:(1)A1B1⊥平面AA1C;(2)AB1∥平面A1C1C.考向二空间向量求线线角【例2】(2021·西安市航天城第一中学)在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为()A.12B.-12C.2 D.【举一反三】1.(2021·广西河池市)如图,在四棱锥P ABCD-中,PA⊥平面ABCD,四边形ABCD为正方形,PA AB=,E为AP的中点,则异面直线PC与DE所成的角的正弦值为().A .5B C .5D .52.(2021·陕西西安市·西安中学)如图,四面体ABCD 中,4CD =,2AB =,E ,F 分别是,AC BD 的中点,若EF AB ⊥,则EF 与CD 所成的角的大小是( )A .6πB .4π C .3π D .2π 3.(2021·安徽高三期末)已知棱长为2的正方体1111ABCD A B C D -中,P ,E ,F ,G 分别为1CC ,CD ,1D D ,11A B 的中点,则异面直线GF 与PE 所成角的余弦值为( )A .13B C D考向三 空间向量求线面角【例3】(2020·北海市北海中学高三月考)在四棱锥P ﹣ABCD 中,PA ⊥底面ABCD ,AD ⊥AB ,AB ∥DC ,AD =DC =AP =2,AB =1,点E 为棱PC 的中点.(1)求证:BE⊥DC;(2)求直线PC与平面PDB所成角的正弦值.【举一反三】-中,PA⊥平面ABC,1.(2020·浙江高三期中)如图,已知三棱锥P ABC⊥===,M、E分别为PB、PC的中点,N为AE的中点.,,2AC BC PA AC BC DB AD(Ⅰ)求证:MN CD ⊥;(Ⅱ)求直线PB 和平面PCD 所成角的正弦值.2.(2021·浙江绍兴市·绍兴一中高三期末)在三棱锥A BCD -中,2AB AD BD ===,BC DC ==,2AC =.(1)求证:BD AC ⊥; (2)若P 为AC 上一点,且34AP AC =,求直线BP 与平面ACD 所成角的正弦值.3.(2021·浙江绍兴市·高三期末)已知三棱柱111ABC A B C -中,平面11ACC A ⊥平面ABC ,11AA AC CA BC ===,1AB =.(Ⅰ)求证:BC ⊥平面11ACC A ;(Ⅱ)求直线1AB 与平面1A BC 所成角的大小.考向四 空间向量求二面角【例4】(2021·盐城市伍佑中学高三期末)在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,AB AC ⊥,1AB AC AA ==,E 是11A C 的中点.(1)求证:AB CE ;(2)求二面角B CE A --的余弦值.【举一反三】1.(2021·湖北高三月考)如图,在四棱锥P ABCD-中,平面PAD⊥平面1,//,,2ABCD AB CD AB AD CD PD AD AB⊥===.(1)求证:平面PBC⊥平面PAB;(2)若2AP DC==,求二面角D PC B--的正弦值.2.(2021·山西吕梁市·高三一模)如图,四棱锥S ABCD-中,//AB CD,BC CD⊥,侧面SCD为等边三角形, 4AB BC ==,2CD =,SB =(1)求证:BC SD ⊥;(2)求二面角B AS D --的余弦值.3.(2021·江西赣州市·高三期末)在如图所示的几何体中,ABC ,ACE △,BCD △均为等边三角形,且平面ACE ⊥平面ABC ,平面BCD ⊥平面ABC .(1)证明://DE AB ;(2)若4AB =,求二面角B CE D --的余弦值.考向五 空间向量求空间距【例5】(2020·上海浦东新区·华师大二附中高三月考)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,侧棱PD ⊥平面ABCD ,E 为PC 的中点,3,4,5AD PD PC ===.(1)证明:直线//PA 平面BDE ;(2)求点A 到平面PBC 的距离.【举一反三】 1.(2021·吉林长春外国语学校)如图,平行四边形ABCD 中,26AD AB ==,,E F 分别为,AD BC 的)建立合适空间直角坐标系,在平面内取一点)求解出AB 和平面的法向量n ;AB n n ⋅=即可求解出点A 到平面α中点.以EF 为折痕把四边形EFCD 折起,使点C 到达点M 的位置,点D 到达点N 的位置,且NF NA =.(1)求证:平面AFN ⊥平面NEB ;(2)若BE =F 到平面BEM 的距离.2.(2020·全国高三专题练习)如图,在直三棱柱111ABC A B C -中,2ABC π∠=,D 是棱AC 的中点,且11AB BC BB ===.(1)求证: 1//AB 平面1BC D ;(2)求直线1AB 到平面1BC D 的距离.1.(2021·北京高三期末)如图,在四棱锥P ABCD -中,90BAD ∠=,//AD BC ,PA AD ⊥,PA AB ⊥,122PA AB BC AD ====. 强化练习(Ⅰ)求证://BC 平面PAD ;(Ⅱ)求平面PAB 与平面PCD 所成锐二面角的余弦值.2.(2021·安徽淮北市·高三一模)如图,在多面体ABCDEFG 中,四边形ABCD 是边长为3的正方形,//EG AD ,//DC FG ,且EG AD =,3DC FG =,DG ⊥面ABCD ,2DG =,N 为EG 中点.(1)若M 是CF 中点,求证://MN 面CDE ;(2)求二面角N BC F --的正弦值.3.(2020·赤峰二中高三三模)如图所示,在平行四边形ABCD 中,4AB =,BC =45ABC ∠=︒,点E 是CD 边的中点,将DAE △沿AE 折起,使点D 到达点P 的位置,且PB =(1)求证;平面PAE ⊥平面ABCE ;(2)求点E 到平面PAB 的距离.4.(2020·陕西省商丹高新学校高三其他模拟)如图所示在长方体1111ABCD A B C D -中,12AA =,4AB =,6AD =,M ,N 分别是1DC ,AC 的中点.(1)求证://MN 平面11ADD A(2)求C 到平面1A MN 的距离.5.(2021·河南高三月考)如图,在四棱锥P ABCD -中,四边形ABCD 为直角梯形,//AD BC ,90ADC ∠=︒,平面PAD ⊥平面ABCD ,Q ,M 分别为AD ,PC 的中点,22PA PD AD CD BC =====.(1)求证:BC ⊥平面PQB ;(2)求二面角A BM P --的余弦值.6.(2021·江苏南通市·高三期末)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AC ,BD 相交于点N ,2DN NB =,已知3PA AC AD ===,BD =30ADB ∠=︒.(1)求证:AC ⊥平面PAD ;(2)设棱PD 的中点为M ,求平面PAB 与平面MAC 所成二面角的正弦值.7.(2021·河南高三期末)如图,直四棱柱1111ABCD A B C D -的底面ABCD 为平行四边形,3AD =,5AB =,3cos 5BAD ∠=,1BD DD =,E 是1CC 的中点.(1)求证:平面DBE ⊥平面1ADD ;(2)求直线1AD 和平面BDE 所成角的正弦值.8.(2021·江西宜春市·高三期末)如图所示,在多面体ABCDEF 中,//AB CD ,AB BC ⊥,22AB BC CD ==,四边形ADEF 为矩形,平面ADEF ⊥平面ABCD ,AF AB λ=.(1)证明://DF 平面BCE ;(2)若二面角C BE F --λ的值.9.(2021·陕西咸阳市·高三一模)如图,在三棱锥P ABC -中,平面PAC ⊥平面ABC ,PC AC ⊥,BC AC ⊥,2AC PC ==,4CB =,M 是PA 的中点.(Ⅰ)求证:PA ⊥平面MBC ;(Ⅱ)设点N 是PB 的中点,求二面角N MC B --的余弦值.10.(2021·宁夏吴忠市·高三一模)如图,在三棱锥P ABC -中,PA ⊥平面ABC ,三角形ABC 是正三角形,PA AB =,点D 、E 、F 分别为棱PA 、PC 、BC 的中点,G 为AD 的中点.(1)求证://GF 平面BDE ;(2)求二面角B DE F --的余弦值.11.(2021·内蒙古赤峰市·高三期末)如图,四棱锥E ABCD -中,底面ABCD 为直角梯形,其中AB BC ⊥,//CD AB ,面ABE ⊥面ABCD ,且224AB AE BE BC CD =====,点M 在棱AE 上.(1)证明:当2MA EM =时,直线//CE 平面BDM ;(2)当AE ⊥平面MBC 时,求二面角E BD M --的余弦值.12.(2021·河南高三月考)如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,M 为PC 的中点.(1)求证://AP 平面BDM ;(2)若PB PC ==CD PC ⊥,求二面角C DM B --的余弦值.13.(2021·安徽高三期末)在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,底面ABCD 为直角梯形,//,90BC AD ADC ∠=︒,11,2BC CD AD E ===为线段AD 的中点,过BE 的平面与线段,PD PC 分别交于点,G F .(1)求证:GF ⊥平面PAD ;(2)若PA PD ==G 为PD 的中点,求平面PAB 与平面BEGF 所成锐二面角的余弦值.14.(2021·江苏常州市·高三开学考试)如图,在四棱锥P ABCD -中,底面四边形ABCD 是矩形,2AB AP BC ==,平面PAB ⊥平面ABCD ,二面角P BC A --的大小为45.(1)求证:PA ⊥平面ABCD ;(2)求直线PB 与平面PAC 所成的角的正弦值.15.(2021·浙江绍兴市)如图,在四棱锥P ABCD -中,PAB △是等边三角形,CB ⊥平面,//PAB AD BC 且22PB BC AD F ===,为PC 中点.(1)求证://DF 平面PAB ;(2)求直线AB 与平面PDC 所成角的正弦值.16.(2021·江西高三其他模拟)如图,在三棱锥P ABC -中,2,AB BC CA PA PC PB ======O 为AC 的中点.(1)证明:平面ABC ⊥平面PBO ;(2)求直线PA 与平面ABC 所成角的正弦值.17.(2021·浙江绍兴市·高三期末)如图,三棱柱111ABC A B C -中,12AB BC AC BB ===,1B 在底面ABC 上的射影恰好是点A ,E 是11A C 的中点.(1)证明:1//A B 平面1B CE ;(2)求1A B 与平面11BCC B 所成角的正弦值.18.(2021·浙江绍兴市·高二期末)如图,在三棱柱111ABC A B C -中,12AA AB AC BC ====,160A AB ∠=,13AC =,点M 为线段1A A 的中点.(1)求证:1AB A C ⊥.(2)求二面角1A AB C 的大小.(3)求直线MC 与平面11A B C 所成角的正弦值.。
3.2.4空间向量求距离

z
G
2
C
4 E
2 x 2 y 0 n EF, n EG
1 1 n ( , ,1) , BE (2,0,0) 3 3 | n BE| 2 11 d . 11 n
1 1 2 2 z ∴ MC ( a , a , 0) , MN (0, a , a ) , MA ( a , 0, 0) P 2 2 2 2 设 n ( x, y, z ) 为平面 MNC 的一个法向量, ∴ n MN , n MC 2 N ∴ n MC ax ay 0 且 C D y 2 a a M n MN y z 0 2 2 2 A 解得 x y z , B 2 x ∴可取 m ( 2,1, 1)
n
A
O
这个结论说明,平面外一点到平面的距离等于连结此点与平面 上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的 绝对值.
例1、已知正方形ABCD的边长为4, CG⊥平面ABCD,CG=2,E、F分别是AB、 AD的中点,求点B到平面GEF的距离。 z
G
x D F A
C
E
y
B
解:如图,建立空间直角坐标系 C-xyz. 由题设 C(0,0,0),A(4,4,0),B(0,4,0), D(4,0,0),E(2,4,0),F(4,2,0),G(0,0,2).
(4)直线与平面的距离
如果一条直线和一个平面平行,那么直 线上各点到这个平面的距离相等,且这条直 线上任意一点到平面的距离叫做这条直线和 平面的距离。
高中数学必修一《空间向量与空间距离》练习

空间向量与空间距离(45分钟 100分)一、选择题(每小题6分,共30分)1.已知△ABC的三个顶点的坐标为A(-1,0,1),B(1,3,5),C(-1,-1,1),则BC边上的中线AD的长为( )A. B.6 C. D.32.在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是( )A. aB. aC. aD. a3.(2013·开封高二检测)四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别为PB,PD的中点,则P到直线EF的距离为( )A.1B.C.D.4.已知正方体ABCD-A1B1C1D1的棱长为3,E为CD的中点,则点D1到平面AEC1的距离为( )A. B. C. D.15.(2013·石家庄高二检测)正方体ABCD-A1B1C1D1的棱长为1,则直线A1C1到平面ACD1的距离为( )A.1B.C.D.二、填空题(每小题8分,共24分)6.(2013·东莞高二检测)平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,则AC1的长为.7.在直四棱柱ABCD-A1B1C1D1中,底面为直角梯形,AB∥CD且∠ADC=90°,AD=1,CD=,BC=2,AA1=2,E是CC1的中点,则A1B1到平面ABE的距离是.8.在长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,则平面A1BC1与平面ACD1的距离是.三、解答题(9题,10题14分,11题18分)9.正方形ABCD的边长为2,E,F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图所示),M是矩形AEFD内一点,如果∠MB'E=∠MB'C',MB'和平面B'C'FE所成的角的正切值为,求点M到直线EF的距离.10.(2013·济南高二检测)如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,其中AB=4,BC=2,CC1=3,BE=1.(1)求||.(2)求点C到平面AEC1F的距离.11.(能力挑战题)如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.(1)求证:B1D⊥平面ABD.(2)求证:平面EGF∥平面ABD.(3)求平面EGF与平面ABD的距离.答案解析1.【解析】选A.易知D(0,1,3),∴=(1,1,2),∴||=.2.【解析】选A.如图所示,建立空间直角坐标系,则A1(a,0,a),M(a,0,),B(a,a,0),D(0,0,0)∴=(0,0,),=(a,0,),=(a,a,0),设平面MBD的法向量为n=(x,y,z),则令x=1,得n=(1,-1,-2)∴点A1到平面MBD的距离为= a.【一题多解】由于M是AA1的中点,故A1与A到平面MBD的距离相等. 又V A-MBD=V B-AMD,即××a×a×h=×××a×a,解得h= a.3.【解析】选D.建系如图,即P(0,0,2),E(1,0,1),F(0,1,1),∴=(-1,0,1),=(-1,1,0).∴在上的投影为==,∴点P到直线EF的距离为=.4.【解题指南】先求平面AEC1的法向量,代入点面距公式求解.【解析】选A.建立如图所示空间直角坐标系,则A(3,0,0),D1(0,0,3),E(0,,0),C1(0,3,3),=(-3,,0),=(-3,3,3),=(0,3,0),设n=(x,y,z)为平面AEC1的法向量,则令x=1,得y=2,z=-1,∴n=(1,2,-1).∴D1到平面AEC1的距离为==.5.【解析】选B.易知A1C1∥平面ACD1,则点A1到平面ACD1的距离即为直线A1C1到平面ACD1的距离.建系如图,易知=(0,0,1)平面ACD1的一个法向量为n=(1,1,1),故所求的距离为=.6.【解析】=++,∴||2=(++)2=||2+||2+||2+2·+2·+2·=1+22+32+2||·||·cos<,>+2||·||·cos<,>+2||·||·cos<,>=14+2×1×2cos 90°+2×1×3cos 60°+2×2×3cos 60°=23,∴||=,即AC1=.答案:7.【解析】以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A(1,0,0),B(1,2,0),E(0,,1),A1(1,0,2),∴=(0,2,0),=(-1,-,1),设平面ABE的法向量为n=(x,y,z),则解得,取z=1,则n=(1,0,1).又易证A1B1∥平面ABE,所以A1B1到平面ABE的距离等于点A1到平面ABE的距离,又=(0,0,2),∴点A1到平面ABE的距离为==.答案:8. 【解析】由AD1∥BC1,A1B∥D1C可证得平面A1BC1∥平面ACD1,建立如图所示的空间直角坐标系,∵AB=4,BC=3,CC1=2,则A1(3,0,2),B(3,4,0),C1(0,4,2),A(3,0,0).∴=(0,4,-2),=(-3,0,2).设平面A1BC1的法向量为n=(x,y,z),则n⊥,n⊥,解得,取z=6,则n=(4,3,6),又=(0,4,0),则平面A1BC1与平面ACD1的距离为==.答案:9.【解析】建立如图所示的空间直角坐标系,作MN⊥EF,垂足为N,则MN⊥平面B'C'FE,连接B'N,则∠MB'N即为MB'与平面B'C'FE所成的角,∴tan∠MB'N=,设M(0,y,z),0<y<2,0<z<1,则由题意可知N(0,y,0),而E(0,0,0),B'(1,0,0),C'(1,2,0),∴=(-1,0,0),=(0,2,0),=(-1,y,z),=(-1,y,0),=(0,0,-z),∴cos∠MB'E==,cos∠MB'C'===,tan∠MB'N===.∵∠MB'E=∠MB'C',∴y=1,z=.因此点M到直线EF的距离为.10.【解析】以D为原点,DA,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系,D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).(1)设F(0,0,a),由=,得(-2,0,a)=(-2,0,2),∴a=2.∴F(0,0,2),=(-2,-4,2).∴||=2.(2)设n=(x,y,z)为平面AEC1F的法向量,由得取z=1,则n=(1,-,1),又=(0,0,3),∴C到平面AEC1F的距离d==.11.【解题指南】寻找条件中的三线两两垂直建立空间直角坐标系,正确地求出图中各点坐标,然后利用向量的坐标运算证明、求解.【解析】如图所示,建立空间直角坐标系,设A1(a,0,0),则B1(0,0,0),F(0,1,0),E(0,0,1),A(a,0,4),B(0,0,4),D(0,2,2),G(,1,0).(1)=(0,2,2),=(-a,0,0),=(0,2,-2).∴·=0+0+0=0,·=0+4-4=0.∴B1D⊥AB,B1D⊥BD.又AB∩BD=B,∴B1D⊥平面ABD.(2)∵=(-a,0,0),=(0,2,-2).=(-,0,0),=(0,1,-1),∴=,=.∴GF∥AB,EF∥BD.又GF∩EF=F,AB∩BD=B,∴平面EGF∥平面ABD.(3)方法一:由(1)(2)知DH为平面EFG与平面ABD的公垂线段.设=λ=(0,2λ,2λ),则=(0,2λ,2λ-1),=(0,1,-1).∵与共线,∴=,即λ=,∴=(0,,),∴=(0,,),∴||=.∴平面EGF与平面ABD的距离为.方法二:由(2)知平面EGF∥平面ABD,设平面ABD的法向量为n=(x,y,z),则n⊥,n⊥,∴解得取z=1,则n=(0,1,1),∵=(0,2,1),∴d===,即平面EGF与平面ABD的距离为.。
空间向量求距离(成稿)

C'
A' B'⋅BB' B' E = A' B
C B
一、求点到平面的距离
uur r PA ⋅ n d= r n
方法指导:若点 为平面 外一点, 为平面α外一点 为平面α内任 方法指导:若点P为平面 外一点,点A为平面 内任 为平面 一点,平面的法向量为n,则点P到平面 到平面α的距离公式 一点,平面的法向量为 ,则点 到平面 的距离公式 为
习题课(三) ——空间距离习题课
知识要点
点到平面的距离
一点到它在一个平面内的正射影的距离叫做这一 一点到它在一个平面内的正射影的距离叫做这一 个点到这个平面的距离。 个点到这个平面的距离。
直线到与它平行平面的距离 两个平行平面的距离
两条异面直线的距离
练习
练习1.如图 已知正三角形 练习 如图,已知正三角形 如图 已知正三角形ABC的边长为 的边长为 6cm,点O到△ABC各顶点的距离都是 各顶点的距离都是4cm, , 到 各顶点的距离都是 , 求点O到这个三角形所在平面的距离 到这个三角形所在平面的距离。 求点 到这个三角形所在平面的距离。
A1
1
D A X B
C Y
练习4、在边长为1的正方体ABCD-A1B1C1D1中, M、N、E、F分别是棱A1B1、A1D1、B1C1、 C1D1的中点,求平面AMN与平面EFDB的距离。
z
d=
AB ⋅ n
A1
ND1Leabharlann F EC1n
A
M B1 D B
C
y
x
四、求异面直线的距离
方法指导:①作直线a、b的方向向量a、b,求a、 b的法向量n,即此异面直线a、b的公垂线的方 向向量;②在直线a、b上各取一点A、B,作向 量AB;③求向量AB在n上的射影d,则异面直线 a、b间的距离为
考点27 空间向量求空间距离 ——2021年高考数学专题复习真题练习

考点27 空间向量求空间距离【题组一 两点距】1.已知点,,则的最小值为( ).()2,,M t t ()()1,1,N t t t t R --∈MNA .B C D 1152.在空间直角坐标系中,设,若a 的值是( ) (1,2,),(2,3,4)A a B ||AB =A .3或5B .或C .3或D .或53-5-5-3-3.设点M 是棱长为2的正方体ABCD -A 1B 1C 1D 1的棱AD 的中点,点P 在面BCC 1B 1所在的平面内,若平面D 1PM 分别与平面ABCD 和平面BCC 1B 1所成的锐二面角相等,则点P 到点C 1的最短距离是( )A B C .1 D【题组二 点线距】1.已知正方体ABCD A 1B 1C 1D 1的棱长为2,点E 是A 1B 1的中点,则点A 到直线BE 的距离是( )A BC D【题组三 点面距】1.如图,在直三棱柱中,,,为的中点.111ABC A B C -1AB BC BB ==11AB A B E = D AC(1)求证:平面;BD ⊥11A ACC (2)若,且,求到平面的距离. 1AB =1AC BD ⋅=1B 1A BD2.如图,在四棱锥中,底面为直角梯形,,,为的中点,P ABCD -ABCD //AD BC 2BAD π∠=E AD ,平面平面.22AD AP PD BC AB ====PAD ⊥ABCD(1)求证:平面平面;PBC ⊥PCE (2)记点到平面的距离为,点到平面的距离为,求的值. B PCD 1d E PAB 2d 21d d3.如图,在多面体中,平面⊥平面,,,DE AC ,AD=BD=1.ABCDE ABD ABC AB AC ⊥AE BD ⊥P 12(Ⅰ)求AB 的长;(Ⅱ)已知,求点E 到平面BCD 的距离的最大值.24AC ≤≤4.如图,四棱锥中,底面为矩形,侧面为正三角形,,,平面P ABCD -ABCD PAD 2AD =3AB =平面,为棱上一点(不与、重合),平面交棱于点. PAD ⊥ABCD E PB P B ADE PC F(1)求证:;AD EF(2)若二面角,求点到平面的距离. ––B AC E B AEC【题组四 线面距】1.如图,在四棱锥O −ABCD 中,底面ABCD 是边长为2的正方形,OA ⊥底面ABCD ,OA=2,M ,N ,R 分别为OA,BC,AD的中点,求直线MN与平面OCD的距离及平面MNR与平面OCD的距离.2.在底面是直角梯形的四棱锥PABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA=AB=BC=2,AD=1,则AD到平面PBC的距离为________.如何学好数学1.圆锥曲线中最后题往往联立起来很复杂导致k算不出,这时你可以取特殊值法强行算出k过程就是先联立,后算代尔塔,用下伟达定理,列出题目要求解的表达式,就ok了2.选择题中如果有算锥体体积和表面积的话,直接看选项面积找到差2倍的小的就是答案,体积找到差3倍的小的就是答案,屡试不爽!3.三角函数第二题,如求a(cosB+cosC)/(b+c)coA之类的先边化角然后把第一题算的比如角A等于60度直接假设B和C都等于60°带入求解。
空间向量基本定理及范围最值高二数学选择性必修第一册)(原卷版)

专题2空间向量基本定理及空间范围与最值目录【题型一】空间向量基底.................................................................................................................1【题型二】基底表示向量.................................................................................................................2【题型三】共面.................................................................................................................................3【题型四】空间向量概念综合.......................................................................................................4【题型五】空间向量数量积.............................................................................................................5【题型六】空间向量求长度.............................................................................................................6【题型七】数量积最值与范围.........................................................................................................8【题型八】空间长度最值与取值范围.............................................................................................8【题型九】空间角度范围最值.........................................................................................................9【题型十】轨迹.............................................................................................................................11培优第一阶——基础过关练...........................................................................................................12培优第二阶——能力提升练...........................................................................................................14培优第三阶——培优拔尖练.. (16)【题型一】空间向量基底【典例分析】(2022·全国·高二课时练习)已知{},,a b c 是空间的一组基底,则下列向量中能与a b +,a b -构成一组基底的是()1.(2023·全国·高二专题练习)已知{},,a b c 是空间一个基底,p a b =+,q a b =-,一定可以与向量p ,q 构成空间另一个基底的是()A .aB .bC .cD .123p q -2.(2021·全国·高二课时练习)若{,,}a b c →→→为空间的一组基底,则下列各项中能构成基底的一组向量是()A .{},,a a b a b →→→→→+-B .{},,b a b a b→→→→→+-C .{},,c a b a b→→→→→+-D .{},,2a b a b a b→→→→→→+-+3.(2021·上海市松江二中高二期中)已知向量{},,a b c 是空间的一组基底,则下列可以构成基底的一组向量是()A .a b +,a ,a b -B .a b +,b ,a b-C .a b +,c ,a b-D .a b +,2a b -,a b-【题型二】基底表示向量【典例分析】(2022·河南·洛宁县第一高级中学高二阶段练习)如图,在平行六面体1111ABCD A B C D -中,1AA a =,AB b =,AD c =uuu r r,点P 在1A C 上,且1:2:3A P PC =,则AP 等于()A .233555a b c++B .322555a b c++C .-223555a b c++D .322555a b c--1.(2022·全国·高二课时练习)已知向量{},,a b c 是空间的一个基底,向量{},,a b a b c +-是空间的另一个基底,一向量p 在基底{},,a b c 下的坐标为(1,2,3),则向量p 在基底{},,a b a b c +-下的坐标为()A .1332(2),,B .31(,,3)22-C .13(3,,)22-D .13(,,3)22-2.(2022·全国·高二专题练习)如图的平行六面体ABCD ﹣A 1B 1C 1D 1中,点M 在BB 1上,点N 在DD 1上,且BM 12=BB 1,D 1N 13=D 1D ,若1MN xAB y AD z AA =++,则x +y +z =()A .17B .16C .23D .323.(2022·全国·高二课时练习)在四面体OABC 中,OA a =,OB b =,OC c =,点D 满足BD BC λ=,E 为AD 的中点,且111244OE a b c =++,则λ=()A .12B .14C .13D .23【题型三】共面【典例分析】(2022·全国·高二课时练习)已知空间中四个点O ,A ,B ,C ,{},,OA OB OC 为空间的一组基底,则下列说法正确的是()A .O ,A ,B ,C 四点共线B .O ,A ,B ,C 四点共面,但不共线C .O ,A ,B ,C 四点不共面D .1OA OB OC ===1.(2021·全国·高二课时练习)已知空间四点()4,1,3A ,()2,3,1B ,()3,7,5C -,(),1,3D x -共面,则x 的值为()A .4B .1C .10D .112.(2022·重庆市巫山大昌中学校高二期末)已知A ,B ,C 三点不共线,O 是平面ABC 外一点,下列条件中能确定点M 与点A ,B ,C 一定共面的是A .OM OA OB OC =++B .23OM OA OB OC=++C .111222OM OA OB OC =++D .111333OM OA OB OC=++3.(2022·全国·高二期末)已知A,B,C 三点不共线,对于平面ABC 外的任一点O,下列条件中能确定点M 与点A,B,C 一定共面的是A .OM OA OB OC =++B .2OM OA OB OC=--C .1123OM OA OB OC =++D .111236OM OA OB OC=++【题型四】空间向量概念综合【典例分析】(2022·全国·高二)下列命题中正确的个数是().①若a 与b 共线,b 与c 共线,则a 与c 共线.②向量a ,b ,c 共面,即它们所在的直线共面.③如果三个向量a ,b ,c 不共面,那么对于空间任意一个向量p ,存在有序实数组(),,x y z ,使得p xa yb zc =++.④若a ,b 是两个不共线的向量,而c a b λμ=+(,λμ∈R 且0λμ≠),则{},,a b c 是空间向量的一组基底.A .0B .1C .2D .3【变式训练】1.(2021·广东·顺德市李兆基中学高二期中)以下命题①||||a b -||a b =+是,a b 共线的充要条件;②若{,,}a b c 是空间的一组基底,则{,,}a b b c c a +++是空间的另一组基底;③|()|||||||a b c a b c ⋅=⋅⋅.其中正确的命题有()A .0个B .1个C .2个D .3个2.(2019·安徽·阜阳市第三中学高二期末(理))以下四个命题中正确的是()A .空间的任何一个向量都可用其他三个向量表示B .若{,,}a b c 为空间向量的一组基底,则{},,a b b c c a +++构成空间向量的另一组基底C .ABC ∆为直角三角形的充要条件是0AB AC ⋅=D .任何三个不共线的向量都可构成空间向量的一个基底3.(2022·全国·高二课时练习)在以下命题中,不正确的个数为()①a b a b +-=是a ,b 共线的充要条件;②若a ∥b ,则存在唯一的实数λ,使a =λb ;③对空间任意一点O 和不共线的三点A ,B ,C ,若OP =2OA -2OB -OC ,则P ,A ,B ,C 四点共面;④若{a ,b ,c }为空间的一个基底,则{a +b ,b +c ,c +a }构成空间的另一个基底;⑤|(a ·b )·c |=|a |·|b |·|c |.A .2B .3C .4D .5【题型五】空间向量数量积【典例分析】(2021·辽宁实验中学高二期中)已知正四面体ABCD 的棱长为2,E 为AB 中点,F 为BC 中点,则ED AF →→⋅=()A .12B .1C .32D .21.(2022·江苏·泗阳县实验高级中学高二阶段练习)设正四面体ABCD 的棱长为a ,E ,F 分别是BC ,AD 的中点,则AE AF →→的值为()A .214aB .212aC .a 2D .4a 22.(2022·全国·高二课时练习)四面体OABCE ,F ,G 分别为OA ,OC ,BC 中点,则GE GF ⋅=___________.3.如图,空间四边形ABCD 的每条边和对角线长都等于1,点E ,F ,G 分别是AB ,AD ,DC 的中点,则FG AB ⋅=()A .4B .14C .12D .2【题型六】空间向量求长度【典例分析】(2022·全国·高二课时练习)如图,平行六面体1111ABCD A B C D -的底面ABCD 是边长为1的正方形,且1160A AD A AB ∠=∠=︒,12AA =,则线段1AC 的长为()A 6B 10C 11D .3【提分秘籍】基本规律1.在空间直角坐标系中,设()1111,,P a b c ,()2222,,P a b c ,则12,P P 两点间的距离1212PP PP ==_()()()222212121a a b b c c -+-+-__.2.2222||||()()()()222OP OA OB OC OA OB OC OA OB OC OA OB OA OC OB OC=++=++=+++++1.(2022·全国·高二专题练习)在平行六面体1111ABCDA B C D -中,11AB BC BB ===,11ABB ABC B BC ∠=∠=∠3π=,12AE BD =,则1||B E =()A 33B .5C .32D .32.(2022·广东汕头·高二期末)如图,在平行六面体1111ABCD A B C D -中,M 为AC 与BD 的交点,若111111===A B A D A A ,1190AA D ∠=,1111160AA B B A D ∠∠==,则1B M 的值为()A .12B C .1D .23.(2021·全国·高二课时练习)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,且6AB AP ==,2AD =,60BAD BAP DAP ∠=∠=∠=︒,E ,F 分别为PB ,PC 上的点,且2PE EB =,PF FC =,EF =()A .1BC .2D 【题型七】数量积最值与范围【典例分析】(2022·全国·高二课时练习)已知MN 是正方体内切球的一条直径,点Р在正方体表面上运动,正方体的棱长是2,则PM PN ⋅的取值范围为()A .[]0,4B .[]0,2C .[]1,4D .[]1,2【变式训练】1.(2021·全国·高二专题练习)已知球O 的半径为2,A 、B 是球面上的两点,且AB =若点P 是球面上任意一点,则PA PB ⋅的取值范围是()A .[]1,3-B .[]2,6-C .[]0,1D .[]0,32.(2022·全国·高二课时练习)已知123,,e e e 是空间单位向量,12233113e e e e e e ⋅=⋅=⋅=,若空间向量a 满足()120,0a xe ye x y =+>>,4a =,则3a e ⋅的最大值是_______.3.(2022·全国·高二专题练习)正四面体A BCD -的棱长为4,空间中的动点P 满足PB PC +=AP PD ⋅的取值范围为()A .4⎡-+⎣B .C .44⎡-⎣D .[]14,2-【题型八】空间长度最值与取值范围【典例分析】(2021·全国·高二期末)如图,直三棱柱111ABC A B C -中,侧棱长为2,AC =1BC =,90ACB ∠=︒,点D 是11A B 的中点,F 是侧面11AA B B (含边界)上的动点.要使1AB ⊥平面1C DF ,则线段1C F 的长的最大值为A .52B .2C .133D .5【变式训练】1.(2021·全国·高二专题练习)棱长均为3的三棱锥S ABC -,若空间一点P 满足(1)SP xSA ySB zSC x y z =++++=,则SP 的最小值为()A .6B .63C .36D .12.(2019·湖北武汉·高一期末)设点M 是棱长为4的正方体1111ABCD A B C D -的棱AD 的中点,点P 在面11BCC B 所在的平面内,若平面1D PM 分别与平面ABCD 和平面11BCC B 所成的锐二面角相等,则点P 到点1C 的最短距离是A .222B .455C .2D .2633.(2018·北京一零一中双榆校区高二期中)正方体ABCD -A 1B 1C 1D 1的棱长为1,平面A 1B 1C 1D 1内的一动点P ,满足到点A 1的距离与到线段C 1D 1的距离相等,则线段PA 长度的最小值为A .22B .32C .52D .2【题型九】空间角度范围最值【典例分析】(2022·全国·高二专题练习)如图,在棱长为33的正方体1111ABCD A B C D -中,点P 是平面11A BC 内一个动点,且满足1||||5213DP PB +=+,则直线1B P 与直线1AD 所成角的取值范围为()(参考数据:43sin 53,sin 37)55︒=︒=A .[37︒,53]︒B .[37︒,90]︒C .[53︒,90]︒D .[37︒,127]︒设直线l 的方向向量为u r ,平面sin θ=___cos ϕ___=___u u (4)求平面与平面的夹角平面与平面相交,形成四个二面角,把这四个二面角中不大于cos θ=____12cos ,n n 〈〉_____=____【变式训练】1.(2022·江西·赣州市赣县第三中学高二阶段练习(理))在长方体1111ABCD A B C D -中,2AB AD ==,11AA =,O 是AC 的中点,点P 在线段11A C 上,若直线OP 与平面1ACD 所成的角为θ,则cos θ的取值范围是()A .33⎣⎦B .33⎣⎦C .,43⎣⎦D .3733⎣⎦2.(2022·全国·高二专题练习)如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,E 、F 分别为AB 、BC 的中点,设异面直线EM 与AF 所成的角为θ,则cos θ的最大值为()A .15B .35C .25D .453.(2018·上海·曹杨二中高二期末)在正方体1111ABCD A B C D -中,点P (异于点B )是棱上一点,则满足BP 与1AC ,所成的角为45°的点P 的个数为A .0B .3C .4D .6【题型十】轨迹【典例分析】(2023·全国·高二专题练习)在直三棱柱111ABC A B C -中,AB AC ⊥,12AB AC AA ===,P 为该三棱柱表面上一动点,若1CP B P =,则P 点的轨迹长度为()A .B .C .D .1.(2021·全国·高二专题练习)空间向量AB ,AC ,AD ,,2AB AC π=,,3AB AD π=,,3AC AD π=,且2AB AC ==,4AD =,若点P 满足AP xAB y AC z AD =++,且1≥x ,1y ≥,1z ≥,5x y x ++≤,则动点P 的轨迹所形成的空间区域的体积为__________.2.(2022·全国·高二课时练习)如图,已知正方体1111ABCD A B C D -的棱长为1,E 、F 分别是棱AD 、11B C 上的中点.若点P 为侧面正方形11ADD A 内(含边)动点,且存在x 、y R ∈,使1B P xBE yBF =+成立,则点P 的轨迹长度为_________.3.(2021·全国·高二期末)已知三棱锥A BCD -的所有棱长均为2,E 为BD 的中点,空间中的动点P 满足PA PE ⊥,PC AB ⊥,则动点P 的轨迹长度为()A .1116πB C .112D 培优第一阶——基础过关练1.(2022·全国·高二课时练习)若{},,a b c 为空间的一个基底,则下列各组向量中一定能构成空间的一个基底的是______.(填序号)①a ,a b +,a b -;②b ,a b +,a b -;③c ,a b +,a b -;④a b +,a b -,2a b +.2.(2022·浙江·高二开学考试)在平行六面体1111ABCD A B C D -中,E 为11C D 的中点,F 为1BB的中点,,,AE a AF b AD c ===,则1AA =()A .4332a b c --B .4433a b c --C .424333a b c --D .3423a b c --3.(2022·江苏镇江·高二开学考试)已知四棱锥P ABCD -的底面是平行四边形,侧棱PB 、PC 、PD 上分别有一点E 、F 、G ,且满足23PE PB =,12PG PD =uuu r uuu r ,PF PC λ=,若A 、E 、F 、G 四点共面,则实数λ=__________.4.(2022·全国·高二课时练习)在空间四点O ,A ,B ,C 中,若{},,OA OB OC 是空间的一个基底,则下列命题不正确的是()A .O ,A ,B ,C 四点不共线B .O ,A ,B ,C 四点共面,但不共线C .O ,A ,B ,C 四点不共面D .O ,A ,B ,C 四点中任意三点不共线5.(2022·全国·高二课时练习)已知四面体ABCD ,所有棱长均为2,点E ,F 分别为棱AB ,CD 的中点,则AF CE ⋅=()A .1B .2C .-1D .-26.(2022·全国·高二专题练习)已知斜三棱柱111ABC A B C -所有棱长均为2,113A AB A AC π∠=∠=,点E 、F 满足112AE AA =,12BF BC =uu u r uu u r ,则EF =()A B C .2D7.(2022·全国·高二课时练习)已知空间向量a ,b ,c 满足0a b c ++=,1a =,2b =,c =,则a 与b 的夹角为()A .30°B .45︒C .60︒D .90︒8.(2021·浙江省杭州学军中学高二期中)如图,二面角AB αβ--的大小为θ,P ,Q 分别在平面α,β内,PM AB ⊥,NQ AB ⊥,PM m =,QN n =,1PQ =,则MN =()AB CD 9.(2022·全国·高二课时练习)已知(5,3,1)a =,22,,5b t ⎛⎫=-- ⎪⎝⎭.若a 与b 的夹角为钝角,则实数t 的取值范围是________.培优第二阶——能力提升练1.(2021·全国·高二课时练习)设,,x a b y b c z c a =+=+=+且{},,a b c 是空间的一组基底,给出下列向量组:①{},,a b x ;②{,,}x y z ③{,,}b c z ④{,,}x y a b c ++其中可以作为空间的基底的向量组是___________(填序号).2.(2022·福建·厦门海沧实验中学高二期中)如图,在四面体O ABC -中,OA a =,OB b =,OC c =,且2OM MA =,BN NC =,则MN =()A .221332a b c ++B .221332a b c +-r r rC .211322a b c -++D .121232a b c -+3.(2021·福建·厦门双十中学高二期中)已知(2,1,3),(1,4,2),(3,5,)a b c λ=-=-=-,若,,a b c 三向量共面,则实数λ=_____.4.(2021·河北·石家庄市第十二中学高二期中)下列关于空间向量的说法中,正确的有___________.①若向量a ,b 与空间任意向量都不能构成基底,则//a br r ②若非零向量a ,b ,c 满足,a b ⊥,b c ⊥,则有//a c ③a b a b -=+是a ,b 共线的充分不必要条件④若AB ,CD 共线,则//AB CD5.(2022·全国·高二课时练习)如图,在三棱柱11ABC A B C -中,底面ABC 为正三角形,侧棱垂直于底面,14,6AB AA ==.若E 是棱1BB 的中点,则异面直线1A E 与1AC 所成角的余弦值为()A B C D 6.(2021·安徽·高二阶段练习)在平行六面体1111ABCD A B C D -中,4AB =,2AD =,13AA =,113BAD BAA A AD π∠=∠=∠=,12CM MC =,则AM 的长为()A .B C .D 7.(2022·全国·高二专题练习)已知MN 是棱长为4的正方体内切球的一条直径,点P 在正方体表面上运动,则PM PN ⋅的取值范围为()A .[14],B .[012],C .[08],D .[16],8.(2022·河南·洛宁县第一高级中学高二阶段练习)如图,三棱锥O ABC -各棱的棱长是1,点D 是棱AB 的中点,点E 在棱OC 上,且OE OC λ=,则DE 的最小值为()A .1 2B .22CD .19.(2020·浙江·湖州中学模拟预测)已知点P 是正方体1111ABCD A B C D -表面上一动点,且满足||2||PA PB =,设1PD 与平面ABCD 所成的角为θ,则θ的最大值为()A .4πB .3πC .6πD .2π培优第三阶——培优拔尖练1.(2019·安徽蚌埠·高二期末(理))已知()a 1,2,3=-,()b 1,14=--,,()c 1,3,m =-,则“m 1=”是“a ,b ,c 构成空间的一个基底”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.(2022·云南·罗平县第一中学高二开学考试)如图,平行六面体1111ABCD A B C D -中,AC 与BD 的交点为M ,设AB a =,AD b =,1AA c =,则选项中与向量1C M uuuu r 相等的是()A .1122---a b cB .1122a b c ++C .1122--a b cD .1122+-a b c 3.(2022·全国·高二课时练习)在正方体1111ABCD A B C D -中,点M 和N 分别是矩形ABCD 和11BB C C 的中心,若点P 满足DP =mDA nDM k DN ++,其中m n k R ∈、、,且1m n k ++=,则点P 可以是正方体表面上的点________.4.(2021·全国·高二专题练习)下列命题正确的是()A .若a 与b 共线,b 与c 线,则a 与c 共线B .向量a ,b ,c 共面,即它们所在的直线共面C .若a ∥b ,则存在唯一的实数λ,使a =λbD .零向量是模为0,方向任意的向量5.(2022·全国·高二课时练习)如图所示,空间四边形的各边和对角线长均相等,E 是BC 的中点,那么().A .AE BC AE CD⋅<⋅B .AE BC AE CD ⋅=⋅C .AE BC AE CD ⋅>⋅D .AE BC ⋅与AE CD ⋅不能比较大小6.(2022·全国·高二单元测试)如图在平行六面体1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,侧棱12AA =且1160A AD A AB ∠=∠=︒,则1AC =()A .B C .D 7.(2021·全国·高二专题练习)已知棱长为2的正方体1111ABCD A B C D -,点A 在空间直角坐标系O xyz -的x 轴上移动,点C 在平面yOz 上移动,则1OC OB ⋅的最大值是()A .2B .1C .4+D .68.(2022·全国·高二专题练习)如图,已知正方体1111ABCD A B C D -的棱长为1,则线段1AD 上的动点P 到直线11A C 的距离的最小值为()A .1B .2C .4D .39.(2022·江西鹰潭·高二期末(理)P ABC -中,5AB AC PB PC ====,4PA =,6BC =,点M 在平面PBC 内,且AM =设异面直线AM 与BC 所成的角为α,则cos α的最大值为()A 25B .5C .25D。
高中数学立体几何专:空间距离的各种计算(含答案)doc(K12教育文档)

高中数学立体几何专:空间距离的各种计算(含答案)doc(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学立体几何专:空间距离的各种计算(含答案)doc(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学立体几何专:空间距离的各种计算(含答案)doc(word版可编辑修改)的全部内容。
高中数学立体几何空间距离1.两条异面直线间的距离和两条异面直线分别垂直相交的直线,叫做这两条异面直线的公垂线;两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离.2.点到平面的距离从平面外一点引一个平面的垂线,这点和垂足之间的距离叫做这个点到这个平面的距离. 3.直线与平面的距离如果一条直线和一个平面平行,那么直线上各点到这平面的距离相等,且这条直线上任意一点到平面的距离叫做这条直线和平面的距离。
4.两平行平面间的距离和两个平行平面同时垂直的直线,叫做这两平行平面的公垂线,它夹在两个平行平面间的公垂线段的长叫做这两个平行平面的距离.题型一:两条异面直线间的距离【例1】 如图,在空间四边形ABCD 中,AB =BC =CD =DA =AC =BD =a ,E 、F 分别是AB 、CD 的中点。
(1)求证:EF 是AB 和CD 的公垂线; (2)求AB 和CD 间的距离;【规范解答】 (1)证明:连结AF ,BF ,由已知可得AF =BF 。
又因为AE =BE ,所以FE ⊥AB 交AB 于E 。
同理EF ⊥DC 交DC 于点F .所以EF 是AB 和CD 的公垂线.(2)在Rt △BEF 中,BF =a 23,BE =a 21,所以EF 2=BF 2—BE 2=a 212,即EF =a 22.由(1)知EF 是AB 、CD 的公垂线段,所以AB 和CD 间的距离为a 22. 【例2】 如图,正四面体ABCD 的棱长为1,求异面直线AB 、CD 之间的距离. 设AB 中点为E ,连CE 、ED .∵AC =BC ,AE =EB 。
考点27 空间向量求空间距离(练习) (原卷版)

考点27 空间向量求空间距离【题组一 两点距】1.已知点()2,,M t t ,()()1,1,N t t t t R --∈,则MN 的最小值为( ).A .115BC .5D .52.在空间直角坐标系中,设(1,2,),(2,3,4)A a B ,若||AB =a 的值是( ) A .3或5 B .3-或5- C .3或5-D .3-或5 3.设点M 是棱长为2的正方体ABCD -A 1B 1C 1D 1的棱AD 的中点,点P 在面BCC 1B 1所在的平面内,若平面D 1PM 分别与平面ABCD 和平面BCC 1B 1所成的锐二面角相等,则点P 到点C 1的最短距离是( )A B .2 C .1 D【题组二 点线距】1.已知正方体ABCD A 1B 1C 1D 1的棱长为2,点E 是A 1B 1的中点,则点A 到直线BE 的距离是( )A BC D【题组三 点面距】1.如图,在直三棱柱111ABC A B C -中,1AB BC BB ==,11AB A B E =,D 为AC 的中点.(1)求证:BD ⊥平面11A ACC ;(2)若1AB =,且1AC BD ⋅=,求1B 到平面1A BD 的距离.2.如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,//AD BC ,2BAD π∠=,E 为AD 的中点,22AD AP PD BC AB ====,平面PAD ⊥平面ABCD .(1)求证:平面PBC ⊥平面PCE ;(2)记点B 到平面PCD 的距离为1d ,点E 到平面PAB 的距离为2d ,求21d d 的值.3.如图,在多面体ABCDE 中,平面ABD ⊥平面ABC ,AB AC ⊥,AE BD ⊥,DE12AC ,AD=BD=1. (Ⅰ)求AB 的长;(Ⅱ)已知24AC ≤≤,求点E 到平面BCD 的距离的最大值.4.如图,四棱锥P ABCD -中,底面ABCD 为矩形,侧面PAD 为正三角形,2AD =,3AB =,平面PAD ⊥平面ABCD ,E 为棱PB 上一点(不与P 、B 重合),平面ADE 交棱PC 于点F .(1)求证:AD EF ;B AC E,求点B到平面AEC的距离.(2)若二面角––【题组四线面距】1.如图,在四棱锥O−ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M,N,R分别为OA,BC,AD的中点,求直线MN与平面OCD的距离及平面MNR与平面OCD的距离.2.在底面是直角梯形的四棱锥PABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA=AB=BC=2,AD=1,则AD到平面PBC的距离为________.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【题组一 两点距】
1.已知点 , ,则 的最小值为( ).
A. B. CБайду номын сангаас D.
2.在空间直角坐标系中,设 ,若 ,则实数a的值是( )
A.3或5B. 或 C.3或 D. 或5
3.设点M是棱长为2的正方体ABCD-A1B1C1D1的棱AD的中点,点P在面BCC1B1所在的平面内,若平面D1PM分别与平面ABCD和平面BCC1B1所成的锐二面角相等,则点P到点C1的最短距离是( )
(1)求证:平面 平面 ;
(2)记点 到平面 的距离为 ,点 到平面 的距离为 ,求 的值.
3.如图,在多面体 中,平面 ⊥平面 , , ,DE AC,AD=BD=1.
(Ⅰ)求AB的长;
(Ⅱ)已知 ,求点E到平面BCD的距离的最大值.
4.如图,四棱锥 中,底面 为矩形,侧面 为正三角形, , ,平面 平面 , 为棱 上一点(不与 、 重合),平面 交棱 于点 .
A. B. C.1D.
【题组二 点线距】
1.已知正方体ABCD A1B1C1D1的棱长为2,点E是A1B1的中点,则点A到直线BE的距离是( )
A. B.
C. D.
【题组三 点面距】
1.如图,在直三棱柱 中, , , 为 的中点.
(1)求证: 平面 ;
(2)若 ,且 ,求 到平面 的距离.
2.如图,在四棱锥 中,底面 为直角梯形, , , 为 的中点, ,平面 平面 .
(1)求证: ;
(2)若二面角 的余弦值为 ,求点 到平面 的距离.
【题组四 线面距】
1.如图,在四棱锥O−ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M,N,R分别为OA,BC,AD的中点,
求直线MN与平面OCD的距离及平面MNR与平面OCD的距离.
2.在底面是直角梯形的四棱锥P ABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA=AB=BC=2,AD=1,则AD到平面PBC的距离为________.
