数值传热学第五章1
数值传热学第五章-数值计算

2016-1-30
太 原 理 工 大 学
9 /70
Thermal
这就是中心差分格式求解对流换热问题时仅限于低
Fw Fe Re(低的F/D)的原因 . aP Dw De aW aE Fe Fw 2 2
若E 200, W 100 P 50
两个值均不 符合实际
若E 100, W 200 P 250
aW Dw Fw 2 1 2 3
aE De Fe 2 1 2 1 违背了正系数规则
aP aE aW 1 3 2, 而 anb 1 3 4 这样,aP anb , 违反了斯卡巴勒准则( 主对角占优)
ui 0
i-1 W
w
二类迎风格式) 控制容积界面上值的规定: 界面上的值等于界面上风侧 网格节点上的值。
e P e E
Fe 0 Fe 0
i
P
e
i+1
E
ui 0
类似地,w界面上
w W Fw 0 w P Fw 0
上述条件语句紧凑格式的写法:
Γe、Γw可以用算术平均法或调和平均法求得。
定义:
D 扩散传导性. x
Thermal
F u 对流或流动强度,可正 、可负,由流动方向定
整理后的离散化方程 其中:
2016-1-30
a p P aE E aWW
Fw 2 太 原 理 工 大 学 aW Dw
7 /70
太 原 理 工 大 学
3 /70
Thermal
哈尔滨工业大学 计算传热学 第五章 对流-扩散方程的离散格式-2013

aPP aEE aWW
Fe Fw exp( Pw ) aE , aW exp( Pe ) 1 exp( Pw ) 1
(D)
aP aE aW (Fe Fw )
区别就在函数 aE和aW
aE De
Pe aE De exp( Pe ) 1
aE Pe De
该格式计算量比指数小,且指数格式的解差别很小。
§ 5-3
为了在讨论中引入 PE 记
通用表达式
x
i
J*
i+1 i+1/2
x
1 界面i+ 上的值可以用界面两侧节点值表示 2
J * Bi Ai 1 (y)
系数A和B的性质的讨论 (1)当 i i 1 时,扩散量=0, J *完全由对流造成,即
即
aPP aEE aW W
显然不论那种格式,仅仅是 A(| P |) 表达式的区别。
A( P )
A(|P |)
中心 1 0.5 | P | 迎风 1 混合 [| 0,1 0.5 | P | |] 指数 | P | [exp(| P |) 1]
1.0
迎风
指数 乘方
乘方 | 0, (1 0.1| P |)5 |
中心
混合
P
§ 5-4
原始的假扩散概念
关于假扩散的讨论
一维非稳态对流方程(纯对流,没有扩散)
u t x
显示迎风差分格式
in1 in
t
u
in in 1
x
, o(x, t )
将上式在(i,n)点做Taylar级数展开,保留二阶。
上述若对任何成立,必得
B( P ) A( P ) A( P ) B( P )
传热学第四版第5章汇总

粘性耗散产生的耗散热可以忽略不计
除高速的气体流动及一部分化工用流体等情况的对流换热 外,对工程中常见的对流换热问题大都可以作上述假定
5-2对流换热问题的数学描写
微元体能量平衡分析
热力学第一定律
dU
d
qm
out
h
1 2
v2
gz out
qm
in
h
1 2
v2
gz in
表面换热系数的一般函数形式
单相强制对流换热,非高速流动时:
h f u,l, ,, , cp
5-1对流换热概说
对流换热的分类
对流换热
无相变
有相变
强制对流 自然对流 混合对流 沸腾换热 凝结换热
5-1对流换热概说
强制对流
内部流动
外部流动
圆管内强制对流
其他形状截面管 道内的对流换热
外掠单根圆 管的对流换热
U
c p dxdy
t
d
5-2对流换热问题的数学描写
微元体能量平衡分析
dτ时间内通过x、y方向各截面进出微元体的焓
x截面流入微元体的焓
qm
in
hin
x
Hx
cputdyd
x+dx截面流出微元体的焓
q m
out
hout
xdx
H xdx
cp
t
t x
dx
u
u x
dx
dyd
5-2对流换热问题的数学描写
实验法
通过实验获得表面传热系数的计算式仍是目前工程设 计的主要依据。为了减少实验次数、提高实验测定结 果的通用性,传热学的实验测定应当在相似原理指导 下进行
【免费下载】数值传热学第五章作业

5-2解:根据课本p158式(5—1a )得一维稳态无源项的对流-扩散方程如下所示: (取常物性)22x x u ∂∂Γ=∂∂φφρ边界条件如下:L L x x φφφφ====,;,00由(5—2)得方程的精确解为: 11)/(00--=--⋅Pe L x Pe L e e φφφφΓ=/uL Pe ρ将分成15等份,有:L ∆=P Pe 15对于中心差分、一阶迎风、混合格式和QUICK 格式分别分析如下:1)(CD)中心差分节点离散方程: 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ10,2 =i 2)一阶迎风节点离散方程: ∆-∆++++=P P i i i 2)1(11φφφ10,2 =i 3)混合格式当时,节点离散方程:,1=∆P 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ10,2 =i 当时,节点离散方程: , 10,5=∆P 1-=i i φφ10,2 =i 4)QUICK 格式,节点离散方程: , ⎥⎦⎤⎢⎣⎡--++++++=+-∆∆-∆∆+∆)336(81221211111i i i i i i P P P P P φφφφφφ2=i , ⎥⎦⎤⎢⎣⎡---++++++=+--∆∆-∆∆+∆)35(812212112111i i i i i i i P P P P P φφφφφφφ2≠i用matlab 编程如下:(本程序在x/L=0-1范围内取16个节点进行离散计算,假设y(1)= =0,y(16)==1,程序中Pa 为,x 为题中所提的x/L 。
由于本程序假设y(1)=0φL φ∆P =0,y(16)==1,所以)0φL φy y y y y y L =--=--=--010)1()16()1(00φφφφPa=input('请输入Pa=')x=0:1/15:1Pe=15*Pa;y=(exp(Pe*x)-1)/(exp(Pe)-1)plot(x,y,'-*k') %精确解hold ony(1)=0,y(16)=1;for i=2:15y(i)=((1+0.5*Pa)*y(i-1)+(1-0.5*Pa)*y(i+1))/2;endplot(x,y(1:16),'-or') %中心差分hold onfor i=2:15y(i)=((1+Pa)*y(i-1)+y(i+1))/(2+Pa);endplot(x,y(1:16),'-.>g') %一阶迎风hold onfor i=2:15if Pa==1y(i)=((1+0.5*Pa)*y(i-1)+(1-0.5*Pa)*y(i+1))/2;elsey(i)=y(i-1)endendplot(x,y(1:16),'-+y') %混合格式hold onfor i=2:15if i==2y(i)=y(i+1)/(2+Pa)+(1+Pa)*y(i-1)/(2+Pa)+(Pa/(2+Pa))*(6*y(i)-3*y(i-1)-3*y(i+1))/8 elsey(i)=y(i+1)/(2+Pa)+(1+Pa)*y(i-1)/(2+Pa)+(Pa/(2+Pa))*(5*y(i)-y(i-1)-y(i-2)-3*y(i+1))/8 endendplot(x, y(1:16),'-<b') %QUICK 格式hold onlegend('精确解','中心差分','一阶迎风','混合格式','QUICK 格式')运行结果如下图所示:当 :1=∆P当:5=∆P当:10=∆P5-3 解:根据课本式(5-19)得:乘方格式:⎪⎪⎩⎪⎪⎨⎧<-≤≤--+≤≤->=∆∆∆∆∆∆∆∆10,010,)1.01(100,)1.01(10,055P P P P P P P P D a e E 当时有:1.0=∆P 951.0)1.01.01()1.01(55=⨯-=-=∆P D a e E 301.0/3)()()()()()(===Γ=Γ=∆ee e e e e e e e P u x u u x D ρδρρδ5297.2830951.0951.0=⨯==e E D a 由系数关系可得:∆=-P D a D a e E w W 53.3130)951.01.0((=⨯+=⨯+=∆w e E W D D a P a根据式(5-51g )得: 205.01.010=⨯=∆∆=tx a P p ρ根据式(4-12)得: (本题方程中无源项)0P W E P a fa fa a ++=当采用隐式时,则得到:1=f 0597.62253.315297.280=++=++=P W E P a fa fa a 即:时,,,,1.0=∆P 5297.28=E a 53.31=W a 20=p a 0597.62=P a 当时,按照以上算法得出:10=∆P ,, , 0=E a 3=W a 20=p a 5=P a。
数值传热学第5章作业答案
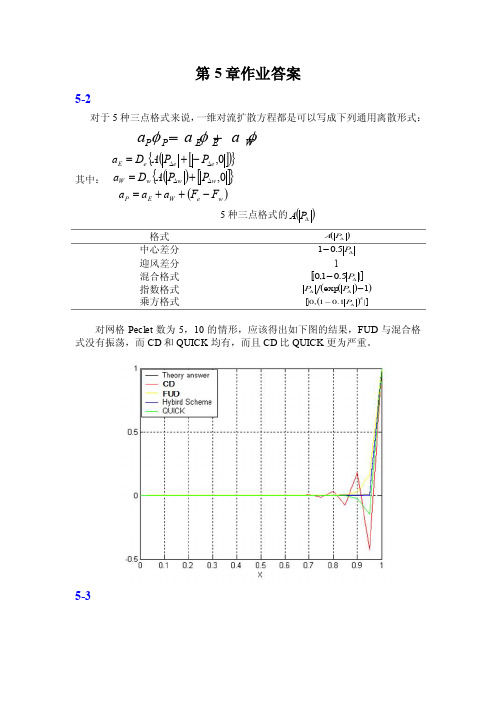
第5章作业答案5-2对于5种三点格式来说,一维对流扩散方程都是可以写成下列通用离散形式:P P E E W Wa a a φφφ=+ 其中: [](){}()[]{}()w e W E P w w w W e e e E F F a a a P P A D a P P A D a -++=+=-+=∆∆∆∆0,0,5种三点格式的()∆P A格式()∆P A迎风差分 1混合格式 []|5.01,0|∆-P 指数格式 ()()1exp -∆∆P P对网格Peclet 数为5,10的情形,应该得出如下图的结果,FUD 与混合格式没有振荡,而CD 和QUICK 均有,而且CD 比QUICK 更为严重。
5-3不同网格∆P 数下各系数计算结果如下∆P E aW a 0P a P a 0.1 28.53 31.53 2 62.05910 0 3255-5 四个节点之值如下一阶迎风 混合格式 乘方格式 二阶迎风(边界一阶) 二阶迎风(边界二阶)1φ 94.26 73.96 79.01 58.57 91.122φ 147.61 91.10 115.13 76.65 144.19 3φ 82.14 72.40 74.19 69.33 81.34 4φ 126.99 85.31 102.70 87.38 124.505-7不计扩散项,采用QUICK 离散i 控制容积的非稳态与对流项得:12117338n nn n n ni i i i i i x utφφφφφφ+--+--++∆=-∆ ((0)u >采用离散扰动分析法,对i+1得到扰动为78n i u t ρε∆,对i-1 得到扰动为38ni u t xε∆-∆,符号不变原则要求:0832≥∆Γ∆+∆∆-ninin i x t x t u εερερ,由此得:38≤=Γ∆∆P xu ρ5-9根据三阶迎风格式的定义:⎪⎩⎪⎨⎧<∆--+->∆+-+=∂∂-++--+0,62360,6632112211u x u xx i i i i i i i i φφφφφφφφφ仿照QUICK 格式,令三阶迎风格式的控制容积右界面上的值的形式为:⎪⎩⎪⎨⎧<+--+>+--+=0,220,22u a u a EEE P E P WP E E P e φφφφφφφφφφφ同理可以写出w φ的计算式。
传热学课件第5章

第五章 对流换热原理
传热学C Heat Transfer
§5-1 对流换热概述
一、对流换热的定义和机理
对流换热:流体流过固体壁面时所发生的热 量传递过程。
机理:既有热对流,也有导热,不是基本的热量传 热方式。
传热学C Heat Transfer
二、牛顿冷却公式
hx— 壁面x处局 系部 W 数 ( m 表 2C ) 面
由以上得:
hx
tw
t
t y
y0,x
它揭示了对流换热问题的 本质
传热学C Heat Transfer
五、局部对流换热系数与边界层的关系
传热学C Heat Transfer
平均对流传热系数:
h 1 At
AhxtxdAx
对于长度为 l 的平板:
1. 定义:当流体流过固体壁面时, 由于流体粘性的作用,使得在固 体壁面附近存在速度发生剧烈 变化的薄层称为流动边界层或 速度边界层。
2. 速度边界层厚度d 的规定:速度等于99%主流 速度。
传热学C Heat Transfer
3. 特点:通常情况下,边界层厚度d是比壁面尺度l 小一个数量级以上的小量。 d << l
传热学C Heat Transfer
例如,对于外掠平板的对流换热现象,可以得到雷
诺数Re、普朗特数Pr和努赛尔数Nu。如果是
两个相似的外掠平板的对流换热现象,则必有:
R'eR"e Pr ' Pr" N'uN"u
根据相似的这种性质,在实验中就只需测量各准 则所包括的量,避免了测量的盲目性,解决了实验 中测量那些量的问题。
Gr gtL3 2
数值传热学习题答案(汇总版)
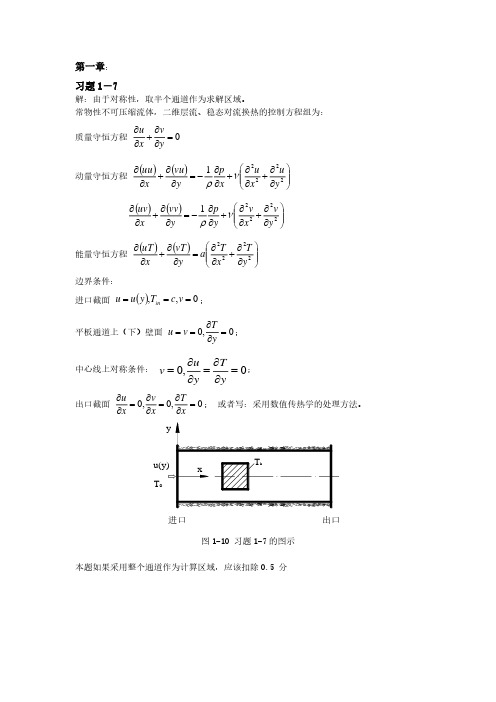
2-4-9
= rP rS
式(2-4-9)也可以写成 a PTP = a E TE + aW TW + b 的形式。而且两种结果是一致的。
2—6:
n n TE −TW dT P , n = 解:将 , dx 2x n n TE −2TPn + TW d 2T P , n = , dx2 x 2
dk = f (x ) 代入原方程,得: dx
令
2-4-4
rk rk a E = , aW = , a P = a E + aW , b x w x e
= SrP r ,
式(2-4-4)可以写成 a PTP = a E TE + aW TW + b 的形式。 2. 再用 Taylor 展开法导出 k
2 2 uE + uP u = , 2 2 e
2 2 uW + uP u = 2 2 w
t u ut N − uP y = (y ) , n n
t
t ut u p − uS y = (y ) 。 s s
t
(y ) n = (y ) s = y
n n n n TE −TW TE −2TPn + TW k + f (x ) +S=0 整理得: 2x x 2
4kT P= 2k + xf ( x)T E+2k − xf ( x)T W +2x 2 S
− 2k 时, a E 会成为负值, x 2k 当 f(x)> 时, aW 会成为负值。 x
rk dr = rk r r dr dr dr
w
e
1 d
传热学第五章对流换热

1.流动边界层(Velocity boundary layer )
如果流体为没有粘性流体,流体流过平板时,流速在截 面上一直保持不变。 如果流体为粘性流体,情况会如何呢?我们用一测速仪 来测量壁面附近的速度分布。测量发现在法向方向上, 即y方向上,壁面上速度为零,随着y方向的增加,流速 急剧增加,到达一薄层后,流速接近或等于来流速度, 德国科学家普朗特L.Prandtl研究了这一现象,并且在 1904年第一次提出了边界层的、分类 三、对流换热的机理 四、影响因素 五、研究方法 六、h的物理意义
一.定义
流体流过与其温度不同的固体表面时所发生的热量交换称为 对流换热。 对流换热与热对流不同, 既有热对流,也有导热; 不是基本传热方式。 对流换热遵循牛顿冷却定律:
qw tw
x
y
t∞
u∞
图5-1 对流换热过程示意
圆管内强制对流换热 其它形式截面管道内的对流换热 外掠平板的对流换热 外掠单根圆管的对流换热 外掠圆管管束的对流换热 外掠其它截面形状柱体的对流换热 射流冲击换热
外部流动
对 流 换 热
有相变
自然对流(Free convection) 混合对流 沸腾换热 凝结换热
大空间自然对流 有限空间自然对流
大容器沸腾 管内沸腾 管外凝结 管内凝结
λ ∂t 换热微分方程(描写h的本质,hx = − ∆t ( ∂y ) y =0 dA) 连续性方程(描写流体流动状态,即质量守恒) 动量微分方程(描写流动状态,即动量守恒) 能量微分方程(描写流体中温度场分布)
对流换热微分方程组 先作假设: (1)仅考虑二维问题; (2)流体为不可压缩的牛顿流体,稳定流动; (3)常物性,无内热源; (4)忽略由粘性摩擦而产生的耗散热。 以二维坐标系中的微元体为分析对象,根据热力学第一定 律,对于这样一个开口系统,有:
传热学第5章1

Φ = ∫ qx dA = ∫ hx ( tw − tf ) x dA = ( tw − tf ) ∫ hx dA A A A
1 h( 对照式 Φ = A h( tw-tf ) 可得 h = ∫A hx dA A
如何确定表面传热系数的大小是对流换热计算的 核心问题,也是本章讨论的主要内容。 核心问题,也是本章讨论的主要内容。
3)能量微分方程(能量守恒) 能量微分方程(能量守恒)
y
单位时间由导热进入微元体 Φλ , x+dx 的净热量和由对流进入微元体的 dy Φλ , x Φh , x Φh , x+dx 净热量之和等于微元体热力学能 Φλ , y Φh , y 的增加, 的增加, dU 0 x Φλ + Φh = dx dτ 单位时间由导热进入微元体的净热量
流体导热系数
Department of Power Engineering, North China Electric Power University (Beijing 102206) 杨立军 知识产权与使用权归华北电力大学能源与动力工程学院所有
NCEPU
按照牛顿冷却公式 ∂t qx = hx ( tw − t∞ ) x = −λ ∂y λ ∂t hx = − ( tw − t∞ ) x ∂ y y =0, x
qx = hx ( tw − tf ) x
杨立军 知识产权与使用权归华北电力大学能源与动力工程学院所有
Department of Power Engineering, North China Electric Power University (Beijing 102206)
NCEPU
等壁温, 等壁温,( tw − tf ) x = tw − tf = 常数
大学课件_计算传热学_第五章非稳态问题的求解方法

第5章 非稳态问题的求解方法1.1 通用输运方程()()()()()t t f q Γv tφφρφρφφ,grad div div =++-=∂∂ ( 5-1 )5.1 显式Euler 方法考虑1D, 定速度,常物性,无源项的特例22xx u t ∂∂Γ+∂∂-=∂∂φρφφ ( 5-2 ) 时间向前,空间中心差分,得FD 与FV 相同形式代数方程()t x x u nin i n i n i n i nin i∆⎥⎦⎤⎢⎣⎡∆-+Γ+∆--+=-+-++21111122φφφρφφφφ( 5-3 ) 可写成()ni n i n i n i c d c d d 1112221-++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-+-=φφφφ ( 5-4 ) 其中()xtu c and x t d ∆∆=∆Γ∆=2ρ ( 5-5 ) d 表示时间步长与特征扩散时间()Γ∆/2ξρ的比。
后者代表一个扰动由于扩散通过∆x 一段距离所需时间。
c 表示时间步长与特性对流传递时间x u ∆/的比。
后者代表一个扰动由于对流通过∆x 一段距离所需时间。
c 成为Courant number, 为CFD 中一个关键的参数。
此格式为时间为1阶精度,空间为2阶精度。
方程(4)内的系数在某些条件下,可能会是负值。
用矩阵表示:n n A φφ=+1 ( 5-6 )观察函数:()∑---=-=in i ni n n 211φφφφε( 5-7 )如果系数矩阵A 的本征值中有大于1,则ε随着n 的增加而增加。
如果本征值全部小于1,则ε是递减的。
一般本征值很难求得,对于本特例,它的解可用复数形式表示ji n n j e ασφ= ( 5-8 )其中,α为波数,可取任意值。
∙ 无条件发散:φn 无条件随n 增加→|σ|>1 ∙无条件稳定:φn 无条件随n 降低→|σ|<1代入差分方程,得到本征值为:()αασsin 2cos 21c i d +1-+= ( 5-9 )考虑特殊情况,∙ 无扩散:d=0, →σ >0, 无条件发散,充分条件∙无对流:c=0, →当cos α= -1时,σ最大,→d<1/2,无条件收敛,充分条件从另一个稳定条件考虑,要求系数矩阵A 的所有系数为正,可得到类似稳定性条件:(充分条件)d c d 2and 5.0<<( 5-10 )第一个条件要求()Γ∆<∆22x t ρ ( 5-11 )表示,每当∆x 减少一半,时间步长需减少到1/4. 第二个条件要求2Pe or2<<Γ∆cell xu ρ ( 5-12 )这同前述的用1D 稳态对流/扩散问题的CDS 要求是一致的。
传热学第五章

例2:流体外掠平板对流换热边界层温度场相似问题 温度沿 x、y 方向变化 如果在空间 对应点上: 几何相 似倍数
' x1 " x1
=
' r2 " r2
=
r3'
" r3
= .... =
' um " um
R'
几何相 似倍数
=
' u2 " u2
=
' u3 " u3
= .... =
' u max
∂x
∂y
∂y
Cu Cl Ca
” ∂t” ” ∂t” ” ∂ 2 t” =a u +v 2 ∂x” ∂y” ∂y”
hl — — 努谢尔特数( Nusslet ) λ ρul ul = Re = — 雷诺数 ( Reynolds ) η ν Nu = ν a ∆p Eu = ρu 2 Pr = — — 普朗特数 (Prandtl) — — 欧拉数 (Euler) ul — 贝克利数 (Peclet)20 a
17
∂u” ∂v” + =0 ∂x” ∂y”
Cu Cl u 'l ' υ " =1 ⇒ =1 Re ' = Re" Cυ υ ' u "l " C∆p Cl ∆p ' u 'l ' ρ "u "2 υ " = 1 ⇒ ' '2 ' =1 C ρ Cu Cυ ρ u υ ∆p" u "l "
Eu ' Re ' = Eu " Re "
第五版传热学课件第五章
惯性力
对稳态流动:
体积力
压强梯度
黏滞力
u v 0
当只有重力场作用时:
X g x
Y g y
四、能量微分方程式
推导依据—— 内能增量=导热热量+对流热量
1.导热热量:
t x dy x t y dx y 2t x dx 2 dxdy x方向导入的净热量: x x x x
u x p 2 u v x 表面法向应力 表面切向应力 yx xy v y x y p 2 y
将其代入Navier-Stokes方程,并采用连续方程化简,得到:
2u 2u u u u p x方向: u x v y X x x 2 y 2 2v 2v v v v p y方向: u x v y Y y x 2 y 2
冷凝器
锅炉
四、换热表面几何因素 (壁面尺寸、粗糙度、形状及与流体的相对位置)
定型尺寸——换热中有决定意义的尺寸,以此特征 尺寸作为分析计算的依据,能准确反映物体形状对 换热的影响
对流表面传热系数h的多参数函数
h f u, t w , t f , , c p , , , , l
1 1 11 1
1
1 1 ? 1 2
~02
小量,可除去
3.y方向动量方程:
2v 2v v v p u v 2 2 x x y y y
11 1
第五章传热(本专业)(1)精品PPT课件
三种传热方式的比较:
传导 对流 辐射
注:三种传热方式往往共存
5.1.3 工程上常用的换热方式
⒈混合式换热
冷热两种流体直接接触换热,如凉水塔,湿式混 合冷凝器。 优点:传热速度快、效率高、设备简单等。
2. 蓄热式换热
计算:
厚度为b 的无限大平壁,壁 面两侧温度t1、t2 ,t1>t2 , 取厚度为dx 的薄层,由傅
立叶定律:
q dt
dx dt q dx
对上式积分,积分限为:
t : t1 t2
x:0
λ取一平均值,视为常 数,积分得:
q
t1
t2
t
Q
qA
A
t1
t2
说明:
①将上式写成速率方程的一般形式为:
分率、分子量及导热系数。
气体的 导热系数:
1-水蒸气;2-氧;3-二氧化碳;4-空气; 5-氮;6-氩
5.2.4 平壁的稳定热传导
㈠单层平壁的稳定热传导
平壁模型:
▪ 平壁材质均匀,λ可视为常数;
▪ 平壁内只有一维温度梯度,导热方向垂直于壁面 ─等温面为平行于侧面的平面;
▪ 导热平壁的长和宽>>壁厚b ,忽略边缘热损失。
─等温面为与圆筒同心的圆筒面;
▪ 筒壁材质均匀,λ视为常数。
计算:
内、外半径r1、r2 , 内外壁温度t1、t2(t1>t2), A=2πrl,导热系数λ,由傅
立叶定律:
QArq2rLddrt
分离变量: dt Q dr
2L r
积分: d t2 t r2 Q dr
t1
r1 2L r
传热学第五章对流传热理论基础课件

研究对流换热的方法:
(1)分析法 (2)实验法 (3)比拟法 (4)数值法
第五章 对流换热
3
5 对流换热的影响因素
其影响因素主要有以下五个方面:(1)流动起因; (2)流动状态; (3)流 体有无相变; (4)换热表面的几何条件; (5)流体的热物理性质
以流体外掠平板为例:
我们所要得到的是:
(1)当地热流密度和总的换热量
u v 0 x y
( u
u
u x
v
u y
)
Fx
p x
(
2u x 2
2u y2 )
( v
u
v x
v
v y
)
Fy
p y
(
2v x 2
2v y 2
)
c
p
t
u
t x
v
t y
2t x2
2t y 2
第五章 对流换热
29
4个方程,4个未知量 —— 可求得速度场(u,v)和 温度场(t)以及压力场(p), 既适用于层流,也适用 于紊流(瞬时值)
dy
c p
(vt) y
dydx
第五章 对流换热
32
Q导热
2t x2
dxdy+
2t y2
dxdy
Q对流
c p
(ut) x
dxdy
c p
(v t) y
dxdy
c
p
u
t x
v
t y
t
u x
t
v y
dxdy
c
p
u
t x
v
t y
dxdy
U
cpdxdy
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由 aPφP = aEφE + aWφW 可得
φP
= aEφE + aWφW
aE + aW
=
(De
−
1 2
Fe )φE
+
(Dw
+
1 2
Fw )φW
(De
−
1 2
Fe
)
+
(Dw
+
1 2
Fw
)
均分网格 常物性
φP
=
(1 −
1 2
F D
)φE
+
(1 +
1 2
(D + D)/ D
F D
)φW
(1 −
1 2
PΔ )φE
exp( ρuL ) −1
Γ
计算,其中
ρuL = Pe
Γ
基于整个长度,这里 Pe = 2PΔ PΔ = 4
控制容积积分法给出的是控制容积内导数的积分 中值的离散形式:
∫1 e ∂φ dx = φe −φw
Δx w ∂x
Δx
6/54
5.2 对流项的中心差分及迎风差分 5.2.1 一维模型方程的分析解 5.2.2 一维对流-扩散方程的中心差分离散 5.2.3 对流项的迎风差分 1. 控制容积法的定义 2. 紧凑形式 3. 对流项一阶迎风、扩散项中心差分的离散方程
ρuL
Γ
x L
)
−1 =
exp(Pe
x) L
−1
φL −φ0 exp(ρuL / Γ) −1 exp(ρuL / Γ) −1 exp(Pe) −1
8/54
特点分析
Pe=0,纯扩散,直线分布
随Pe的增加,曲线不断下凸; 当Pe=10时,大部分地区
φ φ0
当x接近含严重的数值计算误差。 2. 影响到数值解的稳定性 (stability)
著名的中心差分CD,三阶迎风TUD以及QUICK 都只是条件稳定。 3.影响到数值解的经济性 (economics)
4/54
5.1.2 两种构造对流项离散格式的方法 1. Taylor 展开法-给出一点上导数的差分表示式
7/54
5.2 对流项的中心充分及迎风差分
5.2.1 一维对流-扩散模型方程的分析解
d (ρuφ) = d (Γ dφ ), ρ,u,Γ 均为已知的常数
dx dx dx
x = 0, φ = φ0; x = L, φ = φL
该常微分方程的分析解为:
φ −φ0
=
exp( ρ ux
/
Γ)
−1
=
exp(
aE
=
De
−
1 2
Fe
aW
=
Dw
+
1 2
Fw
aP = aE + aW + (Fe − Fw )
如果在迭代求解过程中连续性方程能够满足-质量
守恒得到保证,则: Fe − Fw = 0
为保证代数方程迭代求解的收敛性,我们要求计算
中质量守恒一定要满足,于是 aP = aE + aW
13/54
3. 中心差分离散方程特性分析
数值传热学
第五章 对流扩散方程的离散格式(1)
主讲
西安交通大学能源与动力工程学院 热流中心 CFD-NHT-EHT CENTER
2010年10月13日, 西安
1/54
第5 章 对流-扩散方程的离散格式 5.1 对流项离散格式的重要性及两种离散方式 5.2 对流项的中心充分及迎风差分 5.3 混合格式及乘方格式 5.4 五种三点格式系数的特性及其应用
+
Γw
(δ x)w W
=
−
1 2
(
ρ
u)e
+
Γe
(δ x)e
+
1 2
(
ρ
u
)
w
+
Γw
(δ x)w W
+ [(ρu)e
− (ρu)w]
=
aE
+ aW
+ [(ρu)e
− (ρu)w]
aE
aW
定义界面扩导
Γ
δx
= D,
界面流量 F = ρu
12/54
一维稳态无源项对流扩散方程CD格式的离散形式:
aPφP = aEφE + aWφW
9/54
上述变化趋势与Peclet数的物理意义相一致:
Pe = ρuL = ρu
Γ Γ/L
对流作用 扩散作用
Pe小-扩散占优势,故变量接近于直线分布;
Pe大-对流占优势,上游的作逐渐明显, 流体上游
的信息传到下游;传热学理论分析中当Pe大于100
时可以不计轴向导热即据此而得。
我们希望所构建的离散方程形式也具有这样的
物理特性。
10/54
5.2.2 一维对流-扩散方程的中心差分离散
1. 对一维模型方程在P控制容积内做积分,取分段
线性型线,经整理可得:
φP
[
1 2
(
ρ
u
)e
+
Γe
(δ x)e
−
1 2
(
ρ
u
)
w
+
Γw ]
(δ x)w
=
φE
[
Γe
(δ x)e
−
1 2
(
ρ
u
)e
]
+
φW
[
Γw
(δ x)w
+
1 2
(
ρu
)w
5.1.2 两种构造对流项离散格式的方法 5.1.3 两种对流项离散格式间的联系
3/54
5.1 对流项离散格式的重要性及两种离散方式
5.1.1 对流项离散格式的重要性 对流项从数学上只是一阶导数,但其物理背景(强
烈的方向性)使其离散成为数值计算中的一个难点: 1. 影响到数值解的准确性(accuracy)
]
aP
aE
aW
故得:
aPφP = aEφE + aWφW
11/54
2. 系数间关系的寻找
将 aP 做如下变化:
aP
=
1 2
(
ρu)e
+
Γe
(δ x)e
−
1 2
(
ρ
u
)
w
+
Γw
(δ x)w W
=
1 2
(
ρu)e
− (ρu)e
+ (ρu)e
+
Γe
(δ x)e
−
1 2
(
ρu)w
+ (ρu)w
− (ρu)w
5.5 关于假扩散的讨论 5.6 克服或减轻假扩散的方法 5.7对流-扩散方程离散形式稳定性分析 5.8 多维对流-扩散方程的离散及边界条件的处理 2/54
5.1 对流项离散格式的重要性及两种离散方式
5.1.1 对流项离散格式的重要性 1.影响到数值解的准确性 2.影响到数值解的稳定性 3.影响到数值解的经济性
如CD
∂φ
∂x )P
= φE − φW
2Δx
= φi+1 − φi−1
2Δx
2. 控制容积积分法-给出界面上被求函数的插值方式
∫1
e ∂φ
dx
= φe − φw
分段线性,均分网格
Δx w ∂x
Δx
= (φE + φP ) / 2 − (φP + φW ) / 2 = φE −φW
Δx
2Δx
5/54
5.1.3 两种对流项离散格式间的联系 1. 同一种格式的两种构造方式的截差相同; 2. 同一种格式的两种构造方式的截差首项的系数不同。 3. Taylor 展开给出的是一点上的离散形式,而
+
(1 +
1 2
PΔ
)φW
2
PΔ 称为网格Peclet数。给定 φE ,φW 据上式可算出
φP
。
PΔ
=
ρu(δ
Γ
x)
14/54
给定 φW = 100,φE = 200
由前式对 PΔ = 0,1, 2, 4
得出结果如右。
PΔ = 2
精确解据
φ −φ0 φL −φ0
=
exp( ρuL x ) −1
ΓL
