三角函数诱导公式及经典记忆方法
【高中数学经典】三角函数的诱导公式重难点题型(举一反三)
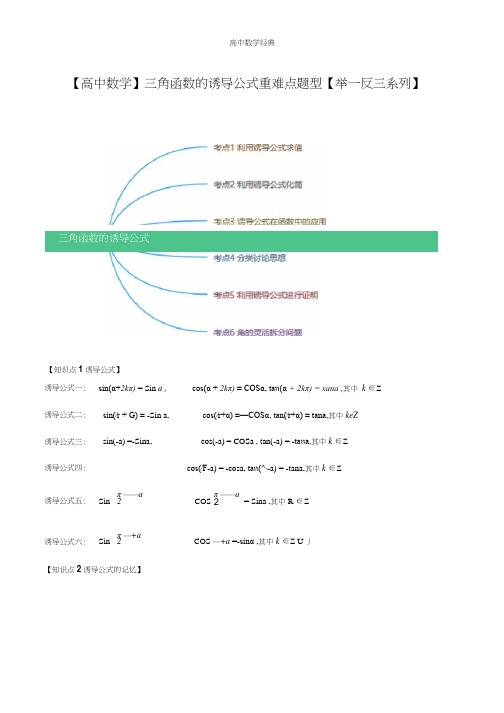
【高中数学】三角函数的诱导公式重难点题型【举一反三系列】三角函数的诱导公式【知识点1诱导公式】【知识点2诱导公式的记忆】诱导公式一: sin(α+2kπ) = Sin a ,cos(α + 2kπ) = COSα, taιι(α + 2kπ) = xana ,其中 k ∈Z 诱导公式二: sin(∕r + G) = -Sin a,cos(∕r+α) =—COSα, tan(∕r+α) = tana,其中keZ 诱导公式三: sin(-a) =-Sina, cos(-a) = COSa , tan(-a) = -taιιa ,其中k ∈Z诱导公式四:cos(∕F -a) = -cosa, taιι(^∙-a) = -tana,其中k ∈Z 诱导公式五: Sin π ——a 2 COS π ——a 2 = Sina ,其中R ∈Z诱导公式六:Sin π —+a 2 COS —+a =-sinα ,其中k ∈Z U 丿记忆11诀“奇变偶不变,符号看象限”,意思是说角k-90 ±a(k 为常整数)的三角函数值:当k 为奇数 时,正弦变余弦,余弦变正弦;当k 为偶数时,函数名不变,然后α的三角函数值前面加上当视Q 为锐角 时原函数值的符号.【考点1利用诱导公式求值】【方法点拨】对任意角求三角函数值,一般遵循“化负为正,化大为小”的化归方向,但是在具体的转化 过程中如何选用诱导公式,方法并不唯一,这就需要同学们去认真体会,适当选择,找出最好的途径,完 成求值.【例1】(2018秋•道里区校级期末)已知点P(l,l)在角Q 的终边上,求下列各式的值.T 、 COS (Λ^ + α)sin(^∙ - a)(I )------------------------------------- ;tan(∕r + α) + sin 2 (彳-a)sin(- + α)cos(- 一 a) (II) 、 2 、——召——cos^ a - sm^ a + tan(;T - a)【分析】由条件利用任意角的三角函数的定义求得smα, cosα, Sna 的值,再利用诱导公式即可求得要 求式子的值.【答案】解:∙.∙角α终边上有一点P(l,l),.x = l , y = l , r =|OP I= √7,Sill CL = — = _ , COS Ct = — = — , tan Ct — -- = It r 2 r 2 X([) cos(∕r + α)sin(%-α)、 -、,兀、 tan(^∙ + α) + sιn^ (― 一 a) ./3∕r 3π([[)SInq-+Q )COS (T _Q ) _ (γosα)(-smα) cos 2 a - sin 2 a + tan(∕r -a) cos 2a - sin 2a 一 tan a【点睛】本题主要考查任意角的三角函数的定义,诱导公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.【变式1-1】 (2019春•龙潭区校级月考)己知tan(^+ «) = -!,求下列各式的值:-COSa ∙smα ton a + cos 2(x(]) 2COS (Λ∙-α)-3sin(∕r+ α)4cos(α - 2πy ) + sin(4∕r - a)(2) siιι(α-7π)cos(a + 5π).【分析】(1)由诱导公式化简后,原式分子分母除以cosα,利用同角三角函数间的基本关系化简,将tana 的值代入计算即可求出值;(2)由诱导公式化简后,原式分母“1”化为sin 2a + ∞s 2a,然后分子分母除以∞s 2a,利用同角三角函数间的基本关系化简,>'J tana 的值代入计算即可求出值.【答案】解:∙.∙tan(∕r + a) = tana =-扌,【点睛】此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键,属于基本知识的 考查.【变式1-21(2018春•陆川县校级月考)若COSa = - , a 是第四象限角,求sm(d_2”) + sin(--3∕τ)cos(-3”) 3 COS (龙-a)-COS (-Λ∙ - a) COS(a - 4π)的值.【分析】由条件利用诱导公式进行化简所给的式子,可得结果.【答案】解:∙.∙cosa =扌,a 是第四象限角,- -sina = 一JI-COS 订=_£ ,Sin(Q - 2π) + siιι(-a -3π)cos(a- 3π) _ Sillcr + Siila ・(一COS a) _ Sin a(l- COS a) _3 3 _ ∙√5 cos(∕r — a)-cos(-x-a)cos(a-4;F) — CoSa+ cosa∙cosa COSa(COSa — 1) 亠(一 1) 2【点睛】本题主要考查应用诱导公式化简三角函数式,属于基础题.【变式1-3】 (2019春•沈阳校级月考)己知SlnQ 是方程5√-7x-6 = 0的根,求sin(-a -—龙)∙sin(- π 一 a)∙tan 2 (2π - a) 4 5【分析】把SinQ 代入到方程中解出即可求出Sina 的值进而求出tan'a 的值,然后把所求的式子利用诱导公 式及同角三角函数间的基本关系进行化简,将tan j 的值代入即可求出值.【答案】解:∙.∙sinα是方程SJC-IX-6 = O 的根,二Sina = -O 或Sina = 2 (舍).5+iτ . ■> 9 “16 , 9∣ √ sm^ α = —, cos^ a = — => taιι^ a = —• 25 25 16(1) 2 COS (Λ∙ -Qf)-3 sin(π + a)4cos(α - 2π) + sin(4∕r - a) 3sinα-2cosα 4cosα-siιια 3 tail α - 2 4-tana(2) sin(α — 7π)cos(α + 5π) = Sm a COS a =SlnQCOSa SUra + COS I atanatan 2a + l 的值.「•原式=∞s α∙(-COS α)∙tan^ aSin α∙(- Sin a)∙cos2 asin2 aCOSa•(—COS α) •—____________ COS-CLSill α∙(- Sill α)∙cos2a1cos2a=sec^ a = l +tail" α = l + —=—16 16【点睛】此题要求学生灵活运用诱导公式及同角三角函数间的基本关系化简求值,解这道题的思路是利用已知求出正切函数的平方,所求的式子也要化为关于正切函数平方的关系式.【考点2利用诱导公式化简】【方法点拨】灵活应用诱导公式,应用的原则是:负化正,大化小,化到锐角就终了taιι(Λ∙ - α)cos(2∕τ —α)sin(-α + —)【例2】(2019秋•颍泉区校级期中)化简: ------------- ------ —-------- .cos(-α - π) sm(-∕r - a)【分析】由已知利用诱导公式即可化简得解.tan(∕r —α)cos(2∕r - α)sin(-α + —) 【答案]解: -------- ------ ---------- 一一cos(_a 一π)sιn(-π一a)(一tan a) COS ◎(一COS a) _ -------------------------- =—1.(一COSa)SiiIa【点睛】本题主要考查了诱导公式在三角函数化简求值中的应用,属于基础题.【变式2-1] (2019春•兰考县校级期末)化简:sιn(4—⑵ CoS(I■ + ◎) tan(5 一Q) + a) COS(2Λ,-a)sin(3τr —a) sin(- + O)【分析】利用诱导公式以及同角三角函数基本关系式化简求解即可.【答案】解sin(4Λ∙-α)cos(-÷α) _ tan(5Λ∙-a) _ sin(-αχ-Sina) _ -tana _ Sin Z a十1 I-Sin Z aSm(爭+ a)cos0-a) sm(3^-a)sin(^÷ a) " <-cosa>cos<-a> SInaCoS八CoSF 品- cos2【点睛】本题考查诱导公式以及同角三角函数基本关系式的应用,考查计算能力.sin(8 - 5Λ∙)COS( ------- θ)cos(lπ一θ)【变式2・2】(2019春•东莞市校级期末)化简----------------- F -------------------------sin(8 - #) sin(-3^∙ - θ)【分析】由条件利用诱导公式进行化简所给的式子,可得结果.【答案】解:sin(8 —5π) cos(-壬一 &)cos(7∕r —θ) Sin(^ - π >cos(y + &)・cos(/r -θ)Sin(O -夢)sin(-3;T — 6)-Sin(^- —8)∙sin(∕r - θ)-siu8»(-sin&)・(一cos8) .;---- =—Sln σ • COS8∙sin θ【点睛】本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.【变式2-3】(2019春•西安月考)化简:血Sr)SIn(-2—&)CoS(6”也cos(8 - π)siιι(5Λ∙ + θ)【分析】由条件利用诱导公式化简所给的三角函数式,可得结果.r M tan(2∕r-8)sin(-2 広一 &) COS(6兀一&) - tan 0∙(-Sill ^)∙cos θ sin 8L ⅛ 杀J W • ----------------------------------------------- = ----------------------------- =-------- = t∩ιι θ ‘COS(O - π)sin(5∕r + θ)- COS 8・(一Sm θ) COS θ【点睛】本题主要考查利用诱导公式进行化简求值,属于基础题.【考点3诱导公式在函数中的应用】cos(- + x) cos(-x) siιι(- - x)【例3】(2019春•怀化期末)已知/(X) = 一 -------------------- - -- 2——sm(-Λ- - X)CoS(2/T - x)(I )化简/(x);(II)若X是第三象限角,且tmιx = 2,求/⑴的值.【分析】(【)由己知利用诱导公式即可化简得解;(II)由tanx=2,可得SinX=2cosx,根据角的范围利用同角三角函数基本关系式即可求解.【答案】解:([)∕α)=Eτ∙(⅜χ.SillACOSX(II) ∙.∙ta∏Λ = 2, ..sinx = 2COSΛ'» 代Asin3 x+cos2 x = l,得:5cos2 x = l,∙.∙x是第三彖限角,.■- /(X) = COSX = --Y .【点睛】本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.【变式3-1】(2019春•大武口区校级期末)己知./(«) =—)su,cos(";)_ sin(-^- - a) cos(y + a) sin(- + a)(1)化简/(«):(2)若/(a) = *,求3sin2α-4siιιαcosof + 5cos2a的值.【分析】(1)直接利用诱导公式化简求解即可.(2)求出正切函数值,利用同角三角函数基本关系式化简表达式为正切函数的形式,代入求解即可.【答案】解:(1)弘)=一Smgm"(Yθsα)=toιm-COS a∙(- Sm QXOS a3 f(a)=-,可得:taιια = -,r . “° 3siιF α — 4sinαcosα + 5cos% 3tan 2α-4taιια + 53SIn- α-4sιnαCOS a + Scos~a = ----------------- ; -------; ----------- = ------------ ; ---------- ,siιι^ a + cos~a taιι^ α + l 将tanα =丄代入, 3Jg得 3siιι2 α-4siιιαCOS a + 5cos 1a = 一 •5 【点睛】本题考查诱导公式以及同角三角函数基本关系式的应用,考查转化思想以及计算能力•【变式3-2】 (2018秋•红塔区校级期末)己知/(α)=泅(2兀一Q )述S + ?COS (FF )cos (∕r - a ) tan (3;T - a )(1) 将/(◎)化为最简形式;(2) f (a )- f (rγ + α) = » 且 Qe (O ,兀),求 tana 的值.【分析】(1)由题意利用诱导公式,化简所给的式子,可得结果.(2)由题意可得Sina+cosa 的值,再利用同角三角函数的基本关系,求得Sina-CoSa 的值,可得Sina 的 COSa 的值,从而求得tana 的值.【答案】解:(1)由题意可得,f(a) = (~SmQf)tanQfeCOSQf) =Sinα . (-cos α)(-taιια)(2) f(a)-f(rγ + Qf) = Sina-Sm(^ + α) = Sinα + COSa = 4©»] 24平方可得 1 + 2SinaCOSQ = ----- .. 2siιιαcosα = -一<0, 25 25π 49 7因为α e (0,兀),所以 α∈(-,Λ-) ∙ SinQ-COSa>0 , (Sina-COSa)2 =1-2SmaCOSa =—,所以SinQ-COSQ = E ②, 由①②可得:Sma = —,cosα = --,5 5 4 结果.(2)利用诱导公式化简要求的式子为sin&-cos0>0,再计算(Sin^-CoS^)2的值,可得要求式子的值.4所以taιια =——• 3【点睛】本题主要考查利用诱导公式,同角三角函数的基本关系,属于基础题.【变式0 (沁秋•汕头校级期中)己知函数蚀少二:(穿1 (1)若 f(θ)×siii — -COS^ = 0,求SineCOSe 的值.(2)若/(B)MosO= £ ,且彳v&v 普,求/(2019Λ--θ)-∞S (2018Λ∙-θ)的值; 【分析】 (1)由题意利用诱导公式求得诚=2,再根据SineCOSe = sin8cos8 sin 2 8+cos' θ总’计算求得【答案】解:(I)函数fg = (SE • +迓哄E = SIn“OS"S1∏Λ∙=若 f(0)×siιι--COS θ = sin&・--COSe = 0 •则 tan 。
三角函数诱导公式及推导

三角函数诱导公式及推导-CAL-FENGHAI.-(YICAI)-Company One1三角函数诱导公式:所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
常用公式:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)= tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)= cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)= cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαsin(π/2-α)=cosαcos(π/2+α)=-sinαcos(π/2-α)=sinαtan(π/2+α)=-cotαtan(π/2-α)=cotαcot(π/2+α)=-tanαcot(π/2-α)=tanα推算公式:3π/2 ±α与α的三角函数值之间的关系:sin(3π/2+α)=-cosαsin(3π/2-α)=-cosαcos(3π/2+α)=sinαcos(3π/2-α)=-sinαtan(3π/2+α)=-cotαtan(3π/2-α)=cotαcot(3π/2+α)=-tanαcot(3π/2-α)=tanα诱导公式记忆口诀:“奇变偶不变,符号看象限”。
《诱导公式》记忆口诀

应用诱导公式可将任意角的三角函数值问题转化为0到90间的角的三角函数值的问题,
基本步骤是:
运用诱导公式解题本质上是多次运用"化归”思想方法,化负角为正角,化大角为周内角, 再化为锐角,但是,诱导公式较多,符号难辨,容易混淆,我们可以分两种情况记忆:
一、“函数名不变,符号看象限”
对于一二,二-:,,亠很,2二-:,2k•亠很(k二z)的三角函数值,把:-看成锐角。
—a
ji-a
+a
2n:-a
2k兀(kez)
sin
—sinaБайду номын сангаас
sina
—sina
—sina
sina
cos
cosa
—cosa
—cosa
cosa
cosa
tan
-ta na
-ta na
tana
-ta na
-tana
二、“函数名改变,符号看象限”
13_'
对于—±a丄土a的三角函数值,把a看成锐角。
2'2
—-Ot
2
Tt—+a
2
3兀
——_a
2
3兀
—+a
2
sin
cosa
cosa
-cosa
-cosa
cos
si n。
— sin。
-si n。
si n。
根据以上的记忆技巧,我们很容易求任意角的三角函数的三角函数值。
三角函数诱导公式及推导

三角函数诱导公式:所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
常用公式:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)=-cosαtan(π+α)= tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)= cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)= cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαsin(π/2-α)=cosαcos(π/2+α)=-sinαcos(π/2-α)=sinαtan(π/2+α)=-cotαtan(π/2-α)=cotαcot(π/2+α)=-tanαcot(π/2-α)=tanα推算公式:3π/2 ±α与α的三角函数值之间的关系:sin(3π/2+α)=-cosαsin(3π/2-α)=-cosαcos(3π/2+α)=sinαcos(3π/2-α)=-sinαtan(3π/2+α)=-cotαtan(3π/2-α)=cotαcot(3π/2+α)=-tanαcot(3π/2-α)=tanα诱导公式记忆口诀:“奇变偶不变,符号看象限”。
三角函数诱导公式大全

三角函数诱导公式大全三角函数诱导公式是数学中的重要内容,常用的诱导公式有以下几组:公式一:对于任意角α,终边相同的角的同一三角函数的值相等,即sin(2kπ+α)=sinα,cos(2kπ+α)=cosα,tan (2kπ+α)=tanα,cot(2kπ+α)=cotα。
公式二:对于任意角α,π+α的三角函数值与α的三角函数值之间的关系,即sin(π+α)=-sinα,cos(π+α)=-cosα,tan(π+α)=tanα,cot(π+α)=cotα。
公式三:对于任意角α,α与-α的三角函数值之间的关系,即sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα,cot(-α)=-cotα。
公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系,即sin(π-α)=sinα,cos(π-α)=-cosα,tan(π-α)=-tanα,cot(π-α)=-cotα。
公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系,即sin(2π-α)=-sinα,cos(2π-α)=cosα,tan(2π-α)=-tanα,cot(2π-α)=-cotα。
公式六:对于π/2±α与α的三角函数值之间的关系,即sin(π/2+α)=cosα,cos(π/2+α)=-sinα,tan(π/2+α)=-cotα,cot(π/2+α)=-tanα,sin(π/2-α)=cosα,cos (π/2-α)=sinα,tan(π/2-α)=cotα,cot(π/2-α)=tanα。
为了更好地记忆这些公式,可以使用以下口诀:奇变偶不变,符号看象限。
具体来说,对于k·π/2±α(k∈Z)的个三角函数值,当k是偶数时,得到α的同名函数值,函数名不改变;当k是奇数时,得到α相应的余函数值,即sin→cos,cos→sin,tan→cot,cot→tan。
(完整版)诱导公式总结大全

e an dAl l t h i ng si nt he i r诱导公式1 所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin (2k π+α)=sin α cos (2k π+α)=cos α tan (2k π+α)=tan α cot (2k π+α)=cot α 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)=-sin α cos (π+α)=-cos α tan (π+α)=tan α cot (π+α)=cot α 公式三: 任意角α与 -α的三角函数值之间的关系: sin (-α)=-sin α cos (-α)=cos α tan (-α)=-tan α cot (-α)=-cot α 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)=sin α cos (π-α)=-cos α tan (π-α)=-tan αe an dAl l t 同角三角函数的基本关系式 倒数关系 tan α ·cot α=1 sin α ·csc α=1 cos α ·sec α=1 商的关系 sin α/cos α=tan α=sec α/csc α cos α/sin α=cot α=csc α/sec α 平方关系 sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α)同角三角函数关系六角形记忆法 构造以"上弦、中切、下割;左正、右余、中间1"的正六边形为模型。
倒数关系 对角线上两个函数互为倒数; 商数关系 六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。
(主要是两条虚线两端的三角函数值的乘积)。
三角函数诱导公式口诀

三角函数诱导公式口诀正弦角余弦角相互抒。
正弦角(sinθ)余弦角(cosθ)先来讲。
180°减去角度与这角个360°多,角度相等就像呼啦圈儿转向着方式相同。
不过值负号前加在正弦角上这你最好记牢。
认真数微多余度所以这点也要好好考。
180°异或角度是个性质,它并不负任何责任,180°-角度取其相抒正弦给余弦算。
对着45°看看你能明白,左加90°,又左旋90°,180°看见镜像都可以把余弦值记得夸。
上面是正弦余弦记得挺好离不开。
接下来我们来说正切这个大家伙。
余切的乙字旁方角只要把它变个样。
根号3往俩角度减,不加在这个方程里能变成样是猜得着。
它跟正切角度很相熟。
对两个角度的积微加,相减规律出来时可真不容易。
其实这三个也可以归一,就是去除分母的根号3,这就是技巧所在。
此时就别再纠结那个角度分子S型后平方根喽。
三角函数本质没变化,只是横坐标扩展或者还原。
若角在这区,可明白大小关系,节省记忆,提高效率。
三角函数进行计算之前,常需要一个0°-90°之间的锐角。
这时候就需要用到副函数呢。
余弦角互倒千万口诀记牢。
tan顶舵舵员,一驾车两个命名确保角度的后面焦。
就分母加个字母S变tan,横坐标倒在它前面,分母的倒数成除法,保证記得够牢。
试想正切角翻过机过渡,横纵线色彩相同还需刻画得足够细致。
副函数到此为止,同学们可以高兴发音啦。
从余切送回应正黏帝迈把右边再看一下。
我们来看看另一个重要的逆函数,这个函数叫做弧度函数。
简单点说,就是将角度转化为弧度。
弧度与角度成反而正,240°弧度报告单位不是固定也别固执。
单位直接乘以π一周两百三,这样加π/3逼的角也算的精确地道。
π加π/6真不是个难的数,抢着转弯就红头喜燕飞的精神强。
让我多对红弧代替黄弧向后转足百分之六。
π+3π/4,有折才美味。
一点减运算无难度,带了个弧后就剩这点。
三角函数诱导公式万能公式和差化积公式倍角公式等公式总结及其推导

三角函数诱导公式万能公式和差化积公式倍角公式等公式总结及其推导一、三角函数诱导公式1、万能公式a sin(A+B) = a sinAcosB + a cosAsinBa cos(A+B) = a cosAcosB - a sinAsinB2、差化积公式sinAcosB - cosAsinB = sin(A-B)cosAcosB + sinAsinB = cos(A-B)3、倍角公式sin2A = 2sinAcosAcos2A = cos2A - sin2A = 2cos2A - 1 = 1 - 2sin2A4、和差公式sin(A±B) = sinAcosB±cosAsinBcos(A±B) = cosAcosB∓sinAsinB二、推导1、万能公式推导过程设定A+B=C,则有:a sin(A + B)= a sinC左右两侧同时乘以cosB:a sin(A + B)cosB = a sinCcosB左右两侧同时乘以sinB:a sin(A + B)sinB = a sinCsinB将上式整合即可得:a sin(A + B)= a sinAcosB + a cosAsinB同理,可推导出:a cos(A + B) = a cosAcosB - a sinAsinB2、差化积公式推导过程设定A=B,则有:sinAcosB - cosAsinB = sinAcosA - cosAcosA 经过整合可得:sinAcosB - cosAsinB = sinA -cosA将A=B替换为A-B,即可得sinAcosB - cosAsinB = sin(A-B)同理:cosAcosB + sinAsinB = cosAcosA + sinAsinA 经过整合可得:cosAcosB +sinAsinB = cosA +sinA将A=B替换为A-B,即可得cosAcosB +sinAsinB = cos(A-B)3、倍角公式的推导过程由于A为任意角度,对其两侧两边可以分别进行乘以cosA及sinA,得到:sinAcosA + sinAcosA = cosA*sinA + cosA*sinA经过整合可得:sin2A = 2sinAcosAcos2A = cosAcosA - sinAcosA经过整合可得:cos2A = 2cos2A - 1再把上式中的cos2A代入:2cos2A - 1 = 1 - 2sin2A4、和差公式推导过程设定A+B=C,则有:sin(A + B)= sinC将左右两侧分别乘以cosB及sinB:。
三角函数的8个诱导公式(汇总)

三角函数的8个诱导公式(汇总)三角函数的8个诱导公式1. 正弦函数的诱导公式sin(-x) = -sin(x)这个公式表明,正弦函数的值在x轴上是关于原点对称的。
也就是说,如果一个角度的正弦值为a,那么它的相反数的正弦值就是-a。
这个公式在解三角形问题时非常有用,为它可以帮助我们计算负角度的正弦值。
2. 余弦函数的诱导公式cos(-x) = cos(x)这个公式表明,余弦函数的值在y轴上是关于原点对称的。
也就是说,如果一个角度的余弦值为a,那么它的相反数的余弦值也是a。
这个公式同样也可以帮助我们计算负角的余弦值。
3. 正切函数的诱导公式tan(-x) = -tan(x)这个公式表明,正切函数的值在原点上是关于y轴对称的。
也就是说,如果一个角的正切值为a,那么它的相反数的正切值就是-a。
这个公式在计算负角的正切值时非常有用。
4. 余切函数的诱导公式cot(-x) = -cot(x)这个公式表明,余切函数的值在原点上是关于x轴对称的。
也就是说,如果一个角的余切值为a,那么它的相反数的余切值就是-a。
这个公式同样也可以帮助我们计算负角的余切值。
5. 正弦函数的平方的诱导公式sin^2(x) + cos^2(x) = 1这个公式是三角函数中最著名的公式之一,它表明正弦函数的平方加上余弦函数的平方等于1。
这个公式在解三角形问题时非常有用,为它可以帮助我们计算三角形中的未知边长。
6. 正切函数的平方的诱导公式tan^2(x) + 1 = sec^2(x)这个公式表明,正切函数的平方加1等于其对应的正割函数的平方。
这个公式在计算三角形中的未知边长时非常有用。
7. 余切函数的平方的诱导公式cot^2(x) + 1 = csc^2(x)这个公式表明,余切函数的平方加1等于其对应的余割函数的平方。
这个公式同样也可以帮助我们计算三角形中的未知边长。
8. 正弦函数和余弦函数的诱导公式sin(x + π/2) = cos(x)cos(x + π/2) = -sin(x)这两个公式表明,正弦函数和余弦函数之间存在一种特殊的关系,即它们的相位差为π/2。
高中数学常用三角函数公式及口诀

常用三角函数公式及口诀常用的诱导公式有以下几组:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα (k∈Z)cos(2kπ+α)=cosα (k∈Z)tan(2kπ+α)=tanα (k∈Z)cot(2kπ+α)=cotα (k∈Z)公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)注意:在做题时,将a看成锐角来做会比较好做。
诱导公式记忆口诀规律总结上面这些诱导公式可以概括为:对于π/2*k ±α(k∈Z)的三角函数值,①当k是偶数时,得到α的同名函数值,即函数名不改变;②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan.(奇变偶不变)然后在前面加上把α看成锐角时原函数值的符号。
诱导公式记忆方法

所在象限的原三角函数值的符号可记忆
水平诱导名不变;符号看象限。
#
各种三角函数在四个象限的符号如何判断,也可以记住口诀“一全正;二正弦(余割);三两切;四余弦(正割)”.
这十二字口诀的意思就是说:
第一象限内任何一个角的四种三角函数值都是“+”;
第二象限内只有正弦是“+”,其余全部是“-”;
当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。
所以sin(2π-α)=-sinα
上述的记忆口诀是:
奇变偶不变,符号看象限。
公式右
边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α
①当k是偶数时,得到α的同名函数值,即函数名不改变;
②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan.
(奇变偶不变)
然后在前面加上把α看成锐角时原函数值的符号。
(符号看象限)
例如:
sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。
第三象限内切函数是“+”,弦函数是“-”;
第四象限内只有余弦是“+”,其余全部是“-”.
上述记忆口诀,一全正,二正弦,三内切,四余弦
#
还有一种按照函数类型分象限定正负:
函数类型 第一象限 第二象限 第三象限 第四象限
正弦 ...........+............+............—............—........
同角三角函数基本关系
同角三角函数的基本关系式
倒数关系:
tanα ·cotα=1
三角函数诱导公式及记忆口诀

诱导公式是指三角函数中,利用周期性将角度比较大的三角函数,转换为角度比较小的三角函数的公式。
接下来给大家分享三角函数常用的诱导公式及记忆口诀。
三角函数的诱导公式诱导公式一:终边相同的角的同一三角函数的值相等设α为任意锐角,弧度制下的角的表示:sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)诱导公式二:π+α的三角函数值与α的三角函数值之间的关系设α为任意角,弧度制下的角的表示:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα诱导公式三:任意角α与-α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα诱导公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系sin(π-α)=sinαcos(π-α)=-cosαcot(π-α)=-cotα诱导公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα诱导公式六:π/2±α及3π/2±α与α的三角函数值之间的关系sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotα三角函数诱导公式记忆口诀奇变偶不变,符号看象限。
三角函数诱导公式记忆口诀

三角函数诱导公式记忆口诀三角函数诱导公式是学习数学中的一个重要内容,也是解决三角函数相关问题的基础。
通过记忆口诀,我们可以更加方便地掌握这些公式。
下面将介绍三角函数诱导公式,并给出一些记忆方法。
一、正弦函数的诱导公式正弦函数是三角函数中最基本的函数之一,它的诱导公式是:sin(α±β) = sinαcosβ±cosαsinβ这个公式可以帮助我们计算两个角的正弦值之和或差。
为了记忆这个公式,我们可以联想“正正相乘,余余相减”。
二、余弦函数的诱导公式余弦函数也是三角函数中的重要函数,它的诱导公式是:cos(α±β) = cosαcosβ∓sinαsinβ这个公式可以帮助我们计算两个角的余弦值之和或差。
为了记忆这个公式,我们可以联想“余余相乘,正正相减”。
三、正切函数的诱导公式正切函数是三角函数中另一个重要的函数,它的诱导公式是:tan(α±β) = (tanα±tanβ)/(1∓tanαtanβ)这个公式可以帮助我们计算两个角的正切值之和或差。
为了记忆这个公式,我们可以联想“正正相加,余余相除”。
四、余切函数的诱导公式余切函数是正切函数的倒数,它的诱导公式是:cot(α±β) = (cotαcotβ∓1)/(cotβ±cotα)这个公式可以帮助我们计算两个角的余切值之和或差。
为了记忆这个公式,我们可以联想“余余相加,正正相除”。
五、正割函数的诱导公式正割函数是余弦函数的倒数,它的诱导公式是:sec(α±β) = (secαsecβ±tanαtanβ)/(secβ±tanαtanβ)这个公式可以帮助我们计算两个角的正割值之和或差。
为了记忆这个公式,我们可以联想“正余相乘,余正相除”。
六、余割函数的诱导公式余割函数是正弦函数的倒数,它的诱导公式是:csc(α±β) = (cscαcscβ∓cotαcotβ)/(cscβ±cotαcotβ)这个公式可以帮助我们计算两个角的余割值之和或差。
三角函数诱导公式记忆方法

三角函数诱导公式记忆方法
奇变偶不变:பைடு நூலகம்
例:sin(kπ/2+α)中k是奇数的话(如π/2、3π/2、5π/2……)sin就变cos,偶数就不变(如0、π、2π、3π……)
同理cos(kπ/2+α)中k是奇数的话(如π/2、3π/2、5π/2……)cos就变sin,偶数就不变(如0、π、2π、3π……)类似的,有tan变cot、cot变tan
sin2cos把看作锐角第一象限时2是第二象限角sin2此时是正数因此cos符号为正cos2sin把看作锐角第一象限时2是第二象限角cos2此时是负数因此sin符号为负sin2cos把看作锐角第一象限时2还是第一象限角sin2此时是正数因此cos符号为正cos2sin把看作锐角第一象限时2还是第一象限角cos2此时是正数因此cos符号为正
符号看象限:
例:sin(π/2+α)=cosα把α看作锐角(第一象限)时,π/2+α是第二象限角,sin(π/2+α)此时是正数因此cosα符号为正
cos(π/2+α)=-sinα把α看作锐角(第一象限)时,π/2+α是第二象限角,cos(π/2+α)此时是负数因此sinα符号为负
sin(π/2-α)=cosα把α看作锐角(第一象限)时,π/2-α还是第一象限角,sin(π/2-α)此时是正数因此cosα符号为正
高1数学-三角函数-诱导公式

高一数学诱导公式知识点1.诱导公式一~四(1)公式一:sin(α+2k π)=sin α,cos(α+2k π)=cos α,tan(α+2k π)=tan α,其中k ∈Z .(2)公式二:sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α.(3)公式三:sin(-α)=-sin α,cos(-α)=cos α,tan(-α)=-tan α.(4)公式四:sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)=-tan α.2.诱导公式的记忆2k π+α(k ∈Z ),π+α,π-α,-α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.3.诱导公式五~六(1)公式五:sin ⎝⎛⎭⎫π2-α=cos α;cos ⎝⎛⎭⎫π2-α=sin α. 以-α替代公式五中的α,可得公式六.(2)公式六:sin ⎝⎛⎭⎫π2+α=cos α;cos ⎝⎛⎭⎫π2+α=-sin α. 4.诱导公式的理解、记忆与灵活应用公式一~四归纳:α+2k π(k ∈Z ),-α,π±α的三角函数值,等于角α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名不变,符号看象限”.公式五~六归纳:π2±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号,简记为:“函数名改变,符号看象限”或“正变余、余变正、符号象限定”.六组诱导公式可以统一概括为“k ·π2±α(k ∈Z )”的诱导公式.当k 为偶数时,函数名不改变;当k 为奇数时,函数名改变;前面加一个把α视为锐角时原函数值的符号,记忆口诀为“奇变偶不变,符号看象限”.题型一 给角求值【例1】求下列各三角函数值.(1)sin(-83π); (2)cos 196π; (3)sin[(2n +1)π-23π].【过关练习】1.求下列三角函数值.(1)sin ⎝⎛⎭⎫-436π;(2)cos 296π;(3)tan(-855°).2.sin 585°的值为( )A .-22 B.22 C .-32 D.323.cos(-16π3)+sin(-16π3)的值为( ) A .-1+32B.1-32C.3-12 D.3+12题型二 给值求值问题【例1】已知cos(α-75°)=-13,且α为第四象限角,求sin(105°+α)的值.【例2】已知cos ⎝⎛⎭⎫α+π6=35,π2≤α≤3π2,求sin ⎝⎛⎭⎫α+2π3的值.【过关练习】1.已知cos(α-π)=-513,且α是第四象限角,则sin α等于( ) A .-1213 B.1213 C.512 D .±12132.已知sin(5π2+α)=15,那么cos α等于( ) A .-25 B .-15 C.15 D.253.若sin(3π+α)=-12,则cos(7π2-α)等于( ) A .-12 B.12 C.32 D .-324.已知cos(π+α)=-35,π<α<2π,求sin(α-3π)+cos(α-π)的值.5.已知sin ⎝⎛⎭⎫π6+α=33,求cos ⎝⎛⎭⎫α-π3的值.题型三 三角函数式的化简【例1】化简下列各式.(1)tan (2π-α)sin (-2π-α)cos (6π-α)cos (α-π)sin (5π-α);(2)1+2sin 290°cos 430°sin 250°+cos 790°.【过关练习】1.化简:(1)sin (540°+α)·cos (-α)tan (α-180°);(2)cos (θ+4π)·cos 2(θ+π)·sin 2(θ+3π)sin (θ-4π)sin (5π+θ)cos 2(-π+θ).2.化简:cos (180°+α)sin (α+360°)sin (-α-180°)cos (-180°-α).题型四 利用诱导公式证明恒等式【例1】求证:tan (2π-α)sin (-2π-α)cos (6π-α)sin ⎝⎛⎭⎫α+3π2cos ⎝⎛⎭⎫α+3π2=-tan α.【过关练习】1.求证:2sin ⎝⎛⎭⎫θ-3π2cos ⎝⎛⎭⎫θ+π2-11-2sin 2 (π+θ)=tan (9π+θ)+1tan (π+θ)-1.题型五 诱导公式的综合应用【例1】已知f (α)=sin (α-3π)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-π-α)sin (-π-α). (1)化简f (α);(2)若α是第三象限的角,且cos ⎝⎛⎭⎫α-3π2=15,求f (α)的值; (3)若α=-31π3,求f (α)的值.【过关练习】1.已知角α终边经过点P (-4,3),求cos (π2+α)sin (-π-α)cos (11π2-α)sin (9π2+α)的值.2.已知tan(3π+α)=2,则sin (α-3π)+cos (π-α)+sin (π2-α)-2cos (π2+α)-sin (-α)+cos (π+α)= .【补救练习】1.cos 600°的值为( ) A.32 B.12 C .-32 D .-122.若sin α=12,则cos(π2+α)的值为( ) A.12 B.32 C .-12 D .-323.化简下列各式.(1)sin(-193π)cos 76π; (2)sin(-960°)cos 1 470°-cos(-240°)sin(-210°).4.已知sin(π+α)=-13.计算: (1)cos ⎝⎛⎭⎫α-3π2; (2)sin ⎝⎛⎭⎫π2+α; (3)tan(5π-α).1.sin 2(π+α)-cos(π+α)cos(-α)+1的值为( )A .1B .2sin 2αC .0D .22.tan(5π+α)=m ,则sin (α-3π)+cos (π-α)sin (-α)-cos (π+α)的值为( ) A.m +1m -1 B.m -1m +1C .-1D .1 3.若sin(π-α)=log 8 14,且α∈⎝⎛⎭⎫-π2,0,则cos(π+α)的值为( ) A.53B .-53C .±53D .以上都不对4.已知cos ⎝⎛⎭⎫π6+θ=33,则cos ⎝⎛⎭⎫5π6-θ= .5.已知sin ⎝⎛⎭⎫α-π6=13,则cos ⎝⎛⎭⎫α+π3的值为( ) A .-233 B.233 C.13 D .-136.已知sin ⎝⎛⎭⎫α-π4=13,则cos ⎝⎛⎭⎫π4+α的值等于( ) A .-13 B.13 C .-223 D.2237.已知f (α)=tan (π-α)·cos (2π-α)·sin (π2+α)cos (-α-π),化简f (α)= .1.若sin(π+α)+cos ⎝⎛⎭⎫π2+α=-m ,则cos ⎝⎛⎭⎫32π-α+2sin(2π-α)的值为( ) A .-2m 3 B.2m 3 C .-3m 2 D.3m 22.已知cos(π2+φ)=32,且|φ|<π2,则tan φ等于( ) A .-33 B.33C .- 3 D.3 3.式子cos 2(π4-α)+cos 2(π4+α)= . 4.若cos(α-π)=-23,求sin (α-2π)+sin (-α-3π)cos (α-3π)cos (π-α)-cos (-π-α)cos (α-4π)的值.5.在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角.6.已知cos ⎝⎛⎭⎫π2+α=2sin ⎝⎛⎭⎫α-π2,求sin 3(π-α)+cos (α+π)5cos ⎝⎛⎭⎫5π2-α+3sin ⎝⎛⎭⎫7π2-α的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数诱导公式及记忆方法一、同角三角函数的基本关系式(一)基本关系1、倒数关系tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=12、商的关系sinα/cosα=tanαsecα/cscα=tanαcosα/sinα=cotαcscα/secα=cotα3、平方关系sin2α+cos2α=1 1+tan2α=sec2α 1+cot2α=csc2α(二)同角三角函数关系六角形记忆法构造以"上弦、中切、下割;左正、右余、中间1”的正六边形为模型。
1、倒数关系对角线上两个函数互为倒数;2、商数关系六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积.(主要是两条虚线两端的三角函数值的乘积,下面4个也存在这种关系.).由此,可得商数关系式。
3、平方关系在带有阴影线的三角形中,上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方.二、诱导公式的本质所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
(一)常用的诱导公式1、公式一: 设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα,k∈z cos(2kπ+α)=cosα,k∈ztan(2kπ+α)=tanα,k∈z cot(2kπ+α)=cotα, k∈zsec(2kπ+α)=secα,k∈z csc(2kπ+α)=cscα,k∈z2、公式二:α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosαtan(π+α)= tanα cot(π+α)= cotαsec (π+α) =-secα csc (π+α) =—cscα3、公式三:任意角α与—α的三角函数值之间的关系:sin(-α)=-sinα cos(-α)= cosαtan(-α)=-tanα cot(-α)=-cotαsec (—α) = secα csc (-α) =-cscα4、公式四:利用公式二和公式三可以得到π—α与α的三角函数值之间的关系:sin(π-α)= sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotαsec (π—α) =—secα csc (π-α) = cscα5、公式五:利用公式一和公式三可以得2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα cos(2π-α)= cosαtan (2π-α)=-tanα cot (2π-α)=-cotα sec (2π—α) = secα csc (2π—α) =-cscα 6、公式六:2π+α与α的三角函数值之间的关系:sin (2π+α)= cosα cos (2π+α)=-sinα tan(2π+α)=-cotα cot (2π+α)=-tanαsec (2π+α) =—cscα csc (2π+α) = secα7、公式七:2π—α与α的三角函数值之间的关系:sin (2π-α)= cosα cos(2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanαsec (2π—α) = cscα csc (2π—α) = secα8、推算公式:23π+α与α的三角函数值之间的关系: sin (23π+α)=-cosα cos (23π+α)= sinα tan (23π+α)=-cotα cot (23π+α)=-tanα sec (23π+α) = cscα csc (23π+α) =-secα 9、推算公式:23π—α与α的三角函数值之间的关系:sin(23π-α)=-cosα cos(23π-α)=-sinα tan (23π-α)= cotα cot(23π-α)= tanα sec (23π—α) =-cscα csc (23π-α) =—secα 诱导公式记忆口诀:“奇变偶不变,符号看象限”.“奇、偶"指的是2π的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变"是指正弦变余弦,正切变余切。
(反之亦然成立)“符号看象限”的含义是:把角α看做锐角,不考虑α角所在象限,看n·(π/2)±α是第几象限角,从而得到等式右边是正号还是负号. 符号判断口诀:“一全正;二正弦;三两切;四余弦"。
这十二字口诀的意思就是说:第一象限内任何一个角的四种三角函数值都是“+”; 第二象限内只有正弦是“+”,其余全部是“-”;第三象限内只有正切和余切是“+",其余全部是“-”; 第四象限内只有余弦是“+”,其余全部是“-”。
“ASCT"意即为“all(全部)”、“sin”、“tan"、“cos" (二)其他三角函数知识1、两角和差公式sin (α+ β)= sinαcosβ+ cosαsinβ sin (α-β)= sinαcosβ-cosαsinβ cos (α+ β)= cosαcosβ-sinαsinβ cos(α-β)= cosαcosβ+ sinαsinβtan (α+ β)=(tanα+tanβ )/(1-tanα·tanβ) tan (α-β)=(tanα-tanβ)/(1+tanα·tanβ)2、二倍角的正弦、余弦和正切公式 sin2α=2sinαcosαcos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α tan2α=αα2tan -12tan3、半角的正弦、余弦和正切公式sin 22α=2cos -1α cos 22α=2cos 1α+tan 22α=ααcos 1cos -1+ tan 2α=ααsin cos -1=ααcos 1sin +4、万能公式sinα=2tan 122tan 2αα+ cosα=2tan 12tan -122αα+ tanα=2tan -122tan 2αα5、三倍角的正弦、余弦和正切公式sin3α=3sinα-4sin 3α cos3α=4cos 3α-3cosα tan3α=α—α—α233tan 1tan 3tan6、三角函数的和差化积公式 sinα+sinβ=2sin 2βα+·cos2β—α sinα-sinβ= 2cos2βα+·sin 2β—αcosα+cosβ= 2cos 2βα+·cos 2β—α cosα-cosβ=-2sin 2βα+·sin 2β—α7、三角函数的积化和差公式sinα·cosβ=21[sin (α+β)+sin (α-β)] cosα·sinβ=21[sin (α+β)-sin (α-β)]cosα·cosβ=21[cos(α+β)+cos(α-β)]sinα·sinβ=-21[cos(α+β)-cos(α-β)]三、公式推导过程(一)万能公式推导 sin2α=2sinαcosα=αααα22sin cos cos sin 2+ (因为cos 2α+sin 2α=1) 再把上面的分式上下同除cos 2α,可得sin2α=2tan 122tan2αα+ 然后用2α代替α即可.同理可推导余弦的万能公式。
正切的万能公式可通过正弦比余弦得到. (二)三倍角公式推导tan3α=ααcos3sin3=αα—ααααααcos sin2sin cos2sin 2cos cos sin2+=αα—αα—αα—ααααcos sin 2sin cos cos sin sin cos cos sin 22222+ 上下同除以cos 3α,得: tan3α=α—α—α233tan 1tan 3tansin3α=sin(2α+α)=sin2αcosα+cos2αsinα=2sinαcos 2α+(1-2sin 2α)sinα=2sinα-2sin 3α+sinα-2sin 3α=3sinα-4sin 3αcos3α=cos(2α+α)=cos2αcosα-sin2αsinα=(2cos 2α-1)cosα-2cosαsin 2α=2cos 3α-cosα+(2cosα-2cos 3α)=4cos 3α-3cosα即 sin3α=3sinα-4sin 3αcos3α=4cos 3α-3cosα (三)和差化积公式推导首先,我们知道sin (α+β)=sin αcos β+cos αsin β, sin (α—β)=sin αcos β—cos αsin β我们把两式相加就得到sin(α+β)+sin(α-β)=2sin αcos β所以,sin αcos β=2sin sin β)—(αβ)(α++同理,若把两式相减,就得到cos αsin β=2sin sin β)—(α—β)(α+同样的,我们还知道cos(α+β)=cos αcos β-sin αsin β,cos(α-β)=cos αcos β+sin αsin β所以,把两式相加,我们就可以得到cos (α+β)+cos(α-β)=2cos αcos β所以我们就得到,cos αcos β=2cos cos β)—(αβ)(α++同理,两式相减我们就得到sin αsin β= —2cos cos β)—(α—β)(α+ 这样,我们就得到了积化和差的四个公式:sin αcos β=2sin sin β)—(αβ)(α++ cos αsin β=2sin sin β)—(α—β)(α+ cos αcos β= 2cos cos β)—(αβ)(α++ sin αsin β=—2cos cos β)—(α—β)(α+ 好,有了积化和差的四个公式以后,我们只需一个变形,就可以得到和差化积的四个公式.我们把上述四个公式中的α+b 设为x, α—β设为y,那么α=2y x +, β=2yx - 把α,β分别用x,y 表示就可以得到和差化积的四个公式:sinx+siny=2sin2y x +cos 2yx - sinx —siny=2cos 2y x +sin 2yx -cosx+cosy=2cos 2y x +cos 2yx -cosx —cosy=—2sin 2y x +sin 2yx -。
