抛物线上的点到准线的公式
抛物线基础知识
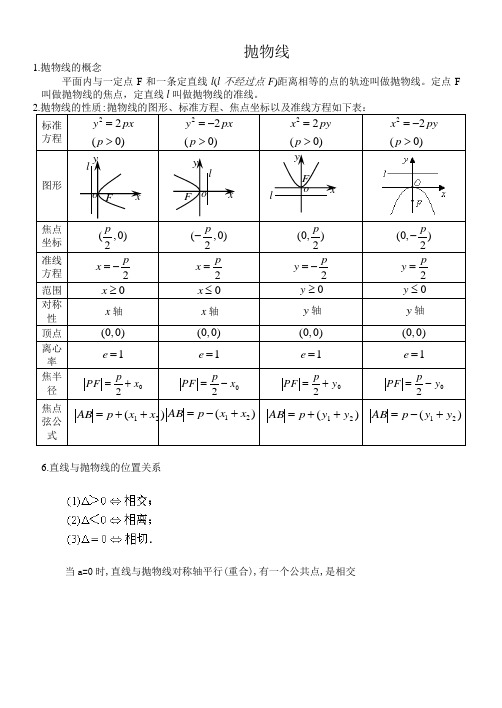
抛物线
1.抛物线的概念
平面内与一定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线。
定点F 叫做抛物线的焦点,定直线l叫做抛物线的准线。
6.直线与抛物线的位置关系
当a=0时,直线与抛物线对称轴平行(重合),有一个公共点,是相交
练习:
1. 2(0)y ax a =≠的焦点坐标是
2. 24y x =的焦点坐标是 准线方程是
3. 顶点在原点,焦点为(0,-2)的抛物线的方程为
4. 抛物线22(0)y px p =>点()23-,到其焦点的距离是5,则p=_______ 5.根据下列条件写出抛物线的标准方程
(1) 焦点是F (3,0)
(2) 准线方程是1
4
x =-
(3) 焦点到准线距离是2
6.求顶点在原点,对称轴为坐标轴,过点(2,-8)的抛物线方程,并指出焦点和准线。
7.垂直于x 轴的直线交抛物线24y x =点A,B,且⎜AB ⎜=AB 的方程
8.抛物线的顶点在原点,焦点在直线240x y --=上,求抛物线的标准方程
9.过抛物线2
20y x =的焦点作倾角为
34
π
的弦,此弦的长度是
10.已知动点M 到定点A (1,0)与定直线x=3的距离之和等于4,求点M 的轨迹方程。
高中抛物线数学公式有哪些

高中抛物线数学公式有哪些高中抛物线数学公式有哪些高中抛物线数学公式1、抛物线:y=ax__+bx+c就是y等于ax的平方加上bx再加上c。
a0时,抛物线开口向上;a0时抛物线开口向下;c=0时抛物线经过原点;b=0时抛物线对称轴为y轴。
2、顶点式y=a(x+h)__+k就是y等于a乘以(x+h)的平方+k,-h是顶点坐标的x,k是顶点坐标的y,一般用于求最大值与最小值。
3、抛物线标准方程:y^2=2px它表示抛物线的焦点在x的正半轴上,焦点坐标为(p/2,0)。
4、准线方程为x=-p/2由于抛物线的焦点可在任意半轴,故共有标准方程:y^2=2pxy^2=-2p__^2=2pyx^2=-2py。
高考数学冲刺策略1、拓实基础,强化通性通法。
高考对基础知识的考查既全面又突出重点。
抓基础就是要重视对教材的复习,尤其是要重视概念、公式、法则、定理的形成过程,运用时注意条件和结论的限制范围,理解教材中例题的典型作用,对教材中的练习题,不但要会做,还要深刻理解在解决问题时题目所体现的数学思维方法。
2、抓住重点内容,注重能力培养。
高中数学主体内容是支撑整个高中数学最重要的部分,也是进入大学必须掌握的内容,这些内容都是每年必考且重点考的。
象关于函数(含三角函数)、平面向量、直线和圆锥曲线、线面关系、数列、概率、导数等,把它们作为复习中的重中之重来处理,要一个一个专题去落实,要通过对这些专题的复习向其他知识点辐射。
3、细心审题、耐心答题,规范准确,减少失误。
计算能力、逻辑推理能力是考试大纲中明确规定的两种培养的能力。
可以说是学好数学的两种最基本能力,在数学试卷中的考查无处不在。
并且在每年的阅卷中因为这两种能力不好而造成的失分占有相当的比例。
所以我们在数学复习时,除抓好知识、题型、方法等方面的教学外,还应通过各种方式、机会提高和规范学生的运算能力和逻辑推理能力。
4、定期重复巩固。
即使是复习过的数学内容仍须定期巩固,但是复习的次数应随时间的增长而逐步减小,间隔也可以逐渐拉长。
抛物线及其标准方程

抛物线1.抛物线的定义平面内与一个定点F 和一条定直线l (l 不过F )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线.其数学表达式:|MF |=d (其中d 为点M 到准线的距离).2.抛物线的标准方程与几何性质1(1)定点不在定直线上.(2)当定点在定直线上时,轨迹为过定点F 与定直线l 垂直的一条直线.2.抛物线的方程特点方程y =ax 2(a ≠0)可化为x 2=1ay ,是焦点在y 轴上的抛物线.3.结论设AB 是过抛物线y 2=2px (p >0)焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则:(1)x 1x 2=p 24,y 1y 2=-p 2;(2)|AF |=p 1-cos α,|BF |=p 1+cos α,弦长|AB |=x 1+x 2+p =2psin 2α(α为弦AB 的倾斜角),S △OAB =p 22sin α;(3)1|FA |+1|FB |=2p;(4)以弦AB 为直径的圆与准线相切;(5)以AF 或BF 为直径的圆与y 轴相切;(6)过焦点弦的端点的切线互相垂直且交点在准线上.(7)过抛物线y 2=2px (p >0)的顶点O (0,0)作互相垂直的两条射线且都与抛物线相交,交点为A ,B (如图).则直线AB 过定点M (2p,0);反之,若过点M (2p,0)的直线l 与抛物线y 2=2px (p >0),交于两点A ,B ,则必有OA ⊥OB .1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线.()(2)若直线与抛物线只有一个交点,则直线与抛物线一定相切.()(3)方程y =ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线,且其焦点坐标是⎪⎭⎫⎝⎛0,4a,准线方程是x =-a 4.()(4)抛物线既是中心对称图形,又是轴对称图形.()2.抛物线y =14x 2的准线方程是()A .y =-1B .y =-2C .x =-1D .x =-23.若抛物线y 2=2px (p >0)的焦点是椭圆x 23p +y 2p=1的一个焦点,则p =()A .2B .3C .4D .84.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点.如果x 1+x 2=6,那么|AB |=()A .6B .8C .9D .105.已知抛物线C 1:x 2=2py (p >0)的准线与抛物线C 2:x 2=-2py (p >0)交于A ,B 两点,C 1的焦点为F ,若△FAB 的面积等于1,则C 1的方程是()A .x 2=2y B .x 2=2y C .x 2=yD .x 2=22y 6.(教材改编)设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是________.7.焦点在直线2x +y +2=0上的抛物线的标准方程为_______________抛物线的定义及应用例:1.动圆与定圆A :(x +2)2+y 2=1外切,且和直线x =1相切,则动圆圆心的轨迹是()A .直线B .椭圆C .双曲线D .抛物线(2)(2020·全国卷Ⅰ)已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =()A .2B .3C .6D .9(3)若点P 到点F(0,2)的距离比它到直线y +4=0的距离小2,则P 的轨迹方程为()A .y 2=8xB .y 2=-8xC .x 2=8yD .x 2=-8y(4)在y =2x 2上有一点P ,它到A (1,3)的距离与它到焦点的距离之和最小,则点P 的坐标是()A .(-2,1)B .(1,2)C .(2,1)D .(-1,2)(5).已知F 是抛物线C :y 2=8x 的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则|FN |=________.(6).已知椭圆x 24+y 23=1的右焦点F 为抛物线y 2=2px (p >0)的焦点,点P 的坐标为(3,2).若点M 为该抛物线上的动点,则|MP |+|MF |的最小值为__________.(7).若点A 的坐标为(3,2),F 是抛物线y 2=2x 的焦点,点M 在抛物线上移动时,使|MF |+|MA |取得最小值的M 的坐标为()A .(0,0)B .⎪⎭⎫⎝⎛121C .(1,2)D .(2,2)(8).已知M 是抛物线x 2=4y 上一点,F 为其焦点,点A 在圆C :(x +1)2+(y -5)2=1上,则|MA |+|MF |的最小值是___________.(9).已知P 是抛物线y 2=4x 上一动点,则点P 到直线l :2x -y +3=0和y 轴的距离之和的最小值是()A .3B .5C .2D .5-1(10).已知抛物线y =12x 2的焦点为F ,准线为l ,M 在l 上,线段MF 与抛物线交于N 点,若|MN |=2|NF |,则|MF |=______.抛物线的标准方程例:(1)(2020·全国卷Ⅰ)已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =()A .2B .3C .6D .9(2)(2021·山西吕梁二模)如图,过抛物线x 2=2py (p >0)的焦点F 的直线l 交抛物线于A ,B 两点,交其准线于点C ,若|BC |=2|BF |,且|AF |=2,则p =()A .1 B.2C .2D .2-2(3).顶点在原点,对称轴为坐标轴,且过点P (-4,-2)的抛物线的标准方程是()A .y 2=-xB .x 2=-8yC .y 2=-8x 或x 2=-yD .y 2=-x 或x 2=-8y(4).如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 交抛物线于点A ,B ,交其准线于点C ,若|BC |=2|BF |,且|AF |=6,则此抛物线方程为()A .y 2=9xB .y 2=6xC .y 2=3xD .y 2=3x(5).已知抛物线x 2=ay 与直线y =2x -2相交于M ,N 两点,若MN 中点的横坐标为3,则此抛物线的方程为()A .x 2=32yB .x 2=6yC .x 2=-3yD .x 2=3y(6).抛物线y 2=2px (p >0)的焦点为F ,O 为坐标原点,M 为抛物线上一点,且|MF |=4|OF |,△MFO 的面积为43,则抛物线的方程为()A .y 2=6xB .y 2=8xC .y 2=16xD .y 2=152x(7).抛物线C :y 2=2px (p >0)的焦点为F ,点O 是坐标原点,过点O ,F 的圆与抛物线C 的准线相切,且该圆的面积为36π,则抛物线的方程为__________.抛物线的几何性质例:(1)(2020·全国卷Ⅲ)设O 为坐标原点,直线x =2与抛物线C :y 2=2px (p >0)交于D ,E 两点,若OD ⊥OE ,则C 的焦点坐标为()A .⎪⎭⎫⎝⎛041,B .⎪⎭⎫⎝⎛021,C .(1,0)D .(2,0)(2)已知抛物线y 2=2px (p >0),过其焦点且斜率为-1的直线交抛物线于A ,B 两点,若线段AB 的中点的横坐标为3,则该抛物线的准线方程为()A .x =1B .x =2C .x =-1D .x =-2(3)已知直线l 过点(1,0)且垂直于x 轴.若l 被抛物线y 2=4ax 截得的线段长为4,则抛物线的焦点坐标为______________.(4).若双曲线C :2x 2-y 2=m (m >0)与抛物线y 2=16x 的准线交于A ,B 两点,且|AB |=43,则m 的值是____________.(5).在平面直角坐标系xOy 中有一定点A (4,2),若线段OA 的垂直平分线过抛物线y 2=2px (p >0)的焦点,则该抛物线的准线方程是_____________(6).已知抛物线y 2=4x 的焦点F ,准线l 与x 轴的交点为K ,P 是抛物线上一点,若|PF |=5,则△PKF 的面积为()A .4B .5C .8D .10(7)(2021·新高考Ⅰ卷)已知O 为坐标原点,抛物线C :y 2=2px (p >0)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ ⊥OP .若|FQ |=6,则C 的准线方程为__________________.(8).过抛物线:y 2=2px (p >0)的焦点F 作倾斜角为60°的直线l ,若直线l 与抛物线在第一象限的交点为A ,并且点A 也在双曲线:x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线上,则双曲线的离心率为()A.213B.13C.233D.5(9).如图,已知抛物线y 2=4x 的焦点为F ,过点F 且斜率为1的直线依次交抛物线及圆(x -1)2+y 2=14于A ,B ,C ,D 四点,则|AB |+|CD |的值是()A .6B .7C .8D .9直观想象、数学运算——抛物线中最值问题的求解方法与抛物线有关的最值问题是历年高考的一个热点,由于所涉及的知识面广,题目多变,一般需要通过数形结合或利用函数思想来求最值,因此相当一部分同学对这类问题感到束手无策.下面就抛物线最值问题的求法作一归纳.1.定义转换法【典例1】(2021·上海虹口区一模)已知点M(20,40),抛物线y2=2px(p>0)的焦点为F.若对于抛物线上的任意点P,|PM|+|PF|的最小值为41,则p的值等于________.2.平移直线法【典例2】抛物线y=-x2上的点到直线4x+3y-8=0的距离的最小值是________.[切入点]解法一:求出与已知直线平行且与抛物线相切的直线方程,从而求两平行线间的距离.解法二:求出与已知直线平行且与抛物线相切的直线与抛物线的切点坐标,从而求切点到已知直线的距离.3.函数法【典例3】若点P在抛物线y2=x上,点Q在圆(x-3)2+y2=1上,则|PQ|的最小值为________.[切入点]P、Q都是动点,转化为圆心与点P的最值.1.(2021·东北三省四市二模)若点P为抛物线y=2x2上的动点,F为抛物线的焦点,则|PF|的最小值为()A.2 B.12C.14D.182.(2021·云南省高三统一检测)设P,Q分别为圆x2+y2-8x+15=0和抛物线y2=4x上的点,则P,Q两点间的最小距离是________.直线与抛物线的位置关系1.直线与抛物线的位置关系2=2px,=kx+m,得k2x2+2(mk-p)x+m2=0.(1)相切:k2≠0,Δ=0.(2)相交:k2≠0,Δ>0.(3)相离:k2≠0,Δ<0.2.焦点弦的重要结论抛物线y2=2px(p>0)的焦点为F,过F的焦点弦AB的倾斜角为θ,则有下列性质:(1)y1y2=-p2,x1x2=p24.(2)|AF|=x1+p2=p1-cosθ;|BF|=x2+p2=p1+cosθ;|AB|=x1+x2+p=2psin2θ.(3)抛物线的通径长为2p,通径是最短的焦点弦.(4)S△AOB=p22sinθ.(5)1|AF|+1|BF|为定值2p.(6)以AB为直径的圆与抛物线的准线相切.(7)以AF(或BF)为直径的圆与y轴相切.(8)过焦点弦的端点的切线互相垂直且交点在准线上.1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)直线与抛物线有且仅有1个公共点,则它们相切.()(2)所有的焦点弦中,以通径的长为最短.()(3)直线l过(2p,0),与抛物线y2=2px交于A、B两点,O为原点,则OA⊥OB.()(4)过准线上一点P作抛物线的切线,A、B为切点,则直线AB过抛物线焦点.() 2.过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有() A.1条B.2条C.3条D.4条3.过抛物线y 2=4x 的焦点的直线l 交抛物线于P (x 1,y 1),Q (x 2,y 2)两点,如果x 1+x 2=6,则|PQ |=()A .9B .8C .7D .64.如图,过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于点A ,B ,交其准线l 于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线的方程为()A .y 2=9xB .y 2=6xC .y 2=3xD .y 2=3x5.设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为__________.直线与抛物线的位置关系【例1】(1)过点(0,3)的直线l 与抛物线y 2=4x 只有一个公共点,则直线l 的方程为__________.(2)已知抛物线C :x 2=2py ,直线l :y =-p2,M 是l 上任意一点,过M 作C 的两条切线l 1,l 2,其斜率为k 1,k 2,则k 1k 2=________.焦点弦问题【例2】(1)(2021·石家庄市质检)已知抛物线y 2=4x 的焦点为F ,过点F 和抛物线上一点M (2,22)的直线l 交抛物线于另一点N ,则|NF |∶|FM |等于()A .1∶2B .1∶3C .1∶2D .1∶3(2)(2021·湖南五市十校摸底)过抛物线C :y 2=2px (p >0)的焦点F 的直线l 与抛物线交于M 、N 两点(其中M 点在第一象限),若MN →=3FN →,则直线l 的斜率为________.(3)过抛物线y 2=4x 焦点F 的直线交抛物线于A 、B 两点,交其准线于点C ,且A 、C 位于x 轴同侧,若|AC |=2|AF |,则|BF |等于()A .2B .3C .4D .5(2020·山东卷)斜率为3的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则|AB |=________.直线与抛物线的综合问题例题1:已知以F 为焦点的抛物线C :y 2=2px (p >0)过点P (1,-2),直线l 与C 交于A ,B 两点,M 为AB 的中点,O 为坐标原点,且OM →+OP →=λOF →.(1)当λ=3,求点M 的坐标;(2)当OA →·OB →=12时,求直线l 的方程.例题2:设抛物线C :y 2=2x ,点A (2,0),B (-2,0),过点A 的直线l 与C 交于M ,N 两点.(1)当l 与x 轴垂直时,求直线BM 的方程;(2)证明:∠ABM =∠ABN .例题3:已知抛物线P :y 2=2px (p >0)上的点⎪⎭⎫ ⎝⎛a ,43到其焦点的距离为1.(1)求p 和a 的值;(2)求直线l :y =x +m 交抛物线P 于A ,B 两点,线段AB 的垂直平分线交抛物线P 于C ,D 两点,求证:A ,B ,C ,D 四点共圆.例题4.如图所示,已知抛物线C :y 2=4x 的焦点为F ,直线l 经过点F 且与抛物线C 相交于A ,B 两点.(1)若线段AB 的中点在直线y =2上,求直线l 的方程;(2)若线段|AB |=20,求直线l 的方程.例题5:已知曲线C :y =x 22,D 为直线y =-12上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点;(2)若以E ⎪⎭⎫ ⎝⎛250,为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.。
高三抛物线定理知识点

高三抛物线定理知识点抛物线是高中数学中重要且常见的曲线。
在高三阶段,学生需要掌握抛物线定理,并且能够灵活运用于解决相关问题。
本文将介绍高三抛物线定理的基本概念以及其应用。
一、抛物线的定义与特点抛物线是由平面上距离一个定点距离相等的点构成的图形。
该定点称为焦点,到直线称为准线。
1. 对称性:抛物线以准线为对称轴对称。
2. 焦距:焦点到准线的距离称为焦距,用f表示。
3. 定义域与值域:抛物线的定义域为实数集,值域为y≥d,其中d为抛物线与其准线的最低点的纵坐标。
二、顶点与对称轴在抛物线中,顶点是其中最高(或最低)的点。
对称轴是过焦点和顶点的直线。
1. 顶点:抛物线的顶点坐标为(h,k),其中h和k分别为抛物线的顶点的横坐标和纵坐标。
2. 对称轴:对称轴的方程为 x = h。
三、抛物线的一般方程抛物线的一般方程为 y = ax² + bx + c,其中a≠0。
在高三阶段,学生需要了解如何通过抛物线的顶点和焦点坐标来确定抛物线方程。
四、抛物线的焦点与准线的关系抛物线的焦点坐标为(f,0),其中焦距f的计算公式为 f = 1/4a。
准线的方程为 x = -f。
五、抛物线的平移抛物线可以通过平移进行位置上的变换。
1. 抛物线上下平移:将抛物线原方程中的常数c进行上下平移。
2. 抛物线左右平移:将抛物线原方程中的常数b进行左右平移。
六、抛物线的应用抛物线的定理在物理学、工程学等领域有广泛的应用。
1. 抛物线光学:在光学实验中,抛物线是一种能够将平行光线聚焦于焦点的曲线形状。
2. 抛物线运动:在物理学中,抛物线也描述了平抛运动的轨迹,如投掷物体的运动。
七、高三抛物线定理解题方法1. 根据已知条件绘制抛物线,并确定抛物线的顶点、焦点和准线。
2. 列出抛物线的一般方程,并代入已知条件,解出未知变量。
3. 运用抛物线定理或几何特性,解答相关问题。
八、总结高三抛物线定理是数学中重要的知识点,掌握抛物线的基本概念、性质以及应用方法对于高中数学学习具有重要意义。
初中抛物线解析式

初中抛物线解析式一、抛物线的定义与性质抛物线是一种重要的数学曲线,它的解析式为y=ax^2+bx+c。
其中,a、b、c是常数,且a≠0。
抛物线具有以下几个性质:1. 对称性:抛物线关于直线x=-b/2a对称。
2. 焦点和准线:抛物线上的每一点到焦点F的距离等于该点到准线l的距离,焦点F的坐标为(-b/2a,c-b^2/4a),准线l的方程为y=c-b^2/4a。
3. 开口方向:当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
二、抛物线的应用1. 物理学中的抛物线:抛物线是物理学中一个重要的概念,例如,一个自由落体物体在重力作用下的运动轨迹就是一个抛物线。
2. 弹道学中的抛物线:弹道学研究的是飞行物体在重力作用下的运动轨迹,例如,炮弹、导弹等的飞行轨迹都是抛物线。
3. 建筑设计中的抛物线:抛物线可以被广泛应用于建筑设计中,例如,拱桥、拱顶等的形状都是抛物线。
4. 几何学中的抛物线:抛物线也是几何学中一个重要的概念,它在平面几何和立体几何中都有广泛的应用。
三、我的抛物线故事小时候,我曾经对抛物线产生了浓厚的兴趣。
在数学课上,老师讲解了抛物线的定义与性质,我对它的独特形状和奇妙性质深感着迷。
一天放学后,我在学校操场上看到了一个抛物线形状的秋千。
我迫不及待地坐上去,开始摇晃。
随着秋千的摇摆,我感受到了抛物线的魅力。
我闭上眼睛,想象自己是一个小鸟,飞翔在广阔的天空中。
我飞越高楼大厦,穿越云层,感受到了自由的快乐。
而我的飞行轨迹,竟然也是一个个美丽的抛物线。
这个抛物线秋千成了我童年的乐园,每天放学后,我都会来到这里,享受抛物线带给我的自由与快乐。
四、抛物线的魅力抛物线的魅力在于它的独特性和广泛应用。
无论是物理学、弹道学还是建筑设计,抛物线都扮演着重要的角色。
抛物线不仅是数学的一部分,更是人类思维的延伸和创造力的体现。
它的美丽曲线,让我们感受到数学的魅力和无限可能性。
在抛物线的世界里,我们可以追寻自由和梦想,感受到生活的美好和无限可能。
抛物线的各类公式

抛物线的各类公式抛物线这玩意儿,在数学里那可是相当重要的角色!咱先来说说抛物线的标准方程,一般式是 y = ax² + bx + c (a ≠ 0)。
这其中的 a 可不得了,它决定了抛物线的开口方向和大小。
要是 a大于 0 ,抛物线开口就朝上,像个乐观向上的笑脸;要是 a 小于 0 ,开口就朝下,仿佛一张哭丧的脸。
顶点式是 y = a(x - h)² + k ,这里的(h,k)就是抛物线的顶点坐标。
我给您举个例子,有次我在公园里散步,看到喷泉喷出的水形成的弧线,那可不就是一条抛物线嘛!当时我就想到了抛物线的顶点式。
那个喷泉的最高点,就是顶点(h,k)。
从这个顶点开始,水向两边洒落,形成了对称的美丽弧线。
还有焦点式,y = 4px²,其中 p 是焦点到准线的距离。
咱们再来说说抛物线的对称轴。
对于一般式,对称轴就是 x = -b /2a 。
想象一下,你拿着一把刀,沿着这条对称轴把抛物线切成两半,两边完全对称,是不是很神奇?抛物线的焦半径公式也得了解一下。
焦点在x 轴正半轴上的抛物线,焦半径是 |x + p/2| ;焦点在 x 轴负半轴上的,焦半径是 |x - p/2| 。
给您说个我教学时候的事儿。
有个学生,怎么都搞不明白抛物线的这些公式,愁得直挠头。
我就给他画了个大大的抛物线在黑板上,然后一步一步地给他讲解,从标准方程到顶点式,再到对称轴和焦半径公式。
我一边讲一边观察他的表情,看到他从迷茫逐渐变得恍然大悟,那一瞬间,我心里别提多有成就感了!在解决抛物线相关的题目时,要灵活运用这些公式。
比如求抛物线的顶点、焦点,或者根据给定的条件确定抛物线的方程。
总之,抛物线的各类公式虽然看起来有点复杂,但只要咱们多做几道题,多观察生活中的抛物线现象,就能把它们掌握得妥妥的!就像我在公园里看到的喷泉抛物线,它就在提醒我,数学无处不在,抛物线的公式也能在生活中找到生动的例子。
所以呀,别害怕抛物线的公式,多琢磨多练习,您一定能搞定它们!。
高中数学公式—抛物线及抛物线标准方程_公式总结

高中数学公式—抛物线及抛物线标准方程_公式总结
高中数学公式之抛物线公式:
抛物线:y=ax^2+bx+c
就是y等于ax 的平方加上bx再加上c
a > 0时开口向上
a < 0时开口向下
c = 0时抛物线经过原点
b = 0时抛物线对称轴为y轴
还有顶点式y = a(x+h)^2 + k
就是y等于a乘以(x+h)的平方+k
-h是顶点坐标的x
k是顶点坐标的y
一般用于求最大值与最小值
抛物线标准方程:y^2=2px
它表示抛物线的焦点在x的正半轴上,焦点坐标为(p/2,0) 准线方程为x=-p/2
由于抛物线的焦点可在任意半轴,故共有标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py 以上是小编为大家整理的高中数学公式的抛物线方程,希望便于大家牢记。
抛物线二级定理

抛物线二级定理抛物线二级定理引言在平面几何中,抛物线是一种重要的曲线,具有许多独特的性质和应用。
本文将介绍抛物线二级定理,该定理是关于抛物线的一个基本性质,对于理解抛物线的性质和应用具有重要意义。
一、基本概念1. 抛物线:抛物线是一种平面曲线,由一个固定点(焦点)F和一条直线(准线)L组成,定义为到焦点距离与到准线距离相等的点的轨迹。
2. 焦距:焦距是指焦点到准线的距离。
3. 对称轴:对称轴是指过焦点垂直于准线的直线。
4. 顶点:顶点是指抛物线上离对称轴最近的点。
5. 参数方程:参数方程是指用参数表示曲线上每个点坐标的方程。
6. 标准方程:标准方程是指将抛物线移到以对称轴为x轴、以顶点为原点的坐标系中后得到的方程。
7. 切线:切线是指与曲面相切于一点且在该点处与曲面重合的直线。
8. 法线:法线是指与切线垂直的直线。
二、抛物线二级定理的表述抛物线二级定理又称为焦点定理,它表述了一个点到抛物线焦点的距离等于这个点到抛物线准线距离的平方与这个点到抛物线顶点距离的平方之和的一半。
具体地说,设P(x,y)为抛物线上任意一点,F为焦点,L为准线,V为顶点,则有:PF² = (x-a)² + (y-b)²PL = |y-c|PV² = (x-a)² + (y-b+c)²其中a,b,c分别是标准方程y²=2px中的参数。
则有:PF² = (PL² + PV²)/2三、证明过程1. 基本思路:首先将抛物线移到以对称轴为x轴、以顶点为原点的坐标系中,并将焦点F移到原点O处。
然后通过参数方程求出P(x,y)到O和L的距离,并利用勾股定理和代数运算得到PF²、PL和PV²。
最后代入公式中进行简化即可得到结论。
2. 具体步骤:(1)将抛物线移到以对称轴为x轴、以顶点为原点的坐标系中,此时抛物线的标准方程为y²=2px。
抛物线的标准方程及抛物线与直线的位置关系

抛物线的标准方程及抛物线与直线的位置关系知识点概括:抛物线的概念抛物线的概念1、平面内与一定点F 和一条定直线l (l 不经过点F )距离相等的点的轨迹叫做抛物线。
定点F 叫做抛物线的焦点,定直线l 叫做抛物线的叫做抛物线的准线准线。
2、抛物线的性质、抛物线的性质::抛物线的图形、标准方程、焦点坐标以及准线方程如下表:标准方程22(0)y pxp =>22(0)y pxp =->22(0)x pyp =>22(0)x pyp =->图形焦点坐标 (,0)2p (,0)2p -(0,)2p (0,)2p -准线方程 2p x =-2p x =2p y =-2py =范围 0x ³ 0x £0y ³ 0y £对称性 x 轴x 轴y 轴 y 轴 顶点 (0,0)(0,0)(0,0)(0,0)离心率 1e =1e =1e =1e =焦半径 02x p PF +=02x p PF -=02y p PF +=02y p PF -=焦点弦)(21x x p AB ++=)(21x x p AB +-=)(21y y p AB ++= )(21y y p AB +-=o Fxy l oxy F l xyo F l+2p , (2)12x x 2x 或x 2=43y B.y 2=92x 或x 2=43yC .y 2=92x 或x 2=-43yD .y 2=-92x 或x 2=-42x ;当焦点在y 轴上时,抛物线方程为x 2=42=3,∴p =6. ∴圆心M 的轨迹方程为y 2=12x . 公式3.3.通径:过通径:过通径:过抛物线抛物线的焦点且垂直于对称轴的弦H 1H 2称为通径;通径:称为通径;通径:|H |H 1H 2|=2P 4、焦点弦:过抛物线22y px =(0)p >焦点F 的弦AB ,若1122(,),(,)A x y B x y ,则(1)||AF =x 0=42p ,12y y =-p 2.例1、当a 为任何值时,为任何值时,直线直线(a -1)x -y +2a +1=0恒过定点P ,则过P 点的抛物线的物线的标准方程标准方程为( ) A .y 2=-93y解析:由直线过定点P ,所以îíìx +2=0,-x -y +1=0,得定点P (-2,3).因为抛物线过定点P ,所以,当焦点在x 轴上时,方程为y 2=-93y .选A. 例2、动圆M 经过点A (3,0)且与直线l :x =-3相切,求动圆求动圆圆心圆心M 的轨迹方程.解:设圆M 与直线l 相切于点N . ∵|MA |=|MN |,∴圆心M 到定点A (3,0)和定直线x =-3的距离相等.根据抛物线的定义,M 在以A 为焦点,l 为准线的抛物线上. ∵p例3、已知抛物线C 的焦点F 在x 轴的正半轴上,点A (2,32+2=4,p =4,即抛物线C 的方程为y 2=8x . 巩固练习:1、(2013年山东数学(理))已知抛物线1C .316 B .38 C .233 D .433【答案】【答案】D D 2、(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理))设抛物线2:2(0)C y px p =>的焦点为F ,点M 在C 2)在抛物线内.若抛物线上一动点P 到A 、F 两点距离之和的最小值为4,求抛物线C 的方程.的方程.解:设抛物线方程为y 2=2px (p >0),其准线为x =-p 2,过P 点作抛物线准线的垂线,垂足为H (图略),由定义知,|PH |=|PF |.∴|P A |+|PF |=|P A |+|PH |,故当H 、P 、A 三点共线时,|P A |+|PF |最小. ∴|P A |+|PF |的最小值为p:212y x p =(0)p >的焦点与的焦点与双曲线双曲线2C :2213x y -=的右焦点的连线交1C 于第一于第一象限象限的点M .若1C 在点M 处的切线平行于2C 的一条的一条渐近线渐近线,则p = ( )A 上,5MF =,若以MF 为直径的圆过点)2,0(,则C 的方程为的方程为 ( )A .24y x =或28y x =B .22y x =或28y x = C .24y x =或216y x =D .22y x =或216y x =【答案】【答案】C C3、(2013年上海市春季年上海市春季高考数学高考数学试卷)试卷)已知已知 A B 、为平面内两定点为平面内两定点,,过该平面内动点M 作直线AB 的垂线的垂线,,垂足为N .若2MN AN NB l=×,其中l 为常数,则动点M 的轨迹不可能是的轨迹不可能是 ( ) A .圆.圆 B .椭圆 C .抛物线.抛物线 D .双曲线.双曲线 【答案】【答案】C C+2p , (2)12x x =42p ,12y y =-p 2.(3) (3) 弦长弦长)(21x x p AB ++=,则AB =q 2sin 2p(5)AF 1+BF 1=P24、(2013年高考江西卷(理))抛物线22(0)x py p =>的焦点为F,F,其其准线与双曲线22133x y -=相交于,A B 两点,若ABF D 为等边三角形,则P =_____________【答案】【答案】6 65、(2013年安徽数学(理)试题)已知年安徽数学(理)试题)已知直线直线y a =交抛物线2y x =于,A B 两点两点..若该抛物线上存在点C ,使得ABC Ð为直角为直角,,则a 的取值范围为的取值范围为___ _____. ___ _____. 【答案】),1[+¥6、( 2013年江苏卷(数学))抛物线2x y =在1=x 处的切线与两处的切线与两坐标轴坐标轴围成三角形区域为D (包含三角形内部与包含三角形内部与边界边界).).若点若点),(y x P 是区域D 内的任意一点,则y x 2+的取值范围是的取值范围是__________.__________. 【答案】úûùêëé-21,21、焦点弦:过抛物线22y px =(0)p >焦点F 的弦AB ,若1122(,),(,)A x y B x y , 则(1)||AF =x 0,p x x x x =³+21212,即当x 1=x 2时,通径最短为2p (4) (4) 若若AB 的倾斜角为θ2. 221212120(,),(,),,(,2).22x x A x B x x x M x p pp-< 由22x py =得22x y p=,则,xy p ¢= 所以12,.MAMBx x kkpp==因此直线MA :102(),xy p x x p+=- 直线MB :202().xy p x x p+=-所以211102(),2x x p x x p p +=- ① 222202().2x x p x x p p +=- ② 由①、②得: 0122.x x x =+所以A 、M 、B 三点的横坐标成等差数列. (2)解:由(1)知,当x 0=2时,时, 将其代入①、②并整理得:将其代入①、②并整理得:弦长公式2121221||1||1||AB k x x y y k=+-=+-3.3.点点P(x 0,y 0)和抛物线22y px =(0)p >的位置关系的位置关系(1) (1)点点P(x 0,y 0)在抛物线22y px =(0)p >内Ûy 20<2px 0 (2) (2)点点P(x 0,y 0)在抛物线22y px =(0)p >上Ûy 20=2px 0 (3) (3)点点P(x 0,y 0)在抛物线22y px =(0)p >外Ûy 2>2px 0例1、如图,设抛物线方程为x 2=2py (p >0),M 为直线p y 2-=上任意一点,过M 引抛物线的切线,引抛物线的切线,切点切点分别为A ,B . (1)求证:A ,M ,B 三点的横坐标成三点的横坐标成等差数列等差数列;(2)已知当M 点的坐标为点的坐标为((2,p 2-)时,时, 410AB =,求此时抛物线的方程; (3)是否存在点M ,使得点C 关于直线AB 的对称点D 在抛物线22(0)x py p =>上,其中,点C 满足OC OA OB =+(O 为坐标原点).若存在,求出所有适合题意的点M 的坐标;若不存在,请说明理由. 解:(1)证明:由题意设2211440,x x p --= 2222440,x x p --=所以x 1、x 2是方程22440x x p --=的两根,因此212124,4,x x x x p +==-又22210122122,2ABx x x x x p p k x x p p -+===-所以2.AB k p =由弦长公式2221212241()411616.AB k x x x x p p=++-=++的方程为011(),xy y x x p-=-由点Q 在直线AB 上,并注意到点1212(,)22x x y y ++也在直线AB 上,上,代入得033.xy x p=若D (x 3,y 3)在抛物线上,)在抛物线上, 则2330322,x py x x ==因此x 3=0或x 3=2x 0. 即D (0,0)或202(2,).x D x p(1(1’ ’ 当x 0=0时,则12020x x x +==,此时,点M (0,-2p )适合题意. (2(2’ ’ 当00x ¹,对于D (0,0)又0,AB x k p=AB ⊥CD ,所以222201212201,44AB CDx x x x x k k p px p++===- 即222124,x x p +=-矛盾. 对于202(2,),x D x p 又410AB =,所以p =1或p =2,因此所求,因此所求抛物线抛物线方程为22x y =或24.x y =(3)解:设D (x 3,y 3),由题意得C (x 1+ x2, y 1+ y 2), 则CD 的中点坐标为123123(,),22x x x y y y Q ++++设直线AB ,此时2212222212120002(2,),,224CDx x x x x x p C x kpx px +++==因为22120(2,),2x x C x p+此时直线CD 平行于y 轴,轴,解:(1)证明:设221122(,)(,)A x x B x x 、,(,)(,)E EF F E x y B x y 、则直线AB 的方程:()222121112x x y x x x x x -=-+-, 即:121()y x x x x x =+- 因00(,)M x y 在AB 上,所以012012()y x x x x x =+- ① 又直线AP 方程:2101x yy x y x -=+由210012x y y x y x x yì-=+ïíï=î得:2210010x yx x y x ---= 所以22100012111,E E E x y y y x x x y x x x -+=Þ=-= 同理,同理,200222,F F y y x y x x =-= 所以直线EF 的方程:201201212()y x x y y x x x x x +=-- 令令0x x =-得: 0120012[()]yy x x x y x x =+-将①代入上式得0y y =,即N 点在直线EF 上.即证即证. .yxPNOMAEBF又00,ABx kp=¹所以所以直线直线AB 与直线CD 不垂直,与题设矛盾,,与题设矛盾, 所以00x ¹时,不存在符合题意的M 点. 综上所述,仅存在一点M (0,-2p )适合题意. 例2、已知已知抛物线抛物线2y x =和三个点00000(,)(0,)(,)M x y P y N x y -、、2000(,0)y x y ¹>,过点M 的一条直线交抛物线于A 、B 两点,AP BP 、的延长线分别交的延长线分别交曲线曲线C 于E F 、.(1)证明E F N 、、三点三点共线共线;(2)如果A 、B 、M 、N 四点共线,问:是否存在0y ,使以,使以线段线段AB 为直径的圆与抛物线有异于A 、B 的交点?如果存在,求出0y 的取值范围,并求出该交点到直线AB 的距离;若不存在,请说明理由.由.(2)解:由已知A B M N 、、、.共线,所以()0000,,(,)A y y B y y - 以AB 为直径的为直径的圆的方程圆的方程:()2200x y y y +-=由()22002x y y y x y ì+-=ïí=ïî得()22000210y y y y y --+-=所以0y y =(舍去),01y y =-要使圆与要使圆与抛物线抛物线有异于,A B 的交点,则010y -³所以存在01y ³,使以AB 为直径的圆与抛物线有异于,A B 的交点(),T T T x y 则01T y y =-,所以交点T 到AB 的距离为()00011T y y y y -=--= 例3、已知已知直线直线:1L x my =+(0m ¹)过)过椭圆椭圆2222:1(0)x y C a b a b +=>>的右焦点F ,且交椭圆C 与A ,B 两点.(1)若抛物线243x y =的焦点为椭圆C 的上的上顶点顶点,求椭圆C 的方程;的方程; (2)对于()对于(11)中的椭圆C ,若直线L 交y 轴于点M ,且12,MA AF MB BF l l ==,当m 变化时,求12l l +的值,由已知得222(5)3x x y +=-+-,易知圆2C 上的点位于直线2x =-的右侧.于是20x +>,所于是0254 3.1k y kk ++=+注意:本题中条件” 12,MA AF MB BF l l ==”的处理很好! 巩固练习:1、在直角在直角坐标系坐标系xOy 中,曲线1C 上的点均在圆222:(5)9C x y -+=外,且对1C 上任意一点M ,M 到直线2x =-的距离等于该点与圆2C 上点的距离的上点的距离的最小值最小值. (Ⅰ)求曲线1C 的方程;的方程;(Ⅱ)设000(,)(3)P x y y ¹±为圆2C 外一点,过P 作圆2C 的两条切线,分别与曲线1C 相交于点,A B 和,C D .证明:当P 在直线4x =-上运动时,四点,A B ,,C D 的纵坐标之积为定值的纵坐标之积为定值. .解:(Ⅰ)解法1 :设M 的坐标为(,)x y 以22(5)5x y x -+=+.化简得曲线1C 的方程为220y x =.解法2 :由题设知,由题设知,曲线曲线1C 上任意一点M 到圆心2C (5,0)的距离等于它到直线5x =-的距离,因此,的距离,因此,曲线曲线1C 是以(5,0)为焦点,直线5x =-为准线的抛物线,故其方程为220y x =.(Ⅱ)当点P 在直线4x =-上运动时,上运动时,P P 的坐标为0(4,)y -,又03y ¹±,则过P 且与圆且与圆2C 相切得直线的斜率k 存在且不为0,每条切线都与抛物线有两个,每条切线都与抛物线有两个交点交点,切线方程为0(4),y y k x -=+0即kx-y+y +4k=0.01218.724y yk k +=-=- ②② 由101240,20,k x y y k y x -++=ìí=î得21012020(4)0.k y y y k -++= ③③ 设四点A,B,C,D 的纵坐标分别为1234,,,y y y y ,则0112120(4).y k y yk +×= ④④同理可得0234220(4)y k y y k +×=⑤⑤ 于是由②,④,⑤三式得于是由②,④,⑤三式得于是由②,④,⑤三式得: :010*******400(4)(4)y k y k y y y y k k ++由023222c --=结合0c >,解得1c =.所以抛物线C 的方程为24x y =.(Ⅱ) ) 抛物线抛物线C 的方程为24x y =,即214y x =,求导得12y x ¢= 设()11,A x y ,()22,B x y (其中221212,44x x y y ==),),则切线则切线,PA PB 的斜率分别为整理得2200721890.k y k y ++-= ①① 设过P 所作的两条切线,PA PC 的斜率分别为12,k k ,则12,k k 是方程①的两个实根,故=2012012124004()16y k k y k k k k éù+++ëû==6400 所以,当P 在直线4x =-上运动时,四点A ,B ,C ,D 的纵坐标之积为定值6400.2、(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))已知抛物线C 的顶点为原点为原点,,其焦点()()0,0F c c >到直线l :20x y --=的距离为322.设P 为直线l 上的点上的点,,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点.(Ⅰ) ) 求抛物线求抛物线C 的方程的方程; ;(Ⅱ) ) 当点当点()00,P x y 为直线l 上的定点时上的定点时,,求直线AB 的方程的方程; ; (Ⅲ) ) 当点当点P 在直线l 上移动时上移动时,,求AF BF ×的最小值. 【答案】【答案】((Ⅰ) ) 依题意依题意依题意,,设抛物线C 的方程为24x cy =,112x ,212x , 所以切线PA 的方程为()1112xy y x x -=-,,21BF y =+, 所以()221212121AF BF y y yy y x y×=+++=+-+又点()00,P x y 在直线l 上,所以002x y =+,所以22220000001921225222y x y y y y æö+-+=++=++ç÷èø所以当012y =-时.1617 B .1615 C 即211122x x y x y =-+,即11220x x y y --=同理可得切线PB 的方程为22220x x y y --= 因为切线,PA PB均过点()00,P x y ,所以1220x x y y --=,2002220x x y y --=所以()()1122,,,x y x y 为方程00220x x y y --=的两组解的两组解. . 所以所以直线直线AB 的方程为00220x x y y --=.(Ⅲ) ) 由由抛物线定义可知11AF y =+所以()()()121212111AF BF y y y y y y ×=++=+++联立方程0022204x x y y x y--=ìí=î,消去x 整理得()22200020y y x y y +-+=由一元二次方程根与系数的关系可得212002y y x y +=-,2120y y y = , AF BF ×取得取得最小值最小值,且最小值为92.课后作业:1.抛物线28y x =的准线方程是(方程是( )(A) 2x =- (B) 4x =- (C) 2y =- (D) 4y =- 2.抛物线24x y =上的一点M 到焦点的距离为1,则点M 的纵坐标是(的纵坐标是( )A .87D .0 3.在抛物线y px 22=上横坐标为4的点到焦点的距离为5,则p 的值为(的值为( )则=×OB OA ( )(A )43 (B )-43(C )3 (D )-3 6.已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为(的坐标为( )A. (41,-1)B. (41,1) C. (1,2) D. (1,-2)7.抛物线y 2=4x 的焦点为F ,准线为l,经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ,AK ⊥l,垂足为K ,则△AKF 的面积是(的面积是( ))(A )4 (B )33 (C) ..10.若直线10ax y -+=经过抛物线24y x =的焦点,则实数a = 一、选择题:12345678ABCDBACB题 号答 案二.填空题:9.x A. 12 B. 1 C. 2 D. 4 4.与.与直线直线2x-y+4=0平行的抛物线y=x 2的切线方程是(是() (A) 2x-y+3=0 (B) 2x-y-3=0 (C) 2x-y+1=0 (D) 2x-y-1=0 5、设坐标原点为O ,抛物线x y 22=与过焦点的直线交于A 、B 两点,43 (D)8 8.已知两点M (-2,0)、N (2,0),点P 为坐标平面内的动点,满足||||MN MP MN NP ×+× =0,则动点P (x ,y )的)的轨迹方程轨迹方程为(为( ) (A )x y 82= (B )x y 82-= (C )x y 42= (D )x y 42-= 二.填空题:9.在.在平面直角坐标系平面直角坐标系xOy xOy中,已知抛物线关于中,已知抛物线关于中,已知抛物线关于x x 轴对称,顶点在原点,顶点在原点O O ,且过点P(2,4)P(2,4),则该抛物线的方程是,则该抛物线的方程是 .11.过抛物线x y 42=的焦点F 作垂直于x 轴的直线,交抛物线于A 、B 两点,则以F 为圆心、AB 为直径的圆方程是________________. 12.已知抛物线x y 42=,过点P(4,0)的直线与抛物线相交于A(),(),2211y x B y x 、两点,则y 2221y +的最小值是的最小值是y 82= ; 10. -1. . 11.4)1(22=+-y x ;12. 32 。
抛物线的基本公式

抛物线的基本公式抛物线是一种常见的函数曲线,在数学、物理、化学、工程等学科中有着广泛的应用。
抛物线的绘制主要是通过抛物线基本公式,抛物线基本公式定义为:y = ax2 + bx + c。
抛物线的基本公式是一元二次方程。
其中参数a,b,c分别表示抛物线的顶点、焦点及渐近线。
当a的符号为正时,抛物线的开口朝上,当a的符号为负时,抛物线的开口朝下;b表示抛物线的斜率,c表示抛物线在y轴上的截距。
抛物线基本公式Y = ax2 + bx + c过改变参数a,b,c,可以绘制出不同的抛物线曲线。
当a=0时,即二次项消失,此时抛物线曲线为一条直线,公式变为y=bx+c,b表示直线斜率,当b=0时,此时直线变为水平线,其Y 值为c;当c=0时,此时抛物线曲线会将坐标原点分隔为两部分,是半椭圆,公式变为y= ax2。
从抛物线曲线的图像可以看出,抛物线曲线的顶点为变量a、b、c中最先变化的,当a变化时,抛物线曲线开口方向发生变化,当b 变化时,抛物线曲线的斜率发生变化,当c变化时,抛物线曲线在x 轴上的截距发生变化。
此外,抛物线的基本公式还可以用来求解其它几何关系的问题,比如:给定两条抛物线,求它们的焦点和准线方程,以及求它们的最大公约数的值。
上述只是抛物线的基本公式的最简单应用,实际上抛物线的基本公式可以应用到许多数学和物理问题,比如几何论、牛顿定律、力学、摩擦力等。
抛物线在实际应用中也有多种,如空气动力学中的攻角抛物线、太阳能、加速度及速度抛物线等。
抛物线的基本公式是由古希腊数学家艾克斯托夫 (Archytas)发现的,他发现用赤道定律来求解抛物线的基本公式,并且通过改变参数a,b,c来绘制出不同的抛物线曲线。
虽然古希腊数学家已经发现抛物线的基本公式,但由于抛物线的基本公式的应用甚广,所以在不断的发展和完善中,几百年的发展历史里,也出现了许多不同的抛物线,如高斯抛物线、拉氏抛物线、摩擦力抛物线等等。
总之,抛物线的基本公式不仅可以用于求解几何关系问题,而且用于求解空气动力学、牛顿定律、力学、太阳能、摩擦力等许多数学和物理问题,它的发明至今仍是一个重要的科学研究标志。
抛物线及其性质知识点大全

抛物线及其性质知识点大全1.抛物线的定义:抛物线是平面上各点到定点(焦点)的距离与各点到定直线(准线)的距离相等的点的轨迹。
2.抛物线的一般方程:抛物线的一般方程为 y = ax^2 + bx + c,其中a ≠ 0。
3.抛物线的焦点和准线:-抛物线的焦点是定点F,在焦点F上可以发射经由抛物线反射的平行光线,称为焦光束。
-抛物线的准线是直线L,通过焦点F,且与抛物线没有交点。
4.抛物线的焦距:-抛物线的焦距是焦点F到准线的垂直距离,记为2p。
5.抛物线的顶点:-抛物线的顶点是抛物线的最高点或最低点,坐标记为(h,k)。
-抛物线的顶点坐标可以通过顶点公式h=-b/2a和k=c-b^2/4a计算得到。
6.抛物线的对称轴:-抛物线的对称轴是抛物线的对称线,过顶点,并且与抛物线垂直。
7.抛物线的开口方向:-当a>0时,抛物线开口向上。
-当a<0时,抛物线开口向下。
8.抛物线的图像特点:-抛物线关于对称轴对称。
-抛物线与准线相交于顶点。
-抛物线在焦点处达到最大值或最小值。
-抛物线两侧的点到焦点的距离相等。
9.抛物线的焦点坐标计算:-焦点坐标可以通过焦距公式p=1/4a和焦点公式F(h,k+p)计算得到。
10.抛物线的拟合直线:-抛物线的切线方程和抛物线在焦点处的切线方向一致。
11.抛物线的截距:-抛物线与x轴的交点称为x轴截距,可以通过方程y=0解得。
-抛物线与y轴的交点称为y轴截距,可以直接读出抛物线方程中的常数项。
12.抛物线的平移:-抛物线的平移是通过改变顶点的坐标来实现的,顶点的新坐标为(h+a,k)。
13.抛物线的标准方程:- 当抛物线顶点为原点时,可以将抛物线的方程化为标准方程 y^2 = 4ax,其中焦点坐标为 (a, 0)。
14.抛物线的求导函数:- 抛物线的导数函数为 f'(x) = 2ax + b。
15.抛物线的面积计算:- 抛物线的面积可以通过定积分来计算,公式为 S =∫[x1,x2](ax^2 + bx + c)dx。
抛物线知识点

抛物线知识点在数学的广阔天地中,抛物线是一个非常重要的概念,它不仅在数学理论中有着关键地位,还在实际生活和其他科学领域有着广泛的应用。
接下来,咱们就一起深入探究抛物线的知识点。
首先,咱们来聊聊抛物线的定义。
简单来说,平面内到一定点 F 和一条定直线 l 的距离相等的点的轨迹就是抛物线。
这个定点 F 叫做抛物线的焦点,定直线 l 叫做抛物线的准线。
那抛物线的标准方程都有哪些呢?常见的有四种形式:当抛物线的焦点在 x 轴正半轴上时,标准方程为 y²= 2px(p >0),此时焦点坐标是(p/2,0),准线方程是 x = p/2 。
当焦点在 x 轴负半轴上时,标准方程为 y²=-2px(p > 0),焦点坐标是(p/2,0),准线方程是 x = p/2 。
要是焦点在 y 轴正半轴上,标准方程就是 x²= 2py(p > 0),焦点坐标为(0,p/2),准线方程是 y = p/2 。
而焦点在 y 轴负半轴上时,标准方程是 x²=-2py(p > 0),焦点坐标是(0,p/2),准线方程是 y = p/2 。
了解了标准方程,咱们再看看抛物线的图像特点。
以 y²= 2px(p > 0)为例,它的图像是开口向右的抛物线。
因为 p 决定了抛物线开口的大小,p 越大,开口越宽;p 越小,开口越窄。
而且,抛物线是轴对称图形。
比如 y²= 2px(p > 0)的对称轴就是 x 轴,顶点在原点。
接下来,咱们说说抛物线的性质。
抛物线上任一点到焦点的距离等于到准线的距离。
这是抛物线非常重要的一个性质,在解题中经常会用到。
还有抛物线的焦半径公式。
对于抛物线 y²= 2px(p > 0),若点P(x₀,y₀)在抛物线上,则点 P 到焦点的距离(焦半径)|PF| =x₀+ p/2 。
在实际应用中,抛物线也有着诸多体现。
比如,抛物线在物理学中的平抛运动、卫星轨道等问题中都有应用。
抛物线知识点总结

抛物线知识点总结一、抛物线的定义抛物线是一种特殊的二次曲线,它的数学定义是平面上一点到定点和直线的距离相等,这个定点就是抛物线的焦点,直线就是抛物线的准线。
在直角坐标系中,抛物线的标准方程为:y=ax2+bx+c,其中a≠0。
二、抛物线的性质1. 焦点和准线:抛物线的焦点和准线是抛物线的两个重要属性。
焦点是定点,准线是直线,它们共同决定了抛物线的形状和特性。
2. 对称性:抛物线是关于x轴对称的。
3. 切线和法线:抛物线上的任意一点,它的切线和法线都是经过这个点,且与x轴垂直。
4. 定理一:抛物线的焦点到准线的距离等于焦点到抛物线上任意一点的距离。
5. 定理二:抛物线上任意一点到焦点的距离等于该点到准线的距离。
6. 焦距:抛物线上所有点到焦点的距离的最小值称为抛物线的焦距。
7. 平行于准线的矩形,被含在抛物线内部并且对称。
8. 定理三:抛物线的离心率等于1。
三、抛物线的方程1. 标准方程:y=ax2+bx+c,其中a≠0。
2. 顶点坐标:抛物线的顶点坐标为(-b/2a, c-b2/4a)。
3. 焦点坐标:抛物线的焦点坐标为(-b/2a, c-b2/4a+1/4a)。
4. 焦距:抛物线的焦距为1/|4a|。
四、抛物线的应用抛物线作为一种重要的数学曲线,在各种应用中都有着广泛的应用,如物理、工程、建筑等领域。
1. 物理:在物理学中,抛物线曲线被广泛应用于描述抛体运动的轨迹。
比如,抛体在空中的飞行轨迹、抛物线发射器等都涉及到抛物线的运动规律。
2. 工程:在建筑工程和土木工程中,抛物线曲线常常被用于设计拱形结构或者桥梁的曲线轨迹。
抛物线的弧形轨迹具有良好的支撑性能和稳定性,因此在工程设计中得到了广泛应用。
3. 航天航空:在航天航空技术中,抛物线曲线也被用于设计火箭轨迹和飞行器的运动路径。
比如,抛物线曲线可以描述卫星的发射和轨道运行规律。
4. 光学:在光学中,抛物线曲线也被应用于设计反射镜和折射镜的形状。
抛物线反射镜可以将平行光线汇聚到一个焦点上,因此在光学仪器和望远镜中得到了广泛应用。
抛物线的焦点和准线关系

抛物线的焦点和准线关系抛物线是一种常见的二次函数曲线,具有特定的形状和性质。
在抛物线上,焦点和准线是两个重要的元素,它们之间存在一定的关系。
焦点的定义和性质焦点是抛物线上的一个特殊点,用F表示。
对于一个标准的抛物线,焦点位于顶点之上(对称轴上方),与准线相距相等。
焦点的性质如下:- 抛物线上的任意一点与焦点的距离等于该点到准线的垂直距离。
- 焦点是抛物线的对称中心,对称轴上的任意一点到焦点的距离等于该点到准线的垂直距离。
准线的定义和性质准线是抛物线对称轴上的一条直线,通常表示为x = a,其中a 为常数。
准线与抛物线的焦点之间的距离称为焦距,用p表示。
准线的性质如下:- 准线是抛物线的对称轴,抛物线上的任意一点到准线的距离相等。
- 由焦点到准线的垂直线段长度等于焦距p。
焦点与准线的关系焦点和准线是密切相关的,它们之间的关系可以用以下公式表示:PF = PM其中,PF表示焦点F到抛物线上一点P的距离,PM表示点P 到准线的垂直距离。
这个关系可以进一步转化为:PF = p其中,p表示焦距,也就是焦点到准线的距离。
焦点和准线的关系告诉我们,在抛物线上的任意一点,到焦点的距离等于该点到准线的垂直距离,而且焦距是确定的。
总结抛物线的焦点和准线是抛物线的重要元素,它们之间存在着特定的关系。
焦点是抛物线的对称中心,准线是对称轴,两者之间的关系可以通过焦点与准线的距离来描述。
了解焦点和准线的性质和关系,有助于我们更好地理解和应用抛物线的相关知识。
以上是关于抛物线的焦点和准线关系的简要介绍。
如果需要更详细的内容或有其他问题,请随时与我联系。
抛物线的基本知识点初三

抛物线的基本知识点初三一、抛物线的定义。
1. 平面内与一定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线。
- 点F叫做抛物线的焦点。
- 直线l叫做抛物线的抛物线的准线。
二、抛物线的标准方程。
1. 当焦点在x轴正半轴上时。
- 设其方程为y^2=2px(p>0)。
- 焦点坐标为((p)/(2),0),准线方程为x = -(p)/(2)。
2. 当焦点在x轴负半轴上时。
- 方程为y^2=-2px(p>0)。
- 焦点坐标为(-(p)/(2),0),准线方程为x=(p)/(2)。
3. 当焦点在y轴正半轴上时。
- 方程为x^2=2py(p > 0)。
- 焦点坐标为(0,(p)/(2)),准线方程为y=-(p)/(2)。
4. 当焦点在y轴负半轴上时。
- 方程为x^2=-2py(p>0)。
- 焦点坐标为(0,-(p)/(2)),准线方程为y=(p)/(2)。
三、抛物线的性质。
1. 对称性。
- 对于抛物线y^2=2px(p>0),它关于x轴对称,对称轴方程为y = 0。
- 对于抛物线x^2=2py(p>0),它关于y轴对称,对称轴方程为x = 0。
2. 顶点。
- 四种标准方程形式的抛物线顶点都在原点(0,0)。
3. 离心率。
- 抛物线的离心率e = 1。
四、抛物线的简单应用。
1. 求抛物线上的点到焦点和准线的距离。
- 根据抛物线的定义,抛物线上的点到焦点的距离等于到准线的距离。
- 例如,对于抛物线y^2=2px(p>0)上一点P(x_0,y_0),点P到焦点((p)/(2),0)的距离| PF|=x_0+(p)/(2)(因为点P到准线x = -(p)/(2)的距离为x_0-(-(p)/(2))=x_0+(p)/(2))。
2. 根据已知条件求抛物线方程。
- 如果已知抛物线的焦点坐标或者准线方程等条件,可以求出p的值,进而确定抛物线的方程。
- 例如,已知抛物线焦点为(3,0),因为焦点在x轴正半轴,且(p)/(2)=3,则p = 6,抛物线方程为y^2=12x。
高中抛物线知识点公式大全

高中抛物线知识点公式大全焦点弦AB 的几条性质11(,)A x y 22(,)B x y以AB 为直径的圆必与准线l 相切若AB 的倾斜角为α,则22sin p AB α=若AB 的倾斜角为α,则22cos pAB α= 2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 切线 方程 00()y y p x x =+ 00()y y p x x =-+ 00()x x p y y =+ 00()x x p y y =-+一. 直线与抛物线的位置关系 二. 直线,抛物线,三. ,消y 得:四. (1)当k=0时,直线l 与抛物线的对称轴平行,有一个交点; 五. (2)当k ≠0时,Δ>0,直线l 与抛物线相交,两个不同交点; Δ=0, 直线l 与抛物线相切,一个切点; Δ<0,直线l 与抛物线相离,无公共点。
(3)若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?(不一定)ox ()22,B x yFy ()11,A x y六. 关于直线与抛物线的位置关系问题常用处理方法 直线l :b kx y += 抛物线,)0( p① 联立方程法:⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k 设交点坐标为),(11y x A ,),(22y x B ,则有0 ∆,以及2121,x x x x +,还可进一步求出bx x k b kx b kx y y 2)(212121++=+++=+,2212122121)())((b x x kb x x k b kx b kx y y +++=++=在涉及弦长,中点,对称,面积等问题时,常用此法,比如 1. 相交弦AB 的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21 b. 中点),(00y x M , 2210x x x +=, 2210y y y += ② 点差法:设交点坐标为),(11y x A ,),(22y x B ,代入抛物线方程,得1212px y = 2222px y =将两式相减,可得)(2))((212121x x p y y y y -=+-2121212y y px x y y +=--a. 在涉及斜率问题时,212y y pk AB +=b. 在涉及中点轨迹问题时,设线段AB 的中点为),(00y x M ,021*******y py p y y p x x y y ==+=--, 即0y pk AB =,同理,对于抛物线)0(22≠=p py x ,若直线l 与抛物线相交于B A 、两点,点),(00y x M 是弦AB 的中点,则有px p x p x x k AB 0021222==+=(注意能用这个公式的条件:1)直线与抛物线有两个不同的交点,2)直线的斜率存在,且不等于零)。
抛物线知识点公式大全

抛物线知识点公式大全
1.抛物线方程。
抛物线的一般方程为y=a某²+b某+c,a、b、c为常数。
2.抛物线定义。
现行定义:抛物线是到一个定点和一条给定直线距离相等的点的轨迹。
3.焦点公式。
焦点公式为F(a,b),其中a是抛物线顶点的横坐标,b是焦距的
一半。
4.焦距公式。
焦距公式为f=1/(4a),其中a是抛物线的参数。
5.曲率公式。
在抛物线上任一点(某,y),曲率公式为y''/(1+y'²)³/²,其中
y'和y''分别为y关于某的一阶导数和二阶导数。
6.垂心公式。
抛物线的垂心公式为H(a,b/2),焦点到准线的距离等于抛物线的
参数的一半。
7.切线方程。
对于抛物线,其切线方程为y-y₀=2a(某-某₀)或y=m某+n,其中m是
斜率,n是截距。
8.弧长公式。
对于抛物线的一部分,其弧长公式为∫√(1+y'²)d某,其中y'是函数的一阶导数。
9.面积公式。
对于抛物线围成的区域,其面积公式为y(2a某-某²)/2。
10.对称轴公式。
对于抛物线,其对称轴公式为某=a/2。
抛物线顶点到准线的距离公式

抛物线顶点到准线的距离公式
抛物线方程为:y^2=2px,焦点坐标为(p/2,0)
准线方程为x=-p/2,
故抛物线焦点到准线的距离为p/2-(-p/2)=p
或:
设抛物线是y^2=2px
则准线是x=-p/2
抛物线上一点是(x0,y0)
则距离=|x0+p/2|
扩展资料:
定义域:对于抛物线y1=2px,p>0时,定义域为x≥0,p<0时,定义域为x≤0;对于抛物线x1=2py,定义域为R。
值域:对于抛物线y1=2px,值域为R,对于抛物线x1=2py,p>0时,值域为y≥0,p<0时,值域为y≤0。
设抛物线上一点P的切线与准线相交于Q,F是抛物线的焦点,则PF⊥QF。
且过P作PA 垂直于准线,垂足为A,那么PQ平分∠APF。
过抛物线上一点P作准线的垂线PA,则∠APF的平分线与抛物线切于P。
〈为性质(1)第二部分的逆定理〉从这条性质可以得出过抛物线上一点P作抛物线的切线的尺规作图方法。
准线方程的公式

准线方程的公式准线方程是圆锥曲线中的一个重要概念,它在数学中有着广泛的应用。
咱们先来说说抛物线吧,对于抛物线 y² = 2px (p>0),它的准线方程是 x = -p/2 。
那这个公式到底咋来的呢?其实呀,就像是解开一个神秘的谜题。
记得我之前给学生讲这个知识点的时候,有个学生特别可爱。
那是一个阳光明媚的下午,教室里有点闷热,大家都有点昏昏欲睡。
我正在黑板上写下抛物线的准线方程,这时这个学生突然举起手,皱着眉头问我:“老师,这准线方程到底是咋想出来的呀,感觉好抽象。
”我一听,心里暗喜,这孩子能问出这个问题,说明他在认真思考。
我就走到他身边,拿起一支笔当作抛物线的对称轴,然后以桌面为x 轴,在空中比划着说:“你看啊,抛物线的定义是到定点 F 的距离等于到定直线 l 的距离的点的轨迹。
那对于抛物线 y² = 2px ,这个定点 F 就是(p/2,0),定直线 l 就是 x = -p/2 。
假设抛物线上有一个点(x,y),那根据定义,这个点到焦点的距离就等于它到准线的距离。
”我一边说一边在纸上写着公式,这个学生眼睛紧紧盯着我的笔,慢慢地,他的眉头舒展开了,露出了恍然大悟的表情,大声说:“老师,我懂啦!”那一刻,我心里特别有成就感。
再来说说椭圆,对于椭圆 x²/a² + y²/b² = 1 (a>b>0),它的准线方程是 x = ±a²/c (c = √(a² - b²) )。
双曲线也有准线方程,对于双曲线 x²/a² - y²/b² = 1 ,它的准线方程是 x = ±a²/c (c = √(a² + b²) )。
学习准线方程的时候,可别死记硬背,得理解它背后的原理。
多做几道题,多琢磨琢磨,你就会发现其中的乐趣。
比如说,在做一道关于抛物线的题目时,告诉你抛物线的方程和一个点的坐标,让你求这个点到准线的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛物线上的点到准线的公式
抛物线是我们经常在日常生活中见到的一种曲线,它具有很多特点。
其中,抛物线上的点到准线的公式是一个非常重要的概念。
首先,我们来了解一下什么是抛物线。
抛物线是一种二次曲线,
它的特点是与一个固定点(称为焦点)的距离与一条直线(称为准线)的距离相等。
这个固定点和直线也是抛物线的两个重要元素。
对于抛物线上的任意一点,它到准线的距离与它到焦点的距离有
一定的关系。
这个关系可以用抛物线上点的坐标以及焦点和准线的位
置公式来表示。
具体来说,对于一个一般式的抛物线y = ax² + bx + c,其中a
不等于0,它的焦点坐标为(0,1/4a),准线的方程为y = -1/4a。
则抛物线上一点P(x,y)到准线的距离为:
d=|y + 1/4a|
这个公式可以用来求解抛物线上任意一点到准线的距离。
我们可以举一个具体的例子来说明这个公式的应用。
比如,我们
考虑一个经典的抛物线问题:一个小球从高度为h的位置抛出,落地
时的位置距离投掷点为d。
假设空气阻力可以忽略不计,抛物线与地面平行。
则小球到达地面时的速度为:
v²=2g(h-d)
其中,g是重力加速度,v是速度。
根据这个公式,我们可以计算出小球到达地面时的速度。
然后,我们可以使用抛物线上点到准线的公式,计算小球飞行过程中离地距离最远的点到准线的距离,从而得到小球的最远飞行距离。
这个例子说明了抛物线上点到准线的公式的实际应用价值。
通过这个公式,我们可以解决很多关于抛物线的实际问题,从物理学到工程学、建筑学等各个领域。
总之,抛物线上点到准线的公式是抛物线的重要性质之一,具有很广泛的应用价值。
掌握这个公式可以帮助我们更好地理解抛物线的性质,并解决很多实际问题。
