基于力学分析的主轴轴系结构优化设计
基于机械动力学的传动轴系统优化设计

基于机械动力学的传动轴系统优化设计随着工业技术的不断发展,机械传动系统在各个领域起着至关重要的作用。
而传动轴系统作为机械传动的重要组成部分,其设计与优化对于传动效率、精度和可靠性有着重要影响。
本文将基于机械动力学的理论,探讨传动轴系统的优化设计方法。
一、传动轴系统的基本原理传动轴系统是用于传递功率和运动的一种机械装置。
其主要由轴、轴承、齿轮或皮带等组成。
传动轴系统能够传递旋转运动和扭矩,并将其传递到其他机械装置上。
在传动轴系统中,涉及到的机械动力学知识主要有力矩传递、转速计算、转矩计算等。
力矩传递是指在轴上施加的力矩通过轴承传递到其他部件,而转速和转矩之间的关系可以通过动力学方程进行计算。
在设计传动轴系统时,需要考虑到传动效率和传动精度等因素。
二、传动轴系统的优化设计方法1. 材料选择传动轴系统的材料选择是优化设计的第一步。
常见的材料有钢、铝、钛等。
不同的材料有着不同的强度和韧性特性,需要根据具体的工作条件选择适合的材料。
2. 尺寸设计尺寸设计是保证传动轴系统正常工作的关键。
在设计传动轴系统时,需要根据所需的扭矩和转速等参数,计算轴的直径和长度等尺寸。
同时,还需要考虑到传动轴的刚度和挠度等因素。
3. 轴承选择轴承在传动轴系统中起着支撑和导向作用。
在优化设计中,需要选择合适的轴承类型、尺寸和材料等。
同时,还需要进行轴承的润滑和密封等设计,以保证传动轴系统的正常工作。
4. 传动方式选择传动轴系统的传动方式有多种,如齿轮传动、皮带传动等。
在进行优化设计时,需要根据实际应用需求选择合适的传动方式。
不同的传动方式有着不同的传动效率和精度,需要根据具体情况进行选择。
5. 动力学要求在进行传动轴系统的优化设计时,需要根据具体应用要求考虑动力学要求。
比如,传动轴系统在高速运转时需要考虑离心力对轴的影响,同时还需要考虑传动带来的振动等。
三、案例分析为了更好地理解基于机械动力学的传动轴系统优化设计,我们以某机械设备的传动轴系统设计为例进行分析。
机械工程中的轴的设计与优化

机械工程中的轴的设计与优化在机械工程中,轴是一种常见且重要的零件,它承载着传动力和扭矩,将动力从一个地方传递到另一个地方。
轴的设计与优化对于机械系统的性能和可靠性至关重要。
本文将探讨轴的设计原则、材料选择以及优化方法。
一、轴的设计原则在设计轴时,有几个原则需要遵循。
首先是强度原则,轴必须足够强以承受所施加的载荷。
这可以通过计算所需的最大弯曲应力和剪切应力来确定轴的尺寸和形状。
其次是刚度原则,轴必须具有足够的刚度以保持传动系统的准确性和稳定性。
刚度可以通过增加轴的直径或改变轴的截面形状来提高。
最后是轻量化原则,轴应该尽可能轻量化,以减少系统的惯性负载和能耗。
二、轴的材料选择轴的材料选择是轴设计的重要一环。
常见的轴材料包括钢、铝合金和钛合金。
钢是最常用的轴材料,因为它具有良好的强度、刚度和耐磨性。
铝合金轴适用于重量要求较低的应用,它具有较低的密度和良好的耐腐蚀性。
钛合金轴则具有极高的强度和轻量化特性,但成本较高。
在选择轴材料时,需要考虑载荷、工作环境和成本等因素。
三、轴的优化方法轴的优化方法可以分为几个方面。
首先是几何形状的优化,通过改变轴的截面形状和尺寸,可以提高轴的强度和刚度。
例如,采用变径轴设计可以在轴的不同部位提供不同的强度和刚度。
其次是材料的优化,通过选择合适的材料和热处理工艺,可以提高轴的强度和耐磨性。
例如,采用表面渗碳处理可以增加轴的硬度和耐磨性。
最后是结构的优化,通过改变轴的结构形式,如中空轴、薄壁轴等,可以实现轻量化和刚度的平衡。
除了上述的设计原则和优化方法,还有一些其他的注意事项需要考虑。
例如,轴的表面质量和光洁度对于传动系统的性能和寿命有重要影响。
因此,在加工和装配过程中,需要注意轴的表面处理和润滑。
此外,轴的安装和对中也是轴设计中的重要环节,合理的轴承选择和安装方法可以减少轴和轴承的磨损和故障。
综上所述,轴的设计与优化在机械工程中具有重要意义。
合理的轴设计可以提高机械系统的性能和可靠性,同时满足轻量化和刚度的要求。
风电主轴轴承试验机悬臂梁静力学分析与结构优化设计

设计与分析◆Sheji yu Fenxi
风电主轴轴承试验机悬臂梁静力学分析与结构优化设计
黄 伟1 孙乐乐2 丁建峰3
(1.洛阳LYC轴承有限公司,河南 洛阳 471000;2.华中科技大学,湖北 武汉 430074;3.一拖(洛阳)铸锻有限公司,河南 洛阳 471004)
摘 要:集成应用Solidworks三维软件和Ansys有限元分析软件,建立了风电主轴轴承试验机悬臂梁的三维模型和静力学分析模 型,通过有限元计算得到了悬臂梁在试验加载力作用下的变形、应力和应变分布,根据相应分析结果提出了机构优化方案,改善了该悬 臂梁的静态力学性能,为保证轴承运行的稳定性提供了技术手段支持。
关键词:主轴承悬臂梁;静力学分析;变形量;优化设计
0 引言
在风力发电机组中,主传动链中的主轴承支撑主轴,并通 过 轴 承 座 将 风 轮 作 用 力 传 递 给 机 架 [1]。它 的 性 能 直 接 影 响 整 机的抗振性和寿命。大型风力发电机组的主轴承受力状况复 杂,主轴承的试验通过主轴承试验机开展。
由上述分析可知,在满足使用要求的情况下,有必要对悬 臂梁进行相应的结构优化设计,在接口条件不变的情况下,优 化措施如下:(1)对悬臂梁中心孔处采取通孔处理,直径大小 采用原来最左端腔处的直径;(2)对悬臂梁固定端接触陪试轴 承这一侧的圆环,外径不变,内径减小,使圆环加厚。优化后的 结构如图7所示。
图7 优化后的悬臂梁三维剖面图 在加载力不变的情况下,将修改后的模型导入到Ansys中 进行静力分析,结果如图8所示,可知总体最大变形为90.8 滋m。 如图9所示,应力最大为0.525×108 Pa,即52.5 MPa。 结构优化前后的参数对比如表1所示。 由表1中的数据可知:(1)在重量减少的情况下,与测试轴
主轴系统仿真分析及优化设计

H03水平定向钻机主轴系统仿真分析报告编制:2014年02月26日1、分析目的:系统由主轴、浮动主轴、变径轴、短节组成,在工作时承受回转力矩40000N*M、以及回拖力900KN,在动态工况下为拉扭复合载荷,同时还有来自整机的随机振动。
因此,需要分析系统在拉扭预定载荷条件下的力学分析和模态分析,研究系统的变形、应力、应变、安全系数、固有频率等规律,为系统的优化设计提供理论依据。
2、分析方法:按照系统的工程图,在ansys12.0的workbench 界面中建立系统的三维模型。
同时对主轴、浮动主轴、变径轴、短节单独画分网格,网格总数为60万个。
约束方式为:浮动轴左端固定,右端施加900000N回拖力;主轴轴承位固定约束,同时在花键侧面施加330000N等效回转力。
分别求解系统的力学分析和模态分析。
后处理:利用云图显示系统的总变形、总应变、总应力分布、安全系数分布、和固有频率及各阶振型。
3、参数设置:主要分析系统在不同材料下的仿真对比(45#、40Cr、20CrMnTi),其中:45#的弹性模量为216GP,泊松比为0.28;40Cr的弹性模量为206GP,泊松比为0.3;20CrMnTi弹性模量为207GP,泊松比为0.25。
4、具体分析过程如下:(1)、45号钢分析结果:图1 变形云图图2 应变云图图3 应力云图图4 安全系数云图提示:A、从图1可以看出系统在拉扭复合载荷作用下最大的变形位于短节端部,约为0.47mm.B、从图2可以看出系统在拉扭复合载荷作用下危险截面位于短节端部和主轴矩形花键部位。
C、从图3可以看出系统在拉扭复合载荷作用下危险截面应力约为300MP。
D、从图4可以看出系统在拉扭复合载荷作用下,最小的安全系数是 1.0,短节端部和主轴矩形花键部在设计时需要重点考虑!(2)、40Cr分析结果:图1 变形云图图2 应变云图图3 应力云图图4 安全系数云图提示:A、从图1可以看出系统在拉扭复合载荷作用下最大的变形位于短节端部,约为0.45mm.B、从图2可以看出系统在拉扭复合载荷作用下危险截面位于短节端部和主轴矩形花键部位。
机床主轴结构的优化

3.约束条件 刚度约束
主轴的刚度是一个重要性能指标,其外伸端
挠度y,不得超过规定值 y0,即:
y [y]
若外力F已知,则有 y Fa2L 3EI
其中:I (D4 d 4 ) / 64;E 为材料的弹性模量。
将以上两式代入到 g (x1)中得
g1 ( x)
y
[ y]
Fa 2 L 3EI
700
650
600
扭转角约束曲 挠度约束曲线
线
550
L
500
450
400
可行域
350
300
250
45
50
55
60
65
70
75
80
85
D
1.设计变量
当主轴材料一旦选定,其重量只是内径 d 、 外径 D 、跨距 L,d 的大小又决定于机床的型 号,不能作为设计变,故设计变量取为:
x x1 x2 T [ D L]T
建立模型:
2. 目标函数
根据设计要求,以自重最轻为设计目标,即:
f
(x)
1 4
x2
( x12
d
2
)
建立模型:
建立模型:
机床主轴一般为多支撑空心阶梯轴,为了便于使用 材料力学公式进行结构分,将其简化成的以当量直径表 示的等截面轴,并且为两支撑主轴形式,如下图所示。
该问题考虑因数:主轴自 重。
对于普通车床,并不 要求过高的加工精度,已 选取主轴的自重最轻为目 A 标,外伸端的挠度为约束 条件。
B
C
建立模型:
问题解决:
设计变量
x1
x2
机械工程中滚动轴承的动力学分析与优化设计

机械工程中滚动轴承的动力学分析与优化设计引言:滚动轴承在机械工程中扮演着重要的角色,广泛应用于各个领域,如汽车工业、飞机制造和工业设备等。
滚动轴承的性能对于机械设备的运行稳定性和效率具有重要影响。
本文将针对滚动轴承的动力学分析与优化设计展开讨论。
1. 滚动轴承的工作原理滚动轴承通过滚珠或滚柱在内外圈之间滚动,从而减小了摩擦和阻力,使机械设备的转动更为平稳。
滚动轴承的工作原理基于滚动接触而不是滑动摩擦,因此具有更低的摩擦损失和更高的效率。
2. 滚动轴承的动力学分析方法在滚动轴承的设计与分析过程中,动力学分析方法是至关重要的。
其中一种常用的方法是基于有限元分析,通过建立轴承的数学模型,分析其在不同工况下的应力和变形情况。
另外,还可以采用实验验证的方法,使用测试设备对滚动轴承进行动态载荷测试,以获取其在实际工作中的性能参数。
这些参数可以用于验证数值分析结果和评估轴承的可靠性。
3. 滚动轴承的优化设计滚动轴承的优化设计旨在提高其性能和寿命。
一种常见的优化方法是通过优化轴承结构和减小摩擦损失来提高轴承的效率。
在轴承结构优化方面,可以通过优化内、外圈的几何形状、滚珠或滚柱的数量和分布等参数来提高轴承的刚度和承载能力。
同时,减小摩擦损失也是提高轴承效率的关键。
例如,可以采用更好的润滑方式、改进润滑油的性能以及优化轴承材料的表面处理等方法来减小轴承的摩擦损失。
4. 滚动轴承的故障分析与预测在机械设备运行过程中,轴承故障是一个常见的问题,会导致设备停机和生产损失。
因此,进行轴承故障分析和预测具有重要意义。
通过对轴承运行状态的监测和振动信号的分析,可以判断轴承是否存在异常,并提前采取维护措施。
此外,还可以使用有限元分析和数值模拟方法,模拟轴承在不同故障模式下的动态响应,为故障诊断提供依据。
5. 结论滚动轴承在机械工程中具有重要地位,其动力学分析与优化设计对于提高机械设备的性能和可靠性起着关键作用。
通过动力学分析方法可以得到滚动轴承在不同工况下的应力和变形情况,为轴承结构的优化设计提供依据。
力学结构分析与优化设计方法研究进展

力学结构分析与优化设计方法研究进展近年来,力学结构分析与优化设计方法在工程领域得到了广泛的应用与研究。
力学结构分析是指对工程结构的力学性能进行计算和分析,而优化设计方法则是通过数学模型和算法,寻求最优结构设计方案。
本文将从力学结构分析和优化设计方法的研究进展两个方面进行探讨。
一、力学结构分析的研究进展力学结构分析是工程领域中不可或缺的一部分,它可以帮助工程师预测和评估结构的强度、稳定性、振动特性等。
近年来,随着计算机技术的不断发展和数值计算方法的成熟,力学结构分析的研究也取得了长足的进展。
1.1 有限元方法有限元方法是目前应用最广泛的力学结构分析方法之一。
它将结构分割成有限个小单元,通过建立数学模型和求解有限元方程,得到结构的应力、应变、位移等信息。
有限元方法具有计算精度高、适用范围广等优点,已成功应用于建筑、航空航天、汽车等各个领域。
1.2 多尺度分析方法随着微纳米科技的快速发展,越来越多的结构尺寸达到了微米甚至纳米级别。
针对这种情况,传统的宏观力学模型已经不再适用,因此出现了多尺度分析方法。
多尺度分析方法将结构分为宏观尺度和微观尺度,通过宏观尺度和微观尺度之间的耦合关系,实现对微纳米结构的力学性能分析。
1.3 结构优化方法结构优化是力学结构分析的重要研究内容之一。
通过优化算法和数学模型,寻求结构的最优设计方案。
结构优化方法可以分为拓扑优化、形状优化、尺寸优化等。
这些方法可以帮助工程师在满足设计要求的前提下,减轻结构重量、提高结构刚度等。
二、优化设计方法的研究进展优化设计方法是力学结构分析的重要组成部分,它旨在通过数学模型和算法,寻求最优的结构设计方案。
近年来,随着计算机技术和优化算法的不断发展,优化设计方法也取得了重要的研究进展。
2.1 遗传算法遗传算法是一种模拟生物进化过程的优化算法,它通过模拟遗传、交叉和变异等过程,寻找最优解。
遗传算法具有全局搜索能力强、适应性好等优点,已经广泛应用于结构优化设计中。
4-主轴结构参数优化设计

d )
4
64
4
a
g1( X ) y0
64 Fx 3 ( x 1 x 3 )
2
3 E ( x 2 d )
4 4
0
应当指出,由于对机床主轴有较高的刚度 要求,当满足刚度要求的情况下,其强度 应该有相当的富裕。因此,不需要再提出 主轴强度条件的约束条件。 2、设计变量的边界条件 三个设计变量的边界约束条件为
机床主轴 力学模型
x1 l X x2 D x3 a
一、设计变量和目标函数 与主轴重量设计方案有关设计变量包括主轴 的外径 D 、孔径 d 、两支承跨度 l 和外伸段 长度 a。由于机床主轴的孔径d 主要取决于待 加工棒料的直径,不能作为设计变量处理。
0
解:1、建立优化设计的数学模型
f ( X ) 0 . 785398163
T
( x 1 x 3 )( x 2 d )
2 2
T
X x 1 , x 2 , x 3 l , D , a
g 1 ( X ) 1 97 . 00872722
x 3 ( x1 x 3 )
可见,这是一个3维有5个不等式约束的非线性优化设 计问题。
2、优化方法与结果 采用内点惩罚函数法求解,初始惩罚因子 r (1 ) 2 , 惩罚因子递减系数 e 0 . 2 ,收敛精度 10 。 按照题目给定的设计变量边界条件,取可行域内 的初始点 X 480 ,100 ,120 ,经过17次迭代计算, 得到最优解 T * * * * T X x 1 , x 2 , x 3 300 . 036 , 75 . 244 , 90 . 001
机械工程中心轴承的优化设计方法研究

机械工程中心轴承的优化设计方法研究引言中心轴承是机械设备中不可或缺的关键部件之一,其性能优劣直接影响整个机器的可靠性和效率。
优化设计方法的研究是提高中心轴承性能的关键,本文将介绍一些常用的优化设计方法,以及它们在机械工程中心轴承中的应用。
一、有限元分析优化设计方法有限元分析方法(Finite Element Analysis,FEA)是一种常用的工程分析技术,通过将复杂结构分解为无限小的单元,进行力学参数模拟和计算,得出结构的应力、应变等性能指标。
在中心轴承的优化设计中,有限元分析方法可以用于模拟和分析轴承在不同工况下的受力情况,进而通过调整材料、几何形状等参数,实现优化设计。
二、遗传算法优化设计方法遗传算法是一种模拟自然界遗传和进化原理的计算方法,通过模拟基因的交叉、变异等操作,搜索最优解。
在中心轴承的优化设计中,遗传算法可以应用于寻找最佳的结构参数组合,以达到最优的性能指标。
例如,可以通过遗传算法优化设计中心轴承的材料组成、几何形状等参数,来实现轴承的性能最大化。
三、响应面优化设计方法响应面优化方法是一种利用数学拟合模型来寻找最佳参数设计的方法。
在中心轴承的优化设计中,响应面方法可以通过拟合实验数据,建立参数和性能指标之间的关系模型,从而进行优化设计。
例如,可以通过响应面方法建立中心轴承的载荷能力和几何参数之间的数学模型,以获得最优的设计参数。
四、多目标优化设计方法传统的中心轴承优化设计方法通常只考虑单一的性能指标,而多目标优化方法则可以同时考虑多个性能指标,从而得到更为综合和全面的设计方案。
在中心轴承设计中,可以将多目标优化方法应用于同时优化轴承的载荷能力、摩擦损失、噪音等性能指标。
通过设置权重、约束等条件,可以得到一系列不同的设计方案,供工程师选择。
总结中心轴承的优化设计方法是提高其性能的关键。
本文介绍了一些常用的优化设计方法,包括有限元分析、遗传算法、响应面和多目标优化方法。
这些方法在实际工程中的应用将进一步提高中心轴承的可靠性、寿命和效率。
水轮机主轴的有限元分析及优化设计

即 可 得 应 变 矩阵
。。 ‘
。
单 元 内的 应 力为
丁。
二
〔 〕 二 〔
‘ ,
,
式中,Biblioteka 〔拼一一
拼
而
对称
了 了
拜
一
一
拼
一
对
拼
一
称
拼
了 、
〕
…
拼
件
一
厂
「
一
拼
拼
和 亡 」
为
的零矩阵
〕
’
单 元 刚 度 矩阵 可 由虚 功 原 理 导 得
拼
。 〔
二
・
仁
,
〕 且 仁
‘
“
二
〕 , ‘“ ”
・
注意到
丁
“
‘。
二
,
增
方 巧 媛等
水 轮 机 主 轴 的 有 限 元 分 析 及 优 化设 计
优化方法
由于强度约束 毛 司 为 隐式
。
,
为 了保 证 可 靠 性 和 计 算 精 度
,
,
,
拟 采 用复合形 法
其主
要 思路为
设 设 计 空间为 一个 且 毛 气
。
维空间
则 在 该 空 间 内选 取 复 合 形 多面 体
则有
、〕 一
丁丁
・ 。 〕仁 〕 。 仁
载 荷 移皿 轴 向节 点 载 荷
所做 的功 为
‘
在图
中
,
令单元 的
边 上 有 一 向上 的 虚 位 移 。
,
则均 布载 荷
左
,
一
,
兀
机床主轴结构优化设计(温正方)
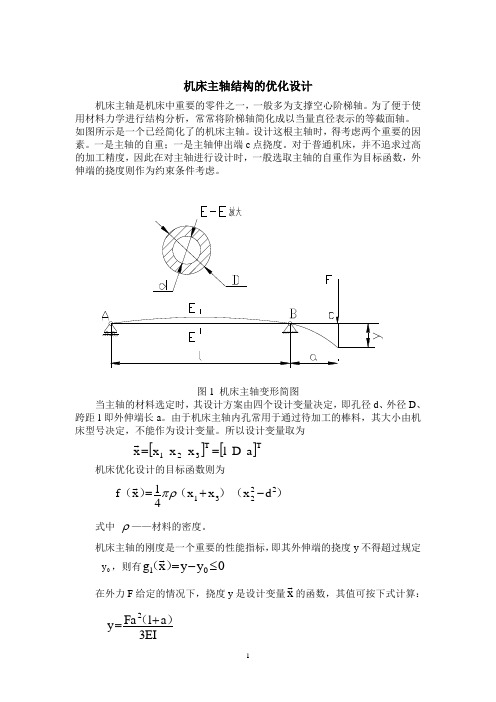
机床主轴结构的优化设计机床主轴是机床中重要的零件之一,一般多为支撑空心阶梯轴。
为了便于使用材料力学进行结构分析,常常将阶梯轴简化成以当量直径表示的等截面轴。
如图所示是一个已经简化了的机床主轴。
设计这根主轴时,得考虑两个重要的因素。
一是主轴的自重;一是主轴伸出端c 点挠度。
对于普通机床,并不追求过高的加工精度,因此在对主轴进行设计时,一般选取主轴的自重作为目标函数,外伸端的挠度则作为约束条件考虑。
图1 机床主轴变形简图当主轴的材料选定时,其设计方案由四个设计变量决定,即孔径d 、外径D 、跨距l 即外伸端长a 。
由于机床主轴内孔常用于通过待加工的棒料,其大小由机床型号决定,不能作为设计变量。
所以设计变量取为[][]T T 321a D l x x x x ==机床优化设计的目标函数则为))(()(22231d x x x 41x f -+=πρ 式中 ρ——材料的密度。
机床主轴的刚度是一个重要的性能指标,即其外伸端的挠度y 不得超过规定0y ,则有0y y x g 01≤-=)( 在外力F 给定的情况下,挠度y 是设计变量x的函数,其值可按下式计算:EI3a l Fa y 2)(+=式中)(44d -D 64I π= 则0y d x E 3x x Fx 64x g 044231231≤--+=)()()(π 此外,通常还应考虑主轴内最大应力不得超过许用应力。
由于机床主轴对刚度要求比较高,当刚度满足要求时,强度尚有相当富裕,因此应力条件约束可以不考虑。
另外,根据设计变量的取值范围有max min l l l ≤≤max min D D D ≤≤max min a a a ≤≤综上所述,可将主轴设计的数学模型表示如下:221321min f x x x x d 4πρ+-()=()() (g ) s.t.2313104422min 132max 4min 252max 6min 373max 64Fx x x g x y 03E x d g x l x 0g x x -l 0g x D x 0g x x -D 0g x a -x 0g x x -a 0π+=-≤-≤≤≤≤≤≤()()()()=-()=()=-()=()=()=在这里做如下假定:取主轴材料选45钢,查得ρ=7.85g/cm3,E=206Gpa ,主轴内径d=300mm ,F=15000N ,许用挠度y 0=0.05mm ,设计变量的初值为x 1=480mm ,x 2=100mm ,x 3=120mm ,上下限为150x 90140x 60650x 300321≤≤≤≤≤≤,,。
基于可靠性分析的主轴优化设计

基于可靠性分析的主轴优化设计
周森# 何晓聪# 寸花英! 窦炜# 张晓龙#
昆明理工大学机电工程学院 云南昆明 ?$"$"" !9 沈机集团昆明机床股份有限公司 云南昆明 ?$"""" #9
摘要 基于 S; 8 _WN DM O 软件对加工中心主轴静刚度进行研究( 在静力学分析基础上& 以主轴质量为约束条件& 对主轴 进行了静刚度优化设计# 在考虑主轴尺寸' 载荷' 材料性能以及轴承刚度等参数随机分布的情况下& 利用概率统计的思想 对优化后的主轴进行了 C 可靠性分析( 结果表明& 优化后主轴刚度提升 #G9 B `C B J H 7 $m& 满足使用要求# 可靠性灵敏度分析 表明外载荷' 轴承刚度以及主轴外径的随机变化对主轴刚度影响较大# 优化后的主轴可ห้องสมุดไป่ตู้度达到 #""m& 安全可靠( 关键词 主轴# 静刚度# 优化# 可靠性分析
$ 1 5 . 2 ,. ! . ONC Q 7 Q B M C Q B X X DN C C ; X 7 H 7 M OB DB DJ M N DQ N 8 c C C [B DP< N K 7 C C Q YPB N P W7 C N P; D S; 8 _WN DM OC ; X Q K 7 8 N = . ON C Q 7 Q B M C Q B X X DN C C ; X Q ON C [B DP< NK 7 C ; [Q B H B o N P; DQ ONW7 C B C ; X C Q 7 Q B M C 7 D7 < Z C B C &K B Q OQ ON C [B DP< N IY7 < B Q Z 7 C M ; DC Q 8 7 B DQ M ; DPB Q B ; D= . ON C B ` C B J H 7 8 N < B 7 WB < B Q Z 7 D7 < Z C B C ; X Q ON; [Q B H B o N PC [B DP< NK 7 C M 7 8 8 B N P; YQ YC B DJQ ONB PN 7 C ; X [8 ; W7 WB < B Q Z7 DP C Q 7 Q B C Q B M C &K OB M OM ; DC B PN 8 N PQ ON8 7 DP; HPB C Q 8 B WYQ B ; D; X J N ; a H N Q 8 B M 7 < PB H N DC B ; DC &N ` Q N 8 D7 < < ; 7 PC &H 7 Q N 8 B 7 < M O7 8 7 M Q N 8 B C Q B M C 7 DP WN 7 8 B DJ C Q B X X DN C C = . ON 8 N C Y< Q C C O; KQ O7 Q Q ON C [B DP< N C Q B X X DN C C M ; Y< PC 7 Q a B C X ZQ ONYC B DJ8 N IYB 8 N H N DQ 7 DP B Q C C Q B X X DN C C B DM 8 N 7 C N P WZ #G9 $m 7 X Q N 8 ; [Q B H B o 7 Q B ; D= 4 N < B 7 WB < B Q Z C N DC B Q B ] B Q Z 7 D7 < Z C B C C O; K N Q O7 Q Q ON 8 7 DP; H ] 7 8 B 7 Q B ; D; X N ` Q N 8 D7 < < ; 7 PC & WN 7 8 B DJ C Q B X X DN C C 7 DP Q ON C [B DP< N PB 7 H N Q N 8 O7 C 7 J 8 N 7 Q B DX < YN DM N ; DQ ON C [B DP< N C Q B X X DN C C = . ON C [B DP< N B C C 7 X N 7 DP 8 N < B 7 W< N7 X Q N 8 ; [Q B H B o 7 Q B ; DK B Q OB Q C C Q B X X DN C C 8 N < B 7 WB < B Q ZB C #""m= @ ) ?A 32 : 5 ! 6[B DP< N # 6Q 7 Q B MC Q B X X DN C C #/ [Q B H B o 7 Q B ; D# 4 N < B 7 WB < B Q Z7 D7 < Z C B C
机床主轴结构的优化课件

软件三
软件介绍:Altair OptiStruct是一款专业的结构优化 软件,基于有限元方法进行结构分析和优化设计。它 广泛应用于汽车、航空航天、机械等领域,为产品设 计提供全面的性能分析和优化建议。
Altair OptiStruct具有强大的建模功能和高效的优化 算法,可以快速建立复杂的三维模型并进行精细的网 格划分。同时,它拥有丰富的材料库和约束条件设置 功能,可以根据实际工况模拟各种复杂的物理场。通 过后处理功能,用户可以直观地查看分析结果并进行 优化设计。此外,它还提供了多种优化策略和算法, 如拓扑优化、形状优化、尺寸优化等,可以帮助用户 快速找到最优设计方案。
CHAPTER 02
机床主轴结构优化设计
优化设计理论与方法
传统优化设计方法
包括数学规划法、拉格朗日乘子法、罚函数法 等,用于求解约束条件下目标函数的最优解。
智能优化设计方法
如遗传算法、粒子群算法、蚁群算法等,利用 生物或自然界的规律进行优化搜索。
多目标优化设计方法
处理多个相互冲突的目标函数,寻求整体最优解。
CHAPTER 04
机床主轴结构优化软件介绍 及使用教程
软件一:ANSYS有限元分析软件
软件介绍:ANSYS是一款全球领先的有限元分析软件 ,广泛应用于机械、电子、土木等领域。它能够进行 结构、流体、电磁等多种物理场的模拟,为产品设计 提供全面的性能分析和优化建议。
ANSYS有限元分析软件具有强大的建模功能和灵活的 网格划分工具,可以快速建立复杂的三维模型并进行 精细的网格划分。同时,它拥有丰富的材料库和边界 条件设置功能,可以根据实际工况模拟各种复杂的物 理场。通过后处理功能,用户可以直观地查看分析结 果并进行优化设计。
基于DOE法的主轴系统的优化设计

}大圆角半径或者凸台厚度 ,能有效地减少应力集 中;且 圆角半径对最大应力影响较大,圆角半径从 l0 m . m增大到 2 m, 5 a r 最大应力下降4 %, , ̄- 8 因此 ; _ 中应确保其加工精度。该方法对主轴零部件的设计 OY -
}加 工具有 一定 的指 导 意义。
l }
lbsdo eD E ( ei xeietipooe ; ema e t oe ibi n l dwt ii ae nt O D s no p r n) rpsdt t macm dls ulads v ,i mn- h g fE m s h h i t oe h }mzn emaiu rs beteadter isfru dcre n i ns o ovx lt d- i gt xm ms esa ojci n a u on onr dt c esfcne ae i h t s v h d o a hk p e
关键词 : 系统 ; 主轴 优化设计 ; 应力集中; 灵敏度分析 【 bt c】 oao reue h r s ocn ao e ehn a ds not i t n e o A s at T i o r c t se ne t tno t cai l ei , i z i t d r v d d e tsc ri nh m c g p m ao m h
第 1 O期 21 0 2年 l 0月
文章编 号 :0 1 3 9 ( 0 )0 0 7 — 2 10 — 9 7 2 1 1 — 0 9 0 2
机 械 设 计 与 制 造
Ma hi e y De in c n r sg & Ma u a t e n f cur 7 9
基 于 DO E法 的主轴 系统 的优 化 设 计 冰
基于弹性力学的机械结构优化设计方法研究

基于弹性力学的机械结构优化设计方法研究简介:在机械工程领域中,结构优化设计是一个重要的研究方向。
弹性力学作为机械结构优化设计的基础理论,通过对材料力学性能和结构拓扑的研究,可以为机械结构的设计提供科学依据。
本文将探讨基于弹性力学的机械结构优化设计方法的研究现状和发展前景。
弹性力学基础理论:弹性力学是研究物体在受力后恢复原状的力学学科。
其基本原理是材料在受力时会发生变形,但是当受力消失后,材料会恢复到原来的状态。
弹性力学的数学模型包括胡克定律和能量原理等。
在机械结构优化设计中,弹性力学的基本原理可以用于确定材料的受力情况和结构的形状变化。
结构拓扑优化设计方法:在机械结构的优化设计中,结构拓扑优化是一种重要的方法。
结构拓扑优化的目标是通过改变结构的连通性,使结构在给定载荷下具有最佳的性能。
该方法可以通过删除或添加材料来调整结构的形状,在满足一定约束条件下,使结构的性能最优化。
拓扑优化设计方法在减少结构重量、提高结构刚度和降低应力等方面具有广泛的应用。
材料的力学性能研究:在机械结构优化设计中,材料的力学性能是一个关键的研究方向。
通过对材料的力学特性进行研究,可以为结构优化设计提供基础。
在材料的力学性能研究中,常用的方法包括拉伸试验、压缩试验、弯曲试验和剪切试验等。
通过对材料试验结果的分析可以得到材料的弹性模量、屈服强度和断裂韧性等重要参数。
这些参数可以作为结构优化设计的输入,提高结构性能。
结构的优化设计实例:为了验证基于弹性力学的机械结构优化设计方法的有效性,我们将给出一个实际的例子。
假设我们要设计一种载荷作用下具有最小变形的机械结构。
我们可以使用有限元方法来模拟和分析该结构在载荷作用下的变形情况。
根据弹性力学的理论,我们可以通过调整结构的材料参数和几何形状,来减小结构的变形。
通过不断迭代计算和优化调整,我们可以得到最优的结构设计方案。
结论:基于弹性力学的机械结构优化设计方法是一个重要的研究领域。
通过对弹性力学理论、结构拓扑优化方法和材料力学性能的研究,可以为机械结构的设计提供科学依据。
基于DOE法的主轴系统的优化设计

基于DOE法的主轴系统的优化设计狄杰建;赵玉侠;张超英;刘峰斌【摘要】应力集中现象经常出现在结构的设计中,为有效的降低应力集中保证结构部件的力学性能与寿命,针对主轴结构提出了基于DOE的方法优化设计主轴部件,建立了以最大应力最小化为目标,倒圆角半径和凸台厚度为设计变量的优化模型并进行求解.结果表明,在工程许可条件下尽可能增大圆角半径或者凸台厚度,能有效地减少应力集中;且圆角半径对最大应力影响较大,圆角半径从0.5mm增大到2mm,最大应力下降48%,因此,加工中应确保其加工精度.该方法对主轴零部件的设计加工具有一定的指导意义.%To avoid or reduce the stress concentration on the mechanical design,optimization method based on the DOE (Design of Experiments proposed;the mathematic model is built and solved,with minimizing the maximum stress as objective and the radius of round corner and thickness of convex plate as design variahles.As the results show,stress concentration can be reduced by enlarging the patue of the round radius or the thickness of the convex plate,with the engineering requirements, and the effect of the radius on the maximum stress is much larger than that of the thickness of the convex plate, with the radius from 0.5mm to 2mm,atid the maximum stress is reduced by 48%.Thus the precision of the manufacturing of the round corner is more important.The presented method is applicable to the design and manufacturing of the components of the axis system.【期刊名称】《机械设计与制造》【年(卷),期】2012(000)010【总页数】2页(P79-80)【关键词】主轴系统;优化设计;应力集中;灵敏度分析【作者】狄杰建;赵玉侠;张超英;刘峰斌【作者单位】北方工业大学机电工程学院,北京100144;北方工业大学机电工程学院,北京100144;北方工业大学机电工程学院,北京100144;北方工业大学机电工程学院,北京100144【正文语种】中文【中图分类】TH12;TH161+.211 引言主轴是高速旋转的运动机构,是任何机械产品的关键零件,它的性能好坏直接决定了机械产品的优良。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图2 Z T 3 0 J 一 1 型镗床主 轴轴系 挠曲线 、剪 力和弯矩 图
图1 J 一 1 型镗床主轴轴系结构 图 Z T 3 0
0
主轴 支 承所使 用 的静 压 轴 承 采 用小 孔 节 流 方 式 ,
利用外部液压站供给压力油, 进入静压轴承周边 的油 腔, 以形 成承 载油 膜 , 由液压 油 的静 压 力 平 衡 外 载 荷 ,
点 , F R = , R = : F: P=G 经计 算 可 知 : 承力 尺 支
=
( + / ) R =( / ) 弯矩 M… = a 1 a 1 P, 2 a 1 P, P。
为 简化轴 系 变形 量 的计 算 , 略 主轴 的微 小 弯 曲 忽
如 图 4所 示 , G。 表示 主轴 自重 , :表示 电动 机 转 G:
1 问题 的来 源
本文 以现有 的 ZT 30型 和对 其 改 进 中 的 ZT J一 l J一
30 2 A型精密镗床主轴轴系结构为基础 , 根据主轴运行 过程 中的受力情况 , 分别转换成力学简图 , 并介入力学 分析 和计 算 , 出相 应 的关键 数 据 , 行 比较 , 得 进 以对 主
理 方式 和手 段 。
中问也 进行 了多次 小 的改 进 , 主要 围绕着 改 善 主 轴 驱 动 结构 和降低 温升进 行 , 动力 传 动从 最 初 的 V带 传 动 改 为多 楔带 传 动 , 后 改成 “ 电主 轴 ” , 接将 电 最 准 型 直 动机转 子安装 在 主轴 上 , 效 地 降低 了径 向 载荷 和 温 有
子 自重 , F, 表示 后静 压 轴 承 支承 力 , 示 前 静 压 轴 F 表 承支 承 反力 。根 据 图 中主 轴 的 受 力状 态 , 转 化成 轴 可 系 的挠 曲线 、 剪力 和弯 矩 图 , 图 2所 示 。其 中 : — 如 0 0
构, 导致主轴偏移的产生 , 降低 了主轴运转的稳定性和
运转精度。现在方案 的改进 , 在不考虑整个轴 系水平 偏移量的前提下 ( 这个水平偏移量对 主轴各项精度的 影响甚微 ) 主要存在 电动机转子 和主轴 自身重量使 ,
主轴 产 生 的变 形 。 3 2 力 学分析 和 计算 .
线代表主轴轴 心线 , 0 表示 前 、 0 、 后静 压轴 承支承
Ab t a t s r c :Ac o d n o t e r q ie n ft e ma h n n c u a y o h a ,u i g t e me h n c lt m7 a c r i g t h e u rme to h c i i g a c r c ft e p ns sn h c a ia he s a g i e,b sn n t e e itn c i e,ma i g s me me h n c la ay e n ac l t n n t e p e — ud a i g o h x si g ma h n k n o c a ia n l s s a d c lu a i s o h r s o s r n r ns tto tt s o p n l h fi g,a d c n ci g o tma e in t o,t e kng te u e a d ta mu ain sae fs i d e s atn n o du tn p i ld sg o h n ma i h sr t r fs i d e s atn r n r ainaia in,a d r d c n h ia a t g a tr n a - tucu e o p n l h i g mo e a d mo e r to lz to f n e u i g t e d s dv n a e f co s o f f ci g t e r t tra c r c ft p n l o s q e l e tn h oao c u a y o he s i d e c n e u nt y,S h c nig a c r c ft e ma h n o l O t e ma hi n c u a y o h c i e t o i mp o e ra l si r v d g e ty,a d p o i i g a k n fmeh d fri n r vd n i d o to o mpr vn n ef c ig t c n c lsr c o i g a d p re t he me ha ia t — n u t e,a h a i ur tt e s me t me,fl n he n e s o r d cn i l g t e d fp o u ig. i Ke wo ds:S i d e S fi y r p n l ha ng;Me h n c lAn l ss t c a ia ay i ;Op i lDe i n;Ma h n n c r c tma sg c i i g Ac u a y
图3 ZI 一 1 型镗 床主轴 轴系挠 曲线 简化 图 . 30 T
3 Z T 30 J - 2 A型镗床轴 系结构 方案分析
3 1 轴 系结构 方案 简述 .
该 方案 是 为 了进 一步 优化 主轴 轴 系 的受 力结 构而 实 施 的 。原 来 的 ZT 30型镗 床 电动 机 转 子 后 置 结 J一 1
代入 各个 已知 参 数 的实 际 数值 后 , 过 计 算 可 以 通 得 到主轴 的总偏移 量 A总= .2 m。 00 58m
需主轴转速通过变频器来调节。 D Pa Nhomakorabea 一
1 一电动机后盖; 、7 1 2 、1 一锁紧螺母 ; 一电机外壳; 一主轴; 一电动机 3 4 5 定子; 一电动机转子 ; 一推力轴承 ; 一后静压轴承 ; 0 后推力盘 ; 2 6 8 9 1- 1 前推力盘 ; 3 前静压轴承;1 -箱盖 ; 5 箱 体; 6 主轴箱前端盖。 1- 4 1- 1-
2 1 轴 系 结构简 述 .
2于是有 0 t [△ + /] , =a n ( △ ) 1。 所 以 △ △+ 1a t 0将 0 代人 , 得 : 总= △ =(+ ) n , 值 a 可
( +口 f ) -( +Ⅱ 2 )
该 型号 机床 主轴 轴 系 结 构 采 用前 、 后静 压 轴 承支 承, 主轴 驱 动通过将 三相 交 流 电动 机 转 子 直联 在 主轴 后端 实 现 ( 1 , 削不 同材 料 和 孔 径 尺 寸 的 工件 所 图 )镗
的市场。通过充分分析论证发现 , 结合力学理论 , 通过 实施 结构 优化 , 主轴 回转精 度还有 较 大的提 升空 间 。
・
7 ・ 6
脚 一 一i 舭 2上 0 i 卜
Dia eh ende r设计与研究 s n sC g Ra
2 Z T 3 0型 镗 床 轴 系结 构 分 析 J 一1
变形 , 留电动机转子 自重引起的主轴整体偏转量 , 保 将
图 2中 的挠 曲线 图 等 效 成 图 3所 示 的形 式 。其 中 , △ 为 转子 中心偏移 量 , 后静 压轴 承偏 移量 , △为 △ 为前 静
子 自重 , 表示后静压轴承支承力 , 表示前静压轴
承 支 承力 。在 方案设 计 时 , 过计 算 , 电动机转 子重 通 将
求为 002m 机床整体 的技术参数和精度指标 较 .0 m, 高 , 以, 所 上述变形 、 自重等不可控因素的轻微波动 , 都
会影 响机 床主轴 的回转精 度和加 精 度 。
ZT 3 0型 精 密 镗床 已成 功应 用 于 生 产 近 6年 , J一 1
点, 对主轴轴系进行优化和完善 , 不失为一种有效的处
的 实际需 求。
关 键词 : 主轴轴 系 力学分 析 优化 设计
中图分 类号 : H1 1 . T 6+5 文献标 识码 : A
加 工精度
T eo t h p i l e in o pn l h f n a e n t e me h nc l n lss ma sg f ide s at g b s d o h c a ia ay i d s i a
主轴是数控机床的核心和关键部件 , 因而主轴轴 系 结构 的优 劣 , 在很 大 程 度 上决 定 了数控 机 床 整 体 的 加工精度 、 运行稳定性和生产效率。对于精密机床 , 主 轴轴系结构的合理性显得更为突出 , 当今一些重要的 生 产加 工领 域 , 密加 工 已成 为发 展 趋 势 和重 要 内容 精
设计与研究 Dia eh en d s『 s ne C g R a
基 于 力学分 析 的主 轴 轴 系结 构 优 化设 计
王海涛 李初晔
( 京航 空制造 工程研 究所 , 京 10 2 ) 北 北 0 04 摘 要: 结合 工件加 工精 度要 求 , 以力学理 论为 指导 , 在现 有机床 的基 础上 , 主轴 轴 系的受 力和 变形状 态进 对 行力 学分析 和计 算 , 进行 了优化 设计 , 并 使轴 系结构 更趋 合理 化 。 而进 一步 降低 影 响主轴 回转 精度 从 的不 利 因素 。 机床 的J -精度得 到显 著提 高 , 使 jr n 为改进 和完善 机械 结构提 供 了一种 思路 , 足 了生产 满
之 一 。力学 是机械 设 计 的基 础 , 以力 学 分 析作 为 切 入
重等的影响, 都会导致主轴偏离 刚转 中心和 自身变形
的产 生 。 由于所 加工孔 的圆柱 度 不大 于 0 0 15Im, . 0 n
表 面粗 糙度 为 R 04I 而且 主轴 回转精 度 的设计 要 . m, x
心 和 主轴重 心 重合 , 于 分析 和 比较方 案 的合 理性 。 便
压轴承偏移量 , 为主轴偏转角度 , 需要求 出主轴总偏
移 量 , A =i△ , 即 Z+ : 以此 与改 进后 的方 案结 果 进 行相
