应力应变关系
应变和应力关系

应变和应力关系嘿,朋友们!咱今儿来聊聊应变和应力这对“好哥们儿”。
你想想啊,这应变就像是个爱调皮捣蛋的小孩子,遇到点情况就变来变去的。
比如说你拉一根橡皮筋,轻轻一拉,它就变长了,这就是它的应变呀。
而应力呢,就像是家长,时刻管着应变这个小家伙,可不能让它随便乱变。
咱生活中到处都能看到应变和应力的影子呢。
就好比你走在路上,不小心踩了个坑,脚就得变形来适应这个坑吧,这就是应变。
而你的身体为了保持平衡,肌肉和骨头就会产生应力来对抗这种变形。
要是没有应力,那你不就直接摔个大跟头啦!再比如说,建房子的时候,那钢材啊、砖块啊都得承受各种力。
要是没有足够的应力来对抗,这房子不就摇摇晃晃的,谁敢住进去呀!这就好像是一场拔河比赛,应变在一边拼命想把东西弄变形,而应力就在另一边紧紧拉住,不让它得逞。
你说这应变和应力是不是很有意思?它们俩就像是一对欢喜冤家,相互制约又相互依存。
没有应变,很多东西都没法变形适应环境;没有应力,那这世界还不得乱了套呀!咱再换个角度想想,人不也一样嘛!我们在生活中会遇到各种各样的困难和挑战,这就像是给我们施加了应力。
我们得像那些坚强的材料一样,产生足够的应力来应对这些应变,不能轻易就被困难给打败了。
有时候我们可能会觉得压力山大,就好像应力太大了,感觉自己都要被压垮了。
但咱可不能就这么轻易放弃呀!得像弹簧一样,压力越大,反弹的力量就越大。
等挺过了这一段,你就会发现自己变得更强大了。
而且呀,我们还得学会灵活应变。
就像水一样,遇到什么形状的容器就能变成什么形状。
不能太死板,要懂得根据不同的情况调整自己。
总之呢,应变和应力这俩家伙可真是无处不在,它们的关系可重要啦!我们得好好了解它们,利用它们,让我们的生活变得更加美好。
别小看了它们,它们可是能决定很多事情的呢!所以呀,我们在生活中要时刻留意应变和应力,让它们为我们服务,而不是让我们被它们牵着鼻子走。
你说是不是这个理儿?。
应力与应变间的关系

22
例题7-7 边长 a = 0.1m 的铜立方块, 无间隙地放入体积较
大, 变形可略去不计的钢凹槽中, 如图 所示。 已知铜的弹 性模量 E=100GPa, 泊松比 =0.34, 当受到P=300kN 的均布 压力作用时, 求该铜块的主应力. 体积应变以及最大剪应力。
P a
y
z
x
23
y
解:铜块上截面上的压应力为
9
3、 特例
(1)平面应力状态下(假设 Z = 0 )
x
1 E
(
x
y)
y
1 E
(
y
x)
z E ( x y)
xy
xy
G
10
(2) 广义胡克定律用主应力和主应变表示时 三向应力状态下:
1
1
E [ 1
(
2
3)]
2
1 E
[
2
(
3
1)]
3
1 E
[
3
( 1
2)]
(7-7-6)
11
平面应力状态下 设 3 = 0, 则
x y z x y y z z x
y
σy
上面
x y z x y y z z x
1、各向同性材料的广义胡克定律 (1)符号规定
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量:拉应力为正
σz
x
o
压应力为负。 z
前面
3
(b)三个剪应力分量: 若正面(外法线与坐标轴
dxdydz
dxdydz(1 1 2 3) dxdydz
dxdydz
应变和应力关系

新能源技术:利用应变和应力原理,优化风力发电机叶片设计,提高风能 利用率和发电效率。
机器人技术:通过研究应变和应力与机器人关节运动的关系,提高机器人 的灵活性和稳定性,拓展机器人的应用领域。
应变和应力对未来科技发展的影响
增强材料性能:通过深入研究应变和应力,可以开发出性能更强的新型材 料,为未来的科技发展提供物质基础。
智能制造:利用应变和应力的知识,可以优化制造过程中的材料性能,提 高生产效率和产品质量,推动智能制造的发展。
生物医学应用:在生物医学领域,应变和应力的研究有助于更好地理解和 控制人体生理机制,为未来的生物医学应用提供支持。
压痕法:利用压痕仪在物体表面压出一定形状的压痕,通过测量压痕的尺寸来计算应力
应变和应力的相互影响
应变和应力之间的关系:应变是应力作用下的物体形状变化,应力是抵抗变形的力。
应变和应力的测量方法:通过应变计和应力计进行测量,应变计测量物体变形,应力计测量物 体受到的力。
应变和应力的相互影响:应变和应力之间存在相互影响,例如在材料屈服点附近,应变和应力 之间会发生突变。
应力的概念
分类:正应力、剪应力、弯 曲应力等
定义:物体受到外力作用时, 内部产生的反作用力
单位:帕斯卡(Pa) 作用效果:使物体产生形变
应变和应力的关系
应变是物体形状 的改变,应力是 物体内部抵抗变
形的力
应变和应力之间 存在线性关系, 即应变正比于应
力
应变和应力之间 的关系可以用胡 克定律表示,即 应力=弹性模量
应变和应力关系
汇报人:XX
应变和应力的定义 应变和应力的测量方法 应变和应力的应用领域 应变和应力的研究进展 应变和应力的未来展望
第四章应力与应变关系

(4-3a)
广义虎克定律
在小变形条件下,应变分量都是微量,(a)式在应变 为零附近做Taylor展开后,忽略2阶以上的微量,例如
对 , 可x 得:
x (f1)0(f1x)0x (f1y)0y (f1z)0z
( f1
yz
)0yz
(f1zx)0zx
(f1xy)0xy
广义虎克定律 展开系数表示函数在其对应变分量一阶导数在应变分 量等于零时的值,而 实( f 1 际) 0 上代表初应力,由于无初应 力假设 等于( f 1零) 0 。 其它分量类推,那么在小变形情况下应力与应变关系 式简化为:
3 t 2 3
和 称 为拉梅(Lame)弹性常数,简称拉梅常数
各向同性体的广义虎克定律
(三)最后通过坐标变换,进一步建立任意正交坐标系应 力与应变关系
在各向同性弹性体中,设 o为x y任z 意正交坐标系,它
的三个轴与坐标系 应O力12主3 轴的方向余弦分别为 、 (l1 ',m1和',n1 ') (l2,',m因2 ',n为2 ')1,(2l3,',m33 ',轴n3是') 主轴,主轴方向的 剪应变和剪应力等于零。 根据转轴时应力分量变换公式得
系O123各轴的方向余弦,知:
l1 n3 cos180 1 m2 cos0 1 l2 l3 m1 m3 n1 n2 cos90 0
各向同性体的广义虎克定律
因此新坐标轴也指向应变主轴方向,剪应变也应该等
于零,且因各向同性时,弹性系数C41,C42和C43应
该不随方向面改变,故取 x, y分, z别为1′,2′和3′轴,同
上式作为虎克定律在复杂受力情况下的一个推广, 因此称为广义虎克定律。式中系数Cm n(m ,n1,是2, ,6) 物质弹性性质的表征,由均匀性假设可知这些弹性性 质与点的位置无关,称为弹性常数。上式也可以写成 矩阵形式
应力与应变间的关系

τ xy
右侧面
σx τ xz
x
γ xy
γ yz
γ zx
O
∠ xOy ∠ yOz
∠zox 。
z
σz
前面
2、各向同性材料的广义胡克定 、 律
(1)线应变的推导 线应变的推导 分别单独存在时, 在σx σy σz 分别单独存在时 x 方 依次为: 向的线应变 εx 依次为
x σ
z
x
x σ
εx ' =
σx
τ = Gγ
或
γ=
τ
G
τ γ γ τ
为剪切弹性模量,单位为N/m G 为剪切弹性模量,单位为N/m2.
三、复杂应力状态下应力与应变的关系 σx σy σz τ x y τ y z τ z x εx ε y ε z γ x y γ y z γ z x
1、各向同性材料的广义胡克定律 (1)符号规定 ) (a)三个正应力分量 拉应力为正 (a)三个正应力分量 三个正应力分量:拉应力为正
因此, 该圆筒变形后的厚度并无变化, 因此 该圆筒变形后的厚度并无变化 仍然为 t =10mm .
G G G
在线弹性范围内, 小变形条件下, 在线弹性范围内 小变形条件下 各向同性材料。 各向同性材料。
1 εx = σx ν (σ y +σz ) E 1 E
[
]
公式的适用范围 : 在线弹性范围内,小 在线弹性范围内 小 变形条件下, 变形条件下 各向同性材 料。
ε y = [σ y ν (σz +σx )]
ν ν ε z = (σ x + σ y ) = (τmax + τmax ) = 0 E E
同理可得,圆筒中任一点 该点到圆筒横截面中心的距离为 该点到圆筒横截面中心的距离为ρ 同理可得 圆筒中任一点 (该点到圆筒横截面中心的距离为ρ) 处 的径向应变为
材料应变与应力的关系

材料应变与应力的关系《材料应变与应力的关系:你知道吗?》我想跟你聊聊材料里一个特别神奇又很实在的事儿,就是应变和应力的关系。
这听起来有点专业,可别被吓着,其实就像咱们生活里常见的一些现象一样好理解。
你看,应力呢,就好比是材料内部的一种“小情绪”。
比如说,你拉一根橡皮筋,你给它施加的这个拉力,在橡皮筋内部就产生了应力。
就好像你给一个人安排了好多工作,这个人就会感觉到压力一样,材料受到外力的时候,内部就有应力了。
那应力是怎么产生的呢?当我们对材料施加力的时候,不管是拉力、压力还是扭力,材料内部的原子啊、分子啊就像一群小伙伴,它们的排列被打乱了,就开始互相“抱怨”,这种互相的作用就是应力。
应变呢,就像是材料的一种“反应”。
还说那根橡皮筋,你拉它的时候,它变长了,这个变长的变化就是应变。
这就好比一个人被安排了太多工作,开始变得很疲惫,这种状态的改变就像是材料的应变。
材料在应力的作用下,它的形状或者尺寸会发生改变,这个改变的程度就是应变。
你可能会想,这应力和应变到底有啥具体关系呢?这就像一场拔河比赛。
如果两队力量差不多,绳子受到的应力就不是特别大,那绳子的应变也就比较小,可能就稍微被拉长一点。
可要是一边的力量超级大,应力就很大,那绳子的应变就大得很,可能都被拉得老长,甚至有可能断掉。
在材料里也是这样,应力越大,一般来说应变就越大。
不过这可不是绝对的哦。
不同的材料对待应力的反应可不一样呢。
就像不同性格的人对待压力的反应不同。
有的材料很“坚强”,像钢铁,你给它很大的应力,它的应变相对比较小。
就好比那些很抗压的人,不管工作压力多大,还是能稳稳地应对,不会轻易改变自己的状态。
而有些材料比较“脆弱”,像玻璃,一点点应力可能就导致很大的应变,一下子就碎了,就像那些心理比较脆弱的人,一点压力就可能崩溃。
那这个应力和应变的关系有啥用呢?哎呀,用处可大了去了。
比如说盖房子,建筑师要知道建筑材料的应力应变关系。
如果选错了材料,应力大的时候应变太大,房子可能就变形了,这可不得了,就像你穿了不合脚的鞋子,走路都难受,房子变形了还能住人吗?再比如说造汽车,汽车的各个部件在行驶过程中受到各种力,要是不了解材料的应力应变关系,部件可能就坏掉了,那多危险啊。
弹性力学弹性体的应力与应变关系

弹性力学弹性体的应力与应变关系弹性力学是一门研究固体材料在外力作用下的变形和应力分布规律的学科。
其中,弹性体是一类能够在外力作用下发生形变,但恢复力可以将其恢复到原始状态的物质。
弹性体的应力与应变关系是弹性力学中的基本概念和重要理论。
一、什么是应力与应变在力学中,应力是物体受来自外界作用的力引起的单位面积内的力的大小。
它是描述物体受力情况的物理量。
应力可分为正应力和剪应力两种,正应力作用于物体的表面上的垂直方向,而剪应力则作用于物体的表面上的切向方向。
应变是描述材料形变程度的物理量,是物体在受力下发生变形时单位长度的变化。
应变也可分为正应变和剪应变两种,正应变是物体长度在受力作用下产生的相对变化量,而剪应变则是物体形状的变化量与原始尺寸之比。
二、背景知识弹性体的应力与应变关系可以通过背景知识来理解。
弹性体的主要特性是能够在外力的作用下发生形变,但当外力消失时,它能够恢复到原来的形状和尺寸。
这是因为弹性体的分子或原子之间存在着弹性力,当外力作用结束时,弹性力将趋于平衡,使得物体恢复到原来的状态。
三、胡克定律胡克定律是描述弹性体应力与应变关系的基本定律。
根据胡克定律,当外力作用于弹性体时,弹性体内部的应力与应变成正比。
具体数学描述如下:σ = Eε其中,σ代表应力,单位为帕斯卡(Pa),E代表弹性模量,单位为帕斯卡(Pa),ε代表应变,为无单位。
胡克定律适用于弹性体在线性弹性范围内,即应力与应变成正比,并且比例系数恒定。
此时的应力-应变关系为线性关系,称为胡克定律。
超出线性弹性范围后,材料会发生塑性变形。
四、弹性模量弹性模量是表征弹性体抵抗形变的能力大小的物理量。
它是胡克定律中比例系数的倒数,可以用来度量弹性体的刚度。
常见的弹性模量有:1. 杨氏模量(Young's Modulus):用E表示,描述的是物体在拉伸或压缩时的应变与应力之间的关系。
2. 剪切模量(Shear Modulus):用G表示,描述的是物体在受剪时的应变与应力之间的关系。
应力-应变

应力-应变
应力-应变关系是材料力学中的重要概念,用于描述材料在受到外力作用下的变形行为。
应力(stress)指单位面积上的力,通常用力(force)除以面积(area)来计算。
应变(strain)则指材料单位长度的变化量,通常用长度变化(change in length)除以初始长度(original length)来计算。
应力和应变之间的关系可以通过材料的应力-应变曲线表示。
在弹性阶段,应力与应变成正比,即呈线性关系,这称为胡克定律。
当超过弹性极限后,材料可能发生塑性变形,应力-应变曲线非线性上升。
最终,在断裂点达到时,材料会发生破坏。
值得注意的是,不同材料具有不同的应力-应变特性,因此需要使用适当的试验方法来确定每种材料的特定应力-应变曲线。
这些实验通常在材料力学测试机上进行,例如拉伸试验、压缩试验或剪切试验等。
总而言之,应力-应变关系是描述材料变形行为的重要概念,可以通过应力-应变曲线来了解材料的力学特性。
应力与应变间的关系

210 × 10 9 = ( − 160 + 0 .3 × 240 ) × 10 − 6 = − 20 .3MPa 1 − 0 .3 2 6
∴σ 1 =44 .3 MPa ;σ 2 =0;σ 3 = − 20 .3MPa ;
0.3 ε 3 = − (σ 3 + σ 1 ) = − ( − 22.3 + 44.3) × 10 6 = − 34.3 × 10 − 6 E 210 × 10 9 实 际上 从排 序的 角度 来 看是 求得 ε 2
µ
注意:主应力和主应变的方向是相同的 注意 主应力和主应变的方向是相同的. 主应力和主应变的方向是相同的
2011-11-30
7
§7-4 应力与应变间的关系
一、单拉下的应力--应变关系 单拉下的应力--应变关系 -y
σx
εx=
σx
E
ε y =− σ x
E
γ ij ≈ 0 (i,j = x,y,z )
µ
ε z =− σ x
E
µ
z
x
y
二、纯剪的应力--应变关系 纯剪的应力--应变关系 --
γ xy =
2011-11-30
τ xy
1 − 2µ θ = (σ 1 + σ 2 + σ 3 ) E 1 − 2µ = (σ x + σ y + σ z ) E
2011-11-30
3(1 − 2 µ ) (σ 1 + σ 2 + σ 3 ) σ m θ = = E 3 k 体积胡克定律, k 为体积弹性模量,
σ m 是三个主应力的平均值
所以, 所以,该点处为平面应力状态
′ σ2
E [ε 1 + µε 2 ] ∴σ 1 = 2 1− µ 210 × 10 9 = ( 240 − 0 .3 × 160 ) × 10 − 6 = 44 .3MPa 1 − 0 .3 2
各向异性材料的应力应变关系

简化后;工程上常用的胡克定律表达式:
i C ij j
S i j=123456
i
ij j
其中:Cij刚度矩阵,[Sij] 柔度矩阵,互为逆矩阵, 即[Cij]= [Sij]1
二:单对称材料应力应变关系
1O2 平面是弹性对称面;沿 3 轴和 3′ 轴方向上的应力和 应变有以下关系:
单对称材料的应力
则柔度系数与工程弹性常数关系为:
同理;沿 2 轴向和 3 轴向的单 向拉伸,还可得:
对于102面 203面和103面的纯剪切;可得:
式中E1,E2,E3和G12,G23,G13分 别为正交各向异性材料的拉压弹 性模量和剪切弹性模量; V12,V23,V13以及V21,V32,V31分 别为主泊松比和副泊松比
其应力应变关系:
应变应力关系:
只有2个独 立弹性常数
2 2正交各向异性材料的工程弹 性常数
用工程弹性常数拉压模量 剪切模量、泊松比来表 示各向异性材料应力应变关系
➢ 柔度系数、刚度系数与工程弹性常数关系 由三个单向拉伸和三个纯剪切示意图来推导
沿 1 轴向单向拉伸时;应力σ ≠ 0 ,其他应力 均为零,可得: 根据胡克定律和泊松效应有:
则用工程弹性常数表达的正交各向异性材料的应 变应力关系为:
由刚度系数矩阵与柔度系数矩阵的可逆性;可得:
式中:
➢ 工程弹性常数的互等关系 由于柔度矩阵的对称性;可得工程弹性常数的互
等关系为:
9个工程弹性常数;3个拉压弹 性模量,3个剪切弹性模量, 3个主泊松比
则刚度矩阵和柔度矩阵分别为:
四:横向各向同性材料的应力应 变关系
三个相互垂直的弹性对称面中有一个是各向同 性的;如单向纤维增强复合材料
第2章 应力-应变关系

P
n F
P
θ
n
P F 2 P cos n F P sin s cos F
σn称为正应力,σs称为剪应力。
x P P
NUDT 12.6
第二章 应力-应变关系
Chap. 02
2.1 符号规定
应力 弹性体 微元体
yx
z
zz
zy
xx
yz
正应力:
外法线 方向
i, j 1,2,3,4,5,6
0 1 0 0 0 2 0 0 0 3 C44 0 0 4 0 C55 0 5 0 0 C66 6 0 0
1
1 C11 C12 C13 C 2 21 C22 C23 3 C31 C32 C33 0 0 4 0 5 0 0 0 6 0 0 0
u w r z x
NUDT 12.6
第二章 应力-应变关系
Chap. 02
2.1 符号规定
正轴与偏轴
正轴(on-axis)应力应变: 偏轴(off-axis)应力应变:
xx xx
yy yy
ij i, j
zz yz zz yz
zx zx
xx , yy , zz
应力分 量指向
zx xy
o
yy yz
xz
yy
xz
y
正负号
xy
zx
zy
yx
剪应力:
xx
xy , xz , yx
zz
x
yz , zx , zy
第四章 应力和应变关系

第四章应力和应变关系内容介绍 知识点应变能原理应力应变关系的一般表达式完全各向异性弹性体 正交各向异性弹性体本构关系 弹性常数各向同性弹性体应变能格林公式 广义胡克定理一个弹性对称面的弹性体本构关系 各向同性弹性体的应力和应变关系 应变表示的各向同性本构关系如果加载缓慢,变形过程中物体与外界进行热交换,但物体的温度保持不变,称为等温过程。
设等温过程中,输入物体的单位体积热量为d Q ,熵的增量为d S ,对于弹性变形等可逆过程,根据热力学第二定律,有因为 ,d Q=TdS , 所以, Q=TS 。
上式中,T 为绝对温度,TS 为输入单位体积的热能。
代入公式可得所以 。
上式中,E 0为物体单位体积的内能,TS 为输入的热能,即U 0=E 0 - TS 。
所以在等温条件下,功能公式仍然成立。
上述公式是从热力学第一和第二定律出发得到的,因此它不受变形的大小和材料的性质的限制。
如果材料的应力应变关系是线性弹性的,则由格林公式,单位体积的应变能必为应变分量的齐二次函数。
因此根据齐次函数的欧拉定理,可得即用张量表示,写作设物体的体积为V ,整个物体的应变能为 。
由于应变能函数的存在,通过格林公式就可求出应力。
本节将通过应变能的推导应力和应变的一般关系。
若将应力表达为应变的函数,则应力和应变关系的一般表达式为这里的函数f i (i =1,2,…,6)取决于材料自身的物理特性。
对于均匀的各向同性材料,单向拉伸或压缩时,应力应变关系可以通过实验直接确定。
但是对于复杂的应力状态,即使是各向同性的材料,也很难通过实验直接确定其关系。
这里不去讨论如何建立一般条件下的应力应变关系,仅考虑弹性范围内的小变形问题。
对于小变形问题,上述一般表达式可以展开成泰勒级数,并且可以略去二阶以上的高阶小量。
例如将的第一式展开,可得上式中(f 1)0表达了函数f 1在应变分量为零时的值,根据应力应变的一般关系式可知,它代表了初始应力。
如果加载很快,变形在极短的时间内完成,变形过程中没有进行热交换,称为绝热过程。
流体力学中应力应变关系

流体力学中应力应变关系流体力学是力学的一个分支,研究的是流体的运动、应力和应变。
在流体力学中,应力和应变之间的关系是一个基础性问题,本文将对流体力学中应力应变关系进行讲解。
一、应力和应变的概念应力是指在物体内部的任意一个点处,单位面积受到的力的大小。
在流体力学中,应力分为正应力和剪应力两种。
正应力是指垂直于物体表面的应力,它的方向和大小与物体表面的法线方向相同。
剪应力是指平行于物体表面的应力,它的方向和大小与物体表面的切线方向相同。
应变是指物体受到应力作用后,形态发生改变的程度。
在流体力学中,应变分为体积应变和剪应变两种。
体积应变是指流体的体积在受到压力作用后发生的变化,它是指流体体积的变化与初始体积的比值。
剪应变是指物体受到剪应力作用后,产生的形变的强度,它是指变形的尺寸与原始尺寸的比值。
流体在受到应力作用时,会发生形变,而应力和应变之间的关系便是描述形变程度的应变和导致形变的应力之间的关系。
在流体力学中,应力和应变之间的关系有两种:1. 线性应力应变关系在一些情况下,流体的应变与应力之间具有线性关系。
这种关系表示为:ε = K σ其中,ε是流体的应变,K是常数,σ是流体的应力。
这种关系在流体受到小应力时是适用的,通常称为胡克定律。
当流体所受到的应力超过一定的范围时,线性应力应变关系不再成立,流体的应变不再是应力的线性函数。
这时,应力和应变的关系可以用更复杂的非线性关系进行描述。
液滴的表面张力、黏度和压缩强度是非线性的。
流变学是研究物质的变形和流动行为的学科,它探究物体在不同的应力作用下,应变的变化规律。
在流体力学的领域中,流体的应力应变关系可以被分成三类:粘弹性流体是一种介于固体和液体之间的物质,它的应变不仅与应力有关,而且与应变历史有关。
它们的应力应变关系可以用弹性模量、黏度和时间来描述。
塑性流体是指流体在受到一定应力作用后会发生永久变形的流体。
在塑性流体中,应变随着应力的增大,在一定的应力范围内也是线性的,但超过一定的范围后便不再线性。
应力和应变之间的关系

应力和应变的关系曲线
描述
应力和应变的关系曲线是描述应力与应变之间关系的图形表示。
形状
在弹性范围内,曲线呈直线上升;超过弹性极限后,曲线出现弯曲。
应用
通过应力和应变的关系曲线,可以确定材料的弹性模量、屈服点和 极限强度等机械性能参数。
04
应力和应变的应用
弹性力学
弹性力学是研究弹性物体在外力作用下 变形和内力的规律的科学。在弹性力学 中,应力和应变是描述物体变形和受力 状态的基本物理量。
公式
σ=Eεsigma = E varepsilonσ=Eε
解释
σ为应力,E为弹性模量,ε为应变。 当应力增加时,应变也相应增加, 且两者成正比关系。
非线性关系
描述
当材料受到超过其弹性极限的应力时 ,应力与应变之间的关系不再是线性 的,而是呈现非线性关系。
特征
在非线性阶段,应变随应力的增加而 急剧增加,可能导致材料发生屈服或 断裂。
设计优化
优化结构设计
通过对应力和应变的分析,优化结构设计,提高结构的承载能力 和稳定性。
考虑材料特性
在设计过程中,充分考虑材料的力学特性和性能,合理选择和使 用材料,以降低应力和应变对结构的影响。
引入减震和隔震措施
通过引入减震和隔震措施,降低地震等外部载荷对结构产生的应 力和应变,提高结构的抗震性能。
时间
蠕变
在长期恒定应力作用下,材料会发生 缓慢的塑性变形,即蠕变。蠕变会影 响材料的应力和应变关系,特别是在 高温和长期载荷作用下。
时间依赖性
某些材料的力学性能会随时间发生变 化,对应力和应变的关系产生影响。 例如,疲劳和时效等现象会导致材料 性能随时间发生变化。
07
应力和应变在工程实践中的 注意事项
应力与应变间的关系
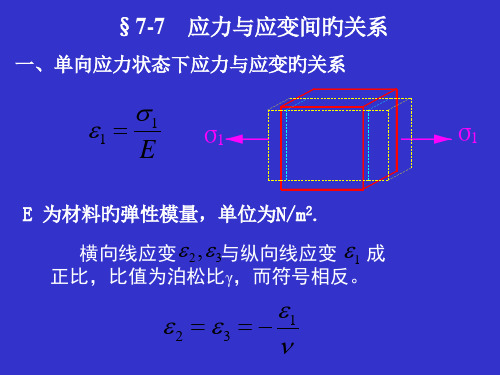
一、单向应力状态下应力与应变旳关系
1
1
E
σ1
σ1
E 为材料旳弹性模量,单位为N/m2.
横向线应变2,3与纵向线应变 1 成
正比,比值为泊松比γ,而符号相反。
2
3
1
二、纯剪切应力状态下应力与应变旳关系
G 或
G
τ γ γτ
G 为剪切弹性模量,单位为N/m2.
三、复杂应力状态下应力与应变旳关系
x y z x y y z z x
y
σy
上面
x y z x y y z z x
1、各向同性材料旳广义胡克定律 (1)符号要求
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量:拉应力为正
σz
x
o
压应力为负。 z
前面
(b)三个剪应力分量: 若正面(外法线与坐标轴
P a
y
z
x
y 解:铜块上截面上旳压应力为
y
P A
300 103 0.12
y x
30MPa
x
(b) Z z
1 [ ( )] 0
xE x
y
z
由
1 [ ( )] 0
zE z
x
y
解得
x
z
(1 1 2
)
y
0.34(1 0.34) 1- 0.342
(30)
-15.5MPa
特例
在平面纯剪切应力状态下:σ 1 σ 3 τ xy
代入得
1 2
E
(1
2
3)
1 2
流体力学中应力应变关系

流体力学中应力应变关系
流体力学中的应力应变关系是指在流体受到外力作用时产生的
应力和应变之间的关系。
在流体力学中,应力和应变都是矢量量,分别表示流体内部的应力状态和形变状态。
应力是力在单位面积上的作用,单位为帕斯卡(Pa)或牛顿/平方
米(N/m)。
在流体力学中,应力分为剪切应力和压力。
剪切应力是指
流体内部的分子或离子在流体流动时发生相互作用所产生的应力,它的方向与流体的流动方向垂直;压力是指流体受到外部压力作用时产生的应力,其方向垂直于受力面。
应变是流体受力后形变程度的量度,它通常用拉伸应变和剪切应变来表示。
拉伸应变是指流体在受力作用下沿着某一方向发生的形变程度,其计算公式为变形量与原始长度的比值,单位为无量纲。
剪切应变是指流体在受到剪切力作用时发生的形变程度,其计算公式为变形量与原始长度的比值,单位为无量纲。
对于牛顿流体,其应力应变关系符合牛顿黏滞定律,即剪切应力与剪切应变成正比,比例系数为黏度。
黏度是流体的特性参数,它反映了流体内部分子或离子在流动时产生的阻力大小。
对于非牛顿流体,其应力应变关系则更加复杂,需要采用不同的模型来描述其流变性质。
在工程应用中,流体力学中的应力应变关系在石油、化工、食品、医药等领域都有广泛应用。
通过研究流体的应力应变关系,可以深入理解流体的流动性质,从而指导工程设计和生产过程中的优化和改进。
- 1 -。
应力与应变间的关系

压应力为负。 z
前面
(b)三个剪应力分量: 若正面(外法线与坐标轴
正向一致的平面)上剪应力矢 的指向与坐标轴正向一致, 或 负面(外法线与坐标轴负向一 致的平面)上剪应力矢的指向 与坐标轴负向一致,则该剪 应力为正, 反之为负。
y
o
z σz
σy
τ yx τ yz τ zy τ zx
上面
τ xy
右侧面
)
y
0.34(1 0.34) 1- 0.342
(30)
-15.5MPa
铜块的主应力为
σ1 σ2 15.5MPa , σ3 30MPa
体积应变和最大剪应力分别为
1 2
E
(1
2
3)
1.95 104
max
1 2
(1
3
)
7.25MPa
(1)概念:构件每单位体积的体积变化, 称为 体积应变用θ表示。
(2)各向同性材料在空间应力状态下的 体积应变
公式推导
2
设单元体的三对平面为主平面, 其 三个边长为d x, d y, d z 变形后的边 长分别为 d x(1+ , d y(1+2 , d z(1+3 , 因此变形后单元体的体 积为:
y
1 E
[ y
( z
x )]
z
1 E
[ z
( x
y )]
(2)剪应变的推导
剪应变 xy , yz ,zx与剪应力xy ,yz ,zx之间的关系为
xy
xy
G
yz
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、三轴压缩状态下的应力-应变关系
• σ-ε关系与土的类似(P35,图4-1),见下 图,应变随荷载的增大而迅速增大。 • 同样,为应力偏量的函数。 • 在应力级位较小时,近似直线,E为常数。 • 与粒料的σ-ε关系有很大不同,凹向相反, 悬浮结构的粒料可能相似(如果细料类似土 的话),这反映了黏结型与嵌锁型的区别。
级配要求
应满足一定的级配要求,可参见有关手册或规范
测试与计算
测试采用三轴试验
计算:
tg
2、应力-应变关系
测定方法
三轴试验
应力-应变关系
ε
注意:该曲线与土的应力-应变曲线的区别
粒料的模量与 受力状态有关
Er k1
k2
θ为主应力之和
1 2 3 1 2 2 3 3
3、变形累积
与土的变形累计规律类似 当较小时,趋于缓慢稳定增加 当较大时,急剧增加 随增加,稳定的增加
4、泊松比
一般0.2-0.5,一般取0.25-0.35
三、稳定类材料
1、强度特性
• 强度来源:黏结力,内摩擦力 • 当采用黏结力、内摩擦力的概念时,总与剪切有关。实际 上,黏结力和内摩擦力提供了各种强度。 • 测试方法 • 三轴压缩试验,P45图5-2 • 梁式试件,4点加荷法,三分点加荷试验,P45图5-2 • 劈裂试验,间接拉伸试验,图 • 同样三种组成状态。由于是整体性材料,所以同样应注意 其水稳定性。细集料(结合料)含量越多,越容易冲刷。 在满足填充要求的前提下,应尽量减少细集料的用量。强 度不是唯一的标准。 • 级配一般采用骨架-填充结构
第五章 路面材料的力学性能
引言 颗粒材料的工程性质 稳定类材料
沥青混合料
水泥混凝土 Miner定律-线性疲劳叠加率
一、 引 言
1、路面材料的类型
2、应力-应变特性:模量E,这是主要力学分析参数
3、强度特性:了解其自身的抗力,了解强度的来源
4、变形特性:变形能力,可恢复的和不可恢复的变 形,对平整度的影响
6、变形特性
累计永久变形忽略不计
7、疲劳特性
概念
• 疲劳是指材料在低于极限荷载的英里作用下发生破坏, 是重复荷载作用下微裂纹的扩展,重复荷载作用的大 小不可太大。疲劳反映了路面的寿命,反映了小吨位 荷载作用下的数千万次的重复作用,滴水穿石的效果。 疲劳设计是路面设计的重要概念,是路面设计的重要 特点。 • 疲劳寿命:指从开始加载至损坏时的荷载作用次数; 通常采用梁式试件测量,四点加荷法。所施加的应力 实际上就是破坏时的应力,成为疲劳强度。 • 疲劳极限:当荷载小于一定数值时,材料永远不会发 生疲劳损坏,这个数值曾经定义为10^7,目前已经不 行。对钢材,应力比0.5。
k为系数,k1=7.0-15.7,k2=0.46-0.64 由于σ1与σ3有关,所以模量还可以表示为:
Er f1 3
f2
荷载-弯沉关系
随着荷载(弯沉)的增大,模量在增加
P
破坏点
l
设计中的考虑
粒料模量的取值比较困难,因为E=F(应力, 棱角,纹理,密度),设计中无法考虑这 么详细
Eg K E0
压碎值、性状 与透水性
压碎值取决于集料的强度和形状,压碎值不足的 危害是很大的,产生变形和强度问题 即便是基层、底基层等层次,虽然整体受力较小, 但局部接触应力可能很大,仍需要限制压碎值 过于密实碎可提高强度,但可能会牺牲水稳定性、 温度稳定性和抗冲刷能力,设计者应设法平衡强 度与稳定性之间的关系 形状可能会影响压碎值,所以采用测试压碎值的 集料的形状应符合要求。集料生产过程中的内部 裂纹会影响压碎值
5、疲劳特性:与寿命有关,与荷载作用次数有关 6、耐久性:自然因素的影响,包括水的作用、水稳 定性、抗剥落特性、抗冻融特性(温度)、自然 老化、抗紫外线。
二、颗粒材料的工程性质
1 2 3 4 泊松比强度ຫໍສະໝຸດ 源应力应变关系变形累积
1、强度来源
强度来源
颗粒类材料由于无结合料的黏结,所以不 是一个整体,是一个结构层,但自身是松 散的。 不能承受拉应力的作用,可以受压或受剪 切。黏结力为零。 内磨檫力提供了抗剪切强度,但取决于粒 料的纹理、密实度、颗粒形状、级配等因 素
加载波形有多种,典型的有三种:
低应力为零:常用方式,沥青路面方式 低应力>零:水泥路面方式 低应力<零:双向加载方式,不常用
• 随着荷载作用次数的增加,材料的抗力(强度、 模量)在不断降低。 • 疲劳寿命与加荷方式、波形、频率等因素有关。 荷载级位越大,疲劳寿命越短;荷载级位越小, 疲劳寿命越长。当然还与材料自身的特性有关, 与黏结料的性质有关,与集料的性质也有关。 一般而言,影响弯拉强度的因素都将影响疲劳 特性。 • 疲劳特性一般用应力或应变与疲劳寿命之间的 关系来表示,两者之间在半对数或双对数坐标 上一般呈线性关系。见图。 • 疲劳方程的离散性一般很大
3、梁式弯拉状态下的应力-应变关系
梁式试件是半拉半压的受力状态,性质应 处于拉、压之间,所得模量略小于三轴 不反映侧限力的影响 应力-应变曲线与上图类似,但损坏区域更 明显,速度更快
4、影响因素
结合料的剂量和活性 龄期
集料的类型(土)
5、参考值域
水泥土:E=(0.7-7)*1000Mpa, μ=0.15-0.35 水泥稳定碎石:(7-28)*1000Mpa, μ=0.15-0.20
颗粒材料的几 种组成状态
骨架结构,不含或很少细料(<0.074)的状态, 见图:强度来源于接触部位的摩擦力,对集料强 度要求高;水稳定性好,透水性好,无冻敏 骨架-填充结构,见图:强度来自于摩擦力,抗剪 切强度有所提高;密度高,透水性差,可能是冻 敏的,取决于填充料;不耐冲刷。三渣多属于这 种结构。 悬浮结构,粗集料悬浮于细集料之中,见图:强 度取决于填充料;密度高,不透水,水敏,冻敏, 不耐冲刷
疲劳方程
常见表达方式:
f
lg N
低应力为零
有高低应力比时的疲劳方程:
f
(1 R) lg N
低应力>0
Rc N R
