六年级数学扇形周长与面积和弓形面积
扇形、三角形、弓形、菱形公式[整理版]
![扇形、三角形、弓形、菱形公式[整理版]](https://img.taocdn.com/s3/m/b6f8b31d91c69ec3d5bbfd0a79563c1ec5dad70c.png)
常用面积公式面积公式扇形面积公式00在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2,所以圆心角为n°的扇形面积:00S=nπR²÷360 00比如:半径为1cm的圆,那么所对圆心角为135°的扇形的周长:00C=2R+nπR÷180 00=2×1+135×3.14×1÷180 00=2+2.355 00=4.355(cm)=43.55(mm) 00扇形的面积:00S=nπR²÷360 00=135×3.14×1×1÷360 00=1.1775(cm²)=117.75(mm²) 00扇形还有另一个面积公式00S=1/2lR 00其中l为弧长,R为半径00扇环面积00圆环周长:外圆的周长+内圆的周长(圆周率X(大直径+小直径)) 0圆环面积:外圆面积-内圆面积(圆周率X大半径的平方-圆周率X小半径的平方\圆周率X(大半径的平方-小半径的平方)) 00用字母表示:00S内+S外(∏R方)00S外—S内=∏(R方-r方)00还有第二种方法:00S=π[(R-r)×(R+r)] 00R=大圆半径00r=圆环宽度=大圆半径-小圆半径00还有一种方法:00已知圆环的外直径为D,圆环厚度(即外内半径之差)为d。
00d=R-r,00D-d=2R-(R-r)=R+r,00可由第一、二种方法推得S=π[(R-r)×(R+r)]=π(D-d)×d,0圆环面积S=π(D-d)×d 00这是根据外直径和圆环厚度(即外内半径之差)得出面积。
这两个数据在现实易于测量,适用于计算实物,例如圆钢管。
三角形面积公式00海伦公式00任意三角形的面积公式(海伦公式):S²=p(p-a)(p-b)(p-c), p=(a+b+c)/2, a.b.c为三角形三边。
六年级上册-1.4扇形的弧长、周长、面积

知识点一、扇形的认识1、弧:如下图1,图上A 、B 两点之间的部分叫做弧,读作弧AB 。
2、扇形:由一条弧和经过这条弧两端的两条半径围成的图形叫做扇形。
下图2就是扇形。
(图1) (图2)3、圆心角:像图1中角AOB 这样,顶点在圆心的角叫做圆心角。
由圆心和两条半径组成,扇形是圆的一部分,我们经常说的21圆、41圆、61圆等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几,那么一般的求法是什么呢?关键是360n 。
(n 表示扇形圆心角的度数)4、扇形的面积公式:3602n r S ⨯=π扇形 5、扇形的弧长公式:3602n r L ⨯=π弧长 6、扇形的周长公式:r n r C 23602+⨯=π扇形 7、几种基本的曲边图形面积求法:(1)弓形,如图:;一般来说,弓形面积=扇形面积—三角形面积 (2)弯角,如图:;弯角的面积=正方形—扇形 (3)谷子,如图:;“谷子”的面积=弓形面积×28、求阴影部分面积的几种方法:①割补平移法;②差不变原理;③阴影=大—白9、方与圆的应用【例题】1、扇形的判断1、判断:(1)因为扇形是它所在圆的一部分,那么圆的一部分一定是扇形。
( )(2)在同一个圆内,圆心角越大,扇形也就越大。
( )(3)以41圆为弧的扇形的圆心角是90度。
( ) 【例题】2、扇形的弧长、周长、面积1、已知扇形的圆心角为60°,半径为2厘米,求这个扇形的周长和面积。
2、画一个半径为3厘米并且圆心角是120°的扇形,并求这个扇形的弧长和面积。
3、求阴影部分面积:(单位:厘米,π取3.14)2、求下列各图形的阴影部分面积是多少平方厘米?(单位:厘米,π取3.14)3、如图,三角形ABC是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,AB长40厘米。
求BC的长度?(π取3.14)1、判断题:(1)圆的一部分就是扇形。
()(2)顶点在圆内的角一定式圆心角。
六年级扇形面积和弧长公式

六年级扇形面积和弧长公式
扇形的面积公式
(1)扇形面积S=l×r/2,其中l为扇形的弧长,r为扇形的半径。
(2)扇形面积S=圆心角的角度×π×r²/360°。
(3)扇形面积S=圆心弧度绝对值|a|×r²/2。
扇形的弧长公式
(1)弧长l=(n÷180)×π×r,其中l是弧长,n是扇形圆心角,π是圆周率,r是扇形半径。
(2)弧长l=|α|×r,l是弧长,其中|α|是弧l所对的圆心角的弧度数的绝对值,r是半径。
扇形的周长公式
周长C=2r+(n÷360)πd,其中n为扇形所对的圆心角的度数,d为扇形的直径。
周长C=2r+(n÷180)πr,其中n为扇形所对的圆心角的度数,r为扇形的半径。
扇形简介
一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形。
显然,它是由圆周的一部分与它所对应的圆心角围成。
圆上A、B两点之间的的部分叫做“圆弧”简称“弧”,读作“圆弧AB”或“弧AB”。
以圆心为中心点的角叫做“圆心角”。
扇形的面积公式和周长公式弧度制

扇形的面积公式和周长公式弧度制在咱们学习数学的奇妙旅程中,扇形可是个有趣的小家伙。
今天咱们就来好好唠唠扇形的面积公式和周长公式,还有那个有点神秘的弧度制。
先来说说扇形的面积公式。
这就好比你去买披萨,扇形的披萨块儿大小怎么算呢?扇形的面积公式是 S = (n/360)×πr² ,这里的 n 表示扇形圆心角的度数,r 是扇形所在圆的半径。
举个例子,有一个扇形,圆心角是 90 度,半径是 5 厘米。
那它的面积就是(90/360)×π×5² = 1/4 × 25π = 6.25π 平方厘米。
这就好像是把整个圆平均分成了 360 份,扇形占了其中的 n 份,所以面积就是相应的比例乘以整个圆的面积。
再聊聊扇形的周长公式。
这就像是给扇形围个漂亮的“篱笆”,得知道需要多长的材料。
扇形的周长公式是 C = L + 2r ,这里的 L 是扇形的弧长,r 还是扇形所在圆的半径。
弧长 L 又等于(n/180)×πr 。
比如说有个扇形,圆心角是 120 度,半径是 8 厘米。
先算弧长 L = (120/180)×π×8 = 16π/3 厘米,那周长 C 就是16π/3 + 2×8 = 16π/3 + 16 厘米。
接下来讲讲弧度制,这可是个有点特别的东西。
咱们平常习惯用角度来衡量圆心角,比如说 30 度、60 度。
但弧度制就不太一样啦,它用弧长和半径的比值来表示圆心角的大小。
还记得有一次我在课堂上讲这些知识,有个同学一脸迷茫地问我:“老师,这弧度制到底有啥用啊?”我笑着回答他:“就好比你用尺子量东西,角度制是一种刻度,弧度制又是另一种刻度,各有各的用处呀。
”然后我给他举了个例子,比如在研究三角函数的时候,弧度制就特别方便,能让计算更简洁呢。
其实在生活中,扇形的面积和周长公式以及弧度制也都有不少用处。
比如说设计师在设计扇子的时候,就得用到扇形的知识,算一算面积和周长,才能做出美观又实用的扇子。
[资料]弓形的面积计算公式
![[资料]弓形的面积计算公式](https://img.taocdn.com/s3/m/5313f10bc381e53a580216fc700abb68a982ad08.png)
关于弓形的公式如下;
F=弓形面积,c=弓形弦长,r=弓形半径,L=弓形弧长,a=弓形圆心角,
h=弓形弦高,√=根号
F=1/2[rL-c(r-h)]
c=2√[h(2r-h)]
r=(c²+4h²)/8h
L=0.01745ra
a=57.296L/r
h=r-1/2√(4r²-c³)
以上公式抄录于《常用金属材料手册》
设弓形AB所对的弧为弧AB,那么:当弧AB是劣弧时,那么S弓形=S 扇形-S△AOB(A、B是弧的端点,O是圆心)。
当弧AB是半圆时,那么S弓形=S扇形=1/2S圆=1/2×πr²。
当弧AB是优弧时,那么S弓形=S 扇形+S△AOB(A、B是弧的端点,O是圆心)计算公式分别是:
S=nπR²/360-ah/2 S=πR²/2 S=nπR²/360+ah/2
弓形面积的通用计算公式
2011-10-02 00:35:03| 分类:几何学| 标签:平面几何|字号大中小订阅
一、已知弓形的底为(2a)、高为h;
二、弓形半径公式:
R=(a2+h2) /(2h);
三、弓形面积的通用计算公式:
S=a(h-R)+R2arccos(1-h/R)(劣弧弓形、优弧弓形,二者通用)。
六年级数学扇形公式

六年级数学扇形公式扇形是我们日常生活中经常接触到的一个几何图形,它是由一个圆心和两条射线组成的。
在学习扇形时,我们需要掌握一些与之相关的基本概念和公式。
我们来了解一下扇形的基本概念。
扇形是由一条半径和一段弧组成的图形,弧是圆周上的一段弧长,而半径是连接圆心和圆上一点的线段。
当我们知道扇形的半径和弧长时,就可以通过公式来计算扇形的面积。
扇形的面积公式为:扇形的面积 = (扇形的弧长 / 圆周长) × 圆的面积。
其中,圆周长是指圆的周长,我们知道圆的周长是2πr,r代表圆的半径。
圆的面积公式是πr²,这个公式在我们之前的学习中已经接触过了。
了解了扇形的面积公式,我们来看一个例子:如果一个扇形的半径为5cm,弧长为8cm,我们要计算这个扇形的面积。
我们可以根据扇形的面积公式计算出圆的面积:圆的面积= π × 5² = 25π cm²。
然后,我们可以计算出圆的周长:圆的周长= 2π × 5 = 10π cm。
接下来,我们将已知的弧长代入扇形的面积公式:扇形的面积= (8 / 10π) × 25π = 20 cm²。
所以,这个扇形的面积为20平方厘米。
除了计算扇形的面积,我们还可以利用扇形的面积公式来解决一些与扇形相关的问题。
例如,如果给定一个扇形的面积和半径,我们可以根据公式来求解弧长。
我们可以通过以下步骤来计算:1. 首先,根据扇形的面积公式,计算出圆的面积。
2. 然后,根据圆的面积公式,计算出圆的半径。
3. 最后,根据扇形的面积公式,计算出扇形的弧长。
通过这样的计算,我们可以得到扇形的弧长。
除了计算扇形的面积和弧长,我们还可以利用扇形的公式计算扇形的周长和圆心角。
但是在这里,由于篇幅有限,就不展开讲解了。
总结起来,六年级数学中的扇形公式是一个非常重要的内容。
掌握了扇形的面积公式,我们可以解决与扇形相关的各种问题。
希望同学们能够通过多做练习,掌握好这一内容,为之后的学习打下坚实的基础。
弧形面积的计算公式

弧形面积的计算公式弧形是数学中常见的一个几何形状,用于描述两个点之间的弧线段。
计算弧形的面积是几何学中的一个经典问题,有多种方法可以解决。
本文将介绍三种常见的计算弧形面积的方法和公式。
一、扇形面积公式扇形是一种特殊的弧形,其两个端点与圆心连线构成一个三角形,我们可以通过计算扇形的三角形面积再减去扇形中央的三角形面积来得到扇形的面积。
扇形面积公式如下:S=(θ/360)×π×r²其中,S表示扇形的面积,θ表示扇形的圆心角(夹角),r表示扇形的半径。
二、弓形面积公式弓形是一种将两个不同的弧线段连接起来的形状,计算弓形的面积可以通过计算各个弧形的面积之和来得到。
弓形面积公式如下:S=S1+S2其中,S表示弓形的面积,S1和S2表示两个弧形的面积。
三、圆环形面积公式圆环形是一种由两个同心圆构成的形状,计算圆环形的面积可以通过计算外圆形的面积减去内圆形的面积来得到。
圆环形面积公式如下:S=π×(R²-r²)其中,S表示圆环形的面积,R表示外圆的半径,r表示内圆的半径。
需要注意的是,这些公式都是在二维平面上计算弧形的面积,如果涉及到三维空间中的弧形,则需要进行相应的扩展。
除了这些基本的计算公式,还有一些更复杂的问题需要考虑,比如计算两个不同半径的圆弧所围成的面积、计算两个非圆形的弧线段所围成的面积等。
这些问题通常需要采用数值计算或者数学模型来求解。
总结起来,计算弧形面积的公式主要包括扇形面积公式、弓形面积公式和圆环形面积公式。
通过学习和理解这些公式,我们可以更好地理解和应用弧形的几何性质。
数学六年级-圆、扇形的周长和面积
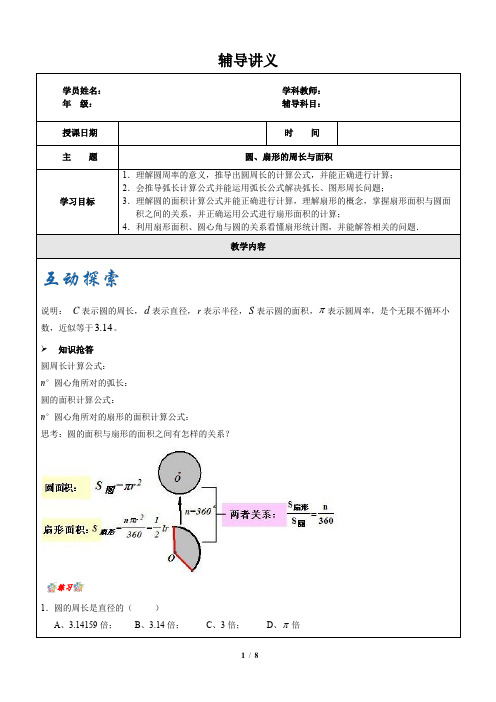
辅导讲义说明:C表示圆的周长,d表示直径,r表示半径,S表示圆的面积,π表示圆周率,是个无限不循环小.3。
数,近似等于14➢知识抢答圆周长计算公式:n°圆心角所对的弧长:圆的面积计算公式:n°圆心角所对的扇形的面积计算公式:思考:圆的面积与扇形的面积之间有怎样的关系?练习1.圆的周长是直径的()A、3.14159倍;B、3.14倍;C、3倍;D、π倍A321CBO2.圆的半径扩大为原来的3倍( )A 、周长扩大为原来的9倍B 、周长扩大为原来的6倍C 、周长扩大为原来的3倍D 、周长不变3.圆的半径不变,圆心角扩大为原来的2倍,则( ) A 、弧长扩大为原来的4倍 B 、弧长扩大为原来的2倍 C 、弧长不变 D 、弧长缩小为原来的一半 4.圆的半径扩大为原来的3倍( )A 、面积扩大为原来的9倍B 、面积扩大为原来的6倍C 、面积扩大为原来的3倍D 、面积不变 5.圆的面积扩大为原来的四倍,则半径( )A 、扩大为4倍;B 、扩大为16倍;C 、不变;D 、扩大为2倍 6.一个扇形的半径扩大2倍,圆心角扩大3倍,则扇形的面积( ) A 、扩大5倍 B 、扩大6倍 C 、扩大18倍 D 、扩大12倍 7.一个扇形的圆心角扩大3倍,弧长扩大6倍,则扇形的面积( ) A 、扩大5倍 B 、扩大6倍 C 、扩大18倍 D 、扩大12倍8.扇形的面积是157平方厘米,它所在的圆面积是1256平方厘米,则扇形的圆心角是 度。
9.已知圆心角为120°的扇形弧长为12.56厘米,则扇形的面积是 平方厘米。
10.已知圆心角为90o 的扇形所在圆的周长是12.56厘米,则扇形的面积是 平方厘米。
【知识梳理1】圆的周长与扇形的弧长例1:如图,点O 、点B 在线段AC 上,AB=120米,BC=70米,O 是圆心,从A 到C 有3条不同的半圆弧线路可走,请你判断走那条半圆弧线路的距离最短?试一试:如图,有一只狗被缚在建筑物的墙角,这个建筑物是边长600厘米的正方形,缚狗的绳子长20米,现狗从A 点出发,将绳拉紧顺时针跑,可跑多少米?【知识梳理2】圆的面积与扇形的面积例2:如图,两个同心圆,大圆的半径为5,小圆的半径为3,求圆环的面积?试一试:求下图中阴影部分的面积与周长:(单位cm ,结果保留 )例3:已知一个扇形的半径为6cm ,周长为20cm ,求扇形的面积。
弧长、扇形、弓形的面积及侧面积

弧长、扇形面积及圆锥侧面积【知识要点】1.弧长公式:半径为R 的圆,其周长是R π2,将圆周分成360份,每一份弧就是1o的弧,1o弧的弧长应是圆周长的3601,而为1803602R R ππ=,因此,on 的弧的弧长就是180R n π,于是得到公式:)(180代表弧长l Rn l π=。
2. (1)扇形的定义:一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形(如图)。
(2)扇形的周长:(3)扇形的面积:如图,阴影部分的面积即为扇形OAB 的面积。
S 扇形=)(3602为扇形圆心角的度数为半径,n R R n π 由上面两公式可知S 扇形=213602n R lR π=.可据已知条件灵活选用公式。
3.弓形的面积(1)由弦及其所对的劣弧组成的图形,S 弓形=S 扇形-S △OAB 。
(2)由弦及其所对的优弧组成的弓形,S 弓形=S 扇形+S △OAB 。
4.圆锥的有关概念:圆锥可以看做是一个直角三角形绕着直角边所在的直线旋转一周而形成的图形,另一条直角边旋转而成的面叫圆锥的底面,斜边旋转而成的面叫圆锥的侧面. 5.圆锥的侧面展开图:圆锥的侧面展开图是一个扇形,如果圆锥的母线长l ,底面半径为,那么这个扇形的半径为,弧长为,因此可得圆锥的侧面积: 圆锥的侧面积。
为底面圆半径为母线长,侧)(221r l rl r l S ππ=⋅=圆锥的表面积。
为底面圆半径为母线长,(底侧表))(r S S r l l r S +=+=π 【典型例题】例1如果一段弧的长度等于半径,则这段弧所对的圆心角的度数一定( )A 、小于60oB 、等于60oC 、大于60oD 、无法确定 AB AB l R l OB OA +=++2·O AB · A BO m· AB Om例2如图,在ABC △中,12023AB AC A BC =∠==,°,,A ⊙与BC 相切于点D ,且交AB AC 、于M N 、两点,则图中阴影部分的面积是 (保留π). 例3 已知扇形的圆心角为120°,弧长为cm π20,这个扇形的面积是多少?例4 已知:如图所示,⊙O 中AB 的长度为4cm π,它所对的圆心角为120°,求弦AB 的长.例5 圆锥的母线长为5cm ,高为3cm ,在它的侧面展开图中,扇形的圆心角是多少度?例6 已知:圆锥的底面半径为r ,母线长为R ,侧面展开图的圆心角为︒n ,求证:︒n =︒⋅360Rr.例7如图,已知△ABC ,AC =BC =6,∠C =90°.O 是AB 的中点,⊙O 与AC 相切于点D 、与BC 相切于点E .设⊙O 交OB 于F ,连DF 并延长交CB 的延长线于G . (1)∠BFG 与∠BGF 是否相等?为什么? (2)求由DG 、GE 和弧ED 围成图形的面积(阴影部分).A·O BA BC DEFGO ANCD BM例8.如图,圆心角都是90º的扇形OAB 与扇形OCD 叠放在一起,连结AC ,BD .(1)求证:AC=BD ;(2)若图中阴影部分的面积是243cm π,OA=2cm ,求OC 的长.例9.图中的粗线CD 表示某条公路的一段,其中AmB 是一段圆弧,AC .BD 是线段,且AC .BD 分别与圆弧 AmB 相切于点A .B ,线段AB =180m ,∠ABD =150°. (1)画出圆弧 AmB 的圆心O ; (2)求A 到B 这段弧形公路的长.例10.如图,PA .PB 是半径为1的O ⊙的两条切线,点A .B 分别为切点,60APB OP AB C O D ∠=°,与弦交于点,与⊙交于点.(1)在不添加任何辅助线的情况下,写出图中所有的全等三角形; (2)求阴影部分的面积(结果保留π).PAOBDCEFOA BC21OAB ClD 例11.如图,一个圆锥的高为33cm ,侧面展开图是半圆. 求:(1)圆锥的母线长与底面半径之比; (2)求BAC ∠的度数;(3)圆锥的侧面积(结果保留π).【经典练习】1、已知圆锥的底面半径是3cm ,母线长为6cm ,则侧面积为________cm 2.(结果保留π) 2.一个扇形的圆心角为90°.半径为2,则这个扇形的弧长为________. (结果保留π) 3.已知扇形的圆心角为120°,半径为15cm ,则扇形的弧长为 cm (结果保留π).4. 如图,扇形OAB ,∠AOB=90︒,⊙P 与OA 、OB 分别相切于点F 、E ,并且与弧AB 切于点C ,则扇形OAB的面积与⊙P 的面积比是 .5.如图,正方形ABCD 边长为4,以BC 为直径的半圆O 交对角线BD 于E .则直线CD 与⊙O 的位置关系是 ,阴影部分面积为(结果保留π) .6.如图,菱形ABCD 中,AB =2 ,∠C =60°,菱形ABCD 在直线l 上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O 所经过的路径总长为 .(结果保留π) A BO ChlrABCDOE(第15题)AB OABOA ’O ’图(十三)图(十四)P7.如图,四边形OABC 为菱形,点B 、C 在以点O 为圆心的⌒EF 上,若OA =1,∠1=∠2,则扇形OEF 的面积为( ) A.6π B. 4π C. 3π D. 32π8.(2010年台湾省)如图(十三),扇形AOB 中,OA =10, ∠AOB =36︒。
圆、扇形、弓形的面积

圆、扇形、弓形的面积【重点难点解析】重点是圆面积,扇形面积、弓形面积公式,要能运用它们解决有关圆的面积、扇形面积、弓形面积的计算与证明问题.难点是扇形面积公式的推导,要理解圆心角为1°的扇形的面积等于圆面积的,圆心角为n°的扇形面积及于圆面积的即,注意:公式中的n没有单位.【基础知识精讲】一、基本公式1.圆的面积:S=πR22.扇形面积:S扇形==lR3.弓形面积:①弓形所含弧为劣弧时 S弓=S扇-S△②弓形所含弧为优弧时 S弓=S扇+S△③弓形所含弧为串圆时 S弓=S圆二、值得注意的问题1.扇形面积公式中的n与弧长公式中的一样,不带单位.2.对于一些没有面积计算公式的几何图形,可采用割补法,转化为学过的几何图形的面积和或差.对于弧形部分,一定要分清圆心和半径.典型例题〔例1〕已知如图7-65,PA切⊙O于A,PO交⊙O于C,且CP=CO,弦AB∥OP,⊙O的半径为2,求阴影部分的面积.图7-65解:连OA,OB∵PA为⊙O切线,∴OA⊥AP∵OA=OC=CP=OP∴∠OPA=30°,∴∠AOP=60°∵AB∥OP,∴∠OAB=∠AOPB=60°∵OA=OB,∴△AOB为等边三角形∴∠AOB=60°∴S扇形OAB==∵AB∥OP,∴S△ABP=S△AOB∴S阴影=S扇形OAB=〔例2〕已知:如图7-66⊙O的半径为R,直径AB垂直于弦CD,以B为圆心,以BC为半径作⊙B 交AB于点E,交AB的延长线于F,连结CB并延长交⊙B于点M,连结AM交⊙O于N,(1)求两圆公共部分的面积S.(2)求证AM·AN=2AE·AF图7-66(1)解:连结BD∵CD为⊙O直径∴∠CBD=90°∵CD⊥AB,OC=OD ∴CB=DB在Rt△CBD中,CD=2R∴BC=CDcos45°=2R· =R∴S=S⊙O+S弓形CDE=πR2+〔π( R)2- ( R)2〕=(π-1)R2(2)证明连AC∵AB为直径∴∠ACB=90°∵BC为⊙B半径∴AC为⊙B的切线∴AC2=AE·AF∵OA=OB ∴CA=CB∵MN·MA=MB·MC=BC·2BC=2BC2=2AC2∴AM·MN=2AE·AF〔例3〕已知:如图7-67,⊙O的长l是半径R的π倍,AC,BC是方程-2x2-(m-1)x+m+1=0的根,OC=1,求弓形AmB的面积.图7-67〔解〕延长线段OC交⊙O于E,F,作OG⊥AB于G,∴GB=ABl==R,∴n=130,∴∠AOB=120°∴∠GOB=60°在Rt△OGB中,sin∠GOB=,∴GB=R·sin60°=R∴AB=R,又cos∠GOB=,∴OG=R,∴S△ABD=AB·OG=× R× R=R2.∵AC、BC是方程-2x2-(m-1)x+m+1=0的根,∴AC·BC=- ①AC+BC=. ②又∵AC·BC=CE·CF=(R-OC)(R+OC)=R2-OC2=R2-1 ③AC+BC=AB=R ④∴由②,④得R=由①,③得R2-1=-解方程组R=R2-1=- 得R=∴S△ABC=R2=·S扇形OAmB==π∴弓形AmB的面积=S扇形OAmB-S△OAB=π- (平方单位).〔说明〕此题是一道代数几何综合问题,解决此题的关键是求出⊙O的半径,综合分析题的图形与已知条件,寻找与半径有关的式子,发现AC+BC=AB,AC·BC=CE·CF,而AB及CE·CF都与半径与关,再由题已知方程的根与系数关系,找到含R的方程组,从而求得R.〔例4〕如图7-68,已知半径为3cm和1cm的两个圆,⊙O1和⊙O2外切于点P,AB是它们的一条外公切线,切点分别为A,B,QP垂直于O1O2于P交AB于Q点,连O1Q和O2Q,求:图中阴影部分面积.图7-68〔解〕连O1A,O2B可求得外公切线长AB=2 =2 (cm)∵QP⊥O1O2,∴QP是⊙O1,⊙O2的内公切线,由切线长定理知AQ=QP=QB,∠=O1QO2=∠AQB=90°.∴QP=AB=(cm)在Rt△QO1P中,tg∠QO1P==,∴∠QO1P=30°,∴∠QO2P=60°∴S阴=S -S -S =O1O2·QP--=×4× - π- =2 - π(cm2).〔说明〕此题就是将一个不规则图形的面积化归为几个已学过的图形面积的和差形式.练习一、填空题1.扇形的弧长是2πcm,半径是10cm,则此扇形的面积是 .2.圆心角为n°,面积为S的扇形的半径是 .3.如果圆的周长是π,则圆的面积是 .4.如下图7-75,C,D是以AB为直径的半圆的三等分点,OC,OD是半径,且半径为长6,CD为弦,则图中阴影部分的面积是 .图7-75 图7-765.如图7-76,Rt△ABC中两直角边AC=4cm,BC=5cm,分别以AB,AC,BC为直径的三个半圆所围成的两个新月形(图中阴影部分)的面积和为平方厘米.图7-776.如图7-77,在△ABC中,∠C=90°,∠A=60°,以A为圆心,以AC的长为半径画弧与AB 相交于D,若图中阴影部分的面积为6πcm2,则AB= cm.7.若扇形的圆心角为150°,弧长为20πcm,则扇形的面积是 .二、选择题1.如图7-78,以边长为a的正三角形的三个顶点为圆心,以边长一半为半径画弧,则三弧所围成的阴影部分的面积是( )A. (2 -π);B. (2 -π);C. +D. a2.2.如图7-79,正方形ABCD的边长为1cm,以CD为直径在正方形内画半圆,再以C为圆心,1cm 长为半径画弧BD,则图中阴影部分的面积为( )A. cm2B. cm2C. cm2D. cm2图7-78 图7-79 图7-803.三个半径为R的圆两两外切,则夹在三个圆之间部分的面积是( )A. R2- πR2B. R2- πR2C.( -1)R2D. R2-R24.如图7-80,在扇形OAB中,∠AOB=90°,再以AB为直径作半圆,所得月牙形面积为( )A.大于S△OABB.等于S△OABC.小于S△OABD.以上都有可能三、解答题1.如图7-81所示,已知正方形ABCD的边长为2,以顶点A为圆心,AB为半径作,由AD的中点E,作EF∥AB,交BC于F,交于G,再以E为圆心,ED为半径作交EF于H,试求图中阴影部分的面积.图7-81 图7-822.如图7-82所示,正三角形ABC的高AD=4cm,以AD为直径作圆分别交AB、AC于E、F,求阴影部分的面积.四、1.如图7-83所示,已知直角梯形ABCD中,∠D=90°,∠A=30°,AB=4,以斜腰AB为直径的半圆切CD于E,交AD于F.求图中阴影部分的面积.图7-83 图7-842.如图7-84所示,已知⊙O1与⊙O2的公共弦为AB,若AB分别为⊙O1和⊙O2的内接正三角形和内接正六边莆的一边,且AB=a,求两圆公共部分的面积.答案:一、1.10πcm2 2. 3. 4.6π 5.10 6.12 7.140πcm2二、1.A 2.C 3.D 4.B。
专题01 扇形、弓形的周长和面积+刘子琳

1、扇形、弓形的周长和面积平面上到定点距离等于定长的点的集合称为圆.扇形、弓形都是圆的一部分,圆中一段弧及过该弧两端点的半径围成的图形称为扇形;由圆得弦及所对的弧围成的图形称为弓形.设圆的半径为r ,则圆的周长为2,C r π=面积2.S r π=若扇形的半径为r ,弧所对的圆心角为,n 则扇形弧长为,180n r l π=扇形周长2,180nC r r π=+面积2.360n r S π=弓形面积则需要考虑弧所对的是优弧还是劣弧,如图1-1,弓形ADB 的面积,ADB AOB S S S ∆=+弓形的周长C =弧长+弦长.由圆、扇形、弓形等构成的图形面积或周长计算通常需要一定技巧,处理这类问题的手段是分解组合、等积变形等等.例1 如图1-2,,AB CD 是O 的两条互相垂直的直径,且2,AB =以点B 为半径画弧AE 交CD 延长线与点,E 又四边形EFGO 为正方形,求阴影部分的面积.分析 将图形分割为AED 区域和DEFGB 区域,其中AED 区域的面积等于扇形ABE 的面积减去扇形AOD 的面积及OBE ∆的面积之和.解注意到,BA BE =且EO 垂直平分,AB 故ABE ∆为正60,ABE OE AB ∠=== 所以ADE ABE AOD OBE S S S S ∆=--CODBAE FGAC2342DEFGB EFGO DOB S S S ππ=--=-2434ππ=-=-故362S π=+-例2 如图1-3.正方形ABCD 的边长为,a 分别以,,,A B C D 为圆心,,a 为半径画弧,求四条弧所围成的阴影部分面积.解 如图1-3将正方形各部分进行分割,面积相等区域用相同的字母表示,于是 244x y z a ++= ① 232.4a x y z π++=②另外,设以点,A D 为圆心的弧交于点,E 则,AE DE AD ADE ==∆为正三角形。
所以222222.6434a a x y z a a ππ++=⨯-=- ③由①②③解得:2(16z a π=-于是22243)3S a z a π=-=+说明 此题关键是发现ADE ∆为正三角形,因此,请读者在解决问题时宜用心掘潜在条件.例3 如图1-4,扇形的半径为20,圆心角为144,,,,,,,B C D E F G H 是扇形弧线八等分点,求阴影部分的面积之和.BACD分析 合理分割,小心拼接解 连接OE 交DF 与点,M 交GC 与点,J 交HB 于点,K 交AI 与点,N 连接OF 与AI 与点,Q 连接OG 交HB 于点,p 连接.OH易证,,QNMF IQO OFM ION S S ∆≅∆=从而区域IHGFQ 为公布部分,故IOF FMNI S S = 又,GJO OKH ∆≅∆所以又区域GHP 为公共部分,故GHKJ HOG S S = 从而区域FMNI 中,23636040.IOF HOG IOG S S S S r ππ=-===由于对称性,于是在区域AIFD 中,80.S π=例4 在一个三边长为50,120,130的三角形内部与外部分别取出与三角形边上至少有一点的距离为2的所有点,求所有这些点构成的区域的面积.解 依题意得,所求面积区域为图1-5中111A B C ∆的外围部分面积.ABC ∆的三个顶点在一起处各有一个小扇形,半径均为2,合在一起恰好为2的圆,故图中ABC ∆外部面积212(50120130)26004.S ππ=⨯+++⨯=+其次,易知,111A B C ∆ABC ∆,且共内心,内切圆半径相差2,由于ABC ∆的内切圆半径为5012013020,2+-=故111A B C ∆的内切圆半径为18.所以 11111181100811008115012010022430.A B C ABC A B C ABC S S ∆∆∆=∆=⨯=⨯⨯⨯=例5 在边长为1的正五边形ABCDE 内,去掉所有与各点距离小于1,求余下部分面积.分析 关键是确定余下部分形状.解 如图1-6所示,分别以,,,,A B C D E 为圆心,以1为半径画弧,这些弧围成一个“曲边五边形”,MNPQR 其余的部分由五个等积的形如“曲边三角形” NBC 的图形组成.注意到曲边三角形NBC 与扇形NDC 的面积之和等于DNC ∆与扇形NCB 的面积之和,所以所求余下面积之和,5()310860605()436036046DNC NCB NDC S S S S πππ∆=+--=+-=-例6 已知正方形和三角形都外切于半径为1的圆,求证:正方形和三角形重叠部分且在圆的外部区域面积大于0.34.证明 当三角形的边与正方形所在边的直线不重合或者平行时,则三角形的边必将正方形减去一个角,此角BEAC ACB ODE F在重叠部分之外,先考虑部分面积的情况. 如图1-7 O 切正方形的边长与点,,E F ABC ∆与点,D 连接,,,,,OE OB OD OC OF 则四边形OEAF 为正方形.设,,1,1,AB x AC y BD x CD CF y ===-==-故有Rt ABC ∆中有222(11)x y x y -+-=+22()22(220, 1.xy x y xy x y x y +=++=+≥+-<<>)2121).2ABC S xy ∆=≤ 由于三角形最大边最多截去正方形三个“角”,从而三角形与正方形重叠面积至少为3,ABC S S ∆-若符合题意得区域面积为,S 则2223231)150.34.ABC S S S Sππ∆≥--≥-⨯-⨯=->证明正方形与三角形重叠部分的面积不可能等于5,但可无限接近. 习题11. ,,90,Rt ABC AC BC C ∆=∠=点D 在AB 上,以点A 为圆心,AD 为半径画弧交BC 交于点,E AC 的延长线与,F 若图中两个阴影部分面积相等,求:.AD DB2.在一块周长为500米的三角形草坪周围修筑一条宽1米的小路,且路的任何一处至少与草坪的某处距离为1米,求路的占地面积.3. AB 是半圆O 的直径,作OD AB ⊥交半圆O 与点,D 分别以点,A B 为圆心,AB 为半径画弧交,AD BD 延长线与,,F E 再以点D 为圆心,DE 为半径画弧,连接,E F ,若2,AB =求图中阴影部分面积.4.直角三角形,2,90,ABC AC CB C ==∠=将ACB ∆绕C 顺时针转90,求AB 扫过的区域面积.5.将一枚半径为1cm 的硬币置于n 边形内,硬币可在里面任意移动,但不可超越边界,求正n 边形内硬币不能接触到部分面积.6. 正三角形的边长为a ,过每两个顶点及中心O 在三角形内作弧,求阴影部分的面积S 阴.7.正三角形的边长为2a为半径画圆,求:圆的公共部分面积.8.ABC ∆的三条边, AB c BC a CA b ===,,作ABC ∆的内切圆,再作此内切圆的三条切线分别平行,,,AB BC CA 又得到三个小三角形,再作这三个小三角形的内切圆,求这四个圆的面积之和.习题11.区域ADEC 是扇形DAF 与ACB ∆公共部分,若图中阴影部分面积相等,2222221451,,2,,,2360482ABC DAF AD AD S S AC AD AC AB AB AD AB DB πππ∆======FEABCDOABC2.依题意,路的占地面积由三个矩形和三个扇形组成,三个矩形可拼成一个长500米宽1米的矩形,三个扇形正好拼成一个半径为1米的圆,从而占地面积3.250011(500)S ππ=⨯+⨯=+4.边AB 扫过的区域即图中的阴影部分,它由两个弓形ADB 和BEF 及曲边三角形DBE 组成,故2221113224 2.2242S πππ=⨯-⨯⨯+-⨯=-5.将各顶点处不能接触到部分拼合在一起,围成一个边心距为1cm 的正n 边形,但除去半径为6.连接,,OB OC 作21,.2OBC OH BC S a ∆⊥=⨯=设弧BOC 的圆心为1,O 由垂径定理得1,O B =从而扇形1BO C 中减去1BOCO 得到两个小弓形,两个小弓形恰好拼成“三叶玫瑰”中的一片叶子,所以213()233OBC S a S π∆⎡⎤=⨯-⎢⎥⎣⎦=222213.9632a a a a ππ⎡⎤-=-⎢⎥⎣⎦ 7.由于对称性,可将图中各部分面积分别用,,x y z 表示,相同字母表示面积相等,易知222133...,2)...63x y z x y z a ππ++=++==注意到222222)(2),BN CN a BC +=+==故,BN NC ⊥从而不难知道MN 垂直平,45,BC NBM BNM ∠=∠=22224512()236022NBD NBM y z S S a a a ππ∆⎡⎤+=-=-=-⎢⎥⎣⎦解得,()262a z π=+8. 8.设ABC ∆的面积为S ,半周长为p ,则11AB C ∆的半周长为22, ,p a QB A q -∆的半周长为p b -,33CA B ∆的半周长为,p c -则ABC ∆的内切圆半径Sr P=,又 112233ABCAB C AB C AB C ∆∆∆∆,从而1111212,AB C AB C S p a p a S S r S p p a p ∆∆⎛⎫--===⋅ ⎪-⎝⎭同理2222A BC S p b r S p bp ∆-==⋅-,3332A B C S p cr S p c p ∆-==⋅-,故 ()()()()()222212322222444222241S r r r r p a p b p c S p p p p ab c S p πππ=+++⎡⎤---=+++⎢⎥⎢⎥⎣⎦++=总 又()()()2,S p p a p b p c =--- 故S =总()()()()2223p a p b p c a b c p π---++,这里.2a b cp ++=(第7题图) (第8题图)D CBAMA BC。
六年级奥数:扇形的周长与面积和弓形面积

六年级奥数:扇形的周长与面积和弓形面积圆规和直尺圆规和直尺一块儿住进了文具盒。
圆规说:“我能画圆,你行吗?”“我横竖都会画,你行吗?”直尺很不服气。
文具盒听了,说:“别争了,谁能画一面扇形,谁就最行。
”圆规和直尺都为难了。
文具盒又说:“你俩一块儿合作,不就行了吗?”圆规和直尺同心协力,很快画好了扇形。
从此,它们成了好朋友。
编后语:圆规和直尺各有自己的长处,也各有自己的不足,两者是不应互相瞧不起的。
后来,由于双方的真诚合作,充分发挥了各自的优势,创造了许多新的事物。
这则寓言告诉我们这样一个道理:一个人的智慧和力量是有限的,众人合作就会创造出新事物,新生活。
知识框架圆的知识:1.当一条线段绕着它的一个端点O在平面上旋转一周时,它的另一端点所画成的封闭曲线叫做圆,点O叫做这个圆的圆心.2.连结一个圆的圆心和圆周上任一点的线段叫做圆的半径.3.连结圆上任意两点的线段叫做圆的弦.过圆心的弦叫做圆的直径.4.圆的周长与直径的比叫做圆周率.圆周上任意两点间的部分叫做弧.5.圆周长=直径×π.=半径×2π 圆面积=π×半径2.扇形的知识:1.扇形是圆的一部分,它是由圆心角的两条半径和圆心角所对的弧组成的图形.顶点在圆心的角叫做圆心角.2.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n. 3. 扇形中的弧长= 180r n π.扇形的周长= 180r n π+2r.扇形的面积=3602r n π =.弓形的知识:【例 1】 弦与它所对的弧所组成的图形叫做弓形.【一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)】重点:圆与扇形的面积和周长计算公式;弓形的面积公式。
难点:计算周长时,首先要分清围成这一图形的边有哪些,再正确计算。
计算面积时,首先要根据图形组合的形式,用会求的图形的面积去求的题目所要求的图形面积。
扇形公式数学六年级知识点

扇形公式数学六年级知识点扇形是我们在日常生活中经常遇到的一个图形,它在数学中也有一些相关的知识点和公式。
接下来,我将为大家介绍关于扇形的数学知识。
一、扇形的定义和性质扇形是由一个圆心、半径和一条弧所围成的图形。
我们可以通过一些常见的性质来了解扇形。
1.扇形的面积公式扇形的面积公式是扇形的重要知识点之一,它可以帮助我们计算扇形的面积。
根据扇形的定义,扇形的面积等于扇形的弧长与圆心角的乘积的一半。
即:扇形的面积 = 1/2 ×弧长 ×半径。
2.扇形的周长公式扇形的周长公式可以帮助我们计算扇形的周长。
根据扇形的定义,扇形的周长等于扇形的弧长与半径的和。
即:扇形的周长 = 弧长 + 2 ×半径。
3. 扇形的度数和弧度关系扇形的度数和弧度也是扇形的常见性质之一。
在数学中,我们通常使用度数或者弧度来表示角度的大小。
扇形的度数是指扇形的圆心角的度数。
180度等于π弧度。
二、扇形的应用扇形的知识不仅仅在数学中有应用,我们在日常生活中也会经常用到扇形的概念和公式。
1. 扇形在建筑设计中的运用在建筑设计中,扇形经常被用来设计圆顶、窗户以及圆形的空间布置。
通过掌握扇形的相关知识,可以帮助建筑设计师更好地进行设计和规划。
2. 扇形在计算器和钟表中的应用我们常见的计算器和钟表上通常会有一个扇形区域,这是因为扇形的面积和周长公式可以帮助我们计算出相应的数值。
同样地,通过掌握扇形的知识,我们可以更好地使用计算器和钟表。
3. 扇形在游乐园游戏设计中的应用在游乐园的一些游戏设计中,我们也可以看到扇形的应用。
例如,摩天轮的每个车厢就是一个扇形,游客可以坐在其中,欣赏全景。
通过对扇形的认识,游乐园设计人员可以更好地进行游戏的设计和安排。
总结:扇形是数学中的一个重要概念,它的应用十分广泛。
通过学习扇形的定义、性质和公式,我们可以更好地理解扇形,并在日常生活中应用这些知识。
希望本文对大家的数学学习有所帮助,让我们一起努力提高数学水平!。
弓形(弧形)面积全能公式计算表

弓形(弧形)面积全能公式计算表弓形(弧形)面积计算全能公式表静闲翡翠林于2014年6月27日创建2014年11月16日完善弧(弓)形面积==面积--扇形中的三角形面积弦心距==2√[半径2--(弦长÷2)2]弦心距==半径--矢高扇形中的三角形面积==2√[半径2--(弦长÷2)2]×半径÷2扇形面积==半径2×3.14÷360×弧对应圆心角周长==半径×2×3.14==直径×3.14弧与周长的%==弧÷周长×100弧对应圆心角==(弧÷周长×100)×360÷100弧对应圆心角==弧÷周长×360矢高==半径--弦心距说明:2√[……]:表示括号内的计算结果必须开二次方;弧两端点对应圆心的三角形就是扇形中的三角形(等腰);弦中点到圆心的距离,简称“弦心距”,也可叫“中位线”;弧中点到弦中点的距离,简称“矢高”;弧长、弦长、半径、矢高、中心角等可全部或部分从电子图中获取;以上计算公式可利用电子表格创建一个非常方便的功能计算表如下弓形(弧形)面积全能公式计算表部位名称弧长矢高弦长弦心距半径周长弧/ 周%中心角弧面积123456789计算式:2=5--4 6=5×2×3.14 7=1÷6×100 8=7×360÷100 8=1÷6×3604=5--√[52--(3÷2)2] 9=5×5×3.14÷360×8--3×(5--2)÷2 2居室台顶3.5910.3403.5084.3604.70029.51612.16643.7990.7912居厅台顶4.2660.4764.1214.2244.70029.51614.45352.0311.3213居厅台顶4.2640.3414.1906.2596.60041.44810.28837.0350.9593居室台顶6.9310.9376.7805.6636.60041.44816.72260.2003.675注:计算式中的黑体字是常数,其余数是计算列序的编号;。
六年级专题讲座(六) 圆 扇形 弓形及其组合图形的面积、周长

这一阶段,我们学习了圆:若它的半径为r,则周长为:2πr。
面积为:。
扇形:它是圆的一部分,若它的半径为r,圆心角为,则弧长为:2πr×,周长为:2πr×+2r。
面积为:×环形:由两个同心圆,圆周之间的部分组成。
以后在例题中,还会遇到弓形、“叶形”,将在题中一一说明。
求组合图形的面积、周长,可以用直接法、间接法、割补法、添补法、平移法、旋转法等等。
同学们在解题中一定要认真领会灵活运用,切实提高自己的观察、分析、综合能力。
下面看几个例题。
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
解:例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
六年级下册数学讲义奥数专题讲与练:[第22讲]圆和扇形的周长与面积(二)人教版
![六年级下册数学讲义奥数专题讲与练:[第22讲]圆和扇形的周长与面积(二)人教版](https://img.taocdn.com/s3/m/f5d779d4dd3383c4ba4cd235.png)
扇形:由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形。
扇形是圆的一部分扇形的圆心角占这个圆周角的几分之几扇形的弧长 C =2360n r π⨯扇形的面积 S =2360n r π⨯扇形的周长=+2×半径 2360nr π⨯(易错点是把扇形的周长等同于扇形的弧长)弓形: 弓形一般不要求周长,主要求面积。
一般来说,弓形面积=扇形面积-三角形面积。
(除了半圆)“弯角”:弯角的面积=正方形-扇形“谷子”:“谷子”的面积=弓形面积× 2(“迎春杯”决赛试题)如图中扇形的半径OA =OB =6厘米,∠AOB =45°,AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米。
(π≈3.14)O如图,直角三角形ABC 中,AB 是圆的直径,且AB =20,阴影甲的面积比阴影乙的面积大7,求BC 长。
(π取3.14)如图是一个直径为3cm 的半圆,让这个半圆以A 点为轴沿逆时针方向旋转60°,此时B 点移动到B '点,求阴影部分的面积。
(图中长度单位为cm ,圆周率按3计算)。
(北大附中“资优博雅杯”数学竞赛)如下图,在以 AB 为直径的半圆上取一点,分别以 AC 和 BC 为直径在△ABC 外作半圆AEC 和 BFC 。
已知 AC 的长度为 4,BC 的长度为 3,AB 的长度为 5。
试求阴影部分的面积。
(北大附中“资优博雅杯”数学竞赛)如图,阴影正方形的顶点分别是大正方形EFGH 各边的中点,分别以大正方形各边的一半为直径向外做半圆,再分别以阴影正方形的各边为直径向外作半圆,再分别以阴影正方形的各边为直径向外作半圆,形成8个“月牙形”。
这8个“月牙形”的总面积为32平方厘米,问大正方形EFGH的面积是多少平方厘米?1.圆的周长与面积2.扇形的周长与面积3.常用的数学思想常用的思想:转化思想等积变形借来还去容斥外围入手测试题1.如下图所示,扇形的半径OA =OB =6,∠AOB =45°,AC 垂直OB 于C ,那么途中cm 阴影部分的面积是( ) ( 取3)2cm πA .3B .4.5C .6D .92.如下图所示,甲比乙的面积大,,那么的长为( ) ( 取3)250cm 20AB cm =BC cm πA .5B .8C .10D .15A3.下图是由直径分别为4,6和10的三个半圆所组成的图形,图中阴影部分的面cm cm cm 积是( )cm 2 ( 取3)πA .30B .31.4C .43.5D .604.如下图所示,大半圆半径为4,小半圆直径为4,那么图中阴影部分的面积是cm cm ( ) ( 取3)2cm πA .5B .6C .10D .185.如下图所示,大圆半径为6,那么阴影部分的面积是( )(取3)πA .36B .48C .60D .72。
数学六年级上册——扇形和弓形的计算教案

本教案旨在帮助六年级的学生深入了解扇形和弓形的计算方法,掌握计算面积和周长的基本技巧,并能运用所学知识解决实际问题。
一、知识概述在学习扇形和弓形的计算前,我们先来了解一些相关概念。
1. 扇形扇形是一个由圆心角不超过 $360^{\circ}$ 的圆锥面的一部分,也就是说,扇形是以圆心为起点,所夹的圆弧和两条半径组成的一个部分。
扇形的面积公式为:$$S=\dfrac{\theta}{360^{\circ}}\times \pi r^2$$其中,$\theta$ 表示圆心角的度数,$r$ 表示扇形的半径。
2. 弓形弓形是一个由圆心角超过 $180^{\circ}$ 但不超过$360^{\circ}$ 的圆锥面的一部分,也就是说,弓形是以一条弧为底,两个半径的射线组成的一个部分。
弓形的面积公式为:$$S=\dfrac{\theta-180^{\circ}}{360^{\circ}}\times \pi r^2$$其中,$\theta$ 表示圆心角的度数,$r$ 表示弓形的半径。
3. 周长周长就是一个图形的边界长度。
对于扇形和弓形,周长的计算公式为:$C=2r+\theta r$其中,$\theta$ 表示圆心角的度数,$r$ 表示扇形或弓形的半径。
二、教学具体安排本教案将扇形和弓形的计算分为三个环节,分别是知识讲解、示范演示和练习巩固。
具体安排如下:1. 知识讲解教师可以先介绍扇形和弓形的基本概念和公式,并附上一些实例,帮助学生理解和记忆。
2. 示范演示教师可以选择一些典型的扇形和弓形题目,对解法进行讲解,并进行详细的演示。
演示时可以使用投影仪或者板书等工具来辅助讲解,让学生更加容易理解。
3. 练习巩固在教学的阶段,可以针对性地选择一些习题,让学生自主或配对完成,并对学生的答案进行详细的解答和讲解。
通过练习,让学生巩固所学知识,提高其运用知识解决实际问题的能力。
三、教学重点和难点1. 教学重点主要教学重点是扇形和弓形的面积和周长计算方法,以及解决实际问题的应用。
扇形弓形和面积的计算

扇形弓形和面积的计算扇形、弓形和面积的计算扇形弓形和面积的计算是几何学中的基本问题之一。
在解决这个问题时,我们需要了解扇形和弓形的定义、性质以及计算公式。
本文将详细介绍扇形和弓形的概念,并给出计算它们的面积的方法。
一、扇形的定义和性质:扇形是指以一个圆心角为度数,且半径固定的圆的一部分。
它的边界由圆心、半径和两条半径所夹的弧组成。
扇形在日常生活中经常出现,比如钟面、风扇等。
扇形面积的计算公式为:扇形面积 = (圆心角 / 360°) ×圆的面积其中,圆心角是扇形所对应的圆的圆心的角度,圆的面积是指整个圆的面积。
二、弓形的定义和性质:弓形是指以一条圆周弧为边界的封闭区域,与此同时,它还与圆心有关。
弓形可以理解为一个扇形减去一个三角形。
弓形面积的计算公式为:弓形面积 = 扇形面积 - 三角形面积其中,扇形面积的计算公式我们已经在上面提到过了,而三角形面积可以通过以下公式计算:三角形面积 = (底边长 ×高) / 2有了以上的定义和性质,我们可以通过以下步骤来计算扇形和弓形的面积:步骤一:确定扇形或者弓形所对应的圆的半径和圆心角。
步骤二:根据上述给出的公式计算扇形的面积。
步骤三:如果题目要求计算的是弓形的面积,则根据上述给出的公式计算三角形的面积。
步骤四:将步骤三得到的三角形的面积从步骤二得到的扇形的面积中减去,即可得到弓形的面积。
需要注意的是,计算面积时所用的单位一定要一致,比如长度单位和面积单位要统一。
例如,对于一个半径为5cm的扇形,其圆心角为60°,我们可以按照以下步骤计算其面积:步骤一:半径r = 5cm,圆心角θ = 60°。
步骤二:扇形的面积= (60° / 360°) × π × r² = (1/6) × 3.14 × 5² = 13.09cm²(保留两位小数)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扇形的周长与面积和弓形面积课前预习圆规和直尺圆规和直尺一块儿住进了文具盒。
圆规说:“我能画圆,你行吗?”“我横竖都会画,你行吗?”直尺很不服气。
文具盒听了,说:“别争了,谁能画一面扇形,谁就最行。
”圆规和直尺都为难了。
文具盒又说:“你俩一块儿合作,不就行了吗?” 圆规和直尺同心协力,很快画好了扇形。
从此,它们成了好朋友。
编后语:圆规和直尺各有自己的长处,也各有自己的不足,两者是不应互相瞧不起的。
后来,由于双方的真诚合作,充分发挥了各自的优势,创造了许多新的事物。
这则寓言告诉我们这样一个道理:一个人的智慧和力量是有限的,众人合作就会创造出新事物,新生活。
知识框架圆的知识:1. 当一条线段绕着它的一个端点O 在平面上旋转一周时,它的另一端点所画成的封闭曲线叫做圆,点O 叫做这个圆的圆心.2. 连结一个圆的圆心和圆周上任一点的线段叫做圆的半径.3. 连结圆上任意两点的线段叫做圆的弦.过圆心的弦叫做圆的直径.4. 圆的周长与直径的比叫做圆周率.圆周上任意两点间的部分叫做弧.5. 圆周长=直径×π.=半径×2π 圆面积=π×半径2.扇形的知识:1. 扇形是圆的一部分,它是由圆心角的两条半径和圆心角所对的弧组成的图形.顶点在圆心的角叫做圆心角. 2. 我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.3. 扇形中的弧长= 180r n π.扇形的周长= 180r n π+2r.扇形的面积=3602r n π =.弓形的知识:1. 弦与它所对的弧所组成的图形叫做弓形.【一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)】重难点重点:圆与扇形的面积和周长计算公式;弓形的面积公式。
难点:计算周长时,首先要分清围成这一图形的边有哪些,再正确计算。
计算面积时,首先要根据图形组合的形式,用会求的图形的面积去求的题目所要求的图形面积。
例题精讲【例1】将半径分别为3厘米和2厘米的两个半圆如图放置(小圆过大圆圆心),那么阴影部分的周长是多少厘米?【考点】圆与扇形 【难度】☆ 【题型】解答【解析】法1:阴影部分的周长=大半圆弧长+小半圆弧长+两条线段的长。
=大半圆弧长+小半圆弧长+(小圆直径大圆半径)+大圆半径 法2:阴影部分的周长=大半圆周长+小半圆周长-2×大半圆半径【答案】阴影部分的周长=2π×2×12+2π×3×12+(3−2)+3=5π+4=19.7(厘米)【巩固】 如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π【考点】圆与扇形 【难度】☆☆ 【题型】【解析】设圆的半径为r,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).【答案】20.5厘米【例2】在一个大圆内有许多个小圆,其直径的和等于大圆的直径。
请问:大圆周长与所有小圆周长之和哪一个更长?【考点】圆与扇形 【难度】☆☆ 【题型】【解析】设五个圆的直径分别为d 1,d 2,d 3,d 4,d 5,则d 5=d 1+d 2+d 3+d 4 所有小圆周长的和=πd 1+πd 2+πd 3+πd 4=π(d 1+d 2+d 3+d 4)=πd 5=大圆周长 【答案】大圆周长等于所有小圆周长的和。
【巩固】已知AB=50厘米,求图中各圆的周长总和。
AB【考点】 【难度】☆☆ 【题型】 【解析】各圆周长的和=直径为50厘米的大圆的周长。
【答案】各圆周长的和=50π=157cm【例3】夏天到了,爸爸从商店买了4瓶啤酒,售货员将4瓶啤酒捆扎在一起,如图7所示,捆4圈至少用绳子多少厘米?(接头处忽略不计)【考点】圆与扇形 【难度】☆☆☆ 【题型】【解析】捆每一圈的绳长可分解为四段相等的弧长与四段相等的线段长。
捆每一圈的四段弧长可以拼成一个整圆,每条线段的长度都等于直径的长度。
总绳长=(7×4+7π)×4(厘米)=(28π+112)(厘米)=199.92(厘米) 【答案】总绳长=(7×4+7π)×4(厘米)=(28π+112)(厘米)=199.92(厘米)⌒【巩固】有7根直径5厘米的塑料管,用一根橡皮筋把它们捆成一捆(如下图),此时橡皮筋的长度是多少?【考点】圆与扇形【难度】☆☆☆【题型】【解析】捆每一圈的绳长可分解为6段相等的弧长与6段相等的线段长。
捆每一圈的6段弧长可以拼成一个整圆,每条线段的长度都等于直径的长度。
总绳长=5×6+5π(厘米)【答案】总绳长=5×6+5π(厘米)=45.7(厘米)【例4】三个半径为100厘米且圆心角为60º的扇形如图摆放;那么,这个封闭图形的周长是________厘米.(π取3.14)【考点】圆与扇形【难度】☆☆☆【题型】=314厘米【解析】三个扇形的弧长相当于半径100厘米,圆心角为180度得扇形弧长,2×3.14×180360【答案】314厘米【巩固】分别以一个边长为2厘米的等边三角形的三个顶点为圆心,以2厘米为半径画弧,得到右图;那么,阴影图形的周长是_______厘米.( 取3.14)【考点】圆与扇形【难度】☆☆☆【题型】【解析】每段弧长为六分之一圆弧,因此阴影的周长=六个六分之一圆弧的长度和=一个圆的周长=2×2×3.14=12.56厘米【答案】12.56厘米【例5】求下列各个阴影部分的面积;(答案用表示即可)444【考点】圆与扇形【难度】☆【题型】解答【解析】(1)阴影面积=扇形面积三角形面积=π62×14−6×3÷2=9π−9(2)阴影面积=扇形面积三角形面积=π42×14−4×4÷2=4π−8(3)阴影面积=(扇形面积三角形面积)×2或者阴影面积=扇形面积×2−正方形面积=π42×14×2−4×4=8π−16(4)阴影面积=扇形面积−半圆面积=π22×14−π12×12=12π(5)阴影面积=正方形面积扇形面积=4×4−π42×14=16−4π【巩固】下列图形中的正方形的边长为4,求各个阴影部分面积的大小;(答案用表示即可)【考点】圆与扇形【难度】☆【题型】解答【解析】(1)阴影面积=4倍叶子的面积=4×(2×2−π22÷4)=16−4π(2)阴影面积=正方形面积1个圆面积=4×4−π22=16−4π【答案】(1)16−4π(2)16−4π【例6】在直角三角形中,已知三角形的两条直角边分别为3厘米和4厘米,以三角形的顶点为圆心的三个圆,半径长都是1厘米,求图中阴影部分的面积。
(π取3)【考点】圆与扇形【难度】☆☆☆【题型】【解析】阴影面积=直角三角形面积减去三个扇形面积之和三个扇形面积之和=半径为1的圆的面积【答案】阴影面积=3×4÷2−π×12=6−π(厘米)=3(厘米)【巩固】图中三个圆的周长都是25.12厘米,不用测量,计算出图中阴影部分的总面积。
【考点】圆与扇形【难度】☆☆☆【题型】【解析】先求出扇形的半径三个小扇形和在一起是一个角度为360-90=270度的扇形【答案】阴影部分的面积=(25.12÷3.14÷2)2×360−90360=37.68(平方厘米)【例7】两个圆半径都是1厘米,且图中两个阴影部分面积相等,求长方形ABOO’的面积。
(π取3)【考点】圆与扇形【难度】☆☆☆【题型】【解析】直接去求,设阴影部分的面积为a ,则长方形ABOO’的面积=14×π×12+14×π×12−a +a =12π=0.5平方厘米 【答案】0.5平方厘米【巩固】下图中,正方形的边长是5cm,图形的总面积是多少?(π取3)【考点】圆与扇形 【难度】☆☆☆ 【题型】【解析】一个圆的面积+四分之三圆的面积+(正方形面积-四分之一圆的面积) =一又二分之一圆面积+正方形面积=37.5π+25=137.5平方厘米 【答案】137.5平方厘米【例8】如下图所示,AB 是半圆的直径,O 是圆心,AC ̂=CD ̂=DB ̂,M 是CD ̂的中点,H 是弦CD 的中点.若N 是OB 上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是 ________平方厘米.【考点】圆与扇形 【难度】☆☆☆ 【题型】【解析】连接OC 、OD 、OH由于C 、D 是半圆的两个三等分点,M 是CD̂的中点,H 是弦CD 的中点,所以这个图形是对称的,由对称性可知CD 与AB 平行,所以,三角形CHN 和三角形CHO 的面积相等。
所以阴影部分的面积等于扇形COD 的面积的一半,而扇形COD 的面积又等于半圆面积的三分之一,所以阴影部分的面积等于半圆的六分之一,为12÷6=2平方厘米 【答案】2平方厘米 【巩固】如图,C 、D 是以AB 为直径的半圆的三等分点,O 是圆心,且半径为6.求图中阴影部分的面积.【考点】圆与扇形 【难度】☆☆☆ 【题型】 【解析】连接OC 、OD 、CD由于由于C 、D 是半圆的两个三等分点,所以三角形AOC 和三角形COD 都是正三角形,那么CD 与AB 平行,所以三角形AOC 和三角形COD 的面积相等,那么所以阴影部分的面积等于扇形COD 的面积。
为π×62×16==6π=18.84 【答案】18.84【例9】图中圆的直径AB 是4厘米,平行四边形ABCD 的面积是7平方厘米,角ABC 等于30°,求阴影部分的面积(π取3)【考点】圆与扇形 【难度】☆☆☆ 【题型】 【解析】连接CO ,,则阴影部分的面积=平行四边形ABCD 的面积扇形AOC 面积三角形COB 面积 阴影部分的面积=7−16×π×22−14×7=214−23π=3.25平方厘米或者是阴影部分的面积=72−(16×π×22−12×π×74)=214−23π=3.25平方厘米【答案】3.25平方厘米【巩固】三角形ABC 的面积是31.2平方厘米,圆的直径AC=6CM ,BD:DC=3:1,求阴影部分的面积。
