bipt概率论第四章试题含答案
概率论与数理统计第四章习题及答案

概率论与数理统计习题 第四章 随机变量的数字特征习题4-1 某产品的次品率为,检验员每天检验4次,每次随机地取10件产品进行检验,如发现其中的次品数多于1个,就去调整设备,以X 表示一天中调整设备的次数,试求)(X E (设诸产品是否为次品是相互独立的).解:设表示一次抽检的10件产品的次品数为ξP =P (调整设备)=P (ξ>1)=1-P (ξ≤1)= 1-[P (ξ=0)+ P (ξ=1)]查二项分布表1-=.因此X 表示一天调整设备的次数时X ~B (4, . P (X =0)=⎪⎪⎭⎫ ⎝⎛04××=.P (X =1)=⎪⎪⎭⎫ ⎝⎛14××=, P (X =2)= ⎪⎪⎭⎫⎝⎛24××=.P (X =3)=⎪⎪⎭⎫ ⎝⎛34××=, P (X =4)= ⎪⎪⎭⎫ ⎝⎛44××=. 从而E (X )=np =4×=习题4-2 设随机变量X 的分布律为Λ,2,1,323)1(1==⎭⎬⎫⎩⎨⎧-=+j j X P jjj ,说明X的数学期望不存在.解: 由于1111133322(1)((1))3j j j j j j j j j P X j j j j ∞∞∞++===-=-==∑∑∑,而级数112j j ∞=∑发散,故级数11133(1)((1))j jj j j P X j j∞++=-=-∑不绝对收敛,由数学期望的定义知,X 的数学期望不存在. 习题X-2 0 2 k p求)53(),(),(22+X E X E X E .解 E (X )=(-2)+0+2=由关于随机变量函数的数学期望的定理,知E (X 2)=(-2)2+02+22=E (3X 2+5)=[3 (-2)2+5]+[3 02+5]+[322+5]=如利用数学期望的性质,则有E (3X 2+5)=3E (X 2)+5=3+5=4.135)(3)53(,8.23.04.0)(,2.03.023.004.02)(222222)2(=+=+=⨯+⨯=-=⨯+⨯+⨯-=-X E X E X E X E习题4-4 设随机变量X 的概率密度为⎩⎨⎧≤>=-0,0,0,)(x x e x f x 求XeY X Y 2)2(;2)1(-==的数学期望.解22)(2)0(2)(2)2()()(00=-=+-=+⋅===∞-∞+-∞-+∞-∞-+∞∞-⎰⎰⎰⎰xx xx e dx e xe dx xe dx x dx x xf X E Y E I3131)()()(0303022=-==⋅==∞-∞+-∞+---⎰⎰xx x x X edx e dx e e e E Y E II 习题4-5 设),(Y X 的概率密度为⎩⎨⎧≤≤≤=其它,0,10,12),(2x y y y x f求)(),(),(),(22Y X E XY E Y E X E +.解 各数学期望均可按照⎰⎰+∞∞-+∞∞-=dxdy y x f y x g Y X g E ),(),()],([计算。
概率论与数理统计第四章测试题

概率论与数理统计第四章测试题第4章 随机变量的数字特征一、选择题1.设两个相互独立的随机变量X 和Y 的方差分别为4和2,则随机变量3X-2Y 的方差是 (A) 8 (B) 16 (C) 28 (D) 44 2.若随机变量X 和Y 的协方差(),0Cov X Y =,则以下结论正确的是( ) (A)X与Y 相互独立 (B) D(X+Y)=DX+DY(C)D(X-Y)=DX-DY (D) D(XY)=DXDY 3.设随机变量X和Y相互独立,且()()221122,,,XN YN μσμσ,则2Z X Y =+( )(A) ()221212,2N μμσσ++ (B) ()221212,N μμσσ++ (C) ()2212122,4N μμσσ++ (D) ()2212122,4N μμσσ--4.设二维随机变量(X,Y)服从二维正态分布,则随机变量ξ=X+Y 与η=X-Y 不相关的充要条件为(A) EX=EY (B) E(X 2)- (EX)2= E(Y 2)- (EY)2(C) E(X 2)= E(Y 2) (D) E(X 2)+(EX)2=E(Y 2)+ (EY)25.设X 、Y 是两个相互独立的随机变量且都服从于()0,1N ,则()max ,Z X Y =的数学期望()E Z =( ) (A)(B) 0(C)(D)6.设X 、Y 是相互独立且在()0,θ上服从于均匀分布的随机变量,则()min ,E X Y =⎡⎤⎣⎦( ) (A) 2θ (B) θ (C) 3θ(D) 4θ 7.设随机变量X 和Y 的方差存在且不等于0,则D(X+Y)=DX+DY 是X 和Y ( )(A) 不相关的充分条件,但不是必要条件 (B) 独立的充分条件,但不是必要条件 (C) 不相关的充分必要条件 (D) 独立的充分必要条件8.若离散型随机变量X的分布列为(){}()1121,2,2nn nP X n =-⋅==,则()E X =()(A) 2 (B) 0 (C) ln2 (D) 不存在9.将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数,则X 和Y 的相关系数等于(A )-1 (B )0 (C )21 (D )110.设随机变量X 和Y 独立同分布,具有方差2σ>0,则随机变量U=X+Y 和V=X-Y(A )独立 (B) 不独立 (C ) 相关 (D) 不相关11.随机变量X 的方差存在,且E(X)=μ,则对于任意常数C ,必有 。
概率论习题及解答-第四章特征函数

∑n
∑ m
= xiP(Ai) + yjP(Bj) = E(ξ) + E(η).
i=1
j=1
练习4.1.2 假设简单随机变量 ξ 和 η 相互独立, 试证明
E(ξη) = E(ξ)E(η).
证明: 不妨设 ξ(Ω)(= {x1, · · · , xn}, )η((Ω) = {y1, · · · , ym}), 则
的一个新分割, 且
∑n ∑ m
ξ +η =
(xi + yj )1AiBj .
i=1 j=1
所以由数学期望的定义和概率的有限可加性得
∑n ∑ m
∑n ∑ m
∑n ∑ m
E(ξ + η) =
(xi + yj)P(AiBj) =
xiP(AiBj) +
yj P(AiBj )
i=1 j=1
i=1 j=1
i=1 j=1
解: 记 ξ = min{ξ1, ξ2, · · · , ξn}, η = max{ξ1, ξ2, · · · , ξn}, 则 (ξ, η) 的联合密度函数
p(ξ,η)(x, y) = n(n − 1)(y − x)n−2, 0 < x < y < 1,
所以 ξ 和 η 的边缘密度函数分别为 ∫∞
n→∞
2
证明: 令 ζn = ξn − η, 则 0 ζn ↑ ξ − η, 由单调收敛定理和数学期望的线性性质得
lim
n→∞
E(ζn)
=
E(ξ
−
η)
=
E(ξ)
−
E(η).
注意到 E(ζn) = E(ξn) − E(η), 由此得证结论.
概率论与数理统计第四章补充习题

第四章补充习题一、 填空题1、 设随机变量X 则Y X 和的相关系数XY ρ= ,=),(2222Y X Cov Y X 的协方差和 。
2、设随机变量Y X 和的数学期望分别为22和-,方差分别为41和,而相关系数为5.0-,则根据切比雪夫不等式{}≤≥+6Y X P 。
3、设随机变量Y X 与相互独立且均服从正态分布2(0,)N , 则)(Y X E -= ,=-)(Y X D 。
4、随机变量ξ服从指数分布,参数λ= 时,72)(2=ξE 。
5、设随机变量Y X ,,2)(-=X E ,4)(=Y E ,4)(=X D ,9)(=Y D ,5.0-=XY ρ, =-+-)323(22Y XY X E 。
6、设随机变量Y X 与的相关系数9.0=XY ρ,若4.0-=X Z ,则=YZ ρ 。
7、设Y X ,同分布,密度函数均为⎪⎩⎪⎨⎧<<=其它若0102)(2tx xtx f ,使t Y X C E 1))2((=+, 则=C 。
8、设随机变量X 的数学期望和方差均为0,则{}=≠0X P 。
9、将一枚均匀硬币连掷3次,用X 表示正面出现的总次数,Y 表示第一次掷得的正面数, 则=)(XY E ,=),(Y X Cov ,=XY ρ 。
二、选择题1、设随机变量Y X 和独立同分布,记 Y X V Y X U +=-=,,则随机变量V U 与必然( ) (A )不独立, (B) 独立, (C) 相关系数不为零, (D) 相关系数为零。
2、将一枚硬币掷n 次,以Y X 和分别表示正面朝上和反面朝上的次数,则Y X 和的相关系数等于( )。
(A )1- (B) 0 (C)21(D) 1。
3、设随机变量Y X 和相互独立且分别服从正态分布(0, 1)N 和(1, 1)N ,则( )。
(A) {}210=≤+Y X P , (B) {}211=≤+Y X P , (C) {}210=≤-Y X P , (D) {}211=≤-Y X P 。
概率论第四章 习题答案

1 ⎛2⎞ 1 DX = EX − ( EX ) = − ⎜ ⎟ = . 2 ⎝ 3 ⎠ 18 1 2 DZ = 4 DX = 4 × = . 18 9
【解毕】
9.在一次拍卖中,两人竞买一幅名画,拍卖以暗标的形式进行,并以最高价成交.设两人 的出价相互独立且均服从(1,2)上的均匀分布,求这幅画的期望成交价. 解:设两人的出价分别为随机变量 X , Y ,则这幅画的期望成交价为 Z = max { X , Y } 由题意知, X 与Y 独立,且 X ∼ U (1, 2); Y ∼ U (1, 2) 先求 Z 的分布函数 当 1 < z < 2 时, F ( z ) = P ( Z £ z ) = P (max { X , Y } £ z ) = P ( X £ z ,Y £ z )
= P( X £ z ) P (Y £ z ) = ( z -1)2
当 z £ 1 时, F ( z ) = 0 ;当 z ³ 2 时, F ( z ) = 1 于是 Z 的密度函数为 f ( z ) = ï í
ì2( z -1),1 < z < 2 ï ï 0, 其它 ï î 5 3
EZ = ò
+¥
3 X .求: ( 1)常数 a, b, c; (2) Ee . 4
【解】 (1)由概率密度的性质知,有
+∞ 2 4
1=
又因为
−∞
∫
f ( x )dx = ∫ axdx + ∫ ( cx + b )dx = 2a + 6c + 2b.
0 2
+∞
2
4
2 = EX =
−∞
∫ xf ( x )dx = ∫ xiaxdx + ∫ x ( cx + b )dx
概率论第四章习题答案

第四章复习题答案一、单项选择1.设随机变量X 具有分布P{X=k}=51,k=1,2,3,4,5,则E (X )=( B ) A.2 B.3 C.4D.52.设随机变量X 与Y 相互独立,X 服从参数为2的指数分布,Y ~B (6,21),则E(X-Y)=( A )A .-1B .21C .2D .5 3.设二维随机变量(X ,Y )的协方差Cov(X ,Y )=61,且D (X )=4,D (Y )=9,则X 与Y 的相关系数XY ρ为( B )()(),XY Cov X Y D X D Y ρ=A .2161 B .361 C .61 D .1 4. 设随机变量X 和Y 独立同分布,X ~N (μ,σ2),则( B ) A.2X ~N (2μ,2σ2) B.2X -Y ~N (μ,5σ2) C.X +2Y ~N (3μ,3σ2)D.X -2Y ~N (3μ,5σ2)5.设EX 2=8,DX =4,则E (2X )=( D ) A.1 B.2 C.3 D.46.对任意两个随机变量X 和Y ,由D (X +Y )=D (X )+D (Y )可以推断( A ) A.X 和Y 不相关B.X 和Y 相互独立C.X 和Y 的相关系数等于-1D.D (XY )=D (X )D (Y )7.已知随机变量X 服从参数为2的泊松分布,则随机变量X 的方差为( D ) A .-2 B .0 C .21D .2 8.设随机变量X 与Y 相互独立,且X ~B (16,0.5),Y 服从参数为9的泊松分布,则D (X -2Y +3)=( C )A.-14B.-11C.40D.439.已知随机变量X 服从参数为2的指数分布,则随机变量X 的期望为( D )A .-21B .0C .21D .2 二、填空1.设随机变量X 服从正态分布N (2,4),Y 服从均匀分布U (3,5),则E (2X-3Y )= ___-8___. 2.设随机变量X 与Y 相互独立,其分布律分别为则E (XY )=__2______.3.设X ,Y 为随机变量,已知协方差Cov(X ,Y )=3,则Cov(2X ,3Y )=____18___. 4.设X~N (0,1),Y~B (16,21),且两随机变量相互独立,则D(2X+Y)= __8______ 5.设随机变量X 的概率密度为⎩⎨⎧≤≤=,,0;10,2)(其他x x x f 则E (X )=__23______.6.已知E (X )=2,E (Y )=2,E (XY )=4,则X ,Y 的协方差Cov (X,Y )=____0_____. 7.设随机变量X ~N (0,4),则E (X 2)=_____4____.8.设X ~N (0,1),Y =2X -3,则D (Y )=____4__. 三、计算1.某柜台做顾客调查,设每小时到达柜台的顾额数X 服从泊松分布,则X~P (λ),若已知P (X=1)=P (X=2),且该柜台销售情况Y (千元),满足Y=21X 2+2.试求:(1)参数λ的值;21!2!e e λλλλ--=,=2λ.(2)一小时内至少有一个顾客光临的概率;{}{}21101-P X P X e -≥=-== (3)该柜台每小时的平均销售情况E (Y ). ()==2E Y λ2. 2021年东京奥运会即将召开,某射击队有甲、乙两个射手,他们的射击技术可用下表给出。
概率论第四、五章课后习题答案

第四章 随机变量的数字特征2.某产品的次品率为0.1,检验员每天检验4次,每次随机地取10件产品进行检验,如发现其中的次品数多于1,就去调整设备。
以X 表示一天中调整设备的次数,试求E (X )。
(设诸产品是否为次品是相互独立的。
)解:先求检验一次,决定需要调整设备的概率。
设抽检出次品件数为Y ,则Y ~b (10,0.1).记需调整设备一次的概率为p ,则2639.01.09.01109.01}1{}0{1)1(910=⨯⨯⎪⎪⎭⎫ ⎝⎛--==-=-=>=Y P Y P Y P p 又因各次检验结果相互独立,故)2639.0,4(~b X X 的分布律为于是0556.12639.0444)1(43)1(62)1(41)(43223=⨯==⨯+-⨯+-⨯+-⨯=p pp p p p p p X E以后将会知道若X ~b (n ,p ),则np X E =)(.6.(1)设随机变量X 的分布律为求)53(),(),(22+XE X E X E(2)设)(~λπX ,求)11(+X E解:(1)E (X )=(-2)⨯0.4+0⨯0.3+2⨯0.3=-0.2 由关于随机变量函数的数学期望的定理,知E (X 2)=(-2)2⨯0.4+02⨯0.3+22⨯0.3=2.8E (3X 2+5)=[3⨯ (-2)2+5]⨯0.4+[3⨯ 02+5]⨯0.3+[3⨯22+5]⨯0.3=13.4如利用数学期望的性质,则有E (3X 2+5)=3E (X 2)+5=3⨯2.8+5=13.4(2)因)(~λπX ,故!}{k ek X P k λλ-==)1(1)1()1!(!)!1()!1(}{11)11(1100λλλλλλλλλλλλλλλλ--∞=-∞=-∞=+-∞=-∞=-=-=-==+=+==+=+∑∑∑∑∑eeej ej ek ek ek X P k X E j jj jk k k k k7. (1)设随机变量X 的概率密度为⎩⎨⎧≤>=-0,00,)(x x e x f x求(I)Y =2X ;(II) Y =e -2X 的数学期望(2)设随机变量n X X X ,,2,1 相互独立,且都服从(0,1)上的均匀分布,(I)求},,max{2,1n X X X U =的数学期望;(II)求},,min{2,1n X X X V =的数学期望。
概率论第四章习题解答(全)

(0.9)10 (0.9)9 3486 0.3874 0.7361
则需要调整设备的概率
P{Y 1} 1 P{Y } 1 0.7361 0.2639
(3)求一天中调整设备的次数 X 的分布律 由于 X 取值为 0,1,2,3,4。 p 0.2369 ,则 X B (4, 0.2369) 于是
个随机变量,其概率密度为
1 x, 0 x 1500, 15002 1 f ( x) ( x 3000),1500 x 3000, 2 1500 0, 其它
求 E( X ) 解 按连续型随机变量的数学期望的定义有
0 1500
E ( X ) xf ( x)dx xf ( x)dx
X p
2
3
4
9
1 8
5 8
1 8
1 8
所以
1 5 1 1 15 E( X ) 2 3 4 9 。 8 8 8 8 4
(2)因为 Y 的取值为 2,3,4,9 当 Y 2 时,包含的字母为“O”,“N”,故
P{Y 2}
1 C2 1 ; 30 15
当 Y 3 时,包含的 3 个字母的单词共有 5 个,故
P (Ck ) P ( Ak | A1 A2 Ak 1 ) P ( Ak 1 | A1 A2 Ak 2 ) P ( A2 | A1 ) P ( A1 )
而
P{ X 1} P ( A1 )
1 2
1 1 P{ X 2} P ( A1 A2 ) P ( A2 | A1 ) P ( A1 ) 3 2 1 2 1 1 1 P ( A2 | A1 A2 ) P ( A2 | A1 ) P ( A1 ) , 4 3 2 4 3 一般地,若当 X k 时,盒中共有 k 1 只球,其中只有一只白球,故 P ( X k ) P ( A1 A2 Ak 1 Ak ) P ( Ak | A1 A2 Ak 1 ) P ( Ak 1 | A1 A2 Ak 2 ) P ( A2 | A1 ) P ( A1 ) 1 k 1 k 2 1 2 1 1 1 k 1 k k 1 4 3 2 k k
概率论与数理统计第四章习题参考答案

=
⎡ E⎢
1
⎢⎣ n −1
n i =1
(Xi
−
⎤ X )2 ⎥
⎥⎦
=
1 n −1
⎡ E⎢
⎢⎣
n i =1
X
2 i
−
nX
2⎤ ⎥ ⎥⎦
=
1 n −1
⎡n ⎢ ⎢⎣ i=1
E
(
X
2 i
)
−
nE( X
2⎤ )⎥ ⎥⎦
∑[ ] [ ] =
1 n −1
⎧ ⎨ ⎩
n i =1
D(X i ) + E 2 (X i )
X −µ 3/2
<
⎫ 1.96⎬
=
0.95
⎭
故,正态总体均值 µ 的 95%的置信区间为 (X − 2.94, X + 2.94)
代入样本值得正态总体均值 µ 的 95%的置信区间为(-2.565,3.315)。
(2)当σ 未知时,由 T = X − µ ~ t(n − 1) 即T = X − µ ~ t(3) ,所以
n
−a n
=0 =0
无解。由此不能求得
a,
b
的极大似然估计量。
⎩ ∂b
b−a
解:X
的概率密度为
f
(x)
=
⎪⎧ ⎨b
1 −
a
,
a
≤
x
≤
b
,
⎪⎩ 0, 其它
似然函数为 L(a, b) = 1 , θ1 ≤ xi ≤ θ 2 ,i = 1,2,L, n , (b − a)n
对于给定的样本值 (x1 , x2 ,L, xn )
−
n
D(
概率论第四章习题答案

概率论第四章习题答案概率论是数学中的一个重要分支,它研究了随机现象的规律性和不确定性。
在概率论的学习过程中,习题是不可或缺的一部分,通过解答习题可以加深对概率论知识的理解和运用。
本文将针对概率论第四章的习题进行解答,以帮助读者更好地掌握这一章节的内容。
第一题:某班级有30名学生,其中有10名男生和20名女生。
从中随机选取2名学生,求选出的两名学生都是男生的概率。
解答:首先,计算总的样本空间。
从30名学生中选取2名学生,共有C(30, 2)= 435种可能的选法。
然后,计算选出的两名学生都是男生的样本空间。
从10名男生中选取2名学生,共有C(10, 2) = 45种可能的选法。
所以,选出的两名学生都是男生的概率为P = 45/435 = 1/9。
第二题:某班级有30名学生,其中有10名男生和20名女生。
从中随机选取4名学生,求选出的学生中至少有1名男生的概率。
解答:首先,计算总的样本空间。
从30名学生中选取4名学生,共有C(30, 4)= 27,405种可能的选法。
然后,计算选出的学生中全是女生的样本空间。
从20名女生中选取4名学生,共有C(20, 4) = 4,845种可能的选法。
所以,选出的学生中至少有1名男生的概率为P = 1 - 4,845/27,405 =22,560/27,405 ≈ 0.822。
第三题:某班级有30名学生,其中有10名男生和20名女生。
从中随机选取6名学生,求选出的学生中至少有3名男生的概率。
解答:首先,计算总的样本空间。
从30名学生中选取6名学生,共有C(30, 6) = 593,775种可能的选法。
然后,计算选出的学生中全是女生或者只有1名男生或者只有2名男生的样本空间。
从20名女生中选取6名学生,共有C(20, 6) = 38,760种可能的选法。
从10名男生中选取1名学生,共有C(10, 1) = 10种可能的选法。
从10名男生中选取2名学生,共有C(10, 2) = 45种可能的选法。
概率论第四章习题解答
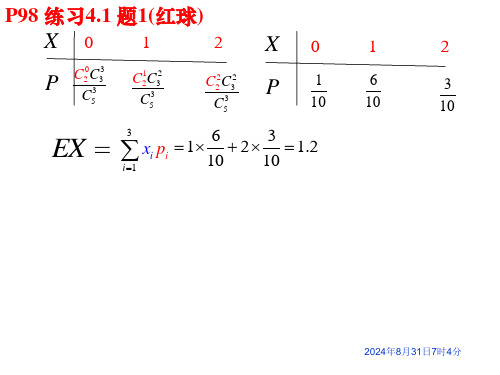
X9
EX 9
9
9
8 9
20
2024年8月31日7时4分
P104 练习4.2 题1 SD 1
1,1
f XY
x,
y
1 0
0 x 1, x y x 其它
yx
DZ D2X 1 4DX
EX xf x, ydxdy
0D
y x 1
1 0
x x
xdy
dx
1 2x2dx 2
P113 习题四 一 填空题 7 X与Y相互独立
f
X
x
2x
0
0
x 其它
1,fY
y
x y t
FT t PT t P X Y t fXY x, y dxdy
x yt
1当t 0时:FT t 0dxdy 0
0
x yt
2 当0 t时:FT
t
t
dx
tx 25e5x5 ydy
0
0
1 e5t 5te5t
t,0
x
FT
t
1
e5t
0
5te5t
t0 t0
33
2 EX 2
xi2 pij
i1 j1
20.1 30.3 30.1 2
33
3 EY 2
yi2 pij
12 0.212 0.112 0.1 22 0.1
22 0.132 0.332 0.1 4.8
i1 j1
12 0.2 12 0.1 12 0.1
12 0.1 12 0.1 0.6
2024年8月31日7时4分
P100 练习4.1 题12
2
f XY
x,
y
x
(完整版)概率论第四章答案

习题4-11. 设随机变量X求()E X ;E (2-3 X );2()E X ;2(35)E X +.解 由定义和数学期望的性质知2.03.023.004.0)2()(-=⨯+⨯+⨯-=X E ; (23)23()23(0.2) 2.6E X E X -=-=-⨯-=; 8.23.023.004.0)2()(2222=⨯+⨯+⨯-=X E ; 4.1358.235)(3)53(22=+⨯=+=+X E X E . 2. 设随机变量X 的概率密度为,0,()0,0.xe xf x x -⎧>⎪=⎨⎪⎩≤求Xe Z X Y 22-==和的数学期望.解()(2)2()22x E Y E X E X x x ∞-====⎰e d ,2201()()3Xx x E Z E ee e dx ∞---==⋅=⎰. 3. 游客乘电梯从底层到电视塔顶观光, 电梯于每个整点的第5分钟、第25分钟和第55分钟从底层起行. 假设一游客在早八点的第X 分钟到达底层侯梯处, 且X 在区间[0, 60]上服从均匀分布. 求该游客等候电梯时间的数学期望. 解已知X 在[0,60]上服从均匀分布, 其概率密度为1,060,()600,.x f x =⎧⎪⎨⎪⎩≤≤其它记Y 为游客等候电梯的时间,则5,05,25,525,()55,2555,65,5560.X X X X Y g X X X X X -<-<==-<-<⎧⎪⎪⎨⎪⎪⎩≤≤≤≤因此, 6001()[()]()()()60E Y E g X g x f x dx g x dx ∞-∞===⎰⎰()5255560525551(5)(25)(55)(65)60x dx x dx x dx x dx =-+-+-+-⎰⎰⎰⎰=11.67(分钟)..14. 某保险公司规定, 如果在一年内顾客的投保事件A 发生, 该公司就赔偿顾客a 元. 若一年内事件A 发生的概率为p , 为使该公司受益的期望值等于a 的10%, 该公司应该要求顾客交多少保险费?解 设保险公司要求顾客交保费c 元. 引入随机变量⎩⎨⎧=.A ,0,A 1不发生事件发生事件,X 则{1},{0}1P X p P X p ====-. 保险公司的受益值1,,0.c a X Y c X -=⎧=⎨=⎩, 于是 ()(){1}{0}E Y c a P X c P X ap c =-⨯=+⨯==-+. 据题意有10%ap c a -+=⨯, 因此应要求顾客角保费(0.1)c p a =+.习题4-21. 选择题(1) 已知(1,(3))E D X X =-= 则2[3(2)]()E X-=.(A) 9. (B) 6. (C) 30. (D) 36. 解22[3(2)]3(44)E X E X X -=-+23[()4()4]E X E X =-+23{()[()]4()4}D X E X E X =+-+ 3(3144)36=⨯+++=.可见,应选(D).(2) 设~(,),(6,( 3.6))B n p E D X X X ==, 则有( ).(A)10, 0.6n p ==. (B) 20, 0.3n p ==. (C) 15, 0.4n p ==. (D) 12, 0.5n p ==.解 因为~(,),B n p X 所以E (X )=n p,D (X )=np (1-p ), 得到np =6, np (1-p )=3.6 . 解之,n=15 , p =0.4 . 可见,应选(C).(3) 设X 与Y 相互独立,且都服从2(,)N μσ, 则有( ).(A) ()()()E X Y E X E Y -=+. (B) ()2E X Y μ-=.(C)()()()D X Y D X D Y -=-. (D) 2()2D X Y σ-=.解 注意到0)()()(=-=-Y E X E Y XE .由于X 与Y 相互独立,所以22)()()(σ=+=-Y D X D Y X D . 选(D).(4) 在下列结论中, 错误的是( ).(A) 若~(,),().X B n p E X np =则(B) 若()~1,1X U -,则()0D X =. (C) 若X 服从泊松分布, 则()()D X E X =.(D) 若2~(,),X N μσ 则~(0,1)X N μσ-.解)1,1(~-U X , 则3112212)()(22==-=a b X D . 选(B). 2. 已知X , Y 独立, E (X )= E (Y )=2, E (X 2)= E (Y 2)=5, 求E (3X -2Y ),D (3X -2Y ).解 由数学期望和方差的性质有E (3X -2Y )= 3E (X )-2 E (Y )=3×2-2×2=2,(32)9()4()D X Y D X D Y -=+})]([)({4})]([)({92222Y E Y E X E X E -⨯+-⨯=13)45(4)45(9=-⨯+-⨯=.3. 设随机变量X 1, X 2, X 3相互独立, 其中X 1服从区间[0, 6]上的均匀分布,22~0,2X N (), 3~3X P (), 记12323Y X X X =-+, 求E (Y )和D (Y ) .解 由题设知21122(60)()3,()3,()0,()4,12E X D X E X D X -=====3321111(),()39E X D X λλ====.由期望的性质可得123123()(23)()2()3()13203 4.3E Y E X X X E X E X E X =-+=-+=-⨯+⨯=又123,,X X X 相互独立, 所以123123()(23)()4()9()1344920.9D Y D X X X D X D X D X =-+=++=+⨯+⨯=4. 设两个随机变量X 和Y 相互独立, 且都服从均值为0, 方差为12的正态分布, 求||X Y -的的期望和方差.解 记UX Y =-. 由于11~(0,),~(0,)22X N Y N , 所以()()()0,E U E X E Y =-= ()()()1D U D X D Y =+=.由此~(0,1)U N . 进而2222220 (||)(||)||x x xE X Y E U x dx xe dx e+∞---+∞+∞-∞-====⎰2222(||)()()[()]101E U E U D U E U==+=+=.故而2222 (||)(||)(||)[(||)]11D X Y D UE U E Uπ-==-=-=-.5. 设随机变量]2,1[~-UX, 随机变量⎪⎩⎪⎨⎧<-=>=.0,1,0,0,0,1XXXY求期望()E Y和方差)(YD.解因为X的概率密度为1,12,()30,.Xxf x-=⎧⎪⎨⎪⎩≤≤其它于是Y的分布率为00--11{1}{0}31()d d3XP Y P X f x x x∞=-=<===⎰⎰,{0}{0}0P Y P X====,+2002{1}{0}31()d d3XP Y P X f x x x∞==>===⎰⎰.因此121()1001333E Y=-⨯+⨯+⨯=,222212()(1)001133E Y=-⨯+⨯+⨯=.故有2218()()[()]199D YE Y E Y=-=-=.6. 设随机变量U在区间[-2, 2]上服从均匀分布, 随机变量1,1,1, 1.UXU--=>-⎧⎨⎩若≤若1,1,1, 1.UYU-=>⎧⎨⎩若≤若求E(X+Y), D(X+Y).解(1) 随机变量(X, Y)的可能取值为(-1,-1),(-1,1),(1,-1),(1,1).{1,1}{P X Y P U =-=-=≤1,U -≤-1-211}{1}41d 4P U x =-==⋅⎰≤, {1,1}{P X Y P U =-==≤1,U -1}0>=, {1,1}{1P X Y P U ==-=>-,U ≤1111}21d 4x -==⋅⎰, 211{1,1}{1,1}41d 4P X Y P U U x ===>->==⋅⎰.于是得X 和Y 的联合密度分布为(2) Y X +和)(Y X +的概率分布分别为由此可见22()044E X Y +=-+=;2()[()]2D X Y E X Y +=+=.习题4-31. 选择题(1) 在下列结论中, ( )不是随机变量X 与Y 不相关的充分必要条件(A) E (XY )=E (X )E (Y ). (B) D (X +Y )=D (X )+D (Y ). (C) Cov(X ,Y )=0. (D) X 与 Y 相互独立.解 X 与 Y 相互独立是随机变量X 与Y 不相关的充分条件,而非必要条件. 选(D).(2) 设随机变量X 和Y 都服从正态分布, 且它们不相关, 则下列结论中不正确的是( ).(A) X 与Y 一定独立. (B) (X , Y )服从二维正态分布. (C) X 与Y 未必独立. (D) X +Y 服从一维正态分布.解 对于正态分布不相关和独立是等价的. 选(A).(3) 设(X , Y )服从二元正态分布, 则下列说法中错误的是( ).(A) (X , Y )的边缘分布仍然是正态分布.(B) X 与Y 相互独立等价于X 与Y 不相关. (C) (X , Y )是二维连续型随机变量.(D)由(X , Y )的边缘分布可完全确定(X , Y )的联合分布. 解 仅仅由(X , Y )的边缘分布不能完全确定(X , Y )的联合分布. 选(D)2 设D (X )=4, D (Y )=6, ρXY =0.6, 求D (3X -2Y ) .解(32)9()4()12Cov(,)D X Y D X D Y X Y -=+-)()(126449Y D X D XY ⨯⨯-⨯+⨯=ρ727.24626.0122436≈⨯⨯⨯-+=.3. 设随机变量X , Y 的相关系数为5.0, ,0)()(==Y E X E 22()()2E X E Y ==,求2[()]E XY +.解222[()]()2()()42[Cov(,)()()]E X Y E X E XY E Y X Y E X E Y +=++=++42420.526.ρ=+=+⨯⨯=4. 设随机变量(X , Y )若E (XY )=0.8, 求常数a ,b 解 首先由∑∑∞=∞==111i j ijp得4.0=+b a . 其次由0.8()100.420110.2210.22E XY a b b ==⨯⨯+⨯⨯+⨯⨯+⨯⨯=+ 得3.0=b . 进而1.0=a . 由此可得边缘分布律于是 , . 故 Cov(,)()()()0.8 1.40.50.1X Y E XY E X E Y =-=-⨯=.5. 已知随机变量(,)~(0.5,4;0.1,9;0)X Y N , Z =2X -Y , 试求方差D (Z ), 协方差Cov(,)X Z , 相关系数ρXZ .解 由于X ,Y 的相关系数为零, 所以X 和Y 相互独立(因X 和Y 服从正态分布). 因此25944)()(4)2()(=+⨯=+=-=Y D X D Y X D Z D ,Cov(,)Cov(,2)2Cov(,)Cov(,)2()08X Z X X Y X X X Y D X =-=-=-=.因此80.825XZ ρ===⨯. 6. 设随机变量(X , Y )服从二维正态分布: 2~(1,3)X N , 2~(0,4)Y N ; X 与Y 的相关系数1,232XYX YZ ρ=-=+. 求: (1) E (Z ), D (Z ); (2) X 与Z 的相关系数ρXZ ; (3)问X 与Z 是否相互独立?为什么?解 (1) 由于)3,1(~2N X , )4,0(~2N Y , 所以16)(,0)(,9)(,1)(====Y D Y E X D X E ,而1Cov(,)3462XY X Y ρ==-⨯⨯=-.因此 31021131)(21)(31)23()(=⨯+⨯=+=+=Y E X E Y X E Z E ,1111()()()()2Cov(,)329432X Y D Z D D X D Y X Y =+=++111916Cov(,)943X Y =⨯+⨯+3)6(3141=-⨯++=.(2) 由于1111Cov(,)Cov(,)()Cov(,)9(6)0,323232XY X Z X D X X Y =+=+=⨯+⨯-= 所以0XZ ρ==.(3) 由0=XZ ρ知X 与Z 不相关, 又X 与Z 均服从正态分布, 故知X 与Z 相互独立.7.证明: 对随机变量(X , Y ), E (XY )=E (X )E (Y )或者D (X ±Y )=D (X )+D (Y )的充要条件是X与Y 不相关.证 首先我们来证明)()()(Y E X E XY E =和()()()D X Y D X D Y ±=+是等价的.事实上, 注意到()()()2Cov(,)D X Y D X D Y X Y ±=+±.因此()()()D X Y D X D Y ±=+Cov(,)0()()()X Y E XY E X E Y ⇔=⇔=.其次证明必要性. 假设E (XY )=E (X )E (Y ), 则Cov(,)()()()0X Y E XY E X E Y =-=.进而0XYρ==, 即X 与Y 不相关.最后证明充分性. 假设X 与Y 不相关, 即0=XYρ, 则Cov(,)0X Y =. 由此知)()()(Y E X E XY E =.总习题四1. 设X 和Y 是相互独立且服从同一分布的两个随机变量, 已知X 的分布律为1{},1,2,33P X i i ===. 又设max{,},min{,}U X Y V X Y ==.(1) 写出二维随机变量(U , V )的分布律; (2) 求()E U .解 (1) 下面实际计算一下{1,3}P UV ==.注意到max{,},min{,}U X Y V X Y ==, 因此{1,3}{1,3}{3,1}P U V P X Y P X Y =====+=={1}{3}{3}{1}P X P Y P X P Y ===+==9231313131=⨯+⨯=.(2) 由(,)U V 的分布律可得关于U 的边缘分布律所以13522()1239999E U =⨯+⨯+⨯=. 2. 从学校乘汽车到火车站的途中有3个交通岗. 假设在各个交通岗遇到红灯的事件是相互独立的, 并且概率是25. 设X 为途中遇到红灯的次数, 求随机变量X 的分布律、分布函数和数学期望.解 令X 表示途中遇到红灯的次数, 由题设知2~(3,)XB . 即X 的分布律为从而3127543686(){}01231251251251255k E X kP X k ====⨯+⨯+⨯+⨯=∑. 3. 设随机变量),(Y X 的概率密度为212,01,(,)0,.y y x f x y ⎧⎪=⎨⎪⎩≤≤≤其它求22(),(),(),()E X E Y E XY E X Y +.解 112404()(,)1245xE X xf x y dxdy dx x y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰. 11240003()(,)1235xE X yf x y dxdy dx y y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰.112500031()(,)12362x E XY xyf x y dxdy dx xy y dy x dx ∞∞-∞-∞==⋅===⎰⎰⎰⎰⎰.122222220()()(,)()12xE X Y x y f x y dxdy dx x y y dy ∞∞-∞-∞+=+=+⋅⎰⎰⎰⎰155012423216(4)5653015x x dx =+=+==⎰. 4. 设随机变量(X ,Y )的概率密度为1sin(),0,0,222(,)0,.≤≤≤≤其它ππx y x y f x y ⎧+⎪=⎨⎪⎩求E (X ),D (X ),E (Y ),D (Y ),E (XY )和 Cov(X ,Y ).解22001()(,)sin()24E X xf x y dxdy x x y dxdy πππ+∞+∞-∞-∞==+=⎰⎰⎰⎰.22222200()(,)1sin() 2.282E X x f x y dxdyx x y dxdy ππππ+∞+∞-∞-∞==+=+-⎰⎰⎰⎰于是有2216)]([)()(222-+=-=ππX E X E X D . 利用对称性,有2216)(,4)(2-+==πππY D Y E .又()(,)E XY xyf x y dxdy +∞+∞-∞-∞=⎰⎰22001sin()2xy x y dxdy ππ=+⎰⎰220022001sin()21[sin cos cos sin ]2xdx y x y dyxdx y x y x y dyππππ=+=+⎰⎰⎰⎰12-=π.所以协方差2Cov(,)()()()1216X Y E XY E X E Y ππ=-=--.5. 设随机变量X 与Y 独立, 同服从正态分布1(0,)2N , 求(1)();()E X Y D X Y --;(2) (max{,});(min{,})E X Y E X Y .解 (1) 记Y X -=ξ.由于)21,0(~),21,0(~N Y N X ,所以,0)()()(=-=Y E X E E ξ 1)()()(=+=Y D X D D ξ.由此)1,0(~N ξ. 所以2222(||)(||)||x x E X Y E x dx xedx ξ+∞+∞---∞-==⎰22x e+∞-==101)]([)()()|(|2222=+=+==ξξξξE D E E .故而ππξξξ2121|)](|[)|(||)(||)(|222-=⎪⎪⎭⎫ ⎝⎛-=-==-E E D Y X D .(2) 注意到2||)(),max(Y X Y X Y X -++=, 2||),min(Y X Y X Y X --+=.所以ππ21221|]}[|)()({21)],[max(==-++=Y X E Y E X E Y X E ,ππ21221|]}[|)()({21)],[min(-=-=--+=Y X E Y E X E Y X E .6. 设随机变量),(Y X 的联合概率密度为,02,02,8(,)0,.x yx y f x y +⎧⎪=⎨⎪⎩≤≤≤≤其它求: E (X ), E (Y ), Cov(X ,Y ), ρXY , D (X+Y ).解 注意到),(y x f 只在区域2≤≤0,2≤≤0:y x G 上不为零, 所以()(,)8Gx yE X xf x y dxdy x x y ∞∞-∞-∞+==⎰⎰⎰⎰d d222000117()(1)846dx x x y dy x x dx =+=+=⎰⎰⎰,22()(,)E Xx f x y dxdy ∞∞-∞-∞=⎰⎰222232000115()()843dx x x y dy x x dx =+=+=⎰⎰⎰, 因而 36116735)]([)()(2222=-=-=X E X E X D .又()(,)E XY xyf x y dxdy ∞∞-∞-∞=⎰⎰22220001144()()8433dx xy x y dy x x dx =+=+=⎰⎰⎰. 由对称性知2275()(),()()63E Y E X E Y E X ====, 3611)()(==X D Y D . 这样,4491Cov(,)()()()33636X Y E XY E X E Y =-=-=-, 111XY ρ==-,5()()()2Cov(,)9D X Y D X D Y X Y +=++=.7. 设A , B 为随机事件, 且111(),(|),(|)432P A P B A P A B ===, 令 10A X A =⎧⎨⎩,发生,,不发生, 10B Y B =⎧⎨⎩,发生,,不发生.求: (1) 二维随机变量(X , Y )的概率分布; (2) X 与Y 的相关系数XY ρ.解 由1()(|)3()P AB P B A P A ==得1111()()33412P AB P A ==⨯=, 进而由1(|)2P A B = ()()P AB P B =得1()2()6P B P AB ==. 在此基础上可以求得(1)1{1,1}()12P X Y P AB ====,111{0,1}()()()61212P X Y P AB P B P AB ====-=-=,111{1,0}()()()4126P X Y P AB P A P AB ====-=-=,{0,0}()1()1[()()()]P X Y P AB P A B P A P B P AB ====-=-+-U 11121[]46123=-+-=.故(X , Y )的概率分布为(2) 由(1)因此211(),(),44E X E X ==22113()()[()]41616D XE X E X =-=-=, 22211115(),(),()()[()]6663636E Y E Y D Y E Y E Y ===-=-=. 又由(X , Y )的分布律可得21111()00011011312121212E XY =⨯⨯+⨯⨯+⨯⨯+⨯⨯=. 故11115XYρ-⨯===.。
概率论与数理统计》课后习题答案第四章

习题4.11.设10个零件中有3个不合格. 现任取一个使用,若取到不合格品,则丢弃重新抽取一个,试求取到合格品之前取出的不合格品数X 的数学期望.解 可得X 的概率分布为0123~77711030120120X ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为7771()012310301201204531208E X =⨯+⨯+⨯+⨯==2..某人有n 把外形相似的钥匙,其中只有1把能打开房门,但他不知道是哪一把,只好逐把试开.求此人直至将门打开所需的试开次数X 的数学期望.解 可得X 的概率分布为12~111n X nn n ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为111()121(1)122E X n n n nn n n n =⨯+⨯++⨯++==3.设5次重复独立试验中每次试验的成功率为0.9,若记失败次数为X ,求X 的数学期望。
解 由题意~(5,0.1)X B ,则X 的数学期望为()50.10.5E X =⨯=4.设某地每年因交通事故死亡的人数服从泊松分布.据统计,在一年中因交通事故死亡一人的概率是死亡两人的概率的21,求该地每年因交通事故死亡的平均人数。
解 设该地每年因交通事故死亡的人数为X ,由题意X 服从泊松分布() (0)P λλ>.因1{1}{2}2P X P X === 即121 41!22!ee λλλλλ--=⇒= 于是X 的数学期望为()4E X λ==所以地每年因交通事故死亡的平均人数为4人。
5.设随机变量X 在区间(1,7)上服从均匀分布,求2{()}P X E X <. 解 因X 在区间(1,7)上服从均匀分布,故X 的数学期望为17()42E X +== 于是22{()}{4}1 {22}6P X E X P X P X <=<=<-<<=6.设连续型随机变量X 的概率密度为01() (,0)0 b ax x p x a b ⎧<<=>⎨⎩其它又知()0.75E X =,求,a b 的值解 由密度函数的性质可得()1p x dx +∞-∞=⎰即1111b aax dx b =⇒=+⎰又由()0.75E X =,可得1()0.75b xp x dx x ax dx +∞-∞=⋅=⎰⎰即0.752ab =+ 求解110.752a b a b ⎧=⎪⎪+⎨⎪=⎪+⎩ 可得 3,2a b ==.7.设随机变量X 的概率密度为0<1()2 120 x x p x x x <⎧⎪=-≤<⎨⎪⎩其它求数学期望()E X解12013312201()() (2) ()133E X xp x dxx xdx x x dx x x x +∞-∞==⋅+⋅-=+-=⎰⎰⎰8.设随机变量X 的概率分布为 X -2 -1 0 1 P 0.2 0.3 0.1 0.4 求(1)(21)E X -;(2)2()E X .解 (1) (21)2()1E X E X -=- 其中()20.210.3010.40.3E X =-⨯-⨯++⨯=-则(21)2()12(0.3)1 1.6E X E X -=-=⨯--=-(2)22222()0.2(2)0.3(1)0.100.41 1.5E X =⨯-+⨯-+⨯+⨯=9.假设一部机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作。
概率论第四章部分习题解答

2
2
x2
=
2 2π σ
∫
E (Y ) =
).
m 1 np Φ npq
6
m 2 np p (m 1 ≤ Y n ≤ m 2 ) ≈ Φ npq
五,练习题
1. 设 ~ N(0,1),求下列概率: X 求下列概率:
(1) P( X ≤ 1.5);
(2) P( X > 2.5);
(3) P(| X |< 1.68); (4) P(0.36 ≤ X ≤ 0.64)
E (Y 2 ) =
2
2
∫ 2π
+∞
0
x e dx = (2n - 1)!!
2
x 2n - 2
2
( 2 n 1 )! ! , n 为奇数 ∴ DY = E (Y ) - [ E (Y )] = ( 2 n 1 )! ! [( n 1 )! ! ] 2 , n 为偶数
∴ E (XY ) = E ( X
(4) P ( 0.36 ≤ X ≤ 0.64) = Φ(0.64) Φ( 0.36)
= Φ(0.64) + Φ(0.36) 1 = 0.7389 + 0.6406 1= 0.3795
7
2. 设 ~ N(1,22 ),求下列概率: X 求下列概率:
(1) P( X < 2.2); (3) P(| X |< 3.5);
概率论与数理统计 第四章 随机变量的数字特征 练习题与答案详解

概率论与数理统计 第四章 随机变量的数字特征练习题与答案详解(答案在最后)1.假定每个人生日在各个月份的机会是相同的,求三个人中生日在第一季度的人数的平均.2.100个产品中有5个次品,任取10个,求次品个数的数学期望与方差.3.设随机变量X 的概率密度为)(,e 21)(∞<<-∞=-x x p x试求数学期望EX 及方差DX .4.已知随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧>≤<≤=,,,,,,4140400)(x x x x x F 试求X 的数学期望EX 方差DX .5.对圆的直径作近似测量,设其值均匀地分布在[]b a ,内,求圆面积的数学期望.6.设随机变量X 概率密度为⎪⎩⎪⎨⎧≤≤=其它,,,,020cos )(πx x x f X试求随机变量DY X Y 的方差2=.7.设随机变量ξ只取非负整数值,其概率为{}0)1(1>+==+a a a k P k k,ξ是常数, 试求ξE 及ξD .8.设独立试验序列中,首次成功所需要的次数ξ服从的分布列为:其中q =9.若事件A 在第i 次试验中出现的概率为,i p 设μ是事件A 在起初n 次独立试验中的出现次数,试求μE 及μD .10.随机变量n ξξξ,,,21 独立,并服从同一分布,数学期望为,μ方差为2σ,求这些随机变量的算术平均值∑==ni i n 11ξξ的数学期望与方差.11.设μ是事件A 在n 次独立试验中的出现次数,在每次试验中,)(p A P =再设随机变量η视μ取偶数或奇数而取数值0及1,试求ηE 及ηD .12.设随机变数ξ之概率分布如下:求: (1) ; ]]1[2[2+ξE (2) ])[(2ξξE E -.13.随机变量,)(~x f X⎪⎩⎪⎨⎧<<-≤≤=其它,,,,,,021210)(x x x x x f试计算n EX n (为正整数).14.随机变量aX Y p n B X e ),,(~=,求随机变量Y 的期望和方差. 15.某种产品每件表面上的疵点数服从泊松分布,平均每件上有8.0个疵点.规定疵点数不超过1个为一等品,价值10元,疵点数大于1不多于4为二等品,价值为8元,4个以上者为废品,求:)1( 产品的废品率;)2( 产品的平均价值.16.一个靶面由五个同心圆组成,半径分别为25,20,15,10,5厘米,假定射击时弹着点的位置为Z Y Z ,),(为弹着点到靶心的距离,且),(Y Z 服从二维正态分布,其密度为200222001),(y x ey x f +-=π,现规定弹着点落入最小的圆域为5分,落入其他各圆域(从小到大)的得分依次为4分,3分,2分,1分,求:)1( 一次射击的平均得分;)2( 弹着点到靶心的平均距离.17.若ξ的密度函数是偶函数,且∞<2ξE ,试证ξ与ξ不相关,但它们不相互独立.18.若ξ与η都是只能取两个值的随机变量,试证如果它们不相关,则独立.答案详解1.每个生日在第一季度的概率是41=p .设X 表示三个人中生日在第一季度的人数,则X 服从二项分布,,⎪⎭⎫⎝⎛B 413从而X 的平均为43413)(=⨯=X E2.5.0=EX ,11045=DX3.x -e 21为偶函数,⋅x x-e 21为奇函数,所以,由积分性质知0d e 21=⋅=-∞∞-⎰x x EX x(奇函数在对称区间上的积分值为零)=DX x x P X E x X d )()]([2⎰∞∞--=⨯=-∞∞-⎰x x xd e 212x x x d e 02-∞⎰)(d )(202x x x x --∞-=-=⎰ x x x d e 200⎰∞-+∞2d e 20==⎰∞-x x x 4.342==DX EX ,5.设圆的直径为随机变量X ,圆的面积为随机变量,Y 则24)(X X f Y π==,随机变量X 的概率密度为⎪⎩⎪⎨⎧≤≤-=其它,,,,01)(b x a ab x p X , 于是)(12112 d 14d )()())(()(2232b ab a a b x ab x ab x x x p x f X f E Y E b aX ++=⋅-⋅=-⋅===⎰⎰∞∞-πππ6.2220π-=DY7.⎥⎦⎤⎢⎣⎡++=+⋅=∑∑∞=∞=+101)1(11)1(k k k k k a a k a a a k E ξ, 令,且,则10)1(<<=+p p a a ,211)1()1()(p p p p p p p kp k k kk -='-='=∑∑∞=∞= 故a aa a aaE =+-+⋅+=2)11(111ξ.采用同样的方法并利用a E =ξ得⎥⎦⎤⎢⎣⎡++=∑∞=k k a a k a E )1(11122ξ[]k k p k k a ∑∞=+-+=11)1(11 ∑∑∞=∞=-+++=11)1(1111k k k k p k k a kp a ,2322122)1(21)1(1)(1a a p a p a p p a p a p a p a k k +=-⋅++="⎥⎦⎤⎢⎣⎡-++=''++=∑∞=故)1()2()(2222a a a a a D +=-+=E -E =ξξξ 8.21pqD pE ==ξξ,9.设,21n μμμμ+++= 其中⎩⎨⎧=出现次试验若第出现次试验若第A i A i i ,0,1μ,则∑∑===E =ni i ni i p E 11μμ,由试验独立得诸i μ相互独立,从而知=μD )1(11i ni i ni i p p D -=∑∑==μ10.nD E 2,σξμξ== 11.事件A 出现奇数次的概率记为b ,出现偶数次的概率记为a ,则.,++=++=---3331122200n n n n n n n n q p C pq C b q p C q p C a 利用,,n n p q b a q p b a )(1)(-=-=+=+可解得事件A 出现奇数次的概率为 n n p p q b )21(2121])(1[21--=--=,顺便得到,事件A 出现偶数次的概率为n p a )21(2121-+=.η服从两点分布,由此得,{}{}===出现奇数次事件A P P 1ηn p )21(2121--, {}{}===出现偶数次事件A P P 0ηn p )21(2121-+, 所以,=ηE n p )21(2121--,=ηD ][)21(2121[n p --])21(2121n p -+n p 2)21(4141--=.12.(1) 117; (2) 46513.x x f x EX n n d )(⎰∞∞-=x x x x x x n n d )2(d 2110-⋅+⋅=⎰⎰12)212(012212+-+⋅++=+++n x n x n x n n n)21122212(2122+++-+-+++=++n n n n n n n )2)(1(222++-=+n n n 14.n a n a n a p q p q DY p q EY 22)e ()e ()e (+-+=+=, 15.(1) 0.0014; (2) 9.616.(1) 007.3; (2) π2517.设)(x f 是ξ的密度函数,则)()(x f x f =-,由)(x xf 是奇函数可得,0=ξE 从而0=ξξE E .又由于)(x f x x 是奇函数及,2∞<ξE 得ξξξξE E x x f x x E ===⎰∞∞-0d )(,故ξ与ξ不相关.由于ξ的密度函数是偶函数,故可选0>c 使得当{}10<<P <c ξ时,也有{}10<<P <c ξ,从而可得 {}{}{}{}c c P c P c P c P <<=<≠<<ξξξξξ,,其中等式成立是由于{}{}c c <⊂<ξξ,由此得不独立与ξξ.18.设⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛2,2,1, , 1q p d c p b a q :,:ηξ.作两个随机变量 ⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--=**2211,0, ,0, q p d c d q p b a b :,:ηηξξ, 由ξ与η不相关即ηξξηE E E ⋅=得)(bd d b E E +--=**ξηξηηξbd dE bE E E +--=ξηηξ**=--=ηξηξE E d E b E ))((,而,,,}{)(}{)(} {))((d c P d c b a P b a E E d c b a P d c b a E -=-⋅-=-=-=-=--=********ηξηξηξηξ由上两式值相等,再由0))((≠--d c b a 得,,}{}{}{d c P b a P d c b a P -=-==-=-=****ηξηξ 即}{}{}{c P a P c a P =⋅====ηξηξ,. 同理可证}{}{}{d P a P d a P =⋅====ηξηξ,, }{}{}{c P b P c b P =⋅====ηξηξ,, }{}{}{d P b P d b P =⋅====ηξηξ,,从而ξ与η独立.。
《概率论与数理统计》习题及答案第四章

《概率论与数理统计》习题及答案第 四 章1.一个袋子中装有四个球,它们上面分别标有数字1,2,2,3,今从袋中任取一球后不放回,再从袋中任取一球,以,X Y 分别表示第一次,第二次取出的球上的标号,求(,)X Y 的分布列.解(,)X Y 的分布列为其中(1,1)(1)(1|1)0P X Y P X P Y X =======余者类推。
2.将一枚硬币连掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值,试写出(,)X Y 的分布列及边缘分布列。
解一枚硬币连掷三次相当于三重贝努里试验,故1~(3,).2X B 331()(),0,1,2,32k P X k C k ===,于是(,)X Y 的分布列和边缘分布为01013818i p ⋅其中(0,1)(0)(1|0)0P X Y P X P Y X =======,13313(1,1)(1)(1|1)()128P X Y P X P Y X C =======⨯=,余者类推。
3.设(,)X Y 的概率密度为又(1){(,)|1,3}D x y x y =<<;(2){(,)|3}D x y x y =+<。
求{(,)}P X Y D ∈ 解(1)1321{(,)}(6)8P x y D x y dxdxy ∈=--⎰=321(6)8x x y dxdy --- =)落在圆222()x y r r R +≤<内的概率. 解(1)22223201(R x y R CR dxdy C R C r drd ππθ+≤==-⎰⎰⎰⎰333233R R C R C πππ⎡⎤=-=⎢⎥⎣⎦, ∴33C R π=.(2)设222{(,)|}D x y x y r =+≤,所求概率为322323232133r r r Rr R R R πππ⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦. 5.已知随机变量X 和Y 的联合概率密度为 求X 和Y 的联合分布函数.解1设(,)X Y 的分布函数为(,)F x y ,则解2由联合密度可见,,X Y 独立,边缘密度分别为 边缘分布函数分别为(),()X Y F x F y ,则 设(,)X Y 的分布函数为(,)F x y ,则6.设二维随机变量(,)X Y 在区域:0D x <<求边缘概率密度。
概率论与数理统计第四章课后习题及参考答案

概率论与数理统计第四章课后习题及参考答案1.在下列句子中随机地取一个单词,以X 表示取到的单词包含的字母的个数,试写出X 的分布律,并求)(X E .Have a good time解:本题的随机试验属于古典概型.所给句子共4个单词,其中有一个单词含一个字母,有3个单词含4个字母,则X 的所有可能取值为1,4,有41)1(==X P ,43)4(==X P ,从而413434411)(=⋅+⋅=X E .2.在上述句子的13个字母中随机地取一个字母,以Y 表示取到的字母所在的单词所含的字母数,写出Y 的分布律,并求)(Y E .解:本题的随机试验属于古典概型.Y 的所有可能取值为1,4,样本空间Ω由13个字母组成,即共有13个样本点,则131)1(==Y P ,1312)4(==Y P ,从而1349131241311)(=⋅+⋅=Y E .3.一批产品有一、二、三等品及废品4种,所占比例分别为60%,20%,10%和10%,各级产品的出厂价分别为6元、8.4元、4元和2元,求产品的平均出厂价.解:设产品的出厂价为X (元),则X 的所有可能取值为6,8.4,4,2,由题设可知X 的分布律为X 68.442P6.02.01.01.0则16.51.021.042.08.46.06)(=⨯+⨯+⨯+⨯=X E (元).4.设随机变量X 具有分布:51)(==k X P ,5,4,3,2,1=k ,求)(X E ,)(2X E 及2)2(+X E .解:3)54321(51)(=++++=X E ,11)54321(51)(222222=++++=X E ,274)(4)()44()2(222=++=++=+X E X E X X E X E .5.设离散型随机变量X 的分布列为k k kk X P 21)!2)1((=-=, ,2,1=k ,问X 是否有数学期望.解:因为∑∑∞=∞==⋅-111212)1(k k k k kkk 发散,所以X 的数学期望不存在.6.设随机变量X 具有密度函数⎪⎩⎪⎨⎧≤≤-=其他.,0,22,cos 2)(2πππx x x f 求)(X E 及)(X D .解:因为x x 2cos 在]2,2[ππ-上为奇函数,所以0d cos 2d )()(222=⋅==⎰⎰-∞+∞-πππx x x x x f x X E ,2112d cos 2d )()(2222222-=⋅==⎰⎰-∞+∞-ππππx x x x x f x X E ,故2112)]([)()(222-=-=πX E X E X D .7.设随机变量X 具有密度函数⎪⎩⎪⎨⎧<<-≤<=其他.,0,21,2,10,)(x x x x x f 求)(X E 及)(X D .解:1d )2(d d )()(2112=-+==⎰⎰⎰∞+∞-x x x x x x x f x X E ,67d )2(d d )()(2121322=-+==⎰⎰⎰∞+∞-x x x x x x x f x X E ,61)]([)()(22=-=X E X E X D .8.设随机变量X 在)21,21(-上服从均匀分布,求)sin(X Y π=的数学期望与方差.解:由题可知X 的密度函数为⎪⎩⎪⎨⎧<<-=其他.,0,2121,1)(x x f 则0d 1sin d )(sin )][sin()(2121=⋅===⎰⎰-∞+∞-x x x x f x X E Y E πππ,21d 1sin d )(sin )]([sin )(21212222=⋅===⎰⎰-∞+∞-x x x x f x X E Y E πππ,21)]([)()(22=-=Y E Y E Y D .9.某正方形场地,按照航空测量的数据,它的边长的数学期望为350m ,又知航空测量的误差随机变量X 的分布列为X (m)30-20-10-0102030P05.008.016.042.016.008.005.0而场地边长随机变量Y 等于边长的数学期望与测量误差之和,即X Y +=350,求场地面积的数学期望.解:设场地面积为S ,则2Y S =,16.01042.0016.0)10(08.0)20(05.030)(⨯+⨯+⨯-+⨯-+⨯-=X E 005.03008.020=⨯+⨯+,16.01042.0016.0)10(08.0)20(05.0)30()(222222⨯+⨯+⨯-+⨯-+⨯-=X E 18605.03008.02022=⨯+⨯+,故)350700(])350[()()(2222++=+==X X E X E Y E S E 122686350)(700)(22=++=X E X E .10.A ,B 两台机床同时加工零件,每生产一批较大的产品时,出次品的概率如下表所示:A 机床次品数X 0123概率P7.02.006.004.0B 机床次品数X 0123概率P8.006.004.010.0问哪一台机床加工质量较好.解:44.004.0306.022.017.00)(=⨯+⨯+⨯+⨯=X E ,8.004.0306.022.017.00)(22222=⨯+⨯+⨯+⨯=X E ,6064.0)]([)()(22=-=X E X E X D ,44.010.0304.0206.018.00)(=⨯+⨯+⨯+⨯=Y E ,12.110.0304.0206.018.00)(22222=⨯+⨯+⨯+⨯=Y E ,9264.0)]([)()(22=-=Y E Y E Y D ,)()(Y E X E =,但)()(Y D X D <,故A 机床加工质量较好.11.设随机变量X 与Y 相互独立,且方差存在,试证:22)]()[()()]([)()()(Y E X D Y D X E Y D X D XY D ++=,由此得出)()()(Y D X D XY D ≥.证:22)]([])[()(XY E XY E XY D -=222)]()([)(Y E X E Y X E -=2222)]([)]([)()(Y E X E Y E X E -=2222)]([)]([})]([)(}{)]([)({Y E X E Y E Y D X E X D -++=22)]()[()()]([)()(Y E X D Y D X E Y D X D ++=.因为)(X D ,)(Y D ,2)]([X E ,2)]([Y E 非负,所以)()()(Y D X D XY D ≥.12.已知随机变量X 的密度函数为⎩⎨⎧≤≤++=其他.,010,)(2x c bx x a x f又已知5.0)(=X E ,15.0)(=X D ,求a ,b ,c .解:c b a x c bx x a x x f ++=++==⎰⎰∞+∞-2131d )(d )(1102,c b a x c bx x a x x x f x X E 213141d )(d )()(5.0102++=++===⎰⎰∞+∞-,⎰⎰++-=-==∞+∞-1222d )()5.0(d )()]([)(15.0xc bx x a x x x f X E x X D 41314151-++=c b a ,解之得12=a ,12-=b ,3=c .13.设),(Y X 的分布律为(1)求)(X E 及)(Y E ;(2)设XYZ =,求)(Z E ;(3)设2)(Y X Z -=,求)(Z E .解:(1)2)13.00(3)1.001.0(2)1.01.02.0(1)(=++⨯+++⨯+++⨯=X E ,0)1.01.01.0(1)3.001.0(0)01.02.0()1()(=++⨯+++⨯+++⨯-=Y E ,(2)1.01)3.001.0(00)31(1.021(2.01)(⨯+++⨯+⨯-+⨯-+⨯-=Z E 1511.0311.021-=⨯+⨯+,(3)1.0)01(0)]1(3[1.0)]1(2[2.0)]1(1[)(2222⨯-+⨯--+⨯--+⨯--=Z E 51.0)13(1.0)12(1.0)11(3.0)03(0)02(22222=⨯-+⨯-+⨯-+⨯-+⨯-+.14.设随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤+=其他.,0,10,20,3),(y x yx y x f求)(X E ,)(Y E ,)(Y X E +及)(22Y X E +.解:⎰⎰∞+∞-∞+∞-=y x y x f x X E d d ),()(911d d 31020=+⋅=⎰⎰y x y x x ,⎰⎰∞+∞-∞+∞-=y x y x yf Y E d d ),()(95d d 31020=+⋅=⎰⎰y x y x y ,⎰⎰∞+∞-∞+∞-+=+y x y x f y x Y X E d d ),()()(916d d 3)(1020=+⋅+=⎰⎰y x y x y x ,⎰⎰∞+∞-∞+∞-+=+y x y x f y x Y X E d d ),()()(2222613d d 3)(102022=+⋅+=⎰⎰y x y x y x .15.),(Y X 在区域}1,0,0|),{(≤+≥≥=y x y x y x D 上服从均匀分布,求)(X E ,)23(Y X E -及)(XY E .解:由题可知),(Y X 的联合密度函数为⎩⎨⎧≤≤-≤≤=其他.,0,10,10,2),(y y x y x f ⎰⎰∞+∞-∞+∞-=y x y x f x X E d d ),()(31d d 21010==⎰⎰-yy x x ,⎰⎰∞+∞-∞+∞--=-y x y x f y x Y X E d d ),()23()23(31d d )23(21010=-=⎰⎰-yy x y x ,⎰⎰∞+∞-∞+∞-=y x y x xyf XY E d d ),()(121d d 21010==⎰⎰-y y x xy .16.设二维随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧>+≤+=.1,0,1,1),(2222y x y x y x f π证明:随机变量X 与Y 不相关,也不相互独立.证:⎰⎰⎰⎰⋅=⋅=∞+∞-∞+∞-πθθππ201d d cos 1d d 1)(r r r y x x X E ,同理,0)(=Y E ,⎰⎰⎰⎰⋅⋅=⋅=∞+∞-∞+∞-πθθθππ201d d sin cos 1d d 1)(r r r r y x xy XY E ,0)()()(),cov(=-=Y E X E XY E Y X ,故随机变量X 与Y 不相关.当11≤≤-x 时,ππ21112d 1d ),()(22x y y y x f x f x x X -===⎰⎰---∞+∞-,其他,0)(=x f X ,故⎪⎩⎪⎨⎧≤≤--=其他.,0,11,12)(2x x x f X π同理,⎪⎩⎪⎨⎧≤≤--=其他.,0,11,12)(2y y y f Y π易得)()(),(y f x f y x f Y X ≠,故随机变量X 与Y 不相互独立.17.设随机变量1X ,2X 的概率密度分别为⎩⎨⎧≤>=-.0,0,0,e 2)(21x x x f x ,⎩⎨⎧≤>=-.0,0,0,e 4)(42y y y f y 试用数学期望的性质求:(1))(21X X E +及)32(221X X E -;(2)又设1X ,2X 相互独立,求)(21X X E .解:由题可知1X ~)2(E ,2X ~)4(E ,则21)(1=X E ,41)(2=X E ,161)(2=X D ,81)]([)()(22222=+=X E X D X E .(1)43)()()(2121=+=+X E X E X X E ,85)(3)(2)32(221221=-=-X E X E X X E .(2)81)()()(2121==X E X E X X E .18.(1)设1X ,2X ,3X 及4X 独立同在)1,0(上服从均匀分布,求)51(41∑=k k kX D ;(2)已知随机变量X ,Y 的方差分别为25和36,相关系数为4.0,求Y X U 23+=的方差.解:(1)由题易得121)(=i X D ,)51(41∑=k k kX D )(5141∑==k kkX D )](4)(3)(2)([514321X D X D X D X D +++=21)4321(121512222=+++⋅=.(2)由已知25)(=X D ,36)(=Y D ,4.0)()(),cov(==Y D X D Y X XY ρ,得12),cov(=Y X ,)2,3cov(2)2()3()23()(Y X Y D X D Y X D U D ++=+=513),cov(232)(2)(322=⋅⋅++=Y X Y D X D .19.一民航送客车载有20位旅客自机场开出,旅客有10个车站可以下车,如果到达一个车站没有旅客下车就不停车,以X 表示停车的次数,求)(X E (设每位旅客在各个车站下车是等可能的,并设各旅客是否下车相互独立).解:引入随机变量⎩⎨⎧=站无人下车.,在第站有人下车;,在第i i X i 01,10,,2,1 =i .易知1021X X X X +++= .按题意,任一旅客在第i 站不下车的概率为9.0,因此20位旅客都不在第i 站下车的概率为209.0,在第i 站有人下车的概率为209.01-,也就是209.0)0(==i X P ,209.01)1(-==i X P ,10,,2,1 =i .由此209.01)(-=i X E ,10,,2,1 =i .进而)()()()()(10211021X E X E X E X X X E X E +++=+++= 784.8)9.01(1020=-=(次).20.将n 只球(1~n 号)随机地放进n 只盒子(1~n 号)中去,一只盒子装一只球.若一只球装入与球同号的盒子中,称为一个配对,记X 为总的配对数,求)(X E .解:引入随机变量⎩⎨⎧=号盒子.号球未放入第第号盒子号球放入第第i i i i X i ,0,,1,n i ,,2,1 =,则n X X X X +++= 21,显然n X P i 1)1(==,则nX P i 11)0(-==,n i ,,2,1 =,从而nX E i 1)(=,n i ,,2,1 =,于是1)()()()()(2121=+++=+++=n n X E X E X E X X X E X E .21.设随机变量),(Y X 的分布律为试验证X 和Y 是不相关的,但X 和Y 不是相互独立的.证:0)25.00(2)025.0(1)025.0()1()25.00(2)(=+⨯++⨯++⨯-++⨯-=X E ,5)25.00025.0(4)025.025.00(1)(=+++⨯++++⨯=Y E ,0)4(25.0)8(0225.0125.0)1(02)(⨯-+⨯-+⨯+⨯+⨯-+⨯-=XY E 025.0804=⨯+⨯+,所以0)()()(),cov(=-=Y E X E XY E Y X ,故X 与Y 不相关.易知25.025.00)2(=+=-=X P ,5.0025.025.00)1(=+++==Y P ,0)1,2(==-=Y X P ,有)1()2()1,2(=-=≠=-=Y P X P Y X P ,故X 与Y 不相互独立.22.设二维随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤+=其他.,0,10,10,),(y x y x y x f 求)(X E ,)(Y E ,)(X D ,)(Y D ,)(XY E ,),cov(Y X 及XY ρ.解:127d d )(d d ),()(1010=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,125d d )(d d ),()(1010222=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,14411)]([)()(22=-=X E X E X D ,由轮换对称性,得127)(=Y E ,14411)(=Y D ,31d d )(d d ),()(1010=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x xy y x y x xyf XY E ,1441)()()(),cov(-=-=Y E X E XY E Y X ,111)()(),cov(-==Y D X D Y X XY ρ.23.设X ~),(2σμN ,Y ~),(2σμN ,且X ,Y 相互独立.求Y X Z βα+=1和Y X Z βα-=2的相关系数(α,β是不为0的常数).解:由题可知μ==)()(Y E X E ,2)()(σ==Y D X D ,则2222)]([)()(σμ+=+=X E X D X E ,2222)]([)()(σμ+=+=Y E Y D Y E ,μβαβα)()()(1+=+=Y X E Z E ,μβαβα)()()(2-=-=Y X E Z E ,222221)()()()()(σβαβαβα+=+=+=Y D X D Y X D Z D ,222222)()()()()(σβαβαβα+=+=-=Y D X D Y X D Z D ,)()])([()(222221Y X E Y X Y X E Z Z E βαβαβα-=-+=))(()()(22222222σμβαβα+-=-=Y E X E ,222212121)()()()(),cov(σβα-=-=Z E Z E Z Z E Z Z ,22222121)()(),cov(21βαβαρ+-==Z D Z D Z Z Z Z .24.设),(Y X 的联合概率密度为⎩⎨⎧≤≤≤≤--=.,0,10,10,2),(其他y x y x y x f (1)求),cov(Y X ,XY ρ和)32(Y X D -;11(2)X 与Y 是否独立?解:(1)125d d )2(d d ),()(1010=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,41d d )2(d d ),()(1010222=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ,61d d )2(d d ),()(1010=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x xy y x y x xyf XY E ,14411)]([)()(22=-=X E X E X D ,由轮换对称性,125)(=Y E ,14411)(=Y D ,1441)()()(),cov(-=-=Y E X E XY E Y X ,111)()(),cov(-==Y D X D Y X XY ρ,)3,2cov(2)3()2()32(Y X Y D X D Y X D -+-+=-144155),cov(12)(3)(222=-+=Y X Y D X D .(2)当10≤≤x 时,x y y x y y x f x f X -=--==⎰⎰∞+∞-23d )2(d ),()(10,其他,0)(=x f X ,故⎪⎩⎪⎨⎧≤≤-=其他.,0,10,23)(x x x f X 同理,⎪⎩⎪⎨⎧≤≤-=其他.,0,10,23)(y y y f Y 因为)()(),(y f x f y x f Y X ≠,故X 与Y 不相互独立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C. X 与 Y 独立
D. X 与 Y 不独立
8. 已知随机变量 X 与 Y 的相关系数为 ,求 X1 = 2X + 1 与 Y1 = 2Y + 1的相关系数为 .
A.
B. −
C. 0
D. 1
9. 已知 D( X ) = 4,D(Y ) = 9,XY = 0.6,则 D(3X − 2Y )=
.
A. 28.8
(1) E( X ) = , E(Y ) = ;(2) E( X +Y ) = ;(3) E( XY ) =
.
10. 填写 1~6 题的方差.
11. 设随机变量 X 服从参数为 2 的泊松分布,则 E( X 2 ) = .
12. 设随机变量 X ~ N(1, 4) , Y ~ N(2,9) ,且 X 与 Y 独立, Z = 2X − 3Y −1 ,则
4
8
16
64
4. (1) E( X )= 3 , E(Y )= 4 ;(2) E( XY )=1;(3) D( X )= 3 , D(Y )= 2 ;
4
3
80
9
(4) D(2X − 3Y +1)= 43 . 20
5. f (z) =
1
− ( z−9)2
e 194 ; 6. = 1;
194
7.
X
01 2
三、综合练习
(一) 填空题 1. 设随机变量 X 的分布律为
X
-2 0 2
p k
0.4 0.3 0.3
则 E(X ) =
.
2. 若随机变量 X 服从 b(1,0.3) ,则 E( X ) =
.
3. 设离散型随机变量 X 服从参数为 2 的泊松( Poisson)分布,则随机变量 Z = 3X − 2 的期
(X
,Y
)
的联合概率密度为
f
( x,
y)
=
Ae−2x−3y ,
0,
x 0, y 0, 其它.
(1) E(2X +3Y +1) =
;(2) E(6XY ) =
.
(提示:第三章(1)求边缘概率密度;(2)判断随机变量 X 与Y 是否独立)
9.若二维正态分布 ( X ,Y ) ~ N(1,2,4,9,0) ,则
1
1
1
8
4
1
1
2
8
2
(1)求 E( X ) , E(Y ) ;(2) D( X ) , D(Y ) ;(3) E(4X +8Y +1) .
4.
设二维连续型随机变量(X ,Y ) 的概率密度为
f (x, y) =
3 x2 y, 2
0 x 1,0 y 2,
0,
其它.
(提示:可以先求边缘概率密度.然后判断随机变量 X 与Y 是否独立.)
B. P{X + Y 1} = 1 2
C. P{X − Y 0} = 1 2
D. P{X − Y 1} = 1 2
7. 设二维随机变量 ( X , Y ) 满足 E(XY ) = E(X )E(Y ) ,则下列说法正确的是 .
A. D(XY ) = D(X )D(Y )
B. D(X + Y ) = D(X − Y )
7.设有十只同种电器元件,其中有两只废品,装配仪器时,从这批元件中任取一只,如是 废品,则扔掉,重新任取一只,如仍是废品,则扔掉再取一只,试求取得正品之前,已取出 废品只数的分布、期望和方差.
8.设随机变量的 X 概率密度为, f (x) = 1 e− x , − x + ,求 X 的数学期望和方差. 2
V = X − 3Y 的方差及协方差. 11.一工厂生产的某种设备的寿命 X (以年计)服从指数分布,概率密度为
f
(
x)
=
1 4
−
e
x 4
之内损坏可予以调换。若工厂售出一台设备赢利 100 元,调 换一台设备厂方需花费 300 元。试求厂方出售一台设备净赢利的数学期望. 12*.游客乘电梯从底层到电视塔顶层观光;电梯于每个整点的 10 分钟、30 分钟和 50 分钟 从底层起行。假设一游客在早 8 点的第 X 分钟到达底层候机处,且 X 在[0,60]上均匀分布,
求(1) E( X ) , E(Y ) ;(2) E( XY ) ;(3) D( X ) , D(Y ) ;(4) D(2X − 3Y +1) .
5.设 X ~ N(1, 4) ,Y ~ N(2,9) ,且 X 与Y 独立, Z = 2X + 3Y +1,求 Z 的分布密度.
6.设随机变量 X 服从参数为 的泊松分布,且已知 E[(X −1)(X − 2)] = 1求参数 .
A. 1
B. −1
C. 1
D. 0
5. 设两个相互独立的随机变量 X 与 Y 的方差分别为 4 和 2,则随机变量 3X − 2Y 的方差
为
.
A. 8
B. 20
C. 28
D. 44
6. 设随机变量 X 与 Y 独立且 X ~ N(0, 1),Y ~ N(1, 1) ,则下列等式成立的是 .
A. P{X + Y 0} = 1 2
C. − 1 4
D. 3 4
3. 已知随机变量 X ~ b(n, p) ,且 E( X ) = 2.4 , D( X ) = 1.44 ,则二项分布的参
数 n, p 的值为 .
A. 4,0.6
B. 6,0.4 C. 10,0.24
D. 100,0.24
4. 设随机变量 X ~ () ,且 E[(X −1)(X − 2)] = 1,则参数 为 .
x 3.
求 E( X ), D( X )
2.已知随机变量
X
的概率密度为
f
(x)
=
Ax, 0,
0 x 1, 其它.
求:(1)常数 A ;(2) E( X ) , E(3X +1) ;(3) D( X ) ;(4) E(4X 2 +1) .
3. 已知随机变量 X 与Y 的联合分布律为
X Y
0
1
9.已知随机变量 X 的概率密度为.
ax, 0 x 2
f (x) = cx + b, 2 x 4
0,
其它
且 E(X ) = 2, P(1 X 3) = 34 ,求(1) a,b, c 的值; (2)求 E(eX ) .
10.已知随机变量 X ,Y 的方差分别为 25 和 36,相关系数为 0.4,求:U = 3X + 2Y 与
E(Y ) = 2 ; E( X +Y ) = 3 ; E( XY ) = 2 .
10. 2.76 ; 0.21 ; 18 ; 97 ; 8 ; 36 ;
11. 6 12. Z ~ N (−5, 97) ; E(Z 2 ) = 122 ;13. 18.4
14. D( X ) = 1/12 ; D(Y ) = 1/3 ; D(6X + 3Y +1) = 6 .
望为
.
4. 设随机变量 X ~ N(1, 4) ,Y ~ N(2,9) ,且 X 与 Y 独立,Z = 2X − 3Y −1 ,则 E(Z ) =
.
5.若随机变量 X ~ (5) , Y ~ U(2,5) ,则 E(4Y − 5X ) = .
6. 设随机变量 X 服从均值为 3 的指数分布,则 E(2X )=
2
32
,
则 E(Z) =
, D(Z ) =
.
(二)选择题
1.若随机变量 X 服从 (0.4) ,则 E(7 − 5X ) = .
A. 9
B. -9
C. 5
2. 设二维随机变量 ( X ,Y ) 的联合分布律为
D. -5
Y
-1
2
X
1
1
-1
4
2
1
0
1
4
则 E( XY ) =
.
A. − 3 4
B. − 1 2
2. (1) A=2 ;(2) E( X )= 2 E(3X +1)=3 ;(3) D( X )= 1 ;(4) E(4X 2 +1)=3.
3
18
3.(1) E( X )= 3 , E(Y )= 13 ;(2) D( X )= 3 , D(Y )= 15 ;(3) E(4X +8Y +1)=17 .
15. D(2X + 3Y +1) = 2 ; 16. D( X ) = 4 ; D(Y ) = 9 ; D( X − Y ) = 13 .
17. −1 18. 1/3,3 (二)选择题 1. C 2. C 3. B 4. D 5. B 6. B 3. A 4. C
(三)综合题
1. E( X )=0.6 , D( X )=2.24
Z~
; E(Z2) =
.
13 .设 X 表示 10 次独立重复射击命中目标的次数,每次命中目标的概率为 0.4,则 X 2 的数
学期望为 .
14. 设随机变量 (X ,Y ) 在区域 D = (x, y) 0 x 1,0 y 2 上服从均匀分布,则
D( X ) = ; D(Y ) = ; D(6X + 3Y +1) =
.
15.设二维随机变量 ( X ,Y ) 的联合概率密度为
f
( x,
y)
=
Ae−2x−3y ,
0,
x 0, y 0, 其它.
((1)求边缘概率密度.(2)判断随机变量 X 与Y 是否独立.)
则 D(2X + 3Y +1) =
