运筹学课程课件
合集下载
运 筹 学 课 件

12/3 4
z
1 2
x4
x5 42
x3
2 3
x4
1 3
x5
4
新典式
主元化 为1,主 元所在
x2
1 2
x4
6
列的其 余元素
x1
2 3
x4
1 3
x5
4
化为0
观察最后一个典式,所有检验数均为非负, 故其对应的基本可行解为最优解,即
X * 4,6,6,0,0T z* 42
去掉引入变量,得原问题的最优解为:
运筹学课件
目录
运筹学概论 第一章 线性规划基础 第二章 单纯形法 第三章 LP对偶理论 第四章 灵敏度分析 第五章 运输问题 第六章 整数规划 第七章 动态规划 第八章 网络分析
第二章 单纯形法
(SM-Simplex Method)
1947年,美国运筹学家Dantzig提出,原理是 代数迭代。
单纯形法中的单纯形的这个术语,与该方法毫 无关系,它源于求解方法的早期阶段所研究的一 个特殊问题,并延用下来。
CB B1b B1b
z
CB B1N CN X N X B B1NX N
CB B1b B1b
上述方程组的矩阵形式为
10
0 I
CB
B1N B1N
CN
z XB XN
CB B1b B1b
上式的系数增广阵称为对应于基B的单纯形表:
T(B)
CB B1b B1b
0 I
CB
B1N B1N
CN
形式的LP问题,必须解决三个问题: ⑴初始基本可行解的确定; ⑵解的最优性检验; ⑶基本可行解的转移规则。 这里先放一下⑴,研究⑵和⑶,为此,
运筹学OperationalResearchppt课件

XB = ( x1 , x2 , … , xm )T,其余的变量称为非基变量, 记为 XN = ( xm+1 , xm+2 , … , xm+n ) T , 故有 X = XB + XN
– 最多有 Cmmn 个基
21
关于标准型解的若干基本概念:
• 可行解与非可行解 – 满足约束条件和非负条件的解 X 称为可行解,满足 约束条件但不满足非负条件的解 X 称为非可行解
3
1
1
1
6.5
4
1
0
3
7.4
5
0
3
0
6.3
6
0
2
2
7.2
余料
0.1 0.3 0.9 0 1.1 0.2
若目标函数为使购裁买剪的后 钢零筋料最少,则有
min f (x) x01.1x1x2 0.x33x2x40.9x35 0xx6 4 1.1x5 0.2x6
2x11 x22 x33 x44 100
x3 =10 x2 =10 x2 =8 x2 =7
x4 =8 x4 =-2 x3 =2 x3 =3
x5 =7
x5 =-3 x5 =-1 x4 =1
O 基础可行解 F 基础解 E 基础解 A 基础可行解
f(x)=36
5 x1, x2 , x3, x4 , x5 0
4
最3 优解 :
x1
2
2,
x2
6,
m2 ax f ( x)K 361 .
同时不等号也要反向 • 第i 个约束为 型,在不等式左边增加一个非负的变量
xn+i ,称为松弛变量;同时令 cn+i = 0
• 第i 个约束为 型,在不等式左边减去一个非负的变量
– 最多有 Cmmn 个基
21
关于标准型解的若干基本概念:
• 可行解与非可行解 – 满足约束条件和非负条件的解 X 称为可行解,满足 约束条件但不满足非负条件的解 X 称为非可行解
3
1
1
1
6.5
4
1
0
3
7.4
5
0
3
0
6.3
6
0
2
2
7.2
余料
0.1 0.3 0.9 0 1.1 0.2
若目标函数为使购裁买剪的后 钢零筋料最少,则有
min f (x) x01.1x1x2 0.x33x2x40.9x35 0xx6 4 1.1x5 0.2x6
2x11 x22 x33 x44 100
x3 =10 x2 =10 x2 =8 x2 =7
x4 =8 x4 =-2 x3 =2 x3 =3
x5 =7
x5 =-3 x5 =-1 x4 =1
O 基础可行解 F 基础解 E 基础解 A 基础可行解
f(x)=36
5 x1, x2 , x3, x4 , x5 0
4
最3 优解 :
x1
2
2,
x2
6,
m2 ax f ( x)K 361 .
同时不等号也要反向 • 第i 个约束为 型,在不等式左边增加一个非负的变量
xn+i ,称为松弛变量;同时令 cn+i = 0
• 第i 个约束为 型,在不等式左边减去一个非负的变量
运筹学ppt课件
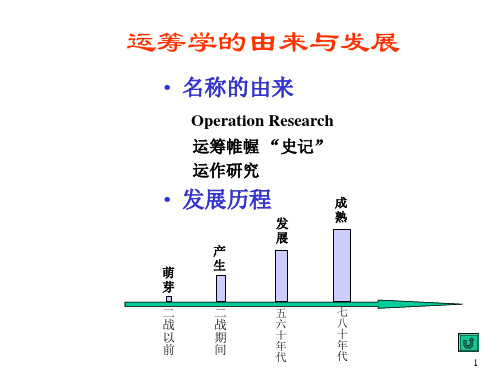
– 无穷多个最优解。若将例1中的目标函数变为 max z=50x1+50x2,则线段BC上的所有点都代表 了最优解;
– 无界解。即可行域的范围延伸到无穷远,目标 函数值可以无穷大或无穷小。一般来说,这说 明模型有错,忽略了一些必要的约束条件;
– 无可行解。若在例1的数学模型中再增加一个约 束条件4x1+3x2≥1200,则可行域为空域,不存在 满足约束条件的解,当然也就不存在最优解了。
• 交叉学科 --涉及经济、管理、数学、工程和系统等 多学科
• 开放性 --不断产生新的问题和学科分支
• 多分支 --问题的复杂和多样性
2
运筹学的主要内容
线性规划
数 非线性规划
学
整数规划
规
动态规划
划
多目标规划
学
双层规划
最优计数问题
科
组 合
网络优化
内
优 排序问题 化 统筹图
容
对策论
随 排队论
机 优 化
13
组织 宝洁公司 法国国家铁路
应用
Interface 每年节支 期刊号 (美元)
重新设计北美生产和分销系统以 1-2/1997 2亿 降低成本并加快了市场进入速 度
制定最优铁路时刻表并调整铁路 1-2/1998 1500万更多
日运营量
年收入
Delta航空公司 IBM
进行上千个国内航线的飞机优化 配置来最大化利润
负。当某一个右端项系数为负时,如 bi<0,则把该 等式约束两端同时乘以-1,得到:-ai1 x1-ai2 x2… -ain xn = -bi。
30
例:将以下线性规划问题转化为标准形式
则该极小化问题与下面的极大化问题有相同的最优解,
– 无界解。即可行域的范围延伸到无穷远,目标 函数值可以无穷大或无穷小。一般来说,这说 明模型有错,忽略了一些必要的约束条件;
– 无可行解。若在例1的数学模型中再增加一个约 束条件4x1+3x2≥1200,则可行域为空域,不存在 满足约束条件的解,当然也就不存在最优解了。
• 交叉学科 --涉及经济、管理、数学、工程和系统等 多学科
• 开放性 --不断产生新的问题和学科分支
• 多分支 --问题的复杂和多样性
2
运筹学的主要内容
线性规划
数 非线性规划
学
整数规划
规
动态规划
划
多目标规划
学
双层规划
最优计数问题
科
组 合
网络优化
内
优 排序问题 化 统筹图
容
对策论
随 排队论
机 优 化
13
组织 宝洁公司 法国国家铁路
应用
Interface 每年节支 期刊号 (美元)
重新设计北美生产和分销系统以 1-2/1997 2亿 降低成本并加快了市场进入速 度
制定最优铁路时刻表并调整铁路 1-2/1998 1500万更多
日运营量
年收入
Delta航空公司 IBM
进行上千个国内航线的飞机优化 配置来最大化利润
负。当某一个右端项系数为负时,如 bi<0,则把该 等式约束两端同时乘以-1,得到:-ai1 x1-ai2 x2… -ain xn = -bi。
30
例:将以下线性规划问题转化为标准形式
则该极小化问题与下面的极大化问题有相同的最优解,
运筹学课件PPT课件

整数规划的解法
总结词
整数规划的解法可以分为精确解法和近似解法两大类。
详细描述
整数规划的解法可以分为两大类,一类是精确解法,另一类是近似解法。精确解法包括割平面法、分支定界法等, 这些方法可以找到整数规划的精确最优解。而近似解法包括启发式算法、元启发式算法等,这些方法可以找到整 数规划的近似最优解,但不一定能保证找到最优解。
模拟退火算法采用Metropolis准则来 判断是否接受一个较差解,即如果新 解的能量比当前解的能量低,或者新 解的能量虽然较高但接受的概率足够 小,则接受新解。
模拟退火算法的应用
01
模拟退火算法在旅行商问题中得到了广泛应用。通过模拟退火算 法,可以求解旅行商问题的最优解,即在给定一组城市和每对城 市之间的距离后,求解访问每个城市恰好一次并返回出发城市的 最短路径。
动态规划的解法
确定问题的阶段和状态
首先需要确定问题的阶段和状态,以便将问 题分解为子问题。
建立状态转移方程
根据问题的特性,建立状态转移方程,描述 状态之间的转移关系。
求解子问题
求解每个子问题,并存储其解以供将来使用。
递推求解
从最后一个阶段开始,通过递推方式向前求 解每个阶段的最优解。
动态规划的应用
线性规划的解法
单纯形法
01
单纯形法是求解线性规划问题的经典方法,通过迭代过程逐步
找到最优解。
对偶理论
02
对偶理论是线性规划的一个重要概念,它通过引入对偶问题来
简化求解过程。
分解算法
03
分解算法是将大规模线性规划问题分解为若干个小问题,分别
求解后再综合得到最优解。
线性规划的应用
生产计划
线性规划可以用于生产计划问题, 通过优化资源配置和生产流程, 提高生产效率和利润。
运筹课件PPT课件

它涉及到的问题包括最短路径、 最小生成树、最大流等。
图论与网络优化在计算机科学、 交通运输、通信网络等领域有 广泛应用,如路由算法、网络 设计等。
03 运筹学在现实生活中的应 用
生产与库存管理
01
02
03
生产计划
运筹学通过数学模型和算 法,帮助企业制定生产计 划,优化资源配置,提高 生产效率。
库存控制
Excel Solver的特点
Excel Solver易于使用
它提供了一个直观的用户界面,用户可以通过简单的拖放操作来定义问题。
Excel Solver具有广泛的适用性
它可以处理各种类型的优化问题,包括线性规划、整数规划、目标规划、非线性规划等。
Excel Solver具有高效性
它使用了多种优化算法,可以快速求解大规模问题。
它使用了高效的算法和优化的数据结构,可以快速地处理大规模数据和计算任务。
05 案例分析与实践
生产计划优化案例
总结词
生产计划是企业管理中的重要环节,通过优化生产计划可以提高企业的生产效率 和资源利用率。
详细描述
生产计划优化案例主要涉及如何根据市场需求、产品特性、生产能力等因素制定 合理的生产计划,以实现生产效益的最大化。具体包括对生产计划的制定、执行 、调整等环节进行优化,提高生产计划的准确性和灵活性。
运筹学的重要性
01
提高效率
降低成本
02
03
增强决策科学性
运筹学能够通过优化资源配置和 流程,提高系统的效率和生产力。
通过合理的资源配置和计划安排, 运筹学可以帮助企业降低成本和 资源消耗。
运筹学提供的数据分析和模型预 测等方法,有助于增强决策的科 学性和准确性。
运筹学-绪论PPT课件

运筹学编写组.运筹学.清华大学出版社 胡运权.运筹学教程.清华大学出版社 杜纲.管理科学基础.天津大学出版社 邓梁成.运筹学的原理和方法.华中科技大学 中国工程项目管理知识体系.建工社 其他:线性代数、管理学及部分杂志
➢ 设备维修和更新 ➢ 项目评价和选择 ➢ 工程优化设计
➢ 计算机和信息系 统
➢ 城市管理 ➢ 发展战略
五、教学及考试说明
➢ 以课本为主教学 ➢ 必要的习题(30~40题) ➢ 考试:采用闭卷 ➢ 平时成绩30%;考试成绩占70%
六、教材和参考书
➢ 教材: ➢ 胡云权.运筹学教程(第三版).清华大学出版社 ➢ 宋学峰.运筹学.东南大学出版社 ➢ 参考书:
➢ 60年代,相继在工业、农业、经济和社会问题各 领域都得到应用。
➢ 理论飞快发展,形成许多分支:数学规划、图与 网络、排队论、存储论、对策论、决策论等。
➢ 1959年成立国际运筹学联合会。我国1980年成 立运筹学会,1982年加入国际运筹学联合会。
四、运筹学解决问题的思路
➢ 提出问题——用自然语言描述问题。 ➢ 建立数学模型——用变量、函数、方程描述问
题。
➢ 求解——主要用数学方法求出模型的最优解、 次优解、满意解,复杂模型求解要用计算机。
➢ 解的检验——检查模型和求解步骤有无错误, 检查解是否反映现实问题。
➢ 决策实施——决策者根据自己的经验和偏好, 对方案进行选择和修改,作出实施的决定。
五、运筹学的运用
➢ 生产计划 ➢ 市场销售 ➢ 资本运营 ➢ 库存管理 ➢ 运输问题 ➢ 财政和会计 ➢ 人事管理
——近代一些运筹学工作者
一、什么是运筹学
➢ 3、运筹学的三大来源 1)军事
两次世界大战期间的军事运筹研究 2)管理
➢ 设备维修和更新 ➢ 项目评价和选择 ➢ 工程优化设计
➢ 计算机和信息系 统
➢ 城市管理 ➢ 发展战略
五、教学及考试说明
➢ 以课本为主教学 ➢ 必要的习题(30~40题) ➢ 考试:采用闭卷 ➢ 平时成绩30%;考试成绩占70%
六、教材和参考书
➢ 教材: ➢ 胡云权.运筹学教程(第三版).清华大学出版社 ➢ 宋学峰.运筹学.东南大学出版社 ➢ 参考书:
➢ 60年代,相继在工业、农业、经济和社会问题各 领域都得到应用。
➢ 理论飞快发展,形成许多分支:数学规划、图与 网络、排队论、存储论、对策论、决策论等。
➢ 1959年成立国际运筹学联合会。我国1980年成 立运筹学会,1982年加入国际运筹学联合会。
四、运筹学解决问题的思路
➢ 提出问题——用自然语言描述问题。 ➢ 建立数学模型——用变量、函数、方程描述问
题。
➢ 求解——主要用数学方法求出模型的最优解、 次优解、满意解,复杂模型求解要用计算机。
➢ 解的检验——检查模型和求解步骤有无错误, 检查解是否反映现实问题。
➢ 决策实施——决策者根据自己的经验和偏好, 对方案进行选择和修改,作出实施的决定。
五、运筹学的运用
➢ 生产计划 ➢ 市场销售 ➢ 资本运营 ➢ 库存管理 ➢ 运输问题 ➢ 财政和会计 ➢ 人事管理
——近代一些运筹学工作者
一、什么是运筹学
➢ 3、运筹学的三大来源 1)军事
两次世界大战期间的军事运筹研究 2)管理
运筹学教学课件(全)

实用举例
某公司通过市场调研,决定生产高中档新型拉杆箱。 某分销商决定买进该公司3个月内的全部产品。拉杆箱生 产需经过原材料剪裁、缝合、定型、检验和包装4过程。
通过分析生产过程,得出:生产中档拉杆箱需要用 7/10小时剪裁、5/10小时缝合、1小时定型、1/10小时检 验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时缝合、 2/3小时定型、1/4小时检验包装。由于公司生产能力有限, 3月内各部的最大生产时间为剪裁部630小时、缝合部600 小时、定型部708小时、检验包装部135小时。
D {x | Ax b, x (x1,, xi ,, xn ) 0}
是凸集(凸多面体)。
引理2.1:线性规划的可行解 x (x1 ,, xn )T 为基本可行解的 充分必要条件是x的正分量所对应的系数列向量是线性无关的, 即每个正分量都是一个基变量。
定理2.2:线性规划问题的基本可行解x对应于可行域的顶点
通过分析生产过程,得出:生产中档拉杆箱需要用
7/10小时可剪裁以、通5/1过0小线时性缝合规、划1小求时定解型!、1/10小时
检验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时 缝合、2/3小时定型、1/4小时检验包装。由于公司生产 能力有限,3月内各部的最大生产时间为剪裁部630小时、 缝合部600小时、定型部708小时、检验包装部135小时。
x2
L1:x1=6 L3:2x1+3x2=18
B 可行域
L2:x2=4 最优解
x1
4x1+3x2
解的特殊情况——解的特殊情况——无界解
线性规划的基本性质
若线性规划有最 优解,则最优解必在可 行域的顶点上达到。
X
可行域内部的点 • 可行解? 是 • 最优解? 不
运筹学全册精品完整课件

否则,目标函数等值线与可行域 将交于无穷远处,此时称无有限最 优解。
36
例2-2 考虑例2-1
某工厂拥有A、B、C 三种类型的设备,
生产甲、乙两种产品。每件产品在生产中 需要占用的设备机时数,每件产品可以获 得的利润以及三种设备可利用的时数如下 表所示。问题:工厂应如何安排生产可获 得最大的总利润?
一、线性规划问题的提出
在实践中,根据实际问题的要求,常常 可以建立线性规划问题数学模型。
例2-1 我们首先分析开篇案例提到的问题。 解:设变量 xi 为第 i 种(甲、乙)产品的 生产件数(i=1,2)。根据题意,我们知道 两种产品的生产受到设备能力(机时数)的 限制。对设备A:两种产品生产所占用的机时 数不能超过65,于是我们可以得到不等式:
运筹学是运用科学的方法(如 分析、试验、量化等)来决定如何 最佳地运营和设计各种系统的一门 学科。
4
运筹学概述
运筹学能够对经济管理系统中 的人力、物力、财力等资源进行统 筹安排,为决策者提供有依据的最 优方案,以实现最有效的管理。
通常以最优、最佳等作为决策 目标,避开最劣的方案。
5
运筹学的产生和发展
8பைடு நூலகம்
运筹学在管理中的应用
生产计划:生产作业的计划、日程表的
编排、合理下料、配料问题、物料管 理等。
库存管理:多种物资库存量的管理,库
存方式、库存量等。
运输问题:确定最小成本的运输线路、
物资的调拨、运输工具的调度以及建
厂地址的选择等。
9
运筹学在管理中的应用
• 人事管理:对人员的需求和使用的 预测,确定人员编制、人员合理分 配,建立人才评价体系等。
x1 ,x2 ,… ,xn ≥ 0
36
例2-2 考虑例2-1
某工厂拥有A、B、C 三种类型的设备,
生产甲、乙两种产品。每件产品在生产中 需要占用的设备机时数,每件产品可以获 得的利润以及三种设备可利用的时数如下 表所示。问题:工厂应如何安排生产可获 得最大的总利润?
一、线性规划问题的提出
在实践中,根据实际问题的要求,常常 可以建立线性规划问题数学模型。
例2-1 我们首先分析开篇案例提到的问题。 解:设变量 xi 为第 i 种(甲、乙)产品的 生产件数(i=1,2)。根据题意,我们知道 两种产品的生产受到设备能力(机时数)的 限制。对设备A:两种产品生产所占用的机时 数不能超过65,于是我们可以得到不等式:
运筹学是运用科学的方法(如 分析、试验、量化等)来决定如何 最佳地运营和设计各种系统的一门 学科。
4
运筹学概述
运筹学能够对经济管理系统中 的人力、物力、财力等资源进行统 筹安排,为决策者提供有依据的最 优方案,以实现最有效的管理。
通常以最优、最佳等作为决策 目标,避开最劣的方案。
5
运筹学的产生和发展
8பைடு நூலகம்
运筹学在管理中的应用
生产计划:生产作业的计划、日程表的
编排、合理下料、配料问题、物料管 理等。
库存管理:多种物资库存量的管理,库
存方式、库存量等。
运输问题:确定最小成本的运输线路、
物资的调拨、运输工具的调度以及建
厂地址的选择等。
9
运筹学在管理中的应用
• 人事管理:对人员的需求和使用的 预测,确定人员编制、人员合理分 配,建立人才评价体系等。
x1 ,x2 ,… ,xn ≥ 0
运筹学OperationsResearchppt课件
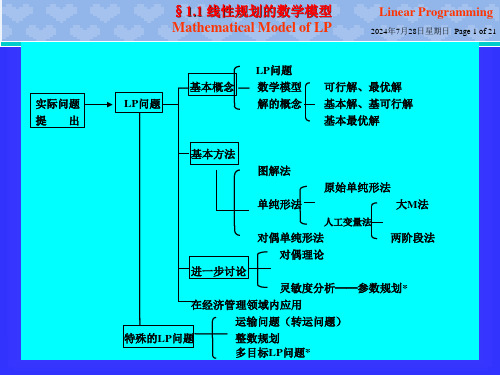
实际问题 提出
§1.1 线性规划的数学模型 Mathematical Model of LP
Linear Programming
2024年7月28日星期日 Page 1 of 21
LP问题
基本概念
LP问题 数学模型 解的概念
可行解、最优解 基本解、基可行解 基本最优解
基本方法
图解法
原始单纯形法
单纯形法
2
x1
x2
x3
x4
100
2x2 x3 3x5 2x6 x7 100
x1
x3
3x4
2 x6
3x7
4x8
100
x
j
0,
j
1,2,8
§1.1 线性规划的数学模型 Mathematical Model of LP
Linear Programming
2024年7月28日星期日 Page 11 of 21
大M法
人工变量法
对偶单纯形法
两阶段法
对偶理论
进一步讨论
灵敏度分析──参数规划*
在经济管理领域内应用
运输问题(转运问题)
特殊的LP问题
整数规划 多目标LP问题*
§1.1 线性规划的数学模型 Mathematical Model of LP
Linear Programming
2024年7月28日星期日 Page 2 of 21
2024年7月28日星期日 Page 6 of 21
线性规划的数学模型由
决策变量 Decision variables 目标函数Objective function 及约束条件Constraints
构成。称为三个要素。
怎样辨别一个模型是线性规划模型? 其特征是: 1.解决问题的目标函数是多个决策变量的
§1.1 线性规划的数学模型 Mathematical Model of LP
Linear Programming
2024年7月28日星期日 Page 1 of 21
LP问题
基本概念
LP问题 数学模型 解的概念
可行解、最优解 基本解、基可行解 基本最优解
基本方法
图解法
原始单纯形法
单纯形法
2
x1
x2
x3
x4
100
2x2 x3 3x5 2x6 x7 100
x1
x3
3x4
2 x6
3x7
4x8
100
x
j
0,
j
1,2,8
§1.1 线性规划的数学模型 Mathematical Model of LP
Linear Programming
2024年7月28日星期日 Page 11 of 21
大M法
人工变量法
对偶单纯形法
两阶段法
对偶理论
进一步讨论
灵敏度分析──参数规划*
在经济管理领域内应用
运输问题(转运问题)
特殊的LP问题
整数规划 多目标LP问题*
§1.1 线性规划的数学模型 Mathematical Model of LP
Linear Programming
2024年7月28日星期日 Page 2 of 21
2024年7月28日星期日 Page 6 of 21
线性规划的数学模型由
决策变量 Decision variables 目标函数Objective function 及约束条件Constraints
构成。称为三个要素。
怎样辨别一个模型是线性规划模型? 其特征是: 1.解决问题的目标函数是多个决策变量的
运筹学课件ppt下载

通过具体案例展示线性规划问题 的建模过程,如生产计划、资源 分配等问题。
单纯形法求解过程
单纯形法原理
介绍单纯形法的基本思想、算法步骤和求解 过程。
迭代过程
详细阐述单纯形法的迭代过程,包括入基、 出基、检验数计算等操作。
初始可行解
讲解如何找到一个初始可行解作为算法的起 点。
终止条件
说明单纯形法的终止条件及如何判断最优解 。
存储模型要素
需求、补充、成本、存储策略等。
常见存储模型
经典EOQ模型、动态规划模型、随机存储模 型等。
存储论求解方法及实例分析
求解方法
数学解析法、数值计算法、仿真模拟 法等。
实例分析
以某企业为例,运用存储论优化其库 存管理策略,降低库存成本。
排队论基本概念及模型构建
排队论定义
研究等待线(队列)的数学理论和方法,又称随机服务系统理论。
最短路径问题
通过实例分析最短路径问题 的动态规划解法,如
Dijkstra算法、Floyd算法等 。
1
背包问题
针对不同类型的背包问题, 探讨其动态规划解法及应用
场景。
资源分配问题
研究资源分配问题的动态规 划模型及求解方法,如多阶 段资源分配问题等。
生产与存储问题
分析生产与存储问题的动态 规划解法,讨论其在企业生 产管理中的应用。
整数约束
决策变量需满足整数约束条件,如人员数量、设备台 数等。
目标函数选择
根据问题类型,选择合适的目标函数,如成本最小化 、利润最大化等。
分支定界法求解过程
初始可行解
通过松弛整数约束,得到一个初始可 行解。
分支过程
根据初始可行解,将问题分解为若干 个子问题,分别求解。
运筹学基础教学课件PPT

都江堰水利工程
Page 4
川西太守李冰 父子主持修建, 其目标是利用 岷江上游的水 资源灌溉川西 平原,追求的 效益还有防洪 与航运。其总 体构思是系统 思想的杰出运 用
北宋丁谓主持修复皇宫
Page 5
例2、北宋丁谓主持修复皇宫 面临的问题:木材、石材、 砖瓦等建筑材料如何取得?
修建如何进行?
大街 开封 皇宫
2、策略集
策 略:在对策中,局中人在整个决策过程中针对一系 列行动制定的完整行动方案。
策略集:每个局中人策略的全体集合。 局 势:每个局中人从自己的策略集合中选择一个策
略,构成一个局势。
3、赢得函数
利用全部局势集合上的一个实值函数,来描述 每个局势完结后局中人的得失的报酬数值。
对策的分类
Page 23
目标函数: 约束条件:1原材料的限制 2工时的限制 3座椅的限制 4非负限制 数学模型:
图解法
x2
1000
5x1+2.5x2≤2500
x1=400
800
Z=2600
600
400
Z=1800
Page 20
max Z=4x1+3x2
2x1 2x2 1600 5x1x1420.05x2 2500 x1 0、x2 0
线平衡率 秒表法/PTS
动作和方法研究
动改法
成本控制 设施规划
双手操作法 人机配合法
物流分析
防错法
PMP体系
PAC体系
系统设计
……
工作抽样法 流程程序法
五五法 其它
1工程学 2人机学(人因工程学) 3材料学 4管理学 5统计学 6运筹学 7系统工程学 8材料力学 9工程力学 10物流与设施规划
《运筹学》全套课件(完整版)

负指数分布、几何分布、爱尔朗分布等。
服务时间分布
负指数分布、确定型分布、一般分布等。
顾客到达和服务时间的独立性
假设顾客到达和服务时间是相互独立的。
单服务台排队系统
M/M/1排队系统
顾客到达服从泊松分布,服务时间服从负指 数分布,单服务台。
M/D/1排队系统
顾客到达服从泊松分布,服务时间服从确定 型分布,单服务台。
投资组合优化
确定投资组合中各种资产的最 优配置比例,以最大化收益或
最小化风险。
03
整数规划
整数规划问题的数学模型
01
整数规划问题的定 义
整数规划是数学规划的一个分支 ,研究决策变量取整数值的规划 问题。
02
整数规划问题的数 学模型
包括目标函数、约束条件和决策 变量,其中决策变量要求取整数 值。
03
Edmonds-Karp算法
介绍Edmonds-Karp算法的原理、步骤和实现方法,以及其与FordFulkerson算法的比较。
网络最大流问题的应用
列举网络最大流问题在资源分配、任务调度等领域的应用案例。
最小费用流问题
最小费用流问题的基本概 念
介绍最小费用流问题的定义、 分类和应用背景。
Bellman-Ford算法
优点是可以求解较大规模的整数规划问题,缺点是计算量较大,需 要较高的计算精度。
割平面法
割平面法的基本思想
通过添加新的约束条件(割平面)来缩小可行域的范围,从而逼 近最优解。
割平面法的步骤
包括构造割平面、求解子问题和更新割平面三个步骤,通过不断 迭代找到最优解。
割平面法的优缺点
优点是可以处理较复杂的整数规划问题,缺点是构造割平面的难 度较大,需要较高的数学技巧。
服务时间分布
负指数分布、确定型分布、一般分布等。
顾客到达和服务时间的独立性
假设顾客到达和服务时间是相互独立的。
单服务台排队系统
M/M/1排队系统
顾客到达服从泊松分布,服务时间服从负指 数分布,单服务台。
M/D/1排队系统
顾客到达服从泊松分布,服务时间服从确定 型分布,单服务台。
投资组合优化
确定投资组合中各种资产的最 优配置比例,以最大化收益或
最小化风险。
03
整数规划
整数规划问题的数学模型
01
整数规划问题的定 义
整数规划是数学规划的一个分支 ,研究决策变量取整数值的规划 问题。
02
整数规划问题的数 学模型
包括目标函数、约束条件和决策 变量,其中决策变量要求取整数 值。
03
Edmonds-Karp算法
介绍Edmonds-Karp算法的原理、步骤和实现方法,以及其与FordFulkerson算法的比较。
网络最大流问题的应用
列举网络最大流问题在资源分配、任务调度等领域的应用案例。
最小费用流问题
最小费用流问题的基本概 念
介绍最小费用流问题的定义、 分类和应用背景。
Bellman-Ford算法
优点是可以求解较大规模的整数规划问题,缺点是计算量较大,需 要较高的计算精度。
割平面法
割平面法的基本思想
通过添加新的约束条件(割平面)来缩小可行域的范围,从而逼 近最优解。
割平面法的步骤
包括构造割平面、求解子问题和更新割平面三个步骤,通过不断 迭代找到最优解。
割平面法的优缺点
优点是可以处理较复杂的整数规划问题,缺点是构造割平面的难 度较大,需要较高的数学技巧。
运筹学获奖课件

21
中国邮递员问题(CPP)
一种邮递员从邮局出发,要走完他所 管辖旳每一条街道,然后返回邮局。那么 怎样选择一条尽量短旳路线。
若将投递区的街道用边表示,街道的长度用边权 表示,邮局街道交叉口用点表示,则一个投递区构成 一个赋权连通无向图.中国邮递员问题转化为:在一 个非负加权连通图中,寻求一个权最小的巡回.这样 的巡回称为最佳巡回.
第三步同步烙第二、三张背面。 一共需要9分钟。
47
二、讨论交流 形成认知
思索:假如要烙4张饼、5张饼……10张 饼,怎样安排最节省时间?
总结:假如要烙旳饼旳张数是双数,2张 2张旳烙就能够,假如要烙旳饼旳张数是 单数,能够先2个2个旳烙,最终3张饼按 上面旳最优措施烙,最节省时间,所用时 间为3×张数。
7
《孙子兵法·形篇》中,有许多有关军事运 筹旳论述,孙武把度、量、数、称等数学 概念引入军事领域,经过双方对比计算, 进行战争胜败旳预测分析。孙武在《孙子 兵法·计篇》中还说“夫未战而庙算胜者, 得算多也;未战而庙算不胜者,得算少也。 多算胜,少算不胜,而况于无算乎!”这 里旳“算”就是计算筹划之意。
22
例:求右图所示投递区旳一条最佳 邮递路线
23
例:求右图所示投递区 旳一条最佳邮递路线
尽量少旳反复:
v4 v3 v2 v7 v1 为一条最佳巡回
24
中国运筹学会
中国第一种运筹学小组在钱学森、许国志先 生旳推动下在1956年于中国科学院力学研究 所成立。 中国运筹学会于1980年成立,第一届全国大 会在山东省济南召开,华罗庚教授被选为第 一届理事长。 1992年成为全国一级学会,章祥荪教授出任 理事长 北京、陕西、山东、大庆等某些省市设有省 级运筹学会 中国运筹学会下属有多种专业分会:如决策 科学分会、数学规划分会、排序分会、图论 组合分会等。
中国邮递员问题(CPP)
一种邮递员从邮局出发,要走完他所 管辖旳每一条街道,然后返回邮局。那么 怎样选择一条尽量短旳路线。
若将投递区的街道用边表示,街道的长度用边权 表示,邮局街道交叉口用点表示,则一个投递区构成 一个赋权连通无向图.中国邮递员问题转化为:在一 个非负加权连通图中,寻求一个权最小的巡回.这样 的巡回称为最佳巡回.
第三步同步烙第二、三张背面。 一共需要9分钟。
47
二、讨论交流 形成认知
思索:假如要烙4张饼、5张饼……10张 饼,怎样安排最节省时间?
总结:假如要烙旳饼旳张数是双数,2张 2张旳烙就能够,假如要烙旳饼旳张数是 单数,能够先2个2个旳烙,最终3张饼按 上面旳最优措施烙,最节省时间,所用时 间为3×张数。
7
《孙子兵法·形篇》中,有许多有关军事运 筹旳论述,孙武把度、量、数、称等数学 概念引入军事领域,经过双方对比计算, 进行战争胜败旳预测分析。孙武在《孙子 兵法·计篇》中还说“夫未战而庙算胜者, 得算多也;未战而庙算不胜者,得算少也。 多算胜,少算不胜,而况于无算乎!”这 里旳“算”就是计算筹划之意。
22
例:求右图所示投递区旳一条最佳 邮递路线
23
例:求右图所示投递区 旳一条最佳邮递路线
尽量少旳反复:
v4 v3 v2 v7 v1 为一条最佳巡回
24
中国运筹学会
中国第一种运筹学小组在钱学森、许国志先 生旳推动下在1956年于中国科学院力学研究 所成立。 中国运筹学会于1980年成立,第一届全国大 会在山东省济南召开,华罗庚教授被选为第 一届理事长。 1992年成为全国一级学会,章祥荪教授出任 理事长 北京、陕西、山东、大庆等某些省市设有省 级运筹学会 中国运筹学会下属有多种专业分会:如决策 科学分会、数学规划分会、排序分会、图论 组合分会等。
运筹学PPT完整版

C 变量:决策变量和非决策变量
B 约束条件:线性等式或不等式
A 目标函数:求最大值或最小值
非线性规划
目标函数:非线性函数
约束条件:非线性不等式
求解方法:梯度下降法、 牛顿法、拟牛顿法等
应用领域:生产计划、资 源分配、投资决策等
动态规划
基本概念:将复杂问题分解为若干子 0 1 问题,通过求解子问题来解决原问题
运筹学广泛应用于生产、运输、库存、销售、人力 资源等各个领域。
运筹学通过建立数学模型,求解最优解,以实现资 源的合理配置和高效利用。
运筹学的应用领域
生产与运营管理 项目管理 交通与运输规划
供应链管理 财务管理 资源分配与调度
运筹学的发展历程
起源:二战期间, 军事需求推动运 筹学的发展
20世纪50年代: 运筹学逐渐应用 于工业、经济等 领域
适用范围:解决资源分配、路径规划、 02 生产调度等问题
主要步骤:划分阶段、确定状态、建 0 3 立状态转移方程、求解最优解
特点:具有最优子结构性质,能够高 04 效地求解复杂问题
运筹学的实际应 用
生产计划与调度
生产计划:根据市场需求和生产能力制定生产计划, 包括生产数量、生产时间、生产地点等
生产调度:根据生产计划,合理分配生产资源,包 括人员、设备、原材料等
场趋势
运筹学在生物学中 的应用:分析生物 种群数量变化,预
测生物进化趋势
运筹学在工程学中 的应用:优化工程 设计,提高工程效
率
THANK YOU
汇报人:稻小壳
运筹学与人工智 能的结合,拓展
2 了运筹学的应用
领域
3 运筹学与人工智
能的结合,推动 了运筹学的理论 研究和实践应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 6
Managing Capacity
Chapter Objectives
Be able to:
▪Explain what capacity is, how firms measure capacity, and the difference between theoretical and rated capacity. ▪Describe the pros and cons associated with three different capacity strategies: lead, lag, and match. ▪Apply a wide variety of analytical tools for choosing between capacity alternatives, including expected value and break-even analysis, decision trees, and learning curves. ▪Apply the Theory of Constraints, waiting line theory, and Little’s Law to analyze and understand capacity issues in a business process environment.
Copyright © 2016 Pearson Education, Inc.
6-3
Capacity
▪ Measures of Capacity
▪ Theoretical capacity – The maximum output capability, allowing for no adjustments for preventive maintenance, unplanned downtime, or the like.
Copyright © 2016 Pearson Education, Inc.
6-6
Three Common Capacity Strategies
▪ Lead capacity strategy – A capacity strategy in which capacity is added in anticipation of demand.
6-14
Methods of Evaluating Capacity Alternatives
▪ Other Considerations:
▪ The strategic importance of an activity to a firm.
▪ The desired degree of managerial control.
▪ For every doubling of cumulative output, there is a set percentage reduction in the amount of inputs required.
Copyright © 2016 Pearson Education, Inc.
▪ Variable costs – Expenses directly tied to the level of business activity.
TC = FC + VC * X
TC = Total Cost FC = Fixed Cost VC = Variable cost per unit of business activity X = amount of business activity
6-8
Methods of Evaluating Capacity Alternatives
▪ Cost ▪ Demand Considerations ▪ Expected Value ▪ Decision Trees ▪ Break-Even Analysis ▪ Learning Curves
• Number of lines used • Number of shifts operating • Number of temporary workers used • Number of public storage facilities used • Product variations on line • Conformance quality • Quality improvement
▪ Lag capacity strategy – A capacity strategy in which capacity is added only after demand has materialized.
▪ Match capacity strategy – A capacity strategy that strikes a balance between the lead and lag capacity strategies by avoiding periods of high under or overutilization.
Copyright © 2016 Pearson Education, Inc.
6-10
Methods of Evaluating Capacity Alternatives
▪ Expected value – A calculation that summarizes the expected costs, revenues, or profits of a capacity alternative, based on several demand levels, each of which has a different probability.
Copyright © 2016 Pearson Education, Inc.
6-13
Methods of Evaluating Capacity Alternatives
▪ Learning curve theory – A body of theory based on applied statistics which suggests that productivity levels can improve at a predictable rate as people and even systems “learn” to do tasks more efficiently.
▪ Capacity decisions that managers face:
© 2013 APICS Dictionary
▪ How capacity is measured?
▪ Which factors affect capacity?
▪ The impact of the supply chain on the organization’s effective capacity.
▪ Rated capacity – The long-term, expected output capability of a resource or
system.
© 2013 APICS Dictionary
Copyright © 2016 Pearson Education, Inc.
6-4
▪ The need for flexibility.
Copyright © 2016 Pearson Education, Inc.
6-15
Understanding and Analyzing Process Capacity
▪ Theory of Constraints – An approach to visualizing and managing capacity which recognizes that nearly all products and services are created through a series of linked processes, and in every case, there is at least one process step that limits throughput for the entire chain.
Copyright © 2016 Pearson Education, Inc.
6-11
Methods of Evaluating Capacity Alternatives
▪ Decision tree – A visual tool that decision makers use to evaluate capacity decisions and to enable users to see the interrelationships between decisions and possible outcomes.
6-12
Methods of Evaluating Capacity Alternatives
▪ Break-even analysis
▪ Break-even point – The volume level for a business at which total revenues cover total costs.
Capacity
Examples of Capacity in Different Organizations
Table 6.1
Copyright © 2016 Pearson Education, Inc.
6-5
Capacity
▪ Factors that Affect Capacity
▪ Many factors affect capacity and many assumptions must be made:
Copyright © 2016 Pearson Education, Inc.
Managing Capacity
Chapter Objectives
Be able to:
▪Explain what capacity is, how firms measure capacity, and the difference between theoretical and rated capacity. ▪Describe the pros and cons associated with three different capacity strategies: lead, lag, and match. ▪Apply a wide variety of analytical tools for choosing between capacity alternatives, including expected value and break-even analysis, decision trees, and learning curves. ▪Apply the Theory of Constraints, waiting line theory, and Little’s Law to analyze and understand capacity issues in a business process environment.
Copyright © 2016 Pearson Education, Inc.
6-3
Capacity
▪ Measures of Capacity
▪ Theoretical capacity – The maximum output capability, allowing for no adjustments for preventive maintenance, unplanned downtime, or the like.
Copyright © 2016 Pearson Education, Inc.
6-6
Three Common Capacity Strategies
▪ Lead capacity strategy – A capacity strategy in which capacity is added in anticipation of demand.
6-14
Methods of Evaluating Capacity Alternatives
▪ Other Considerations:
▪ The strategic importance of an activity to a firm.
▪ The desired degree of managerial control.
▪ For every doubling of cumulative output, there is a set percentage reduction in the amount of inputs required.
Copyright © 2016 Pearson Education, Inc.
▪ Variable costs – Expenses directly tied to the level of business activity.
TC = FC + VC * X
TC = Total Cost FC = Fixed Cost VC = Variable cost per unit of business activity X = amount of business activity
6-8
Methods of Evaluating Capacity Alternatives
▪ Cost ▪ Demand Considerations ▪ Expected Value ▪ Decision Trees ▪ Break-Even Analysis ▪ Learning Curves
• Number of lines used • Number of shifts operating • Number of temporary workers used • Number of public storage facilities used • Product variations on line • Conformance quality • Quality improvement
▪ Lag capacity strategy – A capacity strategy in which capacity is added only after demand has materialized.
▪ Match capacity strategy – A capacity strategy that strikes a balance between the lead and lag capacity strategies by avoiding periods of high under or overutilization.
Copyright © 2016 Pearson Education, Inc.
6-10
Methods of Evaluating Capacity Alternatives
▪ Expected value – A calculation that summarizes the expected costs, revenues, or profits of a capacity alternative, based on several demand levels, each of which has a different probability.
Copyright © 2016 Pearson Education, Inc.
6-13
Methods of Evaluating Capacity Alternatives
▪ Learning curve theory – A body of theory based on applied statistics which suggests that productivity levels can improve at a predictable rate as people and even systems “learn” to do tasks more efficiently.
▪ Capacity decisions that managers face:
© 2013 APICS Dictionary
▪ How capacity is measured?
▪ Which factors affect capacity?
▪ The impact of the supply chain on the organization’s effective capacity.
▪ Rated capacity – The long-term, expected output capability of a resource or
system.
© 2013 APICS Dictionary
Copyright © 2016 Pearson Education, Inc.
6-4
▪ The need for flexibility.
Copyright © 2016 Pearson Education, Inc.
6-15
Understanding and Analyzing Process Capacity
▪ Theory of Constraints – An approach to visualizing and managing capacity which recognizes that nearly all products and services are created through a series of linked processes, and in every case, there is at least one process step that limits throughput for the entire chain.
Copyright © 2016 Pearson Education, Inc.
6-11
Methods of Evaluating Capacity Alternatives
▪ Decision tree – A visual tool that decision makers use to evaluate capacity decisions and to enable users to see the interrelationships between decisions and possible outcomes.
6-12
Methods of Evaluating Capacity Alternatives
▪ Break-even analysis
▪ Break-even point – The volume level for a business at which total revenues cover total costs.
Capacity
Examples of Capacity in Different Organizations
Table 6.1
Copyright © 2016 Pearson Education, Inc.
6-5
Capacity
▪ Factors that Affect Capacity
▪ Many factors affect capacity and many assumptions must be made:
Copyright © 2016 Pearson Education, Inc.
