三次函数的零点问题
三次函数的图象与性质

解:(1)由原式,得 = 3 − 2 − 4 + 4,
∴ ′ = 3 2 − 2 − 4.
1
1
(2)由′ −1 = 0,得 = 2.此时有 = ( 2 − 4)( − 2),
′ = 3 2 − − 4.
4
令′ = 0,得 = 3或 = −1
= −
求导:’ = 3 2 − 3 = 3( + 1)( − 1)
令’ = 0,则 = ±1.
列表:
−∞, −
−
−,
, +∞
’
+
0
−
0
+
增
极大
减
极小
增
y
y
o
−1
x
1
′ 图象
x
o
−1
1
图象
探究二:三次函数 = 3 + 2 + + ( ≠ 0)在R上
2 + 12 ≤ + 6,
由题意可知,1 ≥ −2, 2 ≤ 2,即൝
2 + 12 ≤ 6 − .
解不等式组,得−2 ≤ ≤ 2.
优解:因为′ = 3 2 − 2 − 4的图象是开口向上且过点(0,4)
的抛物线,
4 + 8 ≥ 0,
由条件,得′ −2 ≥ 0, ′ 2 ≥ 0,即ቊ
解:(1) ′ = 3 2 − 3 = 3( 2 − )
当 < 0时,对,有′ > 0,所以 的单调增区间为(−∞, +∞);
当 > 0时,由′ > 0,解得 < − 或 > ;由′ < 0,解得− < <
三次函数的零点问题

三次函数的零点问题
在数学中,三次函数是指一个至多存在三次幂次的多项式函数。
对
于三次函数来说,它的零点问题是一个非常重要的问题,这在许多数
学和工程问题中都有广泛的应用。
三次函数可以表示为f(x)=ax^3+bx^2+cx+d,其中a、b、c和d都是
常数,x是一个变量。
三次函数的图像通常是一个S形曲线,在x轴上
存在一个或多个交点,这些交点就是三次函数的零点。
在三次函数中,求解零点问题的一种方法是通过因式分解,通过寻
找a、b、c和d的共同因子来找到零点。
如果三次函数可以因式分解,则不难看出函数的零点。
但是,在大多数情况下,三次函数并不容易
因式分解,因此必须使用其他方法来解决零点问题。
另一种解决零点问题的方法是使用数值方法,例如二分法和牛顿法。
这些方法不需要将三次函数转化为标准的形式,而是直接以数值方式
计算函数的零点。
这种方法通常需要大量的计算,因此需要使用计算
机来进行计算。
除此之外,还有一种特殊的三次函数,称为“卡迈隆函数”。
这个函
数的形式是f(x)=x^3-3x,它只有一个实零点,值为0。
这个函数具有
一些非常有用的性质,因此它在计算机图形学和密码学中经常被使用。
总之,三次函数的零点问题在数学和工程领域中有着深远的影响。
无论是使用因式分解还是数值方法,找到函数的零点都是一个非常重
要的问题。
同时,特殊的三次函数卡迈隆函数也具有非常有用的性质,在许多计算问题中都有广泛的应用。
谈二次函数与三次函数的零点式应用

谈二次函数与三次函数的零点式应用作者:黄旭东来源:《中学数学杂志(高中版)》2015年第05期对于二次函数f(x)=ax2+bx+c(a≠0)若有根x1,x2,则可写成零点式f(x)=ax-x1x-x2(a≠0).同理对一个三次函数f(x)=ax3+bx2+cx+d(a≠0)若有根x1,x2,x3,则可写成零点式f(x)=ax-x1x-x2x-x3(a≠0),其应用广泛,下面简单讨论其应用.1巧证不等式例1证明:-33≤sinx2-cosx≤33.证明依题设结构,构造以±33为零点的二次函数,记f(t)=t-33t+33,由二次函数图像性质,欲证-33≤sinx2-cosx≤33成立,只需证f(sinx2-cosx)≤0即可.由f(sinx2-cosx)=sin2x2-cosx2-13=3sin2x-2-cosx232-cosx2=-1-2cosx232-cosx2≤0成立,故原不等式成立.点评此题证明没用到三角中变形求值域方法,而是由结构巧妙构造二次函数零点式,依二次函数的函数值与不等式解集之间的紧密关系,数与形有机结合,方法美妙,令人印象深刻.对于证a≤f(x)≤b的形式的不等式,一般可考虑构造二次函数零点式来解决.例2(数学通报201412期问题征解2217)设长方体的长宽高分别为a,b,c(a>b>c),p 为长方体各棱长之和,为表面积,d为一条对角线,求证:a>13p4+d2-12s,c解析由求证结构形式,不妨构造以x1=13p4+d2-12s,x2=13p4-d2-12s为零点的二次函数,由韦达定理知x1+x2=p6=23a+b+c,x1x2=19p216-d2+12s=19[a+b+c2-a2+b2+c2+ab+bc+ac]=13ab+bc+ac,构造二次函数f(x)=3(x-x1)(x-x2)=3x2-2a+b+cx+ab+bc+ac,由函数对称轴为x=a+b+c3,又a>b>c,故a>a+b+c3>c,又由f(a)=3a2-2a+b+ca+ab+bc+ac=a2-ab+bc-ac=(a-b)(a-c)>0,f(c)=3c2-2a+b+cc+ab+bc+ac=c2+ab-bc-ac=(c-b)(c-a)>0,故c13p4+d2-12s,c点评此题用一般方法较难下手,而构造二次函数的零点式,问题的解决得以易乎寻常的顺畅.2巧比大小例3设函数f(x)=ax2-x,g(x)=x-a(a>0),若p,q是方程f(x)-g(x)=0的两根,且满足0证明由f(x)-g(x)=0的两根为p,q,构建零点式,则f(x)-g(x)=a(x-p)(x-q),由x∈(0,p),且00,即f(x)>g(x).又f(x)-p-a=g(x)+a(x-p)(x-q)-p-a=x-p+a(x-p)(x-q)=x-pax-q+1a,由0综上所述,gx例4已知三次函数f(x)=x3+ax2+bx+c,方程f(x)-x=0的三根满足0解析由题意,x1,x2,x3为方程f(x)-x=0的三根,构建零点式得f(x)-x=x-x1x-x2x-x3,由-ca+b+c=-f(0)[f(1)-1]=x1x2x31-x11-x21-x3,又由0点评例3与例4是涉及到二次或三次函数的根的不等关系的证明问题,若按常规采用一般式方程进行处理,问题将变得较为复杂.一般地,一些二次或三次函数的题目中涉及方程的根时,常利用其零点式进行化归处理,可大大优化解题过程与步骤.例5(2010年湖北龙泉中学考试题)已知实数a1a1a2+a1a3+a2a3=b1b2+b1b3+b2b3,且a1b1b2b3;(4)(1-a1)(1-a2)(1-a3)A.1B.2C.3D.4解析由三次方程根与系数关系,构建三次函数f(x)=x-a1x-a2x-a3=x3-a1+a2+a3x2+a1a2+a1a3+a2a3x-a1a2a3,a1b1b2+b1b3+b2b3x-b1b2b3,b1b1b2+b1b3+b2b3,则函数g(x)即为函数f(x)向下作了部分平移而得,如右图示:故由图知(1)(2)显然正确,且a1a2a30,即(1-a1)(1-a2)(1-a3)>(1-b1)(1-b2)(1-b3),则(4)不对.故正确的为2个,选B.点评在一些题目中,根据一元二次方程或一元三次方程的根与系数的关系可构造二次函数或三次函数零点式,巧妙解决一些数学问题,可起到让人耳目一新的效果.3解决不定方程问题例6两个正整数的和比积小2015,并且其中一个是完全平方数,则较大数与较小数的差是.解析由两正数的和与积,联想二次函数零点式,不妨设此两正整数分别为m,n(m>n>0),记f(x)=(x-m)(x-n),依题意,mn-m-n=2015,故f(1)=(1-m)(1-n)=2016=25×7×32,由m,n中有一个为完全平方数,则m-1=672,n-1=3,或m-1=84,n-1=24,或m-1=288,n-1=7.故m=673,n=4,或m=85,n=25,或m=289,n=8.所以m-n=669或60或281.例7已知函数f(x)=x2+ax-a+2(a∈Z)有两个不同的正整数零点,求整数a的值.解析不妨设此函数零点为m,n,则f(x)=x-mx-n,则由题意,m+n=-a,mn=2-a,故mn-m-n=2,则f(1)=1-m1-n=3,由m,n为不同的正整数零点,则m-1=1,n-1=3,或m-1=3,n-1=1.所以两正整数只能为2,4,则a=-6.点评当涉及两数和与积结构时,可联想二次函数零点式,在解决不定方程问题时,有时可使有关问题的解法变得简洁、明快.零点式的应用是相当广泛的,不但二次与三次可利用其零点式解决问题,甚至一次函数也是如此.如像不等式证明中af(x)可构建一次函数零点式f(t)=t-a,也可用零点视角来研究.当然二次函数与三次函数零点式的应用肯定不止本文中所提到的这些,由于本人知识水平有限,欢迎同行进行交流与补充.作者简介黄旭东,1975年6月生,湖北黄石人,中级职称.主研方向为中学数学解题规律与教学规律.发表文章若干篇.。
三次函数图像与性质(解析版)

专题2-2三次函数图像与性质【题型1】求三次函数的解析式【题型2】三次函数的单调性问题【题型3】三次函数的图像【题型4】三次函数的最值、极值问题【题型5】三次函数的零点问题【题型6】三次函数图像,单调性,极值,最值综合问题【题型7】三次函数对称中心【题型8】三次函数的切线问题【题型9】三次函数根与系数的关系1/342/34【题型1】求三次函数的解析式(1)一般式:()³²f x ax bx cx d =+++(a ≠0)(2)交点式:()123()()()f x a x x x x x x =---(a ≠0)1.若三次函数()f x 满足()()()()00,11,03,19f f f f ''====,则()3f =()A .38B .171C .460D .965【解析】待定系数法,求函数解析式设()³²f x ax bx cx d =+++,则()232f x ax bx c '=++,由题意可得:()()()()0011031329f d f a b c d f c f a b c ⎧==⎪=+++=⎪⎨==⎪⎪=+'=⎩'+,解得101230a b c d =⎧⎪=-⎪⎨=⎪⎪=⎩,则()3210123f x x x x =-+,所以()32310312333171f =⨯-⨯+⨯=.【题型2】三次函数的单调性问题三次函数是高中数学中的一个重要内容,其考点广泛且深入,主要涉及函数的性质、图像、最值、零点以及与其他函数的综合应用等方面。
以下是对三次函数常见考点的详细分析:1.三次函数的定义与形式∙定义:形如f (x )=ax 3+bx 2+cx +d (其中a ≠=0)的函数称为三次函数。
∙形式:注意系数a ,b ,c ,d 的作用,特别是a 的正负决定了函数的开口方向(a >0开口向上,a <0开口向下)。
专题17 三次函数的图像与性质(解析版)

专题17 三次函数的图像与性质一、例题选讲题型一 运用三次函数的图像研究零点问题遇到函数零点个数问题,通常转化为两个函数图象交点问题,进而借助数形结合思想解决问题;也可转化为方程解的个数问题,通过具体的解方程达到解决问题的目的.前者由于是通过图形解决问题,故对绘制的函数图象准确度和细节处要求较高,后者对问题转化的等价性和逻辑推理的严谨性要求较高.下面的解法是从解方程的角度考虑的.例1,(2017某某,某某,某某,某某三调)已知函数3()3 .x x a f x x x x a ⎧=⎨-<⎩≥,,,若函数()2()g x f x ax =-恰有2个不同的零点,则实数a 的取值X 围是.【答案】3(2)2-,【解析】:函数()2()g x f x ax =-恰有2个不同的零点,即方程2()0f x ax -=恰有2个不相等的根,亦即方程(Ⅰ)20x ax ax ≥⎧⎨-=⎩和(Ⅱ)3260x a x x ax <⎧⎨--=⎩共有2个不相等的根. 首先(Ⅰ)中20x ax -=,即(2)0a x -=,若2a =,则2x ≥都是方程20x ax -=的根,不符合题意,所以2a ≠,因此(Ⅰ)中由20x ax -=解得0x =,下面分情况讨论(1)若0x =是方程(Ⅰ)的唯一根,则必须满足0a ≥,即0a ≤,此时方程(Ⅱ)必须再有唯一的一个根,即30260x a x x ax <≤⎧⎨--=⎩有唯一根,因为0x ≠,由3260x x ax --=,得226x a =+必须有满足0x a <≤的唯一根,首先60a +>,其次解得的负根需满足0a <≤,从而解得302a -<≤,(2)若0x =不是方程(Ⅰ)的唯一根,则必须满足0a <,即0a >,此时方程(Ⅱ)必须有两个不相等的根,即30260a x ax x ax ⎧>⎪<⎨⎪--=⎩有两个不相等的根,由3260x x ax --=,得0x a =<适合,另外226x a =+还有必须一满足,0x a a <>的非零实根,首先60a +>,a≥,从而解得02a <≤,但前面已经指出2a ≠,故02a <<,综合(1),(2),得实数a 的取值X 围为3(,2)2-.例2,(2017某某学情调研)已知函数f (x )=⎩⎪⎨⎪⎧12x -x3,x ≤0,-2x ,x >0.)当x ∈(-∞,m ]时,f (x )的取值X 围为[-16,+∞),则实数m 的取值X 围是________.【答案】 [-2,8]【解析】思路分析 由于f (x )的解析式是已知的,因此,可以首先研究出函数f (x )在R 上的单调性及相关的性质,然后根据f (x )的取值X 围为[-16,+∞),求出它的值等于-16时的x 的值,借助于函数f (x )的图像来对m 的取值X 围进行确定.当x ≤0时,f (x )=12x -x 3,所以f ′(x )=12-3x 2.令f ′(x )=0,则x =-2(正值舍去),所以当x ∈(-∞,-2)时,f ′(x )<0,此时f (x )单调递减;当x ∈(-2,0]时,f ′(x )>0,此时f (x )单调递增,故函数f (x )在x ≤0时的极小值为f (-2)=-16.当x >0时,f (x )=-2x 单调递减,f (0)=0,f (8)=-16,因此,根据f (x )的图像可得m ∈[-2,8].解后反思 根据函数的解析式来得到函数的相关性质,然后由此画出函数的图像,借助于函数的图像可以有效地进行解题,这就是数形结合的魅力.题型二 三次函数的单调性问题研究三次函数的单调性,往往通过导数进行研究.要特别注意含参的讨论.例3,已知函数32()3f x x x ax =-+()a ∈R ,()|()|g x f x =.(1)求以(2,(2))P f 为切点的切线方程,并证明此切线恒过一个定点;(2)若()g x kx ≤对一切[0,2]x ∈恒成立,求k 的最小值()h a 的表达式;(3)设0a >,求()y g x =的单调增区间.解析 (1)2()36f x x x a '=-+,(2)f a '=,过点P 的切线方程为()224y a x a =-+-,即4y ax =-,它恒过点(0,- 4);(2)()g x kx ≤即32|3|x x ax kx -+≤. 当0x =时,上式恒成立;当(0,2]x ∈时,即2|3|x x a k -+≤对一切(0,2]x ∈恒成立,设2max ()|3|,[0,2]h a x x a x ∈=-+, ①当94a ≥时,2max |3|x x a -+在0x =时取得,∴()h a a =;②当94a <时,2max 99(),984|3|max{,}994()48a a x x a a a a a ⎧<<⎪⎪-+=-=⎨⎪-⎪⎩≤; 由①②,得9(),8()99()48a a g a a a ⎧>⎪⎪=⎨⎪-⎪⎩≤; (3)32()3f x x x ax =-+,22()363(1)3f x x x a x a '=-+=-+-,令()0f x =,得0x =或230x x a -+=,当94a <时,由230x x a -+=,解得132x =232x =令()0f x '=,得23(1)30x a -+-=,当3a <时,由23(1)30x a -+-=,解得31x =41x =+1)当3a ≥时,()y g x =的单调增区间为(0,)+∞;2)当934a <≤时,()y g x =的单调增区间为3(0,)x 和4(,)x +∞;3)当904a <<时,()y g x =的单调增区间为3(0,)x 和14(,)x x 和2(,)x +∞.例4,(2018某某期末) 若函数f(x)=(x +1)2|x -a|在区间[-1,2]上单调递增,则实数a 的取值X 围是________.【答案】 (-∞,-1]∪⎣⎢⎡⎭⎪⎫72,+∞思路分析 由于条件中函数的解析式比较复杂,可以先通过代数变形,将其化为熟悉的形式,进而利用导数研究函数的性质及图像,再根据图像变换的知识得到函数f(x)的图像进行求解.函数f(x)=(x +1)2|x -a|=|(x +1)2(x -a)|=|x 3+(2-a)x 2+(1-2a)x -a|.令g(x)=x 3+(2-a)x 2+(1-2a)x -a,则g ′(x)=3x 2+(4-2a)x +1-2a =(x +1)(3x +1-2a).令g ′(x)=0得x 1=-1,x 2=2a -13.①当2a -13<-1,即a<-1时,令g ′(x)>0,即(x +1)(3x +1-2a)>0,解得x<2a -13或x>-1;令g ′(x)<0,解得2a -13<x<-1.所以g(x)的单调增区间是⎝ ⎛⎭⎪⎫-∞,2a -13,(-1,+∞),单调减区间是⎝ ⎛⎭⎪⎫2a -13,-1. 又因为g(a)=g(-1)=0,所以f(x)的单调增区间是⎝ ⎛⎭⎪⎫a ,2a -13,(-1,+∞),单调减区间是(-∞,a),⎝ ⎛⎭⎪⎫2a -13,-1,满足条件,故a<-1(此种情况函数f(x)图像如图1). ,图1)②当2a -13=-1,即a =-1时,f(x)=|(x +1)3|,函数f(x)图像如图2,则f(x)的单调增区间是(-1,+∞),单调减区间是(-∞,-1),满足条件,故a =-1.,图2)③当2a -13>-1,即a>-1时,令g ′(x)>0,即(x +1)(3x +1-2a)>0,解得x<-1或x>2a -13;令g ′(x)<0,解得-1<x<2a -13.所以g(x)的单调增区间是(-∞,-1),⎝ ⎛⎭⎪⎫2a -13,+∞,单调减区间是⎝ ⎛⎭⎪⎫-1,2a -13. 又因为g(a)=g(-1)=0,所以f(x)的单调增区间是⎝ ⎛⎭⎪⎫-1,2a -13,(a,+∞),单调减区间是(-∞,-1),⎝ ⎛⎭⎪⎫2a -13,a ,要使f(x)在[-1,2]上单调递增,必须满足2≤2a -13,即a ≥72,又因为a>-1,故a ≥72(此种情况函数f(x)图像如图3).综上,实数a 的取值X 围是(-∞,-1]∪⎣⎢⎡⎭⎪⎫72,+∞.,图3)例5,(2018某某期末)已知函数f(x)=⎩⎪⎨⎪⎧-x3+x2,x<0,ex -ax ,x ≥0,其中常数a ∈R .(1) 当a =2时,求函数f (x )的单调区间;(2) 若方程f (-x )+f (x )=e x -3在区间(0,+∞)上有实数解,某某数a 的取值X 围;规X 解答 (1) 当a =2时,f(x)=⎩⎪⎨⎪⎧-x3+x2,x<0,ex -2x ,x ≥0.①当x<0时,f ′(x)=-3x 2+2x<0恒成立,所以f(x)在(-∞,0)上递减;(2分)②当x ≥0时,f ′(x)=e x -2,可得f(x)在[0,ln 2]上递减,在[ln 2,+∞)上递增.(4分)因为f(0)=1>0,所以f(x)的单调递减区间是(-∞,0)和[0,ln 2],单调递增区间是[ln 2,+∞).(5分)(2) 当x>0时,f(x)=e x -ax,此时-x<0,f(-x)=-(-x)3+(-x)2=x 3+x 2.所以可化为a =x 2+x +3x在区间(0,+∞)上有实数解.(6分) 记g(x)=x 2+x +3x ,x ∈(0,+∞),则g ′(x)=2x +1-3x2=(x -1)(2x2+3x +3)x2.(7分) 可得g(x)在(0,1]上递减,在[1,+∞)上递增,且g(1)=5,当x →+∞时,g(x)→+∞.(9分)所以g(x)的值域是[5,+∞),即实数a 的取值X 围是[5,+∞).(10分)题型三 三次函数的极值与最值问题①利用导数刻画函数的单调性,确定函数的极值;② 通过分类讨论,结合图象,实现函数的极值与零点问题的转化.函数,方程和不等式的综合题,常以研究函数的零点,方程的根,不等式的解集的形式出现,大多数情况下会用到等价转化,数形结合的数学思想解决问题,而这里的解法是通过严谨的等价转化,运用纯代数的手段来解决问题的,对抽象思维和逻辑推理的能力要求较高,此题也可通过数形结合的思想来解决问题,可以一试.例6,(2018苏锡常镇调研)已知函数32()1f x x ax bx a b =+++∈,,R . (1)若20a b +=,① 当0a >时,求函数()f x 的极值(用a 表示);② 若()f x 有三个相异零点,问是否存在实数a 使得这三个零点成等差数列?若存在,试求出a 的值;若不存在,请说明理由;规X 解答 (1)①由2()32f x x ax b '=++及02=+b a ,得22()32f x x ax a '=+-,令()0f x '=,解得3ax =或a x -=.由0>a 知,(,)()0x a f x '∈-∞->,,)(x f 单调递增,(,)()03a x a f x '∈-<,,)(x f 单调递减,(,)()03ax f x '∈+∞>,,)(x f 单调递增,因此,)(x f 的极大值为3()1f a a -=+,)(x f 的极小值为35()1327a a f =-. ② 当0a =时,0b =,此时3()1f x x =+不存在三个相异零点; 当0a <时,与①同理可得)(x f 的极小值为3()1f a a -=+,)(x f 的极大值为35()1327a a f =-. 要使)(x f 有三个不同零点,则必须有335(1)(1)027a a +-<,即332715a a <->或.不妨设)(x f 的三个零点为321,,x x x ,且321x x x <<,则123()()()0f x f x f x ===,3221111()10f x x ax a x =+-+=, ①3222222()10f x x ax a x =+-+=, ②3223333()10f x x ax a x =+-+=, ③②-①得222212121212121()()()()()0x x x x x x a x x x x a x x -+++-+--=, 因为210x x ->,所以222212121()0x x x x a x x a ++++-=, ④ 同理222332232()0x x x x a x x a ++++-=, ⑤⑤-④得231313131()()()()0x x x x x x x a x x -+-++-=,因为310x x ->,所以2310x x x a +++=,又1322x x x +=,所以23ax =-.所以()03af -=,即22239a a a +=-,即327111a =-<-,因此,存在这样实数a =满足条件.例7,(2017⋅某某)已知函数32()1(0,)f x x ax bx a b =+++>∈R 有极值,且导函数'()f x 的极值点是()f x 的零点.(极值点是指函数取极值时对应的自变量的值)(1)求b 关于a 的函数关系式,并写出定义域;(2)证明:33b a >;(3)若(),'()f x f x 这两个函数的所有极值之和不小于72-,求a 的取值X 围.解析(1)2'()32f x x ax b =++有零点,24120a b ∆=->,即23a b >,又''()620f x x a =+=,解得3a x =-,根据题意,()03a f -=,即3210333a a a a b ⎛⎫⎛⎫⎛⎫-+-+-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,化简得2239b a a =+,又203a a b >⎧⎨>⎩,所以3a >,即223(3)9b a a a =+>;(2)设2433224591()3(427)(27)81381g a b a a a a a a a =-=-+=--,而3a >,故()0g a >,即23b a >;(3)设12,x x 为()f x 的两个极值点,令'()0f x =得12122,33b ax x x x =+=-, 法一:332212121212()()()()2f x f x x x a x x b x x +=++++++ 22121212121212()[()3][()2]()2x x x x x x a x x x x b x x =++-++-+++3324242232()202732739a ab a a a a =-+=-++=.记()f x ,()f x '所有极值之和为()S a ,12()()0f x f x +=,2'()33a a f b -=-, 则221237()()()'()3392a a a S a f x f x f b a =++-=-=--≥, 而23()()3a S a a =-在(3,)a ∈+∞上单调递减且7(6)2S =-,故36a <≤.法二:下面证明()f x 的图像关于(,())33a af --中心对称,233232()1()()()1333327a a a ab a f x x ax bx x b x =+++=++-++-+23()()()()3333a a a ax b x f =++-++-,所以()()2()0333a a a f x f x f --+-+=-=,所以12()()0f x f x +=,下同法一.例8,(2018某某学情调研)已知函数f(x)=2x 3-3(a +1)x 2+6ax,a ∈R .(1) 曲线y =f (x )在x =0处的切线的斜率为3,求a 的值;(2) 若对于任意x ∈(0,+∞),f (x )+f (-x )≥12ln x 恒成立,求a 的取值X 围;(3) 若a >1,设函数f (x )在区间[1,2]上的最大值,最小值分别为M (a ),m (a ),记h (a )=M (a )-m (a ),求h (a )的最小值.思路分析 第(3)问,欲求函数f(x)在区间[1,2]上的最值M(a),m(a),可从函数f(x)在区间[1,2]上的单调性入手,由于f ′(x)=6(x -1)(x -a),且a >1,故只需分为两大类:a ≥2,1<a <2.当1<a <2时,函数f(x)在区间[1,2]上先减后增,进而比较f(1)和f(2)的大小确定函数最大值,由f(1)=f(2)得到分类的节点a =53.规X 解答 (1) 因为f(x)=2x 3-3(a +1)x 2+6ax,所以f ′(x)=6x 2-6(a +1)x +6a,所以曲线y =f(x)在x =0处的切线的斜率k =f ′(0)=6a,所以6a =3,所以a =12.(2分)(2) f(x)+f(-x)=-6(a +1)x 2≥12ln x对任意x ∈(0,+∞)恒成立,所以-(a +1)≥2lnxx2.(4分)令g(x)=2lnx x2,x >0,则g ′(x)=2(1-2lnx )x3.令g ′(x)=0,解得x = e.当x ∈(0,e)时,g ′(x)>0,所以g(x)在(0,e)上单调递增;当x ∈(e,+∞)时,g ′(x)<0,所以g(x)在(e,+∞)上单调递减.所以g(x)max =g(e)=1e,(6分)所以-(a +1)≥1e ,即a ≤-1-1e,所以a 的取值X 围为⎝⎛⎦⎥⎤-∞,-1-1e .(8分)(3) 因为f(x)=2x 3-3(a +1)x 2+6ax,所以f ′(x)=6x 2-6(a +1)x +6a =6(x -1)(x -a),令f ′(x)=0,则x =1或x =a.(10分)f(1)=3a -1,f(2)=4.由f(1)=f(2)得到分类的节点a =53.①当1<a ≤53时,当x ∈(1,a)时,f ′(x)<0,所以f(x)在(1,a)上单调递减;当x ∈(a,2)时,f ′(x)>0,所以f(x)在(a,2)上单调递增.又因为f(1)≤f(2),所以M(a)=f(2)=4,m(a)=f(a)=-a 3+3a 2,所以h(a)=M(a)-m(a)=4-(-a 3+3a 2)=a 3-3a 2+4.因为h ′(a)=3a 2-6a =3a(a -2)<0,所以h(a)在⎝ ⎛⎦⎥⎤1,53上单调递减,所以当a ∈⎝ ⎛⎦⎥⎤1,53时,h(a)的最小值为h ⎝ ⎛⎭⎪⎫53=827.(12分)②当53<a <2时,当x ∈(1,a)时,f ′(x)<0,所以f(x)在(1,a)上单调递减;当x ∈(a,2)时,f ′(x)>0,所以f(x)在(a,2)上单调递增.又因为f(1)>f(2),所以M(a)=f(1)=3a -1,m(a)=f(a)=-a 3+3a 2,所以h(a)=M(a)-m(a)=3a -1-(-a 3+3a 2)=a 3-3a 2+3a -1.因为h ′(a)=3a 2-6a +3=3(a -1)2>0.所以h(a)在⎝ ⎛⎭⎪⎫53,2上单调递增,所以当a ∈⎝ ⎛⎭⎪⎫53,2时,h(a)>h ⎝ ⎛⎭⎪⎫53=827.(14分)③当a ≥2时,当x ∈(1,2)时,f ′(x)<0,所以f(x)在(1,2)上单调递减,所以M(a)=f(1)=3a -1,m(a)=f(2)=4,所以h(a)=M(a)-m(a)=3a -1-4=3a -5,所以h(a)在[2,+∞)上的最小值为h(2)=1.综上,h(a)的最小值为827.(16分)二、达标训练1,(2017某某暑假测试) 已知函数f (x )=⎩⎪⎨⎪⎧1x,x >1,x3,-1≤x ≤1,)若关于x 的方程f (x )=k (x +1)有两个不同的实数根,则实数k 的取值X 围是________.【答案】 ⎝ ⎛⎭⎪⎫0,12【解析】思路分析 方程f (x )=k (x +1)的实数根的个数可以理解为函数y =f (x )与函数y =k (x +1)交点的个数,因此,在同一个坐标系中作出它们的图像,由图像来观察它们的交点的个数.在同一个直角坐标系中,分别作出函数y =f (x )及y =k (x +1)的图像,则函数f (x )max =f (1)=1,设A (1,1),B (-1,0),函数y =k (x +1)过点B ,则由图可知要使关于x 的方程f (x )=k (x +1)有两个不同的实数根,则0<k <k AB =12.2,(2017苏北四市期末) 已知函数f (x )=⎩⎪⎨⎪⎧sinx ,x <1,x3-9x2+25x +a ,x ≥1,)若函数f (x )的图像与直线y =x 有三个不同的公共点,则实数a 的取值集合为________.【答案】 {-20,-16}【解析】当x <1时,f(x)=sin x,联立⎩⎪⎨⎪⎧y =sinx ,y =x ,得x -sin x =0,令u(x)=x -sin x(x <1),则u ′(x)=1-cos x ≥0,所以函数u(x)=x -sin x(x <1)为单调增函数,且u(0)=0,所以u(x)=x -sin x(x <1)只有唯一的解x=0,这表明当x <1时,函数f(x)的图像与直线y =x 只有1个公共点.因为函数f(x)的图像与直线y =x 有3个不同的公共点,从而当x ≥1时,函数f(x)的图像与直线y =x 只有2个公共点.当x ≥1时,f(x)=x 3-9x 2+25x +a,联立⎩⎪⎨⎪⎧y =x3-9x2+25x +a ,y =x ,得a =-x 3+9x 2-24x,令h(x)=-x 3+9x 2-24x(x ≥1),则h ′(x)=-3x 2+18x -24=-3(x -2)(x -4).令h ′(x)=0得x =2或x =4,列表如下:32数a =-20或a =-16.综上所述,实数a 的取值集合为{-20,-16}.3,(2019某某,某某二模)已知函数f(x)=⎪⎩⎪⎨⎧>+-≤+0,3120,33x x x x x 设g(x)=kx +1,且函数y =f(x)-g(x)的图像经过四个象限,则实数k 的取值X 围为________.【答案】 ⎝⎛⎭⎪⎫-9,13【解析】解法1 y =⎩⎪⎨⎪⎧|x +3|-(kx +1),x ≤0,x 3-(k +12)x +2,x>0,若其图像经过四个象限.①当x>0时,y =x 3-(k +12)x +2,当x =0时,y =2>0,故它要经过第一象限和第四象限,则存在x>0,使y=x 3-(k +12)x +2<0,则k +12>x 2+2x ,即k +12>⎝ ⎛⎭⎪⎫x2+2x min .令h(x)=x 2+2x (x>0),h ′(x)=2x -2x2=2(x3-1)x2,当x>1时,h ′(x)>0,h(x)在(1,+∞)上递增;当0<x<1时,h ′(x)<0,h(x)在(0,1)上递减,当x =1时取得极小值,也是最小值,h(x)min =h(1)=3,所以k +12>3,即k>-9.②当x ≤0时,y =|x +3|-(kx +1),当x =0时,y =2>0,故它要经过第二象限和第三象限,则存在x<0,使y =|x +3|-(kx +1)<0,则k<|x +3|-1x,即k<⎝⎛⎭⎪⎫|x +3|-1x max .令φ(x)=|x +3|-1x=⎩⎪⎨⎪⎧-1-4x ,x ≤-3,1+2x ,-3<x<0,易知φ(x)在(-∞,-3]上单调递增,在(-3,0)上单调递减,当x =-3时取得极大值,也是最大值,φ(x)max =φ(-3)=13,故k<13.综上,由①②得实数k 的取值X 围为⎝⎛⎭⎪⎫-9,13.解法2 可根据函数解析式画出函数图像,当x>0时,f(x)=x 3-12x +3,f ′(x)=3x 2-12=3(x +2)(x -2),可知f(x)在区间(0,2)上单调递减,在区间(2,+∞)上单调递增,且 f(2)=-13<0,当x ≤0时,f(x)=|x +3|.g(x)=kx +1恒过(0,1),若要使y =f(x)-g(x)经过四个象限,由图可知只需f(x)与g(x)在(-∞,0)和(0,+∞)上分别有交点即可(交点不可为(-3,0)和切点).①当k>0时,在(0,+∞)必有交点,在(-∞,0)区间内,需满足0<k<13.②当k<0时,在(-∞,0)必有交点,在(0,+∞)内,只需求过定点(0,1)与函数f(x)=x 3-12x +3(x>0)图像的切线即可,设切点为(x 0,x30-12x 0+3),由k =3x20-12=x30-12x 0+3-1x 0,解得x 0=1,切线斜率k =-9,所以k∈(-9,0).③当k =0也符合题意.综上可知实数k 的取值X 围为⎝⎛⎭⎪⎫-9,13.4,(2018苏中三市,苏北四市三调)已知函数310() 2 0ax x f x x ax x x -≤⎧⎪=⎨-+->⎪⎩, ,,的图象恰好经过三个象限,则实数a 的取值X 围是 ▲ .【答案】a <0或a >2【解析】当a <0时,10y ax x =-,≤的图象经过两个象限,3|2|0y x ax x =-+->在 (0,+∞)恒成立,所以图象仅在第一象限,所以a <0时显然满足题意; 当a ≥0时,10y ax x =-,≤的图象仅经过第三象限,由题意 3|2|0y x ax x x =-+->,的图象需经过第一,二象限.【解法1】(图像法)3|2|y x x =+-与y ax =在y 轴右侧的图象有公 共点(且不相切).如图,3|2|y x x =+-=332,022,2x xx x xx,设切点坐标为3000(,2)x x x ,231yx,则有32000231x x x x ,解得01x ,所以临界直线l 的斜率为2,所以a >2时,符合.综上,a <0或a >2.【解法2】(函数最值法)由三次函数的性质知,函数图象过第一象限,则存()g x 在0x,使得3|2|0,yxax x即2|2|x a xx 设函数22221,02|2|()21,2x x x x g x x xx x x,当02x,322222()2x g x xx x()g x 在(0,1)单调递减,在(1,2)单调递增,又2x时,函数为增函数,所以函数的最小值为2,所以a >2,则实数a 的取值X 围为a <0或a >2.5,(2019某某期末)已知函数f(x)=ax 3+bx 2-4a(a,b ∈R ).(1) 当a =b =1时,求f (x )的单调增区间;(2) 当a ≠0时,若函数f (x )恰有两个不同的零点,求b a的值;(3) 当a =0时,若f (x )<ln x 的解集为(m ,n ),且(m ,n )中有且仅有一个整数,某某数b 的取值X 围.解后反思 在第(2)题中,也可转化为b a =4x2-x 恰有两个不同的实数解.另外,由g(x)=x 3+kx 2-4恰有两个不同的零点,可设g(x)=(x -s)(x -t)2.展开,得x 3-(s +2t)x 2+(2st +t 2)x -st 2=x 3+kx 2-4,所以⎩⎪⎨⎪⎧-(s +2t )=k ,2st +t2=0,-st2=-4,解得⎩⎪⎨⎪⎧s =1,t =-2,k =3.解:(1)当a =b =1时,f(x)=x 3+x 2-4,f ′(x)=3x 2+2x.(2分)令f ′(x)>0,解得x>0或x<-23,所以f(x)的单调增区间是⎝⎛⎭⎪⎫-∞,-23和(0,+∞).(4分)(2)法一:f ′(x)=3ax 2+2bx,令f ′(x)=0,得x =0或x =-2b3a,(6分)因为函数f(x)有两个不同的零点,所以f(0)=0或f ⎝ ⎛⎭⎪⎫-2b 3a =0.当f(0)=0时,得a =0,不合题意,舍去;(8分)当f ⎝ ⎛⎭⎪⎫-2b 3a =0时,代入得a ⎝ ⎛⎭⎪⎫-2b 3a +b ⎝ ⎛⎭⎪⎫-2b 3a 2-4a =0,即-827⎝ ⎛⎭⎪⎫b a 3+49⎝ ⎛⎭⎪⎫b a 3-4=0,所以ba =3.(10分)法二:由于a ≠0,所以f(0)≠0,由f(x)=0得,b a =4-x3x2=4x2-x(x ≠0).(6分)设h(x)=4x2-x,h ′(x)=-8x3-1,令h ′(x)=0,得x =-2, 当x ∈(-∞,-2)时,h ′(x)<0,h(x)递减;当x ∈(-2,0)时,h ′(x)>0,h(x)递增,当x ∈(0,+∞)时,h ′(x)>0,h(x)单调递增,当x>0时,h(x)的值域为R ,故不论b a取何值,方程b a=4-x3x2=4x2-x 恰有一个根-2,此时函数f (x )=a (x +2)2(x -1)恰有两个零点-2和1.(10分)(3)当a =0时,因为f (x )<ln x ,所以bx 2<ln x ,设g (x )=ln x -bx 2,则g ′(x )=1x-2bx =1-2bx2x(x >0),当b ≤0时,因为g ′(x )>0,所以g (x )在(0,+∞)上递增,且g (1)=-b ≥0,所以在(1,+∞)上,g (x )=ln x -bx 2≥0,不合题意;(11分)当b >0时,令g ′(x )=1-2bx2x=0,得x =12b,所以g (x )在⎝ ⎛⎭⎪⎪⎫0,12b 递增,在⎝⎛⎭⎪⎪⎫12b ,+∞递减, 所以g (x )max =g ⎝⎛⎭⎪⎪⎫12b =ln12b -12,要使g (x )>0有解,首先要满足ln12b -12>0,解得b <12e. ①(13分)又因为g (1)=-b <0,g (e 12)=12-b e>0,要使f (x )<ln x 的解集(m ,n )中只有一个整数,则⎩⎪⎨⎪⎧g (2)>0,g (3)≤0,即⎩⎪⎨⎪⎧ln2-4b>0,ln3-9b ≤0,解得ln39≤b <ln24. ②(15分)设h (x )=lnx x,则h ′(x )=1-lnx x2,当x ∈(0,e)时,h ′(x )>0,h (x )递增;当x ∈(e,+∞)时,h ′(x )<0,h (x )递减.所以h (x )max =h (e)=1e>h (2)=ln22,所以12e >ln24,所以由①和②得,ln39≤b <ln24.(16分)(注:用数形结合方法做只给2分)6,(2019某某,某某一模)若函数y =f(x)在x =x 0处取得极大值或极小值,则称x 0为函数y =f(x)的极值点.设函数f(x)=x 3-tx 2+1(t ∈R ).(1) 若函数f (x )在(0,1)上无极值点,求t 的取值X 围;(2) 求证:对任意实数t ,函数f (x )的图像总存在两条切线相互平行;(3) 当t =3时,函数f (x )的图像存在的两条平行切线之间的距离为4,求满足此条件的平行线共有几组.规X 解答 (1)由函数f(x)=x 3-tx 2+1,得f ′(x)=3x 2-2tx.由f ′(x)=0,得x =0,或x =23t.因为函数f(x)在(0,1)上无极值点,所以23t ≤0或23t ≥1,解得t ≤0或t ≥32.(4分)(2)令f ′(x)=3x 2-2tx =p,即3x 2-2tx -p =0,Δ=4t 2+12p.当p >-t23时,Δ>0,此时3x 2-2tx -p =0存在不同的两个解x 1,x 2.(8分)设这两条切线方程为分别为y =(3x21-2tx 1)x -2x31+tx21+1和y =(3x22-2tx 2)x -2x32+tx22+1.若两切线重合,则-2x31+tx21+1=-2x32+tx22+1,即2(x21+x 1x 2+x22)=t(x 1+x 2),即2=t(x 1+x 2).而x 1+x 2=2t 3,化简得x 1·x 2=t29,此时(x 1-x 2)2=(x 1+x 2)2-4x 1x 2=4t29-4t29=0,与x 1≠x 2矛盾,所以,这两条切线不重合.综上,对任意实数t,函数f(x)的图像总存在两条切线相互平行.(10分)(3)当t =3时f(x)=x 3-3x 2+1,f ′(x)=3x 2-6x.由(2)知x 1+x 2=2时,两切线平行.设A(x 1,x31-3x21+1),B(x 2,x32-3x22+1),不妨设x 1>x 2,则x 1>1.过点A 的切线方程为y =(3x21-6x 1)x -2x31+3x21+1.(11分)所以,两条平行线间的距离 d =|2x32-2x31-3(x22-x21)|1+9(x21-2x 1)2=|(x2-x1)|1+9(x21-2x 1)2=4,化简得(x 1-1)6=1+92,(13分)令(x 1-1)2=λ(λ>0),则λ3-1=9(λ-1)2,即(λ-1)( λ2+λ+1)=9(λ-1)2,即(λ-1)( λ2-8λ+10)=0.显然λ=1为一解,λ2-8λ+10=0有两个异于1的正根,所以这样的λ有3解.因为x 1-1>0,所以x 1有3解,所以满足此条件的平行切线共有3组.(16分)7,(2018某某,某某一调)已知函数g(x)=x 3+ax 2+bx(a,b ∈R )有极值,且函数f (x )=(x +a )e x 的极值点是g (x )的极值点,其中e 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)(1) 求b 关于a 的函数关系式;(2) 当a >0时,若函数F (x )=f (x )-g (x )的最小值为M (a ),证明:M (a )<-73.思路分析 (1) 易求得f(x)的极值点为-a -1,则g ′(-a -1)=0且g ′(x)=0有两个不等的实数解,解之得b 与a 的关系.(2) 求导得F ′(x)=(x +a +1)(e x -3x +a +3),解方程F ′(x)=0时,无法解方程e x -3x +a +3=0,构造函数h(x)=e x -3x +a +3,证得h(x)>0,所以-a -1为极小值点,而且得出M(a),利用导数法证明即可.规X 解答 (1) 因为f ′(x)=e x +(x +a)e x =(x +a +1)e x ,令f ′(x)=0,解得x =-a -1.列表如下:所以x =-a -1时,f(x)取得极小值.(2分)因为g ′(x)=3x 2+2ax +b,由题意可知g ′(-a -1)=0,且Δ=4a 2-12b>0,所以3(-a -1)2+2a(-a -1)+b =0,化简得b =-a 2-4a -3.(4分)由Δ=4a 2-12b =4a 2+12(a +1)(a +3)>0,得a ≠-32.所以b =-a 2-4a -3⎝⎛⎭⎪⎫a ≠-32.(6分)(2) 因为F(x)=f(x)-g(x)=(x +a)e x -(x 3+ax 2+bx),所以F ′(x)=f ′(x)-g ′(x)=(x +a +1)e x -[3x 2+2ax -(a +1)(a +3)]=(x +a +1)e x -(x +a +1)(3x -a -3)=(x +a +1)(e x -3x +a +3).(8分)记h(x)=e x -3x +a +3,则h ′(x)=e x -3,令h ′(x)=0,解得x =ln 3.列表如下:所以x =ln 3时,h(x)取得极小值,也是最小值,此时,h(ln 3)=e ln 3-3ln 3+a +3=6-3ln 3+a=3(2-ln 3)+a=3ln e23+a>a>0.(10分)所以h(x)=e x -3x +a +3≥h(ln 3)>0,令F ′(x)=0,解得x =-a -1.列表如下:所以x =-a -1时,F(x)取得极小值,也是最小值.所以M(a)=F(-a -1)=(-a -1+a)e -a -1-[(-a -1)3+a(-a -1)2+b(-a -1)]=-e -a -1-(a +1)2(a +2).(12分)令t =-a -1,则t<-1,记m(t)=-e t -t 2(1-t)=-e t +t 3-t 2,t<-1,则m ′(t)=-e t +3t 2-2t,t<-1.因为-e -1<-e t <0,3t 2-2t>5,所以m ′(t)>0,所以m(t)单调递增.(14分)所以m(t)<-e -1-2<-13-2=-73,即M(a)<-73.(16分)。
三次函数零点存在性问题探讨

求 m 的取值范围. 【答案】(1)见解析;(2) 3,1 .
【解析】(1) f x 3x2 3a 3 x2 a ,
当 a 0 时,对 x R ,有 f x 0 , f x 的单调增区间为 , , 当 a 0 时,由 f x 0 解得 x a 或 x a , 由 f x 0 解得 a x a ,
0得
x1
1 3
,
x2
1,
当
x
,
1 3
时,f
(x)
0
;当
x
1 3
,1
时,f
(x)
0
;当
x
1,
时,f
(
x)
0
,
x1
1 3
与
x2
1分别为
f
x
的极大值点与极小值点,
f
( x)极大值
f
( 1) 3
a
5 27
,
f
( x)极小值
的两个极值为
f
(0)
b,
f
2a 3
4 27
a3
b
,
则函数
f
(x)
有三个不同的零点等价于
f
0
f
2a 3
0
三次函数性质总结.
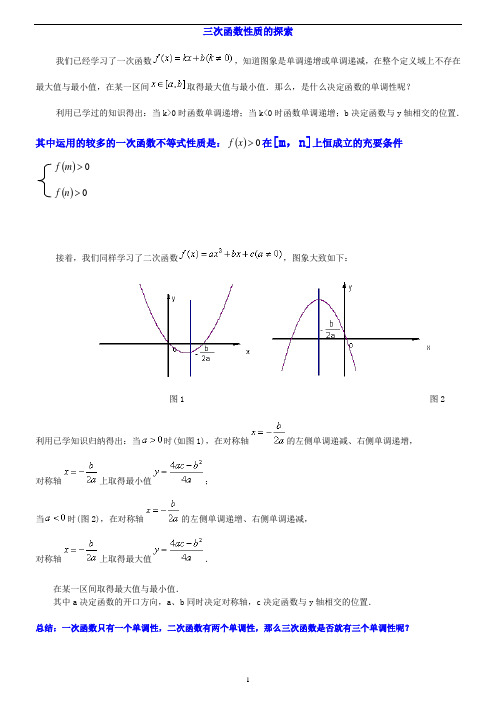
三次函数性质的探索我们已经学习了一次函数,知道图象是单调递增或单调递减,在整个定义域上不存在最大值与最小值,在某一区间取得最大值与最小值.那么,是什么决定函数的单调性呢?利用已学过的知识得出:当k>0时函数单调递增;当k<0时函数单调递增;b决定函数与y轴相交的位置.其中运用的较多的一次函数不等式性质是:()0>f在[m,n]上恒成立的充要条件x()0>fm()0>fn接着,我们同样学习了二次函数,图象大致如下:图1 图2利用已学知识归纳得出:当时(如图1),在对称轴的左侧单调递减、右侧单调递增,对称轴上取得最小值;当时(图2),在对称轴的左侧单调递增、右侧单调递减,对称轴上取得最大值.在某一区间取得最大值与最小值.其中a决定函数的开口方向,a、b同时决定对称轴,c决定函数与y轴相交的位置.总结:一次函数只有一个单调性,二次函数有两个单调性,那么三次函数是否就有三个单调性呢?三次函数专题一、定义:定义1、形如32(0)y ax bx cx d a =+++≠的函数,称为“三次函数”(从函数解析式的结构上命名)。
定义2、三次函数的导数232(0)y ax bx c a '=++≠,把2412b ac ∆=-叫做三次函数导函数的判别式。
由于三次函数的导函数是二次函数,而二次函数是高中数学中的重要内容,所以三次函数的问题,已经成为高考命题的一个新的热点和亮点。
特别是文科。
系列探究1:从最简单的三次函数3x y =开始反思1:三次函数31y x =+的相关性质呢? 反思2:三次函数31y x =-+的相关性质呢? 反思3:三次函数()311y x =-+的相关性质呢?(2012天津理)(4)函数22)(3-+=x x f x在区间(0,1)内的零点个数是 B (A )0 (B )1 (C )2 (D )3系列探究2:探究一般三次函数)0()(23>+++=a d cx bx ax x f 的性质:先求导2()32(0)f x ax bx c a '=++>1.单调性:(1)若22120b ac =-≤△(),此时函数()f x 在R 上是增函数;(2)若22120b ac =->△(),令2()320f x ax bx c '=++=两根为12,x x 且12x x <,则()f x 在12(,),()x x -∞+∞上单调递增,在12(,)x x 上单调递减。
一个三次函数的解题方法与技巧

一个三次函数的解题方法与技巧引言三次函数是一种常见的数学函数形式,其方程为y = ax^3 + bx^2 + cx + d。
解三次函数可以帮助我们找到函数的根、极值以及曲线的行为。
本文将介绍一些解三次函数的方法与技巧,帮助读者更好地理解和解决相关问题。
方法一:因式分解当三次函数的形式比较简单,并且存在因式分解的可能时,我们可以尝试使用因式分解的方法来解题。
通过因式分解,我们可以将三次函数拆解成若干个一次因子与一个二次因子相乘的形式,从而更容易找到函数的根。
方法二:求导数与极值对于三次函数,我们可以通过求导数的方法找到函数的极值点。
通过求函数的一阶导数和二阶导数,并令导数等于零,我们可以求得函数的极值点和曲线的转折点。
方法三:图像分析与差值法利用数学软件或手绘曲线图,我们可以通过观察曲线的特征来了解函数的行为。
通过分析曲线的上升段、下降段以及拐点,我们可以推断函数的根和极值点的位置。
此外,还可以运用差值法,通过代入特定值来估算函数的零点。
方法四:牛顿法和二分法如果以上方法无法解决问题,我们可以尝试使用数值计算的方法。
牛顿法和二分法是两种常用的数值计算方法,可以较快地逼近函数的根。
牛顿法通过迭代计算函数的切线与x轴的交点,逐步逼近根的位置。
二分法则通过不断将区间一分为二,判断根位于哪一半区间内,逐步逼近根的位置。
总结解三次函数的方法与技巧多种多样,我们可以根据题目的不同特点和要求选择合适的方法来解决问题。
因式分解、求导数与极值、图像分析与差值法以及数值计算方法都是常用的解题手段,但需要根据具体情况选择合适的方法。
希望本文的介绍对读者在解题过程中有所帮助。
求三次函数的极值评分标准

求三次函数的极值评分标准
三次函数极值点公式为:f'(x)=0。
最高次数项为3的函数叫做三次函数(cubic function),三次函数的图象是一条曲线。
如y=ax³+bx²+cx+d(a≠0,b,c,d为常数)。
函数在数学上的定义:给定一个非空的数集A,对A施加对应法则f,记作f(A),得到另一数集B,也就是B=f(A).那么这个关系式就叫函数关系式,简称函数。
三次函数的一般形式:f(x)=ax3+bx2+cx+d (a≠0,x∈R)
求复杂函数极值点最常用的方法是对函数求导,所以我们有
f’(x)=3ax2+2bx+c (a≠0,x∈R)
判断是否存在极值:
(1)判别式△=b2-3ac≤0 , f’(x)≥0恒成立,f(x)不存在极值点
(2)判别式△=b2-3ac>0 , f’(x)存在两个零点,f(x)存在极大值和极小值
我们也可以这样表述:
(3)f(x)有极值的充要条件:f’(x)有两个不同的零点;
(4)f(x)在区间(m,n)有一个极值的充要条件:f’(x)在区间(m,n)有一个零点(非重根);
(5)f(x)在区间(m,n)有两个极值的充要条件:f’(x)在区间(m,n)有两个不同零点。
高中数学三次函数的所有题型及解答总计

高中数学三次函数的所有题型及解答总计由于三次函数在高考中出现频率最高,且四次函数、分式函数等都可转化为三次函数来解决,故以三次函数为例来研究根的情况,设三次函数)0()(23≠+++=a d cx bx ax x f其导函数为二次函数:)0(23)(2/≠++=a c bx ax x f ,判别式为:△=)3(412422ac b ac b -=-,设0)(/=x f 的两根为1x 、2x ,结合函数草图易得: (1) 若032≤-ac b ,则0)(=x f 恰有一个实根;(2) 若032>-ac b ,且0)()(21>⋅x f x f ,则0)(=x f 恰有一个实根; (3) 若032>-ac b ,且0)()(21=⋅x f x f ,则0)(=x f 有两个不相等的实根; (4) 若032>-ac b ,且0)()(21<⋅x f x f ,则0)(=x f 有三个不相等的实根.说明:(1)(2)0)(=x f 含有一个实根的充要条件是曲线)(x f y =与x 轴只相交一次,即)(x f 在R 上为单调函数(或两极值同号),所以032≤-ac b (或032>-ac b ,且0)()(21>⋅x f x f );(3)0)(=x f 有两个相异实根的充要条件是曲线)(x f y =与x 轴有两个公共点且其中之一为切点,所以032>-ac b ,且0)()(21=⋅x f x f ;(4)0)(=x f 有三个不相等的实根的充要条件是曲线)(x f y =与x 轴有三个公共点,即)(x f 有一个极大值,一个极小值,且两极值异号.所以032>-ac b 且0)()(21<⋅x f x f . 【例题1】:设函数13-31)(23++=x x x x f ,求函数)(x f 的单调区间。
解析:)(x f 的定义域为R ,3-2)(2x x x f +=′03-2)(2>+=′x x x f ⇒),或(∞1,-3)∞-(+∈x ,此时为)(x f 的单调递增区间; 03-2)(2<+=′x x x f ⇒-3,1)(∈x ,此时为)(x f 的单调递减区间。
三次函数的性质:单调区间和极值 课件(湘教版选修2-2)

课前探究学习
课堂讲练互动
点评 f(x)为增函数,一定可以推出f′(x)≥0,但反之不一 定.因为f′(x)≥0,即为f′(x)>0或f′(x)=0,当函数在某个区间 内恒有f′(x)=0,则f(x)为常函数,不具有单调性,所以f′(x)≥ 0是f(x)为增函数的必要不充分条件.
课前探究学习
课堂讲练互动
预习测评
1.下列说若有最值与极值,则其极大值便是最
大值,极小值便是最小值
B.闭区间上图象连续不断的函数一定有最值,也一定有极
值
C.若函数在其定义域上有最值,则一定有极值,反之,若
有极值则一定有最值
D.若函数在给定区间上有最值,则最多有一个最大值,一
在(- 在(-∞,u)上 ∞,+ 递增 ;在(u,v) ∞)上 上 递减 ;在(v,
递增 +∞)上 递增
在 x=u 处取极大 无 值;在 x=v
处取极小值
课前探究学习
课堂讲练互动
当a<0时, F′(x)的零点
F(x)、 F′(x)的性质
F′(x)的符号
F(x)的单调性
F′(x)的极值
无
F′(x) <0
课前探究学习
课堂讲练互动
解 (1)由f′(x)=x2+x-2=0得,f′(x)的零点为x=-2或x
=1,
当x变化时f′(x)变化情况如下表:
x
(-3,-2) (-2,1) (1,3)
f′(x)
+
-
+
比较f(-3),f(-2),f(1)和f(3)知,在区间[-3,3]上,
当x=3时,f(x)max=1016;x=1时,f(x)min=32.
2 3
)和(1,+∞),f(x)的递减
二次函数与三次函数的性质

二次函数与三次函数的性质函数是数学中的重要概念,而二次函数和三次函数是函数的两种特殊形式。
它们在数学和实际应用中都扮演着重要的角色。
本文将探讨二次函数和三次函数的性质,并比较它们之间的异同点。
一、二次函数的性质二次函数是一个以二次项为最高次幂的多项式函数。
它的一般形式为:f(x) = ax^2 + bx + c其中,a、b、c为实数且a不等于0。
二次函数的性质如下:1. 平移性质:二次函数可以沿x轴和y轴的方向进行平移。
当函数表达式中加上常数h时,图像沿x轴的正方向平移h个单位;当函数表达式中加上常数k时,图像沿y轴的正方向平移k个单位。
2. 对称性质:二次函数的图像关于抛物线的对称轴对称。
对称轴的方程为x = -b/2a,即抛物线的顶点坐标为(-b/2a, f(-b/2a))。
3. 开口方向:当a大于0时,二次函数的图像开口向上;当a小于0时,二次函数的图像开口向下。
4. 最值:当二次函数的开口向上时,函数的最小值为顶点的纵坐标;当二次函数的开口向下时,函数的最大值为顶点的纵坐标。
5. 零点:二次函数的零点是函数图像与x轴的交点,即f(x) = 0的解。
一般来说,二次函数有两个零点。
二、三次函数的性质三次函数是一个以三次项为最高次幂的多项式函数。
它的一般形式为:f(x) = ax^3 + bx^2 + cx + d其中,a、b、c、d为实数且a不等于0。
三次函数的性质如下:1. 平移性质:与二次函数类似,三次函数也可以进行平移。
当函数表达式中加上常数h时,图像沿x轴的正方向平移h个单位;当函数表达式中加上常数k时,图像沿y轴的正方向平移k个单位。
2. 对称性质:三次函数的图像可能存在关于某个点的对称性,这取决于函数的具体形式。
3. 开口方向:三次函数的图像可能存在开口向上或开口向下的情况,这取决于函数的a的正负。
4. 最值:三次函数没有固定的最值。
它的图像可能存在局部最小值或局部最大值,但不一定存在全局最小值或全局最大值。
与三次函数零点有关的取值范围问题专题

与三次函数零点有关的取值范围问题1.函数f(x)=1+x +x 22+x 33零点的个数是________.2.已知函数f(x)=x 3-3x +c 的图象与x 轴恰有两个公共点,则实数c 的值为________.3.已知函数f(x)=ax 3-3x 2+1,若f(x)存在唯一的零点x 0,且x 0>0,则实数a 的取值范围是________.4.若函数f(x)=23x 3-2ax 2-3x 在(-1,1)内有且只有一个极值点,则实数a 的取值范围是________.5.已知函数f(x)=14x 4+a 3x 3+12x 2(a ∈R ,a ≠0)有且仅有3个极值点,则实数a 的取值范围是________.6.若函数f(x)=a 3x 3-12(a +1)x 2+x -13(a>0)在[0,2]上有两个零点,则实数a 的取值范围是________.7.设函数f(x)=x 3-92x 2+6x -a.(1)对于任意实数x ,f ′(x)≥m 恒成立,求实数m 的最大值;(2)若方程f(x)=0有且仅有一个实根,求实数a 的取值范围.=1 024,求满足条件的正整数a的取值集合.8.已知函数f(x)=ax3+|x-a|,a∈R.(1)若函数g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;(2)当a>0时,若对于任意的x1∈[a,a+2],都存在x2∈[a+2,+∞),使得f(x1)f(x2)1.答案:1.解析:∵f ′(x )>0恒成立,∴函数f (x )单调递增,∴零点个数是1.2.答案:±2.解析:函数f (x )=x 3-3x +c 在(-∞,-1)和(1,+∞)上递增,(-1,1)上递减,由题意f (-1)f (1)=0,即(2+c )(-2+c )=0,解得c =±2.3.答案:(-∞,-2). 解析:当a =0时,不合题意;当a ≠0时,令f ′(x )=3ax 2-6x =0,得x =0或x =2a,①当a >0时,由图象及f (0)=1知函数f (x )有负数零点,舍去;②当a <0时,由图象及f (0)=1,只需满足f ⎝ ⎛⎭⎪⎫2a >0,即a ⎝ ⎛⎭⎪⎫2a 3-3⎝ ⎛⎭⎪⎫2a 2+1>0,解得a <-2.综上:a <-2.4.答案:⎝⎛⎭⎪⎫-∞,-14∪⎝ ⎛⎭⎪⎫14,+∞. 解析:∵f ′(x )=2x 2-4ax -3,∴根据题意f ′(-1)·f ′(1)<0,解得a >14或a <-14.5.答案:(-∞,-2)∪(2,+∞).解析:可转化为f ′(x )=x 3+ax 2+x 有三个不同的零点,从而x 2+ax +1=0有两个不等的非零实根,故Δ=a 2-4>0,∴a ∈(-∞,-2)∪(2,+∞).6.答案:⎝ ⎛⎦⎥⎤0,12. 解析:f ′(x )=a ⎝ ⎛⎭⎪⎫x -1a (x -1), ①当12>1,即0<a <1时,f (0)=-13<0,f (1)=-16(a -1)>0,(ⅰ)当2≤1,即0<a ≤12时,1a ≥2,f (2)=13(2a -1)≤0,因为f (x )在区间[0,1]上为增函数,在[1,2]上为减函数,∴f (x )在区间[0,1]和(1,2]上各有一个零点,即在[0,2]上有两个零点;(ⅱ)当2a >1,即12<a<1时,)f(x )增极大值 减 极小值增 ∴x ∈[0,1],f (x )<0,∵f (x )在[1,2]上为增函数,∴f (x )在区间(1,2]有一个零点,即在[0,2]上有一个零点,不满足题设.综上,a 的取值范围是⎝ ⎛⎦⎥⎤0,12. 7.答案:(1)-34;(2)(-∞,2)∪(52,+∞).解析:(1)f ′(x )=3x 2-9x +6=3(x -1)(x -2),∵x ∈R ,∴f ′(x )≥m 即3x 2-9x +6-m ≥0恒成立,∴Δ=81-12(6-m )≤0,得m ≤-34,即m 的最大值为-34. (2)∵当x <1或x >2时,f ′(x )>0,f (x )在(-∞,1)和(2,+∞)上递增;当1<x <2时,f ′(x )<0,f (x )在(1,2)上递减;∴当x =1时,f (x )取极大值f (1)=52-a ,当x =2时, f (x )取极小值f (2)=2-a ,故当f (1)<0或f (2)>0时,方程f (x )=0仅有一个实根,解得a <2或a>52.(或由f (1)f (2)<0,亦可解得a <2或a >52)8.答案:(1)当a ≥1时,有两个解;当-1<a <1时,有三个解;当a ≤-1时,有两个解;(2){1}.解析:(1)f (x )=g (x )即为ax 3+|x -a |=x 4,∴x 4-ax 3=|x -a |,∴x 3(x -a )=|x -a |,即x =a 或⎩⎪⎨⎪⎧x >a ,x =1或⎩⎪⎨⎪⎧x <a ,x =-1,①当a ≥1时,方程f (x )=g (x )有两个不同的解a ,-1;②当-1<a <1时,方程f (x )=g (x )有三个不同的解a ,-1,1;③当a ≤-1时,方程f (x )=g (x )有两个不同的解a ,1.(2)当a >0时,x ∈(a ,+∞)时,f (x )=ax 3+x -a ,f ′(x )=3ax 2+1>0,∴函数f (x )在(a ,+∞)上是增函数,且f (x )>f (a )=a 4>0, ∴当x ∈[a ,a +2]时,f (x )∈[f (a ),f (a +2)],1 024f (x )∈⎣⎢⎡⎦⎥⎤1 024f (a +2),1 024f (a ),当x ∈[a +2,+∞)时,f (x )∈[f (a +2),+∞).∵对任意的x 1∈[a ,a +2],都存在x 2∈[a +2,+∞),使得f (x 1)f (x 2)=1 024,∴⎣⎢⎡⎦⎥⎤1 024f (a +2),1 024f (a ) [f (a +2),+∞),∴1 024f (a +2)≥f (a +2),∴f (a +2)2≤1 024,即f (a +2)≤32,也即a (a +2)3+2≤32,∵a >0,显然a =1满足,而a ≥2时,均不满足.∴满足条件的正整数a的取值的集合为{1}.。
与三次函数零点有关的取值范围问题

与三次函数零点有关的取值范围问题函数的零点个数、两个函数图象的交点个数等问题在近几年的数学高考中屡屡出现,例题:若13x 3-x 2+ax -a =0只有一个实数根,求实数a 的取值范围.变式1已知函数f(x)=13x 3+12ax 2+1有且只有一个零点,求实数a 的取值范围.变式2已知函数f(x)=13x 3-(k +1)2x 2,g(x)=13-kx ,若函数f(x)与g(x)的图象有三个不同的交点,求实数k 的取值范围.串讲1已知函数f(x)=ax 3-3x 2+1,若f(x)存在唯一的零点x 0,且x 0>0,则a 的取值范围是__________.串讲2已知函数f(x)=13x 3-12(a +1)x 2+ax ,设a >1,试讨论函数f(x)在区间[0,a +1]内零点的个数.(2018·全国卷Ⅱ)已知函数f(x)=13x 3-a(x 2+x +1).(1)若a =3,求f(x)的单调区间; (2)证明:f(x)只有一个零点.(2018·苏州调研)已知函数f(x)=x 3-3x 2+ax +3,f(x)在x 1处取极大值,在x 2处取极小值.(1)若a =0,求函数f(x)的单调区间和零点个数;(2)在方程f(x)=f(x 1)的解中,较大的一个记为x 3:在方程f(x)=f(x 2)的解中,较小的一个记为x 4,证明:x 4-x 1x 3-x 2为定值;(3)证明:当a ≥1时,f(x)>ln x.答案:(1)f(x)的增区间为(-∞,0),(2,+∞);减区间为(0,2),f(x)有3个零点;(2)(3)略.解析:(1)当a =0时,f(x)=x 3-3x 2+3,f ′(x)=3x 2-6x ;当f′(x)>0时,x >2或x <0; 当f′(x)<0时,0<x <2;即函数f(x)的单调增区间为(-∞,0),(2,+∞); 单调减区间为(0,2);3分又f(-1)=-1<0,f(0)=3>0,f(2)=-1<0,f(3)=3>0,所以f(x)有3个零点.…4分(2)因为f(x)=f(x 1),则x 3-3x 2+ax +3=x 13-3x 12+ax 1+3,可知x 3-3x 2+ax =x 13-3x 12+ax 1.因为f′(x 1)=0,即a =6x 1-3x 12,即x 3-x 13+3x 12-3x 2+ax -ax 1 =(x -x 1)[x 2+x(x 1-3)-2x 12+3x 1]=(x -x 1)2(x +2x 1-3)=0,可知x 3=3-2x 1, 同理,由f(x)=f(x 2)可知7分x 3-x 23+3x 22-3x 2+ax -ax 2=(x -x 2)[x 2+x(x 2-3)-2x 22+3x 2]=(x -x 2)2(x +2x 2-3)=0;得到x 4=3-2x 2;x 4-x 1x 3-x 2=3-2x 2-x 13-2x 1-x 2=1-x 21-x 1=1-(2-x 1)1-x 1=-1.10分(3)证法一:要证f(x)=x 3-3x 2+ax +3>ln x ,即要证x 3-3x 2+3>ln x -ax.11分设u(x)=x 3-3x 2+3(x >0),则u′(x)=3x 2-6x ;当u′(x)>0时,x >2;当u′(x)<0时, 0<x <2;可知[u(x)]min =u(2)=-1;12分再设v(x)=ln x -ax(x >0),则v′(x)=1x -a ;当v′(x)>0时,0<x <1a ;当v′(x)<0时,x >1a;可知,v(x)max =v ⎝⎛⎭⎫1a =-ln a -1.14分 因为a ≥1,所以1a ≤1,-ln a -1≤-1,且v(x)和u(x)分别在1a 和2处取最大值和最小值,因此v(x)<u(x)恒成立,即当a ≥1时,f(x)>ln x.证法二:一方面,易证ln x ≤x -1;(略)另一方面,当a ≥1时,x 3-3x 2+ax +3≥x 3-3x 2+x +3;又(x 3-3x 2+x +3)-(x -1)=(x +1)(x -2)2≥0;所以,x 3-3x 2+ax +3≥x 3- 3x 2+x +3≥x -1≥ln x ,且不存正数x ,使得其中等号同时成立,故f(x)>ln x.例题1答案:(0,+∞).解法1令f(x)=13x 3-x 2+ax -a ,则f′(x)=x 2-2x +a.∵f(x)=0有一个实数根, ∴f ′(x)=0的Δ≤0或者 f(x)极大值<0或者f(x)极小值>0.①f′(x)=0的Δ≤0,解得a≥1; ②当a <1时,设x 1,x 2为f ′(x)=x 2-2x +a =0的两个根(x 1<x 2),f(x)在(-∞,x 1)和(x 2,+∞)上单调递增,在(x 1,x 2)上单调递减.1° 若f(x)极大值<0,即f(x 1)<0,∴f(x 1)=13x 13-x 12+ax 1-a =13x 1(2x 1-a)-(2x 1-a)+ax 1-a =23x 12+⎝ ⎛⎭⎪⎫23a -2x 1=23(2x 1-a)+⎝ ⎛⎭⎪⎫23a -2x 1=⎝ ⎛⎭⎪⎫23a -23x 1-23a =23[](a -1)x 1-a <0,∴x 1>a a -1,即1-1-a >a a -1,解得(1-a)1-a <1,即(1-a)3<1,得0<a <1;2° 若f(x)极小值>0,即f(x 2)>0,同理f(x 2)=23[(a -1)x 2-a]>0.∴x 2<a a -1,即1+1-a <a a -1,解得-(1-a)1-a >1,即(1-a)3<-1,得a >2(舍去);综上所述,实数a 的取值范围是(0,+∞).解法2令f(x)=13x 3-x 2+ax -a ,则f′(x)=x 2-2x +a.∵f(x)=0有一个实数根, ∴f ′(x)=0的Δ≤0或者f(x 1)·f(x 2)>0(x 1,x 2是f(x)的极值点0). ①f ′(x)=0的Δ≤0,解得a≥1; ②由x 1,x 2为f′(x)=0的两个根,得⎩⎪⎨⎪⎧x 12-2x 1+a =0x 12=2x 1-a ,x 22-2x 2+a =0x 22=2x 2-a ,(a <1)于是f(x 1)=13x 13-x 12+ax 1-a =13x 1(2x 1-a)-(2x 1-a)+ax 1-a =23x 12+⎝ ⎛⎭⎪⎫23a -2x 1=23(2x 1-a)=⎝ ⎛⎭⎪⎫23a -2x 1=⎝ ⎛⎭⎪⎫23a -23x 1-23a ,同理可得f(x 2)=⎝ ⎛⎭⎪⎫23a -23x 2-23a ,于是有f(x 1)·f(x 2)=⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫23a -23x 1-23a ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫23a -23x 2-23a >0.当a <1时,⎝ ⎛⎭⎪⎫x 1-a a -1⎝ ⎛⎭⎪⎫x 2-a a -1>0x 1x 2-a a -1(x 1+x 2)+⎝ ⎛⎭⎪⎫a a -12>0,又∵x 1,x 2是方程x 2-2x +a =0的根,∴x 1+x 2=2,x 1x 2=a ,化简可得a(a 2-3a +3)>0,解得0<a <1;综上所述,实数a 的取值范围是(0,+∞).说明:显然解法2避免了再分类,更显简洁;同时利用“降幂”思想进行代换,可化繁为简.变式联想变式1答案:(-36,+∞).解法1∵函数f(x)=13x 3+12ax 2+1有且只有一个零点.∴13x 3+12ax 2+1=0有且只有一个实根,∵x =0不适合方程,∴a =-2x 2-2x 3有且只有一个实根,设g(x)=-2x 2-2x3,有g ′(x)=4x 3-23(x≠0),①当x <0时,g ′(x)<0,∴g(x)在(-∞,0)上递减,且g(x)∈R;②当x >0时,令g ′(x )=0,得x =36∴g (x )在(0,+∞)上有最大值g (36)=-36,且g (x )∈ (-∞,-36],综上所述,实数a 的取值范围是(36,+∞).解法2令f (x )=13x 3+12ax 2+1,则f ′(x )=x 2+ax .∵f (x )=0有一个实数根,∴f ′(x )=0的Δ≤0或者f (x 1)·f (x 2)>0(x 1,x 2是f (x )的极值点).①f ′(x )=0的Δ≤0, 解得a =0;②f ′(x )=0得x 1=0,x 2=-a (a ≠0),f (x 1)·f (x 2)=-13a 3+12a 3+1>0,即16a 3>-1,∴a >-36且a ≠0.综上所述,实数a 的取值范围是(36,+∞).说明:显然解法2更显简洁. 变式2答案:(-∞,1-3)∪(1+3,+∞).解析:∵f(x)与g(x)的图象有三个不同的交点,∴f(x)=g(x)有三个不等实根.令h(x)=f(x)-g(x)=13x 3-(k +1)2x 2+kx -13,则h′(x)=x 2-(k +1)x +k =(x -k)(x -1),根据题意得k≠1且h(1)·h(k)<0,化简可得k -12⎝ ⎛-16k 3+12k 2-⎭⎪⎫13<0,即-k -112(k -1)(k 2-2k -2)<0,∴k 2-2k -2>0,解得k >1+3或k <1-3,∴实数k 的取值范围是(-∞,1-3)∪(1+3,+∞).串讲激活串讲1答案:(-∞,-2).解析:①当a =0时,-3x 2+1=0时,x =±33,所以此时不符合题意; ②当a >0时,f ′(x)=3ax 2-6x =3x(ax -2),当f′(x)>0时,解得x >2a 或x <0,则f(x)在(-∞,0)上单调递增,因为f(0)=1,f(-1)=-a -2<0,则存在一零点在(-∞,0)上,所以此时不符合题意;③当a <0时,当f′(x)>0时,解得2a <x <0,f ′(x)<0时,解得x <2a 或x >0,所以函数f(x)在⎝ ⎛⎭⎪⎫-∞,2a 上单调递减,在⎝ ⎛⎭⎪⎫2a ,0上单调递增,在(0,+∞)上单调递减,若f(x)在R 上存在唯一的零点x 0,且x 0>0,则f ⎝ ⎛⎭⎪⎫2a =8a2-12a 2+1>0,即-4a2+1>0,整理得a 2>4,整理得a 2>4,解得a <-2或a >2(舍去),综上所述,当a <-2时满足题意.串讲2答案:当1<a <3时,f(x)在区间[0,a +1]内有一个零点;当a =3时,f(x)在区间[0,a +1]内有两个零点;当3<a≤2+3时,f(x)在区间[0,a +1]内有三个零点;当a >2+3时,f(x)在区间[0,a +1]内有两个零点.解析:f′(x)=x 2-(a +1)x +a =(x -1)(x -a),当a >1时,函数f(x)在(0,1)和(a ,a +1)上单调递增,在(1,a)上单调递减,又f(0)=0,f(a)=12a 2-16a 3,f(a +1)=-16(a+1)(a 2-4a +1),解不等式f(a)>0得1<a <3,解不等式f(a +1)>0得1<a <2+3,于是如下讨论:①当1<a <3时,f(x)在区间[0,a +1]内有一个零点; ②当a =3时,f(x)在区间[0,a +1]内有两个零点;③当3<a≤2+3时,f(x)在区间[0,a +1]内有三个零点; ④当a >2+3时,f(x)在区间[0,a +1]内有两个零点.新题在线答案:(1)f(x)在(-∞,3-23)和(3+23,+∞)的单调递增,在(3-23,3+23)的单调递减;(2)略.解析:(1)当a =3时,f(x)=13x 3-3x 2-3x -3,f ′(x)=x 2-6x -3.令f′(x)=0,解得x =3-23或x =3+2 3.当x∈(-∞,3-23)∪(3+23,+∞)时,f ′(x)>0;当x∈(3-23,3+23)时,f ′(x)<0.故f(x)在(-∞,3-23),(3+23,+∞)单调递增,在(3-23,3+23)单调递减.(2)∵x 2+x +1>0,∴f(x)=0等价于x 3x 2+x +1-3a =0.设g(x)=x 3x 2+x +1-3a ,则g ′(x)=x 2(x 2+2x +3)(x 2+x +1)2≥0,仅当x =0时g′(x)=0,∴g(x)在(-∞,+∞)单调递增.故g(x)至多有一个零点,从而f(x)至多有一个零点.又f(3a -1)=-6a 2+2a -13=-6⎝ ⎛⎭⎪⎫a -162-16<0,f(3a +1)=13>0,故f(x)有一个零点.综上,f(x)只有一个零点.。
三次函数的性质;单调区间和极值资料

变式训练:
1.讨论函数f(x)=x3 +ax+5的增减性。
2.已知f(x)=x3 +ax2 +(a+6)x+1有极大值和极小值,
则a的取值范围为( D)
A.-1<a<2 B.-3<a<6 C.a<-1或a>2 D.a<-3或a>6
3.已知函数f (x) x3 ax在R上递增, 则a的取值范围是 _______ .
9
三次函数图象与x轴交点问题
三次函数f(x)=ax3 +bx2 +cx+d(a 0)图象的性质揭示了 一元三次方程ax3 +bx2 +cx+d=0(a 0)根的实质. 由f(x)的图象的性质不难看出: 方程实数根的个数即f(x)图象与轴的交点个数.
三次函数f(x)的导数F '(x) 3ax2 2bx c(a 0)
1.若=4b2 -12ac 0即b2 3ac,则三次函数f(x)无极值, 图象在R上为单调函数,其图象与x轴有且有一个交点. 即方程ax3 +bx2 +cx+d=0(a 0)有且有一个实数根.
a>0
a<0
10
2.若=4b2 -12ac>0即b2>3ac,则三次函数f(x)有2个极值点x1x2 , 不妨设极大值为f(x1),极小值f(x2 ),其图象与x轴交点情况 取决于2个极值点与x轴的关系:
14
变式训练
1.方程x3-6x2+9x-4=0的实数根个数是( B ) A.3 B.2 C.1 D.0
2.设a为实数,函数f (x) x3 x2 x a. (1)求f (x)的极值;
人教版高考总复习一轮数学精品课件 第四章 一元函数的导数及其应用-第四节 三次函数的图象与性质

[, ]上恒成立,可得 ≤ + , + ≥ ⋅ = ,当且仅当 = 时取等号,可
得 ≤ .故选D.
2
3
(2)已知函数 = 3 + 2 + + 在 = − 与 = 1处都取得极值.
①求,的值与函数 的单调区间;
解 = 3 + 2 + + ,′ = 3 2 + 2 + ,由
−
−
> ,
−
< ,
即
−
−
−
−
+ > ,
解得 < −.故选B.
−
−
+
+ < ,
(2)(2023扬州校考)设为实数,函数 = − 3 + 3 + .
①求 的极值.
解 ′ = −3 2 + 3,令′ = 0,得 = −1或 = 1.当 ∈ −∞, −1 时,′ < 0;
− ,
3
−
3
和极小值点三等分,类似地,对极小值也有类似结论.
自测诊断
1.已知三次函数 =
1 3
3
− 4 − 1 2 + 152 − 2 − 7 + 2在上是增函数,
则实数的取值范围是() D
A. < 2或 > 4B.−4 < < −2C.2 < < 4D.2 ≤ ≤ 4
为
1 ,2
1 ,2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:导数与三次函数问题
[真题1] (2009年安徽卷)设a <b,函数2
()()y x a x b =--的图像可能就是( )
[命题探究] 考题的命制,直接给出函数图像,然后设计了四个选项,意在通过对问题的判断, 直接考查三次函数的性质:单调区间与极值问题。
这里,函数的化简、图像的观察等等,不仅需要
扎实的基本功,而且还需要熟练的解题技巧。
[知识链接]
1、三次函数3
2
()(0)f x ax bx cx d a =+++≠图象
a>0
a<0
∆>0
∆≤0
∆>0
∆≤0
图 象
2.函数3
2
()(0)f x ax bx cx d a =+++≠单调性、极值点个数情况。
'
()f x =2
32ax bx c ++, 记∆=2
2
,(其中x 1,x 2就是方程'
=0的根,且x 1<x 2)
a>0
a<0
∆>0
∆≤0
∆>0
∆≤0
单 调 性 在12(,),(,)x x -∞+∞上,
就是增函数; 在12(,)x x 上,就是减
函数;
在R 上就是增函数
在12(,)x x 上,就是增函
数;
在12(,),(,)x x -∞+∞上,就是减函数;
在R 上就是减函数
极值点个数
2 0 2 0
专题:三次函数的零点问题
1、(2006全国卷Ⅱ)设a 为实数,函数.)(2
3
a x x x x f +--= (Ⅰ)求)(x f 的极值、
(Ⅱ)当a 在什么范围内取值时,曲线x x f y 与)(=轴仅有一个交点、
x
x 1 x 2
x 0
x
x 1
x 2
x
x 0
x
2、(2009江西卷文)(本小题满分12分) 设函数3
2
9()62
f x x x x a =-
+-. (1)对于任意实数x ,()f x m '≥恒成立,求m 的最大值; (2)若方程()0f x =有且仅有一个实根,求a 的取值范围. 3、已知函数a ax x a x x f ---+=
232
131)(,x 其中a>0、
(I)求函数)(x f 的单调区间;
(II)若函数)(x f 在区间(-2,0)内恰有两个零点,求a 的取值范围;
(III)就是否存在常数a,使得函数)(x f 在区间(-2,0)内恰有一个零点,若存在,求a 的取值范围,若不存在,说明理由;
4、(2009陕西卷文)(本小题满分12分) 已知函数3
()31,0f x x ax a =--≠
()I 求()f x 的单调区间;
()II 若()f x 在1x =-处取得极值,直线y=m 与()y f x =
的图象有三个不同的交点,求m 的取值
范围。
5、【2102高考福建文12】已知f(x)=x ³-6x ²+9x-abc,a <b <c,且f(a)=f(b)=f(c)=0、现给出如下结论: ①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;④f(0)f(3)<0、 其中正确结论的序号就是
A 、①③
B 、①④
C 、②③
D 、②④ 6、(湖南21)已知函数43219
()42
f x x x x cx =+-+有三个极值点。
(I)证明:275c -<<;
(II)若存在实数c,使函数)(x f 在区间[],2a a +上单调递减,求a 的取值范围。
7、(全国二理 22)已知函数3
()f x x x =-.
(1)求曲线()y f x =在点(())M t f t ,处的切线方程;
(2)设0a >,如果过点()a b ,可作曲线()y f x =的三条切线,证明:()a b f a -<<.。
