中心复合设计CCD
中心复合设计详解

中心复合设计详解中心复合设计(Central Composite Design,CCD)是实验设计中常用的一种方法,它结合了全因子设计和部分因子设计的优点,通过添加中心点和轴向点来评估响应面的曲率,从而更准确地预测最优解。
以下是中心复合设计的详细解释:基本概念:中心点:所有因子的中间水平组合,用于估计纯误差。
轴向点:在因子空间中沿着坐标轴方向取点,用于估计响应面的曲率。
立方体点:全因子设计或部分因子设计的角点,用于估计主效应和交互效应。
设计构造:选择需要考察的因子和水平。
确定全因子或部分因子的角点(立方体点)。
添加中心点,通常重复多次以更好地估计实验误差。
添加轴向点,这些点位于因子空间的坐标轴上,距离中心点的距离(α值)是事先确定的,通常是为了使设计旋转或正交。
设计特点:能够评估非线性关系:通过轴向点和中心点,可以检测响应面是否存在曲率,从而判断因子与响应之间是否存在非线性关系。
高效性:相比于全因子设计,中心复合设计需要的实验次数较少。
灵活性:可以通过调整α值来平衡设计的旋转性和正交性。
可扩展性:容易添加额外的中心点或轴向点以增加设计的精度。
实验步骤:根据实验目的确定因子和水平。
构造中心复合设计,确定实验点。
进行实验并记录响应数据。
使用统计软件(如Minitab、Design-Expert等)拟合响应面模型。
分析模型的有效性,包括残差分析、模型显著性检验等。
利用模型预测最优解并进行验证实验。
应用领域:中心复合设计广泛应用于各种需要优化多个因子影响的过程,如化工、制药、食品科学、机械工程等领域。
它特别适用于当对因子的主效应、交互效应以及二次效应感兴趣时,且预期响应面可能存在曲率的情况。
注意事项:在选择α值时需谨慎,以确保设计的旋转性或正交性符合实验需求。
中心点的重复次数应根据实验误差的预期大小来确定。
在分析响应面模型时,应注意检查模型的假设条件是否满足,如正态性、同方差性等。
响应曲面设计

线后分段完成试验,前次试验设计的点 上做过的试验结果,在后续的试验设计 中继续有用。
精品文档
中心复合试验(shìyàn)设计 CCD
旋转性(rotatable)设计 将来在某点处预报值的方差仅与该店
到试验中心的距离有关,即响应变量的预 测精度在意设计中心为球心的球面上是相 同的,可保证均匀(jūnyún)一致的精度。
2、包含二次项的回归方程
一般的形式如下:
Y=bo+b1x1+b2x2+b11x12+b22x22+b12x1x2+ε
由于增加了两个因子各自的平方项,需要增加试验点。
先后分为几个阶段完成全部试验的策略,称为序贯试验
策略
精品文档
一、响应曲面设计(shèjì)概论
3、怎样获得响应的曲面图形? 大概(dàgài)的步骤如下:
10.00
12.31
+1.732 90.00
200.00
14.00
精品文档
模型 拟合 (móxíng)
• 以远志皂苷元为因变量,对各因素进行多元线性回归和 二项式拟合,模型(móxíng)如下:
• 多元线性回归:Y=b0+b1x1+b2x2+b3x3 二项式:
Y=b0+b1x1+b2x2+b3x3+b4x12+b5x22+b6x32+b7x1x2+b8x1 x3+b9x2x3
需要12+3次试验,4个因子需要24+3次试
验。
精品文档
Box-Behnken试验设计(shèjì)特点
1、在因素相同时,比中心复合设计的试验次数少 2、没有将所有试验因素同时安排为高水平的试验组合,对 某些有安全要求或特别需求的试验尤为适用 3、具有近似旋转性,无序贯性。
响应表面试验设计方法及MINITAB优化(CCD_BBD)

非线性回归结果
输出结果:二次多项式回归方差分析表
此值小于0.05的项显著有效,回归的整体、二次项和交叉 乘积项都显著有效,但是一次项的效果不显著。 Source Regression Linear Square Interaction Residual Error Lack-of-Fit Pure Error Total S = 0.9960 DF Seq SS 9 36.465 3 7.789 3 13.386 3 15.291 10 9.920 5 7.380 5 2.540 19 46.385 R-Sq = 78.6% Adj SS 36.465 7.789 13.386 15.291 9.920 7.380 2.540 Adj MS 4.0517 2.5962 4.4619 5.0970 0.9920 1.4760 0.5079 F 4.08 2.62 4.50 5.14 2.91 P 0.019 0.109 0.030 0.021 0.133
这两个二次项回归系数有很 小的改变,这是由于旋转设 计只具有近似正交性
指标最优化
目标是 最大值
下限设 为10
目标值 设为20
因子最优 水平值
最优预 测值
例6.2-1 大豆施肥量最优化设计
在研究大豆产量Y的试验中,考虑氮肥A、磷肥B、
钾肥C这三种肥料的施肥量。每个因素取两个基本水平, 采用中心复合试验,其中:
2 中心复合试验设计 基本概念
立方点 轴向点 中心点 区组 序贯试验 旋转性
立方点(cube point)
立方点,也称立方体点、角点,即2水平对 应的“-1”和“+1”点。各点坐标皆为+1或-1。 在k个因素的情况下,共有2k个立方点
DOE常见题型及知识结构

DOE常见题型及知识结构出品社区咨询培训托管关于实验设计的考试大纲1.术语(理解)了解试验设计在改进阶段的用法;掌握试验设计的基本概念,包括变量的独立性、因素和水平、响应、处理、误差等;识别试验设计的不同类型和应用条件。
2.试验设计原理(应用)掌握试验设计的原理,包括检出力、样本量、平衡、重复、仿行、顺序、有效性、随机化、区组、交互作用、混杂和分辨力等;理解饱和设计、投影特性和效应稀疏原理。
3.试验计划(评估)通过确定目标,选择因子和水平、响应和测量方法,选择适当的设计来规划、组织和评估试验。
4.单因子试验设计(评估)设计和实施完全随机化、随机化区组的试验设计;理解一次一因素(OFAT)试验的缺点。
5.两水平部分因子试验设计(评估)理解筛选设计的重要性;设计、分析和解释两水平部分因子试验,并理解由于混杂而导致的部分因子试验的局限性。
6.全因子试验设计(评估)设计、实施和分析全因子试验;理解当因子数量增加时,全因子试验的缺点。
7.响应曲面设计(分析)设计、实施和分析响应曲面设计来进行优化;理解并应用响应曲面法,包括CCD, Box-Behnken等;理解三种CCD 设计(CCI,CCC,CCF)的特点;理解和使用最速上升法;理解可旋转性的概念。
8.混料设计与调优运算(了解)了解几种混料设计的基本方法;了解调优运算。
术语(理解)•需要理解的内容:375-377–实验设计的目的1)哪些X 显著影响Y ;2)找出Y 间的关系式,从而找出X 取什么值时Y 最优;375–作用1)删选主要选用部分因子实验和Placket-Burman–作用2)全因子设计,响应曲面设计了解试验设计在改进阶段的用法;掌握试验设计的基本概念,包括变量的独立性、因素和水平、响应、处理、误差等;识别试验设计的不同类型和应用条件。
66. 下列哪项设计是适合作为改进阶段开始的筛选实验(Screening Experiment):A. 8 因子的全因子实验B. 8 因子的部分因子实验C. 中心复合设计(CCD) D. Box-Behnken 设计解析: 【真题】6. 下列哪项是全因子实验设计的主要优势()(1 分)A.实验次数少B.可得到最优的模型C.可得到所有因子的主效应与交互效应D.以上全不对解析: 【真题】41. 以下哪个不是DOE 的目的? (1 分)•A.筛选输入变量•B.筛选输出变量•C.优化输出变量•D.确定输入变量的设定范围•需要理解的内容:408–实验次数安排2k−P +m–混杂的快速记忆分辨度为几就伸出几个手指,然后把这几个手指分为两个部分,这两个部分就是混杂;作用、混杂和分辨力等;理解饱和设计、投影特性和效应稀疏原理。
中心组合设计方法CCD介绍课件ppt

• 目的: 如何設定因子之水準(區間), 使反應變數
達到最佳值.
2021/3/10
2
RSM之基本原理
• 真正的函數關係 Y = f(x1, x2) + e 反應曲面(Response Surface) = f(x1, x2)
• 若因子之區間縮小, 則 f(x1, x2) 可用多項式來趨近. 如: Y = b0+b1x1+b2x2+…+bkxk+e (first order) Y = b0+bixi+biix2i+ bijxixj+e (second order)
• Face-centered Central Composite Design (FCCD)
– 除了 a = 1以外, 其餘 與 CCDs同
– 當部份因子之水準數 只有三個, 或為離散性 質時
– 可旋轉性 (Rotatability) 較差, 應儘量避免使用
2021/3/10
33
二階 Model 之 RSM 設計(3/4)
Chapter 11
Part I :反應曲面技術
(Response Surface Methodology)
2021/3/10
1
Why/When to Use RSM?
• 已知此反應變數(Response Variable)受數個因子 之影響.
– 必須經由實驗設計所證實.
• 吾人想知道此反應變數之最佳值
2021/3/10
49
混合設計之目的
• 前所提及的反應曲面技術設計, 每一因子水準 之選擇皆與其他因子無關 (Independent); 然而, 實際的系統中, 常會因為某一因子水準之選擇, 而使得另一因子的水準必須固定在某一數值上 (Dependent). 此時, 吾人便必須使用混合設計 (Mixture Designs) 才能將此種現象呈現出來.
响应曲面设计概述-2023年学习资料

关于《RSM》-RSM是利用合理的实验设计方法并通过实-验的到一定的数据,采用多元二次回归-方程来拟合因素与响应值 间的函数关-系,通过对回归方程的分析来寻求最优-的工艺参数,解决多变量问题的一种统-计方法。
中心复合设计实验方案的确定-3、中心点个数的选择-在满足旋转性的前提下,适当的选择中心点数,可以使整个试验区-域内 预测值具有一致均匀精度。一般至少选2-5次。-因子数-立方点-星号点-合计-4-13--Behnkeni试验设计-Box-Behnken desingn
中心复合设计实验方案的确定-第三步:如果确定试验区域已经接近最优区域,则可选-择三类点直接进行中心复合设计。需要考 的问题如-下:-1、如何选择全因子设计部分-2、如何确定星号点的位置(即确定α值-3、如何确定中心点的个数
中心复合设计实验方案的确定-1、如何选择全因子设计部分-一般选择全因子设计(因子数在2-4之间,因子数>5时考虑采 用部分因子设计。-2、如何确定星号点的位置(多考虑旋转性-F=K2或F=1/2K205个因素ā=F1/4-F为因子 验点的总数,K为因子的个数-即可满足旋转性,又可满足序贯性,称为中心复合贯序设计-CCC。-Q=2K/4
中心复合试验设计CCD-◆0,t怕-中心点(center point-l,1◆--“----------1,1-中 点,即时设计中心,表示-在图上,坐标皆为“0”.--a,0-10,0-ta,0-,------------0-+1 l-◆0,a-序贯试验设计(顺序试验-线后分段完成试验,前次试验设计-的点上做过的试验结果,在后续的-试验设计中继 有用。
@中心复合试验设计-central composite desingn
中心复合设计CCD
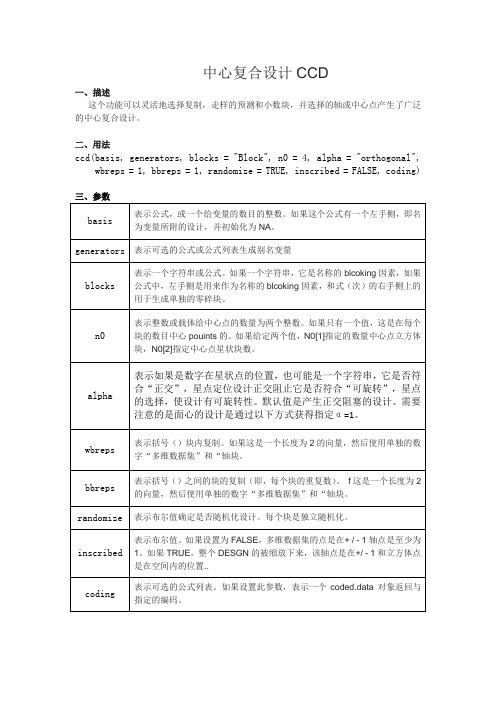
中心复合设计CCD一、描述这个功能可以灵活地选择复制,走样的预测和小数块,并选择的轴或中心点产生了广泛的中心复合设计。
二、用法ccd(basis, generators, blocks = "Block", n0 = 4, alpha = "orthogonal", wbreps = 1, bbreps = 1, randomize = TRUE, inscribed = FALSE, coding)三、参数四、详细信息中央复合设计的CCD响应面勘探中使用的流行的设计。
他们被堵塞的设计组成的至少一种的多维数据集的块(两水平因子或部分因子,附加中心点),和至少一个星状块(点沿每个轴的位置-α+α-),加上中心点。
一切都被假定为规模的编码的多维数据集的设计部分,其中为每个变量的值-1和1,中心点0。
使用的编码参数,如果需要的话,编码可以提供。
基础参数确定一个基本的设计,用来创建立方体块。
例如,basis = ~A+B+C会生成一个基本的8次试验的设计。
如果你需要额外的变量,可使用generators,例如,generators = c(D~-A*B, E~B*C)加在上面定义关系会产生一个5因素设计I = ABD = BCE = ACDE 。
如果你想立方体点分为零碎块,给块参数公式。
例如,basis =A+B+C+D+Egenerators =F~-A*C*D, 和blocks =Day ~c(A*B*C,C*D*E)。
阻挡变量将被命名为“Day”,将其分为4块8和32运行的基本设计(半部分6因素)运行每一个的基础上,结合标志的A * B * C 和C * D * E 。
请注意,这一天将混淆与发电机组,及其相互作用,以及所有这些别名:Day = ABC = CDE = ABDE = -BDF = -ADCF = -BCEF = -AEF。
对于每个模块,我们将添加N0(N0 [1 ])的中心点。
中心复合设计原理

中心复合设计原理(Central Composite Design,简称CCD)是一种用于实验设计的统计方法。
它是响应面分析设计中常用的一种方法,用于确定多个因素对某个响应变量的最佳组合。
中心复合设计原理包括两个主要的设计因素:中心点和星点。
中心点是在每个因素的水平范围内选择中间值,用于确定对响应变量的基本影响。
而星点则是在每个因素的水平范围外选择几个点,用于评估因素对响应变量的非线性影响。
中心复合设计原理的步骤如下:
1. 确定需要研究的因素和响应变量:确定对响应变量有潜在影响的因素,并定义响应变量。
2. 选择因素的水平:确定每个因素的水平范围,通常选择低水平、高水平和中心水平。
3. 构建试验设计表:根据因素的水平和中心点与星点的数量,构建一个试验设计表。
这个表将列出每个因素在每个水平上的设置。
4. 进行试验:按照试验设计表进行实际试验,并记录响应变量的观测结果。
5. 进行数据分析:使用统计方法分析试验结果,建立响应面模型,评估因素对响应变量的影响。
6. 进行优化:基于建立的响应面模型,确定使响应变量达到最佳水平的因素组合。
中心复合设计原理的优点是可以同时研究多个因素,并且考虑了线性和非线性的影响。
它可以帮助研究人员确定最佳的因素组合以优化响应变量,从而提高产品或工艺的性能。
然而,中心复合设计原理也有一些限制,如对因素间相互作用的假设较强,样本容量要求较高等。
在实际应用中,需要根据具体情况和实验要求来选择合适的设计方法。
六西格玛考试复习知识要点

《六西格玛管理》知识要点孙肃清整理序言:为帮助大家学习和掌握六西格玛管理知识,加深对六西格玛管理知识的认识,从容应对考试。
以红书《六西格玛管理》为基础,适当参照蓝书《六西格玛管理统计指南-MINITAB使用指南》,编撰了这篇《知识要点》。
所谓要点,即:主要的知识点,重要的概念、公式和方法、可能的考点以及重难点。
希望能对大家有所裨益。
特别需要提醒的是:第一至第四章、第九第十章的多选题会多一些,而历次考试丢分较多的往往是多选题。
第一章六西格玛管理概论1.1 六西格玛管理的发展1.1.1 质量概念的演进和质量管理的发展1.质量概念的演进质量:一组固有特性满足要求的程度。
(ISO9000:2005)(1)质量概念中主体的演进质量概念中的主体是指“什么的质量”。
⏹产品的质量。
包括性能、可信性等实物质量。
⏹产品和服务的质量。
扩展到包括准时交付、周期时间等服务质量。
⏹产品、服务和过程的质量。
过程质量涉及5M1E,质量体现Q(实物质量)、C(成本)、D(交付)、E(环境)、S(安全)的综合质量。
⏹产品、服务、过程和体系的质量。
体系质量即管理系统的质量。
(2)质量概念中客体的演进质量概念中的客体是指“满足什么要求的质量”。
⏹符合性质量。
满足标准或规范要求。
⏹适用性质量。
满足顾客要求的程度,关键看对顾客是否适用。
⏹顾客及相关方综合满意的质量。
大质量概念,综合满足顾客、股东、员工、供应商及合作伙伴、社会等利益相关方(也称为五大利益相关方)的程度。
2.质量管理的发展经历了质量检验、统计质量控制、全面质量管理三大历史阶段。
(1)质量检验阶段。
(二战以前)三权分立:设计+制造+检验聚焦于产品质量。
代表人物:F.W.泰勒(科学管理之父)。
工人自检、工长监督检查、检验员专检。
两个问题:⏹事后检验,死后验尸;⏹全数检验,成本太高。
(2)统计质量控制(SQC)阶段(20世纪40-50年代)数理统计方法与质量管理结合,过程控制,形成了质量的预防性控制与事后检验相结合的管理方式。
三水平四因子的中心复合设计

三水平四因子的中心复合设计中心复合设计(Central Composite Design,CCD)是一种实验设计方法,通常用于多因素、多水平的实验设计。
这种方法可以帮助研究者探索并理解多个变量之间的相互作用,以便找出最优化的条件或找出最佳的实验设计配置。
中心复合设计的具体步骤包括:1.确定因素和水平:确定要研究的因素和它们的水平。
通常,每个因素都有两个或多个水平,这些水平可以是离散的或连续的。
2.确定实验设计点:在因素空间中确定实验设计点。
中心复合设计通常包括中心点、轴点和星点。
中心点是所有因素都处于零水平的点,轴点是因素水平达到最极端的点,星点则是在因素空间中随机选取的点。
3.实施实验:在确定的实验设计点上进行实验,并收集数据。
4.数据分析和模型拟合:对收集到的数据进行统计分析,通常使用回归分析方法来拟合一个数学模型。
这个模型可以帮助理解因素之间的相互作用,以及如何优化实验条件。
5.优化条件确定:根据数学模型的结果,确定最优化的实验条件。
这通常是通过求解数学模型来得到的。
6.验证实验:在最优化的条件下进行验证实验,以确认实验结果的可靠性和可重复性。
中心复合设计的主要特点:1.中心点重复多次,可以更准确地估计随机误差和模型中的纯误差项。
2.设计中含有轴向点(即远离中心点的试验条件),以充分估计二次项和其他高阶项效应。
3.通过较少的实验次数就能获取较多的信息,从而有效地降低实验成本,提高效率。
三水平四因子的中心复合设计是指在三个水平上对四个因素进行中心复合设计。
具体的实验设计点和数据收集、分析和模型拟合等步骤与上述过程类似。
需要注意的是,由于因素数量和水平的增加,实验设计和数据分析的复杂性也会相应增加。
因此,在进行三水平四因子的中心复合设计时,需要更加谨慎地选择实验设计和分析方法,以确保实验结果的准确性和可靠性。
星点设计效应面法

报告内容
一、引言 二、CCD效应面法基本概念 三、CCD效应面法基本原理 四、CCD效应面法操作环节
一、引言
在药学制剂工艺优化和处方筛选过程中,常需同步考察 多种原因对成果旳影响,并对成果进行优化。当原因水平数 较少时可采用析因设计;较多时需采用试验次数较少旳试验 设计优化法。
国内目前用得比较成熟旳措施为均匀设计和正交试验设 计措施,虽然上述两种措施在试验处理时能够取得较佳点, 基本能够满足一般试验旳要求。但是它们还存在某些问题: 如试验旳精度不够,建立旳数学模型预测性较差,选择旳试 验取值仅仅是接近最佳取值,无法精确找到最佳点,不能灵 敏地考察各原因间旳交互作用等等。
模型旳复有关系数r=0. 9838,先删除最不可信旳b3和b8项,
重新拟合,再根据P值依次删除b6和b7项,再拟合,成果见表4。
四、CCD效应面法操作环节
4.3 多元线性或非线性拟合
实例:采用星点设计效应面法优选远志旳提取工艺。 表 4 简化后二次多项式非线性估计成果
估计值 原则误
t
P
b0
-160. 4345 33. 9894
三、CCD效应面法基本原理
• 宏观上讲,效应面优化法就是经过描绘效应对考察原因旳 效应面,从效应面上选择较佳旳效应区,从而回推出自变 量取值范围即最佳试验条件旳优化法。使用起来直观、以 便、效果很好。
• 简朴地说,效应面优化法就是经过拟合效应变量对考察原 因变量旳效应面,即函数f不可能用数学模型表述,效应 对原因旳真实效应面只是假想旳,但能够用某一数学模型 f ' 近似地模拟函数f,根据该模型能够描绘效应面,从效 应面上选择最优旳效应域,利用f’求得自变量x1, x2,…, xn取值范围即最佳试验条件旳优化法。数学模型f与f ' 旳近 似程度直接关系到效应面旳近似程度与优选条件旳精确度。
ccd中心复合设计 matlab -回复

ccd中心复合设计matlab -回复CCD中心复合设计MatlabCCD中心复合设计是一种用于设计、分析和优化复杂实验的统计方法。
Matlab是一种强大的数值计算和编程工具,可以广泛应用于各种工程和科学领域。
本文将介绍如何使用Matlab来实施CCD中心复合设计,并逐步回答相关问题。
第一步:了解CCD中心复合设计的基本概念和原理。
CCD中心复合设计是一种响应面设计,它是通过改变实验条件来研究响应变量与输入因素之间的关系。
在CCD中,输入因素通常被称为X1、X2、X3等,而响应变量通常被称为Y。
中心复合设计与传统的复合设计相比,更加高效和经济。
它通过在每个输入因素的中心点周围添加一组复合点来实现这一点。
第二步:建立CCD中心复合设计的数学模型。
在Matlab中,可以使用多项式回归模型来描述CCD中心复合设计的数学模型。
假设一个典型的模型为:Y = b0 + b1*X1 + b2*X2 + b3*X3 + b12*X1*X2 + b13*X1*X3 + b23*X2*X3 + b11*X1^2 + b22*X2^2 + b33*X3^2其中,b0、b1、b2等为回归系数。
第三步:设计实验矩阵。
根据CCD中心复合设计的原理,可以使用Matlab中的ccdesign函数来生成实验矩阵。
这个函数需要指定因子的个数和每个因子的水平数。
例如,设有三个因子X1、X2和X3,每个因子的水平数为5,可以使用以下代码生成实验矩阵:factors = 3; 因子个数levels = 5; 每个因子的水平数design = ccdesign(factors, 'center', levels);生成的实验矩阵design将包含27个试验点,其中9个是中心点。
第四步:进行实验和数据采集。
根据实验矩阵设计的方案,对每个试验点进行实验,并记录对应的响应变量值Y。
第五步:拟合回归模型。
在Matlab中,可以使用polyfit函数对实验数据进行多项式拟合,进而得到回归模型的系数。
中心复合设计CCD

中心复合设计CCD一、描述这个功能可以灵活地选择复制,走样的预测和小数块,并选择的轴或中心点产生了广泛的中心复合设计。
二、用法ccd(basis, generators, blocks = "Block", n0 = 4, alpha = "orthogonal", wbreps = 1, bbreps = 1, randomize = TRUE, inscribed = FALSE, coding)三、参数四、详细信息中央复合设计的CCD响应面勘探中使用的流行的设计。
他们被堵塞的设计组成的至少一种的多维数据集的块(两水平因子或部分因子,附加中心点),和至少一个星状块(点沿每个轴的位置-α+α-),加上中心点。
一切都被假定为规模的编码的多维数据集的设计部分,其中为每个变量的值-1和1,中心点0。
使用的编码参数,如果需要的话,编码可以提供。
基础参数确定一个基本的设计,用来创建立方体块。
例如,basis = ~A+B+C会生成一个基本的8次试验的设计。
如果你需要额外的变量,可使用generators,例如,generators = c(D~-A*B, E~B*C)加在上面定义关系会产生一个5因素设计I = ABD = BCE = ACDE 。
如果你想立方体点分为零碎块,给块参数公式。
例如,basis =A+B+C+D+Egenerators =F~-A*C*D, 和blocks =Day ~c(A*B*C,C*D*E)。
阻挡变量将被命名为“Day”,将其分为4块8和32运行的基本设计(半部分6因素)运行每一个的基础上,结合标志的A * B * C 和C * D * E 。
请注意,这一天将混淆与发电机组,及其相互作用,以及所有这些别名:Day = ABC = CDE = ABDE = -BDF = -ADCF = -BCEF = -AEF。
对于每个模块,我们将添加N0(N0 [1 ])的中心点。
minitab实验之试验设计

Minitab 实验之试验设计实验目的:本实验主要引导学生利用Minitab 统计软件进行试验设计分析,包括全因子设计、部分因子设计、响应曲面设计、混料设计、田口设计以及响应优化,并能够对结果做出解释。
实验仪器:Minitab 软件、计算机 实验原理:“全因子试验设计”(full factorial design )的定义是:所有因子的所有水平的所有组合都至少要进行一次试验的设计。
由于包含了所有的组合,全因子试验所需试验的总次数会比较多,但它的优点是可以估计出所有的主效应和所有的各阶交互效应。
所以在因子个数不太多,而且确实需要考察较多的交互作用时,常常选用全因子设计。
一般情况下,当因子水平超过2时,由于试验次数随着因子个数的增长而呈现指数速度增长,因而通常只作2水平的全因子试验。
进行2水平全因子设计时,全因子试验的总试验次数将随着因子个数的增加而急剧增加,例如,6个因子就需要64次试验。
但是仔细分析所获得的结果可以看出,建立的6因子回归方程包括下列一些项:常数项、主效应项有6项、二阶交互作用项15项、三阶交互项20项,…,6阶交互项1项,除了常数项、主效应项和二阶交互项以外,共有42项是3阶以及3阶以上的交互作用项,而这些项实际上已无具体的意义了。
部分因子试验就是在这种思想下诞生的,它可以使用在因子个数较多,但只需要分析各因子和2阶交互效应是否显著,并不需要考虑高阶的交互效应,这使得试验次数大大减少。
在实际工作中,常常要研究响应变量Y 是如何依赖于自变量,进而能找到自变量的设置使得响应变量得到最佳值(望大、望小或望目)。
如果自变量的个数较少(通常不超过3个),则响应曲面方法(response surface methodology ,RSM )是最好的方法之一,本方法特别适合于响应变量望大或望小的情形。
通常的做法是:先用2水平因子试验的数据,拟合一个线性回归方程(可以包含交叉乘积项),如果发现有弯曲的趋势,则希望拟合一个含二次项的回归方程。
minitab实验之试验设计(2)解读

分析要点三:分析评估各项效应的显著性。计算结果显示,4个主效应中,加热温度、加热时间和保温时间是显著的,只有转换时间不显著;6个2因子水平交互效应中,只有加热时间*保温时间是显著的。说明本例中还有不显著的自变量和2因子交互作用,改进模型时应该将这些主效应和交互作用删除。
加热温度*保温时间3.062 1.531 1.500 1.02 0.337
加热时间*转换时间1.263 0.631 1.500 0.42 0.685
加热时间*保温时间7.113 3.556 1.500 2.37 0.045
转换时间*保温时间0.837 0.419 1.500 0.28 0.787
S = 6.00146 PRESS = 1778.45
稳健参数设计(robust parameter design)(也称健壮设计、鲁棒设计,简称参数设计)是工程实际问题中很有价值的统计方法。它通过选择可控因子的水平组合来减少一个系统对噪声变化的敏感性,从而达到减小此系统性能波动的目的。过程的输入变量有两类:可控因子和参数因子。可控因子是指一旦选定就保持不变的变量,它包括产品或生产过程设计中的设计参数,而噪声因子是在正常条件下难以控制的变量。在做参数设计时,就是把可控因子的设计当做研究的主要对象,与此同时让噪声因子按照设定的计划从而系统改变其水平的方法来表示正常条件下的变化,最终按照我们预定的望大、望小或望目地目标选出最佳设置。田口玄一博士在参数设计方法方面贡献非常突出,他在设计中引进信噪比的概念,并以此作为评价参数组合优劣的一种测度,因此很多文献和软件都把稳健参数设计方法称为田口方法(Taguchi design)。
第七章 响应面设计法

例1:某药物毫微球包封率的 优化
• 已知在155F下蒸发35分钟,得到的包封
率是40%。
为
•
设首次优化区间为(150,160F)、 (30,40分)
什 么 除
• 自变量规范化:
以 5
• 采用22析因设计(加5个中心对照点)?
• 通过中心对照点检验弯曲性,拟合一阶 方程,对模型进行统计检验
• 2因素的等径设计(Equiradial design for 2 factors)
• 大于2因素的等径设计(Equiradial design for more than 2 factors)
一、2因素等径设计
• 按单纯形形状可以分为:三角形Triangle、正方形square、正五 边形pentagon和正六边形hexagon四种。
否定先前的模型是没有根据的放弃模型不用更是不应该的欲发现真正的最优试验条件调整试验范围是必f检验给出的显著性与否是判断回归模型是否有效的当然依据一般情况下回归平方和与剩余平方和的比值越大则模型的可信度愈高表现在复相关系数或相关系数上r数值就越大一元线性回归分析常用相关系数表述相关关系的大小且r值可正可负但是建模的过程中我们不能简单地追求高的回归平方和与剩余平值模型的建立一定要根据专业的知识进行数理统计中一个重要的概念是自由度若选进方程中的项过多使误差自由度为1甚至为0虽然r2更加接近于1模型看上去很完美但这时有关的结论的可靠性是很差的
最速上升(或下降)法步骤
• 确定优化区域:x1(x1i,x1j),….. xn(xni,xnj) • 将自变量范围规范在(-1,1)之间 • 根据试验(如析因设计)结果确定线性模型 • 假定x1=x2=…..=xn=0为原点或基点 • 选取一个过程变量的步长△xj,通常以回归系数绝对
三类中心复合设计的比较参考文档

1.1 一些概念
1.1 一些概念
1.2 CCDs简介
因子点:立方体的顶点。主要用于估 计线性项以及交互项。 中心点:位于图形中间的点。中心点 提供关于模型中是否存在曲性的信息 可以提供有关纯误差项的信息。 轴向点:“星”点。如果存在曲性, 轴向点可用于估计纯二次项。不能提 供有关交互作用项的信息。
2.2 从设计的稳健性方面进行比较
三、举例
发动机连杆装配的例子进行模拟分析, 已知有三个因子(底座基准面的 平面度、连杆长度和连杆的垂直度) 显著地影响目标函数(损失函数和 加工成本之和), 将三个因子的公差水平设为五个和三个水平来模拟这 三个设计, 并将利用JMP分析所得到的实验结果总结于表1中。
三、举例
从模型系数的估计精度可看出, CCC的估计精度最高, 尤其是平方效应 的估计, CCI最差, CCI明显地不如CCC 有效, 这表明设计空间对模型参 数的估计精度有影响。而从优化点的坐标值可推断出, 设计域同时极大 地影响着优化点的位置。
三、举例
从设计点的预测误差来看, CCC、CCI的轴向点和析因点性能相似; CCF 轴向点要显著地好于析因设计点, 这说明球形设计的一致精度比立方域 要好。对于被CCI排除但仍然在CCF的操作域之内的各个顶点而言, 意 味着预测误差增加了27%(36.1575435/28.3826518 -1)。从中心点的预测 方差来看, CCF具有最高的精度, 误差小, 这说明CCF设计对中心点的数 目是稳健的。
2.1 从设计域及其复杂性上比较
为了成功地运行任一安排的试验, 操作域必须包括设计域。这意味着过 程必须能够在设计域上具有可操作性, 因此, 正确的选择CCDs的第一步 就是将设计域与操作域相比较。 在球形域中, 当对给定变量的最大尺寸进行变动时, 可以不必考虑操作 域问题。如果实验者能够充分推测出优化目标存在于所研究的变量区 域内, 一般采用球形域。在许多实际情况下, 当过程不能够在设计域的 一个或者多个边界点上操作时, 设计域与操作域相同, 这时设计域是个 立方体。 如果过程不能在区域的一个或者多个立方体的顶点上操作, 那么CCF是 不合适的, 这就留给实验者两个选择: 减少变量的区域产生一个新的CF, 或者产生一个CCI。由于将轴向点放在变量范围的上下界, 析因点就落 在了设计空间的内部, CCI限制了由变量所定义的区域的真实设计空间。
ccd中心复合设计 matlab

ccd中心复合设计 matlab标题:基于CCD中心复合设计的MATLAB应用概述:本文将介绍基于CCD中心复合设计的MATLAB应用,通过该设计方法,可以有效提高实验效率和准确性。
本文将从设计理论、实验步骤和结果分析三个方面进行详细阐述。
设计理论:CCD中心复合设计是一种多因素实验设计方法,通过减少实验次数,节省资源和时间,同时兼顾各因素的重要性。
该设计方法结合了中心复合设计和CCD设计的优势,能够更好地解决多因素实验的问题。
在MATLAB中,可以利用Design of Experiments (DOE)工具箱来实现CCD中心复合设计。
实验步骤:在MATLAB环境中安装并加载DOE工具箱。
然后,定义实验因素和水平,并生成CCD中心复合设计的实验方案。
接下来,根据实验方案,进行实验数据的采集和记录。
最后,利用MATLAB进行数据分析和结果的统计。
结果分析:通过CCD中心复合设计,我们可以有效地探究多因素对实验结果的影响,并对各因素进行优化和调整。
利用MATLAB的数据分析工具,我们可以进行方差分析、回归分析和优化算法等,以获得准确的实验结果和最佳的实验参数组合。
总结:基于CCD中心复合设计的MATLAB应用可以提高多因素实验的效率和准确性。
通过合理设计实验方案、采集数据和进行数据分析,我们可以得到准确的实验结果,并优化实验参数。
MATLAB的强大功能和DOE工具箱的支持,使得实验设计和数据分析更加简单和高效。
在实际应用中,我们可以将CCD中心复合设计与MATLAB相结合,来解决各种复杂实验设计和数据分析的问题。
通过合理利用资源和时间,我们可以在科学研究和工程实践中取得更好的效果。
