2010全国赛A题
2010第六届全国大学生化学实验竞赛笔试试题-终

第七届全国大学生化学实验邀请赛笔试试卷2010.7选手编号:答题需知:1.考试时间为2小时。
2.考生必须遵守考场纪律。
3.题目为单项选择题,每题1分,共100分。
4.请将答案请写在答题纸上。
一、 实验室安全知识与基础知识部分1.关于实验室某插座的说法正确的是()A. 三相电插座,上侧为零线,其与其它任意一线之间的电压为380 V;B. 三相电插座,上侧为零线,其与其它任意一线之间的电压为220 V;C. 三相电插座,下侧为零线,其与其它任意一线之间的电压为380 V;D. 三相电插座,下侧为零线,其与其它任意一线之间的电压为220 V。
2.停电检修时,在一经合闸即可送电到工作地点的开关或闸刀的操作把手上,应悬挂如下( )种标示牌。
A. “在此工作”;B.“止步,高压危险”;C.“禁止合闸,有人工作”; D. “危险,请勿触摸”。
3.扑救液体爆炸物品火灾时,()用沙土盖压,以防造成更大伤害。
A. 必须;B. 禁止;C. 可以;D. 无所谓。
4.关于液氮使用说法中错误的是()A. 皮肤接触致冷剂会引起冻伤;B. 少量致冷剂接触眼睛会导致失明;C. 液氮的快速蒸发可能会造成现场空气缺氧;D. 在易燃物上方使用较多液氮不会引起易燃物着火。
5.下列关于进入实验室工作的各种说法中错误的是()A. 不得在实验室储藏食品、饮食、抽烟。
不得将小孩及亲友等与专业无关人员带进化学实验室。
B. 接触危险品时必须穿工作服,戴防护眼镜,穿不露脚趾的滿口鞋,长发须束起。
C. 保持实验室门和走道畅通,熟悉在紧急情况下的逃离路线和紧急疏散方法,清楚灭火器材、紧急喷淋器、洗眼器的位置。
铭记急救电话。
D. 做实验期间,如实验需要在一定温度下反应5小时,可以到资料室查阅资料。
晚上、节假日做某些危险实验的室内应有二人以上,方可实验。
6.防止毒物危害的最佳方法是()。
A. 穿工作服;B.佩戴呼吸器具;C. 使用无毒或低毒的代替品;D. 不做实验。
2010全国中学生生物学联赛试卷与答案

2010全国中学生生物学联赛试卷与答案注意事项:1.使用2B铅笔在机读卡上做答;2.试题按学科分类,单选与多选混排,每小题只标明分值,分值不代表是否为多选,是否多选可从题干中判断。
答案完全正确才可得分:3.答题时间120分钟,全卷共l20道题l60分。
第一部分29道题(40分)1. 在细胞质膜的组成中,胆固醇分子(1分)A.仅存在于高等动物细胞中B.仅存在于高等植物细胞中C.高等动植物细胞中都存在D.还未确定2. 细胞质膜上具备的钠钾泵每消耗一一个ATP分子将会(1分)A.向细胞内转入2个K+向细胞外转出2个Na+B.向细胞内转入2个Na+向细胞外转出2个K+C.向细胞内转入3个K+向细胞外转出2个Na+D.向细胞内转入2个K+向细胞外转出3个Na+3. 构成溶酶体的各种酶完成合成最终是在那一个部位(1分)A.在游离核糖体上B.在粗面内质网的核糖体上C.同时在游离和粗面内质网核糖体上D.在这两种核糖体上轮流进行4. 下列分子中不能通过无蛋白脂双层膜的是哪一项(1分)A.二氧化碳B.乙醇C.尿素D.葡萄糖5. 以下哪种组蛋白不属于核小体的核心蛋白(1分)A.HlB.H2AC.H2BD.I-13E.H46. 下列哪些细胞器具有质子泵(2分)A.内质网B.高尔基体C.溶酶体D.线粒体E.叶绿体7. 线粒体在合成ATP过程中需要下列哪些条件(2分)A.基质中含有0:B.基质中含ADPC.基质中的H+浓度大于膜间隙D.基质中的H+浓度小于膜间隙8. 在细胞减数分裂过程中会出现下列哪些现象(2分)A.同源染色体配对B.DNA复制C.同源染色体间交换D.基因发生变异9. 电子显微镜下的细胞质膜体现出“暗一亮一暗”的结构,一般认为主要原因有哪些:(2分)A.磷脂分子的亲水头易被染色B.外在膜蛋白的存在C.胞外基质和膜下细胞骨架的存在D.跨膜蛋白的存在10.下面关于组蛋白的说法哪些是正确的:(3分)A.组蛋白普遍存在于真核细胞B.组蛋白在物种间很保守,进化缓慢C.组蛋白富含组氨酸D.组蛋白呈现碱性E.组蛋白的修饰会影响基因的表达11. 人体内嘌呤核苷酸分解代谢的主要终产物是以下哪一种? (1分)A.尿素B.尿酸C.丙氨酸D.肌酸E.肌酸酐12. Q—D一葡萄糖和B-D-葡萄糖的主要区别是下列哪一个?(1分)A.第l位碳原子上的羟基B.第2位碳原子上的羟基C.第5位碳原子上的羟基D.第4位碳原子上的羟基13. 按照脂肪酸的分类,油酸应该属于哪一类脂肪酸? (1分)A.软脂肪酸B.花生四烯酸C.硬脂肪酸D.不饱和脂肪酸14. 在氨基酸的分类中,下面哪一个氨基酸属于芳香族氨基酸?(1分)A.丙氨酸B.丝氨酸C.色氨酸D.亮氨酸15. 蛋白质的肽键是以下列哪一种方式形成的?(1分)A.a一氨基与a一羧基缩合而成B.a一氨基与8~羧基缩合而成C.岱一氨基与a一羧基缩合而成D.D一氨基与8一羧基缩合而成16. 下列哪一个是DNA和RNA二者的主要区别?(1分)A.酯键B.核糖C.碱基D.磷酸基17. 同工酶具有以下哪个特性?(1分)A.具有相同的蛋白质分子结构B.理化性质相同C.催化相同的化学反应D.免疫性能相同18. 使用离心机离心l00毫升样品之前最重要的操作步骤是平衡,正确的操作是以下哪一个?(1分)A.目测B.用量筒量取同样体积的样品溶液分别倒入两个离心管中C.用托盘天平平衡两个离心管,然后将样品溶液分别倒入离心管D.将样品溶液分别倒入两个离心管中,然后用托盘天平进行平衡19. 以下关于酶的描述,哪些是不正确的?(2分)A.大多数酶的化学本质是蛋白质B.所有的酶都必须结合辅基或辅酶才能发挥催化作用;C.都具有立体异构专一性D.能显著地改变化学反应速率20. 在生物大分子的分离纯化过程中,能将生物大分子与无机盐及有机小分子分离的方法是以下哪些?(3分)A.离子交换层析B.凝胶过滤层析C.滤纸过滤D.透析E.离心21. 植物的微生物病害可引起植物机能失灵,代谢紊乱而导致植物生存能力下降,甚至死亡或极大地减少产量。
全国大学生数学建模竞赛历年赛题

全国大学生数学建模竞
赛历年赛题
Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT
全国大学生数学建模竞赛历年赛题
2009:AB
CD
2010:A储油罐的变位识别与罐容表标定
B2010年上海世博会影响力的定量评估
C输油管的布置
D对学生宿舍设计方案的评价
2011:A城市表层土壤重金属污染分析
B交巡警服务平台的设置与调度
C企业退休职工养老金制度的改革
D天然肠衣搭配问题
2012:A葡萄酒的评价
B太阳能小屋的设计
C脑卒中发病环境因素分析及干预
D机器人避障问题
2013:A车道被占用对城市道路通行能力的影响
B碎纸片的拼接复原
C古塔的变形
D公共自行车服务系统
2014:A嫦娥三号软着陆轨道设计与控制策略B创意平板折叠桌
C生猪养殖场的经营管理
D储药柜的设计
2015:A太阳影子定位
B“互联网+”时代的出租车资源配置
C月上柳梢头
D众筹筑屋规划方案设计。
全国数学建模大赛题目

附件2:实际储油罐的检测数据
2010高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
B题 2010年上海世博会影响力的定量评估
2010年上海世博会是首次在中国举办的世界博览会。从1851年伦敦的“万国工业博览会”开始,世博会正日益成为各国人民交流历史文化、展示科技成果、体现合作精神、展望未来发展等的重要舞台。请你们选择感兴趣的某个侧面,建立数学模型,利用互联网数据,定量评估2010年上海世博会的影响力。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。按照有关规定,需要定期对罐容表进行重新标定。图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度和横向偏转角度)之间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
全国研究生数学建模竞赛题目

中国研究生数学建模竞赛试题汇总2021赛题汇总2021-A:相关矩阵组的低复杂度计算和存储建模2021-B:空气质量预报二次建模2021-C:帕金森病的脑深部电刺激治疗建模研究2021-D:抗乳腺癌候选药物的优化建模2021-E:信号干扰下的超宽带(UWB)精确定位问题2021-F:航空公司机组优化排班问题2020赛题汇总2020-A:芯片相噪算法2020-B:汽油辛烷值建模2020-C:面向康复工程的脑信号分析和判别建模2020-D:无人机集群协同对抗2020-E:能见度估计与预测2020-F:飞行器质心平衡供油策略优化2019赛题汇总2019-A: 无线智能传播模型2019-B:天文导航中的星图识别2019-C:视觉情报信息分析2019-D:汽车行驶工况构建2019-E:全球变暖?2019-F:多约束条件下智能飞行器航迹快速规划2018赛题汇总2018-A :关于跳台跳水体型系数设置的建模分析2018-B:光传送网建模与价值评估2018-C:对恐怖袭击事件记录数据的量化分析2018-D:基于卫星高度计海面高度异常资料获取潮汐调和常数方法及应用2018-E:多无人机对组网雷达的协同干扰2018-F:机场新增卫星厅对中转旅客影响的评估方法2017赛题汇总2017-A:无人机在抢险救灾中的优化运用2017-B:面向下一代光通信的VCSEL激光器仿真模型(华为命题)2017-C:航班恢复问题2017-D:基于监控视频的前景目标提取2017-E:多波次导弹发射中的规划问题2017-F:构建地下物流系统网络2016赛题汇总2016-A:多无人机协同任务规划2016-B:具有遗传性疾病和性状的遗传位点分析2016-C:基于无线通信基站的室内三维定位问题2016-D:军事行动避空侦察的时机和路线选择2016-E:粮食最低收购价政策问题研究2015赛题汇总2015-A:水面舰艇编队防空和信息化战争评估模型2015-B:数据的多流形结构分析2015-C:移动通信中的无线信道“指纹”特征建模2015-D:面向节能的单/多列车优化决策问题2015-E:数控加工刀具运动的优化控制2015-F:旅游路线规划问题2014赛题汇总2014-A:小鼠视觉感受区电位信号(LFP)与视觉刺激之间的关系研究2014-B:机动目标的跟踪与反跟踪2014-C:无线通信中的快时变信道建模2014-D:人体营养健康角度的中国果蔬发展战略研究2014-E:乘用车物流运输计划问题2013赛题汇总2013-A:变循环发动机部件法建模及优化2013-B:功率放大器非线性特性及预失真建模2013-C:微蜂窝环境中无线接收信号的特性分析2013-D:空气中PM2.5问题的研究2013-E:中等收入定位与人口度量模型研究2013-F:可持续的中国城乡居民养老保险体系的数学模型研究2012赛题汇总2012-A:基因识别问题及其算法实现2012-B:基于卫星无源探测的空间飞行器主动段轨道估计与误差分析2012-C:有杆抽油系统的数学建模及诊断2012-D:基于卫星云图的风矢场(云导风)度量模型与算法探讨2011赛题汇总2011-A:基于光的波粒二象性一种猜想的数学仿真2011-B:吸波材料与微波暗室问题的数学建模2011-C:小麦发育后期茎秆抗倒性的数学模型2011-D:房地产行业的数学建模2010赛题汇总2010-A:确定肿瘤的重要基因信息2010-B:与封堵溃口有关的重物落水后运动过程的数学建模2010-C:神经元的形态分类和识别2010-D:特殊工件磨削加工的数学建模2009赛题汇总2009-A:我国就业人数或城镇登记失业率的数学建模2009-B:枪弹头痕迹自动比对方法的研究2009-C:多传感器数据融合与航迹预测2009-D:110警车配置及巡逻方案2008赛题汇总2008-A:汶川地震中唐家山堰塞湖泄洪问题2008-B:城市道路交通信号实时控制问题2008-C:货运列车的编组调度问题2008-D:中央空调系统节能设计问题2007赛题汇总2007-A:建立食品卫生安全保障体系数学模型及改进模型的若干理论问题2007-B:机械臂运动路径设计问题2007-C:探讨提高高速公路路面质量的改进方案2007-D:邮政运输网络中的邮路规划和邮车调度2006赛题汇总2006-A:Ad Hoc网络中的区域划分和资源分配问题2006-B:确定高精度参数问题2006-C:维修线性流量阀时的内筒设计问题2006-D:学生面试问题2005赛题汇总2005-A:Highway Traveling time Estimate and Optimal Routing 2005-B:空中加油2005-C:城市交通管理中的出租车规划2005-D:仓库容量有限条件下的随机存贮管理2004赛题汇总2004A:发现黄球并定位2004B:实用下料问题2004C:售后服务数据的运用2004D:研究生录取问题。
2010年全国高中学生化学竞赛试题及参考答案

中国化学会第24届全国高中学生化学竞赛(省级赛区)试卷气体常数R=8.31447 J K-1 mol-1 法拉第常数F=96485 C mol-1 阿佛加德罗常数N A=6.022142×1023 mol-1第1题 (15分)1-12009年10月合成了第117号元素,从此填满了周期表第七周期所有空格,是元素周期系发展的一个里程碑。
117号元素是用249Bk轰击48Ca靶合成的,总共得到6个117号元素的原子,其中1个原子经p次α衰变得到270Db后发生裂变;5个原子则经q次α衰变得到281Rg后发生裂变。
用元素周期表上的117号元素符号,写出得到117号元素的核反应方程式(在元素符号的左上角和左下角分别标出质量数和原子序数)。
1-2 写出下列结构的中心原子的杂化轨道类型:[(C6H5)IF5]-(C6H5)2Xe[I(C6H5)2]+1-3 一氯一溴二(氨基乙酸根)合钴(III)酸根离子有多种异构体,其中之一可用第2题 (5 分)最近我国有人报道,将0.1 mol L-1的硫化钠溶液装进一只掏空洗净的鸡蛋壳里,将蛋壳开口朝上,部分浸入盛有0.1 mol L-1的氯化铜溶液的烧杯中,在静置一周的过程中,蛋壳外表面逐渐出现金属铜,同时烧杯中的溶液渐渐褪色,并变得混浊。
2-1设此装置中发生的是铜离子和硫离子直接相遇的反应,已知φӨ(Cu2+/Cu)和φӨ(S/S2-)分别为0.345V和 -0.476 V,nFEӨ=RT ln K,EӨ表示反应的标准电动势,n为该反应得失电子数。
计算25o C下硫离子和铜离子反应得到铜的反应平衡第3题 (7 分) 早在19世纪人们就用金属硼化物和碳反应得到了碳化硼。
它是迄今已知的除金刚石和氮化硼外最硬的固体。
1930年确定了它的理想化学式。
左下图是2007年发表的一篇研究论文给出的碳化硼晶胞简图。
第4题 (8分)O—O键长112 pm 121 pm 128 pm 149 pm化学式2[Co2O2(NH3)10]4+,其O—O的键长为147 pm;B的化学式为Co(bzacen)PyO2,其O—O的键长为126 pm,Py是吡啶(C5H5N),bzacen是四齿配体[C6H5−C(O-)=CH−C(CH3)=NCH2−]2。
2010年全国高中数学联赛预赛试题汇编

函数值域与最值1、 (2010年江西省预赛试题)函数21)(2+-=x x x f 的值域是2、 (2010年安徽省预赛试题)函数242)(xx x x f --=的值域是3、 (2010年山西省预赛试题)若],0[π∈x ,函数xx xx y cos sin 1cos sin ++=的值域是 4、 (2010年辽宁省预赛试题)函数|cos |3|sin |2)(x x x f +=的值域是5、 (2010年全国联赛一试试题)函数xx x f 3245)(---=的值域是6、(2010年河北省预赛试题)已知关于x 的不等式kx x ≥-+2有实数解,则实数k 的取值范围是7、(2010年江西省预赛试题)设多项式)(x f 满足:对R x ∈∀,都有xxx f x f 42)1()1(2-=-++,则)(x f 的最小值是8、(2010年四川省预赛试题)已知函数424)42()(24224+++-++=xxx k k xx f 的最小值是0,则非零实数k 的值是9、(2010年全国联赛一试试题)已知函数xx a y sin )3cos(2-=的最小值为3-,则实数a 的取值范围是10、(2010年全国联赛一试试题)函数)1,0(23)(2≠>-+=a a aax f xx在区间]1,1[-∈x 上的最大值为8,则它在这个区间上的最小值是 11、(2010年福建省预赛试题)已知函数|2|)(a x x x f -=,试求)(x f 在区间]1,0[上的最大值)(a g12、(2010年辽宁省预赛试题)已知131≤≤a ,若12)(2+-=x axx f 在]3,1[上的最大值为)(a M ,最小值为)(a N ,令)()()(a N a M a g -=函数性质与导数的应用1、(2010年河北省预赛试题)函数)1(+=x f y 的反函数是)1(1+=-x fy,且4007)1(=f ,则=)1998(f2、(2010年山西省预赛试题) 函数2)(2-=axx f ,若2))2((-=f f ,则=a3、(2010年辽宁省预赛试题)不等式xx 256log )1(log >+的整数解的个数为4、(2010年吉林省预赛试题)已知1)1,1(=f ,),(),(**N n m N n m f ∈∈,且对任意*,Nn m ∈都有:①2),()1,(+=+n m f n m f ;②)1,(2)1,1(m f m f =+,则)2008,2010(f 的值为5、(2010年山东省预赛试题)若函数xe ex xf -=ln)(,则=∑=)2011(20101k ke f6、(2010年山东省预赛试题)函数432)(23+++=x xx x f 的图像的对称中心为7、(2010年山东省预赛试题)已知函数)0(4321)(2>--=a x axx f ,若在任何长度为2的闭区间上总存在两点21,x x ,使41|)()(|21≥-x f x f 成立,则a 的最小值为8、(2010年福建省预赛试题)函数)(cossin)(*22N k x x x f kk∈+=的最小值为9、(2010年河南省预赛试题)设11)(+-=x x x f ,记)()(1x f x f =,若))(()(1x f f x f n n =+,则=)(2010x f10、(2010年湖北省预赛试题)对于一切]21,2[-∈x ,不等式0123≥++-x xax恒成立,则实数a 的取值范围为11、(2010年甘肃省预赛试题)设0>a ,函数|2|)(a x x f +=和||)(a x x g -=的图像交于C点且它们分别与y 轴交于A 和B 点,若三角形ABC 的面积是1,则=a 12、(2010年甘肃省预赛试题)函数RR f →:对于一切Rz y x ∈,,满足不等式13、(2010年黑龙江省预赛试题)设)(x f 是连续的偶函数,且当0>x 时是严格单调函数,则满足)43()(++=x x f x f 的所有x 之和为14、(2010年贵州省预赛试题)已知函数2232)(aax xx f --=,且方程8|)(|=x f 有三个不同的实根,则实数=a 15、(2010年安徽省预赛试题)函数=y 的图像与xey =的图像关于直线1=+y x 对称16、(2010年浙江省预赛试题)设442)1()1()(x x x xk x f --+-=,如果对任何]1,0[∈x ,都有)(≥x f ,则k 的最小值为17、(2010年湖南省预赛试题)设函数xx x x f 2cos )24(sinsin 4)(2++⋅=π,若2|)(|<-m x f 成立的充分条件是326ππ≤≤x ,则实数m 的取值范围是18、(2010年新疆维吾尔自治区预赛试题)已知函数221)(xxx f +=,若)1011()1001(...)31()21(),101(...)2()1(f f f f n f f f m ++++=+++=,则=+n m19、(2010年河北省预赛试题)已知函数)1)(1ln(1221)(2≥+++-=m x x mxx f(1)若曲线)(:x f y C=在点)1,0(P 处的切线l 与C 有且只有一个公共点,求m 的值;(2)求证:函数)(x f 存在单调递减区间],[b a ,并求出单调递减区间的长度a b t -=的取值范围。
全国大学生数学建模竞赛赛题综合评析
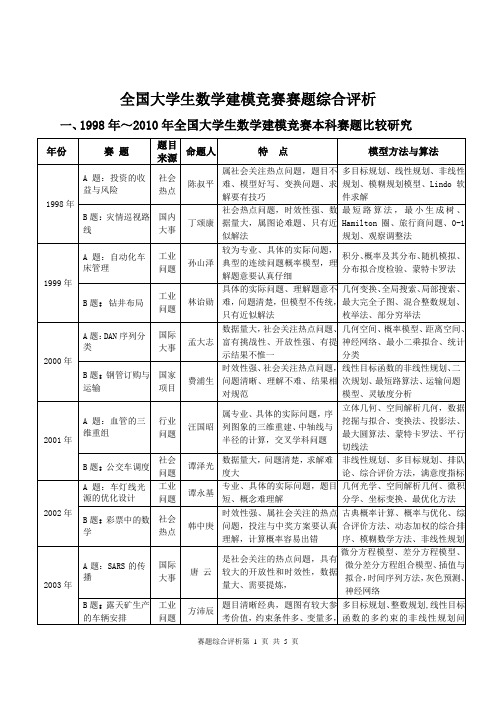
社会热点
叶其孝、周义仓
开放性强、社会关注性强,突出数据来源的可靠性、结论解释的合理性
数据收集与处理、问题的分析与假设,初等数学方法、一般统计方法、多目标规划、回归分析、综合评价方法、灰色预测
2009年
A题:制动器试验台的控制方法分析
工业问题
方沛辰、刘笑羽
问题具体、专业性强,要花时间读懂、理解清楚问题
出版社的资源配置
孟大志
艾滋病疗法的评价及疗效的预测
边馥萍
易拉罐形状和尺寸的最优设计(C题)
叶其孝
煤矿瓦斯和煤尘的监测与控制(D题)
韩中庚
2007年
中国人口增长预测
唐云
乘公交,看奥运
方沛辰、吴孟达
手机“套餐”优惠几何(C题)
韩中庚
体能测试时间安排(D题)
刘雨林
2008年
数码相机定位
谭永基
高等教育学费标准探讨
叶其孝、周义仓
地面搜索(C题)
肖华勇
NBA赛程的分析与评价(D题)
姜启源
2009年
制动器试验台的控制方法分析
方沛辰、刘笑羽
眼科病床的合理安排
吴孟达、毛紫阳
卫星和飞船的跟踪测控(C题)
周义仓
会议筹备(D题)
王宏健
2010年
储油罐的变位识别与罐容表标定
韩中庚
2010年上海世博会影响力的定量评估
杨力平
输油管的布置(C题)
1
6
8
付鹂
重庆大学
1
6
9
姜启源
清华大学
4
3
10
陈叔平
浙江大学、贵州大学
2
5
11
2010年全国高中数学联赛湖北省预赛试题及答案

2010年全国高中数学联赛湖北省预赛2010年全国高中数学联赛湖北省预赛由湖北省数学竞赛组织委员会主办并具体组织活动,委托华中师范大学数学竞赛与普及研究所命题。
试题以《高中数学竞赛大纲(2006年修订稿)》为依据,所涉及的知识范围不超出现行《全日制普通高级中学数学教学大纲》和《普通高中数学课程标准》中所规定的教学内容和要求,在数学思想方法的要求上有所提高,主要考查学生对基本知识和基本技能的掌握情况,以及综合、灵活运用知识的能力,适当考虑全国联赛对参赛学生的要求。
湖北省预赛按高一、高二年级分开命题,试题包括8道填空题和4道解答题,全卷满分120分,考试时间为120分钟。
湖北省预赛于2010年5月16日(星期日)上午8:00至10:00举行,约5万名学生参加,由各地市(州)安排考试并组织阅卷,从中选出约9000人参加全国高中数学联赛。
试 题一、填空题(每小题8分,共64分)1.数列}{n a 满足:3,121==a a ,且)(||*12N n a a a n n n ∈-=++.记}{n a 前n 项的和为n S ,则=100S .2.在△ABC 中,已知B ∠的平分线交AC 于K .若BC =2,CK =1,223=BK ,则△ABC 的面积为 .3.设100<n ,则使得nb a )(+的展开式中有连续三项的系数成等差数列的最大整数n 为 .4.在小于20的正整数中,每次不重复地取出3个数,使它们的和能被3整除,不同的取法种数为 .5.若z y x ,,均为正实数,且1222=++z y x ,则xyzz S 2)1(2+=的最小值为 .6.设椭圆1422=+y x 的左、右焦点分别为21,F F ,M 为椭圆上异于长轴端点的一点,122F MF θ∠=,△12MF F 的内心为I ,则=θcos ||MI .7.对于一切]21,2[-∈x ,不等式0123≥++-x x ax 恒成立,则实数a 的取值范围为 .8.将总和为200的10个数放置在给定的一个圆周上,且任意三个相邻的数之和不小于58.所有满足上述要求的10个数中最大数的最大值为 .二、解答题(本大题共3小题,共56分)9.(16分)已知二次函数c bx ax x f ++=2)(的图象经过点)0,2(-,且不等式221)(22+≤≤x x f x 对一切实数x 都成立. (1)求函数)(x f 的解析式;(2)若对一切]1,1[-∈x ,不等式)2()(xf t x f <+恒成立,求实数t 的取值范围. 10.(20分)设313116234++++=x x x x P ,求使P 为完全平方数的整数x 的值.11.(20分)已知直线x y =与椭圆C :1111622=+y x 交于B A ,两点,过椭圆C 的右焦点F 、倾斜角为α的直线l 交弦AB 于点P ,交椭圆C 于点N M ,.(1)用α表示四边形MANB 的面积;(2)求四边形MANB 的面积取到最大值时直线l 的方程.解 答1.89 提示:由已知可得k k a a =+9.89)(11192110099100=++++=+=a a a a a S S .2.16715 提示:由余弦定理可得b c b =-+22228 ① 又BC AB CK AK =,则 211cb =- ② 由①②,3,25==c b .又由81cos =C 可得873sin =C , 故△ABC 的面积16715sin 21==C ab S . 3.98 提示:设nb a )(+的展开式中有连续三项的系数分别为)11(,,11-≤≤+-n k C C C k n k n k n ,由题意得 112+-+=k nk n k n C C C .依组合数定义展开并整理得024)14(22=-++-k n k n .故)(2981422,1N n k k n ∈+±+=(1).22)12(98+=+m k ,222-+=m m k ,代入(1),得2)1(21-+=m n ,222-=m n .由1002)1(2<-+m ,98=n .4.327 提示:把这19个数按被3除所得的余数分类可以有三类:1A :3,6,9,12,15,18; 2A :1,4,8,11,14,17;3A :2,5,7,10,13,14,19.这样,满足题设条件的取法有且只有四种情形:(1)在1A 中任取3个数,有2036=C 种取法; (2)在2A 中任取3个数,有2036=C 种取法; (3)在3A 中任取3个数,有3537=C 种取法;(4)在321,,A A A 中各取一个数,有252766=⨯⨯种取法.因此,取法总数为:32725235220=++⨯(种). 5.223+ 提示:因 22212z y x xy -=+≤,所以 ]1)1)][(1(2[1)1(1)1()1(2)1(222-++-+=-+=-+≥+=z z z z z z z z z xyz z S ]12)1[(31+++-=z z 2232231+=-≥.当且仅当12,12-==-=y x z 时等号成立.所以 223min +=S .6.32- 提示:先证明下面的结论:已知△ABC 的内心为I ,则AB +AC -BC =2AI A cos2⋅. 证明:设△ABC 的内切圆与边AB 、AC 分别切于D 、E 两点,则AD =AE =12(AB +AC -BC ),又AD =2AI A cos2⋅,所以AB +AC -BC =2AI Acos 2⋅. 对于本题的△12MF F ,有12122cos MF MF F F MI θ+-=⋅.又2214x y +=中2,1,a b c ====,所以1224MF MF a +==,122FF c ==,从而32)324(21)(21cos ||2121-=-=-+=⋅F F MF MF MI θ. 7.110-≤≤-a 提示:记1)(23++-=x x ax x f ,已知条件即0)(≥x f 对一切⎥⎦⎤⎢⎣⎡-∈21,2x 恒成立.(1)当0=x 时,对一切实数a ,01)(>=x f .(2)当]21,0(∈x 时,01)(23≥++-=x x ax x f 可化为321x x x a --≥.设321)(xx x x g --=,则)3)(1(1)(4-+-='x x x x g .当]21,0(∈x 时,0)(>'x g ,所以函数)(x g 在区间]21,0(上单调递增,从而10)21()]([max -==g x g .因此10-≥a .(3)当]0,2(-∈x 时,01)(23≥++-=x x ax x f 可化为321xx x a --≤. 设321)(xx x x g --=,则)3)(1(1)(4-+-='x x x x g .当)0,1(-∈x 时0)(>'x g ;当1-=x 时0)(='x g ;当)1,2(--∈x 时.所以函数)(x g 在区间)1,2(--上单调递减,在区间)0,1(-上单调递增,从而1)1()]([min -=-=g x g .因此1-≤a .综合可知:110-≤≤-a .8.26 提示:设所有放置中的最大数为A ,则200583≤⨯+A ,所以.26≤A 事实上26,6,26,26,6,26,26,6,26,26满足.9.(1)由已知,对2≥n 有11)1()1(11---=--=+n a n n a n a n a n n n n , 两边同除以n 并整理,得)111()1(111nn a n na n n ---=--+, 于是,)111(111)1(1112121---=⎪⎭⎫ ⎝⎛---=⎥⎦⎤⎢⎣⎡--∑∑-=-=+n k k a k ka n k n k k k , 即2),111(1)1(12≥---=--n n a a n n ,所以123)111(1)1(12--=---=-n n n a a n n ,2,231≥-=n n a n .又1=n 时也成立,故*,231N n n a n ∈-=. (2)当2≥k ,有)131431(31)13)(43(1)23(122---=--<-=k k k k k a k ,所以2≥n 时,有⎥⎦⎤⎢⎣⎡---++-+-+<+=∑∑==)131431()8151()5121(31112212n n a a nk k n k k.6761113121311=+<⎪⎭⎫ ⎝⎛--+=n又1=n 时,.67121<=a .故对一切*N n ∈,有6712<∑=nk k a .10.)10(3)13(22--++=x x x P .所以,当10=x 时,2131=P 是完全平方数.下证没有其它整数x 满足要求.(1)当10>x 时,有22)13(++<x x P ,又03132)3(222>++=+-x x x x P ,所以22)3(x x P +>, 从而2222)13()3(++<<+x x P x x . 又Z x ∈,所以此时P 不是完全平方数.(2)当10<x 时,有22)13(++>x x P .令Z y y P ∈=,2, 则|13|||2++>x x y ,即|13|1||2++≥-x x y , 所以 222)13(1||2++≥+-x x y y , 即 01|13|2)10(32≥+++---x x x .解此不等式,得x 的整数值为6,5,4,3,0,1,2----±±,但它们对应的P 均不是完全平方数. 综上所述,使P 为完全平方数的整数x 的值为10.11.(1)直线MN 的倾斜角为α,记θ=∠MFO ,则πθα=+,θα22222222cos 2cos 2||c a ab c a ab MN -=-=. 而AB 与MN 所成的角为θπ+4,则四边形MANB 面积θθθθπ2222cos cos sin ||2)4sin(||||21c a ab OA MN AB S MANB -+⋅⋅=+⋅=.而5,11,16222===c b a ,A 点坐标为⎪⎪⎭⎫⎝⎛9334,9334,且9664||=OA , 从而,αααθθθ22cos 516cos sin 933352cos 516cos sin 933352--⋅=-+⋅=MANB S , 其中59334334arctan0+≤<α或πα<≤+59334334arctan.(2)记αααα2cos 516cos sin )(--=f ,而)(αf 只可能在⎪⎪⎭⎫⎢⎣⎡-∈πα,59334334arctan 时才可能取到最大值.对)(αf 求导数得到:222)cos 516()sin cos 10)(cos (sin )cos 516)(sin (cos )(ααααααααα----+='f . 令0)(='αf ,则有0)tan 10)(1(tan )11tan 16)(tan 1(2=--++αααα. 化简得到 011tan 21tan 6tan 1623=+++ααα. 所以 0)11tan tan 8)(1tan 2(2=+-+ααα.而 011tan tan 82=+-αα无实根,则21tan -=α. 经检验21tan -=α,符合⎪⎪⎭⎫⎢⎣⎡-∈πα,59334334arctan . 故所求直线l 的方程为:2521+-=x y .。
2010年全国初中数学竞赛(海南赛区)

第1页(共4页)2010年全国初中数学竞赛(海南赛区)初 赛 试 卷一、选择题(本大题满分50分,每小题5分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母1. 若x 为实数,则代数式|x|-x 的值一定是 A. 正数B. 非正数C. 非负数D. 负数2.已知(a+b)2=8,(a-b)2=12,则ab 的值为 A .1B .-1C .4D .-43.若bk <0,则直线y=kx+b 一定通过 A .第一、二象限 B .第二、三象限 C .第三、四象限D .第一、四象限4.甲、乙两人下棋,甲获胜的概率为30%,和棋的概率为50%,那么乙不输的概率为 A .20% B .50%C .70%D .80%5.已知20102011-20102009=2010x×2009×2011,那么x 的值是A .2008B .2009C .2010D .20116. 一项工程,甲建筑队单独承包需要a 天完成,乙建筑队单独承包需要b 天完成. 现两队联合承包,那么完成这项工程需要A. b a +1天B.(b a 11+)天 C. b a ab+天 D. ab 1天第2页(共4页)7.在平面上,如果点A 和点B 到点C 的距离分别为3和4,那么A 、B 两点的距离d 应该是 A. d=1B. d=5C. d=7D. 1≤d ≤78.如图1,在直角梯形ABCD 中, AB ∥CD ,∠ABC=90°,动点P 从点B 出发,沿B →C →D 的线路匀速运动至点D 停止.设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是 A .3B .4C .5D .69.如图3,C 是⊙O 外一点,CA 、CB 分别与⊙O 相切于点A 、B ,P 是上一点,若∠C=x °,则∠APB 的度数是A .x °B .(90-2x)°C .(90-x)°D .(180-x)°10.如图4,在等腰直角三角形ABC 中,∠C=90°,D 为BC 的中点,将△ABC 折叠,使 点A 与点D 重合,EF 为折痕,则sin ∠BED 的值是A .53B .43C .32D .75二、填空题(本大题满分40分,每小题5分)11.已知点P 在直角坐标系中的坐标为(0,1),O 为坐标原点,∠QPO=150°,且P 到Q 的距离为2,则Q 的坐标为 .12.点A ,B 是在数轴上不同的两个点,它们所对应的数分别是-4,5322-+x x ,且点A 、B 到原点的距离相等,则x 的值为 .13.50名学生中,会讲英语的有36人,会讲日语的有20人,既不会讲英语也不会讲日语的有8B AOC图3Px ° m BAC 图4FED图2 yxO 25图1 ABC DP第3页(共4页)人,则既会讲英语又会讲日语的人数为 人.14.已知3122=+x x ,且x <0,则x x 1+的值是 . 15.设c <b <0<a ,a+b+c=1,a cb M +=,b ca N +=,c b a P +=,则M,N,P 之间 的关系是 .16.如图5,已知矩形ABCD ,AB=2,BC=3,MB=MC ,则点D 到AM 的距离为 .17.如图6,在梯形ABCD 中,AD ∥BC ,AB=CD=AD=1,∠B:∠A=1:2,M 、N 分别是AD 、BC 的中点,P 是直线MN 上的一点,则PC+PD 的最小值为 .18.如图7,在平行四边形ABCD 中,P 为BC 上任一点,连结DP 并延长交AB 延长线于Q ,则BQ ABBP BC -= .三、解答题(本大题满分30分,每小题15分)19.如图8,△ABC 是边长为1的等边三角形,P 是AB 边上的一个动点(P 与B 不重合),以线段CP 为边作等边△CPD (D 、A 在BC 的同侧),连结AD . (1)判断四边形ABCD 的形状,并给予证明;(2)设BP=x ,△PAD 的面积为y ,求出y 关于x 的函数关系式,并求出△PAD 面积的最大值及取得最大值时x 的值.CBDA图8PCBDA图5M图6CBDA图7PQ第4页(共4页)20.某单位欲购买A 、B 两种电器.根据预算,共需资金15750元.购买一件A 种电器和两件B种电器共需资金2300元;购买两件A 种电器和一件B 种电器共需资金2050元. (1)购买一件A 种电器和一件B 种电器所需的资金分别是多少元? (2)若该单位购买A 种电器不超过5件,则可购买B 种电器至少有多少件?(3)为节省开支,该单位只购买A 、B 两种电器共6件,并知道获政府补贴资金不少于700元;自己出资金不超过4000元;其中政府对A 、B 两种电器补贴资金分别为每件100元和150元.请你通过计算求出有几种购买方案?2010年全国初中数学竞赛(海南赛区)初赛试卷参考答案一、选择题1. 若x ≥0,则|x|-x=x-x=0;若x <0,则|x|-x=-x-x=-2x >0,故选C.2.由题意有a 2+2ab+b 2=8,a 2-2ab+b 2=12,两式相减得4ab=-4,得ab=-1,故选B .3.由bk <0,知b >0,k <0或b <0,k >0,前者直线经过第一、二、四象限,后者直线经过第一、三、四象限,因而必经过第一、四象限,选D .4.由已知条件知乙胜的概率为20%,又和棋概率为50%,故乙不输的概率为70%,选C .5.由20102011-20102009=2010x×2009×2011,20102009(2010-1)(2010+1)= 2010x×2009×2011,则有20102009×2009×2011= 2010x×2009×2011,则有x=2009,选B .6. 两队联合承包每天完成工程的b a 11+,完成这项工程需要的时间为1÷(b a 11+)=b a ab + 天.选C.7.根据题意可知符合条件的点A 和点B 分别在以点C 为圆心的两个同心圆上. 故选D. 8.由图象可知,直角梯形的高BC=2,上底CD=3,所以33221=⨯⨯=∆BCD S ,选A .9.分别连结OA 、OB ,则OA ⊥CA ,OB ⊥CB ,即可求得,选B .10.由已知条件知∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,∴∠BED=∠CDF ,设CD=1,CF=x ,则CA=CB=2,所以DF=FA=2-x ,在Rt △CDF 中,有x 2+1=(2-x)2,解第5页(共4页)得x=43,所以sin ∠BED=sin ∠CDF=53=DF CF ,选A .二、填空题11.(1,1+3)或(-1,1+3);在直角坐标系中,以P(0,1)为顶点,作出∠QPO=150°可求得.12.由45322=-+x x 解得511=x . 13.英语、日语至少会一门的人数为50-8=42人,设既会英语又会日语的为x 人,则只会英语的为(36-x)人;只会日语的为(20-x)人,于是得(36-x)+x +(20-x)=42,解得x=14.14.由3122=+x x ,得5122=++x x ,所以5)1(2=+x x ,又x <0,所以51-=+x x .15.由a+b+c=1可得a a cb 11=++,则M=11-=+a a c b ,同理11-=+=b b c a N ,P=11-=+c c b a ,由c <b <0<a ,得b c a 111>>,111111->->-b c a,∴M >P >N . 16.过D 作DG ⊥AM ,则有2×3=2221⨯⋅+⋅BMAB DG AM ,DG=2.4;17.3;当P 在对角线AC 与MN 的交点处时PC+PD 最小.18.1;∵ BQ AQ BP AD BP BC ==,∴ 1==-=-=-BQ BQBQ AB AQ BQ AB BQ AQ BQ AB BP BC .三、解答题 19.(1)四边形ABCD 是梯形或菱形,证明如下:① 当点P 不与点A 重合时,∵ △ABC 与△CPD 都是等边三角形, ∴ ∠ACB=∠DCP=60°,∴ ∠1=∠2,又AC=BC ,DC=PC ,∴△ADC ≌△BPC ,∴∠DAC=∠B=∠BCA=60°,∴ AD ∥BC.又∠1=∠2<60°,∴ ∠DCB <120°,即 ∠B +∠DCB <180°,∴ DC 与AB 不平行, ∴ 四边形ABCD 是梯形.② 当点P 与点A 重合时,PC 与AC 重合,此时AB=BC=CA=AD=DC ,四边形ABCD 是菱形,综上所述,四边形ABCD 是梯形或菱形.C BD A P1 2M第6页(共4页)(2)由(1)知∠BAD=120°,AD=BP=x ,过P 作DA 延长线的垂线PM ,M 为垂足,则∠PAM=60°,∠APM=30°,又BP=x ,AB =1,∴ AP=1-x ,∴ AM=)1(21x -,PM=)1(23x -∴163)21(43)(43)1(23212122+--=--=-⋅=⋅=x x x x x PM AD y (0<x <1). 当21=x 时,y 取最大值为163,即当21=x 时△PAD 面积取得最大面积为163. 20.(1)设购买一件A 种电器和一件B 种电器所需的资金分别为a 元和b 元.依题意得: ⎩⎨⎧=+=+2050223002b a b a 解之得⎩⎨⎧==850600b a (答略) (2)设该单位购买A 、B 两种电器分别为m 件和n 件.则600m+850n=15750 ,153151217+-=n m .∵ A 种电器不超过5件,∴ 153151217+-n ≤5. ∴ n ≥15,即可购买B 种电器至少有15件. (3)设购买A 种电器x 件,则购买B 种电器为(6-x)件,依题意得:⎩⎨⎧≥-+≤-+700)6(1501004000)6(700500x x x x , 解之得1≤x ≤4 .∵ x 取整数,∴ x=1,2,3,4. 即共有4种购买方案.。
全国初中数学联赛试题及答案(2010年).doc

2010年全国初中数学联合竞赛试题第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( B )A .1.B .2.C .3.D .4.2.若实数,,a b c 满足等式3||6b =,9||6b c =,则c 可能取的最大值为 ( C )A .0.B .1.C .2.D .3.3.若b a ,是两个正数,且 ,0111=+-+-a b b a 则 ( C )A .103a b <+≤. B .113a b <+≤. C .413a b <+≤. D .423a b <+≤. 4.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为( A )A .-13.B .-9.C .6.D . 0.5.在△ABC 中,已知︒=∠60CAB ,D ,E 分别是边AB ,AC 上的点,且︒=∠60AED ,CEDB ED =+,CDE CDB ∠=∠2,则=∠DCB( B ) A .15°. B .20°. C .25°. D .30°.6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则123a a a a ++++( D ) A .28062. B .28065. C .28067. D .28068.二、填空题:(本题满分28分,每小题7分)1.已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += 13 .2.二次函数c bx x y ++=2的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知AC AB 3=,︒=∠30CAO ,则c = 19 .3.在等腰直角△ABC 中,AB =BC =5,P 是△ABC 内一点,且PA ,PC =5,则PB =.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放____15___个球.第二试 (A )一.(本题满分20分)设整数,,a b c (a b c ≥≥)为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数.解 由已知等式可得222()()()26a b b c a c -+-+-= ① 令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.于是,等式①变为222()26m n m n +++=,即 2213m n mn ++= ② 由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ (1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.(2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.二.(本题满分25分)已知等腰三角形△ABC 中,AB =AC ,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD//AC ,交⊙I 于点D.证明:PD 是⊙I 的切线.证明 过点P 作⊙I 的切线PQ (切点为Q )并延长,交BC 于点N.因为CP 为∠ACB 的平分线,所以∠ACP =∠BCP.又因为PA 、PQ 均为⊙I 的切线,所以∠APC =∠NPC.又CP 公共,所以△A CP ≌△NCP ,所以∠PAC =∠PNC.由NM =QN ,BA =BC ,所以△QNM ∽△BAC ,故∠NMQ =∠ACB ,所以MQ//AC.又因为MD//AC ,所以MD 和MQ 为同一条直线.又点Q 、D 均在⊙I 上,所以点Q 和点D 重合,故PD 是⊙I 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点P (1,)a ,Q (2,10)a .(1)如果,,a b c 都是整数,且8c b a <<,求,,a b c 的值.(2)设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为C.如果关于x 的方程20x bx c +-=的两个根都是整数,求△ABC 的面积.解 点P (1,)a 、Q (2,10)a 在二次函数2y x bx c =+-的图象上,故1b c a +-=,4210a c a +-=,解得93b a =-,82c a =-.(1)由8c b a <<知8293,938,a a a a -<-⎧⎨-<⎩解得13a <<.又a 为整数,所以2a =,9315b a =-=,8214c a =-=.(2) 设,m n 是方程的两个整数根,且m n ≤.由根与系数的关系可得39m n b a +=-=-,28mn c a =-=-,消去a ,得98()6m n m n -+=-,NC A两边同时乘以9,得8172()54mn m n -+=-,分解因式,得(98)(98)10m n --=. 所以981,9810,m n -=⎧⎨-=⎩或982,985,m n -=⎧⎨-=⎩或9810,981,m n -=-⎧⎨-=-⎩或985,982,m n -=-⎧⎨-=-⎩解得1,2,m n =⎧⎨=⎩或10,913,9m n ⎧=⎪⎪⎨⎪=⎪⎩或2,97,9m n ⎧=-⎪⎪⎨⎪=⎪⎩或1,932,3m n ⎧=⎪⎪⎨⎪=⎪⎩又,m n 是整数,所以后面三组解舍去,故1,2m n ==.因此,()3b m n =-+=-,2c mn =-=-,二次函数的解析式为232y x x =-+. 易求得点A 、B 的坐标为(1,0)和(2,0),点C 的坐标为(0,2),所以△ABC 的面积为1(21)212⨯-⨯=.第二试 (B )一.(本题满分20分)设整数,,a b c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).解 不妨设a b c ≥≥,由已知等式可得222()()()26a b b c a c -+-+-= ① 令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.于是,等式①变为222()26m n m n +++=,即 2213m n mn ++= ② 由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩(1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.(2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )一.(本题满分20分)题目和解答与(B )卷第一题相同.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数4)1(2-+++=p k px x y 的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.解 由题意知,方程04)1(2=-+++p k px x 的两根21,x x 中至少有一个为整数.由根与系数的关系可得4)1(,2121-+=-=+p k x x p x x ,从而有p k x x x x x x )1(4)(2)2)(2(212121-=+++=++ ①(1)若1k =,则方程为0)2(22=-++p px x ,它有两个整数根2-和2p -.(2)若1k >,则01>-k .因为12x x p +=-为整数,如果21,x x 中至少有一个为整数,则21,x x 都是整数.又因为p 为质数,由①式知2|1+x p 或2|2+x p .不妨设2|1+x p ,则可设12x mp +=(其中m 为非零整数),则由①式可得212k x m -+=, 故121(2)(2)k x x mp m -+++=+,即1214k x x mp m-++=+. 又12x x p +=-,所以14k p mp m--+=+,即 41)1(=-++mk p m ② 如果m 为正整数,则(1)(11)36m p +≥+⨯=,10k m ->,从而1(1)6k m p m-++>,与②式矛盾.如果m 为负整数,则(1)0m p +<,10k m -<,从而1(1)0k m p m -++<,与②式矛盾. 因此,1>k 时,方程04)1(2=-+++p k px x 不可能有整数根.综上所述,1=k .。
数学建模2010A题

承诺书
我们仔细阅读了中国大学生数学建模竞赛的竞赛规则. 我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮 件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问 题. 我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其 他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正 文引用处和参考文献中明确列出。 我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性.如有违反竞 赛规则的行为,我们将受到严肃处理。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生 纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变.按照有 关规定,需要定期对罐容表进行重新标定.图1是一种典型的储油罐尺寸及形状示 意图,其主体为圆柱体,两端为球冠体.图2是其罐体纵向倾斜变位的示意图,图 3是罐体横向偏转变位的截面示意图。
我们参赛选择的题号是(从A/B/C/D 中选择一项填写):
A
ﻩ我们的参赛报名号为(如果赛区设置报名号的话):
所属学校(请填写完整的全名):
南通大学
参赛队员 (打印并签名) :1.
2.
3。
指导教师或指导教师组负责人 (打印并签名):
7月 7日
日期: 2016 年
赛区评阅编号(由赛区组委会评阅前进行编号):
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。 (1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两 端平头的椭圆柱体),分别对罐体无变位和倾斜角为 =4.10的纵向变位两种情况 做了实验,实验数据如附件1所示.请建立数学模型研究罐体变位后对罐容表的影 响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。 (2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型, 即罐内储油量与油位高度及变位参数(纵向倾斜角度 和横向偏转角度 )之 间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据(附件2), 根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为 10cm的罐容表标定值。进一步利用附件2中的实际检测数据来分析检验你们模型 的正确性与方法的可靠性。
历年全国赛数学建模题目

目录1996年全国大学生数学建模竞赛题目 (2)A题最优捕鱼策略 (2)B题节水洗衣机 (2)1997年全国大学生数学建模竞赛题目 (3)A题零件的参数设计 (3)B题截断切割 (4)1998年全国大学生数学建模竞赛题目 (5)A题投资的收益和风险 (5)B题灾情巡视路线 (6)1999创维杯全国大学生数学建模竞赛题目 (7)A题自动化车床管理 (7)B题钻井布局 (8)C题煤矸石堆积 (9)D题钻井布局(同 B 题) (9)2000网易杯全国大学生数学建模竞赛题目 (10)A题 DNA分子排序 (10)B题钢管订购和运输 (12)C题飞越北极 (15)D题空洞探测 (15)2001年全国大学生数学建模竞赛题目 (17)A题血管的三维重建 (17)B题公交车调度 (18)C题基金使用计划 (20)D题公交车调度 (20)2002高教社杯全国大学生数学建模竞赛题目 (21)A题车灯线光源的优化设计 (21)B题彩票中的数学 (21)C题车灯线光源的计算 (23)D题赛程安排 (23)2003高教社杯全国大学生数学建模竞赛题目 (24)A题 SARS的传播 (24)B题露天矿生产的车辆安排 (28)C题 SARS的传播 (29)D题抢渡长江 (30)2004高教社杯全国大学生数学建模竞赛题目 (31)A题奥运会临时超市网点设计 (31)B题电力市场的输电阻塞管理 (35)C题饮酒驾车 (39)D题公务员招聘 (39)2005高教社杯全国大学生数学建模竞赛题目 (42)A题: 长江水质的评价和预测 (42)B题: DVD在线租赁 (43)C题雨量预报方法的评价 (44)D题: DVD在线租赁 (45)2006高教社杯全国大学生数学建模竞赛题目 (46)A题: 出版社的资源配置 (46)B题: 艾滋病疗法的评价及疗效的预测 (46)C题: 易拉罐形状和尺寸的最优设计 (47)D题: 煤矿瓦斯和煤尘的监测与控制 (48)2007高教社杯全国大学生数学建模竞赛题目 (53)A题:中国人口增长预测 (53)2008高教社杯全国大学生数学建模竞赛题目 (56)A题数码相机定位 (56)B题高等教育学费标准探讨 (57)C题地面搜索 (57)2009高教社杯全国大学生数学建模竞赛题目 (59)A题制动器试验台的控制方法分析 (59)B题眼科病床的合理安排 (60)C题卫星和飞船的跟踪测控 (61)D题会议筹备 (61)2010全国高教社杯数学建模题目 (65)A题储油罐的变位识别与罐容表标定 (65)B题 2010年上海世博会影响力的定量评估 (66)A题最优捕鱼策略为了保护人类赖以生存的自然环境,可再生资源(如渔业、林业资源)的开发必须适度.一种合理、简化的策略是,在实现可持续收获的前提下,追求最大产量或最佳效益.考虑对某种鱼(鳀鱼)的最优捕捞策略:假设这种鱼分四个年龄组,称1龄鱼,…,4龄鱼,各年龄组每条鱼的平均重量分别为 5.07,11.55,17.86,22.99(g),各年龄组鱼的自然死亡率为0.8(1/年),这种鱼为季节性集产卵繁殖,平均每条4龄鱼的产卵量为1.109× (个),3龄鱼的产卵量为这个数的一半,2龄鱼和1龄鱼不产卵,产卵和孵化期为每年的最后4个月,卵孵化并成活为1龄鱼,成活率(1龄鱼条数与产卵总量n之比)为1.22× /(1.22× +n).渔业管理部门规定,每年只允许在产卵孵化期前的8个月内进行捕捞作业.如果每年投入的捕捞能力(如渔船数﹑下网次数等)固定不变,这时单位时间捕捞量与各年龄组鱼群条数成正比,比例系数不妨称捕捞强度系数.通常使用13mm网眼的拉网,这种网只能捕3龄鱼和4龄鱼,其两个捕捞强度系数之比为0.42:1.渔业上称这种方式为固定努力量捕捞.1)建立数学模型分析如何实现可持续捕获(即每年开始捕捞时鱼场中各年龄组鱼群不变),并且在此前提下得到最高的年收获量(捕捞总重量).2)某渔业公司承包这种鱼的捕捞业务5年,合同要求5年后鱼群的生产能力不能受到太大破坏. 已知承包时各年龄组鱼群的数量分别为:122,29.7,10.1,3.29(×条),如果任用固定努力量的捕捞方式,该公司应采取怎样的策略才能使总收获量最高.(北京师范大学刘来福提供)B题节水洗衣机我国淡水资源有限,节约用水人人又责,洗衣在家庭用水中占有相当大的份额,目前洗衣机已相当普及,节约洗衣机用水十分重要.假设在放入衣服和洗涤剂后洗衣机的运行过程为:加水-漂水-脱水-加水-漂洗-脱水-…-加水-漂洗-脱水(称"加水-漂洗-脱水"为运行一轮).请为洗衣机设计一种程序(包括运行多少轮﹑每轮加水量等),使得在满足一定洗涤效果的条件下,总用水量最少.选用合理的数据进行计算,对照目前常用的洗衣机的运行情况,对你的模型和结果做出评价.A题零件的参数设计一件产品由若干零件组装而成,标志产品性能的某个参数取决于这些零件的参数。
奥数-2010年全国初中数学竞赛湖南省初赛试题(含答案)

2010年全国初中数学联赛湖南省初赛试题一、 填空题(7×4=28)1、下列计算正确的是 ( ) A 、10220aa a⨯= B 、1025aa a÷=C 、 0(3)0π-= D 、236(2)8a a =2、估算832⨯÷的运算结果应在 ( )A 、0到1之间B 、1到2之间C 、2到3之间D 、3到4之间3、如图,将三角尺的直角顶点放在直尺的一边上,已知∠1=30°,∠2=50°,则∠3的度数等于 ( )A 、50°B 、30°C 、25°D 、20°4、如图,已知⊙O 的半径为R ,D 是直径AB 延长线上的一点,DC 是⊙O 的切线,C 是切点,连结AC 。
若∠CAB=30°,则BD 的长为( ) A 、2R B 、3R C 、R D 、32R5、如图,AD 、BE 是锐角△ABC 的两条高,则△CDE 与△ABC 的面积比等于 ( ) A 、2sin C B 、2cos C C 、2tan C D 、21tan C6、把26个英文字母按规律分成5组,现在还有5个字母D 、M 、Q 、X 、Y 、Z ,请你按原规律补上,其顺序依次为**□ 2.HIO □ 3. NS □ 4.BCKE □ 5.V ATYWU □ A 、QXZMD B 、DMQZX C 、ZXMDQ D 、QXZDM 7、二次函数2yax bx c =++的图像如图所示,则一次函数24y bx b ac =+-与反比例函数a b cyx++=在同一坐标系的图像大致为()二、填空题(8×4=32)8、为了加快3G网络建设,电信运营企业将根据各自发展规划,今明两年预计完成3G投资2800亿元左右。
请将2800亿元用科学计数法表示为元。
9、数轴上的点A、B、C分别对应数0、-1、x,若C与A的距离大于C于B的距离,则x的取值范围是。
2010年全国初中数学联赛试题和答案

2010年全国初中数学联合竞赛试题参考答案第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( )A .1.B .2.C .3.D .4.2.若实数,,a b c 满足等式3||6b =,9||6b c =,则c 可能取的最大值为 ()A .0.B .1.C .2.D .3.3.若b a ,是两个正数,且,0111=+-+-ab b a 则 ( ) A .103a b <+≤. B .113a b <+≤. C .413a b <+≤. D .423a b <+≤. 4.若方程2310x x --=的两根也是方程420x ax bxc +++=的根,则2a b c +-的值为 ()A .-13.B .-9.C .6.D . 0.5.在△ABC 中,已知︒=∠60CAB ,D ,E 分别是边AB ,AC 上的点,且︒=∠60AED ,CE DB ED =+,CDE CDB ∠=∠2,则=∠DCB ( )A .15°.B .20°.C .25°.D .30°.6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则12320092010a a a a a +++++= ( )A .28062.B .28065.C .28067.D .28068.二、填空题:(本题满分28分,每小题7分)1.已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += .2.二次函数c bx x y ++=2的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知AC AB 3=,︒=∠30CAO ,则c = .3.在等腰直角△ABC 中,AB =BC =5,P 是△ABC 内一点,且PA PC =5,则PB =_____.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放_______个球.第二试 (A )一.(本题满分20分)设整数,,a b c (a b c ≥≥)为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数.二.(本题满分25分)已知等腰三角形△ABC 中,AB =AC ,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD//AC ,交⊙I 于点D.证明:PD 是⊙I 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点P (1,)a ,Q (2,10)a .(1)如果,,a b c 都是整数,且8c b a <<,求,,a b c 的值.(2)设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为 C.如果关于x 的方程20x bx c +-=的两个根都是整数,求△ABC 的面积..第二试 (B )一.(本题满分20分)设整数,,a b c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).第二试 (C )三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数4)1(2-+++=p k px x y 的图象与x轴的两个交点的横坐标至少有一个为整数,求k 的值.。
爽爽文档汇编之2020年全国大学生英语竞赛C类试题参考答案及作文评分标准

2010年全国大学生英语竞赛C类试题参考答案及作文评分标准2010 National English Contest for College Students (Level C - Preliminary)Part I Listening Comprehension (30 marks)Section A (5 marks)1. B2. C3. A4. C5. CSection B (10 marks)6. B7. C8. A9. A 10. B 11. A 12. C 13. B 14. C 15. ASection C (5 marks)16. C 17. C 18. A 19. B 20. BSection D (10 marks)21. train sets 22. the under-fives 23. month 24. packaging 25. five 26.storage 27. November 3rd 28. drivers 29. production lines 30. shiftPart II Vocabulary and Structure (15 marks)31. D 32. C 33. A 34. C 35. B 36. D 37. A 38. C 39. C 40. B 41. A 42. A 43. B 44.B 45. DPart III Cloze (10 marks)46.adaptation 47. in 48. ignored 49. from 50.deny 51. spinning 52. representing 53.However 54. that/which 55. talePart IV Reading Comprehension (40 marks)Section A (10 marks)56. F 57. F 58. T 59. Dwyfach Coggages 60. The beachSection B (10 marks)61. threatened 62. move 63. bamboo 64. habitats 65. includingSection C (10 marks)66. C 67. D 68. C 69. A 70. BSection D (10 marks)71. give an indication signal 72. breathing 73. lack of eye contace 74. their internal world 75. BPart V Translation (20 marks)Section A (10 marks)76. 奥巴马政府在新预算中承认了这个问题,该预算包括了一个五千万美元的预防性方案.。
2010年全国高中数学联赛二试试题及答案解析

1 n ⎛1 1⎞ k An − Ak = ⎜ − ⎟ ∑ ai + ∑ ai n i = k +1 ⎝ n k ⎠ i =1
=
1 n ⎛1 1⎞ k ai − ⎜ − ⎟ ∑ ai ∑ n i = k +1 ⎝ k n ⎠ i =1
⎧1 n ⎛1 1⎞ k ⎫ < max ⎨ ∑ ai , ⎜ − ⎟ ∑ ai ⎬ ⎝ k n ⎠ i =1 ⎭ ⎩ n i = k +1 ⎧1 ⎛1 1⎞ ⎫ ≤ max ⎨ (n − k ), ⎜ − ⎟ k ⎬ ⎝k n⎠ ⎭ ⎩n
(40 分)
即 K 为 BC 的中点,矛盾!从而 A, B, D, C 四点共圆.
注 1:“ PK = P 的幂(关于⊙O) + K 的幂(关于⊙O)”的证明:延长 PK 至点 F,使
2
得
PK ⋅ KF = AK ⋅ KE ,
则 P,E,F,A 四点共圆,故
④
∠PFE = ∠PAE = ∠BCE ,
(m)
⎡1⎤ ⎢ ⎥
(r ) 为整数.
⎛ ⎝
1⎞⎡ 1⎤ ⎛ 1⎞ ⎟ ⎢ k + ⎥ = ⎜ k + ⎟ ( k + 1) 为 2⎠⎢ 2⎥ ⎝ 2⎠
(10 分)
k = 2v + α v +1 ⋅ 2v +1 + α v + 2 ⋅ 2v + 2 + " ,
这里, α i = 0 或者 1, i = v + 1, v + 2, " . 于是
k n−k k n−k = ∑ Cn 2 + ∑ Cn 2 (−1) k = (2 + 1) n + (2 − 1) n k =0 k =0
2010年全国中学生英语能力竞赛初二年级组初赛试题(附答案)-全Word版[1]
![2010年全国中学生英语能力竞赛初二年级组初赛试题(附答案)-全Word版[1]](https://img.taocdn.com/s3/m/d593fb87a0116c175f0e4856.png)
2010年全国中学生英语能力竞赛(NEPCS)初赛初二年级组试题(总分:150分答题时间:120分钟)笔试部分(共九大题,共120分)Ⅰ.Multiple-choice(选择填空)(共15小题,每小题1分,共15分)Beneath each of the following sentences there are four choices marked A, B, C and D, Choose the answer that best completes the sentence. (从A,B, C, D四个选项中选出可以填入空白处的最佳选项)(答案涂在答题纸上)31. After school we usually play basketball for half an hour on playgroundA. the, aB. /; theC. /; anD. the; /32. Here are some flowers you our best wishes.A. to; forB. for; withC. of; toD. form; to33. ——Who taught Japanese?——Nobody, I just learned it byA. your; myselfB. you ; IC. yours ; meD. you; myself34. I stopped and on the bed to have a rest.A. to work; to lieB. to work; liedC. working; layD. working ; lying35. Cherry, Lily’s sister, at the aquarium yesterday and she also watched a movie dolphins.A. were; onB. are; fromC. was; aboutD. is; of36. Jane is very happy because she is off today. The underlined(划线的)word can be replaced(被代替)by ““A. at that timeB. at onceC. nowD. for a second37. Our Chinese teacher is in the office at the moment. The underlined wants can be replaced by“”.A. at that timeB. at onceC. nowD. for a second38. ——Can you speak English?——Yes, but only . I know I should try harder.A. a littleB. a fewC. littleD. few39.——Tony, is your brother as active as you?——No, he’s a quiet boy. He is than me.A. outgoingB. more activeC. less outgoingD. much active40. She began to play the violin she was six years old.A. whenB. becauseC. butD. as41. About of the workers in our company were born in the .A. two – thirds; 1980B. two-thirds; 1980C. two-third; 1980D. two third; 198042. ——Hello, what did you do last Sunday?——.——That sounds great.A. I went to the ExpoB. I will go shoppingC. I am making my reportD. I visit my grandparents43. ——Where’re Barry and Harry?—— I’m not sure. They in the library .A. will beB. maybeC. may beD. must be44. ——What’s the matter with you ?————Oh, I’m sorry to hear that.A. I have a headacheB. I had a good timeC. It fits me wellD. Don’t worry45. ——Could you send me an e-mail about the meeting next week?——Of curse,——It’******************..A. What’s your mobile phone number?B. Which city do you live in ?C. How is the meeting going ?D. Can I have your e-mail address?Ⅱ.Reading comprehension(阅读理解)(共15小题;选择题5小题,每小题1分;非选择题10小题,每小题2分,共25分)A)Read the following passage which is followed by five questions. For each of them there are four choices marked A, B, C, and D. Choose the one that fits best according to the passage.(阅读下面的短文,根据短文内容从每题所给的A,B,C,D四个选项中选出能回答所提问题或完成所给句子的最佳选项)(答案涂在答题纸上)It can be dangerous to travel on the ocean. Ships sometimes sink a ling way from land, When this happens, the people have to get into small lifeboats. If another ship does not come to help them quickly enough. or they do not have any food or water. they may die.Most people believe that we must not drink sea water. They believe that if we do. we will be very ill because of the salt in the water. But a doctor named Alain Bombard did not believe this. He thought that people could stay alive at sea by dinking sea water and eating small fish, animals and plants from the ocean, On October 19, 1953. he set out to prove he was right by crossing the Atlantic Ocean in a small boat. He did not take any food or water with him.Every day, Dr Bombard drank just a little sea water. He also caught fish . He took small plants from the ocean, which gave him more food.Dr Bombard became hot. and quite ill, but after sixty-five days at sea, he was still alive, He traveled 1,700 kilometers from one side of the Atlantic Ocean to the other.He had lost 20 kilograms in weight, but he proved that people can survive on sea water and the animals and plants in the ocean.46. Alain Bombard was .A. an old sailorB. a doctorC. a fishermanD. a cook47. He wanted to prove .A. sea water was dangerousB. fish were good for peopleC. sailors often diedD. people could drink sea water and not die48. During his journey. Alain Bombard lived on .A. sea waterB. food that he cookedC. sea water, fish and small plantsD. bread and rice49. When did he land on the other side of the Atlantic Ocean?A. In October, 1954B. In January. 1954C. In December. 1953D. In October. 195350. Which picture show Alain Bombard’s life on the sea?B)The fallowing two passages are followed by several questions. Respond to the questions according to the passage.(阅读下列两篇短文,然后按短文后的要求完成所给出的题目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2010高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
A 题 储油罐的变位识别与罐容表标定
通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)
为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数, 并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
(先检测误差补偿的可靠性,然后进行计算0-10,10-20…..)
附件1:小椭圆储油罐的实验数据
附件2:实际储油罐的检测数据
地平线 图1 储油罐正面示意图
油位探针
2
误差补偿公式:
油位探针
地平线 图2 储油罐纵向倾斜变位后示意图
(b) 小椭圆油罐截面示意图
水平线
1.2m
(a) 小椭圆油罐正面示意图
图4 小椭圆型油罐形状及尺寸示意图
图3 储油罐截面示意图
(b )横向偏转倾斜后正截面图
地平线
油位探针
(a )无偏转倾斜的正截面图。
