人教A版高中数学选修4-5课件基本不等式
合集下载
高中数学新人教A版选修4-5课件:第一讲不等式和绝对值不等式1.1.2基本不等式

1
年销售收入为 150% 32 3- t+1 + 3 + 2t.
首 页
探究一
探究二
J 基础知识 Z 重点难点
ICHU ZHISHI
探究三
由题意,生产 x 万件化妆品正好销完,
由年利润=年销售收入-年生产成本-促销费,
-t2 +98t+35
得年利润 y=
(t≥0).
2(t+1)
-t2 +98t+35
1 2x+y 2
1
(x,y∈R+)中,用的是不等式链中的
其变形去解题,如 xy= ×(2x)y≤
2
2
2
2
1 (2x+y)
1
a+b 2
(x,y∈R+)也可以,这两种解法比较,
.但是 xy= ×(2x)y≤ ×
ab≤
2
2
2
2
可以发现,求得的最值不一样,这说明选择不同的重要不等式的变形形式,求
得的值或范围是不同的,所以我们在选择重要不等式的变形形式时,要使
论有关的不等关系,得出有关理论参数的值.
(4)作出问题结论:根据③中得到的理论参数的值,结合题目要求得出问
题的结论.
J 基础知识 Z 重点难点
首 页
ICHU ZHISHI
HONGDIAN NANDIAN
1
1.下列各式中,最小值等于 2 的是(
x
A.
y
y
+
x
B.
1
C.tanθ+θ
2
3
S 随堂练习
1
的最大值,转化为求 (2x)y 的最大值,即
年销售收入为 150% 32 3- t+1 + 3 + 2t.
首 页
探究一
探究二
J 基础知识 Z 重点难点
ICHU ZHISHI
探究三
由题意,生产 x 万件化妆品正好销完,
由年利润=年销售收入-年生产成本-促销费,
-t2 +98t+35
得年利润 y=
(t≥0).
2(t+1)
-t2 +98t+35
1 2x+y 2
1
(x,y∈R+)中,用的是不等式链中的
其变形去解题,如 xy= ×(2x)y≤
2
2
2
2
1 (2x+y)
1
a+b 2
(x,y∈R+)也可以,这两种解法比较,
.但是 xy= ×(2x)y≤ ×
ab≤
2
2
2
2
可以发现,求得的最值不一样,这说明选择不同的重要不等式的变形形式,求
得的值或范围是不同的,所以我们在选择重要不等式的变形形式时,要使
论有关的不等关系,得出有关理论参数的值.
(4)作出问题结论:根据③中得到的理论参数的值,结合题目要求得出问
题的结论.
J 基础知识 Z 重点难点
首 页
ICHU ZHISHI
HONGDIAN NANDIAN
1
1.下列各式中,最小值等于 2 的是(
x
A.
y
y
+
x
B.
1
C.tanθ+θ
2
3
S 随堂练习
1
的最大值,转化为求 (2x)y 的最大值,即
5.5基本不等式1(1) 课件(人教A版选修4-5)

b2 (2)已知:a, b R , 且a 2 1, 求a 1 b 2 的最大值. 2 1 1 (3)设 为锐角,求(sin )(cos )的最小值. sin cos
作业
课本作业;P10
5、6
的最小值
x y
a b 1, x y
a b ay xb x 解: y ( x y) 1 ( x y)( ) a b x y x y
ay xb 2 ab2 ( a b) x y
ay xb 当且仅当 x y
即
x a 时 y b
变形.
已知
x, y 都是正数,求证:
1 如果积
xy
是定值 P, 那么当 x y 时,和 x y
有最小值 2 P 2 如果和 x y 是定值
S , 那么当 x y 时,积
xy
1 2 S 有最大值 4 证:∵ x, y R ∴ x y xy
x 1当 xy P (定值)时, y P 2
即(ab cd )(ac bd ) 4abcd
练习1
1. 巳知a 0, b 0, 1 1 求证 : ( a b)( ) 4. a b
2. 巳知a, b, c均为正数,求证: (a+b)(b+c)(c+a) 8abc
例2
Байду номын сангаас
求证:(1)在所有周长相同的矩形 中,正方形的面积最大;(2)在所有面 积相同的矩形中,正方形的周长最短。
ab
中的“ = ”号成立.
这句话的含义是:
当 ab 当
ab ab a b 2
ab ab 2
1.1.2.基本不等式 课件(人教A选修4-5)

a+b 如果 a,b 都是正数,我们就称 2 为 a,b 的算术平均,
ab 为 a,b 的几何平均.
4.利用基本不等式求最值 对两个正实数 x,y, (1)如果它们的和 S 是定值,则当且仅当 x=y 时,它们的 积 P 取得最 大 值; (2)如果它们的积 P 是定值,则当且仅当 x=y 时,它们的 和 S 取得最 小 值.
行证明.
(2)本题证明过程中多次用到基本不等式,然后利用同 向不等式的可加性或可乘性得出所证的不等式,要注意不 等式性质的使用条件,对“当且仅当……时取等号”这句话 要搞清楚.
[通一类] 1.设a,b,c∈R+,
求证: a2+b2+ b2+c2+ c2+a2≥ 2(a+b+c).
证明:∵a2+b2≥2ab, ∴2(a2+b2)≥(a+b)2. 又 a,b,c∈R+, ∴ a2+b2≥
每吨面粉的价格为1 800元,面粉的保管等其他费用为平
均每吨每天3元,购买面粉每次需支付运费900元. (1)求该厂多少天购买一次面粉,才能使平均每天所支付 的总费用最少? (2)某提供面粉的公司规定:当一次购买面粉不少于210 吨时,其价格可享受9折优惠,问该厂是否考虑利用此 优惠条件?请说明理由.
2
2 2 |a+b|= (a+b). 2 2
2
2 2 2 2 同理: b +c ≥ (b+c), c +a ≥ (a+c). 2 2
三式相加, 得 a2+b2+ b2+c2+ c2+a2≥ 2(a+b+c).
当且仅当 a=b=c 时取等号.
[研一题]
[例 2] 1 9 已知 x>0,y>0,且x+y=1,
[精讲详析]
本题考查基本不等式在证明不等式中的应
用,解答本题需要分析不等式的特点,先对a+b,b+c,c+ a分别使用基本不等式,再把它们相乘或相加即可.
5.3 证明不等式的基本方法 课件(人教A版选修4-5)
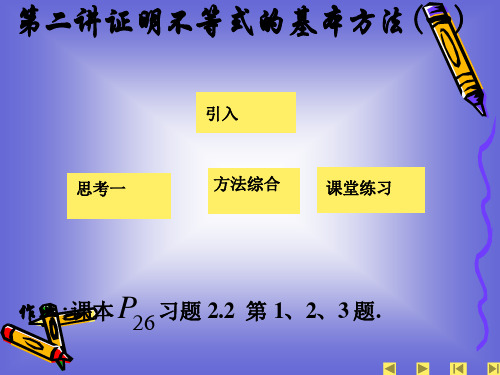
只要证 ( 1 x1 1 x2 )2 ≥ ( 1 x1 x2 1)2
即证: 2 x1 x2 2 1 x1 x2 x1x2 ≥ 2 x1 x2 2 1 x1 x2
只要证: x1 x2 ≥ 0
x1 x2 ≥ 0 成立,故原不等式也成立。
课堂练习:
1 1 x y 1.已知 a, b, x, y R 且 , x y ,求证: . a b xa yb 2.(课本第 23 页习题 2.1 第 4 题)已知 a, b, c 是正数,
求证: a 2a b2b c 2c ≥ a b c ba c c a b 3.(课本第 22 页例 2)已知 a , b, m 都是正数,并且 a b ,
∴a b a b
a b
b a
= (a b)(lg a lg b) ∵ a b 与 lg a lg b 同号,∴ (a b)(lg a lg b) >0
(a lg a b lg b) (b lg a a lg b) 0 a lg a b lg b b lg a a lg b,
思考一:已知 a , b 是正数,且 a b ,求证:a 3 b3 a 2b ab2
尝试 1:作差比较,作差——变形——定符号
根据 a-b>0 a>b,欲证 a>b 只需证 a-b>0.
证明: (a 3 b3 ) (a 2b ab2 ) = a 2 (a b) b2 (a b) ∵ = (a2 b2 )(a b) = (a b)(a b)2
课外练习: 1.若实数 x 1 ,求证: 3(1 x 2 x4 ) (1 x x 2 )2 . 2.非负实数 x1、x2,且 x1+x2≤1, 求证: 1 x1 1 x2 ≥ 1 x1 x2 1 3.已知 a , b 是不相等正数,且 a3 b3 a2 b2 ,
1.1.1.不等式的基本性质 课件(人教A选修4-5)

[通一类] x 1 2 2 1.x∈R,比较(x+1)(x + +1)与(x+ )· +x+1)的大小. (x 2 2 x x 2 2 解:因为(x+1)(x + +1)=(x+1)· +x+1- )=(x+ (x 2 2
x 1)(x +x+1)- (x+1), 2
2
1 2 1 2 (x+ )(x +x+1)=(x+1- )(x +x+1) 2 2 1 2 =(x+1)(x +x+1)- (x +x+1). 2
f1=a+b, ∴ f-1=a-b.
1 a=2[f1+f-1], ∴ b=1[f1-f-1]. 2 ∴f(-2)=4a-2b=3f(-1)+f(1). ∵1≤f(-1)≤2,3≤f(1)≤4. ∴6≤f(-2)≤10.
法二:设 f(x)=ax2+bx, 则 f(1)=a+b,f(-1)=a-b. 令 m(a+b)+n(a-b)=f(-2)=4a-2b,
[精讲详析] 本题考查对不等式的性质的理解, 解答本题 需要利用不等式的性质或利用特殊值逐项判断. (1)错误.因为当取 a=4,b=2,c=6 时,有 a>b,c> b 成立,但 a>c 不成立. a (2)错误.因为 a、b 符号不确定,所以无法确定b>1 是 a 否成立,从而无法确定 lgb>0 是否成立.
[例 3] 已知 60<x<84,28<y<33.求 (1)x-y 的取值范围; x (2)y 的取值范围. [精讲详析] 本题考查不等式性质的灵活应用. 解答问
题(1)需要先求出-y 的取值范围,然后利用不等式的同向 1 可加性解决; 解答问题(2)需要先求出y 的取值范围, 然后利 用不等式的有关性质求解.
2
1 1 2 ∴作差,得(x+1)(x + x+1)-(x+ )(x +x+1) 2 2
1.1.1 不等式的基本性质 课件(人教A选修4-5)

返回
1 1 4.已知a,b,x,y都是正数,且a>b,x>y, x y 求证: > . x+a y+b 证明:因为a,b,x,y都是正数,
1 1 x y 且a>b.x>y,所以a>b, a b 所以x<y. a b 故x+1<y+1, x+a y+b x y 即 x < y .所以 > . x+a y+b
返回
2.不等式的基本性质
由两数大小关系的基本事实,可以得到不等式的一些 基本性质: (1)如果a>b,那么b<a;如果b<a,那么a>b.即 a>
b⇔b<a . (2)如果a>b,b>c,那么 a>c .即a>b,b>c⇒ a>c .
(3)如果a>b,那么a+c> b+c . (4)如果a>b,c>0,那么ac > bc;如果a>b,c<0,那么 ac < bc.
n n
n
a>
n
b (n=2k+
返回
返回
[例 1]
1 1 4 已知 x,y 均为正数,设 m= + ,n= ,试比 x y x+y
较 m 和 n 的大小.
[思路点拨]
变形 转化为因式 与0比较 两式作差 ――→ ―――→ 乘积形式
判断正负,得出大小
返回
[解]
x+y 1 1 4 4 m-n= x + y - = xy - = x+y x+y
返回
(2)a>b,c>d⇒a+c>b+d,即两个同向不等式可以相 加,但不可以 相减 ;而a>b>0,c>d>0⇒ac>bd,即已知的两 个不等式同向且两边为 正值 时,可以相乘,但不可以 相除 . (3)性质(5)、(6)成立的条件是已知不等式两边均为 正值 , 并且n∈N,n≥2,否则结论不成立.而当n取正奇数时可放宽 条件,a>b⇒a >b (n=2k+1,k∈N),a>b⇒ 1,k∈N+).
5.3 证明不等式的基本方法 课件(人教A版选修4-5)

= (a b)(lg a lg b) ∵ a b 与 lg a lg b 同号,∴ (a b)(lg a lg b) >0
(a lg a b lg b) (b lg a a lg b) 0 a lg a b lg b b lg a a lg b,
2.非负实数 x1、x2,且 x1+x2≤1, 求证: 1 x1 1 x2 ≥ 1 x1 x2 1
证明: x1 ≥ 0, x2 ≥ 0, x1 x2 ≤1, 1 x1 ≥ 0,1 x2 ≥ 0,1 x1 x2 ≥ 0 要证 1 x1 1 x2 ≥ 1 x1 x2 1,
只要证 a 2 ab b2 ab ,只要证 a 2 2ab b2 0 . ∵ a b 0 ,∴ (a b)2 0 即 a 2 2ab b2 0 得证.
注:分析法的思维特点是:执果索因.对于思路不 明显,感到无从下手的问题宜用分析法探究证明途径. 另外,不等式的基本性质告诉我们可以对不等式做这 样或那样的变形,分析时贵在变形,不通思变,变则通! (如课本第 24 页例 3)
∵ a , b 是正数,且 a b ,∴ a b 0 , (a b)2 >0
∴ (a3 b3 ) (a2b ab2 ) >0,∴ a 3 b3 a 2b ab2
注:比较法是证明不等式的基本方法,也是 最重要的方法,另外, 有时还可作商比较(如课本 第 22 页例 3).
am a . 求证: bm b 4.(课本第 24 页例 2)已知 a1 , a2 ,, an R ,且 a1a2 an 1 ,
求证: (1 a1 )(1 a2 )(1 an ) ≥ 2n 5.(课本第 26 页习题 2.2 第 9 题)已知 a 1 , b 1 , 求证: 1 ab a b
5.3 证明不等式的基本方法 课件(人教A版选修4-5)

第二讲证明不等式的基本方法(一)
引入
思考一
方法综合
课堂练习
作业:课本 P 习题 2.2 第 1、2、3 题. 26
第二讲证明不等式的基本方法(一)
前面已经学习了一些证明不等式的方法,我们知 道,关于数的大小的基本事实、不等式的基本性质、 基本不等式以及绝对值不等式 x ≤ a 和 x ≥ a 的解 集的规律等,都可以作为证明不等式的依据.下面, 我们来进一步学习体会证明不等式的基本方法. 思考一: 已知 a , b 是正数,且 a b ,求证: a 3 b3 a 2b ab2
∴a b a b
a b
b a
课外练习: 1.若实数 x 1 ,求证: 3(1 x 2 x4 ) (1 x x 2 )2 . 2.非负实数 x1、x2,且 x1+x2≤1, 求证: 1 x1 1 x2 ≥ 1 x1 x2 1 3.已知 a , b 是不相等正数,且 a3 b3 a2 b2 ,
4 求证: 1 a b . 3
4. 比较 loga (1 x) 与 loga (1 x)
的大小( a 0且a 1,0 x 1).
作业:课本 P 习题 2.2 第 1、2、3 题. 26
1.若实数 x 1 ,求证: 3(1 x 2 x4 ) (1 x x 2 )2 . 证明:采用差值比较法: 2 4 2 2 3(1 x x ) (1 x x ) = 3 3 x2 3 x4 1 x2 x4 2 x 2 x2 2 x3 = 2( x 4 x 3 x 1) = 2( x 1)2 ( x 2 x 1) 1 2 3 2 = 2( x 1) [( x ) ]. 2 4 1 2 3 2 x 1, ( x 1) 0, 且( x ) 0, 2 4 12 3 2 ∴ 2( x 1) [( x ) ] 0, ∴ 3(1 x 2 x4 ) (1 x x 2 )2 . 2 4
引入
思考一
方法综合
课堂练习
作业:课本 P 习题 2.2 第 1、2、3 题. 26
第二讲证明不等式的基本方法(一)
前面已经学习了一些证明不等式的方法,我们知 道,关于数的大小的基本事实、不等式的基本性质、 基本不等式以及绝对值不等式 x ≤ a 和 x ≥ a 的解 集的规律等,都可以作为证明不等式的依据.下面, 我们来进一步学习体会证明不等式的基本方法. 思考一: 已知 a , b 是正数,且 a b ,求证: a 3 b3 a 2b ab2
∴a b a b
a b
b a
课外练习: 1.若实数 x 1 ,求证: 3(1 x 2 x4 ) (1 x x 2 )2 . 2.非负实数 x1、x2,且 x1+x2≤1, 求证: 1 x1 1 x2 ≥ 1 x1 x2 1 3.已知 a , b 是不相等正数,且 a3 b3 a2 b2 ,
4 求证: 1 a b . 3
4. 比较 loga (1 x) 与 loga (1 x)
的大小( a 0且a 1,0 x 1).
作业:课本 P 习题 2.2 第 1、2、3 题. 26
1.若实数 x 1 ,求证: 3(1 x 2 x4 ) (1 x x 2 )2 . 证明:采用差值比较法: 2 4 2 2 3(1 x x ) (1 x x ) = 3 3 x2 3 x4 1 x2 x4 2 x 2 x2 2 x3 = 2( x 4 x 3 x 1) = 2( x 1)2 ( x 2 x 1) 1 2 3 2 = 2( x 1) [( x ) ]. 2 4 1 2 3 2 x 1, ( x 1) 0, 且( x ) 0, 2 4 12 3 2 ∴ 2( x 1) [( x ) ] 0, ∴ 3(1 x 2 x4 ) (1 x x 2 )2 . 2 4
第一讲 不等式和绝对值不等式 知识归纳 课件(人教A选修4-5)

对于不等式恒成立求参数范围问题,常见类型及其解法
如下:
(1)分离参数法:
运用“f(x)≤a⇔f(x)max≤a,f(x)≥a⇔f(x)min≥a”可解决恒成立
中的参数范围问题.
(2)更换主元法:
不少含参不等式恒成立问题,若直接从主元入手非常 困难或不可能时,可转换思维角度,将主元与参数互换,
常可得到简捷的解法.
5 ②当- ≤x≤2 时, 2 3 原不等式变形为 2-x-2x-5>2x,解得 x<- . 5 5 3 ∴解集为{x|- ≤x<- }. 2 5 ③当 x>2 时,原不等式变形为 x-2-2x-5>2x, 7 解得 x<- ,∴原不等式无解. 3 3 综上可得,原不等式的解集为{x|x<- }. 5
2|≤1+2|y-2|+2≤5,即|x-2y+1|的最大值为5.
答案:5
3.(2011· 陕西高考)若不等式|x+1|+|x-2|≥a对任意x∈R 恒成立,则a的取值范围是________.
解析:令 f(x)=|x+1|+|x-2|= -2x+1x≤-1, 3-1<x<2, 2x-1x≥2, ∴f(x)≥3. ∵|x+1|+|x-2|≥a 对任意 x∈R 恒成立,∴a≤3.
[解析]
x+3z 由 x-2y+3z=0 得 y= , 2
2 2 y2 x +9z +6xz 6xz+6xz 则xz= ≥ =3, 4xz 4xz
当且仅当 x=3z 时取“=”.
[答案]
3ቤተ መጻሕፍቲ ባይዱ
1 1 1 [例 3] 设 a, c 为正实数, b, 求证:3+ 3+ 3+abc≥2 3. a b c 1 [证明]因为 a,b,c 为正实数,由平均不等式可得 3+ a
1.1.1.不等式的基本性质 课件(人教A选修4-5)

12 3 3 ∵x -x+1=(x- ) + ≥ >0, 2 4 4
2
∴当 x>1 时,(x-1)(x2-x+1)>0. 即 x3-1>2x2-2x; 当 x=1 时,(x-1)(x2-x+1)=0, 即 x3-1=2x2-2x; 当 x<1 时,(x-1)(x2-x+1)<0, 即 x3-1<2x2-2x.
[悟一法]
运用不等式的性质时要注意条件,如倒数法则要求两数 同号;两边同乘一个数,不等号方向是否改变要视此数的正 负而定;同向不等式可以相加,异向不等式可以相减.
[通一类]
1 2.(2011· 广州二模)设 a,b 为正实数,则“a<b”是“a-a 1 <b-b成立的” A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.即不充分又不必要条件 ( )
a 3 b 2 又∵ y= =-1,x= =-1, -3 -2 a b ∴y =x,因此⑤不正确. 由不等式的性质可推出②④恒成立. 即恒成立的不等式有②④.
c d 2.已知三个不等式:ab>0,bc-ad>0,a-b>0(其中 a,b, c,d 均为实数),用其中两个不等式作为条件,余下的一个 不等式作为结论组成一个命题,可组成的正确命题有几个?
(3)错误.此命题当 a、b、c、d 均为正数时才正确. (4)正确.因为 a>b,且 a、b 同号, 1 1 1 所以 ab>0,两边同乘以ab,得a<b. (5)错误.只有当 cd>0 时,结论才成立. (6)正确.因为 c>d,所以-d>-c,又 a>b, 所以 a-d>b-c.综上可知(4)(6)正确.
[例 3] 已知 60<x<84,28<y<33.求 (1)x-y 的取值范围; x (2)y 的取值范围. [精讲详析] 本题考查不等式性质的灵活应用. 解答问
高中数学新人教A版选修4-5课件:第一讲不等式和绝对值不等式1.1.1不等式的基本性质

探究四
探究一不等式的基本性质
对于考查不等式的基本性质的选择题,解答时,一是利用不等式的相关
性质,其中,特别要注意不等号变号的影响因素,如数乘、取倒数、开方、平
方等;二是对所含字母取特殊值,结合排除法去选正确的选项,这种方法一般
要注意选取的值应具有某个方面的代表性,如选取 0、正数、负数等.
J 基础知识 Z 重点难点
几乎都有类似的前提条件,但结论会根据不同的要求有所不同,因而这需要
根据本题的四个选项来进行判断.选项 A,还需有 ab>0 这个前提条件;选项
B,当 a,b 都为负数时不成立,或一正一负时可能也不成立,如 2>-3,但 22>(-3)2
1
a
b
不正确;选项 C,c2+1>0,由 a>b 就可知c2+1 > c2 +1,故正确;选项 D,当 c=0 时不
A.P≥Q
B.P>Q
C.P≤Q
1
−
a+1+ a
解析:P-Q=( a + 1 − a)-( a − a-1)=
a-1- a+1
=
D.P<Q
.
( a+1+ a)( a+ a-1)
∵a≥1,∴ a-1 < a + 1,即 a-1 − a + 1<0.
又∵ a + 1 + a>0, a + a-1>0,
a-1- a+1
格依据不等式的性质和运算法则进行运算,是解答此类问题的基础.在使用
不等式的性质中,如果是由两个变量的范围求其差的范围,一定不能直接作
5.1不等式的基本性质 课件(人教A版选修4-5)

(开方法则)
性质是求解和证明不等式的基础. 例1(1) 已知a > b, c < d , 求证:a-c > b-d (2) 已知a>b> 0,c>d>0, 求证:ac>bd
c c (3) 已知a>b> 0, c <0, 求证: a b
1 1 思考 已知 a>b, 试判断 与 的大小关系. a b 1 1 性质 a b, ab 0 ; a b 1 1 a b, ab 0 . a b
(1) a b b a (对称性) (2) a b, b c a c (传递性) (3) a b a c b c (加法法则) (i ) a b c a c b.
(ii ) a b, c d a c b d
B. 必要不充分条件
D. 既不充分也已知a > 0,a2-2ab+c2 =0,bc>a2,试 比较a、b、c的大小。
1. 设a, b是两个实数,它们在数轴上所对应 的点分别为A, B,那么, 当点A在点B的左 边时, a<b; 当点A在点B的右边时, a>b。 A a a< b B b
x
B b a>b
A a
x
2. 关于实数a, b的大小关系,有以下事实:
a b ab0 a b ab0 a b ab0
c 例2 已知a>b>c,且a+b+c =0, 则 的取值 a (-2,-0.5) 范围是___________。 思考 已知 f(x) =ax2 +c,且 - 4≤f(1)≤ -1, -1≤f(2)≤5,求f(3)的取值范围。 [-1, 20] 练习 1.对于实数a, b, c,给出下列命题: (1)若a>b,则ac2>bc2; (2)若ac2>bc2,则a>b; (3)若a>b,c<d,则a+c<b+d; (4)若a>b,c>d,则ac>bd; (5)若a<b<0,则 a2>ab>b2 (2) 、(5) 其中,正确命题的序号是________________.
性质是求解和证明不等式的基础. 例1(1) 已知a > b, c < d , 求证:a-c > b-d (2) 已知a>b> 0,c>d>0, 求证:ac>bd
c c (3) 已知a>b> 0, c <0, 求证: a b
1 1 思考 已知 a>b, 试判断 与 的大小关系. a b 1 1 性质 a b, ab 0 ; a b 1 1 a b, ab 0 . a b
(1) a b b a (对称性) (2) a b, b c a c (传递性) (3) a b a c b c (加法法则) (i ) a b c a c b.
(ii ) a b, c d a c b d
B. 必要不充分条件
D. 既不充分也已知a > 0,a2-2ab+c2 =0,bc>a2,试 比较a、b、c的大小。
1. 设a, b是两个实数,它们在数轴上所对应 的点分别为A, B,那么, 当点A在点B的左 边时, a<b; 当点A在点B的右边时, a>b。 A a a< b B b
x
B b a>b
A a
x
2. 关于实数a, b的大小关系,有以下事实:
a b ab0 a b ab0 a b ab0
c 例2 已知a>b>c,且a+b+c =0, 则 的取值 a (-2,-0.5) 范围是___________。 思考 已知 f(x) =ax2 +c,且 - 4≤f(1)≤ -1, -1≤f(2)≤5,求f(3)的取值范围。 [-1, 20] 练习 1.对于实数a, b, c,给出下列命题: (1)若a>b,则ac2>bc2; (2)若ac2>bc2,则a>b; (3)若a>b,c<d,则a+c<b+d; (4)若a>b,c>d,则ac>bd; (5)若a<b<0,则 a2>ab>b2 (2) 、(5) 其中,正确命题的序号是________________.
人教A版高中数学选修4-5第一讲二绝对值不等式上课课件

证明
3x 2 y 3a 3b 3 x a 2 y b
2 xa 3 yb
3 2 5
所以:3x 2 y 3a 2b 5 .
例2
两个施工队分别被安排在公路沿线的两 个地点施工,这两个地点分别位于公路路碑 的第10km和第20km处。现要在公路沿线建两 个施工队的共同临时生活区,每个施工队每 天在生活区和施工区地点之间往返一次。要 使两个施工队每天往返的路程之和最小,生 活区应该建在何处?
分析
本题是绝对值不等式的应用,第一把 实际问题划归为数学问题,即归结为求解 形如y x a x b 的函数的极值问题, 这类问题借助于绝对值三角不等式解答。
解:设生活区建于公路路碑的第xkm处,两个施 工队每天往返的路程之和为S(x)km,
则S x 2 x 10 x 20 .
因 :x 10 x 20 x 10 20 x 10, 且 x 1020 x 0 取等 。
因此:a b a b .
其几何意义是三角形的两边之和大于 第三边(如下图)。
x
a+b b
由此可称 定理1为绝 对值三角
不等式
a
y
0
(2)当向量a,b共线时,分以下两种情况: 如果向量a,b方向相同时,a b a b ; 如果向量a,b方向相反时,a b a b .
一般地,我们有 a b a b .
.. . . x . . .. x
0 a b a+b
a+b b a 0
图1
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两 中情况.
如果a>0,b>0时,如图2-1,a b a b .
.. b a+b
3x 2 y 3a 3b 3 x a 2 y b
2 xa 3 yb
3 2 5
所以:3x 2 y 3a 2b 5 .
例2
两个施工队分别被安排在公路沿线的两 个地点施工,这两个地点分别位于公路路碑 的第10km和第20km处。现要在公路沿线建两 个施工队的共同临时生活区,每个施工队每 天在生活区和施工区地点之间往返一次。要 使两个施工队每天往返的路程之和最小,生 活区应该建在何处?
分析
本题是绝对值不等式的应用,第一把 实际问题划归为数学问题,即归结为求解 形如y x a x b 的函数的极值问题, 这类问题借助于绝对值三角不等式解答。
解:设生活区建于公路路碑的第xkm处,两个施 工队每天往返的路程之和为S(x)km,
则S x 2 x 10 x 20 .
因 :x 10 x 20 x 10 20 x 10, 且 x 1020 x 0 取等 。
因此:a b a b .
其几何意义是三角形的两边之和大于 第三边(如下图)。
x
a+b b
由此可称 定理1为绝 对值三角
不等式
a
y
0
(2)当向量a,b共线时,分以下两种情况: 如果向量a,b方向相同时,a b a b ; 如果向量a,b方向相反时,a b a b .
一般地,我们有 a b a b .
.. . . x . . .. x
0 a b a+b
a+b b a 0
图1
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两 中情况.
如果a>0,b>0时,如图2-1,a b a b .
.. b a+b
1.1.2 基本不等式 课件(人教A选修4-5)

3 (2)设 0<x< ,求函数 y=4x(3-2x)的最大值; 2 1 9 (3)已知 x>0,y>0,且 + =1,求 x+y 的最小值. x y
[思路点拨]
根据题设条件,合理变形,创造能用基
本不等式的条件,求最值.
2x 2 [解] (1)∵x>0,∴f(x)= 2 = . 1 x +1 x+x 1 1 1 ∵x+x≥2,∴0< ≤ . 1 2 x+x ∴0<f(x)≤1,当且仅当x=1时取“=”.即f(x)值域 为(0,1] 3 (2)∵0<x< ,∴3-2x>0. 2 2x+3-2x 2 9 ∴y=4x(3-2x)=2[2x(3-2x)]≤2[ ]= . 2 2 3 当且仅当2x=3-2x,即x= 时,等号成立. 4 9 ∴y=4x(3-2x)的最大值为 . 2
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并 求出最小总费用.
解:(1)如题图所示,设矩形的另一边长为a m. 则y=45x+1 由已知xa=360,得a= x 3602 所以y=225x+ x -360(x>0). (2)∵x>0, 3602 ∴225x+ x ≥2 225×3602=10 800. 3602 ∴y=225x+ x -360≥10 440, 3602 当且仅当225 x= 时,等号成立. x 即当x=24 m时,修建围墙的总费用最小,最小总费 用是10 440元.
a2 b2 c2 ∴( b +b)+( c +c)+( a +a) ≥2(a+b+c). a2 b2 c2 即 b + c + a ≥a+b+c. a2 b2 c2 当且仅当 b =b, c =c, a =a, 即a=b=c时取等号.
5.1.2不等式的基本性质(2) 课件 (人教A版选修4-5)
(1)1-x (2)x(1-x) 解题回顾:同向不等式可以做加法运算,异向不等式可以 做减法运算。当同向不等式两边都为正时,可以做乘法运 算。本题常见的错误是将取值范围扩大。 变式:设f(x)=ax2+bx,且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的 取值范围.
1 1 1 a 0, A 1 a 2 , B 1 a 2 , C ,D , 1 a 1 a 例5、已知 2 则A、、B、C、 的大小关系是 ( )
A、A<B<C<D; C、D<B<A<C;
B、D<A<B<C; D、B<D<A<C
【解题回顾】本题采用了赋值法,使问题得以简化、明
朗.赋值法是解选择题、开放题等常用的方
法.它将复杂的问题简单化,是我们常用的 数学方法.
作业
• P10 1 、 3 、 4 Nhomakorabea例1已知a b 0,c d 0,求证 a d b . c
e e 例2、已知a>b>0,C<d<0,e<0,求证: a c bd
【解题回顾】在证明不等式时要依据不等式的性质进行,不能
自己“制造”性质来进行.
例3:在三角形ABC中,求A-B的取值范围.
1 2 例4、已知 x ,求下列式子的取值范围。 3 3
不等式的基本性质
(第二课时)
【知识回顾】
1、不等式的概念: 同向不等式; 异向不等式; 同解不等式.
2、比较两个实数大小的主要方法:
(1)作差比较法:作差——变形——定号——下结论; (2)作商比较法:作商——变形——与1比较大小——下
结论. 大多用于比较幂指式的大小.
1 1 1 a 0, A 1 a 2 , B 1 a 2 , C ,D , 1 a 1 a 例5、已知 2 则A、、B、C、 的大小关系是 ( )
A、A<B<C<D; C、D<B<A<C;
B、D<A<B<C; D、B<D<A<C
【解题回顾】本题采用了赋值法,使问题得以简化、明
朗.赋值法是解选择题、开放题等常用的方
法.它将复杂的问题简单化,是我们常用的 数学方法.
作业
• P10 1 、 3 、 4 Nhomakorabea例1已知a b 0,c d 0,求证 a d b . c
e e 例2、已知a>b>0,C<d<0,e<0,求证: a c bd
【解题回顾】在证明不等式时要依据不等式的性质进行,不能
自己“制造”性质来进行.
例3:在三角形ABC中,求A-B的取值范围.
1 2 例4、已知 x ,求下列式子的取值范围。 3 3
不等式的基本性质
(第二课时)
【知识回顾】
1、不等式的概念: 同向不等式; 异向不等式; 同解不等式.
2、比较两个实数大小的主要方法:
(1)作差比较法:作差——变形——定号——下结论; (2)作商比较法:作商——变形——与1比较大小——下
结论. 大多用于比较幂指式的大小.
3.1不等式的基本性质(1)(人教A版选修4-5)

用数学式子表示为:
a b a b 0; a b a b 0; a b a b 0.
a b a b 0; a b a b 0; a b a b 0.
上式中的左边部分反映的是实数的大小顺 序,而右边部分则是实数的运算性质,合起来 就成为实数的大小顺序与运算性质之间的关系。 这一性质不仅可以用来比较两个实数的大小, 而且是推导不等式的性质、不等式的证明、解 不等式的主要依据。
2.
0
基本理论
X
• 1.实数在数轴上的性质:
• 研究不等式的出发点是实数的大小关系。数 轴上的点与实数1-1对应,因此可以利用数 轴上点的左右位置关系来规定实数的大小:
A a a<b
B b x
B b a>b
A a x
设a,b是两个实数,它们在数轴上所对应的点分别是 A,B,那么,当点A在点B的左边时,a<b;当点A在点B的右 边时,a>b. 关于a,b的大小关系,有以下基本事实:如果a>b,那么 a-b是正数;如果a=b,那么a-b等于零;如果a<b,那么a-b 是负数;反过来也对.
思考?
从上述事实出发,你认为可以用什么方法
比较两个实数的大小?
要比较两个实数a与b的大小,可以转化为比
较它们的差a - b 与0的大小。在这里,0为实数
比较大小提供了“标杆”。
例1、试比较 2x4+1 与 2x3+x2 的大小 2 4 3 4
• 解: (2x +1) - (2x +x ) = 2x +1 - 2x3 _ x2 • = (2x4 - 2x3 )- (x2 -1) • = 2x3 (x -1) - (x -1) (x +1) • = (x-1) [2x3 - (x +1) ] • = (x-1)[(2x3-2x2) + (2x2-2x) + (x-1)] • = (x -1)2 (2x2 + 2x + 1) • = (x -1)2 [2 (x + 1/2)2 + 1/2] • 技能: • 分组组合;添项、拆项;配方法。
1.1.1.不等式的基本性质 课件(人教A选修4-5)

2
[例 2]
[研一题] 下列命题中正确的是
(
)
(1)若 a>b,c>b,则 a>c; a (2)若 a>b,则 lgb>0; (3)若 a>b,c>d,则 ac>bd; 1 1 (4)若 a>b>0,则a<b; a b (5)若 c>d,则 ad>bc;
(6)若a>b,c>d,则a-d>b-c. A.(1)(2) C.(3)(6) B.(4)(6) D.(3)(4)(5)
2
1 1 2 ∴作差,得(x+1)(x + x+1)-(x+ )(x +x+1) 2 2
2
x 1 2 2 =(x+1)(x +x+1)- (x+1)-(x+1)(x +x+1)+ (x +x+1) 2 2
2
1 2 1 2 1 = (x +x+1)- (x +x)= >0, 2 2 2 x 1 2 ∴(x+1)(x + +1)>(x+ )(x +x+1). 2 2
[通一类] x 1 2 2 1.x∈R,比较(x+1)(x + +1)与(x+ )· +x+1)的大小. (x 2 2 x x 2 2 解:因为(x+1)(x + +1)=(x+1)· +x+1- )=(x+ (x 2 2
x 1)(x +x+1)- (x+1), 2
2
1 2 1 2 (x+ )(x +x+1)=(x+1- )(x +x+1) 2 2 1 2 =(x+1)(x +x+1)- (x +x+1). 2
[例 3] 已知 60<x<84,28<y<33.求 (1)x-y 的取值范围; x (2)y 的取值范围. [精讲详析] 本题考查不等式性质的灵活应用. 解答问
题(1)需要先求出-y 的取值范围,然后利用不等式的同向 1 可加性解决; 解答问题(2)需要先求出y 的取值范围, 然后利 用不等式的有关性质求解.
[例 2]
[研一题] 下列命题中正确的是
(
)
(1)若 a>b,c>b,则 a>c; a (2)若 a>b,则 lgb>0; (3)若 a>b,c>d,则 ac>bd; 1 1 (4)若 a>b>0,则a<b; a b (5)若 c>d,则 ad>bc;
(6)若a>b,c>d,则a-d>b-c. A.(1)(2) C.(3)(6) B.(4)(6) D.(3)(4)(5)
2
1 1 2 ∴作差,得(x+1)(x + x+1)-(x+ )(x +x+1) 2 2
2
x 1 2 2 =(x+1)(x +x+1)- (x+1)-(x+1)(x +x+1)+ (x +x+1) 2 2
2
1 2 1 2 1 = (x +x+1)- (x +x)= >0, 2 2 2 x 1 2 ∴(x+1)(x + +1)>(x+ )(x +x+1). 2 2
[通一类] x 1 2 2 1.x∈R,比较(x+1)(x + +1)与(x+ )· +x+1)的大小. (x 2 2 x x 2 2 解:因为(x+1)(x + +1)=(x+1)· +x+1- )=(x+ (x 2 2
x 1)(x +x+1)- (x+1), 2
2
1 2 1 2 (x+ )(x +x+1)=(x+1- )(x +x+1) 2 2 1 2 =(x+1)(x +x+1)- (x +x+1). 2
[例 3] 已知 60<x<84,28<y<33.求 (1)x-y 的取值范围; x (2)y 的取值范围. [精讲详析] 本题考查不等式性质的灵活应用. 解答问
题(1)需要先求出-y 的取值范围,然后利用不等式的同向 1 可加性解决; 解答问题(2)需要先求出y 的取值范围, 然后利 用不等式的有关性质求解.
