切线长定理(用)(PPT34页)
合集下载
《切线长定理》PPT课件

E O CD
P
OA⊥PA,OB ⊥PB,AB ⊥OP
B
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC (3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP (4)写出图中所有的等腰三角形 △ABP △AOB
(5)若PA=4、PD=2,求半径OA
外切圆的半径:交点到三
内切圆的半径:交点到三
角形任意一个定点的距离。 h 角形任意一边的垂直距离。15
分析题目已知:如
图, △ABC的内切圆
⊙O与BC 、CA、
AB 分别相交于点
A
D 、 E 、 F ,且
E
AB=9厘米,BC
FO
=14厘米,CA =13
厘米,求AF、BD、 B D CE的长。
h
C
16
A
几何语言: PA、PB分别切⊙O于A、B
PA = PB ∠OPA=∠OPB
反思:切线长定理为证明线段相等、角相 等提 供了新的方法
h
6
我们学过的切线,常有 六五个 性质:
1、切线和圆只有一个公共点; 2、切线和圆心的距离等于圆的半径; 3、切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点; 5、经过切点垂直于切线的直线必过圆心。 6、从圆外一点引圆的两条切线,它们的切线长相等, 圆心和这一点的连线平分两条切线的夹角。
解:设Rt△ABC的内切圆与三边相切于D、E、F,
连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
A
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
F
设AD= x , BE= y ,CE= r
切线长定理(共33张PPT)

试用文字语言叙述你所发现的结论
切线长定理
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等。
几何语言:
反思:切线长定理为证明线段相等、角相等提供新的方法
O
P
A
B
试一试
A
P
O
B
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
a+b-c
2
ab
a+b+c
· O
A
B
C
D
E
F
O
A
B
C
D
E
思考:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
例题讲解
例1、已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。 求证:AC∥OP
P
A
C
B
D
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有相等的线段
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长。
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
切线长定理
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等。
几何语言:
反思:切线长定理为证明线段相等、角相等提供新的方法
O
P
A
B
试一试
A
P
O
B
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
a+b-c
2
ab
a+b+c
· O
A
B
C
D
E
F
O
A
B
C
D
E
思考:如图,AB是⊙O的直径, AD、DC、BC是切线,点A、E、B 为切点,若BC=9,AD=4,求OE的长.
例题讲解
例1、已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。 求证:AC∥OP
P
A
C
B
D
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有相等的线段
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长。
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
切线长定理课件

切线长定理的再一个推论
总结词
切线长定理的再一个推论是,若两圆在 同一直线上相切,则它们的切线互相平 行。
VS
详细描述
这个推论是切线长定理的进一步应用。当 两圆在同一直线上相切时,它们的切线不 仅长度相等,而且平行。这个推论在解决 涉及直线和圆的问题时非常有用,特别是 在几何证明和解析几何中。通过掌握这个 推论,学生可以更好地理解几何图形的性 质和关系,提高解决几何问题的能力。
切线长定理的另一个推论
总结词
切线长定理的另一个推论是,若两圆相切于同一点,则该点的切线与两圆心的连线垂直 。
详细描述
这个推论说明了当两圆在同一点相切时,该点的切线与两圆心的连线之间此,该点的切
线与两圆心的连线互相垂直。这个推论在证明几何定理和解决几何问题时非常有用。
切线长定理在数学、物理、工程等领 域有着广泛的应用,通过学习和掌握 这个定理,我们可以更好地理解和应 用相关领域的知识。
通过本次课件的学习,我们深入了解 了切线长定理的证明过程和实际应用 ,掌握了利用切线长定理解决实际问 题的技巧和方法。
展望
随着数学和其他学科的发展,切线长定理的应用范围将会更加广泛,我 们可以通过不断学习和探索,深入了解这个定理的更多应用和推广。
切线长定理的证明方法二
利用三角形的全等定理进行证明。首先,作辅助线连接圆心和切点,将切线分为两段。然后,根据三角形的全等定理,证明三 角形全等,从而得到切线长的平方等于半径的平方和。
切线长定理的证明方法三
利用向量进行证明。首先,根据向量的数量积公式,向量的数 量积等于两向量的模长乘以其夹角的余弦值。然后,利用切线 的性质,切线和半径垂直,从而夹角为90度。结合数量积公式 ,可以证明切线长的平方等于半径的平方和。
人教版数学九年级上册24.2.3切线长定理课件(共26张PPT)

三角形外心、内心的区别:
名称
外心
内心
图形
性质
三角形的外心到三角形三个 三角形的内心到三角形
顶点的距离相等
三条边的距离相等
位置 外心不一定在三角形内部 内心一定OC=90°+
1 2
∠A
例2 如图, △ABC的内切圆⊙O与BC,CA, AB
分别相交于点D , E , F ,且AB=9,BC =14,
CA =13,求AF,BD,CE的长.
解:设AF=x,则AE=x,
A
CD=CE=AC-AE=13-x,
E
BD=BF=AB-AF=9-x.
F
由BD+CD=BC,可得
(13-x)+(9-x)=14.解得,x=4. B
D
C
因此,AF=4,BD=5,CE=9.
随堂练习 1.如图,△ABC的内切圆⊙O与BC,CA,AB分 别相切于点D,E,F,且AB=11cm,BC=14cm, CA=13cm,则AF的长为( C ) A.3cm B.4cm C.5cm D.9cm
解:∵ 点O是△ABC的内心,
∴∠OBC= 1 ∠ABC= 1 ×50°=25°,
2
2
∴∠OCB= 1 ∠ACB = 1×75°=37.5° ,
2
2
∴∠BOC=180°-25°-37.5°=117.5° B
A O
C
【选自教材P100 练习 第2题】
5. △ABC的内切圆半径为r, △ABC的周长为l,求△ABC的
2.如图,点O是△ABC的内心,若∠BAC=86°, 则∠BOC=( C ) A.172° B.130° C.133° D.100°
3.如图,已知VP、VQ为⊙T的切线,P,Q为
课时九切线长定理课件.ppt
半径为_斜__边__的__一__半__.
2.直角三角形内切圆的圆心(内心)在_三__角__形__内__部_, 半径r=____a+_b_-c_____.
2
知识拓展 4.Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半 径是____1___. 5.直角三角形的外接圆半径为5cm,内切圆半径为 1cm,则此三角形的周长是_2_2_c_m___.
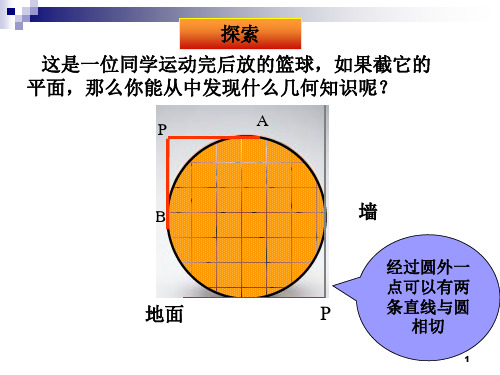
探索
这是一位同学运动完后放的篮球,如果截它的 平面,那么你能从中发现什么几何知识呢?
P
A
B
地面
墙
经过圆外一
点可以有两
P
条直线与圆 相切
1
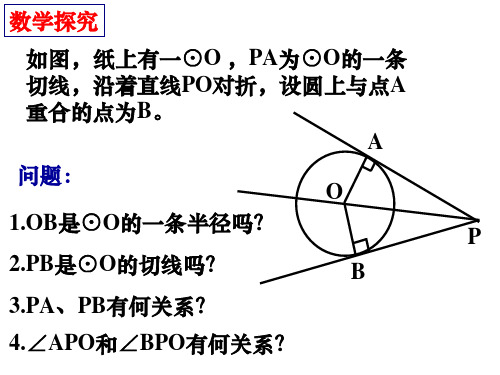
问题2、经过圆外一点P,如何作已知⊙O的
切线?
A
。
P
O
B
思考:假设切线PA已作出,A为切点,
则∠OAP=90°,连接OP,可知A在怎样
的圆上?
2
过⊙O外一点作⊙O的切线
依据。必须掌握并能灵活应用。
13
数学探究 三角形的内切圆: 与三角形各边都相切的圆叫做三角形的内切圆
三角形的内心: 三角形的内切圆的圆心叫 做三角形的内心
三角形的内心是三角形三 条角平分线的交点,它到 三角形三边的距离相等。 B
A
D
O
F
E
C
14
练习四 已知:△ABC是⊙O外切三角形,切点
为D,E,F。若BC=14 cm ,AC=9cm,AB=
例1.如图所示PA、PB分别切圆O于A、B, 并与圆O的切线分别相交于C、D, 已知 PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD的度数
A D
P
·O
E
34第三课时切线长定理用课件
22cm
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________,半径为___________.
2.直角三角形内切圆的圆心(内心)在__________,半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.(1)写出图中所有的垂直关系;(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图,过半径为6cm的⊙O外一点P作圆的切线PA、PB,连结PO交⊙O于F,过F作⊙O切线分别交PA、PB于D、E,如果PO=10cm, 求△PED的周长。
数学探究
思考:连结AB,则AB与PO有怎样的位置关系? 为什么?
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
练习四 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
知识小结
直角三角形的外接圆与内切圆
1.直角三角形外接圆的圆心(外心)在__________,半径为___________.
2.直角三角形内切圆的圆心(内心)在__________,半径r=___________.
a
b
c
斜边中点
斜边的一半
三角形内部
课前训练
1、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.(1)写出图中所有的垂直关系;(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.
练习
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
P
B
O
A
二、填空
25
(3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A
A 16cm
D 8cm
C 12cm
B 14cm
D
C
B
E
A
P
例2、如图,过半径为6cm的⊙O外一点P作圆的切线PA、PB,连结PO交⊙O于F,过F作⊙O切线分别交PA、PB于D、E,如果PO=10cm, 求△PED的周长。
数学探究
思考:连结AB,则AB与PO有怎样的位置关系? 为什么?
(2)填空:AB+CD AD+BC(>,<,=)
=
DN=DP,AP=AL,BL=BM,CN=CM
比较圆的内接四边形的性质:
圆的内接四边形:角的关系
圆的外切四边形:边的关系
练习四 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
初中九年级下册数学《切线长定理》PPT精品课件

切线长定理
2020/11/20
1
A
O
P
2020/11/20
B
过圆外一点作圆的切线,这点 和切点之间的线段的长,叫做这点 到圆的切线长。
2
A
O
P
B
• 切线是直线,不能度量;
• 切线长是线段的长,这条线段的两个端 点分别是圆外一点和切点,可以度量。
2020/11/20
3
A
1
O
M的两条切线,
内切圆圆心:三角形三个 内角平分线的交点。
内切圆的半径:交点到三 角形任意一边的垂直距离。
2020/11/20
9
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
谢谢大家!本文档为精心编制而成,您可以在下载后自由修改和打印,希望下载对您有帮助!
2020/11/20
10
有什么关系? 又OA=OB,OP=OP, 地理课件:
历史课件:
∴Rt△AOP≌Rt△BOP(HL)
∴PA=PB,∠1=∠2
2020/11/20
4
A
O
P
B
• 切线长定理:
• 从圆外一点引圆的两条切线,它们的切线 长相等,这一点和圆心的连线平分两条切 线的夹角。
2020/11/20
5
切线长定理的拓展
A
D
O HC
P
B
(1)写出图中所有的垂直关系
(2)图中有哪些线段相等(除半径 外)、弧相等?
2020/11/20
6
2020/11/20
7
o.
o.
2020/11/20
8
三角形外接圆
C
2020/11/20
1
A
O
P
2020/11/20
B
过圆外一点作圆的切线,这点 和切点之间的线段的长,叫做这点 到圆的切线长。
2
A
O
P
B
• 切线是直线,不能度量;
• 切线长是线段的长,这条线段的两个端 点分别是圆外一点和切点,可以度量。
2020/11/20
3
A
1
O
M的两条切线,
内切圆圆心:三角形三个 内角平分线的交点。
内切圆的半径:交点到三 角形任意一边的垂直距离。
2020/11/20
9
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
谢谢大家!本文档为精心编制而成,您可以在下载后自由修改和打印,希望下载对您有帮助!
2020/11/20
10
有什么关系? 又OA=OB,OP=OP, 地理课件:
历史课件:
∴Rt△AOP≌Rt△BOP(HL)
∴PA=PB,∠1=∠2
2020/11/20
4
A
O
P
B
• 切线长定理:
• 从圆外一点引圆的两条切线,它们的切线 长相等,这一点和圆心的连线平分两条切 线的夹角。
2020/11/20
5
切线长定理的拓展
A
D
O HC
P
B
(1)写出图中所有的垂直关系
(2)图中有哪些线段相等(除半径 外)、弧相等?
2020/11/20
6
2020/11/20
7
o.
o.
2020/11/20
8
三角形外接圆
C
《切线长定理》示范公开课PPT教学课件【九年级数学下册北师大版】

只要证明OC1CD,即LOCD = 90°即可,由LOCD LOCB + LBCD,已知LBCD =LBAC,故只要证明LOCB + LBAC = 90°就可以了,但LOCB与LBAC既没有共同的顶点,又不在同一个三角形中,故可延长CO交O0于点E,连接EB,由圆周角定理的推论,可Q LBAC =LBEC.而LBCELBCD =LBAC,故只要证明LOCB + LBAC = 90°就可以了,但LOCB与LBAC既没有共同的顶点,又不在同一个三角形中,故可延由LOCD LOCB + LBCD,已知LBCD =LBAC,故只要证明LOCB + LBAC = 90°就可以了长CO交O0于点E,连接EB,由圆周角定理的推论,可Q LBAC =LBEC.而LBCE与LBEC都是同一个三角形的内角,因此只要证明LCBE = 90°就行了x这是很角形的内角,因此只要证明LCBE = 90°就行了x这是很
例 如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
分析:
A
O
设 ⊙O的半径为r,连接OD,OE,OF
由切线的性质及切线长定理可得四边形OECF为正方形.
从而CF=CE=OE=OF=r,所以AF=10-r,BE=24-r,
再由切线长定理可得,AD=AF=10-r,BD=BE=24-r,
∠BIC
2.如图,PA,PB分别与⊙O相切于A,B两点.C是弧AB上任意一点,过点C作⊙O的切线,分别与PA,PB相交于D,E两点,若PA = PB =5 cm,求△PDE的周长.
O
P
A
B
C
D
E
解:∵PA,PB,DE是圆的切线∴PA=PB,DC=DA,CE=BE,
例 如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
分析:
A
O
设 ⊙O的半径为r,连接OD,OE,OF
由切线的性质及切线长定理可得四边形OECF为正方形.
从而CF=CE=OE=OF=r,所以AF=10-r,BE=24-r,
再由切线长定理可得,AD=AF=10-r,BD=BE=24-r,
∠BIC
2.如图,PA,PB分别与⊙O相切于A,B两点.C是弧AB上任意一点,过点C作⊙O的切线,分别与PA,PB相交于D,E两点,若PA = PB =5 cm,求△PDE的周长.
O
P
A
B
C
D
E
解:∵PA,PB,DE是圆的切线∴PA=PB,DC=DA,CE=BE,
