2020年高职单招数学考试样卷模拟试题(带答案)
2020年职业教育对口数学模拟试题(带答案)

机密★启用前山东省高等职业教育对口招生数学模拟试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间90分钟.考试结束后,将本试卷和答题卡一并交回.2.本次考试允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.第Ⅰ卷(选择题,共60分)一、选择题(本大题共30小题,每小题2分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项选出)1.已知集合A={ x 1≤x≤4},B={ x x- a>0}, 若A ⊆ B,则实数a的取值范围为()(A) (1,+∞) (B) (-∞,1)(C) [1,+∞) (D) (-∞,1]2.已知方程x2 +a x+ (a+3)=0有实根,则a的取值范围()(A) {a|a>6或a<- 2} (B) {a| -2≤a ≤6}(C) {a|a≥6或a≤- 2} (D) {a| -2< a < 6}3. 已知圆的方程为22-+-=,则点(1,2)(3)(5)16x y-().(A)在圆内(B)在圆上(C)在圆外(D)与圆心重合4.函数y=f (x) 的图象与直线x=k (k 是常数)的交点的个数()(A) 有且只有一个(B) 至少有一个(C) 至多有一个(D) 有一个或两个5.若x > y > 0, 0 < a < 1, 则下列各式成立的是()(A) a x≤a y(B) log a x < log a y(C) a x ≥a y(D) log a x > log a y6. 设a , b是实数,则a2+b2 ≠ 0的充要条件是()(A) a ≠ 0 (B) b ≠ 0 (C) a ≠ 0且b ≠ 0 (D) a ≠ 0或b ≠ 0 7.二次函数 y =x 2+px +q 的顶点在第二象限, 则p 和q 的符号是( )(A) p > 0, q >0 (B) p > 0, q < 0 (C) p < 0, q < (D) p < 0, q > 0 8.在数列3,4,7,12,x ,28, … 中,x 的值是( ).(A ) 18 (B ) 19 (C ) 20 (D ) 21 9. 过点()1,0且平行于y 轴的直线方程是( ).(A )1y = (B ) 1y =- (C )1x = (D ) 1x =-10.在四边形ABCD 中,若→A B = 2→a ,→C D = - 3 →a , ∣→A D ∣=∣→B C ∣ , 则 四边形ABCD 是( ) (A) 平行四边形 (B)菱形 (C) 等腰梯形 (D) 矩形 11.函数y =3 sin (ω x + π3 )(ω > 0)的最小正周期为π3, 则ω等于( )(A) 3 (B) 6 (C) 52(D) 912. 若平面α∥平面β,P 是平面α、β外一点,过P 的两条直线AB 、CD 交平面α于A 、C ,交平面β于B 、D ,且P A =6,AB =2,BD =12,则AC 的长是( ). (A ) 10 (B ) 9 (C ) 8 (D ) 713. 若双曲线的焦点在x 轴上,并且6a =、2b =,则双曲线的标准方程为( ). (A) 221364x y -= (B ) 221436x y -= (C ) 22162x y -= (D ) 22126x y -=14. 某数学兴趣小组成员的数学中考成绩如下:116 99 108 93 100 111 98 95 106 113 若102分以上(包括102)为优秀, 则优秀率为( ).(A ) 0.30 (B ) 0.40 (C ) 0.50 (D ) 0.60 15.0.3()log (2)f x x =,若()0f a =,则实数a 的值是( ).(A )16 (B ) 1 (C ) 0 (D ) 1216. 抛甲、乙两粒骰子,甲骰子点数不小于乙骰子点数的概率是( ). (A )512 (B ) 12 (C ) 712 (D ) 2317. 若椭圆的方程为224312x y +=,则它的焦点坐标为( ). (A ) ()()1,01,0-、 (B ) ()()0,10,1-、(C ) ((0,、 (D ))()、18.有四条线段,长度分别是2cm ,3cm ,4cm ,5cm ,从中任取两条, 长度之和不小于8cm 的概率是( ).(A) 14(B) 12(C) 13(D) 119.不等式 | 3- 2x | ≥ 5 的解集是( )(A) [-1, 4 ] (B) (- ∞, - 1]∪[ 4,+∞) (C) (- ∞, - 4)∪[ 1,+∞) (D) [- 4, 1]20.已知f (x )是奇函数,且x ≥ 0时,f (x )= 2x -x 2,则当x < 0时,f (x ) 的解析式为( )(A) f (x ) = x 2+2x (B) f (x ) = - x 2- 2x (C) f (x ) = x 2- 2x (D) f (x ) = - x 2+2x 21.设函数log ()4a x f x =,且1(16)2f =,则a 的值为( ). (A ) 4 (B ) 8 (C )18(D ) 1422.已知∣→a ∣= 4,→b 在 →a 方向上的射影的数量为- 3,则 →a ·→b =( ) (A) - 12 (B) - 7 (C) - 34 (D) 3423. 若抛物线的焦点在x 轴正半轴上,焦点到准线的距离是12,则它的 标准方程是( ).(A ) 2y x =- (B ) 2y x = (C ) 2x y =- (D ) 2x y = 24.5人参加4项比赛,每人限报一项,报名方法有( )(A) 45 (B) 54 (C) 20 (D) 25 25.函数y = 2sin 2x +4sin x +2 的最大值和最小值分别为( )(A) 6, 0 (B) 6, - 1 (C) 8, 0 (D) 8, - 1 26.等差数列前10项和1060S =,则110a a +等于( ).(A )10 (B ) 11 (C ) 12 (D ) 13 27. 函数()f x 在()5,5-上是增函数,下列选项错误的是( ).(A ) (2)(0)f f ->(B ) (1)(1)f f -< (C ) (2)(3)f f < (D ) (0)(4)f f < 28.△ABC 中:AB =10,S △= 160, 则边AC 的最小值为( )(A) 32 (B) 16 (C) 8 (D) 16 3 29.函数22y x x =+与22y x x =-的图像( ).(A ) 关于x 轴对称 (B ) 关于y 轴对称(C ) 关于原点对称 (D ) 关于x 轴和y 轴都不对称 30.在等比数列{a n }中,a 1+ a 2=30,a 3+ a 4=120,那么a 5+ a 6 =( ) (A) 210 (B) 240 (C) 480 (D) 700第Ⅱ卷(非选择题,共40分)二、填空题(本大题共4小题,每小题3分,共12分)31. 某超市大米3.5元/千克,现设x表示购买大米的重量(千克),y表示应付款数(元),将,x y 的函数关系用列表法表示为:32.若正四棱锥的体积为12,底面对角线的长为_____.33. 若圆的方程222230x y by b+--=,则圆心坐标为_______,半径为_______.34.已知t anα是方程x2-2x-3=0的一个根,且α是第一象限的角,则cosα·tanα= . 三、解答题(本大题共4小题,共28分)35. (7分)设二次函数的图象的顶点是(-2, 32)与x轴的两个交点之间的距离是6,求这个二次函数的解析式.36. (7分) 角α.37.(7分) 如图,正三棱柱ABC —A 1B 1C 1的底面边长为a ,在侧棱BB 1上取BD =2a,在侧棱CC 1上截取CE =a ,过A 、D 、E 作棱柱的截面,试证明截面ADE 与侧面ACC 1A 1垂直。
2020对口高职数学试卷
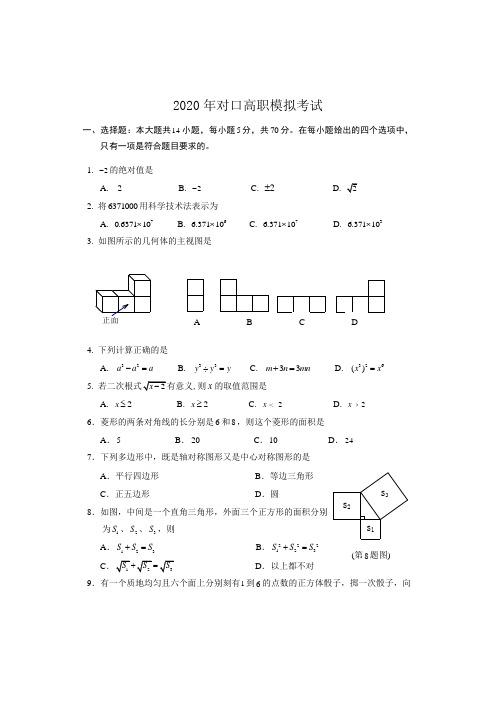
2020年对口高职模拟考试一、选择题:本大题共14小题,每小题5分,共70分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 2-的绝对值是A. 2B. 2-C. 2±D.2.将6371000用科学技术法表示为A. 70.637110⨯ B.66.37110⨯ C. 76.37110⨯ D. 36.37110⨯3.如图所示的几何体的主视图是4. 下列计算正确的是A.32a a a-=B.33y y y÷=C.33m n mn+=D.326()x x=5. ,则x的取值范围是A. 2x≤ B. 2x≥ C. x<2 D. x﹥26.菱形的两条对角线的长分别是6和8,则这个菱形的面积是A.5B.20C.10D.247.下列多边形中,既是轴对称图形又是中心对称图形的是A.平行四边形B.等边三角形C.正五边形D.圆8.如图,中间是一个直角三角形,外面三个正方形的面积分别为1S、2S、3S,则A.123S S S+=B.222123S S S+=C=D.以上都不对9.有一个质地均匀且六个面上分别刻有1到6的点数的正方体骰子,掷一次骰子,向正面S2S3S1上一面的点数为1的概率是A .0 B.C.D .110.母线长为5,底面半径长为3的圆锥的侧面积为A .12πB .15πC .24πD .30π 11.不等式1x -<0的解集在数轴上表示为A .B .C .D . 12.抛物线28y x =-+的顶点坐标是A .(0, 8)B .(8, 0)C .(0, 8)-D .(1-, 8) 13. 已知集合{}2,3,5,6A =,集合{}1,3,4,6,7B =,则集合AB =A . {}2,5B . {}3,6C . {}2,5,6D . {}1,2,3,4,5,6,7 14. 数据1,2-,3,4-,3的中位数和众数分别是A . 1, 3B . 2-, 3C . 3, 1D . 4-, 3 二、填空题:本大题共6小题,每小题5分,共30分。
最新2020年高职单招数学模拟试题二

2020年高职单招数学模拟试题二2020年高职单招数学模拟试题二 班级: 姓名: 一、选择题(本大题共10小题,每小题5分,共50分.) 1、已知集合{}{}7,6,5,3,2,1,8,6,4,2,1==B A ,设B A P =,则集合P 的真子集个数为( )A .8B .7C .6D .52、设向量a =()21x ,-,b =()14x ,+,则“3x =”是“a //b ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件3、若角α的终边在第二象限且经过点(1,3)P -,则sin α等于( )A .32B .32-C .12-D .124、在ABC ∆中,3,5a b ==,1sin 3A =,则sinB =( ) A .15 B .59C .53D .1 5、下列几何体各自的三视图中,有且仅有两个视图相同的是( )A .①②B .①③C .①④D .②④6、抛物线y =14x 2的准线方程是( )A .y =-1B .y =-2C .x =-1D .x =-27、某大学数学系共有本科生1000人,其中一、二、三、四年级的人数比为4∶3∶2∶1,要用分层抽样的方法从所有本科生中抽取一个容量为200的样本,则应抽取三年级的学生人数为( )A .80B .40C .60D .208、用0、1、2、3、4、5组成没有重复数字的两位数,共有( )A 15个B 20个C 25个D 30个9、在等差数列}{n a 中,若10121=+a a ,则=+++111032a a a a ( ) A、10 B、20 C、30 D、4010、直线y= 2x 与圆 x 2+y 2-2x -4y -1=0的位置关系是 ( )A 、 相离B 、相切C 、相交但不过圆心D 、相交且过圆心二、填空题(本大题共3小题,每小题4分,共12分。
)11、幂函数)(x f y =的图像经过点 _________________;12___________. 13、322x ->的解集为____________________三、解答题(本人题共3小题,共38分)14、设U={小于9的正整数},{123}A =,,,{3456}B =,,,,求u C A ,U C B , U U C A C B 。
2020年吉林省高职高专院校单独招生统一考试数学

2020年吉林省高职高专院校单独招生统一考试数学一、选择题1.−5的相反数是A.5B.−5C.±5D.152.下列各角为钝角的是A.700B.1300C.2400D.32003.已知集合A={0,1,2,3,4},B={3,4,5,6},由既属于A又属于B的元素组成的集合是A.∅B.{3}C.{3,4}D.{0,3,4}4.下面几何体中,从正面观察得到的平面图形(主视图)为圆的几何体是5.校园内有一个开满鲜花的矩形花坛,长为8m,宽为5m,则其面积是A.20m2B.26m2C.30m2D.40m26.梯形内角和等于A.1800B.2700C.3600D. 54007. 下面数列为递增数列的是A.2,4,6,8,10,⋯B.−2,−4,−6,−8,−10,⋯C.2,2,2,2,⋯D.−2,4,−6,8,−10,⋯8.空间两条直线的位置关系有A.平行、相交、异面B. 平行、相交C. 相交、异面D. 平行、异面9.化简:3(m+n)+2m=A.3m+2nB.2m+3nC.5m+2nD.5m+3n10.sin300=A.1B.√32C.√22D.1211.在直角三角形中,一个锐角的度数是200,则另一个锐角的度数是A.200B.500C.700D.90012.计算:25×27=A.210B.212C.214D.23513.∠β是五边形内角∠α的外角,则下列等式正确的是A. ∠α=∠βB. ∠α+∠β=900C. ∠α+∠β=1800D. ∠α+∠β=360014.下列运算,正确的是A.(a+2b)2=a2+2ab+b2B.(a+2b)2=a2+4ab+b2C.(a+2b)2=a2+4ab+2b2D.(a+2b)2=a2+4ab+4b215.函数y=√x−2的定义域是A.[2,+∞)B.(2,+∞)C.(−∞,2]D.(−∞,2)16.一艘货船在B处时测得小岛A在北偏西300方向,同时测得航标灯C在西南方向,则∠ABC的度数是A.300B.600C.900D.105017.下列角度转换为弧度运算正确的是radA.300=π4radB.1200=π2radC.450=π3D.1800=πrad18.已知数列1,−2,3,−4,x,−6,7,⋯,按其排列的规律,x值是A.4B.5C.6D.−519.某地为了保护水土资源,实施山林绿化工程,如果2017年的绿化面积是8万公顷,以后每年的绿化面积都比上一年多1万公顷,那么2020年的绿化面积是A.9万公顷B. 10万公顷C. 11万公顷D. 12万公顷20.已知正方体的棱长是2cm,则它的表面积是A.4cm2B.12cm2C.24cm2D.36cm221.已知两点A(0,0)和B(1,1),则线段AB的长度是A.1B.√2C.√3D.222.下列函数为偶函数的是A.y=x2B.y=x3C.y=x2+xD.y=x3+x2+x的值是23.当x=1时,函数y=4xA.2B.3C.4D.524.在等比数列中,首项a1=1,公比q=2,则a4=A.4B.6C.8D.1025.方程3x−9=0的解是A.2B.3C.4D.526.垂直于同一平面的两条直线的位置关系是A.垂直B.平行C.异面D.相交27.函数y=sin2x的最小正周期是A.π2B.πC.3π2D.2π28.从某社区随机抽取8名老人测量血压,测得他们的舒张压(单位:mmHg)分别为:73,80,88,73,99,102,89,76,则这8为老人舒张压的平均数是A.83B.84C.85D.8629.甲乙丙丁四位同学参加米接力赛,甲必须排在第一棒,则所有不同的接力方案有A.3种B.4种C.5种D.6种30.已知向量a⃗=(2,−3),b⃗⃗=(6,3),则a⃗+b⃗⃗=A.(8,3)B.(8,−3)C.(8,0)D.(0,8)31.直线2x−3y−6=0经过点的坐标是A.(2,0)B.(0,2)C.(3,0)D.(0,3)32.现有花色分别为红桃A、方块A、黑桃A、梅花A四张扑克牌,从中任取一张扑克牌为红色的概率是A.12B.13C.14D.1633.已知sin(π−α)=12,则sinα=A.−12B.12C.−√22D.√2234.已知圆x2+y2=4,则圆心坐标和半径分别是A.(0,0),2B.(0,0),4C.(1,1),2D.(1,1),435.直线经过A(1,2)和B(2,3)两点,则直线AB的斜率是A.−35B.35C.−1D.136.已知椭圆x 29+y24=1,则椭圆与x轴的交点坐标是A.(−3,0),(3,0)B.(0,−3),(0,3)C.(−2,0),(2,0)D.(0,−2),(0,2)二、多选题37.满足不等式2.7<x<6.3的所有正整数有A.3B.4C.5D.638.下列函数中,在其定义域内是增函数的有A.y=1xB.y=√xC.y=xD.y=x339.长方体ABCD−A1B1C1D1中,下列说法正确的有A.AB‖D1C1B.D1D⊥平面ABCDC.平面A1ADD1‖平面B1BCC1D.棱A1A与棱C1C所在直线是异面直线三、解答题40某学校要建矩形运动场地,场地相邻两边借用两面墙,另两条边长的和为16m.设矩形的长为xm.(1)求矩形运动场地面积S关于x的函数解析式,并指出函数的定义域(2)当x为何值时,场地面积S最大?最大面积是多少?41.已知{a n}是首项为1,公差为3的等差数列,S n表示{a n}的前n项和(1)求等差数列{a n}的通项公式a n(2)求等差数列{a n}的前6项和S642.已知正方体ABCD−A1B1C1D1,点O是底面ABCD对角线的交点(1)求证:C1O‖平面AB1D1(2)若正方体的棱长为2,求三棱锥A1−AB1D1的体积(3)求直线C1O与平面BB1D1D所成角的正切值。
2020年高职单招考试数学模拟试卷

2020年高职单招考试模拟试题(长线备考、每周一套题,助你成功!多省份适用!有答案解析!)一、选择题(共10小题;共50分)1. 若集合,,则A. B. C. D.2. 不等式的解集为3. 若,则等于A. B. C. D.4. 函数的零点是A. C.5. 若直线过圆的圆心,则的值为B. C.6. 设数列的前项和,则的值为A. B. C. D.7. 设,用二分法求方程在内近似解的过程中得,,,,则方程的根落在区间A. B. D.8. 执行如图所示的程序框图,则输出的值为A. B. C. D.9. 已知函数,则A. 是偶函数,且在上是增函数B. 是奇函数,且在上是增函数C. 是偶函数,且在上是减函数D. 是奇函数,且在上是减函数10. 某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况注:“累计里程”指汽车从出厂开始累计行驶的路程.在这段时间内,该车每千米平均耗油量为A. 升B. 升C. 升D. 升二、填空题(共3小题;共15分)11. 现有三张识字卡片,分别写有“中”、“国”、“梦”这三个字.将这三张卡片随机排序,则能组成“中国梦”的概率是.12. 若,则.13. 设双曲线的两个焦点为,,一个顶点是,则的方程为.三、解答题(共3小题;共35分)14. 在中,内角,,所对的边分别是,,,已知,,.(1)求;(2)求的值.15. 如图,在四棱锥中,底面是矩形,,,,、分别是、的中点.(1)证明:;(2)求三棱锥的体积.16. 已知椭圆.(1)求椭圆的离心率;(2)设为原点,若点在直线上,点在椭圆上,且,求线段长度的最小值.答案第一部分1. C2. A 【解析】不等式可化为:,所以,所以,所以不等式的解集为.注:先保证x2前的系数为正,才有“大于取两边,小于取中间的规律”3. D4. A 【解析】令得,或 .5. B【解析】圆化为标准方程为,所以圆心为,代入直线得.6. C 【解析】.(想想S4表示什么?前4项的和!所以S4=a1+a2+a3+a4 ,S3=a1+a2+a3)7. C8. C9. B 【解析】,所以,即函数为奇函数,又由函数为增函数,为减函数,故函数为增函数.10. B【解析】汽车每次加油时把油箱加满,第二次加油升,说明这段时间总消耗油量为升,这段时间内汽车行驶的里程为千米,所以每千米平均耗油量为升.第二部分12.13.第三部分14. (1)因为,,,所以由余弦定理得:则.(2)由正弦定理得,,所以,,所以.15. (1)在中,、分别是、的中点,所以.因为四边形为矩形,所以,所以,又因为,,所以.(2)连接,,,过作交于点,则,且.在中,,,,所以所以所以16. (1)由题意,椭圆的标准方程为所以,,从而因此故椭圆的离心率(2)设点,的坐标分别为,,其中,因为,所以即,解得又,所以因为且当时等号成立,所以,故线段长度的最小值为.。
2020职业学校对口单招数学模拟试题

B. 2 1, 2 1
C. 2 1, 2 1
D.
0, 2 1
8.直线
xy
5 3
3t 3t
(为参数)的倾斜角为
A . 300
B . 600
D. 150 0 9.平面 与平面 , 都相交,则这三个平面可能有
C . 1200
A.1 条或 2 条交线
B. a1 a 2 D. a 2 a 2
4.首项为 15 的等差数列,从第 6 项开始为正数,则公差 d 的取值范围为
A. d 3
B . d 15 4
C . 3 d 15 4
D. 3 d 15 4
5.若 a 2,3, b 4,1 y,且源自a // b ,则 y 6
2
(1)求 f 0; (2)求 f x 的解析式; (3)设 0, ,则 f 3 ,
2
2 2
求 的值.
19.已知数列an 是等差数列,且 a1 2 , a1 a2 a3 12 . (1)求数列an 的通项公式; (2)令 bn an 3n n N ,求数列 bn 前 n
项和 Sn .
20.为了对某课题进行研究,用分层抽样的方法从三所高校 A,B,C 的相关人中 抽取若干人组成研究小组,有关数据如下表(单位:人).
高校
相关人数
抽取人数
A
54
x
B
36
2
C
72
y
(1)求 x , y ;(2)若从高校 B,C 抽取的人中选 2 人作专题发言,求这 2 人均来自
高校 C 的概率.
22.铁矿石 A 和 B 的含铁率 a ,冶炼每万吨铁矿石的 CO2 的排放量 b 及每万吨铁
高职单招数学卷+答案 (1)

单独招生考试招生文化考试数学试题卷(满分120分,考试时间120分钟)一、选择题:(本题共10小题,每小题6分,共60分)1.已知函数f (x )的图象关于直线x =1对称,当x2>x1>1时,[f (x2)﹣f (x1)](x2﹣x1)<0恒成立,设a =f (−12),b =f (2),c =f (e ),则a ,b ,c 的大小关系为()A.c >a >bB.c >b >aC.a >c >bD.b >a >c2.已知函数y =f (x )在区间(﹣∞,0)内单调递增,且f (﹣x )=f (x ),若a =f (log 123),b =f (2﹣1.2),c =f (12),则a ,b ,c 的大小关系为()A.a >c >bB.b >c >aC.b >a >cD.a >b >c3.设函数f (x )=ex+x ﹣2,g (x )=lnx+x2﹣3.若实数a ,b 满足f (a )=0,g (b )=0,则()A.g (a )<0<f (b )B.f (b )<0<g (a )C.0<g (a )<f (b )D.f (b )<g (a )<04.下列命题是假命题的是()A.(0,sin 2x x xπ∀∈> B.000,sin cos 2x R x x ∃∈+=C.,30xx R ∀∈> D.00,lg 0x R x ∃∈=5.已知11tan(),tan()tan()62633πππαββα++=-=-+=则()A.16B.56C.﹣1D.16.下列函数中,在定义域内单调递增且是奇函数的是()A.y =log 2(x 2+1−x)B.y =sinxC.y =2x ﹣2﹣xD.y =|x ﹣1|7.设函数f (x )=x (ex+e ﹣x ),则对f (x )的奇偶性和在(0,+∞)上的单调性判断的结果是()A.奇函数,单调递增B.偶函数,单调递增C.奇函数,单调递减D.偶函数,单调递减8.若函数f (x )=xln (x +a +x 2)为偶函数,则a 的值为()A.0B.1C.﹣1D.1或﹣19.设函数f (x )=ln|2x+1|﹣ln|2x ﹣1|,则f (x )()A.是偶函数,且在(12,+∞)单调递增B.是奇函数,且在(−12,12)单调递增C.是偶函数,且在(−∞,−12)单调递增D.是奇函数,且在(−∞,−12)单调递增10.已知函数f (x )是定义在R 上的偶函数,且在[0,+∞)上单调递增,则三个数a =f (﹣log313),b =f (2cos2π5),c =f (20.6)的大小关系为()A.a >b >cB.a >c >bC.b >a >cD.c >a >b 二、填空题:(共30分.)1.若圆锥曲线15222=++-k y k x 的焦距与k 无关,则它的焦点坐标是__________.2.定义符号函数⎪⎩⎪⎨⎧-=101sgn x 000<=>x x x ,则不等式:x x x sgn )12(2->+的解集是__________.3.若数列}{n a ,)(*N n ∈是等差数列,则有数列)(*21N n na a ab nn ∈+++=也为等差数列,类比上述性质,相应地:若数列}{n C 是等比数列,且)(0*N n C n ∈>,则有=n d __________)(*N n ∈4.若n S 是数列}{n a 的前n 项的和,2n S n =,则=++765a a a ________.三、解答题:(本题共6小题,每小题10分,共30分.解答应写出文字说明、证明过程或演算步骤.)1.圆C 的圆心在x 轴上,并且过点A(-1,1)和B(1,3),求圆C 的方程。
高职单招数学卷+答案 (4)

单独招生考试招生文化考试数学试题卷(满分120分,考试时间90分钟)一、选择题:(本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知定义在R 上的函数f(x)=2|x﹣m|﹣1(m 为实数)为偶函数,记a=f (log0.53),b=f(log25),c=f(2+m),则a,b,c 的大小关系为()A.a<b<cB.a<c<bC.c<a<bD.c<b<a2.函数f(x)=ln(x2﹣2x﹣8)的单调递增区间是()A.(﹣∞,﹣2)B.(﹣∞,﹣1)C.(1,+∞)D.(4,+∞)3.已知函数()sin cos (0)()()44f x a x b x ab f x f x ππ=-≠-=满足,则直线0ax by c ++=的斜率为()A.1C. D.﹣14.已知偶函数()f x 在区间[0,)+∞上单调递增,则满足1(21)()3f x f -<的x 的取值范围是()A.1[0,3B.12(,33C.12[,)23D.11(,325.已知函数f (x)=(a −2)x ,x ≥2(12)x−1,x <2,满足对任意的实数x1≠x2,都有f(x 1)−f(x 2)x 1−x 2<0成立,则实数a 的取值范围为()A.(1,+∞)B.(−∞,138]C.(−∞,138)D.(138,+∞)6.若函数f (x)=(1−2a)x +3a ,x <12x−1,x ≥1的值域为R,则a 的取值范围是()A.[0,12) B.(12,1]C.[﹣1,12)D.(0,12)7.已知函数f(x)=lg(ax2+(2﹣a)x +14)的值域为R,则实数a 的取值范围是()A.(1,4)B.(1,4)∪{0}C.(0,1]∪[4,+∞)D.[0,1]∪[4,+∞)8.函数f(x)在定义域R 内可导,若f(1+x)=f(3﹣x),且当x∈(﹣∞,2)时,(x﹣2)f(x)<0,设a=f(0),b=f(),c=f(3),则a,b,c 的大小关系是()A.a>b>cB.c>a>bC.c>b>aD.b>c>a9.已知函数f(x)=2x,则函数f(f(x))的值域是()A.(0,+∞)B.(1,+∞)C.[1,+∞)D.R10.已知函数f(x)=lnx −12ax 2+(a﹣1)x+a(a>0)的值域与函数f(f(x))的值域相同,则a 的取值范围为()A.(0,1]B.(1,+∞)C.(0,43]D.[43,+∞)11、已知54cos ,0,2=⎪⎭⎫⎝⎛-∈x x π,则x tan =()A、34B、34-C、43D、43-12、在∆ABC 中,AB=5,BC=8,∠ABC=︒60,则AC=()A、76B、28C、7D、12913、直线012=+-y x 的斜率是();A、-1B、0C、1D、214、点P(-3,-2)到直线4x-3y+1=0的距离等于()A、-1B、1C、2D、-215、过两点A (2,)m -,B(m ,4)的直线倾斜角是45︒,则m 的值是()。
2020年职业教育对口数学模拟试题(带答案)

机密★启用前山东省高等职业教育对口招生数学模拟试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间90分钟.考试结束后,将本试卷和答题卡一并交回.2.本次考试允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.第Ⅰ卷(选择题,共60分)一、选择题(本大题共30小题,每小题2分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项选出) 1.设集合A={1,2,4,5},B={2,5,6,7},则A ∪B 等于﹙ ﹚ (A ){2,5}(B ){1,2,,3,4,5,6,7}(C ){1,2,4,5,6,7} (D ){2,4,5} 2. 对于命题p :x >3,命题q :x >1,则p 是q 的﹙ ﹚ (A )充分条件 (B )必要条件(C )充要条件 (D )既不充分也不必要条件 3.函数y =2x -1的定义域是( )(A ){x ︱x >0} (B ){x ︱x <0} (C ){x ︱x =0} (D )x ∈R 4.设log a 13>1,则a 的取值范围是( )(A )(13 ,1) (B )(0,13)(C)(0,1) (D)(1,+∞)5.等差数列{a n}中,a1=3, a100=36,则a5+a96=()(A)39 (B)36 (C)38 (D)426.已知:∣→a∣= 4, ∣→b∣= 3,<→a,→b>= 60°,则∣→a+2→b∣=()(A)13 (B)10 (C)27(D)219 7.已知f (2x)=x2+x+1,则f (-2) = ( )(A)0 (B)1 (C)3 (D)68.直线y-3=k (x+2)恒过点()(A)(3,-2)(B)(-2,3)(C)(2,-3) (D)(-3,2)9.某同学到4个景点旅游,每个景点游览一天,则不同的游览次序有()种。
2020年四川省单招数学真题(含答案)(中职类)

四川省2020年普通高等学校高职教育单独招生文化考试(中职类)数学第I 卷(共50分)一、单项选择题.本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是复核要求的,请将其选出,错选、多选或未选均无分.1.函数3x 2f(x)-=的定义域是()A.{x|x≠2}B.{x|x≠3}C.{x|x>3}D.{x|x>3}2.已知集合A={1},B={-1,a},且A∩B={1},则a=()A.-2B.0C.1D.23.已知3log 2=b ,则b=()A.2B.6C.8D.94.不等式|x+1|>2的解集为()A.[-3,1] B.(-∞,-3]∪[1,+∞)C.(-3,1)D.(-∞,-3)∪(1,+∞)5.在等差数列{an}中,a2=1,a4=5,则a6=()A.5B.7C.9D.116.为了得到函数x y sin 2=的图像,只需要把函数x y sin =的图像()A.横坐标缩短为原来的21倍,纵坐标不变B.横坐标伸长为原来的2倍,纵坐标不变C.纵坐标缩短为原来的21倍,横坐标不变D.纵坐标伸长为原来的2倍,横坐标不变7.设a、b 均为大于0且不等于1的常数,探究函数x x b x g a x f ==)()(和在同一直角坐标系下的图像如图所示,则下列结论正确的是()A.a>b>1B.b>a>1C.1>a>b>0D.1>b>a>08.从4名女同学和2名男同学中,任选2人参加志愿者活动,则其中有两人都是女同学的概率为()A.21B.52 C.53 D.549.已知)(x f y =是定义在R 上的奇函数,且当x>0时,13)(+=xx f ,则=-)1(f ()A.-4B.-2C.34 D.410.△ABC 的内角A、B、C 的对边分别为a、b、c,已知22cos ,21sin ==B A ,a=2,则c=()A.226- B.226+ C.26- D.26+第II 卷(共50分)二、填空题.本大题共3个小题,每小题4分,共12分.请在每小题的空格中填上正确答案,错填、不填均无分.11.在等比数列{an}中,a1=1,a2=3,则a4=.12.某中学高一年级学生700人,高二学生人数为700,高三年级人数为600,现学校决定采取分层抽样的方法,要从这三个年级抽取100名学生进行学习情况调查,则抽取高三年级人数为.13.已知直线033=-+y x 与圆2)122=+-y x (相交于A、B 两点,则线段AB 的长度为.二、解答题.本大题共3个小题,第14题12分,第15、16题各13分,共38分.解答应写出文字说明、证明过程或演算步骤.14.已知向量a=(2,-3),b=(3,2)(1)求向量a+2b 与向量b-a 的坐标;(2)判断向量a 与b 是否垂直.15.如图,在四棱锥P-ABCD 中,底面ABCD 为正方形,平面PAC ⊥底面ABCD ,PA=PC=AC=2,O 为AC 中点.(1)证明:PO⊥底面ABCD.(2)求四棱锥P-ABCD 的体积.16.已知双曲线C:12222=-b y a x (a>0,b>0)的一个顶点为(4,0),渐近线方程为x y 43±=.(1)求双曲线的标准方程;(2)设点A(8,m )为双曲线上的一个点,求点A 到双曲线C 右焦点的距离.四川省2020年普通高等学校高职教育单独招生文化考试(中职类)·数学参考答案一、单项选择题.本大题共10个小题,每小题5分,共50分1.B 2.C 3.C 4.D 5.C 6.D7.A8.B9.A10.D二、填空题.本大题共3个小题,每小题4分,共12分.11.8112.3013.2三、解答题.本大题共3个小题,第14题12分,第15、16题各13分,共33分.14.(1)a+2b=(2,-3)+2(3,2)=(2,-3)+(6,4)=(8,1)……………(3分)b-a=(3,2)-(2,-3)=(1,5)…………………………(6分)(2)因为a·b=2×3+(-3)×2=0…………………………(9分)所以a⊥b……………………………………………………(12分)15.(1)因为在△PAC 中,PA=PC,O 为AC 的中点所以PO⊥AC……………………………………………………(2分)又因为平面PAC⊥底面ABCD,AC 为平面PAC 和地面ABCD 的交线所以,PO⊥地面ABCD.………………………………………………(5分)(2)已知底面ABCD 为正方形所以,AB⊥BC,AB=BC.在等腰直角△ABC 中,222=+=BC AB AC 所以,AB=BC=1.正方形ABCD 的面积SABCD=1.………………………………………………(8分)已知O 为AC 的中点,所以AO=2221=AC 在直角△PAO 中,PO=2622=-AO PA .……………………………………(11分)由(1)知,PO⊥地面ABCD,所以,四棱锥P-ABCD 的体积VP-ABCD=661263131=⨯⨯=ABCD S PO ·..………(12分)16.(1)由双曲线c 的一个顶点(4,0),得a=4又由渐近线方程为xy 43±=可得43=ab ,b=3………………………………………………(4分)所以,双曲线的标准方程为:191622=-y x …………………………………………(6分)(2)由点(8,m)在双曲线上,所以1916822=m -,解得272=m …………………………………………(8分)双曲线C 的焦距5342222=+=+=c a c 所以,右焦点的坐标为:(5,0)…………………………………………(10分)点A 到双曲线C 右焦点的距离:6)082=-+m ()(25-…………………………(13分)。
2020年高职单招数学模拟试题七

、选择题已知集合M 0,1,2 2. 3. 4. 5. 6.(A ) 1 在等比数列 a n 中, (A)6 (B)8 已知向量a A. (- 1,11) (3,1),b 数学模拟试题七,B 1,4,那么集合 AUB 等于( (B ) (C ) 2,3 (D ) 123,4 已知a 1 (2,5), B. 2包 4,那么a 5等于 (C)10 (D)16 那么2a+b 等于( (4,7) C. (1,6) D (5,-4) 函数y log 2(x+1)的定义域是( (A) 0, (B) ( 1,+ (C) (1,) (D) 1, 如果直线3x (A) 3 函数y=sin 标缩短到原来的 (A) 4 7.在函数 (A) y 8. sin 11 6 y 0与直线mx y 1 0平行,那么m 的值为( 1 (B) 3 (D) 3x 的图象可以看做是把函数y 二sinx 的图象上所有点的纵坐标保持不变,横坐 1倍而得到,那么的值为() (B) (C) 的值为 9.不等式x 2 A. x x 10.已知平面 2x , (B) 3x+2//平面y log 2 x , 0的解集是 B. x x>1 ,直线m 平面 1 2 x 中,奇函数的是 (D) 3 C. (C) (B) y log 2 x (D) (D)乎 x1 x 2 D. x x 1,或 x 2那么直线m 与平面 的关系是() A.直线m 在平面 内 B.直线m 与平面 相交但不垂直 C.直线m 与平面 垂直 D.直线m 与平面 平行.填空题11 •在ABC中,a . 3 , b 2 , c 1,那么A的值是()112 •当x>0时,2x 一的最小值是()2x13. 从数字1,2,3,4,5中随机抽取两个数字(不允许重复),那么这两个数字的和是奇数的概率为()三、解答题14. 在三棱锥P-ABC中,侧棱PA丄底面ABC,ABLBC,E,F分别是BC,PC 的中点.(I)证明:EF//平面PAB;(II)证明:EF L BC.15. 已知向量a=(2sin x,2sin x) , b=(cos x, sin x),函数f (x)=a b+1 .1(I) 如果f (x)=,求sin 4x的值;2(II) 如果x (0,),求f (x)的取值范围.216. 已知圆C的方程是x2+y2 2y+m=0 .如果圆C与直线y=0没有公共点,求实数m的取值范围?。
2020年职业教育对口数学模拟试题1(带答案)

机密★启用前山东省高等职业教育对口招生考试数学模拟试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间90分钟.考试结束后,将本试卷和答题卡一并交回.2.本次考试允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.第Ⅰ卷(选择题,共60分)一、选择题(本大题共30小题,每小题2分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项选出)1.设M ={ x x≥2}, a = 2 ,则下列关系中正确的是()(A) {a} ⊆M(B) a ∉M (C) a ⊆ M(D) a∈M2. 设命题“p∨q”为真,“p∧q”为假,则()(A) p和q都假(B) p和q都真(C) p和⌝q真假相同(D) p和⌝q真假不同3.如果a– b>a , a + b>b , 那么下列式子中正确的是()(A) a + b>0(B) a– b < 0 (C)a⨯b< 0 (D)ab >04.设f (x) = ax2 + b x+ c,且方程f (x) =0 的两根分别在区间(1,2)和(2,3)内,则必有()(A) f (1)⋅f (2) > 0 (B) f (1)⋅f (2) < 0(C) f (1)⋅f (3) < 0 (D) f (2)⋅f (3) > 05.将- 256π化成k·2π +α( k ∈ Z, 0≤α < 2π ) 的形式为()(A) - 256π = - 5π +56π(B) -256π = - 6π +116π(C) - 256π = - 4π -16π(D) -256π = - 3π -76π6.设函数f (x) = x2+2x , 则f (2)⋅ f (12) = ()(A) 1 (B) 3 (C) 5 (D) 10 7.在等差数列{a n}中,a1= -1 , a n+1=a n + 2,则a13等于()(A) 34 (B) 35 (C) 23 (D) 78 8.已知函数f (x)是一次函数且f [f (x) ]= 9x+1 , 则f (x) =( )(A) 3x +14 (B) - 3x - 12(C) 3x +14 或 - 3x - 12 (D) 3x - 12 或 3x +149.设cos α= - 45 ( π < α < 32π ), 则sin α·tan α的值是( )(A )920 (B )- 920 (C )710 (D )- 71010.函数 y = 4 - x +1x -1的定义域是( ) (A) (1, 4] (B) (-∞, 4] (C) (-∞, 1) ∪ (1, +∞) (D) (-∞, 1) ∪ (1, 4] 11.下列几个命题中,正确命题的个数为( )① 对于函数f (x ) , 若f (-2) = - f (2) ,则f (x )一定是奇函数 ②若函数f (x ), 在[a , b ] 上是增函数, 则它在(a , b ) 上也一定是增函数. ③若f (x )在R 上是奇函数, 则它在[a , b ]一定是奇函数 . ④若f (x )在R 上是奇函数 , 则f (x )的图象一定过原点 .⑤已知f (x )是偶函数且在(0, +∞)上是增函数, 则f (x )在(-∞, 0)上是减函数 . (A)1 (B) 2 (C) 3 (D) 4 12.设x >0, 且a x < b x < 1, (a , b ∈R +), 则( )(A) b < a < 1 (B) a < b < 1 (C) 1 < b < a (D) 1 < a < b 13.函数 y = lg(x 2+1 – x ) 在定义域内是( )(A) 奇函数 (B)既是奇函数又是偶函数 (C) 偶函数 (D) 既不是奇函数又不是偶函数 14.下列命题中,不正确的是( ).(A ) 过平面外一点,有且仅有一个平面与已知平面平行(B ) 两条直线都和一个平面平行,则过这两条直线的平面也和该平面平行 (C ) 垂直于同一直线的两个平面平行 (D ) 一条直线和两个平行平面所成的角相等 15.式子32 - l o g 3 2 的值为( )(A) 9(B) 2 (C) 29 (D) 9216.数列{}n a 的通项公式是(2)11n na n -=-+,则它的前三项是( ).(A ) 151232---,, (B ) 70 13-,, (C ) 12 33--,, (D ) 132 32--,,17.等比数列{a n }的各项都是正数,若a 1 =81,a 5=16,则它的前5项的和是( ) (A) 179 (B) 211 (C) 243 (D) 27518. 有6张卡片上分别写有0, 1, 2, 3, 4, 5, 将它们放入袋子中,摸出一张是数字小于2的概率是( ). (A )12 (B ) 14 (C ) 13(D ) 16 19.如果向量→a 和向量→b 不平行,那么与→a 、→b 都不平行的向量是( ) (A) 2→a (B) - 3→b (C) →a +→b (D) -→a20.已知函数 y =lg [(a 2-1) x 2 + (a +1) x +1 ], 若函数的定义域为(-∞, +∞),则实数a 的取值范围是( )(A) a ≤-1 (B) a > 53(C) a ≤-1或 a > 53 (D) -1 ≤a < 5321. 已知圆C :22(3)8x y ++=,下列各点中,在圆内的点是( ).(A ) (1,1)- (B ) (1,2)- (C ) (0,0) (D ) (2,2)- 22.已知∣→a ∣= 5,∣→b ∣= 4,<→a , →b > = 60°则 →a ·→b 等于( )(A) - 10 (B) 10 (C) - 10 3 (D) 10 3 23.函数y =4 sin2 x 取最小值时,x 的取值集合是( )(A) {x | x = π4 + 2k π, k ∈Z }(B) {x | x = - π2+ 2k π, k ∈Z }(C) {x | x = -π4 + k π , k ∈Z }(D) {x | x = π2 + k π , k ∈Z }24.设1F 、2F 为定点,并且128F F =,若动点M 满足124MF MF -=, 则点M 的轨迹是( ).(A ) 双曲线 (B ) 椭圆 (C ) 圆 (D ) 线段25.若双曲线的两个焦点坐标为()13,0F -、()23,0F ,并且2a =,则其标准方程为( ). (A ) 22154x y -= (B ) 22145x y -=(C ) 22145y x -= (D ) 22154y x -=26. 甲,乙两个样本,甲的样本方差是0.065,乙的样本方差是0.056,那么样本甲与样本乙的波动大小应是( ).(A ) 甲的波动比乙的大 (B ) 甲的波动比乙的小 (C ) 甲与乙的波动相同 (D ) 无法判定27. 点(1,1)P 在圆22()()4x a y a -++=外部,则a 的取值范围是( ). (A ) 11a -<< (B ) 1a 0<< (C ) 1a <-或1a > (D ) 1a =± 28. 在椭圆中,若62a b ==,,则该椭圆的标准方程为( ). (A ) 221364x y +=(B ) 221436x y +=(C ) 221364x y +=或221436x y +=(D ) 22126x y +=或22162x y +=29. 要从某校五年级85名学生中抽取20名学生作为一个样本,用抽签的方法选取是( ). (A ) 分层抽样 (B ) 系统抽样 (C ) 简单随机抽样 (D ) 无法确定 30. 有15个样本,按从小到大的顺序排列分成5个组,如下表:第四组的频率为( (A )13 (B ) 14 (C ) 12 (D ) 15第Ⅱ卷(非选择题,共40分)二、填空题(本大题共4小题,每小题3分,共12分)31. 若函数f (x ) 在[0, 1 ] 上是增函数, 则适合条件f (1- a ) > f ( 12) 的实数a 的取值范围是 .32.函数y =11+2 sin x的定义域是 .33. 在球内相距为9cm的两个平行截面,面积分别为249πcm和2400πcm,且截面位于球心同一侧,则球的表面积为_________.34. 若椭圆的标准方程为221259x y+=,则其长轴长为,椭圆上一点P到焦点F1的距离等于6,则点P到另一个焦点的距离是.三、解答题(本大题共4小题,共28分)35. (7分)在28届雅典奥运会上,中国获得射箭女子团体银牌,从电视实况转播中,我们可以清楚看到箭在空中飞行的轨迹是抛物线,设箭出口与靶中心10环平行,都距地面1.5m,相距70m,在中间35m处,箭飞行达到最大高度3m,建立直角坐标系如图所示,试求箭飞行的轨迹所对应二次函数的解析式.36.(7分)已知函数y =3cos 2x +12sin2x 32.(1)求函数的最大值及取得最大值时x 的值;(2)画出函数在一个周期内的图像.37. (7分) 已知P A⊥⊙O所在平面,AB为⊙O的直径,C是圆周上的任意一点,过A作AE ⊥PC于E,判断AE与平面PBC的关系,并说明理由.38.(本小题7分)椭圆C: x2a2+y2b2= 1(a>b> 0)的两个焦点分别为F1,F2,点P在椭圆C上,且PF1⊥PF2, |PF1| =6, |PF2| =8,(1)求椭圆的方程。
