matlab最小树算法
最小生成树matlab代码

最小生成树简介最小生成树(Minimum Spanning Tree)是图论中的一个重要概念。
它是一种用于连接所有节点的树,同时使得树中边的权值之和最小。
最小生成树在许多领域中都有广泛的应用,例如网络设计、电力传输、交通规划等。
算法Kruskal算法Kruskal算法是一种常用的解决最小生成树问题的算法。
它的基本思想是通过不断选择图中权值最小的边,并且保证这些边不会形成环,直到选择了足够多的边为止。
具体步骤如下:1.初始化一个空的最小生成树集合。
2.将图中所有边按照权值从小到大排序。
3.遍历排序后的边,如果当前边不会导致最小生成树形成环,则将该边添加到最小生成树集合中。
4.最终得到的最小生成树集合即为所求。
Prim算法Prim算法是另一种解决最小生成树问题的经典算法。
它的基本思想是从一个起始节点开始,逐步扩展最小生成树,直到覆盖所有节点。
具体步骤如下:1.初始化一个空的最小生成树集合。
2.随机选择一个起始节点,并将其加入到最小生成树集合中。
3.在最小生成树集合和图的剩余节点之间找到连接两部分的最小权值边,将该边和连接的节点加入到最小生成树集合中。
4.重复步骤3,直到最小生成树覆盖了所有节点。
应用场景网络设计最小生成树在网络设计中有着广泛应用。
例如,在计算机网络中,我们希望通过最小的成本将所有节点连接起来。
最小生成树提供了一种方法来实现这一目标,通过构建一个权值最小的树形网络,可以节省物理资源,提高网络传输效率。
电力传输在电力传输领域,最小生成树被用于设计最优的电力传输网络。
通过选择最小的成本边连接所有电力站点,可以减少电力传输的总成本,并优化电力的分布。
交通规划最小生成树在交通规划中也有着广泛的应用。
例如,在城市道路规划中,我们希望通过最小的道路建设成本将所有地区连接起来。
最小生成树算法可以帮助我们找到连接所有区域的最短路径,从而实现高效的交通规划。
MATLAB代码实现function [T] = minSpanningTree(G)% 输入参数:% G: 输入图的邻接矩阵表示% 输出参数:% T: 最小生成树的邻接矩阵表示n = size(G, 1); % 节点个数visited = zeros(1, n); % 记录节点是否被访问过T = zeros(n); % 初始化最小生成树的邻接矩阵visited(1) = 1; % 从第一个节点开始构建最小生成树while sum(visited) < n % 当所有节点都被访问过时停止minEdge = inf; % 最小权值边的权值minIndex = 0; % 最小权值边的终点for i = 1:nif visited(i) == 1for j = 1:nif visited(j) == 0 && G(i, j) < minEdgeminEdge = G(i, j);minIndex = j;endendendendvisited(minIndex) = 1; % 将新节点标记为已访问T(minIndex, :) = G(minIndex, :); % 将该边添加到最小生成树中T(:, minIndex) = G(:, minIndex);endend总结最小生成树是一种重要的图论概念,常用于解决连接所有节点的问题。
Primf及Krusf最小成树及matlab源代码

11
2013年8月21日11 Nhomakorabea
例 、一个乡有7个自然村,其间道路如图 所示,要以村为中心建有线广播网络,如 要求沿道路架设广播线,应如何架设?
a
18
19 14 16 12
b
7
8
5
c
3
e
f
g
27
21
d
12
数学建模-图论
四、最小生成树问题及其算法
Prim 算法 Matlab 程序如下:
function T =Primf(a) l=length(a); a(a==0)=inf; k=1:l; listV(k)=0; listV(1)=1; e=1; while(e<l) min=inf; for i=1:l if listV(i)==1 for j=1:l if listV(j)==0 & min>a(i,j) min=a(i,j); b=a(i,j); s=i; d=j; end end end end
10
数学建模-图论
四、最小生成树问题及其算法
求最小生成树的 Prim 算法的思想如下:
从连通图 G=<V,E>的某一顶点 v 出发,选择与其关联的具有最小权的边 (u0,v),将其顶点加入到生成树的顶点集合 U 中。以后每一步从一个顶点 在 U 中而另一顶点不在 U 中的各条边中选择权值最小的边(u,v) ,把它的 顶点加入到集合 U 中,如此下去,直到图中的所有顶点都加入到生成树顶点 集合 U 中为止,这时得到一颗最小生成树。
0 2 2 0 4 4 0 8 A 8 0 4 5 3 7 8 5 3 7 8 0 3 7 3 0 6 7 6 0 4
数学建模-最小生成树-kruskal算法及各种代码之欧阳史创编

kruskal算法及代码---含伪代码、c代码、matlab、pascal等代码K r u s k a l算法每次选择n- 1条边,所使用的贪婪准则是:从剩下的边中选择一条不会产生环路的具有最小耗费的边加入已选择的边的集合中。
注意到所选取的边若产生环路则不可能形成一棵生成树。
K r u s k a l算法分e 步,其中e 是网络中边的数目。
按耗费递增的顺序来考虑这e 条边,每次考虑一条边。
当考虑某条边时,若将其加入到已选边的集合中会出现环路,则将其抛弃,否则,将它选入。
目录Kruskal算法1.算法定义举例描述Kruskal算法的代码实现1.伪代码C代码实现matlab代码实现pascal代码实现Kruskal算法1.算法定义举例描述Kruskal算法的代码实现1.伪代码C代码实现matlab代码实现pascal代码实现算法定义克鲁斯卡尔算法假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网,则按照克鲁斯卡尔算法构造最小生成树的过程为:先构造一个只含 n 个顶点,而边集为空的子图,若将该子图中各个顶点看成是各棵树上的根结点,则它是一个含有 n 棵树的一个森林。
之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,也就是说,将这两个顶点分别所在的两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。
依次类推,直至森林中只有一棵树,也即子图中含有 n-1条边为止。
举例描述克鲁斯卡尔算法(Kruskal's algorithm)是两个经典的最小生成树算法的较为简单理解的一个。
这里面充分体现了贪心算法的精髓。
大致的流程可以用一个图来表示。
这里的图的选择借用了Wikipedia上的那个。
非常清晰且直观。
首先第一步,我们有一张图,有若干点和边如下图所示:第一步我们要做的事情就是将所有的边的长度排序,用排序的结果作为我们选择边的依据。
matlabKruskal最小生成树算法

matlabKruskal最小生成树算法clear all;clc;a = rand(100,100);%随机生成100*100的方阵graph_adjacent = (a+a')/2;len = length(graph_adjacent);%计算图中的顶点数temp = graph_adjacent;%将原图内容拷贝到temp中,以防对原图做改动superedge = zeros(len-1,2);%用于保存生成最小生成树的边i = 1;%指向superedge的下标for j = 1:lentag(j) = j;%关联标志初始化,将每个顶点的关联标志设为其本身end;%以下的循环完成kruskal算法ticwhile(superedge(len-1,1)==0)[Y,I] = sort(temp);%将temp的每列按从小到大排序,数组Y保存temp 排序后的结果,I中保存相应结果对应的在temp中的下标cost_min = min(Y(1,:));%找出权值最小的边index = find(Y(1,:)==cost_min);%找出权值最小的边对应的顶点index = index(1);%一条边对应两个节点,且不同的边的权值可能一样,这里为了方便处理人为规定了顺序,取标号最小的顶点进行处理anotherpoint = I(1,index);%找到该边对应的另一个顶点%将该边对应的权值修改为最大,防止该边在下次循环中再次被选为最优边temp(index,anotherpoint)=100;temp(anotherpoint,index)=100;if(tag(anotherpoint)~=tag(index))%当两个点不属于一个连通集时,这两个点之间的边为最小生成树的边superedge(i,:)=[index,anotherpoint];%将其加入最小生成树的边集中i=i+1;%下标加1%下面的语句的作用是将两个连通分支变成一个连通分支,即tag 值一样for j=1:len %以index的tag值为标准if((tag(j)==tag(anotherpoint))&&(j~=anotherpoint))%遍搜tag数组,先将和anotherpoint tag值一样的点的tag值变为index 的tag值tag(j)=tag(index);endendtag(anotherpoint)=tag(index);%将anotherpoint的tag值变为index的tag值endendtoc%s=0;for ii=1:len-1k=sprintf('最小生成树第%d条边:(%d,%d),权值为%d',ii,superedge(ii,1),superedge(ii,2),graph_adjacent(superedg e(ii,1),superedge(ii,2)));%格式化字符串disp(k);%显示disp(' ');%空一行%s=s+graph_adjacent(superedge(ii,1),superedge(ii,2)); %求最小生成树的代价end%显示最小生成树的代价%disp('最小生成树的总代价为:') %disp(s);。
Kruskal算法寻找最小树的matlab程序

Kruskal算法寻找最小树的matlab程序function tree=kruskal(d) %矩阵d为无向图的权矩阵,且是对称矩阵N=size(d,1);k=0; %记录图中边的条数I=max(max(d)); %I作为无穷大edge=zeros(N*(N-1)/2,3);%用于存储图中所有的边,边的条数最多为n*(n-1)/2for i=1:N-1 %因为权矩阵是对称阵,所以只用上三角矩阵。
for j=i+1:Nif d(i,j)<Ik=k+1;edge(k,1)=i;edge(k,2)=j;edge(k,3)=d(i,j);endendendedge=edge(1:k,:); %删除多余的行。
o_edge=edge; %用于存储排序后的边及边的端点。
for i=1:k-1 %用选择排序法进行升序排序for j=i+1:kif o_edge(i,3)>o_edge(j,3)temp=o_edge(i,:);o_edge(i,:)=o_edge(j,:);o_edge(j,:)=temp;endendendtree=zeros(N-1,3); %用于存放最小树中的边及边的端点,最小树中的边数为节点数减1 tree(1:2,:)=o_edge(1:2,:); %两条边一定不能构成圈,所以前面最小的两条边一定在最小树中。
line=3;for i=3:kif line==N %如果line=N说明tree矩阵已填满,最小树已经找到,跳出循环break;elseif line<Nif isempty(find(tree(:,1:2)==o_edge(i,1), 1))||isempty(find(tree(:,1:2)==o_edge(i,2), 1))%判断tree中已经确定的的所有边中的节点是否和新增加的边的两个端点都重复,若新边的两个端点不都重复,则为真%直接说明新边符合条件,加入tree中。
shortestpathtree matlab 函数

shortestpathtree matlab 函数矩阵中的所有节点之间都有一些路径连接着。
某些路径可能是直接的,而有些可能需要经过其他节点。
寻找从一个节点到另一个节点的最短路径是图论中一个经典的问题。
在 MATLAB 中,可以使用 shortestpathtree 函数来解决这个问题。
首先,让我们了解一下最短路径树(Shortest Path Tree)是什么。
最短路径树是一个有向图,它以某个源节点为根节点,并将所有其他节点连接到根节点的最短路径。
最短路径树通常用于网络中的路由选择和通信网络中的拓扑控制。
在 MATLAB 中,你可以使用 shortestpathtree 函数来计算具有有向边的有向图的最短路径树。
这个函数采用一个邻接矩阵作为输入,并返回一个有向图的最短路径树。
邻接矩阵是一个 N×N 的矩阵,其中 N 是图中节点的数量。
邻接矩阵的第 i 行第 j 列的元素表示从节点 i 到节点 j 是否有一条边。
如果有边连接,则该元素的值为非零,否则为零。
在有向图中,边是有方向的,所以邻接矩阵是对称的。
为了使用 shortestpathtree 函数,我们首先需要创建一个邻接矩阵。
我们可以使用 MATLAB 中的矩阵操作来实现这一点。
例如,我们可以使用 zeros 函数创建一个全零矩阵,然后使用索引操作将适当的元素设置为非零值,从而表示边的存在。
例如,假设我们有一个图,其中有四个节点,从节点 1 到节点 3 有一条权重为2 的边,从节点 1 到节点 4 有一条权重为 5 的边,从节点 2 到节点 3 有一条权重为 1 的边,从节点 2 到节点 4 有一条权重为 3 的边。
我们可以通过以下方式创建邻接矩阵:matlabadjacency_matrix = zeros(4);adjacency_matrix(1, 3) = 2;adjacency_matrix(1, 4) = 5;adjacency_matrix(2, 3) = 1;adjacency_matrix(2, 4) = 3;现在我们已经创建了邻接矩阵,我们可以使用 shortestpathtree 函数来计算最短路径树。
matlab 普里姆算法

matlab 普里姆算法普里姆算法是一种最小生成树算法,用于求解给定图的最小生成树。
该算法基于贪心策略,每次选择当前已选中的点集到未选中的顶点集中距离最近的一条边,将该边所连接的点加入到已选中的点集中。
在实现普里姆算法时,我们需要使用一个优先队列用于存储当前已选中的点集到未选中的顶点集中的边,以及每个顶点到已选中的点集中最小距离。
在每次选取最小距离的边时,我们将该边所连接的点加入到已选中的点集中,并将该点与未选中的点集中的所有点之间的距离加入到优先队列中,同时更新已选中的点集到未选中的顶点集中的最小距离。
该过程重复进行,直到所有的顶点都已经被加入到已选中点集中,最终得到的图就是原图的最小生成树。
下面是使用matlab实现普里姆算法的示例代码:function MST = prim_algorithm(graph)% graph为邻接矩阵,MST为最小生成树的邻接矩阵表示n = size(graph, 1); % 获取图中节点数key = Inf(1,n); % 存储每个顶点与已选中点集的最小距离mst = zeros(n, n); % 存储最小生成树的邻接矩阵表示visited = false(1,n); % 存储每个顶点是否已加入到已选中点集中pq = PriorityQueue(n); % 创建优先队列start = 1; % 从任意一个顶点开始寻找最小生成树key(start) = 0; % 起始点距离已选中点集的最小距离为0pq.insert(start, 0); % 将起始点加入到优先队列中while ~pq.isempty() % 当优先队列非空时进行迭代[u, cost] = pq.deleteMin(); % 选取距离已选中点集最近的边visited(u) = true; % 将选中的顶点加入到已选中点集中if u ~= start % 将当前边加入到最小生成树的邻接矩阵中mst(parent(u), u) = cost;mst(u, parent(u)) = cost;endfor v = 1:n % 更新与已选点集中每个顶点的最小距离if ~visited(v) && graph(u,v) < key(v)parent(v) = u;key(v) = graph(u,v);if pq.contains(v)pq.updatePriority(v, key(v));elsepq.insert(v, key(v));endendendendMST = mst;end该代码中借助matlab的优先队列类PriorityQueue实现了优先队列的功能,其中包括了队列插入、队列删除、队列是否为空、队列中是否包含某元素以及队列中某元素优先级的更新等方法。
最小生成树matlab代码

最小生成树matlab代码在Matlab中,最小生成树可以通过Kruskal算法和Prim算法来实现。
本文将分别介绍两种算法的代码实现,并对其进行详细解析。
Kruskal算法Kruskal算法是基于贪心算法的最小生成树算法。
其基本思想是将边按照权值从小到大进行排序,然后逐个加入到树中,直到树连通为止。
如果加入一条边使得形成环,则不加入该边。
定义一个函数Kruskal(weight,n)来实现Kruskal算法。
参数weight是一个n*n的矩阵,表示图的邻接矩阵;n表示图中节点的个数。
该函数的返回值为最小生成树的边集。
function edges=Kruskal(weight,n)%初始化[rows,cols,vals]=find(weight);edge_num=length(rows);%边数edges=zeros(n-1,2);%初始化,存放最小生成树的边%边按照权重从小到大排序[~,idx]=sort(vals);rows=rows(idx);cols=cols(idx);%初始化并查集par=1:n;rank=zeros(1,n);%依次加入边n_edge=0;%表示已加入的边数for i=1:edge_num%如果两个节点已经在同一连通块中,则不能加入当前边if FindPar(par,rows(i))==FindPar(par,cols(i))continue;end%将当前边加入到最小生成树中n_edge=n_edge+1;edges(n_edge,:)=[rows(i),cols(i)];%将两个节点合并Union(par,rank,rows(i),cols(i));%如果当前已经加入足够的边,则退出循环if n_edge==n-1break;endendFindPar函数和Union函数是实现并查集的两个函数,用于判断是否形成环以及将两个节点合并。
具体代码如下:%查找节点的祖先function par=FindPar(par,idx)if par(idx)==idxpar=idx;elsepar=FindPar(par,par(idx));end%将两个节点合并function Union(par,rank,x,y)x_par=FindPar(par,x);y_par=FindPar(par,y);if rank(x_par)>rank(y_par)par(y_par)=x_par;elsepar(x_par)=y_par;if rank(x_par)==rank(y_par)rank(y_par)=rank(y_par)+1;endendPrim算法Prim算法也是一种贪心算法,基本思想是从任意一个点开始,找到与该点相邻的最短边,然后将这个边连接的点加入到集合中,继续寻找与该集合相邻的最短边。
Matlab中求解最小生成树

数学建模——Matlab中求解最小生成树关键词:Matlab、最小生成树、破圈法、避圈法、运筹学要求:选择一道编程题自己独立完成,必须自己编写源代码,不能从网上下载。
先编写算法的通用程序,然后以例子运行,论文内容包括程序代码、程序说明、例子运行结果,最终程序文件连同论文一起发至e-mail,便于老师运行程序是否正确。
编程使用C或MATLAB。
选择题目:编写实现生成树、最小生成树的程序(包括避圈法、破圈法)。
题目分析:本题要求编写实现生成树、最小生成树的程序,首先来了解一下关于关于生成树的概念:1、树的概念:树是无向图的特殊情况,即对于一个N个节点的无向图,其中只有N-1条边,且图中任意两点间有且只有一条路径,即图中不存在环,这样的图称为树。
2、生成树的概念:对于一个无向连通图G=(V,E),其中V代表顶点,E代表边,对它做一次遍历,每个节点经过一次,那么图中的N个节点再加上遍历过程中经过的N-1条边所构成的子图就是图G的一个生成树。
3、最小生成树的概念:对于一个无向连通图G=(V,E),给它的每条边(u,v)赋一个权值w(u,v)。
若图G 的生成树不止一个,那么其中包含的N-1条边的权值之和的最小的生成树就是图G的最小生成树。
4、关于运筹学中最小生成树有2种不错的算法,即避圈法和破圈法,下面来看一下求解最小生成树的算法:先看一下图示法表示的最小生成树:<1>避圈法求解上面无向带权连通图的基本步骤是:每步从未选的边中选取边e,使它与已选边不构成圈,且e是未选边中的最小权边,直到选够n-1条边为止。
<2>破圈法基本思想如下:(1) 每次从图中选取任意一个圈, 然后去掉该圈中权值最大的边(如果存在多条相同权值的最大边,可以任意选择一条去掉即可) 使之不构成圈.(2) 重复上述过程. 直到图中不再含圈且所有顶点均包含在图中为止, 就构成最小生成树.它的算法图解如下:5、我们在用matlab程序求解最小生成树的时候需要用到无向图的邻接矩阵,首先来了解一下邻接矩阵的概念。
Matlab中避圈法求解最小生成树

end
end
P(2,y)=P(1,y);
elseif P(2,y)<P(1,y)
for l=(y+1):m
%准备工作
T=zeros(n); %最小生成树的加权邻接矩阵
WW=W;
for i=1:n
for j=1:n
if W(i,j)==inf WW(i,j)=0;
end
end
end
m=((nnz(WW))/2); %图的边线的数目
%编程工具Matlab;程序名称MST_k.m.
%这是一个通过避圈法求解连通带权图的最小生成树的程序.
n=input('请输入图的顶点数目:n= ')
W=input('请输入图的加权邻接矩阵:[W(1,1),..,W(1,n);..;W(n,1),..,W(n,n)]=')
%用W(i,i)="inf" 代替 "=0"
end
W(a,b)=inf;
else %如果条件|E|=|V|-1成立
MST=T;
input('这个图的最小生成树的加权邻接矩阵是:')
MST
break
end
Байду номын сангаас
end
if j<(n-1) %如果条件|E|<|V|-1成立
input('这个图没有最小生成树.')
end
j=0; %最小生成树的边线的数目
%主要步骤
for i=1:m %被选择边线的数目
matlab 最小值算法

在MATLAB中,寻找数组或矩阵中的最小值是一个常见的任务。
MATLAB提供了多种用于寻找最小值的函数和算法,这些方法适用于不同类型的数据和不同的应用场景。
以下是一些在MATLAB中寻找最小值的常见方法和相关函数:### 1. **`min` 函数:**`min` 函数是MATLAB中最基本和最常用的寻找最小值的方法之一。
它可以用于矩阵、数组或者向量,返回最小元素的值以及对应的索引。
语法:```matlab[minValue, index] = min(A);```- `minValue`:返回矩阵或数组中的最小值。
- `index`:返回最小值所在的索引。
示例:```matlabA = [4, 2, 8; 1, 7, 5; 6, 3, 9];[minValue, index] = min(A);disp('最小值:');disp(minValue);disp('最小值索引:');disp(index);```### 2. **`min` 函数的多输出形式:**`min` 函数还支持多输出形式,可以同时返回每列或每行的最小值及其索引。
语法:```matlab[minValues, indices] = min(A, [], dim);```- `minValues`:返回每列或每行的最小值。
- `indices`:返回最小值所在的索引。
- `dim`:指定沿着哪个维度进行操作,可以是`1` 表示按列操作,`2` 表示按行操作。
示例:```matlabA = [4, 2, 8; 1, 7, 5; 6, 3, 9];[minValues, indices] = min(A, [], 1);disp('每列的最小值:');disp(minValues);disp('每列最小值的索引:');disp(indices);```### 3. **`min` 函数的应用场景:**- **查找最小元素:** 最直观的用法是查找矩阵或数组中的最小元素,以便进一步的分析和处理。
通过使用prim算法(反圈法)求解最小支撑树问题

一.实验目的通过使用prim算法(反圈法)求解最小支撑树问题..二.实验内容设图G =(V,E),其生成树的顶点集合为U。
①.把v0放入U。
②.在所有u∈U,v∈V-U的边(u,v)∈E中找一条最小权值的边,加入生成树。
③.把②找到的边的v加入U集合。
如果U集合已有n个元素,则结束,否则继续执行②。
其算法的时间复杂度为O(n^2)Prim算法实现:图用邻接阵表示,路径不通用无穷大表示,在计算机中可用一个大整数代替。
采用堆,可以将复杂度降为O(m log n),如果采用Fibonaci堆可以将复杂度降为O(n log n + m)三.使用环境Windows XP 环境下MATLAB 编写四.调试过程程序如下:#include<stdio.h>#include<stdlib.h>#include<string.h>#define INFINITY 1000#define max_name 50#define max_vertex_num 50typedef char vertex[max_name];//顶点名字串typedef int adjMatrix[max_vertex_num][max_vertex_num];//邻接距阵typedef struct{vertex adjvex; //邻接矩阵int lowcost; //权值}close[max_vertex_num];//定义一个结构以便在后面closedge 使用typedef struct//定义图{vertex vexs[max_vertex_num]; //顶点集adjMatrix arcs; //边int vexnum,arcnum;//点个数,边个数}MGraph;int LocateVex(MGraph G,vertex u)//若G中存在顶点u,则返回该点在图中位置;否则返回其他信息;{int i;for(i=0;i<G.vexnum;++i)if(strcmp(u,G.vexs[i])==0)return i;return 1;}void CreateGraph(MGraph &G){int i,j,k,w;vertex v1,v2;printf("输入无向图顶点数和边数: \n");scanf("%d %d",&G.vexnum,&G.arcnum);printf("输入各顶点的值:\n", G.vexnum);for(i=0;i<G.vexnum;++i) //构造顶点集scanf("%s",&G.vexs[i]);for(i=0;i<G.vexnum;++i) //初始化邻接方阵for(j=0;j<G.vexnum;++j)G.arcs[i][j]=INFINITY;printf("输入一条边依附的顶点及权值:\n",G.arcnum);//输入一条边依附的顶点及权值for(k=0;k<G.arcnum;++k){scanf("%s%s%d",v1,v2,&w);i=LocateVex(G,v1);//v1在图中位置j=LocateVex(G,v2);//v2在图中位置G.arcs[i][j]=G.arcs[j][i]=w; //置于对称弧}}int minimum(close c,MGraph G)//求出下一个节点第k个顶点{int i=0,j,k,min;min=INFINITY;//初始化k=-1;for(j=0;j<=G.vexnum;j++)//求最小if(c[j].lowcost<min&&c[j].lowcost>0){min=c[j].lowcost;k=j;}return k;}void PRIM(MGraph G,vertex u){int i,j,k=0;close closedge;//一个结构bool isbreak=false;k=LocateVex(G,u);//u在图中位置返回G.vexs[i]中下标for(j=0;j<=G.vexnum;++j) //辅助数组初始化closedge从O 开始{if(j!=k)//没有自己到自己的closedge[k].lowcost=0;strcpy(closedge[j].adjvex,u);closedge[j].lowcost=G.arcs[k][j];//列}int flag[1000];flag[0]=0;int count=1;for(i=1;i<G.vexnum;++i){k=minimum(closedge,G);if(k==-1){isbreak=true;break;}printf("%s-%s%d\n",closedge[k].adjvex,G.vexs[k],G.arcs[k][LocateVex(G,closedge[k].adjvex)]); //输出生成树的边closedge[k].lowcost=0; // 第k个顶点并入U集flag[count]=k;count++;for(j=0;j<G.vexnum;++j)if(G.arcs[k][j]<closedge[j].lowcost)//新顶点并入U后重新选择最小边{strcpy(closedge[j].adjvex,G.vexs[k]);closedge[j].lowcost=G.arcs[k][j];}}if(isbreak){printf("此图不连通,无最小支撑树!\n访问过的点为:\n");for(i=0;i<count;i++){printf("%s ",G.vexs[flag[i]]);}printf("\n");}}void main(){MGraph G;CreateGraph(G);printf("最小生成树的各条边为: \n");PRIM(G,G.vexs[0]);}五.实验结果此处給出两个赋权图, 用prim算法找出赋权图上的最小树.图1结果如下:注释 :图1中有7个点10条边, 最后结果输出最小生成树为:图1最小权值W=5+1+2+3+4+1= 16图2结果如下:注释 :图2中有7个点10条边,但较图1(4-5)(5-6)无边相連,固输入权值为0.所以结果出现了两个連通子图.结果如下:而整个图2不連通,无最小支撑树.六.实验总结1.无向图的生成树就是从图的边集中选择一些边,使得这些边构成一个连通无环图,也就是树。
数学建模最小生成树例题

数学建模最小生成树例题例题1:某城市计划建设一条高速公路,需要在若干个村庄之间选择一条最优路径。
已知各个村庄之间的距离,请使用最小生成树算法为高速公路选择最优路径。
参考答案:最小生成树算法可以用于解决此类问题。
常用的最小生成树算法有Kruskal算法和Prim算法。
1. Kruskal算法:按照边的权重从小到大排序,依次将边加入生成树,如果加入的边与已选择的边不构成环,则加入,否则不加入。
2. Prim算法:首先选择权重最小的边加入生成树,然后从剩余的边中选择一条与已选择的边相连且权重最小的边加入生成树,直到所有边都加入生成树。
例题2:一个通信网络由若干个节点和边组成,节点代表城市,边代表通信线路。
已知各个城市之间的距离和通信需求,请使用最小生成树算法为该通信网络设计一个最优的通信线路网。
参考答案:最小生成树算法可以用于解决此类问题。
通过最小生成树算法,我们可以找到一个包含所有节点且边的总权重最小的树形结构,以满足各个城市之间的通信需求。
常用的最小生成树算法有Kruskal算法和Prim算法。
1. Kruskal算法:按照边的权重从小到大排序,依次将边加入生成树,如果加入的边与已选择的边不构成环,则加入,否则不加入。
2. Prim算法:首先选择权重最小的边加入生成树,然后从剩余的边中选择一条与已选择的边相连且权重最小的边加入生成树,直到所有边都加入生成树。
例题3:一个城市的电力网由多个节点和边组成,节点代表发电厂或变电站,边代表输电线路。
已知各个节点之间的电抗和传输功率,请使用最小生成树算法为该城市电力网设计一个最优的输电线路。
参考答案:最小生成树算法可以用于解决此类问题。
通过最小生成树算法,我们可以找到一个包含所有节点且边的总电抗最小的树形结构,以满足各个节点之间的电力传输需求。
常用的最小生成树算法有Kruskal算法和Prim算法。
1. Kruskal算法:按照边的电抗从小到大排序,依次将边加入生成树,如果加入的边与已选择的边不构成环,则加入,否则不加入。
matlab 最小值 优化算法

matlab 最小值优化算法
Matlab 中有多种优化算法可以用于寻找函数的最小值,其中常用的算法包括:
1. fminsearch:使用无约束的模式搜索算法,通过迭代来寻找最小值。
2. fminunc:使用有约束的优化算法,可以处理具有边界约束和线性等式约束的问题。
3. fmincon:使用求解约束最优化问题的算法,可以同时处理无约束、等式约束和不等式约束。
4. ga:使用遗传算法进行优化,适用于多个变量以及多个约束条件的问题。
5. particleswarm:使用粒子群优化算法进行优化,适用于连续和离散的变量,也可以处理多个约束条件的问题。
根据具体的问题和约束条件,可以选择合适的优化算法进行求解。
评估这些算法的性能和效果可以参考官方文档或者相关的学术论文。
最小生成树(MATLAB)

prim算法设置两个集合P和Q,其中P 用于存放G的最小生成树中的顶点,集合Q存放G的最小生成树中的边。
令集合P的初值为P={V1}(假设构造最小生成树时,从顶点V1出发),集合Q的初值为。
Prime算法的思想是,从所有p ∈P,v∈V-P的边中,选取具有最小权值的边pv,将顶点v加入集合P中,将边pv 加入集合Q中,如此不断重复,直到P=V时,最小生成树构造完毕,这时集合Q中包含了最小生成的所有边。
(找最小的权,不连成圈即可)•clc;clear;•M=1000;•a(1,2)=50; a(1,3)=60;•a(2,4)=65; a(2,5)=40;•a(3,4)=52;a(3,7)=45;•a(4,5)=50; a(4,6)=30;a(4,7)=42;•a(5,6)=70;•a=[a;zeros(2,7)];•a=a+a';a(find(a==0))=M;•result=[];p=1;tb=2:length(a);•while length(result)~=length(a)-1•temp=a(p,tb);temp=temp(:);•d=min(temp);•[jb,kb]=find(a(p,tb)==d);•j=p(jb(1));k=tb(kb(1));•result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[];•end•result•例、一个乡有7个自然村,其间道路如图所示,要以村为中心建有线广播网络,如要求沿道路架设广播线,应如何架设?Kruskal算法每步从未选的边中选取边e,使它与已选边不构成圈,且e 是未选边中的最小权边,直到选够n-1条边为止。
•clc;clear;•M=1000;•a(1,2)=50; a(1,3)=60;•a(2,4)=65; a(2,5)=40;•a(3,4)=52;a(3,7)=45;•a(4,5)=50; a(4,6)=30;a(4,7)=42;•a(5,6)=70;•[i,j]=find((a~=0)&(a~=M));•b=a(find((a~=0)&(a~=M)));•data=[i';j';b'];index=data(1:2,:);•loop=max(size(a))-1;•result=[];•while length(result)<loop•temp=min(data(3,:));•flag=find(data(3,:)==temp);•flag=flag(1);•v1=data(1,flag);v2=data(2,flag);•if index(1,flag)~=index(2,flag)•result=[result,data(:,flag)];•end•if v1>v2•index(find(index==v1))=v2;•else•index(find(index==v2))=v1;•end•data(:,flag)=[];•index(:,flag)=[];•end•result中国邮递员问题中国邮递员问题也可以表示为:在一个有奇点的连通图中。
随机森林最小叶子数调参matlab

随机森林最小叶子数调参matlab
随机森林是一种常用的机器学习算法,它可以用于分类和回归任务。
在随机森林的构建过程中,需要对一些参数进行调参,以达到更好的性能。
其中,最小叶子数是一个重要的参数,它决定了每个子树的最小样本数。
因此,调整最小叶子数可以影响随机森林的泛化能力和效率。
在Matlab中,我们可以使用TreeBagger函数来构建随机森林模型。
这个函数包含了许多参数,可以通过输入不同的值来调整模型的性能。
其中,'MinLeafSize'参数可以用来设置最小叶子数。
默认情况下,它的值为1,也就是每个子树至少需要一个样本。
如果将最小叶子数设置得太小,可能会出现过拟合的情况。
而如果将最小叶子数设置得太大,可能会出现欠拟合的情况。
因此,需要通过实验来找到最佳的最小叶子数。
具体来说,我们可以使用交叉验证的方法来评估不同最小叶子数下的模型性能。
首先,将数据集分为训练集和测试集。
然后,在训练集上使用TreeBagger函数构建随机森林模型,并设定不同的最小叶子数。
接着,使用测试集来评估模型性能,并记录下每个最小叶子数下的评估指标(如准确率、召回率、F1值等)。
最后,选择在测试集上表现最优的最小叶子数作为模型的参数。
总之,调整随机森林的最小叶子数是一个重要的步骤,可以帮助我们优化模型的性能。
在Matlab中,可以使用TreeBagger函数和交叉验证的方法来实现这个过程。
最小生成树算法的matlab代码实现
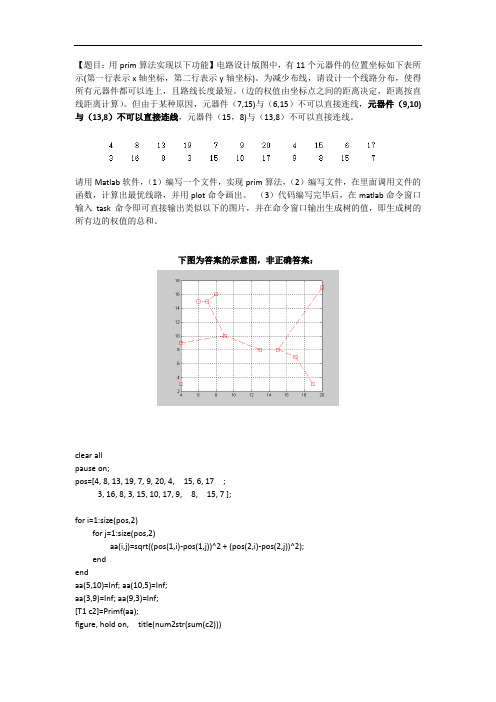
【题目:用prim算法实现以下功能】电路设计版图中,有11个元器件的位置坐标如下表所示(第一行表示x轴坐标,第二行表示y轴坐标)。
为减少布线,请设计一个线路分布,使得所有元器件都可以连上,且路线长度最短。
(边的权值由坐标点之间的距离决定,距离按直线距离计算)。
但由于某种原因,元器件(7,15)与(6,15)不可以直接连线,元器件(9,10)与(13,8)不可以直接连线,元器件(15,8)与(13,8)不可以直接连线。
请用Matlab软件,(1)编写一个文件,实现prim算法,(2)编写文件,在里面调用文件的函数,计算出最优线路,并用plot命令画出。
(3)代码编写完毕后,在matlab命令窗口输入task命令即可直接输出类似以下的图片,并在命令窗口输出生成树的值,即生成树的所有边的权值的总和。
下图为答案的示意图,非正确答案:clear allpause on;pos=[4, 8, 13, 19, 7, 9, 20, 4, 15, 6, 17 ;3, 16, 8, 3, 15, 10, 17, 9, 8, 15, 7 ];for i=1:size(pos,2)for j=1:size(pos,2)aa(i,j)=sqrt((pos(1,i)-pos(1,j))^2 + (pos(2,i)-pos(2,j))^2);endendaa(5,10)=Inf; aa(10,5)=Inf;aa(3,9)=Inf; aa(9,3)=Inf;[T1 c2]=Primf(aa);figure, hold on, title(num2str(sum(c2)))for i=1:size(T1,2)plot([pos(1,T1(1,i)),pos(1,T1(2,i)) ], [pos(2,T1(1,i)),pos(2,T1(2,i)) ] ,'-bs'), endplot([pos(1,3),pos(1,9) ], [pos(2,3),pos(2,9) ] ,'-rs'),plot([pos(1,5),pos(1,10) ], [pos(2,5),pos(2,10) ] ,'-rs'),grid onhold offfunction [Tree cost]=Primf(a)l=length(a);a(a==0)=inf;k=1:l;listOfVector(k)=0;listOfVector(1)=1;e=1;while (e<l)min=inf;for i=1:lif listOfVector(i)==1for j=1:lif listOfVector(j)==0 & min>a(i,j) %避圈min=a(i,j);b=a(i,j);s=i;d=j;endendendendlistOfVector(d)=1;distance(e)=b;source(e)=s;destination(e)=d;e=e+1;endTree=[source;destination];for g=1:e-1cost(g)=a(Tree(1,g),Tree(2,g));endcost;。
数学建模-最小生成树-kruskal算法及各种代码之欧阳与创编

kruskal算法及代码---含伪代码、c代码、matlab、pascal等代码K r u s k a l算法每次选择n- 1条边,所使用的贪婪准则是:从剩下的边中选择一条不会产生环路的具有最小耗费的边加入已选择的边的集合中。
注意到所选取的边若产生环路则不可能形成一棵生成树。
K r u s k a l 算法分e 步,其中e 是网络中边的数目。
按耗费递增的顺序来考虑这e 条边,每次考虑一条边。
当考虑某条边时,若将其加入到已选边的集合中会出现环路,则将其抛弃,否则,将它选入。
目录Kruskal算法1.算法定义举例描述Kruskal算法的代码实现1.伪代码C代码实现matlab代码实现pascal代码实现Kruskal算法1.算法定义举例描述Kruskal算法的代码实现1.伪代码C代码实现matlab代码实现pascal代码实现算法定义克鲁斯卡尔算法假设WN=(V,{E}) 是一个含有n 个顶点的连通网,则按照克鲁斯卡尔算法构造最小生成树的过程为:先构造一个只含n 个顶点,而边集为空的子图,若将该子图中各个顶点看成是各棵树上的根结点,则它是一个含有n 棵树的一个森林。
之后,从网的边集E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,也就是说,将这两个顶点分别所在的两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。
依次类推,直至森林中只有一棵树,也即子图中含有n-1条边为止。
举例描述克鲁斯卡尔算法(Kruskal's algorithm)是两个经典的最小生成树算法的较为简单理解的一个。
这里面充分体现了贪心算法的精髓。
大致的流程可以用一个图来表示。
这里的图的选择借用了Wikipedia上的那个。
非常清晰且直观。
首先第一步,我们有一张图,有若干点和边如下图所示:第一步我们要做的事情就是将所有的边的长度排序,用排序的结果作为我们选择边的依据。
