【资料】高等土力学(李广信)2.7-lade-duncan模型和清华弹塑性模型汇编
高等土力学(李广信)1-5章部分习题答案(最新版)

• 1-1拟在一种砂土上进行各种应力路径的三轴试验,施加的各向等压应力都是σc =100kPa ,首先完成了常规三轴压缩试验(CTC ),当时,试样破坏。
根据莫尔-库仑强度理论,试预测在CTE 、TC 、TE 、RTC 和RTE 试验中试样破坏时与各为多少?CTE 、TC 、TE 、RTC 、RTE 试验中的应力条件-两个未知数,两个方程。
莫尔-库仑强度理论:c =0;σ1/σ3=3.809(1)• CTC : σc = σ3=100kPa (2-1)• CTE (三轴挤长): σa =σ3=100kPa (2-2)• RTC (减压三轴压缩) : σa =σ1=100kPa (2-3)• RTE (减载三轴伸长) : σc = σ1=100kPa (2-4)• TC (p=c 三轴压) :2σ3+ σ1=300kPa (2-5)• CTE (p=c 三轴伸) :• 答案σ3+ 2σ1=300kPa (2-6)CTE : σ3= 100 kPa σ1-σ3 =208.9 kPaTC : σ3= 58.95 kPa σ1-σ3 =123.15 kPaTE :σ3= 41.8 kPa σ1-σ3 =87.3 kPaRTC :σ3= 32.4 kPa σ1-σ3 =67.6 kPaRTE : σ3= 32.4 kPa σ1-σ3 =67.6 kPa1-4解析,应力推导公式1-5答案: 567天,U =94%;n=100,U =99%-时间? 2222(1)31()()1()1(2)(3)1(4)331(5)3(6)(7)y x z x z x y x z x xx z x y x b b ctg z y q b b b b z q z b b y b z p z y b p z z y σσσσθσσσσσσσσσσσσ-'=-'='+=-=-''''=-+-=-+=''-+'=--='+=-=+=+221000028194%0.0046100,1000080.01, 2.3t v v t U e c t T H n te t h ββπβπ-=−−→=-====1-6答案:• 蠕变比尺为1,仍为120年2-1.什么叫材料的本构关系?在上述的本构关系中,土的强度和应力-应变有什么联系?答:材料的本构关系是反映材料的力学性质的数学表达式,表现形式一般为应力-应变-强度-时间的关系,也成为本构定律,本构方程。
2023年高等土力学试题考博专用

参考书目《高等土力学》李广信第1章土工实验及测试一、简述土工实验的目的和意义。
1)揭示土的一般或特有的物理力学性质。
2)针对具体土样的实验,揭示区域性土、特殊土、人工复合土的物理力学性质。
3)拟定理论计算和工程设计的参数。
4)验证理论计算的对的性及实用性。
5)原位测试、原型监测直接为土木工程服务,也是分析和实现信息化施工的手段。
第2章土的本构关系★二、广义讲,什么是土的本构关系?与其他金属材料比,它有什么变形特性(应力应变特性)?(2.3节)P51土的本构关系广义上讲是指反映土的力学性状的数学表达式,表达形似一般为应力-应变-强度-时间的关系。
与金属材料相比,土的变形特性包含:①土应力应变的非线性。
由于土由碎散的固体颗粒组成,土的宏观变形重要不是由土颗粒自身变形,而是由于颗粒间位置的变化。
这样在不同的应力水平下由相同应力增量引起的应变增量就不会相同,即表现出非线性。
②土的剪胀性。
由于土石由碎散颗粒组成的,在各向等压或等比压缩时,孔隙总是减少的,从而可发生较大的体积压缩,这种体积压缩大部分死不可恢复的,剪应力会引起土塑性体积变形,这叫剪胀性,另一方面,球应力又会产生剪应变,这种交叉的,或者耦合的效应,在其他材料中很少见。
③土体变形的弹塑性。
在加载后再卸载到本来的应力状态时,土一般不会完全恢复到本来的应变状态,其中有一部分变形是可以恢复的,部分应变式不可恢复的塑性应变,并且后者往往占很大的比例。
④土应力应变的各向异性和土的结构性。
不仅存在原生的由于土结的各向构异性带来的变形各向异性,并且对于各向受力不同时,也会产生心的变形和各向异性。
⑤土的流变性。
土的变形有时会表现出随时间变化的特性,即流变性。
与土的流变特性有关的现象只要是土的蠕变和应力松弛。
影响土的应力应变关系的应力条件重要有应力水平,应力途径和应力历史。
★三、何为土的剪胀性,产生剪胀的因素?P52(2.3.2)土体由于剪应力引起的体积变化称为剪胀性,广义的剪胀性指剪切引起的体积变化,既涉及体胀,也涉及体缩,但后者常被称为“剪缩”。
清华大学-《土力学》(李广信)学课后习题答案

d
1-2: 已知:Gs=2.72
设 Vs=1cm3
s 2.72 g / cm3
ms 2.72 g ms 2.72 g *10 16 KN / m3 V 1.7 m V 2.72 0.7 *1 g s V w g *10 20.1KN / m3 V 1.7 则 w 20.1 10 10.1KN / m3
又 hA hB hC 35cm
hA 5cm, hB 10cm, hC 20cm
V kA hA 1*103 cm / s LA
V加水 V * A * t=0.1cm3
2-2 解:
icr
Gs 1 2.70 1 1.076 1 e 1 0.58 h 20 1*9.8* 6.53 N L 30
流塑状态
乙: I L
坚硬(半固态)
I p wL w p 15
属于粉质粘土(中液限粘质土)
乙土较适合作天然地基 1-9:
A甲 I p甲 P0.002甲 53 36 0.31 0.75 55
属非活性粘土
A乙
I p乙 P0.002乙
70 35 1.3 1.25 27
乙:
I p wL wp 8 设Vs 1则ms sVs 2.68 g mw ms w 2.68* 22% 0.4796 g 则VV 0.4796cm3 ms mw 2.68 0.4796 2.14 g / cm3 1 0.4796 Vs VV ms 2.68 1.84 g / cm3 Vs Vw 1.4796
土的弹塑性模型

土的弹塑性模型近年来,根据弹塑性理论建立的土的弹塑性模型发展很快,各国学者提出的弹塑性本构模型很多。
下面几节分别介绍剑桥模型,修正剑桥模型,Lade-Duncan 模型,以及清华模型的基本概念。
一.剑桥模型英国剑桥大学Roscoc 和他的同事(1958 ~ 1963 )在正常固结粘土和超固结粘土试样的排水和不排水三轴试验的基础上,发展了Rendulic (1937)提出的饱和粘土有效应力和孔隙比成唯一关系的概念,提出完全状态边界面的思想。
他们假定土体是加工硬化材料,服从相关联流动规则,根据能量方程,建立剑桥模型。
剑桥模型从理论上阐明了土体弹塑性的变形特性,标志着土的本构理论发展新阶段的开始。
1.临界状态线和Roscoe 面各向等压固结过程中,孔隙比e 或比容()1e υυ=+与有效应力的关系可用下式表示: ln N p υλ'=- (1) 式中 N —— 当 1.0p '=时的比容。
因此exp N p υλ-⎛⎫'= ⎪⎝⎭(2)(a ),p q ''平面(b ),ln p υ'平面图1 临界状态线正常固结粘土排水和不排水三轴试验表明:它们有条共同的破坏轨迹,与排水条件无关。
破坏轨迹在,p q ''平面上是一条过原点的直线,在,ln p υ'平面上也是直线,目与正常固结线平行,分别如图(a )和(b 〕 所示。
破坏轨迹线可用下式表示:cs csq Mp '= (3)ln cs csp υλ'=Γ- (4) 式中 CS ——表示临界状态;M——,p q''平面上临界状态线斜率;Γ—— 1.0p'=时土体的比容;csυ'平面上临界状态线斜率。
λ——,ln p一旦土体的应力路径到达这条线,土体就会发生塑性流动。
这时土体被认为处于临界状态,破坏轨迹被称为临界状态线。
临界状态线在,,''空间为一条空间曲线,如下图2所示。
清华大学-土力学(李广信)课后习题答案

85000m3
1-4: 甲:
I p wL wP 40 25 15
设Vs 1则
ms s *Vs 2.7g
mw 2.7 *30% 0.81g
又因为 Sr 100%
VV
mw w
0.81
ms mw 2.7 0.81 1.94g / 9.4KN / m3
则可得: d 1.78g / cm3
1-7: 设 S=1, 则Vs Sh h 则压缩后:
ms VsGs 2.7h mw msw 2.7h * 28%
则Vw
mw w
2.7h * 28%
Vs Vw 2.7h * 28% h 1.95 则 h 1.11cm
hV 2.0 1.11 0.89cm
1
sat
1
又 sat粘土 sat砂层 ,故只考虑 sat粘土 就可以
icr sat粘土 1 2.04 1 1.04g / cm3
1-9:
A甲
I p甲
53 36
0.31 0.75
P0.002甲
55
属非活性粘土
A乙
I p乙
70 35
1.3 1.25
P0.002乙
27
属活性粘土
乙土活动性高,可能为伊利石,及少量的高岭石,工程性质乙土的可能较
2-1 解:
第二章
根据渗流连续原理,流经三种土样的渗透速度 v 应相等,即 vA vB vC
根据达西定律,得: RA
hA LA
RB
hB LB
RC
hC LC
hA : hB : hC 1: 2 : 4
又 hA hB hC 35cm
hA 5cm, hB 10cm, hC 20cm
高等土力学(李广信)2.5 土的弹塑性模型的一般原理

面重合,即f=g。
不相适应(不相关联)的流动(nonassociated
flow rule):塑性势面不必与屈服面重合fg。
dpij
dij
Drucker 假说:对于稳定材 料:
图2-42 Drucker 假说
认为A与A´在同一屈服面上
图2-41
三轴试验与真三轴试验确定塑性应变增量方向
2.5.3流动规则与硬化定律
1. 流动规则 (flow rule) 2. 硬化定律 (strain-hardening law)
1. 流动规则(flow rule):用以确定塑性应变增量 向量的方向的规则(或者确定塑性应变增量的 各个分量间的比例关系)-塑性应变增量向量 正交于塑性势面。所以也称为正交规则。
d
ijd
P ij
0
屈服面的外凸 与塑性应变增 量向量的正交
锥形屈服面与帽子屈服面 q
dpij dpij
p 图2-43 与两种屈服面的正交的塑性应变
表现土的塑性剪胀与剪缩,锥形屈服面会使剪胀量过 大,一般采用不相适应的流动规则
2. 加工(应变)硬化定律 (strain-hardening law): 是确定在一定的应力增量作用下引起的塑性应变增
2.5.2屈服准则与屈服面
1. 屈服准则 2. 屈服函数 3. 屈服面与屈服轨迹 4. 土的屈服面与屈服轨迹的一般形式 5.土的屈服面与屈服轨迹的确定
1. 屈服准则(yield criterion)
判断是否发生塑性变形的准则 -判断加载与卸载的准则
ABBຫໍສະໝຸດ AABA B
A、B在屈服面上, A B不在屈服面上
Lade-Duncan模型读书报告

荷载作用下砂土的应力-应变关系(砂土本构模型)是表征砂土力学特性的基本关系,也是分析砂土强度和变形等一系列特性的基础.目前,国内外具体建立的砂土本构模型大致可以分为以下3类.1)弹性模型,如:Hooke定律和Duncan-Chang模型.2)符合相关流动法则的弹塑性模型,如:Mohr-Coulomb模型、Drucker-Prager模型、统一空间滑动面(SMP)模型、清华弹塑性模型等.3)符合非相关流动法则的弹塑性模型,如:Lade-Duncan模型、修正Lade-Duncan模型、Single-Harding模型等.在一般情况下,砂土的应力-应变关系受中间主应力、剪胀性及应力路径相关性等因素的影响呈非线性.采用弹性模型来描述砂土特性往往有较大偏差.Lade等通过大量试验研究发现,砂土塑性应变增量方向不正交于屈服面.因此,采用非相关流动法则的砂土本构模型更符合实际.Lade-duncan 模型是由LADE P V和DUNCAN J M于1975年在期刊JournaloftheSoilMechanicsandFoundationsDivision上提出的,论文名称为Elasto-plastic stress-straintheory for cohesionless soil 。
Lade和Duncan根据真三轴仪上砂土试验成果,建立了一个适应三维空间的弹塑性应力-应变模型。
Lade-Duncan弹塑性模型该模型基于砂土的真三轴试验得出,其应变总量由弹性应变总量与塑性应变总量组成,可表示为{dε}={dεe}+{dεp}。
弹性应变增量dεe采用广义虎克定律求得。
假定砂土在生成和受荷过程中是各向同性。
砂土破坏条件与屈服函数分别表示为I31I3=kf,f=I31I3式中:kf为与砂土密实度有关的常数,通过试验确定。
该模型认为:随着塑性变形的发展,土体内部应力增大,屈服面逐渐扩大,破坏面为屈服面的极限状态[12];土体受力时服从非关联流动准则,塑性势函数g采用类似屈服函数形式的表达式,即g=I31-K2I3,式中:K2为取决于f的常数,与侧压力σ3大小无关.L-d模型有如下特点:1.采用不相适应的流动准则2.以塑性功为硬化参数 3.过坐标原点的射线屈服轨迹-圆锥形屈服面 4.主要适用于沙土L-D模型中参数分为以下4类:弹性常数...,破坏常数,塑性势常数,塑性功常数,因为原模型只有锥面,即只有剪涨,在静水压力下,没有塑性体应变,不能反映土在各向等压的应力下不产生屈服的现象,所以Lade又针对Lade-Duncan弹塑性模型进行了修正,形成了两套屈服面,将原来的直线屈服轨迹改为弯曲的并增加了“帽子”屈服面,即圆锥面加帽子面,以反映比例加载条件、应变软化和强度随围压变化等因素。
高等土力学-习题解答-李广信

第3章习题摩尔-库仑公式推导:ϕ+ϕσ+σ=σ-σcos c sin 223131 即: 231231]cos c 2sin )[()(ϕ+ϕσ+σ=σ-σ,同理有;232232]cos c 2sin )[()(ϕ+ϕσ+σ=σ-σ; 221221]cos c 2sin )[()(ϕ+ϕσ+σ=σ-σ破坏面条件:{}{}{}0]cos c 2sin )[()(]cos c 2sin )[()(]cos c 2sin )[()(221221232232231231=ϕ+ϕσ+σ=σ-σ⨯ϕ+ϕσ+σ=σ-σ⨯ϕ+ϕσ+σ=σ-σ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧+⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧π-θ-θπ+θ=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧σσσ1112321I 31I 31I 31)6cos()sin()6cos(J 32 将该式代入上式得:0cos C J )3sin sin (cos sin I 3121=ϕ+ϕθ+θ-ϕ π平面上各轴的投影:在1σ轴上的投影:2S 2321321=σ-σ-σ在2σ轴上的投影:2S 2322312=σ-σ-σ在3σ轴上的投影:2S 2323213=σ-σ-σ如: 1σ=400kPa, 2σ=3σ=100kPa. 则在三个轴上的投影分别为: 141kPa, -71kPa, -71kPa.1、临界状态:是指土在常应力和常孔隙比下不断变形的状态。
临界孔隙比:表示土在这种密度状态下,受剪作用只产生剪应变而不产生体应变。
水力劈裂:由于孔隙水压力的升高,引起土体产生拉伸裂缝发生和发展的现象。
饱和松砂的流滑:饱和松砂在受静力剪切后,因体积收缩导致超孔压骤然升高,从而失去强度和流动的现象。
真强度理论:为了反映孔隙比对粘土抗剪强度及其指标的影响,将抗剪强度分为受孔隙比影响的粘聚分量与不受孔隙比影响的摩擦分量。
通过不同的固结历史,形成等孔隙比的试样,在不同的法向压力下剪切,试样破坏时的孔隙比相同,强度包线即为孔隙比相同的试样的强度包线,该强度称为在此孔隙比时的真强度。
11高等土力学-大作业

2011年“高等土力学”大作业1. 推导土弹塑性应力应变关系的一般表达式。
简述土弹塑性本构关系的三大支柱的主要内容。
2. K-G 模型(Domachuk 模型)中,K 和G 分别如何确定,其中2t )1(f f i q q R G G -=如何得到? 3. 分别详述Lade-Duncan 模型、清华(黄文熙)模型、南科所模型、松岗元模型,并评述之。
4. 详述Biot 固结理论及其与Terzaghi 一维固结理论的异同。
5. 详述沉降计算几种方法:弹塑性理论法、应力路径法、剑桥模型法等。
6. 分别推导Prandtl 、Reissner 和Terzaghi 条件下地基极限承载力公式。
7. 详述强度折减法及其应用。
8. 对深埋基础,Meyerhof 、Vesic 和Terzaghi 分别如何得到极限承载力?地基承载力的深度、宽度修正系数是如何得到的?9. 说明临界状态土力学的要点。
2010年“高等土力学”课程考试试题(二)1. 什么是加工硬化?什么是加工软化?绘出它们的典型的应力应变关系曲线。
2.试绘出下述试验的应力路径:(1)侧限压缩试验;(2)无侧限压缩试验;(3)普通三轴试验的:(a ) CU 试验(有效应力及总应力);(b )CD 试验(除CU 试验的有效应力路径外,其余都必须给出路径线的倾角或其正切值);3.定性绘出很疏松和密实状态的同一种砂土的在固结不排水试验中的应力-应变-孔压(σ1-σ3)~ε1~u 关系曲线。
4.用同样密度、同样组成的天然粘土试样和重塑粘土试样进行三轴试验,一般哪一个的抗剪强度高一些?在正常固结土地基中进行十字板剪切试验,作用在园柱形剪切体上的侧向抗剪强度h τ和作用在其上下端面上的抗剪强度vτ一般哪一个大?为什么?5.在软粘土地基上修建两个大型油罐,一个建成以后分期逐渐灌水,6个月以后排水加油;另一个建成以后立即将油加满。
后一个地基发生破坏,而前一个则安全。
绘制二者地基中心处的有效应力路径,并解释为什么。
高等土力学主要知识点整理(李广信版)

第二章 土的本构关系(一)概述材料的本构关系是反映其力学性能的数学表达式,一般为应力-应变时间-强度的关系,也称本构定律、本构方程。
土的强度是土受力变形的一个阶段,即微小应力增量小,发生无限大(或不可控制)应变增量,实际是本构关系一个组成部分,是土受力变形的最后阶段。
第一应力不变量kk z y x I σσσσ=++=1第二应力不变量kk yz xz xy z y z x y x I στττσσσσσσ=---++=2222第三应力不变量22232xyz xz y yz x yz xz xy z y x I τστστστττσσσ---+= 坐标系选择使剪应力为零 3211σσσ++=I ,3231212σσσσσσ++=I 3213σσσ=I 球应力张量)(31)(3131321332211σσσσσσσσ++=++==kk m 偏应力张量ii kk ij ij s δσσ31-=,其中⎩⎨⎧=≠=j i j i ii 10δ,克罗内克解第一偏应力不变量01≡=kk s J 第二偏应力不变量()()()[]23123222126121σσσσσσ-+-+-==ji ij s s J 第二偏应力不变量()()()213312321322227131σσσσσσσσσ------==ki jk ij s s s J 1.土的应力应变特性:非线性(应变/加工硬化、应变/加工软化)、剪胀性、弹塑性、各向异性、结构性、流变性(蠕变、应力松弛)。
加工硬化:应力随应变增加而增加,但增加速率越来越慢,最后趋于稳定(正常固结黏土、松砂)加工软化:应力一开始随应变增加而增加,超过一个峰值后,应力随应变增加而减小,最后趋于稳定(超固结黏土、松砂)剪胀性:剪应力引起的体积变化,含剪胀和剪缩土的结构性:由土颗粒空间排列集合、土中各相和颗粒间作用力造成,可明显提高土的强度和刚度。
灵敏度:原状黏性土与重塑土的无侧限抗压强度之比土的蠕变:应力状态不变条件下,应变随时间逐渐增长的现象,随土的塑性、活动性、含水量增加而加剧土的应力松弛:维持应变不变,材料内应力随时间逐渐减小的现象压硬性:土的变形模量(指无侧限,压缩模指完全侧限)随围压而提高的现象。
高等土力学考试题复习思考题与参考答案汇总

硕士研究生《高等土力学》复习思考题一(a)、将下面描述“土力学和岩土工程”的英文译成中文Soil MechanicsThis class presents the application of principles of soil mechanics. It considers the following topics: the origin and nature of soils; soil classification; the effective stress principle; hydraulic conductivity and seepage; stress-strain-strength behavior of cohesionless and cohesive soils and application to lateral earth stresses; bearing capacity and slope stability; consolidation theory and settlement analyses; and laboratory and field methods for evaluation of soil properties in design practice.Soil amongst most variable and difficult of all materials to understand and model1. Complex stress-strain (non-linear , irreversible 不可逆的)2. Properties highly variable function of soil types and stress history3. Properties change with time, stress, environment, …4. Every site has different soil conditions - new challenge5. Soil "hidden" underground and data on small fraction of deposit Geotechnical EngineeringThis course describes the application of soil mechanics in the analysis and design of foundations (shallow and deep) and earth retaining structures. The lectures include an overview of geotechnical site investigation methods and in situ tests used to estimate engineering parameters. The course emphasizes the importance of parameter selection in calculations of ultimate and serviceability limit state calculations for both shallow and deep foundations, and discusses methods of soil improvement. The section on earth retaining structures considers systems ranging from gravity walls to composite construction (reinforced earth), from structural support to field monitoring of excavations (bracing, tieback anchors etc.).(1)What is consolidation?Consolidation is a time-related(时间性) process of increasing the density(增加密度) of a saturated soil by draining some of the water out of the voids.(2)The shear strength of a soil [土的抗剪强度] (τf ) at a point on a particular plane was originally expressed by Coulomb as a linear function of the normal stress (σ’f ) on the plane at the same point by'tan ''φστ⋅+=f f cwhere c’ is cohesion [粘聚力] and φ’ is internal angle of friction [内摩擦角].(3)Ultimate bearing capacity (qu) is defined as the pressure which would cause shear failure of the supporting soil immediately below and adjacent to a foundation. (当基底压力增大到极限承载力时,地基出现剪切破坏)(4)Allowable bearing capacity (qa) is defined as the maximum pressure which may be applied to the soil such that the above two requirements are satisfied. From first requirement, qa is defined as: (地基的容许承载力 qa 定义为当上述两个条件满足时的基底最大压力.当条件一满足时qa 定义如下)sua F q q =(5)A foundation must satisfy two fundamental requirements: (设计基础要满足两个要求 ) (a) the factor of safety Fs against shear failure of the supporting soil must be adequate, a value between 2 and 3 normally being specified (地基达到剪切破坏的安全糸数 Fs 要适当,一般在2至3之间 )(b)the settlement of the foundation should be tolerable and, in particular , differential settlement should not cause any unacceptable damage of the structure (基础的沉降和沉降差必须在该建筑物所允许的范围之内)Example 5.5A saturated clay has the following properties:7.2,15.0s ==G λof the soil. Prove that a 1% increase in water content can cause a 20% reduction in the undrained shear strength.SolutionFor undrained triaxial (UU or CU) tests of saturated soils, the volume of the specimen is not allowed to change during axial compression or extension. Therefore, the effective mean stress at failure is given byf f 0ln p e e e '-==Γλor⎪⎭⎫⎝⎛-='Γλ0f exp e e pwhere e0 is the initial void ratio and eis the void ratio on the CSL when p' =1. Theundrained shear strength is therefore⎪⎭⎫ ⎝⎛-='==Γλ0f f u exp 222e e M p M q cnts. The onlyvariable is the initial void ratio. This indicates that the undrained shear strength depends only the initial void ratio. For saturated soil, we have e=wGs. Therefore, for two initial void ratio, e1 and e2, the corresponding undrained shear strength cu1 and cu2 are related to each other as()⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=ΓΓλλλλ12s 1221u2u1exp exp exp exp w w G e e e e e e c cFor water content increase of 1%, with7.2,15.0s ==G λ, we have()2.115.001.07.2exp u2u1=⎪⎭⎫⎝⎛=c cTherefore, the undrained shear strength is decreased by 20%.一(b)、《高等土力学》研究的主要内容。
高等土力学-课件

ε
1、沉降计算问题
σ
τf
ε
2、土压力问题 3、边坡稳定问题 4、地基承载力问题
强度问题加变形问题
极限平衡分析 条分法 k=1.4
强度问题加变形问题
上海倒楼问题 成寿寺邮电出版社基坑(上抬)
相互作用问题
有限土体土压力问题
深、大基础承载力问题 Pu=cNC + rdNq + rbNr/2
内蒙鄂尔多斯某砼搅拌站
(1930年,美国哈佛大学工硬化 加工软化
εa
不同应力路径下来做三轴试验:
1、常规 σr不变 σa增加
三轴压缩
σr不变 σa减小
三轴挤压(三轴拉伸)
其他
σa不变 σr增加 三轴挤压 σa不变 σr减小 三轴压缩 σa增大 σr减小 但平均应力不变
三轴压缩
σr增大 σa减小 但平均应力不变 三轴挤压
J.H.Atkinson, P.L.Bransby
主要内容
1、引言 2、土工试验 3、应力分析、应变分析 4、屈服准则 5、几个模型
Duncan— Chang Model Lade—Duncan Model Cambridge Model 6、渗流问题 7、简单的测试与讨论
李广信 70万字
龚晓南 24万字
高等土力学
(Advanced Soil Mechanics)
张钦喜
北京工业大学
2014.09
高等土力学(32h) (Advanced Soil Mechanics)
主要参考文献:
1、土的本构关系 蒋彭年 科学出版社 1982 2、土的塑性力学 屈智炯 成都科技大学出版社
1987 3、土的塑性力学 龚晓南 浙江大学出版社
土的本构关系研究现状与发展方向

土的本构关系研究现状与发展方向作者:吴玺杨觅来源:《武汉科技报·科教论坛》2013年第10期【摘要】本文介绍了土的本构关系的研究历程,概述了土的本构关系的研究现状和目前常见的理论模型,讨论了经典模型的建立依据和适用条件,分析了各模型的优缺点,并对土的本构模型的研究方向进行了评述。
【关键词】土力学;土的本构模型;现状;发展方向一、土的本构关系的概述土体是在漫长的地质历史中形成的。
土是一种复杂的多孔材料,在受到外界荷载作用后,其变形具有以下特性:1.土体的变形具有明显的非线性,如:土体的压缩试验e-p曲线、三轴剪切试验的应力应变关系曲线、现场承载板试验所得p-s曲线等;2.土体在剪切应力作用下会产生塑性应变,同时球应力也引起塑性应变;3.土体尤其是软粘土,具有十分明显的流变特性;4.由于土体的构造或沉积等原因,使土具有各向异性;5.紧砂、超固结粘土等在受剪后都表现出应变软化的特性;6.土体的变形与应力路径有关,证明不同的加载路径会出现较大的差别;7.剪胀性等。
为了更好地描述土体的真实力学变形特性,建立其应力、应变和时间的关系,在各种试验和工程实践经验的基础上提出一种数学模型,即:土体的本构关系。
二、常见的土的本构模型(一)线弹性本构关系线性弹性模型是假设土的应力与应变成正比,强度是无限的。
线性弹性模型对计算地基中的垂直应力分布是很有用的,得到的结果比较符合实际,但是计算地基的位移和沉降,该模型只适用于不排水加荷的情况,并且对破坏要有较大的安全系数,不能发生屈服。
土的线弹性模型简单,但适用范围有限。
(二)非线性弹性本构关系土的非线弹性模型理论可以分为三类:弹性模型、超弹性(Hyper Elastic)模型(又称Green超弹性模型)和次弹性( Hypo Elastic)模型。
其中影响最大、最具有代表性的主要是邓肯一张( Duncan- Chang)(即D-C)模型。
这类模型理论基础有局限性,不能反映不同应力路径的影响,不能反映土的剪胀性等。
高等土力学(李广信)3.6-土的强度理论

1. 特雷斯卡(Tresca)准则与广义特雷斯卡 (extended Tresca)准则
2k
1
3
J2
sin
π 2
k
0
广义形式
1
3
2k
I 1
J2
sin
π 2
k
1 2
I1
0
图3-79 特雷斯卡与米泽斯准则
六棱柱的表面:
J2
sin
π 2
k
0
锥面 图3-80 广义的形式
2. 米泽斯(Von Mises)和广义米泽斯(extended Von Mises)准则
1
2
sin 2 13 sin 2 12 sin 2 23
1 2
sin
其中:
sin
ij
i i
j j
3.6.2 土的经典强度理论
1. 特雷斯卡(Tresca)准则及其广义准则 2. 米泽斯(Von Mises)准则及其广义准则 3. 莫尔-库仑(Mohr-Coulomb)强度准则 4. 三个强度准则的讨论
kf
1
3
2
13
1 2 2
1 2
2 3 2
2 3
kf
9
tg212+ tg223+ tg213=kf
图3-91 不同强度参数平面上的强度轨迹
3. 双剪应力强度理论 12面体应力的概念
13
1 2
1
3
12
1 2
1
2
23
1 2
2
3
主正应力
13
1 2
1
3
12
1 2
1
2
23
1 2
高等土力学第四讲2012

p
q p
帽子屈服面
p
12
浙江工业大学建筑工程学院
3)二者的联合形式
q
P
普遍形式的屈服面
13
浙江工业大学建筑工程学院
5.土的屈服面与屈服轨迹的确定 1)假设屈服面与屈服函数
2)通过试验试加载勾画屈服轨迹
3)通过试验确定塑性应变增量的方向和Drucker 公设确定塑性势面=屈服轨迹(清华弹塑性模型)
4. 土的屈服面与屈服轨迹的形状
5.土的屈服面与屈服轨迹的确定
6
浙江工业大学建筑工程学院
1. 屈服准则(yield criterion) 判断是否发生塑性变形的准则 -判断加载与卸载的准则
A B B
B
A
A
A
B
A、B在屈服面上, A B不在屈服面上 屈服-弹塑性应变的判断准则
加卸载的判断(应变硬化情况)
f d ij 0 ij
为加载,同时发生弹性、 塑性变形
f 0
f d ij 0 ij
为中性变载,只产生弹性变形
f d ij 0 ij
为卸载,只产生弹性变形
f <0 在屈服面之内,弹性变形
9
浙江工业大学建筑工程学院
3. 屈服面与屈服轨迹 屈服面-屈服准则在应力空间中的几何表示: 1)三维应力空间:屈服面 2)二维应力空间:屈服轨迹
e
{d}
24
浙江工业大学建筑工程学院
g f D D d =Dd d T f g A+ D
T g f D D = D T d f g A+ D =D ep d
高等土力学-李广信-清华版
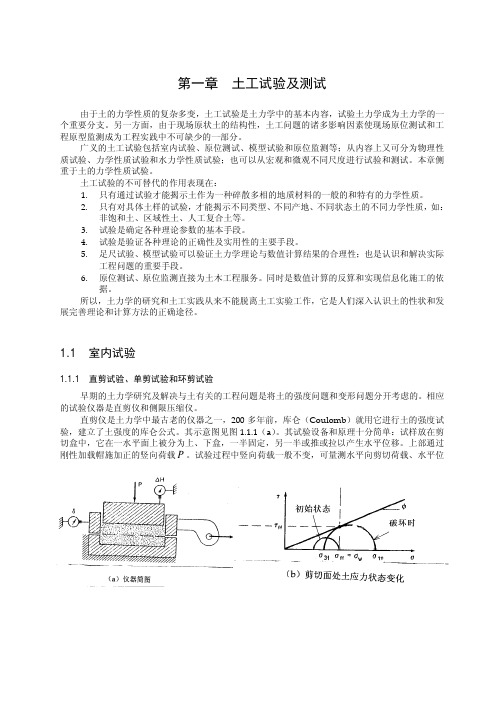
第一章 土工试验及测试
(6) 减载的三轴伸长(RTE:Reduced triaxial extension)试验 试样首先在σ c 下等向压缩固结,然后保持室压σ c 不变,轴向σ a 减小,即 ∆σ 3 = ∆σ a < 0 ,
∆σ 1 = ∆σ 2 = ∆σ c = 0 ,试样被轴向伸长,可达到破坏。由于室压不变,试样伸长,所以这种试验 也被称为三轴伸长试验。这时θ = 30o 或 b = 1.0 。当σ 3 < 0 时,试样中实际上存在拉应力,可引起
三轴试验。对于所有的三轴试验,试样受到的三个主应力总有两个是相等的。所以常用平均主应力 p
和广义剪应力σc) q=(σa‐σc) 在一般应力状态下,为了表示中主应力的大小,常用另外两个参数表示:
(1.1.1) (1.1.2)
b = (σ 2 − σ 3 ) /(σ 1 − σ 3 )
第一章 土工试验及测试
由于土的力学性质的复杂多变,土工试验是土力学中的基本内容,试验土力学成为土力学的一 个重要分支。另一方面,由于现场原状土的结构性,土工问题的诸多影响因素使现场原位测试和工 程原型监测成为工程实践中不可缺少的一部分。
广义的土工试验包括室内试验、原位测试、模型试验和原位监测等;从内容上又可分为物理性 质试验、力学性质试验和水力学性质试验;也可以从宏观和微观不同尺度进行试验和测试。本章侧 重于土的力学性质试验。
土工试验的不可替代的作用表现在: 1. 只有通过试验才能揭示土作为一种碎散多相的地质材料的一般的和特有的力学性质。 2. 只有对具体土样的试验,才能揭示不同类型、不同产地、不同状态土的不同力学性质,如:
非饱和土、区域性土、人工复合土等。 3. 试验是确定各种理论参数的基本手段。 4. 试验是验证各种理论的正确性及实用性的主要手段。 5. 足尺试验、模型试验可以验证土力学理论与数值计算结果的合理性;也是认识和解决实际
(完整word版)高等土力学思考题与概念题

思虑题第一章:1. 对于砂土,在以下三轴排水试验中, 哪些试验在量测试样体变时应试虑膜嵌入(membrane penetration)的影响? HC, CTC, CTE, RTC, RTE, 以及均匀主应力为常数的 TC TE 试验。
2.对于砂土,在惯例三轴固结不排水 (CU) 压缩试验中,围压 为常数,其膜嵌入 (membrane penetration)效应付于试验量侧的孔隙水压力有没有影响,为何?对于惯例三轴固结排水试验对于试验有无影响? 3.对于砂土,在惯例三轴固结不排水 (CU) 压缩试验中,围压 为常数,其膜嵌入 (membrane penetration)效应付于试验的不排水强度有没有影响, 4.在周期荷载作用下饱和砂土的动强度 d (或 d )怎样表示?定性绘出在相同围压 3,不一样初始固结比1/ 3 下的动强度曲线。
5.在必定围压下, 对小于、等于和大于临界孔隙比 e cr 密度条件下的砂土试样进行固结不排水三轴试验时,损坏时的膜嵌入对于量侧的孔隙水压力有何影 响?对其固结不排水强度有什么影响(无影响、偏大仍是偏小)?6.在土工离心模型试验中进行固结试验,假如模型比尺为 100,达到相同固结度,模型与原型对比,固结时间为多少?7.举出三种土工原位测试的方法,说明其工作原理、获得的指标和用途。
8.对于粗颗粒土料,在室内三轴试验中常用哪些方法模拟?各有什么优弊端?9.真三轴试验仪器有什么问题影响试验结果?用改制的真三轴试验仪进行试验,其应力范围有何限制?10. 在饱和土三轴试验中, 孔压系数 A 和 B 反应土的什么性质?怎样提升孔压系数 B ?11. 在 p, q 坐标、 , 坐标和在 平面坐标下画出下边几种三轴试验的应力路径(标出应力路径的斜率) 。
(1) CTC (惯例三轴压缩试验) (2) p =常数, b=0.5=常数,真三轴试验; (3) RTE (减压的三轴伸长试验) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p-q平
面
平面上
图2-69 塑性应变增量的方向与屈服轨迹
f gph2q210(1)
kh krh
近似为椭圆屈服轨迹
k2p2 k2 1q2 p
h
r2
(2)
k2 1
硬化参数h
根据正交性,式(1)微分+式(2),得到:
f gph2q210
kh krh
d d V p pd dq pr2xk2 r2 1 xx2k2k2 r 21 (3)
高等土力学(李广信)2.7-LadeDuncan模型和清华弹塑性模型
1.弹性应变的确定
ij iej ipj
dij diejdipj
1.弹性应变 eij的确定
n
E
kur
pa
3
pa
假设泊松比常数
有关常数通过三轴试验的初始模量确定E
2. 破坏面、屈服面、塑性势面及其函数式
破坏面函数: 屈服函数: 塑性势函数:
3)塑性剪胀部分的参数
塑性势函数中的参数
2 Sfp R 3 pa t
常数S, t, R
p d3p gp 3 d1p gp 1
2f(I1,1,3,p)
3Hale Waihona Puke 塑性剪胀部分的参数剪胀变形的塑性功Wp中的参数:
1
1
fp
aebWp
Wp
pa
q
a
1
e W
pa
p峰
q
(1)
b 1
(2)
qW p峰
l
Wp峰
从式(5)和此图中
两个点确定 r, k 两个
常数
图2-70 三轴试验确定屈服函数中的参数
3. 硬化参数的确定 h
k2p2 k2r21q2 p k2 1
f1 I13 I3 kf
f I13 I3 k
gI13k2I3 0
q
破坏面、屈服面、塑性势面的 几何形状
破坏轨迹 屈服轨迹
p 塑性势轨迹
图2-61 破坏面、屈 服面、塑性势面在 子午面上的轨迹
图2-62
在平面上的破坏、屈服面轨迹
3.硬化参数与应力应变关系
硬化参数: 塑性功Wp
Wp
d p ij ij
ft:初应力水平
a
M
p
a
(
p
3 a
)l
d
1
( f f t ) u lt
rf
K f ft ( f f t ) u lt
破坏比
Lade-Duncan模型的参数
弹性常数:K,n,
破坏常数:K1 塑性势常数(K2): A 塑性功常数:M, l, rf, ft,
2.7.2 修正的Lade-Duncan模型
原模型只有锥面,亦即只有剪胀; 在静水压力下,没有塑性体应变; 所以作者进行修正。
图2-64 只有塑性剪胀 的屈服面
两套屈服面:圆锥面+帽子屈服面。 破坏面、屈服面、塑性势面的子午线是微弯的 可反映土的应变软化。
1. 弹性变形与两种塑性应变
dijdiejdicjdipj
d
p ij
塑性剪胀应变
p: 是试验数据 I1,1,3 :相应的应力
通过以上关系式确定各应力状态下的k2 绘制K2与f的直线,确定常数A
K2
f
k2
3I12 1p 3 1 p3
图2-63 参数K2的试验确定
K 2A f27(1A )
对于承德中密砂A=0.415
塑性功Wp中的常数-假设
(f
ft )
Wp a dWp
4. 有关参数的确定
1)弹性参数E、:
三轴卸载
2)塑性塌陷部分的参数:c和p从三 轴试验确定
Wc
cPa
fc pa 2
p
3)塑性剪胀部分的参数
强度参数:和m: 不同围压下的破坏试验
1
I13
I3
27I1
pa
m
pa/I1 与(I13/I3-27)的双对数坐标曲线:
lg ( I 1 3 /I 3 2 7 ) lg 1 m lg ( I 1 /p a )
其中:
x
p q
1
设
Z
arctg
dVp d p
(4)
Z
arctg
dVp d p
(4)
d dV p pd dq p r2xk2 r2 1 xx2k2k2 r2 1 (3)
代入公式(4)
tg zr2xk2 r2 1xx2k2k2 r2 1
(5)
Z
arctg
dv p d p
Pa
p
3 a
(3)
q3 pa
(4)
图2-67
承德中密砂Wp与塑性剪胀屈服函数fp间的关系
修正的Lade-Duncan模型中14个常数
Kur, n, , 弹性 m, 破坏与屈服
c, p, 塑性塌陷 R, S, t, 塑性剪胀的塑性势函数
P, l, 硬化参数
2.7.4 清华弹塑性模型
1. 弹性参数的确定 2. 屈服面的确定 3. 硬化参数的确定 4. 模型的三维形式
微分
dicj
dc
fc
ij
应力应变关系:
dc
dWc 2 fc
(二次齐次
方程)
3. 塑性剪胀应变 破坏面方程:
屈服面方程:
塑性势方程: 硬化参数 :
d
p ij
1
I13
I3
27I1
pa
m
fp
I13
I3
27I1
pa
m
gp
I13
272
pa I1
m
I3
Wp
q
p 图2-66
微弯的破坏面、屈服面与塑性势面
塑性功增量
dWp d
p ij
ij
dgij ij
应力应变关系
dWp dipjij
d g ij
ij
g
ij
ij
3g
(三阶齐次方程)
所以:
d dWp
3g
d
p ij
d
g
ij
4. 模型的参数的确定
1)弹性参数:,Kur, n:三轴试验卸、再加载(或
者曲线初始段)曲线 2)强度参数:kf : 试样破坏时kf =I13/I3 3)塑性势函数中k2 4)硬化参数:塑性功中参数
d
c ij
塑性塌陷应变
破坏面
塑性剪胀屈服面 塑性塌陷屈服面
静水压力轴
0
图2-65 修正模型的双重屈服面
2.塑性塌陷应变 屈服面函数
d
c ij
fc I12 2I2
硬化参数:塑性功;相适应流动法则 Wc ijdicj
d w cid j icjid j c fc ijdc ij fcij= dc2fc
1. 弹性变形参数 K, G
K K0 p
各向等压试验
n
G
G0 pa
3
pa
常规三轴试验
2. 屈服面的确定
vp v ve
p e
计算三轴试验下各应力状态下的塑性应变, 绘制应力-塑性应变间关系曲线-在应力坐 标下塑性应变增量的方向。
p
kPa
3kPa
5kPa
0
vp
图2-68 三轴试验的塑性应变路径
f I13 I3 k
gI13k2I3 0
3)塑性势函数中k2 假设
K 2A f27(1A )
f
I13 I3
k
K2是f的函数, 关键是确定常数A
pd d1 3 p p g g 1 333 I1 I212 kk 2 21 3 23
k2
3I12 1p 3 1 p3
K 2A f27(1A )
