精选高一数学下学期周练试题4.9
2020学年高一数学下学期周练(九)新版、新人教版

2019学年下期高一数学周练(九)一.选做题:1.已知98απ=,则角α的终边所在的象限是 ( )A .第一象限B .第二象限C .第三象限D .第四象限2.已知sin 2cos 5,tan 3sin 5cos ααααα-=-+那么的值为( ) A .-2 B .2 C .2316 D .-23163. 设扇形的周长为8cm ,面积为42cm ,则扇形的圆心角是( )radA .1B .2C .πD .1或2 4.下列函数同时具有“最小正周期是π,图象关于点(6π,0)对称”两个性质的函数是A .)62cos(π+=x y B .)62sin(π+=x yC . )62cos(π+=xyD . )62sin(π+=x y5.与向量a =(-5,12)垂直的单位向量为 ( )A .125,1313⎛⎫-⎪⎝⎭ B .125,1313⎛⎫-- ⎪⎝⎭C .125125,,13131313⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭或 D .125125,,13131313⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭或 6.设e 是单位向量,3,3,AB e CD e AC BD ==-=u u u r r u u u r r u u u r u u u r,则四边形ABCD 是 ( )A .梯形B .菱形C .矩形D .正方形7.)2cos()2sin(21++-ππ等于 ( )A .sin2-cos2B .cos2-sin2C .±(sin2-cos2)D .sin2+cos28.设向量1e u r 、2e u u r 满足:122,1e e ==u r u u r ,1e u r ,2e u u r 的夹角是60︒,若1227te e +u r u u r 与12e te +ur u u r 的夹角为钝角,则t 的范围是( )A .1(7,)2-- B .14141[7,)(,]2----UC .14141(7,)(,)2----U D .1(,7)(,)2-∞--+∞U9.函数)sin(ϕω+=x y 的部分图象如右图,则ϕ、ω可以取的一组值是 ( )A. ,24ππωϕ==B. ,36ππωϕ==C. ,44ππωϕ==D. 5,44ππωϕ==10.已知a r ,b r 满足:||3a =r ,||2b =r ,||4a b +=r r ,则||a b -=r r( )O y 1 2 3A .3B .5C .3D .10 11.已知函数()f x 与()g x 的图像在R 上不间断,由下表知方程f(x)=g(x)有实数解的区间是( )x -1 0 1 2 3 f(x) -0.677 3.011 5.432 5.980 7.651 g(x)-0.5303.4514.8905.2416.892A .(-1,0)B .(0,1)C .(1,2)D .(2,3) 12. 已知函数f(x)=sin(2x+ϕ),其中ϕ为实数,若f(x)≤|f(6π)|对x ∈R 恒成立,且f(2π)>f(π),则f(x)的单调递增区间是( ) A.[,]36k k ππππ-+(k ∈Z) B.[,]2k k πππ+ (k ∈Z)C.2[,]63k k ππππ++ (k ∈Z) D.[,]2k k πππ- (k ∈Z)二、填空题:13、已知点A(-1,5)和向量a ={2,3},若AB =3a ,则点B 的坐标为 . 14、 设21,y ax a =+-当11x -≤≤时,函数有唯一零点,则实数a 的取值范围是 。
【高一数学试题精选】高一数学下册每周一练测试题及答案

高一数学下册每周一练测试题及答案
5 高一数学“每周一练”系列试题(39)
一、选择题本大题共10小题,每小题2分,满分x (其中a>0且a≠1) 在同一坐标系中的图象可能为
()
A. B. c. D.
10、已知,,,则下列关系中正确的是()
A.B.C.D.
二、填空题本大题共5小题,每小题5分,满分25分.
11、函数的递增区间是=
12、在平面直角坐标系中,角的终边关于一、三象限的角平分线对称,且角的终边经过点,则=
13、如图,菱形ABcD的边长为1,,E、F分别
为AD、cD的中点,则=
14、已知函数是定义在上的奇函数,且当时,
,则=
15、已知函数,对于上的任意有如下条
① ;② ③ ,
其中能使恒成立的条是(填写序号)
三、解答题本大题共6小题,共75分。
解答须写出字说明,证明过程或演算步骤.
16、(本题14分)已知全集,,
(1)用列举法表示集合(2)求,,。
17、(本题14分)判断下列函数的奇偶性
(1);(2)。
苏教版高中数学必修4高一第二学期周练试卷.docx

& 鑫达捷致力于精品文档 精心制作仅供参考 &鑫达捷高一数学第二学期周练(五)班级 学号 姓名 得分一、填空题:1.平面四边形ABCD 和点O ,若OA OC OB OD +=+u u u r u u u r u u u r u u u r,则四边形ABCD 是 四边形.2.(1,2),(2,3),(2,0),(,)A B C D x y ---,且2AC BD =u u u r u u u r,则x y += 3.1,2,a b a b λ===r r r r ,则a b -r r=4.设12,e e u r u u r 是两个不共线的向量,已知122,AB e ke =+u u u r u r u u r 12123,2CB e e CD e e =+=-u u u r u r u u r u u u r u r u u r,若A B D 、、三点共线,则k =5.函数sin 2cos tan sin cos tan x x xy x x x=++的值域为 6.442cos sin 2sin x x x -+的值为7.若cos()63x π-=5cos()6x π+=8.函数()sin()42xf x π=-的最小正周期为9.函数()2tan (0)f x x ωω=>在,43ππ⎡⎤-⎢⎥⎣⎦上单调递增,则ω的范围是10.已知()3sin()(0)6f x x πωω=->和()2cos(2)1g x x ϕ=++的图象的对称轴完全相同,若0,2x π⎡⎤∈⎢⎥⎣⎦,则()f x 的取值范围是11.若函数2()sin 2cos f x x x =+在2,3πθ⎡⎤-⎢⎥⎣⎦上的最大值为1,则θ的值是12.为了得到sin(2)3y x π=-的图象,只需将cos(2)3y x π=-的图象向右平移 个长度单位.13.已知坐标平面内(1,2),(3,1),(1,2)OA OB OM ==-=-u u u r u u u r u u u u r,p 是直线OM 上一点,当22PA PB +u u u r u u u r 最小时,OP uuu r的坐标为14.下列说法正确的序号是①a b r r 与不共线,则a b λr r与也不共线 ②函数tan y x =在第一象限内是增函数③函数()sin ,()sin f x x g x x ==均是周期函数 ④函数()4sin(2)3f x x π=+在,03π⎡⎤-⎢⎥⎣⎦上是增函数 ⑤函数()sin(2)23f x a x π=++的最大值为2a +二、解答题:15.若sin α是方程25760x x --=的一个根,且α是第三象限角,求233sin()cos()tan ()22cos()sin()αππαπαπαπα--⋅-⋅--+. 16.如图,ABC ∆中,D E 、为边AB 的两个三等分点,=3,2CA a CB b =u u u r r u u u r r,试a b r r 、表示向量CD CE u u u r u u u r、. 17.已知(1,0),(0,2),(1,1)A B C -,(1)求与AB u u u r共线的单位向量;(2)若ABCD 是平行四边形,求点D 的坐标;(3)若(5,8)a =r,试用AB AC u u u r u u u r 、表示a r . 18.已知定义在R 上的函数()sin()(,0,0)2f x A x A πωϕϕω=+<>>的最小正周期为π,且对一切x R ∈,都有()()412f x f π≤=.(1)求()f x 的表达式;(2)若()()6g x f x π=-,求()g x 的单调递减区间;(3)求()()f x g x +的最大值.19.已知向量(,)u x y =r 与向量(,2)v y y x =-r 的对应关系可用()v f u =r r表示.(1)设(1,1),(1,0)a b ==r r ,求向量()()f a f b r r及的坐标;(2)证明:对于任意向量a b r r 、及常数m n 、,恒有()()()f ma nb mf a nf b +=+r r r r成立; (3)求使()(3,5)f c =r成立的向量c r .20.阅读与理解:给出公式:sin()sin cos cos sin αβαβαβ+=+; cos()cos cos sin sin αβαβαβ-=+;我们可以根据公式将函数()sin g x x x =化为:1()2(sin )2(sin cos cos sin )2sin()22333g x x x x x x πππ=+=+=+(1)根据你的理解将函数()sin cos()6f x x x π=+-化为()sin()f x A x ωϕ=+的形式.(2)求出上题函数()f x 的最小正周期、对称中心. (3)求函数在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值、最小值及相应的x 的值.。
2021学年高一下学期周练数学试题

高一数学测试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的) 1、化简:22cos sin 44ππθθ⎛⎫⎛⎫---=⎪ ⎪⎝⎭⎝⎭( ) A 、sin 2θ B.sin 2θ- C.cos 2θ D.cos 2θ- 2、已知2sin 3α=,则()cos 2πα-=( ) A 、519- C.195 3、已知3tan 5α=-,则sin 2α= A 、1517 B 、1517- C 、817- D 、8174、00000000sin 24cos 6sin 66sin 6sin 21cos39cos 21sin 39--化简后的结果是( ) A 、0cos18 B 、0tan18 C 、1- D 、1 5、为了得到函数sin 3cos3y x x =+的图象,可以将函数2y x =的图象( )A 、向右平移12π个单位 B 、向右平移4π个单位 C 、向左平移12π个单位 D 、向左平移4π个单位6、若函数()()sin cos 0g x a x x a =>的最大值为12,则函数()sin cos f x x a x =+的图象的一条对称轴方程为( )A 、0x =B 、34x π=- C 、4x π=-D 、54x π=-7、在ABC ∆中,已知2sin cos sin ,A B C =那么ABC ∆一定是( )A 、直角三角形B 、等腰三角形C 、等腰直角三角形D 、正三角形 8、在ABC ∆中,已知5,7,8a b c ===,则三角形的面积为( ) A 、153 B 、103 C 、53 D 、10 9、在ABC ∆中,角A ,B ,C 的对边分别为,,,1,3,6a b c a b A π===,则B 等于( )A 、3πB 、3π或23π C 、6π或56π D 、23π 10、在ABC ∆中,D 是BC 边上任意一点(D 与B ,C 不重合),且22AB AD BD DC =+⋅,则ABC ∆一定是( )A 、直角三角形B 、等边三角形C 、等腰三角形D 、等腰直角三角形11、在ABC ∆中,若3cos ,,156A B b π=-==,则a =A 、85B 、45C 、165D 、5812、已知钝角三角形ABC 的面积是12,1,2AB BC ==,则AC =( )A 、5B 、5C 、2D 、1 二、填空题(本大题共4小题,每小题5分,共20分) 13、已知5,,sin 25παπα⎛⎫∈= ⎪⎝⎭,则tan 2α=. 14、设0,2πθ<<向量()sin 2,cos a θθ=,()cos ,1b θ=,若a //b ,则tan θ=.15、如图,在ABC ∆中,2AB =,点D 在边BC 上,2BD DC =,310cos ,10DAC ∠=25cos 5C ∠=,则AC =16、如图,在河床的一岸边选取A ,B 两点,观察对岸的点C ,测得075A =,045B =,且200AB m =,则A ,C 两点间的距离为m .17、(本小题12分)已知0,0,44ππαβ<<<<且()3sin sin 2,βαβ=+24tan1tan 22αα=-求αβ+的值.18、(本小题12分)已知函数()sin 32f x x x =+,记函数()f x 的最小正周期为β,向量()2,cos ,1,tan ,024a b βπααα⎛⎫⎛⎫==+<< ⎪ ⎪⎝⎭⎝⎭,且73a b ⋅=. (1)求()f x 在区间24,33ππ⎡⎤⎢⎥⎣⎦上的最值; (2)求()22cos sin 2cos sin ααβαα-+-的值.19、(本小题12分)已知函数())22sin cos 2330,0f x a x x x a ωωωω=+>>的最大值为2,且最小正周期为π.(1)求函数()f x 的解析式及其对称轴方程; (2)若()43f a =,求sin 46πα⎛⎫+ ⎪⎝⎭的值.20、在锐角三角形ABC 中,角A ,B ,C 所对的边分别为,,a b c .已知4,6,b c ==且sin 23a B =.(1)求角A 的大小;(2)若D 为BC 的中点,求线段AD 的长.21、在ABC ∆中,角A ,B ,C 所对的边分别为,,a b c ,且cos cos 2.cos cos b C c Ba A a A+=(1)求A ;(2)若2,a =求ABC ∆周长的最大值.22、已知函数())233sin cos f x x x x x R =+∈. (1)求4f π⎛⎫⎪⎝⎭的值; (2)若0,2x π⎛⎫∈ ⎪⎝⎭,求()f x 的最大值; (3)在ABC ∆中,若()()1,2A B f A f B <==,求BC AB的值.。
高一数学下学期周考卷-高一数学试题

高一数学下学期周考卷高一数学试题一、选择题(每题1分,共5分)1. 下列函数中,奇函数是()A. y = x^2B. y = x^3C. y = |x|D. y = x + 12. 已知等差数列{an},a1=1,a3=3,则公差d为()A. 1B. 2C. 3D. 43. 不等式2x 3 > 0的解集是()A. x > 1.5B. x < 1.5C. x > 3D. x < 34. 下列关于x的方程中,无解的是()A. x^2 4x + 4 = 0B. x^2 2x + 1 = 0C. x^2 + 2x + 1 = 0D. x^2 3x + 2 = 05. 若向量a与向量b的夹角为60°,|a| = 2,|b| = 3,则向量a与向量b的数量积为()A. 3B. 6C. 9D. 12二、判断题(每题1分,共5分)1. 任何两个等差数列的乘积仍然是等差数列。
()2. 一次函数的图像是一条直线。
()3. 一元二次方程的解一定有两个实数根。
()4. 平行四边形的对角线互相平分。
()5. 若两个角互为补角,则它们的正切值互为倒数。
()三、填空题(每题1分,共5分)1. 已知等差数列{an},a1=1,a3=3,则a5=______。
2. 若函数f(x) = 2x + 1是单调递增的,那么f(3) > f(2)的解为______。
3. 向量a = (2, 3),向量b = (4, 1),则向量a与向量b的数量积为______。
4. 若一元二次方程x^2 4x + 3 = 0的两个根为x1和x2,则x1 + x2 =______。
5. 在直角坐标系中,点A(2, 3)关于原点的对称点坐标为______。
四、简答题(每题2分,共10分)1. 简述等差数列的定义。
2. 举例说明一次函数的实际应用。
3. 如何求解一元二次方程的解?4. 简述向量数量积的性质。
5. 举例说明平行四边形在实际生活中的应用。
高一数学下学期周练试题(承智班,4.9)(2021年整理)

河北省定州市2016-2017学年高一数学下学期周练试题(承智班,4.9)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(河北省定州市2016-2017学年高一数学下学期周练试题(承智班,4.9))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为河北省定州市2016-2017学年高一数学下学期周练试题(承智班,4.9)的全部内容。
河北省定州市2016—2017学年高一数学下学期周练试题(承智班,4.9)一、选择题1.已知三棱锥中,,,,,,则关于该三棱锥的下列叙述正确的为()A.表面积 B.表面积为C.体积为 D.体积为2.已知三棱锥中,,,,,,则三棱锥的外接球的表面积为()A。
B. C。
D。
3.如图,正方体中,点为线段上一动点,点为底面内(含边界)一动点,为的中点,点构成的点集是一个空间几何体,则该几何体为( )(A)棱柱(B)棱锥(C)棱台(D)球4.将正三棱柱截去三个角(如图(1)所示A、B、C分别是△GHI三边的中点)得到几何体如图(2),则该几何体按图(2)所示方向的侧视图(或称左视图)为()A B C D5.球面上有3个点,其中任意两点的球面距离都等于大圆周长的,经过3个点的小圆的周长为,那么这个球的半径为()A.B.C.2D.6.已知地球的半径为,球面上两点都在北纬45°圈上,它们的球面距离为,点在东经30°上,则两点所在其纬线圈上所对应的劣弧的长度为( )A.B.C.D.7.、是半径为的球的球面上两点,它们的球面距离为,求过、的平面中,与球心的最大距离是( )A.B.C.D.8.已知A,B两地都位于北纬45°,又分别位于东经30°和60°,设地球半径为R,则A,B的球面距离约为( )A.B.C.D.9.设地球半径为R,则东经线上,纬度分别为北纬和的两地A,B的球面距离为( ) A.B.C.D.10.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( ) A.B.C.D.11.六棱柱的底面是正六边形,侧棱垂直于底面,且侧棱于底面边长,则直线与所成角的余弦值为()A.B.C.`D.12.一个容器形如倒置的等边圆锥,如下图所示,当所盛水深是容器高的一半时,将容器倒转,那么水深是容器高的()A.B。
2021年高一下学期第9周数学周末练习

2021年高一下学期第9周数学周末练习姓名班级成绩一.填空题(本大题共14小题,每小题5分,共70分)1.在中,,则的大小为.2.变量满足,则的最小值为;3.若三点共线,则的值等于___________.4.不等式的解集是.5.函数的定义域为.6.是等边三角形,是等腰直角三角形,,交于,;则.7.若为不等式组表示的平面区域,则当从连续变化到1时,动直线扫过中的那部分区域的面积为.8.过点的直线与端点为、的线段有公共点,则直线的倾斜角的取值范围是.9.若、、、,、为常数,且,则的最小值是.10.函数的最大值是.11.如果函数的图象与轴有两个交点,则点在平面上的区域(不包含边界)为.①②③④12.已知正数、满足,则的最小值是.13.在 +9× = 60的两个中,分别填入两自然数,使它们的倒数和最小,应分别填上14.不等式所表示的平面区域内的整点个数为.一中高一数学xx春学期第九周双休练习答题卡1、__________________ 6、__________________ 11、________________2、__________________ 7、__________________ 12、________________3、__________________ 8、__________________ 13、________________4、_________________ 9、_________________ 14、________________5、_________________ 10、_________________二.解答题(本大题共6小题,共90分)15.画出由三条直线,,围成的三角形及其内部区域(包括边界),并用不等式组表示出该区域.(14分)16.(1)不等式表示的平面区域包含点和点,求的取值范围.(2)点和点在直线的同侧,求的取值范围.(14分)17.已知的面积为,2=A+C,求的最小值及相应的和的值.(15分)18.已知线性约束条件:,(1)求的最大值;(2)求的取值范围.(15分)19.某村计划建造一个室内面积为72m2的矩形蔬菜温室。
2020-2021学年高一数学下学期第四次周测试题

2020-2021学年高一数学下学期第四次周测试题1.若sin(π+α)+)2cos(απ+=-m ,则)23cos(απ-+2sin(6π-α)的值为( )A .-23m B.-32m C .23mD .32m2.若角A ,B ,C 是△ABC 的三个内角,则下列等式中一定成立的是( )A .cos(A +B )=cosC B .sin(A +B )=-sin C C .cos A +C 2=sin BD .sin B +C 2=cos A23.四条线段的长度分别是1,3,5,7,从这四条线段中任取三条,则所取出的三条线段能构成一个三角形的概率是( )A .14 B .13 C .12 D .254.下列三角函数:①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π); ④ cos [(2n +1)π-6π];⑤sin[(2n +1)π-3π](n ∈Z).其中函数值与sin 3π的值相同的是( )A .①②B .①③④C .②③⑤D .①③⑤5.函数)252sin(π+=x y 的图象的一条对称轴方程是( ) A .2π-=x B .4π-=x C .8π=x D .π45=x6.已知︱cos θ︱=cos θ,︱tan θ︱=-tan θ,则2θ在 ( )A 第二、四象限B 第一、三象限C 第一、四象限或终边在x 轴上D 第二、四象限或终边在x 轴上7.设πα32=,则)125tan()2sin(πααπ-+-=( ) A .222- B .222+C .232+D .232-[]的取值范围是()的上满足在x x 23sin 2,0.8≥π ⎥⎦⎤⎢⎣⎡6,0.πA ⎥⎦⎤⎢⎣⎡ππ65,6.B ⎥⎦⎤⎢⎣⎡ππ32,3.C ⎥⎦⎤⎢⎣⎡ππ,65.D 9.若角α的终边落在直线0=+y x 上,则=-+-ααααcos cos 1sin 1sin 22( ) A .2 B.-2 C .1 D .0的大小关系为()与 156sin 14sin .10156sin 14sin .<A 156sin 14sin .>B 156sin 14sin .=C的形式为改写成将)20,(22018.11πϕπϕα≤≤∈+-=︒z k k12.已知cos(75°+α)=13,且-180°<α<-90°,则cos(15°-α)=________.13.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,则由此求出的平均数减去实际平均数的值是______. 14.________790cos 250sin 430cos 290sin 21=︒+︒︒︒+化简:________)4sin()(.15为的图象的对称轴的方程函数π-=x x f大小需要查表计算才能比较.D16. (本题10分)已知α为第三象限角,且)sin()tan()tan()23cos()2sin()(παπααπαππαα-----+-=f(1)化简)(αf(2)若的值求)(,51)23cos(απαf =-17.(本题15分))32sin()(π+=x x f 函数(1)的图象用五点法画出)(x f(2)写出函数的对称轴,对称中心和单调增减区间【感谢您的阅览,下载后可自由编辑和修改,关注我每天更新】。
2021年高一数学下学期周练试题

2021年高一数学下学期周练试题1.若-9,a,-1成等差数列,-9,m,b,n,-1成等比数列,则ab=________. 2.在公差不为零的等差数列中,有,数列是等比数列,且,则.3.已知为等差数列,为其前n项和,则使得达到最大值的n等于.4. 已知数列{a n}为等差数列,若,则数列{|a n|}的最小项是第__ __项.5.设为等比数列的前项和,,则___6.设为等比数列的前项和,已知,,则公比___7.设数列{}是公比为的等比数列,,若数列{}的连续四项构成集合,则值为8.在等差数列中,,其前项的和为.若,则_9.已知是首项为1的等比数列,是的前n项和,且,则数列的前5项和为___. 10.设等差数列的前n项和为,若,则中最大的是_ _.11. 已知等差数列的前项和分别为和,若,且是整数,则的值为.12.在中,,,面积,则=________________.13.在周长为16的中,,则的取值范围是 .14.如图,圆内接∆中,是的中点,.若,则15.在中,,.(Ⅰ)求; (11)设的外心为,若,求,的值.16.已知锐角△ABC的三个内角A、B、C对边分别是a、b、c, .(1)求证:角A、C、B成等差数列;(2)若角A是△的最大内角,求的范围(3)若△ABC的面积,求△ABC 周长的最小值17.已知数列为等差数列,且.(1) 求数列的通项公式;(2) 令,求证:数列是等比数列;(3)令,求数列的前n项和.18.已知数列的首项,.(1)求证:数列为等比数列;(2) 记,若,求最大正整数.19.已知由正数组成的两个数列,满足.(1)求证:为等差数列; (2)已知分别求数列的通项公式;(3)求数列的前n 项和.20.如图,某市市区有过市中心O 南北走向的解放路,为了解决南徐新城的交通问题,市政府决定修建两条公路:延伸从市中心O 出发北偏西60°方向的健康路至B 点;在市中心正南方向解放路上选取A 点,在A 、B 间修建南徐新路.(1)如果在A 点处看市中心O 和B 点视角的正弦值为35,求在B 点处看市中心O 和A 点视角的余弦值;(2) 如果△AOB 区域作为保护区,已知保护区的面积为154 3 km 2,A 点距市中心的距离为3 km ,求南徐新路的长度;(3) 如果设计要求市中心O 到南徐新路AB 段的距离为4 km ,且南徐新路AB 最短,请你确定A 、B 两点的位置.1.解析 由已知得a =-9-12=-5,b 2=(-9)×(-1)=9且b <0,∴b =-3,∴ab =(-5)×(-3)=15.答案 15;2.16 ; 3、6 ; 4.6 ;5. ;6.解析:两式相减得, ,.7.;8.;9.解析:显然q1,所以,所以是首项为1,公比为的等比数列, 前5项和.10.8;11. 15 ;12.;13 . ;14、 .15.(1) ;(2),.16. (1)省略;(2);(3)△ABC 周长的最小值为6.17、解析: (1)∵数列为等差数列,设公差为,由,,得, .∴. ………… 2分. …………………… 5分(2)∵,∴,∴数列是首项为9,公比为9的等比数列 . …………………… 10分(3)∵,,∴∴ )111(41)3121(41)211(41+-++-+-=n n S n = 16分18.19、(1)证明: …………………………………………………………2分 ,…………………………………………4分 是等差数列。
2021年高一下学期数学周练试题4

2021年高一下学期数学周练试题4一.填空题(本大题共14小题,每小题5分,共70分)1、若为等差数列, 26 .2、若是一个等比数列的连续三项,则的值为 -4 .3、在等比数列{a n }中,已知S n =3n -b ,则b 的值为_____1 __.4、已知1是a 2与b 2的等比中项,又是与的等差中项,则的值是 1或 .5、若等比数列的前2项的和为12, 前4项的和为36, 则前6项的和为 84 .6、在数列{a n }中,a 1=1,a n +1=(n ∈N *),则是这个数列的第 6 项.7、设函数f (x )满足f (n +1)=(n ∈N *)且f (1)=2,则f (20)为 97 .8、在中,分别为角的对边,且,则角B 的值_____________.9、数列{a n }的通项公式为,若,则 99 .10、等比数列{a n },a n >0,q ≠1,且a 2、a 3、2a 1成等差数列,则等于11、已知中,,3,5,0,AB AC AB AC BC ==⋅<=且则 8 .12、等差数列{a n }中,等比数列{b n }中,则等于 16或-16 .13、实数a ,b ,5a ,7,3b ,…,c 组成等差数列,且a +b +5a +7+3b +…+c =2500,则c 的值为 99 .14、已知两灯塔A 、B 与观测点C 的距离都等于km,灯塔A 在观测点C 的北偏东,灯塔B 在观测点C 的南偏东,则灯塔A 与B 的距离为 km.请将以上填空题的答案填到下面对应的横线上,否则不计分1、 262、 -43、 _14、 1或5、 846、 6 _7、 978、9、 99 10、 11、 8 12、16或-1613、 99 14、15. 已知公差不为0的等差数列{}中,,成等比数列,求集合A ={x |x =,n ∈且100<x <200}的元素个数及所有这些元素的和.(本小题满分14分)【解】设{a n }公差为d ,则a 2=a 1+d ,a 4=a 1+3d …………………………………………2分 ∵a 1、a 2、a 4成等比数列,∴(a 1+d )2=a 1(a 1+3d )d=a 1.………………………3分 又∵a 1+(a 1+d )+(a 1+2d )+(a 1+3d )=4a 1+6d=20.………………………………5分 解得:a 1=d=2,∴x=a n =2+2(n -1)=2n∴A={x|x=2n ,n ∈N *且100<x<200}∵100<2n<200,∴50<n<100.…………………………………………………………7分 ∴集合A 中元素个数99-51+1=49(个)……………………………………………10分 由求和公式得:S=×49=7350.…………………………………………14分16. 在中,角的对边分别为,的面积为,且,(本小题满分14分)()22222222223cos 1cos cos 2()26011sin sin 606222cos 2cos607ABC C CC C ABC C S ab C ab ab c a b ab C a b ab a b ab a b ∆=∴==-∆∴=︒==︒=∴==+-=+-︒∴+-=∴+=2解:由已知得21-cos 或舍………………………………………………4分在中,……………………………………………………6分又即………………9分由132,33,2a b a b ∴====…………………………………………12分或………………………………………………14分17. 已知三个实数成等比数列,三个实数的积为103 ,在这三个数中,如果最小的数除以2,最大的数减去7,所得三个数依次成等差数列,求等比数列中的三个实数及等差数列的公差.(本小题满分15) 解:设成等比数列的三个数为,a ,aq ,由·a ·aq =103,解得a =10,即等比数列,10,10q .…………………………2分(1)当q >1时,依题意,+(10q -7)=20.解得q 1=(舍去),q 2=.…………………5分此时等比数列中的三个数分别为4,10,25,………………………………………………………7分 因此成等差数列的三个数为2,10,18,公差d =8.………………………………………………8分(2)当0<q <1,依题意,(-7)+5q =20,解得q 1=5(舍去),q 2=,……………………11分此时等比数列中的三个数分别为25,10,4,……………………………………………………13分 因此成等差数列的三个数为18、10、2,公差为-8.…………………………………………14分 综上所述,d =±8.…………………………………………………………………………………15分 18.在数列{a n }中,已知a 1=1,a n =a n -1+a n -2+…+a 2+a 1.(n ∈N *,n ≥2),求这个数列的通项公式。
赣榆区高一数学下学期周练9(无答案)(2021年整理)

江苏省连云港市赣榆区2016-2017学年高一数学下学期周练9(无答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省连云港市赣榆区2016-2017学年高一数学下学期周练9(无答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省连云港市赣榆区2016-2017学年高一数学下学期周练9(无答案)的全部内容。
江苏省连云港市赣榆区2016—2017学年高一数学下学期周练9(无答案)一、填空题(本大题共 14 小题,每小5分,共70分.请把答案填写在答题卡的相应位置上.)1、函数)1tan()(+=x x f π的最小正周期为2、已知α为第二象限角,则错误!所在的象限是第 象限。
3、已知向量(5,3)a =,(2,)b y =,且a ∥b ,则实数y 的值为__________4、已知(0<θ<π),则cosθ= .5、在ABC ∆中,已知3,4,5AB AC BC ===,则AB BC •= .6、过点()4,3-的圆2522=+y x 的切线方程___ ___。
(用一般式表示)7、将函数sin 2y x =的图象向左平移(0)ϕϕ>个单位,若所得图象过点3(,)62π,则ϕ的最小值为 8、在平行四边形ABCD 中,AC 为一条对角线,若(2,4),(1,3)AB AC ==,则BD = .9、已知平面向量a ,b 不共线,()c ka b k R =+∈,d a b =-,如果c ∥d ,则实数k 的值等于10、已知1sin()63x π+=,则25sin()sin ()63x x ππ-+-的值是__________ 11、函数⎥⎦⎤⎢⎣⎡∈++=32,6,3sin 3cos 22ππx x x y 的值域为_ ___. 点,点F12、如图,在矩形ABCD 中,22AB BC ==,,点E 为BC 的中在边CD 上,若2=•AF AB ,则BF AE •的值是__________a e -与e 13、已知e 为单位向量,且向量a e +与e 的夹角为6π,向量的夹角为3π,则||a =__________ 14、已知直线3+=ax y 与圆22280x y x ++-=相交于A 、B 两点,点00(,)P x y 在直线x y 2=上,且PB PA =,则0x 的取值范围为____ ___.二、解答题(本大题共6小题,共90分,解答应必要的文字说明,证明过程或演算步骤.)15、已知||4,||8a b ==,a 与b 的夹角120︒.(1) 计算||,|42|a b a b +-;(2) 当k 为何值时,(2)()a b ka b +⊥-。
精选高一数学下学期周练试题17_1017_20班

江西省樟树市2016-2017学年高一数学下学期周练试题(1)(7-10,17-20班)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一 项是符合题目要求的). 1.直线10x y +-=的倾斜角α= A .30° B .45°C.60° D .135°2. 在y 轴上的截距为2,且与直线34y x =--垂直的直线的斜截式方程为( ) A .123y x =+B .123y x =-- C.1233y x =-+ D.1233y x =+ 3.函数()f x 是定义在(2,2)-上的奇函数,当(0,2)x ∈时,()21xf x =-,则21(log )3f 的值为A .23-B .2-C .2D .234.(普通班做)点P 为x 轴上的一点,点P 到直线3460x y -+=的距离为6,则点P 的坐标为 A .(8,0)B .(12,0)-C .(8,0)或(12,0)-D .(0,0)(重点班、素质班做)圆222410x y x y +-++=的半径为A .1B C .4 D .25.已知直线1l 经过两点(1,2)(1,4)---、,直线2l 经过两点(2,1)(,6)x 、,且12//l l ,则x = A .2B.﹣2 C .4D .16.一个几何体的三视图如右图所示,则此几何体的体积是 A .112B .80 C .72 D .647. 过坐标原点且与点的距离都等于1的两条直线的夹角为A .60°B .45°C.90°D .120°8. 已知212()log (2)f x x x =-的单调递增区间是 A .(1,)+∞B .(2,)+∞C .(,0)-∞D .(,1)-∞9.如果0AC >,且0BC <,那么直线0Ax By C ++=不通过 (第6题图) A .第一象限 B .第二象限C .第三象限 D .第四象限10.直线12:310,:2(1)10l ax y l x a y ++=+++=,若12//l l ,则实数a 的值为 A .﹣3B .2C .﹣3或2D .3或﹣211.(普通班做)对于任意a R ∈,直线(1)10a x y a --++=恒过定点P ,则P 点坐标为A .(1,2)- B.(1,0)C.(1,2)-- D.(0,1)a +(重点班、素质班做)已知点(1,3),(2,1)A B --,若直线:21l y kx k =-+与线段AB 没有交点, 则k 的取值范围是 A .12k ≥或2k ≤- B .2k ≤-C .12k >或2k <- D .122k -≤≤ 12.(普通班做)已知函数2()log ,(4,8)f x x x =∈,则函数28()()()f x f x f x =+的值域为 A .[8,10)B .26(,10)3C .26(8,)3D .25(,10)3(重点班、素质班做)定义在(1,)+∞上的函数()f x 满足下列两个条件:(1)对任意的(1,)x ∈+∞恒有(2)2()f x f x =成立; (2)当(1,2]x ∈时,()2f x x =-;记函数()()(1)g x f x k x =--,若函数()g x 恰有两个零点,则实数k 的取值范围是A .[1,2)B .4[,2)3C.4[,2]3D .4(,2)3二、填空题(本大题4小题,每小题5分,共20分).13.设集合{}||1|3P x x =+≤,1|(),(2,1)3xQ y y x ⎧⎫==∈-⎨⎬⎩⎭,则PQ =.14.(普通班做)若直线3440x y ++=与3420x y +-=平行,则这两条平行线间的距离为. (重点班、素质班做)已知两条平行直线12:320,:680l x ay l x y m ++=++=之间的距离为2,m =. 15.已知()f x 是(,0)(0,)-∞+∞上偶函数,当(0,)x ∈+∞时,()f x 是单调增函数,且(1)0f =,则(1)0f x +<的解集为.16.(普通班做)将一张坐标纸折叠一次,使点(2,6)点(4,6)重合,则与点(4,1)-重合的点的坐标____.(重点班、素质班做)已知点(,)P x y 在直线40x y +-=上,点(,)Q x y 在圆22:220O x y x y +++=上则PQ 的最小值为.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)求经过两条直线1:40l x y +-=和2:20l x y -+=的交点,且分别与直线210x y --=(1)平行的直线方程; (2)垂直的直线方程.18. (本小题满分12分) 已知△ABC 的顶点坐标分别是(5,1),(1,1),(1,3)A B C (1)求AB 中垂线的方程; (2)求△ABC 的面积.19. (本小题满分12分)在坐标系中有两点(2,3),(3,4)P Q .求(1)在y 轴上求出一点M ,使得MP+MQ 的值最小;(2)在x 轴上求出一点N ,使得NQ ﹣NP 的值最大.20.(本小题满分12分)已知直线:120()l kx y k x R -++=∈. (1)若直线l 不经过第四象限,求k 的取值范围;(2)若直线l 交x 轴负半轴于点A ,交y 轴正半轴于点,B O 为坐标原点,设ABC ∆的面积为S ,求S 的最小值及此时直线l 的方程.21.(本小题满分12分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M 是BD 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)若N 是BC 的中点,证明:AN∥平面CME ; (2)证明:平面BDE⊥平面BCD . (3)求三棱锥D ﹣BCE 的体积.22.(本小题满分12分)(普通班做)已知二次函数2(),()21f x ax bx g x x =+=-.(1)当1a =时,若函数()f x 的图象恒在函数()g x 的图象上方,试求实数b 的取值范围; (2)若()y f x =对任意的x R ∈均有(2)()f x f x -=-成立,且()f x 的图象经过点2(1,)3A .①求函数()y f x =的解析式;②若对任意3x <-,都有()2()f x kg x x<成立,试求实数k 的最小值. (重点班、素质班做)已知函数()121x af x =-+(a 为常数)为R 上的奇函数.(1)求实数a 的值;(2)对(0,1]x ∈,不等式()21xs f x ⋅≥-恒成立,求实数s 的取值范围;(3)令2()1()g x f x =-,若关于x 的方程(2)()0g x mg x -=有唯一实数解,求实数m 的取值范围.江西省樟树中学2019届高一下学期第1次周练文科数学答案一、选择题(本大题共12小题,每小题5分,共60分。
【数学周练】高一下数学周练及答案
高一下数学周练一、选择题(每小题5分,共35分)1、若一个正三棱柱的三视图如下图所示,则这个正三棱柱的体积为()A.8B.C.D.2、棱锥的三视图如下图,则该棱锥的全面积(单位:)为( )A.48+12B.48+24C.36+12D.36+243、如下图是无盖正方体纸盒的平面展开图,则直线在原正方体中的位置关系是()A.平行B.相交且垂直C.异面D.相交成角4、正四棱锥的顶点都在同一球面上,若该棱锥的高为,底面边长为,则该球的表面积为()A. B. C.D.5、长方体的一个顶点上三条棱长分别是,且它的个顶点都在同一球面上,则这个球的表面积是 ( )A. B. C. D.都不对6、如图,在三棱锥中,,且分别是棱的中点,则和所成的角等于()A. B. C. D.7、下列命题中,正确命题的个数是( )①如果是两条平行直线,那么平行于经过的任何一个平面;②如果直线和平面满足,那么与平面内的任何一条直线平行;③如果直线满足,那么;④如果直线和平面满足,那么;⑤如果平面的同侧有两点到平面的距离相等,那么.A.0B.1C.2D.3二、填空(每小题5分,共15分)8、如右图是一个棱长为的无盖正方体盒子的平面展开图,为其上四个点,则以为顶点的三棱锥的体积为__________.9、如右图所示,分别是正方体的面、面的中心,则四边形在该正方体的面上的正投影可能是下列图中的__________(要求把可能的序号填上).10、已知四棱锥S—ABCD的底面为正方形且侧棱长相等,底面上的四个顶点A、B、C、D在球心为O的半球底面圆周上,顶点S在半球面上,则半球O的体积和正四棱锥S—ABCD的体积之比为__________.三、解答题(每小题12分,共24分)11、四面体及其三视图如图所示,平行于棱,的平面分别交四面体的棱于点.(1)求四面体的体积;(2)证明:四边形是矩形.12、如图,四棱锥P﹣ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.(1)求证:AF∥平面PCE;(2)求证:平面PCE⊥平面PCD;(3)求三棱锥C﹣BEP的体积.周练10答案解析第1题答案C第1题解析由三视图知正三棱柱的底面边长为4,高为2,第2题答案A第2题解析棱锥的直观图如图所示:是的等腰直角三角形,底面,,为中点,由底面是边长为6的等腰直角三角形知其底面积是.又直角三角形斜边的中点到两直角边的距离都是3,棱锥高为4,所以三个侧面中与底面垂直的侧面三角形高是4,底面边长为,其余两个侧面的斜高为.故三个侧面中与底面垂直的三角形的面积为,另两个侧面三角形的面积都是,故此几何体的全面积是,故选A第3题答案D第3题解析如图,连接,得正三角形,∴在原正方体中相交成角.第4题答案A第4题解析利用球心到各顶点距离相等列式求解.如图,设球心为,半径为,则中,,解得,该球的表面积为.第5题答案B第5题解析如图所示,设球的半径为R,则球的直径,所以球的表面积,故选B.第6题答案B第6题解析如图所示,取的中点,连接.∵分别为的中点,∴,且.∴为与所成的角,∵,∴,∵,∴,∴,∴是等腰直角三角形,∴,即与所成的角为.第7题答案C第7题解析如图,在正方体中,,在过的平面内,故命题①不正确;平面平面,但不平行于,故命题②不正确;平面平面但与相交,所以③不正确;④中,假设与相交,因为,所以与相交,这与矛盾,故,即④正确;⑤显然正确.第8题答案第8题解析根据题意,可画出图形为:∴.第9题答案(2)(3)第9题解析其中(2)可以是四边形在正方体的面或面上的正投影;(3)可以是四边形在正方体的面上的正投影;四边形在正方体任何一个面上的正投影都不是(1)(4).第10题答案.第10题解析设球O的半径为R,则四棱锥的高为R,底面边长为,体积是,半球体积是,故体积之比是.第11题答案(1)(2)略第11题解析(1)由该四面体的三视图可知,,,平面,四面体体积.(2)证明:平面,平面平面,平面平面,,同理,四边形是平行四边形,又平面,.四边形是矩形.第12题答案(1)略;(2)略;(3).第12题解析(1)取PC的中点G,连接FG、EG,∴FG∴,形ABCD为矩形,E为AB的中点,∴,∴,∴四边形AEGF是平行四边形,∴,又EG⊂平面PCE,AF ⊄平面PCE,∴AF∥平面PCE;(2)∵PA⊥底面ABCD,∴PA⊥AD,PA⊥CD,又AD⊥CD,PA∩AD=A,∴CD⊥平面ADP,又AF⊂平面ADP,∴CD⊥AF,在Rt△PAD中,∠PDA=45°,∴△PAD为等腰直角三角形,∴PA=AD=2,∵F是PD的中点,∴AF⊥PD,又CD∩PD=D,∴AF⊥平面PCD,∵AF∥EG,∴EG⊥平面PCD,又EG⊂平面PCE,∴平面PCE⊥平面PCD;(3)PA⊥底面ABCD在Rt△BCE中,BE=1,BC=2,∴三棱锥C﹣BEP的体积.。
河南省2021学年高一数学下学期周练试题四

高一数学下学期周练试题(四)一、单项选择(每题5分,共85分)1、已知扇形面积为38π,半径是l ,则扇形的圆心角是( ) A. 316π B. 38π C. 34π D. 32π2、若角600°的终边上有一点(﹣4,a ),则a 的值是( ) A. 4 B. 43- C.433 D. 433- 3、将一张坐标纸折叠一次,使得点()0,2与点()4,0重合,点()7,3与点(),m n 重合,则m n +的值为A. 5B. 6C. 345D. 7 4、设函数()πsin 3,2f x x x ⎛⎫=-∈ ⎪⎝⎭R ,则下列结论正确的是 A. ()f x 是最小正周期为3π的奇函数 B. ()f x 是最小正周期为3π的偶函数 C. ()f x 是最小正周期为2π3的奇函数 D. ()f x 是最小正周期为2π3的偶函数 5、已知函数错误!未找到引用源。
是定义域为R 的偶函数. 当错误!未找到引用源。
时,错误!未找到引用源。
若关于x 的方程错误!未找到引用源。
(错误!未找到引用源。
),有且仅有6个不同实数根,则实数错误!未找到引用源。
的取值范围是( ) A .错误!未找到引用源。
B .错误!未找到引用源。
C .错误!未找到引用源。
D .错误!未找到引用源。
6、对于函数()()x x x x x f sin cos 21cos sin 21--+=,下列说法正确的是( ) A.该函数的值域是[]1,1- B.当且仅当222πππ+<<k x k (Z k ∈)时,()0>x fC.当且仅当22ππ+=k x (Z k ∈)时,该函数取得最大值1D.该函数是以π为最小正周期的周期函数7、函数1tan 4y x π⎛⎫=--⎪⎝⎭的定义域为( ) A. 4k k πππ⎛⎤+ ⎥⎝⎦,, k Z ∈ B. 2k k πππ⎛⎤+ ⎥⎝⎦,, k Z ∈C. 42k k ππππ⎛⎤-+⎥⎝⎦,, k Z ∈ D. 4k k πππ⎛⎤-⎥⎝⎦, , k Z ∈ 8、已知函数()()sin (0,)2f x x πωϕωϕ=+><的最小正周期为4π,且对x R ∀∈,有()3f x f π⎛⎫≤ ⎪⎝⎭成立,则()f x 的一个对称中心坐标是( )A. 2,03π⎛⎫- ⎪⎝⎭ B. ,03π⎛⎫- ⎪⎝⎭ C. 2,03π⎛⎫ ⎪⎝⎭ D. 5,03π⎛⎫ ⎪⎝⎭ 9、一棱长为6的正四面体内部有一个可以任意旋转的正方体,当正方体的棱长取最大值时,正方体的外接球的表面积是( ) A.B.C.D.10、在梯形ABCD 中,AD∥BC,已知AD =4,BC =6,若CD mBA nBC =+ (m ,n∈R),则mn=( )A. -3B. -13 C. 13D. 311、如果函数()f x 对任意的实数x ,都有()()1f x f x =-,且当12x ≥时, ()()2log 31f x x =-,那么函数()f x 在[]2,0-的最大值与最小值之差为( )A. 4B. 3C. 2D. 112、设()f x 是R 上的周期为2的函数,且对任意的实数x ,恒有()()0f x f x --=,当[]1,0x ∈-时, ()112xf x ⎛⎫=- ⎪⎝⎭,若关于x 的方程()()log 10a f x x -+= (0a >且1a ≠)恰有五个不相同的实数根,则实数a 的取值范围是( )A . []3,5B . ()3,5C . []4,6 D . ()4,6 13、函数()()sin ln 2xf x x =+的图象可能是14、已知函数,若a ,b ,c 互不相等,且f (a )=f (b )=f(c ),则a+b+c 的取值范围是( )A .(2,2018)B .(2,2019)C .(3,2018)D .(3,2019)15、已知圆的方程为2268160x y x y +--+=,设该圆过点()3,5的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为A. 122B. 32C. 62D. 4216、若圆2244100x y x y ++--=上至少有三个不同的点到直线:0l ax by +=的距离为22,则直线l 的斜率的取值范围是( )A. 23,23⎡⎤-+⎣⎦B. 23,32⎡⎤---⎣⎦C. 23,23⎡⎤--+⎣⎦ D. 23,23⎡⎤---⎣⎦17、一观览车的主架示意图如图所示,其中O 为轮轴的中心,距地面32m (即OM 长),巨轮的半径为30m ,AM =2BP =m ,巨轮逆时针旋转且每12分钟转动一圈.若点M 为吊舱P 的初始位置,经过t 分钟,该吊舱P 距离地面的高度为()h t m ,则()h t =( )hPA OMBA.ππ30sin()30122t -+B.ππ30sin(3062t -+ C.ππ30sin()3262t -+ D.ππ30sin(62t -二、填空题(每题5分,共20分)18、化简: +AB AC BD CD AD --+=__________.19、16/17世纪之交,随着天文、航海、工程、贸易以及军事的发展,改进数字计算方法成了当务之急,约翰•纳皮尔正是在研究天文学的过程中,为了简化其中的计算而发明了对数.后来天才数学家欧拉发现了对数与指数的关系,即b a N = ⇔ log a b N =.现在已知23a=,34b =,则ab =__________.20、设函数()()f x x R ∈满足()()cos f x f x x π-=+,当0x π-<≤时,f(x)=0,则136f π⎛⎫= ⎪⎝⎭__________. 21、已知(),0,{ 2,0,xlgx x f x x >=≤则函数()()2231y f x f x =-+的零点个数是__________.三、解答题(共45分)22、如图,在四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,底面ABCD 是平行四边形,45ABC ∠=,2AD AP ==,22AB DP ==,E 为CD 的中点,点F 在线段PB 上.(Ⅰ)求证:AD PC ⊥;(Ⅱ)当三棱锥B EFC -的体积等于四棱锥P ABCD -体积的16时,求PFPB的值. 23、设两个非零向量a 与b 不共线.(1)若AB a b =+,()28,3BC a b CD a b =+=-,求证:,,A B D 三点共线; (2)试确定实数k ,使ka b +与a kb +共线.24、已知线段PQ 的端点Q 的坐标为()2,3-,端点P 在圆()()22814C x y -+-=:上运动. (Ⅰ)求线段PQ 中点M 的轨迹E 的方程;(Ⅱ)若一光线从点Q 射出,经x 轴反射后,与轨迹E 相切,求反射光线所在的直线方程. 25、将函数sin y x =的图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得的图象向左平移6π个单位长度后得到函数()f x 的图象. (1)写出函数()f x 的解析式;(2)求函数()f x 数的单调递增区间与对称中心的坐标;(3)求实数a 和正整数n ,使得()()F x f x a =-在[]0,n π上恰有2017个零点.参考答案一、单项选择CBCDC BCABA CDABA BB二、填空题 18、AD 19、2 20、32- 21、5三、解答题22、(Ⅰ)证明:在平行四边形ABCD 中,连接AC , 因为22AB =,2BC =,45ABC ∠=, 由余弦定理得2842222cos454AC =+-⋅⋅⋅=, 得2AC =,所以90ACB ∠=,即BC AC ⊥,又AD ∥BC , 所以AD AC ⊥,又2AD AP ==,22DP =,所以PA AD ⊥,AP AC A ⋂=, 所以AD ⊥平面PAC ,所以AD PC ⊥. (Ⅱ)因为E 为CD 的中点,1,4BEC ABCD S S ∆∴=四边形 ,,.PAD ABCD PAD ABCD AD PA AD PA ABCD ⊥⋂=⊥∴⊥侧面底面,侧面底面平面 设F 到平面ABCD 的距离为,h1,6B EFC F BEC P ABCD V V V ---==111,363BEC ABCD S h S PA ∆∴⋅⨯=⋅⋅⋅2,3h PA ∴=所以1.3PF PB =23、(1)证明:∵AB a b =+,()28,3BC a b CD a b =+=- ∴()()28355BD BC CD a b a b a b AB =+=++-=+= ∴AB 与BD 共线,又它们有公共点B ,∴,,A B D 三点共线 (2)若ka b +和a kb +共线∴存在实数λ,使ka b +()a kb λ=+ 即ka b a k b λλ+=+ ∴{1k k λλ==解得1k =±24、(1)设()()00,,,M x y P x y ,0022{ 32x xy y -=⇒+=0022{ 23x x y y =+=- 则代入()()2200814x y -+-= 轨迹E 的方程为()()22321x y -+-= (2)设()2,3Q -关于x 轴对称点()'2,3Q --设过()'2,3Q --的直线():32y k x +=+,即230kx y k -+-= ∵2322311k k d k -+-==+,()22551k k -=+,()2225211k k k -+=+22450240k k -+=()()34430k k --=∴43k =或34k = ∴反射光线所在()4:323y x +=+即4310x y --= ()3324y x +=+即3460x y --=25、(1)将函数sin y x =的图象上所有点的横坐标缩短到原来的12倍,所得图象对应的解析式为sin2y x =,再将所得的图象向左平移6π个单位长度,所得图象对应的解析式为y sin 2263x sin x ππ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦。
2021年高一下学期数学周练试卷(文科4.19) 含答案

2021年高一下学期数学周练试卷(文科4.19) 含答案一、选择题1. 在数列1,1,2,3,5,8,x ,21,34,55,…中,等于( )A .11B .12C .13D .142. 给出下列结论:①数列{a n }前n 项和S n =n 2-2n +1,则{a n }是等差数列. ②数列{a n }前n 项和S n =7n 2-8n ,则a 100=1385. ③数列{a n }前n 项和S n =2n -1,则{a n }是等比数列.④数列{a n }前n 项和S n =1,则a n =1.其中正确的个数为( ) A .0 B .1 C .2 D .3 3.在数列中,, ,则( )A .B .C .D . 4.数列中,若,,则等于( )A .B .C .D .5.设数列{a n }是公比为a (a ≠1),首项为b 的等比数列,S n 是前n 项和,对任意的n ∈N + ,点(S n ,S n +1)在 ( )A .直线y =ax -b 上B .直线y =bx +a 上C .直线y =bx -a 上D .直线y =ax +b 上 6. 已知数列,,,…,,…,使数列前n 项的乘积不超过的最大正整数n 是 ( )A .9B .10C .11D .12 7在数列中,,,,其中、为常数,则( )A -1B 0C -2 D. 18. 已知数列{a n }的通项公式a n =log 2n +1n +2(n ∈N +),设其前n 项和为S n ,则使S n <-5成立正整数n ( )A .有最小值63B .有最大值63C .有最小值31D .有最大值31 9. 设记不超过的最大整数为[],令{}=-[],则{},[],( )A.是等差数列但不是等比数列B.是等比数列但不是等差数列C.既是等差数列又是等比数列D.既不是等差数列也不是等比数列10. 古希腊人常用小石子在沙滩上摆成各种性状来研究数, 例如:他们研究过图1中的1,3,6,10,…, 由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数。
高一数学下学期周练试题(2)(7-10班,17-20班)(2021年整理)

班)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江西省樟树市2016-2017学年高一数学下学期周练试题(2)(7-10班,17-20班))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江西省樟树市2016-2017学年高一数学下学期周练试题(2)(7-10班,17-20班)的全部内容。
17—20班)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有 项是符合题目要求的).1。
已知集合{}{}2|2,|20A x y x B x x x ==-=-<,则A 。
AB φ= B. A B R = C. B A ⊂ D 。
A B ⊂2. 如果直线l 过点(1,2)P ,且l 不经过第四象限,那么l 的斜率的取值范围是A.[0,2] B 。
[0,2) C. 1[0,]2 D 。
1[,0]2-3. 若直线3x ﹣4y+12=0与两坐标轴交点为A 、B,则以AB 为直径的圆的方程是A .x 2+y 2+4x ﹣3y=0B .x 2+y 2﹣4x ﹣3y=0C .x 2+y 2+4x ﹣3y ﹣4=0D .x 2+y 2﹣4x ﹣3y+8=04. 为了得到函数4lg 10x y +=的图象,只需把函数lg y x =的图象上所有的点 A .向左平移4个单位长度,再向上平移1个单位长度B .向右平移4个单位长度,再向上平移1个单位长度C .向左平移4个单位长度,再向下平移1个单位长度D .向右平移4个单位长度,再向下平移1个单位长度5.如右图为某几何体的三视图,图中四边形为边长为1的正方形,两条虚线互相垂直,则该几何体体积为A .16 B.45 C .15 D .566.夹在两条平行线1:340l x y -=与1:34200l x y --=之间的圆的最大面积为A 。
高一数学下学期周练试题一 试题

HY中学2021-2021学年高一数学下学期周练试题〔一〕姓名:班级:得分:一、单项选择题〔5×10=50〕1.集合,集合,那么〔〕A. B.C. D.2.集合,,,那么〔〕A. B. C. D.3.表示集合中整数元素的个数,设集合,,那么〔〕A. B. C. D.4.如图,集合,,,那么图中阴影局部表示的集合为〔〕A. B.C. D.5.集合,,,那么〔〕A. B. C. D.6.集合,,〔〕A. B.C. D.7.设集合,,那么〔〕A. B. C. D.8.集合,且},那么〔〕A. B. C. D.9.集合,,那么〔〕A. B. C. D.10.集合,,那么集合( )A. B. C. D.二、解答题〔20分〕11.设全集,集合,,. 〔1〕求;〔4分〕〔2〕假设,务实数的取值范围.〔6分〕12.全集,集合,.〔1〕求,.〔4分〕〔2〕集合,假设,务实数的取值范围.〔6分〕参考答案11.〔1〕; 〔2〕.12.〔1〕,或者〔2〕励志赠言经典语录精选句;挥动**,放飞梦想。
厚积薄发,一鸣惊人。
关于努力学习的语录。
自古以来就有许多文人留下如头悬梁锥刺股的经典的,而近代又有哪些经典的高中励志赠言出现呢?小编筛选了高中励志赠言句经典语录,看看是否有些帮助吧。
好男儿踌躇满志,你将如愿;真巾帼灿烂扬眉,我要成功。
含泪播种的人一定能含笑收获。
贵在坚持、难在坚持、成在坚持。
功崇惟志,业广为勤。
耕耘今天,收获明天。
成功,要靠辛勤与汗水,也要靠技巧与方法。
常说口里顺,常做手不笨。
不要自卑,你不比别人笨。
不要自满,别人不比你笨。
高三某班,青春无限,超越梦想,勇于争先。
敢闯敢拼,**协力,争创佳绩。
丰富学校体育内涵,共建时代校园文化。
奋勇冲击,永争第一。
奋斗冲刺,誓要蟾宫折桂;全心拼搏,定能金榜题名。
放心去飞,勇敢去追,追一切我们为完成的梦。
翻手为云,覆手为雨。
二人同心,其利断金。
高一数学周练(含答案)

高一数学周练一、单选题(共40分)1.若集合{4},{31}M x N x x =<=≥∣,则M N ⋂=( ) A .{}02x x ≤< B .123x x ⎧⎫≤<⎨⎬⎩⎭C .{}316x x ≤<D .1163x x ⎧⎫≤<⎨⎬⎩⎭2.函数 y = ) A .3,2⎛⎫-∞- ⎪⎝⎭B .3,2⎡⎫-+∞⎪⎢⎣⎭C .[)0,+∞D .(],3∞--][)0,+∞.3.“角α,β的终边关于y x =轴对称”是“22sin sin 1αβ+=”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】A【分析】根据三角函数的性质的即可判断求解.【详解】若角α,β的终边关于y x =轴对称,则sin α=cos β,则2222sin sin cos sin =1αβββ+=+;若22sin sin 1αβ+=,则22sin =cos αβ,则sin α=±cos β,则角α,β的终边关于y x =或y =-x 轴对称;综上,“角α,β的终边关于y x =轴对称”是“22sin sin 1αβ+=”的充分不必要条件. 故选:A.4.已知方程ln 112x x =-的实数解为0x ,且()0,1x k k ∈+,*k ∈N ,则k =( ) A .1 B .2 C .3 D .4【答案】D【解析】先转化为两个简单函数判断交点所在区间的大致范围,再由零点判定定理确定即可.【详解】解:112lnx x =-,令()g x lnx =,()112h x x =-在同一坐标系画出图象可得 由图可知01x >,令()211f x lnx x =+-,()()129(27)0f f ln =-->,()()23(27)(35)0f f ln ln =-->, ()()34(35)(43)0f f ln ln =-->, ()()45(43)(51)0f f ln ln =--<,()04,5x ∴∈4k ∴=,故选:D .【点睛】本题主要考查函数零点所在区间的求法,图象法和零点判定定理.将函数的零点问题转化为两个函数交点的问题是常用的手段,属于基础题.5.如图是下列四个函数中的某个函数在区间[3,3]-的大致图像,则该函数是( )A .3231x xy x -+=+B .321x xy x -=+C .22cos 1x xy x =+ D .22sin 1xy x =+6.将函数()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ,若C关于y 轴对称,则ω的最小值是( ) A .16B .14C .13D .127.记函数()sin (0)4f x x b ωω⎛⎫=++> ⎪⎝⎭的最小正周期为T .若23T ππ<<,且()y f x =的图象关于点3,22π⎛⎫ ⎪⎝⎭中心对称,则2f π⎛⎫= ⎪⎝⎭( )A .1B .32C .52 D .38.已知函数()131,0ln ,0x x f x x x +⎧-⎪=⎨>⎪⎩若函数()()g x f x a =-有3个零点,则a 的取值范围是( ) A .()0,1 B .(]0,2C .()2,+∞D .()1,+∞【答案】A【分析】要使函数()()g x f x a =-有三个零点,则()f x a =有三个不相等的实根,即()f x 与y a =的图象有三个交点,结合函数的性质及图象即可得出.【详解】要使函数()()g x f x a =-有三个零点,则()f x a =有三个不相等的实根,即()f x 与y a =的图象有三个交点, 当1x ≤-时,113x f x在(],1-∞-上单调递减,()0,1f x ; 当10-<≤x 时,()131x f x +=-在(]1,0-上单调递增,()0,2f x ;当0x >时,()ln f x x =在()0,∞+上单调递增,()f x ∈R ; 由()f x 与y a =的图象有三个交点,结合函数图象可得()0,1a ∈, 故选:A.二、多选题(共20分)9.已知函数f (x )=2sin (2x ﹣6π),则如下结论:其中正确的是( ) A .函数f (x )的最小正周期为π; B .函数f (x )在[6π,512π]上的值域为[1; C .函数f (x )在7(,)312ππ上是减函数;D .函数y =f (x )的图象向左平移6π个单位得到函数y =2sin2x 的图象,10.下列结论正确的是( )A .若α,β的终边相同,则αβ-的终边在x 的非负半轴上B .函数()log 1a f x x =+(0a >且1a ≠)恒过定点(),2aC .函数()22x f x x =-只有两个零点D .己知一扇形的圆心角60α=︒,且其所在圆的半径3R =,则扇形的弧长为π11.如图,摩天轮的半径为40m ,其中心O 点距离地面的高度为50m ,摩天轮按逆时针方向匀速转动,且20min 转一圈,若摩天轮上点P 的起始位置在最高点处,则摩天轮转动过程中( )A .转动10min 后点P 距离地面10mB .若摩天轮转速减半,则转动一圈所需的时间变为原来的12C .第17min 和第43min 点P 距离地面的高度相同D .摩天轮转动一圈,点P 距离地面的高度不低于70m 的时间为5min 【详解】解:摩天轮2010t t ππ=,(02)ϕπ是以轴正半轴为始边,轴正半轴为始边,为终边的角为P 的纵坐标为又由题知,P 点起始位置在最高点处,2π5070,1102t,020t , 0210t ππ,103t ππ或52310tπππ,解得1003t 或50203t , 20min 3,故D 错误. 故选:AC .12.给出下面四个结论,其中正确的是( ) A .函数()()ln sin f x x =的定义域是()0,π. B .()sin sin 122x xf x =+的值域为52,2⎡⎤⎢⎥⎣⎦.C .函数()sin 2f x x x =-+在区间()2,4上有唯一一个零点.D .角πα6=是1cos 22α=-的必要不充分条件.三、填空题(共20分)13.已知sin π3a ⎛⎫- ⎪⎝⎭=13,则cos 5π()6a -=________.【详解】sin 14.定义在R 上的偶函数()f x ,当],(0x ∈-∞时,()f x 单调递减,则()()231f x f x +<-的解集为______.15.已知α为第二象限角,cos 2sin()24απα⎛⎫--+= ⎪⎝⎭,则cos α=___________.16.函数sin(2)4y x π=+的图像与直线y =a 在(0,98π)上有三个交点,其横坐标分别为1x ,2x ,3x ,则123x x x ++的取值范围为_______.8442⎝⎭πππ利用对称性求出答案四、解答题(共70分)17.已知全集U =R ,集合{}2|2150A x x x =--<,集合()(){}2|210B x x a x a =-+-<. (1)若1a =,求UA 和B ;(2)若A B A ⋃=,求实数a 的取值范围. )UA ={x ∴x {|3U A x x ∴=-或5}x ,若1a =,则集合{|(2B x x =-(2)因为A B A ⋃=,所以当B =∅时,221a a =-,解当B ≠∅时,即1a ≠时,)可知集合{|A x =-22135a a --,解得15a,且综上所求,实数a 的取值范围为:15a-.【点睛】本题主要考查了集合的基本运算,考查了一元二次不等式的解法,是基础题.18.已知函数()()()sin 20f x x ϕϕ=+<<π的图象关于点,012⎛⎫- ⎪⎝⎭对称.(1)求ϕ的值;(2)将函数()y f x =的图象向右平移6π个单位,然后将所得的图象上各点的横坐标缩小到原来的12倍(纵坐标不变),得到函数()y g x =的图象.当0,4x π⎡⎤∈⎢⎥⎣⎦时,求函数()g x 的值域.19.已知函数2()2sin 1f x x x θ=+-,1[]2x ∈. (1)当6πθ=时,求()f x 的最大值和最小值;(2)若()f x 在1[]2x ∈上是单调函数,且[0,2)θπ∈,求θ的取值范围.443366【详解】试题分析:(1)当时,在上单调递减,在上单调递增当时,函数有最小值当时,函数有最小值(2)要使在31[,]22x ∈-上是单调函数,则或即或,又解得:20.已知函数()sin()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示.(1)写出函数f (x )的最小正周期T 及ω、φ的值;(2)求函数f (x )在区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值与最小值.,44ππ⎡⎤-⎢⎥⎣⎦当23x π+=21.已知二次函数2()21(0)g x mx mx n m =-++>在区间[0,3]上有最大值4,最小值0. (1)求函数()g x 的解析式; (2)设()2()g x x f x x-=.若()220x xf k -⋅在[3,3]x ∈-时恒成立,求k 的取值范围.22.已知函数()21log 1x f x x -=+. (1)若()1f a =,求a 的值;(2)判断函数()f x 的奇偶性,并证明你的结论;(3)若()f x m ≥对于[)3,x ∈+∞恒成立,求实数m 的范围. 【答案】(1)3- (2)奇函数,证明见解析f a=,)()1-3为奇函数,证明如下:,解得:x。
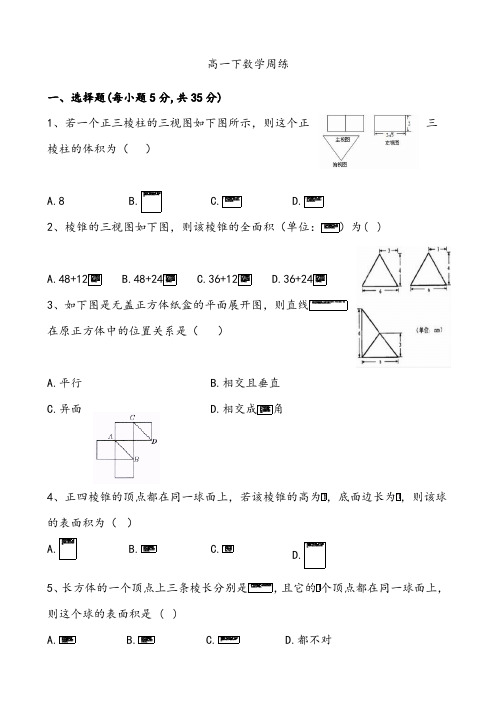
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省定州市2016-2017学年高一数学下学期周练试题(4.9)
一、选择题
1.正方形绕某一条对角线所在直线旋转一周,所得几何体是()
A.圆柱 B.圆锥
C.圆台 D.两个圆锥
2.如图是由哪个平面图形旋转得到的()
A. B. C. D.
3.将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括()A.一个圆台、两个圆锥 B.两个圆台、一个圆柱
C.两个圆台、一个圆锥
D.一个圆柱、两个圆锥
4.下列结论正确的是()
A.圆锥的顶点与底面圆周上的任意一点的连线都是母线
B.以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥
C.棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥
D.各个面都是三角形的几何体是三棱锥
5.如图所示,观察四个几何体,其中判断正确的是().
A.(1)是棱台 B.(2)是圆台
C.(3)是棱锥 D.(4)不是棱柱
6.下列命题中正确的个数是()
①由五个面围成的多面体只能是三棱柱;
②用一个平面去截棱锥便可得到棱台;
③仅有一组对面平行的五面体是棱台;
④有一个面是多边形,其余各面是三角形的几何体是棱锥.
A.0个 B.1个
C.2个 D.3个
7.如图所示,观察四个几何体,其中判断正确的是().
A.(1)是棱台 B.(2)是圆台
C.(3)是棱锥 D.(4)不是棱柱
8.如下图,能推断这个几何体可能是三棱台的是()
A.,,,
网
科
]
B.,,,,,[来
:学
源
C.,,,,,
D.,,
9.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体积为()
A. B. C. D.
10.在正方体中,M是棱的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
A.B.C.D.
11.已知地球的半径为,球面上两点都在北纬45°圈上,它们的球面距离为
,点在东经30°上,则两点所在其纬线圈上所对应的劣弧的长度为()A.
B.
C.
D.
12.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.
B.
C.
D.
二、填空题
13.已知圆柱的底面半径为1,母线长与底面的直径相等,则该圆柱的表面积为.14.平面截半径为2的球所得的截面圆的面积为,则球心到平面的距离为.15.若圆锥的内切球与外接球的球心重合,且内切球的半径为,则圆锥的体积为.
16.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点。
三、解答题
17.如图,在直四棱柱中,底面是边长为的正方形,
分别为线段的中点.
(1)求证:平面;
(2)四棱柱的外接球的表面积为,求异面直线与所成的角的大小.
18.设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
参考答案
1.D
【解析】
试题分析:连接正方形的两条对角线知对角线互相垂直,故绕对角线旋转一周形成两个圆锥.
考点:旋转体.
【易错点晴】一条平面曲线绕着它所在的平面内的一条定直线旋转所形成的曲面叫作旋转面;该定直线叫做旋转体的轴;封闭的旋转面围成的几何体叫作旋转体.等腰三角形绕过底边上的高的直线旋
转一周构成的图形性就是一个旋转体——圆锥.还有圆柱、圆台、球等都是旋转体.圆绕过圆心的直线旋转一周所成的球.
2.D
【解析】
试题分析:A.应旋转为中间是圆柱,上下是圆锥,B.应旋转为上下同底的两个圆锥,C.应旋转为上面是圆柱,线面是圆锥,只有D旋转后是如图的几何体,故选D.
考点:旋转体
3.D
【解析】
试题分析:把等腰梯形分割成两个直角三角形和一个矩形,由旋转体的定义可知所得几何体包括一个圆柱、两个圆锥.故选D.
考点:旋转体.
4.A
【解析】
试题分析:如图2,若不是直角三角形,或是直角三角形但旋转轴不是直角边,所得
的几何体都不是圆锥,B错误;若该棱锥是六棱锥,由题设知,它是正六棱锥,易证正六棱锥的侧棱长必大于底面边长,这与题设矛盾,C错误;如图1是由两个相同的三棱锥叠放在一起构成的几何体,它的各个面都是三角形,但它不是三棱锥,D错误;易知A正确,故选A.
考点:锥体及其性质.
5.C
【解析】
试题分析:图①不是由棱锥截来的,所以①不是棱台;
图②上、下两个面不平行,所以②不是圆台;
图③是棱锥.
图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱考点:几何体的结构特征
【解析】
试题分析:①中,由五个面围成的多面体可以是四棱锥,所以不正确;②中,用一个平行于底面的平面截棱锥才能得到一个棱台;③中,仅有一组对面平行的五面体,可以是三棱柱;④中,有一个个面是多边形,其余各面是三甲型的几何体不一定是棱锥,如三棱台,所以选A.
考点:多面体的特征.
7.C
【解析】
试题分析:根据几何体的结构特征可知,(1)不是棱台,棱台的侧棱延长后应交于一点,(2)不是圆柱,圆柱的上下底面互相平行,(3)为棱锥,(4)是棱柱。
考点:几何体的结构特征。
8.C
【解析】
试题分析:根据棱台是由棱锥截成的,A、,故A不正确;B、,故B
不正确;C、,故C正确,D、满足这个条件的是一个三棱柱,不是三棱台,
故选C.
考点:棱台的结构特征.
9.D
【解析】
试题分析:根据正四棱柱的几何特征得:该球的直径为正四棱柱的体对角线,故
,即得,所以该球的体积,故选D.
考点:正四棱柱的几何特征;球的体积.
10.C
【解析】
如图,以D为原点,建立空间直角坐标系,
不妨设,则A(1,0,0),,,P(1,y,1),则,
,∴,∴OP⊥AM.选C.
【解析】
如图,设球心为,北纬45°圈的中心为,
由两点的球面距离为,所以=,
为等边三角形.于是.
由,
.即=.
两点在其纬线圈上所对应的劣弧.选C.
12.B
【解析】由勾股定理可得球的半径为,从而根据球的体积公式可求得该球的体积为:
.故选B.
13.
【解析】
试题分析:因为圆柱的表面积为,所以圆柱的表面积为
考点:圆柱的侧面积
14.
【解析】
试题分析:由题意得:截面圆的半径为1.截面圆圆心与球心距离、截面圆的半径1及球的半径2构成直角三角形三边,利用勾股定理可得距离为.
考点:球的相关知识.
15.
【解析】
试题分析:过圆锥的旋转轴作轴截面,得△及其内切圆和外切圆,且两圆同圆心,即△的内心与外心重合,易得△为正三角形,由题意的半径为,∴△的
边长为,∴圆锥的底面半径为,高为,∴.
考点:圆锥的体积.
16.5,4,3
【解析】
试题分析:面最少的三棱柱是三棱柱,它有五个面;面数最少的棱锥是三棱椎,它有4个顶点;顶点最少的一个棱台是三棱台,它有三条侧棱.故答案为:5,4,3.
考点:棱锥的结构特征.
17.(1)证明见解析;(2).
【解析】
试题分析:(1)由题意可知,要证明平面,则可证明;(2)通过外接球的表面积为可求出四棱柱的高,再通过平移找出异面直线与所成的平面角,从而求解. 试题解析:(1)连接,在中,分别为线段的中点,∴为中位线,∴,而面,面,∴平面.
(2)由(1)知,故即为异面直线与所成的角.
∵四棱柱的外接球的表面积为,
∴四棱柱的外接球的半径,
设,则,解得,
在直四棱柱中,∵平面,平面,
∴,在中,,
∴,
∴异面直线与所成的角为.
考点:1.直线与平面平行的判定;2.异面直线所成的夹角.
18.
【解析】
试题分析:本题实质是体积问题,我们知道题中球取出前后水的体积是不变的,通过开始时的圆锥体积减去球的体积得出水的容积,球取出后,水变成了圆锥,圆锥的高就是我们要求的水面高度.
试题解析:如图为圆锥轴截面,球心为,可得
(3分)
(5分)
设取出球后,水面高为,则
(8分)
因为(10分)
所以(12分)
考点:圆锥的体积与圆锥的性质.。
