进制转换表

合集下载

进制转换对照

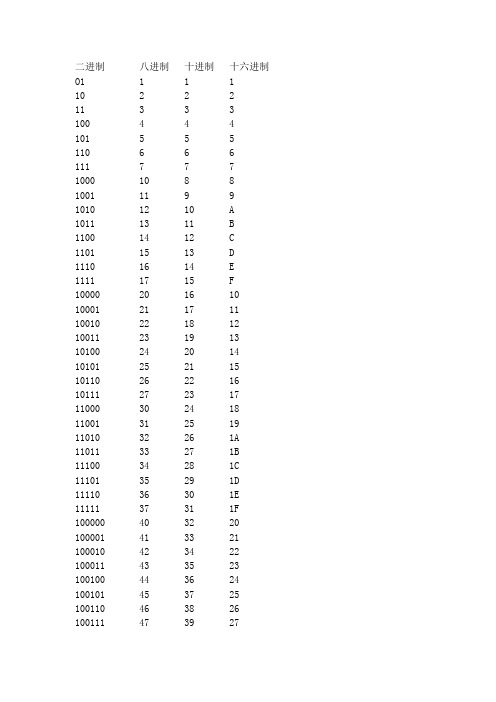
二进制八进制十进制十六进制O1 1 1 110 2 2 211 3 3 3100 4 4 4101 5 5 5110 6 6 6111 7 7 71000 10 8 81001 11 9 91010 12 10 A1011 13 11 B1100 14 12 C1101 15 13 D1110 16 14 E1111 17 15 F 10000 20 16 10 10001 21 17 11 10010 22 18 12 10011 23 19 13 10100 24 20 14 10101 25 21 15 10110 26 22 16 10111 27 23 17 11000 30 24 18 11001 31 25 19 11010 32 26 1A 11011 33 27 1B 11100 34 28 1C 11101 35 29 1D 11110 36 30 1E 11111 37 31 1F 100000 40 32 20 100001 41 33 21 100010 42 34 22 100011 43 35 23 100100 44 36 24 100101 45 37 25 100110 46 38 26 100111 47 39 27101001 51 41 29 101010 52 42 2A 101011 53 43 2B 101100 54 44 2C 101101 55 45 2D 101110 56 46 2E 101111 57 47 2F 110000 60 48 30 110001 61 49 31 110010 62 50 32 110011 63 51 33 110100 64 52 34 110101 65 53 35 110110 66 54 36 110111 67 55 37 111000 70 56 38 111001 71 57 39 111010 72 58 3A 111011 73 59 3B 111100 74 60 3C 111101 75 61 3D 111110 76 62 3E 111111 77 63 3F 1000000 100 64 40 1000001 101 65 41 1000010 102 66 42 1000011 103 67 43 1000100 104 68 44 1000101 105 69 45 1000110 106 70 46 1000111 107 71 47 1001000 110 72 48 1001001 111 73 49 1001010 112 74 4A 1001011 113 75 4B 1001100 114 76 4C 1001101 115 77 4D 1001110 116 78 4E 1001111 117 79 4F1010001 121 81 511010010 122 82 521010011 123 83 531010100 124 84 541010101 125 85 551010110 126 86 561010111 127 87 571011000 130 88 581011001 131 89 591011010 132 90 5A1011011 133 91 5B1011100 134 92 5C1011101 135 93 5D1011110 136 94 5E1011111 137 95 5F1100000 140 96 601100001 141 97 611100010 142 98 621100011 143 99 631100100 144 100 64要将二进制转为16进制，只需将二进制的位数由右向左每四位一个单位分隔，分的不够的前边补零，用四位数的二进制数来代表一个16进制。

各进制转换(含小数)

各进制转换(含小数)
1.带小数的二进制转换为十进制：
例如二进制数 1011.0111，在转换过程中将其分为整数部分和小数部分分别转换，整数部分转换方式没有变化，即每位乘以2的对应该位数上的幂，此整数的幂为0~3，而对于小数部分来说，对应的2的幂则应该是-1~-4。

1011.0111 = (1*2^3+0*2^2+1*2^1+1*2^0) +
(0*2^-1+1*2^-2+1*2^-3+1*2^-4
=8+0+2+1+0+1/2^2+1/2^3+1/2^4
=11.4375
2.带小数的十进制转换为二进制：
我们知道十进制整数转换为二进制的方法是除2取余，直至商为0，最后将所得余数以逆序排列即可得到二进制数。

而对于十进制小数则刚好相反，转换的方法是乘2取整，将小数乘以2然后截取整数部分，再把截取后的小数乘以2再截取整数，以此类推，直至小数部分为0，最后将截取所得到整数以顺序排列即可得出对应的二进制数。

例如 0.4375
0.4375*2 = 0.875 0
0.875*2 = 1.75 (1)
(1.75-1)*2 = 1.5 (1)
(1.5-1)*2 = 1 (1)
1-1 = 0(到此结束)
所以所得二进制数为0.0111。

需要注意的是并不是所有十进制小数都可以完全转换为二进制数，因为如果要实现完全转换必须乘2到最后不剩小数部分。

这时通常是根据精度要求转换到小数后某一位为止。

进制转换表

Plc课程知识点一基础知识1 数字电路基础2 plc基础3 编程基础二编程入门1逻辑控制程序编制2定时器程序编制3计数器程序编制三编程软件及仿真软件的使用二、八、十、十六进制数数值=6×1000+5×100+0×10+5×1=6505B1011=1×8+0×4+1×2+1×0=K11H3AE=3×256（16的2次方）+A(10)×16（16的一次方）+E（14）×1（16的零次方）=K942 8421BCD码用四位二进制数表示十进制数的编码方式称为BCD码又称二—十进制。

最长用的是8421BCD码十进制数58的二进制数表示和BCD码表示1．二进制数表示K58=B11101058/2=29 029/2=14 (1)14/2=7 07/2=3 (1)3/2=1 (1)1/2=0 (1)2 。

8421BCD码表示5 80101 1000K58=01011000BCD格雷码在各种控制系统的角度、长度测量和定位控制中，经常使用绝对式旋转编码器作为位置传感器，其算输出的二进制编码为格雷码。

格雷码是一种无权二进制编码，它的特点是任何相邻的吗组之间只有一位数位发生改变，是一种错误很少的可靠性编码。

十进制转化成N进制口诀：除N取余，逆序排列K58=B11101058/2=29 029/2=14 (1)14/2=7 07/2=3 (1)3/2=1 (1)1/2=0 (1)k8000=H1f408000/16=500 0500/16=31 (4)31/16=1 (15)1/16=0 (1)k302=b100101110302/2=151 0151/2=75 (1)75/2=37 (1)37/2=18 (1)18/2=9 09/2=4 (1)4/2=2 02/2=1 01/2=0 (1)十进制转化成二进制例：K200=B？200÷2=100.。

二进制八进制16进制转换表

二进制八进制16进制转换表二进制、八进制和十六进制是计算机中常用的进制表示方法。

在计算机科学和信息技术领域，我们经常需要进行不同进制之间的转换。

下面是一个二进制、八进制和十六进制转换表，方便大家在实际应用中进行转换。

首先，我们来看二进制转换为八进制和十六进制的方法。

二进制是由0和1组成的数字系统，每一位的权值是2的幂次方。

八进制是由0到7组成的数字系统，每一位的权值是8的幂次方。

十六进制是由0到9和A到F组成的数字系统，每一位的权值是16的幂次方。

在二进制转换为八进制时，我们将二进制数从右往左每三位一组进行分组，然后将每组转换为对应的八进制数。

例如，二进制数1101011可以分组为011和010和110，分别对应的八进制数是3和2和6，所以1101011的八进制表示为326。

在二进制转换为十六进制时，我们将二进制数从右往左每四位一组进行分组，然后将每组转换为对应的十六进制数。

例如，二进制数1101011可以分组为0110和1011，分别对应的十六进制数是6和B，所以1101011的十六进制表示为6B。

接下来，我们来看八进制转换为二进制和十六进制的方法。

八进制数每一位的权值是8的幂次方，而二进制数每一位的权值是2的幂次方。

所以，八进制数可以直接转换为二进制数，每一位八进制数对应的三位二进制数。

例如，八进制数326可以转换为对应的二进制数011010110。

在八进制转换为十六进制时，我们先将八进制数转换为对应的二进制数，然后将二进制数从右往左每四位一组进行分组，最后将每组转换为对应的十六进制数。

例如，八进制数326转换为二进制数011010110，可以分组为0110和1011，分别对应的十六进制数是6和B，所以326的十六进制表示为6B。

最后，我们来看十六进制转换为二进制和八进制的方法。

十六进制数每一位的权值是16的幂次方，而二进制数每一位的权值是2的幂次方。

所以，十六进制数可以直接转换为二进制数，每一位十六进制数对应的四位二进制数。

二进制，八进制，十进制和十六进制之间的互相转换【超详细】！

⼆进制，⼋进制，⼗进制和⼗六进制之间的互相转换【超详细】！在进⾏讲解之前，我们先在下⾯放置⼀个对应表，因为在理解下⾯转换的时候，你可以随时查看该表。

㈠：⼆进制转⼗进制⑴⼆进制转⼗进制的第⼀个⽅法是要从右到左⽤⼆进制的每个数去乘以2的相应次⽅,⼩数点后则是从左往右2的0次⽅是1（任何数的0次⽅都是1，0的0次⽅⽆意义）2的1次⽅是22的2次⽅是42的3次⽅是82的4次⽅是162的5次⽅是322的6次⽅是642的7次⽅是1282的8次⽅是2562的9次⽅是5122的10次⽅是1024㈡⼗进制转⼆进制⽅法为：⽤2整除⼗进制整数，可以得到⼀个商和余数；再⽤2去除商，⼜会得到⼀个商和余数，如此进⾏，直到商为⼩于1时为⽌，然后把先得到的余数作为⼆进制数的低位有效位，后得到的余数作为⼆进制数的⾼位有效位，依次排列起来。

具体如下图所⽰：㈢⼆进制转⼋进制⼆进制数转换成⼋进制数：从⼩数点开始，整数部分向左、⼩数部分向右，每3位为⼀组⽤⼀位⼋进制数的数字表⽰，不⾜3位的要⽤“0”补⾜3位，就得到⼀个⼋进制数。

（具体⽤法如下图）㈣：⼋进制转成⼆进制⼋进制转换成⼆进制数：⼋进制数通过除2取余法，得到⼆进制数，每个⼋进制对应三个⼆进制，不⾜时在最左边补充零。

（具体⽤法如下图）㈤⼆进制转⼗六进制⽅法为：与⼆进制转⼋进制⽅法近似，⼋进制是取三合⼀，⼗六进制是取四合⼀。

（注意事项，4位⼆进制转成⼗六进制是从右到左开始转换，不⾜时补0）。

（具体⽤法如下图）㈥⼗六进制转⼆进制⼗六进制转⼆进制：⼗六进制数通过除2取余法，得到⼆进制数，每个⼗六进制对应四个⼆进制，不⾜时在最左边补充零。

（具体⽤法如下图）（七）、⼗进制转⼋进制或者⼗六进制有两种⽅法第⼀：间接法—把⼗进制转成⼆进制，然后再由⼆进制转成⼋进制或者⼗六进制。

这⾥不再做图⽚⽤法解释。

第⼆：直接法—把⼗进制转⼋进制或者⼗六进制按照除8或者16取余，直到商为0为⽌。

（⼋）、⼋进制或者⼗六进制转成⼗进制⽅法为：把⼋进制、⼗六进制数按权展开、相加即得⼗进制数。

八进制转十六进制表格

八进制转十六进制表格八进制转十六进制表格在计算机科学中，数字通常使用二进制、八进制或十六进制表示。

其中，八进制和十六进制是比较常用的进制系。

如果需要将八进制转换成十六进制，可以使用如下的表格来进行转换：八进制数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7--- | --- | --- | --- | --- | --- | --- | --- | ---十六进制数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7八进制数 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17--- | --- | --- | --- | --- | --- | --- | --- | ---十六进制数 | 8 | 9 | A | B | C | D | E | F对于一个八进制数来说，将每个位上的数字与上表中的对应关系进行匹配，就能得到其对应的十六进制数。

例如，八进制数726转换成十六进制数的过程如下：1. 将726拆分为每一位上的数字，得到7、2和6。

2. 根据上表可知，数字7对应十六进制数7，数字2对应十六进制数2，数字6对应十六进制数6。

3. 因此，726的十六进制表示为762。

需要注意的是，八进制和十六进制之间只是进制的不同，它们所表示的数值是相等的。

因此，进行进制转换不会改变原数的大小，只是改变了其表现形式。

除了使用表格进行转换，还有一些其他的方法可以将八进制转换成十六进制。

例如，可以先将八进制数转换成二进制数，再将二进制数转换成十六进制数。

或者直接使用计算器或程序完成转换。

不管采用何种方法，都需要对进制转换的原理有基本的了解，才能正确地进行转换。

总之，八进制和十六进制是计算机科学中常用的进制系，掌握其转换方法对于进行编程和计算具有重要意义。

通过使用表格等工具，可以更加便捷地进行进制转换，提高计算的效率和准确性。

二进制八进十六进制转换表

二进制八进十六进制转换表在计算机科学和电子工程领域，二进制、八进制和十六进制是常用的数制。

通过将数值转换成不同的进制，我们可以更好地理解和表示数字。

下面是一个二进制、八进制和十六进制的转换表，可作为参考使用。

1. 二进制转八进制和十六进制将二进制数转换为八进制和十六进制相对简单，只需要将二进制数按照位数分组。

- 八进制：每三个二进制位为一组，从低位向高位对应地分组，再将每组转换成相应的八进制数。

下表是常用的二进制转八进制的对应关系。

二进制八进制000 0001 1010 2011 3100 4101 5110 6111 7- 十六进制：每四个二进制位为一组，从低位向高位对应地分组，再将每组转换成相应的十六进制数。

下表是常用的二进制转十六进制的对应关系。

二进制十六进制0000 00001 10010 20011 30100 40101 50110 60111 71000 81001 91010 A1011 B1100 C1101 D1110 E2. 八进制和十六进制转二进制将八进制和十六进制数转换为二进制也很简单，只需要将八进制数每一位对应转换为对应的三个二进制位，将十六进制数每一位对应转换为对应的四个二进制位即可。

- 八进制转二进制：下表是常用的八进制转二进制的对应关系。

八进制二进制0 0001 0012 0103 0114 1005 1016 1107 111- 十六进制转二进制：下表是常用的十六进制转二进制的对应关系。

十六进制二进制0 00001 00013 00114 01005 01016 01107 01118 10009 1001A 1010B 1011C 1100D 1101E 1110F 1111通过以上转换表，我们可以方便地将不同进制的数值进行转换。

这对于计算机科学和电子工程领域的学习和应用是非常重要的。

总结：本文提供了一个二进制、八进制和十六进制的转换表，可帮助读者快速而准确地进行数值转换。

进制转换

进制转换对照表(0~255) - 十进制，十六进制，八进制，二进制Dec Hex Oct Bin0 1 2 3 4 5 6 7 8 9101112131415 0123456789ABCDEF00000100200300400500600701001101201301401501601700000000000000010000001000000011000001000000010100000110000001110000100000001001000010100000101100001100000011010000111000001111Dec Hex Oct Bin16171819202122232425262728293031101112131415161718191A1B1C1D1E1F02002102202302402502602703003103203303403503603700010000000100010001001000010011000101000001010100010110000101110001100000011001000110100001101100011100000111010001111000011111Dec Hex Oct Bin32333435363738394041424344454647202122232425262728292A2B2C2D2E2F04004104204304404504604705005105205305405505605700100000001000010010001000100011001001000010010100100110001001110010100000101001001010100010101100101100001011010010111000101111Dec Hex Oct Bin48495051525354555657585960616263303132333435363738393A3B3C3D3E3F06006106206306406506606707007107207307407507607700110000001100010011001000110011001101000011010100110110001101110011100000111001001110100011101100111100001111010011111000111111Dec Hex Oct Bin64656667686970 4041424344454610010110210310410510601000000010000010100001001000011010001000100010101000110Dec Hex Oct Bin808182838485865051525354555612012112212312412512601010000010100010101001001010011010101000101010101010110Dec Hex Oct Bin969798991001011026061626364656614014114214314414514601100000011000010110001001100011011001000110010101100110Dec Hex Oct Bin1121131141151161171187071727374757616016116216316416516601110000011100010111001001110011011101000111010101110110717273747576777879 4748494A4B4C4D4E4F1071101111121131141151161170100011101001000010010010100101001001011010011000100110101001110010011118788899091929394955758595A5B5C5D5E5F1271301311321331341351361370101011101011000010110010101101001011011010111000101110101011110010111111031041051061071081091101116768696A6B6C6D6E6F1471501511521531541551561570110011101101000011010010110101001101011011011000110110101101110011011111191201211221231241251261277778797A7B7C7D7E7F167170171172173174175176177011101110111100001111001011110100111101101111100011111010111111001111111Dec Hex Oct Bin128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 808182838485868788898A8B8C8D8E8F20020120220320420520620721021121221321421521621710000000100000011000001010000011100001001000010110000110100001111000100010001001100010101000101110001100100011011000111010001111Dec Hex Oct Bin144145146147148149150151152153154155156157158159909192939495969798999A9B9C9D9E9F22022122222322422522622723023123223323423523623710010000100100011001001010010011100101001001010110010110100101111001100010011001100110101001101110011100100111011001111010011111Dec Hex Oct Bin160161162163164165166167168169170171172173174175A0A1A2A3A4A5A6A7A8A9AAABACADAEAF24024124224324424524624725025125225325425525625710100000101000011010001010100011101001001010010110100110101001111010100010101001101010101010101110101100101011011010111010101111Dec Hex Oct Bin176177178179180181182183184185186187188189190191B0B1B2B3B4B5B6B7B8B9BABBBCBDBEBF26026126226326426526626727027127227327427527627710110000101100011011001010110011101101001011010110110110101101111011100010111001101110101011101110111100101111011011111010111111Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 C0C1C2C3C4C5C6C7C8C9CACBCCCDCECF30030130230330430530630731031131231331431531631711000000110000011100001011000011110001001100010111000110110001111100100011001001110010101100101111001100110011011100111011001111208209210211212213214215216217218219220221222223D0D1D2D3D4D5D6D7D8D9DADBDCDDDEDF32032132232332432532632733033133233333433533633711010000110100011101001011010011110101001101010111010110110101111101100011011001110110101101101111011100110111011101111011011111224225226227228229230231232233234235236237238239E0E1E2E3E4E5E6E7E8E9EAEBECEDEEEF34034134234334434534634735035135235335435535635711100000111000011110001011100011111001001110010111100110111001111110100011101001111010101110101111101100111011011110111011101111240241242243244245246247248249250251252253254255F0F1F2F3F4F5F6F7F8F9FAFBFCFDFEFF36036136236336436536636737037137237337437537637711110000111100011111001011110011111101001111010111110110111101111111100011111001111110101111101111111100111111011111111011111111一：简述：进位计数制：是人们利用符号来计数的方法。

进制转换对照

进制转换表(常见分数、小数)

进制转换表（常见分数、小数）
本文档提供了常见分数和小数之间的进制转换表。

通过这份表格，您可以快速准确地进行进制转换，方便您在研究和工作中的使用。

分数转小数
小数转分数
为了方便使用，本文档也提供了一些常见小数转分数的参考。

请注意，这是一个常见分数和小数进制转换的简单参考表格，可能不包含所有分数和小数的转换。

如果您在使用过程中遇到其他分数或小数的转换问题，建议使用特殊的转换工具或咨询数学专业知识。

希望这份进制转换表能对您有所帮助！。