节点导纳矩阵法
14节点导纳矩阵

14节点导纳矩阵14节点导纳矩阵是描述电力系统中节点之间相互连接关系的一种数学工具。
本文将介绍14节点导纳矩阵的构成和作用,以及如何利用导纳矩阵进行电力系统分析。
导纳矩阵是描述电力系统中节点之间导纳关系的一种矩阵形式。
它由14行14列组成,每个元素表示对应节点之间的导纳值。
导纳是指电路元件对电流的响应程度,是电路的重要参数之一。
14节点导纳矩阵的构成是基于电力系统的拓扑结构和电路元件的导纳值。
拓扑结构描述了电力系统中各节点之间的连接关系,而电路元件的导纳值则代表了电路元件对电流的响应程度。
在14节点导纳矩阵中,对角线元素表示各节点的自导纳值,非对角线元素表示各节点之间的互导纳值。
自导纳值可以理解为节点本身的电流响应能力,而互导纳值则表示节点之间的电流传输能力。
利用14节点导纳矩阵可以进行电力系统的各种分析。
例如,可以通过求解导纳矩阵的特征值和特征向量来判断电力系统的稳定性。
特征值表示系统的固有频率,特征向量则表示系统的振荡模式。
导纳矩阵还可以用于计算电力系统中节点之间的电压和电流分布。
通过对导纳矩阵进行运算,可以得到各节点的电压和电流值,从而了解电力系统的工作状态。
除了稳定性分析和电压电流计算,导纳矩阵还可以用于故障分析和电力系统的优化设计。
在发生故障时,可以通过修改导纳矩阵中对应元素的值来模拟故障情况,并分析故障对电力系统的影响。
在电力系统的优化设计中,可以通过调整导纳矩阵中的元素值来改变电力系统的结构和参数,以达到提高电力系统效率和可靠性的目的。
14节点导纳矩阵是描述电力系统中节点之间导纳关系的重要工具。
它可以用于电力系统的稳定性分析、电压电流计算、故障分析和优化设计等方面。
通过对导纳矩阵的分析和运算,可以更好地了解和优化电力系统的工作状态。
节点导纳矩阵

z10
I10
3 V3 1 I3 I13
z13
因此a的导纳矩阵为:
1
z12
1 z13
1 z10
1 z12
1 z13
Y
1 z12
1 z12
0
1
z13
1
0
z13
1
2
3
z12
z23
z20
若将节点1与节点2互换,根据图e,按照上述原则可得导纳矩阵为
1
z12
Y
1 z12
0
1 z12
2
I2 I12
1
I1
I13 0
3 I3
z12
z13
z10
I10
•
•
I 1 I 21 Y12
•
I
•
2 I
21
1 z12
Y22
•
I 3 0 Y32
同理得第三列元素为:
2
I2
•
•
I 1 I 31 Y13
I12 0
•
1
z12
I 2 0 z12 Y23
•
•
I 3 I 31 Y33
1
I1
Y11
1 z12
1 z13
1 z10
y12
y10
y13
节点2的自导纳应为:
Y22
1 z12
y12
(4) 导纳矩阵的非对角元素 等于节点
纳并取负号:
1
Yij
zij
yij
和节点
间的支路导
按照上述原则无论电力系统如何复杂都可以根据输电线路的参数和接线拓 扑,直接求出导纳矩阵。
一下包括变压器、移相器时,导纳矩阵的的形成方法。
节点导纳矩阵的计算

目录摘要 (1)1 题目 (1)2 节点导纳矩阵的计算原理 (2)2.1节点方程 (2)2.2节点导纳矩阵元素的物理意义 (5)3 计算过程 (6)4 用MATLAB计算 (7)4.1程序清单: (7)4.2 输出结果与分析 (9)5 小结 (10)参考文献 (11)成绩评定表节点导纳矩阵的计算1 题目电力系统如下图所示,图中所有串联支路参数均为阻抗标幺值,所有对支路参数均为导纳标幺值。
求设网络的节点导纳矩阵。
图一2 节点导纳矩阵的计算原理2.1节点方程在图2中的简单电力系统中,若略去变压器的励磁功率和线路电容,负荷用阻抗表示,便可得到一个有5个基点(包括零电位点)和7条支路的等值网络,如图3所示。
图2图3将接于节点1和4的电势源和阻抗的串联组合变换成等值的电流源和导纳的并联组合,便得到图4的等值网络。
其中:••=1101E y I ••图4以零电位点作为计算节点电压的参考点,根据基尔霍夫电流定律,可以写出4个独立节点的电流平衡方程如下上述方程组经过整理可以写成:式中:⎪⎪⎪⎭⎪⎪⎪⎬⎫=+-+-=-+-=-+-++-=-+•••••••••••••••••••••4440343424244324232342243223220121212112110)()(0)()(0)()()()(I V y V V y V V y V V y V V y V V y V V y V y V V y I V V y V y ⎪⎪⎪⎭⎪⎪⎪⎬⎫=++=++=+++=+•••••••••••••4444343242434333232424323222121212111000I V Y V Y V Y V Y V Y V Y V Y V Y V Y V Y V Y V Y 34433424422423322312211234244044342440443423331224232022121011;;;;;;;;y Y Y y Y Y y Y Y y Y Y y y y Y y y y Y y y Y y y y y Y y y Y -==-==-==-==++=++=+=+++=+=一般地,对于有n 个独立节点的网络,可以列写n 个节点方程:也可以用矩阵写成:或缩写成:YV=I矩阵Y 称为节点导纳矩阵。
节点导纳矩阵
2019/12/5
电气工程基础-系统篇
3
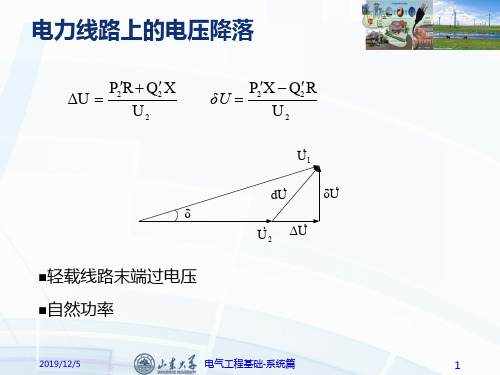
3.3.1 电力网络方程
对任意节点i,根据KCL
U i
U i
U j
U j
Ii n Iij n yij Ui U j
yij yij
j0
j0
ji
ji
Iij
1
I1
y10
2
y13 y12 y23
I2
3
y30
y34
4
y40
I4
简化等值网络
2019/12/5
电气工程基础-系统篇
11
2019/12/5
电气工程基础-系统篇
I YU
12
3.3.2 功率方程和节点分类 I Y U
以极坐标形式表示节点电压、直角坐标形式表示导纳
Ui Uie ji Ui cosi jsini
13
节点分类
节点 已知变 待求变
类型 量
量
适用节点
备注
PQ P和Q
PV P和U
平衡节 U和δ 点?
U 和δ Q和δ P和Q
按给定有功、无功功率发电的 P Q 节 点 占
发电厂节点和没有其他电源的 系 统 节 点
变电站接点
总数的大
部分, PV
有一定无功功率储备的发电厂 节 点 占 少
节点和一定无功功率电源的变 部 分 ( 某
G
1)若以同获时2 得给同定时末满端3 足负两荷4个功限率制始条端件电的压YT1结,果必(须Y2l 前反推复回推Y2l 代算算(Y法T迭2 )代
z 1 12 2
z23
z 3
34 4
节点导纳矩阵.ppt

2 1 3 1 3 2 4 2 5 2
y y y y y
4 5 3 1 2
这些是各节点的互导纳;其余节点互导纳为0; 上式反映了各节点电压与注入电流的关系,I 1 ~ I 5 为各节点 注入的电流,除 I I 外其他都为0
1
5
通过以上的例子,节点方程的阶数等于网络的节点数n,展开一般 形式为:
导纳矩阵的对称性和稀疏性对于计算机解算电力系统问题有很大的影 响,如果能充分利用该特点,会大大提高计算机的速度并节约内存。
1.2节点导纳矩阵的形成与修改 主要分为三个部分:导纳矩阵的形成、特殊元件的处理与导纳矩阵的修 改。 导纳矩阵的形成可以分为以下几点: (1) 导纳矩阵的阶数等于电力网络的节点数; (2) 导纳矩阵各行的非对角元素中非零元素的个数等于对应节点所连的不 接地支路数; (3) 导纳矩阵各对角元素,即各节点的自导纳等于相应节点所连支路的导 纳之和:
节点2的自导纳应为:
Y22
(4) 导纳矩阵的非对角元素 纳并取负号:
1 y12 z12
等于节点 和节点 间的支路导
1 Yij yij zij
按照上述原则无论电力系统如何复杂都可以根据输电线路的参数和接线拓 扑,直接求出导纳矩阵。 一下包括变压器、移相器时,导纳矩阵的的形成方法。 当节点 i 、 j 之间为变压器支路时对导纳矩阵的影响: (1) 增加非零非对角元素
1
3
V1=1
I1I13I3 Nhomakorabeaz12 z10
z13
I10
I 1 I 12 I 13 I I 2 I I 3 I
12
含四种受控源电路的节点导纳矩阵系统列写法

一、概述在电力系统分析中,受控源是一种被广泛使用的模型,在各种电路和系统的分析中都有重要的应用。
受控源电路的节点导纳矩阵系统列写法是一种用来表示受控源电路的方法,能够方便地进行分析和计算。
本文将重点介绍含四种受控源电路的节点导纳矩阵系统列写法,包括其原理、方法和应用。
二、含四种受控源电路的节点导纳矩阵1. 受控电压源受控电压源是一个电压源,其输出电压由电路中的某个变量控制。
在节点导纳矩阵系统列写法中,受控电压源可以表示为:$I_k = -G_{NK}V_k + H_{NK}V_m$其中,$I_k$为电流,$V_k$为电压,$G_{NK}$为导纳矩阵的元素,$H_{NK}$表示受控源的系数。
2. 受控电流源受控电流源是一个电流源,其输出电流由电路中的某个变量控制。
在节点导纳矩阵系统列写法中,受控电流源可以表示为:$V_k = -B_{NK}I_k + E_{NK}I_m$其中,$V_k$为电压,$I_k$为电流,$B_{NK}$为导纳矩阵的元素,$E_{NK}$表示受控源的系数。
3. 受控电压源的双向连接受控电压源的双向连接是一种复杂的受控源模型,其输出电压由电路中的两个变量控制。
在节点导纳矩阵系统列写法中,受控电压源的双向连接可以表示为:$I_k = -G_{NK}V_k + H_{NK}V_m$$I_m = -G_{NM}V_m + H_{NM}V_k$其中,$I_k$和$I_m$分别为电流,$V_k$和$V_m$分别为电压,$G_{NK}$、$H_{NK}$、$G_{NM}$、$H_{NM}$为导纳矩阵的元素。
4. 受控电流源的双向连接受控电流源的双向连接是一种更为复杂的受控源模型,其输出电流由电路中的两个变量控制。
在节点导纳矩阵系统列写法中,受控电流源的双向连接可以表示为:$V_k = -B_{NK}I_k + E_{NK}I_m$$V_m = -B_{NM}I_m + E_{NM}I_k$其中,$V_k$和$V_m$分别为电压,$I_k$和$I_m$分别为电流,$B_{NK}$、$E_{NK}$、$B_{NM}$、$E_{NM}$为导纳矩阵的元素。
电力系统分析第4章 电力网络的数学模型

Vn
I2(1)
•
•
Y (1) n2
V2
Y (1) nn
Vn
I2(1)
式中
Y (1) ij
Yij
Yi1Yj1 Y11
; Ii(1)
I
Yi1 Y11
I1
第四章电力网络的数学模型
4.2 网络方程的解法
➢ 对方程式再作一次消元,其系数矩阵便演变为
Y11
Y (2)
Y12 Y13 Y1n
Y (1) 22
第四章电力网络的数学模型
4.1 节点导纳矩阵
➢一般地,对于有n个独立节点地网络,可以列写n个 节点方程
•
•
•
Y11 V1 Y12 V2 Y1n Vn
•
I1
•
•
•
Y21 V1 Y22 V2 Y2n Vn
•
I2
•
•
• •
Yn1 V1 Yn2 V2 Ynn Vn In
(4-3)
4.1 节点导纳矩阵
➢上述方程经过整理可以写成
•
•
Y11 V1 Y12 V2
0
•
•
•
•
Y21 V1 Y22 V2 Y23 V3 Y24 V4 0
•
•
•
Y32 V2 Y33 V3 Y34 V4 0
•
•
•
Y42 V2 Y43 V3 Y44 V4
•
I
4
(4-2)
第四章电力网络的数学模型
4.1 节点导纳矩阵
➢将电势源和阻抗的串联变 换成电流源和导纳的并联,得 到的等值网络如图所示,其中:
•
•
I 1 y10 E1
节点导纳矩阵法

Y1(23)
Y1(13)
⎥ ⎦
所以:
[ ]y = ⎡⎢⎢YY13((1111))
⎢ ⎢⎣ 0
Y1(31) Y3(31) + Y1(12) + Y2(23)
Y2(12) + Y1(23)
21
利用S参数求待定导纳矩阵
[S] → [ y]:
[ y%] = ([I ] −[S])([I ] + [S])−1
[ y] = ⎡⎣ y0 ⎤⎦[ y%] ⎡⎣ y0 ⎤⎦
其中[ y%]为归一化导纳矩阵,[I ]为单位矩阵,
⎡⎣
⎡
y0
⎤⎦
=
⎢ ⎢
y01
O
0
⎤ ⎥
⎥
⎢ ⎢⎣
0
y0n
⎥ ⎥⎦
y01, y02 ,L, y0n为n端口元件各端外接传输线特性导纳。
3.2 节点导纳矩阵法(待定导纳矩阵法) Admittance Matrix Method
1
一般电路
端点:元件与外部连线的衔接点; 端口:电路网络的输入与输出口, 一个端口由两个端点构成; 节点:元件与元件的端点互相连接 之处; 支路:两个节点之间的通路; 回路:由一个节点出发,再回到该 节点的一组支路。
k =1
k =1
k =1
10
z 性质二:行Βιβλιοθήκη 素之和为零。假设各节点电位都相等且不为零(u1=u2 =L=un ≠ 0)。 由于节点间无电位差,所以各电流都为零。
n
∑ ik = − u j ykj = 0 j =1
k = 1, 2,L, n
又由于u1=u2 =L=un ≠ 0,所以
n
n
n
∑ ∑ ∑ y1 j = y2 j = L = ynj = 0
节点导纳矩阵及潮流计算

目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)节点导纳矩阵 (3)牛顿-拉夫逊法 (4)牛顿-拉夫逊法基本原理 (4)牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。
潮流计算是电力系统分析中的一种最基本的计算,它的任务是对给定的运行条件确定系统的运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题目初始条件: 如图所示电网。
其元件导纳参数为:y 12=, y 23=, y 13=任务及要求:1)根据给定的运行条件,确定图2所示电力系统潮流计算时各节点的类型和待求量;2)求节点导纳矩阵Y ;1???2+j13)给出潮流方程或功率方程的表达式;4)当用牛顿-拉夫逊法计算潮流时,给出修正方程和迭代收敛条件。
2原理介绍节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取,也可根据电路知识中找出改网络的关联矩阵,在节点电压方程的矩阵形式进行求解。
本章节我们主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道,在利用电子数字计算机计算电力系统运行情况时,多采用IYV 形式的节点方程式。
其中阶数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组:11112211211222221122n n n n nn n Y Y Y n Y Y Y n Y Y Y n +++=⎫⎪+++=⎪⎬⎪⎪+++=⎭V V V I V V V I V V VI (2-1) 由此可以得到n 个节点导纳矩阵:111212212212n n n n nn Y Y Y Y Y Y Y Y Y Y ⎛⎫⎪ ⎪= ⎪⎪⎝⎭? (2-2) 它反映了网络的参数及接线情况,因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。
节点导纳矩阵

节点导纳矩阵
节点导纳矩阵是一种重要的数学模型,它用来描述一个网络由端点和连接组成,其中端点有单个变量,它们之间的关系由算法控制。
它可以用来模拟复杂的系统,如电路、社会网络和计算机网络等。
它由一组可以在任何一个给定的节点上改变的变量组成,这些变量通常是电流或电压。
节点导纳矩阵可以用来模拟电路的行为,因为它能够表达电路中不同组件之间的关系。
可以将这种关系用一个导纳矩阵表示,这个矩阵描述了电路中每一节点之间的变化。
例如,一个两端口电路可以用一个2*2的导纳矩阵表示,它表示了每一端口之间的电流之间的关系。
此外,节点导纳矩阵还可以用来模拟社会网络中的行为。
这样的社会网络包括人与人之间的关系,也可以用导纳矩阵来模拟。
这样的社会网络可以用一个N*N的导纳矩阵来表示,它描述了每一个参与者之间的关系。
这样的社会网络可以用来模拟社会系统,如政治、社会和经济系统。
另一方面,节点导纳矩阵还可以用来模拟计算机网络。
计算机网络是由一系列节点和连接组成的复杂系统,它可以用一个N*N的导纳矩阵表示,用来描述每一节点之间的关系。
这样的网络可以用来模拟计算机系统,如互联网和局域网系统。
在总结,节点导纳矩阵是一种非常有用的数学模型,它可以用来模拟复杂的系统,如电路、社会网络和计算机网络等,用来描述
不同组件之间的关系。
它可以用一个N*N的导纳矩阵来表示,这个矩阵描述了每一个节点之间的变化,从而更好地模拟复杂的系统。
节点导纳矩阵在工程领域有着重要的作用,在未来的研究中有望取得更多有用的结果。
节点导纳矩阵

I1
3
U3
I2
电气工程基础-系统篇
6
节点电流方程的矩阵形式
用节点导纳矩阵表示的节点电压方程
Y U Y U Y U Y U I 1 11 1 12 2 1i i 1n n Y U Y U Y U Y U I 2 21 1 22 2 2i i 2n n Y U Y U Y U Y U I n n1 1 n2 2 ni i nn n
3
2
I1
y23
I2
y30
y34
4
y40
I4
简化等值网络
2018/12/27
电气工程基础-系统篇
12
I Y U
2018/12/27
电气工程基础-系统篇
13
3.3.2 功率方程和节点分类
U e ji U cos jsin U i i i i i
节点注入功率
I Y U
以极坐标形式表示节点电压、直角坐标形式表示导纳
Yij Gij jBij
P i Ui
U G
j j 1 n j j 1
n
ij
cos δij Bij sin δij
ij
i 1,2,,n i 1,2,,n
14
Qi U i
2018/12/27
U G
k
I i
l
2 U2
例如
1 U1
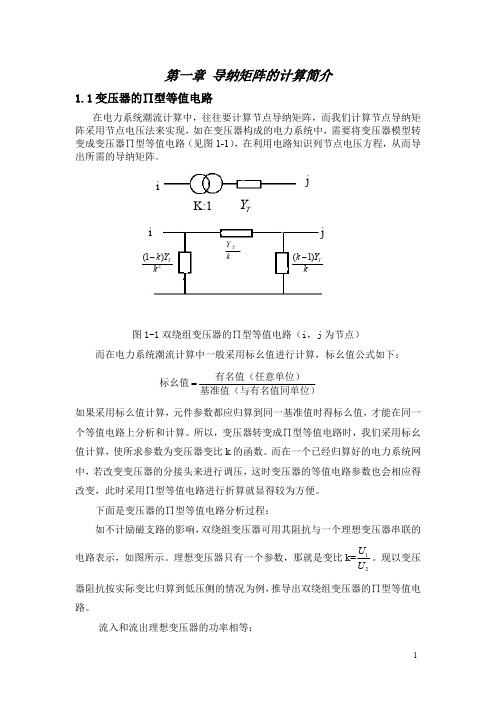
Y Y Y U I 1 11 12 13 1 U I Y Y Y 2 21 22 23 2 0 Y31 Y32 Y33 U 3
节点导纳矩阵计算
(1-11)
由此可以得到 n 个节点导纳矩阵:
Y11 Y12 ... Y1 n Y Y ... Y 21 22 2n Y ...... Yn 1 Yn 2 ... Ynn
它反映了网络的参数及接线情况, 因此导纳矩阵可以看成是对电力网络电气 特性的一 种数学抽象。 由导纳短阵所联系的节点方程式是电力网络广泛应用的一种数学模 型。 通过上面的讨论,可以看出节点导纳矩阵的有以下特点: (1) 导纳矩阵的元素很容易根据网络接线图和支路参数直观地求得,形成节 点导纳矩阵的程序比较简单。 (2)导纳矩阵为对称矩阵。由网络的互易特性变比归算到低压侧的情况为例, 推导出双绕组变压器的∏型等值电 路。 流入和流出理想变压器的功率相等:
1
U 1 I 1 U 2 I 2 / k ( U1 、 U 2 分别为变压器高、低绕组的实际电压) I1 I 2 / k
联立(1-1) 、 (1-2)两个公式解得:
. V1 . V V2 ... V. n
. I1 . I I2 ... I. n
分别为节点注入电流列向量及节点电压列向量;
Y11 Y 21 Y ... Yn1
节点 j 之间的互导纳。
. . . .
Y12 3 的自导纳,
的互导纳。
Y21 y6 , Y13 Y31 y4 , Y23 Y32 y5 称为相应节点之间
因此,在一般情况下,在电力网络中有 n 个节点,则可以按式(1-10)的形 式列出 n 个节点方程式,也可用矩阵的形式表示 I
YV 。其中
5
(3)导纳矩阵是稀疏矩阵。它的对角线元素一般不为零,但在非对角线元素 中则存在不少零元素。在电力系统的接线图中,一般每个节点与平均不超过 3~4 个其他节点有直接的支路连接。因此,在导纳矩阵的非对角线元素中每行仅有 3~4 个非零元素,其余的都是零元素,而且网络的规模越大,这种现象越显著。 导纳矩阵的对称性和稀疏性对于应用计算机求解电力系统问题有很大的影 响。如果能充分地利用这两个特点,如在程序设计中储存导纳矩阵的对角元素和 上三角元素(或下三角元素) ,排除零元素的储存和运算,就可以大大地节省储 存单元和提高计算速度。 节点导纳矩阵的形式可归纳如下: (1)导纳矩阵的阶数等于电力网络的节点数。 (2) 导纳矩阵各行非对角元素中非零元素的个数等于对应节点所连得不接地 支路数。 (3) 导纳矩阵各对角元素,即节点的自导纳等于相应节点之间的支路导纳之 和。 (4) 导纳矩阵非对角元素,即节点之间的互导纳等于相应节点之间的支路导 纳的负值。 而在电力系统中进行潮流计算时,往往要计算不同接线下的运行状况,例如 改变变压器主抽头时,潮流分布也随之变化,以及改变其他设备参数进行计算潮 流分布,此时就需要导出变化时的导纳矩阵就需要对所设计的程序进行参数设 定,而不需要重复上述步骤去导出所求的导纳矩阵。
节点导纳和阻抗矩阵

Y11 Y21 Yn1
Y12 Y22 Yn 2
I Y1n V 1 1 Y2 n V2 I 2 = Ynn Vn In
三、节点导纳矩阵的修改
根据原始节点导纳矩阵和修改的网络接线方式,快速形成修改后 的节点导纳矩阵
(0) Y y + ii ik Y = − yik
− yik yik
(0) (0) + Y y Y − y ii ij ij ij Y= (0) (0) Y ji − yij Y jj +yij
Z1q Z 2q Z iq Z pq Z qq
阻抗矩阵中对应于网络 原有部分的全部元素保 持原有数值不变
Z qq = ziq + Z ii
2. 追加连枝
叠加原理和替代定理
= Z I V i i1 1 + Z i 2 I 2 + + Z ik ( I k − I km ) + + Z im ( I m + I km ) + + Z ip I p =
思考:如果k节点是大地,如何修改?
4-3 节点阻抗矩阵
一、节点阻抗矩阵元素的物理意义
YV = I
其中,Z = Y −1 —节点阻抗矩阵
ZI = V
Z11 Z 21 Z n1
Z12 Z 22 Zn2
V Z1n I 1 1 Z 2n I V 2 2 = Z nn In Vn
Lesson-02节点导纳矩阵及节点网络方程的解法

Vi 1, Vj 0, j 1, 2, , n, j i
Y11V1 Y12V2
Y1nVn
I1
Y21V1 Y22V2
Y2nVn
I
2
...
Yn1V1 Yn2V2 YnnVn In
I1
Y1i
I2 Y2i
Ii Yii
i7
y24
1 y12 i5 2 i6 y23
3
y34 i8 4
I1
i1
i2
y10
y20
i3
i4
y30
y40
I4
导纳形式的节点方程
y10V1 y12 (V1 V2 ) I1
y12 (V2
V1 )
y20V2
y23 (V2
V3 )
y24 (V2
V4 )
0
y23 (V3 V2 ) y34 (V3 V4 ) y30V3 0
李长松 Spring 2016
电力系统计算机辅助分析
稳定性计算
第5/6章
发电机组和 负荷数学模型
第4章
潮流计算
第2章
电力网络 数学模型
第1章
短路计算
第3章
什么是“数学模型”
• A mathematical model is a description for property or behavior of a system (or a process or a phenomenon) using mathematical concepts and language.
Y21V1 Y22V2
Y2nVn
I
2
节点导纳矩阵法

⎤ ⎥ ⎥⎦
⎡⎢⎣VV&&23
⎤ ⎥ ⎦
28
图解建立电路导纳矩阵的步骤
对于第三个元件有:
⎡ ⎢ ⎢
I&1(3) I&2(3)
⎤ ⎥ ⎥
=
⎢⎢⎡YY12((1133))
⎢ ⎢⎣
I&3(3)
⎥ ⎥⎦
⎢⎢⎣Y3(13)
Y1(23) Y2(23) Y3(23)
Y1(33) Y2(33) Y3(33)
⎤ ⎥ ⎥ ⎥ ⎥⎦
k =1
k =1
k =1
10
z 性质二:行元素之和为零。
假设各节点电位都相等且不为零(u1=u2 =L=un ≠ 0)。 由于节点间无电位差,所以各电流都为零。
n
∑ ik = − u j ykj = 0 j =1
k = 1, 2,L, n
又由于u1=u2 =L=un ≠ 0,所以
n
n
n
∑ ∑ ∑ y1 j = y2 j = L = ynj = 0
∑ ⎧
⎪i1
=
−
n
u j y1 j
⎪
j =1
∑ ⎪
n
⎪⎨i2
=
−
u j y2 j
j =1
⎪⎪M
∑ ⎪
⎪in
=−
n
u j ynj
⎩
j =1
6
节点电流方程(基尔霍夫电流定律)
全电路节点方程组:
⎛ ⎜ ⎜ ⎜
i1 i2 M
⎞ ⎟ ⎟ ⎟
=
⎛ ⎜ ⎜ ⎜
− −
y11 y21 M
− y12 − y22
M
L L
2
3.2.1 待定导纳矩阵的定义
节点导纳矩阵的计算及应用综述

Y24 、Y42 、Y35 、Y53 为互导纳,亦即节点之 地时,在两个待测节点中的另外一个向电力
网络注入的电流。如果用矩阵形式表示
y4 y5 y6
y4
y5
0 0
y4
y1 y3 y4
y3
y1 0
Y
y5
抗。由于新增加一个新的节点,因而导纳矩 阵相应增加一阶。导纳矩阵各元素变化情况 如下:j 节点的导纳如式(8)所示,i 节点导纳 矩阵增量如式(9)所示,其他节点导纳矩阵自 导纳不变化。I、j 节点之间的互导纳如式(10) 所示,其他节点互导纳不变化。
4
自导纳 Y jj
1 z ij
(8)
Y ii
有许多比较明显的特点,一一列举如下: (1)节点导纳矩阵是对称矩阵,关于
主对角线对称; (2)节点导纳矩阵是稀疏矩阵,矩阵
内含有大量的零元素; (3)自导纳位于矩阵对角线,为与节
点相连接的导纳之和; (4)互导纳位于矩阵非对角线位置,
为两节点之间导纳的相反数; (5)导纳矩阵维数与节点数相等; 相对于节点阻抗矩阵,节点导纳矩阵具
1
Y 42
1
Y 52
1
Y 33
2
Y 43
2
Y 53
2
Y 34
3
Y 44
3
Y 54 Y 45
4
Y 55
4
5
3
5
4
5
5
(3)
式(3)可以通过叠加原理来解释,叠加原理定 义如下: 叠加原理:有多个激励的响应等于每一激励
电力网节点导纳矩阵计算例题与程序

电力网节点导纳矩阵计算例题与程序————————————————————————————————作者:————————————————————————————————日期:电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0, 图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m②③①YYY④⑤1:1 1.042315Z21=0.04+J0.25Z23=0.08+J0.30Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25% Np is number of node point,Nb is number of braches% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
n
节点电压u j 可为任何值 → 各项系数为零
∑y
k =1
n
k1
= ∑ yk 2 = L = ∑ ykn = 0
k =1 k =1
10
n
n
z 性质二:行元素之和为零。
假设各节点电位都相等且不为零(u1 =u2 = L =un ≠ 0)。 由于节点间无电位差,所以各电流都为零。 ik = −∑ u j ykj = 0
18
微波半导体器件
根据基尔霍夫电流定律: I1 + jωC2 (V2 − V1 ) + ( G1 + jωC1 )(V3 − V1 ) = 0 I 2 + jωC2 (V1 − V2 ) + ( G2 + jωC3 )(V3 − V2 ) − g m (V1 − V3 ) = 0 I 3 + ( G1 + jωC1 )(V1 − V3 ) + ( G2 + jωC3 )(V2 − V3 ) + g m (V1 − V3 ) = 0
20
利用S参数求待定导纳矩阵 实际电路中尚有一些微波元器件,它们 的导纳矩阵或等效电路中 Ykj 不可能精确的 从理论分析中导出。对于这类元器件,一般 采用测量方法测出其散射矩阵参数,然后将 它变换成导纳矩阵参数,再求出待定导纳矩 阵。
21
利用S参数求待定导纳矩阵
[S ] → [ y] :
% ] = ([ I ] − [ S ]) ([ I ] + [ S ]) [y ⎤ % ⎡ ⎤ [ y] = ⎡ ⎣ y0 ⎦ [ y ] ⎣ y0 ⎦
7
节点电流方程(基尔霍夫电流定律)
写成向量形式: I = YU Y : 待定导纳矩阵 I : 外电流向量 U : 节点电压向量 其中 − ykk = ∑ ykj
j =1 j ≠k n
I = [i1 i2 L in ]
T T
U = [u1 u2 L un ]
8
待定导纳矩阵Y
当电路具有n个节点时,Y 为n × n矩阵: ⎛ n ⎜ ∑ y1 j − y12 L ⎜ j =2 n ⎜ ⎜ − y21 ∑ y2 j L j =1 ⎜ j≠2 ⎜ M ⎜ M ⎜ ⎜ − yn1 − yn 2 L ⎜ ⎝ 3个节点时: ⎡ y12 + y13 ⎢ −y 21 ⎢ ⎢ ⎣ − y31 − y12 y21 + y23 − y32 ⎞ − y1n ⎟ ⎟ ⎟ − y2 n ⎟ ⎟ ⎟ M ⎟ ⎟ n −1 ynj ⎟ ∑ ⎟ j =1 ⎠ − y13 ⎤ − y23 ⎥ ⎥ y31 + y32 ⎥ ⎦
19
微波半导体器件
整理得到: − jωC2 − ( G1 + jωC1 ) ⎤ ⎡V1 ⎤ ⎡ I1 ⎤ ⎡ G1 + jω ( C1 + C2 ) ⎥⎢ ⎥ ⎢I ⎥ = ⎢ g − j ω C G + j ω C + C − G + g + j ω C ( ) ( ) m m 2 2 2 3 2 3 ⎥ ⎢V2 ⎥ ⎢ 2⎥ ⎢ ⎢ − ( G2 + jωC3 ) G1 + G2 + g m + jω ( C1 + C3 ) ⎥ ⎣ I3 ⎥ ⎦ ⎢ ⎣V3 ⎥ ⎦ ⎣ − ( G1 + g m + jωC1 ) ⎦⎢ → 待定导纳矩阵 − jωC2 − ( G1 + jωC1 ) ⎡ G1 + jω ( C1 + C2 ) ⎤ ⎥ g j ω C G j ω C C G g j ω C − + + − + + ( ) ( ) [Y ] = ⎢ m 2 2 2 3 2 m 3 ⎢ ⎥ ⎢ − ( G2 + jωC3 ) G1 + G2 + g m + jω ( C1 + C3 ) ⎥ ⎣ − ( G1 + g m + jωC1 ) ⎦
对于理想变压器,是不存在导纳矩 阵的,所以它对应的不定导纳矩阵 也是不存在的。因此在节点导纳矩 阵法中只能对理想变压器作近似处 理,常采用包含一个串联电阻R→0 的近似电路。
17
微波半导体器件 常见的半导体器件有晶体管、场效应管 和各种二极管等。这些器件通常用其集总参 数等效电路表示,因此它们的不定导纳矩阵 原则上可按公式导出。对于晶体管和场效应 管,其等效电路中包含受控电流源,因此其 不定导纳矩阵将受到受控源参数的影响。
5
节点电流方程(基尔霍夫电流定律)
全电路共有n个节点:
n ⎧ ⎪i1 = −∑ u j y1 j j =1 ⎪ n ⎪ ⎪i2 = −∑ u j y2 j j =1 ⎨ ⎪M ⎪ n ⎪ ⎪in = −∑ u j ynj j =1 ⎩
6
节点电流方程(基尔霍夫电流定律)
全电路节点方程组: ⎛ i1 ⎞ ⎛ − y11 ⎜ ⎟ ⎜ i y − 2 ⎜ ⎟ = ⎜ 21 ⎜M⎟ ⎜ M ⎜ ⎜i ⎟ ⎟ ⎜ ⎜−y ⎝ n ⎠ ⎝ n1 − y12 L − y1n ⎞ ⎛ u1 ⎞ ⎟⎜ ⎟ − y22 L − y2 n ⎟ ⎜ u2 ⎟ M M ⎟⎜ M ⎟ ⎟ ⎜ ⎟ ⎟ ⎜ − yn 2 L − ynn ⎠ ⎝ un ⎟ ⎠
⎧1 R ⎪ y = ⎨ jωC ⎪1 jω L ⎩
电阻 电容 电感
15
均匀传输线
θ ⎧ = Y jY tg ⎪ 1 0 2 ⎨ ⎪Y2 = − jY0 csc θ ⎩
⎛ ⎜ − jY0 ctgθ ⎜ Y = ⎜ jY0 csc θ ⎜ ⎜ θ ⎜ jY tg − 0 ⎜ 2 ⎝
jY0 csc θ − jY0 ctgθ − jY0tg
13
3.2.3 微波元器件的待定导纳矩阵 z 在用节点导纳矩阵分析微波电路时,先要 求出电路的导纳矩阵,而电路导纳矩阵[Y] 可从电路各元器件的不定导纳矩阵中求 出,所以我们先讨论如何形成微波电路中 各元器件的不定导纳矩阵。
14
集总参数元件
⎡ y − y⎤ [Y ] = ⎢ ⎥ ⎣− y y ⎦
上式右边第一项:
∑u
j =1 j ≠k
n
k
ykj = uk ∑ ykj = uk ( − ykk ) = −uk ykk
j =1 j ≠k
n
节点电流方程写为: ⎛ ⎞ n n ik = − ⎜ uk ykk + ∑ u j ykj ⎟ = −∑ u j ykj ⎜ ⎟ j =1 j =1 ⎜ ⎟ j≠k ⎝ ⎠
2j
∑y
j =1 j ≠2
n
2j
L
− y2 n M
M − yn 2 L
∑y
j =1
n −1
M − yn 2 L
nj
− yn1
∑y
j =1
n −1
nj
0 − y21 = M − yn1
n
0
L
2j
0 − y2 n =0 M
∑y
j =1 j≠2
L
M − yn 2 L
∑y
j =1
n −1
nj
12
z 性质四:若网络的第t个节点接地(ut=0),则其 不定导纳矩阵降1阶,降阶后的矩阵称为确定导纳 矩阵。
θ
2Hale Waihona Puke 2⎟ ⎟ θ − jY0tg ⎟ 2⎟ θ⎟ 2 jY0tg ⎟ ⎟ 2⎠
16
− jY0tg
θ⎞
理想变压器
⎛ 1 ⎜ ⎜ R ⎜ 1 Y = ⎜− ⎜ nR ⎜ 1− n ⎜ ⎝ nR
1 − nR 1 n2 R n −1 n2 R
⎞ ⎟ ⎟ ⎟ ⎟ ⎟ 2 ( n − 1) ⎟ ⎟ n2 R ⎠ 1− n nR n −1 n2 R
3
节点电流方程(基尔霍夫电流定律)
ik + ∑ ( u j − uk ) ykj = 0
j =1 j ≠k n
展开得到: ik = ∑ uk ykj − ∑ u j ykj
j =1 j ≠k j =1 j≠k n n
4
节点电流方程(基尔霍夫电流定律)
引入符号:ykk = −∑ ykj
j =1 j≠k n
−1
% ] 为归一化导纳矩阵, 其中[ y [ I ]为单位矩阵, ⎡ y01 ⎢ ⎡ y0 ⎤ = ⎢ O ⎣ ⎦ ⎢ ⎢ ⎣ 0
0
⎤ ⎥ ⎥ ⎥ y0 n ⎥ ⎦
y01 , y02 ,L , y0 n为n端口元件各端外接传输线特性导纳。
22
3.2.4 电路导纳矩阵的建立方法
z 1. 建立电路导纳矩阵的步骤: 首先对电路所有节点进行编号,编号从1开始直至n(n 为正整数),接地节点不编号或编为零号。显然,最大 编号数n即为电路的总节点数,由此可得电路导纳矩阵 为n×n矩阵。 对各元件的端点进行编号并建立不定导纳矩阵。 将各元件不定导纳矩阵的元素(除与接地点相关的元素 外)逐一加入电路导纳矩阵。
9
3.2.2 待定导纳矩阵的性质
z 性质一:列元素之和为零。
全部流入电路的外电流总和为零: ⎛ n ⎞ ik = ∑ ⎜ ∑ ykj u j ⎟ = 0 ∑ k =1 k =1 ⎝ j =1 ⎠
n n
∑y
k =1
n
k1 1
u + ∑ yk 2u2 + L + ∑ ykn un = 0
k =1 k =1
∑y
j =1 j ≠2
n
⎛ ⎞ n n n −1 ⎛ n ⎞ ⎜ n ⎛ n −1 ⎞ ⎟ ⎜ ∑ y1 j − ∑ y1 j ⎟ ⎜ ∑ y2 j − ∑ y2 j ⎟ L ⎜ ∑ ynj − ∑ ynj ⎟ j =2 j =1 j =1 1 ⎟ ⎝ j =2 ⎠ ⎜ jj = ⎝ j =1 ⎠ j ≠2 ⎝ ≠2 ⎠ = − y21 M
