结构基本自振周期计算 (1)
结构基本自振周期计算

W
---风荷载组合系数;一般结构可不考虑,风荷载起控制作用的高层建筑应
采用0.2;
精品课件
3.8.3结构抗震承载力验算
(2)截面抗震验算
S R RE
S---包含地震作用效应的结构构件内力组合的设计值; R---结构构件承载力设计值; RE ---承载力抗震调整系数;
精品课件
3.8.3结构抗震承载力验算
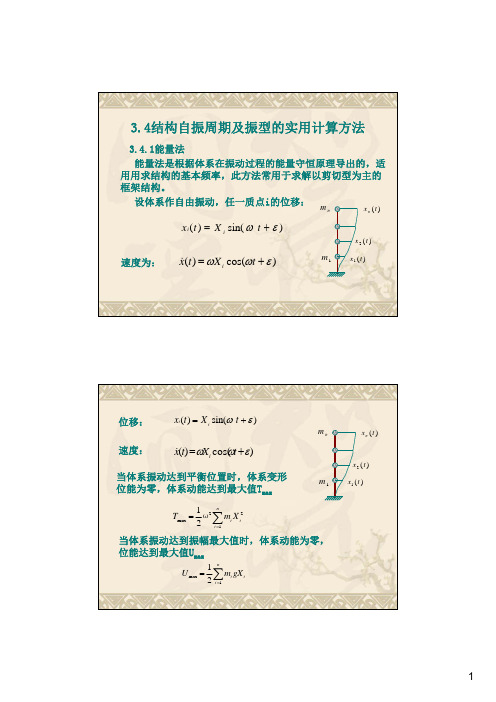
3.4.1能量法
位移: xi(t)Xisi nt()
速度: x (t)Xicots()
mn
当体系振动达到平衡位置时,体系变形
位能为零,体系动能达到最大值Tmax
Tmax12ω2 in1 miXi2
m1
xn (t)
x2 (t) x1 (t )
当体系振动达到振幅最大值时,体系动能为零,
位能达到最大值Umax
无论结构是否有偏心,地震地面运动产生的结构扭 转振动均是存在的。
★扭转作用会加重结构的震害 《规范》规定对质量和刚度明显不均匀、不对称结构 应考虑水平地震作用的扭转效应
精品课件
3.6竖向地震作用
抗震设计中,一般不考虑竖向地震作用的影响 震害表明:
1、在高烈度区,竖向地面运动的影响是明显的 2、竖向地震作用对高层建筑、高耸及大跨结构
3.4结构自振周期及振型的实用计算方法
能量法是根据体求解以剪切型为主的框架结构
mn
xn (t)
设体系作自由振动,任一质点i的位移:
xi(t)Xisi nt()
3.4.1能量法
速度为 x (t)X ico ts()
m1
精品课件
x2 (t) x1 (t )
竖向地震作用。
精品课件
3.8.1地震作用及计算方法
建筑结构抗震考试题库及答案(含各题型)

建筑结构抗震考试题库及答案(含各题型)一、单选题1.钢筋混凝土丙类建筑房屋的抗震等级应根据那些因素查表确定()A、抗震设防烈度、结构类型和房屋层数B、抗震设防烈度、结构类型和房屋高度C、抗震设防烈度、场地类型和房屋层数D、抗震设防烈度、场地类型和房屋高度参考答案:B2.根据地震波传播速度,以下排序正确的是()。
A、纵波>横波>面波(L波)B、横波>纵波>面波C、纵波>面波>横波D、面波>横波>纵波参考答案:A3.下列哪项不属于提高结构延性的构造措施()A、强柱弱梁B、强剪弱弯C、强节点弱构件D、强梁弱柱参考答案:D4.()一般周期长,波速较慢,振幅较大,引起地面水平方向的运动。
A、纵波B、横波C、瑞利波D、勒夫波参考答案:B5.基底剪力法计算水平地震作用可用于下列何种建筑?()A、40米以上的高层建筑B、自振周期T1很长(T1>4s)的高层建筑C、垂直方向质量、刚度分布均匀的多层建筑D、平面上质量、刚度有较大偏心的多高层建筑参考答案:C6.框架柱轴压比过高会使柱产生()A、大偏心受压构件B、小偏心受压构件C、剪切破坏D、扭转破坏参考答案:B7.下列结构延性哪个延性在抗震设计时要求最高()A、结构总体延性B、结构楼层的延性C、构件的延性D、关键杆件的延性参考答案:D8.横波是由震源向四周传播的压缩波,这种波的周期(),振幅()。
A、长,小B、长,大C、短,小D、短,大参考答案:B9.土质条件对地震反应谱的影响很大,土质越松软,加速度谱曲线表现为()A、谱曲线峰值右移B、谱曲线峰值左移C、谱曲线峰值增大D、谱曲线峰值降低参考答案:A10.为保证结构“大震不倒”,要求结构具有()A、较大的初始刚度B、较高的截面承载能力C、较好的延性D、较小的自振周期T1参考答案:C11.纵波、横波和面波(L波)之间的波速关系为()A、VP>VS>VLB、VS>VP>VLC、VL>VP>VSD、VP>VL>VS参考答案:A12.多遇地震烈度所对应的超越概率为()。
建筑结构抗震复习题带答案

建筑结构抗震复习题一、判断题1.振型分解反应谱法既适用于弹性体系,也可用于弹塑性体系×2.结构的刚心就是地震惯性力合力作用点的位置×3.受压构件的位移延性将随轴压比的增加而减小√4.结构的重力荷载代表值等于竖向荷载加上各可变荷载组合值。
×5.震源到震中的垂直距离称为震中距。
×6.对应于一次地震,震级只有一个,烈度也只有一个。
×7.横波一般周期较长,振幅较大,引起地面水平方向的运动。
√8.采用底部剪力法时,突出屋面的屋顶件,由于刚度突变、质量突变,其地震作用的效应乘以增大系数3,此增大部分应向下传递。
×9.采用底部剪力法时,突出屋面的屋顶件,由于刚度突变、质量突变,其地震作用的效应乘以增大系数3,此增大部分应向下传递。
×10.地震波的传播速度,以横波最快,面波次之,纵波最慢。
×11.横波只能在固态物质中传播√12.设防烈度为8度和9度的高层建筑应考虑竖向地震作用×13.众值烈度比基本烈度小度,罕遇烈度比基本烈度大度×14在进行抗震设计时,结构平面凹进的一侧尺寸为其相应宽度的20%时,认为是规则的√15.地震波的传播速度,以横波最快,面波次之,纵波最慢。
×16.在同等场地、烈度条件下,钢结构房屋的震害较钢筋混凝土结构房屋的震害要严重。
×17.钢筋混凝土框架柱的轴压比越大,抗震性能越好。
×18.场地特征周期与场地类别和地震分组有关。
×19.受压构件的位移延性将随轴压比的增加而减小。
√20.选择结构的自振周期应尽可能接近场地卓越周期。
×21.根据液化指数,将液化等级分为三个等级。
√22.质量和刚度明显不对称、不均匀的结构,应考虑水平地震作用的扭转影响√。
23.地震作用对软土的承载力影响较小,土越软,在地震作用下的变形就越小。
×24.结构的重力荷载代表值等于竖向荷载加上各可变荷载组合值。
工程结构抗震计算题大全

(二)计算题工程结构抗震计算1.已知一个水塔,可简化为单自由度体系。
10000m kg =,1kN cm k =,该结构位于Ⅱ类场地第二组,基本烈度为7度(地震加速度为0.10g ),阻尼比0.03ξ=,求该结构在多遇地震下的水平地震作用。
解:(1)计算结构的自振周期22 1.99T s === (2)计算地震影响系数查表2得,0.4g T s =,查表3得,max 0.08α=。
由于0.030.05ξ=≠应考虑阻尼比对地震影响系数形状的调整。
20.050.050.0311 1.160.08 1.60.08 1.60.03ξηξ--=+=+=++⨯0.050.050.030.90.90.940.360.360.03ξγξ--=+=+=++⨯由上图2可知,()0.94max 0.40.08 1.160.02051.99g T T γαα⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭(3)计算水平地震作用0.020*******.812011N F G α==⨯⨯=2.计算仅有两个自由度体系的自由振动频率。
假设[]11122122k k K kk ⎡⎤=⎢⎥⎣⎦ []1200m M m ⎡⎤=⎢⎥⎣⎦解:根据多自由度体系的动力特征方程[][]20K M ω-=,有[][]111212221222000k k m K M kk m ωω⎡⎤⎡⎤-=-=⎢⎥⎢⎥⎣⎦⎣⎦整理得()()4212112221112212210m m k m k m k k k k ωω-++-=解方程得2112211212k k m m ω⎛⎫=+⎪⎝⎭2112221212k k m m ω⎛⎫=++ ⎪⎝⎭3.图示钢筋混凝土框架结构的基本周期10.467T s =,抗震设防烈度为8度,Ⅱ类场地,设计地震分组为第二组(0.40g T s =)。
通过计算已经求得相应于结构基本自振周期的水平地震影响系数值10.139α=,试用底部剪力法计算多遇地震时的层间剪力。
结构基本周期

结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系。
自振周期是结构按某一振型完成一次自由振动所需的时
计特征周期是在抗震设计用的地震影响系数曲线中,反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值;场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期,表示场地土最主要的振动特性。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结
周期相等或接近时,建筑物的震害较为严重。
基本周期应该取决于建筑物的结构形式,各种结构形式都是定数。
结构自振周期是结构在水平作用下的震动周期,是变数。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结构的质量和刚度相关。
经验表明,当建筑物的自振周期与场地的卓越周期相等或接近时,建筑物的震害较为严重。
结构的基本周期可采用结构力学方法计算,对于比较规则的结构,也可以采用近似方法计算:
框架结构 T=()N
框剪结构、框筒结构 T=()N
剪力墙结构、筒中筒结构 T=()N
其中N为结构层数。
也可采用结构分析得到的结构第1平动周期。
自振周期及地震作用计算讲义
n
i
根据能量守恒原理:
g
m
i 1 n i
n
i
Xi
T1
2 i
2
m
i 1
X
1
2
m X
i i 1 n
n
2 i
g
m X
i i 1
2
i
G X
i
n
2 i
G X
i i 1
i 1 n
i
一般假定:将结构重力荷载当成水平荷载作用于质点上 所得的结构弹性曲线为结构的基本振型。
T 1 max 1 2
n
i 1
m i ( 1 x i )
2
mN
xn
M
eq
xm
单质点体系的最大动能为
T 2 max 1 M 2
eq
xm xn
m1 x1
( 1 x m ) 2
x m ---体系按第一振型振动时,相应于折算质点处的最大位移;
T1max
1 n mi (1xi )2 2 i1
ห้องสมุดไป่ตู้
竖向地震作用,烟囱上 抛后下落错位。
9
德阳利森水泥厂生料均化库,受到 竖向地震作用,塔筒上抛后下落。
底部框架底层为薄弱层, 底层墙体叠合塌落。 (9度 区)
10
底部框架结构底层框架叠合塌落(北川11度区)。
中间层叠合塌落(日本阪神大地震)。
11
中间层水平裂缝 中间层水平裂缝。
3.6.1高耸结构及高层建筑的竖向地震作用
台湾省漳化县富贵 名门大楼,16层钢筋混 凝土住宅楼,平面为C 型, 平面不规整,单排 柱框架,柱子间距太大, 数量偏少。
结构基本自振周期计算 (1)

3.6竖向地震作用
抗震设计中,一般不考虑竖向地震作用的影响 震害表明:
1、在高烈度区,竖向地面运动的影响是明显的 2、竖向地震作用对高层建筑、高耸及大跨结构
影响显著。
我国抗震设计《规范》规定,对下列建筑应考虑竖向地震 作用的不利影响: 1、8度和9度时的大跨度结构、长悬臂结构; 2、8度和9度时烟囱和类似的高耸结构; 3、9度时的高层建筑。
有利时,不应大于1.0; 地震作用
Eh
Ev
Eh、 Ev---分别为水平、竖向 仅计算水平地震作用
1.3
0.0
地震作用分项系数, 仅计算竖向地震作用
0.0
1.3
按右表采用;
同时计算水平与竖向地震作用
1.3
0.5
w ---风荷载分项系数,一般取1.4
SGE、SEhk、SEvk、Swk — —重力荷载代表值的效应、水平、竖向地震 作用标准值的效应、风载标准值的效应;
框架-抗震墙结构可近似视为剪弯型杆。
T 1.7 bs
本方法适用于质量及刚度沿高度分布比较均匀的任何体系结构。
补充:自振周期的经验公式
根据实测统计,忽略填充墙布置、质量分布差异等,初 步设计时可按下列公式估算
(1)高度低于25m且有较多的填充墙框架办公楼、旅馆的基本周期
T1 0.22 0.35H / 3 B
W ---风荷载组合系数;一般结构可不考虑,风荷载起控制作用的高层建筑应
采用0.2;
3.8.3结构抗震承载力验算
(2)截面抗震验算
S
R
RE
S ---包含地震作用效应的结构构件内力组合的设计值; R---结构构件承载力设计值; RE ---承载力抗震调整系数;
3.8.3结构抗震承载力验算
建筑结构抗震复习题带答案

建筑结构抗震复习题一、判断题1.振型分解反应谱法既适用于弹性体系,也可用于弹塑性体系×2.结构的刚心就是地震惯性力合力作用点的位置×3.受压构件的位移延性将随轴压比的增加而减小√4.结构的重力荷载代表值等于竖向荷载加上各可变荷载组合值。
×5.震源到震中的垂直距离称为震中距。
×6.对应于一次地震,震级只有一个,烈度也只有一个。
×7.横波一般周期较长,振幅较大,引起地面水平方向的运动。
√8.采用底部剪力法时,突出屋面的屋顶件,由于刚度突变、质量突变,其地震作用的效应乘以增大系数3,此增大部分应向下传递。
×9.采用底部剪力法时,突出屋面的屋顶件,由于刚度突变、质量突变,其地震作用的效应乘以增大系数3,此增大部分应向下传递。
×10.地震波的传播速度,以横波最快,面波次之,纵波最慢。
×11.横波只能在固态物质中传播√12.设防烈度为8度和9度的高层建筑应考虑竖向地震作用×13.众值烈度比基本烈度小1.55度,罕遇烈度比基本烈度大1.55度×14在进行抗震设计时,结构平面凹进的一侧尺寸为其相应宽度的20%时,认为是规则的√15.地震波的传播速度,以横波最快,面波次之,纵波最慢。
×16.在同等场地、烈度条件下,钢结构房屋的震害较钢筋混凝土结构房屋的震害要严重。
×17.钢筋混凝土框架柱的轴压比越大,抗震性能越好。
×18.场地特征周期与场地类别和地震分组有关。
×19.受压构件的位移延性将随轴压比的增加而减小。
√20.选择结构的自振周期应尽可能接近场地卓越周期。
×21.根据液化指数,将液化等级分为三个等级。
√22.质量和刚度明显不对称、不均匀的结构,应考虑水平地震作用的扭转影响√。
23.地震作用对软土的承载力影响较小,土越软,在地震作用下的变形就越小。
×24.结构的重力荷载代表值等于竖向荷载加上各可变荷载组合值。
荷载计算

风、雪荷载执行规范:《建筑结构荷载规范》(GB 50009-2012),1 查询结果所在地点:辽宁沈阳市海拔高度:42.8m基本气温(最低~最高):-24℃~33℃雪荷载准永久值系数分区:Ⅰ2 设计资料2.1 已知条件基本风压:w0=0.55kN/m2基本雪压:s0=0.50kN/m2结构类型:主要受力结构基本自振周期:T1=0.04s建筑宽度:B=22.00m建筑高度:H=3.00m计算位置的高度:z=3.00m结构阻尼比:ζ1=0.01地面粗糙度:C修正系数η:1.00风荷载体型系数:μs=0.10屋面积雪分布系数:μr=1.002.2 计算内容(1)风压高度变化系数(2)结构第1阶振型系数(3)脉动风荷载的背景分量因子(4)脉动风荷载的共振分量因子(5)风振系数(6)风荷载标准值(7)雪荷载标准值3 计算过程和计算结果3.1 风压高度变化系数因为计算点的高度z=3.00m<5.00m超出《荷载规范》表8.2.1的取值范围, 所以离地面高度按5.00m考虑。
查《荷载规范》表8.2.1, 风压高度变化系数μz=0.65考虑修正系数η后, μz=μzη=0.65×1.00=0.653.2 结构第1阶振型系数z/H=3.00/3.00=1.000查《荷载规范》表G.0.3, 结构第1阶振型系数φ1(z)=1.003.3 脉动风荷载的背景分量因子查《荷载规范》表8.4.5-1, 系数k=0.30, 系数a 1=0.26 根据台@公式8.4.6-2B=22.00m>2H=6.00m, 取B=2H=6.00m 脉动风荷载水平方向相关系数x 根据《荷载规范》公式8.4.6-1 脉动风荷载竖直方向相关系数z根据《荷载规范》第8.4.5条 脉动风荷载的背景分量因子B z xz1(z⨯3.000.261.003.4 脉动风荷载的共振分量因子结构第1阶自振频率f 1=1/T 1=1/0.04=25.64Hz 根据《荷载规范》公式8.4.4 地面粗糙度修正系数k w =0.54脉动风荷载的共振分量因子10.013.5 风振系数根据《荷载规范》公式8.4.3 峰值因子g 取2.510m 高度名义湍流强度I 10取0.23 风振系数=z3.6 风荷载标准值根据《荷载规范》公式8.1.1-1w k=βzμsμz w0=1.75×0.10×0.65×0.55=0.06kN/m23.7 雪荷载标准值根据《荷载规范》公式7.1.1s k=μr s0=1.00×0.50=0.50kN/m23.8 结构自重荷载标准值结构总长80.6m,采用直径48mm,壁厚3.5mm钢管,单重3.841kg/m结构总重G=80.6×3.841=310kg=3.1kN总体布置间隔4m一榀,荷载总值N=(0.06+0.5)×4×22.8+3.1=54.17kN q=1.1N/22.8=2.7kN/m。
结构自振周期的近似计算

3.5.3 结构自振周期的近似计算通过结构的频率方程求自振周期比较复杂,这里介绍几种近似计算方法。
动能为势能为由能量守恒,有例.已知:解:3.6 竖向地震作用《规范》规定:设防烈度为8度和9度区的大跨度屋盖结构、长悬臂结构、烟囱及类似高耸结构和9度区的高层建筑,应考虑竖向地震作用。
效应:使建筑物上下颠簸F F3.7 结构平扭耦合地震反应与双向水平地震影响 规范规定:对于质量及刚度明显不均匀、不对称的结构,应考虑水平地震作m用的扭转影响。
刚心)(tug质心分析过程:[受弯钢筋凝土构件的滞回曲线滞回模型:描述结构或构件滞回关系的数学模型。
双线性模型双线性模型一般适用于钢结构梁、柱、节点域构件。
钢筋混凝土梁、柱、墙等一般采用退化三线性模型。
退化三线性模型结构非弹性地震反应分析的简化方法适用范围:不超过12层且层刚度无突变的钢筋混凝土框架结构和填充墙钢筋混凝土框架结构;不超过20层且层刚度无突变的钢框架结构和支撑钢框架结构;式中:N N a h +−5.0)(/---系数,混凝土强度等级不超过C50时,取1.0,C80时为0.94,by二、结构薄弱层位置判别结构薄弱层:塑性变形集中的楼层,即ζy 最小或相对较小的楼层对于ζy 沿高度分布均匀的框架结构,底层作为薄弱层。
3.9 结构抗震验算3.9.1 结构抗震计算方法原则(1 ) 一般情况下,应允许在建筑结构的两个主轴方向分别计算水平地震作用,并进行抗震验算各方向的水平地震作用应由该方向抗侧力构件承担。
(2 )有斜交抗侧力构件的结构,当相交角度大于15°时,应分别计算各抗侧力构件方向的水平地震作用。
(3) 质量和刚度分布明显不对称的结构,应计入双向水平地震作用下的扭转影响,其他情况,应允许采用调整地震作用效应的方法计入扭转影响。
(4) 不同方向的抗侧力结构的共同构件(如框架角柱),应考虑双向水平地震作用的影响。
(5)8、9度时的大跨度和长悬臂结构及9度时的高层建筑,应计算竖向地震作用。
结构周期

1. 结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系:自振周期是结构按某一振型完成一次自由振动所需的时间;基本周期是指结构按基本振型完成一次自由振动所需的时间;设计特征周期是在抗震设计用的地震影响系数曲线中,反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值;场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期,表示场地土最主要的振动特性。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结构的质量和刚度相关。
经验表明,当建筑物的自振周期与场地的卓越周期相等或接近时,建筑物的震害较为严重。
2.经验公式一般情况下,高层钢筋混凝土结构的基本自振周期T1为T1=(0.05~1.10)n(4.3-27)其中:钢筋混凝土框架结构:T1=(0.06~0.09)n(4.3-28)框架-剪力墙结构:T1=(0.06~0.08)n(4.3-29)高层钢结构的基本自振周期T1为T1=(0.10~0.15)n(4.3-30)式中:n——建筑层数。
结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系:结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系:自振周期是结构按某一振型完成一次自由振动所需的时间;基本周期是指结构按基本振型完成一次自由振动所需的时间;设计特征周期是在抗震设计用的地震影响系数曲线中,反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值;场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期,表示场地土最主要的振动特性。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结构的质量和刚度相关。
经验表明,当建筑物的自振周期与场地的卓越周期相等或接近时,建筑物的震害较为严重。
用顶点位移法求自振周期:T=1.7*周期折减系数*(层间侧移开方)折减系数:框架结构取0.6~0.7框剪结构取0.7~0.8抗剪墙取1.0按照行业标准《工程抗震术语标准》(JGJ/97)的有关条文,自振周期:结构按某一振型完成一次自由振动所需的时间。
高层建筑结构设计思考题答案(2)

高层建筑结构设计思考题答案(2)第二章2.1钢筋混凝土房屋建筑和钢结构房屋建筑各有哪些抗侧力结构体系?钢筋混凝土房屋建筑和钢结构房屋建筑各有哪些抗侧力结构体系?每种结构体系举1~2例。
答:钢筋混凝土房屋建筑的抗侧力结构体系有:框架结构(如主体18层、局部22层的北京长城饭店);框架剪力墙结构(如26层的上海宾馆);剪力墙结构(包括全部落地剪力墙和部分框支剪力墙);筒体结构[如芝加哥Dewitt-Chestnut公寓大厦(框筒),芝加哥JohnHancock大厦(桁架筒),北京中国国际贸易大厦(筒中筒)];框架核心筒结构(如广州中信大厦);板柱-剪力墙结构。
钢结构房屋建筑的抗侧力体系有:框架结构(如北京的长富宫);框架-支撑(抗震墙板)结构(如京广中心主楼);筒体结构[芝加哥西尔斯大厦(束筒)];巨型结构(如香港中银大厦)。
2.2框架结构、剪力墙结构和框架----剪力墙结构在侧向力作用下的水平位移曲线各有什么特点?答:(1)框架结构在侧向力作用下,其侧移由两部分组成:梁和柱的弯曲变形产生的侧移,侧移曲线呈剪切型,自下而上层间位移减小;柱的轴向变形产生的侧移,侧移曲线为弯曲型,自下而上层间位移增大。
第一部分是主要的,所以框架在侧向力作用下的水平位移曲线以剪切型为主。
(2)剪力墙结构在侧向力作用下,其水平位移曲线呈弯曲型,即层间位移由下至上逐渐增大。
(3)框架-剪力墙在侧向力作用下,其水平位移曲线呈弯剪型,层间位移上下趋于均匀。
2.3框架结构和框筒结构的结构构件平面布置有什么区别?答:(1)框架结构是平面结构,主要由与水平力方向平行的框架抵抗层剪力及倾覆力矩,必须在两个正交的主轴方向设置框架,以抵抗各个方向的侧向力。
抗震设计的框架结构不宜采用单跨框架。
框筒结是由密柱深梁组成的空间结构,沿四周布置的框架都参与抵抗水平力,框筒结构的四榀框架位于建筑物的周边,形成抗侧、抗扭刚度及承载力都很大的外筒。
2.5中心支撑钢框架和偏心支撑钢框架的支撑斜杆是如何布置的?偏心支撑钢框架有哪些类型?为什么偏心支撑钢框架的抗震性能比中心支撑框架好?答:中心支撑框架的支撑斜杆的轴线交汇于框架梁柱轴线的交点。
2.3结构基本自振周期的计算

K 2 6 .145 10 3 1 .229 10 4
(2)计算结构自振周期
T 2
m 2
K
G g K
2
1000 9 .8 1 .229 10 3
0 .573 s
2
Ø二、多自由度体系的基本自振周期 (1)能量法:
T1 2 t
n
Gi
u
i
i 1
V 3 1960 kN V2 4900 kN
(2)计算各楼层处的水平位移
V1 7840kN
u 1 0 .03136 ( m ) u 2 0 .05586 ( m ) u 3 0 .07546 ( m )
(3)能量法计算基本自振周期
T1 2 t
n
G
iu
2
i
i 1
n
Giu i
i 1
2 0 .8 2940 0 .03136 2 2940 0 .05586 2 1960 0 .07546 2 2940 0 .03136 2940 0 .05586 2940 0 .07546
0 .3834 ( s )
7
§2.4 结构地震反应的时程分析法简述
直接动力分析理论---时程分析法
将实际地震加速度时程记录(简称地震记录 earthquakerecord)作为动荷载输入,进行结构的地震响应分析。
《抗震规范》规定:①特别不规则的建筑、②甲类建筑和下表 所列高度范围的高层建筑,应采用时程分析法进行多遇地震下 的补充计算,可取多条时程曲线计算结果的平均值与振型分解 反应谱法计算结果的较大值。
其他抗震墙 梁 轴压比小于0.15柱 轴压比不小于0.15柱 抗震墙 各类构件
受力状态
周期、振型问题

1、《高层规程》3.2.6规定-----结构基本自振周期大致为:框架结构T1=(0.08~0.10)n, 框—剪和框—筒结构T1=(0.06~0.08)n 剪力墙和筒中筒结构T1=(0.05~0.06)n2、周期比即结构扭转为主的第一自振周期(也称第一扭振周期)Tt 与平动为主的第一自振周期(也称第一侧振周期)T1的比值。
周期比主要控制结构扭转效应,减小扭转对结构产生的不利影响,使结构的抗扭刚度不能太弱。
因为当两者接近时,由于振动藕连的影响,结构的扭转效应将明显增大。
2.2 相关规范条文的控制:[高规]4.3.5条规定,结构扭转为主的第一自振周期Tt与平动为主的第一自振周期T1之比(即周期比),A级高度高层建筑不应大于0.9;B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。
[高规]5.1.13条规定,高层建筑结构计算振型数不应小于9,抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不小于15,对于多塔楼结构的振型数不应小于塔楼数的9倍,且计算振型数应使振型参与质量不小于总质量的90%。
2.3 电算结果的判别与调整要点: (1).计算结果详周期、地震力与振型输出文件。
因SATWE电算结果中并未直接给出周期比,故对于通常的规则单塔楼结构,需人工按如下步骤验算周期比: a)根据各振型的两个平动系数和一个扭转系数(三者之和等于1)判别各振型分别是扭转为主的振型(也称扭振振型)还是平动为主的振型(也称侧振振型)。
一般情况下,当扭转系数大于0.5时,可认为该振型是扭振振型,反之应为侧振振型。
当然,对某些极为复杂的结构还应结合主振型信息来进行判断;b)周期最长的扭振振型对应的就是第一扭振周期Tt,周期最长的侧振振型对应的就是第一侧振周期T1;c)计算Tt / T1,看是否超过0.9(0.85)。
对于多塔结构周期比,不能直接按上面的方法验算,这时应该将多塔结构分成多个单塔,按多个结构分别计算、分别验算(注意不是在同一结构中定义多塔,而是按塔分成多个结构)。
抗震设计讲座之结构自振周期的计算

y N (t )
y(t ) X i sin(it i )
速度为
(t ) X i i cos( y i t i )
y2 (t )
m1
y1 (t )
一、能量法计算基本周期 设体系按i振型作自由振动。 t时刻的位移为
mN
y N (t )
y(t ) X i sin(it i )
x1
M eq
x2 F / k1 F / k2 7.00105 1 / 10720
16.33105 m
能量法的结果为 T1=0.508s
x2
xm x2 16.3310 m
5
M eq
T1 2
m x
i 1 i 2 xm
n
2
i
400 (7 105 ) 2 300 (16.33105 ) 2 38.11t 9.8 ( 16.33105 ) 2
EI
q
悬臂杆的特解为 yi ( x, t ) X i ( x) sin
基本周期为
T1 1.78l 2
2 t Ti
m / EI
振型
重力作为水平荷载所引起的位移为
uT ql 4 / 8EI
q mg
m 8 uT 4 EI gl
T 1 1.6 uT
(2)体系按剪切振动时 框架结构可近似视为剪切型杆。
1 M eq (1 xm ) 2 2
mN
xn
M eq xm
m1
x1
单质点体系的最大动能为
T2 max
xm ---体系按第一振型振动时,相应于折算质点处的最大位移;
T1max T2 max
计算题——精选推荐

计算题1.单层⼚房排架结构如图a 所⽰。
已知W=15.0kN ,q 1=0.8kN /m ,q 2=0.4kN /m 。
试⽤剪⼒分配法计算各柱的柱顶剪⼒。
(提⽰:⽀反⼒系数C 11=0.3,见图b(1);图b(2)、b(3)中的△u 1=2△u 2)2.两跨等⾼排架结构计算简图如题39图所⽰。
排架总⾼13.1m ,上柱⾼3.9m ,q 1=1.5kN /m ,q 2=0.75kN /m ,A 、B 、C 三柱抗侧刚度之⽐为1∶1.7∶1。
试⽤剪⼒分配法求A 柱的上柱下端截⾯的弯矩值。
(提⽰:柱顶不动铰⽀座反⼒R =C 11qH ,C 11=0.34)3.某单层单跨⼚房排架结构如题39图所⽰。
A 柱与B 柱尺⼨相同,在⽜腿顶⾯上分别作⽤有M max =104kN·m 及M min =58kN·m 的⼒矩,吊车横向⽔平刹车⼒为T=30kN 。
试⽤剪⼒分配法计算各柱的柱顶剪⼒。
(提⽰:柱顶不动铰⽀座⽀⼒3535, 1.30,0.70MR C TC C C H=+==)4.某排架计算简图如题40图所⽰。
A 柱与B 柱的抗剪刚度⽐为3∶2,上柱⾼度H 1=4m ,下柱⾼度H 2=9.2m 。
在A 柱和B 柱的⽜腿顶⾯上分别作⽤有M A =129kN ·m ,M B =42kN ·m 。
试⽤剪⼒分配法计算A 柱的柱底弯矩。
(提⽰:反⼒系数C 3A =C 3B =1.35)5.某单层⼚房排架结构计算简图如题37图(a)所⽰。
排架下柱⾼H 1=12.0m ,上柱⾼H 2=3.6m 。
已知:荷载标准值q 1k =0.9kN/m ,q 2k =0.45kN/m ,W k =12.0kN 。
试⽤剪⼒分配法计算A 柱的柱底弯矩标准值。
(提⽰:⽀座反⼒系数C 11=0.34,见图(b);图(c)、图(d)中的121.5u u ?=?)1.某单层⼚房排架结构及风荷载体型系数如图所⽰。
混凝土梁的自由振动周期计算方法

混凝土梁的自由振动周期计算方法一、前言混凝土梁是建筑结构中常见的一种构件,其自由振动周期的计算对于结构设计和分析具有重要的意义。
本文将介绍混凝土梁自由振动周期的计算方法,包括基本理论、计算公式和实际应用。
二、基本理论混凝土梁的自由振动周期是指在一定的约束条件下,梁在不受外力作用时自然振动一次所需的时间。
计算自由振动周期需要用到梁的弹性模量、截面惯性矩、截面面积、长度等参数,其中最重要的是弹性模量和截面惯性矩。
弹性模量是材料的一种力学性质,反映了材料抵抗形变的能力。
混凝土的弹性模量一般根据混凝土试件的压缩强度来确定,可以根据国家标准《混凝土结构设计规范》中的公式计算得出。
截面惯性矩是描述梁截面抗弯刚度的参数,其大小与梁的截面形状有关。
常见的梁截面形状有矩形、圆形、T形、I形等,对于不同形状的截面,截面惯性矩的计算方法也不同。
三、计算公式1. 矩形截面当混凝土梁的截面为矩形时,其截面惯性矩可以根据以下公式计算:$$I=\frac{1}{12}bh^3$$其中,$b$为矩形截面的宽度,$h$为矩形截面的高度。
梁的自由振动周期可以根据以下公式计算:$$T=2\pi\sqrt{\frac{I}{Ebh^3}}$$其中,$E$为混凝土的弹性模量,$I$为截面惯性矩,$b$为矩形截面的宽度,$h$为矩形截面的高度。
2. 圆形截面当混凝土梁的截面为圆形时,其截面惯性矩可以根据以下公式计算:$$I=\frac{\pi}{4}d^4$$其中,$d$为圆形截面的直径。
梁的自由振动周期可以根据以下公式计算:$$T=2\pi\sqrt{\frac{I}{E\pi d^4}}$$其中,$E$为混凝土的弹性模量,$I$为截面惯性矩,$d$为圆形截面的直径。
3. T形截面当混凝土梁的截面为T形时,其截面惯性矩可以根据以下公式计算:$$I=\frac{1}{12}b_1h_1^3+\frac{1}{12}(b_2-b_1)(h_2^3-h_1^3)$$其中,$b_1$为T形截面的上翼缘宽度,$b_2$为T形截面的下翼缘宽度,$h_1$为T形截面的上翼缘高度,$h_2$为T形截面的下翼缘高度。
建筑结构抗震复习题带答案

建筑结构抗震复习题一、判断题1.振型分解反应谱法既适用于弹性体系,也可用于弹塑性体系×2.结构的刚心就是地震惯性力合力作用点的位置×3.受压构件的位移延性将随轴压比的增加而减小√4。
结构的重力荷载代表值等于竖向荷载加上各可变荷载组合值。
×5。
震源到震中的垂直距离称为震中距。
×6。
对应于一次地震,震级只有一个,烈度也只有一个。
×7。
横波一般周期较长,振幅较大,引起地面水平方向的运动。
√8。
采用底部剪力法时,突出屋面的屋顶件,由于刚度突变、质量突变,其地震作用的效应乘以增大系数3,此增大部分应向下传递.×9.采用底部剪力法时,突出屋面的屋顶件,由于刚度突变、质量突变,其地震作用的效应乘以增大系数3,此增大部分应向下传递。
×10.地震波的传播速度,以横波最快,面波次之,纵波最慢.×11.横波只能在固态物质中传播√12.设防烈度为8度和9度的高层建筑应考虑竖向地震作用×13.众值烈度比基本烈度小1。
55度,罕遇烈度比基本烈度大1。
55度×14在进行抗震设计时,结构平面凹进的一侧尺寸为其相应宽度的20%时,认为是规则的√15。
地震波的传播速度,以横波最快,面波次之,纵波最慢。
×16.在同等场地、烈度条件下,钢结构房屋的震害较钢筋混凝土结构房屋的震害要严重。
×17.钢筋混凝土框架柱的轴压比越大,抗震性能越好。
×18。
场地特征周期与场地类别和地震分组有关.×19.受压构件的位移延性将随轴压比的增加而减小。
√20.选择结构的自振周期应尽可能接近场地卓越周期.×21.根据液化指数,将液化等级分为三个等级。
√22。
质量和刚度明显不对称、不均匀的结构,应考虑水平地震作用的扭转影响√。
23。
地震作用对软土的承载力影响较小,土越软,在地震作用下的变形就越小。
×24。
附录F:结构基本自振周期的经验公式

附录F 结构基本自振周期的经验公式F.1 高耸结构F.1.1 一般高耸结构的基本自振周期,钢结构可取下式计算的较大值,钢筋混凝土结构可取下式计算的较小值:H T )013.0~007.0(1= (F.1.1)式中:H ——结构的高度(m)。
F.1.2 烟囱和塔架等具体结构的基本自振周期可按下列规定采用:1,烟囱的基本自振周期可按下列规定计算:1)高度不超过60m 的砖烟囱的基本自振周期按下式计算:dH T 2211022.023.0-⨯+= (F.1.2-1) 2)高度不超过150m 的钢筋混凝土烟囱的基本自振周期按下式计算:dH T 2211010.041.0-⨯+= (F.1.2-2) 3)高度超过150m ,但低于210m 的钢筋混凝土烟囱的基本自振周期按下式计算:dH T 2211008.053.0-⨯+= (F.1.2-3) 式中:H ——烟囱高度(m);d ——烟囱1/2高度处的外径(m)。
2,石油化工塔架(图F.1.2)的基本自振周期可按下列规定计算:图F.1.2 设备塔架的基础形式(a)圆柱基础塔;(b)圆筒基础塔;(c)方形(板式)框架基础塔;(d)环形框架基础塔1)圆柱(筒)基础塔(塔壁厚不大于30mm)的基本自振周期按下列公式计算: 当H 2/D 0<700时2311085.035.0D H T -⨯+= (F.1.2-4)当H 2/D 0≥700时2311099.025.0D H T -⨯+= (F.1.2-5) 式中:H ——从基础底板或柱基顶面至设备塔顶面的总高度(m);D 0——设备塔的外径(m);对变直径塔,可按各段高度为权,取外径的加权平均值。
2)框架基础塔(塔壁厚不大于30mm)的基本自振周期按下式计算:2311040.056.0D H T -⨯+= (F.1.2-6) 3)塔壁厚大于30mm 的各类设备塔架的基本自振周期应按有关理论公式计算。
4)当若干塔由平台连成一排时,垂直于排列方向的各塔基本自振周期T 1可采用主塔(即周期最长的塔)的基本自振周期值;平行于排列方向的各塔基本自振周期T 1可采用主塔基本自振周期乘以折减系数0.9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FEVK G V max eq
V max 0.65 H max
Geq 0.75 Gi
FVi
Gi H i
n
FEVK ---质点i的竖向地震作用标准值。
影响显著。
我国抗震设计《规范》规定,对下列建筑应考虑竖向地震 作用的不利影响: 1、8度和9度时的大跨度结构、长悬臂结构; 2、8度和9度时烟囱和类似的高耸结构; 3、9度时的高层建筑。
3.6.1高耸结构及高层建筑的竖向地震作用
分析结果表明: 高耸结构和高层建筑竖向第一振型的地震内力与竖向 前5个振型按“平方和开方”组合的地震内力相比较, 误差仅在5%--15%。 竖向第一振型的数值大致呈倒三角形式
1.建筑结构的偏心
m
主要原因:结构质量中心与刚度 中心不重合
质心:在水平地震作用下, 惯性力的合力中心
刚心:在水平地震作用下, 结构抗侧力的合力中心
质心
ug (t)
刚心
3.5结构的扭转地震效应
2.地震地面运动存在扭转分量 地震波在地面上各点的波速、周期和相位不同。建
筑结构基底将产生绕竖直轴的转动,结构便会产生扭转 振动。
高耸结构和高层建筑竖向地震作用可按与底部剪力法 类似的方法计算。
3.6.1高耸结构及高层建筑的竖向地震作用
(1)竖向反应谱及竖向振动周期 竖向地震反应谱: 与水平地震反应谱的形状相差不大 竖向反应谱的加速度峰值约为水平反应谱的1/2至2/3。 可利用水平地震反应谱进行分析。
V 0.65 H
Ⅰ类场地的竖向和水平平均反应谱
x2 (t)
m1
x1 (t)
3.4.1能量法
位移: xi(t) X i sin( t ) 速度: x(t) Xi cos(t )
mn
当体系振动达到平衡位置时,体系变形
位能为零,体系动能达到最大值Tmax
Tmax
1ω2 2
n i 1
mi
X
2 i
m1
xn (t)
x2 (t) x1 (t)
3.4结构自振周期及振型的实用计算方法
3.4.1能量法
能量法是根据体系在振动过程的能量守恒原理导出的, 适用用求结构的基本频率
此方法常用于求解以剪切型为主的框架结构
mn
xn (t)
设体系作自由振动,任一质点i的位移:
速度为
xi(t) X i sin( t )
x(t) X i cos(t )
3.6.1高耸结构及高层建筑的竖向地震作用
竖向振动周期: 计算结果表明:高耸结构和高层建筑竖向振动周
期较短,基本周期在0.1~0.2s范围内 小于场地的特征周期Tg 《建筑抗震规范》直接取竖向地震影响系数:
V max 0.65 H max
3.6.1高耸结构及高层建筑的竖向地震作用
(2)竖向地震作用计算----底部剪力法
无论结构是否有偏心,地震地面运动产生的结构扭 转振动均是存在的。
★扭转作用会加重结构的震害 《规范》规定对质量和刚度明显不均匀、不对称结构 应考虑水平地震作用的扭转效应
3.6竖向地震作用
抗震设计中,一般不考虑竖向地震作用的影响 震害表明:
1、在高烈度区,竖向地面运动的影响是明显的 2、竖向地震作用对高层建筑、高耸及大跨结构
根据实测统计,忽略填充墙布置、质量分布差异等,初 步设计时可按下列公式估算
(1)高度低于25m且有较多的填充墙框架办公楼、旅馆的基本周期
T1 0.22 0.35H / 3 B
H---房屋总高度;B---所考虑方向房屋总宽度。 (2)高度低于50m的钢筋混凝土框架-抗震墙结构的基本周期
T1 0.33 0.00069H 2 / 3 B
当体系振动达到振幅最大值时,体系动能为零, 位能达到最大值Umax
1 n
U max 2 i1 mi gX i
3.4.1能量法
Tmax
1ω2 2
n i 1
mi
X
2 i
U max
1 2
n i 1
mi gX i
根据能量守恒原理: Tmax=UmaxLeabharlann ng mi X i
i 1
n
mi
X
2 i
i 1
(b):弯曲型(c):剪切型(d):弯剪型
3.4.3顶点位移法
抗震墙结构可视为弯曲型杆,即弯曲型结构。 Tb 1.6 b
框架结构可近似视为剪切型杆。
Ts 1.8 s
框架-抗震墙结构可近似视为剪弯型杆。
T 1.7 bs
本方法适用于质量及刚度沿高度分布比较均匀的任何体系结构。
补充:自振周期的经验公式
等效原则:两个体系的动能相等 多质点体系的最大动能为
mN xn M eq xm
T1max
1 2
n i 1
mi (1xi )2
单质点体系的最大动能为
T2 max
1 2
M eq
(1xm )2
m1 x1
xm xn
xm ---体系按第一振型振动时,相应于折算质点处的最大位移;
3.4.2折算质量法(等效质量法)
(3)高度低于50m的规则钢筋混凝土抗震墙结构的基本周期
T1 0.04 0.038H / 3 B
自振周期的经验公式
在实测统计基础上,再忽略房屋宽度和层高的影响等, 有下列更粗略的公式
(1)钢筋混凝土框架结构 T1 (0.08 ~ 0.10)N N---结构总层数。
(2)钢筋混凝土框架-抗震墙或钢筋混凝土框架-筒体结构
T1 (0.06 ~ 0.08) N
(3)钢筋混凝土抗震墙或筒中筒结构
T1 (0.04 ~ 0.05) N
(4)钢-钢筋混凝土混合结构
T1 (0.06 ~ 0.08) N
(5)高层钢结构
T1 (0.08 ~ 0.12) N
3.5结构的扭转地震效应
一、产生扭转地震反应的原因
两方面:建筑自身的原因和地震地面运动的原因。
T1max
1 2
n i 1
mi (1xi )2
T1max T2max
T2 max
1 2
M eq (1xm )2
n
mi
x
2
i
M eq
i 1
xm2
1
1
M eq
T1 2 M eq
---单位水平力作用下顶点位移。
3.4.3顶点位移法
顶点位移法是根据在重力荷载水平作用时算得的 顶点位移来求解基本频率的一种方法
T1
2 1
2
n
mi
X
2 i
i 1 n
2
g mi X i
i 1
n
Gi
X
2 i
i 1
n
Gi X i
i 1
一般假定:将结构重力荷载当成水平荷载作用于质点上 所得的结构弹性曲线为结构的基本振型
3.4.2折算质量法(等效质量法)
基本原理:将多质点体系用单质点体系代替。
使单质点体系的自振频率和原体系的基本频率相等或相近
