初二数学压轴几何证明题(含答案)

合集下载

部编版初二数学八年级上册期中压轴专题(带答案解析)

初二期中压轴专题一、解答题1．如图1，在Rt△ACB中，∠BAC=90°，AB=AC，分别过B、C两点作过点A的直线l的垂线，垂足为D、E；(1)如图1，当D、E两点在直线BC的同侧时，猜想，BD、CE、DE三条线段有怎样的数量关系？并说明理由．(2)如图(2)，将(1)中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线l上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．(3)如图3，∠BAC=90°，AB=22，AC=28．点P从B点出发沿B→A→C路径向终点C运动；点Q从C 点出发沿C→A→B路径向终点B运动．点P和Q分别以每秒2个和3个单位的速度同时开始运动，只要有一点到达相应的终点时两点同时停止运动；在运动过程中，分别过P和Q作PF⊥l于F，QG⊥l于G．问：点P运动多少秒时，△PFA与△QAG全等？(直接写出结果即可)2．如图，在四边形ABCD中，AD=BC=10，AB=CD，BD=14，点E从D点出发，以每秒2个单位的速度沿DA向点A匀速移动，点F从点C出发，以每秒5个单位的速度沿C→B→C，作匀速移动，点G 从点B出发沿BD向点D匀速移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动，假设移动时间为t秒．(1)试证明：AD∥BC．(2)在移动过程中，小明发现有△DEG与△BFG全等的情况出现，请你探究这样的情况会出现几次？并分别求出此时的移动时间t和G点的移动距离．3．如图，在△ABC中，AB=AC，∠BAC=90°，BD平分∠ABC，交AC于点D，AF⊥BD，垂足为点E，交BC于点F．求证：AD=CF．4．解答下列问题：(1)如图1，在△ABC中，AB=AC，点D在AC上，且AD=BD=BC，求∠A的度数．(2)如图2，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE．①若∠EDM=84°，求∠A的度数：②若以E为圆心，ED为半径作弧，与射线DM没有交点(除D点外)，直接写出∠A的取值范围．5．在△ABC中，AB=AC，∠BAC=90°，点D为AC上一动点．(1)如图1，点E、点F均是射线BD上的点并且满足AE=AF，∠EAF=90°．求证：△ABE≌△ACF．(2)在(1)的条件下，求证：CF⊥BD．(3)由(1)我们知道∠AFB=45°，如图2，当点D的位置发生变化时，过点C作CF⊥BD于F，连接AF．那么∠AFB的度数是否发生变化？请证明你的结论．6．如图，已知△ABC中，AB=AC=10 cm，BC=8 cm，点D为AB的中点．(1)如果点P在线段BC上以3 cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1 s后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？(2)若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？7．如图，在△ABC中，∠ABC>60°，∠BAC<60°，以AB为边作等边△ABD(点C，D在边AB的同侧)，连接CD．(1)若∠ABC=90°，∠BAC=30°，求∠BDC的度数．(2)当∠BAC=2∠BDC时，请判断△ABC的形状并说明理由．(3)当∠BCD等于多少度时，∠BAC=2∠BDC恒成立．8．解答：(1)如图1，△ABC与△ADE均是顶角为40°的等腰三角形，BC、DE分别是底边，求证：BD=CE．(2)如图2，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．填空：∠AEB的度数为；线段BE与AD之间的数量关系是．(3)拓展探究如图3，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．9．如图，已知△ABC中，AB=AC=24厘米，BC=18厘米，点D为AB的中点．(1)如果点P在线段BC上以3厘米/秒得速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，设运动时间为x．①PC=____(用含x的代数式表示)；②若点Q的运动速度与点P的运动速度相等，当x为何值时，以B，P，D为顶点的三角形与△CQP全等；③若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD≌△CPQ？(2)如果点Q以(1)③中的运动速度从点C出发，点P以3厘米/秒的速度从点B出发，都逆时针沿△ABC 三边运动，点P，Q同时出发，运动时间为y．当y取何值时，点P与点Q第二次相遇？10．如图(1)，AB=4cm，AC⊥AB，BD⊥AB，AC=BD=3cm．点P在线段AB上以1cm/s的速度由点A 向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t(s)．(1)若点Q的运动速度与点P的运动速度相等，当t=1时，△ACP与△BPQ是否全等，并判断此时线段PC 和线段PQ的位置关系，请分别说明理由．(2)如图(2)，将图(1)中的“AC⊥AB，BD⊥AB”为改“∠CAB=∠DBA=60°”，其他条件不变．设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．初二期中压轴专题答案及解析一、解答题1．【答案】(1)解：猜想：DE=BD+CE．理由：∵BD⊥直线l，CE⊥直线l，∴∠BDA=∠CEA=90°，∵∠BAC=90°，∴∠BAD+∠CAE=90°，∵∠BAD+∠ABD=90°，∴∠CAE=∠ABD，在△ADB和△CEA中，∠ ∠∠ ∠ ，∴△ADB≌△CEA(AAS)，∴AE=BD，AD=CE，∴DE=AE+AD=BD+CE．(2)解：成立．∵∠BDA=∠BAC=α，∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α，∴∠CAE=∠ABD，在△ADB和△CEA中，∠ ∠∠ ∠ ，∴△ADB≌△CEA(AAS)，∴AE=BD，AD=CE，∴DE=AE+AD=BD+CE．(3)解：①当0≤t<时，点P在AB上，点Q在AC上，此时有BP=2t，CG=3t，AB=22，AC=28．当PA=QA即22-2t=28-3t，也即t=6时，∵PF⊥l，QG⊥l，∠BAC=90°，∴∠PFA=∠QGA=∠BAC=90°，∴∠PAF=90°-∠GAQ=∠AQG．在△PFA和△AGQ中，∠ ∠∠ ∠ ，∴△PFA≌△AGQ(AAS)．②当≤t≤11时，点P在AB上，点Q也在AB上，此时相当于两点相遇，则有2t+3t=50，解得t=10；③当11<t≤时，点Q停在点B处，点P在AC上，当PA=QA即2t-22=22，解得t=22(舍去)．综上所述：当t等于6或10时，△PFA与△QAG全等．【解析】(1)根据BD⊥直线l，CE⊥直线l得∠BDA=∠CEA=90°，而∠BAC=90°，根据等角的余角相等得∠CAE=∠ABD，然后根据“AAS”可判断△ADB≌△CEA，则AE=BD，AD=CE，于是DE=AE+AD=BD+CE；(2)利用∠BDA=∠BAC=α，则∠DBA+∠BAD=∠BAD+∠CAE=180°-α，得出∠CAE=∠ABD，进而得出△ADB≌△CEA即可得出答案；(3)易证∠PFA=∠QGA，∠PAF=∠AQG，只需PA=QA，就可得到△PFA与△QAG全等，然后只需根据点P和点Q不同位置进行分类讨论即可解决问题．2．【答案】(1)证明：在△ABD和△CDB中，，∴△ABD≌△CDB(SSS)，∴∠ADB=∠CBD，∴AD∥BC．(2)解：设G点的移动距离为x，当△DEG与△BFG全等时，∵∠EDG=∠FBG，∴DE=BF、DG=BG或DE=BG、DG=BF，①∵BC=10，2，∴当点F由点C到点B，即0<t≤2时，则：，解得：，或，解得：(不合题意舍去)；②当点F由点B到点C，即2<t≤4时，则，解得：，或，解得：，∴综上所述：△DEG与△BFG全等的情况会出现3次，此时的移动时间分别是秒、秒、秒，G点的移动距离分别是7、7、．【解析】(1)由SSS证得△ABD≌△CDB，得出∠ADB=∠CBD，即可得出结论；(2)设G点的移动距离为x，当△DEG与△BFG全等时，由∠EDG=∠FBG，得出DE=BF、DG=BG或DE=BG、DG=BF，①当点F由点C到点B，即0<t≤2时，则：，或，解方程组即可得出结果；②当点F由点B到点C，即2<t≤4时，则，或，解方程组即可得出结果．3．【答案】证明：过点A作∠BAC的平分线AG，交BD于点G，∵AB=AC，∴∠ABC=∠C．∵∠BAC=90°，∴∠ABC=∠C=45°．∵AG平分∠BAC，∴∠BAG=∠CAG=∠ABC=45°，∴∠BAG=∠C．∵AE⊥BD，∴∠ABG+∠BAE=90°．∵∠CAF+∠BAE=90°，∴∠ABG=∠CAF．在△ABG和△CAF中，∠ ∠，∠ ∠∴△ABG≌△CAF(ASA)，∴AG=CF．∵BD平分∠ABC，∴∠ABG=∠CBD，∵∠ABG=∠CAF，∴∠CAF=22.5°．∵∠CAG=45°，∴∠GAE=∠CAG-∠CAF=45-22.5°=22.5°，∴∠GAE=∠CAF．∵AE⊥BD，∴∠AEG=∠AED=90°．在△GAE和△DAE中，∠ ∠，∠ ∠∴△GAE≌△DAE(ASA)，∴AG=AD．∵AG=CF，∴AD=CF．【解析】过点A作∠BAC的平分线AG，交BD于点G，构造全等三角形：△ABG≌△CAF(ASA)，△GAE≌△DAE(ASA)，根据全等三角形的对应边相等和等量代换证得结论．4．【答案】(1)解：设∠A=x°，∵AD=BD，∴∠ABD=∠A=x°，∴∠BDC=∠A+∠ABD=2x°，∵BD=BC，∴∠C=∠BDC=2x°，∵AB=AC，∴∠ABC=∠C=2x°，在△ABC中，∠A+∠ABC+∠C=180°，∴x+2x+2x=180，解得：x=36，∴∠A=36°．(2)解：①∵AB=BC=CD=DE，∴∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，根据三角形的外角性质，∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，又∵∠EDM=84°，∴∠A+3∠A=84°，解得：∠A=21°；②∵以E为圆心，ED为半径作弧，与射线DM上没有交点(除D点外)，∴E到射线AM的距离大于DE，∴∠EDM≥90°，则∠EDM=4∠A≥90°，即∠A≥22.5°，∵△CDE为等腰三角形，∴∠ECD=∠CED=3∠A＜90°，∴∠A<30°，∴∠A的取值范围是22.5°≤∠A<30°．【解析】(1)先设∠A=x°，然后由等腰三角形的性质，求得∠ABC=∠C=2x°，然后由三角形的内角和定理，得到方程：x+2x+2x=180，解此方程即可求得答案；(2)①根据等边对等角可得∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，再根据三角形外角的性质可得∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，然后用∠A表示出∠EDM，计算即可求解；②先判断出E到射线AM的距离小于DE，进而得出∠EDM≥90°，根据△CDE为等腰三角形，得到∠ECD=∠CED=3∠A＜90°，解不等式组即可得出结论．5．【答案】(1)证明：∵∠BAC=∠BAE+∠EAD=90°，∠EAF=∠CAF+∠EAD=90°，∴∠BAE=∠CAF，在△ABE和△ACF中∠ ∠∴△ABE≌△ACF(SAS)．(2)证明：∵∠BAC=90°，∴∠ABE+∠BDA=90°；由(1)得△ABE≌△ACF，∴∠ABE=∠ACF，∴∠BDA+∠ACF=90°；又∵∠BDA=∠CDF，∴∠CDF+∠ACF=90°，∴∠BFC=90°，∴CF⊥BD．(3)解：∠AFB=45°不变化，理由如下：过点A作AF的垂线交BM于点E∵CF⊥BD，∴∠BAC=90°，∴∠ABD+∠ADB=90°，同理∠ACF+∠CDF=90°；∵∠CDF=∠ADB，∴∠ABD=∠ACF，同(1)理得∠BAE=∠CAF．在△ABE和△ACF中，∠ ∠，∠ ∠∴△ABE≌△ACF(ASA)，∴AE=AF，∴△AEF是等腰直角三角形，∴∠AFB=45°．【解析】(1)根据SAS证明△ABE≌△ACF即可；(2)根据全等三角形的性质和垂直的判定解答即可；(3)根据全等三角形的判定和性质解答即可．6．【答案】(1)解：①全等，理由如下：∵t=1 s，∴BP=CQ=3×1=3 cm，∵AB=10 cm，点D为AB的中点，∴BD=5 cm．又∵PC=BC-BP，BC=8 cm，∴PC=8-3=5 cm，∴PC=BD．又∵AB=AC，∴∠B=∠C，在△BPD和△CQP中，∠ ∠ ，∴△BPD≌△CQP(SAS)．②∵v P≠v Q，∴BP≠CQ，若△BPD≌△CPQ，∠B=∠C，则BP=PC=4 cm，CQ=BD=5 cm，∴点P，点Q运动的时间t＝= s，∴ cm/s．(2)解：设经过秒后点P与点Q第一次相遇，由题意，得，解得，∴点P共运动了×3=80 cm．△ABC周长为：10+10+8=28 cm，若是运动了三圈即为：28×3=84 cm，∵84-80=4 cm<AB的长度，∴点P、点Q在AB边上相遇，∴经过 s点P与点Q第一次在边AB上相遇．【解析】(1)①根据时间和速度分别求得两个三角形中的边的长，根据SAS判定两个三角形全等；②根据全等三角形应满足的条件探求边之间的关系，再根据路程=速度×时间公式，先求得点P运动的时间，再求得点Q的运动速度；(2)根据题意结合图形分析发现：由于点Q的速度快，且在点P的前边，所以要想第一次相遇，则应该比点P多走等腰三角形的两个腰长．7．【答案】(1)解：∵△ABD为等边三角形，∴∠BAD=∠ABD=60°，AB=AD．又∵∠BAC=30°，∴AC平分∠BAD，∴AC垂直平分BD，∴CD=CB，∴∠BDC=∠DBC=∠ABC-∠ABD=90°-60°=30°．(2)解：△ABC是等腰三角形．理由：设∠BDC=x，则∠BAC=2x，∠CAD=60°-2x，∠ADC=60°+x，∴∠ACD=180°-∠CAD-∠ADC=60°+x，∴∠ACD=∠ADC，∴AC=AD．∵AB=AD，∴AB=AC，即△ABC是等腰三角形．(3)解：当∠BCD=150°时，∠BAC=2∠BDC恒成立．如图：作等边△BCE，连接DE，则BC=EC，∠BCE=60°．∵∠BCD=150°，∴∠ECD=360°-∠BCD-∠BCE=150°，∴∠DCE=∠DCB．又∵CD=CD，∴△BCD≌△ECD，∴∠BDC=∠EDC，即∠BDE=2∠BDC．又∵△ABD为等边三角形，∴AB=BD，∠ABD=∠CBE=60°，∴∠ABC=∠DBE=60°+∠DBC．又∵BC=BE，∴△BDE≌△BAC(SAS)，∴∠BAC=∠BDE，∴∠BAC=2∠BDC．【解析】(1)先由等腰三角形三线合一的性质证明AC为BD的垂直平分线，从而可得到CD=CB，则∠BDC=∠DBC=∠ABC-∠ABD；(2)设∠BDC=x，则∠BAC=2x，∠CAD=60°-2x，∠ADC=60°+x，然后可证明∠ACD=∠ADC，则AC=AD，于是可得到AB=AC；(3)当∠BCD=150°时，∠BAC=2∠BDC恒成立，如答图所示：作等边△BCE，连接DE，则BC=EC，∠BCE=60°．先证明△BCD≌△ECD，从而可得到∠BDE=2∠BDC，然后再证明△BDE≌△BAC，从而可得到∠BAC=∠BDE．8．【答案】(1)证明：∵∠BAC=∠DAE=40°，∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，在△BAD和△CAE中，∠ ∠ ，∴△BAD≌△CAE，∴BD=CE．(2)60° BE=AD(3)解：∵△ACB和△DCE均为等腰直角三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=90°，∠CDE=∠CED=45°，∴∠ACB-∠DCB=∠DCE-∠DCB，即∠ACD=∠BCE，在△ACD和△BCE中，∠ ∠ ，∴△ACD≌△BCE，∴BE=AD，∠BEC=∠ADC．∵点A，D，E在同一直线上，∴∠ADC=180-45=135°，∴∠BEC=135°，∴∠AEB=∠BEC-∠CED=135°-45°=90°；∵∠DCE=90°，CD=CE，CM⊥DE，∴CM=DM=EM，∴DE=DM+EM=2CM，∴AE=AD+DE=BE+2CM．【解析】(1)根据全等三角形的判定方法，判断出△BAD≌△CAE，即可判断出BD=CE；(2)∵△ACB和△DCE均为等边三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=60°，∠CDE=∠CED=60°，∴∠ACB-∠DCB=∠DCE-∠DCB，即∠ACD=∠BCE，在△ACD和△BCE中，∠ ∠ ，∴△ACD≌△BCE，∴BE=AD；∠ADC=∠BEC，∵点A，D，E在同一直线上，∴∠ADC=180°-60°=120°，∴∠BEC=120°，∴∠AEB=∠BEC-∠CED=120°-60°=60°．故答案为：60°；BE=AD．(3)首先根据△ACB和△DCE均为等腰直角三角形，可得AC=BC，CD=CE，∠ACB=∠DCE=90°，据此判断出∠ACD=∠BCE，然后根据全等三角形的判定方法，判断出△ACD≌△BCE，即可判断出BE=AD，∠BEC=∠ADC，进而判断出∠AEB的度数为90°即可，最后根据∠DCE=90°，CD=CE，CM⊥DE，可得CM=DM=EM，所以DE=DM+EM=2CM，据此判断出AE=BE+2CM 即可．9．【答案】(1)解：①由运动知，BP=3x，∴PC=BC-BP=18-3x(0≤x≤6)；②当点Q的运动速度与点P的运动速度相等时，由运动知，BP=CQ，∵△ABC是等腰三角形，∴∠B=∠C，∵以B，P，D为顶点的三角形与△CQP全等，∴只有PC=BD，∵点D是AB的中点，∴BD=AB=12，∴PC=18-3x=12，∴x=2；③∵V P≠V Q，∴BP≠CQ，又∵∠B=∠C，要使△BPD≌△CPQ，只能BP=CP=9，∵△BPD≌△CPQ，∴CQ=BD=12．∴点P的运动时间(秒)，此时V Q=(厘米/秒)．(2)解：因为V Q>V P，只能是点Q追上点P，即点Q比点P多走△ABC的周长和AB+AC的路程之和，设经过y秒后P与Q第二次相遇，依题意得4y=3y+2×24+2×24+18，解得y=114(秒)，∴点P、Q在BC边上相遇，即经过了114秒，点P与点Q第二次在BC边上相遇．【解析】(1)①直接由运动即可得出结论；②先求得BP=CQ，PC=BD=12，然后根据等边对等角求得∠B=∠C，最后根据SAS即可证明；③因为V P≠V Q，所以BP≠CQ，又∠B=∠C，要使△BPD与△CQP全等，只能BP=CP=9，根据全等得出CQ=BD=12，然后根据运动速度求得运动时间，根据时间和CQ的长即可求得Q的运动速度；(2)因为V Q>V P，只能是点Q追上点P，即点Q比点P多走△ABC的周长和AB+AC的路程之和，据此列出方程，解这个方程即可求得．10．【答案】(1)解：当t=1时，AP=BQ=1，BP=AC=3，又∠A=∠B=90°，在△ACP和△BPQ中，∠ ∠ ，∴△ACP≌△BPQ(SAS)．∴∠ACP=∠BPQ，∴∠APC+∠BPQ=∠APC+∠ACP=90°．∴∠CPQ=90°，即线段PC与线段PQ垂直．(2)解：①若△ACP≌△BPQ，则AC=BP，AP=BQ，则，解得；②若△ACP≌△BQP，则AC=BQ，AP=BP，则，解得：；综上所述，存在或，使得△ACP与△BPQ全等．【解析】(1)利用SAS证得△ACP≌△BPQ，得出∠ACP=∠BPQ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；(2)由△ACP≌△BPQ，分两种情况：①AC=BP，AP=BQ，②AC=BQ，AP=BP，建立方程组求得答案即可．。

八年级上册数学几何压轴大题

八年级上册数学几何压轴大题在数学几何的学习中，大题是测试学生对知识点掌握和解题能力的重要方式。

本文将为大家展示八年级上册数学几何压轴大题，帮助同学们更好地理解数学几何知识和提高解题能力。

大题一：平面图形的性质与判断1. 已知三角形ABC中，角A=90度，AB=5cm，BC=12cm，求角C的度数和边AC的长度。

解析：由已知条件可得三角形ABC为直角三角形。

根据直角三角形的性质，角C为90度，边AC可以通过勾股定理求得。

勾股定理表达式如下：AC² = AB² + BC²代入已知值，得：AC² = 5² + 12² = 25 + 144 = 169通过开方运算，可得：AC = √169 = 13因此，角C的度数为90度，边AC的长度为13cm。

2. 如果一个四边形的两条对角线相等，这个四边形是否一定是矩形？请给出理由。

解析：不一定。

对于四边形来说，两条对角线相等是矩形的充分条件，但并非必要条件。

除了矩形之外，还存在其他特殊的四边形，如菱形和正方形，它们的两条对角线也相等。

因此，只知道两条对角线相等无法准确判断四边形的类型，还需进一步观察其他条件。

大题二：空间几何图形的投影与旋转1. 一个正方体的边长为3cm，将它围绕其中一个顶点逆时针旋转90度，再向下投影到地面上，求投影图形的面积。

解析：首先我们可以通过观察得知，正方体的一个顶点以及连接这个顶点的3条边组成一个等边三角形，且边长为3cm。

这个等边三角形在投影到地面时会变为一个边长为3cm的正三角形。

正三角形的面积计算公式为：正三角形的面积 = 边长的平方× √3 / 4代入已知值，得：正三角形的面积= 3² × √3 / 4 = 9√3 / 4 ≈ 3.9cm²因此，投影图形的面积约为3.9cm²。

2. 一个圆锥的底面半径为6cm，高为8cm，将它绕底面的直径旋转一周，求旋转体的体积。

八年级上学期数学期末专题：几何证明综合(原题和解析)

【期末压轴题】专题05：几何证明综合（原卷版）学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列六个命题①有理数与数轴上的点一一对应①两条直线被第三条直线所截，内错角相等①平行于同一条直线的两条直线互相平行；①同一平面内，垂直于同一条直线的两条直线互相平行；①直线外一点到这条直线的垂线段叫做点到直线的距离①如果一个角的两边分别平行于另一个角的两边，那么这两个角相等，其中假命题的个数是（）A．2个B．3个C．4个D．5个2．下列几个命题中，真命题有（）①两条直线被第三条直线所截，内错角相等；①如果1∠=∠；∠和2∠是对顶角，那么12①一个角的余角一定小于这个角的补角；①三角形的一个外角大于它的任一个内角．A．1个B．2个C．3个D．43．下面说法正确的个数有（）x-<-的（1）不等式两边乘（或除以）同一个数，不等号的方向不变；（2）5-是324解；（3）三角形的外角等于与它不相邻的两个内角的和；（4）如果ABC的三个内角满∠=∠-∠，那么ABC一定是直角三角形；（5）三角形的高所在的直线交于一足A C B点，这一点不在三角形内就在三角形外A．1个B．2C．3个D．4个4．下列命题中假命题有（）①两条直线被第三条直线所截，同位角相等①如果两条直线都与第三条直线平行，那么这两条直线也互相平行①点到直线的垂线段叫做点到直线的距离①过一点有且只有一条直线与已知直线平行①若两条直线都与第三条直线垂直，则这两条直线互相平行．A．5个B．4个C．3个D．2个5．下列命题为真命题的是（）A ．如果0mn =，那么0m =且0n =B ．两边分别相等的两个直角三角形全等C ．三角形的三条角平分线相交于一点，并且这一点到三个顶点的距离相等D ．如果两条直线互相平行，则其中一条直线上任意一点到另一条直线的距离都相等 6．一副三角板如图摆放，点F 是45°角三角板ABC 的斜边的中点，4AC =．当30°角三角板DEF 的直角顶点绕着点F 旋转时，直角边DF ，EF 分别与AC ，BC 相交于点M ，N ．在旋转过程中有以下结论：①MF NF =；①四边形CMFN 有可能为正方形；①MN 长度的最小值为2；①四边形CMFN 的面积保持不变：①CMN △面积的最大值为2，其中正确的个数是（）A ．2B ．3C ．4D ．57．如图，在Rt ABC △中，90BAC ∠=︒，AB AC =，D 为BC 边上一点，将ABD △绕点A 逆时针旋转90°得到ACE ，点B 、D 的对应点分别为点C 、E ，连接BE ，将AC 平移得到DF （点A 、C 的对应点分别为点D 、F ），连接AF ，若AB =2BD =，则AF 的长为（）A ．B ．6C ．D 8．如图，等腰Rt ABC 中，AB ＝AC ，①BAC ＝90°，AD ①BC 于点D ，①ABC 的平分线分别交AC 、AD 于E 、F 两点，M 为EF 的中点，AM 的延长线交BC 于点N ，连接DM ，下列结论：①DF ＝DN ；①DMN 为等腰三角形；①DM 平分①BMN ；①AE ＝23EC ；①AE ＝NC ，其中正确结论有（）A ．2个B ．3个C ．4个D ．5个9．如图，凸四边形ABCD 中，90,90,60,3,A C D AD AB ∠=︒∠=︒∠=︒==若点M 、N 分别为边,CD AD 上的动点，则BMN △的周长最小值为（）A ．B ．C ．6D ．310．如图，Rt ABC 中，90ACB ∠=︒且CA CB =，D 为ABC 外一点，连接AD ，过D 作DE DA ⊥交BC 于点E ，F 为DE 上一点且DF DA =，连接BF ，CD ．将线段CD 绕点C 逆时针旋转90︒到线段CG ，连接DG 分别交BF 、BA 于点M 、N ，连接BG 、CF ．下列结论：①BM FM =；①CG =；①BCG AND ∠>∠；①CF AD +>；①若2BG =，BC =CF =2ADFC S =四边形）A ．2个B ．3个C ．4个D ．5个 11．如图，在ABC 中，点E 在边AC 上，EB ＝EA ，①A ＝2①CBE ，延长BD 到F ，使DF ＝DB ，连接CF ，过点C 作CD ①BF 于点D ，BD ＝16，AC ＝22，则边BC 的长为（）A ．B ．C ．D ．12．如图，把含30°的直角三角板ABC 绕点B 顺时针旋转至如图EBD ，使BC 在BE 上延长AC 交DE 于F ，若AF =4，则AB 的长为（）A．2B ．C ．D ．3二、填空题 13．如图，在平面直角坐标系中，点()6,0A ，点()0,P m ，将线段PA 绕着点P 逆时针旋转90°，得到线段PB ，连接AB ，OB ，则BO BA +的最小值为__________．14．如图，在ABC 中，CA BC =，8AB =，5AC =，点D 是AB 边上的一个动点，点E 与点A 关于直线CD 对称，连接CE ，DE ，AE ，当ADE 是直角三角形时，求AD 的长为_____________．15．如图，已知30B ∠=，45C ∠=，150BDC ∠=，且5BD CD ==，则AB =_________16．如图，在矩形ABCD 中，点E 在线段AD 上，连接BE 、CE ，点F 在线段BE 上，连接CF ，若①EBC ＝2①ECD ，DE ＝2，BF ＝9，tan①EFC ＝43，则线段CE 的长为______．17．如图，在等腰ABC 中，120ACB ∠=︒，8AC BC ==，D 、E 为边AB 上两个动点，且6DE =，则CDE △周长的最小值是________．18．如图，点D 是等边①ABC 内部的一点，①ADC ＝120°，AB 2＝19，23AD CD =，则线段BD 的长度是 ___．19．如图所示，①AOB ＝50°，①BOC ＝30°，OM ＝11，ON ＝6．点P 、Q 分别是OA 、OB 上动点，则MQ +PQ +NP 的最小值是 ___．20．①ABC中，①ACB＝60°，AC＝4，BC＝13，以AB为边作等边①ABD，过D作DE①BC 于E，则BE的长为____．三、解答题21．如图，AD与BC交于点O，①AD=BC；①①A=①C；①AB=CD，请以①①①中的两个作为条件，另一个为结论，写出一个真命题，并加以证明．已知：求证：证明：22．如图，在Rt①ABC中，①C=90°，AB=10cm，AC=6cm，动点P从点B出发，沿射线BC以4cm/s的速度运动，设运动时间为t秒．（1）当t= 时，AP平分①ABC的面积．（2）当①ABP为等腰三角形时，求t的值．（3）若点Q是边AB上一点，且QP①BC，垂足为P，请用无刻度的直尺和圆规，作出点P、点Q，使得QA=QP．（4）若点E、F为BC、AB上的动点，求AE+EF的最小值．23．在①ABC中，P是BC边上的一动点，连接AP．（1）如图1，①BAC＝90°，AB＝AC，①BAP＝15°，且PC．求：①ABP的面积．（2）如图2，若①BAC＝90°，AB＝AC，AP为边作等腰Rt①APE，连接BE，F是BE的中点，连接AF，猜想PE，PB，AF之间有何数量关系？并证明你的结论．（3）如图3，作PD①AB于D，PE①AC于E，若①B＝75°，①C＝45°，BC＝9﹣当DE最小时，请直接写出DE的最小值．24．如图，在Rt ABC中AB=10，BC①AC，P为线段AC上一点，点Q，P关于直线BC对称，QD①AB于点D，DQ与BC交于点E，连结DP，设AP=m．（1）若BC=8，求AC的长，并用含m的代数式表示PQ的长；（2）在（1）的条件下，若AP=PD．求CP的长：（3）连结PE，若①A=60°，PCE与PDE的画积之比为1：2，求m的值．25．定义：如图1，点M、N把线段AB分割成AM、MN和BN，若以AM、MN、BN为边的三角形是一个直角三角形，则称点M ，N 是线段AB 的勾股分割点．（1）已知点M 、N 是线段AB 的勾股分割点，MN AM >，MN BN >，若2AM =，3MN =，则BN =_________；（2）如图，在等腰直角ABC 中，AC BC =，90ACB ∠=︒，M ，、N 为直线AB 上两点，满足45MCN ∠=︒．①如图2，点M 、N 在线段AB 上，求证：点M 、N 是线段AB 的勾股分割点；小林同学在解决第（2）小题时遇到了困难，陈老师对小林说：要证明勾股分割点，则需设法构造直角三角形，你可以把CBN 绕点C 逆时针旋转90°试一试．请根据陈老师的提示完成第（2）小题的证明过程；①如图3，若点M 在线段AB 上，点N 在线段AB 的延长线上，AM =，BN =，求BM 的长．26．如图，在ABC 中，45A ∠=︒．（1）如图1，若AC =2AB =，求ABC 的面积；（2）如图2，D 为ABC 外的一点，连接CD ，BD 且CD CB =，ABD BCD ∠=∠，过点C 作CE AC ⊥交AB 的延长线于点E ，求证：2BD AB +=；（3）如图3，在（2）的条件下，作AP 平分CAE ∠交CE 于点P ，过E 点作EM AP ⊥交AP 的延长线于点M ，点K 为直线AC 上点的一个动点，连接MK ，过M 点作MK MK '⊥，且始终满足MK MK '=，连接AK '，若AC =AK MK ''+取得最小值时()2AK MK ''+的值．27．如图（1），CD 、BE 是①ABC 的两条高，M 为线段BC 的中点．（1）求证：MD ＝ME ．（2）若①ABC ＝70°，①ACB ＝42°，求①DME 的度数．（3）若将锐角①ABC 变为钝角①ABC ，如图（2），①BAC ＝α，请直接写出①DME 的度数．（用含α的式子表示）28．如图，在ABC 中，AB AC =，过点A 作线段AD ，使AB AD =，连接BD ，CD ．（1）如图1，当30ABC ∠=︒时，求BDC ∠度数；（2）如图2，求证：11802BDC BAC ∠+∠=︒；（3）如图3，在（1）的条件下，过点D 作DF BC ⊥，垂足为点F ，并反向延长DF 到点E ，使DA DE =，连接AE 交DC 于点M ，若2BD DM ==，求AE 的长．29．如图，已知ABC 是等腰直角三角形，动点P 在斜边AB 所在的直线上，以PC 为直角边作等腰直角PCQ ，其中①PCQ ＝90°，探究并解决下列问题：（1）如图1，若点P 在线段AB 上时，猜想P A 2，PB 2，PQ 2三者之间的数量关系；（2）如图2，若点P 在AB 的延长线上，在（1）中所猜想的P A 2，PB 2，PQ 2三者之间的数量关系仍然成立，请利用图2进行证明；（3）若动点P 满足PA PB ＝23，求PC AC的值（请利用图3进行探求）． 30．在平面直角坐标系中，O 为原点，点()2,0A ，点()0,2B ，把ABO 绕点B 逆时针旋转，得A BO ''△，点A ，O 旋转后的对应点为A '，O '，记旋转角为α．（1）如图①，当点O '落在边AB 上时，求点O '的坐标；（2）如图①，当60α=︒时，求AA '的长及点A '的坐标．【期末压轴题】专题05：几何证明综合（解析版）学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列六个命题①有理数与数轴上的点一一对应①两条直线被第三条直线所截，内错角相等①平行于同一条直线的两条直线互相平行；①同一平面内，垂直于同一条直线的两条直线互相平行；①直线外一点到这条直线的垂线段叫做点到直线的距离①如果一个角的两边分别平行于另一个角的两边，那么这两个角相等，其中假命题的个数是（）A．2个B．3个C．4个D．5个【标准答案】C【思路点拨】利用实数的性质、平行线的性质及判定、点到直线的距离等知识分别判断后即可确定答案．【精准解析】解：①实数与数轴上的点一一对应，故原命题错误，是假命题，符合题意；①两条平行直线被第三条直线所截，内错角相等，故原命题错误，是假命题，符合题意；①平行于同一条直线的两条直线互相平行，正确，是真命题，不符合题意；①同一平面内，垂直于同一条直线的两条直线互相平行，正确，是真命题，不符合题意；①直线外一点到这条直线的垂线段的长度叫做点到直线的距离，故原命题错误，是假命题，符合题意；①如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补，故原命题错误，是假命题，符合题意，假命题有4个，故选：C．【名师指导】本题主要考查了命题与定理的知识，解题的关键是了解实数的性质、平行线的性质及判定、点到直线的距离的定义等知识，难度不大．2．下列几个命题中，真命题有（）①两条直线被第三条直线所截，内错角相等；①如果1∠=∠；∠和2∠是对顶角，那么12①一个角的余角一定小于这个角的补角；①三角形的一个外角大于它的任一个内角．A．1个B．2个C．3个D．4【标准答案】B【思路点拨】根据平行线的性质对①进行判断；根据对顶角的性质对①进行判断；根据余角与补角的定义对①进行判断；根据三角形外角性质对①进行判断．【精准解析】解：两条平行直线被第三条直线所截，内错角相等，所以①错误；如果①1和①2是对顶角，那么①1=①2，所以①正确；一个角的余角一定小于这个角的补角，所以①正确；三角形的外角大于任何一个与之不相邻的一个内角，所以①错误．故选：B．【名师指导】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．3．下面说法正确的个数有（）（1）不等式两边乘（或除以）同一个数，不等号的方向不变；（2）5-是324x-<-的解；（3）三角形的外角等于与它不相邻的两个内角的和；（4）如果ABC的三个内角满足A C B∠=∠-∠，那么ABC一定是直角三角形；（5）三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外A．1个B．2C．3个D．4个【标准答案】C【思路点拨】利用不等式性质2可判断（1）；利用解不等式求解可判断（2）；利用三角形外角性质可判断（3）；利用三角形内角和与条件组成方程组可判断（4）；利用直角三角形高所在直线交点可判断（5）即可．【精准解析】解（1）不等式两边乘（或除以）同一个正数，不等号的方向不变，故（1）不正确；（2）324x-<-，移项合并得32x<-，系数化1得23x<-，①5-是324x-<-的解正确，故（2）正确；（3）三角形的外角等于与它不相邻的两个内角的和，故（3）正确；（4）如果ABC 的三个内角满足A C B ∠=∠-∠，又①180A B C ∠+∠+∠=︒①180C B B C ∠-∠+∠+∠=︒解得90C ∠=︒①ABC 一定是直角三角形，故（4）正确；（5）三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外直角三角形的高所在的直线交于一点，在三角形边上，故（5）不正确；①说法正确的个数有3个．故选择C ．【名师指导】本题考查不等式的性质，不等式的解法与解，三角形外角性质，直角三角形判定，三角形高所在直线的交点位置，掌握不等式的性质，不等式的解法与解，三角形外角性质，直角三角形判定，三角形高所在直线的交点位置是解题关键．4．下列命题中假命题有（）①两条直线被第三条直线所截，同位角相等①如果两条直线都与第三条直线平行，那么这两条直线也互相平行①点到直线的垂线段叫做点到直线的距离①过一点有且只有一条直线与已知直线平行①若两条直线都与第三条直线垂直，则这两条直线互相平行．A ．5个B ．4个C ．3个D ．2个【标准答案】B【思路点拨】根据平行线的性质和判定，点到直线距离定义一一判断即可．【精准解析】解：①两条直线被第三条直线所截，同位角相等，错误，缺少平行的条件；①如果两条直线都与第三条直线平行，那么这两条直线也互相平行，正确；①点到直线的垂线段叫做点到直线的距离，错误，应该是垂线段的长度；①过一点有且只有一条直线与已知直线平行，错误，应该是过直线外一点；①若两条直线都与第三条直线垂直，则这两条直线互相平行，错误，条件是同一平面内．故选B ．【名师指导】本题主要考查命题与定理，解决本题的关键是要熟练掌握平行线的性质和判定，点到直线距离定义．5．下列命题为真命题的是（）A ．如果0mn =，那么0m =且0n =B ．两边分别相等的两个直角三角形全等C ．三角形的三条角平分线相交于一点，并且这一点到三个顶点的距离相等D ．如果两条直线互相平行，则其中一条直线上任意一点到另一条直线的距离都相等【标准答案】D【思路点拨】分清“或”与“且”的区别，可判断A ，利用全等三角形的判定方法可判断B ，利用角平分线的性质可判断C ，利用平行线间的距离处处相等性质可判断D ．【精准解析】A ．①0mn =，①m =0或n =0，如果0mn =，那么0m =且0n =不是真命题，故选项A 不正确B. ①有两边对应相等的两个直角三角形全等，①两边分别相等的两个直角三角形全等不是真命题，故选项B 不正确；C. ①三角形的三条角平分线相交于以点，这点到三边的距离相等，①三角形的三条角平分线相交于一点，并且这一点到三个顶点的距离相等不是真命题，故选项C 不正确；D. 如果两条直线互相平行，则其中一条直线上任意一点到另一条直线的距离都相等是真命题，故选项D 正确．故选择D ．【名师指导】本题考查真命题，由正确的题设能推出结论正确，是真命题，否则是假命题是解题关键． 6．一副三角板如图摆放，点F 是45°角三角板ABC 的斜边的中点，4AC =．当30°角三角板DEF 的直角顶点绕着点F 旋转时，直角边DF ，EF 分别与AC ，BC 相交于点M ，N ．在旋转过程中有以下结论：①MF NF =；①四边形CMFN 有可能为正方形；①MN 长度的最小值为2；①四边形CMFN 的面积保持不变：①CMN △面积的最大值为2，其中正确的个数是（）A ．2B ．3C ．4D ．5【标准答案】C【思路点拨】利用两直角三角形的特殊角、性质及旋转的性质分别判断每一个结论，找到正确的即可．【精准解析】解：①连接CF ，①F 为AB 中点，AC =BC ，①ACB =90°，①AF =BF =CF ，CF ①AB ，①①AFM +①CFM =90°．①①DFE =90°，①CFM +①CFN =90°，①①AFM =①CFN ．同理，①①A +①MCF =90°，①MCF +①FCN =90°，①①A =①FCN ，在①AMF 与①CNF 中，AFM CFN AF CFA FCN ∠=∠⎧⎪=⎨⎪∠=∠⎩， ①①AMF ①①CNF （ASA ），①MF =NF ．故①正确；①当MF ①AC 时，四边形MFNC 是矩形，此时MA =MF =MC ，根据邻边相等的矩形是正方形可知①正确；①连接MN ，当M 为AC 的中点时，CM =CN ，根据边长为4知CM =CN =2，此时MN最小，最小值为①错误；①当M 、N 分别为AC 、BC 中点时，四边形CDFE 是正方形．①①ADF ①①CEF ，①S ①CEF =S ①AMF①S 四边形CDFE =S ①AFC ．故①正确；①由于①MNF 是等腰直角三角形，因此当MF 最小时，FN 也最小；即当DF ①AC 时，MF 最小，此时FN =12AC =2．①MN =当①CMN 面积最大时，此时①MNF 的面积最小．此时S ①CMN =S 四边形CFMN -S ①FMN =S ①AFC -S ①DEF =4-2=2，故①正确．故选：C ．【名师指导】此题考查的知识点有等腰直角三角形，全等三角形的判定与性质等知识点，综合性强，难度较大，是一道难题．7．如图，在Rt ABC △中，90BAC ∠=︒，AB AC =，D 为BC 边上一点，将ABD △绕点A逆时针旋转90°得到ACE ，点B 、D 的对应点分别为点C 、E ，连接BE ，将AC 平移得到DF（点A 、C 的对应点分别为点D 、F ），连接AF ，若AB =2BD =，则AF 的长为（）A ．B ．6C ．D【标准答案】A【思路点拨】由旋转的性质可得BD ＝CE ＝2，①ACE ＝①ABD ＝45°，由勾股定理可求BE ，由“SAS ”可证①ABE ①①DF A ，可得BE ＝AF ．【精准解析】解：（1）①①BAC ＝90°，AB ＝AC＝①①ABC ＝①ACB ＝45°，BC6，①将①ABD 绕点A 逆时针旋转90°得到①ACE ，①BD ＝CE ＝2，①ACE ＝①ABD ＝45°，AD ＝AE ，①DAE ＝90°，①①BCE ＝90°，①BE①①BAC ＝①DAE ＝90°，①①BAC +①DAE ＝180°，①①BAE +①DAC ＝180°，①AC 平移得到DF ，①AC ＝DF ＝AB ，AC ①DF ，①①ADF +①DAC ＝180°，①①ADF ＝①BAE ，在①ABE 和①DF A 中，AB DF BAE ADF AE AD =⎧⎪∠=∠⎨⎪=⎩，①①ABE ①①DF A （SAS ），①BE ＝AF ＝故选：A【名师指导】本题考查了旋转的性质，勾股定理，全等三角形的判定和性质等知识，灵活运用性质性质解决问题是本题的关键．8．如图，等腰Rt ABC 中，AB ＝AC ，①BAC ＝90°，AD ①BC 于点D ，①ABC 的平分线分别交AC 、AD 于E 、F 两点，M 为EF 的中点，AM 的延长线交BC 于点N ，连接DM ，下列结论：①DF ＝DN ；①DMN 为等腰三角形；①DM 平分①BMN ；①AE ＝23EC ；①AE ＝NC ，其中正确结论有（）A ．2个B ．3个C ．4个D ．5个【标准答案】C【思路点拨】先根据等腰直角三角形的性质得出BD AD =，DBF DAN ∠=∠，BDF ADN ∠=∠，进而证DFB DAN △≌△，即可判断①，再证ABF CAN △≌△，推出CN AF AE ==，即可判断①；根据全等三角形的判定与性质可得M 为AN 的中点，进而可证得12DM AM NM AN ===，由次可判断①，再根据等腰三角形的性质及外角性质可判断①，最后再根据垂直平分线的判定与性质以及直角三角形的勾股定理可判断①．【精准解析】解：90BAC ∠=︒，AC AB =，AD BC ⊥，45ABC C ∴∠=∠=︒，AD BD CD ==，90ADN ADB ∠=∠=︒， 45BAD CAD ∴∠=︒=∠， BE 平分ABC ∠，122.52ABE CBE ABC ∴∠=∠=∠=︒， 9022.567.5BFD AEB ∴∠=∠=︒-︒=︒，67.5AFE BFD AEB ∴∠=∠=∠=︒，AF AE ∴=，又①M 为EF 的中点，①AM BE ⊥，90AMF AME ∴∠=∠=︒，9067.522.5DAN CAN MBN ∴∠=∠=︒-︒=︒=∠，在FBD 和NAD 中，FBD DAN BD ADBDF ADN ∠=∠⎧⎪=⎨⎪∠=∠⎩FBD NAD ∴△≌△（ASA ），DF DN ∴=，故①正确；在AFB △和CNA 中4522.5BAF C AB ACABF CAN ∠=∠=︒⎧⎪=⎨⎪∠=∠=︒⎩AFB CAN ∴△≌△（ASA ），AF CN ∴=，AF AE =，AE CN ∴=，故①正确；在ABM 和NBM 中ABM NBM BM BMAMB NMB ∠=∠⎧⎪=⎨⎪∠=∠⎩ABM NBM ∴△≌△（ASA ），AM NM ∴=，①点M 是AN 的中点，又①90ADN ∠=︒， ①12DM AM NM AN ===，DM NM =， DMN ∴是等腰三角形，故①正确；DM AM =，22.5DAM ADM ∴∠=∠=︒，45DMN DAM ADM ∴∠=∠+∠=︒，9045DMB DMN DMN ∴∠=︒-∠=︒=∠，DM ∴平分BMN ∠，故①正确；如图，连接EN ，①AM NM =，AM BE ⊥，①BE 垂直平分AN ，①EA ＝EN ，22.5ENA EAN ∴∠=∠=︒，45CEN ENA EAN ∴∠=∠+∠=︒，又①45C ∠=︒，①90ENC ∠=︒，且EN CN =，在Rt ENC 中，22222EC EN CN EN =+=， ①EC ，AE ∴，故①错误，即正确的有4个，故选：C ．【名师指导】本题考查了全等三角形的判定与性质，三角形外角性质，三角形内角和定理，直角三角形斜边上中线性质，等腰三角形的判定与性质，垂直平分线的判定与性质以及勾股定理等相关知识的应用，能熟练运用相关图形的判定与性质是解此题的关键，主要考查学生的推理能力．9．如图，凸四边形ABCD 中，90,90,60,3,A C D AD AB ∠=︒∠=︒∠=︒==M 、N 分别为边,CD AD 上的动点，则BMN △的周长最小值为（）A ．B ．C ．6D ．3【标准答案】C【思路点拨】由轴对称知识作出对称点，连接两对称点，由两点之间线段最短证明B B '''最短，多次用勾股定理求出相关线段的长度，平角的定义及角的和差求出角度的大小，最后计算出BMN ∆的周长最小值为6．【精准解析】解：作点B 关于CD 、AD 的对称点分别为点B '和点B ''，连接B B '''交DC 和AD 于点M 和点N ，DB ，连接MB 、NB ；再DC 和AD 上分别取一动点M '和N '（不同于点M 和)N ，连接M B '，MB''，N B '和N B '''，如图1所示：B B M B M N N B ''''''''''<++，B M BM '''=，B N BN ''''=，BM M N BN B B '''''''∴++>，又B B B M MN NB ''''''=++，MB MB '=，NB NB ''=，NB NM BM BM M N BN ''''∴++<++，BMN l NB NM BM ∆∴=++时周长最小；连接DB ，过点B '作B H DB '''⊥于B D ''的延长线于点H ，如图示2所示：在Rt ABD △中，3AD =，AB =∴DB =230∴∠=︒，530∴∠=︒，DB DB ''=，又1260ADC ∠=∠+∠=︒，301∴∠=︒，730∴∠=︒，DB DB '=，1257120B DB '''∴∠=∠+∠+∠+∠=︒，DB DB DB '''===又6180B DB '''∠+∠=︒，660∴∠=︒，HD ∴=3HB '=，在Rt ①B HB '''中，由勾股定理得：6B B '''．6BMN l NB NM BM ∆∴=++=，故选：C ．【名师指导】本题综合考查了轴对称-最短路线问题，勾股定理，平角的定义和两点之间线段最短等相关知识点，解题的关键是掌握轴对称-最短路线问题，难点是构建直角三角形求两点之间的长度．10．如图，Rt ABC 中，90ACB ∠=︒且CA CB =，D 为ABC 外一点，连接AD ，过D 作DE DA ⊥交BC 于点E ，F 为DE 上一点且DF DA =，连接BF ，CD ．将线段CD 绕点C 逆时针旋转90︒到线段CG ，连接DG 分别交BF 、BA 于点M 、N ，连接BG 、CF ．下列结论：①BM FM =；①CG =；①BCG AND ∠>∠；①CF AD +>；①若2BG =，BC =CF =2ADFC S =四边形）A ．2个B ．3个C ．4个D ．5个【标准答案】C【思路点拨】先证明()BCG ACD SAS △≌△，得到对应边相等，对应角相等，依次得出①正确和①错误，由等腰直角三角形的性质和勾股定理，得出①正确，由三角形的三边关系，可以得出①正确，利用勾股定理逆定理和三角形面积公式即可判定①正确．【精准解析】解:①90ACB ∠=︒，90GCD ∠=︒，①75=∠∠，又①CA CB =且CD CG =，①()BCG ACD SAS △≌△，①BG AD =，2CAD ∠=∠，①=BG AD DF =①=90ADE ∠︒，①=360180CAD CED ACB ADE +∠︒--=︒∠∠∠，①=1CAD ∠∠，①1=2∠∠，①3=1+4=2+4=GBM ∠∠∠∠∠∠，又①=DMF GMB ∠∠，=BG DF ，①()DMF GMB AAS △≌△，①GM DM =，BM FM =，故①正确；①222CD CG DG +=，①()2222CG DM =，CD =①CG ，故①正确；CF AD CF DF CD +=+>，即CF AD +>，故①正确； ①==45CAN CDN ︒∠∠，86NDC =+∠∠∠，85NAC =+∠∠∠，①5=6∠∠，①7=6∠∠，故①错误；如图，连接AF ，若2BG =，BC =CF =①==2BG AD DF =，①2228AF AD DF =+=，即AF①2222AF CF BC AC +==，①AF CF ⊥，①11S =+S 2222ADF AFC ADFC S =⨯⨯+△△四边形①正确；故选：C ．．【名师指导】本题综合考查了全等三角形的判定与性质、勾股定理及其逆定理、等腰直角三角形等内容，解决本题的关键是能正确分析图形中的相等关系，能在相等的边和角中进行转化，能构造直角三角形进行求解等．11．如图，在ABC中，点E在边AC上，EB＝EA，①A＝2①CBE，延长BD到F，使DF ＝DB，连接CF，过点C作CD①BF于点D，BD＝16，AC＝22，则边BC的长为（）A．B．C．D．【标准答案】A【思路点拨】过点C作CH AB∥交BF于点H，由此可得①A＝①ECH，①EBA＝①EHC，再根据EB＝EA可得①A＝①EBA，进而可得AC＝BH＝22，结合DF＝DB＝16可得BF＝32，DH＝6，FH＝10，再利用垂直平分线的性质可得BC＝CF，进而可得①F＝①CBE，再结合①A＝2①CBE，①EHC＝①HCF＋①F可得CH＝FH＝10，最后利用勾股定理计算即可求得答案．【精准解析】解：如图，过点C作CH AB∥交BF于点H，①CH AB∥，①①A＝①ECH，①EBA＝①EHC，①EB＝EA，①①A＝①EBA，①①ECH＝①EHC，①EC＝EH，①EC＋EA＝EH＋EB，即AC＝BH＝22，又①DF＝DB＝16，①BF＝BD＋DF＝32，DH＝BH－BD＝6，①FH＝BF－BH＝32－22＝10，①CD①BF，DF＝DB，①BC＝CF，①①F＝①CBE，又①①A＝2①CBE，①①EHC＝①ECH＝2①F，又①①EHC＝①HCF＋①F，①①HCF＋①F＝2①F，①①HCF＝①F，①CH＝FH＝10，①在Rt DCH中，CD，8①在Rt BCD中，BC故选：A．【名师指导】本题考查了平行线的性质，等腰三角形的判定，三角形的外角性质，垂直平分线的性质以及勾股定理的应用，根据题意作出正确的辅助线并能熟练运用相关图形的性质是解决本题的关键．12．如图，把含30°的直角三角板ABC 绕点B 顺时针旋转至如图EBD ，使BC 在BE 上延长AC 交DE 于F ，若AF =4，则AB 的长为（）A ．2B ．C ．D ．3【标准答案】C【思路点拨】连接AE ，可证明①ABE 为等边三角形AE =AB ，①AEF 为直角三角形，再结合含30°角的直角三角形的性质和勾股定理可求得AE ，从而得出AB ．【精准解析】解：连接AE ，由题意可知，在Rt ①ABC 中，①①BAC =30°，①ACB =90°，①①ABC =60°，根据旋转的性质可知,30BE AB BED BAC =∠=∠=︒，①①ABE 为等边三角形，①AE =AB ，①AEB =60°，①EAF =30°，①①AEF =90°，①122EF AF ==,AB AE == 故选：C ．【名师指导】本题考查勾股定理，旋转的性质，含30°角的直角三角形，等边三角形的性质和判定．能正确作出辅助线构筑等边三角形是解题关键．二、填空题13．如图，在平面直角坐标系中，点()6,0A ，点()0,P m ，将线段PA 绕着点P 逆时针旋转90°，得到线段PB ，连接AB ，OB ，则BO BA +的最小值为__________．【标准答案】【思路点拨】过点B 作BC ①y 轴于点C ，作O 关于直线BC 的对称点D ，连接AD ，BD ，由题意易得①BCP ①①POA ，则有PC =OA =6，BC =OP =m ，则有CO =6+m ，DO =12+2m ，由三角不等关系可知AB BD AD +≥，进而问题可求解．【精准解析】解：过点B 作BC ①y 轴于点C ，作O 关于直线BC 的对称点D ，连接AD ，BD ，如图所示：①PA PB ⊥，①90BPC APO ∠+∠=︒，①90PAO APO ∠+∠=︒，①BPC PAO ∠=∠，①90,BCP POA BP PA ∠=∠=︒=，①①BCP ①①POA ，①点()6,0A ，点()0,P m ，①PC =OA =6，BC =OP =m ，①CO =6+m ，由轴对称可知：,OC CD BD OB ==，①DO =12+2m ，由三角不等关系可知AB BD AD +≥，即AB OB AD +≥，①AB +OB 的最小值即为AD 的长，①AD =①当m =0时，AD 最短，为AD故答案为【名师指导】本题主要考查图形与坐标、勾股定理、轴对称的性质及全等三角形的判定与性质，熟练掌握图形与坐标、勾股定理、轴对称的性质及全等三角形的判定与性质是解题的关键． 14．如图，在ABC 中，CA BC =，8AB =，5AC =，点D 是AB 边上的一个动点，点E 与点A 关于直线CD 对称，连接CE ，DE ，AE ，当ADE 是直角三角形时，求AD 的长为_____________．【标准答案】1或7.【思路点拨】根据题意分两种情况：①当点D 在AF 上时；①当点D 在BF 上时；进行讨论即可求解．【精准解析】解：作CF ①AB 于F ，①在①ABC 中，CA BC =，8AB =，5AC =，①AF =4，①3CF =，①如图1，当点D 在AF 上时，①①ADE =90°，①①ADC =①EDC =（360°-90°）÷2=135°．①①CDF =45°．①CF =DF ．①AD =AF -DF =AF -CF =4-3=1．①如图2，当点D 在BF 上时，①①ADE =90°，①①CDF =45°．①CF =DF ．①AD =AF +DF =AF +CF =4+3=7．故答案为：1或7.【名师指导】本题主要考查勾股定理，等腰三角形的性质以及轴对称的性质，解本题的关键是注意运用数形结合的思想解决问题．15．如图，已知30B ∠=，45C ∠=，150BDC ∠=，且5BD CD ==，则AB =_________【标准答案】【思路点拨】延长CD交AB于E，根据题意可求得①BDE=①B =30°，再根据等腰三角形的判定和三角形外角性质求得BE=DE，①AED=2①B=60°，过E作EF①BD于F，过A作AP①CE于P，利用等腰三角形的性质和含30°角在直角三角形的性质可得BF= 12BD，BE=2EF，AE=2EP，AP= ，根据勾股定理和等腰直角三角形判定分别求出BE、DE、EP，进而求得AE即可解答．求解即可．【精准解析】解：延长CD交AB于E，①①BDC=150°，①B=30°，①①BDE=①B =30°，①BE=DE，①AED=2①B=60°，过E作EF①BD于F，过A作AP①CE于P，则BF= 12BD=52，在Rt①BEF中，①B=30°，①BE=2EF，由勾股定理得：BF2+EF2=BE2，解得：BE= ，即DE，在Rt①APE中，①AED=60°，则①EAP=30°，①AE=2EP，①AP= ，①AP①CE，①C=45°，①①CAP=45°，①CP=AP，①EP+CP=DE+CD，CD=5，①EP+5，解得：EP，①AE=2EP①AB=BE+AE=故答案为：【名师指导】本题考查等腰三角形的判定与性质、含30°角的直角三角形的性质、勾股定理、三角形的外角性质、解一元一次方程等性质，理解题意，添加适当的辅助线，掌握相关知识间的联系与运用是解答的关键．16．如图，在矩形ABCD 中，点E 在线段AD 上，连接BE 、CE ，点F 在线段BE 上，连接CF ，若①EBC ＝2①ECD ，DE ＝2，BF ＝9，tan①EFC ＝43，则线段CE 的长为______．【标准答案】【思路点拨】过点C 作CH BE ⊥于H ，证明()ABE HCB AAS ≅，得到AB CH CD ==，继而证明t R CDE ≅t ()R CHE HL ，结合已知tan①EFC ＝43，设4,3AB CH CD x FH x ====，在Rt ABE △中，根据勾股定理得222BE AB AE =+，结合因式法解一元二次方程得到2x =，从而解得8CD =，最后在Rt CDE △中，有应用勾股定理解题即可．【精准解析】解：过点C 作CH BE ⊥于H ，设①ECD =,2EBC αα∠=。

专题07几何证明解答题之压轴题训练(1)(原卷版)-2021-2022学年第一学期八年级压轴题训练

专题07 几何证明解答题之压轴题训练（1）1.（徐汇龙华2019期中27）在△ABC 中，D 为AB 的中点，F 为BC 上一点，DF ∥AC ，延长FD 至E ，且DE=DF,联结AE 、AF.（1）求证：∠E=∠C;（2）如果DF 平分∠AFB ，求证：AC ⊥AB.2.（2019曹杨中学10月27）如图，在直角△ABC 中，∠BAC=90°，AB=AC ，点D 为射线BC 上一动点，联结AD ，以AD 为一边且在AD 的右侧作Rt △ADE ，且AD=AE. 解答下列问题：（1）当点D 在线段BC 上时（与点B 不重合），如图a ，联结线段CE ，那么CE 、BD 之间的位置关系为，数量关系为；（2）当点D 在线段BC 的延长线上时，如图b ，（1）中的结论是否仍然成立，并说明理由；（3）如果点D 在线段BC 上运动，如图c ，联结AD ，以AD 为一边且在AD 的右侧作∠EAD=45°，交边BC 于点E ，请问线段BD 、DE 、EC 所围成的三角形的形状，并说明理由.3.（2019复附10月27）已知△ABC 中，记∠BAC=α，∠ACB=β.FEDCBA图c图b图aAB CDE ABEEBA（1）如图a ，若AP 平分∠BAC ，BP 、CP 分别是△ABC 的外角∠CBM 和∠BCN 的平分线，BD ⊥AP ，用含α的代数式表示∠BPC 的度数，用含β的代数式表示∠PBD 的度数，并说明理由.（2）如图b ，若点P 为△ABC 的三条内角平分线的交点，BD ⊥AP 于点D ，猜想（1）中的两个结论是否发生变化，补全图形并直接写出你的结论.∠BPC= ；∠PBD= .4. (2019浦东一署10月29) 已知:如图，点A 、B 、C 在同一直线上，AB=2，BC=1，分别以AB 、BC 为边，在AC 同侧作等边△ABD 和等边△BCE ，分别联结AE 、CD. （1）找出图中的全等三角形（不添加辅助线），并证明你的结论；（2）线段AE 与线段CD 的关系是：AE CD （填＞、＝、＜）；AE 与CD 的夹角是：；（3）△ABD 固定不动，使△BCE 绕着点B 旋转， ①这时（2）得出的结论还成立吗（不要求证明）？②在旋转过程中，线段DC 的长是变化的，它的变化范围是 ; ③在下面的备用图中，画出在△BCE 旋转过程中，BC 与AB 垂直时的图形.5.（2019位育10月25）已知△ABC 和△ADE 都是等腰直角三角形，其中∠ABC=∠ADE=90°，连接BD 、EC ，点M 为EC 的中点，连接BM 、DM.（1）如图1，当点D 、E 分别在AC 、AB 上时，求证：△BMD 为等腰直角三角形；ABCPNMPDCBA图a图b备用图备用图DDABAB B ACDE（2）如图2，将图1中的△ADE 绕点A 逆时针旋转45°，使点D 落在AB 上，此时（1）中的结论“△BMD 为等腰直角三角形”还成立吗？请对你的结论加以证明；（3）如图3，将图2中的△ADE 绕点A 逆时针旋转90°时，△BMD 为等腰直角三角形的结论是否仍成立？若成立，请证明；若不成立，请说明理由.6.（2019上宝25）如图，在长方形 ABCD 中，AB=3，AD=，点 P 为对角线 B D 上异于 B 、D 的一个动点，联结 A P ，将△ABP 沿 A P 所在直线翻折，使得点 B 落在 E 处；（1）当∠DPA=45°时，求点 E 到直线 A B 的距离；（2）联结 A E,交线段 B D 于点 F ，当△EFP 为直角三角形时，求线段 B P 的长度；（3）当∠DPE=30°时，请直接．．写出△ABP 的面积.7.（青浦实验2019期中25）如图点O 是等边ABC 内一点，110,AOB BOC α︒∠=∠=，∠ACD=∠BCO ，OC=CD ，（1）试说明：COD 是等边三角形；（2）当150α︒=时，试判断AOD △的形状，并说明理由；（3）当BOC ∠为多少度时，AOD △是等腰三角形图3图2图1ABCDEMABCDEMME DCB A备用图AB CDDCBA8.（徐教院附2019期中29）已知在△ABC 中，AB ＝AC 在射线AC 上取一点D ，以D 为顶点、DB 为一条边作∠BDF ＝∠A ，点E 在AC 的延长线上，∠ECF ＝∠ACB (1)如图(1)，当点D 在边AC 上时，求证:①∠FDC ＝∠ABD; ②DB ＝DF ；(2)如图(2)，当点D 在AC 的延长线上时，请判断DB 与DF 是否相等，并说明理由.9.（川中南2019期中26）在△ABC 中，∠ACB=90°，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于点D ，BE ⊥MN 于点E.（1）当直线MN 绕点C 旋转到图1所示位置时，求证：DE=ADBE ；（2）当直线MN 绕点C 旋转到图２、图３所示位置时，补全图形，并探索线段DE 、AD 、BE 之间的数量关系（直接写出答案）．110°αODBAABC D EFFEDCBA图(1)图(2)10.（浦东南联合2019期中26）已知：点O 是△ABC 内一点，射线AO 、BO 交BC 、AC 于点D 、E .（1）若射线AO 、BO 分别平分∠B AC 、∠ABC ;①如图（1），设∠ACB =x °．试用含x 的代数式表示∠AOB 的大小;②如图（2），若AC =BC , ∠ACB =36°，射线BE 与射线AM 交于点M ，且∠BAC =∠OAM =∠AOM ．求证：AM =CM ;（2）联结CO ，若AO =BO =CO ,且△AOB 中有一个内角是50°，请直接写出∠ACB 的度数．11.（浦东四署2019期中26）在等腰△OAB 和等腰△OCD 中，OA=OB ，OC=OD ，连接AC 、BD 交于点M.（1）如图1，若∠AOB=∠COD=40°.①AC 与BD 的数量关系为； ②∠AMB 的度数为；（2）如图2，若∠AOB=∠COD=90°.①判断AC 与BD 之间存在怎样的数量关系？并说明理由； ②求∠AMB 的度数.图1图2图3ABCMNAB CM NE NMDC BA12.（浦东四署2020期末26）阅读下面的材料，然后解答问题：我们新定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形. （1）理解并填空：①根据奇异三角形的定义，请你判断：等边三角形一定是奇异三角形吗？（填“是”或“不是”）②若某三角形的三边长分别为1、2，则该三角形（填“是”或“不是”）奇异三角形.（2）探究：在Rt ABC ∆，两边长分别是a 、c ，且2250,100a c ==，则这个三角形是否是奇异三角形？请说明理由.13.（川中南2020期末25）（1）问题发现如图1，△ACB 和△DCE 均为等边三角形，点A ，D ，E 在同一直线上，连接BE ．填空：①∠AEB 的度数为；②线段AD ，BE 之间的数量关系为 ; （2）拓展探究如图2，△ACB 和△DCE 均为等腰直角三角形，∠ACB ＝∠DCE ＝90°，点A ，D ，E 在同一直线上，CM 为△DCE 中DE 边上的高，连接BE ，请判断∠AEB 的度数及线段CM ，AE ，BE 之间的数量关系，并说明理由．图1图2ABCDOMMOD CB A14.（西南模2019期中28）如图，等边ABE ∆，点D 为射线AE 上一点，延长BE 至点C ，使得EC=AD ，联结CD 并延长交射线AB 于点F.（1）当点D 在边AE 上时，如图1，若ED=AD ，则_____CFA DBC ︒∠-∠=；（2）当点D 在边AE 上时，如图2，若ED AD ≠，则（1）的结论还成立吗？若成立，请证明；若不成立，写出CFA ∠与DBC ∠的数量关系并证明；（3）当点D 在边AE 的延长线上时，则（1）的结论还成立吗？若成立，请证明；若不成立，写出CFA ∠与DBC ∠的数量关系并证明.15.（建平实验2019期中28）已知Rt △ABC 中，AC=BC ，∠C=90°，D 为AB 边中点，∠EDF 绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F. （1）当点E 在AC 边上时（如图1），求证CE=BF ；（2）在（1）的条件下，求证：△ABC △CEF △DEF 21S S S =+；（3）当∠EDF 绕D 点旋转到图3的位置即点E 、F 分别在AC 、CB 边的延长线上时，上述（2）结论是否成立？若成立，请给予证明；若不成立，△ABC △CEF △DEF S S S 、、又有怎样的数量关系？请写出你的猜想，不需证明.图1图2M EDCBAABCDE ABCDEF FEDC BA图1图2。

初二数学压轴几何证明题(含答案)

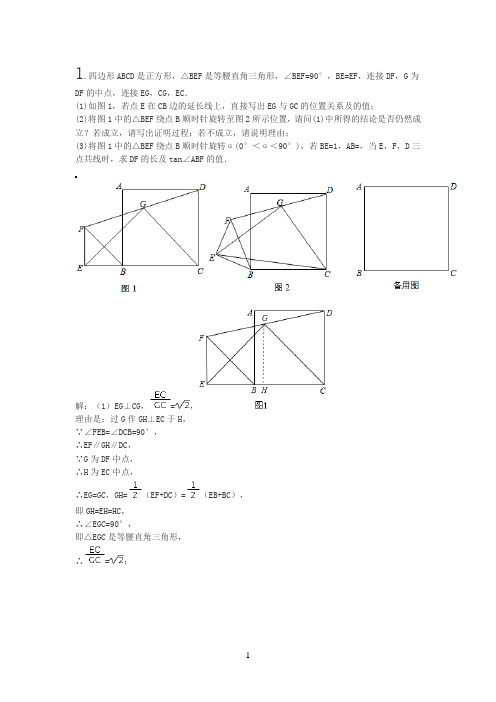
1.四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF，连接DF，G为DF的中点，连接EG，CG，EC．(1)如图1，若点E在CB边的延长线上，直接写出EG与GC的位置关系及的值；(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置，请问(1)中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；(3)将图1中的△BEF绕点B顺时针旋转α(0°＜α＜90°)，若BE=1，AB=，当E，F，D三点共线时，求DF的长及tan∠ABF的值．解：（1）EG⊥CG，=，理由是：过G作GH⊥EC于H，∵∠FEB=∠DCB=90°，∴EF∥GH∥DC，∵G为DF中点，∴H为EC中点，∴EG=GC，GH=（EF+DC）=（EB+BC），即GH=EH=HC，∴∠EGC=90°，即△EGC是等腰直角三角形，∴=；（2）解：结论还成立，理由是：如图2，延长EG到H，使EG=GH，连接CH、EC，过E作BC的垂线EM，延长CD，∵在△EFG和△HDG中∴△EFG≌△HDG（SAS），∴DH=EF=BE，∠FEG=∠DHG，∴EF∥DH，∴∠1=∠2=90°-∠3=∠4，∴∠EBC=180°-∠4=180°-∠1=∠HDC，在△EBC和△HDC中∴△EBC≌△HDC．∴CE=CH，∠BCE=∠DCH，∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°，∴△ECH是等腰直角三角形，∵G为EH的中点，∴EG⊥GC，=，即（1）中的结论仍然成立；（3）解：连接BD，∵AB=，正方形ABCD，∴BD=2，∴cos∠DBE==，∴∠DBE=60°，∴∠ABE=∠DBE-∠ABD=15°，∴∠ABF=45°-15°=30°，∴tan∠ABF=，∴DE=BE=，∴DF=DE-EF=-1．解析：（1）过G作GH⊥EC于H，推出EF∥GH∥DC，求出H为EC中点，根据梯形的中位线求出EG=GC，GH=（EF+DC）=（EB+BC），推出GH=EH=BC，根据直角三角形的判定推出△EGC是等腰直角三角形即可；（2）延长EG到H，使EG=GH，连接CH、EC，过E作BC的垂线EM，延长CD，证△EFG≌△HDG，推出DH=EF=BE，∠FEG=∠DHG，求出∠EBC=∠HDC，证出△EBC≌△HDC，推出CE=CH，∠BCE=∠DCH，求出△ECH是等腰直角三角形，即可得出答案；（3）连接BD，求出cos∠DBE==，推出∠DBE=60°，求出∠ABF=30°，解直角三角形求出即可．2.已知正方形ABCD和等腰直角三角形BEF，BE=EF，∠BEF=90°，按图1放置，使点E在BC 上，取DF的中点G，连接EG，CG．(1)延长EG交DC于H，试说明：DH=BE．(2)将图1中△BEF绕B点逆时针旋转45°，连接DF，取DF中点G(如图2)，莎莎同学发现：EG=CG且EG⊥CG．在设法证明时他发现：若连接BD，则D，E，B三点共线．你能写出结论“EG=CG且EG⊥CG”的完整理由吗？请写出来．(3)将图1中△BEF绕B点转动任意角度α(0＜α＜90°)，再连接DF，取DF的中点G(如图3)，第2问中的结论是否成立？若成立，试说明你的结论；若不成立，也请说明理由．（1）证明：∵∠BEF=90°，∴EF∥DH，∴∠EFG=∠GDH，而∠EGF=∠DGH，GF=GD，∴△GEF≌△GHD，∴EF=DH，而BE=EF，∴DH=BE；（2）连接DB，如图，∵△BEF为等腰直角三角形，∴∠EBF=45°，而四边形ABCD为正方形，∴∠DBC=45°，∴D，E，B三点共线．而∠BEF=90°，∴△FED为直角三角形，而G为DF的中点，∴EG=GD=GC，∴∠EGC=2∠EDC=90°，∴EG=CG且EG⊥CG；（3）第2问中的结论成立．理由如下：连接AC、BD相交于点O，取BF的中点M，连接OG、EM、MG，如图，∵G为DF的中点，O为BD的中点，M为BF的中点，∴OG∥BF，GM∥OB，∴四边形OGMB为平行四边形，∴OG=BM，GM=OB，而EM=BM，OC=OB，∴EM=OG，MG=OC，∵∠DOG=∠GMF，而∠DOC=∠EMF=90°，∴∠EMG=∠GOC，∴△MEG≌△OGC，∴EG=CG，∠EGM=∠OCG，又∵∠MGF=∠BDF，∠FGC=∠GDC+∠GCD，∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°，∴EG=CG且EG⊥CG．解析：（1）由∠BEF=90°，得到EF∥DH，而GF=GD，易证得△GEF≌△GHD，得EF=DH，而BE=EF，即可得到结论．（2）连接DB，如图2，由△BEF为等腰直角三角形，得∠EBF=45°，而四边形ABCD为正方形，得∠DBC=45°，得到D，E，B三点共线，而G为DF的中点，根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC，于是∠EGC=2∠EDC=90°，即得到结论．（3）连接AC、BD相交于点O，取BF的中点M，连接OG、EM、MG，由G为DF的中点，O为BD的中点，M为BF的中点，根据三角形中位线的性质得OG∥BF，GM∥OB，得到OG=BM，GM=OB，而EM=BM，OC=OB，得到EM=OG，MG=OC，又∠DOG=∠GMF，而∠DOC=∠EMF=90°，得∠EMG=∠GOC，则△MEG≌△OGC，得到EG=CG，∠EGM=∠OCG，而∠MGF=∠BDF，∠FGC=∠GDC+∠GCD，所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°．3.已知正方形ABCD和等腰Rt△BEF，BE=EF，∠BEF=90°，按图①放置，使点F在BC上，取DF的中点G，连接EG、CG．(1)探索EG、CG的数量关系和位置关系并证明；(2)将图①中△BEF绕B点顺时针旋转45°，再连接DF，取DF中点G(如图②)，问(1)中的结论是否仍然成立．证明你的结论；(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间)，再连接DF，取DF的中点G(如图③)，问(1)中的结论是否仍然成立，证明你的结论．解：（1）EG=CG且EG⊥CG．证明如下：如图①，连接BD．∵正方形ABCD和等腰Rt△BEF，∴∠EBF=∠DBC=45°．∴B、E、D三点共线．∵∠DEF=90°，G为DF的中点，∠DCB=90°，∴EG=DG=GF=CG．∴∠EGF=2∠EDG，∠CGF=2∠CDG．∴∠EGF+∠CGF=2∠EDC=90°，即∠EGC=90°，∴EG⊥CG．（2）仍然成立，证明如下：如图②，延长EG交CD于点H．∵BE⊥EF，∴EF∥CD，∴∠1=∠2．又∵∠3=∠4，FG=DG，∴△FEG≌△DHG，∴EF=DH，EG=GH．∵△BEF为等腰直角三角形，∴BE=EF，∴BE=DH．∵CD=BC，∴CE=CH．∴△ECH为等腰直角三角形．又∵EG=GH，∴EG=CG且EG⊥CG．（3）仍然成立．证明如下：如图③，延长CG至H，使GH=CG，连接HF交BC于M，连接EH、EC．∵GF=GD，∠HGF=∠CGD，HG=CG，∴△HFG≌△CDG，∴HF=CD，∠GHF=∠GCD，∴HF∥CD．∵正方形ABCD，∴HF=BC，HF⊥BC．∵△BEF是等腰直角三角形，∴BE=EF，∠EBC=∠HFE，∴△BEC≌△FEH，∴HE=EC，∠BEC=∠FEH，∴∠BEF=∠HEC=90°，∴△ECH为等腰直角三角形．又∵CG=GH，∴EG=CG且EG⊥CG．解析：（1）首先证明B、E、D三点共线，根据直角三角形斜边上的中线等于斜边的一半，即可证明EG=DG=GF=CG，得到∠EGF=2∠EDG，∠CGF=2∠CDG，从而证得∠EGC=90°；（2）首先证明△FEG≌△DHG，然后证明△ECH为等腰直角三角形．可以证得：EG=CG且EG ⊥CG．（3）首先证明：△BEC ≌△FEH ，即可证得：△ECH 为等腰直角三角形，从而得到：EG=CG 且EG ⊥CG ．已知，正方形ABCD 中，△BEF 为等腰直角三角形，且BF 为底，取DF 的中点G ，连接EG 、CG ．（1）如图1，若△BEF 的底边BF 在BC 上，猜想EG 和CG 的数量关系为______；（2）如图2，若△BEF 的直角边BE 在BC 上，则（1）中的结论是否还成立？请说明理由；（3）如图3，若△BEF 的直角边BE 在∠DBC 内，则（1）中的结论是否还成立？说明理由．解：（1）GC=EG ，（1分）理由如下：∵△BEF 为等腰直角三角形， ∴∠DEF=90°，又G 为斜边DF 的中点， ∴EG=DF ， ∵ABCD 为正方形， ∴∠BCD=90°，又G 为斜边DF 的中点，∴CG= DF ， ∴GC=EG ；（2）成立．如图，延长EG 交CD 于M ，∵∠BEF=∠FEC=∠BCD=90°，∴EF ∥CD ，∴∠EFG=∠MDG ，又∠EGF=∠DGM ，DG=FG ，∴△GEF ≌△GMD ，∴EG=MG ，即G 为EM 的中点．∴CG 为直角△ECM 的斜边上的中线，∴CG=GE= EM ；（3）成立．取BF 的中点H ，连接EH ，GH ，取BD 的中点O ，连接OG ，OC ．∵CB=CD ，∠DCB=90°，∴CO= BD1 2 1 21212．∵DG=GF，∴GH∥BD，且GH= BD，OG∥BF，且OG= BF，∴CO=GH．为等腰直角三角形．∵△BEF∴EH= BF∴EH=OG．∵四边形OBHG为平行四边形，∴∠BOG=∠BHG．∵∠BOC=∠BHE=90°．∴∠GOC=∠EHG．∴△GOC≌△EHG．∴EG=GC．此题考查了正方形的性质，以及全等三角形的判定与性质．要求学生掌握直角三角形斜边上的中线等于斜边的一半，以及三角形的中位线与第三边平行且等于第三边的一半．掌握这些性质，熟练运用全等知识是解本题的关键．解析：（1）EG=CG，理由为：根据三角形BEF为等腰直角三角形，得到∠DEF为直角，又G为DF中点，根据在直角三角形中，斜边上的中线等于斜边的一半，得到EG为DF的一半，同理在直角三角形DCF中，得到CG也等于DF的一半，利用等量代换得证；（2）成立．理由为：延长EG交CD于M，如图所示，根据“ASA”得到三角形EFG与三角形GDM 全等，由全等三角形的对应边相等得到EG与MG相等，即G为EM中点，根据直角三角形斜边上的中线等于斜边的一半得到EG与CG相等都等于斜边EM的一半，得证；（3）成立．理由为：取BF的中点H，连接EH，GH，取BD的中点O，连接OG，OC，如图所示，1212因为直角三角形DCB中，O为斜边BD的中点，根据斜边上的中线等于斜边的一半得到OC等于BD 的一半，由HG为三角形DBF的中位线，根据三角形的中位线平行于第三边且等于第三边的一半，得到GH等于BD一半，OG等于BF的一半，又根据直角三角形斜边上的中线等于斜边的一半得到EH等于BF的一半，根据等量代换得到OG与EH相等，再根据OBHG为平行四边形，根据平行四边形的性质得到对边相等，对角相等，进而得到∠GOC与∠EHG相等，利用“SAS”得到△GOC与△EHG全等，利用全等三角形的对应边相等即可得证．。

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题1、如图，AB＞AC，∠BAC的平分线与BC边的中垂线GD相交于点D，过点D作DE⊥AB于点E，DF⊥AC于点F，求证：BE=CF．2、如图，△ABC中，∠ACB=90°，AC=BC，将△ABC绕点C逆时针旋转角α．（0°＜α＜90°）得到△A1B1C1，连接BB1．设CB1交AB于D，A1B1分别交AB、AC于E、F．（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以说明（△ABC与△A1B1C1全等除外）；（2）当△BB1D是等腰三角形时，求α．3、如图，在△ABC中，∠BAC=120°，AD，BE分别为△ABC的角平分线，连结DE．（1）求证：点E到DA，DC的距离相等；（2）求∠DEB的度数．4、在△ABC中，∠ACB=90°，AC=BC，直线，MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．（1）当直线MN绕点C旋转到如图1的位置时，求证：DE=AD+BE；（2）当直线MN绕点C旋转到如图2的位置时，求证：DE=AD﹣BE；（3）当直线MN绕点C旋转到如图3的位置时，线段DE、AD、BE之间又有什么样的数量关系？请你直接写出这个数量关系，不要证明．5、概念学习：规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．理解概念（1）如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB，请写出图中两对“等角三角形”．概念应用（2）如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．求证：CD为△ABC的等角分割线．（3）在△ABC中，∠A＝42°，CD是△ABC的等角分割线，直接写出∠ACB的度数．6、如图,∠ABC=∠BAD=90°，点E，F分别是AC，BC的中点。

特训07 几何证明解答压轴题 2024-2025学年上海八年级数学上期末复习(原卷版)

特训07几何证明压轴题（上海精选，八大题型，含四大热点+二大新方向）目录：题型1：传统解答证明题题型2：热点1-几何中的分类讨论题型3：热点2-动态几何-翻折问题题型4：热点3-动态几何-旋转问题题型5：热点4-新定义题题型6：热点5-几何证明与列函数解析式题型7：新方向-数学活动题题型8：新方向延伸-情景探究题题型1：传统解答证明题1．（22-23八年级上·上海长宁·期末）在Rt ABC △中，已知90BAC ∠=︒，AB AC >，点D 在射线BC 上，连接AD ，2ADB B ∠=∠．(1)如图1，若AD 的垂直平分线经过点B ，求C ∠的度数；(2)如图2，当点D 在边BC 上时，求证：2BC AD =；(3)若2AC =，5BD CD =，请直接写出CD 的长．2．（23-24八年级上·上海徐汇·阶段练习）在ABC V 中，CAB ∠和CBA ∠的平分线AD BE 、交于点P ，连接CP ．(1)求证：CP 平分ACB ∠；(2)当ABC V 为等边三角形时，求证：EP PD =；(3)当ABC V 不是等边三角形，且60ACB ∠=︒时，（2）中的结论是否还成立？若成立，请加以证明，若不成立，说明理由．3．（24-25八年级上·上海闵行·期中）在ABC V 中，90ACB ∠=︒，AC BC =，点D 为边BC 上一点，连结AD ，过点C 作CE AD ⊥于点F ，交AB 于点E ，点G 是线段AD 上一点．(1)如图1，连结CG ，如果ACG B ∠=∠，求证：AG CE =；(2)如图2，连结BG 交CE 于点P ，如果点P 恰为BG 的中点，求证：2AG FP =；(3)已知等腰直角三角形的腰长和底边长之比为1）的基础上，连结DE 、EG ，当1CD DE ==时，求四边形CDEG 的面积题型2：热点1-几何中的分类讨论4．（23-24八年级上·上海长宁·期末）已知在Rt ABC 中，90ABC ∠=︒，点P 在边AC 上，连接BP ．(1)如图1，如果点P 在线段的垂直平分线上，求证：AP PC =；(2)过点P 作PD BP ⊥，交边BC 于点D ，①如图2，如果点P 是线段AC 的中点，且2BD CD =，求C ∠的度数；，且线上一点，以AD 为腰作等腰直角DAF △，使90DAF ∠=︒，连接CF ．(1)请判断CF 与BC 的位置关系，并说明理由；(2)若8BC =，4CD BC =，求线段AD 的长；(3)如图2，在（2）的条件下，将DAF △沿线段DF 翻折，使点A 与点E 重合，连接CE ，求线段CE 的长．题型4：热点3-动态几何-旋转问题6．（21-22八年级上·上海·期末）已知△ABC 和△ADE 都是等腰直角三角形，其中∠ABC =∠ADE =90°，连接BD 、EC ，点M 为EC 的中点，连接BM 、DM ．(1)如图1，当点D 、E 分别在AC 、AB 上时，求证：△BMD 为等腰直角三角形；(2)如图2，将图1中的△ADE 绕点A 逆时针旋转45°，使点D 落在AB 上，此时（1）中的结论“△BMD 为等腰直角三角形”还成立吗？请对你的结论加以证明；(3)如图3，将图2中的△ADE 绕点A 逆时针旋转90°时，△BMD 为等腰直角三角形的结论是否仍成立？若成立，请证明；若不成立，请说明理由．题型5：热点4-新定义题7．（23-24八年级下·上海金山·期末）（1）性质证明：已知：如图1，BP CP 、分别是ABC V 的外角平分线，求证：AP 平分BAC ∠；根据上述证明可以得到这样一条性质：三角形一个内角的平分线和其他两个内角的外角平分线交于一点，我们把这个交点叫做这个三角形的旁心．图1中点P 就是ABC V 的一个旁心．（2）性质应用：①如图2，已知点O 是ABC V 的一个旁心，求证：1902O ABC ∠=︒-∠；②已知点1O 、2O 、3O 是ABC V 的三个旁心，2AB =，在123O O O 中，130O ∠=︒，1213O O O O =，且23O O 经过点B ，求123O O O 的面积．题型6：热点5-几何证明与列函数解析式8．（23-24八年级上·上海虹口·期末）如图，ABC V 中，90,60,6ACB B BC ∠=︒∠=︒=，点D 、E 分别是边AB BC、上的一个动点，且BD BE =,过点D 作DG AB ⊥交射线BC 于点G ，交线段AC 于点F ，设BD x =．(1)如图1，当点G 与点C 重合时，求DCE △的面积；(2)如图2，设当点G 在BC 的延长线上时，FC y =，并写出定义域；(3)若DEF 为直角三角形，求x 的值．9．（23-24八年级上·上海浦东新·期末）如图，在Rt ABC △中，90BAC ∠=︒，6AB =，60C ∠=︒，AD 是BC 边上的中线，动点P 从点AAD 向终点D 运动，动点M 从点D 出发以每秒DB 上运动，点M 与点P 同时出发，设动点运动时间为x．(1)求AD 的长；(2)若动点M 在线段DB 上运动，设PMB ABCS y S =△△，求y 关于x 的函数解析式，并写出定义域；(3)若动点M 在射线DB 上运动，当点P 运动到终点D 时，点M 也停止运动，直接写出当116PMB ABC S S =△△时，x 的值．10．（21-22八年级上·上海·期末）已知：在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，左右作平行移动的等边三角形DEF的两个顶点E、F始终在边BC上，DE、DF分别与AB相交于点G、H．(1)如图1，当点F与点C重合时，点D恰好在斜边AB上，求△DEF的周长；(2)如图2，在△DEF作平行移动的过程中，图中是否存在与线段CF始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由；(3)假设C点与F点的距离为x，△DEF与△ABC的重叠部分的面积为y，求y与x的函数关系式，并写出定义域．11．（21-22八年级上·上海·期末）如图，已知在Rt△ABC中，∠C=90°，∠CAB=60°，AB=10，点F是AB 中点，点D是射线CB上的一个动点，△ADE是等边三角形，联结EF．(1)当点D在线段CB上时，①求证：△AEF≌△ADC；②联结BE，设C、D间距离为x，BE yBF ，求y关于x的函数解析式及定义域；(2)当∠DAB=15°时，求△ADE的面积（直接写出答案）．12．（21-22八年级上·上海·期末）如图，在ABC V 中，90ACB ∠=︒，4B C =，30A ∠=︒，D 是边AC 上不与点A 、C 重合的任意一点，DE AB ⊥，垂足为点E ，M 是BD 的中点．(1)求证：CM EM =；(2)如果设AD x =，CM y =，求y 与x 的函数解析式，并写出函数的定义域；(3)当CME △的面积为时，求x的值．13．（21-22八年级上·上海·期末）如图，在Rt △ABC 中，∠C =90°，AB =BC =D 是边AB 的中点，点E 是边AC 上一个动点，作线段DE 的垂直平分线分别交边AC 、BC 于点M 、N ，设AM =x ，ME =y ．(1)当点E 与点C 重合时，求ME 的长；(2)求y 关于x 的函数解析式，并写出函数的定义域；(3)当MN 经过△ABC 一边中点时，请直接写出ME 的长．14．（22-23八年级上·上海青浦·期末）如图，在ABC V 中，D 是AB 的中点，E 是边AC 上一动点，连接DE ，过点D 作⊥DF DE 交边BC 于点F （点F 与点B 、C 不重合），延长FD 到点G ，使DG DF ＝，连接EF AG 、，已知1068AB BC AC ===，，．(1)求证：AC AG ⊥；(2)设AE x CF y ==，，求y 与x 的函数解析式，并写出自变量x 的取值范围；(3)当BDF V 是以BF 为腰的等腰三角形时，求AE 的长．15．（19-20八年级上·上海徐汇·阶段练习）如图，在△ABC 中，∠ACB=90°,AC=BC=4点D 是边AB 上的动点(点D 与点A 、B 不重合)，过点D 作DE ⊥AB 交射线BC 于点E ，联结AE,点F 是AE 的中点，过点D 、F 作直线，交AC 于点G,联结CF 、CD ．(1)当点E 在边BC 上，设DB=x ,CE=y①写出y 关于x 的函数关系式及定义域；②判断△CDF 的形状，并给出证明;(2)如果AE=3，求DG 的长.题型7：新方向-数学活动题16．（23-24八年级上·上海徐汇·阶段练习）某同学在一次课外活动中用硬纸片做了两个直角三角形，Rt ABC △中，∠B=90°，30A ∠=︒，6cm BC =．Rt DEF △中，∠D=90°，45E ∠=︒，4cm DE =．该同学将DEF 的直角边DE 与ABC V 的斜边AC 重合在一起，并将DEF 沿AC 方向移动，在移动过程中，D 、E 两点始终在AC 边上．(1)当DEF 移动至什么位置，即AD 的长为多少时，F 、C 的连线与AB 平行？(2)当DEF 移动至什么位置，即AD 的长为多少时，以线段AD 、FC 、BC 的长为三边长的三角形是直角三角形？(3)在DEF 的移动过程中，是否存在某个位置，使得15FCD ∠=︒？如果存在，求出AD 的长；如果不存在，说明理由．17．（24-25九年级上·上海浦东新·期中）图①中的板凳又叫“四脚八叉凳”，是中国传统象具，图②是四脚八叉凳的几何示意图．四脚八叉凳的榫卯结构体现了古人含蓄内敛的审美观．榫眼的设计很有讲究，木工一般用铅笔画出凳面的对称轴，以对称轴为基准向两边各取相同的长度，确定榫眼的位置，如图③所示．板凳的结构设计体现了数学的对称美．现在老师给同学们准备了凳面的木板和凳腿的木棒，请同学们根据要求准确找到榫眼的位置，安装板凳．【驱动任务一】根据“四脚八叉凳”的几何示意图画出它的主视图，如图④【驱动任务二】若A 、B 、C 在同一条直线上，且AB 与地面垂直，如图⑤，小组同学选取25cm 的木棒作为凳脚进行制作，成品凳面与地面距离为7cm ，但是同学们发现此高度缺乏舒适感，所以决定重新调整打孔位置，经过计算发现，将榫眼外移__________cm 时可将凳高调整为20cm ．【驱动任务三】根据做板凳的经验和对剩余材料的整理，同学们打算制作如图⑥所示的简易桌子，桌子的主视图如图⑦所示，正方形桌面AC 的边长为45cm ，135cm长的木棒恰好能截成和BC ，则成品桌子的高度为．面还有一个有趣的结论：(1)【问题发现】如图1所示，若AD 是BAC ∠的角平分线，可得到结论：AB BD AC DC=．小李的解法如下：过点D 作DE AB ⊥于点E ，DF AC ⊥于点F ，过点A 作AG BC ⊥于点G ，∵AD 是BAC ∠的角平分线，且DE AB ⊥，DF AC ⊥，∴．∵1212ABD ADC AB DE S AB S AC AC DF ⨯==⨯△△，1212ABD ADC B AG D S BD S CD CD AG ⨯=⨯=△△，∴AB BD AC DC =；(2)【类比探究】如图2所示，若AD 是BAC ∠的外角平分线，AD 与BC 的延长线交于点D ．求证：AB BD AC DC=；(3)【直接应用】如图3所示，在Rt ABC △中，90C ∠=︒，AD 是BAC ∠的平分线，且交BC 于D ，若15BD =，9CD =，请利用小李的方法在不添加辅助线的情况下求出AB ；(4)【拓展应用】如图4所示，在ABC V 中，90ABC ∠=︒，9AB =，12BC =，将ABC V 先沿BAC ∠的平分线AD 折叠，B 点刚好落在AC 上的E 点，剪掉重叠部分（即四边形ABDE ），再将余下部分（ABC V ）沿DEC ∠的平分线EF 折叠，再剪掉重叠部分（即四边形DEGF ），直接写出剩余部分的面积为．19．（22-23八年级上·上海·阶段练习）已知ABC V ，AD是一条角平分线．(1)【探究发现】如图1所示，若AD 是BAC ∠的角平分线，可得到结论：AB BD AC DC=．小红的解法如下：过点D 作DE AB ⊥于点E ，DF AC ⊥于点F ，过点A 作AG BC ⊥于点G ，AD 是BAC ∠的角平分线，且DE AB ⊥，DF AC ⊥，∴_________________，（_________________________________________）1212ABD ADC AB DE S S AC DF ⨯==⨯△△______________， 1212ABD ADC BD AG S BD S CD CD AG ⨯==⨯ △△，AB BD AC DC ∴=(2)【类比探究】如图2所示，若AD 是BAC ∠的外角平分线，AD 与BC 的延长线交于点D ．求证：AB BD AC CD=(3)【拓展应用】如图3所示，在ABC V 中，60BAC ∠=︒，BF 、CE 分别是ABC ∠、ACB ∠的角平分线且相交于点D，若2ED CD =，直接写出FC BC 的值是__________．。

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

北师大版八年级下册数学期末几何压轴题专练(含答案)

八下数学期末复习专题几何压轴题专练1．如图1，在△ABC中，AB＝AC，点D是直线BC上一点（不与点BC重合），以AD 为一边在AD的右侧作△ADE，使AD＝AE，△DAE＝△BAC，连接CE.设△BAC＝α，△DCE＝β.（1）求证：△DAB△△EAC.（2）当点D在线段BC上运动时，①α＝50°，则β＝°.②猜想α与β之间的数量关系，并对你的结论进行证明.（3）如图2，当点D在线段BC的反向延长线上运动时，猜想α与β之间的数量关系，并对你的结论给出证明.2．如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4.（1）如图1，当△DAG＝30°时，求BE的长；（2）如图2，当点E是BC的中点时，求线段GC的长；（3）如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长. 3．如图（1）如图1，在□ABCD中，AE平分△BAD交CD边于点E，已知AB=5cm，AD=3cm，则EC等于cm。

（2）如图2，在□ABCD中，若AE，BE分别是△DAB，△CBA的平分线，点E在DC边上，且AB=4，则▱ABCD的周长为。

（3）如图3，已知四边形ABCD是平行四边形，AD=BC，若AF，BE分别是△DAB，△CBA的平分线。

求证：DF=EC（4）在（3）的条件下，如果AD=3，AB=5，则EF的长为。

4．已知,在▱ABCD中, AB⊥BD, AB＝BD, E为射线BC上一点,连接AE交BD 于点F．（1）如图1,若点E与点C重合,且AF=√5,求AB的长;（2）如图2,当点E在BC边上时,过点D作DG⊥AE于G,延长DG交BC于H,连接FH．求证: AF=DH+FH;（3）如图3,当点E在射线BC上运动时,过点D作DG⊥AE于G, M为AG 的中点,点N在BC边上且BN=1,已知AB=5√2,请直接写出MN的最小值．5．如图，在△ABC中，△ACB＝90°，AC＝a，BC＝b，a＞b，点P是边AB上一点，连接CP，将△ACP沿CP翻折得到△QCP．（1）若PQ△AB，由折叠性质可得△BPC＝°；（2）若a＝8，b＝6，且PQ△AB，求C到AB的距离及BP的长；（3）连接BQ，若四边形BCPQ是平行四边形，直接写出a与b之间的关系式．6．如图，在平行四边形ABCD中，AB△AC，对角线AC，BD相交于点O，将直线AC 绕点O顺时针旋转一个角度α(0°<α≤90°)，分别交线段BC，AD于点E，F，连接BF.（1）如图1，在旋转的过程中，写出线段AF与EC的数量关系，并证明；（2）如图2，当旋转至90°时，判断四边形ABEF的形状，并说明理由；（3）若AB＝1，BC＝√5，求当α等于多少度时，BF＝DF？7．在Rt△ABC中，∠ABC=90°，BA=BC=4，将△ABC绕点C顺时针旋转得到△A1B1C，其中点A，B的对应点分别为点A1，B1.连接AA1，BB1交于点D.（1）如图1，当点A1落在BC的延长线上时，求线段AB1的长；（2）如图2，当△ABC旋转到任意位置时，求证：点D为线段AA1中点；（3）若△A1B1C从图1的位置绕点C继续顺时针旋转α（0°<α≤90°），当直线AB与直线A1B1相交构成的4个角中最小角为30°时，求α的值.8．如图①，在平行四边形ABCD中，AD＝BD＝2，BD△AD，点E为对角线AC上一动点，连接DE，将DE绕点D逆时针旋转90°得到DF，连接BF．（1）求证BF＝AE；（2）如图②，若F点恰好落在AC，求OF的长；（3）如图③，当点F落在△OBC的外部，构成四边形DEMF时，求四边形DEMF 的面积.9．如图（1）如图①，在Rt△ABC中，AB＝AC，D为BC边上一点(不与点B，C重合)，将线段AD绕点A逆时针旋转90°得到AE，连接EC，证明线段BC，DC，EC之间满足的等量关系;（2）如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，探索线段AD，BD，CD之间满足的等量关系，并证明结论;（3）如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°若BD＝12，CD＝4，求AD的长.10．把△ABC绕着点A逆时针旋转α，得到△ADE.（1）如图1，当点B恰好在ED的延长线上时，若α=60°，求△ABC的度数；（2）如图2，当点C恰好在ED的延长线上时，求证：CA平分△BCE；（3）如图3，连接CD，如果DE=DC，连接EC与AB的延长线交于点F，直接写出△F的度数（用含α的式子表示）.11．如图1，在平面直角坐标系中.直线y=−12x+3与x轴、y轴相交于A、B两点，动点C在线段OA上，将线段CB绕着点C顺时针旋转90∘得到CD，此时点D 恰好落在直线AB上时，过点D作DE⊥x轴于点E．（1）求证：△BOC△ △CED；（2）如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点D的坐标及△BCD平移的距离；（3）若点P在y轴上，点Q在直线AB上.是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q点坐；若不存在，请说明理由．12．在等边三角形ABC中，AD⊥BC于D，AB=2．（1）如图①，点E为AD的中点，则点E到AB的距离为；（2）如图②，点M为AD上一动点，求12AM+MC的最小值．（3）（问题解决）如图③，A，B两地相距600km，AC是笔直地沿东西方向向两边延伸的一条铁路，点B到AC的距离为360km．今计划在铁路线AC上修一个中转站M，再在BM间修一条笔直的公路．如果同样的物资在每千米公路上的运费是铁路上的两倍，那么为使通过铁路由A到M再通过公路由M到B的总运费达到最小值，中转站M应修在使AM=（千米）处．13．已知Rt△ABC中，△BAC=90°，AB=AC，点E为△ABC内一点，连接AE，CE，CE△AE，过点B作BD△AE，交AE的延长线于D．（1）如图1，求证BD=AE；（2）如图2，点H为BC中点，分别连接EH，DH，求△EDH的度数；（3）如图3，在（2）的条件下，点M为CH上的一点，连接EM，点F为EM的中点，连接FH，过点D作DG△FH，交FH的延长线于点G，若GH：FH=6：5，△FHM 的面积为30，△EHB=△BHG，求线段EH的长．14．阅读下面材料，并解决问题：（1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求△APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′△△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出△APB ＝；（2）基本运用请你利用第（1）题的解答思想方法，解答下面问题：已知如图②，△ABC中，△CAB＝90°，AB＝AC，E、F为BC上的点且△EAF＝45°，求证：EF2＝BE2+FC2；（3）能力提升如图③，在Rt△ABC中，△C＝90°，AC＝1，△ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且△AOC＝△COB＝△BOA＝120°，求OA+OB+OC的值．15．在△ABC和△ADE中，∠BAC=∠DAE=90°，且AB=AC，AD=AE.（1）如图1，如果点D在BC上，且BD=4，CD=3，求DE的长；（2）如图2，AD与BC相交于点N，点D在BC下方，连接BD，且AD⊥BD，连接CE并延长与BA的延长线交于点F，点M是CA延长线上一点，且CM=AF，求证：CF=AN+MN；（3）如图3，若AD=AB，△ADE绕着点A旋转，取DE中点M，连接BM，取BM中点N，连接AN，点F为BC中点，连接DN，若DN恰好经过点F，请直接写出DF:DN:AN的值.16．如图1，△ABC是直角三角形，△ACB＝90°，点D在AC上，DE△AB于E，连接BD，点F是BD的中点，连接EF，CF.（1）EF和CF的数量关系为；（2）如图2，若△ADE绕着点A旋转，当点D落在AB上时，小明通过作△ABC和△ADE斜边上的中线CM和EN，再利用全等三角形的判定，得到了EF和CF的数量关系，请写出此时EF和CF的数量关系；（3）若△AED继续绕着点A旋转到图3的位置时，EF和CF的数量关系是什么？写出你的猜想，并给予证明.17．我们定义：如图1、图2、图3，在ΔABC中，把AB绕点A顺时针旋转α(0∘<α<180∘)得到AB′，把AC绕点A逆时针旋转β得到AC′，连接B′C′，当α+β=180∘时，我们称ΔAB′C′是ΔABC的“旋补三角形”，ΔAB′C′边B′C′上的中线AD叫做ΔABC的“旋补中线”，点A叫做“旋补中心”.图1、图2、图3中的ΔAB′C′均是ΔABC的“旋补三角形”.（1）①如图2，当ΔABC为等边三角形时，“旋补中线” AD与BC的数量关系为：AD=BC；②如图3，当∠BAC=90∘，BC=8时，则“旋补中线” AD长为.（2）在图1中，当ΔABC为任意三角形时，猜想“旋补中线” AD与BC的数量关系，并给予证明.18．在平行四边形ABCD中，∠BAD的角平分线交直线BC于点E，交直线DC于点F．（1）在（图25-1）中证明CE=CF；（2）若∠ABC=90°，G是EF的中点（如图25-2），求∠BDG的度数；（3）若∠ABC=120°，FG//CE，FG=CE，分别连接BD、DG（如图25--3），直接写出∠BDG的度数．19．在△ABCD中，对角线AC、BD交于点O，将过点A的直线l绕点A旋转，交射线CD于点E，BF△l于点F，DG△l于点G，连接OF，OG．（1）如图①当点E与点C重合时，请直接写出线段OF，OG的数量关系；（2）如图②，当点E在线段CD上时，OF与OG有什么数量关系？请证明你的结论；（3）如图③，当点E在线段CD的延长线上时，上述的结论是否仍成立？请说明理由．20．如图，在平行四边形ABCD中，AB△AC，对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转一个角度α（0°＜α≤90°），分别交线段BC，AD于点E，F，连接BF.（1）如图1，在旋转的过程中，求证：OE＝OF；（2）如图2，当旋转至90°时，判断四边形ABEF的形状，并证明你的结论；（3）若AB＝1，BC＝√5，且BF＝DF，求旋转角度α的大小.21．如图1，在Rt△ABC中，△A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD ＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点.（1）观察猜想：图1中，线段PM与PN的数量关系是，位置关系是；（2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值.22．如图，已知函数y=﹣12x+b的图象与x轴、y轴分别交于点A、B，与函数y=x的图象交于点M，点M的横坐标为2．（1）求点A的坐标；（2）在x轴上有一动点P（a，0）（其中a＞2），过点P作x轴的垂线，分别交函数y=﹣12x+b和y=x的图象于点C、D．①若OB=2CD，求a的值；②是否存在这样的点P，使以B、O、C、D为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．答案与解析1．【答案】（1）证明：∵△DAE＝△BAC，∴△CAD﹣△DAE＝△CAD﹣△BAC，∴△CAE＝△BAD，在△DAB和△EAC中，{AB=AC∠BAD=∠CAF AD=AE∴△DAB△△EAC（SAS）（2）解：①130；②α+β＝180°，理由：由（1）知，△DAB△△EAC，∴△ABC＝△ACE，在△ABC中，AB＝AC，△BAC＝α，∴△ABC＝△ACB＝12（180°﹣△BAC）＝12（180°﹣α）＝90°﹣12α，∴β＝△ACB+△ACE＝△ACB+△ABC＝90°﹣12α+90°﹣12α＝180°﹣α，∴α+β＝180°（3）解：β＝α；理由：∵△DAE＝△BAC，∴△DAE﹣△BAE＝△BAC﹣△BAE，∴△CAE＝△BAD，在△DAB和△EAC中，{AB=AC∠BAD=∠CAB AD=AE∴△DAB△△EAC（SAS），∴△ABD＝△ACE，在△ABC中，AB＝AC，△BAC＝α，∴△ABC＝△ACB＝12（180°﹣△BAC）＝12（180°﹣α）＝90°﹣12α，∴△ACE＝△ABD＝180°﹣△ABC＝180°﹣（90°﹣12α）＝90°+12α，∴β＝△ACE﹣△ACB＝90°+ 12α﹣（90°﹣12α）＝α.2．【答案】（1）解：∵四边形ABCD是矩形，∴△BAD＝90°，∵△DAG ＝30°，∴△BAG ＝60°由折叠知，△BAE ＝12△BAG ＝30°，在Rt△BAE 中，△BAE ＝30°，AB ＝3，∴BE ＝√3（2）解：如图4，连接GE ，∵E 是BC 的中点，∴BE ＝EC ，∵△ABE 沿AE 折叠后得到△AFE ，∴BE ＝EF ，∴EF ＝EC ，∵在矩形ABCD 中，∴△C ＝90°，∴△EFG ＝90°，∵在Rt△GFE 和Rt△GCE 中，{EG =EG EF =EC∴Rt△GFE△Rt△GCE （HL ），∴GF ＝GC ；设GC ＝x ，则AG ＝3+x ，DG ＝3﹣x ，在Rt△ADG 中，42+（3﹣x ）2＝（3+x ）2，解得x ＝43. （3）解：BE ＝323．【答案】（1）2（2）12（3）证明：∵在▱ABCD 中，CD△AB ，∴△DFA=△FAB.又∵AF是△DAB的平分线∴△DAF=△FAB，∴△DAF=△DFA，∴AD=DF，同理可得EC=BC.∵AD=BC，∴DF=EC（4）14．【答案】（1）解：如图1中，∵AB⊥BD,∴∠ABD=90°,∵AB=BD,∠BAD=45°,∴∠BDA=∠BAD=45°,∵四边形ABCD是平行四边形,∴E、C重合时BF=12BD=12AB,在RtΔABF中,∵AF2=AB2+BF2,∴(√5)2=(2BF)2+BF2,∴BF=1, AB=2,∴AB=2;（2）证明：如图2中，在AF上截取AK=HD,连接BK,∵AB⊥BD, DG⊥AE,∴∠ABF=∠FGD=90°,∵∠AFD=∠ABF+∠2=∠FGD+∠3, ∠ABF=∠FGD=90°,∴∠2=∠3,在ABK和ΔDBH中, {AB=BD ∠2=∠3 AK=HD,∴ΔABK≅ΔDBH,∴BK=BH, ∠6=∠1,∵四边形ABCD是平行四边形,∴AD//BC,∴∠4=∠1,由（1）知∠4=45°,∴∠l=∠6=45°,∴∠5=∠ABD−∠6=45°,∠5=∠1,在ΔFBK和ΔFBH中, {BF=BF ∠5=∠1 BK=BH,∴ΔFBK≅ΔFBH,∴KF=FH,∵AF=AK+KF，∴AF=DH+FH；（3）解：MN的最小值为√149−52．5．【答案】（1）45（2）解：如图，作CH△AB于H由翻折的性质可知：△APC=△QPC∵CH△AB，△BPC=45°∴CH=PH在Rt△ABC中，AB=√AC2+BC2=√82+62=10∵12⋅AB ⋅CH =12⋅AC ⋅BC ，即 5CH =24 ∴CH= 245；（3）解：如图:连接BQ由翻折的性质可得：PA=PQ ，△QPC=△APC∵四边形BCPQ 是平行四边形∴PQ=BC=PA=b ，PQ//BC ，∴△QPC+△PCB=180°∵△BPC+△APC=180°∴△PCB=△BPC∴PB=BC=b∴AP=PB=b ，AB=2b ，在Rt△ABC 中，则有（2b ）2=a 2+b 2∴a 2=3b 2∵a>0.b>0，∴a= √3b ．6．【答案】（1）解：AF=CE.理由如下：∵四边形ABCD 为平行四边形，∴AD // CB ，OA=OC.∴△FAO=△ECO.在 △AOF 和 △COE 中，∵{∠AOF =∠COE,OA =OC,∠FAO =∠ECO,∴△AOF ≌△COE(ASA) .∴AF=CE.（2）解：当旋转至90°时，四边形ABEF为平行四边形.理由如下：∵△AOF= 90°，△BAC= 90°，∴AB //EF.又∵四边形ABCD是平行四边形，∴AD//BC，即AF//BE.∴四边形ABEF为平行四边形（3）解：当α等于45度时，BF＝DF.理由如下：∵AB=1，BC= √5，AB△AC，∴AC= √BC2−AB2=√(√5)2−12=2.∵四边形ABCD为平行四边形，∴OA=12AC=12×2=1，BO=DO.∴OA=AB=1.点O在线段BD的垂直平分线上.∴△ABO为等腰直角三角形.∴△AOB= 45°.当F在线段BD的垂直平分线上时，BF=DF，∴FO垂直平分BD.∴△BOF=90°.∴∠AOF=∠BOF−∠AOB=90°−45°=45°，即α=45°.∴当α等于45度时，BF＝DF.7．【答案】（1）解：∵Rt△ABC中，∠ABC=90°，BA=BC=4，∴∠ACB=45°，AC=√AB2+BC2=√42+42=4√2.∵△ABC绕点C顺时针旋转得到△A1B1C，∴∠A1CB1=45°，B1C=BC=4.∴∠ACB1=180°−∠ACB−∠A1CB1=90°.∴AB1=√AC2+B1C2=√(4√2)2+42=4√3（2）证明：过点A1作A1E//AB交BB1的延长线于点E，∴∠ABD=∠DEA1.∵B1C=BC，∴∠CBB1=∠CB1B.∵∠ABC=∠A1B1C=90°，∴∠ABD+∠CBB1=∠CB1B+∠A1B1E=90°.∴∠A1B1E=∠ABD=∠DEA1.∴A1B1=A1E.∵AB=A1B1，∴AB=A1E.∵∠ADB=∠A1DE，∴△ADB≅△A1DE.∴AD=∠A1D.∴点D为线段AA1中点（3）解：如图3，当直线AB与直线A1B1相交于点A上方，延长BC交A1B1于点E，∵∠ABC=90°，∠P=30°，∴∠PEB=60°.∵∠CA1B1=45°，∴∠A1CE=∠PEB−∠CA1E=15°.如图4，当直线AB与直线A1B1相交于点A下方，延长BC交A1B1的延长线于点E，∵∠ABC=90°，∠P=30°，∴∠PEB=60°.∵∠A1B1C=90°，∴∠B1CE=∠A1B1C−∠PEB=30°.∴∠A1CE=∠B1CE+∠A1CB=75°.∴当直线AB与直线A1B1相交构成的4个角中最小角为30°时，α的值为15°或75°.8．【答案】（1）证明：根据旋转的性质可得，DE=DF，△EDF=90°∵BD△AD∴△ADB=90°∴△ADE=△BDF∵AD=BD∴△ADE△△BDF∴BF=AE（2）过点D 作DG△AC 于点G ，∵DE=DF ，△EDF=90°∴△DEF=△DFE=45°，△DEA=135°根据（1）可得，△ADE△△BDF∴△BFD=△DEA=135°，AE=BF∴△BFO=90°∵四边形ABCD 为平行四边形∴OB=OD∴△DGO△△BFO∴DG=BF ，OF=OG∴DG=EG=AE=BF设DG=a （a ＞0），则AG=2a在直角三角形ADG 中，∵AG 2+DG 2=AD 2∴（2a ）2+a 2=22解得a=2√55 ∴OF=OG=12×2√55=√55（3）过点D 作DN△AC 于点N ，将△DEN 绕点D 逆时针旋转90°得到△DFH ，∴DH=DN ，△DNE=△DH=90°，△DEN=△DFG∵△DEF=△FME=90°∴△DEM+△DFM=180°∴△DFH+△DFM=180°∴点H ，点F ，点M 三点共线∵△DHF=△DNM=△FMN=90°∴四边形DNMG 为矩形∵DN=DH∴四边形DNMH 为正方形∴S 四边形DEMF=S 四边形DNMH=（2√55）2=459．【答案】（1）解：∵线段AD绕点A逆时针旋转90°得到AE∵Rt△ABC中AB=AC∴∠BAD=∠CAE∴△ABD≌△ACE(SAS)∴DB=EC∴BC=DC+DB=DC+EC（2）解：连结CE∵Rt△ABC与Rt△ADE中AB＝AC，AD＝AE∴∠B=∠ACE=45°，DE2=AD2+AE2=2AD2，∵由（1）同理可得△ABD≌△ACE∴DB=EC,∠ABD=∠ACE=45°∴∠ECD=90°∴Rt△ECD中，DE2=EC2+CD2=BD2+CD2∴2AD2=BD2+CD2（3）解：过点A作AE⊥AD，且AE=AD，连结DE,CE∵∠ABC=∠ACB=45°∴AB⊥AC,AB=AC∵AE⊥AD,AE=AD∴由（1）同理可得△ABD≌△ACE∴DB=EC=12∵∠ADC=45°∴∠EDC=∠ADC+∠ADE=90°∴DE=√CE2−CD2=√122−42=8√2∴等腰直角△ADE中AD=810．【答案】（1）解：∵α=60°，△ABC△△ADE，∴ AD=AB，△ABC=△ADE.∴ △ABD=△DAB=60°.∴ △ABC=△ADE=△DAB+△ABD=120°.（2）解：∵ AC=AE,△EAC= α，∴ △E=△ACE.∵ △ABC△△ADE，∴ △ACB=△E.∴ △ACB=△ACE.∴ CA平分△BCE.（3）解：△F= 90°−α.如下图：延长AD交EF于点G，则根据图形旋转的性质得，△GAF=α，∵△ABC△△ADE∴AC=AE，∴△AEC为等腰三角形，在△AED和△ACD中，{AE=AC DE=CD AD=AD，∴ △AED △ △ACD（SSS），∴ △DAE=△DAC，∴ AD平分△EAC，∵△AEC为等腰三角形，∴AG△EF，即△AGF=90°，∴∠EAF=3∠CAF=32α，∴∠F=180°−∠GAF−∠AGF=90°−α.11．【答案】（1）证明：∵∠BOC=∠BCD=∠CED=90∘，∴∠OCB+∠DCE=90∘，∠DCE+∠CDE=90∘，∴∠BCO=∠CDE，∵BC=CD，∴△BOC△ △CED．（2）解：∵△BOC△ △CED，∴OC=DE=m，BO=CE=3，∴D(m+3,m)，把D(m+3,m)代入y=−12x+3得到，m=−12(m+3)+3，∴2m=−m−3+6，∴m=1，∴D(4,1)，∵B(0,3)，C(1,0)，∴直线BC的解析式为y=−3x+3，设直线B′C′的解析式为y=−3x+b，把D(4,1)代入得到b=13，∴直线B′C′的解析式为y=−3x+13，∴C′(133,0)，∴CC′=103，∴△BCD平移的距离是103个单位．（3）点Q的坐标为(3,32)或(5,12)或(−3,92).12．【答案】（1）√34（2）解：如图，作CN⊥AB，垂足为N，此时12AM+MC最小，最小值等于CN，∵在正三角形ABC中，AB=BC=AC=2，∠ANC=90°，∴AN=1，由勾股定理得，CN=√3由（1）知，MN=12AM∴MN+CM=12AM+MC=CN=√3，即12AM+MC的最小值为√3（3）( 480−120√3 )13．【答案】（1）证明：∵CE△AE，BD△AE，∴△AEC＝△ADB＝90°，∵△BAC＝90°，∴△ACE+CAE＝△CAE+△BAD＝90°，∴△ACE＝△BAD，在△CAE与△ABD中{∠ACE=∠BAD ∠AEC=∠ADB AC=AB∴△CAE△△ABD（AAS），∴AE＝BD；（2）解：连接AH∵AB＝AC，BH＝CH，∴△BAH＝12∠BAC=12×90°=45°，△AHB＝90°，∴△ABH＝△BAH＝45°，∴AH＝BH，∵△EAH＝△BAH﹣△BAD＝45°﹣△BAD，△DBH＝180°﹣△ADB﹣△BAD﹣△ABH＝45°﹣△BAD，∴△EAH＝△DBH，在△AEH与△BDH中{AE=BD∠EAH=∠DBH AH=BH∴△AEH△△BDH（SAS），∴EH＝DH，△AHE＝△BHD，∴△AHE+△EHB＝△BHD+△EHB＝90°即△EHD＝90°，∴△EDH ＝△DEH ＝ 180°−90°2=45° ；（3）解：过点M 作MS△FH 于点S ，过点E 作ER△FH ，交HF 的延长线于点R ，过点E 作ET△BC ，交HR 的延长线于点T ．∵DG△FH ，ER△FH ，∴△DGH ＝△ERH ＝90°，∴△HDG+△DHG ＝90°∵△DHE ＝90°，∴△EHR+△DHG ＝90°，∴△HDG ＝△HER在△DHG 与△HER 中{∠HDG =∠HER ∠DGH =∠ERH DH =EH∴△DHG△△HER （AAS ），∴HG ＝ER ，∵ET△BC ，∴△ETF ＝△BHG ，△EHB ＝△HET ，△ETF ＝△FHM ，∵△EHB ＝△BHG ，∴△HET ＝△ETF ，∴HE ＝HT ，在△EFT 与△MFH 中{∠ETF =∠FHM ∠EFT =∠MFH EF =FM，∴△EFT△△MFH （AAS ），∴HF ＝FT ，∴HF·MS 2=FT·ER 2， ∴ER ＝MS ，∴HG＝ER＝MS，设GH＝6k，FH＝5k，则HG＝ER＝MS＝6k，HF·MS 2=5k·6k2=30，k＝√2，∴FH＝5 √2，∴HE＝HT＝2HF＝10 √2．14．【答案】（1）150°（2）解：如图2，把△ABE绕点A逆时针旋转90°得到△ACE′，由旋转的性质得，AE′＝AE，CE′＝BE，△CAE′＝△BAE，△ACE′＝△B，△EAE′＝90°，∵△EAF＝45°，∴△E′AF＝△EAE′-△EAF=45°，∴△EAF＝△E′AF，在△EAF和△E′AF中，{AE=AE′∠EAF=∠E′AFAF=AF∴△EAF△△E′AF（SAS），∴E′F＝EF，∵△CAB＝90°，AB＝AC，∴△B＝△ACB＝45°，∴△E′CF＝45°+45°＝90°，由勾股定理得，E′F2＝CE′2+FC2，即EF2＝BE2+FC2．（3）解：如图3，将△AOB绕点B顺时针旋转60°至△A′O′B处，连接OO′，∵在Rt△ABC中，△ACB＝90°，AC＝1，△ABC＝30°，∴AB＝2，∴BC＝√AB2−AC2=√3，∵△AOB绕点B顺时针方向旋转60°，△ABC=30°，∴△A′BC＝△ABC+60°＝30°+60°＝90°，∵△C＝90°，AC＝1，△ABC＝30°，∴AB＝2AC＝2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B＝AB＝2，BO＝BO′，A′O′＝AO，∴△BOO′是等边三角形，∴BO＝OO′，△BOO′＝△BO′O＝60°，∵△AOC＝△COB＝△BOA＝120°，∴△COB+△BOO′＝△BO′A′+△BO′O＝120°+60°＝180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C＝√BC2+A′B2=√(√3)2+22=√7，∴OA+OB+OC＝A′O′+OO′+OC＝A′C＝√7．15．【答案】（1）解：连接EC，又AB=AC，AD=AE，∴BD=CE=4，∠ACE=∠ABC，∵∠ABC+∠ACB=90°∴∠ACE+∠ACB=90°∴△ACE是直角三角形，∴DE=√CD2+CE2=√32+42=5；（2）解：∵∠BAD+∠DAC=90°,∠EAC+∠DAC=90°∴∠BAD=∠EAC∵{AB=AC∠BAD=∠EACAD=AE∴△BAD≅△CAE(SAS)∴∠ABD=∠ACE∵AD⊥BD∴∠BAD=90°−∠ABD∵∠BAC=90°∴∠DAC=90°−∠BAD∴∠DAC=∠ABD∴∠ACF=∠DAC∴AD//CF过点A作AP//BC交FC于点P，∴四边形ANCP是平行四边形∴AN=CP，NC=AP∵AP//BC∴∠FAP=∠ABC=45°{PA=NC∠PAF=∠NCM AF=CN∴△PAF≅△NCM(SAS)∴MN=PF∴AN+MN=CP+FP=CF；（3）DF:DN:AN=1:2:216．【答案】（1）EF＝CF（2）EF＝CF（3）解：猜想，EF＝CF，理由：如图3中，取AB的中点M，AD的中点N，连接MC，MF，EN，FN.∵BM＝MA，BF＝FD，∴MF△AD，MF＝12AD，∵AN＝ND，∴MF＝AN，MF△AN，∴四边形MFNA是平行四边形，∴NF＝AM，△FMA＝△ANF，在Rt△ADE中，∵AN＝ND，△AED＝90°，∴EN＝12AD＝AN＝ND，同理CM＝12AB＝AM＝MB，在△AEN和△ACM中，△AEN＝△EAN，△MCA＝△MAC，∵△MAC＝△EAN，∴△AMC＝△ANE，又∵△FMA＝△ANF，∴△ENF＝△FMC，∵AM＝FN，AM＝CM，∴CM＝NF，在△MFC和△NEF中，{MF=EN∠FMC=∠ENFMC=NF，∴△MFC△△NEF（SAS），∴FE＝FC.17．【答案】（1）12；4（2）解：结论：AD=12BC.理由：如图1中，延长AD到M，使得AD=DM，连接B′M，C′M，∵B′D=DC′，AD=DM，∴四边形AC′MB′是平行四边形，∴AC′=B′M=AC，∵∠BAC+∠B′AC′=180∘，∠B′AC′+∠AB′M=180∘，∴∠BAC=∠MB′A，∵AB=AB′，∴ΔBAC≅ΔAB′M，∴BC=AM，∴AD=12BC.18．【答案】（1）证明：在平行四边形ABCD中，AB△CD，AD△BC∴△BAF=△F，△DAF=△CEF又∵AE平分△BAD∴△BAF=△DAF∴△F=△CEF∴CE=CF（2）如图，连接CG、BG.∵ABCD是平行四边形，△ABC＝90°∴平行四边形ABCD是矩形∴AB=DC，AB△DC，AD△BC，△BAD＝△ADC=△BCD＝△ECF＝90° ∴△F=△BAE，△DBC=△ADB∵△BAD＝90° ，△BAE＝12△BAD=45°∴AB=BE，△F=△BAE=45°∴CE=CF∴BC=BE+EC=AB+CF=CD+CF=DF又∵G 是EF 的中点，△ECF ＝90° ,CE=CF∴CG=FG=12EF,△ECG=12△ECF=45° ∴△ECG=△F∴△DFG△△BCG∴△FDG ＝△CBG ，DG=BG∴△DBG=△BDG∵△DBC=△ADB,△FDG ＝△CBG∴△DBC+△CBG=△ADB+△FDG即△DBG=△ADB+△FDG∴△BDG=△ADB+△FDG又∵△BDG+（△ADB+△FDG ）=90°∴△BDG=12△ADC=45° （3）如图，连接GB 、GE 、GC 。

初二数学数学全等三角形压轴几何题试题含答案

初二数学数学全等三角形压轴几何题试题含答案一、全等三角形旋转模型1．问题背景：如图1，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，120ABC ∠=︒，60MBN ∠=︒，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．探究图中线段AE ，CF ，EF 之间的数量关系．小李同学探究此问题的方法是：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，再证明BFC BFE △≌△，可得出结论，他的结论就是_______________；探究延伸1：如图2，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由．探究延伸2：如图3，在四边形ABCD 中，BA BC =，180BAD BCD ∠+∠=︒，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？并说明理由．实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O 处）北偏西30的A 处舰艇乙在指挥中心南偏东70︒的B 处，并且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东50︒的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E 、F 处，且指挥中心观测两舰艇视线之间的夹角为70︒，试求此时两舰艇之间的距离．答案：E解析：EF=AE+CF ．探究延伸1：结论EF=AE+CF 成立．探究延伸2：结论EF=AE+CF 仍然成立．实际应用：210海里．【分析】延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；探究延伸1：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；探究延伸2：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；实际应用：连接EF ，延长AE ，BF 相交于点C ，然后与探究延伸2同理可得EF=AE+CF ，将AE 和CF 的长代入即可．【详解】解：EF=AE+CF理由：延长FC 到G ，使CG AE =，连接BG ，在△BCG 和△BAE 中，90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩，∴BCG BAE △≌△（SAS ），∴BG=BE ，∠CBG=∠ABE ，∵∠ABC=120°，∠MBN=60°，∴∠ABE+∠CBF=60°，∴∠CBG+∠CBF=60°，即∠GBF=60°，在△BGF 和△BEF 中，BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△BGF ≌△BEF （SAS ），∴GF=EF ，∵GF=CG+CF=AE+CF ，∴EF=AE+CF ．探究延伸1：结论EF=AE+CF 成立．理由：延长FC 到G ，使CG AE =，连接BG ，在△BCG 和△BAE 中，90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩，∴BCG BAE △≌△（SAS ），∴BG=BE ，∠CBG=∠ABE ，∵∠ABC=2∠MBN ，∴∠ABE+∠CBF=12∠ABC ， ∴∠CBG+∠CBF=12∠ABC ，即∠GBF=12∠ABC ，在△BGF 和△BEF 中，BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△BGF ≌△BEF （SAS ），∴GF=EF ，∵GF=CG+CF=AE+CF ，∴EF=AE+CF ．探究延伸2：结论EF=AE+CF 仍然成立．理由：延长FC 到G ，使CG AE =，连接BG ，∵180BAD BCD ∠+∠=︒，∠BCG+∠BCD=180°，∴∠BCG=∠BAD在△BCG 和△BAE 中，BC BA BCG BAE CG AE =⎧⎪∠=∠⎨⎪=⎩，∴BCG BAE △≌△（SAS ），∴BG=BE ，∠CBG=∠ABE ，∵∠ABC=2∠MBN ，∴∠ABE+∠CBF=12∠ABC ， ∴∠CBG+∠CBF=12∠ABC ，即∠GBF=12∠ABC ，在△BGF 和△BEF 中，BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△BGF ≌△BEF （SAS ），∴GF=EF ，∵GF=CG+CF=AE+CF ，∴EF=AE+CF ．实际应用：连接EF ，延长AE ，BF 相交于点C ，∵∠AOB=30°+90°+(90°-70°)=140°，∠EOF=70°，∴∠EOF=12∠AOB ∵OA=OB ，∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°，∴符合探索延伸中的条件∴结论EF= AE+CF 仍然成立即EF=75×1.2+100×1.2=210（海里）答：此时两舰艇之间的距离为210海里．【点睛】本题考查了全等三角形的判定与性质．作辅助线构造全等三角形是解题的关键． 2．（1）如图1，在OAB 和OCD 中，OA=OB ，OC=OD ，∠AOB=∠COD=40°，连接AC ，BD 交于点M ．求：①AC BD的值； ②∠AMB 的度数．（2）如图2，在OAB 和OCD 中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC 交BD 的延长线于点M ．请判断AC BD的值及∠AMB 的度数，并说明理由；（3）在（2）的条件下，将OCD 点O 在平面内旋转，AC ，BD 所在直线交于点M ，若OD=2，OB=23，请直接写出当点C 与点M 重合时AC 的长．答案：A解析：（1）①1，②40°；（2）AC BD =3，∠AMB=90°，见解析；（3）23或43 【分析】（1）①根据已知条件证明△COA ≌△DOB ，即可证明AC=BD ；②根据△COA ≌△DOB 可得∠CAO=∠DBO ，根据已知条件可得∠OAB+∠ABO=140°，然后在△AMB 中，根据等角的转换即可得到答案；（2）根据已知条件证明△AOC ∽△BOD ，可得∠CAO=∠DBO ，进而可得∠MAB=∠OAB+∠DBO ，最后可得∠AMB=180°-（∠OAB+∠ABM+∠DBO ）=90°；（3）分两种情况讨论，根据题（2），同理可得OAC OBD △△，90AMB ∠=︒，3AC BD=，设BD=x ，则3AC x = 用x 表示出AM 、BM 的长，在Rt AMB 中，根据勾股定理222AM BM AB +=列出方程，求解即可．【详解】解：（1）①如图1，∵∠AOB=∠COD=40°，∴∠COA=∠DOB ，∵OC=OD ，OA=OB ，∴△COA ≌△DOB （SAS ），∴AC=BD ， ∴AC BD =1， ②∵△COA ≌△DOB ，∴∠CAO=∠DBO ，∵∠AOB=40°，∴∠OAB+∠ABO=140°，在△AMB 中，∠AMB=180°﹣（∠CAO+∠OAB+∠ABD ）=180°﹣（∠DBO+∠OAB+∠ABD ）=180°﹣140°=40°，（2）如图2，AC BD=3，∠AMB=90°，理由是：在Rt △COD 中，∠DCO=30°，∠DOC=90°， ∴3tan 30OD OC =︒= 同理得：3tan 303OB OA =︒=， ∴OD OB OC OA=， ∵∠AOB=∠COD=90°，∴∠AOC=∠BOD ，∴△AOC ∽△BOD ，∴AC OC BD OD=3∠CAO=∠DBO ，在△AMB 中，∠AMB=180°﹣（∠MAB+∠ABM ）=180°﹣（∠OAB+∠ABM+∠DBO ）=90°；（3）AC 的长为23或43．①如图，点C 与点M 重合，同理可得：OAC OBD △△，90AMB ∴∠=︒，3AC BD =，设BD=x ，则3AC x =，在Rt ODC 中，30OCD ∠=︒，OD=2，4CD ∴=，在Rt AOB 中，30OAB ∠=︒，OB=23，43AB ∴=，在Rt AMB 中，222AM BM AB +=，即222(3)(4)(43)x x ++=，解得：x=2或-4(舍)，AC=323x =；②如图，点C 与点M 重合，同理可得：90AMB ∠=︒，3AC BD =设BD=x ，则3x ，在Rt COD 中， 90OCD ∠=︒，OD=2，4CD ∴=，4BC x =-，在Rt AOB 中，30OAB ∠=︒，3OB =243AB OB ∴==，在Rt AMB 中，222AM BM AB +=，即222(3)(4)(43)x x +-=，解得：x=4或-2（舍），AC=343x =，综上所述，AC 的长为23或43．【点睛】本题主要考查三角形的综合运用，涉及全等三角形与相似三角形的性质和判定、勾股定理、解一元一次方程、图形旋转证明、特殊角的三角函数值等知识点，难度较大，第（1）题证明△COA ≌△DOB 是关键，第（2）题证明△AOC ∽△BOD 是关键，第（3）题要特别注意分情况讨论． 3．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是，位置关系是；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．解析：（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492．【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =，点P ，M 是CD ，DE 的中点， //PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =，利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠，90BAC ∠=︒，90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，22AM ∴=在Rt ABC ∆中，10AB AC ==，52AN =22522MN ∴=最大，222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大．方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大．【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．4．如图，在ABC 中，,AB AC BAC α=∠=，过A 作AD BC ⊥于点D ，点E 为直线AD 上一动点，把线段CE 绕点E 顺时针旋转α，得到线段EF ，连接FC 、FB ，直线AD 与BF 相交于点G ．（1）（发现）如图1，当60α=︒时，填空： ①AE BF的值为___________； ②AGB ∠的度数为___________；（2）（探究）如图2，当120α=︒时，请写出AE BF的值及AGB ∠的度数，并就图2的情形给出证明；（3）（应用）如图3，当90α=︒时，若23,15AB ACE =∠=︒，请直接写出DFG 的面积．答案：G解析：（1）1；60°；（2）3AE BF =∠G =30°，理由见解析；（3）333 【分析】（1）①根据已知条件可以证明三角形ABC 和三角形EFC 都是等边三角形，然后根据等边三角形的性质证明△AEC ≌△BFC ，即BF =AE 从而得出答案；②根据①中的证明∠ABG =90°，∠BAG =30°，从而计算出∠AGB 的度数；（2）根据题目已知条件可以计算出3BC =，同理可以证得3CF CE =，再证ECA FCB ∠=∠即△ACE ∽△BCF ，从而得到比值和角的度数；（3）根据第（2）问的计算结论分E 在AD 上和E 在DA 的延长线上分类讨论求解即可．【详解】解：（1）①∵AB =AC ，CE =EF ，∠BAC =∠FEC =60°∴△ABC 和△EFC 都是等边三角形∴∠ACB =∠ECF =60°，AC =CB ，CE =CF∴∠ACE =∠BCF∴△ACE ≌△BCF∴A E =BF ，即1AE BF= ②∵△ACE ≌△BCF∴∠EAC =∠CBF由①可知△ABC 是等边三角形∴AD 平分∠BAC ，BD ⊥AD∴∠CAE =∠CBF =30°∴∠AGB =∠180°-∠CBF -∠BDG =60°（2）3AE BF =，理由如下： ∵AB =AC ，∠BAC =120°，AD ⊥BC∴∠ABD =30°=∠ACB∴BD AB AC CD === ∴BC =同理∵∠FEC =120°，EF =EC ∴CF =∴BC CF AC CE=，∠ACB =∠ECF =30° ∴△ACE ∽△BCF∴∠CAE =∠CBF∴3AE AC BF BC == ∵AD ⊥BC ，∠BAC =120°，∴∠CAE =∠CBF =60°又∵∠BDG =90°∴∠G =30°（3）第一种情况，如图所示，当E 在AD 上时 ∵AB AC ==∠BAC =90°，AD ⊥BC∴sin 4562BC AD BD CD AB =====∠DAC =45° ∵∠ACE =15° ∴∠CED =∠CAD +∠ACE =60° ∴2tan 60DC DE ==∴AE AD DE =-=BC CF AC CE==，∠ACB =∠ECF =45° 又∵AD ⊥BC ，∠BAC =90°，∴∠CAE =∠CBF =45°∴△ACE ∽△BCF∴2BF BC AE AC == ∴()262232BF =-=- ∵∠ADC =∠BDG∴∠G =∠ACB =45° ∴223BG BD ==∴2FG BG BF =-=过点D 作DM ⊥BG 交BG 于M ，∵∠G =∠ACB =45°，∠BDG =90° ∴=6DG BD CD ==∴232DM DG == ∴132DFG S FG DM ==△ 第二种情况：当E 在DA 的延长线上时过点D 作DM ⊥BG 交BG 于M ，同上可证2BF BC AE AC==，6BG BD ==，3DM =∵∠ACE =15°，∠DAC =45°∴∠DEC =30° ∵AD ⊥CD ，6CD =∴32tan 30DC DE ==∴=6DG BD CD ==326AE DE AD =-=∴2623FB AE ==-∴6FG BF BG =+=1332DFG S FG DM ==△故答案为：3或33．【点睛】本题主要考查了相似三角形的性质与判定，旋转的性质，三角函数等知识点，解题的关键在于能够熟练的掌握相关知识点．5．在ABC 中，,AB AC BAC α=∠=，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接,DB DC ．（1）如图1，当60α=︒时，请直接写出线段PA 与线段CD 的数量关系是__________，DCP ∠为______度；（2）如图2，当120α=︒时，写出线段PA 和线段DC 的数量关系，并说明理由；（3）如图2，在（2）的条件下，当23AB =13BP PC +的最小值．答案：A解析：（1）PA ＝DC ，60；（2）CD 3PA ．理由见详解；（232【分析】（1）先证明△ABC ，△PBD 是等边三角形，再证明△PBA ≌△DBC ，进而线段PA 与线段CD 的数量关系，利用全等三角形的性质以及三角形内角和等于180°，解决问题即可；（2）证明△CBD ∽△ABP ，可得3CD BC PA AB== （3）过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ，过点B 作BG ⊥BA 于点G ，当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小，由BGP CNP ∽，得13GP NP BP CP ==，结合勾股定理求出GP ，从而得CP ，进而即可求解．【详解】（1）①证明： ∵将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，∴PB ＝PD ，∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝60°，∴△ABC ，△PBD 是等边三角形，∴∠ABC ＝∠PBD ＝60°，∴∠PBA ＝∠DBC ， ∵BP ＝BD ，BA ＝BC ，∴△PBA ≌△DBC （SAS ）， ∴PA ＝DC ．设BD 交PC 于点O ，如图1，∵△PBA ≌△DBC ，∴∠BPA ＝∠BDC ，∵∠BOP ＝∠COD ，∴∠OBP ＝∠OCD ＝60°，即∠DCP ＝60°．故答案是：PA ＝DC ，60；（2）解：结论：CD 3．理由如下：∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝120°，∴BC ＝2•AB •cos30°3，BD ═2BP •cos30°3，∴BC BD BA BP=3 ∵∠ABC ＝∠PBD ＝30°，∴∠ABP ＝∠CBD ，∴△CBD ∽△ABP ，∴3CD BC PA AB==∴CD ＝3PA ；（3）过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ，过点B 作BG CA ⊥于点G ，则BG =AB ×sin ∠BAG =23×sin60°=3，AG = AB ×cos ∠BAG =3．当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小， ∵∠BGP =∠CNP =90°，∠BPG =∠CPN ， ∴BGP CNP ∽，∴13GP NP BP CP ==，设GP =x ，则AP =3-x ，BP =3x ，∴()22233x x +=，解得：x =324， ∴BP =924，AP =3-324， ∴CP =AC +AP =23+3-324=33-324， ∴13BP PC +最小值=924+13×(33-324)=3+22．【点睛】本题属于几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等知识，第（1）（2）题解题的关键是正确寻找全等三角形或相似三角形解决问题，第（3）题的关键是过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ．6．已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF ⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）求证：EG ＝CG ；（2）将图①中BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．答案：E解析：（1）见解析；（2）依然成立，见解析；（3）依然成立，EG⊥CG【分析】（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG＝EG；（2）结论仍然成立，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点；再证明△DAG≌△DCG，得出AG＝CG；再证出△DMG≌△FNG，得到MG＝NG；再证明△AMG≌△ENG，得出AG＝EG；最后证出CG＝EG；（3）结论依然成立，证明方法类似（2）．【详解】（1）证明：∵四边形ABCD是正方形，∴∠DCF＝90°，在Rt△FCD中，∵G为DF的中点，∴CG＝12FD，同理，在Rt△DEF中，EG＝12 FD，∴CG＝EG．（2）解：（1）中结论仍然成立，即EG＝CG．证法：如图，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点，在△DAG与△DCG中，∵AD＝CD，∠ADG＝∠CDG，DG＝DG，∴△DAG≌△DCG（SAS），∴AG＝CG；在△DMG与△FNG中，∵∠DGM＝∠FGN，FG＝DG，∠MDG＝∠NFG，∴△DMG≌△FNG（ASA），∴MG＝NG；∵∠EAM＝∠AEN＝∠AMN＝90°，∴四边形AENM是矩形，在矩形AENM中，AM＝EN，在△AMG与△ENG中，∵AM＝EN，∠AMG＝∠ENG，MG＝NG，∴△AMG≌△ENG（SAS），∴AG＝EG，∴EG＝CG．（3）解：（1）中的结论仍然成立．理由如下：如图，过F作CD的平行线并延长CG交于M点，连接EM、EC，过F作FN垂直于AB于N，∵G为FD中点，∴FG=GD，∵MF∥CD，∴∠FMG=∠DCG，∠GDC=∠GFM，∴△CDG≌△MFG，∴CD＝FM，∵NF∥BC，∴∠NFH+∠NHF=∠EHB+∠EBH，又∵∠NHF=∠EBH，∴∠NFH=∠EBH，∴∠EFM＝∠EBC，又∵BE=EF，则△EFM≌△EBC，∠FEM＝∠BEC，EM＝EC∵∠FEC+∠BEC＝90°，∴∠FEC+∠FEM＝90°，即∠MEC＝90°，∴△MEC是等腰直角三角形，∵G为CM中点，∴EG＝CG，EG⊥CG．【点睛】本题考查全等三角形的判定和性质、矩形的判定与性质，正方形的性质，旋转的性质，解题的关键是掌握相关性质．7．探究：（1）如图①，在△ABC中，∠ACB＝90°，CD⊥AB于点D，若∠B＝28°，则∠ACD的度数是．拓展：（2）如图②，∠MCN＝90°，射线CP在∠MCN的内部，点A、B分别存CM、CN 上，分别过点A、B作AD⊥CP、BE⊥CP于点D、E，若AC＝CB，则AD、DE、BE三者间的数量关系为．请说明理由；应用：（3）如图③，点A、B分别在∠MCN的边CM、CN上，射线CP在∠MCN的内部，点D、E在射线CP上，连结AD、BE、AE，且使∠MCN＝∠ADP＝∠BEP．当AC＝BC 时，△≌△；此时如果CD＝2DE，且S△CBE＝6，则△ACE的面积是．答案：D解析：（1）28°（2）DE＝AD﹣BE；理由见解析（3）ACD；CBE；9【分析】（1）利用直角三角形的两锐角互余，即可得出结论；（2）利用同角的余角相等判断出∠CAD＝∠BCE，进而判断出△ACD≌△CBE，即可得出结论；（3）利用等式的性质判断出∠ADC＝∠CEB，进而判断出△ACD≌△CBE，得出S△ACD＝S△CBE，再求出S△ADE＝3，即可得出结论．【详解】解：探究：∵CD⊥AB，∴∠CDB＝90°，∵∠B＝28°，∴∠BCD＝90°﹣∠B＝68°，∵∠ACB＝90°，∴∠ACD＝90°﹣∠BCD＝28°，故答案为：28°；拓展：(2)∵∠MCN ＝90°，∴∠ACD+∠BCE ＝90°，∵AD ⊥CP ，BE ⊥CP ，∴∠ADC ＝∠BEC ＝90°，∴∠ACD+∠CAD ＝90°，∴∠CAD ＝∠BCE ，在△ACD 和△CBE 中，ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△CBE （AAS ），∴CD ＝BE ，AD ＝CE ，∴DE ＝CE ﹣CD ＝AD ﹣BE ，故答案为：DE ＝AD ﹣BE ；应用：(3)∵∠MCN ＝∠ACD+∠BCD ，∠MCN ＝∠ADP ，∴∠ADP ＝∠ACD+∠BCD ，∵∠ADP ＝∠ACD+∠CAD ，∴∠CAD ＝∠BCE ，∵∠ADP ＝∠BEP ，∴∠ADC ＝∠CEB ，在△ACD 和△CBE 中，ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△CBE （AAS ），∴S △ACD ＝S △CBE ，∵S △CBE ＝6，∴S △ACD ＝6，∵CD ＝2DE ，∴S △ACD ＝2S △ADE ，∴S △ADE ＝12S △ACD ＝3， ∴S △ACE ＝S △ACD +S △ADE ＝9，故答案为：ACD ，CBE ，9．【点睛】此题是三角形综合题，主要考查了直角三角形的性质，同角的余角相等，等式的性质，全等三角形的判定和性质，判断出△ACD ≌△CBE 是解本题的关键．8．如图1，ABC ∆中，CA CB =，ACB α∠=，D 为ABC ∆内一点，将CAD ∆绕点C按逆时针方向旋转角α得到CBE ∆，点,A D 的对应点分别为点,B E ，且,,A D E 三点在同一直线上．（1）填空：CDE ∠=______（用含α的代数式表示）；（2）如图2，若60α=︒，请补全图形，再过点C 作CF AE ⊥于点F ，然后探究线段CF ，AE ，BE 之间的数量关系，并证明你的结论；（3）如图3，若90α=︒，52AC =，直接写出四边形ABEC 面积的最大值______．解析：（1）1802α-；（2）233AE BE CF =+；证明见解析；（3）25(21)2+．【分析】（1）由旋转的性质可得CD CE =，DCE α∠=，即可求解；（2）由旋转的性质可得AD BE =，CD CE =，60DCE ∠=︒，可证CDE ∆是等边三角形，由等边三角形的性质可得33DF EF CF ==，即可求解；（3）如图3中，过点C 作CF BE ⊥交BE 的延长线于F ，设AE 交BC 于J ．证明90ACJ BEJ，推出点E 在以AB 为直径的圆上运动，即图中BC 上运动，当CEEB 时，四边形ABEC 的面积最大，此时EC EB =，分别求出ABC ∆，BCE ∆的面积即可解决问题．【详解】解：（1）如图1中，将CAD ∆绕点C 按逆时针方向旋转角α得到CBE ∆ACD BCE ∴∆≅∆，DCE α∠=CD CE ∴=1802CDE α︒-∴∠=．故答案为：1802α︒-．（2）233AE BE CF =+理由如下：如图2中，将CAD ∆绕点C 按逆时针方向旋转角60︒得到CBE ∆ACD BCE ∴∆≅∆AD BE ∴=，CD CE =，60DCE ∠=︒ CDE ∴∆是等边三角形，且CF DE ⊥ 33DF EF CF ∴==AE AD DF EF =++ 233AE BE CF ∴=+．（3）如图3中，过点C 作CWBE 交BE 的延长线于W ，设AE 交BC 于J ．CAD ∆绕点C 按逆时针方向旋转90︒得到CBE ∆，CAD CBE ，CAD CBE ∴∠=∠， AJC BJE ，90ACJBEJ，∴点E 在以AB 为直径的圆上运动，即图中BC 上运动，当CEEB 时，四边形ABEC的面积最大，此时EC EB =，CD CE =，90DCE ∠=︒， 45CED ∴∠=︒， 90AEW AEB ， 45CEW ， CF EW ， 45WCE CEW ，CWEW ，设CWEWx ，则EC EB ==，在Rt BCW 中，222BC CW BW ，222(2)(52)x xx ，225(22)2x ，21225(21)222BCESBE CW x ， 2521252115252222ABCBCEABECS SS四边形．【点睛】本题考查了圆的性质，等腰三角形的性质，全等三角形的判定和性质，解直角三角形等知识，熟悉相关性质，灵活运用所学知识解决问题是解题的关键． 9．问题解决一节数学课上，老师提出了这样一个问题：如图①，点P 是等边ABC 内的一点，6PA =，8PB = ，10PC =．你能求出APB ∠的度数和等边ABC 的面积吗？小明通过观察、分析、思考，形成了如下思路：如图①将BPC △绕点B 逆时针旋转60°，得到BPA △，连接PP '，可得BPP '是等边三角形，根据勾股定理逆定理可得AP P '是直角三角形，从而使问题得到解决．（1）结合小明的思路完成填空：PP '=_____________，APP '∠=_______________，APB ∠=_____________ ，ABC S = ______________．（2）类比探究Ⅰ如图②，若点P 是正方形ABCD 内一点，1PA = ，2PB =，3PC =，求APB ∠的度数和正方形的面积．Ⅱ如图③，若点P 是正方形ABCD 外一点，3PA = ，1PB =，PC =APB ∠的度数和正方形的面积．答案：B解析：（1）8，90˚，150˚，25336+；（2）Ⅰ135APB ∠=︒， 722ABCD S =+正方形；Ⅱ45APB ∠=︒， 1032ABCD S =-正方形【分析】（1）根据小明的思路，然后利用等腰三角形和直角三角形性质计算即可；（2）Ⅰ将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′，求出∠APB 的度数；先利用旋转求出∠PBP'=90°，BP'=BP=2，AP'=CP=3，利用勾股定理求出PP'，进而判断出△APP'是直角三角形，得出∠APP'=90°，即可得出结论；过B 作BE ⊥AP 于点E ，然后利用勾股定理求出AB 的长度即可求出正方形面积；Ⅱ将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′，求出∠APB 的度数；先利用旋转求出∠PBP'=90°，BP'=BP=2，AP'=CP=3，利用勾股定理求出PP'，进而判断出△APP'是直角三角形，得出∠APP'=90°，即可得出结论；过B 作BF ⊥AP 于点F ，然后利用勾股定理求出AB 的长度即可求出正方形面积；【详解】解:（1）由题易有P BP '∆是等边三角形，AP P '∆是直角三角形 ∴PP '=BP=8，90?APP '=∠，60?P PB '=∠，∴APB ∠=APP '∠+=P PB '∠150˚，如图1，过B 作BD ⊥AP 于点D∵APB ∠=150° ∴30?BPD =∠在Rt △BPD 中，30?BPD =∠，BP=8∴BD=4，PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483 ∴ABCS=234AB =25336+ （2）Ⅰ．如图2，将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′， ∴△ABP'≌△CBP ，∴∠PBP'=90°，BP'=BP=2，AP'=CP=3，在Rt △PBP'中，BP=BP'=2，∴∠BPP'=45°，根据勾股定理得，PP'=2BP=22， ∵AP=1，∴AP 2+PP'2=1+8=9， ∵AP'2=32=9， ∴AP 2+PP'2=AP'2，∴△APP'是直角三角形，且∠APP'=90°， ∴∠APB=∠APP'+∠BPP'=90°+45°=135°；过B 作BE ⊥AP 于点E ， ∵∠APB=135° ∴∠BPE=45°∴△BPE 是等腰直角三角形 ∴BE=BP=22BP 2 ∴2∴AB 2=AE 2+BE 22∴2722ABCD S AB ==+正方形Ⅱ．如图3，将△BPC 绕点B 逆时针旋转90°，得到△BP′A ，连接PP′， ∴△ABP'≌△CBP ，∴∠PBP'=90°，BP'=BP=1，11在Rt △PBP'中，BP=BP'=1，∴∠BPP'=45°，根据勾股定理得，PP'=2BP=2， ∵AP=3，∴AP 2+PP'2=9+2=11， ∵AP'2=（11）2=11， ∴AP 2+PP'2=AP'2，∴△APP'是直角三角形，且∠APP'=90°， ∴∠APB=∠APP'-∠BPP'=90°-45°=45°．过B 作BF ⊥AP 于点F ∵∠APB=45°∴△BPF 为等腰直角三角形 ∴PF=BF=22BP =22 ∴AF=AP-PF=3-22∴AB 2=AF 2+BF 2=1032- ∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题，主要考查了正方形的性质，旋转的性质，直角三角形的性质和判定，勾股定理，正确作出辅助线是解本题的关键． 10．在等腰Rt ABC △中，AB AC =、90BAC ∠=︒．（1）如图1，D ，E 是等腰Rt ABC △斜边BC 上两动点，且45DAE ∠=︒，将ABE △绕点A 逆时针旋转90后，得到AFC △，连接DF ．①求证：AED AFD ≌．②当3BE =，9CE =时，求DE 的长．（2）如图2，点D 是等腰Rt ABC △斜边BC 所在直线上的一动点，连接AD ，以点A 为直角顶点作等腰Rt ADE △（E 点在直线BC 的上方），当3BD =，9BC =时，求DE 的长．答案：D解析：（1）①证明见解析；②5；（2）35或317 【分析】（1）①证明∠DAE=∠DAF=45°即可利用SAS 证明全等；②由①中全等可得DE=DF ，再在Rt △FDC 中利用勾股定理计算即可；（2）连接BE ，根据共顶点等腰直角三角形证明全等，再利用勾股定理计算即可。

初二数学压轴题及答案

【例一】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.（1）求证：OE是CD的垂直平分线.解：证明：∵E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA∴ED=EC∵OE=OE∴Rt△OED≌Rt△OEC∴OC=OD∵OE平分∠AOB∴OE是CD的垂直平分线.（2）若∠AOB=60º，请你探究OE，EF之间有什么数量关系？并证明你的结论。

解：OE=4EF理由如下：∵OE平分∠AOB，∠AOB=60º，∴∠AOE=∠BOE=30º∵ED⊥OA ∴OE=2DE∵∠EFD=90º，∠DEO=90º-∠DOE=90º-30º=60º∴∠EDF=30º∴DE=2EF∴OE=4EF【例二】如图（1）点P是等腰三角形ABC底边BC上的一动点，过点P作BC的垂线，交AB于点Q，交CA的延长线于点R。

请观看AR与AQ，它们相等吗？并证明你的猜想。

解：AR=AQ,理由如下:∵AB=AC,∴∠B=∠C.∵RP⊥BC,∴∠B+∠BQP=∠C+∠PRC=90°,∴∠BQP=∠PRC.∵∠BQP=∠AQR,∴∠PRC=∠AQR,∴AR=AQ;（2）如图(2)如果点P沿着底边BC 所在的直线，按由C向B的方向运动到CB的延长线上时，(1)中所得的结论还成立吗？请你在图(2)中完成图形，并给予证明.解：猜想仍然成立.证明如下:∵AB=AC, ∴∠ABC=∠C.∵∠ABC=∠PBQ,∴∠PBQ=∠C,∵RP⊥BC,∴∠PBQ+∠BQP=∠C+∠PRC=90°,∴∠BQP=∠PRC, ∴AR=AQ.【例三】在△ABC中，AB＝AC，D是AB上一点，过点D作DE∥BC，交AC于点E．（1）如图1，求证：DB＝EC；（2）现将图1中的△ADE绕点A逆时针旋转一个角度，如图2，连接DB、EC．①结论DB＝EC是否仍然成立？若成立，请给予证明；若不成立，请说明理由；【解答】∵AB＝AC，∴∠B＝∠C，又∵DE∥BC，∴∠ADE＝∠B，∠AED＝∠C，∴∠ADE＝∠AED，∴AD＝AE，∴AB﹣AD＝AC﹣AE，∴BD＝CE．②延长BD交EC于点P（请自己在图2中画出图形并表明字母），若∠ACB＝70°，请求出∠BPC的度数．【解答】如图2﹣2中．设AC交BD于点O．∵AB＝AC，∴∠ABC ＝∠ACB＝70°，∴∠BAC＝180°﹣70°﹣70°＝40°，∵△ADB≌△AEC，∴∠ABO＝∠PCO，∵∠AOB＝∠POC，∴∠BPC＝∠BAO＝40°．【例四】如图，点B在线段AC上，点E在线段BD上，∠ABD＝∠DBC，AB＝DB，EB＝CB，M，N分别是AE，CD的中点。

初二数学压轴几何证明题(含答案)

1.四边形是正方形，△是等腰直角三角形，∠90°，，连接，G 为的中点，连接，，．(1)如图1，若点E在边的延长线上，直接写出与的位置关系及的值；(2)将图1中的△绕点B顺时针旋转至图2所示位置，请问(1)中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；(3)将图1中的△绕点B顺时针旋转α(0°＜α＜90°)，若1，，当E，F，D三点共线时，求的长及∠的值．解：（1）⊥，=，理由是：过G作⊥于H，∵∠∠90°，∴∥∥，∵G为中点，∴H为中点，∴，（）=（），即，∴∠90°，即△是等腰直角三角形，∴=；（2）解：结论还成立，理由是：如图2，延长到H，使，连接、，过E作的垂线，延长，∵在△和△中∴△≌△（），∴，∠∠，∴∥，∴∠1=∠2=90°-∠3=∠4，∴∠180°-∠4=180°-∠1=∠，在△和△中∴△≌△．∴，∠∠，∴∠∠∠∠∠∠90°，∴△是等腰直角三角形，∵G为的中点，∴⊥，=，即（1）中的结论仍然成立；（3）解：连接，∵，正方形，∴2，∴∠，∴∠60°，∴∠∠∠15°，∴∠45°-15°=30°，∴∠，∴，∴1．解析：（1）过G作⊥于H，推出∥∥，求出H为中点，根据梯形的中位线求出，（）=（），推出，根据直角三角形的判定推出△是等腰直角三角形即可；（2）延长到H，使，连接、，过E作的垂线，延长，证△≌△，推出，∠∠，求出∠∠，证出△≌△，推出，∠∠，求出△是等腰直角三角形，即可得出答案；（3）连接，求出∠，推出∠60°，求出∠30°，解直角三角形求出即可．2.已知正方形和等腰直角三角形，，∠90°，按图1放置，使点E在上，取的中点G，连接，．(1)延长交于H，试说明：．(2)将图1中△绕B点逆时针旋转45°，连接，取中点G(如图2)，莎莎同学发现：且⊥．在设法证明时他发现：若连接，则D，E，B三点共线．你能写出结论“且⊥”的完整理由吗？请写出来．(3)将图1中△绕B点转动任意角度α(0＜α＜90°)，再连接，取的中点G(如图3)，第2问中的结论是否成立？若成立，试说明你的结论；若不成立，也请说明理由．（1）证明：∵∠90°，∴∥，∴∠∠，而∠∠，，∴△≌△，∴，而，∴；（2）连接，如图，∵△为等腰直角三角形，∴∠45°，而四边形为正方形，∴∠45°，∴D，E，B三点共线．而∠90°，∴△为直角三角形，而G为的中点，∴，∴∠2∠90°，∴且⊥；（3）第2问中的结论成立．理由如下：连接、相交于点O，取的中点M，连接、、，如图，∵G为的中点，O为的中点，M为的中点，∴∥，∥，∴四边形为平行四边形，∴，，而，，∴，，∵∠∠，而∠∠90°，∴∠∠，∴△≌△，∴，∠∠，又∵∠∠，∠∠∠，∴∠∠∠∠∠∠∠∠45°+45°=90°，∴且⊥．解析：（1）由∠90°，得到∥，而，易证得△≌△，得，而，即可得到结论．（2）连接，如图2，由△为等腰直角三角形，得∠45°，而四边形为正方形，得∠45°，得到D，E，B三点共线，而G为的中点，根据直角三角形斜边上的中线等于斜边的一半得到，于是∠2∠90°，即得到结论．（3）连接、相交于点O，取的中点M，连接、、，由G为的中点，O为的中点，M为的中点，根据三角形中位线的性质得∥，∥，得到，，而，，得到，，又∠∠，而∠∠90°，得∠∠，则△≌△，得到，∠∠，而∠∠，∠∠∠，所以有∠∠∠∠∠∠∠∠45°+45°=90°．3.已知正方形和等腰△，，∠90°，按图①放置，使点F在上，取的中点G，连接、．(1)探索、的数量关系和位置关系并证明；(2)将图①中△绕B点顺时针旋转45°，再连接，取中点G(如图②)，问(1)中的结论是否仍然成立．证明你的结论；(3)将图①中△绕B点转动任意角度(旋转角在0°到90°之间)，再连接，取的中点G(如图③)，问(1)中的结论是否仍然成立，证明你的结论．解：（1）且⊥．证明如下：如图①，连接．∵正方形和等腰△，∴∠∠45°．∴B、E、D三点共线．∵∠90°，G为的中点，∠90°，∴．∴∠2∠，∠2∠．∴∠∠2∠90°，即∠90°，∴⊥．（2）仍然成立，证明如下：如图②，延长交于点H．∵⊥，∴∥，∴∠1=∠2．又∵∠3=∠4，，∴△≌△，∴，．∵△为等腰直角三角形，∴，∴．∵，∴．∴△为等腰直角三角形．又∵，∴且⊥．（3）仍然成立．证明如下：如图③，延长至H，使，连接交于M，连接、．∵，∠∠，，∴△≌△，∴，∠∠，∴∥．∵正方形，∴，⊥．∵△是等腰直角三角形，∴，∠∠，∴△≌△，∴，∠∠，∴∠∠90°，∴△为等腰直角三角形．又∵，∴且⊥．解析：（1）首先证明B、E、D三点共线，根据直角三角形斜边上的中线等于斜边的一半，即可证明，得到∠2∠，∠2∠，从而证得∠90°；（2）首先证明△≌△，然后证明△为等腰直角三角形．可以证得：且⊥．（3）首先证明：△≌△，即可证得：△为等腰直角三角形，从而得到：且⊥．已知，正方形中，△为等腰直角三角形，且为底，取的中点G，连接、．（1）如图1，若△的底边在上，猜想和的数量关系为；（2）如图2，若△的直角边在上，则（1）中的结论是否还成立？请说明理由；（3）如图3，若△的直角边在∠内，则（1）中的结论是否还成立？说明理由．解：（1），（1分）理由如下： ∵△为等腰直角三角形，∴∠90°，又G 为斜边的中点， ∴ ， ∵为正方形， ∴∠90°，又G 为斜边的中点，∴ ，∴；（2）成立．如图，延长交于M ，∵∠∠∠90°，∴∥，∴∠∠，又∠∠，，1212∴，即G 为的中点．∴为直角△的斜边上的中线，∴ ；（3）成立．取的中点H ，连接，，取的中点O ，连接，．∵，∠90°，∴． ∵，∴∥，且，∥，且， ∴．∵△为等腰直角三角形．∴∴．∵四边形为平行四边形，∴∠∠．∵∠∠90°．∴∠∠．121 212 1 2∴．此题考查了正方形的性质，以及全等三角形的判定与性质．要求学生掌握直角三角形斜边上的中线等于斜边的一半，以及三角形的中位线与第三边平行且等于第三边的一半．掌握这些性质，熟练运用全等知识是解本题的关键．解析：（1），理由为：根据三角形为等腰直角三角形，得到∠为直角，又G为中点，根据在直角三角形中，斜边上的中线等于斜边的一半，得到为的一半，同理在直角三角形中，得到也等于的一半，利用等量代换得证；（2）成立．理由为：延长交于M，如图所示，根据“”得到三角形与三角形全等，由全等三角形的对应边相等得到与相等，即G为中点，根据直角三角形斜边上的中线等于斜边的一半得到与相等都等于斜边的一半，得证；（3）成立．理由为：取的中点H，连接，，取的中点O，连接，，如图所示，因为直角三角形中，O为斜边的中点，根据斜边上的中线等于斜边的一半得到等于的一半，由为三角形的中位线，根据三角形的中位线平行于第三边且等于第三边的一半，得到等于一半，等于的一半，又根据直角三角形斜边上的中线等于斜边的一半得到等于的一半，根据等量代换得到与相等，再根据为平行四边形，根据平行四边形的性质得到对边相等，对角相等，进而得到∠与∠相等，利用“”得到△与△全等，利用全等三角形的对应边相等即可得证．。

苏科版八年级上册几何压轴题专题(解析版)

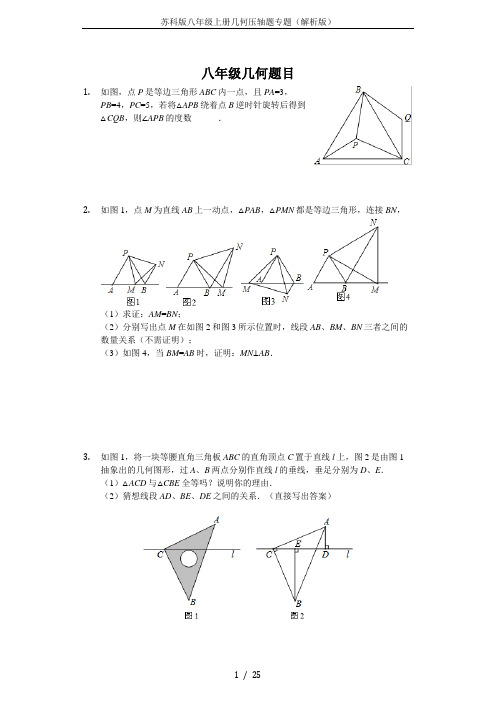
苏科版八年级上册几何压轴题专题（解析版）八年级几何题目1.如图，点P是等边三角形ABC内一点，且PA=3，PB=4，PC=5，若将△APB绕着点B逆时针旋转后得到△CQB，则∠APB的度数______．2.如图1，点M为直线AB上一动点，△PAB，△PMN都是等边三角形，连接BN，（1）求证：AM=BN；（2）分别写出点M在如图2和图3所示位置时，线段AB、BM、BN三者之间的数量关系（不需证明）；（3）如图4，当BM=AB时，证明：MN⊥AB．3.如图1，将一块等腰直角三角板ABC的直角顶点C置于直线l上，图2是由图1抽象出的几何图形，过A、B两点分别作直线l的垂线，垂足分别为D、E．（1）△ACD与△CBE全等吗？说明你的理由．（2）猜想线段AD、BE、DE之间的关系．（直接写出答案）1/ 254.（1）问题发现如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，求∠AEB的度数．（2）拓展探究如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请求∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．5.如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．试回答：（1）图中等腰三角形是______ ．猜想：EF与BE、CF之间的关系是______ ．理由：（2）如图②，若AB≠AC，图中等腰三角形是______ ．在第（1）问中EF与BE、CF间的关系还存在吗？（3）如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O 点作OE∥BC交AB于E，交AC于F．这时图中还有等腰三角形吗？EF与BE、CF关系又如何？说明你的理由．苏科版八年级上册几何压轴题专题（解析版）6.如图1，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，（1）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数；（2）何时△PBQ是直角三角形？（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数．7.如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（点D不与点B、C重合），连接AD，作∠ADE=40°，DE交线段AC于点E．（1）当∠BDA=115°时，∠EDC=______°，∠AED=______°；（2）线段DC的长度为何值时，△ABD≌△DCE，请说明理由；（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求∠BDA的度数；若不可以，请说明理由．8.如图，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的速度都为1cm/s．当点P到达点B时，P，Q两点3/ 25停止运动，设点P的运动时间为t（s）．（1）当t为何值时，△PBQ是直角三角形？（2）连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．9.【新知理解】如图①，若点A、B在直线l同侧，在直线l上找一点P，使AP+BP的值最小．作法：作点A关于直线l的对称点A'，连接A'B交直线l于点P，则点P即为所求．【解决问题】如图②，AD是边长为6cm的等边三角形ABC的中线，点P、E分别在AD、AC 上，则PC+PE的最小值为______cm；【拓展研究】如图③，在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD．（保留作图痕迹，并对作图方法进行说明）苏科版八年级上册几何压轴题专题（解析版）10.在△ABC中，∠C=90°，AC=BC=2，将一块三角板的直角顶点放在斜边AB的中点P处，将此三角板绕点P旋转，三角板的两直角边分别交射线AC、CB与点D、点E，图①，②，③是旋转得到的三种图形．（1）观察线段PD和PE之间的有怎样的大小关系，并以图②为例，加以说明；（2）△PBE是否构成等腰三角形？若能，指出所有的情况（即求出△PBE为等腰三角形时CE的长）；若不能请说明理由．11.（1）观察猜想如图①点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE=90°，AD=AE，则BC、BD、CE之间的数量关系为______；（2）问题解决如图②，在Rt△ABC中，∠ABC=90°，CB=4，AB=2，以AC为直角边向外作等腰Rt△DAC，连结BD，求BD的长；（3）拓展延伸如图③，在四边形ABCD中，∠ABC=∠ADC=90°，CB=4，AB=2，DC=DA，请直接写出BD的长．12.如图，四边形ABCD是正方形，E是直线CD上的点，将△ADE沿AE对折得△AFE，直线EF交边BC于点G，连接5/ 25AG．(1)求证：△ABG≌△AFG；(2)当DE是线段CD的一半时，请你在备用图中利用尺规作图画出符合题意的图形(保留作图痕迹，不写作法)(3)在(2)的条件下，求∠EAG的度数．13.如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B 开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．（1）出发2秒后，求△PBQ的面积；（2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？（3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．14.如图，边长为4cm的等边△ABC中，点P、Q分别是边AB、BC上的动点（端点除外），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ，CP交于点M，在点P，Q运动的过程中．苏科版八年级上册几何压轴题专题（解析版）（1）求证：△ABQ≌△CAP；（2）∠QMC的大小是否发生变化？若无变化，求∠QMC的度数；若有变化，请说明理由；（3）连接PQ，当点P，Q运动多少秒时，△PBQ是直角三角形？15.已知△ABC中，AB=AC，BC=6．点P从点B出发沿射线BA移动，同时点Q从点C出发沿线段AC的延长线移动，点P、Q移动的速度相同，PQ与直线BC相交于点D．（1）如图①，过点P作PF∥AQ交BC于点F，求证：△PDF≌△QDC；（2）如图②，当点P为AB的中点时，求CD的长；（3）如图③，过点P作PE⊥BC于点E，在点P从点B向点A移动的过程中，线段DE的长度是否保持不变？若保持不变，请求出DE的长度，若改变，请说明理由．16.如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B 开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．7/ 25（1）出发2秒后，求PQ的长；（2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？（3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．17.如图1，△ABC是等边三角形，点E在AC边上，点D是BC边上的一个动点，以DE为边作等边△DEF，连接CF．（1）当点D与点B重合时，如图2，求证：CE + CF = CD；（2）当点D运动到如图3的位置时，猜想CE、CF、CD之间的等量关系，并说明理由；（3）只将条件“点D是BC边上的一个动点”改为“点D是BC延长线上的一个动点”，如图4，猜想CE、CF、CD之间的等量关系为___________________（不必证明）．苏科版八年级上册几何压轴题专题（解析版）18.如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB、AC引垂线，垂足分别为E、F点．（1）当点D在BC的什么位置时，DE=DF？并证明．（2）在满足第一问的条件下，连接AD，此时图中共有几对全等三角形？并请给予写出．（3）过C点作AB边上的高CG，请问DE、DF、CG的长之间存在怎样的等量关系？并加以证明．9/ 25答案和解析1.【答案】150°【解析】解：连接PQ，由题意可知△ABP≌△CBQ则QB=PB=4，PA=QC=3，∠ABP=∠CBQ，∵△ABC是等边三角形，∴∠ABC=∠ABP+∠PBC=60°，∴∠PBQ=∠CBQ+∠PBC=60°，∴△BPQ为等边三角形，∴PQ=PB=BQ=4，又∵PQ=4，PC=5，QC=3，∴PQ2+QC2=PC2，∴∠PQC=90°，∵△BPQ为等边三角形，∴∠BQP=60°，∴∠BQC=∠BQP+∠PQC=150°,∴∠APB=∠BQC=150°.首先证明△BPQ为等边三角形，得∠BQP=60°，由△ABP≌CBQ可得QC=PA，在△PQC 中，已知三边，用勾股定理逆定理证出得出∠PQC=90°，可求∠BQC的度数，由此即可解决问题．本题考查旋转的性质、等边三角形的判定和性质、勾股定理的逆定理等知识，解题的关键是勾股定理逆定理的应用，属于中考常考题型．2.【答案】（1）证明：∵△PAB和△PMN是等边三角形，∴∠BPA=∠MPN=60°，AB=BP=AP，PM=PN=MN，∴∠BPA-∠MPB=∠MPN-∠MPB，∴∠APM=∠BPN．在△APM和△BPN中{AP=PB∠APM=∠BPN PM=PN，∴△APM≌△BPN（SAS），∴AM=BN；（2）解：图2中BN=AB+BM；图3中BN=BM-AB，（3）证明：∵△PAB和△PMN是等边三角形，∴∠ABP=∠PMN=60°，AB=PB，∴∠PBM=120°，∵BM=AB=PB，∴∠BMP=30°，∴∠BMN=∠PMN+∠BMP=90°，∴MN⊥AB．【解析】本题考查了等边三角形的性质的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键．（1）根据等边三角形的性质就可以得出∠BPA=∠MPN=60°，AB=BP=AP，PM=PN=MN，进而就可以得出△APM≌△BPN，得出结论；（2）由（1）中的方法证得△APM≌△BPN，得出图2中，BN=AB+BM；得出图3中，苏科版八年级上册几何压轴题专题（解析版）11 / 25BN =BM -AB ；（3）由等边三角形的性质得出∠ABP =∠PMN =60°，就可以得出∠PBM =120°，求得∠BMP =30°，进而就可以得出∠BMN =90°，得出结论．3.【答案】证明：（1）△ACD 与△CBE 全等.理由如下：∵AD ⊥CE ，BE ⊥CE ，∴∠ADC =∠CEB =90°，又∵∠ACB =90°，∴∠ACD =∠CBE =90°-∠ECB ．在△ACD 与△CBE 中，{∠ADC =∠CEB∠ACD =∠CBE AC =BC，∴△ACD ≌△CBE （AAS ）；（2）AD =BE -DE .【解析】【分析】本题考查全等三角形的判定与性质，余角的性质，关键是根据AAS 证明三角形全等. （1）观察图形，结合已知条件，可知全等三角形为：△ACD 与△CBE ．根据AAS 即可证明；（2）由（1）知△ACD ≌△CBE ，根据全等三角形的对应边相等，得出CD =BE ，AD =CE ，从而求出线段AD 、BE 、DE 之间的关系.【解答】解：（1）见答案；（2）∵△ACD ≌△CBE ，∴CD =BE ，AD =CE ，又∵CE =CD -DE ，∴AD =BE -DE .4.【答案】解：（1）∵△ACB 和△DCE 均为等边三角形，∴CA =CB ，CD =CE ，∠ACB =∠DCE =60°，∴∠ACD =60°-∠CDB =∠BCE ，在△ACD 和△BCE 中，{AC =BC ∠ACD =∠BCE CD =CE，∴△ACD ≌△BCE （SAS ），∴∠ADC =∠BEC ，∵△DCE 为等边三角形，∴∠CDE =∠CED =60°，∵点A ，D ，E 在同一直线上，∴∠ADC =120°，∴∠BEC =120°，∴∠AEB =∠BEC -∠CED =60°. （2）∠AEB =90°，AE =BE +2CM .理由：∵△ACB 和△DCE 均为等腰直角三角形，∴CA =CB ，CD =CE ，∠ACB =∠DCE =90°，∴∠ACD =∠BCE ，在△ACD 和△BCE 中，{CA=CB∠ACD=∠BCE CD=CE，∴△ACD≌△BCE（SAS），∴AD=BE，∠ADC=∠BEC，∵△DCE为等腰直角三角形，∴∠CDE=∠CED=45°，∵点A，D，E在同一直线上，∴∠ADC=135°，∴∠BEC=135°，∴∠AEB=∠BEC-∠CED=90°，∵CD=CE，CM⊥DE，∴DM=ME．∵∠DCE=90°，∴DM=ME=CM．∴AE=AD+DE=BE+2CM.【解析】本题考查了全等三角形的判定与性质和等腰三角形的判定与性，证明三角形全等是解决问题的关键.（1）先证出∠ACD=∠BCE，那么△ACD≌△BCE，根据全等三角形证出∠ADC=∠BEC，求出∠ADC=120°，得出∠BEC=120°，从而证出∠AEB=60°；（2）证明△ACD≌△BCE，得出∠ADC=∠BEC，最后证出DM=ME=CM即可.5.【答案】(1)△AEF、△OEB、△OFC、△OBC、△ABC；EF=BE+CF；理由如下：∵OB、OC平分∠ABC、∠ACB，∴∠ABO=∠OBC，∠ACO=∠OCB；∵EF∥BC，∴∠EOB=∠OBC=∠EBO，∠FOC=∠OCB=∠FCO；即EO=EB，FO=FC；∴EF=EO+OF=BE+CF;(2)△EOB、△FOC;当AB≠AC时，△EOB、△FOC仍为等腰三角形，（1）的结论仍然成立．（证明过程同（1））;(3)△EOB和△FOC仍是等腰三角形，EF=BE-FC;理由如下：同（1）可证得△EOB是等腰三角形；∵EO∥BC，∴∠FOC=∠OCG,∵OC平分∠ACG，∴∠ACO=∠FOC=∠OCG，∴FO=FC，故△FOC是等腰三角形,∴EF=EO-FO=BE-FC．【解析】解：（1）图中是等腰三角形的有：△AEF、△OEB、△OFC、△OBC、△ABC；EF、BE、FC的关系是EF=BE+FC．理由如下：∵OB、OC平分∠ABC、∠ACB，∴∠ABO=∠OBC，∠ACO=∠OCB,∵EF∥BC，∴∠EOB=∠OBC=∠EBO，∠FOC=∠OCB=∠FCO,即EO=EB，FO=FC,苏科版八年级上册几何压轴题专题（解析版）13 / 25 ∴EF =EO +OF =BE +CF ;（2）当AB ≠AC 时，△EOB 、△FOC 仍为等腰三角形，（1）的结论仍然成立．（证明过程同（1））;（3）△EOB 和△FOC 仍是等腰三角形，EF =BE -FC ．理由如下：同（1）可证得△EOB 是等腰三角形；∵EO ∥BC ，∴∠FOC =∠OCG ,∵OC 平分∠ACG ，∴∠ACO =∠FOC =∠OCG ，∴FO =FC ，故△FOC 是等腰三角形,∴EF =EO -FO =BE -FC ．（1）由AB =AC ，可得∠ABC =∠ACB ；又已知OB 、OC 分别平分∠ABC 、∠ACB ；故∠EBO =∠OBC =∠FCO =∠OCB ；根据EF ∥BC ，可得：∠EOB =∠OBC =∠EBO ，∠FOC =∠FCO =∠BCO ；由此可得出的等腰三角形有：△AEF 、△OEB 、△OFC 、△OBC 、△ABC ；已知了△EOB 和△FOC 是等腰三角形，则EO =BE ，OF =FC ，则EF =BE +FC ．（2）由（1）的证明过程可知：在证△OEB 、△OFC 是等腰三角形的过程中，与AB =AC 的条件没有关系，故这两个等腰三角形还成立．所以（1）中得出的EF =BE +FC 的结论仍成立．（3）思路与（2）相同，只不过结果变成了EF =BE -FC ．此题主要考查了等腰三角形的判定，平行线的性质、角平分线的定义等知识．进行线段的等量代换是正确解答本题的关键．6.【答案】解：（1）∠CMQ =60°不变． ∵等边三角形中，AB =AC ，∠B =∠CAP =60°又由条件得AP =BQ ，∴△ABQ ≌△CAP （SAS ），∴∠BAQ =∠ACP ，∴∠CMQ =∠ACP +∠CAM =∠BAQ +∠CAM =∠BAC =60°．（2）设时间为t ，则AP =BQ =t ，PB =4-t①当∠PQB =90°时，∵∠B =60°，∴PB =2BQ ，得4-t =2t ，t =43；②当∠BPQ =90°时，∵∠B =60°，∴BQ =2BP ，得t =2（4-t ），t =83；∴当第43秒或第83秒时，△PBQ 为直角三角形．（3）∠CMQ =120°不变．∵在等边三角形中，BC =AC ，∠B =∠CAP =60°∴∠PBC =∠ACQ =120°，又由条件得BP =CQ ，∴△PBC≌△QCA（SAS）∴∠BPC=∠MQC又∵∠PCB=∠MCQ，∴∠CMQ=∠PBC=180°-60°=120°【解析】（1）因为点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，所以AP=BQ．AB=AC，∠B=∠CAP=60°，因而运用边角边定理可知△ABQ≌△CAP．再用全等三角形的性质定理及三角形的角间关系、三角形的外角定理，可求得CQM的度数．（2）设时间为t，则AP=BQ=t，PB=4-t．分别就①当∠PQB=90°时；②当∠BPQ=90°时利用直角三角形的性质定理求得t的值．（3）首先利用边角边定理证得△PBC≌△QCA，再利用全等三角形的性质定理得到∠BPC=∠MQC．再运用三角形角间的关系求得∠CMQ的度数．此题是一个综合性很强的题目．本题考查等边三角形的性质、全等三角形的判定与性质、直角三角形的性质．难度很大，有利于培养同学们钻研和探索问题的精神．7.【答案】（1）25；65；（2）当DC=2时，△ABD≌△DCE，理由：∵∠C=40°，∴∠DEC+∠EDC=140°，又∵∠ADE=40°，∴∠ADB+∠EDC=140°，∴∠ADB=∠DEC，又∵AB=DC=2，在△ABD和△DCE中{∠ADB=∠DEC ∠B=∠CAB=DC，∴△ABD≌△DCE（AAS）；（3）当∠BDA的度数为110°或80°时，△ADE的形状是等腰三角形，∵∠BDA=110°时，∴∠ADC=70°，∵∠C=40°，∴∠DAE=70°，∴∠AED=180°-70°-40°=70°，∴△ADE的形状是等腰三角形；∵当∠BDA的度数为80°时，∴∠ADC=100°，∵∠C=40°，∴∠DAE=40°，∴∠DAE=∠ADE，∴△ADE的形状是等腰三角形．【解析】【分析】此题主要考查学生对等腰三角形的判定与性质，全等三角形的判定与性质，三角形外角的性质等知识点的理解和掌握，此题涉及到的知识点较多，综合性较强，但难度不大，属于基础题．苏科版八年级上册几何压轴题专题（解析版） 15 / 25（1）利用邻补角的性质和三角形内角和定理解题；（2）当DC =2时，利用∠DEC +∠EDC =140°，∠ADB +∠EDC =140°，求出∠ADB =∠DEC ，再利用AB =DC =2，即可得出△ABD ≌△DCE ．（3）当∠BDA 的度数为110°或80°时，△ADE 的形状是等腰三角形．【解答】解：（1）∠EDC =180°-∠ADB -∠ADE =180°-115°-40°=25°；∠AED =∠EDC +∠C =40°+25°=65°．故答案为25；65；（2）、（3）见答案.8.【答案】解：（1）设时间为t ，则AP =BQ =t ，PB =5-t①当∠PQB =90°时，∵∠B =60°，∴PB =2BQ ，得5-t =2t ，t =53； ②当∠BPQ =90°时，∵∠B =60°，∴BQ =2BP ，得t =2（5-t ），t =103；∴当第53秒或第103秒时，△PBQ 为直角三角形．（2）∠CMQ =60°不变．在△ABQ 与△CAP 中，{AB =AC∠B =∠CAP =60°AP =BQ，∴△ABQ ≌△CAP （SAS ），∴∠BAQ =∠ACP ，∴∠CMQ =∠ACP +∠CAM =∠BAQ +∠CAM =∠BAC =60°．【解析】（1）需要分类讨论：分∠PQB =90°和∠BPQ =90°两种情况；（2）∠CMQ =60°不变．通过证△ABQ ≌△CAP （SAS ）得到：∠BAQ =∠ACP ，由三角形外角定理得到∠CMQ =∠ACP +∠CAM =∠BAQ +∠CAM =∠BAC =60°．本题考查了全等三角形的判定与性质，等边三角形的性质．掌握判定三角形全等的方法，分类讨论是解决问题的关键．9.【答案】【解决问题】3√3【拓展研究】方法1：如图③，作B 关于AC 的对称点E ，连接DE 并延长，交AC 于P ，点P 即为所求，连接BP ，则∠APB =∠APD ．方法2：如图④，作点D关于AC的对称点D'，连接D'B并延长与AC的交于点P，点P即为所求，连接DP，则∠APB=∠APD．【解析】解：（1）【解决问题】如图②，作点E关于AD的对称点F，连接CF，交AD于点P，则PE=PF，当点F，P，C在一条直线上时，PC+PE=PC+PF=CF（最短），AB=3（cm），当CF⊥AB时，CF最短，此时BF=12∴Rt△BCF中，CF=√BC2−BF2=√62−32=3√3（cm），∴PC+PE的最小值为3√3cm，故答案为：3√3；（2）【拓展研究】方法1：如图③，作B关于AC的对称点E，连接DE并延长，交AC于P，点P即为所求，连接BP，则∠APB=∠APD．苏科版八年级上册几何压轴题专题（解析版） 17 / 25方法2：如图④，作点D 关于AC 的对称点D '，连接D 'B 并延长与AC 的交于点P ，点P 即为所求，连接DP ，则∠APB =∠APD ．（1）作点E 关于AD 的对称点F ，连接CF ，则PE =PF ，根据两点之间线段最短以及垂线段最短，得出当CF ⊥AB 时，PC +PE =PC +PF =CF （最短），最后根据勾股定理，求得CF 的长即可得出PC +PE 的最小值；（2）根据轴对称的性质进行作图．方法1：作B 关于AC 的对称点E ，连接DE 并延长，交AC 于P ，连接BP ，则∠APB =∠APD ．方法2：作点D 关于AC 的对称点D '，连接D 'B 并延长与AC 的交于点P ，连接DP ，则∠APB =∠APD ．本题属于轴对称-最短路线问题，本题考查了勾股定理、轴对称的性质，利用轴对称作图与基本作图等知识点的综合应用，熟知两点之间，线段最短以及垂线段最短是解答此题的关键．10.【答案】解：（1）PD =PE ．以图②为例，如图，连接PC∵△ABC 是等腰直角三角形，P 为斜边AB 的中点，∴PC =PB ，CP ⊥AB ，∠DCP =∠B =45°，又∵∠DPC +∠CPE =90°，∠CPE +∠EPB =90°∴∠DPC =∠EPB∴△DPC ≌△EPB （ASA ）∴PD =PE ；（2）能，①当EP =EB 时，CE =12BC =1．②当EP =PB 时，点E 在BC 上，则点E 和C 重合，CE =0．③当BE =BP 时，若点E 在BC 上，则CE =2-√2．若点E 在CB 的延长线上，则CE =2+√2．【解析】（1）连接PC ，通过证明△DPC ≌△EPB ，得出PD =PE ．（2）分EP =EB 、EP =PB 时、BE =BP 三种情况进行解答．本题考查了等腰三角形的性质与判定；此题是分类讨论题，应分情况进行论证，不能漏解．辅助线的作出是解答本题的关键．11.【答案】（1）BC =AB +AC =BD +CE（2）问题解决如图②，过D 作DE ⊥AB ，交BA 的延长线于E ，由（1）同理得：△ABC ≌△DEA ，∴DE =AB =2，AE =BC =4，Rt △BDE 中，BE =6，由勾股定理得：BD =√62+22=2√10；（3）拓展延伸如图③，过D 作DE ⊥BC 于E ，作DF ⊥AB 于F ，同理得：△CED ≌△AFD ，∴CE =AF ，ED =DF ，设AF =x ，DF =y ，则{x +y =42+x =y，解得：{x =1y =3， ∴BF =2+1=3，DF =3，由勾股定理得：BD =√32+32=3√2．【解析】解：（1）观察猜想结论：BC =BD +CE ，理由是：如图①，∵∠B =90°，∠DAE =90°，∴∠D +∠DAB =∠DAB +∠EAC =90°，∴∠D =∠EAC ，∵∠B =∠C =90°，AD =AC ，∴△ADB ≌△EAC ，∴BD =AC ，EC =AB ，∴BC =AB +AC =BD +CE ；（2）见答案；（3）见答案；【分析】（1）观察猜想：证明△ADB ≌△EAC ，可得结论：BC =AB +AC =BD +CE ；（2）问题解决：作辅助线，同理证明：△ABC ≌△DEA ，可得DE =AB =2，AE =BC =4，最后利用勾股定理求BD 的长；（3）拓展延伸：同理证明三角形全等，设AF =x ，DF =y ，根据全等三角形对应边相等列方程组可得结论．本题考查了全等三角形的性质定理与判定定理、勾股定理，解决本题的关键是证明：△CED ≌△AFD ，并运用了类比的思想依次解决问题．12.【答案】解：（1）证明：∵四边形ABCD 为正方形，∴AB =AD ，∠B =∠D =90°，∵将△ADE 沿AE 对折得△AFE ，∴AF =AD =AB ，∠AFE =∠D =90°，在Rt △ABG 与Rt △AFG 中，AF =AB ,AG =AG ,∴△ABG ≌△AFG （HL ）；（2）如图所示：苏科版八年级上册几何压轴题专题（解析版）19 / 25（3）∵△AFE ≌△ADE ，△ABG ≌△AFG ，∴∠EAF =∠EAD ，∠GAF =∠GAB ，∵在正方形ABCD 中，∠BAD =90°．∴∠EAG =∠EAF +∠GAF =12×90°=45°．【解析】此题主要考查了折叠的性质、正方形的性质和全等三角形的性质及判定，综合利用各性质定理是解答此题的关键．（1）利用正方形的性质和折叠的性质可得AF =AB ，∠AFE =∠D ，由HL 定理可证得Rt △ABG ≌Rt △AFG ；（2）首先作出CD 的垂直平分线，与CD 相交于点E ，再以E 点为圆心，DE 为半径作弧，A 点为圆心，AF 为半径作弧，两弧相交于点F ，连接AF ，AE ，EF ，延长EF 与BC 相交于点G ，如图所示；（3）由△AFE ≌△ADE ，△ABG ≌△AFG ，利用全等三角形的性质可得∠EAF =∠EAD ，∠GAF =∠GAB ，易得∠EAG =∠EAF +∠GAF =12∠BAD ，可得结论. 13.【答案】解：（1）当t =2时，则AP =2cm ，BQ =2t =4cm ，∵AB =16cm ，∴BP =AB -AP =16-2=14（cm ），在Rt △BPQ 中，S △PBQ =12BP ×BQ =28cm 2．（2）由题意可知AP =t ，BQ =2t ，∵AB =16cm ，∴BP =AB -AP =(16-t )cm ，当△PQB 为等腰三角形时，则有BP =BQ ，即16-t =2t ，解得t =163，∴出发163秒后△PQB 能形成等腰三角形.（3）①当CQ =BQ 时，如图1所示，则∠C =∠CBQ ，∵∠ABC =90°，∴∠CBQ +∠ABQ =90°，AC =√AB 2+BC 2=√162+122=20cm ．又∵∠A +∠C =90°，∴∠A =∠ABQ ，∴BQ =AQ ，∴CQ =AQ =12AC =10cm ，∴BC +CQ =22cm ，∴t =22÷2=11． ②当CQ =BC 时，如图2所示，则BC +CQ =24cm ，∴t =24÷2=12． ③当BC =BQ 时，如图3所示，过B 点作BE ⊥AC 于点E ，则BE =AB⋅BC AC =12×1620=485cm ，∴CE =√BC 2−BE 2=√122−(485)2=365cm ， ∴CQ =2CE =14.4cm ，∴BC +CQ =26.4cm ，∴t =26.4÷2=13.2．综上所述：当出发的时间为11秒或12秒或13.2秒时，△BCQ 为等腰三角形．【解析】本题主要考查了勾股定理、等腰三角形的性质和判定，三角形的面积和分类讨论思想等知识．用时间t 表示出相应线段的长，注意方程思想的应用．（1）可求得AP 和BQ ，则可求得BP ，最后用三角形面积公式即可得出结论；（2）用t 可分别表示出BP 和BQ ，根据等腰三角形的性质可得到BP =BQ ，可得到关于t 的方程，可求得t 的值；（3）利用等腰三角形的性质可分BQ =CQ 、CQ =BC 和BQ =BC 三种情况，分别得到关于t 的方程，可求得t 的值．14.【答案】（1）证明：∵△ABC 是等边三角形，∴∠ABQ =∠CAP =60°，AB =CA ，∵点P 、Q 的速度相同，∴AP =BQ ，在△ABQ 和△CAP 中，{AB =CA∠ABQ =∠CAP AP =BQ ，苏科版八年级上册几何压轴题专题（解析版） 21 / 25 ∴△ABQ ≌△CAP （SAS ）；（2）解：∠QMC 的大小不发生变化，∵△ABQ ≌△CAP ，∴∠BAQ =∠ACP ，∴∠QMC =∠QAC +∠ACP =∠QAC +∠BAQ =60°；（3）解：设点P ，Q 运动x 秒时，△PBQ 是直角三角形，则AP =BQ =x ，PB =（4-x ），当∠PQB =90°时，∵∠B =60°，∴BP =2BQ ，即4-x =2x ，解得，x =43，当∠BPQ =90°时，∵∠B =60°，∴BQ =2BP ，即2（4-x ）=x ，解得，x =83，∴当点P ，Q 运动43秒或83秒时，△PBQ 是直角三角形．【解析】（1）根据等边三角形的性质、三角形全等的判定定理证明；（2）根据全等三角形的性质得到∠BAQ =∠ACP ，根据三角形的外角的性质解答；（3）分∠PQB =90°和∠BPQ =90°两种情况，根据直角三角形的性质计算即可．本题考查的是全等三角形的判定、直径三角形的性质，掌握等边三角形的性质、灵活运用分情况讨论思想是解题的关键．15.【答案】解：（1）∵AB =AC ，∴∠B =∠ACB ．∵PF ∥AC ，∴∠PFB =∠ACB∴∠B =∠PFB ，∴BP =FP由题意，BP =CQ ，∴FP =CQ∵PF ∥AC ，∴∠DPF =∠DQC ．又∠PDF =∠QDC ，∴△PFD ≌△QCD ；（2）如图，过P 点作PF ∥AC 交BC 于F∵点P 为AB 的中点，∴F 为BC 的中点，∴FC =12BC =3由（1）知△PFD ≌△QCD ，CD =DF∴CD =DF =12FC =32；（3）线段DE 的长度保持不变．如图，过点P 作PF ∥AC 交BC 于F ，由（1）知PB =PF∵PE ⊥BC ，∴BE =EF由（1）知△PFD ≌△QCD ，CD =DF ，∴DE =EF +DF =12BC =3．【解析】（1）根据全等三角形的判定定理ASA 进行证明；（2）过点P 作PF 平行与AQ ，由平行线的性质和等腰三角形的性质得出∠B =∠PFB ，证出BP =PF ，得出PF =CQ ，由ASA 证明△PFD ≌△QCD ，得出DF =CD =12CF ，再证出F 是BC 的中点，即可得出结果；（3）过点P 作PF ∥AC 交BC 于F ，首先证明BE =EF ，根据DF =FC ，即可解决问题．本题是三角形综合题目，考查了等腰三角形的性质与判定、全等三角形的判定与性质、等腰直角三角形的判定与性质等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．16.【答案】解：（1）∵BQ =2×2=4（cm ），BP =AB -AP =16-2×1=14（cm ），∠B =90°， ∴PQ =√42+142=√212=2√53（cm ）；（2）BQ =2t ，BP =16-t ，根据题意得：2t =16-t ，解得：t =163，即出发163秒钟后，△PQB 能形成等腰三角形；（3）①当CQ =BQ 时，如图1所示，则∠C =∠CBQ ，∵∠ABC =90°，∴∠CBQ +∠ABQ =90°．∠A +∠C =90°，∴∠A =∠ABQ ，∴BQ =AQ ，∴CQ =AQ =10，∴BC +CQ =22，∴t =22÷2=11秒． ②当CQ =BC 时，如图2所示，则BC +CQ =24，∴t =24÷2=12秒． ③当BC =BQ 时，如图3所示，过B 点作BE ⊥AC 于点E ，则BE =AB⋅BC AC =12×1620=485，∴CE =√BC 2−BE 2=√122−(485)2=365， ∴CQ =2CE =14.4，∴BC +CQ =26.4，∴t =26.4÷2=13.2秒．综上所述：当t 为11秒或12秒或13.2秒时，△BCQ 为等腰三角形．苏科版八年级上册几何压轴题专题（解析版）23 / 25【解析】本题考查了勾股定理、三角形的面积以及等腰三角形的判定和性质，注意分类讨论思想的应用．（1）根据点P 、Q 的运动速度求出AP ，再求出BP 和BQ ，用勾股定理求得PQ 即可；（2）设出发t 秒钟后，△PQB 能形成等腰三角形，则BP =BQ ，由BQ =2t ，BP =8-t ，列式求得t 即可；（3）当点Q 在边CA 上运动时，能使△BCQ 成为等腰三角形的运动时间有三种情况： ①当CQ =BQ 时，则∠C =∠CBQ ，可证明∠A =∠ABQ ，则BQ =AQ ，则CQ =AQ ，从而求得t ；②当CQ =BC 时，则BC +CQ =12，易求得t ；③当BC =BQ 时，过B 点作BE ⊥AC 于点E ，则求出BE ，CE ，即可得出t ． 17.【答案】（1)证明：如图2：∵△ABC 与△BEF 都为等边三角形，∴∠ABC =∠EBF =60°，AB =BC =CD ，EB =BF ，∴∠ABC -∠EBC =∠EBF -∠EBC ，即∠ABE =∠CBF ，在△ABE 和△CBF 中，{AB =BC ∠ABE =∠CBF EB =FB，∴△ABE ≌△CBF （SAS ），∴AE =CF ，则CD =AC =AE +EC =FC +EC ；(2)CE =CF +CD ，理由为：证明：过D 作DG ∥AB ，交AC 于点G ，连接CF ，∵DG ∥AB ，∴∠CGD =∠CDG =60°，△CDG 为等边三角形，∵△DEF 为等边三角形，∴∠EDF =∠GDC =60°，ED =FD ，GD =CD ，∴∠EDF -∠GDF =∠GDC -∠GDF ，即∠EDG =∠FDC ，在△EDG 和△FDC 中，{ED =FD ∠EDG =∠FDC DG =DC，∴△EDG ≌△FDC （SAS ），∴EG =FC ，则CE =CG +EG =CG +CF =CF +CD ；(3)CF =CE +CD .【解析】【分析】此题考查了全等三角形的判定与性质，等边三角形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．（1）由三角形ABC 与三角形EBF 都为等边三角形，利用等边三角形的性质得到一对角相等，两对边相等，利用等式的性质得到夹角相等，利用SAS 得到三角形ABE 与三角形CBF 全等，利用全等三角形对应边相等得到AE =CF ，由AC =AE +EC，等量代换即可得证；（2）CE=CF+CD，理由为：过D作DG∥AB，交AC于点G，连接CF，如图所示，由DG与AB平行，利用两直线平行同位角相等，确定出三角形GDC为等边三角形，再由三角形EDF为等边三角形，利用等边三角形的性质得到两对边相等，再利用等式的性质得到夹角相等，利用SAS得到三角形EGD与三角形FCD全等，利用全等三角形对应边相等得到EG=FC，由EC=EG+GC，等量代换即可得证；（3）CF=CE+CD，理由为：过D作DG∥AC，交FC于点G，同（2）即可得证．【解答】（1）见答案；（2）见答案；（3）CF=CE+CD，理由为：证明：过D作DG∥AC，交FC于点G，∵GD∥AC，∴∠GCD=∠DGC=60°，即△GCD为等边三角形，∵△EDF为等边三角形，∴∠EDF=∠GDC=60°，∴∠EDF-∠EDG=∠GDC-∠EDG，即∠FDG=∠EDC，在△ECD和△FGD中，{ED=FD∠EDC=∠FDG CD=GD，∴△ECD≌△FGD（SAS），∴EC=FG，则FC=FG+GC=EC+CD．故答案为：CF=CE+CD.18.【答案】（1）当点D在BC的中点上时，DE=DF，证明：∵D为BC中点，∴BD=CD，∵AB=AC，∴∠B=∠C，∵DE⊥AB，DF⊥AC，∴∠DEB=∠DFC=90°，∵在△BED和△CFD中{∠B=∠C∠DEB=∠DFC BD=CD，∴△BED≌△CFD（AAS），∴DE=DF．苏科版八年级上册几何压轴题专题（解析版）25 / 25 （2）解：有3对全等三角形，有△BED ≌△CFD ，△ADB ≌△ADC ，△AED ≌△AFD ， ∵由（1）知△BED ≌△CFD ，∴DE =DF ，BE =CF ，∵AB =AC ，∴AE =AF ，在△AED 和△AFD 中{AD =AD AE =AF DE =DF，∴△AED ≌△AFD （SSS ），∵在△ADB 和△ADC 中{AB =AC AD =AD BD =CD∴△ADB ≌△ADC （SSS ），∴有3对全等三角形，有△BED ≌△CFD ，△ADB ≌△ADC ，△AED ≌△AFD ；（3）CG =DE +DF证明：连接AD ，∵S 三角形ABC =S 三角形ADB +S 三角形ADC ， ∴12AB ×CG =12AB ×DE +12AC ×DF ， ∵AB =AC ，∴CG =DE +DF ．【解析】（1）根据AAS 证△BED ≌△CFD ，根据全等三角形的性质推出即可；（2）求出DE =DF ，AE =AF ，根据SSS 证出△AED ≌△AFD 即可，根据SSS 证出△ABD ≌△ACD 即可；（3）连接AD ，根据三角形的面积公式求出即可．本题考查了全等三角形的性质和判定的应用，主要考查学生运用定理进行推理的能力．。

专题全等三角形压轴题(30题)(解析版)

八年级上册数学《第十二章全等三角形》专题全等三角形压轴题训练（30题）1．（2022秋•忠县期末）在△ABC中，点D、E分别在AB、AC边上，设BE与CD相交于点F．（1）如图①，设∠A＝60°，BE、CD分别平分∠ABC、∠ACB，证明：DF＝EF．（2）如图②，设BE⊥AC，CD⊥AB，点G在CD的延长线上，连接AG、AF；若∠G＝∠6，BD＝CD，证明：GD＝DF．【分析】（1）在BC上截取BM＝BD，连接FM，证明△BFD≌△BFM，△ECF≌△MCF，进而可以解决问题；（2）根据已知条件证明△BDF≌△CDA，进而可以解决问题．【解答】证明：（1）如图，在BC上截取BM＝BD，连接FM，∵∠A＝60，∴∠BFC＝90°+60°÷2＝120°，∴∠BFD＝60°，∵BE平分∠ABC，∴∠1＝∠2，在△BFD和△BFM中，BD=BM∠1=∠2，BF=BF∴△BFD≌△BFM（SAS），∴∠BFM＝∠BFD＝60°，DF＝MF，∴∠CFM＝120°﹣60°＝60°，∵∠CFE＝∠BFD＝60°，∴∠CFM＝∠CFE，∵CD平分∠ACB，∴∠3＝∠4，又CF＝CF，在△ECF和△MCF中，∠CFE=∠CFMFC=FC，∠3=∠4∴△ECF≌△MCF（ASA），∴EF＝MF，∴DF＝EF；（2）∵BE⊥AC，CD⊥AB，∴∠BDF＝∠CDA＝90°，∴∠1+∠BFD＝90°，∠3+∠CFE＝90°，∠BFD＝∠CFE，∴∠1＝∠3，∵BD＝CD，在△BDF和△CDA中，∠BDF=∠CDABD=CD，∠1=∠3∴△BDF≌△CDA（ASA），∴DF＝DA，∵∠ADF＝90°，∴∠6＝45°，∵∠G＝∠6，∴∠5＝45°∴∠G＝∠5，∴GD＝DA，∴GD＝DF．【点评】本题属于三角形的综合题，考查了全等三角形的判定与性质，角平分线的性质，解决本题的关键是掌握全等三角形的判定与性质．2．如图，△ABC中，AB＝AC，D为AC边上一点，E为AB延长线上一点，且CD＝BE，DE与BC相交于点F．（1）求证：DF＝EF．＝5，求EG的长．（2）过点F作FG⊥DE，交线段CE于点G，若CE⊥AC，CD＝4，S△EFG【分析】（1）过点D作DH∥AB交BC于点H，根据等腰三角形的性质及平行线的性质得到∠BEF＝∠HDF，∠DHC＝∠DCH，则DH＝CD，结合∠BFE＝∠HFD，即可利用AAS判定△BEF≌△HDF，根据全等三角形的性质即可得解；（2）根据三角形的面积公式求解即可．【解答】（1）过点D作DH∥AB交BC于点H，∵AB＝AC，∴∠ABC＝∠ACB，∵DH∥AB，∴∠DHC＝∠ABC，∴∠DHC＝∠ACB＝∠DCH，∴DH＝CD，∵CD＝BE，∴DH＝BE，∵DH∥AB，∴∠BEF＝∠HDF，在△BEF和△HDF中，∠BFE=∠HFD∠BEF=∠HDFBE=DH，∴△BEF≌△HDF（AAS），∴DF＝EF；（2）连接DG，∵DF＝EF，FG⊥DE，∴S△DFG ＝S△EFG＝5，∴S△DEG＝10，∵CE⊥AC，CD＝4，∴S△DEG =12EG•CD=12EG×4，∴12EG×4＝10，∴EG＝5．【点评】此题考查了全等三角形的判定与性质，利用AAS判定△BEF≌△HDF是解题的关键．3．如图1，在等腰直角三角形ABC中，AB＝AC，∠BAC＝90°，点P为BC边上的一个动点，连接AP，以AP为直角边，A为直角顶点，在AP右侧作等腰直角三角形PAD，连接CD．（1）当点P在线段BC上时（不与点B重合），求证：△BAP≌△CAD；（2）当点P在线段BC的延长线上时（如图2），试猜想线段BP和CD的数量关系与位置关系分别是什么？请给予证明．【分析】（1）证得∠BAP＝∠CAD，根据SAS可证明△BAP≌△CAD；（2）可得∠BAP＝∠CAD，由SAS可证明△BAP≌△CAD，可得BP＝CD，∠B＝∠ACD，则结论得证．【解答】（1）证明：∵∠BAC＝∠PAD＝90°，∴∠BAC﹣∠PAC＝∠PAD﹣∠PAC，即：∠BAP＝∠CAD，在△BAP和△CAD中AB=AC∠BAP=∠CAD，PA=DA∴△BAP≌△CAD（SAS）；（2）猜想：BP＝CD，BP⊥CD．证明：∵∠BAC＝∠PAD＝90°，∴∠BAC+∠PAC＝∠PAD+∠PAC，即：∠BAP＝∠CAD，在△BAP和△CAD中AB=AC∠BAP=∠CAD，PA=DA∴△BAP≌△CAD（SAS），∴BP＝CD（全等三角形的对应边相等），∠B＝∠ACD（全等三角形的对应角相等），∵∠B+∠ACB＝90°，∴∠ACD+∠ACB＝90°，即：BP⊥CD．【点评】本题考查了全等三角形的判定与性质，等腰直角三角形的性质，根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键．4．在△ABC中，∠ABC＝90°．点G在直线BC上，点E在直线AB上，且AG与CE相交于点F，过点A 作边AB的垂线AD，且CD∥AG，EB＝AD，AE＝BC．（1）如图①，当点E在△ABC的边AB上时，求∠DCE的度数；（2）如图②，当点E在线段BA的延长线上时，求证：AB＝BG．【分析】（1）如图①，连接ED，根据已知条件得到△ADE≌△BEC（SAS），根据全等三角形的性质得到∠AED＝∠BCE，ED＝CE，于是得到结论；（2）如图②，连接DE，根据已知条件得到△ADE≌△BEC（SAS），根据全等三角形的性质得到∠AED ＝∠BCE，ED＝CE，根据等腰三角形的性质得到∠EDC＝∠ECD，推出AF平分∠DAE，于是得到结论．【解答】解：（1）如图①连接ED，∵AD⊥AB，∴∠DAE＝90°，∵∠ABC＝90°，∵AD＝EB，AE＝BC，∴△ADE≌△BEC（SAS），∴∠AED＝∠BCE，ED＝CE，∴∠AED+∠BEC＝∠BCE+∠BEC；∴∠AED+∠CEB＝90°，∴∠DEC＝90°，∴∠DCE＝45°；（2）如图②，连接DE，∵AD⊥AB，∴∠DAE＝90°，∵∠ABC＝90°，∴∠DAE＝∠ABC，∵AD＝EB，AE＝BC，∴△ADE≌△BEC（SAS），∴∠ADE＝∠BEC，ED＝CE，∵ED＝CE，∴∠EDC＝∠ECD，即∠ADE+∠ADC＝∠ECD，∴∠BEC+∠DAF＝∠AFC，∵∠BEC+∠EAF＝∠AFC，∴∠DAF＝∠EAF，∴AF平分∠DAE，∵∠DAE＝90°，∴∠EAF＝45°，∵∠EAF＝∠BAG，∴∠BAG＝45°，∵∠ABC＝90°，∴∠ABG＝90°，∴∠BGA＝∠BAG，∴AB＝BG．【点评】本题考查了平行线的性质，全等三角形的判定和性质，角平分线的定义，等腰直角三角形的判定和性质，正确的识别图形是解题的关键．5．在Rt△ABC中，∠ABC＝90°，点D是CB延长线上一点，点E是线段AB上一点，连接DE．AC＝DE，BC＝BE．（1）求证：AB＝BD；（2）BF平分∠ABC交AC于点F，点G是线段FB延长线上一点，连接DG，点H是线段DG上一点，连接AH交BD于点K，连接KG．当KB平分∠AKG时，求证：AK＝DG+KG．【分析】（1）证明Rt△ACB≌Rt△DEB即可解决问题；（2）作BM平分∠ABD交AK于点M，证明△BMK≌△BGK，△ABM≌△DBG，即可解决问题．【解答】证明：（1）在Rt△ACB和Rt△DEB中，AC=DEBC=BE，∴Rt△ACB≌Rt△DEB（HL），∴AB＝BD，（2）如图：作BM平分∠ABD交AK于点M，∵BM平分∠ABD，KB平分∠AKG，∴∠ABM＝∠MBD＝45°，∠AKB＝∠BKG，∵∠ABF＝∠DBG＝45°∴∠MBD＝∠GBD，在△BMK和△BGK中，∠MBD=∠GBDBK=BK，∠AKB=∠BKG∴△BMK≌△BGK（ASA），∴BM＝BG，MK＝KG，在△ABM和△DBG中，AB=BD∠ABM=∠DBG，BM=BG∴△ABM≌△DBG（SAS），∴AM＝DG，∵AK＝AM+MK，∴AK＝DG+KG．【点评】本题考查了全等三角形的判定与性质，解决本题的关键是得到△BMK≌△BGK．6．（2023春•市南区期末）如图，在△ABC中，AB＝AC，AD⊥BC于点D，E为AC边上一点，连接BE与AD交于点F，G为△ABC外一点，满足∠ACG＝∠ABE，∠FAG＝∠BAC，连接EG．（1）求证：△ABF≌△ACG；（2）求证：BE＝CG+EG．【分析】（1）根据已知条件可得∠BAD＝∠CAG，然后利用ASA即可证明△ABF≌△ACG；（2）结合（1）的结论，再证明△AEF≌△AEG，即可解决问题．【解答】（1）证明：∵∠BAC＝∠FAG，∴∠BAC﹣∠CAD＝∠FAG﹣∠CAD，∴∠BAD＝∠CAG，在△ABF和△ACG中，∠BAD=∠CAGAB=AC，∠ABF=∠ACG∴△ABF≌△ACG（ASA）；（2）证明：∵△ABF≌△ACG，∴AF＝AG，BF＝CG，∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD，∵∠BAD＝∠CAG，∴∠CAD＝∠CAG，在△AEF和△AEG中，AF=AG∠FAE=∠GAE，AE=AE∴△AEF≌△AEG（SAS）．∴EF＝EG，∴BE＝BF+FE＝CG+EG．【点评】本题考查了全等三角形的判定与性质，解决本题的关键是得到△AEF≌△AEG．7．（2022秋•新市区校级期中）已知：如图，BD为△ABC的角平分线，且BD＝BC，E为BD延长线上的一点，BE＝BA，过E作EF⊥AB，F为垂足．求证：（1）AD＝AE＝EC．（2）BA+BC＝2BF．【分析】（1）由△BCD和△BEA为等腰三角形，∠ABD＝∠EBC，得出∠BCD＝∠BEA，由△ABD≌△EBC可得∠BCE＝∠BDA，由∠BCE＝∠BCD+∠DCE，∠BDA＝∠DAE+∠BEA得出∠BCD+∠DCE＝∠DAE+∠BEA，进而得出∠DCE＝∠DAE，即可证明AE＝EC；（2）过点E作EG⊥BC交BC的延长线于点G，由“HL”得出Rt△BFE≌Rt△BGE和Rt△BFE≌Rt△BGE，从而得出BF＝BG，FA＝CG，再通过等量代换即可得出结论．【解答】（1）证明：∵BD为△ABC的角平分线，∴∠ABD＝∠EBC，在△ABD与△EBC中，AB=EB∠ABD=∠EBD，BD=BC∴△ABD≌△EBC（SAS），∴∠BCE＝∠BDA，∵∠BCE＝∠BCD+∠DCE，∠BDA＝∠DAE+∠BEA，∴∠BCD+∠DCE＝∠DAE+∠BEA，∵BD＝BC，BE＝BA，∴△BCD和△BEA为等腰三角形，∵∠ABD＝∠EBC，∴∠BCD＝∠BEA，∴∠DCE＝∠DAE，∴AE＝EC，∵△ABD≌△EBC，∴AD＝EC，∴AD＝EC＝AE；（2）证明：如图，过点E作EG⊥BC交BC的延长线于点G，∵BE平分∠ABC，EF⊥AB，EG⊥BG，∴EF＝EG，在Rt△BFE与Rt△BGE中，EF=EGBE=BE，∴Rt△BFE≌Rt△BGE（HL），∴BF＝BG，在Rt△AFE与Rt△CGE中，EF=EGEA=EC，∴Rt△AFE≌Rt△CGE（HL），∴FA＝CG，∴BA+BC＝BF+FA+BG﹣CG＝BF+BG＝2BF．【点评】本题考查了全等三角形的判定与性质，掌握三角形全等的判定方法是解决问题的关键．8．（2023春•余江区期末）如图，大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处，AC＝BC，DC＝EC，连接AE、BD，点A恰好在线段BD上．（1）找出图中的全等三角形，并说明理由；（2）当AD＝AB＝4cm，则AE的长度为　cm．（3）猜想AE与BD的位置关系，并说明理由．【分析】（1）根据SAS证明△CBD≌△CAE即可；（2）根据全等三角形的性质解答即可；（3）根据全等三角形的性质和垂直的定义解答即可．【解答】解：（1）△CBD≌△CAE，理由如下：∵∠ACB＝∠DCE＝90°，∴∠ACB+∠ACD＝∠DCE+∠ACD，即∠BCD＝∠ACE，在△CBD与△CAE中，BC=AC∠BCD=∠ACE，DC=EC∴△CBD≌△CAE（SAS）；（2）∵△CBD≌△CAE，∴BD＝AE＝AD+AB＝4+4＝8（cm），故答案为：8；（3）AE⊥BD，理由如下：AE与CD相交于点O，在△AOD与△COE中，∵△CBD≌△CAE，∴∠ADO＝∠CEO，∵∠AOD＝∠COE，∴∠OAD＝∠OCE＝90°，∴AE⊥BD．【点评】此题考查全等三角形的判定和性质，关键是根据SAS得出△CBD与△CAE全等解答．9．已知，△ABC中，∠ACB＝90°，AC＝BC，点E是BC上一点，连接AE（1）如图1，当AE平分∠BAC时，EH⊥AB于H，△EHB的周长为10m，求AB的长；（2）如图2，延长BC至D，使DC＝BC，将线段AE绕点A顺时针旋转90°得线段AF，连接DF，过点B作BG⊥BC，交FC的延长线于点G，求证：BG＝BE．【分析】（1）根据等腰三角形的性质得到∠B＝45°，根据角平分线的性质得到CE＝EH＝BH，根据全等三角形的性质得到AH＝AC，于是得到结论；（2）先连接AD，依据AAS判定△ADF≌△ABE，得到DF＝BE，再判定△BCG≌△DCF，得出DF＝BG，进而得到BG＝BE．【解答】解：（1）∵∠ACB＝90°，AC＝BC，∴∠B＝45°，∵AE平分∠BAC时，EH⊥AB于H，∴CE＝EH＝BH，在Rt△ACE与Rt△AHE中，CE=EH AE=AE，∴Rt△ACE与Rt△AHE（HL），∴AH＝AC，∴AH＝BC，∵△EHB的周长为10m，∴AB＝AH+BH＝BC+BH＝10m；（2）如图所示，连接AD，线段AE绕点A顺时针旋转90°得线段AF，则AE＝AF，∠EAF＝90°，∵AC⊥BD，DC＝BC，∴AD＝AB，∠ABE＝∠ADC＝45°，∴∠BAD＝90°＝∠EAF，∴∠BAE＝∠DAF，∴△ABE≌△ADF（SAS），∴DF＝BE，∠ADF＝∠ABE＝45°，∴∠FDC＝90°，∵BG⊥BC，∴∠CBG＝∠CDF＝90°，又∵BC＝DC，∠BCG＝∠DCF，∴△BCG≌△DCF（ASA），∴DF＝BG，∴BG＝BE．【点评】本题主要考查了旋转的性质，等腰直角三角形的性质以及全等三角形的判定与性质的综合运用，解决问题的关键是作辅助线构造全等三角形，依据全等三角形的对应边相等得出结论．10．在△ABC中，∠ABC＝45°，AM⊥MB，垂足为M，点C是BM延长线上一点，连接AC．（1）如图①，点D在线段AM上，且DM＝CM．求证：△BDM≌△ACM；（2）如图②，在（1）的条件下，点E是△ABC外一点，且满足EC＝AC，连接ED并延长交BC于点F，且F为线段BC的中点，求证：∠BDF＝∠CEF．【分析】（1）利用SAS即可证明△BMD≌△AMC．（2）延长EF到点G，使得FG＝EF，证△BMD≌△AMC得AC＝BD，再证△BFG≌△CFE可得BG＝CE，∠G＝∠E，从而得BD＝BG＝CE，即可得∠BDG＝∠G＝∠CEF．【解答】（1）证明：∵∠ABM＝45°，AM⊥BM，在△BMD和△AMC中，DM=CM∠BMD=∠AMC BM=AM，∴△BMD≌△AMC（SAS）；（2）证明：延长EF到点G，使得FG＝EF，连接BG．如图所示：∵△BMD≌△AMC∴BD＝AC，又∵CE＝AC，∴BD＝CE，在△BFG和△CFE中，BF=FC∠BFG=∠EFC FG=FE，∴△BFG≌△CFE（SAS），∴BG＝CE，∠G＝∠CEF，∴BD＝CE＝BG，∴∠BDF＝∠G＝∠CEF．∴∠BDF＝∠CEF．【点评】本题主要考查全等三角形的判定与性质，等腰直角三角形的性质等知识点，熟练掌握全等三角形的判定与性质是解题的关键．11．如图1，在△ABC中，∠A＝120°，∠C＝20°，BD平分∠ABC，交AC于点D．（1）求证：BD＝CD．（2）如图2，若∠BAC的角平分线AE交BC于点E，求证：AB+BE＝AC．（3）如图3，若∠BAC的外角平分线AE交CB的延长线于点E，则（2）中的结论是否成立？若成立，给出证明，若不成立，写出正确的结论．【分析】（1）根据∠A＝120°，∠C＝20°，可得∠ABC的度数，再根据BD平分∠ABC，可得∠DBC＝∠C＝20°，进而可得结论；（2）如图2，过点E作EF∥BD交AC于点F，证明△ABE≌△AFE，可得BE＝EF＝FC，进而可得AB+BE ＝AC；（3）如图3，过点A作AF∥BD交BE于点F，结合（1）和AE是∠BAC的外角平分线，可得FE＝AF＝AC，进而可得结论BE﹣AB＝AC．【解答】（1）证明：∵∠A＝120°，∠C＝20°，∴∠ABC＝180°﹣120°﹣20°＝40°，∵BD平分∠ABC，∴∠ABD＝∠DBC=12∠ABC＝20°，∴∠DBC＝∠C＝20°，∴BD＝CD；（2）证明：如图2，过点E作EF∥BD交AC于点F，∴∠FEC＝∠DBC＝20°，∴∠FEC＝∠C＝20°，∴∠AFE＝40°，FE＝FC，∴∠AFE＝∠ABC，∵AE是∠BAC的平分线，∴∠BAE＝∠FAE，在△ABE和△AFE中，∠BAE=∠FAE∠ABE=∠AFE，AE=AE∴△ABE≌△AFE（AAS），∴BE＝EF，∴BE＝EF＝FC，∴AB+BE＝AF+FC＝AC；（3）（2）中的结论不成立，正确的结论是BE﹣AB＝AC．理由如下：如图3，过点A作AF∥BD交BE于点F，∴∠AFC＝∠DBC＝20°，∴∠AFC＝∠C＝20°，∴AF＝AC，∵AE是∠BAC的外角平分线，∴∠EAB=12（180°﹣∠ABC）＝30°，∵∠ABC＝40°，∴∠E＝∠ABC﹣∠EAB＝10°，∴∠E＝∠FAE＝10°，∴FE＝AF，∴FE＝AF＝AC，∴BE﹣AB＝BE﹣BF＝EF＝AC．【点评】本题考查了全等三角形的判定与性质，解决本题的关键是掌握全等三角形的判定与性质．12．（2022秋•渝北区校级期末）已在等腰Rt△ABC中，∠ABC＝90°，AB＝CB，D为直线AB上一点，连接CD，过点C作CE⊥CD，且CE＝CD，连接DE，交AC于点F．（1）如图1，当点D在线段AB上，且∠DCB＝30°时，请探究DF，EF，CF之间的数量关系，并说明理由；（2）如图2，在（1）的条件下，在FC上任取一点G，连接DG，作射线GP使∠DGP＝60°，交∠DFG 的平分线于点Q，求证：FD+FG＝FQ．【分析】（1）在EF上找到G点使得FG＝CF，易证△CFG是等边三角形，可得CG＝CF＝GF，即可求得∠ECG＝∠ACD，即可证明△ECG≌△CDF，可得DF＝EG，即可解题；（2）在FP上找到H点，使得FH＝FG，易证△FGH是等边三角形，可得∠GHF＝∠FGH＝60°，GH ＝FG＝FH，即可求得∠FGD＝∠QGH，即可证明△DFG≌△QHG，可得DF＝QH，即可解题．【解答】（1）解：EF＝DF+CF；在EF上找到G点使得FG＝CF，如图2，∵∠BCD＝30°，∠ACB＝45°，∴∠ACD＝15°，∴∠CFG＝∠CDE+∠ACD＝60°，∵FG＝CF，∴△CFG是等边三角形，∴CG＝CF＝GF，∠FCG＝60°，∴∠GCE＝90°﹣15°﹣60°＝15°，在△ECG和△CDF中，CG=CF∠ECG=∠ACD，CE=CD∴△ECG≌△CDF，（SAS）∴DF＝EG，∵EF＝EG+GF，∴EF＝DF+CF；（2）证明：在FQ上找到H点，使得FH＝FG，如图3，∵FQ平分∠DFG，∴∠QFG＝60°，∵FG＝FH，∴△FGH是等边三角形，∴∠GHF＝∠FGH＝60°，GH＝FG＝FH，∵∠AFD＝∠CDE+∠ACD＝60°，∴∠GHQ＝∠DFG＝120°，∵∠FGD+∠DGH＝60°，∠DGH+∠QGH＝60°，∠QGH＝∠DGF，∴∠FGD＝∠QGH，在△DFG和△QHG中，∠DFG=∠QHG=120°FG=HG，∠FGD=∠QGH∴△DFG≌△QHG，（ASA）∴DF＝QH，∵FQ＝FH+QH，∴FQ＝FG+FD．【点评】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ECG≌△CDF和△DFG≌△QHG是解题的关键．13．（2022春•运城期末）综合与探究如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，CE的延长线交BD于点F．（1）求证：△ACE≌△ABD．（2）若∠BAC＝∠DAE＝50°，请直接写出∠BFC的度数．（3）过点A作AH⊥BD于点H，求证：EF+DH＝HF．【分析】（1）可利用SAS证明结论；（2）由全等三角形的性质可得∠AEC＝∠ADB，结合平角的定义可得∠DAE+∠DFE＝180°，根据∠BFC+∠DFE＝180°，可求得∠BFC＝∠DAE，即可求解；（3）连接AF，过点A作AJ⊥CF于点J．结合全等三角形的性质利用HL证明Rt△AFJ≌Rt△AFH，Rt△AJE≌Rt△AHD可得FJ＝FH，EJ＝DH，进而可证明结论．【解答】（1）证明：∵∠BAC＝∠DAE．∴∠CAE＝∠BAD．在△ACE和△ABD中，AC=AB∠CAE=∠BAD，AE=AD∴△ACE ≌△ABD （SAS ）；（2）解：∵△ACE ≌△ABD ，∴∠AEC ＝∠ADB ，∴∠AEF +∠AEC ＝∠AEF +∠ADB ＝180°．∴∠DAE +∠DFE ＝180°，∵∠BFC +∠DFE ＝180°，∴∠BFC ＝∠DAE ＝∠BAC ＝50°；（3）证明：如图，连接AF ，过点A 作AJ ⊥CF 于点J ．∵△ACE ≌△ABD ，∴S △ACE ＝S △ABD ，CE ＝BD ，∵AJ ⊥CE ，AH ⊥BD ．∴12CE ⋅AJ =12BD ⋅AH ，∴AJ ＝AH ．在Rt △AFJ 和Rt △AFH 中，AF =AF AJ =AH ，∴Rt △AFJ ≌Rt △AFH （HL ），∴FJ ＝FH ．在Rt △AJE 和Rt △AHD 中，AE =AD AJ =AH ，∴Rt △AJE ≌Rt △AHD （HL ），∴EJ ＝DH ，∴EF +DH ＝EF +EJ ＝FJ ＝FH ．【点评】本题主要考查全等三角形的判定与性质，掌握全等三角形的判定条件是解题的关键．14．（2022春•沙坪坝区校级期中）如图，在△ABC 中，∠ABC 、∠ACB 的平分线交于点D ，延长BD 交AC 于E ，G 、F 分别在BD 、BC 上，连接DF 、GF ，其中∠A ＝2∠BDF ，GD ＝DE ．（1）当∠A ＝80°时，求∠EDC 的度数；（2）求证：CF ＝FG +CE ．【分析】（1）方法一：先求∠ABC 和∠ACB 的和为100°，再根据角平分线求∠DBC +∠DCB ＝50°，再根据外角即可解决问题；方法二：在BC 上取点M ，使CM ＝CE ，证明△CDE ≌△CDM （SAS ），可得DE ＝DM ，∠DEC ＝∠DMC ，∠EDC ＝∠MDC ，证明∠BDM ＝180°−12∠ABC ﹣∠DMB ＝180°−12∠ABC ﹣∠AEB ＝∠A ＝80°，进而可以解决问题．（2）结合（1）然后证明△DGF ≌△DMF （SAS ），可得GF ＝MF ，进而可以解决问题．【解答】（1）解：方法一：∵∠A ＝80°，∴∠ABC +∠ACB ＝100°，∵BE 平分∠ABC 、CD 平分∠ACB ，∴∠DBC +∠DCB ＝50°，∴∠EDC ＝∠DBC +∠DCB ＝50°；方法二：如图，在BC 上取点M ，使CM ＝CE ，∵CD 平分∠ACB ，∴∠ACD＝∠BCD，在△CDE和△CDM中，CE=CM∠ECD=∠MCDCD=CD，∴△CDE≌△CDM（SAS），∴DE＝DM，∠DEC＝∠DMC，∠EDC＝∠MDC，∵GD＝DE，∴GD＝MD，∵∠DEC+∠AEB＝180°，∠DMC+∠DMF＝180°，∴∠AEB＝∠DMF，∵BE平分∠ABC，∴∠ABE＝∠CBE=12∠ABC，∴∠BDM＝180°−12∠ABC﹣∠DMB＝180°−12∠ABC﹣∠AEB＝∠A＝80°，∴∠EDM＝100°，∴∠EDC＝50°；（2）证明：∵∠A＝2∠BDF，∴∠BDM＝2∠BDF，∴∠FDM＝∠BDF，在△DGF和△DMF中，DG=DM∠GDF=∠MDFDF=DF，∴△DGF≌△DMF（SAS），∴GF＝MF，∴CF＝CM+FM＝CE+GF．∴CF＝FG+CE．【点评】本题考查了全等三角形的判定与性质，角平分线的定义，解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF．15．如图，在△ABC中，∠C＝90°，AD是∠BAC的角平分线交BC于点D，过D作DE⊥BA于点E，点F在AC上，且BD＝DF．（1）求证：AC＝AE；（2）求证：∠BAC+∠FDB＝180°；（3）若AB＝9.5，AF＝1.5，求线段BE的长．【分析】（1）证△ACD≌△AED（AAS），即可得出结论；（2）设∠DAC＝∠DAE＝α，在AB上截取AM＝AF，连接MD，证△FAD≌△MAD（SAS），得FD＝MD，∠ADF＝∠ADM，再证Rt△MDE≌Rt△BDE（HL），得∠DME＝∠B，然后证∠FDB＝90°+90°﹣2α＝180°﹣2α，即可得出结论；（3）求出MB＝AB﹣AM＝8，由全等三角形的性质得ME＝BE，即可求解．【解答】（1）证明：∵AD平分∠BAC，∴∠DAC＝∠DAE，∵DE⊥BA，∴∠DEA＝∠DEB＝90°，∵∠C＝90°，∴∠C＝∠DEA＝90°，在△ACD和△AED中，∠C=∠DEA∠DAC=∠DAE，AD=AD∴△ACD≌△AED（AAS），∴AC＝AE；（2）证明：设∠DAC＝∠DAE＝α，∵∠C＝∠DEA＝90°，∴∠ADC＝90°﹣α，∠ADE＝90°﹣α，则∠FDB＝∠FCD+∠DFC＝90°+∠DFC，在AB上截取AM＝AF，连接MD，如图所示：在△FAD和△MAD中，AF=AM∠DAF=∠DAM，AD=AD∴△FAD≌△MAD（SAS），∴FD＝MD，∠ADF＝∠ADM，∵BD＝DF，∴BD＝MD，在Rt△MDE和Rt△BDE中，MD=BDDE=DE∴Rt△MDE≌Rt△BDE（HL），∴∠DME＝∠B，∵∠DAC＝∠DAE＝α，∴∠DAC+∠ADF＝∠ADM+∠ADM，在△FAD中，∠DAC+∠ADF＝∠DFC，在△AMD中，∠DAE+∠ADM＝∠DME，∴∠DFC＝∠DME，∴∠DFC＝∠B，∵∠C＝90°，在△ABC中，∠B＝90°﹣2α，∴∠DFC＝90°﹣2α，∴∠FDB＝90°+90°﹣2α＝180°﹣2α，∵∠BAC＝∠DAC+∠DAE＝2α，∴∠FDB+∠BAC＝180°﹣2α+2α＝180°；（3）解：∵AF＝AM，且AF＝1.5，∴AM＝1.5，∵AB＝9.5，∴MB＝AB﹣AM＝9.5﹣1.5＝8，由（2）得：Rt△MDE≌Rt△BDE，∴ME＝BE，∴BE=12BM=4，即BM的长为4．【点评】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识；证明△FAD≌△MAD和Rt△MDE≌Rt△BDE是解题的关键．16．在△ABC中，AB＝AC，D是直线BC上一点，以AD为一条边在AD的右侧作△ADE，使AE＝AD，∠DAE＝∠BAC，连接DE，CE．（1）如图，当点D在BC延长线上移动时，求证：BD＝CE．（2）设∠BAC＝α，∠DCE＝β．①当点D在线段BC的延长线上移动时，α与β之间有什么数量关系？请说明理由．②当点D分别在线段BC上、线段BC的反向延长线上移动时，α与β之间有什么数量关系？请说明理由.【分析】（1）根据SAS证△BAD≌△CAE，可得结论；（2）①由△BAD≌△CAE，推出∠B＝∠ACE，根据三角形外角性质求出即可；②α+β＝180°或α＝β，根据三角形外角性质求出即可．【解答】（1）证明：∵∠DAE＝∠BAC，∴∠DAE+∠CAD＝∠BAC+∠CAD，∴∠BAD＝∠CAE，在△BAD和△CAE中，AB=AC∠BAD=∠CAE，AD=AE∴△BAD≌△CAE（SAS），（2）解：①当点D在线段BC的延长线上移动时，α与β之间的数量关系是α＝β，理由是：由（1）知△BAD≌△CAE，∴∠B＝∠ACE，∵∠ACD＝∠B+∠BAC＝∠ACE+∠DCE，∴∠BAC＝∠DCE，∵∠BAC＝α，∠DCE＝β，∴α＝β；②分三种情况：i）当D在线段BC上时，如图2，α+β＝180°，理由是：同理可证明：△ABD≌△ACE（SAS），∴∠ADB＝∠AEC，∠ABC＝∠ACE，∵∠ADC+∠ADB＝180°，∴∠ADC+∠AEC＝180°，∴∠DAE+∠DCE＝180°，∵∠BAC＝∠DAE＝α，∠DCE＝β，∴α+β＝180°，ii）当点D在线段BC反向延长线上时，如图3，α＝β．如图3，同理可证明：△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵∠ACE＝∠ACD+∠DCE，∠ABD＝∠ACD+∠BAC，∴∠ACD+∠DCE＝∠ACD+∠BAC，∴∠BAC＝∠DCE，∵∠BAC＝α，∠DCE＝β，∴α＝β；ii）当点D在线段BC的延长线上时，如图1，α＝β．综上，当点D在BC上移动时，α＝β或α+β＝180°．【点评】本题是三角形的综合题，考查了全等三角形的性质和判定，三角形的外角性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．17．（2022春•南海区校级月考）如图，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD．以AD为直角边且在AD的上方作等腰直角三角形ADF．（1）若AB＝AC，∠BAC＝90°．①当点D在线段BC上时（与点B不重合），试探讨CF与BD的数量关系和位置关系；②当点D在线段BC的延长线上时，①中的结论是否仍然成立，请在图②中画出相应的图形并说明理由；（2）如图③，若AB≠AC，∠BAC≠90°，∠BCA＝45°，点D在线段BC上运动，试探究CF与BD 的位置关系．【分析】（1）①根据同角的余角相等求出∠CAF＝∠BAD，然后利用“边角边”证明△ACF和△ABD全等，根据全等三角形的性质及等腰直角三角形的性质求解即可；②先求出∠CAF＝∠BAD，然后与①的思路相同求解即可；（2）过点A作AE⊥AC交BC于E，可得△ACE是等腰直角三角形，根据等腰直角三角形的性质可得AC＝AE，∠AED＝45°，再根据同角的余角相等求出∠CAF＝∠EAD，然后利用“边角边”证明△ACF 和△AED全等，根据全等三角形对应角相等可得∠ACF＝∠AED，然后求出∠BCF＝90°，从而得到CF ⊥BD．【解答】解：（1）①CF＝BD，CF⊥BD，理由如下：∵∠BAC＝90°，△ADF是等腰直角三角形，AB＝AC，∴∠CAF+∠CAD＝90°，∠BAD+∠CAD＝90°，∠B＝∠ACB＝45°，∴∠CAF＝∠BAD，在△ACF和△ABD中，AC=AB∠CAF=∠BAD，AF=AD∴△ACF≌△ABD（SAS），∴CF＝BD，∠ACF＝∠B＝45°，∵∠ACB＝45°，∴∠FCB＝45°+45°＝90°，∴CF⊥BD；②①中的结论成立，理由如下：如图②：∵∠BAC＝90°，△ADF是等腰直角三角形，AB＝AC，∴∠BAC＝∠DAF＝90°，∠B＝∠ACB＝45°，∴∠BAC+∠CAD＝∠DAF+∠CAD，即∠CAF＝∠BAD，在△ACF和△ABD中，AC=AB∠CAF=∠BAD，AF=AD∴△ACF≌△ABD（SAS），∴CF＝BD，∠ACF＝∠B，∴∠BCF＝∠ACF+∠ACB＝45°+45°＝90°，∴CF⊥BD；（3）如图③，过点A作AE⊥AC交BC于E，∵∠BCA＝45°，∴△ACE是等腰直角三角形，∴AC＝AE，∠AED＝45°，∵∠CAF+∠CAD＝90°，∠EAD+∠CAD＝90°，∴∠CAF＝∠EAD，在△ACF和△AED中，AC=AE∠CAF=∠EAD，AF=AD∴△ACF≌△AED（SAS），∴∠ACF＝∠AED＝45°，∴∠BCF＝∠ACF+∠BCA＝45°+45°＝90°，∴CF⊥BC．【点评】此题是三角形综合题，主要考查了全等三角形的判定与性质，等腰直角三角形的性质，作出合理的辅助线根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键．18．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）△ABC≌△ADE吗？为什么？（2）求∠FAE的度数；（3）延长BF到G，使得FG＝FB，试说明CD＝2BF+DE．【分析】（1）由“SAS”可证△ABC≌△ADE；（2）由等腰直角三角形的性质可得∠AEC＝∠ACE＝45°，由全等三角形的性质可得∠ACB＝∠AED＝45°，即可求解；（3）由全等三角形的性质可得∠ABC＝∠ADE，BC＝DE，由线段垂直平分线的性质和等腰三角形的性质可得AB＝AG＝AD，∠ABG＝∠AGB＝∠ADC，由“AAS”可证△ACD≌△ACG，可得CD＝CG，可得结论．【解答】证明：（1）△ABC≌△ADE，理由如下：∵∠BAD＝∠CAE＝90°，∴∠EAD＝∠CAB，在△ABC和△ADE中，AB=AD∠BAC=∠DAE，AC=AE∴△ABC≌△ADE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠AEC＝∠ACE＝45°，∵△ABC≌△ADE，∴∠ACB＝∠AED＝45°，∵AF⊥CB，∴∠FAC＝45°，∴∠FAE＝135°；（3）∵△ABC≌△ADE，∴∠ABC＝∠ADE，BC＝DE，∴∠ADC＝∠ABG，∵AF⊥BF，BF＝FG，∴AB＝AG，∴AG＝AD，∠ABG＝∠AGB＝∠ADC，又∵∠ACG＝∠ACD＝45°，∴△ACD≌△ACG（AAS），∴CD＝CG，∴CD＝BG+CB＝2BF+DE．【点评】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的判定和性质，线段垂直平分线的性质等知识，证明△ACD≌△ACG是解题的关键．19．Rt△ABC中，∠C＝90°，点D在直线AC上，点E在直线AB上，∠ADE＝∠ABC．（1）如图1，当点D、E分别在边AC、AB上时，求证：DE⊥AB；（2）如图2，当点D在CA延长线上，点E在BA延长线上时，DE、BC延长线交于点F，作∠EAC的角平分线AG交DF于点G，求证：∠D+2∠DGA＝90°；（3）如图3，在（2）的条件下，连接BG交CD于点H，若∠DGH＝∠DHG，∠AGB＝3∠CBH，求∠DGA的度数．【分析】（1）根据直角三角形的两锐角互余得到∠ABC+∠A＝90°，等量代换得出∠ADE+∠A＝90°，进而得出∠AED＝90°，根据垂直的定义即可得解；（2）过点G作GN∥FB交CD于点N，根据平行线的性质及垂直的定义推出∠AEG＝∠ANG＝90°，根据角平分线定义得出∠EAG＝∠NAG，利用AAS证明△EAG≌△NAG，根据全等三角形的性质及直角三角形的性质即可得解；（3）根据直角三角形的性质及对顶角相等得出∠DGH＝90°−13∠AGB，根据等腰三角形的性质推出∠DGH＝90°−12∠D，则90°−13∠AGB＝90°−12∠D，进而推出∠AGB=32∠D，则∠DGA+32∠D＝90°−12∠D，结合（2）求解即可．【解答】（1）证明：∵∠C＝90°，∴∠ABC+∠A＝90°，∵∠ADE＝∠ABC，∴∠ADE+∠A＝90°，∴∠AED＝90°，∴DE⊥AB；（2）证明：如图2，过点G作GN∥FB交CD于点N，则∠GNC＝∠ACB＝90°，∴GN⊥CD，∵∠ACB＝90°，∴∠ABC+∠BAC＝90°，∵∠ADE＝∠ABC，∠BAC＝∠DAE，∴∠ADE+∠DAE＝90°，∴∠DEA＝90°，∴BE⊥DF，∴∠AEG＝∠ANG＝90°，∵AG平分∠EAC，∴∠EAG＝∠NAG，在△EAG和△NAG中，∠AEG=∠ANG∠EAG=∠NAGAG=AG，∴△EAG≌△NAG（AAS），∴∠DGA＝∠NGA，∴∠DGN＝2∠DGA，∵∠D+∠DGN＝90°，∴∠D+2∠DGA＝90°；（3）解：∵∠AGB＝3∠CBH，∴∠CBH=13∠AGB，∵∠DHG＝∠CHB＝90°﹣∠CBH，∴∠DGH＝90°−13∠AGB，∵∠DGH＝∠DHG，∴∠DGH=12（180°﹣∠D）＝90°−12∠D，∴90°−13∠AGB＝90°−12∠D，∴∠AGB=32∠D，∵∠DGH＝∠DGA+∠AGB，∴∠DGA+∠AGB＝90°−12∠D，∴∠DGA+32∠D＝90°−12∠D，∴2∠D+∠DGA＝90°，由（2）知，∠D+2∠DGA＝90°，∴∠D＝∠DGA，∴3∠DGA＝90°，∴∠DGA＝30°．【点评】此题是三角形综合题，考查了直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、平行线的性质等知识，熟练掌握直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质并作出合理的辅助线是解题的关键．20．（2023春•新市区期末）在△ABC中，∠ACB＝90°，AC＝BC，D是直线AB上一点（点D不与点A、B重合），连接DC并延长到E，使得CE＝CD，过点E作EF⊥直线BC，交直线BC于点F．（1）如图1，当点D为线段AB上的任意一点时，用等式表示线段EF、CF、AC的数量关系，并证明；（2）如图2，当点D为线段BA的延长线上一点时，依题意补全图2，猜想线段EF、CF、AC的数量关系是否发生改变，并证明；（3）如图3，当点D在线段AB的延长线上时，直接写出线段EF、CF、AC之间的数量关系．【分析】（1）过D作DH⊥CB于H，由“AAS”可证△FEC≌△HDC，可得CH＝FC，DH＝EF，可得结论；（2）过D作DH⊥CB于H，由“AAS”可证△FEC≌△HDC，可得CH＝FC，DH＝EF，可得结论．（3）过D作DH⊥CB交CB的延长线于H，由“AAS”可证△FEC≌△HDC，可得CH＝FC，DH＝EF，可得结论．【解答】解：（1）结论：AC＝EF+FC．理由如下：过D作DH⊥CB于H，∴∠DHC＝∠DHB＝90°，∵EF⊥CF，∴∠EFC＝∠DHC＝90°，在△FEC和△HDC中，∠EFC=∠DHC=90°∠FCE=∠DCH，EC=DC∴△FEC≌△HDC（AAS），∴CH＝FC，DH＝EF，∵∠ACB＝90°，AC＝BC，∴∠B＝45°，∵∠DHB＝90°，∴∠B＝∠HDB＝45°，∴DH＝HB＝EF，∵BC＝CB+HB，∴AC＝FC+EF；（2）依题意补全图形，结论：AC＝EF﹣CF，理由如下：过D作DH⊥CB交BC的延长线于H，∵EF⊥CF，∴∠EFC＝∠DHC＝90°，在△FEC和△HDC中，∠FCE=∠DCH∠EFC=∠DHC=90°，EC=DC∴△FEC≌△HDC（AAS），∴CH＝FC，DH＝EF，∵∠DHB＝90°，∴∠B＝∠HDB＝45°，∴DH＝HB＝EF，∵BC＝HB﹣CH，∴AC＝EF﹣CF；（3）AC＝CF﹣EF．如图3，过D作DH⊥CB交CB的延长线于H，同理可证△FEC≌△HDC（AAS），∴CH＝FC，DH＝EF，∵∠DHB＝90°，∴∠B＝∠HDB＝45°，∴DH＝HB＝EF，∵BC＝CH﹣BH，∴AC＝CF﹣EF．【点评】本题是三角形综合题，考查了全等三角形的判定和性质，添加恰当辅助线构造全等三角形是本题的关键．21．如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．（1）如果AB＝AC，∠BAC＝90°，①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD所在直线的位置关系为，线段CF、BD的数量关系为　；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；（2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F 不重合），并说明理由．【分析】（1）当点D在BC的延长线上时①的结论仍成立．由正方形ADEF的性质可推出△DAB≌△FAC，所以CF＝BD，∠ACF＝∠ABD．结合∠BAC＝90°，AB＝AC，得到∠BCF＝∠ACB+∠ACF＝90°．即CF⊥BD．（2）当∠ACB＝45°时，过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，可推出∠ACB＝∠AGC，所以AC＝AG，由（1）①可知CF⊥BD．【解答】证明：（1）①正方形ADEF中，AD＝AF，∵∠BAC＝∠DAF＝90°，∴∠BAD＝∠CAF，又∵AB＝AC，∴△DAB≌△FAC，∴CF＝BD，∠B＝∠ACF，∴∠ACB+∠ACF＝90°，即CF⊥BD．②当点D在BC的延长线上时①的结论仍成立．由正方形ADEF得AD＝AF，∠DAF＝90度．∵∠BAC＝90°，∴∠DAF＝∠BAC，∴∠DAB＝∠FAC，又∵AB＝AC，∴△DAB≌△FAC，∴CF＝BD，∠ACF＝∠ABD．∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∴∠ACF＝45°，∴∠BCF＝∠ACB+∠ACF＝90度．即CF⊥BD．（2）当∠ACB＝45°时，CF⊥BD（如图）．理由：过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，∵∠ACB＝45°，∠AGC＝90°﹣∠ACB，∴∠AGC＝90°﹣45°＝45°，∴∠ACB＝∠AGC＝45°，∴AC＝AG，∵∠DAG＝∠FAC（同角的余角相等），AD＝AF，∴△GAD≌△CAF，∴∠ACF＝∠AGC＝45°，∠BCF＝∠ACB+∠ACF＝45°+45°＝90°，即CF⊥BC．【点评】本题考查三角形全等的判定和直角三角形的判定，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．22．（1）如图1，∠B＝∠D＝90°，E是BD的中点，AE平分∠BAC，求证：CE平分∠ACD．（2）如图2，AM∥CN，∠BAC和∠ACD的平分线并于点E，过点E作BD⊥AM，分别交AM、CN于B、D，请猜想AB、CD、AC三者之间的数量关系，请直接写出结论，不要求证明．（3）如图3，AM∥CN，∠BAC和∠ACD的平分线交于点E，过点E作不垂直于AM的线段BD，分别交AM、CN于B、D点，且B、D两点都在AC的同侧，（2）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．【分析】（1）过点E作EF⊥AC于F，根据角平分线上的点到角的两边的距离相等可得OB＝OE，从而求出OE＝OD，然后根据到角的两边距离相等的点在角的平分线上证明；（2）如图2，过E作EF⊥AC于F，根据平行线的性质得到BD⊥CD，由角平分线的性质得到BE＝EF，证得Rt△AEF≌Rt△ABE，根据全等三角形到现在得到AF＝AB，同理CF＝CD，等量代换得到结论；（3）成立，如图3，在AC上截取AF＝AB，根据角平分线的定义得到∠BAE＝∠FAE，推出△ABE≌△AFE，根据全等三角形的性质得到∠AFE＝∠ABE，根据角平行线的性质得到∠ABE+∠CDE＝180°，求得∠CFE＝∠CDE，证得△CEF≌△CDE，根据全等三角形的性质即可得到结论．【解答】解：（1）如图1，过E作EF⊥AC于F，∵∠B＝90°，AE平分∠BAC，∴EF＝BE，∵E是BD的中点，∴BE＝DE，∴EF＝DE，∵∠D＝90°，∴CE平分∠ACD；（2）如图2，过E作EF⊥AC于F，∵AM∥CN，BD⊥AM，∴BD⊥CD，∵AE平分∠BAC，∴BE＝EF，在Rt△AEF与Rt△ABE中，BE=EF AE=AE，∴Rt△AEF≌Rt△ABE，∴AF＝AB，同理CF＝CD，∵AC＝AF+CF，∴AC＝AB+CD；（3）成立，如图3，在AC上截取AF＝AB，∵AE平分∠BAC，∴∠BAE＝∠FAE，在△ABE与△AFE中，AB=AF∠BAE=∠FAEAE=AE，∴△ABE≌△AFE，∴∠AFE＝∠ABE，∵AM∥CN，∴∠ABE+∠CDE＝180°，∵∠AFE+∠EFC＝180°，∴∠CFE＝∠CDE，∵CE平分∠ACD，∴∠FCE＝∠DCE，在△CEF与△CDE中，∠CFE=∠CDE ∠FCE=∠DCE CE=CE，∴△CEF≌△CDE，∴CF＝CD，∵AC＝AF+CF，∴AC＝AB+CD．【点评】本题考查了全等三角形的判定和性质，角平分线的性质，角平分线的定义，平行线的性质，正确的作出辅助线构造全等三角形是解题的关键．23．将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F．（1）求证：AF+EF＝DE；（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图②中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图③．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．【分析】（1）我们已知了三角形BED和CAB全等，那么DE＝AF+CF，因此只要求出EF＝CF就能得出本题所求的结论，可通过全等三角形来实现，连接BF，那么证明三角形BEF和BCF全等就是解题的关键，这两三角形中已知的条件有BE＝BC，一条公共边，根据斜边直角边定理，这两个直角三角形就全等了，也就得出EF＝CF，也就能证得本题的结论了；（2）解题思路和辅助线的作法与（1）完全一样；（3）结论不成立．结论：AF＝DE+EF．同（1）得CF＝EF，由△ABC≌△DBE，可得AC＝DE，AF＝AC+FC＝DE+EF．【解答】（1）证明：连接BF（如图①），∵△ABC≌△DBE（已知），∴BC＝BE，AC＝DE．∵∠ACB＝∠DEB＝90°，∴∠BCF＝∠BEF＝90°．在Rt△BFC和Rt△BFE中，BF=BFBC=BE∴Rt△BFC≌Rt△BFE（HL）．∴CF＝EF．又∵AF+CF＝AC，∴AF+EF＝DE．（2）解：画出正确图形如图②∴（1）中的结论AF+EF＝DE仍然成立；（3）不成立．结论：AF＝DE+EF．。

初二压轴题(几何证明直角三角形后)

1.如图，在Rt △ABC 中，90BAC ∠=︒，AB = AC ，点M 、N 在边BC 上．（1）如图1，如果AM = AN ，求证：BM = CN ；（2）如图2，如果M 、N 是边BC 上任意两点，并满足45MAN ∠=︒，那么线段BM 、MN 、 NC 是否有可能使等式222MN BM NC =+ 成立？如果成立，请证明；如果不成立，请说明理由．2.如图,把矩形ABCD 折叠,使点C 落在AB 上的点C ˋ处(C ˋ与A 、B 不重合),点D 落在点D ˋ处,此时C ˋD ˋ交AD 于点E,折痕为MN. （1）如果AB=1,BC=34,当C ˋ点在什么位置时,可使△NBC ˋ≌△C ˋAE; （2）如果AB=BC=1,使△NBC ˋ≌△C ˋAE 的C ˋ点还存在吗？,若存在,求出C ˋ点的位置;若不存在,请说明理由.3.已知：在△ABC 中，∠CAB 和∠ABC 的平分线AD 、BE 交于点P 。

（1）当△ABC 为等边三角形（如图1）时，求证：EP =DP ；（2）当△ABC 不是等边三角形，但∠ACB =600（如图2）时，（2）中的结论是否还成立？若成立，请证明；若不成立，请说明理由。

ABCM NED `C `NMDCBAAB（图1） AB CDEP（图2）4.已知在∆ABC 中，AD ⊥BC ，垂足为D 点在边BC 上，BF ⊥AC 分别交射线DA 、射线CA 于点E 、F ，若BD=4，∠BAD= 45. （1）如图5：若∠BAC 是锐角，则点F 在边AC 上，① 求证：∆BDE ≌∆ADC ； ② 若DC=3，求AE 的长；（2）若∠BAC 是钝角，AE=1，求AC 的长5.已知在△ABC 中，45ABC ︒∠=，高AD 所在的直线与高BE 所在的直线交于点F ，过点F 作FG ∥BC ，交直线AB 于点G ,联结CF .（1）当△ABC 是锐角三角形时（如图a 所示），求证：AD FG CD =+；（2）当BAC ∠是钝角时（如图b 所示），①写出线段AD 、CD 、FG 三者之间的数量关系，不必写出证明过程，直接写结论；②当BE FE =,4BD =时，求FG 的长.6.已知：如图，D 是等腰直角三角形ABC 的斜边AB 上一动点，CE ⊥CD ，且CE =CD ．试探究：（1）在点D 的运动过程中，是否存在与线段AD 始终相等的线段？如果存在，请证明；如果不存在，请说明理由．（2）△ACD 与△EDB 能否全等？如果能，请指出这两个三角形全等时点D 的位置，并证明你的判断；如果不能，请说明理由．A BD CEF图5A BD C备用图GFEDCB A第27（a ）题GFEDBA第27（b ）题CABDE7.在△ABC 中，∠ACB =90°，D 是AB 的中点，过点B 作∠CBE =∠A ，BE 与射线CA 相交于点E ，与射线CD 相交于点F ．(1)如图, 当点E 在线段CA 上时, 求证：BE ⊥CD ；(2)如果BE =CD ，那么线段AC 与BC 之间具有怎样的数量关系？并证明你所得到的结论；(3)如果△BDF 是等腰三角形，求∠A 的度数．8.已知ABC ∆中，AC =BC , =120C ∠,点D 为AB 边的中点，60EDF ∠=,DE 、DF 分别交AC 、BC 于E 、F 点．（1）如图（图1），若EF ∥AB ．求证：DE =DF ．（2）如图（图2），若EF 与AB 不平行．则问题（1）的结论是否成立？说明理由．（图1）ABECD F（图2）ABECD F9.如图（图1）,已知ABC ∆中, BC =3, AC =4, AB =5,直线MD 是AB 的垂直平分线，分别交AB 、AC 于M 、D 点. （1）求线段DC 的长度；（2）如图（图2），联接CM ，作ACB ∠的平分线交DM 于N .求证:CM ＝MN .10.在△ABC 中，AD ⊥BC ，垂足为点D （D 在BC 边上），BE ⊥AC ，垂足为点E ，M 为AB 边的中点，联结ME 、MD 、ED 。

人教版八年级上册几何压轴题专项训练含答案

人教版八年级上册几何压轴题专项训练1．已知，如图，△ABC为等边三角形，AE＝C D，A D、BE相交于点P，B Q⊥A D于Q．（1）求证：BE＝A D；（2）求∠BP Q的度数；（3）若P Q＝3，PE＝1，求A D的长．2．如图，已知在△ABC中，∠BAC为直角，AB＝AC，D为AC上一点，CE⊥B D于E，交BA的延长线于F．（1）求证：△ABD≌△ACF；（2）若B D平分∠ABC，求证：CE＝B D；（3）若D为AC上一动点，∠AED如何变化，若变化，求它的变化范围；若不变，直接写出它的度数．3．如图1，△ABE是等腰三角形，AB＝AE，∠BAE＝45°，过点B作BC⊥AE于点C，在B C上截取C D＝C E，连接A D、D E，并延长A D交BE于点P；（1）求证：A D＝BE；（2）试说明A D⊥BE；（3）如图2，将△C D E绕着点C旋转一定的角度，那么A D与BE的位置关系是否发生变化，说明理由．4．如图，已知△AB C中，AB＝AC＝10厘米，∠ABC＝∠ACB，B C＝8厘米，点D为AB 的中点，如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动，设点P运动的时间为t．（1）用含有t的代数式表示线段P C的长度；（2）若点Q的运动速度与点P的运动速度相等，经过1秒后△BP D与△C Q P是否全等，请说明理由；（3）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BP D与△C Q P全等？5．以点A为顶点作等腰Rt△ABC，等腰Rt△ADE，其中∠BAC＝∠DAE＝90°，如图1所示放置，使得一直角边重合，连接B D、CE．（1）试判断B D、CE的数量关系，并说明理由；（2）延长B D交C E于点F，试求∠BFC的度数；（3）把两个等腰直角三角形按如图2放置，（1）、（2）中的结论是否仍成立？请说明理由．6．如图1，在△AB C中，AB＝AC，点D是BC边上一点（不与点B，C重合），以AD为边在A D的右侧作△A DE，使A D＝AE，∠DAE＝∠BA C，连接CE．设∠BAC＝α，∠BCE ＝β．（1）求证：△CAE≌△BA D；（2）探究：当点D在BC边上移动时，α、β之间有怎样的数量关系？请说明理由；（3）如图2，若∠BA C＝90°，CE与BA的延长线交于点F．求证：EF＝D C．7．如图，∠BA D＝∠CAE＝90°，AB＝A D，AE＝A C，AF⊥CB，垂足为F．（1）求证：△ABC≌△A D E；（2）求∠FAE的度数；（3）求证：C D＝2BF+DE．8．如图，在平面直角坐标系中，OA＝OB，AC＝C D，已知两点A（4，0），C（0，7），点D在第一象限内，∠D CA＝90°，点B在线段O C上，AB的延长线与D C的延长线交于点M，A C与B D交于点N．（1）点B的坐标为：；（2）求点D的坐标；（3）求证：C M＝C N．9．已知：如图1所示，等腰直角三角形AB C中，∠BAC＝90°，AB＝AC，直线M N经过点A，B D⊥M N于点D，CE⊥M N于点E．（1）求证：△BAD≌△ACE；（2）试判断线段D E，B D，CE之间的数量关系，并说明理由；（3）当直线M N运动到如图2所示位置时，其余条件不变，判断线段DE，B D，C E之间的数量关系．10．如图，已知△ABC和△C D E均为等边三角形，且点B、C、D在同一条直线上，连接A D、BE，交CE和AC分别于G、H点，连接G H．（1）请说出A D＝BE的理由；（2）试说出△BCH≌△AC G的理由；（3）试猜想：△C G H是什么特殊的三角形，并加以说明．11．（1）如图1，△ABC和△D C E都是等边三角形，且B，C，D三点在一条直线上，连接A D，BE相交于点P，求证：BE＝A D．（2）如图2，在△BC D中，若∠B C D＜120°，分别以BC，C D和B D为边在△BC D外部作等边△ABC，等边△C D E，等边△B DF，连接A D、BE、CF恰交于点P．①求证：A D＝BE＝CF；②如图2，在（2）的条件下，试猜想PB，PC，P D与BE存在怎样的数量关系，并说明理由．12．已知：在等边△ABC中，点D、E、F分别为边AB、BC、A C的中点，点G为直线BC 上一动点，当点G在CB延长线上时，有结论“在直线EF上存在一点H，使得△D G H 是等边三角形”成立（如图①），且当点G与点B、E、C重合时，该结论也一定成立．问题：当点G在直线BC的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．13．如图，在△AB C中，AB＝BC＝AC＝20cm．动点P，Q分别从A，B两点同时出发，沿三角形的边匀速运动．已知点P，点Q的速度都是2cm/s，当点P第一次到达B点时，P，Q两点同时停止运动．设点P的运动时间为t（s）．（1）∠A＝度；（2）当0＜t＜10，且△AP Q为直角三角形时，求t的值；（3）当△AP Q为等边三角形时，直接写出t的值．14．如图，在三角形AB C中，AB＝8，BC＝16，AC＝12．点P从点A出发以2个单位长度/秒的速度沿A→＞B→C→A的方向运动，点Q从点B沿B→C→A的方向与点P同时出发；当点P第一次回到A点时，点P，Q同时停止运动；用t（秒）表示运动时间．（1）当t＝秒时，P是AB的中点．（2）若点Q的运动速度是个单位长度/秒，是否存在t的值，使得BP＝2B Q．（3）若点Q的运动速度是a个单位长度/秒，当点P，Q是AC边上的三等分点时，求a 的值．15．如图，等边△ABC的边长为15cm，现有两点M，N分别从点A，点B同时出发，沿三角形的边顺时针运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次到达B点时，M，N同时停止运动（1）点M、N运动几秒后，M，N两点重合？（2）点M、N运动几秒后，△A M N为等边三角形？（3）当点M，N在BC边上运动时，能否得到以M N为底边的等腰三角形A M N？如存在，请求出此时M，N运动的时间．16．如图，已知△ABC中，AB＝A C＝10cm，BC＝8cm，点D为AB的中点．（1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段C A 上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1s后，△BP D与△C Q P是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BP D与△C Q P全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？参考答案1．（1）证明：∵△ABC为等边三角形，∴AB＝CA，∠BAE＝∠C＝60°，在△AEB与△C D A中，，∴△AEB≌△C D A（SAS），∴BE＝A D；（2）解：由（1）知，△AEB≌△C D A，则∠ABE＝∠CA D，∴∠BA D+∠AB D＝∠BA D+∠CA D＝∠BAC＝60°，∴∠BP Q＝∠BAD+∠AB D＝60°；（3）解：如图，由（2）知∠BP Q＝60°．∵B Q⊥A D，∴∠PB Q＝30°，∴P Q＝BP＝3，∴BP＝6∴BE＝BP+PE＝7，即A D＝7．2．解：（1）∵∠BA C是直角，CE⊥B D，∴∠BAC＝∠CAF＝∠BEC＝90°，∴∠C D E+∠D C E＝90°，∠AB D+∠A DB＝90°，∵∠A DB＝∠C D E，∴∠AB D＝∠ACF，在△AB D和△ACF中，，∴△AB D≌△ACF（ASA）；（2）由（1）知，△AB D≌A CF，∴B D＝CF，∵B D⊥CE，B D平分∠ABC，∴BC＝BF，∵B D⊥CE，∴CE＝EF，∴CE＝CF＝B D；（3）∠AE D不变化理由：如图，过点A作A G⊥⊥CF于G，作A H⊥B D于H，由（1）证得△BAD≌△CAF（ASA），∴S BA D＝S CAF，B D＝CF，△△∴B D•A H＝CF•AG，而B D＝CF，∴A H＝A G，∵A H⊥EB，A G⊥E G，∴EA平分∠BEF，∴∠BEA＝∠BE G＝45°，即：∠AE D不变化．3．解：（1）∵BC⊥AE，∠BAE＝45°，∴∠CBA＝∠CAB，在△BCE和△ACD中，，∴△BCE≌△ACD（SAS），∴A D＝BE．（2）∵△BCE≌△AC D，∴∠EBC＝∠DAC，∵∠B DP＝∠A D C，∴∠BP D＝∠D C A＝90°，∴A D⊥BE．（3）A D⊥BE不发生变化．理由：如图（2），∵△BCE≌△ACD，∴∠EBC＝∠DAC，∵∠BFP＝∠AF C，∴∠BPF＝∠ACF＝90°，∴A D⊥BE．4．解：（1）由运动知，BP＝3t，∵BC＝8，∴PC＝BC﹣BP＝8﹣3t；（2）全等，理由：当t＝1时，BP＝3，CP＝5，C Q＝3，∵点D是AB的中点，∴B D＝AB＝5，∴CP＝B D，，∴△BP D≌△C Q P（SAS）；（3）∵BP＝3t，C P＝8﹣3t，设点Q的运动速度为xcm/s，∴C Q＝xt，当△BP D≌△C Q P时，∴BP＝C Q，∴3t＝x t，∴x＝3（不符合题意），当△BP D≌△CPQ时，∴BP＝CP，B D＝C Q，∴3t＝8﹣3t，5＝x t，∴t＝，x＝，∴点Q的运动速度为cm/s时，能够使△BP D与△C Q P全等．5．解：（1）CE＝B D，理由如下：∵等腰Rt△ABC，等腰Rt△A DE，∴AE＝A D，AC＝AB，在△EAC与△DAB中，，∴△EAC≌△DAB（SAS），∴CE＝B D；（2）∵△EA C≌△DAB，∴∠ECA＝∠DBA，∴∠ECA+∠CBF＝∠DBA+∠CBF＝45°，∴∠ECA+∠CBF+∠D C B＝45°+45°＝90°，∴∠BFC＝180°﹣90°＝90°；（3）成立，∵等腰Rt△ABC，等腰Rt△A DE，∴AE＝A D，AC＝AB，在△EAC与△DAB中，∴△EAC≌△DAB（SAS），∴CE＝B D；∵△EAC≌△DAB，∴∠ECA＝∠DBA，∴∠ECA+∠CBF＝∠DBA+∠CBF＝45°，∴∠ECA+∠CBF+∠D C B＝45°+45°＝90°，∴∠BFC＝180°﹣90°＝90°．6．（1）证明：∵∠DAE＝∠BAC，∴∠DAE﹣∠DAC＝∠BA C﹣∠D A C，∴∠CAE＝∠BAD．∵A D＝AE，AC＝AB，∴△CAE≌△BAD（SAS）．（2）解：α+β＝180°，理由如下：由△CAE≌△BAD，∴∠ACE＝∠B．∵AB＝AC，∴∠B＝∠ACB．∴∠ACE＝∠B＝∠ACB．∴∠BCE＝β＝2∠B，在△ABC中，∠BA C＝α＝180°﹣2∠B．∴α+β＝180°．（3）证明：由（1）知，△CAE≌△BA D，∴CE＝B D．∵∠BAC＝90°，AB＝AC，∴∠B＝∠ACB＝45°，由（2）得，∠BCF+∠BA C＝180°．∴∠BCF＝90°．∴∠F＝∠B＝45°，∴CF＝CB．∴CF﹣CE＝CB﹣B D．∴EF＝D C．7．证明：（1）∵∠BA D＝∠CAE＝90°，∴∠BAC+∠CA D＝90°，∠CA D+∠DAE＝90°，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CFA＝90°，∴∠CAF＝45°，∴∠FAE＝∠FAC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得F G＝FB，∵AF⊥B G，∴∠AF G＝∠AFB＝90°，在△AFB和△AFG中，∴△AFB≌△AF G（SAS），∴AB＝A G，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝A D，∠CBA＝∠E DA，CB＝E D，∴A G＝A D，∠ABF＝∠C D A，∴∠G＝∠C D A，∵∠G CA＝∠D C A＝45°，在△C G A和△C D A中，，∴△C G A≌△C D A（AAS），∴C G＝C D，∵C G＝CB+BF+FG＝CB+2BF＝DE+2BF，∴C D＝2BF+D E．8．解：（1）∵A（4，0），∴OA＝OB＝4，∴B（0，4），故答案为：（0，4）．（2）∵C（0，7），∴O C＝7，过点D作DE⊥y轴，垂足为E，∴∠DE C＝∠A O C＝90°，∵∠D CA＝90°，∴∠EC D+∠B CA＝∠EC D+∠E D C＝90°∴∠BCA＝∠E D C，∴△DE C≌△C O A（AAS），∴DE＝O C＝7，E C＝OA＝4，∴OE＝O C+E C＝11，∴D（7，11）；（3）证明：∵BE＝OE﹣OB＝11﹣4＝7∴BE＝DE，∴△DBE是等腰直角三角形，∴∠DBE＝45°，∵OA＝OB，∴∠OBA＝45°，∴∠DBA＝90°，∴∠BAN+∠ANB＝90°，∵∠D CA＝90°，∴∠C D N+∠D N C＝90°，∵∠D N C＝∠ANB，∴∠C D N＝∠BAN，∵∠D CA＝90°，∴∠AC M＝∠D C N＝90°，∴△D C N≌△ACM（ASA），∴C M＝C N．9．（1）证明：∵B D⊥M N，CE⊥M N，∴∠B DA＝∠AEC＝90°，∴∠BA D+∠AB D＝90°，又∵∠BAC＝90°，∴∠BA D+∠CAE＝90°，∴∠AB D＝∠CAE，∴△BA D≌△ACE（AAS），（2）解：DE＝BD+C E．理由如下：由（1）得：△BAD≌△ACE，∴B D＝AE，A D＝CE，又DE＝AE+A D，∴DE＝B D+CE，（3）DE＝CE﹣BD，同（1）可得：△BA D≌△ACE，故B D＝AE，A D＝CE，又DE＝A D﹣AE，∴DE＝CE﹣B D．10．解：（1）∵△ABC和△C D E均为等边三角形∴AC＝BC，EC＝D C∠ACB＝∠EC D＝60°∴∠AC D＝∠ECB∴△AC D≌△BCE∴A D＝BE；（2）∵△AC D≌△BCE∴∠CB H＝∠CAG∵∠ACB＝∠ECD＝60°，点B、C、D在同一条直线上∴∠ACB＝∠ECD＝∠AC G＝60°又∵AC＝BC∴△AC G≌△BCH；（3）△C G H是等边三角形，理由如下：∵△AC G≌△BCH∴C G＝C H（全等三角形的对应边相等）又∵∠AC G＝60°∴△C G H是等边三角形（有一内角为60度的等腰三角形为等边三角形）；11．（1）证明：∵△ABC和△D C E都是等边三角形，∴BC＝AC，CE＝C D，∠ACB＝∠D C E＝60°，∴∠ABC+∠ACE＝∠D CE+∠ACE，即∠BCE＝∠ACD，∴∠BCE≌△ACD（SAS），∴BE＝A D；（2）①证明：∵△ABC和△C D E是等边三角形，∴AB＝BC，C D＝BE，∠ACB＝∠D C E＝60°，∴∠ACB+∠BC D＝∠D CE+∠BC D，即∠AC D＝∠BCE，∴△AC D≌△BCE（SAS），∴A D＝BE，同理：△AB D≌△CBF（SAS），∴A D＝CF，即A D＝BE＝CF；②解：结论：PB+P C+P D＝BE，理由：如图2，AD与BC的交点记作点Q，则∠A Q C＝∠B Q P，由①知，△AC D≌△BCE，∴∠CA D＝∠CBE，在△AC Q中，∠C A D+∠A Q C＝180°﹣∠ACB＝120°，∴∠CBE+∠B Q P＝120°，在△BP Q中，∠APB＝180°﹣（∠CBE+∠B Q P）＝60°，∴∠DPE＝60°，同理：∠APC＝60°，∴∠CP D＝120°，在PE上取一点M，使P M＝P C，∴△CP M是等边三角形，∴CP＝C M，∠PC M＝∠C M P＝60°，∴∠C M E＝120°＝∠CP D，∵△C D E是等边三角形，∴C D＝CE，∠D C E＝60°＝∠PCM，∴∠PC D＝∠M C E，∴△PC D≌△M C E（SAS），∴P D＝M E，∴BE＝PB+P M+M E＝PB+P C+P D．12．证明：连接D E、EF、DF．（1）当点G在线段BE上时，如图①，在EF上截取E H使E H＝B G．∵D、E、F是等边△ABC三边中点，在△DB G和△DEH中，，∴△DB G≌△DEH（SAS），∴D G＝D H．∴∠B D G＝∠E D H．∵∠B DE＝∠G D E+∠B D G＝60°，∴∠G D H＝∠G D E+∠E D H＝60°∴在直线EF上存在点H使得△D G H是等边三角形．（2）当点G在射线EC上时，如图②，在EF上截取E H使E H＝B G．由（1）可证△DB G≌△DE H．∴D G＝D H，∠BD G＝∠E D H．∵∠B DE＝∠B D G﹣∠E D G＝60°，∴∠G D H＝∠E D H﹣∠E D G＝60°．∴在直线EF上存在点H使得△D G H是等边三角形．（3）当点G在BC延长线上时，如图③，与（2）同理可证，结论成立．综上所述，点G在直线BC上的任意位置时，该结论成立．13．解：（1）∵AB＝BC＝A C，∴△ABC为等边三角形，∴∠A＝60°，故答案为：60．（2）∵∠A＝60°，当∠AP Q＝90°时，∠A QP＝90°﹣60°＝30°．∴QA＝2PA．即20﹣2t＝2t×2．解得．当∠A QP＝90°时，∠AP Q＝90°﹣60°＝30°．∴PA＝2QA．即2（20﹣2t）＝2t．解得．∴当0＜t＜10，且△AP Q为直角三角形时，t的值为．（3）①由题意得：AP＝2t，AQ＝20﹣2t，∵∠A＝60°，∴当A Q＝AP时，△AP Q为等边三角形，∴2t＝20﹣2t，解得t＝5，②当P于B重合，Q与C重合，则所用时间为：4÷2＝20，综上，当△AP Q为等边三角形时，t＝5或20．14．解：（1）∵AB＝8，点P的运动速度为2个单位长度/秒，∴当P为AB中点时，即4÷2＝2（秒）；故答案为：2．（2）由题意可得：当BP＝2B Q时，P，Q分别在AB，BC上，∴点Q只能在BC上运动，当点P在AB上，∴BP＝8﹣2t，BQ＝t，则8﹣2t＝2×t，解得t＝，当点P在BC上时，BP＝2t﹣8，B Q＝，∴2t﹣8＝2×t，解得t＝12．当点P运动到AC上时，不存在BP＝2B Q；故t＝12或，使得BP＝2B Q．（3）当点P为靠近点A的三等分点时，如图1，AB+BC+CP＝8+16+8＝32，此时t＝32÷2＝16，∵BC+C Q＝16+4＝20，∴a＝20÷16＝，当点P为靠近点C的三等分点时，如图2，AB+BC+CP＝8+16+4＝28，此时t＝28÷2＝14，∵BC+C Q＝16+8＝24，∴a＝24÷14＝．综上可得：a的值为或．15．解：（1）设运动t秒，M、N两点重合，根据题意得：2t﹣t＝15，∴t＝15，答：点M，N运动15秒后，M、N两点重合；（2）如图1，设点M、N运动x秒后，△A M N为等边三角形，∴AN＝A M，由运动知，AN＝15﹣2x，A M＝x，∴15﹣2x＝x，解得：x＝5，∴点M、N运动5秒后，△A M N是等边三角形；（3）假设存在，如图2，设M、N运动y秒后，得到以M N为底边的等腰三角形A M N，∴A M＝A N，∴∠A M N＝∠ANM，∵△ABC是等边三角形，∴AB＝AC，∠C＝∠B＝60°，∴△AC N≌△ABM（A AS），∴CN＝B M，∴C M＝B N，由运动知，C M＝y﹣15，BN＝15×3﹣2y，∴y﹣15＝15×3﹣2y，∴y＝20，故点M，N在BC边上运动时，能得到以M N为底边的等腰三角形A M N，此时M，N运动的时间为20秒．16．解：（1）①∵t＝1s，∴BP＝C Q＝3×1＝3cm，∵AB＝10cm，点D为AB的中点，∴B D＝5cm．又∵PC＝BC﹣BP，BC＝8cm，∴PC＝8﹣3＝5cm，∴PC＝B D．又∵AB＝AC，∴∠B＝∠C，在△BP D和△C Q P中，∴△BP D≌△C Q P（SAS）．②∵v≠，vP Q∴BP≠C Q，若△BP D≌△CPQ，∠B＝∠C，则BP＝PC＝4cm，C Q＝B D＝5cm，∴点P，点Q运动的时间s，∴cm/s；（2）设经过x秒后点P与点Q第一次相遇，由题意，得x＝3x+2×10，解得．∴点P共运动了×3＝80cm．△ABC周长为：10+10+8＝28cm，若是运动了三圈即为：28×3＝84cm，∵84﹣80＝4cm＜AB的长度，∴点P、点Q在AB边上相遇，∴经过s点P与点Q第一次在边AB上相遇．∴CN＝B M，∴C M＝B N，由运动知，C M＝y﹣15，BN＝15×3﹣2y，∴y﹣15＝15×3﹣2y，∴y＝20，故点M，N在BC边上运动时，能得到以M N为底边的等腰三角形A M N，此时M，N运动的时间为20秒．16．解：（1）①∵t＝1s，∴BP＝C Q＝3×1＝3cm，∵AB＝10cm，点D为AB的中点，∴B D＝5cm．又∵PC＝BC﹣BP，BC＝8cm，∴PC＝8﹣3＝5cm，∴PC＝B D．又∵AB＝AC，∴∠B＝∠C，在△BP D和△C Q P中，∴△BP D≌△C Q P（SAS）．②∵v≠，vP Q∴BP≠C Q，若△BP D≌△CPQ，∠B＝∠C，则BP＝PC＝4cm，C Q＝B D＝5cm，∴点P，点Q运动的时间s，∴cm/s；（2）设经过x秒后点P与点Q第一次相遇，由题意，得x＝3x+2×10，解得．∴点P共运动了×3＝80cm．△ABC周长为：10+10+8＝28cm，若是运动了三圈即为：28×3＝84cm，∵84﹣80＝4cm＜AB的长度，∴点P、点Q在AB边上相遇，∴经过s点P与点Q第一次在边AB上相遇．∴CN＝B M，∴C M＝B N，由运动知，C M＝y﹣15，BN＝15×3﹣2y，∴y﹣15＝15×3﹣2y，∴y＝20，故点M，N在BC边上运动时，能得到以M N为底边的等腰三角形A M N，此时M，N运动的时间为20秒．16．解：（1）①∵t＝1s，∴BP＝C Q＝3×1＝3cm，∵AB＝10cm，点D为AB的中点，∴B D＝5cm．又∵PC＝BC﹣BP，BC＝8cm，∴PC＝8﹣3＝5cm，∴PC＝B D．又∵AB＝AC，∴∠B＝∠C，在△BP D和△C Q P中，∴△BP D≌△C Q P（SAS）．②∵v≠，vP Q∴BP≠C Q，若△BP D≌△CPQ，∠B＝∠C，则BP＝PC＝4cm，C Q＝B D＝5cm，∴点P，点Q运动的时间s，∴cm/s；（2）设经过x秒后点P与点Q第一次相遇，由题意，得x＝3x+2×10，解得．∴点P共运动了×3＝80cm．△ABC周长为：10+10+8＝28cm，若是运动了三圈即为：28×3＝84cm，∵84﹣80＝4cm＜AB的长度，∴点P、点Q在AB边上相遇，∴经过s点P与点Q第一次在边AB上相遇．∴CN＝B M，∴C M＝B N，由运动知，C M＝y﹣15，BN＝15×3﹣2y，∴y﹣15＝15×3﹣2y，∴y＝20，故点M，N在BC边上运动时，能得到以M N为底边的等腰三角形A M N，此时M，N运动的时间为20秒．16．解：（1）①∵t＝1s，∴BP＝C Q＝3×1＝3cm，∵AB＝10cm，点D为AB的中点，∴B D＝5cm．又∵PC＝BC﹣BP，BC＝8cm，∴PC＝8﹣3＝5cm，∴PC＝B D．又∵AB＝AC，∴∠B＝∠C，在△BP D和△C Q P中，∴△BP D≌△C Q P（SAS）．②∵v≠，vP Q∴BP≠C Q，若△BP D≌△CPQ，∠B＝∠C，则BP＝PC＝4cm，C Q＝B D＝5cm，∴点P，点Q运动的时间s，∴cm/s；（2）设经过x秒后点P与点Q第一次相遇，由题意，得x＝3x+2×10，解得．∴点P共运动了×3＝80cm．△ABC周长为：10+10+8＝28cm，若是运动了三圈即为：28×3＝84cm，∵84﹣80＝4cm＜AB的长度，∴点P、点Q在AB边上相遇，∴经过s点P与点Q第一次在边AB上相遇．。

初二数学平行四边形压轴：几何证明题

初二数学平行四边形压轴：几何证明题1.在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，顺次连接EF 、FG 、GH 、HE ．（1）请判断四边形EFGH 的形状，并给予证明；（2）试探究当满足什么条件时，使四边形EFGH 是菱形，并说明理由。

2.如图，在直角三角形ABC 中，∠ACB=90°，AC=BC=10，将△ABC 绕点B 沿顺时针方向旋转90°得到△A 1BC 1．（1）线段A 1C 1的长度是，∠CBA 1的度数是．（2）连接CC 1，求证：四边形CBA 1C 1是平行四边形．3. 如图，矩形ABCD 中，点P 是线段AD 上一动点，O 为BD 的中点， PO 的延长线交BC 于Q.（1）求证：OP=OQ ；（2）若AD=8厘米，AB=6厘米，P 从点A 出发，以1厘米/秒的速度向D 运动（不与D 重合）.设点P 运动时间为t 秒，请用t 表示PD 的长；并求t 为何值时，四边形PBQD 是菱形．4.已知：如图，在□ABCD 中，AE 是BC 边上的高，将△ABE 沿BC 方向平移，使点E 与点C 重合，得△GFC. ⑴求证：BE =DG ；⑵若∠B =60︒，当AB 与BC 满足什么数量关系时，四边形ABFG 是菱形？证明你的结论.5. 如图，在四边形ABCD 中，AD ∥BC ，E 为CD 的中点，连结AE 、BE ，BE ⊥AE ，延长AE 交BC 的延长线于点F ．求证：（1）FC ＝AD ；（2）AB ＝BC ＋AD ．6.如图，在△ABC 中，AB=AC ，D 是BC 的中点，连结AD ，在AD 的延长线上取一点E ，连结BE ，CE.（1）求证：△ABE ≌△ACE（2）当AE 与AD 满足什么数量关系时，四边形ABEC 是菱形？并说明理由.A B E F C G D H B A 1 C 1A C AD G CB F E A QCD P B OA BE D C A D EF C B7.如图，在平行四边形ABCD 中，点E 是边AD 的中点，BE 的延长线与CD 的延长线交于点F.（1）求证：△ABE ≌△DFE（2）连结BD 、AF ，判断四边形ABDF 的形状，并说明理由.8. 如图，已知点D 在△ABC 的BC 边上，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ．（1）求证：AE ＝DF ；（2）若AD 平分∠BAC ，试判断四边形AEDF 的形状，并说明理由．9. 如图，在平行四边形中，点E F ，是对角线BD 上两点，且BF DE =．（1）写出图中每一对你认为全等的三角形；（2）选择（1）中的任意一对全等三角形进行证明．10.在梯形ABCD 中，AD ∥BC,AB=DC ，过点D 作DE ⊥BC ，垂足为点E ，并延长DE 至点F ，使EF=DE.连接BF 、CF 、AC.（1）求证：四边形ABFC 是平行四边形；（2）若CE BE DE ⋅=2,求证：四边形ABFC 是矩形.11.如图，△ABC 中，AB=AC ，AD 、AE 分别是∠BAC 和∠BAC 的外角平分线，BE ⊥AE. （1）求证：DA ⊥AE（2）试判断AB 与DE 是否相等？并说明理由。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF，连接DF，G 为DF的中点，连接EG，CG，EC．(1)如图1，若点E在CB边的延长线上，直接写出EG与GC的位置关系及的值；(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置，请问(1)中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；(3)将图1中的△BEF绕点B顺时针旋转α(0°＜α＜90°)，若BE=1，AB=，当E，F，D三点共线时，求DF的长及tan∠ABF的值．解：（1）EG⊥CG，=，理由是：过G作GH⊥EC于H，∵∠FEB=∠DCB=90°，∴EF∥GH∥DC，∵G为DF中点，∴H为EC中点，∴EG=GC，GH=（EF+DC）=（EB+BC），即GH=EH=HC，∴∠EGC=90°，即△EGC是等腰直角三角形，∴=；（2）解：结论还成立，理由是：如图2，延长EG到H，使EG=GH，连接CH、EC，过E作BC的垂线EM，延长CD，∵在△EFG和△HDG中∴△EFG≌△HDG（SAS），∴DH=EF=BE，∠FEG=∠DHG，∴EF∥DH，∴∠1=∠2=90°-∠3=∠4，∴∠EBC=180°-∠4=180°-∠1=∠HDC，在△EBC和△HDC中∴△EBC≌△HDC．∴CE=CH，∠BCE=∠DCH，∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°，∴△ECH是等腰直角三角形，∵G为EH的中点，∴EG⊥GC，=，即（1）中的结论仍然成立；（3）解：连接BD，∵AB=，正方形ABCD，∴BD=2，∴cos∠DBE==，∴∠DBE=60°，∴∠ABE=∠DBE-∠ABD=15°，∴∠ABF=45°-15°=30°，∴tan∠ABF=，∴DE=BE=，∴DF=DE-EF=-1．解析：（1）过G作GH⊥EC于H，推出EF∥GH∥DC，求出H为EC中点，根据梯形的中位线求出EG=GC，GH=（EF+DC）=（EB+BC），推出GH=EH=BC，根据直角三角形的判定推出△EGC是等腰直角三角形即可；（2）延长EG到H，使EG=GH，连接CH、EC，过E作BC的垂线EM，延长CD，证△EFG≌△HDG，推出DH=EF=BE，∠FEG=∠DHG，求出∠EBC=∠HDC，证出△EBC≌△HDC，推出CE=CH，∠BCE=∠DCH，求出△ECH是等腰直角三角形，即可得出答案；（3）连接BD，求出cos∠DBE==，推出∠DBE=60°，求出∠ABF=30°，解直角三角形求出即可．2.已知正方形ABCD和等腰直角三角形BEF，BE=EF，∠BEF=90°，按图1放置，使点E 在BC上，取DF的中点G，连接EG，CG．(1)延长EG交DC于H，试说明：DH=BE．(2)将图1中△BEF绕B点逆时针旋转45°，连接DF，取DF中点G(如图2)，莎莎同学发现：EG=CG且EG⊥CG．在设法证明时他发现：若连接BD，则D，E，B三点共线．你能写出结论“EG=CG且EG⊥CG”的完整理由吗？请写出来．(3)将图1中△BEF绕B点转动任意角度α(0＜α＜90°)，再连接DF，取DF的中点G(如图3)，第2问中的结论是否成立？若成立，试说明你的结论；若不成立，也请说明理由．（1）证明：∵∠BEF=90°，∴EF∥DH，而∠EGF=∠DGH，GF=GD，∴△GEF≌△GHD，∴EF=DH，而BE=EF，∴DH=BE；（2）连接DB，如图，∵△BEF为等腰直角三角形，∴∠EBF=45°，而四边形ABCD为正方形，∴∠DBC=45°，∴D，E，B三点共线．而∠BEF=90°，∴△FED为直角三角形，而G为DF的中点，∴EG=GD=GC，∴∠EGC=2∠EDC=90°，∴EG=CG且EG⊥CG；（3）第2问中的结论成立．理由如下：连接AC、BD相交于点O，取BF的中点M，连接OG、EM、MG，如图，∵G为DF的中点，O为BD的中点，M为BF的中点，∴OG∥BF，GM∥OB，∴四边形OGMB为平行四边形，∴OG=BM，GM=OB，而EM=BM，OC=OB，∴EM=OG，MG=OC，∵∠DOG=∠GMF，而∠DOC=∠EMF=90°，∴∠EMG=∠GOC，∴EG=CG，∠EGM=∠OCG，又∵∠MGF=∠BDF，∠FGC=∠GDC+∠GCD，∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°，∴EG=CG且EG⊥CG．解析：（1）由∠BEF=90°，得到EF∥DH，而GF=GD，易证得△GEF≌△GHD，得EF=DH，而BE=EF，即可得到结论．（2）连接DB，如图2，由△BEF为等腰直角三角形，得∠EBF=45°，而四边形ABCD为正方形，得∠DBC=45°，得到D，E，B三点共线，而G为DF的中点，根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC，于是∠EGC=2∠EDC=90°，即得到结论．（3）连接AC、BD相交于点O，取BF的中点M，连接OG、EM、MG，由G为DF的中点，O为BD的中点，M为BF的中点，根据三角形中位线的性质得OG∥BF，GM∥OB，得到OG=BM，GM=OB，而EM=BM，OC=OB，得到EM=OG，MG=OC，又∠DOG=∠GMF，而∠DOC=∠EMF=90°，得∠EMG=∠GOC，则△MEG≌△OGC，得到EG=CG，∠EGM=∠OCG，而∠MGF=∠BDF，∠FGC=∠GDC+∠GCD，所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°．3.已知正方形ABCD和等腰Rt△BEF，BE=EF，∠BEF=90°，按图①放置，使点F在BC上，取DF的中点G，连接EG、CG．(1)探索EG、CG的数量关系和位置关系并证明；(2)将图①中△BEF绕B点顺时针旋转45°，再连接DF，取DF中点G(如图②)，问(1)中的结论是否仍然成立．证明你的结论；(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间)，再连接DF，取DF的中点G(如图③)，问(1)中的结论是否仍然成立，证明你的结论．解：（1）EG=CG且EG⊥CG．证明如下：如图①，连接BD．∵正方形ABCD和等腰Rt△BEF，∴∠EBF=∠DBC=45°．∴B、E、D三点共线．∵∠DEF=90°，G为DF的中点，∠DCB=90°，∴EG=DG=GF=CG．∴∠EGF=2∠EDG，∠CGF=2∠CDG．∴∠EGF+∠CGF=2∠EDC=90°，即∠EGC=90°，∴EG⊥CG．（2）仍然成立，证明如下：如图②，延长EG交CD于点H．∵BE⊥EF，∴EF∥CD，∴∠1=∠2．又∵∠3=∠4，FG=DG，∴△FEG≌△DHG，∴EF=DH，EG=GH．∵△BEF为等腰直角三角形，∴BE=EF，∴BE=DH．∵CD=BC，∴CE=CH．∴△ECH为等腰直角三角形．又∵EG=GH，∴EG=CG且EG⊥CG．（3）仍然成立．证明如下：如图③，延长CG至H，使GH=CG，连接HF交BC于M，连接EH、EC．∵GF=GD，∠HGF=∠CGD，HG=CG，∴△HFG≌△CDG，∴HF=CD，∠GHF=∠GCD，∴HF∥CD．∵正方形ABCD，∴HF=BC，HF⊥BC．∵△BEF是等腰直角三角形，∴BE=EF，∠EBC=∠HFE，∴△BEC≌△FEH，∴HE=EC，∠BEC=∠FEH，∴∠BEF=∠HEC=90°，∴△ECH为等腰直角三角形．又∵CG=GH，∴EG=CG 且EG ⊥CG ．解析：（1）首先证明B 、E 、D 三点共线，根据直角三角形斜边上的中线等于斜边的一半，即可证明EG=DG=GF=CG ，得到∠EGF=2∠EDG ，∠CGF=2∠CDG ，从而证得∠EGC=90°；（2）首先证明△FEG ≌△DHG ，然后证明△ECH 为等腰直角三角形．可以证得：EG=CG 且EG ⊥CG ．（3）首先证明：△BEC ≌△FEH ，即可证得：△ECH 为等腰直角三角形，从而得到：EG=CG 且EG ⊥CG ．已知，正方形ABCD 中，△BEF 为等腰直角三角形，且BF 为底，取DF 的中点G ，连接EG 、CG ．（1）如图1，若△BEF 的底边BF 在BC 上，猜想EG 和CG 的数量关系为______；（2）如图2，若△BEF 的直角边BE 在BC 上，则（1）中的结论是否还成立？请说明理由；（3）如图3，若△BEF 的直角边BE 在∠DBC，则（1）中的结论是否还成立？说明理由．解：（1）GC=EG ，（1分）理由如下：∵△BEF 为等腰直角三角形， ∴∠DEF=90°，又G 为斜边DF 的中点， ∴EG= DF ， ∵ABCD 为正方形， ∴∠BCD=90°，又G 为斜边DF 的中点，∴CG= DF ，∴GC=EG；（2）成立．如图，延长EG 交CD 于M ， 1 21 2∵∠BEF=∠FEC=∠BCD=90°，∴EF∥CD，∴∠EFG=∠MDG，又∠EGF=∠DGM，DG=FG ，∴△GEF≌△GMD，∴EG=MG，即G 为EM 的中点．∴CG 为直角△ECM 的斜边上的中线，∴CG=GE= EM ；（3）成立．取BF 的中点H ，连接EH ，GH ，取BD 的中点O ，连接OG ，OC ．∵CB=CD，∠DCB=90°，∴CO= BD ． ∵DG=GF，∴GH∥BD，且GH= BD ，OG∥BF，且OG= BF ， ∴CO=GH．∵△BEF 为等腰直角三角形．∴EH= BF∴EH=OG．∵四边形OBHG 为平行四边形，∴∠BOG=∠BHG．∵∠BOC=∠BHE=90°．∴∠GOC=∠EHG．∴△GOC≌△EHG．∴EG=GC．1 1 21 2 1 2。

初二数学压轴几何证明题(含答案)

部编版初二数学八年级上册期中压轴专题(带答案解析)

八年级上册数学几何压轴大题

八年级上学期数学期末专题：几何证明综合(原题和解析)

专题07几何证明解答题之压轴题训练(1)(原卷版)-2021-2022学年第一学期八年级压轴题训练

初二数学压轴几何证明题(含答案)

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

特训07 几何证明解答压轴题 2024-2025学年上海八年级数学上期末复习(原卷版)

人教版八年级数学上册期末专题复习：几何压轴题强化训练试题(含答案)

北师大版八年级下册数学期末几何压轴题专练(含答案)

初二数学 数学全等三角形压轴几何题试题含答案

初二数学压轴题及答案

初二数学压轴几何证明题(含答案)

苏科版八年级上册几何压轴题专题(解析版)

专题 全等三角形压轴题(30题)(解析版)

初二压轴题(几何证明直角三角形后)

人教版八年级上册几何压轴题专项训练 含答案

初二数学平行四边形压轴：几何证明题

初二数学数学全等三角形压轴几何题试题含答案

专题全等三角形压轴题(30题)(解析版)

人教版八年级上册几何压轴题专项训练含答案