刚体平面运动-习题解答
第八章-2 刚体的平面运动

aB aAx aAy aBA a
√ √
√
n BA
aAy
A
aAx
方向 √ √ 大小
√
?
√
? AB
将上式向 轴投影
a BA
2 AB
aAy
AB
n a BA
n aB a Ax a Ay 2 aBA 74.36(cm / s 2 )
aB 1 n (a Ax a Ay ) aBA 2 2
a
① 加速度没有投影定理。 ② 加速度瞬心存在,但一般不与速度瞬心重合。 ③ 由于加速度瞬心寻找很困难,求解中只用基点法。
半径为 R 的轮子 在水平面上纯滚,已知某瞬 时轮心的速度为 vO,加速 度为aO .求轮上速度瞬心的 加速度和 B 点的加速度。
例
aBY aO aBX B O C aCX
aB
B
aAx
n aB BA
§8-5 运动综合应用举例
工程中的机构大都由数个物体组成,各物体间通过联 结点而传递运动。为分析机构的运动,首先要分清各 物体都作什么运动,计算联结点的速度和加速度。 平面运动理论用来分析同一平面运动刚体,或刚体间 接触处没有相对滑动的机构的运动量联系。当两刚体 相接触而有相对滑动时,则需要点的合成运动理论。 复杂机构可能同时有平面运动和点的合成运动问题, 应分清关系、综合处理。
B’ B
30°
vB’A
vB' A 30 3 mm/ s
AE
vB ' A 3 rad / s AB 2
从而得槽杆AE的角速度
求加速度
1、选滑块B为动点,动系与槽杆AE固结。 aa = a e + a r+ a C ( 4 ) 2、以 A 点为基点,求 B’点的加速度
第八章刚体的平面运动
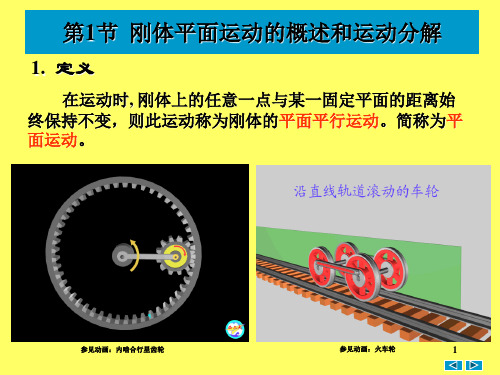
其中,i ,j 为x,y 轴的单位矢量。
14
2. 速度投影定理
同一平面图形上任意两点的速度在这两点连
线上的投影相等。
证明:
vB =vA +vBA
vBA vB
∵(vB )AB= (vA )AB+ (vBA) AB
A
B
vA
vA
而vBA 垂直AB,在AB两点连线上的投影为零
∴ (vB )AB= (vA )AB
O
30 A 60 60 B vB 已知方向,可求出连杆CB的速度瞬
vA
心Cv2。
36
例题
刚体的平面运动
例题8
因为
CCv2 CB tan 30
3l 3
故得连杆CB角速度的大小
C
Cv2
Cv1
vC
CB
vC CCv 2
3 l
vA
它的转向沿逆时针。于是滑块B 速
度的大小为
O
30 A
vA
60 60 B vB
M3和M4各点的加速度大小。
39
例题
刚体的平面运动
例题9
解: 因在此瞬时O点的加速度是已知的,
M3
故选O点为基点,则齿轮节圆边缘上任一
点M 的加速度为:
aO vO M4
M2
RO
a O
因为任一瞬时齿轮的角速度 vO ,
R
M1
因此,可对此式求导数,从而求得齿轮
的角加速度
O
ψ
A vB
vA=u
vB
u
tan
,
vBA
u
sin
,
所以
AB
vBA l
u l
刚体的平面运动习题答案

刚体的平面运动习题答案刚体的平面运动习题答案刚体的平面运动是力学中的一个重要课题,它涉及到物体在平面上的运动规律和力的作用方式。
在学习这一课题时,我们常常会遇到一些习题,下面我将为大家提供一些关于刚体平面运动的习题答案,希望能够帮助大家更好地理解和掌握这一知识点。
1. 习题一:一个质量为m的刚体在水平地面上受到一个水平力F的作用,求刚体受力情况下的加速度。
解答:根据牛顿第二定律,刚体的加速度与作用在其上的合外力成正比,与刚体的质量成反比。
因此,刚体的加速度可以表示为a = F/m。
2. 习题二:一个质量为m的刚体以速度v沿x轴正方向运动,受到一个大小为F的力沿y轴正方向作用,求刚体的加速度和运动轨迹。
解答:由于刚体受到的力只有在y轴上的F,所以刚体在x轴方向上不受力,即不会有加速度。
而在y轴方向上,刚体受到的力F会引起加速度的产生。
根据牛顿第二定律,我们可以得到刚体在y轴方向上的加速度为a = F/m。
至于刚体的运动轨迹,由于在x轴方向上没有加速度,刚体将以匀速直线运动,而在y轴方向上有加速度,刚体将在y轴上做匀加速运动。
3. 习题三:一个质量为m的刚体受到一个大小为F的力作用,该力的方向与刚体的速度方向相同,求刚体在力作用下的加速度。
解答:由于力的方向与速度方向相同,所以刚体受到的力将会增加其速度。
根据牛顿第二定律,刚体的加速度可以表示为a = F/m。
4. 习题四:一个质量为m的刚体受到一个大小为F的力作用,该力的方向与刚体的速度方向相反,求刚体在力作用下的加速度。
解答:由于力的方向与速度方向相反,所以刚体受到的力将会减小其速度。
根据牛顿第二定律,刚体的加速度可以表示为a = -F/m。
5. 习题五:一个质量为m的刚体受到一个大小为F的力作用,该力的方向与刚体的速度方向成一定的夹角θ,求刚体在力作用下的加速度。
解答:对于这个习题,我们可以将力F分解为两个分力F1和F2,其中F1与刚体的速度方向相同,F2与刚体的速度方向垂直。
第6章刚体的平面运动习题解答080814

,(逆时针)、
,
杆OB得角速度为
,(逆时针)、
两齿轮啮合点M得速度为,则轮1得角速度为
,(逆时针)、
6-9如图所示,轮O在水平面上匀速滚动而不滑动,轮缘上固连销钉连接滑块B,此滑块在摇杆得槽内滑动,并带动摇杆绕轴转动。已知轮得半径m,在图示位置时,就是轮得切线,轮心得速度m/s,摇杆与水平面得夹角为。求摇杆得角速度与角加速度。
解:如图所示,对各构件进行速度分析、
1)杆作平面运动、因,所以杆为瞬时平移,得
、
2)杆作平面运动、由找得杆得速度瞬心为D点,所以,杆上得速度分布好像与三角板一起绕作定轴转动一样,得
,方向如图示、
3)杆作平面运动、由找得杆得速度瞬心为,故有
,(顺时针);
,(方向向上).
6—5图示四连杆机构中,连杆由一块三角板ABD构成。已知曲柄得角速度rad/s,mm,mm,mm。当mm铅直时,AB平行于,且、A、D在同一直线上,角。求三角板ABD得角速度与点D得速度.
解:1)速度分析、
动齿轮A在定齿轮O上作纯滚动,所以,动齿轮A上与定齿轮O接触得这点就就是动齿轮得A得速度瞬心,于就是有
,,(逆时针)、
、
选BE杆上得B点为动点,套筒C为动系,如图(a)。由速度合成定理
,
得
,
、
式中、从而杆BE得角速度为
,(顺时针)、
当选BE杆上得为动点时,牵连速度为零,又因为杆相对于套筒就是作平移,从而杆BE上得点得速度为
解出
,
,
于就是,杆得角速度为
,(逆时针);
杆得角速度为
,(顺时针)、
选取滑块上得销钉C为动点,摇杆为动系,则
第二章习题解答
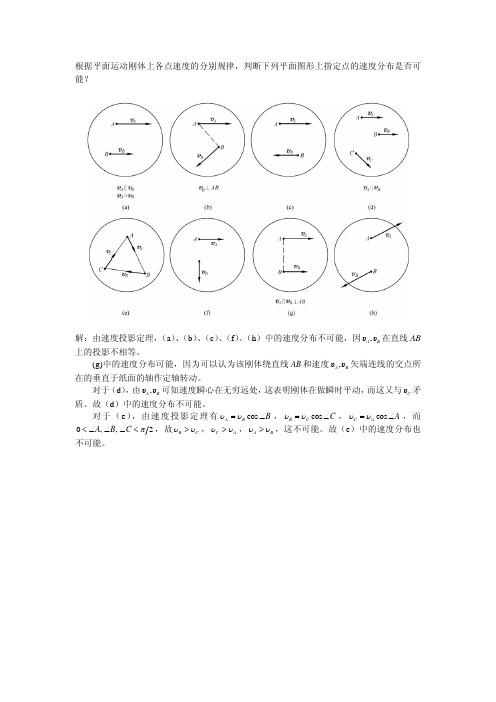
v B = v A + ωAB × rAB
将式(a)向 v A 方向投影,并考虑到 ϕ = 90D ,得:
(a)
ω AB ⋅ 2r sin 30D = v A
ω AB =
将式(a)向 v B 方向投影,得:
ωr
2r sin 30D
=ω
vB = ω AB × 2r cos 30D = 3ω r
ωO B =
反平行四边形机构中, AB = CD = 2a AC = BD = 2c , a > c 。求 BD 杆的动瞬心轨迹和 定瞬心轨迹。
解:显然, P 点为 BD 杆的速度瞬心。 连结 AD, 则 ΔADC ≅ ΔADB , 故 ∠DAB = ∠CDA , PA = PD , PB = PC ,可知: PA + PC = PD + PB = 2a ,即速度瞬心 P 到 A、C 两点及到 D,B 两点的距 离之和始终为常数,因此 P 点的动瞬心轨迹和定瞬心轨迹分别为以 B、 D 为焦点的椭圆和以 A、C 为焦点的椭圆。
ν A = ω AB AD
又,
AD = OA OC / sin θ R cos θ = = tan θ tan θ sin 2 θ
得到:
ω AB = ν A / AD =
v sin 2 θ (逆时针) R cos θ
已知 OA 杆以匀角速度 ω e = ω 逆时针转动, 圆盘 B 相对 AB 杆以 ω r = 4ω 作顺时针纯滚动, 圆盘半径为 r , OP = 3r 。求圆盘中心 B 的速度大小。
o
(a)
ω AB =
由式(a)得:
ω0 r
l
v B = v A + ωAB × rAB = 0
刚体平面运动习题

刚体平面运动习题第八章刚体平面运动的练习1.真或假(勾选正确和交叉错误)8-1。
刚体的平面运动是一种运动,在这种运动中,刚体上的任何一点与固定平面之间的距离总是平行的。
()8-2。
平面图形的运动可以看作基点的平移和围绕基点的旋转的组合。
()8-3。
平面图形上任意两点的速度都相等地投影在一个固定的轴上。
()()()8-6。
瞬时速度中心的速度为零,加速度为零。
()8-7。
刚体的平移也是一种平面运动。
()2。
填空(在横线上写出正确答案)8-8。
在直线轨道上纯滚动时,圆轮与地面接触点的速度为。
8-9。
平面图上任意两点的速度在上投影中相等。
8-10。
瞬时刚体平移时的角速度是:刚体上每个点的速度;每个点的加速度。
3.简短回答问题8-11。
确定图中所示平面运动物体的瞬时速度中心的位置。
AbabaccωOboaωOdbω(b)Co(a)(c)图8-11 (d)8-12。
如果一个刚体在一个平面上运动,下面平面图中A和B的速度方向是正确的吗?问题8-12图(c)8-13。
下图中O1A和AC的速度分布是否正确?8-14。
当圆形车轮在曲线上滚动时,某一瞬时车轮中心的速度vo和加速度ao,而车轮的半径是R,即车轮中心的角度加速度是多少?如何确定瞬时速度中心的加速度的大小和方向?蟹爪兰O1VβA01ωO2P 8-13图8-148-15。
为什么用基点法计算平面图中单个点的加速度时没有科里奥利加速度?4.计算问题8-16。
椭圆规AB由曲柄OC驱动,曲柄OC以均匀的角速度ω O绕O轴旋转。
如图所示,如果以C为基点,OC=BC=AC=r,试着找出椭圆规AB的平面运动方程。
8-17。
半径为R的齿轮由曲柄OA驱动,沿半径为R的固定齿轮滚动,如图所示。
曲柄以均匀的角加速度α绕O轴旋转,并设定初始角速度ω。
角加速度α?0.角落??0.如果选择移动齿轮的中心C点作为基点,试着找出移动齿轮的平面运动方程。
yay rarαφBMMoxorBx 8-16图ωOO图8-178-18。
理论力学课后习题答案-第6章--刚体的平面运动分析

理论力学课后习题答案-第6章--刚体的平面运动分析为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:Rv R v A A ==ωRv R v B B 22==ωBA ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
解:杆BC 的瞬心在点P ,滚子O 的瞬心在点DBD v B ⋅=ωBPBD BPv B BC ⋅==ωω︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
hv AC v AP v ABθθω2000cos cos ===ωω习题6-5图OO 1ABCOO 1ABCD习题6-3解图习题6-3图v Av B ωωCBOϕθ ωCBO ϕθω vv B PD习题6-4图习题6-4解图ωB习题6-6图习题6-6解图l ϕυl2BO 1ωABAυB υO1O ABωω解:图(a )中平面运动的瞬心在点O ,杆BC 的瞬心在点C 。
图(b )中平面运动的杆BC 的瞬心在点P ,杆AD 做瞬时平移。
6-6 图示的四连杆机械OABO 1中,OA = O 1B =21AB ,曲柄OA 的角速度ω= 3rad/s 。
试求当示。
ϕ= 90°而曲柄O 1B 重合于OO 1的延长线上时,杆AB 和曲柄O 1B 的角速度。
解:杆AB 的瞬心在O 3===ωωOAvAABrad/s ωl v B3=2.531===ωωl v BBO rad/s6-7 绕电话线的卷轴在水平地面上作纯滚动,线上的点A 有向右的速度v A = 0.8m/s ,试求卷轴中心O 的速度与卷轴的角速度,并问此时卷轴是向左,还是向右方滚动?解:如图333.16.08.03.09.0==-=AOv ωrad/s 2.1689.09.0=⨯==OOv ωm/s 卷轴向右滚动。
理论力学7—刚体的平面运动2
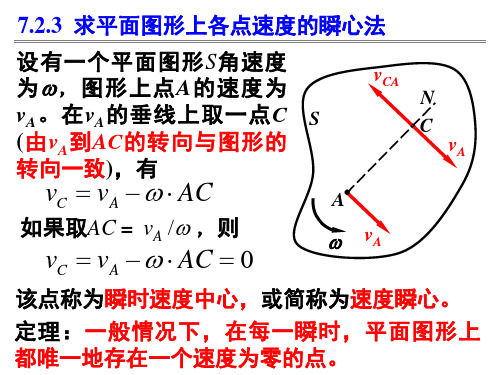
vC
vC C C 2 w BC
3 rw 3
习题7-12 图示小型精压机的传动机构,OA= O1B=r=0.1m,EB=BD=AD=l=0.4 m,在 图示瞬时OA⊥AD,O1B⊥ED,O1D在水平位 置,OD和EF在铅直位置。已知曲柄OA的转速 n=120 rpm,求此时压头F 的速度。
a C O r r
t
w
O
vO
n aCO
aO aO
aO r
vO r
aO
2
t aCO
C
aCO rw
n 2
r(
)
2
vO r
w
vO r
,
aO r
a C O a O , a C O vO / r
t n 2
取如图的投影轴, 将各矢量 投影到投影轴上得
y
aCx aO aCO 0
A2 A4
vA2
A1
v A 3 2 rw 2 v
2 rw 2v
例7-7 曲柄肘杆式压床如图。已知曲柄OA长r, 以匀角速度w 转动,AB = BC = BD = l,当曲柄 与水平线成30º 角时,连杆AB处于水平位置,而 肘杆DB与铅垂线也成30º 角。试求图示位置时, 杆AB、BC的角速度以及冲头C 的速度。 解:连杆AB作平面运动,瞬 D 30º 心在点C1,则
7.2.3 求平面图形上各点速度的瞬心法
设有一个平面图形S角速度 vCA 为 w ,图形上点A的速度为 N vA 。在vA 的垂线上取一点C S C (由vA 到AC的转向与图形的 vA 转向一致),有 vC v A w A C A 如果取AC= vA /w ,则 w vA vC v A w A C 0
第八章刚体的平面运动习题解答

故
向
即
8-21图8-48所示机构中,圆轮A的半径R=0.2m,圆轮B的半径r=0.1m,两轮均在水平轨道上作纯滚动。在图示瞬时,A轮上C点在最高位置,轮心速度vA=2m/s,加速度aA=2m/s2,试求轮B滚动的角速度和角加速度。
图8-48
加速度分析
圆轮A
杆BC
故
向
8-22轮O在水平面上作纯滚动,如图8-49所示。轮缘上固定销钉B,此销钉可在摇杆O1A的槽内滑动,并带动摇杆绕轴O1转动。已知轮心O的速度是一常量,vO=0.2m/s,轮的半径R=0.5m,图示位置时,O1A是轮的切线,摇杆与水平面的夹角为 。试求该瞬时摇杆的角速度和角加速度。
图8-59
以O为动点,杆AB为动系
(1)速度分析
(2)加速度分析
圆轮O
以O为基点,分析C点
向y
8-33图8-60所示机构中,已知曲柄OA以匀角速度 绕定轴O转动,OA=100mm,l=500mm。在图示位置, ,试确定杆BD的角速度和角加速度。
图8-60
以A为动点,杆AB为动系
(1)速度分析
(2)加速度分析
图8-33
瞬心法
基点法
8-7在如图8-34所示的筛动机构中,筛子BC的摆动是由曲柄连杆机构所带动。已知曲柄长OA=0.3m,转速为n=40r/min。当筛子运动到与点O在同一水平线上时, ,试求此时筛子BC的速度。
图8-34
速度投影定理
8-8长为l=1.2m的直杆AB作平面运动,某瞬时其中点C的速度大小为vC=3m/s,方向与AB的夹角为 ,如图8-35所示。试求此时点A可能有的最小速度以及该瞬时杆AB的角速度。
8-20半径为r的圆盘可在半径为R的固定圆柱面上纯滚动,滑块B可在水平滑槽内滑动,如图8-47所示。已知r=125mm,R=375mm;杆AB长l=250mm。图示瞬时,vB=500mm/s,aB=750mm/s2;O、A、O1三点位于同一铅垂线上,试求此时圆盘的角加速度。
刚体平面运动

刚体平面运动一、是非题(正确或是用√,错误或否用×,填入括号内。
)1. 刚体的平动和定轴转动均是刚体平面运动的特例。
( √ )2. 刚体作瞬时平动时,刚体的角速度和角加速度在该瞬时一定都等于零。
( × )3. 轮子作平面运动时,如轮上与地面接触点C 的速度不等于零,即相对地面有滑动,则此时轮子一定不存在瞬时速度中心。
( × )4. 若在作平面运动的刚体上选择不同的点作为基点时,则刚体绕不同基点转动的角速度是不同的。
( × )5. 某刚体作平面运动,若A 和B 是其平面图形上的任意两点,则速度投影定理[][]AB B AB A v v =永远成立。
( √ )6. 作平面运动的刚体,某瞬时若角速度、角加速度同时为零,则此时刚体上各点的速度与加速度均相等。
( √ )7. 接上题,在上述条件下,有结论:刚体作平动。
( × )8. 设A 为平面运动刚体上的任意一点,I 为刚体在某时刻的速度瞬心,则A 点的运动轨迹在此处的曲率半径等于A 、I 间的距离。
( × )9. 我们知道,作平面运动的刚体上任意两点A 、B 之间有相对速度,因此,如果将一坐标系固定在此刚体上,在此坐标系中所观察到的A 、B 点之速度一般来说不相等。
( × )10. 刚体作平面运动时,若某瞬时其上有二点加速度相同,则此瞬时刚体上各点的速度都相同。
( √ )11. 平面图形上任意两点的速度在任一直线上的投影始终相等。
( × )12. 平面图形瞬时平动时,其上任意两点的加速度在这两点连线上的投影相等。
( √ )13. 刚体平动必为刚体平面运动的特例,但刚体定轴转动不一定是刚体平面运动的特例。
( × )14. 请判断下述说法是否正确:A. 刚体的平动是平面运动的特殊情况。
( × )B. 刚体的平面运动是平动的特殊情况。
( × )C. 刚体的定轴转动是平面运动的特殊情况。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)章节题库-刚体的平面运动(圣才出品)

第8章刚体的平面运动一、选择题1.图8-1所示平面图形上A、B两点的加速度与其连线垂直且ɑA≠ɑB,则此瞬时平面图形的角速度ω、角加速度α应该是()。
A.ω≠0,α=0B.ω=0,α≠0C.ω=0,α=0D.ω≠0,α≠0图8-1【答案】B2.图8-2所示各平面图形的速度分布为:(a)v A=-v B,v A不垂直AB,这种速度分布是()。
A.可能的B.不可能的不垂直AB,,这种速度分布是()。
A.可能的B.不可能的图8-2【答案】B;B3.在图8-3所示机构中,则ω1()ω2。
A.=B.>C.<图8-3【答案】C4.在图8-4所示机构的几种运动情况下,平面运动刚体的速度瞬心为:(a)();(b)();(c)();(d)()。
A.无穷远处B.B点C.A、B两点速度垂线的交点D.A点E.C点图8-4【答案】D;B;A;C5.已知图8-5所示平面图形上B点的速度v B,若以A为基点,并欲使是B点相对于A点的速度,则A点的速度v A()。
A.与AB垂直B.沿AB方向,且由A指向BC.沿AB方向,且由B指向AD.与AB成φ角图8-5【答案】B二、填空题1.边长为L的等边三角形板在其自身平面内运动,已知B点的速度大小为,方向沿CB,A点的速度沿AC方向。
如图8-6所示,则此时三角板的角速度大小为______;C点的速度大小为______。
图8-6【答案】2.已知作平面运动的平面图形上A点的速度v A,方向如图8-7所示。
则B点所有可能速度中最小速度的大小为______,方向______。
【答案】;沿AB方向图8-73.已知作平面运动的平面图形(未画出)上某瞬时A点的速度大小为v A,方向如图8-8所示,B点的速度方位沿mn,AB=l,则该瞬时刚体的角速度ω为______,转向为______。
【答案】;顺时针图8-8三、判断题1.作平面运动的平面图形上(瞬时平移除外),每一瞬时都存在一个速度瞬心。
()【答案】对2.研究平面运动图形上各点的速度和加速度时,基点只能是该图形上或其延展面上的点,而不能是其他图形(刚体)上的点。
理论力学-刚体地平面运动

第七章 刚体的平面运动一、是非题 1.刚体作平面运动时,绕基点转动的角速度和角加速度与基点的选取无关。
( )2.作平面运动的刚体相对于不同基点的平动坐标系有相同的角速度与角加速度。
( )3.刚体作平面运动时,平面图形两点的速度在任意轴上的投影相等。
( )4.某刚体作平面运动时,若A 和B 是其平面图形上的任意两点,则速度投影定理AB B AB A u u ][][ 永远成立。
( )5.刚体作平面运动,若某瞬时其平面图形上有两点的加速度的大小和方向均相同,则该瞬时此刚体上各点的加速度都相同。
( )6.圆轮沿直线轨道作纯滚动,只要轮心作匀速运动,则轮缘上任意一点的加速度的方向均指向轮心。
( )7.刚体平行移动一定是刚体平面运动的一个特例。
( )二、选择题1.杆AB 的两端可分别沿水平、铅直滑道运动,已知B 端的速度为B u ,则图示瞬时B 点相对于A点的速度为 。
①u B sin; ②u B cos; ③u B /sin; ④u B /cos。
2.在图示啮合行星齿轮转动系中,齿轮Ⅱ固定不动。
已知齿轮Ⅰ和Ⅱ的半径各为r1和r2,曲柄OA以匀角速度0逆时针转动,则齿轮Ⅰ对曲柄OA的相对角速度1r应为。
①1r=(r2/ r1)0(逆钟向);②1r=(r2/ r1)0(顺钟向);③1r=[(r2+ r1)/ r1] 0(逆钟向);④1r=[(r2+ r1)/ r1] 0(顺钟向)。
3.一正方形平面图形在其自身平面运动,若其顶点A、B、C、D的速度方向如图(a)、图(b)所示,则图(a)的运动是的,图(b)的运动是的。
①可能;③不确定。
②不可能;4.图示机构中,O1A=O2B。
若以1、与2、2分别表示O1A杆与O2B杆的1角速度和角加速度的大小,则当O1A∥O2B时,有。
①1=2,1=2;②1≠2,1=2;③1=2,1≠2;④1≠2,1≠2。
三、填空题1.指出图示机构中各构件作何种运动,轮A(只滚不滑)作;杆BC作;杆CD作;杆DE作。
《理论力学》第八章-刚体平面运动试题及答案

理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
如曲柄OA 以匀角加速度a 绕O 轴转动,且当运动开始时,角速度00=w ,转角0=j 。
求动齿轮以中心A为基点的平面运动方程。
解:图示,A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2,故有 ∠CAC 2=r R /j ,所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ,N 用铰C 连结,作平面平行运动。
已知AC=BC=600mm ,在题附图所示位置s mm v s mm v B A /100,/200==,方向如图所示。
试求C 点的速度。
解:由速度投影定理得()()0==BC C BC B v v 。
则v C 必垂直于BC 连线,v C 与AC 连线的夹角为30°。
由()()AC A AC C v v = 即得:s mm v v A C /200== ,方向如题4-6附图示。
解毕。
8-9 图所示为一曲柄机构,曲柄OA 可绕O 轴转动,带动杆AC 在套管B 内滑动,套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。
已知:OA =BD =300mm ,OB =400mm ,当OA 转至铅直位置时,其角速度ωo =2rad/s ,试求D 点的速度。
C 12Aj C解 (1)平面运动方法: 由题可知:BD AC w w =确定AC 杆平面运动的速度瞬心。
套筒中AC 杆上一点速度沿套筒(为什么?)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析?关键求AC 杆角加速度(=BD 杆角速度) 基点法,分析AC 杆上在套筒内的点(B’):(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小:× ∠ ∠ × 方位:× ∠ ∠ ∠ 再利用合成运动方法:动点:套筒内AC 杆上的点B’,动系:套筒。
第八章刚体平面运动河南科技大学理论力学课后

如图 a 听示.在诵动机掏中. OA 制•■:-迎 H R = 40 r . min . OA = 03 mZBAO =90° 樓此斷时踊f BC 的速度,解離于UC 作平移.如圏 0所示的位置.巾与GBO 夹瀚沏3(r . n- OA-応卞"° xO30 - 0.40 n in.'sJ30由速度投靈定理仟/屈=(%)应潯订日应」Vj = v 3 co&60°\<=5启■中如=PA 毋屈由儿何光系PA = Q A + PO[ = O A + q 。
: co-t30D = 0.10 + 0 05^3 tnVj> - PD ■肉上=(亠4£) + PA)宓型 ~ (0.05 + 0.10 + 0.05-^) x 1 07 =0.253 m8-3一 -- 08^ = 2.51 mscos 60°8-4 W㈣连打机杓r 连杆曲卜嗣环1块 雷枫曲D 如阳 齐斤石-机椅由曲榊 蒂功。
己知曲稱的角=2rads : = 0,1m F 水O X O 2 = 0.05m - .lD=0.05m :蚩Q*船買时平行于11Q 与"5在同1直线上;曲卩=30J 求角&ABD 的角速度和点Q 的速度(a)0>)常 三桶板ABD f$平面运动.在图 所示应置的速度瞬心莊点P ,设三角柢箱速度为由題涯徊 ljAB U :沟0」0x2O .IO +.V?二 1 07 rals 疫】節子的IS 动是由曲柄杆机掏所带动.已知曲柄「BC ■, O I- ■ R 陀£ I:时. 把JM 值优入上式,得图 总所示机构申.己知;a4-3Z> = D£ = 01iu . £P = 0.1V3m :=4rad/s n 在图 g 所示位豐时.^9iOA UWI 哉阳 亚山 且丘D 川尸祀网1 枯鬥线卜-<岷自于更求杆肚的用恕煜Hl A F 的这燧n解 机构中,杆肿• 3C UI£F 作平面运动,曲柄①I 和「角块CDE {] 轴转动,而 滑块歩尸悴平務,此时杆a hv 2. 均沿水平方向M 图 4所示,所^AB 作■时 平移.v s = v i = =U.40m.5叫丄DC. v s ±DB.杆銘的速度・希莊点D 故DC v c = ------ v EDBv nri> =DE -^-= -------- v. =0 40 ms ■ h 向沿打羽就国 b)DC DB由逾度投庠定埋初“ -tos (p =: V £由几何关系知.在△血尸中・V5 .1COS 卩=—,Sill =—v F = —— - 0.462 ni'S ( t :3两H 空的:速麼瞬心在点P I8-7高理转动的製置如團-2折示・杆qq 境q 轴轴动,转速为% ° o 少用钗琏擅1 ■ ■ I ;■ X :丙洁动齿轮m转动时轮II 在半径为与的阖定内齿純上预动,并便半轻为厅的轮】绕a 轴转动•轮I 上装肓砂卷 随同轮1高速转动. MI —= 11. 旳=900 rAiun ■.耒讪垃的4述)<a) (b)8-6解 轮II 柞纯锻功.其速度瞬心在点只 如图 b 所示.* 二 QQg 4r 3)(y 4■=J P* Op = F&Gf]勺fi?2 = ' 二 GJJ' ■ ** r 2轮D ®轮I 的炖点Q 的速廈^c ~ -v Oi 二 2(耳 + )CJ 4码 =土= 2(斤+陀)防4 =十'>厠4 =(1+—)«4 =12fi)4n n八 f\场=12??4 = 10 800 r/'niin (i )口缶=rfi )j =r-(2®}3 = 4r<y 2a c = J{4r/F +=2忑心孑=ll.Slm^ Q = ^48-12 解“)越度分析 、」=R& 时曲瞬时平*矢11 =0 * 叫=1二=人少=2 m/s ・<y# = —^- = r 壮=G>s • y/lr = 2V2r (i?=、迂丘他=2.828 in s (2)加速虺甘析j 二 Re :)2加定轴转动.以討由基点・则=°aBa3 - a A + a £A方向 t4t曲衲CM 以恒定的角連度血=2rad 居境拙口釋动「并借勁连朴曲驱动T 诗为r 的轮子在半栓为R 的圆弧擠中作无滑动的渡动.设OA=AB=R^2r=l^ 求图 N 所示麟 时点丹和点亡的連婕与加連厦oAQA.(a) (b)(c)丸小悬?加卜.戌向曲9向投影.存8-13 8-13-出旦为哎斜屏时曲柄与水平鶴阖康仙.的连村腼写曲柄皿 逵直.滑块B 左圆 形19内滑蚩b 韭时半栓6B4HJ 杆腼 刑成孔"低 UiCM=r ・AB - 2^3r . O {B = 2r t .K 在该解时・■: m s 的i 卩向和法向加辻.度#取=也 <?PS 30O = 4^r&G将听=旳亠(I ; = AT : +玄]+临亠咗4分别向抽刃T 轴广投巒.得al =aicos3G°+占右 cos3(F-aL sin 30fl - a ; m 30°□; = a\ sm d0° + 灯二 sm3O°*f7^ cos30* + iij cos30a 心命6二处知孕% 代人式(lh ⑵.解得口; (2任o —羽述)因此滑块冷的加遽度为晒=2r^0~ ■ <J B =T ' (-a c 一 V5%‘)8-14解\-^\iOA 匕也卫抽峑嗫和加速愷为fm = rc^0 i a A 二 r (y 0 ・ a A = ra 0 以点/为基点分析杆屈上点R 的速度与加遠度,如图 燈为乩图 g 所示.则戌JJ 的逮H.⑴在图2所不机构屮,曲柄CM 长为F •绕轴。
第8章刚体的平面运动习题

第8章 刚体平面运动习题1.是非题(对画√,错画×)8-1.刚体平面运动为其上任意一点与某一固定平面的距离始终平行的运动。
( ) 8-2.平面图形的运动可以看成是随着基点的平移和绕基点的转动的合成.( ) 8-3.平面图形上任意两点的速度在某固定轴上投影相等。
( ) 8-4.平面图形随着基点平移的速度和加速度与基点的选择有关。
( ) 8-5.平面图形绕基点转动的角速度和角加速度与基点的选择有关。
( ) 8-6.速度瞬心点处的速度为零,加速度也为零。
( ) 8-7.刚体的平移也是平面运动。
( ) 2.填空题(把正确的答案写在横线上)8-8.在平直轨道作纯滚动的圆轮,与地面接触点的速度为 。
8-9.平面图形上任意两点的速度在 上投影相等。
8-10.某瞬时刚体作平移,其角速度为 ;刚体上各点速度 ;各点加速度 。
3.简答题8-11.确定图示平面运动物体的速度瞬心位置。
题8-11图(a) (b)(c)8-12.若刚体作平面运动,下面平面图形上A 、B 的速度方向正确吗? 题8-12图(a) (b) (c)8-13.下面图形中O 1A 和AC 的速度分布对吗?8-14.圆轮做曲线滚动,某瞬时轮心的速度o v 和加速度o a ,轮的半径为R ,则轮心的角加速度等于多少?速度瞬心点处的加速度大小和方向如何确定?题8-13图B8-15.用基点法求平面图形个点的加速度时,为什么没有科氏加速度? 4.计算题8-16.椭圆规尺AB 由曲柄OC 带动,曲柄以匀角速度o ω绕O 轴转动,如图所示,若取C 为基点,OC=BC=AC=r ,试求椭圆规尺AB 的平面运动方程。
8-17.半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动,如图所示。
曲柄以匀角加速度α绕O轴转动,设初始时角速度0=ω、角加速度0=α、转角0=ϕ,若选动齿轮的轮心C 点为基点,试求动齿轮的平面运动方程。
题8-16图题8-17图8-18.曲柄连杆机构,已知OA =40cm ,连杆AB =1m ,曲柄OA 绕O 轴以转速180=n r/min 匀速转动,如图所示。
刚体的平面运动-3
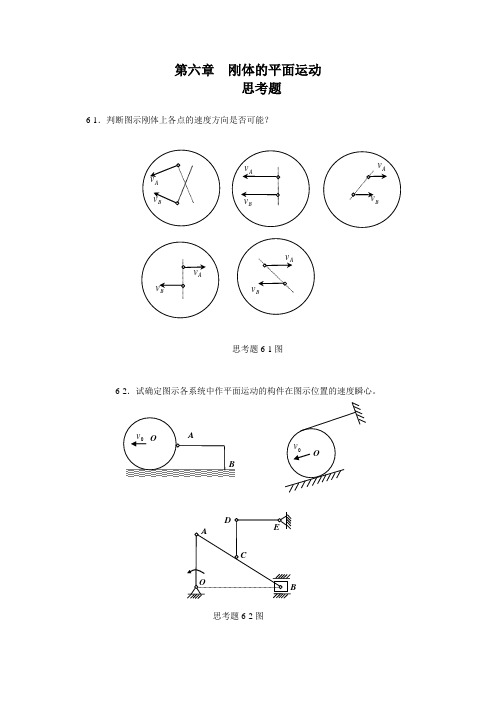
第六章 刚体的平面运动思考题6-1.判断图示刚体上各点的速度方向是否可能?6-2.试确定图示各系统中作平面运动的构件在图示位置的速度瞬心。
思考题6-2图B思考题6-1图6-3.某瞬时平面图形上A 、B 两点的速度矢分别为A v 和B v ,则该瞬时AB 连线上中点C 的速度矢为()2B A C v v v +=,请问此式是否正确?。
6-4.平面图形瞬时平动时,其上任意两点的加速度在这两点连线上的投影相等。
这种说法是否正确?为什么?6-5.刚体的平动和定轴转动都是平面运动的特例吗?刚体的平动与某瞬时刚体瞬时平动有何区别?6-6.刚体的平面运动通常分解为哪两个运动?它们与基点的选取有无关系?用基点法求平面图形上各点的加速度时,要不要考虑科氏加速度?6-7.如图所示机构中,能否根据A 、B 两点的速度A v 、B v 的方向,按图示的方法确定速度瞬心I 的位置,为什么?6-8.图示杆AB 沿墙角在铅直平面滑落时,试画出其动瞬心轨迹和定瞬心轨迹。
思考题6-7图思考题6-8图第六章 刚体的平面运动习 题6-1 筛子的摆动由曲柄连杆机构带动。
已知曲柄OA 的转速40 r/min, 0.3m, n OA BC BE ===。
求图示瞬时筛子CD 的速度。
6-2 杆AB 的A 端沿水平线以等速v 运动,运动时杆恒与一半径为R 的半圆周相切,如图所示,如杆与水平线间的交角为θ,试以角θ表示杆的角速度。
6-3 图示曲柄连杆机构中,曲柄OA 长20cm ,以匀角速度010rad/s ω=转动,连杆AB 长100cm ,求在图示位置时连杆的角速度与角加速度以及滑块B 的加速度。
6-4 在图示曲柄连杆机构中,曲柄OA 绕轴O 转动,其角速度为0ω,角加速度为0α,在某瞬时曲柄与水平线间成60°角,而连杆AB 与曲柄OA 垂直。
滑块B 在圆形槽内滑动,此时半径O 1B 与连杆AB 间夹角为30°。
如果1, , 2OA r AB O B r ===,求该瞬时,滑块B 的切向和法向加速度。
刚体平面运动习题课
大小 方向
? ?
√
BC BC
? BC
BC
2
√
√
√
A
aA
a CB
a CB
n
t
BC
B
BC
2
aB
1
O1
O2
a A a CA a CA a B a CB a CB
t n t n
两式相等:
大小
方向
√ √
AC
AC
? AC
AC
2
√ √
BC BC
? BC
BC
2
√
√
√
√
解出αAC 或 αBC 即可求解 a C
A
aA
AC
AC
a
a CA
t CA
a CB n
n a CB BC
t
BC
B
aB
2
O2
1
O1
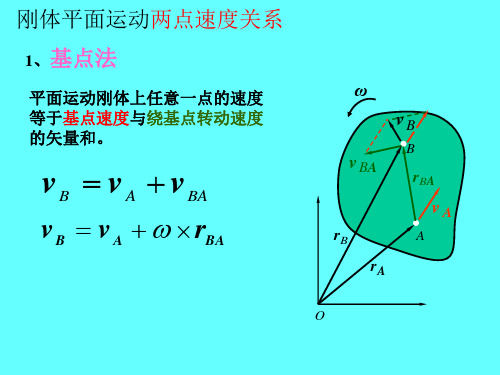
图示机构,已知vA为常矢量,匀质圆盘在水平面上做纯滚动, AB杆长l,圆盘半径为R。试求图示位置时圆盘中心O的速度 和加速度。
B
D
60° M A
vA
解:求角速度。 分析:齿轮、齿条AB都做平面一般运动,齿轮纯滚动,M点为齿 轮的速度瞬心,于是D点的速度方向已知,AB的速度瞬心p已知。 几何关系MAD为等边三角形
MD 2 r sin 60 MA
Ap MA tan 60
2r
sin
2
60
cos 60
a CA
t
C
an CA
加速度分析
aC
大小
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
cm/s 2 将上式向水平轴投影
n 2
n
n
a B cos 60 a B sin 60 a BA 得
2
a B 2( AB AB VB sin 60 / O1 B) 0
1 a B / O1 B 0
6-10. 半径为 R 的圆盘沿水平地面作纯滚动,细杆 AB 长为 L,杆端 B 可沿铅 垂墙滑动。在图示瞬时,已知圆盘的角速度0,角加速度为0,杆与水平面的夹 角为。试求该瞬时杆端 B 的速度和加速度。
t v AO r vCO R , vC 0, v A v, a tAO r , aCO R
由图 B 得
v v O r 0 vO R
解式(1) , (2)得
(1) (2)
vO
由图 C 得
R v Rr
n t n a A aO a tAO a AO , aC aO aCO aCO
a A R 0 ,
n
选A为基点, 则
a B a A a BA a BA
上式投影在BA方向有 a B sin a A cos a BA
n 2
a B ( R 0 cos L AB ) / sin R 0 ctg ( R 2 0 / L sin 3 )
2
方向 :
铅直向下
6-11.如图所示,轮 O 在水平面上滚动而不滑动,轮心以匀速 O 0.2 m s 运动。 轮缘上固连销钉 B,此销钉在摇杆 O1A 的槽内滑动,并带动摇杆绕 O1 轴转动。 已知:轮的半径 R=0.5m,在图示位置时,AO1 是轮的切线,摇杆与水平面间的 交角为 60 。求摇杆在该瞬时的角速度和角加速度。
vC
DC vB DB
vC DE v B 0.40m / s (方向沿杆 EF 如图 9-8b) DC DB
v E DE
由速度投影定理得
v F cos v E
由几何关系知,在 DEF 中,
cos vF 1 3 , sin 2 2
vE 0.462m / s ( ) cos
r1 r2 4 r2
1
(r r ) vC 2(r1 r2 ) r 4 1 3 4 (1 3 ) 4 12 4 r1 r1 r1 r1 ()
n1 12n4 10800r / min
6-6. 图示小型精压机的传动机构,OA=O1B=r=0.1m, EB=BD=AD=l=0.4m。
杆 O1 B 的角速度
1 v B / BO1 2 / 0.3 6.67 rad / s 顺时针 二.求 1
取点 A 为基点,则有 a B a B a A a BA a BA
n
n
将上式向 X 轴投影
n n a B sin a B cos a A sin a BA n n a B a A (a BA / sin ) a B ctg 2 2 OA 2 (v BA / AB sin ) v B ctg / O1 B
6-1 在图示四连杆机构中,已知:匀角速度 O , OA = O1 B = r 。试求在 45 且 AB ⊥ O1 B 的图示瞬时,连杆 AB 的角速度 AB 及 B 点的速度。
解:连杆 AB 作平面运动,由基点法得
v B v A v BA
由速度合成的矢量关系,知
v BA v A cos
rad/s rad/s
顺时针
2 VC / CO2 16 / 10 1.6
AB杆的速度瞬心为点O1 , 故
顺时针
AB V A / O1 A 8 / 10 0.8
有
n n 2
a B V B / O1 B 16 2 / 20 12.8
2
cm/s 2
a BA BA AB 6.4 3 取点A为基点(a A 0), 则有 a B a B a BA a BA
57.8m / s 2
杆 O1 B 的角加速度 @
2 1 a 逆时针 B / O1 B 57.8 / 0.3 192.7 rad / s
6-3.图示机构中,已知:OA=0.1m, DE=0.1m, EF 0.1 3 m ,D 距 OB 线为 h=0.1m; OA 4 rad s 。在图示位置时,曲柄 OA 与水平线 OB 垂直;且 B、D 和 F 在同一铅直线上。又 DE 垂直于 EF。求杆 EF 的角速度和点 F 的速度。
解: (1)求 aB 和AB
V A 常量, a A 0 V A || VB , 且AB不垂直于V A , AB杆作瞬时平动
AB 0, BC VB / BC 10 / 5 2
选A为基点, 则 a B a B a A a BA a BA 由图中几何关系得
解: (1)求 V B C1 为圆盘速度瞬心,故 VA=R0 ∵C2 为杆 AB 速度速度瞬心,故
AB V A / AC 2 R 0 / L sin V B BC 2 AB L cos R 0 / L sin 铅直向下 R 0 ctg
(2)求a B
在图示瞬时, OAAD , O1 BED ,O1D 在水平位置,OD 和 EF 在铅直位置。已 知曲柄 OA 的转速 n 120 r min ,求此时压头 F 的速度。
解:速度分析如图,杆 ED 及 AD 均作平面运动,点 P 是杆 ED 的速度瞬心,故
vF vE vD
由速度投影定理,有
v B OB ,故连杆 AB 的速度瞬心在 AO1 和 BO 延长线的交点 P。设轮Ⅰ与轮Ⅱ
的啮合点为 C。此时 ABP 为直角三角形, 60 ,由几何关系知:
PA
AB 3.00m, PB AB tan 60 1.50 3m cos
PC PB r2 1.2 3m
齿轮的角速度
vC 6rad / s (逆) r1
6-5. 使砂轮高速转动的装置如图所示。杆 O1O2 绕 O1 轴转动,转速为 n4。O2 处用铰链连接一半径为 r2 的活动齿轮 II,杆 O1O2 转动时,轮 II 在半径为 r3 的固 定内齿轮 III 上滚动,并使半径为 r1 的轮 I 绕 O1 轴转动。轮 I 上装有砂轮,随同
n n
rad/s
n
a B a BA a B / cos BC BC / cos 30
2
5 2 2 /( 3 / 2) 40 3 / 3
AB a BA / AB 40 / 3 / 10
4 / 3rad / s 逆时针
2
cm/s 2
(2)求a D 选A为基点则 a D a A a DA a DA
解:由速度投影定理
[V A ] AB [VB ] AB
得 故
VB V A / cos 60 8 / cos 60 16 V B VC VBC cm/s rad/s VC V BC VB 16
cm/s
取点C为基点, 则得
BC VBC / BC 16 / 20 0.8
解:一.求 1
v A OA 0.3 2 0.6 m / s
取 A 为基点,则有 v B v A v BA 得
v B v A ctg 0.6 / 0.3 2 m / s
v BA v A / sin (0.6 / 0.3) (12 0.32 )1 / 2 2.09m
将上 2 式向水平轴投影,得
a Ax aO r aCx aO R
由于 a Ax a, aCx 0, 故可从式(3) , (4)中解得
(3) (4)
aO
Ra Rr
6-8.在图示平面机构中,已知:BC=5cm,AB=10cm,A 点以匀速度 uA=10m/s 沿水平运动,方向向右;在图示瞬时,=30°,BC 杆处于铅垂位置。试求该瞬 (2)AB 杆的角加速度; (3)AB 杆中点 D 的加速度。 时: (1)B 点的加速度;
解
机构中,杆 AB,BC 和 EF 作平面运动,曲柄 OA 和三角块 CDE 作
定轴转动,而滑块 B,F 作平移。此时杆 AB 上 v A , v B 均沿水平方向如图 9-8b 所 示,所以杆 AB 作瞬时平移。 v B v A OA OA 0.40m / s vC DC , v B DB, 杆 BC 的速度瞬心在点 D,故
v D cos v A
解得
vF
vA r 2n l 2 r 2 1.295m / s cos 60 l
6-7.半径为 R 的轮子沿水平面滚动而不滑动,如图所示。在轮上有圆柱部分, 其半径为 r。将线绕于圆柱上,线的 B 端以速度 v 和加速度 a 沿水平方向运动。 求轮的轴心 O 的速度和加速度。
解:因轮子沿水平面滚动而不滑动,所以轮上与地面接触点的速度为 0,且 轮上 C 点的加速度沿水平方向的投影也为 0。以轮心 O 为基点分析轮上点 A 及 点 C 的运动。设轮心 O 的速度为 vO ,加速度为 aO ,则
v A vO v AO , vC vO vCO
设轮子滚动的角速度为 ,角加速度为 ,则
n
a D a DA DA AB 5 4 / 3 20 3 / 3 cm/s 2 方向如图示
6-9.平面机构中在图示=30°位置时,杆 AB 及 O2C 分别处于水平及铅垂位 置,O1A 为铅垂线,O1A=O2C=L=10cm,uA=8cm/s,A=0。试求此瞬时: ( 1) 连杆 BC 的角速度BC; (2)杆 O2C 的角速度2; (3)杆 O1B 的角加速度。
