Matlab小波变换对奇异点的检测
基于小波分析对信号奇异性的检测

D  ̄ e2 ., 2 0 0 7
筇2 6卷
第 6期
V0. 6 No 6 12 .
基 于小 波 分析 对 信 号奇 异 性 的检 测
易 鸿
( J 文婵 学 院 阴 j t 物 理 程技 术系 ,qI 达 州 = jI P t J பைடு நூலகம்50 3 00)
[ 摘 要] 出小波分析对信号奇异性的检测方法, 提 实现小波分析对信号各类奇异 间断点的有
且 一 阶微 分 是 不连 续 的 , 种属 于 第 ~类 型 的 间 断 点 . 这 : 通 常 , Lpe i 指 数来 描 述 函数 的 局 部 奇异 性 . 面 就 给 用 i ht s z 下
b 称八 ), ) ( ,) f 一 Lpe i . n6 是 致 isht n z
丁具 . 应用 Fui’ trl ) e 变换研究 一 个模 拟信号 的频谱 特性 . 必须获得其在时域 中信 号的令部 信息 . 甚至包 括将 来的 信息. 果…个信号仵 某个时 刻的一 个小 的领 域 中发牛 如
点 可导 , 而导数有 界 )在 的
但不连续 时, ish zn指数 仍 为 1 如 果 L ci p t ;
点是奇异的. 一个在 ‰处不
相 埘 来 讲 , 波 变 换 具 有 问 局 部 化 性 质 , 此 币川 小 l j 小波 变 换 来 分 析 信 ’ 奇 异性 及 奇异 位 置 和 奇 异 的 大 j 的 小是 比较 仃 效 的 √J 变 换 突 破 了 F mif 换 在 时 域 没 、 波 u e变
维普资讯
20 0 7年 1 2月
重庆 文 理 学 院 学 报 (『然 科 学 版 ) {
J u n l fCh n q n I ie st fAl M ce c s fNau a c e c d t n) o r a o g i g Ln v ri o t a S in e t r lS in e E i o o y s i
Matlab小波分析在信号处理中的应用

T e U e f M t a a e e n 1 s S n S g a P o e s n h s o a 1 b W v 1 t h a y i i i n 1 r c s i g
肖大 雪
Xi oDa u a x e
( 江西财经大学软件与通信工程学 院, 南昌 江西 3 0 1) 3 0 3
G b r 14 a o 于 96年提 出窗 口傅 立叶变换 , 它可以对时空信号进 行分段或分 块, 即时空一频谱分析 。
展。 至今 , 对于其性质随时间稳定 不变 的信号而言, 处理的理
它度量 了信号在所有不同频率中的振荡信息 。
傅立叶变换 的逆变化为:
1 田
厂) IF ) ( , 寺 (P
( 2 )
意味着信号可展开为不同频率正弦信号 的线性叠加 。
从( 式 中我们可以看 出傅立 叶变换 的核函数是 正弦 函 1 )
摘
‘
要: 文在对傅立 叶变换和窗 口傅立 叶变换 以及小波变换 比较分析的基础上 , 本 重点探讨 了Ma a t b小波分析对普通信 l
g进行分析 、 - 消噪、 压缩和奇异点检测等信号处理 中的各种应用 , 并提 出一些 自己的看法。 关键词: 小波变换 ; 信号处理; 消噪 ; 缩 压 中图分类号 : P 7 T 24 文献标识码 : A 文章编号 :6 1 7 2(0 110 6 5 17 - 9 . 1).0 00 4 2
O Wn e . viws
Ke wo d : a ee a s o ; i a r c s ig De n ii g C mp e so y r s W v lt Tr n f r S g l o e sn ; — o s ; o r si n m n P n
小波技术在110kV线路故障引起站内保护跳闸方式识别应用论文

小波技术在110kV线路故障引起站内保护跳闸方式识别中的应用摘要:正确检测电力线路故障信号对提高电力系统稳定性具有非常重要的意义。
小波技术能够准确地揭示信号在时间和频率方面的分布规律,可以同时分析信号在时域和频域中的特点。
本文介绍了小波变换的定义,小波奇异性检测理论,小波分析在线路故障中的应用。
通过仿真双端供电110kv线路发生a相单相接地故障。
分析了小波技术在甲站506qf出现a相跳闸保护;乙站508qf出现a 相跳闸保护;甲站506qf、乙站508qf同一时间出现a相跳闸保护;甲站506qf出现abc三相跳闸四种保护方式下,a站变末屏a相电压和电流的差异。
根据小波分解原理,计算、对比了信号分解重构下低频和高频部分的小波能量函数值,证明了小波分析能很好地应用于1 1 0 kv线路故障引起站内保护跳闸方式的识别。
展示了小波变换在电力系统中的应用和它独特的优势。
关键词:110kv线路:小波技术:跳闸方式【中图分类号】tm862引言小波分析的应用是和小波分析的理论研究紧密地结合在一起的。
对电力线路的运行情况或故障进行早期诊断和预测是非常重要的。
当电力线路发生故障时,准确、及时地切除故障是减少经济损失最直接的措施。
电力线路出现早期故障征兆,通过采用积极有效的补救措施,阻止故障进一步恶化引起系统瘫痪。
小波变换具有良好的时频局部化特性,能准确定位信号的奇异点,因而在故障检测方面有广泛的应用价值。
输电线路故障引起变电站保护跳闸属于瞬间的暂态电流信号。
利用小波变换模极大值原理对线路故障信号的奇异点进行检测,并应用matlab进行了仿真研究,仿真表明该方法在输电线路发生故障时能快速准确地检测到故障点。
通过仿真分析站内不同保护跳闸方式ct设备暂态信号的特征变化,可以找出故障信息和保护方式之间的内在联系。
1 小波技术和仿真模型建立1.1 小波变换的定义小波变换是将信号和一个时域和频域均具有局部化性质的平移伸缩小波基函数进行卷积,将信号分解成位于不同频带- 时段上的各个成分。
基于小波变换的皮电信号滤波及奇异性检测

⑥
2 0 1 3 S c i . T e c h . E n g r g .
管理科学
基于小波变换的皮 电信号滤波及奇异性检测
李章 勇 姜 瑜 王 伟 刘亚 东
( 重庆 邮电大学 生物 医学工程研究中心 , 重庆 4 0 0 0 6 5 )
摘
要
皮 电信号( G S R) 是 心理 测试 的重要参数指标 。信号 的奇 异点包含 着皮 电信 号的 幅度 变化 、 突变 时间及持 续时 间等
国家 自然科学基金 ( 6 0 9 0 1 0 4 5 ) 项 目、
些特点 : ( 1 ) 容易受到设 备影 响且漂移 比普通 电
重庆市科技攻关( C S T C 2 0 0 9 A C 5 1 4 9 ) 项 口资助
生理信号严重; ( 2 ) 频带很低, 极易受 冲击响应的干 扰, 干扰信号滤波后 的信号容 易和皮电成分重叠 , 有用信息分离 困难 ; ( 3 ) 皮 电信号在心理测试 过程
理方 法 ( 如傅里叶) 无 法 提 取 皮 电信 号 突 变 时 间 和
1 分析方法和实验方案
皮 电信号 除 了 具 有 一 般 生 物 医学 信 号 具 有 的
持续时间, 不能满足要求 , 现有心理特征 点的提取
一
信号弱 、 噪声强 、 随机性强等特点外 , 还具有 自身的
一
2 0 1 2 年9 月1 1日收到
频两域都具有表征信号局部分析 的能力 。国内
外现 已有 相 关 研 究 , 主要 是 将 小 波 用 于 心 电信 号 Q R T检 测 J 、 风 电 异 常 数 据 处 理 J 、 机 械 故 障 检 测 j 、 和地 震信 号 检 测 等 方 面 , 尚无 文 献 将 小 波
小波变换(内附奇异值分析matlab程序)

2、算法及其应用实例
小波在信号的奇异性检测中的应用举例 信号的突变点和奇异点等不规则部分通常包含重要信息,一般信号 的奇异性分为两种情况: (1)信号在某一时刻其幅值发生突变,引起信号的非连续,这种类 型的突变称为第一类型的间断点; (2)信号在外观上很光滑,幅值没有发生突变,但是信号的一阶微 分有突变发生且一阶微分不连续,这种类型的突变称为第二类型的间 断点。 应用小波分析可以检测出信号中的突变点的位置、类型以及变 化的幅度。
程序代码
load nearbrk; x=nearbrk; %使用db4对信号进行2层分解 [c,l]=wavedec(x,2,‘db4’); subplot(411); subplot(4,1,i+2); plot(x); plot(d); ylabel('x'); ylabel(['d',num2str(3-i)]); %对分解的第六层低频系数进行重构 end a=wrcoef('a',c,l,'db4',2); subplot(412); plot(a); ylabel('a2'); for i=1:2 %对分解的第2层到第1层的高频系数 进行重构 a=wrcoef('a',c,l,'db4',3-i);
3、小波分析的优缺点
小波变换与Fourier变换相比,是一个时间和频域的局域变换因而能 有效地从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进 行多尺度细化分析(Multiscale Analysis),解决了Fourier变换不能 解决的许多困难问题。 小波变换存在以下几个优点: 小波变换存在以下几个优点: (1)小波分解可以覆盖整个频域(提供了一个数学上完备的描述) (2)小波变换通过选取合适的滤波器,可以极大的减小或去除所提取得不 同特征之间的相关性 (3)小波变换具有“变焦”特性,在低频段可用高频率分辨率和低时间分 辨率(宽分析窗口),在高频段,可用低频率分辨率和高时间分辨率(窄分 析窗口) 。 (4)小波变换实现上有快速算法(Mallat小波分解算法)。
基于小波分析的信号奇异点判定

基于小波分析的信号奇异点判定作者:康基伟李雪皎郭飞来源:《计算技术与自动化》2017年第02期摘要:在介绍小波变换概念及信号奇异性理论分析的基础上,给出了利用小波系数模极大值对信号奇异点判定的算法,并结合仿真试验对小波分析在信号奇异点上的判定进行了分析,效果良好。
关键词:小波分析;信号检测;奇异点;模极大值中图分类号:文献标识码:Abstract:On the basis of introducing the concept of wavelet transform and the theory of signal singularity, the algorithm of using wavelet modulus maxima to determine the singular points of signals was presented. And according to the result of the simulation experiment, the algorithm was effective for determination of signal singularity based on wavelet analysis.Key words:wavelet analysis; signal detection; singularity; modulus maximum信号的奇异点(突变点)往往蕴含着信号的众多关键信息。
小波变换是在傅里叶变换基础上的进一步完备和拓展,它克服了傅里叶变换在观察局部时频特性方面的不足(仅能判断信号奇异的整体性质,无法具体定位突变点),经改进,不仅具有了良好的波形整体分析能力,更同时具备了出众的时频域局部化分析能力;这在分析非平稳信号的时频特性时,利用其在时—频相平面不同位置处使用不同的窗口(分辨率),可以有效地得到信号在时域和频域的细节信息。
因此,基于小波分析的信号奇异点判定方法适用于非平稳信号里边缘奇异点与峰值奇异点等特征信息的辨识和提取,这将在电力系统故障诊断、地震数据分析、医学成像、语音识别等信号处理领域中发挥重要作用。
小波变换在信号奇异性检测中的应用仿真研究

第2 5卷
第1 期
江
西
科
学
V 12 . o . 5 No 1
Fe 2 07 b. 0
20 0 7年 2月
JANG S ENCE I XI CI
文 章 编 号 :0 1 6 9 20 ) 1 0 6 0 10 —37 ( 0 7 0 — 0 5— 3
S N C e gxag C A i U h n —i , H O Qn n
( oeeo l tcl nier g Xni gU i ri , i in lm q 80 0 R ) C l g f e r a E gnei , i a n esy Xn agWuu u i 30 0P C l E ci n jn v t j
国内 外不少学者已 开始投入到这方面的研究。
1 基本 理 论
1 1 信 号奇 异性 的有 关 定义 .
数 学上 称无 限次 可 导 函数 是 光滑 的或 没有奇
异性 , 函数在某处有间断或某阶导数不连续 , 若 则 称函数在 此处 有奇 异性 , 该点 就是奇 异 点 J 。
奇异性反映了信号 的不规则程度 , 信号的奇异性
信 号 的奇异 性在 小波 变 换 下 的特 征 由定 理 2
() t在点 t 的奇异性 。Lpci 指数 越大 , 。 i hz s t 则函
数 t 越 光 滑 。如 果 函数 f t 在 点 连 续 、 ) () 可
Ab t a t Un i e t dt n l F u e r n fr , e wa ee a so m a o d l c l a o r p r sr c : l r i o a o r r t s m t v ltt n fr h s g o o ai t n p o e t k a i i a o h r zi y b t n t n e u n y d man . h p l a in o e wa ee r n f r i h ee t n o e oh i me a d f q e c o i s T e a p i t ft v lt a s m n t e d tc i ft i r c o h t o o h s g lrt s b el n o u e n ti a e ,i l t n v l a e i me o . i u a y i  ̄ f i t d c d i h s p p r s n i y r mua o ai ts t s t d i d h h Ke r s: a e e a so m , i g lr y d t cin, a l d a n ss L p c i y wo d W v l t n fr S n ua i ee t r t t o F u t ig o i , i s h t z
(完整版)MATLAB小波变换指令及其功能介绍(超级有用)

MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能:一维离散小波变换格式:[cA,cD]=dwt(X,'wname’)[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维 DFT说明:[cA,cD]=dwt(X,'wname’)使用指定的小波基函数’wname’ 对信号X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D)使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解.(2) idwt 函数功能:一维离散小波反变换格式:X=idwt(cA,cD,’wname’)X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明:X=idwt(cA,cD,'wname’) 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X .’wname'为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R)用指定的重构滤波器 Lo_R 和 Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,’wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L)指定返回信号 X 中心附近的 L 个点。
2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能——————----—--——--———--—-—-----————-——————-—--—---——dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换—-—-—--——-—-——-—-—---—-—-——-—————------——-—----—-————---——-(1) wcodemat 函数功能:对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式:Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明:Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵 X 的编码矩阵 Y ;NB 伪编码的最大值,即编码范围为 0~NB,缺省值 NB=16;OPT 指定了编码的方式(缺省值为’mat’),即:别可以实现一维、二维和N 维 DFTOPT='row’ ,按行编码OPT=’col' ,按列编码OPT='mat' ,按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数(缺省值为’1’),即:ABSOL=0 时,返回编码矩阵ABSOL=1 时,返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的Matlab实现(2) dwt2 函数功能:二维离散小波变换格式:[cA,cH,cV,cD]=dwt2(X,'wname’)[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明:[cA,cH,cV,cD]=dwt2(X,'wname’)使用指定的小波基函数 'wname'对二维信号 X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。
基于小波分析的信号突变点探测及其MATLAB仿真

基于小波分析的信号突变点探测及其MATLAB仿真
肖尚辉;黄邦菊
【期刊名称】《宜宾学院学报》
【年(卷),期】2005(005)006
【摘要】小波变换突破了傅立叶分析在时域和频域方面的局部化能力,适合对非平稳信号的处理.信号的突变部分包含了信号的许多重要信息.在介绍了小波分析的概念及其时频方面性质的基础上,分析并仿真了小波变换的时频局部化在信号突变部分探测中的理论与应用.
【总页数】3页(P29-31)
【作者】肖尚辉;黄邦菊
【作者单位】宜宾学院,电子信息系,四川,宜宾,644007;中国民航飞行学院,空中交通管理学院,四川,广汉,618307
【正文语种】中文
【中图分类】TN911.6
【相关文献】
1.小波分析及Matlab仿真在信号检测方面的应用研究 [J], 郑楠;张德强
2.小波分析在信号奇异性探测及瞬态信号检测中的应用 [J], 向阳;蔡悦斌
3.基于模极大值点液体火箭发动机瞬态检测信号重构的小波分析法 [J], 费继友;高铁愉;李宝良;夏学礼
4.基于小波分析的肿瘤基因表达信号突变点检测 [J], 陈军;伍亚舟;易东
5.基于小波分析的信号奇异点判定 [J], 康基伟;李雪皎;郭飞
因版权原因,仅展示原文概要,查看原文内容请购买。
运用小波变换捕捉信号的奇异点

sa gr ( e s na eu rsue no a o ) b sdo eeh oo yo waeet so . T e to s d t u ehe t n e t t t o s es fr t n ae n h cn lg r hi a n n p r i m i t t f vl a fr h h dit t h Dab cis tr n m me se e wi Wa e tn T AB. hog el g t,te rs e v o u eea vl d iee c a e O jd e eekmo n vl e iMA L T ru h an h h es e rd c lt ey l f rne l ,S c u g a me t d i wi p u wa p r r i o df vu we a n h t l
Ab t a t I to id sr, i i t e rma yc n iin o r n i g s se tc l a eppei ei s f . Th a l ic v r f e k g sr c : n per - u t n y t s h i r o d t f u n n t ma ia l t t h i l a e p o y yh t n s ee r d s o e yo la a e y
如何利用小波变换进行异常检测

如何利用小波变换进行异常检测引言:在现代社会,异常检测在各个领域中都起到了至关重要的作用。
异常检测的目标是从大量数据中找出与正常模式不符的异常点或异常行为,以便及时采取措施进行干预和修正。
小波变换作为一种有效的信号处理工具,被广泛应用于异常检测领域。
本文将介绍如何利用小波变换进行异常检测,并探讨其在实际应用中的优势和挑战。
一、小波变换概述小波变换是一种信号分析方法,能够将信号分解成不同频率的成分,从而揭示出信号的时频特性。
与傅里叶变换相比,小波变换具有更好的时域分辨率和频域分辨率,能够更精确地描述信号的瞬时特征。
小波变换通过将信号与一组基函数进行卷积运算,得到信号在不同尺度和位置上的分解系数,从而实现信号的多尺度分析。
二、小波变换在异常检测中的应用1. 异常检测的基本思想异常检测的基本思想是将待检测的信号与正常模式进行比较,通过测量它们之间的差异来判断是否存在异常。
小波变换可以将信号分解成不同尺度的成分,这为异常检测提供了一种新的思路。
通过比较信号在不同尺度上的小波系数,可以捕捉到不同尺度上的异常变化,从而实现对异常的检测和定位。
2. 小波变换的优势相比于其他信号处理方法,小波变换具有以下优势:(1)多尺度分析:小波变换可以将信号分解成不同尺度的成分,从而能够捕捉到信号在不同时间尺度上的变化。
这对于异常检测来说非常重要,因为异常往往表现为在不同时间尺度上的异常变化。
(2)时频局部化:小波变换具有良好的时域分辨率和频域分辨率,能够更精确地描述信号的瞬时特征。
这使得小波变换在异常检测中能够更准确地定位异常点或异常行为。
(3)自适应性:小波变换的基函数可以根据信号的特性进行选择和调整,从而能够适应不同类型的信号和异常模式。
这使得小波变换在不同应用场景中都能够发挥良好的效果。
3. 小波变换在异常检测中的挑战尽管小波变换在异常检测中具有很多优势,但也面临一些挑战:(1)基函数选择:小波变换的效果受到基函数选择的影响。
第5章小波变换的matlab实现

15种 经典类小波:Harr小波、Morlet小波、Mexican
hat小波、Gaussian小波
正交小波:db小波、对称小波、Coiflets小波、
Meyer小波
双正交小波 查看命令
wavemngr('read',1)
1
小波分析示例
一维连续小波
1. coefs = cwt(s,scale,’wname’)
46 43 40 37 34 31 28 25 22 19 16 13 10
7 4 1
100 200 300 400 500 600 700 800 900 1000 time (or space) b
2
scales a
C=cwt(noissin,2:2:128,’db4’,’plot’)
Absolute Values of Ca,b Coefficients for a = 2 4 6 8 10 ...
1.X=waverec(C,L,’wname’) 2.X=waverec(C,L,Lo_R,Hi_R) 例子: A0=waverec(C,L,’db1’); 重构最大误差: Err=max(abs(s-A0))
20
original Level 3 Approximation Original Approximation
低频系数 150 100 0 800
500 1000 1500 2000 2500 3000 3500 4000 30
原始信号 高频系数
700
20
600 10
500 0
400
-10 300
-20 200
100 0
200 400 600 800 1000 1200 1400 1600 1800 2000
图像奇异性表征机理分析比较

图像奇异性表征机理分析比较郑玮【摘要】Singularity in images carry massive essential information,which is crucial to further analysis.We need to adopt different methods accordingto the elements in image singularity. Wavelet transform and curvelet transform are two important methods for sparse representation and are widely used in numerous fields.In this paper, wavelet transform and curvelet transform are used to analyze the effects of different singularity in images.The experimental results and theoretical analysis both demonstrate that wavelet is good at noises in images but cannot represent the edges effectively.On the contrary,curvelet is very suitable for the curve edge.%图像奇异性包含的许多重要信息对于图像的进一步分析具有重要作用。
对于图像中的不同奇异性通常需要采用不同的方法表示。
小波变换和曲波变换作为稀疏表示中的重要方法,具有广泛的应用。
分析了小波变换和曲波变换对于图像奇异性表证的不同效果。
实验结果和理论分析均表明小波变换对于图像中的点奇异性具有很好效果,但对于线奇异性表示则不够稀疏,曲波则可以高效地表示图像边缘的曲线奇异性。
心电信号奇异性检测的几种情况比较

关键词 : 小波 变换 心 电信号 奇异点 信号检 测 中 图分 类号 : 6 F 3 7 文献标识码 . n
文章编号 : 6 2 3 9 ( 0 9 0 ( ) 0 6 -O 1 7 — 7 1 2 0 ) 4a 一 0 2 l 原 始 心 电信 号s n 及 混 有 白噪 声 的 心 电 信 ()
1小波分析理论
设X 腥 平 方 可 积 函数 ,q O的 小波  ̄x( 变换 定 义 为…
数 I, 3 有 】
v f (= )
、 o= } ) , ∞
0f 1 e (: )
号 x n 的R波形 , 上 图是 信号 s ) a r  ̄ () 右 ( 的h a d n
W() 【 ( ( T, 击 ( j r x ̄ a ) I , ) )
波 变 换结 果 , 下 图是 信号 xn 的h ad 波 左 () ar  ̄ ( .) 21 变 换 , 图 中可 以清 楚 的 看 到每 个 R 的 位 从 波 用 、【 , I )对 r 做 小 波 变 换 , ,( 】 t 得 置 , 此利 用 奇 异性 可 以 很准 确 的 检 测 出R 因 a 1 其 零 点 反 映 了 的 极 值 , 实 , , t 可 波 来 , 且 噪 声 对 结 果 的 准 确 性 不 会 有 太 而 现 零 极 点 的检 测 , 因而 可 确 定信 号 的边 缘 ; 大 的影 响 。 下 图是 使 用s m2  ̄ 对s ) 右 y d波 ( 的 n 用1( ) I 对 I 小波变换 , , f 故 得 (t , 口 )其 小 波 变 换 结 果 , 果 显 示 不 如 右 上 图清 晰 , , 结 零点反映了 的转折点, 因而 可确 定 信 号 如 果 对 上 述 三 种 小 波 结 果 作 周期 性 分 段 分 的 尖 峰脉 冲 。 析 , 发 现 使 用 s m2  ̄ 时 小 波 变 换 的 模 会 y d波 数学上 用Lpc i 指 数描 述信 号的奇 异 isht z 极 大值不好定位 。 性 , 是 表 征 函数 局 部 特 征 的一 种 度 量 。 这
小波在奇异性检测中的应用

9.小波在信号奇异性检测及图像边缘提取中的应用无限次可导的函数是光滑的或者是没有奇异性的。
若函数在某处有间断或者某阶导数不连续,则称该函数在此处有奇异性信号的奇异性和非正则结构包含了信号的本质信息。
长期以来,傅立叶变换一直是研究函数奇异性的基本工具,但是由于傅立叶变换缺乏空间局部性,因此只能确定其奇异性的整体性质,傅立叶变换相当于将信号作了平均,局部的特征丢失了。
无法确定奇异点的空间分布情况。
小波变换具有空间局部化性质,小波变换系数由该点附近的局部信息所确定,因此小波变换能够很好的分析信号的奇异点的位置和奇异点的强弱。
奇异点的位置可以通过跟踪小波变换在细尺度下的模极大曲线来检测;而信号点的奇异性强弱(在数学上,通常用Lipshitz 指数来刻画信号奇异性的大小)可以由小波变换模极大值随尺度参数的衰减性来刻画。
S.Mallat 在1992年将Lipschitz 指数(Lipschitz Exponent LE )与小波变换后系数模的局部极大值联系起来,通过小波变换后局部极大值在不同尺度上的衰减速度来衡量信号的局部奇异性。
基于小波变换的信号奇异性检测可以应用于故障诊断、图像的多尺度边缘提取、信号恢复和去噪、语音基因周期检测等领域。
Lipschitz 指数的定义[9]1)设)()(2R L x f ∈,称函数)(x f 在0x R ∈处具有Lipschitz 指数α(0α≥),是指对x R ∀∈,存在常数0x K 和m α=⎢⎥⎣⎦次多项式0x p ,使得000()()ax x f x p t K x x -≤-2)如果存在与0x 无关的常数K ,使得0[,]x a b ∀∈均有00()()ax f x p t K x x -≤-则称函数f 在区间[,]a b 上是一致Lipchitz α的。
3)满足f 在0x 点是Lipschitz α的所有α的上界0α刻画了该点的正则性,称为函数f 在0x 点的Lipschitz 指数;同样可以定义区间上的Lipschitz 指数。
小波变换奇异点检测

基于小波变换的机械振动信号故障检测摘要:正确检测机械故障信号对提高机械设备运行稳定性具有非常重要的意义。
通过简要介绍小波变换应用在信号奇异性检测方面的基本原理,提出基于小波变换的机械故障信号分析方法,该方法既充分利用了小波变换在故障信号分析中的优点,准确的检测到了故障发生的位置。
关键字:小波变换;奇异性检测;Lipschitz 指数;信号处理1 引 言机械故障诊断中由传感器检测到的信号往往十分复杂,且信号中的奇异部分常载有机械设备运行状态特征的重要信息。
因此判断状态信号的奇异点出现时刻,并对信号奇异性实现定量描述,在机械故障诊断信号分析和处理中有着非常重要的意义。
小波分析理论能实现信号的时一频局部化描述,为信号奇异性分析提供有了力的工具。
利用小波奇异性检测理论,本文根据奇异点的局部奇异性信息来诊断机械故障的方法。
2 检测原理通常,采用李普西兹指数来描述函数的局部奇异性。
定义1:设n 是一非负整数,1n n α≤-,如果存在两个常数A 和00h ,及n 次多项式()n P t ,使得对任意的0h h ,均有0()()n f x h P h A h α+-≤,则说f(X)在点x0为Lipschitza 。
如果上式对所有0(,)x ab ∈均成立,且0(,)x h a b +∈,称f(x)在(a, b)上是一致的 Lipschitz a 。
在利用小波分析这种局部奇异性时,小波系数取决于f( x)在0x 的领域内的特性及小波变换所选取的尺度。
在小波变换中,局部奇异可定义为:定义2:设2()()f x L R ∈ ,若f(x)对0x x δ∀∈,小波()x Φ满足且连续可微,并具有n 阶消失矩(n 为正整数),有:(,)Wf s x Ks α≤ (其中K 为常) 则称a 为0x 处的奇异性指(也称Linschitz 指数)。
定义3:对0x x δ∀∈,有0(,)(,)Wf s x Wf x x ≤,则称0x 为小波变换在尺度,下的局部极值点。
基于小波变换的信号奇异性检测及去噪

2、三角函数基作为具有一定周期和波形的光滑函数,对于存在间断 点的信号进行近似时会产生Gibbs现象,因此对于一般的非周期的 非平稳信号,三角基近似不是最优选择。
吉布斯现象(Gibbs):将具有不连续点的周期函数(如矩形脉冲) 进行傅立叶级数展开后,选取有限项进行合成。当选取的项数越 多,在所合成的波形中出现的峰起越靠近原信号的不连续点。当 选取的项数很大时,该峰起值趋于一个常数,大约等于总跳变值 的9%。这种现象称为吉布斯现象。
目录
一、小波变换基础及几种基本常用小波介绍 二、多分辨分析 三、小波变换的信号奇异性检测及去噪
什么是小波变换
像傅立叶分析一样,小波分析就是把一个信号分解为将母小波经
过缩放和平移之后的一系列小波,因此小波是小波变换的基函数。
小波变换可以理解为用经过缩放和平移的一系列小波函数代替傅 立叶变换的正弦波和余弦波进行傅立叶变换的结果。
3、傅里叶变换不能同时进行时域和频域的分析。这是因为信号经过 傅里叶变换后,它的时间特性消失,只能进行频域信息分析。
与 Fourier变换相比,小波变换是时间(空间)频 率的局部化分析,它通过伸缩平移运算对信号 (函数)逐步进行多尺度细化,最终达到高频 处时间细分,低频处频率细分,能自动适应时 频信号分析的要求,从而可聚焦到信号的任意 细节,解决了Fourier变换的困难问题。 小波转换分成两个大类:离散小波变换 (DWT) 和连续小波转换 (CWT)。
软阈值化”和“硬阈值化”是对超过阈值δ的小波系数进行 缩减的两种主要方法,如图1、2 所示。横坐标代表信号原始 小波系数,纵坐标代表阈值化后小波系数。图1 表示的是“软 阈值化”,用数学式表示为:
阈值δ的选取
阈值化处理的关键问题是选择合适的阈值δ。 如果阈值(门限) 太小,去噪后的信号仍然有噪 声存在;相反,如果太大,重要信号特征将被滤掉, 引起偏差。从直观上,对于给定小波系数,噪声 越大,阈值δ就越大。大多数阈值选择过程是针 对一组小波系数,即根据本组小波系数的统计 特性,计算出一个阈值δ。
基于小波奇异性的故障诊断

基于小波奇异性的故障诊断刘伯鸿【摘要】小波变换具有良好的时-频特性,能在不同尺度上分析和处理信号的各种成分,使信号的奇点、突变点放大,提高信号的分辨率、信噪比.因此可以有效地用于电力电子系统故障诊断.在介绍小波变换信号奇异性检测原理的基础上,对电力电子系统奇异性故障信号使用Matlab进行仿真.仿真结果表明,小波变换在故障诊断中有着广泛的应用前景.【期刊名称】《现代电子技术》【年(卷),期】2006(029)024【总页数】2页(P92-93)【关键词】小波变换;故障诊断;奇异点;Matlab【作者】刘伯鸿【作者单位】兰州交通大学,信息与电气工程学院,甘肃,兰州,730070【正文语种】中文【中图分类】TP394信号的奇异点及不规则的突变部分经常带有比较重要的信息,他是信号的重要特征之一。
例如,在电力电子系统故障信号分析处理和机械故障诊断中,故障经常表现为输出信号发生突变,因此,对突变点的检测在故障诊断中具有非常重要的意义。
由于小波变换的时域-频域局部性质,能有效地从信号中提取瞬态突变信息,并进行提取和综合分析,实现准确、可靠、及时诊断的优点,为信号奇异性的故障诊断提供了一个有利的分析工具。
1 小波变换的奇异性检测原理信号的奇异性通常分为2种情况:一种是在某一时刻,其幅值发生突变,引起信号的非连续,信号的突变处是第一种类型的间断点;另一种是信号外观上很光滑,其幅值没有突变,但信号的一阶微分有突变产生,且一阶微分也不连续的,称为第二种类型的间断点。
在数学上,常采用Lipschitz指数[1,2]描述信号奇异点的奇异性。
相关定义如下:定义1 设n是一非负整数,n<α≤n+1,就说f(x)在点x0为李普西兹α,如果存在2个常数A和h0>0,及n次多项式Pn(h),使得对任意的h≤h0,均有:|f(x0+h)-Pn(h)|≤A|h|∂如果上式对所有x0∈(a,b) 均成立,且x0+h∈(a,b) ,称f(x)在(a,b) 上是李普西兹α。
小波变换检测信号突变点的MATLAB实现
⼩波变换检测信号突变点的MATLAB 实现之前在不经意间也有接触过求突变点的问题。
在我看来,与其说是求突变点,不如说是我们常常玩的"找不同"。
给你两幅图像,让你找出两个图像中不同的地⽅,我认为这其实也是找突变点在⽣活中的应⽤之⼀吧。
回到找突变点位置上,以前⾃⼰有过⼀个傻傻的⽅法:就是直接求前后两个采样的的差分值,最后设置⼀个阈值,如果差分值⼤于这个阈值则该点是突变点。
但这个⽅法问题很⼤,实际中突变点幅值有⼤有⼩,你怎么能确定阈值到底是多少呢?还有可能信号本来的差分值就⽐你那突变点的差分值还要⼤。
所以这种⽅法在信号或噪声稍微复杂⼀点就⾏不通了。
这⼏天看到了⼀种船新的信号突变点检测的⽅法-基于⼩波变换的信号突变点检测。
于是乎去学习了⼀下⼩波变换的相关知识和应⽤,学习的不是很深⼊,但也模模糊糊感觉到了⼩波变换确实是检测突变点的⼀⼤利器,下⾯分为两个⼤部分总结⼀下我所学习到的⼩波变换求突变点的实现过程和相关知识理论。
⼀:⼩波变换求信号突变点实现我喜欢直接从应⽤⼊⼿,或者应⽤结合理论。
⼀步⼀步分析代码,看数据和图像的变化⽐⼀步⼀步推公式有趣的多(虽然可能是错误的呀)。
于是在这⾥我就先直接上代码和图像了,这样先让我们对整个过程有个感性的认识。
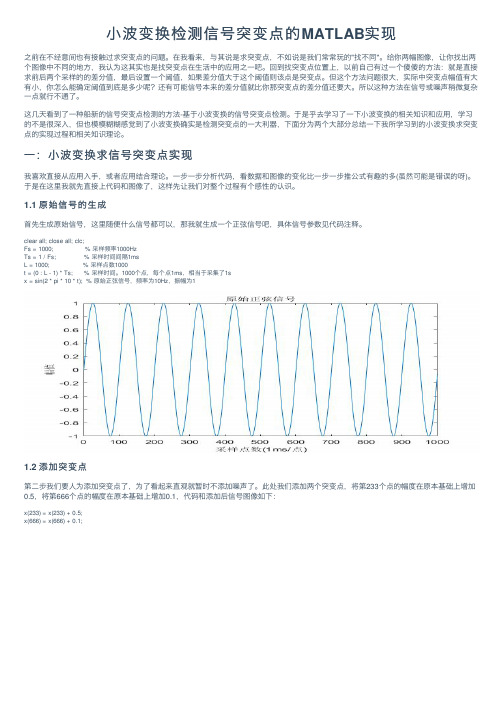
1.1 原始信号的⽣成⾸先⽣成原始信号,这⾥随便什么信号都可以,那我就⽣成⼀个正弦信号吧,具体信号参数见代码注释。
1.2 添加突变点第⼆步我们要⼈为添加突变点了,为了看起来直观就暂时不添加噪声了。
此处我们添加两个突变点,将第233个点的幅度在原本基础上增加0.5,将第666个点的幅度在原本基础上增加0.1,代码和添加后信号图像如下:clear all; close all; clc;Fs = 1000; % 采样频率1000HzTs = 1 / Fs; % 采样时间间隔1msL = 1000; % 采样点数1000t = (0 : L - 1) * Ts; % 采样时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab 小波变换对于奇异点的检测 1.信号的突变性突变信号又称奇异信号,突变信号的突变点经常携带比较重要的信息,是信号的重要特征之一。
在数字信号处理和数字图像处理中具有非常重要的作用和地位,信号的突变性检测是先对原信号在不同尺度上进行“磨光”,再对磨光后信号的一阶或二阶倒数检测其极值点或过零点。
对信号进行磨光处理,主要是为了消除噪声而不是边缘。
传统的信号突变检测方法是基于傅立叶变换的,由某一函数的傅立叶变换趋近于零的快慢来推断该函数是否具有突变性,但它只能反映信号的整体突变性,而对信号的局部突变则无法描述。
这样我们就引入小波变换算法。
2.信号的突变点的检测原理设h(t)是函数f(t)和g(t)的卷积,即:)()()(t g t f t h ⊗=则根据傅立叶变换的性质有:)()()]()([)]('[ωωωω∧∧=⊗=g f j t g t f F j t h F=)()]([ωωω∧∧g f j =)]()[(ωωω∧∧g j f=)]('[)]([)]([)]('[t g F t f F t g F t f F ⊗=⊗所以得到:)(')()()(')('t g t f t g t f t h ⊗=⊗=若将函数f(t)看作是信号,g(t)看作是滤波器,那么信号的导数与滤波器的卷积结果可以看作是滤波器的导数与信号的卷积。
例如,如果选g(t)为高斯函数,则利用其导数可以构造Morlet 小波和Maar 小波,因此,小波变换的突变点和极值点与信号f(t)的突变点和极值点具有对应关系,利用小波可以检测突变信号。
具体过程如下:设)(t θ是一个起平滑作用的低通平稳函数,且满足条件⎰∞∞-=,1)(dt t θ0)(lim =∞→t t θ 通常取)(t θ为高斯函数,即 2/221)(t e t -=πθ假设)(t θ是二次可导的,并且定义2/)1(221)()(t te dt t d t --==πθψ 2/222)2(2)1(21)()(t e t dt t d t --==πθψ 则函数)()1(t ψ、)()2(t ψ满足小波的容许条件:⎰∞∞-=0)()1(dt t ψ,⎰∞∞-=0)()2(dt t ψ 因此可用做小波母函数。
若记1s t s s θθ⎛⎫= ⎪⎝⎭,则()s t θ表示)(t θ在尺度因子s 下的伸缩。
由于小波变换就是将原信号)(t f 同伸缩小波卷积得到的,为此以)(),()2()1(t t ψψ为小波函数定义的卷积型小波变换为: ))(*()(*)(*)()1()1(t f dt d s t dt d s f t f t f w s s s s θθψ=⎪⎭⎫ ⎝⎛== ))(*()(*)(*)(222222)2()2(t f dt d s t dt d s f t f t f w s s s s θθψ=⎪⎪⎭⎫ ⎝⎛== 由此可见,小波变化)(),()2()1(t f w t f w s s 分别是函数)(t f 在尺度s 下由)(t θ平滑后再取一阶、二阶导数。
当s 较小时,用)(t s θ对)(t f 平滑的结果对)(t f 的突变位置影响不大;当s 较大时,则此平滑过程会将)(t f 的一些细小的突变削去,而只剩下大尺寸的突变。
由此我们可知,当小波函数可看作某一平滑函数的一阶导数时,信号小波变换模的局部极值点对应信号的突变点(或边缘)。
当小波函数可看作某一平滑函数的二阶导数时,信号小波变换模的过零点,也对应信号的突变点(或边缘)。
这就是采用检测小波变换系数模的过零点和局部极值点可检测信号突变点(或边缘)的原理。
Matlab 小波变换检测奇异点原始信号是含有奇异点的信号,为确定该奇异点的时间,采用haar 小波进行连续小波变换后,在对系数进行分析处理。
仿真程序如下:figure(1)plot(cuspamax)xlabel('时间');ylabel('幅值');title('频率突变信号');figure(2)[c,l]=wavedec(cuspamax,5,'db6');cfd=zeros(5,1024);for k=1:5d=detcoef(c,l,k);d=d(ones(1,2^k),:);cfd(k,:)=wkeep(d(:)',1024)endcfd=cfd(:);I=find(abs(cfd)<sqrt(eps));cfd(I)=zeros(size(I));cfd=reshape(cfd,5,1024);colormap(pink(64));img=image(flipud(wcodemat(cfd,64,'row')));set(get(img,'parent'),'YtickLabel',[]);title('离散小波变换后系数的绝对值')ylabel('层数');figure(3)ccfs=cwt(cuspamax,1:32,'haar','plot'); title('连续小波变换系数的绝对值')colormap(pink(64));ylabel('尺度')xlabel('时间(或者空间)')程序的运行结果如下图所示:图1 原始信号的示意图图2 db6连续小波变换后系数图3 haar连续小波变换后系数命令行输出结果如下:Name Size Bytes Classcaption 1x71 142 char cuspamax 1x1024 8192 double arraay结论原始信号载入后有矩阵表示,其中矩阵大小为1*1024,矩阵名为cuspamax。
矩阵是以双精度表示相应的图像显示如图1所示。
对原始先信号使用db6小波在尺度1~32上进行连续小波变换。
相应系绝对值的图像如图2所示。
从图3的原始信号连续小波变换系数的示意图可以清楚的看出,在t=710时,小波系数出现了一个倒锥形的区域,以此,可以推断在该区域存在突变点。
小波分析在检测突变点应用中具有傅立叶变换无法比拟的优越性。
傅里叶变换,拉普拉斯变换和Z变换的意义【傅里叶变换】傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值分量和频率分量)。
傅里叶变换是一种解决问题的方法,一种工具,一种看待问题的角度。
我们原来对一个信号其实是从时间的角度去理解的,不知不觉中,其实是按照时间把信号进行分割,每一部分只是一个时间点对应一个信号值,一个信号是一组这样的分量的叠加。
傅里叶变换后,其实还是个叠加问题,只不过是从频率的角度去叠加,只不过每个小信号是一个时间域上覆盖整个区间的信号,但他确有固定的周期,或者说,给了一个周期,我们就能画出一个整个区间上的分信号,那么给定一组周期值(或频率值),我们就可以画出其对应的曲线,就像给出时域上每一点的信号值一样,不过如果信号是周期的话,频域的更简单,只需要几个甚至一个就可以了,时域则需要整个时间轴上每一点都映射出一个函数值。
傅里叶变换就是将一个信号的时域表示形式映射到一个频域表示形式;逆傅里叶变换恰好相反。
这都是一个信号的不同表示形式。
对一个信号做傅里叶变换,可以得到其频域特性,包括幅度和相位两个方面。
幅度是表示这个频率分量的大小,那么相位呢,它有什么物理意义?频域的相位与时域的相位有关系吗?信号前一段的相位(频域)与后一段的相位的变化是否与信号的频率成正比关系?傅里叶变换就是把一个信号,分解成无数的正弦波(或者余弦波)信号。
也就是说,用无数的正弦波,可以合成任何你所需要的信号。
想一想这个问题:给你很多正弦信号,你怎样才能合成你需要的信号呢?答案是要两个条件,一个是每个正弦波的幅度,另一个就是每个正弦波之间的相位差。
所以现在应该明白了吧,频域上的相位,就是每个正弦波之间的相位。
傅里叶变换用于信号的频率域分析,一般我们把电信号描述成时间域的数学模型,而数字信号处理对信号的频率特性更感兴趣,而通过傅立叶变换很容易得到信号的频率域特性。
傅里叶变换简单通俗理解就是把看似杂乱无章的信号考虑成由一定振幅、相位、频率的基本正弦(余弦)信号组合而成,傅里叶变换的目的就是找出这些基本正弦(余弦)信号中振幅较大(能量较高)信号对应的频率,从而找出杂乱无章的信号中的主要振动频率特点。
如减速机故障时,通过傅里叶变换做频谱分析,根据各级齿轮转速、齿数与杂音频谱中振幅大的对比,可以快速判断哪级齿轮损伤。
【拉普拉斯变换】工程数学中常用的一种积分变换。
它是为简化计算而建立的实变量函数和复变量函数间的一种函数变换。
对一个实变量函数作拉普拉斯变换,并在复数域中作各种运算,再将运算结果作拉普拉斯反变换来求得实数域中的相应结果,往往比直接在实数域中求出同样的结果在计算上容易得多。
拉普拉斯变换的这种运算步骤对于求解线性微分方程尤为有效,它可把微分方程化为容易求解的代数方程来处理,从而使计算简化。
在经典控制理论中,对控制系统的分析和综合,都是建立在拉普拉斯变换的基础上的。
在工程学上,拉普拉斯变换的重大意义在于:将一个信号从时域上,转换为复频域(s域)上来表示;在线性系统,控制自动化上都有广泛的应用.【Z变换】在数字信号处理中,Z变换是一种非常重要的分析工具。
但在通常的应用中,我们往往只需要分析信号或系统的频率响应,也即是说通常只需要进行傅里叶变换即可。
那么,为什么还要引进Z变换呢?【三者关系】傅里叶变换的物理意义非常清晰:将通常在时域表示的信号,分解为多个正弦信号的叠加。
每个正弦信号用幅度、频率、相位就可以完全表征。
傅里叶变换之后的信号通常称为频谱,频谱包括幅度谱和相位谱,分别表示幅度随频率的分布及相位随频率的分布。
对一个信号来说,就包含的信息量来讲,时域信号及其相应的傅里叶变换之后的信号是完全一样的。
那傅里叶变换有什么作用呢?因为有的信号主要在时域表现其特性,如电容充放电的过程;而有的信号则主要在频域表现其特性,如机械的振动,人类的语音等。
若信号的特征主要在频域表示的话,则相应的时域信号看起来可能杂乱无章,但在频域则解读非常方便。
在实际中,当我们采集到一段信号之后,在没有任何先验信息的情况下,直觉是试图在时域能发现一些特征,如果在时域无所发现的话,很自然地将信号转换到频域再看看能有什么特征。
信号的时域描述与频域描述,就像一枚硬币的两面,看起来虽然有所不同,但实际上都是同一个东西。
