利用MATLAB编程实现动态画图功能
matlab句柄绘图课件

动态曲线图
使用plot函数和pause函数结合,可以绘制动态曲线图,展示数据随时间变化的趋势。
交互式选择数据
使用axes的pick函数,可以在图表上选择数据点,并获取其坐标值。
交互式缩放和平移
使用axes的zoom、pan和rotate函数,可以在图表上进行缩放、平移和旋转操作。
交互式修改图表属性
成本较高
ห้องสมุดไป่ตู้
01
02
03
THANKS
感谢您的观看。
3D等高线图
使用contour或contour3函数绘制三维等高线图,可以展示三维空间中等高线或等值线的分布情况。
动态散点图
使用scatter函数和pause函数结合,可以绘制动态散点图,展示数据随时间变化的分布情况。
动态曲面图
使用surf或mesh函数和pause函数结合,可以绘制动态曲面图,展示数据随时间变化的形状。
Matlab句柄绘图PPT课件
目录
Matlab句柄图绘图基础句柄图绘图进阶技巧高级句柄图绘图技术实例演示总结与展望
01
CHAPTER
Matlab句柄图绘图基础
句柄图绘图是一种基于图形句柄的绘图方法,通过操作图形对象的句柄,可以方便地控制图形的各个属性,如线条颜色、线型、数据点标记等。
句柄图绘图在Matlab中广泛应用于数据可视化、算法演示等领域,具有灵活性和可定制性强的特点。
图例添加
使用`title`函数,可以为图表添加标题,概括图表的主题或内容。
标题设置
使用`text`函数,可以在图表中添加文本注释,对特定数据点或区域进行说明。
文本注释
03
CHAPTER
高级句柄图绘图技术
利用MATLAB编程实现动态画图功能

自动化专业综合设计报告设计题目:利用MATLAB编程实现动态画图功能所在实验室:自动化系统仿真实验室指导教师:学生姓名班级计082-2 班学号200825502210撰写时间:2012-3-1 成绩评定:一.设计目的a)进一步熟悉Matlab的界面及基本操作;b)了解并掌握Matlab中一些函数的作用与使用;c)学会如何利用Matlab实现绘图功能,并可使坐标系动态设置。
二.设计要求外部输入数据动态设置坐标系,然后绘制图形,并举例演示。
三.设计内容Matlab用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
我设计的题目是利用matlab的GUI编程实现动态的画图功能。
GUI运行时主界面如下:在文本输入框中分别输入x、y、z的值,其中y的值可以是包含x的表达式,z的值可以是包含x和y的表达式。
当y和z的值均为0时,绘制x的曲线;当z的值为0时,绘制二维图形;当z的值不为0时,可以绘制三维图形和三维曲面图。
设计步骤如下:1:打开matlab软件2:建立一个GUI文件,保存到work中3:添加控件主界面,包含的控件有:EditText,StaticText,Axes,PushButton。
其中EditText用于xyz值的输入,StaticText用于显示提示,Axes用于显示绘制的图形,PushButton作为绘图按钮。
4:编写程序程序的编写主要分为两个部分,一个是数据的采集,一个是绘图。
数据采集部分用到的函数主要是str2num、eval函数,具体程序如下: X值输入:function editX_Callback(hObject, eventdata, handles)clchandles.x=str2num(get(hObject,'string'))handles.xhandles=gcboguidata(hObject, handles);Y值输入:function edit2_Callback(hObject, eventdata, handles)clcx=handles.x;handles.y=eval(get(hObject,'string'))handles.yhandles=gcboguidata(hObject, handles);Z值输入:function edit3_Callback(hObject, eventdata, handles)clcx=handles.x;y=handles.y;handles.z=eval(get(hObject,'string'));if handles.z==0set(handles.pushbutton1,'Visible','on');set(handles.pushbutton4,'Visible','off');set(handles.pushbutton5,'Visible','off');elseset(handles.pushbutton1,'Visible','off');set(handles.pushbutton4,'Visible','on');set(handles.pushbutton5,'Visible','on');endhandles.zhandles=gcboguidata(hObject, handles);handles.zhandles=gcboguidata(hObject, handles);绘图部分用到的函数主要有axis(),plot(),plot3(),具体程序如下:绘制二维图形:clcx=handles.x;y=handles.y;handles.x=str2num(get(handles.xhandles,'string'))handles.y=eval(get(handles.yhandles,'string'))handles.z=eval(get(handles.zhandles,'string'));xmin=min(handles.x)-min(handles.x)/10;xmax=max(handles.x)+min(handles.x)/10;ymin=min(handles.y)-min(handles.y)/10;ymax=max(handles.y)+min(handles.y)/10;if y==0q=plot(handles.x)elsev=[xmin xmax ymin ymax]; axis(v);q=plot(handles.x,handles.y);endxlabel('X Öá');ylabel('YÖá');绘制三维图形:function pushbutton4_Callback(hObject, eventdata, handles) clcx=handles.x;y=handles.y;handles.y=eval(get(handles.yhandles,'string'))handles.z=eval(get(handles.zhandles,'string'));xmin=min(handles.x)-min(handles.x)/10;xmax=max(handles.x)+min(handles.x)/10;ymin=min(handles.y)-min(handles.y)/10;ymax=max(handles.y)+min(handles.y)/10;zmin=min(handles.z)-min(handles.z)/10;zmax=max(handles.z)+min(handles.z)/10;v=[xmin xmax ymin ymax zmin zmax];axis(v);q=plot3(handles.x,handles.y,handles.z);绘制三维曲面图:function pushbutton5_Callback(hObject, eventdata, handles) clcx=handles.xy=handles.yhandles.x=eval(get(handles.editX,'string'));handles.y=eval(get(handles.yhandles,'string'))xmin=min(handles.x)-min(handles.x)/10;xmax=max(handles.x)+min(handles.x)/10;ymin=min(handles.y)-min(handles.y)/10;ymax=max(handles.y)+min(handles.y)/10;zmin=min(handles.z)-min(handles.z)/10;zmax=max(handles.z)+min(handles.z)/10;v=[xmin xmax ymin ymax zmin zmax];axis(v);x1=ones(size(handles.y))*handles.x;y1=handles.y*ones(size(handles.x));r=sqrt(x1.^2+ y1.^2)+eps;z=sin(r)./rq=mesh(z);四.设计实验结果及分析当x=-10:0.01:100,y=sin(x),z=0时,得到的图形如下:当x=-10:0.01:10,y=sin(x),z=sin(x)+cos(y)时,得到的图形如下(三维图形):当x=-10:0.1:10,y=x’,z=1时,得到的图形如下(三维曲面图):五.设计感受我之前对于matlab编程的认识只是局限于M文件编程以及命令窗口编程。
matlab动态绘图Animation

matlab动态绘图Animation 主要是查看matlab帮助的Animation动画页⾯1、函数播放录制的电影桢将轴或图形捕获为影⽚帧返回与电影帧相关联的图像数据将图像转换为电影帧创建动画线⼆维彗星图三维彗星图更新数据并处理回调指定数据源后刷新图中的数据线动画2、官⽅例⼦(1)画出sin(x)图像,并且追踪⼀个点%%%创建sinxx = linspace(0,10,1000);y = sin(x);plot(x,y)hold onp = plot(x(1),y(1),'o','MarkerFaceColor','red'); %标记第⼀个点,设置为红⾊hold offaxis manual %将轴限制模式设置为⼿动,以避免在整个动画循环中重新计算限制。
%%%使⽤drawnow动态画图for k = 2:length(x)p.XData = x(k);p.YData = y(k);drawnowend(2)画出sin(x)图像,追踪⼀个点,显⽰坐标变换%%%画出sin(x)图像x = linspace(-6,6,1000);y = sin(x);plot(x,y)axis manual%%%设置图⽚格式ax = gca;h = hgtransform('Parent',ax);hold onplot(x(1),y(1),'o','Parent',h);hold offt = text(x(1),y(1),num2str(y(1)),'Parent',h,...'VerticalAlignment','top','FontSize',14);%%%使⽤drawnow动态画图for k = 2:length(x)m = makehgtform('translate',x(k)-x(1),y(k)-y(1),0);h.Matrix = m;t.String = num2str(y(k));drawnowend(3)这个例⼦展⽰了如何通过更新三⾓形的数据属性来让⼀个三⾓形在圆的内部循环。
matlab动态爱心代码

Matlab动态爱心代码简介动态爱心代码是一种使用Matlab编程语言实现的动画效果,能够在屏幕上以爱心形状展示出美丽的动态效果。
本文将详细介绍Matlab动态爱心代码的实现原理和步骤。
实现原理Matlab动态爱心代码的实现原理基于数学方程。
通过使用心形曲线的参数方程,我们可以在Matlab中绘制出具有爱心形状的曲线。
然后,我们利用Matlab的动画功能,将这个曲线进行平移、旋转和缩放等变换,从而实现动态效果。
实现步骤以下将详细介绍实现Matlab动态爱心代码的步骤:步骤一:绘制心形曲线1.创建一个新的Matlab脚本文件。
2.使用参数方程来定义心形曲线的x和y坐标:–x = 16 * sin(t)^3–y = 13 * cos(t) - 5 * cos(2t) - 2 cos(3t) - cos(4t)3.设置参数t的取值范围,通常选择0到2*pi之间的一段范围。
4.使用plot函数绘制心形曲线:plot(x, y)5.使用axis函数设置坐标轴的显示范围,使爱心曲线充满整个屏幕。
6.使用title函数设置图像的标题,如“动态爱心”。
步骤二:实现动画效果1.使用hold on命令,保持之前绘制的爱心曲线不被删除。
2.使用for循环来不断更新曲线的位置和大小,从而实现动态效果。
3.在循环中,分别使用平移、旋转和缩放等变换函数来更新爱心曲线的坐标。
4.为了使动画效果更加平滑,可以在每次循环之间添加适当的延时。
5.循环结束之后,使用hold off命令来释放资源。
示例代码下面是一个示例的Matlab动态爱心代码:% 步骤一:绘制心形曲线t = 0:0.01:2*pi;x = 16 * sin(t).^3;y = 13 * cos(t) - 5 * cos(2*t) - 2 * cos(3*t) - cos(4*t);plot(x, y);axis([-20 20 -20 20]);title('动态爱心');% 步骤二:实现动画效果hold on;for scale = 0.1:0.1:2% 平移tx = 5 * scale;ty = -3 * scale;x_new = x + tx;y_new = y + ty;% 旋转angle = scale * pi/4;x_new = x_new * cos(angle) - y_new * sin(angle);y_new = x_new * sin(angle) + y_new * cos(angle);% 缩放x_new = x_new * scale;y_new = y_new * scale;plot(x_new, y_new);pause(0.1);endhold off;结论通过以上步骤,我们可以实现一个简单但美丽的Matlab动态爱心代码,展示出令人惊叹的动画效果。
Matlab-制作动画

保存动画的示例1
• 三维动画
[x,y,z]=peaks(30); %peaks产生一个凹凸有致的曲面 surf(x,y,z) %用X和Y定义x-y坐标网格,Z定义网格上每一点的高度,来生成三维曲面 axis([-3 3 -3 3 -10 10]) m=moviein(15); for i=1:15 view(-37.5+24*(i-1),30) m(:,i)=getframe; end movie(m)
surf(sin(2*pi*j/20)*Z,Z) F(j) = getframe; end movie(F,20)
15
其它动画示例程序
clear;clc; [x,y]=meshgrid(-8:.1:8); for j=1:20 f=@(x,y)(sin(sqrt((11-j)*(x.^2+y.^2)))./sqrt((11-j)*(x.^2+y.^2)+eps)); z=f(x,y); surf(x,y,z);shading interp; M(j) = getframe; if j==1 [I,map]=rgb2ind(M(j).cdata,256); imwrite(I,map,'out.gif','DelayTime',.1) else imwrite(rgb2ind(M(j).cdata,map),map,'out.gif','WriteMode','append','DelayTime',.1) end end movie2avi(M,'out.avi')
• 一般格式:
for i=1:n figure(i) F(i)=getframe; end; movie2avi(F,'...filename.avi')
matlab画立体蝴蝶的代码

matlab画立体蝴蝶的代码Matlab是一款强大的工具,可以帮助我们完成许多数据分析、数学建模和图像处理等工作。
在Matlab中,我们可以用简单的代码绘制出许多精美的图像,例如立体蝴蝶。
下面就来介绍一下如何使用Matlab绘制立体蝴蝶的代码。
1.准备工作我们需要在Matlab中打开一个新的文件,然后输入下面这句代码创建一个3D画布:figure('units','normalized','outerposition',[0 0 1 1])这句代码将创建一个全屏的3D画布,供我们后续用来绘制立体蝴蝶。
2.绘制蝴蝶的翅膀接下来,我们需要定义蝴蝶的两个翅膀,具体代码如下:t = 0:pi/10:2*pi;x = sin(t).*(exp(cos(t))-2*cos(4*t)-sin(t/12).^5);y = cos(t).*(exp(cos(t))-2*cos(4*t)-sin(t/12).^5);z = sin(t/2).^2.*cos(5*t+pi/2);plot3(x,y,z,'r','LineWidth',2)这段代码的意思是先设置一个参数t,然后用该参数计算出x、y、z坐标分别对应蝴蝶翅膀上的点的位置。
最后使用plot3函数将这些点连接起来,形成一个立体的蝴蝶翅膀。
这时我们已经完成了蝴蝶的一只翅膀的绘制。
接下来我们需要将另一只翅膀按照一定的规律旋转、平移后绘制出来。
代码如下:hold onfor i=1:3xx = x*cos(pi*i/3) + y*sin(pi*i/3) - 5*(cos(pi*i/3)+1)/2; yy = -x*sin(pi*i/3) + y*cos(pi*i/3);zz = z+2*i;plot3(xx,yy,zz,'r','LineWidth',2)end这段代码首先使用for循环来遍历翅膀的三个位置。
MATLAB动画演示效果
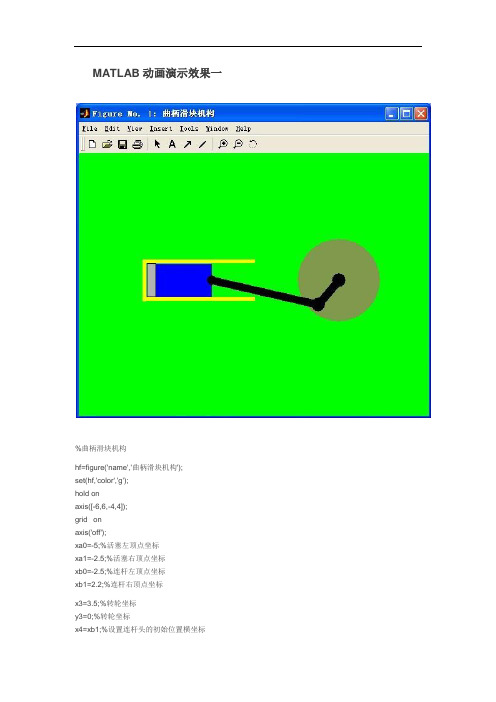
MATLAB动画演示效果一%曲柄滑块机构hf=figure('name','曲柄滑块机构');set(hf,'color','g');hold onaxis([-6,6,-4,4]);grid onaxis('off');xa0=-5;%活塞左顶点坐标xa1=-2.5;%活塞右顶点坐标xb0=-2.5;%连杆左顶点坐标xb1=2.2;%连杆右顶点坐标x3=3.5;%转轮坐标y3=0;%转轮坐标x4=xb1;%设置连杆头的初始位置横坐标y4=0;%设置连杆头的初始位置纵坐标x5=xa1;y5=0;x6=x3;%设置连轴初始横坐标y6=0;%设置连轴初始纵坐标a=0.7;b=0.7c=0.7a1=line([xa0;xa1],[0;0],'color','b','linestyle','-','linewidth',40); %设置活塞a3=line(x3,y3,'color',[0.5 0.6 0.3],'linestyle','.','markersize',300);%设置转轮a2=line([xb0;xb1],[0;0],'color','black','linewidth',10);%设置连杆a5=line(x5,y5,'color','black','linestyle','.','markersize',40);%设置连杆活塞连接头a4=line(x4,y4,'color','black','linestyle','.','markersize',50);%设置连杆连接头a6=line([xb1;x3],[0;0],'color','black','linestyle','-','linewidth',10);a7=line(x3,0,'color','black','linestyle','.','markersize',50);%设置运动中心a8=line([-5.1;-0.2],[0.7;0.7],'color','y','linestyle','-','linewidth',5);%设置汽缸壁a9=line([-5.1;-0.2],[-0.72;-0.72],'color','y','linestyle','-','linewidth',5);%设置汽缸壁a10=line([-5.1;-5.1],[-0.8;0.75],'color','y','linestyle','-','linewidth',5);%设置汽缸壁a11=fill([-5,-5,-5,-5],[0.61,0.61,-0.61,-0.61],[a,b,c]);%设置汽缸气体len1=4.8;%连杆长len2=2.5;%活塞长r=1.3;%运动半径dt=0.015*pi;t=0;while 1t=t+dt;if t>2*pit=0;endlena1=sqrt((len1)^2-(r*sin(t))^2);%连杆在运动过程中横轴上的有效长度rr1=r*cos(t);%半径在运动过程中横轴上的有效长度xaa1=x3-sqrt(len1^2-(sin(t)*r)^2)-(r*cos(t));%活塞在运动过程中的右顶点坐标位置xaa0=xaa1-2.5;%%活塞在运动过程中的左顶点坐标位置x55=x3-cos(t)*r;%连杆在运动过程中横坐标位置y55=y3-sin(t)*r;%连杆在运动过程中纵坐标位置set(a4,'xdata',x55,'ydata',y55);%设置连杆顶点运动set(a1,'xdata',[xaa1-2.5;xaa1],'ydata',[0;0]);%设置活塞运动set(a2,'xdata',[xaa1;x55],'ydata',[0;y55]);set(a5,'xdata',xaa1);%设置活塞与连杆连接头的运动set(a6,'xdata',[x55;x3],'ydata',[y55;0]);set(a11,'xdata',[-5,xaa0,xaa0,-5]);%设置气体的填充set(gcf,'doublebuffer','on');%消除震动drawnow;end文献出处:/blog/static/13485835420091124584320/MATLAB动画效果演示二MATLAB 2009-12-24 17:15:48 阅读135 评论0 字号:大中小订阅%理想弹簧阵子简谐运动%Clearrectangle('position',[12,8.5,2,0.3],'FaceColor',[0.5,0.3,0.4]);axis([0,15,-1,10]);%画顶板hold onplot([13,13],[7,8.5],'r','linewidth',2);%画直线y=2:.2:7;M=length(y);x=12+mod(1:M,2)*2;x(1)=13;x(end-3:end)=13;D=plot(x,y);%弹簧C=0:.1:2*pi;r=0.35;t1=r*sin(C);F1=fill(13+r*cos(C),2+t1,'r');% 球set(gca,'ytick',[0:2:9]);set(gca,'yticklabels',num2str([-1:3]'));plot([0,15],[3.3,3.3],'black');H1=plot([0,13],[3.3,3.3],'y');% 句柄[黄线]Q=plot(0,3.8,'color','r');% 运动曲线;td=[];yd=[];T=0;text(2,9,'理想中的弹簧振子简谐振动','fontsize',16);set(gcf,'doublebuffer','on');while T<12;pause(0.2);Dy=(3/2-1/2*sin(pi*T))*1/2;Y=-(y-2)*Dy+7;Yf=Y(end)+t1;td=[td,T];yd=[yd,Y(end)];set(D,'ydata',Y);set(F1,'ydata',Yf,'facecolor',rand(1,3));set(H1,'xdata',[T,13],'ydata',[Y(end),Y(end)]);set(Q,'xdata',td,'ydata',yd) ;T=T+0.1;end文献出处:/blog/static/1348583542009112451548632/%台球完全碰撞模拟示例axis([-1.6,12.6,-1.6,10.7])%确定坐标轴参数范围hold on %保持当前图形及轴系的所有特性fill([-2,13,13,-2],[-2,-2,11,11],[0,1,0]);%填充底座背景fill([-1,12,12,-1],[-1,-1,10,10],[0,0.5,0]);%填充底座背景ball1=line(0,5,'color','r','marker','.','erasemode','xor','markersize',60);%设置小球颜色,大小,线条的擦拭方式ball2=line(8,9,'color','g','marker','.','erasemode','xor','markersize',60);%设置小球颜色,大小,线条的擦拭方式ball3=line(-1,-1,'color','g','marker','.','erasemode','xor','markersize',80);%设置左下角圆的颜色,大小,线条的擦拭方式ball4=line(12,-1,'color','g','marker','.','erasemode','xor','markersize',80);%设置右下角圆的颜色,大小,线条的擦拭方式ball3=line(-1,10,'color','g','marker','.','erasemode','xor','markersize',80);%设置左上角圆的颜色,大小,线条的擦拭方式ball4=line(12,10,'color','g','marker','.','erasemode','xor','markersize',80);%设置右上角圆的颜色,大小,线条的擦拭方式title('完全非弹碰在模拟台球比赛的应用', 'color','r','fontsize',15);%图形标题pause(1)%设定暂停时间的长度t=0;dt=0.005;%设制初始数值while t<7.2%设定横轴范围t=t+dt;%设制横轴计算公式y=1/2*t+5;%设制纵轴计算公式set(ball1,'xdata',t,'ydata',y)%设制球的运动drawnow;%刷新屏幕end %结束while t<8.8%设定横轴范围t=t+dt;%设制横轴计算公式y=1/2*t+5;%设制纵轴计算公式set(ball2,'xdata',t,'ydata',y)%设制球的运动drawnow;%刷新屏幕end %结束while t<11.5%设定横轴范围t=t+dt;%设制横轴计算公式y=-1/2*t+14.3;%设制纵轴计算公式set(ball2,'xdata',t,'ydata',y)%设制球的运动drawnow;%刷新屏幕end%结束while t>-0.5%设制横轴范围t=t-dt;%设制横轴计算公式y=1/2*t+2.90;%设制纵轴计算公式set(ball2,'xdata',t,'ydata',y)%设制球的运动drawnow;%刷新屏幕end%结束while t<6%设制横轴范围t=t+dt;%设制横轴计算公式y=-1/2*t+2.40;%设制纵轴计算公式set(ball2,'xdata',t,'ydata',y)%设制球的运动drawnow;%刷新屏幕end%结束while t<11.5%设制横轴范围t=t+dt;%设制横轴计算公式y=1/2*t-3.0;%设制纵轴计算公式set(ball2,'xdata',t,'ydata',y)%设制球的运动drawnow;%刷新屏幕end%结束while t>-2%设制横轴范围t=t-dt;%设制横轴计算公式y=-t*7.65/12.9+9.57;%设制纵轴计算公式set(ball2,'xdata',t,'ydata',y)%设制球的运动drawnow;%刷新屏幕end%结束text(2,5,'好!进球了啊!!!恭喜!','fontsize',16,'color','r'); %显示字幕的颜色和大小文献出处:/blog/static/134858354200911245185379/MATLAB动画效果演示四MATLAB 2009-12-24 17:22:18 阅读50 评论2 字号:大中小订阅%能量守恒验证示例fill([6,7,7,6],[5,5,0,0],[0,0.5,0]);%右边竖条的填充hold on; %保持当前图形及轴系的所有特性fill([2,6,6,2],[3,3,0,0],[0,0.5,0]);%左边竖条的填充hold on;% 保持当前图形及轴系的所有特性t1=0:pi/60:pi;plot(4-2*sin(t1-pi/2),5-2*cos(t1-pi/2));%绘制中间的凹弧图形grid;%添加网格线axis([0,9,0,9]);%定义坐标轴的比例%axis('off');%关闭所有轴标注,标记,背景fill([1,2,2,1],[5,5,0,0],[0,0.5,0]);%中间长方形的填充hold on;% 保持当前图形及轴系的所有特性title('31608118');%定义图题x0=6;y0=5;head1=line(x0,y0,'color','r','linestyle','.','erasemode','xor','markersize',30);head2=line(x0,y0,'color','r','linestyle','.','erasemode','xor','markersize',50); %设置小球颜色,大小,线条的擦拭方式t=0;%设置小球的初始值dt=0.001;%设置运动周期t1=0;%设置大球的初始值dt1=0.001;while 1%条件表达式t=t+dt;x1=9-1*t;y1=5;x3=6;y3=5;if t>0x2=6;y2=5;%设置小球的运动轨迹endif t>2.8t=t+dt;a=sin(t-3);x1=6.1;y1=5.1;x3=4-2*sin(1.5*a);y3=5-2*cos(1.5*a);%设置大球的运动轨迹endset(head1,'xdata',x1,'ydata',y1);%设置球的运动set(head2,'xdata',x3,'ydata',y3);drawnow;end文献出处:/blog/static/1348583542009112452218157/。
第二讲 MATLAB 绘图

绘制y=1-exp(0.3*t).*cos(0.7*t)
t=6*pi*(0:100)/100; y=1-exp(-0.3*t).*cos(0.7*t); tt=t(find(abs(y-1)>0.05)); ts=max(tt); plot(t,y,'r-'); grid on; axis([0,6*pi,0.6,max(y)]); title('y=1-exp(-\alpha*t)*cos(\omega*t)'); hold on; plot(ts,0.95,'bo'); hold off; set(gca,'xtick',[2*pi,4*pi,6*pi],'ytick',[0.95,1,1.05,max(y)]); grid on;
绘制曲线
x t cos(3t ) , t 2 y t sin t
t = -pi:pi/100:pi; x = t.*cos(3*t); y = t.*sin(t).^2; plot(x,y)
2015-5-14 10
图形标识
图形标识包括:
图名(title) 坐标轴名(xlabel、ylabel) 图形文本注释(text) 图例(legend)
2015-5-14 22
双纵坐标:plotyy指令
plotyy指令调用格式:
plotyy(x1, y1, x2, y2)
x1-y1曲线y轴在左, x2-y2曲线y轴在右。
例3.7:
x = 0:0.01:20; y1 = 200*exp(-0.05*x).*sin(x); y2 = 0.8*exp(-0.5*x).*sin(10*x); plotyy(x,y1,x,y2);
matlab程序绘图

%计算矩阵A的行数,将行数记为number %将A矩阵的第一列放入到exp_x1数组中 %将A矩阵的第二列放入到exp_x1数组中 %将A矩阵的第三列放入到exp_x1数组中 %将A矩阵的第四列放入到exp_x1数组中
2、利用导入的数据画图
scatter(exp_x1,exp_y1,250,‘r’,‘o’,‘filled’) 点 for i=1:1:number
hold on
-1-3
-2
-1
0
1
2
3
scatter(-3,-0.5,5,'w','d','filled')
hold on scatter(3,4.7,5,'w','d','filled') hold on scatter(3,-0.5,5,'w','d','filled')
注意:在同一个图中画多次画图时 应使用hold on语句,否则后面的 会覆盖前面的
set(gca,‘yticklabel’,{‘0‘, ’ ‘ ,‘100‘,‘ ’,’200‘}) % 只显示0,100,200这三个刻度值
不显示的刻度值 用空格表示
5、数组调用
pp=[10,15,40,1. 0]
set (py(lg1ac)ba)e,l‘('FdoNn_t{Ncahm}e/’d\,e‘tad'e,f'aFuolntt’Si,z‘e'F,opnpt(S2i)ze)’,p scatter(exp_x1,exp_y1,pp(3),'k','p' ,s'efti(lglcead,'')linewidth',pp(4))
Matlab中使用Plot函数动态画图方法总结

Matlab中使用Plot函数动态画图方法总结Matlab除了强大的矩阵运算,仿真分析外,绘图功能也是相当的强大,静态画图没什么问题,由于Matlab本身的多线程编程缺陷,想要动态的画图,并且能够很好的在GUI中得到控制,还不是一件很容易的事情,下面总结几种方法。
一. AXIS 移动坐标系这种方法是最简单的一种方法,适合于数据已经全部生成的场合,先画图,然后移动坐标轴。
实例代码如下:%%%先画好,然后更改坐标系%在命令行中使用Ctrl+C 结束t=0:0.1:100*pi;m=sin(t);plot(t,m);x=-2*pi;axis([x,x+4*pi,-2,2]);grid onwhile 1if x>max(t)break;endx=x+0.1;axis([x,x+4*pi,-2,2]); %移动坐标系pause(0.1);end二. Hold On 模式此种方法比较原始,适合于即时数据,原理是先画上一帧,接着保留原始图像,追加下一幀图像,此种方式比较繁琐,涉及画图细节,并且没有完整并连续的Line对象数据。
例如:%%% Hold On 法% 此种方法只能点,或者分段划线hold offt=0;m=0;t1=[0 0.1]; %要构成序列m1=[sin(t1);cos(t1)];p = plot(t,m,'*',t1,m1(1,:),'-r',t1,m1(2,:),'-b','MarkerSize',5);x=-1.5*pi;grid on;for i=1:100hold ont=0.1*i; %下一个点m=t-floor(t);t1=t1+0.1; %下一段线(组)m1=[sin(t1);cos(t1)];p = plot(t,m,'*',t1,m1(1,:),'-r',t1,m1(2,:),'-b','MarkerSize',5);x=x+0.1;axis([x x+2*pi -1.5 1.5]);pause(0.01);end三. Plot 背景擦除模式这种模式比较适合画动画,效率比较高,刷新闪烁小,适合即时数据,最终的Line结构数据完整。
MATLAB_动态图

surf(Z);
axis tight manual off%保持刻度不随数据的大小而变化,以数据的大小为坐标轴的范围,不显示坐标系 set(gca,'nextplot','replacechildren'); %在当前设置下清清除所有子对象 for k = 1:nFrames
5
移动坐标轴
% ligo 数据来源: /science/GW100916/Lstrain_hp30-968654552-10.txt ligodata=load('D:\LIGOdata.txt'); ligodata=ligodata'; t=linspace(0,10,163840); subplot(2,1,1); plot(t,ligodata); title('LIGO Livingston Observatory data for GW100916'); xlabel('Time[Seconds] from 2010-09-16 06:42:17 UTC (968654552.0)'); ylabel('Gravitational-wave strain amplitude');
for k = 0:3:360
view(k,37.5); drawnow; end
15
切换视角
16
运动轨迹
运动轨迹可以利用comet或comet3来实现 comet(x,y,p) comet3(x,y,z,p)
p可取[0,1],它制定‚彗星‛拖尾的长度,p越大就越长
mov(k) = getframe(gcf);
matlab动画制作例子

matlab动画制作例子
在MATLAB中,你可以使用`pause`和`drawnow`命令来制作动画。
以下是一个简单的例子,它展示了如何创建一个动画,该动画显示一个点在二维平面上沿一圆形路径移动。
```matlab
% 初始化参数
t = 0::2pi; % 时间向量
x = sin(t); % x坐标
y = cos(t); % y坐标
% 创建图形窗口
figure;
% 循环动画
for k = 1:length(t)
% 绘制当前点的位置
plot(x(k), y(k), 'ro');
% 添加标题和标签
title('点在圆上的移动');
xlabel('x');
ylabel('y');
% 暂停并更新图形,以便可以看到动画效果
pause();
drawnow;
end
```
这个脚本将会创建一个动画,显示一个点在二维平面上沿着一个圆形路径移动。
这个动画是通过在一个循环中绘制每个点的位置并暂停一段时间来创建的。
`drawnow`命令将立即更新图形窗口,使得你可以看到动画效果。
注意:MATLAB的版本和环境可能会影响动画的表现。
在一些环境中,可能需要使用不同的命令或参数才能获得最佳的动画效果。
matlab动态波形绘制方法

matlab动态波形绘制方法
在MATLAB中,你可以使用多种方法来绘制动态波形。
下面是一个基本的示例,演示如何使用`plot`函数来绘制动态波形:
```matlab
% 初始化时间向量
t = 0::10;
% 初始化波形数据
y = zeros(size(t));
% 循环来更新波形数据
for i = 1:length(t)
% 假设我们在每个时间点都更新波形数据
y(i) = sin(t(i));
% 使用pause函数暂停绘图,以便你可以看到更新的波形
pause();
% 清除当前图形,以便我们可以重新绘制它
clf;
% 绘制新的波形
plot(t, y);
% 添加标题和标签
title('动态波形');
xlabel('时间 (s)');
ylabel('幅度');
end
```
这个示例中,我们首先创建了一个时间向量`t`和一个与时间向量大小相同的零向量`y`。
然后,我们使用一个for循环来更新`y`的每个元素,并使用
`pause`函数暂停程序以便我们可以看到更新的波形。
在每次循环中,我们都使用`clf`函数清除当前的图形,然后使用`plot`函数绘制新的波形。
最后,我们添加了标题和标签。
注意,这个示例中的`pause`函数将暂停程序秒。
你可以根据需要调整这个值。
如果你希望更快或更慢地更新波形,可以减小或增大这个值。
Matlab——图形绘制——三维立体图形剔透玲珑球动态图——彗星状轨迹图

Matlab——图形绘制——三维⽴体图形剔透玲珑球动态图——彗星状轨迹图三维绘图函数三维绘制⼯具函数view实例:三维螺旋线>> t=0:pi/50:10*pi;plot3(sin(t),cos(t),t)grid %添加⽹格plot3可以画出空间中的曲线>> t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t); %注意⽤点乘 .*也可以同时画出两条空间中的曲线>> t=linspace(0,10*pi,501);>> plot3(t.*sin(t),t.*cos(t),t,t.*sin(t),t.*cos(t),-t);正弦曲线图x=linspace(0,3*pi); % 0到 3pi 间100 个数据点z1=sin(x);z2=sin(2*x);z3=sin(3*x);y1=zeros(100); % 含有100 个数据的0数组y3=zeros(100);y2=y3/2;plot3(x,y1,z1,x,y2,z2,x,y3,z3);⽴体⽹状图实例:>> x=linspace(-2, 2, 25); %在x轴上取25点y=linspace(-2, 2, 25); %在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵zz=xx.*exp(-xx.^2-yy.^2); %计算函数值,zz也是21x21的矩阵mesh(xx, yy, zz); %画出⽴体⽹状图曲⾯图>> x=linspace(-2, 2, 25); %在x轴上取25点y=linspace(-2, 2, 25); %在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵zz=xx.*exp(-xx.^2-yy.^2); %计算函数值,zz也是21x21的矩阵surf(xx, yy, zz);%画出⽴体曲⾯图peaks函数>> z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...- 1/3*exp(-(x+1).^2 - y.^2);>> peaks z也可以对peaks函数取点,再以各种不同的⽅法进⾏绘图meshz 可将曲⾯加上围裙[x,y,z]=peaks;meshz(x,y,z);waterfall 可在x ⽅向或y ⽅向产⽣⽔流效果:[x,y,z]=peaks;waterfall(x,y,z);产⽣在y⽅向的⽔流效果:[x,y,z]=peaks;waterfall(x',y',z');meshc 同时画出⽹状图与等⾼线:[x,y,z]=peaks;meshc(x,y,z);surfc 同时画出曲⾯图与等⾼线:[x,y,z]=peaks;surfc(x,y,z);contour3 画出曲⾯在三度空间中的等⾼线contour3(peaks, 20);contour 画出曲⾯等⾼线在XY 平⾯的投影contour(peaks, 20);剔透玲珑球[X0,Y0,Z0]=sphere(30); %产⽣单位球⾯的三维坐标X=2*X0;Y=2*Y0;Z=2*Z0; %产⽣半径为2 的球⾯的三维坐标surf(X0,Y0,Z0); %画单位球⾯shading interp %采⽤插补明暗处理hold on; mesh(X,Y,Z);hold off %画外球⾯hidden off %产⽣透视效果axis off %不显⽰坐标轴动态图形动画效果——彗星状轨迹图R0=1; %以地球半径为⼀个单位a=12*R0;b=9*R0;T0=2*pi; %T0是轨道周期T=5*T0;dt=pi/100;t=[0:dt:T]';f=sqrt(a^2-b^2); %地球与另⼀焦点的距离th=12.5*pi/180; %卫星轨道与x-y平⾯的倾⾓E=exp(-t/20); %轨道收缩率x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t)); plot3(x,y,z,'g') %画全程轨线[X,Y,Z]=sphere(30);X=R0*X;Y=R0*Y;Z=R0*Z; %获得单位球坐标grid on,hold on,surf(X,Y,Z),shading interp %画地球x1=-18*R0;x2=6*R0;y1=-12*R0;y2=12*R0;z1=-6*R0;z2=6*R0; axis([x1 x2 y1 y2 z1 z2]) %确定坐标范围view([11737]),comet3(x,y,z,0.02),hold off %设视⾓、画运动轨线。
matlab animatedline函数用法

matlab animatedline函数用法Matlab的animatedline函数用于在图形窗口中创建一个动态的线条对象。
它可以用来实时绘制数据、动态可视化等应用。
animatedline函数的用法如下:1. 创建animatedline对象:使用line = animatedline()语句创建一个新的animatedline对象,并将其赋值给变量line。
2. 添加数据点:使用addpoints(line, x, y)语句向animatedline对象中添加一个新的数据点,其中x和y分别是数据点的x和y坐标。
3. 更新图形:使用drawnow语句可以立即更新图形窗口,使得新的数据点可以立即绘制出来。
下面是一个简单的示例代码,演示了animatedline的基本用法:```matlab% 创建图形窗口figure% 创建animatedline对象line = animatedline();% 循环添加数据for t = 0:0.1:10x = t;y = sin(t);% 添加数据点addpoints(line, x, y);% 更新图形窗口drawnow;% 等待一段时间pause(0.1);end```上述代码将在图形窗口中绘制一个sin函数的实时变化曲线。
在每次循环中,将x和y坐标作为数据点添加到animatedline对象中,然后使用drawnow更新图形窗口,最后使用pause函数等待一段时间使动画效果可见。
需要注意的是,在使用animatedline函数时,每次添加一个数据点后需要使用drawnow函数更新图形窗口。
这样可以确保新的数据点立即绘制出来,从而形成动画效果。
以上就是animatedline函数的用法说明,希望对您有所帮助。
Matlab中的动态系统建模与仿真方法介绍

Matlab中的动态系统建模与仿真方法介绍引言:动态系统建模与仿真在各个科学领域扮演着重要的角色。
在众多的建模软件中,Matlab无疑是最为常用和受欢迎的。
本文将介绍Matlab中的动态系统建模与仿真方法,帮助读者理解和掌握这一重要技术。
一、动态系统建模的基础知识动态系统是指在时间上随着一系列因素的变化而产生演化的系统。
建模是指将真实世界的系统用数学方程来描述,并将其转化为计算机可处理的形式。
为了进行动态系统建模,我们需要了解以下几个基础概念:1. 状态变量:动态系统的状态变量描述系统在某一时刻的状态。
例如,对于物理系统来说,位置和速度可以作为系统的状态变量。
2. 输入和输出:输入是指影响系统状态变量的外部参数,而输出是指我们希望观测到的系统的行为或性能指标。
3. 动态方程:动态方程是描述系统状态变化随时间演化的数学方程。
一般来说,动态方程是一个微分方程或差分方程。
二、Matlab中的动态系统建模工具Matlab提供了许多用于动态系统建模和仿真的工具箱。
下面将介绍其中几个常用的工具箱:1. Simulink:Simulink是Matlab的一个可视化仿真环境,用于建模、仿真和分析各种动态系统。
它提供了丰富的模块库,可以轻松构建复杂的系统模型,并进行仿真分析。
2. Control System Toolbox:该工具箱提供了一套功能强大的工具,用于设计和分析控制系统。
它包含了许多常见的控制器设计方法,如比例、积分和微分控制器(PID),以及现代控制理论中的状态空间方法。
3. Signal Processing Toolbox:信号处理是动态系统建模中的一个重要环节。
这个工具箱提供了许多用于信号处理和分析的函数和工具,如傅里叶变换、滤波器设计等。
三、动态系统建模方法在Matlab中,我们可以使用不同的方法来进行动态系统建模,下面介绍几种常见的方法:1. 方程建模法:这是最常见的建模方法之一,通过分析系统的物理特性和因果关系,建立微分方程或差分方程来描述系统动态特性。
Matlab编程实例视频教程系列31:科学绘图 动画 函数绘图 极坐标图 三维图 曲面图

freexyn编程实例视频教程系列31 Matlab作图与动画(绘图)31.0概述1.主要内容1.1 运用Matlab进行作图/数据可视化/动画1.2通过编程实例体会运用Matlab进行作图的思路作者:freexyn31.1 plot基本用法1.随机实例,基本绘图用法2.认识函数plot31.2 线型、标记和颜色1.随机实例,演示作图线型、标记和颜色。
2.说明线型:- -- : -.标记:o + * . x s d ^ v > < p h颜色:y m c r g b w k31.3 标题、标签和图例1.随机实例,演示图像上添加标题、标签和图例。
2.认识函数titlexlabelylabellegend作者:freexyn3.说明\alphaα\upsilonυ\sim~ \angle∠\phiφ\leq≤\ast*\chiχ\infty∞\betaβ\psiψ\clubsuit♣\gammaγ\omegaω\diamondsuit♦\deltaδ\GammaΓ\heartsuit♥\epsilonϵ\DeltaΔ\spadesuit♠\zetaζ\ThetaΘ\leftrightarrow↔\etaη\LambdaΛ\leftarrow←\thetaθ\XiΞ\Leftarrow⇐\varthetaϑ\PiΠ\uparrow↑\iotaι\SigmaΣ\rightarrow→\kappaκ\Upsilonϒ\Rightarrow⇒\lambdaλ\PhiΦ\downarrow↓\muµ\PsiΨ\circº\nuν\OmegaΩ\pm±\xiξ\forall∀\geq≥\piπ\exists∃\propto∝\rhoρ\ni∍\partial∂\sigmaσ\cong≅\bullet•\varsigmaς\approx≈\div÷\tauτ\Reℜ\neq≠\equiv≡\oplus⊕\alephℵ\Imℑ\cup∪\wp℘\otimes⊗\subseteq⊆\oslash∅\cap∩\in∈\supseteq⊇\supset⊃\lceil⌈\subset⊂\int∫\cdot·\oο\rfloor⌋\neg¬\nabla∇\lfloor⌊\times x \ldots... \perp⊥\surd√\prime´\wedge∧\varpiϖ\0∅\rceil⌉\rangle〉\mid| \vee∨\langle〈\copyright©31.4多图、子图和网格1.随机实例,演示创建多图、子图和显示网格。
Matlab如何制作和保存gif动图
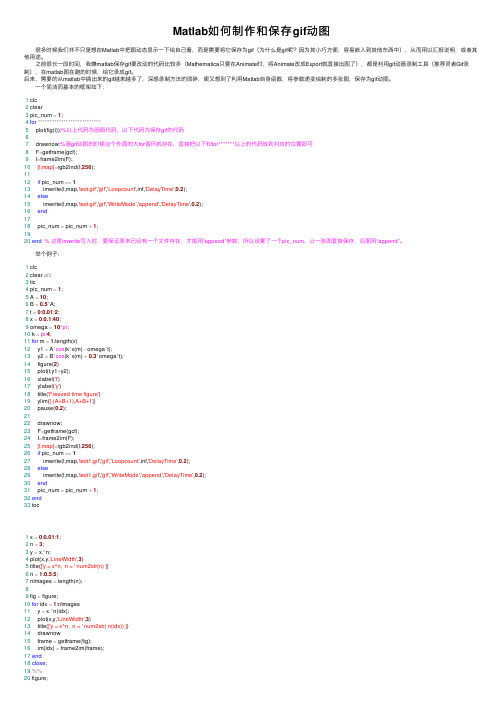
Matlab如何制作和保存gif动图 很多时候我们并不只是想在Matlab中把图动态显⽰⼀下给⾃⼰看,⽽是需要将它保存为gif(为什么是gif呢?因为其⼩巧⽅便,容易嵌⼊到其他东西中),从⽽⽤以汇报说明,或者其他⽤途。
之前很长⼀段时间,我嫌matlab保存gif要改动的代码⽐较多(Mathematica只要在Animate时,将Animate改成Export就直接出图了),都是利⽤gif动画录制⼯具(推荐灵者Gif录制),在matlab图在跑的时候,给它录成gif。
后来,需要的从matlab中搞出来的gif越来越多了,深感录制⽅法的琐碎,便⼜想到了利⽤Matlab⾃⾝函数,将参数递变绘制的多张图,保存为gif动图。
⼀个简洁⽽基本的框架如下:1 clc2 clear3 pic_num =1;4for***************************5 plot(fig(i));%以上代码为画图代码,以下代码为保存gif的代码67 drawnow;%画gif动图的时候这个外⾯的⼤for循环就存在,直接把以下和for*******以上的代码放到对应的位置即可8 F=getframe(gcf);9 I=frame2im(F);10[I,map]=rgb2ind(I,256);1112if pic_num ==113 imwrite(I,map,'test.gif','gif','Loopcount',inf,'DelayTime',0.2);14else15 imwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.2);16end1718 pic_num = pic_num +1;1920end % 这⾥imwrite写⼊时,要保证原来已经有⼀个⽂件存在,才能⽤“append”参数,所以设置了⼀个pic_num,让⼀张图直接保存,后⾯⽤“append”。
MATLAB中的动态系统建模与仿真方法详解

MATLAB中的动态系统建模与仿真方法详解MATLAB是一种广泛应用于科学和工程领域的高级计算机编程语言及集成开发环境。
它拥有强大的数值计算和数据处理能力,被许多研究人员和工程师广泛使用。
在MATLAB中,动态系统建模与仿真是一个重要的应用领域。
本文将详细介绍MATLAB中动态系统建模与仿真的方法。
一、动态系统建模动态系统建模是指将实际的物理或数学系统抽象为数学模型的过程。
在MATLAB中,可以使用多种方法进行动态系统建模,包括基于物理原理的建模、数据拟合建模和系统辨识建模等。
1.基于物理原理的建模基于物理原理的建模是指根据系统的物理特性和运动规律,通过建立方程或微分方程组来描述系统的动态行为。
在MATLAB中,可以使用符号计算工具箱来推导系统的运动方程,并使用ode45等数值求解器对方程进行数值求解。
这种方法适用于已知系统物理特性和运动规律的情况。
2.数据拟合建模数据拟合建模是指通过对实验数据进行分析和拟合,建立与数据拟合程度较高的数学模型。
在MATLAB中,可以使用curve fitting工具箱对数据进行拟合,得到拟合曲线的函数表达式。
这种方法适用于已有实验数据但系统的物理特性未知的情况。
3.系统辨识建模系统辨识是指根据已知的输入-输出数据,利用数学方法建立系统的数学模型。
在MATLAB中,可以使用系统辨识工具箱进行系统辨识建模。
系统辨识工具箱提供了多种经典的辨识算法,包括ARX模型、ARMAX模型和ARIMA模型等。
这种方法适用于已知输入-输出数据但系统的物理特性未知的情况。
二、动态系统仿真动态系统仿真是指利用建立的数学模型,在计算机上模拟系统的动态行为。
MATLAB提供了多种工具和函数,可用于动态系统的仿真分析。
1.数值求解器MATLAB中的ode45函数是一种常用的数值求解器,可用于解决常微分方程初值问题。
ode45函数基于龙格-库塔法,具有较好的公式稳定性和数值稳定性,适合求解各种常微分方程。
MATLAB绘画实验报告

MATLAB绘画实验报告MATLAB绘画实验报告引言:MATLAB是一种强大的科学计算软件,它不仅可以进行数值计算、数据分析和模拟仿真等工作,还可以用于绘制各种图形。
在本次实验中,我将通过使用MATLAB进行绘画,探索其绘图功能的强大之处。
一、绘制基本图形首先,我使用MATLAB绘制了一些基本图形,如直线、曲线和点等。
通过设置不同的参数,我可以控制图形的形状、颜色和线条样式等。
这为我后续的绘图工作奠定了基础。
二、绘制二维图形接下来,我使用MATLAB绘制了一些二维图形,如折线图、散点图和柱状图等。
通过输入数据并选择合适的绘图函数,我可以将数据以直观的方式展示出来。
例如,我可以使用折线图来展示某个变量随时间的变化趋势,或者使用散点图来展示两个变量之间的关系。
三、绘制三维图形除了二维图形,MATLAB还可以绘制各种各样的三维图形。
我使用MATLAB绘制了一些三维曲面图和三维散点图。
通过设置坐标轴和数据,我可以将复杂的数据以立体的方式展示出来。
这对于研究三维数据的分布和趋势非常有帮助。
四、绘制动画除了静态图形,MATLAB还可以绘制动画。
我使用MATLAB编写了一些简单的动画程序,如小球的运动轨迹和图形的变换等。
通过控制时间和参数,我可以实现图形的动态变化,使得观察者可以更好地理解图形背后的规律和特点。
五、图形处理与分析MATLAB不仅可以绘制图形,还可以对图形进行处理和分析。
我使用MATLAB 对一些图形进行了平滑处理、噪声去除和边缘检测等操作。
这些图形处理技术可以帮助我们更好地理解图像中的信息,并提取出我们感兴趣的特征。
六、应用实例最后,我将MATLAB的绘图功能应用到了实际问题中。
我使用MATLAB绘制了一幅地形图,并通过设置不同的参数,展示了地形在不同条件下的变化。
这对于地质学家和地理学家来说非常有用,可以帮助他们更好地理解地球表面的形态和特征。
结论:通过本次实验,我深刻体会到了MATLAB绘图功能的强大之处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动化专业综合设计报告
设计题目:利用MATLAB编程实现动态画图功能
所在实验室:自动化系统仿真实验室
指导教师:
学生姓名
班级
学号
撰写时间:2012-02-24 成绩评定:
一、设计目的
a)进一步熟悉Matlab的界面及基本操作;
b)了解并掌握Matlab中一些函数的作用与使用;
c)学会如何利用Matlab实现绘图功能,并可使坐标系动态设置。
二、设计要求
1.外部输入数据动态设置坐标系,然后绘制图形
2.举例演示
三、设计内容(可加附页)
Matlab用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
我们设计的题目是利用matlab编程实现动态的画图功能。
具体内容体现在:
1):利用外部输入的数据来设置坐标系,使坐标系能够按照自己想要的方式呈现出来,从而更加直观的分析图形。
2):绘制图形,我们举例绘制了一个正弦函数和一个三维的图形。
设计步骤:
1:打开matlab软件
2:建立一个.m文件,保存到work中
3:进行编程
首先从编程的角度分析,要实现两个功能,一个是可以从外部输入数据来改变坐标系。
用到的函数是:
axis([])。
其次是实现画图功能并实现图形的动态变化.
具体思路:
1:定义变量
global xmin xmax ymin ymax zmax zmin m n s y a b q p
2建立函数switch()
Case0
Case1
3:从外部输入,编译
a=-8:0.1:10;
q=a';
a1=ones(size(q))*x;
q1=y*ones(size(a));
r=sqrt(a1.^2+q1.^2)+eps;
z=sin(r)./r;
mesh(z);
四.设计实验结果及分析
结果1:在命令窗口输入n=1; a=-8:0.1:10;
q=a';
a1=ones(size(q))*x;
q1=y*ones(size(a));
r=sqrt(a1.^2+q1.^2)+eps;
z=sin(r)./r;
mesh(z);
四、结论
Matlab不仅有着友好的工作平台编程环境,简单易用的程序语言,强大的科学计算机数据处理能力,出色的图形处理功能,应用广泛的模块集合工具箱实用的程序接口和发布平台。
而且它还可以绘制复杂的二维和多维的图形,可以进行控制系统仿真,是一个很有用的软件.值得我们自动化专业学生学习的一门课.
五、设计感受
以前对matlab只是局限在数学实验上学的那些知识,但是通过此次的课程设计,才了解到matlab在图像图形处理方面的强大功能。
在此要感谢老师对我们的悉心指导,感谢老师给我们的帮助。
在设计过程中我们通过查阅大量资料,与同学交流经验合自学,并向同学请教等方式,使自己学到不少知识,也经历了不少艰辛,但同样收获巨大。
在整个设计中我
懂得了去多东西,也培养了我独立工作的能力,相信会对今后的学习工作有重要影响。
虽然这个设计做的不是太好,但是在设计过程中所学到的东西是最大的收获和财富,是我终生收益。
程序(附)
global xmin xmax ymin ymax zmax zmin m n s y a b q p
function f=myfun(n)
switch n
case 0
xmin=0;
ymin=0;
m=ymin;
ymax=y;
n=ymax;
s=0:0.1:10;
xmax=max(s);
if ymax<ymin
ymax=m;
ymin=n;
if ymax>ymin
ymin=m;
ymax=n;
end
end
plot(s,y);
grid on;
axis([xmin, xmax ,ymin ,ymax])
case 1
a=-8:0.1:10;
q=a';
a1=ones(size(q))*x;
q1=y*ones(size(a));
r=sqrt(a1.^2+q1.^2)+eps;
z=sin(r)./r;
mesh(z);
zmin=0;
b=zmin;
zmax=z;
p=zmax;
if zmax<zmin
zmax=b;
zmin=p;
if zmax>zmin
zmin=b;
zmax=p;
end
end
plot3(a,q,z);
axis([xmin, xmax ,ymin ,ymax,zmin,zmax]) end。
