结构力学第03章习题课
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第3章 静定梁与静定刚架【圣才出品】

第3章 静定梁与静定刚架
3.1 复习笔记【知识框架】
【重点难点归纳】
一、单跨静定梁 ★★★★
1.内力
表3-1-1 内力的基本概念
图3-1-1
图3-1-22.内力与外力间的微分关系及积分关系(1)由平衡条件导出的微分关系式
计算简图如图3-1-3所示,微分关系式为
(Ⅰ)
d d d d d d s
s N
F q x
x M F
x F p x
x ⎧=⎪⎪⎪=
⎨⎪⎪=-⎪⎩-()()
图3-1-3
(2)荷载与内力之间的积分关系
如图3-1-4
所示,结合式(Ⅰ)可得梁的内力积分公式,积分公式及其几何意义见表3-1-2。
图3-1-4
表3-1-2 内力的积分公式及几何意义
3.叠加法作弯矩图
表3-1-3 常用叠加法及其作图步骤
图3-1-5
图3-1-6
二、多跨静定梁 ★★★★
多跨静定梁是由构造单元(如简支梁、悬臂梁)多次搭接而成的几何不变体系,其计算简图见图3-1-7,几何构造、计算原则、传力关系见表3-1-4。
结构力学 第三章 作业参考答案

B
M图(kN m)
(1) (2)
解: (1)求支座反力
∑M = 0 ∑F = 0
A y
取左边或者右边为隔离体,可得:
∑M ∑F
x
C
=0
⇒ FBx =
M h
(3) (4)
=0
最后容易做出结构的弯矩图。
3—18 试作图示刚架的 M 图。
C 0.8kN/m 0.5kN/m D E
14.625 4.225 12.8375
3—19 试作图示刚架的 M 图。
20kN
24 16
C
24
16
B FAx A FBy FAy
FBx
1m
2m
2m
2m
M图(kN m)
(1) (2) (3)
解:对整体:
∑M ∑F
y
A
=0
FBy × 4 + FBx ×1 = 20 × 2 FAy + FBy = 20 FAx − FBx = 0 FBx × 2 − FBy × 2 = 0
40kN m
10kN m M图(kN m)
32.5kN
20kN
20kN F(kN) S
解:求支座反力。取整体:
47.5kN
∑M ∑F
A
=0
FB × 8 − 20 ×10 − 10 ×10 × 3 − 40 = 0 FAy + FB − 10 ×10 − 20 = 0
然后即可做出弯矩图,利用弯矩图即可作出剪力图。
然后即可做出整个刚架的弯矩图。结点受力校核如下图。
D
qL 4 qL 2 qL 2
qL 4
qL 4
E
qL 2 qL 2
03静定梁--习题

3 静定梁
3 静定梁(3 课时)
本章提要 3.l 静定单跨梁的计算 3.2 叠加法绘制直杆弯矩图 3.3 简支斜梁的计算 3.4 静定多跨梁约束力计算与几何组成 3.5 静定多跨梁内力图的绘制 本章小结 思考题 习题
结构力学电子教程
3 静定梁
本章小结
基本内容是静定单跨梁和多跨梁的支座反力、 基本内容是静定单跨梁和多跨梁的支座反力、内力的计算 及内力图的绘制。学习时应强调多做练习,提高熟练程度。 及内力图的绘制。学习时应强调多做练习,提高熟练程度。 要点如下: 要点如下: (1)计算步骤:支座反力、内力、内力图。 )计算步骤:支座反力、内力、内力图。 对静定多跨梁,要注意其几何组成特点, 对静定多跨梁,要注意其几何组成特点,求支座反力的次 序应与组成次序相反。 序应与组成次序相反。 (2)截面内力有弯矩、剪力、轴力;应注意其定义及正负 )截面内力有弯矩、剪力、轴力; 号规定。 号规定。 (3)计算截面内力的基本方法是截面法。在此基础上,也 )计算截面内力的基本方法是截面法。在此基础上, 应能熟练地列出截面法算式,直接计算截面内力。 应能熟练地列出截面法算式,直接计算截面内力。 (4)绘制弯矩图的基本方法是分段叠加法。 )绘制弯矩图的基本方法是分段叠加法。 (5)内力图的纵坐标垂直于杆轴线。弯矩图画在杆件受拉 )内力图的纵坐标垂直于杆轴线。 纤维一侧,不注正负号;剪力图和轴力图注明正负号。 纤维一侧,不注正负号;剪力图和轴力图注明正负号。
= 38kN ⋅ m
MA
A C D
4kN
3kN/m
B
【解】
2m
YA = 10kN
10
2m
2m
6 Q (kN) 38 18 6 M (kN·m)
李廉锟《结构力学》(上册)配套题库【课后习题】(静定梁与静定刚架)【圣才出品】

第3章静定梁与静定刚架复习思考题1.用叠加法作弯矩图时,为什么是竖标的叠加,而不是图形的拼合?答:因为有时叠加弯矩图时的基线与杆轴不重合,如果用图形拼合,不能完全保证叠加后弯矩值是实际同一点的两个弯矩相加后的值。
2.为什么直杆上任一区段的弯矩图都可以用简支梁叠加法来作?其步骤如何?答:(1)因为根据内力分析可以求出直杆任一区段两端的内力,所以直杆任一区段两端均可以看成两端有外力(集中力或集中力偶)的简支梁。
(2)设有直杆任一区段简支梁AB,具体步骤如下①分解作用区段AB上的荷载;②分别作出分解荷载下的弯矩图;③求解出区段AB两端的弯矩M A和M B;④将两端弯矩M A和M B绘出并连以直线(虚线);⑤以步骤④中的虚线为基线叠加各个分解荷载下的弯矩图(竖标叠加),得最终弯矩图。
3.试判断图3-1所示刚架中截面A、B、C的弯矩受拉边和剪力、轴力的正负号。
图3-1答:轴力以受压为负,受拉为正;剪力以使截面顺时针旋转为正。
(1)截面A:左边受拉,剪力为负,轴力为负;(2)截面B:右边受拉,剪力为正,轴力为正;(3)截面C:左边受拉,剪力为正,轴力为正。
4.怎样根据静定结构的几何构造情况(与地基按两刚片、三刚片规则组成,或具有基本部分与附属部分等)来确定计算反力的顺序和方法?答:(1)与地基按两刚片,例如简支梁,支座反力只有三个,对某一端点取矩直接解除约束反力。
(2)与地基按三刚片规则组成,例如三铰刚架,支座反力有四个,考虑结构整体的三个平衡方程外,还需再取刚架的左半部(或右半部,一般取外荷载较少部分)为隔离体建立一个平衡方程方可求出全部反力。
(3)具有基本部分与附属部分时,按先附属后基本的计算顺序,求解支座反力。
5.当不求或少求反力而迅速作出弯矩图时,有哪些规律可以利用?答:当不求或少求反力而迅速作出弯矩图时,如下规律可以利用(1)结构上若有悬臂部分及简支梁部分(含两端铰接直杆承受横向荷载)弯矩图可先行绘制出;(2)直杆的无荷区段弯矩图为直线和铰处弯矩为零;(3)刚结点的力矩平衡条件;(4)外力与杆轴重合时不产生弯矩;(5)外力与杆轴平行及外力偶产生的弯矩为常数;(6)对称性的合理利用;(7)区段叠加法作弯矩图。
结构力学第三版王焕定第3章习题及参考答案
w.
cos α = 2 5
隔离体(b)
FN7 = FN8 = 35 kN
FN6 = FN5 = 65 kN
更多考研资料下载:
co
FN10
FN4
FN3
α α
隔离体(d)
m
40 kN FN4
课后答案网
2-2(b) Fp
θ
再取结点 B 作隔离体
FN4 = 26.67 kN
ww
更多教材下载:
w.
kh
更多考研资料下载:
da
课
后
答
w.
案 网
5 FN3 = − FN1 =33.33 kN 3 4 FN2 = FN1 = − 26.67 kN 3
1 0 8
12
13 6
4 5
7 4×2.5 m
17.5 kN 依次取结点为隔离体,受力图如下所示。 10 kN FN1 FN2
32.5 kN
2×1.25 m
2-2(a) 先求反力,结果如图所示。 10 kN 2
40 kN 3
α
FN8
FN1
α α
α
FN5
案 网
17.5 kN 隔离体(a)
FN9
32.5 kN 隔离体(c)
FN 2 = −30 2 kN=42.42 kN
FN3 = −15 2 kN= − 21.21 kN
更多教材下载:
更多考研资料下载:
co
FN4 45o FN1 FN3 (c)隔离体图
2-6(b)取 2、3 杆件相交的结点作隔离体图(a)所示,往FN2方向投影,列方程得:
( FN3 − FN4 ) sin 2α − 40 kN × cos α = 0, FN3 = 20 kN/sinα + FN4 = − 27.951 kN
结构力学第三章习题参考解答

FAy 6 FAx 2 0
1 ql 2A
1 ql 4
取整体:M A 0
Fy 0
取AC: MC 0
取整体: Fx 0
l
l
0.45ql
FBy
1 2l
ql 3l 2
3 ql 4
FAy
ql
3 4
ql
1 4
ql
FAx
2 ql 2 l4
1 ql 2
FBx
1 ql 2
l 2
1 ql B2 3 ql 4
取左段
FNK
ql cos
3l 4
1 q 3 l 2 2 4
9 ql 2 32
D
C
q
3 ql
4
A
1 ql
l
4
1 ql
4
1 ql 4
3 ql
4
FQ KN
1 ql 2
E
4
1 ql 2 4
9 ql2 32
1 ql
B
4
ql 2 8
M KNm
l
1 ql
4
1 ql
4
1 ql
4
FN KN
1 ql2 4
1 ql 4
3-12解:
q C
q
3 ql
4
A
l
1 ql
B
4
Fy 0
FAy
1 ql 4
1 ql 4
l
l
1 ql
4
取BC:
MC 0
FBx
1 4
ql
取整体:
Fx 0
FAx
ql
1 ql 4
3 ql 4
AD段的最大弯矩 M x 3 qlx 1 qx2 dM 3 ql qx 0
NO3结构力学习题PPT课件

3-17: 求图示抛物线三铰拱的反力,并求截面D和E的内力 。
100kN
10kN/m
FAx A
DC
E
4m FBx
B 5m 5m 5m 5m
FAy
FBy
解:求反力: MB0,FAy100kN,
MA0,FBy100kN M C 01005500kN m
FAx
FBx
FH
悬臂桁架可不求反力
M 60 ,F 2 3 1 1 .2 5 k N M 20,F 673.75kN
F iy0,F 6212.5kN
3-21 试作图示结构二力杆的轴力,绘梁式杆的弯矩图
20kN/m
D A
177.4kN
F
4.37m
C 9m
E
1.2m
B 1m
G 4.37m
177.4kN
A
177.4kN
2-2
A
B
W=3×3-2×2-5=0 CD二元体
三刚片法则 无多几何不变
C
D
2-3
A
B
C
W=3×2-2×1-4=0 三刚片法则 瞬变体系
2-7
D
E
F
A
B
C
W=3×4-2×3-5=1>0 几何可变体系
2-15
C
F
G
A
B
D
E
W=3×9-2×12-3=-2<0
三刚片法则
有两个多余约束的几何不变体系
15kNm 10kN/m
180
B
C
C
180 FQ:kN
A A
解: 求反力:
250 20 A M:kNm
结构力学章节习题及参考答案

习题2.1(6)图
习题2.2填空
(1)习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2)习题2.2(2)图所示体系为__________体系。
习题2-2(2)图
习题2.2(5)图
(6)习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图
(7)习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图
习题2.3对习题2.3图所示各体系进行几何组成分析。
习题2.3图
第3章静定梁与静定刚架习题解答
习题7.2(4)图
习题9.3用力矩分配法计算习题7.3图所示连续梁,作弯矩图和剪力图,并求支座B的反力。
(1)(2)
习题7.3图
习题9.4用力矩分配法计算习题7.4图所示连续梁,作弯矩图。
(1)(2)
习题7.4图
习题9.5用力矩分配法计算习题7.5图所示刚架,作弯矩图。
(1)(2)
习题7.5图
第11章影响线及其应用习题解答
习题11.1是非判断题
(1)习题8.1(1)图示结构BC杆轴力的影响线应画在BC杆上。( )
习题8.1(1)图习题8.1(2)图
(2)习题8.1(2)图示梁的MC影响线、FQC影响线的形状如图(a)、(b)所示。
(3)习题8.1(3)图示结构,利用MC影响线求固定荷载FP1、FP2、FP3作用下MC的值,可用它们的合力FR来代替,即MC=FP1y1+FP2y2+FP3y3=FR 。( )
结构力学-静定结构的内力分析

计算多跨梁的原则:先附属,后基本。
多跨梁
单跨梁
单跨梁内力图
多跨梁内力28 图
[例1] 作多跨静定梁的弯矩图和剪力图
40KN/m
120KN
A
D
B
C
3m
8m
2m
6m
解: (1)作层次图
40KN/m
C
A B
120KN D
29
(2)求反力
40KN/m A
B 8m
C 2m
120KN D
3m 6m
C
120KN D
A
mC 0
FAH
FBH
FAV
l 2 FP1 f
l 2 a1
FA0V
a2
C
FP2
f
B FBH
FBV
l
FP2
C
B
FH
M
0 C
f
FB0V 55
三、 静定拱的内力计算:
1. 静定拱的内力有: M、 FQ 、FN 。
弯矩:使拱内侧受拉为正。
145KN 8m
60KN
60KN
B 235KN
3m
2m
6m
60KN
32
[例2] 作多跨静定梁的弯矩图和剪力图
q
A
B
C
qa
D
E
2qa2 F
a/2 a/2
a
a
a/2 a/2
q
AB
C 7qa/ 8
3qa/8 D
qa D
2qa2
E
F
3qa/8
6qa/8
11qa3/38
作弯矩图: 3qa2
qa2
8
8
龙驭球《结构力学Ⅰ》(第4版)笔记和课后习题(含考研真题)详解(静定结构的受力分析)【圣才出品】

第3章静定结构的受力分析3.1 复习笔记本章详细论述了各类静定结构的受力分析过程与步骤,包括静定平面桁架、静定多跨梁、静定平面刚架、组合结构和三铰拱,介绍了隔离体的最佳截取方法,以及静定结构内力计算的虚位移法。
重视静定结构的基本功训练,有助于培养驾驭基本原理解决复杂问题的能力,为超静定结构的分析与求解打下坚实基础。
一、静定平面桁架桁架由杆件铰接而成,其杆件只承受轴力,杆件截面上应力分布均匀,主要承受轴向拉力和压力,因而能够充分发挥材料的作用,经常使用于大跨度结构中。
1.桁架的类别与组成规律(见表3-1-1)表3-1-1 桁架的类别与组成规律2.桁架杆件内力的求解方法(见表3-1-2)表3-1-2 桁架杆件内力的求解方法二、梁的内力计算的回顾1.截面内力分量符号规定如图3-1-1(图中所示方向为正方向)所示:(1)轴力以拉力为正;(2)剪力以绕微段隔离体顺时针转向为正;(3)在水平杆件中,当弯矩使杆件下部受拉(上部受压)时,弯矩为正。
图3-1-12.截面法(见表3-1-3)表3-1-3 截面法3.荷载与内力之间的微分关系(1)在连续分布的直杆段内,取微段dx为隔离体,如图3-1-2所示。
图3-1-2(2)由平衡条件导出微分关系为(Ⅰ)4.荷载与内力之间的增量关系(1)在集中荷载处,取微段为隔离体,如图3-1-3所示。
图3-1-3(2)由平衡条件导得增量关系为5.荷载与内力之间的积分关系如图3-1-4所示,结合式(Ⅰ)可得梁的内力积分公式,积分公式及其几何意义见表3-1-4。
图3-1-4表3-1-4 内力的积分公式及几何意义6.分段叠加法作弯矩图(1)分段叠加法步骤①求支反力:根据整体受力平衡求出支座反力;②选取控制截面:集中力作用点、集中力偶作用点的左右两侧、分布荷载的起点和终点都应作为控制截面;③求弯矩值:通过隔离体平衡方程求出控制截面的弯矩值;④分段画弯矩图:控制截面间无荷载作用时,用直线连接即可;控制截面间有分布荷载作用时,在直线连接图上还需叠加这一段分布荷载按简支梁计算的弯矩图。
结构力学章节习题及参考答案

结构力学章节习题及参考答案第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6)(b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6)(c)图,故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)习题2.3图(h)第3章(g)静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
结构力学第3章习题及参考答案
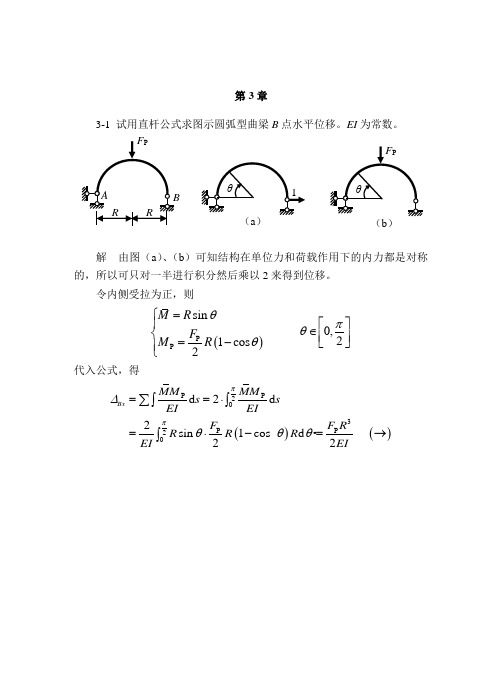
由此解得
按上述思路,再求C截面两侧的转角,为此作出单位弯矩图,如图(c)所示,则
3-15已测得在图示荷载作用下各点竖向位移为H点1.2 cm,G、I点0.1 cm,F、C、J点0.06 cm,D、B点0.05 cm。试求当10 kN竖向力平均分布作用于15个结点上时,H点的竖向位移。
3-6 (a)
解将悬臂梁在K截面切开,取左边部分,并将K截面内力作为荷载作用在K截面上,如图(a-1)所示。(a-1)所示结构悬臂端的竖向位移就是原结构K截面的竖向位移。作出(a-1)所示结构的Mp和 图,并将Mp图按荷载分解。图乘结果为
3-6 (b)
解
3-6 (c)
解
3-6 (d)
解
3-6 (e)
解
3-9试求图示刚架在温度作用下产生的D点的水平位移。梁为高度h=0.8m的矩形截面梁,线膨胀系数为 =10-5 oC-1。
解
3-10图示桁架各杆温度上升t,已知线膨胀系数 。试求由此引起的K点竖向位移。(画出需要的图)
解
*3-11图示梁截面尺寸为b×h=0.2m×0.6m,EI为常数,线膨胀系数为 ,弹簧刚度系数k=48EI/l3(l=2m)。梁上侧温度上升10℃,下侧上升30℃,并有图示支座移动和荷载作用。试求C点的竖向位移。
解
3-6 (f)
解(1)相对水平位移
(2)相对竖向位移
对称结构在对称荷载作用下的反对称位移等于零
解
3-7试求图示结构在支座位移下的指定位移。
3-7 (a)
解
3-7 (b)
解
3-8图示结构各杆件均为截面高度相同的矩形截面,内侧温度上升t,外侧不变。试求C点的竖向位移。线膨胀系数为 。
同济大学 结构力学课后习题及答案解析(完整版)

R=2m
4m
A O
M ( ) 1 (R sin )2 1 2 R(1 cos ) 2
M ( ) 1
B
1 EI
2 1 [1 (R sin )2 1 2 R(1 cos )]Rd 02
= (8-3 ) -1.42 (逆时针)
EI
EI
(d) A q
R EI=常数
O
B
5-7 试用图乘法计算图示梁和刚架的位移:(a) ΔyC ;(b) ΔyD ;(c) ΔxC ;(d) ΔxE ;(e) D ;(f) ΔyE 。 (a)
5-5 已知桁架各杆的 EA 相同,求 AB、BC 两杆之间的相对转角 ΔB 。 5-6 试用积分法计算图示结构的位移:(a) ΔyB ;(b) ΔyC ;(c) B ;(d) ΔxB 。
(a)
q2 q1
A
EI
B
l
以B点为原点,向左为正方向建立坐标。
q( x)
q2
l
q1
x
q1
M
p(x)
1 2
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架,并计算 1、2 杆的内力。设各杆的 EA 均相同。
(a)
(b)
1
1
2
FP
FP
a
a
a
2m
题 6-6 图
6-7 试用力法计算图示组合结构,求出链杆轴力并绘出 M 图。
2
30kN 2m
(a)
a 1.5m
l
A
kθ=
12EI l
2 3
2 3
6 1 20 62 8
3 2
1 6180 3 2
结构力学第三章习题及答案

静定结构计算习题3—1 试做图示静定梁的M 、F Q 图。
解:首先分析几何组成:AB 为基本部分,EC 为附属部分。
画出层叠图,如图(b )所示。
按先属附后基本的原则计算各支反力(c)图。
之後,逐段作出梁的弯矩图和剪力图。
36.67KN15KN •m 20KNM 图(单位:KN/m )13.323.313.33F Q 图(单位:KN )3—3 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =48kN (→) M A =60 KN •m (右侧受拉) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—7 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =20kN (←) F AY =38kN(↑) F BY =62kN(↑) (2)逐杆绘M 图BCM 图(单位:KN/m ) F Q 图(单位:KN )3030F AX F N图(单位:60)20)(3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—9 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =0.75qL (←) F AY =-0.25qL( ) F BY =0.25qL(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—11试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F BX =40KN (←) F AY =30KN (↑) F BY =50kN(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)C(a )qBY 23—17 试求图示抛物线三铰拱的支座反力,并求截面D 和E 的内力。
结构力学 第三章 作业参考答案

∑M = 0 ∑F = 0 ∑F = 0
A
FBy × l − q × l ×
l =0 2
(1) (2) (3)
y
FAy + FBy = 0 FAx + FBx − q × l = 0
FBx × l − FBy × l =0 2
x
取右边部分为隔离体:
∑M
C
=0
(4)
解以上方程可得:
ql ⎧ ⎪ FAx = 4 ⎪ 3ql ⎪ => ⎨ FBx = 4 ⎪ ql ⎪ ⎪ FAy = FBy = 2 ⎩
3—10 试不计算反力绘出梁的 M 图。
16
12
4
A
B
8 2m 2m 4m 4m
12 4m
6m
2m
解:从悬臂端和 AB 开始作图。利用区段叠加法和铰结点的弯矩为零,即可做出全部的弯矩图。
3—12 试不计算反力绘出梁的 M 图。
5
华南农业大学 水利与土木工程学院(College of water conservancy and Civil Engineering, SCAU)
1m
D 80
30
40 E
20 40
40 C F
80 E
40
A
解: (1) 求支座反力
B
40
∑F = 0 ∑M = 0 ∑F = 0
y A x
FC − 10 × 4 − 20 = 0 FA − FB = 0
⇒ FC = 60 kN ⇒ FC = 10 kN
(1) (2) (3)
FB ×1 − 50 − 10 × 4 × 6 − 20 × 10 = 0 ⇒ FB = 10 kN
(1)
结构力学课后练习题+答案

2cm
A CB 2cm 2cm
42、求图示结构 A 点竖向位移(向上为正) AV 。
M EI
EI A
a
EI
EI = ∞ 1
3 EI
K = a3
a
a
43、求图示结构 C 点水平位移 CH ,EI = 常数。
M B
2l
C 6 EI k=
l3
A l
44、求图示结构 D 点水平位移 DH 。EI= 常数。
a/ 2 D
a
A
c1
A'
a
B B'
aห้องสมุดไป่ตู้
c2
35、图示结构 B 支座沉陷 = 0.01m ,求 C 点的水平位移。
C l
A
B
l/2 l/2
—— 25 ——
《结构力学》习题集
36、结构的支座 A 发生了转角 和竖向位移 如图所示,计算 D 点的竖向位移。
A
D
l
l l/ 2
37、图示刚架 A 支座下沉 0.01l ,又顺时针转动 0.015 rad ,求 D 截面的角位移。
P
P
l
l
l
l
18、用力法计算图示结构并作弯矩图。
—— 31 ——
100 kN C EI
《结构力学》习题集
100 kN D
2 EI A
2 EI
4m
B
1m
6m
1m
19、已知 EI = 常数,用力法计算并作图示对称结构的 M 图。
q
q
EA=
l
l
l
20、用力法计算并作图示结构的 M 图。EI =常数。
a
P q
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、本章主要内容回顾 二、习题解答
.
3-1
本章要求:
1、能够灵活运用“隔离体”的平衡建立平衡方程; 2、掌握作梁的内力图的方法及其简便作法,尤其是要 熟练掌握利用分段叠加法作弯矩图; 3、逐步提高由梁到刚架作复杂内力图的能力; 4、从构造分析入手,学会将静定多跨梁拆成单跨梁, 将静定复杂刚架拆成简单单元的分析方法。
M图
(a)
(b)
(c)
(d)
(e)
(f)
(g)
.
(h)
(i)
3-20
3-5 求支座反力,并作梁的内力图。
(a)① 分析体系的几何组成 次序,确定基本部分和附属部分。
该体系的组成次序为先固定 AC , 再 固 定 CE , 最 后 固 定 EF 。 因此基本部分为AC,附属部分为 CE和EF。
② 求支座反力
q
q
a
qa
(c)
qa 2
qa 2
qa
2
qa
qa
qa 2
Q图
qa2 8 qa2 8
qa2 8
qa2 8
5 qa2 8
5 qa2 8
qa 2 2
M图
5 qa2 8 5 qa2 8
qa
qa
2
2
qa
N图
.
3-26
3-8 作图示三铰刚架的内力图。
支座反力: X左
=
25 12
kN(),
X右
=
25 12
kN(),Y左
或 M图 Q图
M图 Q图 或 M图 Q图
.
3-16
3-3 速画M图。
a
P
(a)
Pa
Pa
Pa
M图
q
qa 2
P
P
a
(b)
qa2 qa 2
2
M图
.
a
a
(c)
Pa Pa
2Pa
M图
3-17
q
q
h
(d)
l
qh2 2
qh2 2
M图
q (e) h
l
qh2
2
qh2
M图
(f) h
l
ql 2 8
M图
q
a
a 1.5a a
应用条件:材料服从“虎克定律”,并且是小变形。
理论依据:“力的独立作用原理”。 梁的弯矩图的一般作法:
(1) 选定控制截面(集中力、集中力偶的作用点,分布荷 载的起止点),并求出其弯矩值。
(2) 当控制截面间无荷载时,连接控制截面弯矩的纵坐 标顶点,即可作出直线弯矩图;当控制截面间有荷载作用时, 此直线为叠加基线,再叠加该段按简支梁求得的弯矩图。
Q图
qa2
qa 2
8
qa 2
qa 2 8
M图
5 qa 8
N图
.
3-24
2kN / m
2kN / m
3kN / m
4.5m
3kN / m 3m
3kN / m 3m
(b)
6
6
9
6.75
6.75
9 Q 图(kN )
9 9
9 9
1.13
1.13
12.38
M 图(kNm)
6
6
6.75
N 图(kN )
.
3-25
Pl
4
Al
2
p
Cl
2
Pl
B4
B1
Pl 4
A1
Pl 4
(f )
Pl 4
M图
3kN/ m
A 2m
B
2m C
D 2m
6.0 B1 1.5 2.0
A1
26
D1
M 图(kNm)
.
D1 A1
B1 8.0 10.7 10 6
M 图(kNm)先求支反力
3-14
(g) A 1m B
3kN / m
C
2m
2m
E D
1m
(h)
1kN
A 2m
3kN / m
B 2m
C 2m D
A1 B1 6
E1
10
6
D1
6 D1
A1
B1 2
30
12 6
M 图(kNm) 先求支反力
M 图(kNm)
3-2 判断内力图正确与否,将错误改正。
(a) q
M (b)
M图
M图
或
Q图
Q图 或
.
3-15
(c) M图 Q图
(e)
或 或
或
(d) M图 Q图
ql 2
8
8
2
A
l 2
q
C
l
2
A1
ql 2
8
ql 2
ql 2
4
8
M图
B1
ql 2 8
A1
ql 2 8
.
ql 2
极值点 8
M图
ql 2
B8 B1
ql 2 8
3-13
(c) A
Pl
4
l
2
p
B
Pl
C
l
4
2
A1
Pl 4
(e)
2kN m
A 2m
Pl
Pl
2
4
M图
B1
Pl 4
3kN / m
C
B
D
2m
2m
(d)
.
3-10
2、计算程序
(1) 先计算支座反力;
(2) 在支反力和外荷载的作用下,分别求出各杆端的内 力(截面法),作出各杆的内力图,合起来即得到整个刚架的 内力图;
(3) 最后校核。
3、内力图的作法
第一种作法:分别求出各控制截面的内力M、Q、N, 按绘图规则作出各内力图。
第二种作法:计算各控制截面的弯矩M,作M图;截取
.
3-7
注意:弯矩图的叠加,是指纵坐标(竖距)的叠加,而不 是指图形的简单拼合。
三、静定多跨梁
定义:由若干根梁用铰连接而成用来跨越几个相连跨 度的静定梁称为静定多跨梁。
静定多跨梁是由简支梁、悬臂梁、伸臂梁组合而成的。 1、两种基本形式简图(组成形式) (1)单悬臂式 (2)双悬臂式
.
3-8
静定多跨梁从构造上来讲,可分为基本部分和附属部
20 kN
10kN 2kN / m
A
BC
D
E
F
3m 3m 1.5 2m 2.5m1.5 4.5m
6m
6m
6m
题3-5(a)
6.08
6.75
先 计 算 EF , 求 出 E 点 的 反 力 ,
将其作为外荷载反向作用在CE上。
然后再计算CE,求出C点的反力,
将其作为外荷载反向作用在AC。
最后计算AC。
RF = 4.5kN ()
kN
()
RC
=
67 kN 32
()
RI = 3.125kN ()
③ 作M 图和Q 图(如右图)
.
4 kN
D
E 2 kN m
A
FG B
1m 2m 2m 1m1m1m1m 4m
1 kN / m
C
H
I
1m 4m 1m
题3-5(b)
11
15
8
1
2
9 2
9 4
7 4
1
M 图 (kN m)
15 8
7
1
32
Q 图 (kN)
-
q(lx 2
x2 )
若 ,则有 M中 = M右
q(l - 2x)2 = - q(lx - x2 )
8
2
解得
x1
=
24
2l
x2
=
2+ 4
2l
不合题意,舍去 .
xl x
题3-6 图
q
l
l
q(l - 2x) 2
x
3-23
3-7 作图示刚架的内力图。
q
qa
a
a
a/2
(a)
1 qa 2
5 qa
qa
8
13 qa 8
7 4
1
17 8
3-22
3-6 选择铰的位置x,使中间一跨的跨中弯矩与支座弯矩绝 对值相等。
解:中间一跨的跨中弯矩为
q
M中
=
q(l
- 2x)2 8
中间一跨的支座反力均为
l
q(l - 2x) 2
()
则对左边一跨有如右图所示的等效图。
右边支座处的弯矩为
M右
=
-[ q(l
- 2x) 2
x+
qx2 2
]
=
2 qa 3
2 qa
2 qa 3
2 qa 3
3
4 qa 3
Q图
N图
.
3-29
支座反力:X左 = 2.81q(), X右 = 2.81q(),Y左 = 7.5q(),Y右 = 7.5q()
q
10m
12.5q 12.5q
3.1q
3.1q
9.3q
9.3q
2.5 6m 6m 2.5
(d)
5q 2.5q
2.5q 0.9q
2、截面法
截面法:是指将指定截面切开,取左边部分(或右边部 分)为隔离体,利用隔离体的平衡条件,确定此截面的三个 内力分量。
需要注意的问题:
(1) 隔离体的取法。隔离体与其周围的约束要全部切断, 而以相应的约束力代替。
