射影变换
证明射影变换把直线映成直线

证明射影变换把直线映成直线
射影变换是指将一个射影平面映射到另一个射影平面的变换。
在射影平面上,直线可以表示为一个点集,因此射影变换将直线映射为另一个点集。
要证明射影变换把直线映成直线,可以采用以下步骤:
1. 假设直线L是射影平面P上的一个点集,且L不包含射影平面的无穷远点。
2. 设T为射影变换,将射影平面P映射到另一个射影平面P'。
3. 设L'为直线L在P'上的像点集,即L' = T(L)。
4. 要证明L'是一条直线,需要证明L'满足射影几何中直线的定义:任意两点都在L'上,且L'不包含无穷远点。
5. 由于L在P中不包含无穷远点,因此L'在P'中也不包含无穷远点。
6. 设P1和P2是L上的两个点,则它们在P中不为同一点。
7. 由于T是射影变换,因此它是一一对应的,即对于任意两个不同的点P1和P2,它们在P'中的像点T(P1)和T(P2)也不同。
8. 因此,T(P1)和T(P2)都在L'上,即L'包含P1和P2。
9. 综上,L'是一条直线,证毕。
因此,射影变换将直线映射为直线。
这个结论在射影几何中是非常重要的,因为它保证了射影变换可以保持直线和交点不变,从而可以在射影几何的研究中得到广泛应用。
- 1 -。
空间几何的射影变换

空间几何的射影变换在日常生活中,我们经常面对空间的变换,如照相机拍摄的照片、镜子中的影像等。
这些现象都与几何变换密切相关,其中,射影变换是其中一个重要的变换类型。
在本文中,我们将讨论空间几何的射影变换及其应用。
一、射影变换的基本概念射影几何是解决欧几里德几何中所无法解决的问题的一种方法,它不要求平行线有相交点,也不要求垂直线相交成直角。
在射影几何中,平行线也可能相交,万物是相互联系的,没有孤立的存在。
被称为射影变换的变换是由一组变换组成的,这些变换可以通过投影、切比雪夫变换和对合来定义。
它们可以将几何图形中的点、直线和平面进行映射,并保持它们的基本性质。
射影变换也被称为单个射影坐标系到另一个射影坐标系的变换。
二、射影变换的应用射影变换在计算机视觉、计算机图形学、航空航天技术和游戏开发等领域中经常被使用。
它是许多计算机视觉算法的重要组成部分,如物体检测、目标跟踪和姿态估计等。
在游戏开发中,射影变换用于创建虚拟世界中的相机视图,使玩家可以观察到游戏场景中的不同角度和位置。
另一个重要的应用是医学成像,如CT和MRI。
这些成像技术可以创建三维图像,从而更好地诊断疾病和故障。
射影变换在这些成像技术中扮演着重要的角色,因为它可以将成像平面与三维物体之间建立对应关系,从而实现准确的成像。
三、空间几何的射影变换实现在实现空间几何的射影变换时,需要使用矩阵变换来表示变换矩阵。
通常使用4×4的矩阵表示射影变换,其中前三行表示旋转和缩放,第四行表示平移和尺度变化。
假设有一个点(x,y,z,1)在进行变换时,只需将其分别乘以变换矩阵的每一行即可得到变换后的坐标。
在实际应用中,常用的射影变换包括投影变换、剪裁变换、变换到相机坐标系等。
投影变换用于将三维场景投影到一个二维平面上,常用于计算机图形学和计算机视觉中。
剪裁变换用于筛选出场景中实际可见的区域,同时去掉不必要的区域。
变换到相机坐标系用于将物体的坐标与相机的坐标建立对应关系,从而计算其在视角下的表现形式。
第二章 射影变换-第四节 一维射影变换课件ppt课件
一、一维射影变换
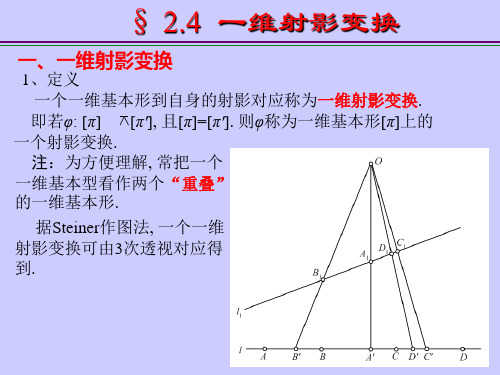
1、定义 一个一维基本形到自身的射影对应称为一维射影变换. [π'], 且[π]=[π']. 则φ称为一维基本形[π]上的 即若φ: [π] 一个射影变换. 注:为方便理解, 常把一个 一维基本型看作两个“重叠” 的一维基本形. 据Steiner作图法, 一个一维 射影变换可由3次透视对应得 到.
a11 a12 0,
a21 a22
0
(2.10)
其中对应点的坐标是关于一维基本形[π]上的同一坐标系取得的.
(ad bc 0)
§ 2.4 一维射影变换
一、一维射影变换
1、定义 2、代数表示 (1). 坐标表示 (2). 参数表示 定理2.16 一维基本形上的一个变换为射影变换其对应元素 的参数λ,λ' 满足一个双线性方程 a 'b c 'd 0 (ad bc 0) (2.13) 证 “=>”. 见教材, 略. “<=”. 设一维基本形(P)上的一个变换φ使得任一对对应元素的 参数λ,λ' 满足双线性方程(2.13). 显然φ是一个双射,只要证φ保交比. 设λi ,λi' (i=1,2,3,4)为任意四对对应元素的参数. 则 b1 d b3 d (ad bc)(1 3 ) 1 '3 ' . a1 c a3 c (a1 c)(a3 c) 同法可以求出λ2'–λ4', λ2'–λ3', λ1'–λ4', 得到 (1 '3 ' )(2 '4 ' ) (1 3 )(2 4 ) . (2 '3 ' )(1 '4 ' ) (2 3 )(1 4 )
认识平面几何的射影变换与旋转变换教案

认识平面几何的射影变换与旋转变换教案平面几何是数学中的一个重要分支,它研究的是平面上的各种图形和它们之间的关系。
在平面几何中,射影变换和旋转变换是两个常见的变换方式。
本文将为大家介绍平面几何中的射影变换和旋转变换,并给出相应的教案。
一、射影变换1.1 什么是射影变换射影变换又称为投影变换,它是平面上的一种映射方式,将一个点或一组点映射到另一个点或一组点上。
射影变换可以通过线性变换和非线性变换实现。
其中线性变换包括平移、缩放、错切等,非线性变换包括对称、相似等。
1.2 射影变换的特点射影变换具有保持直线共线和保持比例关系的特点。
也就是说,经过射影变换后,原来共线的点仍然共线,并且线段的比例关系保持不变。
1.3 射影变换的应用射影变换在现实生活中有很多应用,如建筑投影、影像处理等。
在建筑投影中,射影变换可以实现将三维模型投影到二维平面上,以实现对建筑物的设计和展示。
在影像处理中,射影变换可以实现图像的裁剪、变换、扭曲等操作。
二、旋转变换2.1 什么是旋转变换旋转变换是平面上的一种变换方式,它通过旋转角度将一个图形绕某个旋转中心进行旋转。
旋转变换可以使图形保持原有形状和大小,只是位置和方向发生改变。
2.2 旋转变换的特点旋转变换具有保持形状和大小不变的特点,也就是说,在旋转过程中,图形的所有边长和角度保持不变。
2.3 旋转变换的应用旋转变换在日常生活中有很多应用,如地球自转、电风扇旋转等。
在地球自转中,地球绕自身的轴线进行旋转,形成昼夜交替。
在电风扇旋转中,电风扇的叶片绕中心旋转,产生风力。
三、射影变换与旋转变换教案3.1 教学目标通过本节课的学习,学生将了解射影变换和旋转变换的基本概念和特点,并能灵活应用于解决实际问题。
3.2 教学内容(1)射影变换的定义和特点;(2)射影变换的应用案例分析;(3)旋转变换的定义和特点;(4)旋转变换的应用案例分析。
3.3 教学过程(1)导入:通过引入平面几何中的平移变换,帮助学生理解射影变换和旋转变换的概念;(2)讲解:通过教师讲解射影变换和旋转变换的定义和特点,引导学生理解并记住相关知识;(3)案例分析:通过展示射影变换和旋转变换在实际生活中的应用案例,激发学生的学习兴趣,并培养学生分析和解决问题的能力;(4)练习:设计一系列练习题,让学生巩固所学知识,并提高应用能力;(5)总结:通过课堂小结,帮助学生对本节课的内容进行总结和归纳。
射影与射影变换的性质与应用

射影与射影变换的性质与应用射影几何是几何学的一个分支,主要研究高维空间中的射影与射影变换的性质与应用。
射影几何的研究对于空间形态的描述和数学建模具有重要的意义。
本文将介绍射影与射影变换的基本概念、性质以及在几何学和计算机图形学中的应用。
一、射影的基本概念射影是指从一个几何对象映射到另一个几何对象的操作。
在射影几何中,我们使用齐次坐标来描述几何对象。
齐次坐标是指用n+1个数表示n维空间中的点,通过对这些数进行比例变换可以得到等价的点。
例如,在二维平面中,一个点的齐次坐标可以表示为(x, y, 1),其中x和y是点在平面上的坐标。
二、射影变换的性质射影变换是指通过矩阵乘法对几何对象进行映射的操作。
射影变换具有以下性质:1. 保直线性:射影变换将直线映射为直线,保持直线上的所有点的次序关系。
2. 保比例性:射影变换将平行线段映射为平行线段,并且保持线段之间的比例关系。
3. 保交比性:射影变换可以保持射影空间中的交比关系,即一组点的交比在变换后保持不变。
4. 保角度性:射影变换可以保持两条直线之间的夹角不变。
5. 组合性:射影变换可以通过矩阵乘法的组合实现。
三、射影与射影变换在几何学中的应用1. 透视投影:透视投影是一种射影变换,将三维场景投影到二维平面上。
透视投影在计算机图形学中广泛应用于生成逼真的虚拟场景。
2. 图像处理:射影变换可以用于图像的旋转、缩放和扭曲等操作,以及图像的透视校正和纠正。
3. 几何建模:射影变换可以用于对三维几何模型进行旋转、平移和缩放等操作,以及模型的投影和透视变换。
四、射影与射影变换在计算机图形学中的应用1. 三维渲染:射影变换在三维渲染中用于将三维物体的坐标映射到二维屏幕上,实现真实感的显示。
2. 图形变换:射影变换在图形变换中用于对图形图像进行旋转、平移、缩放和扭曲等操作。
3. 图像合成:射影变换可以用于对多个图像进行叠加和融合,生成新的合成图像。
五、射影与射影变换的应用案例1. 虚拟现实:射影变换在虚拟现实中用于实现真实感的三维场景投影和交互。
射影变换教案

射影变换教案教案标题:射影变换教案教案目标:1. 理解射影变换的概念和基本原理;2. 掌握射影变换的常见类型和应用领域;3. 能够运用射影变换解决相关问题。
教学重点:1. 射影变换的概念和基本原理;2. 射影变换的常见类型和应用领域。
教学难点:1. 射影变换的具体计算方法;2. 射影变换的实际应用。
教学准备:1. 教学投影仪和计算机;2. 射影变换的相关案例和实例。
教学过程:一、导入(5分钟)1. 引入射影变换的概念,并与学生讨论射影变换在日常生活中的应用。
二、理论讲解(15分钟)1. 讲解射影变换的基本概念和原理,包括射影变换的定义、特点和基本性质。
2. 介绍射影变换的常见类型,如平面射影变换、透视射影变换等,并解释其应用领域。
三、示例分析(20分钟)1. 展示射影变换的实际案例和应用,如图像处理、计算机图形学等。
2. 分析示例中的射影变换过程和计算方法,引导学生理解射影变换的具体应用和计算步骤。
四、练习与讨论(20分钟)1. 提供一些射影变换的练习题,让学生运用所学知识解决问题。
2. 引导学生讨论解题思路和方法,共同探讨射影变换的应用和优势。
五、小结与展望(10分钟)1. 对本节课的内容进行小结,强调射影变换的重要性和应用价值。
2. 展望下节课的内容,如射影变换的进阶应用和相关算法。
教学延伸:1. 鼓励学生自主探索射影变换在其他领域的应用,如建筑设计、摄影等。
2. 提供相关学习资源和参考书目,供有兴趣的学生进一步学习和研究。
教学评估:1. 教师观察学生在课堂上的学习态度和参与度;2. 学生完成课后作业,检查其对射影变换的理解和应用能力。
教学反思:1. 教学过程中是否能够引起学生的兴趣和思考;2. 学生对射影变换的理解程度和应用能力是否达到预期目标;3. 教学方法和教学资源是否适合学生的学习需求。
仿射变换和射影变换的概念及应用

仿射变换和射影变换的概念及应用Affine transformation refers to a transformation that preserves straight lines, parallelism, and ratios of distances along a line. It can include translation, rotation, scaling, reflection, and shearing. Affine transformations can be represented using matrices and vectors, and they play a crucial role in various applications such as image processing, computer vision, and 3D graphics.On the other hand, projective transformation, also known as perspective transformation, is a more general transformation that includes affine transformations as a special case. Projective transformations preserve straight lines but not necessarily parallelism or ratios of distances along a line. They are often used to model realistic rendering of 3D scenes onto 2D images, as they can simulate the effect of perspective and depth.Both affine and projective transformations have their own mathematical representations and properties. They are widely used in computer graphics, computer vision, and other related fields to manipulate and transform geometric objects and images.中文回答: 仿射变换和射影变换是几何学和计算机图形学中的两个重要概念。
射影变换、仿射变换、欧式变换、相似变换、等距变换

射影变换、仿射变换、欧式变换、相似变换、等距变换射影变换组成了⼀个群,这个群被称为射影变换群。
仿射变换是射影变换的⼦群。
欧式变换(旋转+平移+等⽐缩放)是仿射变换的⼦群。
相似变换和等距变换则是欧式变换的⼦群。
0.射影变换定义由有限次中⼼射影的积定义的两条直线间的⼀⼀对应变换称为⼀维射影变换。
由有限次中⼼射影的积定义的两个平⾯之间的⼀⼀对应变换称为⼆维射影变换。
性质——交⽐不变性如果平⾯上点场的点建⽴了⼀个⼀⼀对应,并且满⾜:(1)任何共线三点的象仍是共线三点;(2)共线四点的交⽐不变。
则这个⼀⼀对应叫做点场的射影变换,简称射影变换。
矩阵表⽰⽤H表⽰,H为3×3的可逆实矩阵,虽然有9个未知数,但只有8个⾃由度(只与具体⽐率有关),其中h31与h32不为0是它与仿射变换的本质区别,它使得仿射变换的⾮线性效应。
可以把⼀个H分解为:H=SAP,其中S为相似变换,A为仿射变换,P为射影变换。
变换前后共点,共线,交⽐,相切,拐点,切线的不连续性和岐点保持不变。
注:n×n可逆实矩阵称为⼀般线性群GL(n),当把相差⾮零纯量因⼦的矩阵都视为等同时,便得到射影映射群,记为PL(n),在平⾯射影变换时为PL(3)。
射影变换矩阵表⽰:H = { h11, h12, h13h21, h22, h23h31, h32, h33 }其中当最后⼀⾏为(0,0,1)时的变换为仿射变换,在仿射的前提下,当左上⾓2×2矩阵正交时为欧式变换,左上⾓矩阵⾏列式为1时为定向欧式变换。
1、等距变换:它相当于是平移变换和旋转变换的复合,⽤R表⽰变换矩阵,R为3×3矩阵,R={{r11,r12,tx},{r21,r22,ty},{0,0,1}}左上⾓2×2矩阵为旋转部分,tx和ty为平移因⼦,它有三个⾃由度,即旋转,x⽅向平移,y⽅向平移。
等距变换前后长度,⾯积,线线之间的⾓度都不变。
2.相似变换它相当于是等距变换和均匀缩放的⼀个复合,⽤S表⽰变换矩阵,S为3×3矩阵,S={{s*r11,s*r12,tx},{s*r21,s*r22,ty},{0,0,1}}左上⾓2×2矩阵为旋转部分,tx和ty为平移因⼦,它有4个⾃由度,即旋转,x⽅向平移,y⽅向平移和缩放因⼦s。
计算机视觉中的多视图几何第二章3D射影几何和变换

零空间与生成子空间表示
(2)Plucker矩阵 将一条直线由4*4的反对称齐次矩阵表示,连接两点A,B的直线L的矢量表示:L=AB’-BA’ L有若干如下性质: 1、L的秩为2 2、该表示具有描述一条直线所需要的4个自由度,6-2 3、矩阵L与用来确定它的点A,B无关,C=A+aB代替时,那么得到的矩阵是 L’’=AC’-CA’=A(A’+aB’)-(A+aB)A’= AB’-BA’=L
Page *
绝对二次曲线 (1)绝对二次曲线是在π∞上的一条二次曲线,满足 X1²+X2²+X3² =0 X4² 值得注意的是定义一条二次曲线需要定义两个方程 可以写成(x1,x2,x3)I(x1,x2,x3)’=0形式 绝对对偶二次曲线 (1)绝对二次曲线的对偶是3维空间中一种退化的对偶二次曲面,从几何上说,绝对对偶二次曲线由对偶二次曲线的平面组成。想象一个椭球面的所有切平面的集合,然后把椭球面压成饼的情况。
Page *
秩 ∮ 对角线 方程 实现 4 4 (1,1,1,1) X²+Y²+Z²+1=0 无实点 2 (1,1,1,-1) X²+Y²+Z²=1 球面 0 (1,1,-1,-1) X²+Y²=Z²+1 单叶双曲面 3 3 (1,1,1,0) X²+Y²+Z²=0 点(0,0,0,1) 1 (1,1,-1,0) X²+Y²=Z² 过原点的圆锥 2 2 (1,1,0,0) X²+Y²=0 单条直线(Z轴) 0 (1,-1,0,0) X²=Y² 两平面X=+-Y 1 1 (1,0,0,0) X²=0 平面X=0 三次绕线
Page *
设A,B分别是原点和X-方向的理想点
第三章射影变换

第三章 射影变换与射影坐标本章首先引入射影不变量——交比。
然后在此基础上,讨论了一维基本形之间的射影对应与射影变换,以及二维射影对应和射影变换,还定义了一维和二维射影坐标。
§1 交比与调和比点列中四点的交比与调和比定义1.1 共线的四个不同点A ,B ,C ,D 的交比等于单比(ABC )与单比(ABD )的比,记作:(AB ,CD ),即(AB ,CD )=)()(ABD ABC其中A ,B 叫基点偶,C ,D 叫分点偶。
交比又称交叉比和复比。
由交比和单比的定义,我们可AD BC BDAC BDAD BC ACABD ABC CD AB ⋅⋅===)()()(, 其中AC ,BC ,AD ,BD 是有向线段的数量。
我们不难得出:(1) 点偶C ,D 不分离点偶A ,B 时,交比(AB ,CD )﹥0; (2) 点偶C ,D 分离点偶A ,B 时,交比(AB ,CD )﹤0; (3) 当C ,D 重合时,(AB ,CD )=1; (4) 当A ,C 重合时,(AB ,CD )=0。
定理1.1 基点偶与分点偶交换,交比值不改变,即 (AB ,CD )=(CD ,AB ) 证明 由定义1.1,(CD ,AB )=),(CD AB BCAD BDAC CB DA DB CA =⋅⋅=⋅⋅ 定理1.2 基点偶的两个字母交换或分点偶的两个字母交换,交比的值变成原来的交比值的倒数,即(BA ,CD )=(AB ,DC )=),(1CD AB证明(AB ,DC )=),(1)()(1)()(CD AB ABD ABC ABC ABD == 又(BA ,CD )=(CD ,BA )=),(1),(1CD AB AB CD =推论 同时交换每个点偶里的字母,交比的值不改变,即 (AB ,CD )=(BA ,DC ) 定理1.3 交换中间的两个字母或两端的两个字母,交比的值等于1减去原来的交比值,即(AC ,BD )=(DB ,CA )=1-(AB ,CD )证明(AC ,BD )AD CB CD AB ⋅⋅=AD CB BD CB BC AC ⋅++=))(( AD CB BDAC CB BD CB AC ⋅⋅+++=)(AD CB BD AC ⋅⋅+=1=1+)(ADBC BDAC ⋅⋅-=1-(AB ,CD )共线四点1,2,3,4一共有4!=24中不种的排列,所以有24个交比,根据交比的运算性质,它们只有6个不同的交比值,即(12,34)=(34,12)=(21,43)=(43,21)=m(21,34)=(34,21)=(12,43)=(43,12)=m1(13,24)=(24,13)=(31,42)=(42,31)=1-m(13,42)=(42,13)=(31,24)=(24,31)=m-11(14,23)=(23,14)=(41,32)=(32,41)=1-m 1(14,32)=(32,14)=(41,23)=(23,41)=1-m m例1 已知(P 1P 2,P 3P 4)=3,求(P 4P 3,P 2P 1)和(P 1P 3,P 2P 4)的值解 (P 4P 3,P 2P 1)= (P 2P 1 ,P 4P 3)=(P 1P 2,P 3P 4)=3 (P 1P 3,P 2P 4)=1-(P 1P 2,P 3P 4)=1-3=-2下面研究交比的代数表示定理1.4 一直线上的无穷远点分其上任何两点的单比等于1。
任意三角形的射影定理(3篇)

第1篇在几何学中,射影定理是一个重要的定理,它描述了三角形在射影变换下的性质。
射影变换是指将一个几何图形通过一定的方式映射到另一个几何图形上,而保持其某些性质不变。
本文将详细介绍任意三角形的射影定理,包括其定义、证明方法以及在实际应用中的重要性。
一、射影定理的定义射影定理是指在任意三角形中,从一个顶点到对边上的任意点作垂线,那么这个垂线段的长度与这个顶点到对边中点的距离之比等于从该顶点到对边另一端点的距离与从该顶点到对边中点的距离之比。
设三角形ABC,其中点D是BC边上的任意一点,点E是AD的垂足,点F是AC的中点。
根据射影定理,我们有:$$\frac{AE}{EF} = \frac{AB}{AF}$$二、射影定理的证明证明射影定理有多种方法,以下介绍两种常见的证明方法:1. 构造辅助线法(1)作辅助线:在三角形ABC中,作辅助线DE,使得DE垂直于BC,交BC于点D。
(2)证明:在直角三角形ADE和直角三角形AFC中,∠AED=∠AFC=90°,且∠ADE=∠AFC(都是直角)。
根据AAS(角-角-边)全等条件,得到三角形ADE≌三角形AFC。
(3)根据全等三角形的性质,我们有AE=AF。
(4)由于EF是AC的中线,所以EF=AF。
(5)根据射影定理的定义,得到:$$\frac{AE}{EF} = \frac{AB}{AF}2. 利用相似三角形法(1)证明:在直角三角形ADE和直角三角形AFC中,∠AED=∠AFC=90°,且∠ADE=∠AFC(都是直角)。
根据AAS(角-角-边)全等条件,得到三角形ADE≌三角形AFC。
(2)根据全等三角形的性质,我们有AE=AF。
(3)由于EF是AC的中线,所以EF=AF。
(4)根据相似三角形的性质,我们有:$$\frac{AE}{AF} = \frac{DE}{FC}$$(5)由于DE=BC,FC=AC/2,代入上式得到:$$\frac{AE}{AF} = \frac{BC}{AC/2} = \frac{AB}{AF}$$三、射影定理的应用射影定理在几何学、工程学、物理学等领域都有广泛的应用。
射影定理证明

射影定理证明射影定理是代数学中非常重要的一个定理,它在研究代数结构和代数变换时具有广泛的应用。
本文章将对射影定理进行详细的解释和证明,以期帮助读者更深入地理解射影定理的核心思想和应用。
首先,我们来了解一下射影变换的概念。
射影变换是指在二维平面或三维空间中,将任意一条直线或射线映射为另一条直线或射线的变换。
射影变换可以将无穷远处的点映射到有限远处或相反,因此它可以将有限点集变换为具有无穷远点的点集。
在这个过程中,射影定理所关注的是一些特殊的点集,它们由直线或射线所包含。
在理论研究中,我们通常将这样的点集称为“射线”或“直线”,而不管它们是否有穷远点。
在这个意义上,我们可以将射线看作是一些具有方向的“向量”,它们可以表示为起始点加上方向的形式。
在形式化的研究中,一个“射线”可以被表示成一个形如(a,b,c)的三元组,其中a、b和c分别表示“起始点的x坐标”、“起始点的y坐标”和“方向向量的斜率”(如果它存在)。
接下来,我们提出了射影定理的核心思想:它是一个关于“点集和射影变换”的定理,指出如果一个点集在进行完射影变换后,依然保持线性的结构,那么这个点集就被称为“射影空间中的点集”。
换言之,射影定理指出了一个点集何时是“射线”或“直线”的判断标准:当它在射影变换下仍为“射线”或“直线”时,我们才可以把它看作是一个“射线”或“直线”。
接下来,我们详细地说明射影定理的证明过程。
具体来说,我们考虑将一个任意的点集进行射影变换(指已知点集和它们对应的线性关系,计算变换后的射线方程或直线方程),并且假设该点集在射影变换前是一个线性子空间。
根据射影变换的定义,我们可以得到一个矩阵M,它将所有的坐标表示和方向矢量变换为另一个表示方式和矢量。
此外,我们加入一个额外的列(行)以表示“无穷远点”。
这表示了所有“射线”或“直线”的共同性质:它们具有无限的长度,其中包括无穷远处的一些点。
通过使用矩阵M来将我们的原始点集和坐标表示变换为新的点集和坐标表示,我们可以得到一个新的“线性子空间”,其中包括原始点集和无穷远点。
射影。仿射变换的基本知识

射影变换的基本知识定义设为平面上的四个共线点,称两个单比和的比为这四点的交比或复比,记作,其中和称为基础点对,和称为分点对。
定义如果四点的交比,则称点对和调和分离点对和,或称点对与点对调和共轭,这时也称为的第四调和点,交比值称为调和比。
定理:中心射影保持共线四点的交比不变证明:如图为射影中心直线上任意四点在中心射影下的像分别是直线上的设的垂直于的高长度为,的垂直于的长度为则于是同理于是故定义如果平面上的点变换使共线三点还变成共线三点,并且保持共线四点的交比不变,称此变换为平面上的射影变换。
因为正交变换、相似变换、仿射变换都保持共线三点的单比不变,必然保持共线四点的交比不变,所以这些变换都是射影变换。
射影变换的基本不变性质:定理:平面上全部射影变换的集合构成群证明:(1)设是平面上的两个射影变换,是共线四点据定义有且且所以仍是射影变换(2)设是平面的上射影变换且且所以是射影变换故平面上全部射影变换的集合构成群称之为射影变换群,仿射变换群、相似变换群、正交变换群都是它的子群。
§2.6 几个重要的变换群下面讨论正交变换(运动)、相似变换、仿射变换、射影变换,以及它们的基本性质。
这些变换群可以决定四种不同的几何学,即欧氏几何学、相似几何学、仿射几何学和射影几何学。
一、正交变换群定义:平面上保持两点间距离不变的点变换称为正交变换或运动。
即将平面上的点建立一一对应,且对于平面上任意两点,若其对应点分别为,则对应线段的长度。
正交变换具有的基本不变的性质(1)正交变换把直线变成直线,并且保持点和直线的结合关系和共线三点的介于关系。
证明:设是直线上有序的三点,它们共线的充要条件为如果正交变换把它们依次变为,则有于是因此在同一直线上。
就是说,共线点变成共线点,直线变成直线。
(2)正交变换把不共线的点变成不共线的点证明:设为不共线三点,则三点不共线充要条件为如果它们依次变为,则有于是因此不共线由(1)、(2)知,正交变换把相交直线变成相交直线,把角变成角。
射影变换

简介
由有限次中心射影的积定义的两条直线间的一一对应变换称为一维射影变换。 一维射影变换 由有限次中心射影的积定义的两个平面之间的一一对应变换称为二维射影变换。 二维(高维)射影变换 因为正交变换、相似变换、仿射变换都保持共线三点的单比不变,必然保持共线四点的交比不变,所以这些 变换都是射影变换。
射影变换
数学术语
01 简介
03 05 相关知识
目录
02 交比 04 仿射变换
由有限次中心射影的积定义的两条直线间的一一对应变换称为一维射影变换。由有限次中心射影的积定义的 两个平面之间的一一对应变换称为二维射影变换。
因为正交变换、相似变换、仿射变换都保持共线三点的单比不变,必然保持共线四点的交比不变,所以这些 变换都是射影变换。
仿射变换
仿射变换是射影变换的特殊情况,当定义中心射影的线束为互相平行的直线时,变换称为仿射变换,由于线 束中的直线互相平行,显然,仿射变换保持交比不变。
仿射变换
相关知识
射影平面
射影平面就是2维射影空间。它可以视为平面添上一条无穷远直线。它是代数几何、射影几何里最基本的对象。
对射影平面的理解是从局部到整体的扩展过程。先从无穷远元素、射影直线的理解入手,再到射影平面定义 的理解,最后利用射影平面的模型来揭示射影平面的结构,想象它的形状,帮助初学者更好地理解射影平面的结 构与性质。在射影几何的基本内容中,初学者对射影平面尤感兴趣,但又觉得其极为抽象、难以理解,这主要是 与我们的直观认识不一致引起的。因此,从射影平面上的无穷远点、无穷远直线、射影直线的理解入手,在理解 这些抽象概念的同时,即理解射影平面上元素的特点,接着理解射影平面的定义,最后给出射影平面的模型以帮 助理解射影平面的形象。
射影定理的内容

射影定理的内容射影定理是数学中一个经典的定理,它是代数几何中的基本定理之一,也是现代代数几何的核心内容。
本文将从射影空间、射影几何、射影变换以及射影定理等方面来详细介绍射影定理的内容。
一、射影空间射影空间是指一个由向量空间V中的所有一维子空间所构成的集合,记为P(V)。
在射影空间中,每个向量都对应着一个一维子空间,而一维子空间又可以看作是一个向量的所有倍数所组成的集合。
因此,射影空间中的点可以看作是向量的等价类。
射影空间的一个重要性质是它具有同构不变性,即不同的线性变换在射影空间中对应着相同的变换。
这个性质使得射影空间成为了研究几何图形的一个有力工具。
二、射影几何射影几何是指在射影空间中研究几何图形的一种数学分支。
在射影几何中,直线被定义为两个点之间的最小一维子空间,平面被定义为三个点之间的最小二维子空间,等等。
射影几何中的一个重要问题是如何描述一个几何图形。
一个几何图形可以被描述为一个射影空间中的子集,它的维数即为这个子集所在的最小子空间的维数。
三、射影变换射影变换是指从一个射影空间到另一个射影空间的一个双射,它保持了直线和点的性质。
射影变换可以用一个矩阵来表示,这个矩阵是一个非奇异的n+1阶方阵,其中n为射影空间的维数。
射影变换有一些重要的性质。
首先,任何射影变换都可以看作是一个仿射变换和一个伸缩变换的组合,其中仿射变换是指一个将直线变为直线的变换,伸缩变换是指一个将点变为点的变换。
其次,射影变换具有同构不变性,即不同的矩阵在射影空间中对应着相同的变换。
四、射影定理射影定理是代数几何中的一个重要定理,它将射影几何和射影变换联系了起来。
射影定理的内容如下:设X和Y分别为两个射影空间,f:X→Y是一个非常数的射影变换,那么f在X上的像集是一个在Y中的射影子空间。
这个定理的意义是,射影变换可以将一个射影空间中的子集映射到另一个射影空间中的子集,而这个映射后的子集仍然是一个射影子空间。
这个定理是代数几何中的基本定理之一,它在研究射影几何和射影变换中有着重要的应用。
空间解析几何的线性变换平移旋转射影变换的性质

空间解析几何的线性变换平移旋转射影变换的性质在数学中,空间解析几何是一门研究空间中点、线、面等几何要素的位置、形状和相互关系的学科。
空间解析几何涉及线性变换、平移、旋转和射影变换等多个概念和性质。
本文将依次介绍线性变换、平移、旋转和射影变换在空间解析几何中的性质。
一、线性变换线性变换是空间解析几何中非常重要的概念,指的是通过运用线性代数的方法,将一个向量空间中的向量按照某种规则变换为另一个向量空间中的向量。
线性变换有以下性质:1. 保持线性性:线性变换将向量的线性性质保持不变,即对于任意向量a和b以及任意标量c,有T(a+b) = T(a) + T(b)和T(c*a) = c*T(a)。
2. 保持原点:线性变换将原点在变换后仍然保持在原点。
3. 保持共线性:线性变换将共线的向量映射为仍然共线的向量。
二、平移平移是指将点p在空间中沿着某个方向d移动一个指定的距离a得到点p'的操作。
平移有以下性质:1. 平移不改变点的方向:平移不改变点的方向,只是改变了点的位置。
2. 平移保持距离:平移前后,点与点之间的距离保持不变。
3. 平移是线性变换:平移是一种特殊的线性变换,不改变向量的方向和长度。
三、旋转旋转是指将点p绕着某个轴心旋转一个指定的角度θ,得到点p'的操作。
旋转有以下性质:1. 旋转不改变距离:旋转前后,点与点之间的距离保持不变。
2. 旋转保持共面性:旋转前后,点所在的平面保持不变。
3. 旋转是线性变换:旋转是一种特殊的线性变换,不改变向量的方向和长度。
四、射影变换射影变换是指通过将点p在空间中映射到平面上的某个点p',实现空间到平面的变换。
射影变换有以下性质:1. 保持共线性:射影变换将共线的点映射为仍然共线的点。
2. 保持交比:射影变换保持平面上的任意四点的交比不变。
3. 平行线的交点:射影变换后,原来平行的线在平面上可能会相交。
在空间解析几何中,线性变换、平移、旋转和射影变换是重要的概念和操作。
射影变换

P3P4 )
(1 (2
3 )(2 3 )(1
4 ) 4 )
.
(2.2)
§ 2.1 交比
证明定理2.1. 以P1, P2,为基点,参数表示P3, P4. 设
a+λ1b=a', a+λ2b=b'.
从中解出a,
b,
得
a
a' 2
b' 1
,
2 1
b b'a' .
2 1
于是, P1, P2, P3, P4的坐标可表示为 a', b', 2 3 a' 3 1 b', 2 4 a' 4 1 b' 2 1 2 1 2 1 2 1
中的两个著名定理:Menelaus定理、Ceva定理.
§ 2.1 交比
一、点列中四点的交比
二、线束中四直线的交比
1、线束的参数表示
设a, b为线束S(p)中取定的相异二直线. 则对于任意的p∈S(p),
其坐标可表示为
a b
R.
称a, b为基线, λ为参数.
这里a, b, p均表示直线的齐次坐标. 注1 参数λ的几何意义?不易说清楚!容易看出
解:设 P3 P1 1P2, P4 P1 2P2. 则显然2 1, 由
(P1P2 , P3P4 )
1 2
1
1
2.
可得 1 2, 从而P3的坐标为(3,–1,3).
§ 2.1 交比
一、点列中四点的交比 1、定义 2、性质 3、特殊情况
4、调和比 5、交比的计算 (1). 由坐标求交比 (2). 由交比求坐标
即
a', b', a' 3 1 b', a' 4 1 b'.
基于空间射影变换的视角转换方法

基于空间射影变换的视角转换方法空间射影变换是一种在计算机图形学中广泛应用的技术,用于将3D空间中的对象在不同的视角进行投影以呈现出逼真的3D效果。
在计算机视觉和虚拟现实领域,视角转换是一项重要的技术,它可以帮助我们在不同的视角下观察和理解3D场景。
本文将介绍基于空间射影变换的视角转换方法,并探讨其在计算机图形学领域的应用。
一、空间射影变换的基本原理空间射影变换是一种数学方法,通过应用投影矩阵将3D空间中的对象投影到2D平面上。
在计算机图形学中,我们通常使用透视投影或正交投影进行空间射影变换。
透视投影是一种模拟人眼视觉的投影方式,它可以使观察者在观察3D场景时感受到景深和透视效果。
透视投影通常通过透视投影矩阵来实现,其基本原理是根据观察者的位置和视线方向,将3D场景中的对象投影到视平面上。
透视投影可以使得远处的物体看起来比近处的物体小,从而呈现出逼真的3D效果。
正交投影是一种简单而直接的投影方式,它将3D场景中的对象投影到一个平行于观察平面的平面上。
正交投影通常通过正交投影矩阵来实现,其基本原理是将3D场景中的对象在观察者的视线方向上进行投影,保持物体在投影平面上的大小和比例不变。
正交投影不会呈现出透视效果,但可以使得物体在不同视角下呈现出相同的大小和比例。
在计算机图形学中,基于空间射影变换的视角转换方法主要包括以下几个步骤:1.确定观察者的位置和朝向。
通过设定观察者的位置和观察方向,我们可以确定视角转换的基本参数,包括视点、观察方向和上方向。
2.构建投影矩阵。
根据观察者的位置和朝向,我们可以构建透视投影矩阵或正交投影矩阵,用于将3D场景中的对象进行投影。
3.进行坐标变换。
将3D场景中的对象的顶点坐标通过投影矩阵进行坐标变换,将其投影到2D平面上。
4.剔除不可见部分。
通过深度测试或裁剪算法,剔除投影后在观察平面之外的部分,以减少不必要的计算和提高性能。
5.渲染投影图像。
将投影到2D平面上的对象进行光照、纹理映射和渲染,生成最终的投影图像。
射影变换基础

1 T
1
1 1 1
1
k2 1 1 A2 B2 k . A2 B2 k1
k2 (k is a scalar) k1
MA B M so
1 1 1
1 1 1
1
k . A B2 ,
1 2
1 2
A B and A B2 are similar matrices
根据相似矩阵的性质,这两个矩阵具有相同 的特征值。再假定B1也为可逆矩阵,则相 应的特征值不为0,因此根据特征值两两相 除(消去标量k),则得到两个不变量。可见同 一平面两个非退化二次曲线有两个绝对不 变量,当存在退化情况时,有一个特征值 为0,因此只有一个不变量。
1 T
1
1 T
1
if A1 is invertable matrix , A1 M MA I , then k2 .B2 ( M ) B1 M k1 A2 .MA B M , so MA B M
1 1 1 1 1 1 1 1 1 T 1
( M ) A1 M .MA B M
• 由有限次中心射影的积定义的两条直线间 的一一对应变换称为一维射影变换.
二维(高维)射影变换
Def3.2 由有限次中心射影的积定义的两个平面之间的一一对 应变换称为二维射影变换.
交比不变量
• Def 3.3 (交比)若A,B,C,D为直线L上任意四 点,则下式定义的R称为交比(cross ratio)
' ' ' '
线束的射影变换
• 平面上两个线束的射影变换及线束的交比。 如下图所示,平面上有两个线束O,O’,若 它们所有对应线的交点共线,则称这两个 线束的对应为中心射影。类似点列的射影 变换,有限次中心射影的积称为线束间的 射影变换。
二次曲线上的射影变换

二次曲线上的射影变换
射影变换是指将二维平面上的点通过射影矩阵进行变换的操作。
对于二次曲线上的点进行射影变换,可以通过以下步骤进行:
1. 假设二次曲线的方程为Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0,其中A、B、C、D、E、F是常数。
2. 将二次曲线表示为齐次坐标形式,即Ax^2 + Bxy + Cy^2 + Dxz + Eyz + Fz^2 = 0。
3. 构造射影矩阵P,一般形式为:
P = [p11, p12, p13]
[p21, p22, p23]
[p31, p32, p33]
其中p11、p12、...、p33是射影矩阵的元素。
4. 对于二次曲线上的点[x, y, z],通过将射影矩阵P与该点相乘得到变换后的点:
[x', y', z'] = P[x, y, z]
其中[x', y', z']是变换后的点。
5. 将变换后的点[x', y', z']转换为非齐次坐标形式,即[x'/z', y'/z'],即可得到射影变换后的二次曲线上的点。
需要注意的是,射影变换可能会改变二次曲线的形状、位置和方向。
射影矩阵P的选择会影响变换的效果,不同的射影矩阵可能会得到不同的变换结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
射影变换4.1 点列和线束点列和线束定义.两个矢量),,(321a a a 和),,(321b b b 表示不同的点当且仅当这两个矢量线性无关. 在两点A ),,(321a a a 与B ),,(321b b b 的连线上任意一点),,(321x x x X 满足0321321321=b b b a a a x x x即,三点A ),,(321a a a ,B ),,(321b b b 与),,(321x x x X 共线的充分必要条件是0321321321=b b b a a a x x x以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=;以m l ,为基线的线束中,任何一直线p 都可以表示为m l p μλ+=,用齐次坐标可以表示为m l m l p λλμ'+=+=.练习4-11.已知A 和B 的齐次坐标分别为)1,1,5(和)1,0,1(-,求直线AB 上一点C ,使1)(-=ABC ,若B A C λ+=,求出λ.解利用非齐次坐标),(y x 与齐次坐标),,(321x x x 之间的关系31x x x =,32x xy =.这时,)1,5(),(=y x A ,)0,1(),(-=y x B ,再利用BC AC ABC =)(.115-=+-x x ,解得2=x,101-=--y y ,解得21=y .即)21,2(=C ,C 点的齐次坐标为)1,21,2(. 因为B A C 2121+=,所以 1=λ. 注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 2.试证明:三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为0321321321=z z z y y y x x x 证明三点),,(321x x x ,),,(321y y y ,),,(321z z z 共线的充分必要条件为λ=--=--=--333322221111y z x z y z x z y z x z所以0332211321332211321321321=-------=y z y z y z y y y x z x z x z z z z y y y x x x4.已知直线0143=++y x 与02=+y x ,求过两直线的交点与点)0,1,2(的直线方程.解两直线0143=++y x 与02=+y x 的交点为)5,1,3(112143321--=x x x 于是点)5,1,3(--与点)0,1,2(的直线方程为05105012513321321=+-=--x x x x x x即05105321=+-x x x .4.2 点列和线束的交比定义4.2设D C B A ,,,为点列上共线的四点,则这四点的交比为ADBC BDAC CD AB ⋅⋅=),(.定理 4.1取A 和B 为基点,将D C B A ,,,四点的坐标依次表示为a ,b ,b a 1λ+,b a 2λ+,则四点的交比为21),(λλ=CD AB . 定理4.2若D C B A ,,,四点的坐标为)4,3,2,1(21=+i P P i λ,21,P P 点列上两个基点,则),(),(432124142313λλλλλλλλλλλλ=----=CD AB定理4.3将某两点互换,同时互换其余两点,则交比不变.即),(),(),(),(BA DC AB CD DC BA CD AB ===定理4.4只在一对点中互换,交比转为其倒数.即),(1),(CD AB DC AB =,),(1),(CD AB CD BA =定理4.5交换中间两点,则交比为1与原值的差,即),(1),(CD AB BD AC -= 定义4.3当1),(-=CD AB 时,称D C ,调和分割线段AB .调和分割的关系是对等的.因为1),(),(-==CD AB AB CD ,所以,B A ,也调和分割线段CD ,有时也称D C B A ,,,为调和点列.定义4.4称21λλ为四直线d c b a ,,,的交比,记为),(cd ab .即 =),(cd ab 21λλ.注意:用齐次坐标之间的关系定义交比,点列的交比与线束的交比在形式上完全一致.定理4.6设四直线d c b a ,,,,若b a c 1λ+=,b a d 2λ+=,则=),(cd ab 21λλ. 定理4.7若四直线q p a 1μ+=,q p b 2μ+=,q p c 3μ+=,q p d 4μ+=,则 424132314321),(),(μμμμμμμμμμμμ----==cd ab .这个比值也称为数4321,μμμμ的交比.定理4.8两个点列经过中心投影,交比不变.练习4-21. 设E D C B A ,,,,是同一直线上的五点,求证1),)(,)(,(=EC AB DE AB CD AB .证明由交比定义ADBC BDAC CD AB ⋅⋅=),(,1),)(,)(,(=⋅⋅⋅⋅⋅⋅⋅⋅=ACBE BCAE AE BD BE AD AD BC BD AC EC AB DE AB CD AB .2.设C B A ,,三点的坐标分别为)1,1,1(,)1,1,1(-,)1,0,1(,且2),(=CD AB ,求点D 的坐标.解)1,1,1(=A ,)1,1,1(-=B ,则C B A ==+)1,0,1(2121,于是12=λ.设B A D 1λ+=,由2),(21==λλCD AB 可知,21=λ,所以)3,1,3(2-=+=B A D .注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 3.求四点)1,1,2(-A ,)1,1,1(-B ,)0,0,1(C ,)5,5,1(-D 的交比),(CD AB .解利用定理 4.1,取A 和B 为基点,将D C B A ,,,四点的坐标依次表示为a ,b ,b a 1λ+,b a 2λ+,则四点的交比为21),(λλ=CD AB . 这里B AC +=,于是11=λ, B AD 32-=,于是232-=λ,由21),(λλ=CD AB 可知,32),(21-==λλCD AB . 注意:以B A ,为基点的点列中,任何一点X 都可以表示为B A X μλ+=,用齐次坐标可以表示为B A B A X λλμ'+=+=. 7.试证:02321=+-x x x ,023321=-+x x x ,0721=-x x ,0531=-x x 所表示的四直线共点,并求这四直线的交比.解直线0721=-x x 与0531=-x x 的交点为)5,7,1(15017321=--x x x 点)5,7,1(满足四直线,所以,此四直线共点. 四直线与x 轴的交点分别为211-=x ,322=x ,03=x ,514=x ,所以,21),(4321=l l l l .4.3 完全四点形和完全四线形完全四点形和完全四线形定义.定理4.6完全四点形通过每一个对角点有一组调和线束,即通过这个对角点的两边和对角三角形的两边.定理4.10完全四线形的每一条对角线上有一组调和点列,即这条直线上的两个顶点及对角三角形的两个顶点.练习4-32.设XYZ 是完全四点形ABCD 的对边三点形,XY 分别交BD AC ,于M L ,,不用笛沙格定理,证明CM BL YZ ,,共点.证明由四点形ABCD ,根据定理可知,在AC 边上的四点L Y C A ,,,调和共轭, 即1),(-=YL AC .在四点形YBZL 中,LB 与YZ 交于N ,MN 与YL 交于C ',由定理可得),(-='YL CA 所以,点C 应与点C '重合,即CM BL YZ ,,共点.4.4 一维基本图形的射影对应两个点列成射影对应的定义. 两个线束成射影对应的定义. 点列与线束成射影对应的定义.定理4.11 设两个一维基本图形成射影对应,则对应四元素的交比相等. 定理4.12 若两个一维基本图形对应四个元素的交比相等,则必成射影对应. 定理 4.13 如果已知两个一维图形的任意三对对应元素,那么可以确定唯一一个射影对应.练习4-45. 若三角形ABC 的三边AB 、BC 、C A 分别通过共线的三点P ,Q ,R ,二顶点B 与C 各在定直线上,求证顶点A 也在一条直线上.证明根据图形(见第4题图)可知,题图)(第2Λ),,,(21ΛB B B ),,,(21ΛC C C ,则Λ),,,(21ΛB B B P ),,,(21ΛC C C R在这两个射影线束中,PR是自对应元素,所 以Λ),,,(21ΛB B B P ),,,(21ΛC C C R两透视对应的线束对应直线的交点Λ,,,21A A A 共线. 4.5 透视对应定义4.8点列和线束成射影对应,如果对应直线过对应点,这种特殊的射影对应称为透视对应,这时也这两个一维图形处于透视状态.定义4.9两个点列和同一个线束成透视对应,也就是说两个点列成中心射影对应,则称这两个点列成透视对应.定义4.10两个线束和同一个点列成透视对应,则称这两个线束成透视对应. 定理4.14两个射影对应的点列成透视的充要条件是:两个点列的公共点自对应. 定理4.15两个射影对应的线束成透视的充要条件是:两个线束的公共点自对应. 定理4.16(巴卜斯定理)设C B A ,,是直线l 上互异的三点,C B A ''',,是l '上互异的三点,那么三个交点C B C B L '⨯'=,B A B A N '⨯'=,A C A C M '⨯'=共线.定理4.17对于两个不共底的且不成透视对应的射影对应点列,用两次透视对应,可把第一个点列变成第二个点列.也就是说,射影对应是两个透视对应的复合.定理4.18设一个点列与一个线束成射影对应而不成透视对应,那么用三次透视就可以彼此转换.即,这时的射影对应是三个透视对应的复合.题图)(第5A1.如图四边形ABCD 被EF 分成两个四边形AFED 和FBCE ,求证三个四边形ABCD ,AFED ,FBCE 的对角线交点H G K ,,共线.证明因为D ,E ,C 直线l 上互异的三点,A ,F ,B 是直线m 上互异 的三点,由定理4.16(巴卜斯定理),三个交点AE DF G⨯=,AC DB K ⨯=, FC EB H ⨯=共线.4.6 对合对应对合对应定义.定理4.19两个重叠的一维图形(点列、线束)q p μ+,q p μ'+成为对合对应的充分必要条件是:对应元素的参数μ和μ'满足0)(=+'++'d b a μμμμ其中02≠-b ad .定理4.20不重合的两对对应元素,确定唯一一个对合对应.1.求参数为21→,20→的两对对应元素所确定的对合对应. 解利用定理 4.19,这里两对对应元素的参数μ和μ'分别为21,1='=μμ和2,0='=μμ,设0)(=+'++'d b a μμμμ为所求的对合对应,把两对对应参数值代入得)题图(第1DAFBCEGKHlm⎪⎩⎪⎨⎧=+=++0202321d b d b a 解得2:1:1::-=d b a ,因此,这两对对应元素所确定的对合对应为02=-'++'μμμμ.。
