2018届高三数学下学期周练三文
专题12 利用导数解决函数的单调性-学会解题之高三数学万能解题模板【2022版】(原卷版)
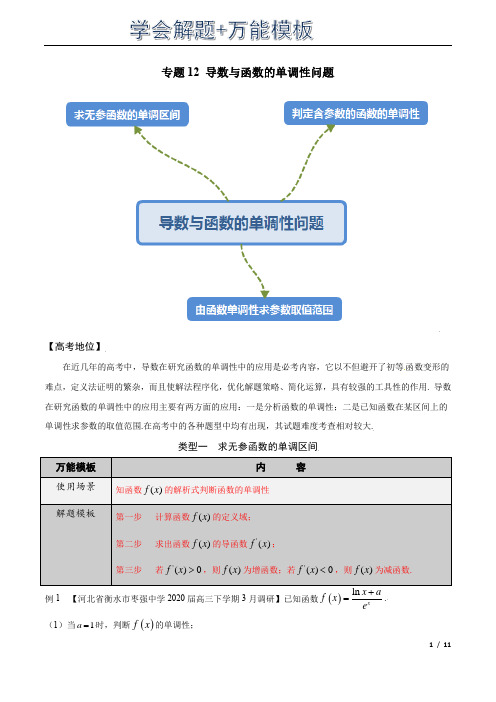
专题12 导数与函数的单调性问题【高考地位】在近几年的高考中,导数在研究函数的单调性中的应用是必考内容,它以不但避开了初等函数变形的难点,定义法证明的繁杂,而且使解法程序化,优化解题策略、简化运算,具有较强的工具性的作用. 导数在研究函数的单调性中的应用主要有两方面的应用:一是分析函数的单调性;二是已知函数在某区间上的单调性求参数的取值范围.在高考中的各种题型中均有出现,其试题难度考查相对较大.类型一 求无参函数的单调区间万能模板 内 容使用场景 知函数()f x 的解析式判断函数的单调性 解题模板第一步 计算函数()f x 的定义域; 第二步 求出函数()f x 的导函数'()f x ;第三步 若'()0f x >,则()f x 为增函数;若'()0f x <,则()f x 为减函数.例1 【河北省衡水市枣强中学2020届高三下学期3月调研】已知函数()ln xx af x e+=. (1)当1a =时,判断()f x 的单调性;【变式演练1】函数,的单调递增区间为__________.【来源】福建省三明第一中学2021届高三5月校模拟考数学试题【变式演练2】已知函数,则不等式的解集为___________.【来源】全国卷地区“超级全能生”2021届高三5月联考数学(文)试题(丙卷)【变式演练3】【黑龙江省哈尔滨六中2020届高三高考数学(文科)二模】已知函数()2sin f x x x =-+,若3(3)a f =,(2)b f =--,2(log 7)c f =,则,,a b c 的大小关系为( ) A .a b c <<B .b c a <<C .c a b <<D .a c b <<【变式演练4】【湖南省湘潭市2020届高三下学期第四次模拟考试】定义在R 上的连续函数()f x ,导函数为()f x '.若对任意不等于1-的实数x ,均有()()()10x f x f x '+->⎡⎤⎣⎦成立,且()()211x f x f x e -+=--,则下列命题中一定成立的是( )A .()()10f f ->B .()()21ef f -<-C .()()220e f f -<D .()()220e f f ->类型二 判定含参数的函数的单调性万能模板 内 容使用场景 函数()f x 的解析式中含有参数解题模板第一步 计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ;第二步 讨论参数的取值范围,何时使得导函数'()f x 按照给定的区间大于0或小于0; 第三步 根据导函数的符号变换判断其单调区间.例2 【黑龙江省大庆市第四中学2020届高三下学期第四次检测】已知函数()()2ln 21f x x x ax a R =+-+∈.(1)讨论()f x 的单调性;【变式演练5】(主导函数是一次型函数)【福建省三明市2020届高三(6月份)高考数学(文科)模拟】已知函数()=1,f x nx ax a R -∈.(1)讨论函数f x ()的单调性;()2sin sin 2f x x x =⋅0,2x π⎡⎤∈⎢⎥⎣⎦()()2ln 1x xf x x e e -=+++()()2210f x f x --+≤【变式演练6】(主导函数为类一次型)【山东省威海荣成市2020届高三上学期期中考试】已知函数()x f x e ax -=+.(I )讨论()f x 的单调性;【变式演练7】(主导函数为二次型)【2020届山西省高三高考考前适应性测试(二)】已知函数()2ln af x x a x x=--,0a ≥. (1)讨论()f x 的单调性;【变式演练8】(主导函数是类二次型)【山西省太原五中2020届高三高考数学(理科)二模】已知函数2()(1)x f x k x e x =--,其中k ∈R.(1)当k 2≤时,求函数()f x 的单调区间;【变式演练9】已知函数,若在区间上单调递增,则的取值范围是( )A .B .C .D .【来源】江西省南昌市新建区第一中学2020-2021学年高三上学期期末考试数学(文)试题类型三 由函数单调性求参数取值范围万能模板 内 容使用场景 由函数单调性求参数取值范围解题模板第一步 计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ; 第二步 根据题意转化为相应的恒成立问题; 第三步 得出结论.例3.【江苏省南通市2019-2020学年高三下学期期末】若()()21ln 242f x x b x =-++在()2,-+∞上是减函数,则实数b 的范围是( ) A .(],1-∞-B .(],0-∞C .(]1,0-D .[)1,-+∞【变式演练11】(转化为任意型恒成立)【四川省绵阳市2020高三高考数学(文科)三诊】函数2()(2)x f x e x ax b =-++在(1,1)-上单调递增,则2816a b ++的最小值为( )A .4B .16C .20D .18()22ln f x x x =-()f x ()2,1m m +m 1,14⎡⎫⎪⎢⎣⎭1,4⎡⎫+∞⎪⎢⎣⎭1,12⎡⎫⎪⎢⎣⎭[)0,1【变式演练12】(转化为变号零点)【山西省运城市2019-2020学年高三期末】已知函数2()ln 1f x x a x =-+在(1,2)内不是单调函数,则实数a 的取值范围是( ) A .[)2,8B .[]2,8C .(][),28,-∞+∞ D .()2,8【变式演练13】(直接给给定单调区间)【辽宁省六校协作体2019-2020学年高三下学期期中考试】已知函数()32113f x x mx nx =+++的单调递减区间是()3,1-,则m n +的值为( ) A .-4B .-2C .2D .4【变式演练14】(转化为存在型恒成立)【四川省仁寿第一中学北校区2019-2020学年高三月考】若f (x )321132x x =-++2ax 在(1,+∞)上存在单调递增区间,则a 的取值范围是( )A .(﹣∞,0]B .(﹣∞,0)C .[0,+∞)D .(0,+∞)【高考再现】1.(2021·全国高考真题(理))设2ln1.01a =,ln1.02b =, 1.041c =-.则( ) A .a b c <<B .b c a <<C .b a c <<D .c a b <<2.(2021·全国高考真题(理))已知且,函数.(1)当时,求的单调区间;(2)若曲线与直线有且仅有两个交点,求a 的取值范围. 3.已知函数. (1)讨论的单调性;(2)设,为两个不相等的正数,且,证明:. 【来源】2021年全国新高考Ⅰ卷数学试题 4.【2017山东文,10】若函数()e xf x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是A . ()2xf x -= B. ()2f x x = C. ()3xf x -= D. ()cos f x x =5.【2017江苏,11】已知函数31()2e ex x f x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,0a >1a ≠()(0)a x x f x x a=>2a =()f x ()y f x =1y =()()1ln f x x x =-()f x a b ln ln b a a b a b -=-112e a b<+<则实数a 的取值范围是 ▲ .6.【2020年高考全国Ⅰ卷文数20】已知函数()()e 2xf x a x =-+.(1)当1a =时,讨论()f x 的单调性; (2)若()f x 有两个零点,求a 的取值范围.7.【2020年高考全国Ⅰ卷理数21】已知函数()2e xf x ax x =+-.(1)当1a =时,讨论()f x 的单调性; (2)当0x ≥时,()3112f x x ≥+,求a 的取值范围. 8.【2020年高考全国Ⅱ卷文数21】已知函数()2ln 1f x x =+. (1)若()2f x x c ≤+,求c 的取值范围; (2)设0a >,讨论函数()()()f x f a g x x a-=-的单调性.9.(2018年新课标I 卷文)已知函数f (x )=ae x −lnx −1∈ (1)设x =2是f (x )的极值点.求a ,并求f (x )的单调区间; (2)证明:当a ≥1e 时,f (x )≥0∈10.【2018年全国普通高等学校招生统一考试理科数学(新课标I 卷)】已知函数f(x)=1x −x +alnx ∈ (1)讨论f(x)的单调性;(2)若f(x)存在两个极值点x 1,x 2,证明:f (x 1)−f (x 2)x 1−x 2<a −2.【反馈练习】1.【2020届广东省梅州市高三总复习质检(5月)】已知0x >,a x =,22xb x =-,()ln 1c x =+,则( )A .c b a <<B .b a c <<C .c a b <<D .b c a <<2.【2020届山东省威海市高三下学期质量检测】若函数()()()1cos 23sin cos 212f x x a x x a x =+++-在0,2π⎡⎤⎢⎥⎣⎦上单调递减,则实数a 的取值范围为( )A .11,5⎡⎤-⎢⎥⎣⎦B .1,15⎡⎤-⎢⎥⎣⎦C .[)1,1,5⎛⎤-∞-⋃+∞ ⎥⎝⎦D .(]1,1,5⎡⎫-∞-⋃+∞⎪⎢⎣⎭3.【河南省十所名校2019—2020学年高三毕业班阶段性测试】若函数()sin24sin f x x x m x =--在[0,2π]上单调递减,则实数m 的取值范围为( ) A .(2,2)-B .[2,2]-C .(1,1)-D .[1,1]-4.【黑龙江哈尔滨市第九中学2019-2020学年高三阶段验收】函数()3f x x ax =+,若对任意两个不等的实数()1212,x x x x >,都有()()121233f x f x x x ->-恒成立,则实数a 的取值范围是( ) A .()2,-+∞B .[)3,+∞C .(],2-∞-D .(),3-∞5.【湖北省武汉市新高考五校联合体2019-2020学年高三期中检测】若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间,则实数a 的取值范围是_______. 6.【四川省宜宾市2020届高三调研】若对(]0,1t ∀∈,函数2()(4)2ln g x x a x a x =-++在(,2)t 内总不是单调函数,则实数a 的取值范围是______7.【河南省南阳市第一中学校2019-2020学年高三月考】若函数()22ln f x x x =-在定义域内的一个子区间()1,1k k -+上不是单调函数,则实数k 的取值范围______.8.若函数在区间是增函数,则的取值范围是_________.【来源】陕西省宝鸡市眉县2021届高三下学期高考模拟文科数学试题 9.已知函数,若对任意两个不同的,,都有成立,则实数的取值范围是________________【来源】江西省景德镇市2021届高三上学期期末数学(理)试题10.【黑龙江省哈尔滨师范大学附属中学2020-2021学年高三上学期开学考试】(1)求函数()sin cos (02)f x x x x x π=+<<的单调递增区间;()cos 2sin f x x a x =+,62ππ⎛⎫⎪⎝⎭a ()()1ln 1xf x x x+=>1x 2x ()()1212ln ln f x f x k x x -≤-k(2)已知函数2()ln 43f x a x x x =-++在1,22⎡⎤⎢⎥⎣⎦上单调递增,求实数a 的范围.11.【黑龙江省哈尔滨三中2020届高三高考数学(文科)三模】函数()()21ln 1x f x x x -=-+. (1)求证:函数()f x 在()0,∞+上单调递增; (2)若m ,n 为两个不等的正数,求证ln ln 2m n m n m n->-+. 12.【湖北省黄冈中学2020届高三下学期适应性考试】已知函数()()ln 1ln f x ax x a x =-+,()f x 的导数为()f x '.(1)当1a >-时,讨论()f x '的单调性; (2)设0a >,方程()3f x x e =-有两个不同的零点()1212,x x x x <,求证121x e x e+>+. 13.【湖南省永州市宁远、道县、东安、江华、蓝山、新田2020届高三下学期六月联考】已知函数()()()ln 12f x a x x a =+-∈R .(1)讨论()f x 的单调性;(2)当0x ≥时,()1xf x e ≥-,求实数a 的取值范围.14.【2020届山西省高三高考考前适应性测试(二)】已知函数()xf x ae ex =-,()()ln 1xg x x b x e =--,其中,a b ∈R .(1)讨论()f x 在区间()0,∞+上的单调性; (2)当1a =时,()()0f x g x ≤,求b 的值.15.【河南省2020届高三(6月份)高考数学(文科)质检】已知函数2()22ln ()f x x ax x a R =-+∈.(1)讨论函数()f x 的单调性;(2)若()f x 存在两个极值点()1221,x x x x >,求证:()()()2121(2)f x f x a x x -<--. 16.【山东省2020年普通高等学校招生统一考试数学必刷卷】已知实数0a >,函数()22ln f x a x a x x=++,()0,10x ∈.(1)讨论函数()f x 的单调性;(2)若1x =是函数()f x 的极值点,曲线()y f x =在点()()11,P x f x ,()()22,Q x f x ()12xx <处的切线分别为12,l l ,且12,l l 在y 轴上的截距分别为12,b b .若12//l l ,求12b b -的取值范围.17.【福建省2020届高三(6月份)高考数学(理科)模拟】已知函数()()()2ln 222f x x a x x =++++,0a >.(1)讨论函数()f x 的单调性; (2)求证:函数()f x 有唯一的零点.18.【山东省潍坊市五县2020届高三高考热身训练考前押题】已知函数()f x 满足222(1)()2(0)2x f f x x f x e -'=+-,21()(1)24x g x f x a x a ⎛⎫=-+-+ ⎪⎝⎭,x ∈R . (1)求函数()f x 的解析式; (2)求函数()g x 的单调区间;(3)当2a ≥且1≥x 时,求证:1ln ln x e x e a x x--<+-.19.【陕西省商洛市商丹高新学校2020届高三下学期考前适应性训练】已知函数3()ln ()f x x a x a R =-∈.∈1)讨论函数()f x 的单调性∈∈2)若函数()y f x =在区间(1,]e 上存在两个不同零点∈求实数a 的取值范围.20.【2020年普通高等学校招生全国统一考试伯乐马模拟考试】已知函数()()22xxf x ax a e e =-++.(1)讨论函数()f x 的单调性; (2)若函数()()()2212x x g x f x ax x a e e =-++-存在3个零点,求实数a 的取值范围. 21.【金科大联考2020届高三5月质量检测】已知函数()()()()()22224ln 2144f x x ax x a x a a x a =--+++∈R .(∈)讨论函数()f x 的单调性;(∈)若0a ≤,证明:函数()f x 在区间)1,a e -⎡+∞⎣有且仅有一个零点.22.已知函数.(1)若,求函数的单调区间; (2)求证:对任意的,只有一个零点.【来源】全国Ⅱ卷2021届高三高考数学(理)仿真模拟试题 23.已知函数. (1)当时,判断的单调性;(2)若有两个极值点,求实数的取值范围.【来源】安徽省合肥六中2021届高三6月份高考数学(文)模拟试题 24.已知函数. (1)求的单调性;(2)设函数,讨论的零点个数. 【来源】重庆市高考康德卷2021届高三模拟调研卷数学试题(三) 25.已知函数, (1)讨论的单调性;(2)若,,,用表示,的最小值,记函数,,讨论函数的零点个数.【来源】山东省泰安肥城市2021届高三高考适应性训练数学试题(二) 26.已知() (1)讨论的单调性;(2)当时,若在上恒成立,证明:的最小值为. 【来源】贵州省瓮安中学高三2021届6月关门考试数学(理)试题27.已知函数.(1)讨论的单调性;()321()13f x x a x x =--+2a =-()f x a ∈R ()f x ()21ln 2f x x ax x ax =-+1a =()f x ()f x a ()()cos sin ,0,2f x x x x x π=-∈()f x ()()(01)g x f x ax a =-<<()g x ()ln()xf x x a x a=+-+a R ∈()f x 4a =()1cos (2sin )2g x x x mx x =++0m >}{min ,m n m n }{()min ()()h x f x g x =,[],x ππ∈-()h x ()ln f x x ax =+a R ∈()f x 1a =()()1f x k x b ≤++()0,∞+221k b k +--1e -+2()2ln ,()f x x ax x a R =+++∈()f x(2)若恒成立,求的最大值.【来源】广东省佛山市五校联盟2021届高三5月数学模拟考试试题 28.已知函数. (1)若,证明:在单调递增; (2)若恒成立,求实数的取值范围.【来源】黑龙江省哈尔滨市第三中学2021届高三五模数学(理)试题 29.已知函数. (1)若在上为增函数,求实数a 的取值范围;(2)设,若存在两条相互垂直的切线,求函数在区间上的最小值.【来源】四川省达州市2021 届高三二模数学(文)试题 30.已知函数. (1)如果函数在上单调递减,求的取值范围; (2)当时,讨论函数零点的个数.【来源】内蒙古赤峰市2021届高三模拟考试数学(文)试题 31.已知函数. (1)若在R 上是减函数,求m 的取值范围;(2)如果有一个极小值点和一个极大值点,求证 有三个零点. 【来源】安徽省淮南市2021届高三下学期一模理科数学试题32.已知函数.(1)若函数在上为增函数,求实数的取值范围; (2)当时,证明:函数有且仅有3个零点. 【来源】重庆市第二十九中学校2021届高三下学期开学测试数学试题()xf x e ≤a ()ln x f x xe ax a x =--0a ≤()f x ()0,∞+()0f x ≥a 21()cos 2f x x ax x =++()f x [0,)+∞21()()2g x f x x =-()g x sin ()1()x g x F x x -+=,2ππ⎡⎤⎢⎥⎣⎦1()ln(1)1f x a x x =-+-()()22g x f x x =-+(1,)+∞a 0a >()y f x =21()e 1()2x f x x mx m =+-+∈R ()f x ()f x 1x 2x ()f x ()e sin 1xf x ax x =-+-()f x ()0,∞+a 12a ≤<()()()2g x x f x =-11/ 11。
江西省南昌市第二中学2018届高三下学期周考数学文试题

南昌二中2018届高三二轮复习周考(二)数学(文)试卷第Ⅰ卷(选择题共60分)一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知R n m ∈,,集合{}m A 7log ,2=,集合{}n m B ,=,若{}1=B A ,则n m +=( ) A .1B .2C .4D .82.已知a 是实数,i 1i a +-是实数,则7cos 3a π的值为( )A.12B. 21- C.0D.23.在矩形ABCD 中,2,4==AD AB ,若向该矩形内随机投一点P ,那么使得ABP ∆与ADP ∆的面积都不小于2的概率为( ) A .81 B. 41 C. 21 D. 43 4.下列语句中正确的个数是( )①R ∈∀ϕ,函数)2sin()(f ϕ+=x x 都不是偶函数 ②命题“若y x = 则y x sin sin =”的否命题是真命题 ③若p 或q 为真 则p ,非q 均为真④“⋅0>”的充分不必要条件是“与夹角为锐角” A. 0 B .1 C .2 D .35.阅读如下程序框图,如果输出5=i ,那么空白的判断框中应填入的条件是( )A .8<sB .8≤sC .9<sD .9≤s 6.一个空间几何体的三视图及尺寸如图所示,则该几何体的体积是( )A .323+πB .33+πC .32+πD .332+π7.已知实数y x ,满足:⎪⎩⎪⎨⎧≤-≤+≥-62602y x y x x , 则12x --=y Z 的最大值( )A .8B .7C .6D .5 8.将函数ϕπϕsin )22cos(cos )sin 21()(2++-=x x x f 的图象向右平移3π个单位后,所得图象关于y 轴对称,则ϕ的取值可能为( ) A . 3π-B .6π-C .3π D .65π 9.函数xx x y --=333的图像大致是( )10.已知定义在R 上的函数)(x f 是奇函数,且满足)()23(x f x f =-,2)2(-=-f ,数列{}n a 满足11-=a ,且12+=nan S n n ({}n a S n 为的前项和n ),则=)(5a f ( ) A .3- B .2- C .3 D .211.在正方体1111D C B A ABCD -中边长为2,点P 是上底面1111D C B A 内一动点,若三棱锥ABC P -的外接球表面积恰为441π,则此时点P 构成的图形面积为( ) A .π B .π1625 C .π1641D .π2 12.若函数)(x f y =,M x ∈对于给定的非零实数a ,总存在非零常数T ,使得定义域M 内的任意实数x ,都有)()(T x f x af +=恒成立,此时T 为)(x f 的假周期,函数)(x f y =是M上的a 级假周期函数,若函数)(x f y =是定义在区间[)∞+,0内的3级假周期且2=T ,当,)2,0[∈x⎪⎩⎪⎨⎧<<-≤≤-=)21)(2()10(221)(f 2x x f x x x 函数m x x x x g +++-=221ln 2)(,若[]8,61∈∃x ,)0(2∞+∈∃,x 使0)()(12≤-x f x g 成立,则实数m 的取值范围是( )A .]213,(-∞ B .]12,(-∞ C .]39,(-∞ D .),12[+∞ 第II 卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量()()R a ∈+-=ααα3sin ,1cos ,()1,4=b的最小值为 . 14.曲线2x y =在点()1,1P 处的切线与直线l 平行且距离为5,则直线l 的方程为 . 15.在△ABC||53cos ||AB A CA B =-则)tan(B A -的最大值为 . 16.已知椭圆15922=+y x 的右焦点为F ,P 是椭圆上一点,点)32,0(A ,当点P 在椭圆上运动时,APF ∆的周长的最大值为.____________三、解答题:共70分。
2022届陕西省西安中学高三下学期三模数学(文)试题(解析版)

2022届陕西省西安中学高三下学期三模数学(文)试题一、单选题1.命题“,sin 10x R x ∀∈+≥”的否定是( ) A .00,sin 10x R x ∃∈+< B .,sin 10x R x ∀∈+< C .00,sin 10x R x ∃∈+≥ D .,sin 10x R x ∀∈+≤【答案】A【分析】利用全称命题的否定方法求解,改变量词,否定结论. 【详解】因为,sin 10x R x ∀∈+≥的否定为00,sin 10x R x ∃∈+<, 所以选A.【点睛】本题主要考查含有量词的命题的否定,一般处理策略是:先改变量词,然后否定结论.2.已知集合{}12{|20}A B x ax =-=+=,,,若A B A ⋃=,则实数a 的取值所组成的集合是( )A .{}12-, B .{}11-,C .{2-,0,1}D .{1-,0,2}【答案】D【分析】A B A ⋃=等价于B A ⊆,分0a =、0a ≠两种情况讨论,从而可得答案. 【详解】A B A B A ⋃=∴⊆,.当0a =时,B 为空集,满足条件.当0a ≠时,20a -+=或220a +=,解得2a =或1a =-. 综上可得,实数a 的取值所组成的集合是{0,2,1}-. 故选:D.【点睛】本题主要考查集合的表示方法,空集的定义,以及并集与子集的定义,属于基础题.3.若a ,b 都是实数,则0”是“220a b ->”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件【答案】A【分析】根据充分条件和必要条件的定义判断即可得正确选项.【详解】0>0a b >≥,所以22a b >,可得220a b ->, 故充分性成立,取2a =-,1b =-,满足220a b ->,但a ,b 无意义得不出0a b ->, 故必要性不成立,所以0a b ->是220a b ->的充分不必要条件, 故选:A.4.2022年举办北京冬奥会促进我国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.下面是2015年至2021年中国雪场滑雪人次(万人次)与同比增长率的统计图,则下面结论中不正确的是( )A .2015年至2021年,中国雪场滑雪人次逐年增加B .2016年至2018年,中国雪场滑雪人次和同比增长率均逐年增加C .2021年与2016年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等D .2021年与2019年相比,中国雪场滑雪人次增长率约为30.5% 【答案】C【分析】根据统计图,结合数据逐一判断即可.【详解】A :由统计图可知中:2015年至2021年,中国雪场滑雪人次逐年增加,所以本选项结论正确;B :由统计图可知:2016年至2018年,中国雪场滑雪人次和同比增长率均逐年增加,所以本选项结论正确;C :2021年与2016年相比,中国雪场滑雪人次的同比增长率近似相等,2021年同比增长人数为:19701750220-=,2016年同比增长人数为:900800100-=,显然不相等,所以本选项结论不正确;D :2021年与2019年相比,中国雪场滑雪人次增长率为1970151030.5%1510-≈,所以本选项结论正确,故选:C5.已知函数()sin 2f x x π⎛⎫=- ⎪⎝⎭,则()f x 是( )A .周期为π的奇函数B .周期为π的偶函数C .周期为2π的奇函数D .周期为2π的偶函数【答案】D【分析】利用诱导公式将函数()y f x =的解析式化简,即可求出该函数的周期,并判断出该函数的奇偶性. 【详解】()sin cos 2f x x x π⎛⎫=-= ⎪⎝⎭,因此,函数()y f x =是周期为2π的偶函数.故选:D.【点睛】本题考查三角函数周期和奇偶性的判断,解题的关键就是利用诱导公式将三角函数解析式化简,考查计算能力,属于基础题. 6.已知F 是抛物线21:2C x y =的焦点,点(,)P m n 在抛物线C 上,且1m =,则||PF =( ) A .178B .32C .98D .52【答案】A【分析】代入已知点得到相应的参数值,根据抛物线的焦半径公式得到117||88PF n =+=.【详解】由212x y =,得14p =,由1m =得2n =,由抛物线的性质,117||88PF n =+=,故选:A.7.数列{}n a ,{}n b 满足1n n a b =,256n a n n =++,*N n ∈,则{}n b 的前10项之和为( ) A .413B .513C .839D .1039【答案】D【解析】求出{}n b 的通项,利用裂项相消法可求前10项之和.【详解】因为1n n a b =,256n a n n =++,故21115623n b n n n n ==-++++,故{}n b 的前10项之和为11111111103445121331339-+-++-=-=, 故选:D.8.天气预报显示,在今后的三天中,每一天下雨的概率为40%,现用随机模拟的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0--9之间整数值的随机数,并制定用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 则这三天中恰有两天下雨的概率近似为( ) A .23B .14C .415 D .15【答案】B【详解】解:阅读随机数表可知,满足题意的数据为:191,271,932,812,393 , 据此可知:这三天中恰有两天下雨的概率近似为51204p == . 本题选择B 选项.9.在等比数列{}n a 中,7a ,11a 是方程2520x x ++=的二根,则3915513a a a a a ⋅⋅⋅的值为( )A .2+22-B .2-C .2D .2-或2【答案】B【分析】利用等比数列的性质、韦达定理列方程组求解.【详解】解:在等比数列{}n a 中,7a ,11a 是方程2520x x ++=的二根,则71171152a a a a +=-⎧⎨=⎩,∴92a =-,则3391599251392a a a a a a a a ⋅⋅===-⋅. 故选:B .10.如图,已知四棱柱1111ABCD A B C D -的底面为平行四边形,E ,F ,G 分别为棱1111,,AA CC C D 的中点,则下列各选项正确的是( )A .直线1BC 与平面EFG 平行,直线1BD 与平面EFG 相交B .直线1BC 与平面EFG 相交,直线1BD 与平面EFG 平行 C .直线1BC 、1BD 都与平面EFG 平行 D .直线1BC 、1BD 都与平面EFG 相交 【答案】A【分析】取AB 的中点H ,证明1BC HG ∥,1BC ∥平面EFG 即得证,再证明直线1BD 与平面EFG 相交即得解.【详解】解:取AB 的中点H ,则11//,=,BH C G BH C G 从而四边形1BC GH 为平行四边形, 所以1BC HG ∥.易知////EH GF EH GF ,,则四边形EGFH 为平行四边形, 从而GH ⊂平面EFG .又1BC ⊄平面EFG ,所以1BC ∥平面EFG .易知11//=BF ED BF ED ,,则四边形1BFD E 为平行四边形,从而1BD 与EF 相交, 所以直线1BD 与平面EFG 相交. 故选:A .11.我们把由半椭圆()222210x y x a b +=≥与半椭圆()222210y x x b c+=<合成的曲线称作“果圆”(其中222a b c =+,0a b c >>>).如图所示,设点0F 、1F 、2F 是相应椭圆的焦点,1A 、2A 和1B 、2B 是“果圆”与x 轴和y 轴的交点,若012F F F ∆是边长为1的等边三角形,则a ,b 的值分别为( )A 71 B 3 1 C .5,3 D .5,4【答案】A【详解】由题意知,222334a b -==⎝⎭,2221124b c ⎛⎫== ⎪⎝⎭-, ∴221a c =-. 又222a b c =+, ∴21b =,1b =. ∴274a =,7a .故选:A.12.已知函数()f x 是定义在R 上的奇函数,当[]0,1x ∈时,()sin f x x π=,且满足当1x >时,()()22f x f x =-,若对任意[],x m m ∈-,()23f x ≤则m 的最大值为( ) A .236B .103C .256D .133【答案】B【解析】由函数的奇偶性和题设条件,求得()[]si 1,1n ,f x x x π∈-=,再根据()()22f x f x =-,画出函数图象,结合图象,即可求解.【详解】由题意,函数()f x 是定义在R 上的奇函数,当[]0,1x ∈时,()sin f x x π=, 当[1,0)x ∈-时,()()sin()sin f x f x x x ππ=--=--=,即()[]si 1,1n ,f x x x π∈-=,又由当1x >时,()()22f x f x =-,可画出函数图象,如图所示.由图知,当35x ≤≤时,()()()444sin 44sin f x f x x x πππ=-=-=; 则当53x -≤≤-时,()()4sin f x f x x π=--=;当53x -≤≤-时,令4sin 23x π=,解得121011,33x x =-=-(舍去), 若对任意[],x m m ∈-,()23f x ≤成立,所以m 的最大值为103. 故选:B.二、填空题13.已知向量()()3,1,1,0,a b c a kb ===+.若a c ⊥,则k =________. 【答案】103-. 【分析】利用向量的坐标运算法则求得向量c 的坐标,利用向量的数量积为零求得k 的值【详解】()()()3,1,1,0,3,1a b c a kb k ==∴=+=+,(),33110a c a c k ⊥∴⋅=++⨯=,解得103k =-, 故答案为:103-. 【点睛】本题考查平面向量的坐标运算,平面向量垂直的条件,属基础题,利用平面向量()()1122,,,p x y q x y ==垂直的充分必要条件是其数量积12120x x y y +=. 14.已知1sin24α=,且233ππα<<,则cos sin αα-=___.【答案】3【分析】根据同角的三角函数关系式,结合二倍角的正弦公式进行求解即可 【详解】因为233ππα<<,所以sin cos αα>, 因此有:222cos sin (cos sin )cos sin 2cos sin 1sin 2ααααααααα-=---+-=--把1sin24α=代入,得13cos sin 14αα-=--, 故答案为:315.在棱长为2的正方体1111ABCD A B C D -中,点E 、F 分别是棱BC ,1CC 的中点,P 是侧面四边形11BCC B 内(不含边界)一点,若1//A P 平面AEF ,则线段1A P 长度的取值范围是_______.【答案】325⎢⎣ 【分析】分别取棱111,BB B C 的中点,M N ,连接MN ,则可证得平面1A MN ∥平面AEF ,由题意可得点P 必在线段MN 上,由此可判断点P 在M 或N 处时,1A P 最长,位于线段MN 的中点时最短,通过解直角三角形即可求得结果【详解】如下图所示,分别取棱111,BB B C 的中点,M N ,连接MN ,1BC , 因为,,,M N E F 为分别为111,BB B C ,BC ,1CC 的中点, 所以MN ∥1BC ,EF ∥1BC , 所以MN ∥EF ,因为MN ⊄平面AEF ,EF ⊂平面AEF , 所以MN ∥平面AEF ,因为1AA ∥NE ,1AA NE =,所以四边形1AA NE 为平行四边形, 所以1A N ∥AE ,因为1A N ⊄平面AEF ,AE ⊂平面AEF , 所以1A N ∥平面AEF , 因为1A NMN N =,所以平面1A MN ∥平面AEF ,因为P 是侧面四边形11BCC B 内一点,且1//A P 平面AEF , 所以点P 必在线段MN 上,在11R t A B M 中,221111415A M A B B M =+=+=, 同理在11R t A B N 中,求得15A N =, 所以1A MN 为等腰三角形,当点P 在MN 的中点O 时,1A P MN ⊥,此时1A P 最短,点P 在M 或N 处时,1A P 最长,因为()222211232522AO A M OM ⎛⎫=-=-= ⎪ ⎪⎝⎭, 115AM A N ==, 因为P 是侧面四边形11BCC B 内(不含边界)一点, 所以线段1A P 长度的取值范围是32,52⎡⎫⎪⎢⎪⎢⎣⎭, 故答案为:32,52⎡⎫⎪⎢⎪⎢⎣⎭【点睛】关键点点睛:此题考查面面平行,线面平行的判断,考查立体几何中的动点问题,解题的关键是通过证明面面平行,找出点P 必在线段MN 上,从而可求出1A P 的最大值和最小值,考查空间想象能力和计算能力,属于较难题16.若函数()ln f x x a =+与函数()22(0)g x x x x =+<的图象有公切线,则实数a 的取值范围是________. 【答案】()ln21-∞+,【分析】设出两个切点,分别表示出切线,利用两切线方程对应系数相等,解出a ,构造新函数()h t ,求导确定()h t 的值域,即是a 的取值范围.【详解】设公切线与函数()ln f x x a =+切于()11,ln x x a +,与函数()22(0)g x x x x =+<切与()2222,2x x x +,则公切线斜率12211()()22k f x g x x x ''====+,故切线方程为()1111ln ()y x a x x x -+=-,即1111ln y x x a x =-++,也可以表示为()()22222222()y x x x x x -+=+-,即()22222y x x x =+-,可得21212122ln 1x x x a x ⎧=+⎪⎨⎪+-=-⎩,2211111111ln 11ln 2124a x x x x ⎛⎫⎛⎫∴=---+=--+ ⎪ ⎪⎝⎭⎝⎭,()212110,220,2x x x x <<∴=+∈,令11t x =,则()0,2t ∈,21ln 4a t t t =-+,令()21ln 4h t t t t =-+,则()()2213112210222t t t h t t t t t --+-++'=-+==>,则()h t 在()0,2上单调递增,当0t →时,()h t =-∞,2t =时,(2)ln 21h =+,故(,ln 21)a ∈-∞+. 故答案为:()ln21-∞+,.【点睛】本题关键点在于利用两个函数的切线相同建立关系,解出关于a 的关系式,换元后构造函数进行求解,对于公切线问题是通法,注意积累掌握. 三、解答题17.在ABC 中,角A ,B ,C 所对的边分别是a ,b ,c,且sin 2sin c B C =. (1)若cos23cos 2sin 0A A B +-=,求角A 的大小; (2)若a =2b =,求ABC 的面积. 【答案】(1)3π;(2【解析】(1)先利用正弦定理求出cos B =6B π=,载代入已知条件可得1cos 2A =,即可求解; (2)由(1)知6B π=,结合已知条件由余弦定理可得c 的值,再利用三角形的面积公式即可求解.【详解】(1)在ABC中,因为sin 2sin c B C =,由正弦定理可得:sin 2sin cos sin sin C B B B C ⋅=,因为(),0B C π∈,,sin 0B ≠,sin 0C ≠ 可得3cos 2B =,又0B π∈(,),所以6B π=,由cos23cos 2sin 0A A B +-=,可得22cos 3cos 20A A +-=,即(2cos 1)(cos 2)0A A -+=, 解得:1cos 2A =或cos 2A =-, 又0cos 1A A π∈<<(,),-1,得1cos 2A =,所以.3A π=(2)由(1)知,6B π=,又23a =,2b =,根据余弦定理得,2222cos b a c ac B =+-, 可得234122232c c =+-⨯⨯⨯, 即2680c c -+=,解得:12c =,24c =, 当12c =时,111sin 2323222ABCS ac B ==⨯⨯⨯=; 当24c =时,111sin 23423222ABCSac B ==⨯⨯⨯=; 所以ABC 的面积为3或23.18.某市从2019年参加高三学业水平考试的学生中随机抽取80名学生,将其数学成绩(均为整数)分成六组[)[)90,100100,110,,…,[]140,150后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[)120130,内的频数; (2)若在同一组数据中,将该组区间的中点值(如:组区间[)100,110的中点值为1001101052+=),作为这组数据的平均分,据此,估计本次考试的平均分; (3)用分层抽样的方法在分数段为[)110,130的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至少有1人在分数段[)120130,内的概率. 【答案】(1)24;(2)121;(3)1415. 【分析】(1)根据频率和为1得分数在[)120130,内的频率,进而即可对于的频数; (2)利用频率分布直方图求解平均数即可;(3)结合已知数据,由分层抽样得[)110,120分数段内抽取2人,[)120130,分数段内抽取4人,再根据古典概型公式并结合对立事件的概率计算求解即可.【详解】解: ()1分数在[)120130,内的频率为 ()10.10.150.150.250.0510.70.3-++++=-=故频数为800.324⨯=()2估计平均分为950.11050.151150.151250.31350.251450.05121x =⨯+⨯+⨯+⨯+⨯+⨯=()3由题意,[)110,120分数段的人数为800.1512⨯=(人).[)120130,分数段的人数为800.324⨯=(人). 用分层抽样的方法在分数段为[)110,130的学生中抽取一个容量为6的样本, 所以需在[)110,120分数段内抽取2人,分别记为12,A A ﹔在[)120130,分数段内抽取4人,分别记为1234,,,B B B B ; 设“从样本中任取2人,至少有1人在分数段[)120130,内”为事件A , 则样本空间{}121112131421222324121314232434,,,,,,,,,,,,,,A A A B A B A B A B A B A B A B A B B B B B B B B B B B B B Ω=共包含15个样本点事件A :“从样本中任取2人,2人都不在在分数段[)120130,内” {}12A A A =,只有1个样本点, 所以()115p A =()()114111515p A p A =-=-= 19.如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB DA ⊥. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.【答案】(1)见解析. (2)1.【详解】分析:(1)首先根据题的条件,可以得到BAC ∠=90,即BA AC ⊥,再结合已知条件BA ⊥AD ,利用线面垂直的判定定理证得AB ⊥平面ACD ,又因为AB ⊂平面ABC ,根据面面垂直的判定定理,证得平面ACD ⊥平面ABC ;(2)根据已知条件,求得相关的线段的长度,根据第一问的相关垂直的条件,求得三棱锥的高,之后借助于三棱锥的体积公式求得三棱锥的体积. 详解:(1)由已知可得,BAC ∠=90°,BA AC ⊥. 又BA ⊥AD ,且AC AD A =,所以AB ⊥平面ACD .又AB ⊂平面ABC , 所以平面ACD ⊥平面ABC .(2)由已知可得,DC =CM =AB =3,DA =32 又23BP DQ DA ==,所以22BP =作QE ⊥AC ,垂足为E ,则QE =13DC . 由已知及(1)可得DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE =1. 因此,三棱锥Q ABP -的体积为111131332Q ABP ABPV QE S-=⨯⨯=⨯⨯⨯⨯︒=. 点睛:该题考查的是有关立体几何的问题,涉及到的知识点有面面垂直的判定以及三棱锥的体积的求解,在解题的过程中,需要清楚题中的有关垂直的直线的位置,结合线面垂直的判定定理证得线面垂直,之后应用面面垂直的判定定理证得面面垂直,需要明确线线垂直、线面垂直和面面垂直的关系,在求三棱锥的体积的时候,注意应用体积公式求解即可.20.已知点A在圆(22:16C x y +=上,()B,(P ,线段AB 的垂直平分线与AC 相交于点D . (1)求动点D 的轨迹方程;(2)若过点()0,1Q -的直线l 斜率存在,且直线l 与动点D 的轨迹相交于M ,N 两点.证明:直线PM 与PN 的斜率之积为定值.【答案】(1)22142x y +=;(2)32-【解析】(1)由圆的方程可得:圆心C ,半径4r =,||||DA DB =,||||DB DC +||||||4||DA DC AC r BC =+===>=,由椭圆的定义即可求解;(2)设:1l y kx =-,11(,)M x y ,22(,)N x y ,联立直线与椭圆的方程,利用根与系数的关系计算12x x +,12x x,再计算1212121212(1)(1)y y kx kx k k x x x x ==⋅即可求解.【详解】(1)由(22:16C x y +=得,圆心C ,半径4r =,点D 在线段AB 的垂直平分线上, ||||DA DB ∴=,||||||||||4||DB DC DA DC AC r BC ∴+=+===>=由椭圆的定义可得动点D的轨迹是以(B,C 为焦点, 长轴长为24a =的椭圆.从而2222,2a c b a c ===-=,故所求动点D 的轨迹方程为22142x y +=.(2)设:1l y kx =-,11(,)M x y ,22(,)N x y由221142y kx x y =-⎧⎪⎨+=⎪⎩消去y 得22(21)420k x kx +--=,显然222(4)8(21)80k k k ∆=-++=+> 12122242,2121k x x x x k k ∴+==-++. 120,0x x ≠≠,∴可设直线PM 与PN 的斜率分别为12,k k 则121212k k ==222121212241)31)()321221kk k x x k x x k k x x k -⨯+-+++==+-+232k =+=-即直线PM 与PN 的斜率之积为定值. 【点睛】方法点睛:求轨迹方程的常用方法(1)直接法:如果动点满足的几何条件本身就是一些几何量,如(距离和角)的等量关系,或几何条件简单明了易于表达,只需要把这种关系转化为,x y 的等式,就能得到曲线的轨迹方程;(2)定义法:某动点的轨迹符合某一基本轨迹如直线、圆锥曲线的定义,则可根据定义设方程,求方程系数得到动点的轨迹方程;(3)几何法:若所求轨迹满足某些几何性质,如线段的垂直平分线,角平分线的性质,则可以用几何法,列出几何式,再代入点的坐标即可;(4)相关点法(代入法):若动点满足的条件不变用等式表示,但动点是随着另一动点(称之为相关点)的运动而运动,且相关点满足的条件是明显的或是可分析的,这时我们可以用动点的坐标表示相关点的坐标,根据相关点坐标所满足的方程,求得动点的轨迹方程;(5)交轨法:在求动点轨迹时,有时会出现求两个动曲线交点的轨迹问题,这类问题常常通过解方程组得出交点(含参数)的坐标,再消去参数即可求出所求轨迹的方程.21.【2018年新课标I 卷文】已知函数()e 1xf x a lnx =--.(1)设2x =是()f x 的极值点.求a ,并求()f x 的单调区间;(2)证明:当1ea ≥时,()0f x ≥.【答案】(1) a =212e ;f (x )在(0,2)单调递减,在(2,+∞)单调递增.(2)证明见解析.【详解】分析:(1)先确定函数的定义域,对函数求导,利用f ′(2)=0,求得a =212e ,从而确定出函数的解析式,之后观察导函数的解析式,结合极值点的位置,从而得到函数的增区间和减区间;(2)结合指数函数的值域,可以确定当a ≥1e 时,f (x )≥e ln 1exx --,之后构造新函数g(x )=e ln 1exx --,利用导数研究函数的单调性,从而求得g (x )≥g (1)=0,利用不等式的传递性,证得结果.详解:(1)f (x )的定义域为()0+∞,,f ′(x )=a e x –1x. 由题设知,f ′(2)=0,所以a =212e . 从而f (x )=21e ln 12e x x --,f ′(x )=211e 2e x x-. 当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.所以f (x )在(0,2)单调递减,在(2,+∞)单调递增. (2)当a ≥1e 时,f (x )≥e ln 1exx --.设g (x )=e ln 1e x x --,则()e 1'e x g x x=-.当0<x <1时,g′(x )<0;当x >1时,g′(x )>0.所以x =1是g (x )的最小值点. 故当x >0时,g (x )≥g (1)=0. 因此,当1a e≥时,()0f x ≥.点睛:该题考查的是有关导数的应用问题,涉及到的知识点有导数与极值、导数与最值、导数与函数的单调性的关系以及证明不等式问题,在解题的过程中,首先要保证函数的生存权,先确定函数的定义域,之后根据导数与极值的关系求得参数值,之后利用极值的特点,确定出函数的单调区间,第二问在求解的时候构造新函数,应用不等式的传递性证得结果.22.平面直角坐标系xOy 中,曲线1C 的参数方程为24x t y t =+⎧⎨=-+⎩(t 为参数),以坐标原点O为极点,x 轴非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2(2cos 2) 3.ρθ-= (1)求曲线1C 的普通方程与2C 的直角坐标方程;(2)求2C 上的动点到1C 距离的取值范围.【答案】(1)1C 的普通方程为60x y +-=.2C 的直角坐标方程为2213x y +=;(2)⎡⎣.【解析】(1)把参数方程化为普通方程,由cos sin x y ρθρθ=⎧⎨=⎩化极坐标方程为直角坐标方程;(2)设2C 上的动点为,sin M αα),求出点M 到直线的距离,利用三角函数知识可得取值范围.【详解】(1)∵直线1C 的参数方程为24x t y t =+⎧⎨=-+⎩(t 为参数),∴消去参数t ,得1C 的普通方程为60x y +-=. ∵曲线2C 的极坐标方程为2(2cos 2)3ρθ-=,22222cos sin )3ρρθθ∴--=(,2C ∴的直角坐标方程为22222)()3x y x y +--=(,即2213x y +=.(2)曲线2C 的参数方程为sin x y αα⎧⎪⎨=⎪⎩(α为参数),设2C 上的动点为,sin M αα),则2C 上的动点到1C 距离|2sin()6|d πα+-==∵[]2sin()2,23πα+∈-,则2C 上的动点到1C 距离的最大值是∴2C 上的动点到1C 距离的取值范围是⎡⎣.【点睛】方法点睛:本题参数方程与普通方程的互化,考查极坐标方程与直角坐标方程的互化,涉及到椭圆上的点到定直线的距离的最值问题时可用椭圆的参数方程,设出点的坐标(对22221x y a b+=可设cos ,sin x a y b αθ==),由点到直线的距离公式把问题转化为三角函数的最值.23.已知函数f (x )=2|x -1|+|x +2|. (1)求不等式f (x )≥6的解集; (2)若2()f x m m≥+对任意x ∈R 恒成立,求实数m 的取值范围. 【答案】(1)(][),22,-∞-+∞.(2)()[],01,2-∞⋃.【解析】(1)根据绝对值的定义分类讨论去掉绝对值符号后可解不等式;(2)分类讨论去绝对值符号后求得函数()f x 的最小值,然后解关于m 的不等式,注意按分母m 的正负分类求解.【详解】(1)由不等式()6f x ≥可得:()2|1||2|6f x x x =-++≥,可化为:22226x x x ≤-⎧⎨---≥⎩或212226x x x -<<⎧⎨-++≥⎩或12226x x x ≥⎧⎨-++≥⎩ 解得:2x -≤或2x ≥,所以原不等式的解集为(][),22,-∞-+∞. (2)因为()3,2212=4,213,1x x f x x x x x x x -≤-⎧⎪=-++-+-<<⎨⎪≥⎩,所以()f x 在(),1-∞上单调递减,在[)1+∞,上单调递增, 所以min()(1)3f x f ==.要()2f x m m ≥+对任意R x ∈恒成立,只需23m m ≥+,即:2320m m m-+≤, 所以()()1200m m m ⎧--≤⎨>⎩或()()1200m m m ⎧--≥⎨<⎩,解得:12m ≤≤或0m <,所以,实数m 的取值范围为()[],01,2-∞⋃.【点睛】方法点睛:本题考查解含绝对值的不等式,绝对值不等式恒成立问题.解含绝对值的不等式的常用方法是利用绝对值的定义分类讨论去绝对值符号,然后解不等式.而不等式恒成立,在解关于参数m 的不等式时注意分式不等式的分类讨论求解.。
届高三数学(理)第一次月考模拟试卷及答案

届高三数学(理)第一次月考模拟试卷及答案2018届高三数学(理)第一次月考模拟试卷及答案高考数学知识覆盖面广,我们可以通过多做数学模拟试卷来扩展知识面!以下是店铺为你整理的2018届高三数学(理)第一次月考模拟试卷,希望能帮到你。
2018届高三数学(理)第一次月考模拟试卷题目一、选择题(本题共12道小题,每小题5分,共60分)1.已知全集U=R,A={x|x2﹣2x<0},B={x|x≥1},则A∪(∁UB)=( )A.(0,+∞)B.(﹣∞,1)C.(﹣∞,2)D.(0,1)2.已知集合A={1,2,3,4},B={y|y=3x﹣2,x∈A},则A∩B=()A.{1}B.{4}C.{1,3}D.{1,4}3.在△ABC中,“ >0”是“△ABC为锐角三角形”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.下列说法错误的是( )A.命题“若x2﹣4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2﹣4x+3≠0”B.“x>1”是“|x|>0”的充分不必要条件C.若p且q为假命题,则p、q均为假命题D.命题p:“∃x∈R使得x2+x+1<0”,则¬p:“∀x∈R,均有x2+x+1≥0”5.已知0A.a2>2a>log2aB.2a>a2>log2aC.log2a>a2>2aD.2a>log2a>a26.函数y=loga(x+2)﹣1(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m>0,n>0,则 + 的最小值为( )A.3+2B.3+2C.7D.117.已知f(x)是定义在R上的偶函数,在[0,+∞)上是增函数,若a=f(sin ),b=f(cos ),c=f(tan ),则( )A.a>b>cB.c>a>bC.b>a>cD.c>b>a8.若函数y=f(x)对x∈R满足f(x+2)=f(x),且x∈[-1 ,1]时,f(x)=1﹣x2,g(x)= ,则函数h(x)=f(x)﹣g(x)在区间x∈[-5 ,11]内零点的个数为( ) A.8 B.10 C.12 D.149设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1= ,an=f(n)(n∈N*),则数列{an}的前n 项和Sn的取值范围是( )A.[ ,2)B.[ ,2]C.[ ,1)D.[ ,1]10.如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )A . B.C. D.11.设函数f(x)=(x﹣a)|x﹣a|+b,a,b∈R,则下列叙述中,正确的序号是( )①对任意实数a,b,函数y=f(x)在R上是单调函数;②对任意实数a,b,函数y=f(x)在R上都不是单调函数;③对任意实数a,b,函数y=f(x)的图象都是中心对称图象;④存在实数a,b,使得函数y=f(x)的图象不是中心对称图象.A.①③B.②③C.①④D.③④12.已知函数,如在区间(1,+∞)上存在n(n≥2)个不同的数x1,x2,x3,…,xn,使得比值= =…= 成立,则n的取值集合是( )A.{2,3,4,5}B.{2,3}C.{2,3,5}D.{2,3,4}第II卷(非选择题)二、填空题(本题共4道小题,每小题5分,共20分)13.命题:“∃x∈R,x2﹣x﹣1<0”的否定是 .14.定义在R上的奇函数f(x)以2为周期,则f(1)= .15.设有两个命题,p:x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0};q:函数y=lg(ax2﹣x+a)的定义域为R.如果p∨q为真命题,p∧q为假命题,则实数a的取值范围是 .16.在下列命题中①函数f(x)= 在定义域内为单调递减函数;②已知定义在R上周期为4的函数f(x)满足f(2﹣x)=f(2+x),则f(x)一定为偶函数;③若f(x)为奇函数,则 f(x)dx=2 f(x)dx(a>0);④已知函数f(x)=ax3+bx2+cx+d(a≠0),则a+b+c=0是f(x)有极值的充分不必要条件;⑤已知函数f(x)=x﹣sinx,若a+b>0,则f(a)+f(b)>0.其中正确命题的序号为 (写出所有正确命题的序号).三、解答题(本题共7道小题,第1题12分,第2题12分,第3题12分,第4题12分,第5题12分,第6题10分,第7题10分,共70分)17.已知集合A={x|x2﹣4x﹣5≤0},函数y=ln(x2﹣4)的定义域为B.(Ⅰ)求A∩B;(Ⅱ)若C={x|x≤a﹣1},且A∪(∁RB)⊆C,求实数a的取值范围.18.已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(1)求实数a,b的值;(2)解关于x的不等式: >0(c为常数).19.已知函数f(x)= 是定义在(﹣1,1)上的奇函数,且f( )= .(1)确定函数f(x)的解析式;(2)证明f(x)在(﹣1,1)上是增函数;(3)解不等式f(t﹣1)+f(t)<0.20.已知关于x的不等式x2﹣(a2+3a+2)x+3a(a2+2)<0(a∈R).(Ⅰ)解该不等式;(Ⅱ)定义区间(m,n)的长度为d=n﹣m,若a∈R,求该不等式解集表示的区间长度的最大值.21.设关于x的方程2x2﹣ax﹣2=0的两根分别为α、β(α<β),函数(1)证明f(x)在区间(α,β)上是增函数;(2)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小.选做第22或23题,若两题均选做,只计第22题的分。
四川省自贡市2023届高三下学期第三次诊断性考试数学(文)试题

故选:D.
6.B
【分析】由等比数列及已知,要Tn 为递增数列只需 a1qn1 1 在 n ,结合 a1 的符号,再根据充分必要性的定义即可得答案.
【详解】由题设
Tn Tn1
an
a1qn1 且 n
2
,要Tn 为递增数列,只需
a1q n 1
2 ,显然 a1q
1,即T2
T1 ,不满足;
a1 1 ,则 a1qn1 1 在 n 2 上恒成立,满足.
所以Tn 为递增数列有 a1 1 且 q 1 .
所以,“数列Tn 为递增数列”是“ a1 0 且 q 1 ”的充分不必要条件.
故选:B.
答案第 2 页,共 18 页
7.C 【分析】对 K 、 H 、 G 、 B 四个点逐一进行分析,找出棱柱中与平面 PEF 平行的棱的条数, 即可判断. 【详解】解:取 AC 的中点 M ,连接 EM , MK , KF , EF ,如图所示:
1在
n
2
上恒成
立,
当 q 0 ,不论 a1 取何值,总存在 a1qn1 0 ,不满足要求;
当0 q 1,
a1 0 ,则 a1qn1 0 ,不满足要求;
a1 0 ,总存在 0 a1qn1 1,不满足要求;
当q 1,
a1 0 ,则 a1qn1 0 ,不满足;
0
a1
1,若 a1
1,q= 3
1.A
参考答案:
【分析】利用复数的除法化简复数 z ,利用复数的模长公式可求得 z 的值.
【详解】由复数的四则运算可得
z
21 i
1 i
1
21 i2 1 i1 i
1
1
i2
1
1
湖南省常德市2018届高三上学期检测考试(期末)数学(文)试题Word版含答案

湖南省常德市2018届高三上学期检测考试(期末)数学(文)试题Word版含答案常德市2017-2018学年度上学期高三数学(文科)检测考试第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合$A=\{1,2,3\},B=\{2,3,4,5\}$,则$A\cap B$中元素的个数为()。
A.2.B.3.C.4.D.5.2.在复平面内,复数$z=1+2i$($i$为虚数单位)对应的点所在的象限为()。
A.第一象限。
B.第二象限。
C.第三象限。
D.第四象限。
3.在某学校图书馆的书架上随意放着有编号为1,2,3,4,5的五本史书,若某同学从中任意选出两本史书,则选出的两本史书编号相连的概率为()。
A.$\frac{1}{10}$。
B.$\frac{1}{5}$。
C.$\frac{2}{5}$。
D.$\frac{1}{2}$。
4.元朝著名数学家XXX《四元玉鉴》中有一首诗:“我有一壶酒,携着XXX走,遇店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”其意思为:“诗人带着装有一倍分酒的壶去春游,先遇到酒店就将酒添加一倍,后遇到朋友饮酒一斗,如此三次先后遇到酒店和朋友,壶中酒恰好饮完,问壶中原有多少酒?”用程序框图表达如图所示,即最终输出的$x=$,那么在这个空白框中可以填入()。
A.$x=x-1$。
B.$x=2x-1$。
C.$x=2x$。
D.$x=2x+1$。
5.已知向量$a=(x,y),b=(1,2),c=(-1,1)$,若满足$a\parallel b,b\perp(a-c)$,则向量$a$的坐标为()。
A.$(\frac{5}{11},\frac{5}{11})$。
B.$(-\frac{5}{11},-\frac{5}{11})$。
C.$(\frac{6}{11},\frac{3}{11})$。
D.$(\frac{5}{11},\frac{6}{11})$。
XXX2018年高三下学期期初考试(3月)数学(文)试题

XXX2018年高三下学期期初考试(3月)数学(文)试题2018年全国高三文科数学统一联合考试一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合$A=\{x|x\leq1\}$,且$A\cap B=\{0,1\}$,则集合$B$可能是(。
)A.$\{x|x\geq\}$B.$\{x|x>-1\}$C.$\{-1,0,1\}$D.$\{0,1,2\}$2.已知向量$a=(1,2)$,$b=(-1,0)$,则$2a-b=$(。
)A.$17$B.$17\vec{a}$C.$5$D.$25$3.若复数$z$在复平面内对应的点的坐标是$(1,-2)$,则$z=$ (。
)A.$1-2i$B.$1+2i$C.$2-i$D.$-2-i$4.《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边同时相向打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果这两只老鼠恰好用了7天把墙打穿,则墙厚为(。
)A.$8255$尺B.$129$尺C.$2079$尺D.$65$尺5.若双曲线$C:-\frac{x^2}{x^2+y^2}=1$的离心率为3,则实数$m=$ (。
)frac{m}{m+1}$A.$1$B.$2$C.$1$或$-2$D.$1$或$2$6.已知命题$p:\exists m\in R$,使得$f(x)=x^2+mx$是偶函数;命题$q:x^2=1\Rightarrow x=1$,现给出下列命题:①$p$;②$q$的逆否命题;③$p\land q$;④$p\lor(\negq)$。
其中真命题的个数为(。
)A.$0$B.$1$C.$2$D.$3$7.如图,网格纸上小正方形的边长为$1$,粗实线画出的是某几何体的三视图,则该几何体的体积为(。
江西省南昌市2018届高三第三次文科数学模拟试题(有解析)(精品资料).doc

【最新整理,下载后即可编辑】江西省南昌市第三次模拟测试卷文科数学一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,若,则()A. B. C. D.【答案】D【解析】所以于是所以。
故选D2. 已知,是虚数单位,若,,则为()A. 或B.C.D. 不存在的实数【答案】A详解:由题得,故,故选A.点睛:考查共轭复数的定义和复数的四则运算,属于基础题.3. “”是“关于的方程有解”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】分析:先求出得,而s有解可得即可.详解:由题得得,s有解可得,故可得“”是“关于的方程有解”的充分不必要条件,故选A.点睛:考查逻辑关系,能正确求解前后的结论,然后根据定义判断是解题关键,属于基础题.4. 已知函数,那么函数的值域为()A. B. C. D.【答案】B【解析】分析:先求出分段函数的每段所在范围的值域,然后两段值域求并集即可.详解:的值域为,y=的值域为:故函数的值域为,选B点睛:考查分段函数的值域求法,明白先求出分段函数的每段所在范围的值域,然后两段值域求并集是关键,属于基础题.5. 在平面直角坐标系中,已知双曲线与双曲线有公共的渐近线,且经过点,则双曲线的焦距为()A. B. C. D.【答案】D【解析】分析:双曲线C与双曲线x2−=1有公共的渐近线,因此设本题中的双曲线C的方程x2−=λ,再代入点P的坐标即可得到双曲线C的方程.然后求解焦距即可.详解:双曲线C与双曲线x2−=1有公共的渐近线,设本题中的双曲线C的方程x2−=λ,因为经过点,所以4-1=λ,解之得λ=3,故双曲线方程为故焦距为:,选D.点睛:本题给出与已知双曲线共渐近线的双曲线经过某个已知点,求该双曲线的方程,着重考查了双曲线的标准方程与简单几何性质,属于基本知识的考查.6. 执行如图所示的程序框图,若输出的,则判断框内应填入的条件是()A. B. C. D.【答案】A【解析】S=0,k=1,k=2,S=2,否;k=3,S=7,否;k=4,S=18,否;k=5,S=41,否;k=6,S=88,是.所以条件为k>5,故选B.7. 已知,则的大小关系为()A. B. C. D.【答案】D【解析】分析:可以先比较同底的对数大小,再结合中间值1,进行比较即可. 详解:,故,选D.点睛:考查对数函数的基本性质和运算公式,比较大小通常先比较同底的然后借助中间值判断不同底的即可.属于基础题.8. 在平面直角坐标系中,为坐标原点,点,则外接圆的半径为()A. B. C. D.【答案】A【解析】分析:求出线段OP,OQ的中垂线所在直线方程,联立方程求得圆心坐标,即可求得则△POQ外接圆的半径.详解::∵k OP=3,k OQ=-1,线段OP,OQ的中点分别为,∴线段OP,OQ的中垂线所在直线方程分别为联立方程可得圆心坐标,所以半径为,故选A.点睛:本题考查了三角形外心的求解,属于中档题.9. 将函数的图象上所有点的横坐标压缩为原来的,纵坐标保持不变,得到图象,若,且,则的最大值为()A. B. C. D.【答案】C【解析】分析:先得出变化后的表达式然后若,且,则取到两次最大值即可得出结论.详解:由题得,若,且,则取到两次最大值,令,要使,最大,故令k=1,k=-2即可,故的最大值为,选C点睛:考查三角函数的伸缩变化和最值,明白取到两次最大值,是解题关键.10. 某几何的三视图如图所示,其中主视图由矩形和等腰直角三角形组成,左视图由半个圆和等腰直角三角形组成,俯视图的实线部分为正方形,则该几何体的表面积为()A. B. C. D.【答案】A【解析】由三视图知几何体的上半部分是半圆柱,圆柱底面半径为1,高为2,其表面积为:,下半部分为正四棱锥,底面棱长为2,斜高为,其表面积:,所以该几何体的表面积为本题选择A选项.点睛:(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.11. 为培养学生分组合作能力,现将某班分成三个小组,甲、乙、丙三人分到不同组,某次数学建模考试中三人成绩情况如下:在组中的那位的成绩与甲不一样,在组中的那位的成绩比丙低,在组中的那位成绩比乙低.若甲、乙、丙三人按数学建模考试成绩由高到低排序,则排序正确的是()A. 甲、丙、乙 B. 乙、甲、丙 C. 乙、丙、甲 D. 丙、乙、甲【答案】C【解析】因为在组中的那位的成绩与甲不一样,在组中的那位的成绩比乙低.所以甲、乙都不在B组,所以丙在B组. 假设甲在A组,乙在C组,由题得甲、乙、丙三人按数学建模考试成绩由高到低排序是乙、丙、甲.假设甲在C组,乙在A组,由题得矛盾,所以排序正确的是乙、丙、甲.故选C.12. 已知双曲线的左、右焦点分别为,以为圆心的圆与双曲线在第一象限交于点,直线恰与圆相切于点,与双曲线左支交于点,且,则双曲线的离心率为()A. B. C. D.【答案】B【解析】设,在三角形中,在直角三角形中,故选B.点睛:本题的关键是寻找关于离心率的方程,一个方程是中的勾股定理,另外一个是直角三角形中勾股定理,把两个方程结合起来就能得到离心率的方程.二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 中国数学家刘徽在《九章算术注》中提出“割圆”之说:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.意思是“圆内接正多边形的边数无限增多的时候,它的周长的极限是圆的周长,它的面积的极限是圆的面积”.如图,若在圆内任取一点,则此点取自其内接正六边形的概率____.【答案】【解析】分析:根据几何概型的概率公式分别求出正六边形的面积和圆的面积即可详解:设圆心为O,圆的半径为1,则正六边形的面积S=则对应的概率P=,故答案为.点睛:本题主要考查几何概型的概率的计算,根据定义求出相应的面积是解决本题的关键.14. 已知函数的图象在点处的切线过点,则__________.【答案】1【解析】分析:求得函数f(x)的导数,可得切线的斜率,由两点的斜率公式,解方程可得a的值.详解:函数f(x)=e x-x2的导数为f′(x)=e x-2x,函数f(x)=e x-x2的图象在点(1,f(1))处的切线的斜率为e-2,切点为(1,e-1),由切线过点(0,a),可得:e-2=得a=1,故答案为:1.点睛:本题考查导数的几何意义,考查两点的斜率公式,以及方程思想和运算能力,属于基础题.15. 已知向量,,则在方向上的投影为__________.【答案】【解析】分析:根据向量的投影和向量的坐标运算即可求出.详解:因为向量,,∴−=(-1,-1),在方向上的投影为故答案为点睛:本题考查了向量的投影和向量的坐标运算,属于基础题请在此填写本题解析!16. 现某小型服装厂锁边车间有锁边工名,杂工名,有台电脑机,每台电脑机每天可给件衣服锁边;有台普通机,每台普通机每天可给件衣服锁边.如果一天至少有件衣服需要锁边,用电脑机每台需配锁边工名,杂工名,用普通机每台需要配锁边工名,杂工名,用电脑机给一件衣服锁边可获利元,用普通机给一件锁边可获利元,则该服装厂锁边车间一天最多可获利__________元.【答案】780【解析】分析:设每天安排电脑机和普通机各x,y台,则一天可获利z=12×8x+10×6y=96x+60y,线性约束条件,画出可行域,利用目标函数的几何意义求解即可.学#科#网...学#科#网...学#科#网...学#科#网...学#科#网...学#科#网...学#科#网...点睛:本题考查线性规划的简单应用,考查约束条件的可行域以及目标函数的最值是解题的关键.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知数列的各项均为正数,且.(1)求数列的通项公式;(2)若,求数列的前项和.【答案】(1);(2)【解析】分析:(1)由得,解得或,又数列{a n}的各项均为正数,可得a n.(2)利用错位相减法求解即可.详解:(1)由得,所以或,又因为数列的各项均为正数,负值舍去所以.(2)由,所以①②由①-②得:所以.点睛:考查数列通项的求法和利用错位相减法求和,能正确分解因式递推式求得通项是解题关键.18. 如图,多面体中,为正方形,,,且.(1)证明:平面平面;(2)求三棱锥的体积.【答案】(1)见解析;(2)【解析】分析:(1)证明面面垂直可通过证明线面垂直得到,证A平面即可,(2)由已知,连接交于,作于,由等体积法:,进而可得出结论.(1)证明:∵,由勾股定理得:又正方形中,且∴平面,又∵面,∴平面平面(2)由已知,连接交于作于,则又由(1)知平面平面,平面平面,面,得面由,知四边形为平行四边形,即,而,进而又由,所以,三棱锥的体积.点睛:考查面面垂直、几何体体积,能正确分析线条关系,利用等体积法转化求体积是解题关键.19. 十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫,某帮扶单位为帮助定点扶贫村真正脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用互联网电商渠道进行销售.为了更好地销售,现从该村的蜜柚树上随机摘下了个蜜柚进行测重,其质量分布在区间内(单位:克),统计质量的数据作出其频率分布直方图如图所示:(1)按分层抽样的方法从质量落在的蜜柚中随机抽取个,再从这个蜜柚中随机抽个,求这个蜜柚质量均小于克的概率;(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有个蜜柚待出售,某电商提出两种收购方案:所有蜜柚均以元/千克收购;低于克的蜜柚以元/个收购,高于或等于的以元/个收购.请你通过计算为该村选择收益最好的方案.【答案】(1);(2)见解析【解析】分析:(Ⅰ)由题得蜜柚质量在[1750,2000)和[2000,2250)的比例为2:3,应分别在质量为[1750,2000),[2000,2250)的蜜柚中各抽取2个和3个.记抽取质量在[1750,2000)的蜜柚为A1,A2,质量在[2000,2250)的蜜柚为B1,B2,B3,则从这5个蜜柚中随机抽取2个,利用列举法能求出这2个蜜柚质量均小于2000克的概率.(Ⅱ)由频率分布直方图可知,蜜柚质量在[1500,1750)的频率为0.1,蜜柚质量在[1750,2000),[2000,2250),[2500,2750),[2750,3000)的频率依次为0.1,0.15,0.4,0.2,0.05.若按A方案收购:根据题意各段蜜柚个数依次为500,500,750,2000,1000,250,求出总收益为457500(元);若按B方案收购:收益为1750×60+325080=250×20×[7×3+13×4]=365000元.方案A的收益比方案B的收益高,应该选择方案A.详解:(1)由题得蜜柚质量在和的比例为,∴应分别在质量为的蜜柚中各抽取个和个.记抽取质量在的蜜柚为,质量在的蜜柚为,则从这个蜜柚中随机抽取个的情况共有以下种:其中质量小于克的仅有这种情况,故所求概率为.(2)方案好,理由如下:由频率分布直方图可知,蜜柚质量在的频率为同理,蜜柚质量在的频率依次为若按方案收购:根据题意各段蜜柚个数依次为于是总收益为(元)若按方案收购:∵蜜柚质量低于克的个数为蜜柚质量低于克的个数为∴收益为元∴方案的收益比方案的收益高,应该选择方案.点睛:本题考查概率的求法,考查两种方案的收益的求法及应用,考查古典概型、列举法等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.20. 已知动圆过点,并与直线相切.(1)求动圆圆心的轨迹方程;(2)已知点,过点的直线交曲线于点,设直线的斜率分别为,求证:为定值,并求出此定值.【答案】(1);(2)【解析】分析:(1)(Ⅰ)由题意圆心为M的动圆M过点(1,0),且与直线x=-1相切,利用抛物线的定义,可得圆心M的轨迹是以(1,0)为焦点的抛物线;(2)先分AB斜率为0和不为0进行讨论,然后结合两点的斜率公式和韦达定理可得为定值.(1)设由得动圆圆心轨迹方程为(2)当斜率为时,直线斜率不存在(不合题意,舍去)当斜率不为时,设方程:,即设由,得,且恒成立∴∴(定值)点睛:考查抛物线的定义,直线与抛物线的综合问题,求定值问题,首先根据题意写出表达式是解题关键.21. 已知函数.(1)求函数的单调区间;(2)当时,恒成立,求的取值范围.【答案】(1)单调递减区间为,单调递增区间为;(2)【解析】分析:(1)求单调区间只需求解导函数的不等式即可;(2)对于当时,恒成立,可先分离参数,然后求出新函数的最小值即可.详解:(1)函数的定义域为,∵,∴,解得或;,解得,∴的单调递减区间为,单调递增区间为.(2)∵在恒成立∴,令,则,当时,;当时,,∴在上单调递减,在上单调递增,∴,∴.点睛:考查函数的单调区间的求法以及恒成立问题转化为最值问题求解的思维,分离参数的是解题关键,属于中档题.22. 在平面直角坐标系中,曲线的参数方程为:(为参数,)将曲线经过伸缩变换:得到曲线.(1)以原点为极点,轴的正半轴为极轴建立坐标系,求的极坐标方程;(2)若直线(为参数)与,相交于两点,且,求的值.【答案】(1);(2)或【解析】试题分析:求得曲线的普通方程,然后通过变换得到曲线方程,在转化为极坐标方程在极坐标方程的基础上结合求出结果解析:(1)的普通方程为,把,代入上述方程得,,∴的方程为.令,,所以的极坐标方程为.(2)在(1)中建立的极坐标系中,直线的极坐标方程为,由得,由得.而,∴.而,∴或.23. 已知函数.(1)求不等式的解集;(2)设,证明:【答案】(1)或;(2)见解析【解析】试题分析:(1)根据绝对值定义将不等式转化为三个不等式组,分别求解集,最后求并集(2)利用分析法证明不等式:,平方作差并因式分解可得结论试题解析:(1)①当时,原不等式可化为,解得;②当时,原不等式可化为,解得,此时原不等式无解;③当时,原不等式可化为,解得.综上, .(2)因为,所以,要证,只需证,即证, 即证,即证,即证.因为,所以,所以成立,所以原不等式成立.。
上海建平中学2023-2024学年高三下学期数学周练及答案

建平中学2023-2024学年第二学期高三年级周练12024.0312三、解答题(共5道大题,其中17题14分,18题14分,19题14分,20题16分,21题18分,共计76分)17.(本题满分14分.本题共2小题,第(1)小题7分,第(2)小题7分.)34519.(本题满分14分.本题共2小题,第(1)小题6分,第(2)小题8分.)第19届亚运会在杭州举行,志愿者的服务工作是亚运会成功举办的重要保障.某高校承办了杭州志愿者选拔的面试工作.先随即抽取了100名候选者的面试成绩,并分成n 组:第一组[45,55),第二组[55,65),第三组[)65,75,第四组[75,85),第五组[]85,95,绘制成如图所示的频率分布直方图,已知第三、四、五组的频率之和为0.7,第一组和第五组的频率相同.(1)现规定分数排名前40%可以加入资深志愿者组,估计资深志愿者组的录取分数约为多少?(精确到0.1)(2)在第四、第五两组志愿者中,采用分层抽样的方法从中抽取5人,然后再从这5人中选出2人,以确定组长人选,求选出的两人来自不同组的概率;(3)已知第四组的平均成绩为80,方差为20,第五组的平均成绩为90,方差为5,则75分以上的志愿者的平均成绩和方差为多少?620.(本题满分16分.本题共有3小题,第(1)小题满分4分,第(2)小题满分6分.第 (3)小题满分6分)已知抛物线24y x =的焦点为F ,直线l 交抛物线于不同的,A B 两点. (1)若直线l 的方程为1yx =−,求线段AB 的长; (2)若直线l 经过点()1,0P −,点A 关于x 轴的对称点为A ′,求证:,,A F B ′三点共线; (3)若直线l 经过点()8,4M −,抛物线上是否存在定点N ,使得以线段AB 为直径的圆恒过点N ?若存在,求出点N 的坐标,若不存在,请说明理由.7参考答案一、填空题8910111213二、选择题13.在10件产品中有3件次品,从中选3件.下列各种情况是互斥事件的有( ) ①A :“所取3件中至多2件次品”, B : “所取3件中至少2件为次品”; ②A :“所取3件中有一件为次品”,B : “所取3件中有二件为次品”; ③A :“所取3件中全是正品”,B :“所取3件中至少有一件为次品”; ④A :“所取3件中至多有2件次品”,B :“所取3件中至少有一件是正品”; A .①③B .②③C .②④D .③④B根据互斥事件的定义即可得到结果.在10件产品中有3件次品,从中选3件,∵所取3件中至多2件次品与所取3件中至少2件为次品,两个事件中都包含2件次品,∴①中的两个事件不是互斥事件. ∵所取3件中有一件为次品与所取3件中有二件为次品是互斥事件, ∴②中的两个事件是互斥事件.∵所取3件中全是正品与所取3件中至少有一件为次品是不能同时发生的, ∴③中的两个事件是互斥事件,∵所取3件中至多有2件次品与所取3件中至少有一件是正品都包含2件次品一件正品,以及1件次品两件正品,以及三件正品,所以④不是互斥事件,故选:B .14.已知α,β是不同的平面,m ,n 是不同的直线,则下列命题不正确的是( ) A .若m ⊥α,m n ∥,n ⊂β,则α⊥β B .若m n ∥,m αβ= ,则n α∥,n β C .若m n ∥,m ⊥α,则n ⊥α D .若m ⊥α,m ⊥β,则αβ∥B运用线面垂直的性质和面面垂直的判定定理即得A 项;满足B 项条件的图形有三种,故B 项错误;利用线面垂直的判定方法即得C 项;利用面面平行的判定方法即得D14三、解答题15161718192021222324。
精选2018届高三数学下学期周练三理

DBA 河南省正阳县第二高级中学2017-2018学年下期高三理科数学周练(三)一·选择题:1.已知a R ∈,则“2a >”是“22a a >”成立的 ( )条件A. 充分不必要B. 必要不充分C.充分必要D. 既不充分也不必要2. 已知集合P={0,1},M={x|xP},则集合M 的子集个数为( )A.8B.16C.32D.643. 已知变量x ,y 满足约束条⎪⎩⎪⎨⎧≤-≥+≥-4211y x y x y x ,则y x z +=3的最大值为( )A. B. C. D.4. 在等差数列{}n a 中,已知22a =,前项和756S =,则公差d =A .B .C .D .5. 如图,三行三列的方阵中有9个数(i=1,2,3;j=1,2,3),从中任取三个数,则至少有两个数位于同行或同列的概率是( )A .37B .47 C. 114 D. 13146. 已知向量(1,1)a =,2(4,2)a b +=,则向量,a b 的夹角的余弦值为( ) AB.D. 7. 已知抛物线24y x =上的点到其准线的距离为,直线交抛物线于,两点,且AB 的中点为(2,1)N ,则到直线的距离为( )A.或 BCD8. 一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是1(0,0,0),(1,0,1,(0,1,1),(,1,0)2),绘制该四面体三视图时, 按照如下图所示的方向画正视图,则得到侧(左)视图可以为( )111213212223313233aa a a a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦9. 若实数,满足422log 4log x y +=+8log ()x y =+,则11x y+的值为( ) A .128 B .256 C .512 D . 10. 设函数()f x 定义如下表:A.4B.5C.2D.311. 4.sin ()((,0)(0,))xf x x xππ=∈-大致的图象是( )A .B . C. D .12. 设函数f(x)=(x -a)2+(ln x 2-2a)2,其中x>0,a ∈R ,存在x 0使得f(x 0)≤b 成立,则实数b 的最小值为( )(A) 15 (B) 25 (C) 45(D) 1二.填空题:13. 有3对双胞胎站成一排,要求每对双胞胎都相邻,则不同的站法种数是.14.已知双曲线22221(0,0)x y a b a b-=>>的渐近线被圆22650x y x +-+=截得的弦长为,则该双曲线的离心率为.15. 定义运算:⎩⎨⎧<≥=∇)0( )0( xy y xy x y x ,例如:343=∇,44)2(=∇-,则函数)2()(22x x x x f -∇=的最大值为____________.16. 在各项都为正数的等比数列{}n a 中,若2018a =则2017201912a a +的最小值为_______.三.解答题:17.已知 △ABC 的三个内角,,的对边分别为,,,并且满足2a =,cos (2)cos a B c b A =-.(1)求角的大小;(2)求△ABC 周长的最大值.18. 如图,ABCD 是边长为3的正方形,DE ⊥平面ABCD ,AF ∥DE ,DE=3AF ,BE 与平面ABCD 所成角为60°.(Ⅰ)求证:AC ⊥平面BDE ;(Ⅱ)求二面角F ﹣BE ﹣D 的余弦值.19. “蛟龙号”从海底中带回的某种生物,甲乙两个生物小组分别独立开展对该生物离开恒温箱的成活情况进行研究,每次试验一个生物,甲组能使生物成活的概率为13,乙组能使生物成活的概率为12,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.(Ⅰ)甲小组做了三次试验,求至少两次试验成功的概率.(Ⅱ)如果乙小组成功了4次才停止试验,求乙小组第四次成功前共有三次失败,且恰有两次连续失败的概率.(Ⅲ)若甲乙两小组各进行2次试验,设试验成功的总次数为X ,求X 的期望.20. 如图,在直角坐标系xOy 中,椭圆:22221y x a b+=()0a b >>的上焦点为,椭圆的离心率为12 ,且过点1,3⎛⎫ ⎪ ⎪⎝⎭.(1)求椭圆的方程;(2)设过椭圆的上顶点的直线与椭圆交于点(不在轴上),垂直于的直线与交于点,与轴交于点,若110F B F H ∙=,且MO MA =,求直线的方程.21. 已知函数()ln()f x x a x =+-有且只有一个零点,其中0a >. (Ⅰ)求的值;(Ⅱ)若对任意的(0,)x ∈+∞,有2()f x kx ≥成立,求实数的最大值; (Ⅲ)设()()h x f x x =+,对任意1212,(1,)()x x x x ∈-+∞≠,证明:不等式1212()()x x h x h x ->-四.选作题:22.在直角坐标系xOy 中,曲线的参数方程为cos 2sin x y αα=⎧⎨=⎩,(为参数),将曲线经过伸缩变换2x x y y '=⎧⎨'=⎩,后得到曲线.在以原点为极点,轴正半轴为极轴的极坐标系中,直线的极坐标方程为cos sin 100ρθρθ--=.(1)说明曲线是哪一种曲线,并将曲线的方程化为极坐标方程;(2)已知点是曲线上的任意一点,求点到直线的距离的最大值和最小值.23.已知函数()||f x x a =+.(1)当1=a 时,求不等式()211f x x ≤+-的解集;(2)若函数()()3g x f x x =-+的值域为,且[]2,1A -⊆,求的取值范围.参考答案:17.(1)60°(2)6 17.(1)略(2 19.(1)727(2)332(3)P(X=0)=1111(1)(1)3322-⨯-⨯⨯=19 P(X=1)=1122211111221332222333C C ⨯⨯⨯⨯+⨯⨯⨯= P(X=2)=11221111221121111333223322332236C C ⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯=P(X=3)=1122111121111332233226C C ⨯⨯⨯⨯+⨯⨯⨯⨯=P(X=4)=11111332236⨯⨯⨯=20.(1)22143y x +=(2)23y x =±+ 21.(1)a=1 (2)12k ≥-(3)构造函数22.(1)圆心在原点,半径为2的圆,其极坐标方程为2ρ=(2)2和2 23.(1)(,1][1,)-∞-+∞(2)(,1][5,)-∞+∞。
江西省等三省十校2018届高三下学期联考数学(文)试卷(含答案)

“三省十校”联考2017-2018学年第二学期高三数学(文科)试题(考试时间:150分钟 总分:150分)第I 卷(选择题 共60分)三、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}{}2|5,|30A x N x B x R x x =∈≤=∈->,则A B ⋂=A. {}3,4,5B.{}4,5 C. {}|35x x <≤ D. {| 0x x <或 }35x <≤2.已知()125i z +=(i 为虚数单位),则复数z 的虚部为 A. 2i B. 1 C. 2- D. 2 3.下列判断正确的是A. “22am bm <”是“a b <”的充要条件B. 命题“32,10x R x x ∀∈--≤”的否定是“32,10x R x x ∃∈--≥” C. 若p q ∧为假命题,则,p q 均为假命题 D. 2x =是24x =的充分不必要条件4.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第一天走了A. 24里B. 48里C. 96里D.192里5.已知抛物线22y px = (0)p >上点()1,M m 到其焦点的距离为5,则该抛物线的焦点坐标为A. ()4,0B. ()0,4-C. ()4,0-D. ()0,46. 平面向量a r 与b r 的夹角为()120,1,0,1a b ==o r r ,则2a b +=r rA.B.C.3D. 77. 已知x ,y 满足约束条件2010220x y x y x y -≤⎧⎪+-≥⎨⎪-+≥⎩,则3z x y =++的最大值是A .3B .4 C.5 D .6(4)已知[x ]表示不超过x 的最大整数。
湖南省长沙市2024届高三下学期三模数学试题含答案

试卷第1页,共6页2024年湖南省长沙市高考三模数学试题(答案在最后)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{12},{21}A xx B x x =-<<=-<<∣∣,则集合()A B A B ⋃⋂=ð()A .()1,1-B .()2,2-C .()()2,11,2--⋃D .(2,1][1,2)--⋃2.已知复数()2i 1i z =⋅-,则复数z 在复平面内对应的点在()A .第一象限B .第二象限C .第三象限D .第四象限3.样本数据16,24,14,10,20,15,12,14的上四分位数为()A .14B .15C .16D .184.已知1cos 3π6α⎛⎫+= ⎪⎝⎭,则ππsin sin 236αα⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭()A .109B .49-C .23D .655.已知向量()1,1a = ,()0,b t = ,若()2a a b ⊥+,则b = ()A .22B .1CD .26.已知等差数列{}n a 的前n 项和为n S ,若210,a a ≥>20100S =,则1011a a ()A .有最小值25B .有最大值25C .有最小值50D .有最大值507.已知三棱锥A BCD -中,AB ⊥平面BCD ,AB =4,BC =3,5CD =,BD =7,则该三棱锥外接球的表面积为()A .196π3B .244π3C .196π5D .244π58.在平面直角坐标系xOy 中,已知圆()22:14C x y -+=,若直线:0l x y m ++=上有且只有一个点P 满足:过点P 作圆C 的两条切线,PM PN ,切点分别为,M N ,且使得四边形PMCN 为正方形,则正实数m 的值为()A .1B.C .3D .7二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.试卷第2页,共6页9.下列说法正确的是()A .某校高一年级共有男女学生500人,现按性别采用分层抽样的方法抽取容量为50人的样本,若样本中男生有30人,则该校高一年级女生人数是200B .数据1,3,4,5,7,9,11,16的第75百分位数为10C .线性回归方程中,若线性相关系数r 越大,则两个变量的线性相关性越强D .根据分类变量x 与y 的成对样本数据,计算得到2 3.937χ=,根据小概率值0.05α=的独立性检验()0.05 3.841=x ,可判断x 与y 有关联,此推断犯错误的概率不大于0.0510.瑞士数学家Jakob Bernoulli 于17世纪提出如下不等式:1x ∀>-,有()()11,111,01r rx rx r x rx r ⎧+≥+≥⎪⎨+≤+≤≤⎪⎩,请运用以上知识解决如下问题:若01a <<,01b <<,a b ¹,则以下不等式正确的是()A .1a b a b +>B .1b a a b +>C .a b b aa b a b +>+D .a b b aa b a b +<+11.若定义在R 上的连续函数()f x 满足对任意的实数,a b 都有()()()f a b f a f b +=⋅且()12f =,则下列判断正确的有()A .函数()f x 的图象关于原点对称B .()f x 在定义域上单调递增C .当()0,x ∈+∞时,()1f x >D .()()()()()()()()()()24620222024...202413520212023f f f f f f f f f f +++++=三、填空题:本题共3小题,每小题5分,共15分.12.根据国家“乡村振兴战略”提出的“推动城乡义务教育一体化发展,高度重视农村义务教育”,某师范大学4名毕业生主动申请到某贫困山区的乡村小学工作,若将这4名毕业生分配到该山区的3所乡村小学,每所学校至少分配1人,则不同分配方案的种数为.13.如图,四边形ABCD 是边长为1的正方形,延长CD 至E ,使得2DE CD =.动点P 从点A 出发,沿正方形的边按逆时针方向运动一周回到A 点,AP AB AE λμ=+,则λμ+的试卷第3页,共6页取值范围为.14.如图所示,直角三角形ABC 所在平面垂直于平面α,一条直角边AC 在平面α内,另一条直角边BCπ6BAC ∠=,若平面α上存在点P ,使得ABP线段CP 长度的最小值为.四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.15.在ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,已知)tan tan 1C B C +=-,(1)求角A .(2)若a =ABC 所在平面内有一点D 满足2π3BDC ∠=,且BC 平分ABD ∠,求ACD 面积的取值范围.16.已知某科技公司的某型号芯片的各项指标经过全面检测后,分为Ⅰ级和Ⅱ级,两种品级芯片的某项指标的频率分布直方图如图所示:试卷第4页,共6页若只利用该指标制定一个标准,需要确定临界值K ,按规定须将该指标大于K 的产品应用于A 型手机,小于或等于K 的产品应用于B 型手机.若将Ⅰ级品中该指标小于或等于临界值K 的芯片错误应用于A 型手机会导致芯片生产商每部手机损失800元;若将Ⅱ级品中该指标大于临界值K 的芯片错误应用于B 型手机会导致芯片生产商每部手机损失400元;假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.(1)设临界值60K =时,将1个Ⅰ级品芯片和1个Ⅱ级品芯片分别应用于A 型手机和B 型手机.求两部手机有损失的概率(计算结果用小数表示);(2)设K x =且[]50,55x ∈,现有足够多的芯片Ⅰ级品、Ⅱ级品,分别应用于A 型手机、B 型手机各1万部的生产,试估计芯片生产商损失费用的最小值.17.已知直三棱柱111ABC A B C -中,1AB AC AA ==,,M N 分别为BC 和1BB 的中点,P 为棱11A C 上的动点,11AN A C ⊥.试卷第5页,共6页(1)证明:平面ANP ⊥平面1A MP ;(2)设111A P A C λ= ,是否存在实数λ,使得平面11AA B B 与平面PMN18.已知函数()()11n n n f x x x x n -+=+++-∈N .(1)判断并证明()n f x 的零点个数(2)记()n f x 在(0,)+∞上的零点为n x ,求证;(i ){}n x 是一个递减数列(ii )121122n n nx x x +≤+++<+ .试卷第6页,共6页19.已知双曲线2222Γ:1(0,0)x y a b a b-=>>的左焦点为()1F,点(M 在双曲线上,直线l 与双曲线Γ交于,A B 两点.(1)若l 经过点()2,0-,且AOB 90∠= ,求AB ;(2)若l 经过点1F ,且,A B 两点在双曲线Γ的左支上,则在x 轴上是否存在定点Q ,使得QA QB⋅为定值.若存在,请求出QAB 面积的最小值;若不存在,请说明理由.答案第1页,共15页参考答案:1.D【分析】利用不等式性质、交集、并集、补集定义求解.【详解】由题意,()()1,1,2,2A B A B ⋂=-⋃=-,所以()][()2,11,2A B A B ⋃⋂=--⋃ð.故选:D.2.A【分析】先利用复数乘法运算化简复数,再根据复数的几何意义确定对应点所在的象限.【详解】因为()22i 1i 2i 2i 22i z =⋅-=-=+,所以该复数在复平面内对应的点为()2,2,在第一象限.故选:A 3.D【分析】根据题意,由百分位数的计算公式,代入计算,即可得到结果.【详解】将数据从小到大排序可得10,12,14,14,15,16,20,24,共8个样本数据,则上四分位数即第75百分位数为80.756⨯=,即为1620182+=.故选:D 4.A【分析】使用诱导公式和二倍角公式,结合已知条件即可求解.【详解】ππππππsin sin 2coscos 2362362αααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-=----+ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭3ππcos cos 26αα⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭2ππcos 2cos 166αα⎛⎫⎛⎫⎛⎫=+-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2111021339⎛⎫⎛⎫=-⋅-= ⎪ ⎪ ⎪⎝⎭⎝⎭.故选:A.5.B【分析】先出求2(1,12)a b t +=+ ,再根据(2)a a b ⊥+ 即可得出t 的值,最后求b的模.【详解】由题意可知,因为(1,1)a =,(0,)b t = ,答案第2页,共15页所以2(1,1)2(0,)(1,12)a b t t +=+=+,又因为(2)a a b ⊥+ ,所以(2)0a a b ⋅+=,即()111120t ⨯+⨯+=,解得1t =-.所以||1b = .故选:B.6.B【分析】由20100S =,利用等差数列的性质推出101110a a +=,再利用基本不等式计算即得.【详解】由12020101120()10()1002a a S a a +==+=可得101110a a +=,因210,a a ≥>则等差数列{}n a 的公差0d ≥,故10110,0a a >>,则121011011()252a a a a +≤=,当且仅当10115a a ==时取等号,即当10115a a ==时,1011a a 取得最大值25.故选:B.7.B【分析】由题意画出图形,利用正弦定理求出BCD △的外接圆的半径,再由勾股定理求出三棱锥外接球的半径,代入球的表面积公式得答案.【详解】如图,设BCD △的外心为M ,过M 作底面的垂线MO ,使12MO BA =,则O 为三棱锥的外接球的球心,在BCD △中,由BC =3,5CD =,BD =7,得2223571cos 2352BCD +-∠==-⨯⨯,答案第3页,共15页故sin 2BCD ∠=,设BCD △的外接圆的半径为r ,则r =,2OM =,∴22226123OB R =+==.∴三棱锥外接球的表面积为2612444π4ππ33R =⨯=.故选:B 8.C【分析】根据直线与圆相切得圆心与点P 的距离,即结合正方形的性质可得符合的点P 的位置,从而可得结论.【详解】由()2214x y -+=可知圆心()1,0C ,半径为2,因为四边形PMCN 为正方形,且边长为圆C 的半径2,所以=PC 所以直线:0l x y m ++=上有且只有一个点P,使得=PC PC l ⊥,所以圆心C 到直线l的距离为,=3m =或5m =-,又0m >,所以3m =.故选:C.9.ABD【分析】利用分层抽样计算判断A ;求出第75百分位数判断B ;利用线性相关系数的意义判断C ;利用独立性检验的思想判断D.【详解】对于A ,该校高一年级女生人数是503020050500-=,A 正确;对于B ,由875%6⨯=,得第75百分位数为911102+=,B 正确;对于C ,线性回归方程中,线性相关系数r 绝对值越大,两个变量的线性相关性越强,C 错答案第4页,共15页误;对于D ,由20.053.937 3.841x χ=>=,可判断x 与y 有关联,此推断犯错误的概率不大于0.05,D 正确.故选:ABD 10.ABC【分析】不妨设a b <,根据选项C 的结构构造函数()a bf x x x =-,利用导数研究其单调性,结合题目不等式结论即可判定正确,再根据题目不等式结论证明得ba a ab >+及ab b a b>+,相加即可判断B 正确,结合C 判断A 正确,得解.【详解】不妨设a b <,先证明C :证明()a bf x x x =-在a x b <<上单调递减即可.()1111a b a b abf x ax bx ax x a ----⎛⎫='-=- ⎪⎝⎭,即要证明10b a b a b a x x a b ---⇔,即要证明111b aa b a b aa b a b a b-+-+->⇔>⇔>,因为()()11111111111a ba babb b a a b a b+-+-⎡⎤=-+>-+=>⎣⎦+-+-,得证,所以a b a b a a b b ->-,即a b b a a b a b +>+,故选项C 正确,D 错误;再证明B :()1111+1bbb a a a b ab a b a a a a a --+-+⎛⎫⎛⎫=≤+=< ⎪ ⎪⎝⎭⎝⎭,因此ba a ab >+,同理a b b a b >+,故1b aa b a b a b a b+>+=++,且1a b b a a b a b +>+>,所以AB 正确.故选:ABC【点睛】方法点睛:利用导数比较大小的基本步骤(1)作差或变形;(2)构造新的函数()h x ;(3)利用导数研究()h x 的单调性或最值;(4)根据单调性及最值,得到所证不等式.11.BCD【分析】直接证明()2xf x =,然后逐个判断选项即可.【详解】由()()()211f f x f x ==-知()0f x ≠恒成立,再由()20222x x x f x f f f ⎛⎫⎛⎫⎛⎫⎛⎫=⋅=> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭知()0f x >恒成立.设()()2log g x f x =,则()()221log 1log 21g f ===,且()()()()()()()()()2222log log log log g x y f x y f x f y f x f y g x g y +=+==+=+.故()11g =,()()()g x y g x g y +=+.由于()()()()()0000020g g g g g =+=+=,故()00g =.而()()()()111g x g x g g x +=+=+,故归纳即知()()g n n n =∈Z .又因为对()0m m ∈≠Z 有()11g x g x g m m ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭,故归纳即知()1n g n g n m m ⎛⎫⎛⎫=⋅∈ ⎪ ⎪⎝⎭⎝⎭Z .特别地有1m g m g m m ⎛⎫⎛⎫=⋅ ⎪ ⎪⎝⎭⎝⎭,故()11111m g g g m m m m m ⎛⎫⎛⎫=⋅=⋅= ⎪ ⎪⎝⎭⎝⎭,所以对(),0m n m ∈≠Z 有1n ng n g m m m⎛⎫⎛⎫=⋅= ⎪ ⎝⎭⎝⎭.这就得到了()()g q q q =∈Q ,从而()()2qf q q =∈Q .设有无理数r ,有理数数列{}n q 使得n q r →,由于()f x 是连续的,故()()n f q f r →,而()22n q r n f q =→,故()2r f r =.这就表明()2xf x =.由于()()11212f f -=≠-=-,故()2x f x =不是奇函数,故其图象并不关于原点对称,A 错误;由于()2xf x =在定义域上单调递增,且当()0,x ∞∈+时,()0221x f x =>=,故B ,C 正确;对于D ,由()()11222x x f x f x ++==可得()()()()()()()()()()24620222024...213520212023f f f f f f f f f f ======,从而()()()()()()()()()()24620222024...202413520212023f f f f f f f f f f +++++=,D 正确.故选:BCD.【点睛】关键点点睛:值得注意的是,如果去掉()f x 是连续函数的条件,并承认选择公理,则此时不能说明对无理数r ,有()2rf r =,且()f x 不一定单调递增.事实上,此时可以构造一个→R Q 的满足()11P =的线性映射()P x ,再取()()2P x f x =,即可得到反例.12.36【分析】把4人分成3组,再分配到3所学校即可.【详解】依题意,有2人去同一所学校,所以不同分配方案的种数为2343C A 6636=⨯=.故答案为:3613.[]0,4【分析】建立适当的平面直角坐标系,讨论,,,P AB P BC P CD P DA ∈∈∈∈四种情况,即可求出λμ+的取值范围.【详解】建立如图所示的平面直角坐标系:则()()1,0,2,1B E -,所以()2,AP AB AE λμλμμ=+=-,当P AB ∈时,有0210λμμ≤-≤⎧⎨=⎩,即01,0λμ≤≤=,此时λμ+的取值范围为[]0,1,当P BC ∈时,有2101λμμ-=⎧⎨≤≤⎩,即()123134λμλμμμ≤+=-+=+≤,此时λμ+的取值范围为[]1,4,当P CD ∈时,有0211λμμ≤-≤⎧⎨=⎩,即()()323234λμλμμλμ≤+=-+=-+≤,此时λμ+的取值范围为[]3,4,当P DA ∈时,有2001λμμ-=⎧⎨≤≤⎩,即()02333λμλμμμ≤+=-+=≤,此时λμ+的取值范围为[]0,3,综上所述,λμ+的取值范围为[]0,4.故答案为:[]0,4.14.63/163【分析】由题意,根据面面垂直的性质可得BC ⊥平面ABC ,利用线面垂直的性质可得BC ⊥CP ,进而213CP BP =-,由三角形的面积公式可得1sin BP θ=,即可求解.【详解】在Rt ABC 中,3π,36BC BAC =∠=,则233AB =,又平面ABC α⊥,平面ABC ,,AC AC BC BC α=⊥⊂ 平面ABC ,所以BC ⊥平面ABC ,连接CP ,CP α⊂,所以BC ⊥CP ,得22213CP BP BC BP =-=-,设ABP θ∠=(0πθ<<),则1sin 2ABP S AB BP θ=⋅ ,即3123sin 323BP θ=⋅⋅,得1sin BP θ=,当sin 1θ=即π2θ=即AB BP ⊥时,BP 取到最小值1,此时CP 取到最小值221161333BP -=-=.故答案为:63【点睛】关键点点睛:本题的解题关键是利用勾股定理和三角形面积公式计算得到213CP BP -1sin BP θ=,而sin 1θ≤,即为所求.15.(1)π3(2)33⎛ ⎝⎭【分析】(1)由两角和的正切公式结合题意化简得tan 3A =(2)设ABC CBD x ∠=∠=,由正弦定理把边化成角,再用三角形面积公式得34sin cos ACD S x x = ,结合导数求解即可.【详解】(1)由题)tan 3tan 31C BC =-,即)tan tan 1tan tan B C B C +=-,即tan tan 1tan tan B CB C+=-所以()tan B C +=()tan πA -=tan A =,又(0,π)A ∈,所以π3A =.(2)由题(1)知π3BAC ∠=,又2π3BDC ∠=,设ABC CBD x ∠=∠=,由BCD △中,2π3BDC ∠=,故π0,3x ⎛⎫∈ ⎪⎝⎭,则π2π2π2π233ACD x x ∠=---=-,由正弦定理有sin sin BC AC BAC x =∠,sin sin BC DCBDC x=∠,则2sin AC CD x ==,故ACD 面积()()2312sin sin π24sin cos 2ACD S x x x x =⋅-= ,令()34sin cos x x x ϕ=,则())224212sin cos 4sin 4sin cos sin cos sin x x x x xx xx x ϕ=-=+-',又π0,3x ⎛⎫∈ ⎪⎝⎭,所以()0x ϕ'>,知函数()34sin cos x x x ϕ=在π0,3⎛⎫ ⎪⎝⎭上单调递增,又()00ϕ=,π3ϕ⎛⎫= ⎪⎝⎭,故ACD 面积的取值范围为0,4⎛⎫ ⎪ ⎪⎝⎭.16.(1)0.163(2)136万元【分析】(1)根据频率分布直方图,I 级品中该指标小于或等于60的频率和II 级品中该指标大于60的频率,即可求解;(2)由题意分别计算A 、B 型手机的损失费用可得()5768f x x =-,结合一次函数的性质即可求解.【详解】(1)临界值60K =时,I 级品中该指标小于或等于60的频率为()0.0020.005100.07+⨯=,II 级品中该指标大于60的频率为0.1,故将1个I 级品芯片和1个II 级芯片分别应用于A 型手机和B 型手机,两部手机有损失的概率为:()()110.0710.10.163--⨯-=;(2)当临界值K x =时,I 级品中该指标小于或等于临界值K 的概率为()0.002100.005500.0050.23x x ⨯+⨯-=-,可以估计10000部A 型手机中有()100000.0050.23502300x x -=-部手机芯片应用错误;II 级品中该指标大于临界值K 的概率为()0.01100.03600.03 1.9x x ⨯+⨯-=-+,可以估计10000部B 型手机中有()100000.03 1.919000300x x -+=-部手机芯片应用错误;故可以估计芯片生产商的损失费用()()()0.085023000.0419000300f x x x =⨯-+⨯-5768x=-又[]50,55x ∈,所以()[]136,176f x ∈,即芯片生产商损失费用的最小值为136万元.17.(1)证明见解析;(2)存在14λ=.【分析】(1)先用线面垂直的判定定理证明AN ⊥平面1A MP ,再使用面面垂直的判定定理即可;(2)使用空间向量法直接求解两平面的夹角(用λ表示),再根据夹角条件,解关于λ的方程即可.【详解】(1)由于在直三棱柱111ABC A B C -中,有1AA ⊥平面ABC ,而AC 在平面ABC 内,故1AA AC ⊥.同时有11//AC A C ,且11AN A C ⊥,故AN AC ⊥.由于AN AC ⊥,1AA AC ⊥,且AN 和1AA 在平面11AA B B 内交于点A ,故AC ⊥平面11AA B B .由于AB 在平面11AA B B 内,故AB AC ⊥.取AB 的中点R ,由于,M R 分别是BC 和BA 的中点,故//MR AC ,而11//AC A C ,故11//MR A C ,即1//MR A P .由于,M R 分别是BC 和BA 的中点,可以得到1111122MR AC AC A P ===,所以有平行四边形1MRPA ,故1//A R MP .设1A R 和AN 交于点T ,由于11111222BN BB AA AB AR ====,1AB A A =,190ABN A AR ∠=︒=∠,从而得到ABN 全等于1A AR ,故19090TRA A RA ANB BAN RAT ∠=∠=∠=︒-∠=︒-∠.这就得到90TRA RAT ∠+∠=︒,从而90RTA ∠=︒,即1AN A R ⊥.而1A R MP ,故AN MP ^.由于11AN A C ⊥,即1AN A P ⊥,而AN MP ^,1A P 和MP 在平面1A MP 内交于点P ,故AN ⊥平面1A MP .由于AN ⊥平面1A MP ,AN 在平面ANP 内,故平面ANP ⊥平面1A MP .(2)有AB AC ⊥,又因为1AA ⊥平面ABC ,AB 和AC 在平面11AA B B 内,故1AA AB ⊥,1AA AC ⊥.由于1,,AB AC AA 两两垂直,故我们能够以A 为原点,1,,AB AC AA分别作为,,x y z 轴正方向,建立空间直角坐标系.由于题设条件和需要求证的结论均只依赖于线段间的比值,不妨设12AB AC AA ===,这就得到()0,0,0A ,()0,2,0B ,()2,0,0C ,()10,0,2A ,()10,2,2B ,()12,0,2C ,()1,1,0M ,()0,2,1N .据题设有111A P A C λ=,显然01λ≤≤,此时()2,0,2P λ.从而有()0,2,0AB = ,()10,0,2AA = ,()2,2,1NP λ=- ,()1,1,1MN =-.设()1,,n p q r = 和()2,,n u v w = 分别是平面11AA B B 和平面PMN 的法向量,则1110n AB n AA ⋅=⋅= ,220n NP n MN ⋅=⋅= .即220q r ==,220u v w u v w λ-+=-++=,从而可取()11,0,0n =,()23,21,22n λλ=+- .此时平面11AA B B 与平面PMN 所成的角的余弦值为121212cos ,n nn n n n ⋅==,=22784142λλ-+=,解得14λ=,所以存在14λ=,使得平面11AA BB 与平面PMN 18.(1)当n 为奇数数,()n f x 有1个零点;当n 为偶数时,()n f x 有2个零点(2)证明见解析【分析】(1)当0x ≥时,利用导数研究函数()n f x 的零点和零点的存在性定理可知其在(0,)+∞内有唯一零点;当0x <时,分类讨论n 为奇、偶数时零点的情况,即可下结论;(2)(i )易知11x =,当2n ≥时可得111()()n n n n f x f x +++>,利用()n f x 的单调性解不等式可得1n n x x +<,即可证明;(ii )由(i )1112n n x x +>>>,求和可得1212n n x x x ++++≥;由2ln 2(22)ln 21n n n ≥+>+得11ln 411ln(1)122n n n ++>>++,利用放缩法和函数单调性解不等式可证得11()22n nx <+,求和,结合等比数列数列前n 项求和公式计算即可证明.【详解】(1)当n 为奇数时,()n f x 有1个零点;当n 为偶数时,()n f x 有2个零点.证明如下:当0x ≥时,由1()1n n n f x x x x -=+++- ,得12()(1)10n n n f x nx n x --'=+-++> ,所以函数()n f x 在(0,)+∞上单调递增,又(0)10n f =-<,(1)10n f n =-≥,所以函数()n f x 在(0,)+∞内有唯一零点;当0x <时,11()(21)1n n f x x x x+=---,若n 为奇数,1210n x x +--<,则()0n f x <,此时()n f x 在(,0)-∞内无零点;若n 为偶数,设1()21n h x x x +=--,则()2(1)n h x n x '=-+,方程()0h x '=有一个解102()1nx n =-+,所以函数()h x 在0(,)x -∞上单调递减,在0(,0)x 上单调递增,且10(2)5(2)0,()(0)0n h h x h +-=---><<,此时()n f x 在(,0)-∞内有1个零点.综上,当n 为奇数时,()n f x 有1个零点;当n 为偶数时,()n f x 有2个零点.(2)(i )由(1)知,当1n =时,1()f x 在在(0,)+∞内的零点11x =,当2n ≥时,()0n n f x =,2(0)10,(1)0,01n n f f x =-<><<,则11111()10()n n n n n n n n n n n f x x x x x f x +++++=+++-=>= ,故1n n x x +<,所以数列{}n x 是一个递减数列;(ii )由(i )知,当1n =时,11x =,当2n ≥时,1111111()()()()1()022222n n n n f -=+++-=-< ,有1((1)02n n f f <,所以1112n n x x +>>>,求和可得1211122n n n x x x -++++≥+= ,当且仅当1n =时等号成立;当3n ≥时,012C C C 22n nn n n n =+++≥+ ,故2ln 2(22)ln 21n n n ≥+>+,则ln 2112n >+,得11ln 411ln(1)122n n n ++>>++,即11ln 4(1)ln(1)2n n +>++,即(1)114(1)2n n ++>+,即(1)1114211(1)2222n n n n n ++++->+,即(1)111111()222222n n n n ++-+>-,即(1)1111()112222()10()112222n n n n n n n nf f x ++-++=->=-,即11()22n nx <+,当2n =时,234x <,所以当2n ≥时,均有11(22n nx <+成立,求和可得1211211111111()()()1[1()]122222222n n n n n nx x x ---+++<+++=++-<+ .综上,121122n n nx x x +≤+++<+ .【点睛】方法点睛:在证明导数与数列不等式综合问题时,常常将上一问的结论直接应用到证明当中去,再综合考虑不等式特征合理选取方法巧妙放缩求和,即可实现问题求解.19.(1)(2)存在,【分析】(1)先利用点在双曲线上和双曲线的性质求出双曲线方程,然后分直线的斜率存在与否讨论,存在时,设出直线方程,利用韦达定理法表示出1212,x x x x +,再代入直线方程表示出12y y ,最后利用向量的数量积为零求出斜率k ,再代入弦长公式求出弦长;(2)假设存在,设直线方程x ty =-,利用韦达定理法表示出QA QB ⋅ ,要使QA QB ⋅为定值,则843421--=-,解出m 后得到点Q 的坐标,再用弦长公式表示出三角形的面积,最后利用换元法和分离常数法结合复合函数的单调性求出面积的最小值.【详解】(1)把(M 代入22221x y a b-=得:22461a b-=,又()1,F c ∴=.又222+=a b c ,解得1,a b ==∴双曲线方程为2212y x -=.若直线l 的斜率不存在时,:2l x =-,此时不妨设((,2,A B --.4620OA OB ⋅=-=-≠,舍去.若l 的斜率存在,设l 方程为()2y k x =+,代入2212y x -=,化简得()()222224420k xk x k ---+=,()()4222Δ16424224160k k kk =+-+=+>,设()()1112,,,A x y B x y ,则22121222442,22k k x x x x k k ++==--,()()()22121212122622242k y y k x k x k x x x x k -⎡⎤=+⋅+=+++=⎣⎦-.90AOB ∠=,得0OA OB ⋅= ,即12120x x y y +=.则222224260.122k k k k k +-+=∴=--.4AB =(2)假设存在(),0Q m ,使得QA QB ⋅为定值.设l 方程为x ty =-,代入2212y x -=,化简得()222140t y --+=.由题意()2222210,Δ48162116160t t t t -≠=--=+>.12122421y y y y t +==-.由题意221210,210,2y y t t <∴-<<.()()1122,,QA QB x m y x m y ⋅=-⋅-()()1122,,ty m y ty m y =-⋅-())()2212121()t y y m t y y m =+-++())2241(21t m t m t =+⋅⋅+-()22284(21t m t --+=++-要使QA QB ⋅ 41=-,解之得0m =.∴存在()0,0Q ,使得QA QB ⋅为定值1-.此时12112QAB S F Q y y =⋅-==答案第15页,共15页222231,1,12322u u t t u =≥=+<-=-,1,2u ⎡∴∈⎢⎣⎭.32QAB S u u∴=- 由复合函数的单调性可知32y u u =-在1,2⎡⎢⎣⎭递减,32y u u∴=-在1u =时取得最大值1.QAB S ∴的最小值为【点睛】关键点点睛:(1)求弦长时,可用弦长公式AB =,韦达定理表示出两根之和和两根之积;(2)对于直线过定点问题时,可采用向量垂直数量积为零,求出关于参数的方程,再讨论定点问题;(3)求圆锥曲线中三角形的面积最值问题时,可用弦长公式表示出面积,再结合换元法或基本不等式或函数的单调性求出面积的最值.。
江西省等三省十校2018届高三下学期联考数学(理)试卷(含答案)
江西省等三省十校2018届高三下学期联考数学(理科)试题(考试时间:120分钟 总分:150分)第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.)1. 已知集合{}2560A x x x =--≤,(){}ln 1B x y x ==-,则A B I 等于A. []1,6-B. (]1,6C. [)1,-+∞D. []2,3 2.设复数z 满足(1)3i z i -=+,则z = A .2 B .2 C .22 D .53.《九章算术》中有如下问题:“今有勾五步,股一十二步,问勾中容圆,径几何? ”其大意:“已知直角三角形两直角边长分别为5步和12步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是 A .215π B . 320π C. 2115π- D . 3120π- 4.执行如右图所示的程序框图,则输出的s 的值是 A .7 B .6 C .5 D .35.在等差数列{}n a 中,已知47,a a 是函数2()43f x x x =-+的两个零点,则{}n a 的前10项和等于A . 18-B . 9C .18D .206.已知Rt ABC ∆,点D 为斜边BC 的中点, 62AB =u u u r , 6AC =u u u r , 12AE ED =u u u r u u u r ,则AE EB ⋅u u u r u u u r等于A. 14-B. 9-C. 9D.147. 已知12e a dx x=⎰,则()()4x y x a ++ 展开式中3x 的系数为A.24B.32C.44D.56 8.函数321y x =-的图象大致是A. B. C. D.9.已知双曲线2222:1(0,0)x y C a b a b-=>>的实轴长为16,左焦点分别为F ,M 是双曲线C 的一条渐近线上的点,且OM MF ⊥,O 为坐标原点,若16OMF S ∆=,则双曲线C 的离心率为A .5B .5C . 3D . 3310.已知函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+≠><< ⎪⎝⎭,若()03f f π⎛⎫=-⎪⎝⎭,则ω的最小值是 A . 3 B . 2 C. D 111. 如图,格纸上小正方形的边长为1,粗实线画出的 是某多面体的三视图,则该多面体的外接球表面积为 A. 31π B. 32π C. 41π D. 48π12.已知函数()f x 的定义域为R ,(2)()f x f x -=--且满足,其导函数'()f x ,当1x <-时,(1)[()(1)'()]0x f x x f x +++<,且(1)4,f =则不等式(1)8xf x -<的解集为A . (),2-∞-B .()2,+∞C . ()2,2-D . ()(),22,-∞-+∞U第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分.)13. 若实数x y ,满足条件1230x x y y x≥⎧⎪-+≥⎨⎪≥⎩,则1y z x =+的最大值为14. 3sin 2,sin 2θθθθ=已知sin +cos =则 . 15. 已知,A B 是以F 为焦点的抛物线24y x =上两点,且满足4AF FB =u u u r u u u r,则弦AB 中点到准线距离为 .16. ∆∆在ABC 中,AB=AC,D 为AC 中点,BD=1,则ABC 的面积最大值为 . 三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或验算步骤.) 17. (12分)已知等比数列{}n a 的公比0q >,2318a a a =,且46,36,2a a 成等差数列.32()1求数列{}n a 的通项公式 ()2记2n nnb a =,求数列{}n b 的前n 项和n T 18. (12分)如图所示,该几何体是由一个直三棱柱ADE BCF -和一个四棱锥P ABCD -组合而成,其中AD AF ⊥,PA PB PC PD ===,2AE AD AB ===. (Ⅰ)证明:AD ⊥平面ABFE ;(Ⅱ)若四棱锥P ABCD -的高2,求二面角C AF P --的余弦值.19. (12分)“中国人均读书4.3本(包括络文学和教科书),比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用,出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天40名读书者进行调查,将他们的年龄分成6段:[)20,30, [)30,40, [)40,50, [)50,60, [)60,70, []70,80后得到如图所示的频率分布直方图.问:(1)估计在40名读书者中年龄分布在[)30,60的人数;(2)求40名读书者年龄的平均数和中位数; (3)若从年龄在[)60,80的读书者中任取2名,求这两名读书者年龄在[)70,80的人数X 的分布列及数学期望.20. (12分)已知椭圆2226:1(2)2x y C b b +=<< ,动圆P :22002()()3x x y y -+-= (圆心P 为椭圆C 上异于左右顶点的任意一点),过原点O 作两条射线与圆P 相切,分别交椭圆于M ,N 两点,且切线长最小值时,tan 2MOP ∠=. (Ⅰ)求椭圆C 的方程;(Ⅱ)判断MON ∆的面积是否为定值,若是,则求出该值;不是,请说明理由。
河北省衡水中学2023届高三下学期第六周周测数学(理)试题

河北省衡水中学2017届高三下学期第六周周测数学(理)试卷第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出地四个选项中,只有一项是符合题目要求地)1、复数2(1)1i z i+=-地共轭复数所对应地点位于复平面地A .第一象限B .第二象限C .第三象限D .第四象限2、已知等比数列{}n a 中,257a a -+=⎰,则6468(2)a a a a ++=地值为A .216π B .24π C .22π D .2π3、已知双曲线2222:1(0,0)x y C a b a b-=>>且经过点,则双曲线C 地标准方程为A .22123x y -=B .22139x y -=C .22146x y -= D .221x y -=4、阅读如图地程序框图,如输入4,6m n ==,则输出地,a i 分别等于A .12,2 B .12,3 C .24,2 D .24,35、已知条件p 关于x 地不等式13x x m -+-<有解;条件():(73)xq f x m =-为减函数,则p 成立是q 成立地A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6、已知不等式组3410043x y x y +-≥⎧⎪≤⎨⎪≤⎩表示地区域D,过区域D 中任意一点P 作圆地两条切线且切点分别为A 、B,当APB ∠最大时,cos APB ∠=AB .12 C..12-7、已知(0,)απ∈,若1tan()43πα-=,则sin 2α=A .45-B .45C .54-D .548、一个几何体地三视图如下图所示,正视图与侧视图为全等地矩形,俯视图为正方形,则该几何体地体积为 A .8 B .4 C .83 D .439、已知F 为抛物线24y x =地焦点,点A 、B 在该抛物线上,0OA OB ⋅=(其中O 为坐标原点),则ABO ∆与BFO ∆面积之差地最小值是A .4B .8C ..10、若函数111ln y x x =,函数223y x =-,则221212()()x x y y -+- 地最小值为A B .1 C D .211、若非零向量a 与向量b 地夹角为钝角,2b = ,且当12t =-时,()b ta t R -∈ ,向量c 满足()()c b c a -⊥- ,则当()c a b ⋅+ 取最大值时,c b -等于A B . C ..5212、已知函数()2ln ()()x x b f x b R x +-=∈,若存在1[,2]2x ∈,使得()()0f x xf x '+>,则实数b地取值范围是A .3(,)2-∞ B .9(,)4-∞ C .(,3)-∞ D .(-∞第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把解析填在答题卷地横线上。
江西省稳派教育2020届高三下学期调研考试(三)数学(文科)试题(含答案)

2019-2020学年高三年级调研考试(三)数学(文)卷一、选择题1.若集合A =x ,y x 2-2x =0,y ∈R ,B =x ,y y 2=2x ,则A ∩B 中元素的个数为()A.1B.2C.3D.4【答案】C【解析】因为A =x ,y x =0 或x =2,y ∈R ,B =x ,y y 2=2x ,所以A ∩B =0,0 ,2,2 ,2,-2 ,故选C .2.已知a +2i 2a ∈R 是纯虚数,则a +i =()A.3 B.5 C.3D.5【答案】B【解析】a +2i 2=a 2-4+4a i ,因为a +2i 2a ∈R 是纯虚数,所以a 2-4=04a ≠0,所以a =±2,由a +i =±2+i =5 ,故选B .3.若a <b <1且ab ≠0,则下列结论恒成立的是()A.a <12B.ab <b 2C.1a >1b>1D.ab +1>a +b【答案】D【解析】取a =23 ,b =34 ,可排除A ,取a =-2,b =-12 ,可排除B ,取a =-2,b =12,可排除C ,由a <b <1可得a -1 b -1 >0,展开得ab +1>a +b ,故选D .4.已知圆x 2+y 2-2x +4y =0关于双曲线C :x 22m -y 2m +1=1m >0 的一条渐近线对称,则m =()A.12B.13C.15D.17【答案】D【解析】圆x 2+y 2-2x +4y =0关于双曲线C :x 22m-y 2m +1=1m >0 的一条渐近线对称,则圆心1,-2 在渐近线y =-m +12mx 上,所以m +12m =2,m =17,故选D .5.已知a ,b 是单位向量,且a +b =2,-1 ,则a -b =()A.1B.2C.3D.2【答案】A【解析】因为a ,b 是单位向量,a +b =2 ,-1 ,两边平方得2a ⋅b =1,所以a -b =a 2-2a ⋅b +b 2=1,故选A .6.已知等差数列a n 的前n 项和为S n ,若a 6=2,a 2+a 10 2a 3+a 9 =12,则S 5=()A.5B.3C.-3D.-5【答案】D【解析】由题意得a 2+a 10 2a 3+a 9 =2a 6a 3+a 3+a 9 =2a 6a 3+2a 6 =4a 3+4 =12,可得a 3=-1,所以S 5=5a 3=-5,故选D .7.新冠肺炎病毒可以通过飞沫方式传染,已知甲通过检测确诊为新冠肺炎,经过追踪发现甲有A ,B ,C ,D ,E 5名密切接触者,现把这5人分为2组(一组2人,一组3人),分别送到2个医院进行隔离观察,则A ,B 在同一个医院的概率为()A.15B.310C.25D.12【答案】C【解析】把A ,B ,C ,D ,E 分为2组(一组2人,一组3人),结果有:AB ,CDE ,AC ,BDE ,AD ,BCE ,AE ,BCD ,BC ,ADE ,BD ,ACE ,BE ,ACD ,CD ,ABE ,CE ,ABD ,DE ,ABC ,共10种,A ,B 在同一个医院的结果有:AB ,CDE ,CD ,ABE ,CE ,ABD ,DE ,ABC ,共4种,所以所求概率P =410 =25 ,故选C .8.已知函数f x =1,x >00,x =0-1,x <0,g x =sinπx ,则下列结论错误的是()A.g f x =0B.f f x =f xC.f x g x =sinπxD.f g x +2 =1【答案】C【解析】由f x =1,x >00,x =0-1,x <0,g x =sinπx ,可得当x >0时,g f x =g 1 =sinπ=0,当x =0时,g f x =g 0 =sin0=0,当x <0时g f x =g -1 =sin -π =0,所以A 正确;当x >0时,f x =1,f f x =f 1 =1,f f x =f x 成立,当x =0时,f 0 =0,f f 0 =f 0 =0,f f x =f x 成立,当x <0时,f x =-1,f f x =f -1 =-1,f f x =f x 成立,所以B 正确,由f 32 g 32 =-1,可知C 错误,由g x ≥-1,g x +2≥1,可知f g x +2 =1正确,故选C .9.已知函数f x =x 3+ax 2-3x +b 满足f x +f -x =2,则f x 的图象在x =1处的切线方程为()A.y =-1B.y =0C.y =x -1D.y =-x +1【答案】A【解析】由f x +f-x=2可得2ax2+2b=2,所以a=0,b=1,f x =x3-3x+1,f x =3x2-3,f1 =-1,f 1 =0,所以f x 的图象在x=1处的切线方程为y=-1,故选A.10.《算法统宗》全称《新编直指算法统宗》,共17卷,是中国古代数学名著,明朝数学家程大位著.书中有这样一道著名的题目:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大、小和尚各几丁?”现给出该问题中求小僧人数的算法的程序框图,则图中①②可分别填入()A.s=3m+n3 ;n=100B.s=3n+m3 ;n=100C.s=3n+m3 ;s=100D.s=3m+n3 ;s=100【答案】D【解析】由程序框图可知,n表示小僧人数,m表示大僧人数,根据“大僧三个更无争,小僧三人分一个”,设馒头数为s,则s=3m+n3 ,所以①中填入s=3m+n3,当s=100时结束程序,输出n,故选D.11.如图,正三角形ABC为圆锥的轴截面,D为AB的中点,E为弧BC的中点,则直线DE与AC所成角的余弦值为()A.13B.12C.22D.34【答案】C【解析】取BC 中点O ,BO 中点F ,连接OD ,OE ,FE ,DF ,则∠ODE 就是直线DE 与AC 所成角.设AB =4,则OD =2,OF =1,OE =2,DF =3 ,EF =OE 2+OF 2 =5 ,DE =DF 2+EF 2 =22 ,所以∠ODE =π4 ,即直线DE 与AC 所成角的余弦值为22,故选C .12.已知椭圆C :x 2a 2 +y 2b2 =1a >b >0 的右焦点为F ,设c =a 2-b 2 ,直线x c +y b =1与椭圆C 在第四象限交于点A ,点A 在x 同上的射影为B ,若AB ⋅AF =49b 2,则椭圆C 的离心率为()A.15B.5 5C.25D.10 5【答案】B【解析】由AB ⊥x 轴可得AB ⋅AF =AB 2,所以AB =2b 3,又AB FB=tan ∠BFA =b c ,所以FB =2c 3 ,所以A 5c 3 ,-2b3,代入椭圆C 的方程得25c 29a 2+49 =1,所以e =5 5,故选B .二、填空题13.若函数f x =x 2,x ≥1a x +1 ,x <1的值域为R ,则a 的取值范围是______.【答案】12 ,+∞ 【解析】当x ≥1时,f x =x 2≥1,若a =0,x <1时,f x =0,f x 的值域不是R ;若a <0,x <1时,f x >2a ,f x 的值域不是R ,若a >0,x <1时,f x <2a ,所以当2a ≥1时,f x 的值域为R ,所以a 的取值范围是12,+∞ .14.正项数列a n 满足a 2=1,a 2n +1a n=2a n +a n +1,则使a n >100的最小的n 值为______.【答案】9【解析】由a 2n +1a n=2a n +a n +1得a 2n +1-a n a n +1-2a 2n =0,即a n +1+a n a n +1-2a n =0,因为a n >0,所以a n +1-2a n =0,a n +1=2a n ,a n =a 2⋅2n -2=2n -2,a 8=64,a 9=128,所以使a n >100的最小的n 值为9.15.已知f x =sin x +π3 ,若方程f x =a 在0,5π3上只有4个不同实根x 1,x 2,x 3,x 4x 1<x 2<x 3<x 4 ,则a x 1+2x 2+2x 3+x 4 的最小值为______.【答案】23π【解析】画出f x 的图象,由图象可知3 2≤a <1,x 1+x 2=2×π6 =π3 ,x 2+x 3=2×2π3 =4π3 ,x 3+x 4=2×7π6 =7π3,相加得x 1+2x 2+2x 3+x 4=4π,所以a x 1+2x 2+2x 3+x 4 的最小值为23 π.16.在△ABC 中,AB =AC =3,BC =3,点D 在BC 上,且BD =2DC ,将△ABD 沿AD 折起,使点B 到达点P 位置,且AP ⊥AC ,则三棱锥P -ACD 的外接球半径为______.【答案】7 2【解析】由题意可得AD =DC =1,AB ⊥AD ,因为AP ⊥AC ,所以三棱锥P -ACD 中,AP ⊥底面ADC ,把三棱锥P -ACD 补成三棱柱,则该三棱柱的外接球就是三棱锥P -ACD 的外接球,球心是三棱柱上下底面外接圆圆心连线的中点,底面外接圆半径r =12 ⋅3 sin120°=1,又AP =3,所以三棱锥P -ACD 外接球半径R =12+3 22 =72.三、解答题17.2020年上半年,随着新冠肺炎疫情在全球蔓延,全球超过60个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为2020年第一季度企业成立年限与倒闭分布情况统计表:企业成立年份20192018201720162015企业成立年限x 12345倒闭企业数量(万家) 5.28 4.72 3.58 2.70 2.15倒闭企业所占比例y %21.4%19.1%14.5%10.9%8.7%(1)由所给数据可用线性回归模型拟合y 与x 的关系,请用相关系数加以说明;(2)建立y 关于x 的回归方程,预测2014年成立的企业中倒闭企业所占比例.参考数据:5i =1y i =74.6 ,5i =1x i y i =190.2 ,5i =1y i-y 2≈10.70,10 ≈3.16,相关系数r =ni =1x i y i -nx yn i =1x i -x 2ni =1y i -y2,样本x i ,y i i =1,2,...,n 的最小二乘估计公式为b =ni =1x i y i -nx yni =1x 2i -nx2 ,a =y -b x .【答案】(1)用线性回归模型拟合y 与x 的关系;(2)4.84%【解析】(1)由表中数据及参考数据可得x =3,5i =1x i -x 2=10 ,5i =1y i -y 2≈10.70,由5i =1x i =15 ,5i =1y i =74.6 ,可得x =3,y =14.92,所以5i =1x i y i -5x y=190.2-5×3×14.92=-33.6 ,所以r ≈-33.610.70×3.16≈-0.99,因为y 与x 的相关系数近似为-0.99,说明y 与x 的相关程度相当高,从而可以用线性回归模型拟合y 与x 的关系.(2)b =5i =1x i y i -5x y5i =1x 2i -5x 2 =-33.655-5×9 =-3.36,则a =y -b x=14.92+3.36×3=25,所以y 关于x 的回归方程y=-3.36x +25.当x =6时,y=-3.36×6+25=4.84,所以预测2014年成立的企业中倒闭企业所占比例为4.84%.18.已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足c tan A tan C+1 -9b =0.(1)求cos A 的值;(2)若点D 在边BC 上,AD 平分角A ,且AD =5 ,求1b+1c 的值.【答案】(1)19 ;(2)23【解析】(1)由c tan Atan C+1 -9b =0及正弦定理可得sin C ⋅sin A cos C +sin C cos Asin C cos A-9sin B =0,即sin A +Ccos A-9sin B =0,因为sin A +C =sin π-B =sin B ,且sin B ≠0,所以cos A =19.(2)因为cos A =19 ,所以sin A =1-cos 2A =459 ,因为AD 平分角A ,所以sin ∠BAD =sin ∠CAD =1-cos A 2=1-19 2=23,由S △ABC =S △ADB +S △ADC ,可得12 bc sin A =12 c ⋅AD sin ∠BAD +12b ⋅AD sin ∠CAD ,12 bc ⋅459 =12 c ⋅5 ⋅23 +12 b ⋅5 ⋅23 ,整理得23bc =b +c ,所以1b+1c =23 .19.如图,在三棱柱ABC -A 1B 1C 1中,AA 1⊥底面ABC ,点D 为BB 1中点,点E 为点B 关于直线AC 的对称点,AB =BC =AA 1=2,AC =22.(1)求证:平面AC 1D ⊥平面ACC 1A 1;(2)求三棱锥E -ADC 1的体积.【答案】(1)见解析;(2)三棱锥E -ADC 1的体积为23【解析】(1)设AC 1的中点为F ,连接BE 与AC 交于G ,则点G 为AC 中点,连接DF ,FG ,则FG ∥CC 1,且FG =12CC 1.又D 为BB 1的中点,所以DB ∥FG ,且DB =FG ,所以四边形BDFG 为平行四边形,所以BG ∥DF ,因为AA 1⊥底面ABC ,所以平面ABC ⊥平面ACC 1A 1,因为AB =BC ,G 为AC 中点,所以BG ⊥平面ACC 1A 1,所以DF ⊥平面ACC 1A 1.又DF ⊂平面AC 1D ,所以平面AC 1D ⊥平面ACC 1A 1.(2)由(1)知BE ∥DF ,所以点E ,B 到平面ADC 1的距离相等,所以V 三棱锥E -ADC 1=V 三棱锥B -ADC 1=V 三棱锥A -BDC 1.由AB =BC =2,AC =22,可得AB ⊥BC ,因为平面ABC ⊥平面BCC 1B 1,AB ⊥平面BCC 1B 1,又△BDC 1的面积S =12 ×1×2=1,所以V 三棱锥A -BDC 1=13 ×AB ×S =13 ×2×1=23,所以三棱锥E -ADC 1的体积为23.20.已知抛物线C :y 2=2px p >0 与直线y =x +1只有一个公共点,点A ,B 是抛物线C 上的动点.(1)求抛物线C 的方程;(2)①若k OA +k OB =1,求证:直线AB 过定点;②若P x 0,y 0 是抛物线C 上与原点不重合的定点,且k PA +k PB =0,求证:直线AB 的斜率为定值,并求出该定值.【答案】(1)y 2=4x ;(2)①见解析;②见解析,定值为-2y 0 .【解析】(1)y 2=2px 与y =x +1联立得y 2-2py +2p =0因为抛物线C 与直线y =x +1只有一个公共点,所以△=2p 2-8p =0,p =2,所以抛物线C 的方程为y 2=4x .(2)①设A y 214 ,y 1 ,B y 224 ,y 2,则k OA +k OB =4y 1 +4y 2=1,所以y 1y 2y 1+y 2 =4,又k AB =y 1-y 2y 214 -y 224=4y 1+y 2 ,所以直线AB 的方程为y -y 1=4y 1+y 2x -y 214,即y =4y 1+y 2 x +y 1-y 21y 1+y 2 =4y 1+y 2 x +y 1y 2y 1+y 2 =4y 1+y 2x +4,当x =0时y =4,所以直线AB 过定点0,4 .②设A y 214 ,y 1 ,B y 224 ,y 2,则k PA +k PB =y 1-y 0y 214 -y 204 +y 2-y 0y 224 -y 204=4y 1+y 0 +4y 2+y 0 =0,所以y 1+y 0+y 2+y 0=0,y 1+y 2=-2y 0,所以直线AB 的斜率k AB =y 1-y 2y 214 -y 224=4y 1+y 2 =-2y 0 .即直线AB 的斜率为定值-2y 0 .21.已知函数f x =ax 2ln x +12-x ln x +1.(1)若a <e2,讨论f x 的单调性;(2)若a =1,x ≥1,求证:f x >32 x 2-2x +1+sin x .【答案】(1)当a ≤0时,f x 在0,1e 上单调递增,在1e,+∞ 上单调递减;当0<a <e 2 时,f x 在0,1e 和12a ,+∞ 上单调递增,在1e ,12a上单调递减;(2)见解析【解析】(1)因为f x =ax 2ln x +12-x ln x +1,所以f x =2ax ln x +2ax -ln x -1=2ax -1 ln x +1 x >0 ,①若a ≤0,则2ax -1<0,当x ∈0,1e时,f x >0,f x 是增函数,当x ∈1e,+∞ 时,f x <0,f x 是减函数;②若0<a <e 2 ,即12a >1e ,当x ∈0,1e 和x ∈12a ,+∞ 时,f x >0,f x 是增函数,当x ∈1e ,12a时,f x <0,f x 是减函数.综上可得,当a ≤0时,f x 在0,1e 上单调递增,在1e,+∞ 上单调递减;当0<a <e 2 时,f x 在0,1e 和12a ,+∞ 上单调递增,在1e ,12a上单调递减.(2)当a =1时,要证f x >32x 2-2x +1+sin x ,只需证f x ≥32 x 2-2x +2,即证x 2-x ln x -1+1x≥0,因为x ≥1,所以x 2-x ≥0,设g x =ln x -1+1x,则g x =1x -1x 2 =x -1x2 ≥0,所以g x 在1,+∞ 上是增函数,g x ≥g 1 =0,ln x -1+1x≥0,所以x 2-x ln x -1+1x≥0,因此f x >32x 2-2x +1+sin x 成立22.平面直角坐标系xOy 中,点A 的坐标为3,3 ,在以坐标原点为极点,x 轴的正半轴为极轴的极坐标系中,曲线C 的极坐标方程为ρ2=2+22 ρsin θ+π4.(1)求曲线C 的参数方程;(2)若P ,Q 是曲线C 上的不同两点,且AP 2+AQ 2=40,求证:线段PQ 的中点M 恒在一条直线上,并求出此直线的直角坐标方程.【答案】(1)曲线C 的参数方程x =1+2cos φy =1+2sin φ(φ为参数);(2)x +y =0【解析】(1)ρ2=2+22 ρsin θ+π4=2+2ρcos θ+2ρsin θ,由ρ2=x 2+y 2,ρcos θ=x ,ρsin θ=y ,得曲线C 的直角坐标方程为x 2+y 2=2+2x +2y ,即x -1 2+y -1 2=4,设x -1=2cos φ,y -1=2sin φ,得曲线C 的参数方程x =1+2cos φy =1+2sin φ(φ为参数).(2)设P 1+2cos φ1,1+2sin φ1 ,Q 1+2cos φ2,1+2sin φ2 ,设M x ,y ,则x =1+cos φ1+cos φ2,y =1+sin φ1+sin φ2,由AP 2+AQ 2=40,得2cos φ1-2 2+2sin φ1-2 2+2cos φ2-2 2+2sin φ2-2 2=40,整理得1+cos φ1+cos φ2+1+sin φ1+sin φ2=0,即x +y =0,所以点M 恒在直线x +y =0上,所以此直线的直角坐标方程为x +y =0.23.已知函数f x =x -m -x -2m .(1)若m =2,求不等式f x >1的解集;(2)若对满足a >b >0的任意实数a ,b ,关于x 的方程f x =a +1a -b b的解集∅,求m 的取值范围.【答案】(1)72,+∞ ;(2)m 的取值范围是-3,3【解析】解:(1)当m =2时,f x =x -2 -x -4 =-2,x <22x -6,2≤x ≤42,x >4,当x <2时,-2>1不成立,当2≤x ≤4时,由2x -6>1,得72<x ≤4,当x >4时,2>1成立,所以不等式f x >1的解集为72,+∞ .(2)因为f x =x -m -x -2m ≤x -m -x -2m =m ,所以-m ≤f x ≤m ,又a +1a -b b =a -b +b +1a -b b ≥33a -b b ⋅1a -b b=3,当a -b =b =1a -b b,即a =2,b =1时取等号,若对满足a >b >0的任意实数a ,b ,关于x 的方程f x =a +1a -b b的解集为∅,则m <3,所以m 的取值范围是-3,3 .。
江西省新余市高三数学上学期第十四次周练试题(零班)理(new)

江西省新余市2018届高三数学上学期第十四次周练试题(零班)理第Ⅰ卷(选择题:共50分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}ln(1)M x y x ==-,集合{|,}x N y y e x R ==∈(e 为自然对数的底数),则 MN =( )A.{|1}x x < B 。
{|1}x x > C 。
{|01}x x << D 。
∅ 2。
若复数z 满足()2z 12i 13i (i -+=+为虚数单位),则Z =( )A 。
—2—4iB 。
-2+4i C.4+2i D.4-2i3.若()f x 为偶函数,且当[)0,x ∈+∞时,()2sin (01)2ln (1)x x f x x x x π⎧≤≤⎪=⎨⎪+>⎩,则不等式()11f x -<的解集为( )A.{}02x x <<B.{}11x x -<<C.{}01x x <<D.{}22x x -<<4.现有5人参加抽奖活动,每人依次从装有5张奖票(其中3张为中奖票)的箱子中不放回地随机抽取一张,直到3张中奖票都被抽出时活动结束,则活动恰好在第4人抽完后结束的概率为( ) A.110 B 。
15 C.310 D 。
255。
已知等差数列{}n a 的公差0d ≠,且1a ,3a ,13a 成等比数列,若11a =,n S 为数列{}n a 的前n 项和, 则2163n n S a ++的最小值为( )A 。
3B 。
4 C.232 D 。
92侧视图212俯视图2正视图6。
已知“整数对”按如下规律排成一列:()()()()()()1,1,1,2,2,1,1,3,2,2,3,1,()1,4,()()2,3,3,2,()4,1,。
设第2017个整数对为(),a b ,若在从a 到b 的所有整数中(含,a b )中任取2个数,则这两个数之和的取值个数为( ) A 。
江西省南昌市2018届高三下学期三模(文科)数学试卷

— 高三文科数学(模拟三)第1页(共4页) —NCS20180607项目第三次模拟测试卷文科数学本试卷分必做题和选做题两部分.满分150分,考试时间120分钟.注意事项:1.答卷前,考生务必将自已的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人的准考证号、姓名是否一致.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答题无效.3.考试结束后,监考员将答题卡收回.一.选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}3,2a M =,{},N a b =,若{}1M N =,则MN = A .{}1,2,3 B .{}0,2,3 C .{}0,1,2 D .{}0,1,32.已知a R ∈,i是虚数单位,若i z a =,_4z z ⋅=,则a 为A .1或1-B .1C .1-D .不存在的实数3.“11m>”是“关于x 的方程sin x m =有解”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件4.已知函数2(1)()ln (1)x x f x x x -≤⎧=⎨>⎩,那么函数()f x 的值域为A .(,1)[0,)-∞-+∞B .(,1](0,)-∞-+∞C .[1,0)-D .R5.在平面直角坐标系中,已知双曲线C 与双曲线2213y x -=有公共的渐近线,且经过点(2)P -,则双曲线C 的焦距为 AB.C. D.6.执行如图所示的程序框图,若输出的57S =,则判断框内应填入的条件是A . 4k >B .5k >C .6k >D .7k >7.已知324log 2,log 3,log 7a b c ===,则,,a b c 的大小关系为A .a b c <<B .b a c <<C .c a b <<D .a c b <<8.在平面直角坐标系中,O 为坐标原点,点(1,3)P 、Q(1,1)-,则POQ ∆外接圆的半径为A.2 BC.2D— 高三文科数学(模拟三)第2页(共4页) —9.将函数()sin()6f x x π=+的图象上所有点的横坐标压缩为原来的12,纵坐标保持不变,得到()g x 图象.若12()()2g x g x +=,且[]12,2,2x x ππ∈-,则12x x -的最大值为A .πB .2πC .3πD .4π10.某几何体的三视图如图所示,其中主视图由矩形和等腰直角三角形组成,左视图由半个圆和等腰直角三角形组成,俯视图的实线部分为正方形,则该几何体的表面积为A.3π+B.4(1)π C.4(π D .4(1)π+11.为培养学生分组合作能力,现将某班分成,,A B C 三个小组,甲、乙、丙三人分到不同组,某次数学建模考试中三人成绩情况如下:在B 组中的那位的成绩与甲不一样,在A 组中的那位的成绩比丙低,在B 组中的那位的成绩比乙低.若甲、乙、丙三人按数学建模考试成绩由高到低排序,则排序正确的是A.甲、丙、乙B.乙、甲、丙 C .乙、丙、甲 D .丙、乙、甲12.已知双曲线2222:1x y C a b-=(0,0)a b >>的左、右焦点分别为12F F 、,以2F 为圆心的圆与双曲线C 在第一象限交于点P ,直线1PF 恰与圆2F 相切于点P ,与双曲线左支交于点Q ,且12PQ F Q =,则双曲线的离心率为ABCD二.填空题:本大题共4小题,每小题5分,共20分.13.中国数学家刘微在《九章算术注》中提出“割圆”之说:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”.意思是“圆内接正多边形的边数无限增加的时候,它的周长的极限是圆的周长,它的面积的极限是圆的面积”.如图,若在圆内任取一点,则此点取自其内接正六边形的概率 .14.已知函数2()x f x e x =-的图象在点(1,(1))f 处的切线过点(0,)a ,则a = .15.已知向量(1,2)m =,(2,3)n =,则m 在m n -方向上的投影为 .16.现某小型服装厂锁边车间有锁边工10名,杂工15名,有7台电脑机,每台电脑机每天可给12件衣服锁边;有5台普通机,每台普通机每天可给10件衣服锁边.如果一天至少有100件衣服需要锁边,用电脑机每台需配锁边工1名,杂工2名,用普通机每台需要配锁边工1名,杂工1名.用电脑机给一件衣服锁边可获利8元,用普通机给一件衣服锁边可获利6元,则该服装厂锁边车间一天最多可获利 元.— 高三文科数学(模拟三)第3页(共4页) —三.解答题:共70分. 解答应写出文字说明、证明过程或演算步骤. 第17题-21题为必考题,每个试题考生都必须作答.第22题、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(本小题满分12分) 已知数列{}n a 的各项均为正数,且22(21)0,n n a na n n N *--+=∈. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若2n n n b a =⋅,求数列{}n b 的前n 项和n T .18.(本小题满分12分) 如图,多面体ABCDEF 中,ABCD 为正方形,2AB =,3AE =,DE =EF =,cos 5CDE ∠=,且//EF BD . (Ⅰ)证明:平面ABCD ⊥平面EDC ;(Ⅱ)求三棱锥A EFC -的体积.19.(本小题满分12分)十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫.某帮扶单位为帮助定点扶贫村真正脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用互联网电商渠道进行销售.为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分布在区间[15003000],内(单位:克),统计质量的数据作出其频率分布直方图如图所示: (Ⅰ)按分层抽样的方法从质量落在[17502000),,[20002250),的蜜柚中随机抽取5个,再从这5个蜜柚中随机抽2个,求这2个密柚质量均小于2000克的概率;(Ⅱ)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有5000个蜜柚待出售,某电商提出两种收购方案:A .所有蜜柚均以40元/千克收购;B .低于2250克的蜜柚以60元/个收购,高于或等于2250的以80元/个收购.请你通过计算为该村选择收益最好的方案.— 高三文科数学(模拟三)第4页(共4页) — 20.(本小题满分12分)已知动圆C 过点(1,0)F ,并与直线1x =-相切.(Ⅰ)求动圆圆心C 的轨迹方程E ;(Ⅱ)已知点(4,4),(8,4)P Q -,过点Q 的直线l 交曲线E 于点,A B ,设直线,PA PB 的斜率分别为12k k ,,求证:12k k 为定值,并求出此定值.21.(本小题满分12分)已知函数21()x x x f x e-+=. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)当[0,2]x ∈时,2()2f x x x m ≥-++恒成立,求m 的取值范围.(二)选考题:共10分.请考生在第(22)、(23)两题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B 铅笔在答题卡上把所选题目的题号涂黑,把答案填在答题卡上.22.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线1C 的参数方程为:cos sin x y θθ=⎧⎨=⎩(θ为参数,[]0,θπ∈),将曲线1C经过伸缩变换:x x y '=⎧⎪⎨'=⎪⎩得到曲线2C . (Ⅰ)以原点为极点,x 轴的正半轴为极轴建立坐标系,求2C 的极坐标方程;(Ⅱ)若直线cos :sin x t l y t αα=⎧⎨=⎩(t 为参数)与12,C C 相交于,A B 两点,且1AB =,求α的值.23.(本小题满分10分)选修4-5:不等式选讲已知函数()|1|f x x =+.(Ⅰ)求不等式()|21|1f x x <+-的解集M ;(Ⅱ)设,a b M ∈,证明:()()()f ab f a f b >--.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省正阳县第二高级中学
2017-2018学年下期高三文科数学周练(三)
一.选择题:
1. 已知集合A={2,a},B={x|1<x<4},若{2}A
B =,则实数a 的值不可能为( )
A .1
B .3
C .4
D .5 2.复数23(1)z i =-++在复平面内对应的点在( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限 3. 已知函数9
4(1)1
y x x x =-+
>-+,当x=a 时,y 取得最小值b ,则a+b=( ) A .-3 B .2 C .3 D .8
4. 在圆221x y +=内任取一点,以该点为中点作弦,
( ) A .1:2 B . 1:3 C .1:4 D .1:5
5.双曲线
22
145
x y -=的左焦点到右顶点的距离为( ) A .1 B .2 C .4 D .5
6.已知函数()sin()(0,0,0)f x A x A ωϕωϕπ=+>><<的部分图象如图所示,则下列判断错误的是( )
A .A=2
B .2ω=
C .f(0)=1
D .56
πϕ=
7. 实数x ,y 满足条件1011x y y x -+≤⎧⎪≤⎨⎪>-⎩
,则22
(2)x y -+的最小值为( )
A.
2
8.P 为抛物线2
4x y =-上一点,A(1,0),则P 到此抛物线的准线的距离与P 到点A 的距离之和的最小值为( )
A .
12 B .2
C .2
D 9. 执行如图所示的程序框图,若输入x 的值为5-,则输出y 的值是 (A) -1 (B) 1 (C) 2 (D) 1
4
10.下列函数中,既是奇函数,又在(1,)+∞上递增的是( ) A .36y x x =- B .22y x x =- C .y=sinx D .33y x x =- 11.若体积为4的长方体的一个面的面积为1,且这个长方体8个顶点都在球O 的球面上,则球O 表面积的最小值为( ) A .12π B .16π C .18π D .24π
12. 若定义在区间]2016,2016[-上的函数)(x f 满足:对于任意的
12,[2016,2016]x x ∈-,都有
1212()()()2016f x x f x f x +=+-,且0>x 时,有
2016)(<x f ,)(x f 的最大值、最小值分别为N M ,,则M+N 的值为
(A )2015 (B )2016 (C )4030 (D )4032
二.填空题:
13. 已知函数f (x )=2
2x -x (2)f ',则函数f (x )的图像在点(2,f (2))处的切线方程是_________.
14. 在△ABC 中,内角 A B C ,,所对的边分别为, , a b c ,且BC ,则c b
b c +取得最大值时,内角A 的值为 .
15.某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为 .
16. 数列{}n a 的通项2
2(cos
sin )33
n n n a n ππ=-,其前n 项和为n S ,则30S =________.
三.解答题:
17. 已知等差数列}{n a 的前n 项和为n S ,数列}{n b 是等比数列,满足31=a ,11=b ,
1022=+S b ,3252a b a =-. (Ⅰ)求数列}{n a 和}{n b 通项公式;
(Ⅱ)令⎪⎩⎪⎨⎧=)
(,)
(,2
为偶数为奇数n b n S c n n n ,设数列}{n c 的前n 项和n T ,求n T 2.
18. 某班甲、乙两名学同参加100米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:
绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(2)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率.
(3)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
19. 如图,多面体ABCDEF 中,四边形ABCD 是边长为2的正方形,四边形EFBD 为等腰
梯形,//EF BD ,1
2
EF BD =
,平面⊥EFBD 平面ABCD .
(1)证明:AC ⊥平面EFBD ;
(2)若2
10
=BF ,求多面体ABCDEF 的体积.
20. 已知抛物线22x py =上点P 处的切线方程为10x y --=. (Ⅰ)求抛物线的方程;
(Ⅱ)设11(,)A x y 和22(,)B x y 为抛物线上的两个动点,其中12y y ≠且124y y +=,线段AB 的垂直平分线l 与y 轴交于点C ,求ABC ∆面积的最大值.
21. 设函数32,0()(0),0
x
x x x f x a axe x ⎧->⎪
=>⎨≤⎪⎩ (1)求曲线g(x)=f(x)+lnx 在点(1,f(1))处的切线方程; (2)若f(x)+f(a)0≥对(,0]-∞恒成立,求实数a 的取值范围
四.选作题:
22. 在直角坐标系xOy 中,曲线1C 的参数方程为cos 2sin x y αα
=⎧⎨
=⎩,
(α为参数),将曲线1C 经过
伸缩变换2x x y y '=⎧⎨'=⎩
,
后得到曲线2C .在以原点为极点,x 轴正半轴为极轴的极坐标系中,直线
l 的极坐标方程为cos sin 100ρθρθ--=.
(1)说明曲线2C 是哪一种曲线,并将曲线2C 的方程化为极坐标方程;
(2)已知点M 是曲线2C 上的任意一点,求点M 到直线l 的距离的最大值和最小值.
C
A
23.已知函数()||f x x a =+.
(1)当1=a 时,求不等式()211f x x ≤+-的解集;
(2)若函数()()3g x f x x =-+的值域为A ,且[]2,1A -⊆,求a 的取值范围.
参考答案:
1-7.BBCCDD 7-12.DDADCD 13.Y=4x-8 14.30°17.(1)121,2n n n a n b -=+=(2)222
(41)213
n n n T n =+-+ 18.(1)乙(2)0.8(3)104:225
19.(1)略(2)20.(1)2
4x y =(2)8
21.(1)y=2x-2 (2)a ≥
22.(1)圆心在原点,半径为2的圆,其极坐标方程为2ρ=(2)2和2 23.(1)(,1][1,)-∞-+∞(2)(,1][5,)-∞+∞。
