物化各种公式概念总结
物化期末公式总结

物化期末公式总结一、热力学方面的公式1. 热力学第一定律:ΔU = Q + W这个公式表示了能量的守恒,其中,ΔU是系统内能的变化,Q是系统吸收或释放的热量,W是系统对外界做功。
2. 热力学第二定律:ΔS≥0这个公式表示了熵的增加趋势,系统在无限接近绝对零度时,熵趋于最小。
3. 热力学第三定律:绝对零度熵为0这个公式表示了在绝对零度下,熵为0。
4. 焓的变化:ΔH = ΔU + PΔV这个公式表示了焓的变化,其中,ΔH是焓的变化,ΔU是系统内能的变化,P是压强,ΔV 是体积的变化。
5. 熵的变化:ΔS = Q/T这个公式表示了熵的变化,其中,ΔS是熵的变化,Q是系统吸收或释放的热量,T是温度。
二、化学反应方程的计算1. 物质的量与摩尔质量:物质的量n = m/M其中,n是物质的量,m是物质的质量,M是摩尔质量。
2. 化学反应的平衡常数:Kc = ([C]^c[D]^d) / ([A]^a[B]^b)其中,[C]、[D]、[A]、[B]分别表示化学反应中的物质浓度,a、b、c、d分别表示化学反应中物质的摩尔系数。
3. 反应速率与物质浓度的关系:v = k[A]^a[B]^b其中,v表示反应速率,k表示速率常数,[A]、[B]分别表示反应物质的浓度。
三、电化学方面的公式1. Faraday定律:m = nFz其中,m是电化学反应的产物质量,n是电子数,F是法拉第定数,z是电化学反应的化学当量。
2. 电池方程:Ecell = Ecathode - Eanode这个公式表示了电池的电动势,Ecell是电池的电动势,Ecathode是阴极半反应的标准电势,Eanode是阳极半反应的标准电势。
3. 纳仑方程:Ecell = E°cell - (RT/nF)lnQ这个公式表示了电池的电动势,E°cell是标准电动势,R是理想气体常量,T是温度,n 是电子数,F是法拉第定数,Q是反应物质浓度的比值。
(完整word版)物理化学重要概念公式总结

第一章 热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律热力学第一定律:ΔU =Q +W 。
焦耳实验:ΔU =f (T ) ; ΔH =f (T )三、基本关系式1、体积功的计算 δW = -p e d V恒外压过程:W = -p e ΔV可逆过程: W =nRT 1221ln ln p p nRT V V =2、热效应、焓等容热:Q V =ΔU (封闭系统不作其他功)等压热:Q p =ΔH (封闭系统不作其他功)焓的定义:H =U +pV ; d H =d U +d(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容 热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂=定压热容与定容热容的关系:nR C C =-V p热容与温度的关系:C p =a +bT +c’T 2四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p e d V 等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程:Q =0 ;利用C V (T 2-T 1)=-p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化:ΔH =Q =n Δ_H ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、热化学物质的标准态;热化学方程式;盖斯定律;标准摩尔生成焓。
摩尔反应热的求算:)298,()298(B H H m f B mr θθν∆=∆∑ 反应热与温度的关系—基尔霍夫定律:)(])([,p B C T H m p BB m r ∑=∂∆∂ν。
物理化学公式及概念

摘自南大物理化学第五版第1页物理化学公式及概念一、气体222111., , 33i i in u p mnu pV mNu u u n===å为根均方速率为根均方速率,,2.,(BBARpV nRT Nk T k N == =理想气体状态方程:玻尔兹曼常数)123.Dalton i i p p p p x p =++= 道尔顿()分压定律:…………;;分压:在同一温度下,各别气体单独存在,并占有与混合气体相同体积时的压力,3334., , 22B t t m B k TE k T E RT u m ===21.5*2245.()2mv kT m Maxwell f v e v kT -æö =ç÷p èø麦克斯韦麦克斯韦(()速率分布定律:06.()lnp MghBoltzmann p RT=-玻尔兹曼分布:7.A BB Av M v M =气体扩散定律:()()228.), m m m a a van der Waals p V b RT p V nb nRT V V æöæö+-=+-=ç÷ç÷èøèø范德华范德华((方程方程::二、热力学第一定律1. 隔离系统(孤立系统)、封闭系统、敞开系统2. 广度性质、强度性质3. 热动平衡、力学平衡、相平衡、化学平衡4. 等温过程、等压过程、等容过程、绝热过程、环状过程5.W p dVd =-体外体积功:6.,U Q W dU Q W D =+=d +d 7. 功与过程、准静态过程、可逆过程8.,pdefHU PV H Q +D =焓:化学分析的重量分析是多少?通过适当的方法如沉淀、挥发、电解等使待测组分转化为另一种纯的、化学组成的固定的化合物而与样品中其他组分得以分离,然后称其质量,根据称得到的质量计算待测组分的含量摘自南大物理化学第五版摘自南大物理化学第五版p v Q Q H U d d -==¶¶æöæö====ç÷ç÷2211pCp V p V -cT D En n def d d ooorBrHHn D D oo o o o H Ho rmHD R Q d =max 21R W Q V p -化学分析有哪些分类?化学分析根据其操作方法的不同,可将其分为滴定分析(比如摘自南大物理化学第五版摘自南大物理化学第五版H D (相变)o2,p oo C dT D *2()f R T M *2()b R T M RTP defC S dp HD ooClausius -克劳修斯21111vap m sub mH H p D æöæD 摘自南大物理化学第五版摘自南大物理化学第五版vap m H D oo 2()ln 11o o or m r moH H K T d K æöD D =Þ=-ç÷or mo H D =ò=´´按法拉第定律计算所需理论电荷量电极上产物的实际质量;11defI Gl k), A c 11mooc cL 1def2;lg oA z z II I+--摘自南大物理化学第五版摘自南大物理化学第五版0.059ooRT[氧化型氧化型]][氧化型氧化型]]E E E E ¶¶¶æöæöæöç÷ç÷ç÷¶æöç÷oRT +[氧化型氧化型]](),x s E E F-11[]1(B defdp dd B rx 具有简单级数反应的速率公式和特征:级数级数 反应类型反应类型 速率公式的定积分式速率公式的定积分式浓度与时间的线性关系线性关系半衰期t 1/2速率常数k 的单位的单位一级一级A →产物→产物 1lnak ta x =-1ln~ta x - 1ln 2k (时间)-1二级二级A+B →产物→产物(a=b) 211k ta x a -=-1~t a x -21k a(浓度)-1·(时间)-1 A+B →产物→产物 (a ≠b)21()ln ()b a x k t a b a b x -=--()ln ~()b a x t a b x --1/21/2()()t A t B ¹ 三级三级A+B+C →产物→产物322111k t éù-=êú21~t2331(浓度)-2·-1(a b c) 2()a x a -ëû()a x -32k a(时间) 零级零级表面催化反应表面催化反应x k t =~x t2ak (浓度)·(时间)-1摘自南大物理化学第五版摘自南大物理化学第五版n 级(n ≠1) 反应物→产物反应物→产物111111()n n kt n a x a --éù-=êú--ëû11~()n t a x -- 1()n A A a -为常数 (浓度)1-n· (时间)-11/2''1/21/2'lg t t t a a æöç÷æöèø=+ç÷æöç÷1e e e x x a x k -==11lnk x a==2121211(ln ln k k a k k eek k k =-+æö-=ç÷2ln 11a E a a E E k d k-æö12[][][],,11111,m M r k k E S r S K -+====与呈线性关系第6页。
物理化学公式总结

物理化学公式总结物理化学是研究物质变化及其中发生的物理现象的学科,公式是物理化学研究的基础工具之一。
本文将对一些常用的物理化学公式进行总结和解析,帮助读者更好地理解这些公式的实际应用。
1. 状态方程状态方程描述了物质的状态及其性质与条件之间的关系。
其中,最为著名的状态方程是理想气体状态方程:PV = nRT。
它表达了气体的压强(P)、体积(V)、摩尔数(n)与温度(T)之间的关系,其中 R 是气体常数。
2. 阿伏伽德罗定律阿伏伽德罗定律是描述理想气体摩尔浓度与分压之间的关系的公式。
根据阿伏伽德罗定律,理想气体的摩尔浓度与其分压成正比:C = kP,其中 C 是摩尔浓度,P 是分压,k 是比例常数。
3. 物质的摩尔浓度物质的摩尔浓度表示单位体积或单位质量物质中包含的物质的量。
它可以用以下公式表示:C = n/V,其中 C 是摩尔浓度,n 是物质的摩尔数,V 是溶液的体积。
4. 热力学公式热力学是研究能量转化和能量变化规律的学科。
热力学公式中最为著名的是热力学第一定律:ΔU = q + w,其中ΔU 是系统内能的变化量,q 是系统吸热量,w 是系统对外做功。
5. 熵的变化熵是描述系统混乱程度的物理量,它可以用来分析物质在化学反应中的状态变化。
熵的变化可以用以下公式表示:ΔS = ΔS_prod - ΔS_react,其中ΔS 是熵的变化量,ΔS_prod 是生成物的总熵变,ΔS_react 是反应物的总熵变。
6. 酸碱中和反应酸碱中和反应是常见的化学反应类型之一。
在酸碱中和反应中,酸和碱反应生成盐和水。
一些重要的酸碱中和反应公式包括酸的离解方程式(例如 HCl -> H+ + Cl-)和碱的离解方程式(例如NaOH -> Na+ + OH-)。
7. 溶解度平衡常数溶解度平衡常数是描述溶液中溶质的溶解程度的物理化学参数。
对于一般的溶液,溶解度平衡常数可以用以下公式表示:Ksp =[A+]^m[B-]^n,其中 Ksp 是溶解度平衡常数,[A+] 是阳离子的浓度,[B-] 是阴离子的浓度,m 和 n 是阳离子和阴离子在化学方程式中的系数。
最全物理化学公式集

最全物理化学公式集以下是一个详细的物理化学公式集合,包含了许多常用的公式和方程式。
这些公式可以帮助学生更好地理解物理化学的理论,并应用于解决相关问题。
1.经典力学:-牛顿第一定律:物体保持匀速直线运动或静止,直到有外力作用。
-牛顿第二定律:物体的加速度与作用在其上的力成正比,与物体的质量成反比。
-牛顿第三定律:对于任何两个物体,彼此之间的作用力大小相等,方向相反。
-动能定理:物体的动能等于其质量乘以速度的平方的一半。
-动量定理:物体的动量变化等于作用在其上的力乘以时间间隔。
-弹性碰撞:在碰撞中,总动量和总动能守恒。
2.热力学:-热力学第一定律:能量不会自行产生或消失,只会转化为其他形式。
-热容量公式:物体吸收或释放的热量与其质量、温度变化以及物体的热容量有关。
-理想气体状态方程:PV=nRT,其中P是压力,V是体积,n是物质的摩尔数,R是气体常数,T是温度。
-熵变方程:ΔS=Q/T,其中ΔS是系统的熵变,Q是吸收或释放的热量,T是温度。
3.电化学:-法拉第定律:通过电解的物质的质量与通过电解的电荷数成正比。
-电动势公式:电动势等于化学反应中产生的能量与电荷数的比值。
- 纳尔斯特方程:E = Eo - (RT/nF)ln(Q),其中E是电池的电动势,Eo是标准电动势,R是气体常数,T是温度,n是电子转移数,F是法拉第常数,Q是反应物的活性。
4.量子力学:-布罗意波长:λ=h/p,其中λ是波长,h是普朗克常数,p是物体的动量。
-不确定性原理:ΔxΔp≥h/(4π),其中Δx是位置的不确定度,Δp是动量的不确定度,h是普朗克常数。
5.光学:- 折射率公式:n₁sinθ₁ = n₂sinθ₂,其中n₁和n₂是介质的折射率,θ₁和θ₂是光线的入射和折射角度。
-焦距公式:1/f=1/u+1/v,其中f是透镜的焦距,u是物体的距离,v是像的距离。
6.分析化学:-摩尔浓度公式:C=n/V,其中C是溶液的摩尔浓度,n是溶质的物质的摩尔数,V是溶液的体积。
物化公式归纳

物化公式归纳物化公式归纳第一章化学热力学基础公式总结1.体积功 We = -Pe △V2.热力学第一定律的数学表达式△U = Q + W 3.n mol 理想气体的定温膨胀过程.定温可逆时:Wmax=-Wmin=4.焓定义式 H = U + PV在封闭体系中,W ′= 0,体系发生一定容过程Qv = △U在封闭体系中,W ′= 0,体系发生一定压过程 Qp = H2 – H1 = △H5.摩尔热容Cm ( J ·K-1·mol-1 ): 定容热容 CV(适用条件 :封闭体系、无相变、无化学变化、W ′=0 定容过程适用对象 : 任意的气体、液体、固体物质)定压热容 Cp(适用条件:封闭体系、无相变、无化学变化、W ′=0 的定压过程适用对象 : 任意的气体、液体、固体物质)单原子理想气体: Cv,m = 1.5R , Cp,m = 2.5R 双原子理想气体:Cv,m = 2.5R , Cp,m = 3.5R 多原子理想气体: Cv,m = 3R , Cp,m = 4RCp,m = Cv,m + R6.理想气体热力学过程ΔU 、ΔH 、Q 、W 和ΔS 的总结=21,T T mp dTnCH 1221lnln P P nRT V V nRT =nC C m =?=21,T T m V dTnC U7.定义:△fHm θ(kJ ·mol-1)-- 标准摩尔生成焓△H —焓变;△rHm —反应的摩尔焓变△rHm θ—298K 时反应的标准摩尔焓变;△fHm θ(B)—298K 时物质B 的标准摩尔生成焓;△cHm θ(B) —298K 时物质B 的标准摩尔燃烧焓。
8.热效应的计算由物质的标准摩尔生成焓计算反应的标准摩尔焓变△rH θm = ∑νB △fH θm ,B 由物质的标准摩尔燃烧焓计算反应的标准摩尔焓变△rH θm = -∑νB △cH θm ,B 9.Kirchhoff (基尔霍夫)方程△rHm (T2) = △rHm (T1) + 如果ΔCp 为常数,则△rHm (T2) = △rHm(T1) + △Cp ( T2 - T1)10.热机的效率为对于卡诺热机= 可逆循环过程< 不可逆循环过程11.熵变定义式(体系经历一可逆过程的热温商之和等于该过程的熵变.)12.热力学第二定律的数学表达式(不等式中, ― > ‖号表示不可逆过程, ― = ‖ 号表示可逆过程― T ‖—环境温度 , 对可逆过程也是体系温度. )13.熵增原理 (孤立体系的熵永不减少) △S 孤立≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡.对于封闭体系△S 孤立= △S 封闭+ △S 环境≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡14.定温定压的可逆相变15.化学反应熵变的计算△rS θm = ∑νBS θm ,B16.△rH θm 和△rS θm 与温度的关系:△rH θ m (T2) = △rH θ m (T1) + △rS θ m (T2) = △rS θ m (T1) +1211Q Q Q Q W R +=-=ηdTC p T T ?21121211Q Q Q Q Q Q W +=+=-21T T T -=2211≤+T Q T Q RBAA B TQ S S S (δ?=-=?∑≥?i iiTQ S (δTQdS δ≥环体环环环境T Q T Q S - ==相变,相变T Hn S m ?=dTC p T T ?21TC p T T ??21第二章自由能、化学势和溶液公式1.第一和第二定律的联合公式为2.吉布斯自由能定义式G = U + PV – TS = H – TS△G =△H -T △S(G----体系的状态函数, ( J ) , 绝对值无法测量) 3.在定温定压下,有如下关系:ΔG=W’最大 4.吉布斯自由能判据< 不可逆过程, 自发过程 = 可逆过程, 平衡态 > 反方向为自发过程5.判断过程方向及平衡条件的总结6定压下.对任意相变或化学变化7.定温物理变化?G 的计算(W’=0的封闭体系). 理想气体定温过程0≥'+--W dV P dU dS T e e δ0,,≤'W P T dG 0,,≤?'W P T G S TGP ?-=)(===?212112lnP P P P T P P nRT dP PnRT dP V G. 纯液体或纯固体的定温过程. 定温定压可逆相变 dG = -SdT + VdP dT =0 dP =0 ?G T , P, W' = 0 。
物理化学公式总结

物理化学公式总结物理化学是研究物质的结构、性质和变化的科学,它使用数学和物理的原理来解释化学现象。
在物理化学的研究过程中,涉及到许多重要的公式,这些公式是揭示物质性质和相互作用规律的基础。
下面我将为大家总结一些物理化学中常见的公式。
1. 热力学公式热力学公式描述了物质在热平衡状态下的性质和能量转化规律。
其中最基本的公式是热力学第一定律(能量守恒定律):∆U = q + w其中,∆U表示系统内能的变化,q表示传递给系统的热量,w 表示系统对外界做的功。
2. 热力学第二定律热力学第二定律描述了能量的定向流动规律。
其中最著名的公式是卡诺热机效率公式:η = 1 - Tc/Th其中,η表示卡诺热机的效率,Tc表示冷热源的温度,Th表示热源的温度。
3. 热力学公式一般表达式根据热力学第一定律,可以推导出一般的热力学公式:dU = TdS - PdV其中,dU表示系统内能的微小变化,T表示温度,dS表示系统的熵变化,P表示压力,dV表示体积的微小变化。
4. 热力学常用关系根据热力学公式一般表达式,可以得到一些重要的热力学关系:Gibbs自由能(G)与焓(H)的关系:G = H - TS其中,G表示Gibbs自由能,H表示焓,T表示温度,S表示熵。
5. 气体状态方程气体状态方程描述了理想气体和实际气体之间的关系。
最常见的气体状态方程是理想气体状态方程:PV = nRT其中,P表示压力,V表示体积,n表示气体的摩尔数,R表示气体常数,T表示温度。
6. 麦克斯韦速率分布定律麦克斯韦速率分布定律描述了气体分子速度的分布规律。
根据麦克斯韦速率分布定律,可以得到气体分子的平均动能(等于温度的能量):KE = (3/2) kT其中,KE表示气体分子的平均动能,k表示玻尔兹曼常数,T表示温度。
7. 热容公式热容公式描述了物质温度变化时的热量和温度之间的关系。
最常用的热容公式是:C = q/∆T其中,C表示热容,q表示吸收或释放的热量,∆T表示温度变化。
物化公式归纳

物化公式归纳物化公式归纳第一章化学热力学基础公式总结1.体积功 We = -Pe △V2.热力学第一定律的数学表达式△U = Q + W 3.n mol 理想气体的定温膨胀过程.定温可逆时:Wmax=-Wmin=4.焓定义式 H = U + PV在封闭体系中,W ′= 0,体系发生一定容过程Qv = △U在封闭体系中,W ′= 0,体系发生一定压过程 Qp = H2 – H1 = △H5.摩尔热容Cm ( J ·K-1·mol-1 ): 定容热容 CV(适用条件 :封闭体系、无相变、无化学变化、W ′=0 定容过程适用对象 : 任意的气体、液体、固体物质)定压热容 Cp(适用条件:封闭体系、无相变、无化学变化、W ′=0 的定压过程适用对象 : 任意的气体、液体、固体物质)单原子理想气体: Cv,m = 1.5R , Cp,m = 2.5R 双原子理想气体:Cv,m = 2.5R , Cp,m = 3.5R 多原子理想气体: Cv,m = 3R , Cp,m = 4RCp,m = Cv,m + R6.理想气体热力学过程ΔU 、ΔH 、Q 、W 和ΔS 的总结=?21,T T m p dTnC H 1221ln ln P PnRT V V nRT =nCC m =?=?21,T T m V dTnC U7.定义:△fHm θ(kJ ·mol-1)-- 标准摩尔生成焓△H —焓变;△rHm —反应的摩尔焓变△rHm θ—298K 时反应的标准摩尔焓变;△fHm θ(B)—298K 时物质B 的标准摩尔生成焓;△cHm θ(B) —298K 时物质B 的标准摩尔燃烧焓。
8.热效应的计算由物质的标准摩尔生成焓计算反应的标准摩尔焓变△rH θm = ∑νB △fH θm ,B 由物质的标准摩尔燃烧焓计算反应的标准摩尔焓变△rH θm = -∑νB △cH θm ,B 9.Kirchhoff (基尔霍夫)方程△rHm (T2) = △rHm (T1) + 如果ΔCp 为常数,则△rHm (T2) = △rHm (T1) + △Cp ( T2 - T1)10.热机的效率为对于卡诺热机= 可逆循环过程 < 不可逆循环过程11.熵变定义式(体系经历一可逆过程的热温商之和等于该过程的熵变.)12.热力学第二定律的数学表达式(不等式中, “ > ”号表示不可逆过程, “ = ” 号表示可逆过程“ T ”—环境温度 , 对可逆过程也是体系温度. )13.熵增原理 (孤立体系的熵永不减少) △S 孤立≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡.对于封闭体系△S 孤立= △S 封闭+ △S 环境≥ 0 > 不可逆过程, 自发过程 = 可逆过程, 体系达平衡14.定温定压的可逆相变15.化学反应熵变的计算△rS θm = ∑νBS θm ,B16.△rH θm 和△rS θm 与温度的关系:△rH θ m (T2) = △rH θ m (T1) +△rS θ m (T2) = △rS θ m (T1) +1211Q Q Q Q W R +=-=ηdTC p T T ?21121211Q Q Q Q Q Q W +=+=-=η121T T T -=02211≤+T Q T Q RBAA B TQS S S )(δ?=-=?∑≥?ii i T Q S (δTQdS δ≥环体环环环境T Q T Q S -==相变,相变T H n S m ?=dTC p T T ??21d TTC pT T ??21第二章自由能、化学势和溶液公式1.第一和第二定律的联合公式为2.吉布斯自由能定义式G = U + PV – TS = H –TS △G =△H -T △S(G----体系的状态函数, ( J ) , 绝对值无法测量) 3.在定温定压下,有如下关系:ΔG=W’最大4.吉布斯自由能判据< 不可逆过程, 自发过程 = 可逆过程, 平衡态 > 反方向为自发过程56定压下.对任意相变或化学变化7.定温物理变化?G 的计算(W’=0的封闭体系) . 理想气体定温过程0≥'+--W dV P dU dS T e e δ0,,≤'W P T dG 0,,≤?'W P T G S TGP ?-=(?===?212112ln P P P P T P PnRT dP P nRT dP V G. 纯液体或纯固体的定温过程. 定温定压可逆相变 dG = -SdT + VdP dT =0 dP =0 ?G T , P, W' = 0 。
物化公式整理整理版
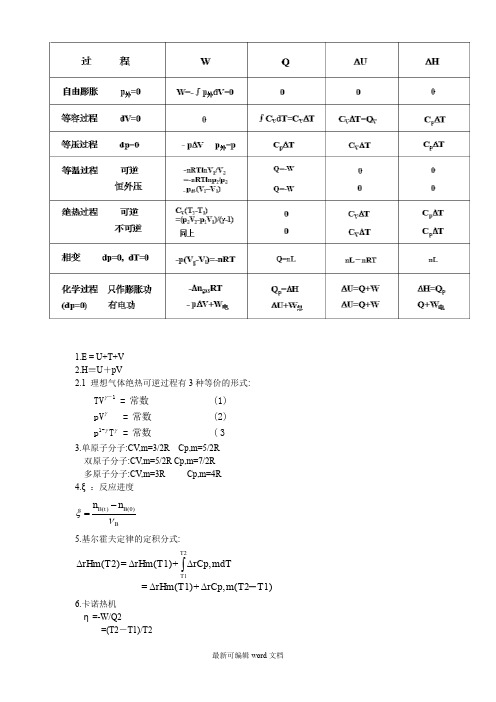
1.E = U+T+V2.H ≡U +pV2.1 理想气体绝热可逆过程有3种等价的形式:(3)常数= T p (2)常数 = pV (1)常数= TV -1-1γγγγ3.单原子分子:CV,m=3/2R Cp,m=5/2R双原子分子:CV,m=5/2R Cp,m=7/2R多原子分子:CV,m=3R Cp,m=4R4.ξ:反应进度B B t B n n νξ)0()(-=5.基尔霍夫定律的定积分式:T1)-m(T2rCp, +rHm(T1)= mdTrCp, +rHm(T1) =rHm(T2)T2T1∆∆∆∆∆⎰6.卡诺热机η=-W/Q2=(T2-T1)/T2=1-(T1/T2)7.熵的微观意义:S=klnWW:宏观状态拥有的微观运动状态的数量k :Boltzmann 常数8.纯物质B 在状态(T,p)的规定熵即为下述过程的熵变:),()0(p T B K B →Kp T B TK p T B S S S S 0,0),(-=∆= 9. 等温过程的熵变: (理想气体)(p1/p2)nRln = S p2/p1=V2/V1∴p2V2=p1V1∵(1) (V2/V1)nRln = S1)/TnRTln(V2/V =-WR/T =QR/T =QR/T ∫=S ∆∆∆δ 10. 绝热过程:绝热可逆过程, 由熵的判别式:0 = S ∆ 绝热可逆 (2)绝热不可逆过程: 对此类过程需设计一条可逆途径, 从相同的始态到相同末态, 再沿可逆途径求算熵变.11. 变温过程: 简单体系A. 等压变温:)Cpln(T2/T1 = (4)(Cp/T)dT =QR/T ∫=SCpdT=QR ⎰∆δδB. 等容变温:ln(T2/T1)C = /T)dT ∫(C =/T Q ∫=SdTC =Q V V R V R δδ∆12.相变过程:平衡相变:平衡相变是一可逆过程, 在等温等压下进行./T Q =Q/T ∫=S R δ∆平衡相变有:H =Qp ∆ 故平衡相变的熵变为:相变H/T =S ∆∆ (6)即:平衡相变的熵变等于相变潜热除以相变温度13.理想气体的混合过程:(1).A, B 先各自等温可逆膨胀到各自的末态;(2).可逆混合.第一步的熵变为:2Rln2= )/V Rln(V +)/V Rln(V =S +S =S1B 1,B 2,A 1,A 2,B A ∆∆∆第二步熵变为零14.赫氏自由能 F ≡U -TS状态函数,广度性质,没有明确的物理意义,具有能量的量纲.15.在等温过程中,一封闭系统所能作的最大功等于系统的亥姆霍兹函数的减少。
物理化学公式大全

物理化学公式集热力学第一定律 功:δW=δW e +δW f1膨胀功 δW e =p 外dV 膨胀功为正,压缩功为负. 2非膨胀功δW f =xdy非膨胀功为广义力乘以广义位移.如δW 机械功=fdL,δW 电功=EdQ,δW 表面功=rdA.热 Q :体系吸热为正,放热为负.热力学第一定律: △U =Q —W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数. 热容 C =δQ/dT1等压热容:C p =δQ p /dT = H/T p 2等容热容:C v =δQ v /dT = U/T v 常温下单原子分子:C v,m =C v,m t =3R/2 常温下双原子分子:C v,m =C v,m t +C v,m r =5R/2 等压热容与等容热容之差:1任意体系 C p —C v =p +U/V T V/T p 2理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v T 1—T 2=p 1V 1—p 2V 2 理想气体多方可逆过程:W =T 1—T 2 热机效率:η= 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β= 焦汤系数: μJ -T ==- 实际气体的ΔH 和ΔU: ΔU=+ ΔH=+化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +RT 化学反应热效应与温度的关系: 热力学第二定律 Clausius 不等式:熵函数的定义:dS=δQR/T Boltzman熵定理:S=klnΩHelmbolz自由能定义:F=U—TS Gibbs自由能定义:G=H-TS 热力学基本公式:1组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU=TdS-pdV dH=TdS+VdpdF=-SdT-pdV dG=-SdT+Vdp2Maxwell关系:==-3热容与T、S、p、V的关系:CV =T Cp=TGibbs自由能与温度的关系:Gibbs-Helmholtz公式=-单组分体系的两相平衡:1Clapeyron方程式:=式中x代表vap,fus,sub.2Clausius-Clapeyron方程式两相平衡中一相为气相:=3外压对蒸汽压的影响: pg 是在惰性气体存在总压为pe时的饱和蒸汽压.吉不斯-杜亥姆公式:SdT-Vdp+=0dU=TdS-pdV+ dH=TdS+Vdp+dF=-SdT-pdV+ dG=-SdT+Vdp+在等温过程中,一个封闭体系所能做的最大功等于其Helmbolz自由能的减少.等温等压下,一个封闭体系所能做的最大非膨胀功等于其Gibbs自由能的减少.统计热力学波兹曼公式:S=klnΩ一种分布的微观状态数:定位体系:ti =N 非定位体系:ti=波兹曼分布:=在A、B两个能级上粒子数之比:=波色-爱因斯坦统计:Ni =费米-狄拉克统计:Ni=分子配分函数定义:q=-i为能级能量q=-i为量子态能量分子配分函数的分离:q=q n q e q t q r q v能级能量公式:平动:εt=转动:εr =振动:εv=分子配分函数表达式:平动:当所有的平动能级几乎都可被分子到达时一维:q t=二维:q t=A 三维:q t=转动:线性q r===为转动特征温度非线性q r=振动:双原子分子q V===为振动特征温度多原子线性:q V=多原子非线性:q V=+1电子运动:q e=2j+1 原子核运动:q n=2Sn热力学函数表达式:F=-kTlnq N定位 F=-kTln非定位S=klnq N+NkT定位 S=kln+NkT非定位G=-kTlnq N+NkTV定位G=-kTln+NkTV非定位U=NkT2 H=NkT2+NkTV=P=NkT CV一些基本过程的ΔS、ΔG、ΔF的运算公式W=0f一些基本过程的W、Q、ΔU、ΔH的运算公式Wf =0溶液-多组分体系体系热力学在溶液中的应用溶液组成的表示法:1物质的量分数:2质量摩尔浓度:3物质的量浓度:4质量浓度拉乌尔定律亨利定律:化学势的各种表示式和某些符号的物理意义:气体:1纯理想气体的化学势标准态:任意温度,p=pφ=101325Pa.μφT为标准态时的化学势2纯实际气体的化学势标准态:任意温度,f=pφ且复合理想气体行为的假想态即p =pφ,γ=1,μφT为标准态时的化学势.3混合理想气体中组分B的化学势因为所以不是标准态时的化学势,是纯B气体在指定T、p时的化学势.溶液:1 理想溶液组分的化学势所以不是标准态时的化学势而是温度为T、溶液上方总压为p时,纯液体B的化学势.2 稀溶液中各组分的化学势溶剂:不是标准态时的化学势而是温度为T、溶液上方总压为p时,纯溶剂A的化学势.溶质:,,均不是标准态时的化学势,均是T,p的函数,它们分别为:当xB =1,mB=1molkg-1,cB=1moldm-3时且服从亨利定律的那个假想态的化学势.4非理想溶液中各组分的化学势溶剂:不是标准态的化学势,而是aA,x =1即xA=1,γA=1的纯组分A的化学势.溶质:,,均不是标准态时的化学势,均是T,p的函数,它们分别为:当aB,x =1,aB,m=1,aB,c=1时且服从亨利定律的那个假想态的化学势. 4活度a的求算公式:ü 蒸汽压法:溶剂aA =γAxA=pA/pA溶质:aB=γBxB=pA/kcü 凝固点下降法:溶剂ü Gibbs-Duhem公式从溶质剂的活度求溶剂质的活度. 5理想溶液与非理想溶液性质:理想溶液:非理想溶液:超额函数:溶液热力学中的重要公式:1 Gibbs-Duhem公式2 Duhem-Margule公式:对二组分体系:稀溶液依数性:1凝固点降低:2沸点升高:3渗透压:化平衡学化学反应亲和势:A=-化学反应等温式:平衡常数的表达式:温度,压力及惰性气体对化学平衡的影响:电解质溶液法拉第定律:Q=nzF m=t+=====r+为离子移动速率,U+U-为正负离子的电迁移率亦称淌度.近似:浓度不太大的强电解质溶液离子迁移数:tB===+=1电导:G=1/R=I/U=kA/l电导率:k =1/ρ 单位:S·m -1 莫尔电导率:Λm =kV m =k/c 单位S·m 2·mol -1科尔劳乌施经验式:Λm = 离子独立移动定律:= 奥斯特瓦儿德稀释定律:= 平均质量摩尔浓度:=平均活度系数:= 平均活度:== 电解质B 的活度:a B == m +=v +m B m -=v -m B 离子强度:I =德拜-休克尔公式:lg =-A|z +z --| 可逆电池的电动势及其应用 Δr G T,p =-W f,max Δr G mT,p =zEFNernst Equation :若电池反应为 cC +dD =gG +hH E =E φ-标准电动势E φ与平衡常数K φ的关系:E φ= 还原电极电势的计算公式:=计算电池反应的有关热力学函数变化值:= =-zEF + Q R =T = zF zF =电极书面表示所采用的规则:负极写在左方,进行氧化反应是阳极,正极写在右方,进行还原反应是阴极 电动势测定的应用:1求热力学函数变量Δr G m 、Δr G m Φ、、及电池的可逆热效应Q R 等. 2求氧化还原反应的热力学平衡常数K Φ值:K Φ= E Φ=E =3求难溶盐的溶度积K sp 、水的离子积K w 及弱酸弱碱的电离常数等. 4求电解质溶液的平均活度系数和电极的值.5从液接电势求离子的迁移数.Pt,H 2p|HClm|HClm’| H 2p,Pt 1-1价型:E j =E =E c +E j = 高价型:M z+A z -m 1|M z +A z -m 2 E j =6利用醌氢醌电极或玻璃电极测定溶液的pH 电解与极化作用E 分解=E 可逆+ΔE 不可逆+IRΔE不可逆=η阴+η阳η阴=φ可逆-φ不可逆阴η阳=φ不可逆-φ可逆阳φ阳,析出=φ阳,可逆+η阳φ阴,析出=φ阴,可逆-η阴η=a+blnjE实际分解=E理论分解+η阴+η阳+IR对电解池,由于超电势的存在,总是使外加电压增加而多消耗电能;对原电池,由于超电势的存在,使电池电动势变小而降低了对外作功的能力.在阴极上,还原电势愈正者,其氧化态愈先还原而析出;同理,在阳机上,则还原电势愈负者其还原态愈先氧化而析出.需外加电压小化学反应动力学半衰期法计算反应级数:kp =kcRT1-n Ea-Ea’=Q化学反应动力学基础二:ZAB==μ=若体系只有一种分子:ZAA==碰撞参数:b=dABsinθ碰撞截面:反应截面:kSCTT=kSCTT==几个能量之间的关系:Ea =Ec+RT/2=E+mRT=式中是反应物形成活化络合物时气态物质的代数和,对凝聚相反应,=0.对气相反应也可表示为:Ea=式中n为气相反应的系数之和原盐效应:弛豫法:%界面现象与T的关系:两边均乘以T,,即的值将随温度升高而下降,所以若以绝热方式扩大表面积,体系的温度必将下降.杨-拉普拉斯公式:ps为曲率半径,若为球面ps =,平面 ps.液滴愈小,所受附加压力愈大;液滴呈凹形,R‘为负值,ps为负值,即凹形面下液体所受压力比平面下要小.毛细管:ps==Δρgh Δρgh=R为毛细管半径开尔文公式:p0和p分别为平面与小液滴时所受的压力对于液滴凸面R‘>0,半径愈小,蒸汽压愈大.对于蒸汽泡凹面R‘<0,半径愈小,蒸汽压愈小.两个不同液滴的蒸汽压:溶液越稀,颗粒越大.液体的铺展:非表面活性物质使表面张力升高,表面活性物质使表面张力降低.吉不斯吸附公式:为表面超额若,>0,正吸附;,<0,负吸附.表面活性物质的横截面积:Am=粘附功:Wa值愈大,液体愈容易润湿固体,液固界面愈牢.内聚功:浸湿功:铺展系数: ,液体可在固体表面自动铺展.接触角:Langmuir等温式:θ:表面被覆盖的百分数.离解为两个分子:混合吸附:即:BET公式:弗伦德利希等温式:乔姆金吸附等温式:吸附剂的总表面积:S=Am Ln n=Vm/22400cm3mol-1气固相表面催化反应速率:单分子反应:产物吸附很弱产物也能吸附双分子反应:AB都吸附AB均吸附,但吸附的B不与吸附的A反应B不吸附胶体分散体系和大分子溶液布朗运动公式:D为扩散系数球形粒子的扩散系数:渗透压:渗透力:F=扩散力=-F沉降平衡时粒子随高度分布公式:瑞利公式:电势表面电势 Stern电势电解质浓度增加电势减小.电泳速度: k=6时为电泳,k=4时为电渗.大分子稀溶液渗透压公式不是吧。
物理化学公式大全

物理化学公式大全物理化学是研究物质的物理性质和化学性质之间的关系的学科。
以下是一些在物理化学中常用的公式:1.热力学方程:-理想气体状态方程:PV=nRT其中P为气体压强,V为气体体积,n为气体摩尔数,R为气体常数,T为气体温度。
-内能变化公式:ΔU=q+w其中ΔU为系统内能变化,q为系统吸取或放出的热量,w为系统对外界做的功。
-能量守恒定律:ΔE=q+w其中ΔE为系统总能量变化,q为系统吸取或放出的热量,w为系统对外界做的功。
2.动力学方程:-反应速率公式:r=k[A]^m[B]^n其中r为反应速率,k为反应速率常数,[A]和[B]分别为反应物A和B的浓度,m和n为反应物的反应级数。
- Arrhenius 公式:k = A * e^(-Ea/RT)其中 k 为反应速率常数,A 为 Arrhenius 常数,Ea 为活化能,R为气体常数,T 为反应温度。
3.量子力学方程:- 波函数公式:Ψ = Σcnφn其中Ψ 为波函数,cn 为系数,φn 为基态波函数。
- Schroedinger 方程:HΨ = EΨ其中H为哈密顿算符,Ψ为波函数,E为能量。
4.热力学方程:- 熵变公式:ΔS = q_rev / T其中ΔS 为系统熵变,q_rev 为可逆过程吸放热量,T 为温度。
- Gibbs 自由能公式:ΔG = ΔH - TΔS其中ΔG 为 Gibbs 自由能变化,ΔH 为焓变化,ΔS 为熵变化,T 为温度。
5.电化学方程:- Nerst 方程:E = E° - (RT / nF) * ln(Q)其中E为电池电势,E°为标准电势,R为气体常数,T为温度,n为电子数,F为法拉第常数,Q为电化学反应的反应物浓度比。
- Faraday 定律:nF = Q其中n为电子数,F为法拉第常数,Q为电荷数。
以上公式只是物理化学中的一小部分,这里列举的是一些常见的、基本的公式,实际上物理化学领域有非常多的公式和方程可供使用。
物化知识点(公式)总结

定压(恒压)过程
若过程的始态、终态的压力相等 , 且过程中的压力恒等于环境的压力 , 即 p1 = p2
= psu , 此过程叫定压过程
(iii)
定容(恒容)过程
系统状态变化过程中体积保持恒定 , V1 = V2 , 此为定容过程。
(iv)
绝热过程
系统状态变化过程中 , 与环境间的能量传递仅可能有功的形式 , 而无热的形 式 , 即 Q =
(4) 吉布斯函数判据: △GT,p≤W’(<不可逆,=可逆)
W’=0 时, △GT,p≤0 (<自发,=平衡)
(5)热力学能判据: W’=0 时, △US,V≤0
(<自发,=平衡)
(6)焓判据: W’=0 时, △HS,p≤0
(<自发,=平衡)
六、热力学基础中重要的定义式 定义式:任何条件下均可使用。 ( 1 ) 体 积 功 δWv ≡
耳温度、临界温度的相关知识。
二、易错、易混淆的基本概念简述
(1)当系统的状态变化时 , 状态函数的改变量只决定于系统的始态和终态 , 而 与变化的过
程或途径无关。即
系统变化时其状态函数的改变量 = 系统终态的函数值 - 系统始态的函数值 在做计算题时,
计算状态函数,在有公式可用的情况下,可以不管具体发生 的过程,直接根据始终态条件
(vii)
自由膨胀过程 ( 向真空膨胀 ) psu=0,Wv=0,
若仅发生气体 pVT 变化的过程,Q=0。
若发生相变、化学变化的过程,Q=△U≠0
(4)饱和蒸气压
在一定温度下,液体与气体达到两相平衡或发生可逆相变的压力为饱和蒸汽压, 简称蒸
汽压。
蒸气压等于外压时的温度称液体的沸点 ; 101. 325 kPa 下的沸点叫正常沸点 ;100
物理化学公式

物理化学公式物理化学是研究物质的物理性质和化学性质之间关系的学科。
在物理化学的研究过程中,我们常常会涉及到一些重要的公式和方程式,这些公式和方程式可以帮助我们理解物质的变化规律和性质。
下面是一些常见的物理化学公式的介绍。
1. 确定物质的相变温度:在物理化学中,相变温度是指物质从一种相变为另一种相的温度。
常见的相变温度公式包括冰点温度公式和沸点温度公式。
冰点温度公式:T(°C) = (Rm - R0)/(Rm - R1) * 100其中,T为冰点温度,R0为纯净冰的电阻,R1为冰与盐混合的电阻,Rm为冰与水混合的电阻。
沸点温度公式:T(°C) = Rm - 0.32其中,T为沸点温度,Rm为纯净液体的电阻。
2. 确定理想气体的状态:理想气体状态方程是气体物理化学中最常用的公式之一。
理想气体状态方程可以用来描述理想气体的压强、体积和温度之间的关系。
理想气体状态方程:PV = nRT其中,P为气体的压强,V为气体的体积,n为气体的物质量,R为气体常数,T为气体的温度。
3. 确定溶解度:溶解度是指在一定温度下,单位体积的溶剂中可以溶解的最大溶质质量。
溶解度可以通过溶质溶解度积常数来表示。
溶质溶解度积常数:Ksp = [A+]^a * [B-]^b其中,Ksp为溶质溶解度积常数,A+和B-分别代表溶质的阳离子和阴离子,a和b分别代表阳离子和阴离子的个数。
4. 确定化学反应速率:化学反应速率是化学反应物质浓度的变化率。
化学反应速率可以通过测定反应物质浓度随时间的变化来确定。
化学反应速率公式:v = - (1/a)(Δ[A]/Δt) =(1/b)(Δ[B]/Δt) = (1/c)(Δ[C]/Δt)其中,v为化学反应速率,a、b、c分别为化学反应中反应物A、B、C的化学计量数,[A]、[B]、[C]分别为反应物A、B、C的浓度,Δt为反应时间。
5. 确定能量变化:在物理化学中,常常需要计算系统的能量变化。
物理化学公式大全

1. 热力学第一定律的数学表示式W Q U +=∆或 'a m bδδδd δd U Q W Q p V W=+=-+ 系统得功为正,对环境作功为负。
上式适用于封闭体系的一切过程。
2. 焓的定义式 3. 焓变(1) )(pV U H ∆+∆=∆式中)(pV ∆为pV 乘积的增量,只有恒压下)()(12V V p pV -=∆在数值上等于体积功。
(2) 2,m 1d p H nC T ∆=⎰此式适用于理想气体单纯pVT 变化的一切过程,或真实气体的恒压变温过程,或纯的液体、固体物质压力变化不大的变温过程。
4. 热力学能(又称内能)变此式适用于理想气体单纯pVT 变化的一切过程。
5. 恒容热和恒压热V Q U =∆ (d 0,'0V W == p Q H =∆ (d 0,'0)p W == 6. 热容的定义式 (1)定压热容和定容热容δ/d (/)p p pC Q T H T ==∂∂δ/d (/)V V V C Q T U T ==∂∂(2)摩尔定压热容和摩尔定容热容,m m /(/)p p p C C n H T ==∂∂ ,m m /(/)V V VC C n U T ==∂∂ 上式分别适用于无相变变化、无化学变化、非体积功为零的恒压和恒容过程。
(3)质量定压热容(比定压热容)式中m 和M 分别为物质的质量和摩尔质量。
(4) ,m ,mp V C C R -= 此式只适用于理想气体。
,m//p p p c C m CM==pVU H +=2,m 1d V U nC T∆=⎰7. 摩尔蒸发焓与温度的关系21vap m 2vap m 1vap ,m ()()d T p TH T H T C T ∆=∆+∆⎰式中 vap ,m p C ∆ = ,m p C (g) —,m p C (l),上式适用于恒压蒸发过程。
8. 体积功(1)定义式 V p W d a m b -=∂ 或 V p W d amb ∑-=(2) )()(1221T T nR V V p W --=--= 适用于理想气体恒压过程。
物理化学公式

物理化学公式物理化学公式是物理学和化学的交叉学科的重要组成部分,被广泛应用于科学和工程领域。
这些公式描述了物质和能量之间的关系,提供了揭示自然界行为的数学工具。
在本文中,将介绍一些物理化学领域的常见公式。
物理化学学科涉及的公式众多且复杂,其中一些是由著名科学家在长期的研究和实验基础上总结出来的。
以下是一些物理化学中常见的公式:1. 理想气体状态方程:PV = nRT其中,P是气体的压强,V是体积,n是摩尔数,R是气体常数,T 是温度。
该公式描述了理想气体在不同温度和压力下的状态。
2. 质量守恒定律:m₁ + m₂ = m₃这是化学反应中最基本的公式,表示反应前后物质的质量守恒。
3. 热力学第一定律(能量守恒定律):ΔU = q + w其中,ΔU表示系统内能的变化,q表示系统吸收的热量,w表示系统对外做功。
这个公式表明了能量在物理化学过程中的守恒。
4. 阿伏伽德罗常数(用于描述分子和原子间的关系):Nₐ = 6.0221 × 10²³ mol⁻¹它表示在摩尔中包含的粒子数目,由此可推导出物质的摩尔质量。
5. 波尔原子模型公式:E = -2.178 × 10⁻¹⁸ (Z²/n²) J其中,E表示氢原子的能量,Z表示核电荷数,n表示电子的主量子数。
这个公式用于描述氢原子的能级和能量。
6. 平均气体动能公式:KE = (3/2) kT其中,KE表示气体分子的平均动能,k是玻尔兹曼常量,T是温度。
这个公式表明了温度和气体分子动能之间的关系。
7. 化学反应速率公式:v = k[A]ⁿ[B]ᵐ这是描述化学反应速率的公式,v表示反应速率,k是速率常数,[A]和[B]分别表示反应物A和B的浓度,ⁿ和ᵐ是反应物在反应速率中的指数。
8. Nernst方程:E = E° - (RT/nF) ln(Q)该方程描述了电池电势的计算,E表示电池的电势,E°是标准电势,R是气体常数,T是温度,n是电子转移数,F是法拉第常数,Q是反应物浓度的比值。
物化中的公式

气 体理想气体状态方程:nRT pV =分压力定义:∑=BBpp道尔顿分压定律:∑=++=BB V RT n p p p )(......21 阿马格定律:∑∑==++=BB BB pRT n V V V V )(......21 范德华方程:RT b V V ap m m=-+))((2或 n R T nb V V an p =-+))((22热力学第一定律体积功的计算:⎰-=21)(V V dV p W 环封闭系统热力学第一定律的数学表达式:W Q U +=∆U Q V ∆=(条件:恒容,无非体积功,封闭系统)H Q p ∆=(条件:恒容,无非体积功,封闭系统) 对于理想气体有:R C C m V m p =-,,当0=dp ,0='W 时,则有 ⎰=∆=21,T T m p p dT nC H Q当0,0='=W dV 时,则有 ⎰=∆=21,T T m V V dT nC U Q理想气体恒温可逆过程:2121ln ln 2121p p nRT V V nRT dV V nRTpdV W V V V V ==-=-=⎰⎰理想气体绝热可逆过程—绝热可逆过程方程式:常数=-1γTV或 常数=γpV 或 常数=-γγT p 1若0=dT ,0=dp ,0='W ,则有 H Q p 相变∆=∑∆=∆Bm f B m r T B H T H ),,()(βν生成物反应物⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆-⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆=∆∑∑Bm C B Bm C B m r T H T H T H )()()(νν基希霍夫公式:⎰∆+∆=∆21)()(12T T p r m r m r dT C T H T H∑=∆=∆=-RTg RT g n V p Q Q B p V p ξν)()(热力学第二定律热机效率:1Q W -=η,121211211T T T T T Q Q Q -=-=+=η⎰⎰==∆2121TQdS S rδ单纯pVT 变化的的熵变计算:1212,ln lnV VnRT T T nC S m V +=∆ 2112,ln lnp p nR T T nC S m p +=∆ 12,12,ln lnV VnC p p nC S m p m V +=∆ 可逆相变过程:TH S 相变∆=∆)()()(环系隔S S S ∆+∆=∆∑=∆)15.298,,()15.298(K B S K S m B m r βν⎰∆+∆=∆TKmp r m r m r dT TC K S T S 15.298,)15.298()(θϑTS U A -≡ TS H G -≡热力学基本方程:pdV TdS dU -=Vdp TdS dH += pdV SdT dA --=V d p SdT dG +-=麦克斯韦关系式:VS S p V T ⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂pS S V p T ⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ T V V S T p ⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂ Tp p S T V ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂-偏摩尔量的定义 BC n p T BB nX X ≠⎪⎪⎭⎫ ⎝⎛∂∂=,, 化学势的定义 BA n n p T BB nG≠⎪⎪⎭⎫ ⎝⎛∂∂≡,,μ化学平衡理想气体反应的标准平衡常数 ∏⎪⎪⎭⎫⎝⎛=B B Bp p K ν化学反应的等温方程式 K RT J RT G p m r ln ln -=∆K RT G m r ln -=∆∑∆=∆Bm f B m r T B G G ),,(βν范特霍夫等压方程 2ln RT H T K m r p∆=⎪⎪⎭⎫ ⎝⎛∂∂ )11(ln 1212T T R H K K m r -∆-=多组分系统热力学与相平衡摩尔分数 ∑=BB B B n n x /质量分数 ∑=BB B B m m w /物质的量浓度 V n c B B /= 质量摩尔浓度 A B B m n b /= 拉乌尔定律:A A A x p p *=亨利定律 B B b B B c B B x B b k c k x k p ,,,===理想液态混合物中任一组分的化学势 B B B x RT ln +=*μμ理想溶液混合物的混合性质0m i x =∆V 0mix =∆H0ln mix >-=∆∑BB B x n R S 0ln mix <=∆∑BB B x n RT G稀溶液凝固点降低 B f f b K T ⋅=∆ 沸点升高 B b b b K T ⋅=∆稀溶液渗透压 RT c B =π 吉布斯相律 2+-=P C F R R S C '--=克拉佩龙方程 **∆∆=Bm Bm V T H dT dp ,,αβα 克劳修斯-克拉佩龙方程 2])/[ln(RT H dT p p d m vap *∆= 121212)(ln T T T T R H p p m vap -∆=*电化学离子的迁移数 -++-++-++++=+=+=U U U v v v Q Q Q t -+--+--+--+=+=+=U U U v v v Q Q Q t 电导 R G /1= κ==R G /1A /l 摩尔电导率 m Λ=κ/c柯尔劳施离子独立运动定律的数学表达式 ∞--∞++∞Λ+Λ=Λ,,m m m νν∞ΛΛ=m m /αννν/1)(--++±⋅=a a a ,式中-++=ννν νννγγγ/1)(--++±⋅= ννν/1)(--++±⋅=b b b ν±=a aννννγνν)/( b b a ±--++⋅⋅=离子强度为 ∑=221B B z b I 德拜-修克尔极限公式: I z Az -+±-=γlg 在25℃时的水溶液中1/2ol)0.509(kg/m =A恒温、恒压、可逆反应过程 z F E W G r m r -='=∆p m r T E zF S )/(∂∂=∆恒温反应过程 ])/([E T E T zF H p m r -∂∂=∆p m r m r T E zFT S T Q )/(,∂∂=∆=能斯特方程(原电池的基本方程): ∏-=BB B a zF RTE E ν)(ln zFE G m r -=∆RTzFE K=ln电极电势的能斯特方程:)()(ln)()(氧化态还原态电极电极a a zF T R E E -= )(阳E =),(理阳E +)(阳η )(阴E =),(理阴E -)(阴η表面现象比表面 VA A S =表面张力又称比表面功 dA W l F r /2//δσ==杨氏方程 θσσσc o s l g l s s g ---+= l g l s s g ----=σσσθ/)(c o s 铺展系数 l g l s s g -----=σσσϕ 拉普拉斯方程 r r r r r r Fp σπσππ2)/(2211121===∆ 液体在毛细管中上升的高度 gr h ρθσc o s 2=开尔文公式 rMp p RT r ρσ2ln=朗缪尔吸附等温式 bpbp+=1θ ∞ΓΓ=/θbpbp+Γ=Γ∞1 液体表面的吸附——吉布斯吸附等温式 TBB c RTc ⎪⎪⎭⎫ ⎝⎛∂∂⋅-=Γσ 化学动力学基础反应速率 dtdc dt dn V dt d V VBB B B ⋅=⋅=⋅==ννξξυ111 质量作用定律 bB a A A A A c c k dtdc =-=υ 零级反应 A A A A k c k dt dc ==-0t k c c A A A =-0, k c t A 20,2/1=一级反应 A A A c k dt dc =- t k c c A AA =0,lnAA k k t 6932.02ln 2/1== 二级反应 2A A A c k dt dc =- 0,11A A A c c t k -=阿伦尼乌斯公式 ⎪⎭⎫⎝⎛-=RT E k k a exp 0 2ln RT E dT k d a =。
物理化学公式大全

物理化学公式大全物理化学是研究物质及其性质与能量变化之间关系的学科。
在物理化学的学习与研究过程中,掌握一些重要的公式是十分关键的。
下面是物理化学公式的大全,帮助你更好地理解和运用这些公式。
1. 热力学公式1.1 热力学第一定律dU = dq + dw其中,dU表示系统内能的变化,dq表示系统吸收的热量,dw表示系统对外界所做的功。
1.2 热力学第二定律(卡诺循环)η = 1 - Tc / Th其中,η表示卡诺循环的热效率,Tc表示循环过程中的低温热源温度,Th表示循环过程中的高温热源温度。
1.3 熵变ΔS = ∫dq / T其中,ΔS表示熵变,dq表示吸收的热量,T表示温度。
2. 电化学公式2.1 奥姆定律I = U / R其中,I表示电流强度,U表示电压,R表示电阻。
2.2 法拉第定律I = nFv其中,I表示电流强度,n表示电离物质的摩尔数,F表示法拉第常数,v表示电离的速率。
2.3 电解质溶液中浓度的关系c = n / V其中,c表示溶液的浓度,n表示溶质的物质的量,V表示溶液的体积。
3. 量子化学公式3.1 玻尔模型电子能级En = - 13.6 / n²其中,En表示第n个电子能级的能量。
3.2 库仑势能E = - (Z × e²) / (4πε₀r)其中,E表示两个带电粒子之间的库仑势能,Z表示电荷的量子数,e表示元电荷,ε₀表示真空介电常数,r表示两个带电粒子的距离。
4. 动力学公式4.1 反应速率常数k = A × e^(-Ea / RT)其中,k表示反应速率常数,A表示指前因子,Ea表示活化能,R 表示气体常数,T表示温度。
4.2 阿伦尼乌斯方程k = Z × f(ΔE)其中,k表示反应速率常数,Z表示碰撞频率,f(ΔE)表示碰撞激活因子,ΔE表示碰撞能量。
5. 其他公式5.1 时间-位移关系x = v₀t + 1/2at²其中,x表示位移,v₀表示初始速度,t表示时间,a表示加速度。
物理化学公式大全

物理化学公式集热力学第一定律功:δW=δW e+δW f(1)膨胀功δW e=p外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f=xdy非膨胀功为广义力乘以广义位移。
如δW(机械功)=fdL,δW(电功)=EdQ,δW(表面功)=rdA。
热Q:体系吸热为正,放热为负。
热力学第一定律:△U=Q—W 焓H=U+pV理想气体的内能和焓只是温度的单值函数。
热容C=δQ/dT(1)等压热容:C p=δQ p/dT=(∂H/∂T)p(2)等容热容:C v=δQ v/dT=(∂U/∂T)v常温下单原子分子:C v,m=C v,m t=3R/2常温下双原子分子:C v,m=C v,m t+C v,m r=5R/2等压热容与等容热容之差:(1)任意体系C p—C v=[p+(∂U/∂V)T](∂V/∂T)p(2)理想气体C p—C v=nR理想气体绝热可逆过程方程:pVγ=常数TVγ-1=常数p1-γTγ=常数γ=C p/ C v理想气体绝热功:W=C v(T1—T2)=(p1V1—p2V2)理想气体多方可逆过程:W=(T1—T2)热机效率:η=冷冻系数:β=-Q1/W可逆制冷机冷冻系数:β=焦汤系数:μJ-T==-实际气体的ΔH和ΔU:ΔU=+ΔH=+化学反应的等压热效应与等容热效应的关系:Q p=Q V+ΔnRT当反应进度ξ=1mol时,Δr H m=Δr U m+RT化学反应热效应与温度的关系:热力学第二定律Clausius不等式:熵函数的定义:dS=δQ R/T Boltzman熵定理:S=klnΩHelmbolz自由能定义:F=U—TS Gibbs自由能定义:G=H-TS热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU=TdS-pdV dH=TdS+VdpdF=-SdT-pdV dG=-SdT+Vdp(2)Maxwell关系:==-(3)热容与T、S、p、V的关系:C V=T C p=TGibbs自由能与温度的关系:Gibbs-Helmholtz公式=-单组分体系的两相平衡:(1)Clapeyron方程式:=式中x代表vap,fus,sub。
物理化学公式汇总

物理化学公式汇总物理化学是一门运用物理学的原理和方法来研究化学现象和规律的学科,其中涉及众多的公式。
这些公式是理解和解决物理化学问题的重要工具。
下面为大家汇总一些常见且重要的物理化学公式。
首先是热力学方面的公式。
热力学第一定律:ΔU = Q + W 。
其中,ΔU 表示系统内能的变化,Q 表示系统吸收的热量,W 表示系统对外做功。
这个公式揭示了能量的守恒与转化关系。
热力学第二定律有多种表述方式,其中克劳修斯表述为:热量不能自发地从低温物体传到高温物体。
开尔文表述为:不可能从单一热源吸取热量使之完全变为有用功而不产生其他影响。
熵增原理的数学表达式为:ΔS ≥ 0 ,其中ΔS 表示熵的变化。
熵是系统混乱度的度量。
理想气体状态方程:pV = nRT 。
p 是压强,V 是体积,n 是物质的量,R 是理想气体常数,T 是温度。
这个公式在研究气体的性质和行为时经常用到。
热力学能的定义式:U = U(T, V) 。
表明热力学能是温度和体积的函数。
接着是热力学函数的相关公式。
焓的定义式:H = U + pV 。
吉布斯自由能的定义式:G = H TS 。
在恒温恒压条件下,ΔG ≤ 0 时反应自发进行。
亥姆霍兹自由能的定义式:A = U TS 。
在恒温恒容条件下,ΔA ≤ 0 时过程自发进行。
然后是化学平衡方面的公式。
标准平衡常数表达式:Kθ =Π(piθ)^νi 。
其中piθ 是平衡时各物质的分压,νi 是化学计量数。
范特霍夫等温方程:ΔG =ΔGθ + RTlnQ 。
Q 是反应商,通过比较ΔG 的正负可以判断反应进行的方向。
再来看电化学方面的公式。
法拉第定律:Q = nZF 。
Q 表示通过电极的电量,n 是电极反应中转移的电子数,Z 是离子的电荷数,F 是法拉第常数。
能斯特方程:E =Eθ (RT / nF)lnQ 。
用于计算非标准状态下的电极电势。
最后是动力学方面的公式。
质量作用定律:对于基元反应 aA +bB → cC + dD ,反应速率 v = kA^aB^b 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律 热力学第一定律:ΔU =Q +W 。
三、基本关系式1、体积功的计算 δW = -p 外d V恒外压过程:W = -p 外ΔV定温可逆过程(理想气体):W =nRT 1221ln ln p p nRT V V = 2、热效应、焓:等容热:Q V =ΔU (封闭系统不作其他功)等压热:Q p =ΔH (封闭系统不作其他功)焓的定义:H =U +pV ; ΔH =ΔU +Δ(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容:热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂= 定压热容与定容热容的关系:nR C C =-V p热容与温度的关系:C p ,m =a +bT +cT 2四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p 外d V等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d pC V (㏑T 2-㏑T 1)=nR(㏑V 1-㏑V 2)(T 与V 的关系)C p (㏑T 2-㏑T 1)=nR(㏑P 2-㏑P 1) (T 与P 的关系)不可逆绝热过程:Q =0 ;利用C V (T 2-T 1)=-p 外(V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化 可逆相变化:ΔH =Q =n ΔH ; W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、实际气体节流膨胀:焦耳-汤姆逊系数:μJ-T (理想气体在定焓过程中温度不变,故其值为0;其为正值,则随p 降低气体T 降低;反之亦然)4、热化学标准摩尔生成焓:在标准压力和指定温度下,由最稳定的单质生成单位物质的量某物质的定压反应热(各种稳定单质在任意温度下的生成焓值为0) 标准摩尔燃烧焓:…………,单位物质的量的某物质被氧完全氧化时的反应焓第二章 热力学第二定律一、基本概念 自发过程与非自发过程二、热力学第二定律热力学第二定律的数学表达式(克劳修斯不等式)T Q dS δ≥ “=”可逆;“>”不可逆三、熵(0k 时任何纯物质的完美结晶丧子为0)1、熵的导出:卡若循环与卡诺定理(页522、熵的定义:T Q dS r δ=3、熵的物理意义:系统混乱度的量度。
4、绝对熵:热力学第三定律5、 熵变的计算(1)理想气体等温过程:2112ln ln p p nR V V nR T Q S r ===∆ (2)理想气体等压过程:12,ln T T nC S m p =∆(3)理想气体等容过程:12,ln T T nC S m V =∆ (4)理想气体pTV 都改变的过程:2112,ln ln p p nR T T nC S m p +=∆ (5)可逆相变化过程:T H n S _∆=∆(6)化学反应过程:)298,()298(B S S m B m r ∑=∆θθν四、赫姆霍兹函数和吉布斯函数1、定义:A=U-TS ;G=H-TS等温变化:ΔA=ΔU -TΔS ;ΔG=ΔH -TΔS2、应用:不做其他功时,ΔG T ,p ≤0 ;自发、平衡3、热力学重要关系式:dU=TdS-pdV ;dH=TdS+Vdp【页72】 dA=-SdT- pdV ;dG=-SdT+Vdp4、ΔA 和ΔG 的求算(1)理想气体等温过程用公式:ΔA=ΔU -TΔS ;ΔG=ΔH -TΔS用基本关系式:d A =-S d T - pdV ;d G =-S d T + Vdp(2)可逆相变过程 ΔA=ΔU -TΔS =W =-nRT ;ΔG =0(3)化学反应过程的ΔG 标准熵法:ΔG=ΔH -TΔS标准生成吉布斯函数法:)298,()298(B G G m f B m r θθν∆=∆∑(4)ΔG 与温度的关系ΔG=ΔH -TΔS ,设ΔH 、ΔS 不随温度变化。
第三章化学势1、化学势的定义。
物理意义:决定物质传递方向的限度的强度因素。
)(,,)(B c c n p T BB n G ≠∂∂=μ ;在T 、p 及其他物质的量保持不变的情况下,增加1molB 物质引起系统吉布斯函数的增量。
(又称偏摩尔量。
1、只有系统的容量性质才有偏摩尔量,故系统强度性质没有偏摩尔量【页8有两种性质定义】2、只有在定稳T ,定压P 下才成为偏摩尔量)2、化学势的应用在等温等压不作其他功时,∑B B μν<0自发;=0平衡;>0逆向自发3、化学时表示式理想气体:)/ln(θθμμp p RT += 纯固体和纯液体:θμμ=拉乌尔定律和亨利定律1、拉乌尔定律p A =p *x A (溶液中该物质蒸汽压=纯该物质蒸汽压*溶液中该物质物质量分数【理想】) 适用于液态混合物和溶液中的溶剂。
2、亨利定律p B =k x,x B (与溶液平衡的溶质蒸汽的分压=亨利系数*溶质在溶液中的摩尔分数)适用于溶液中的溶质。
二、液态混合物和溶液中各组分的化学势1、理想液态混合物x RT T mix p T x ln )(),,(+=θμμ 标准态为:同温下的液态纯溶剂。
2、真实液态混合物x x a RT T mix p T ln )(),,(+=θμμ 标准态为:同温下的液态纯溶剂。
3、理想稀溶液溶剂:A A x A x RT T sln p T ln )(),,(+=θμμ 标准态为:同温下的液态纯溶剂。
溶质:B B x B x RT T sln p T ln )(),,(+=θμμ 标准态为:同温下x B =1且符合亨利定律的溶质。
4、真实溶液溶剂:A x A x A a RT T sln p T ,,ln )(),,(+=θμμ ;a x,A =f x,A x ; 标准态为:同温下的液态纯溶剂。
溶质:B x B x B a RT T sln p T ,ln )(),,(+=θμμ ; a x,B =γx,B x B ; 标准态为:同温下x B =1且符合亨利定律的溶质。
B b B b B a RT T sln p T ,,ln )(),,(+=θμμ; a b,B =γb,B b B ; 标准态为:同温下b B =1且符合亨利定律的溶质。
理想稀溶液的凝固点降低B A m fus f f f x H T RT T ,*∆=∆第四章 化学平衡一、化学平衡常数与平衡常数表达式二、 标准平衡常数的求算:θθK RT T G m r ln )(-=∆三、 范特荷夫等温方程 θθK RT T G m r ln )(-=∆+RT ㏑Q P (页114四、平衡常数与温度的关系θθθm r m r m r S T H T G ∆-∆=∆)(;θθK RT T G m r ln )(-=∆五、平衡常数的各种表示方法:(页121K p 、K x 是气相反应的经验平衡常数。
其与标准平衡常数关系为: K θ=K p (p θ)-△V (产物与反应物计量数之差)=K x (p/ p θ)△V =K n (p/ p θn 总)△V 若△v=0则K θ=K p =K x =K n分解压:固体物质在一定温度下分解达到平衡时产物中气体的总压力第五章 多相平衡一、相律1、系统中所包含的相的总数称为相数,以Ф表示。
最小值为1。
正整数2、一个系统中无论多少气体都为一个气相;系统一般一两个液相;多少固体物质便有多少固相。
3、系统中所含化学物质书称为“物种数”以S 表示,最小值为1.正整数4、足以表示系统中各相组成所需的最少独立物种数称为系统“组分数”,以K 表示。
组分数=物种数-独立化学平衡数-独立浓度关系数 K=S-R-R ,自由度:在不引起旧相消失和新相形成的前提下,可在一定范围内独立变动的强度性质,以f 表示只考虑温度与压力因素的影响时f =K -φ+2,(f =K -φ+1指定温度或压力)。
最小值为0二、单组分系统 1、克-克方程 )11(ln 2112T T R H p p m vap -∆=2、水的相图 三面、三线、一点。
三、二组分系统 1、步冷曲线(页1702、看相图:有“丁”字型相则说明有不稳定化合物生成。
第六章(没学不考)第七章 电化学通过电极电荷量:Q=nF (n 为电极反应时得失电子的物质的量,F 为1mol 电子电荷量,叫法拉第,通常取96.5kC/mol )一、电解质溶液的电导1、电导 G =1/R ; 单位:S(西门子)2、电导率 G =κA /l 或κ=G l /A ; 单位:S/m3、摩尔电导率 Λm =κ/c4、无限稀释摩尔电导率 ∞--∞++∞+=ΛΛΛm νν5、离子的电迁移lE U ∆=++υ ;-++--+++++=+===U U U I I Q Q t υυυ ;1=+-+t t 二、电解质溶液的活度(229页表格1、电解质的化学势(电解质溶液的浓度用m B 或b B 表示)B B B a RT ln +=θμμ;)(;)(;/)(;/1/1/1ννννννθννννγγγγ-+-+-+-+±-+±±±-+±±⋅=⋅=⋅=⋅==m m m m m a a a a a B 2、离子强度 ∑=221B B z m I 电池系列 一、可逆电池的构成电池反应互为逆反应;充放电时电流无穷小。
二、可逆电池热力学1、(△r G m )T,P =-nFE=-QE2、p m r T E zF S )(∂∂=∆4、m r r S T Q ∆= ;电池反应做了其他功。
三、能斯特方程四、可逆电极的种类1、第一类电极:金属电极;气体电极2、第二类电极:微溶盐电极;微溶氧化物电极3、第三类电极:氧化还原电极电池表示式(1)以化学式表示电池中各种物质的组成,并需分别注明固液气等物态。
对气体注明压力,对溶液注明浓度(2)以“|”表示不同物相之间的界面,包括电极与溶液的接界和不同溶液间的接界。
盐桥以“||”(3)电池中的负极(氧化反应)写在左边。
五、电极电势的应用1、判断反应趋势2、求化学反应平衡常数3、求微溶盐活度积4、测离子平均活度±γ 六、电动势E=φ(正极电势)-φ(负)= φ(阴)-φ(阳)无论原电池还是电解池,相对于可逆电极电势φ,当有电流通过电极时,由于电极的极化,阳极电势升高,阴极电势降低,即 φ(阳)=φ+μ,φ(阴)=φ-μ1、浓差极化:电极反应速度比离子迁移速度快造成的。
