(完整版)大学物理学(课后答案)第7章
大学物理课后习题答案 第七章

Q
RT1
ln
V2 V1
8.31 400 ln 0.005 0.001
5.35 103 J
(2) 根据卡诺循环的效率公式可得
1 T2 A净 T1 Q吸
A净
(1
T2 T1
)Q吸
(1
300 ) 5.35 103 400
1.34 103 J
(3)由能量守恒 Q吸 A净 Q放 可得
Pa Va )
1 2 (Pb
Pa ) (Vb
Va )
9.5 102 J
A 100 10.5% Q吸 950
B
C 2 V (L)
62
大学物理上习题册参考解答
10、一定质量理想气体(摩尔热容比为 γ)的某循环过程的 T-V 图如下,其中 CA 为绝
热过程,状态 A(T1,V1)和状态 B(T2,V2)为已知,试问:
RT2
ln
VA VB
R(T1 T2) ln
VA VB
T2 T1 T2
14、一台家用冰箱放在室温为 300K 的房间内,做一盘 2.09105 J 的热量。设冰箱为理想卡诺制冷机。 (1)求做一盘冰块所需要的功;
℃的冰块需从冷冻室取走
(2)若此冰箱能以 2.09102 J / s 的速率取出热量,求冰箱的电功率。
mR mR
60
大学物理上习题册参考解答
6、某理想气体在 P-V 图上等温线与绝热线相交于 A
点(如图所示)。 已知 A 点的压强 P1=2×105Pa,体积 V1=0.5 P ×10-3m3 ,而且 A 点处等温线的斜率与绝热线斜率之比为
0.714,现使气体从 A 点绝热膨胀至 B 点,其体积 V2=1×10-3m3。
大学物理第7章静电场中的导体和电介质课后习题及答案

1第7章 静电场中的导体和电介质 习题及答案1. 半径分别为R 和r 的两个导体球,相距甚远。
用细导线连接两球并使它带电,电荷面密度分别为1s 和2s 。
忽略两个导体球的静电相互作用和细导线上电荷对导体球上电荷分布的影响。
试证明:Rr =21s s。
证明:因为两球相距甚远,半径为R 的导体球在半径为r 的导体球上产生的电势忽略不计,半径为r 的导体球在半径为R 的导体球上产生的电势忽略不计,所以的导体球上产生的电势忽略不计,所以半径为R 的导体球的电势为的导体球的电势为R R V 0211π4e p s =014e s R =半径为r 的导体球的电势为的导体球的电势为r r V 0222π4e p s =024e s r = 用细导线连接两球,有21V V =,所以,所以Rr=21s s 2. 证明:对于两个无限大的平行平面带电导体板来说,证明:对于两个无限大的平行平面带电导体板来说,(1)(1)(1)相向的两面上,电荷的面密度总是相向的两面上,电荷的面密度总是大小相等而符号相反;大小相等而符号相反;(2)(2)(2)相背的两面上,电荷的面密度总是大小相等而符号相同。
相背的两面上,电荷的面密度总是大小相等而符号相同。
相背的两面上,电荷的面密度总是大小相等而符号相同。
证明: 如图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1s ,2s ,3s ,4s (1)取与平面垂直且底面分别在A 、B 内部的闭合圆柱面为高斯面,由高斯定理得内部的闭合圆柱面为高斯面,由高斯定理得S S d E SD +==×ò)(10320s s e故+2s 03=s上式说明相向两面上电荷面密度大小相等、符号相反。
上式说明相向两面上电荷面密度大小相等、符号相反。
(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即电平面产生的场强叠加而成的,即0222204030201=---e s e s e s e s又+2s 03=s 故 1s 4s =3. 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量。
大学物理课后答案第七章.doc

第七章静电场中的导体和电介质一、基本要求1. 掌握导体静电平衡的条件及静电平衡时导体电荷的分布规律;2. 学会计算电容器的电容;3. 了解介质的极化现象及其微观解释;4. 了解各向同性介质中D和E的关系和区别;5. 了解介质中电场的高斯定理;6. 理解电场能量密度的概念。
二、基本内容1. 导体静电平衡(1) 静电平衡条件:导体任一点的电场强度为零(2) 导体处于静电平衡时:①导体是等势体,其表面是等势面;②导体表面的场强垂直于导体表面。
(3) 导体处于静电平衡时,导体内部处处没有净电荷存在,电荷只能分布在导体的表面上。
2. 电容(1) 孤立导体的电容c=勺V电容的物理意义是使导体电势升高单位电势所需的电量。
电容是导体的重要属性之一,它反映导体本身具有储存电荷和储存电能的能力。
它的大小仅由导体的几何形状、大小和周围介质决定,与导体是否带电无关。
(2) 电容器的电容C =—9-V A~ Vq为构成电容器两极板上所带等量异号电荷的绝对值。
V A-V B为A、B两极间电势差。
电容器电容与电容器形状、大小及两极间介质有关,与电容器是否带电无关。
(3) 电容器的串并联串联的特点:各电容器的极板上所带电量相等,总电势差为各电容器上电势差之111 1和。
等效电容由一=—+—+川+一进行计算。
C C C C1 2 n并联的特点:电容器两极板间的电势差相等,不同电容器的电量不等,电容大者电量多。
等效电容为C=C +C ,川*C o 1 2 n(4) 计算电容的一般步骤+ 一%1设两极带电分别为q和q,由电荷分布求出两极间电场分布。
~ = J B%1由V V E dl求两极板间的电势差。
A B A%1根据电容定义求c wV A VB3. 电位移矢量D=£ +人为引入的辅助物理量,定义D E P, D既与E有关,又与P有关。
说明D 0不是单纯描述电场,也不是单纯描述电介质的极化,而是同时描述场和电介质的。
定义式无论对各向同性介质,还是各向号惟会质都适用。
大学物理第7章习题参考答案(钟韶 编)

第七章7-1 (1)由RT MmpV =把p =10atm, T=(47+273)K=320K.m =0.1kg, M=32×10-3kg R =8.31J ·mol -1·K -1代入.证V =8.31×10-3m 3(2) 设漏气后,容器中的质量为m ′,则T R M m V p ''=' 3201.0853*******⨯⨯='⇒⨯'=⇒R MR M m R Mm pV )kg (151='⇒m 漏去的氧气为kg 103.3kg 301kg )1511.0(2-⨯≈=-='-=m m m ∆ 7-2 太阳内氢原子数H Sm M N =故氢原子数密度为3827303)1096.6(341067.11099.134⨯⨯⨯⨯===-ππs H S R m M VN n)(105.8329-⨯=m由P =nkT 知)(1015.11038.1105.81035.17232914K nk p T ⨯=⨯⨯⨯⨯==- 7-3 如图混合前:2221112222111O He T M m T M m RT M m pV RT M m pV =⇒⎪⎪⎭⎪⎪⎬⎫==气有对气有对 ①总内能 222111212523RT M m RT M m E E E +=+=前 ② ①代入②证1114RT M m E =前 混合后:设共同温度为T题7-2图()RT M m T T EF RT M m M m E 21210221125231,2523⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=式得又由后 ③ 又后前E E =,故由(2)(3)知)/53(8211T T T T +=7-4 (1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤≤≤=000002020)(v v v v v av v v v av f (2)由归一化条件⎰∞=01d )(v v f 得020032123d d 000v a av v a v v v a v v v =⇒==+⎰⎰(3)4d d )(00002/02/Nv v v a N v v Nf N v v v v =⎪⎪⎭⎫ ⎝⎛==⎰⎰∆ (4)从图中可看出最可几速率为v 0~2v 0各速率. (5)⎰⎰⎰+⎪⎪⎭⎫ ⎝⎛==∞0002/000d d d )(v v v v va v v v av v v vf v020911611v av ==(6)02/02/097d d d )(d )(0002121v v v v a v v av v v v f v v vf v v v v v v v v v =⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛==⎰⎰⎰⎰ 7-5 氧气未用时,氧气瓶中T T p L V V ====111,atm 130,32 V RTMp V RT Mp m 11111==① 氧气输出压强降到atm 102=p 时 V RTMp V RT Mp m 22222== ② 氧气每天用的质量 000V RTMP m =③L 400,atm 100==V P设氧气用的天数为x ,则021210m m m x m m xm -=⇒-= 由(1)(2)(3)知021021)(V p Vp p m m m x -=-=)(6.932400110130天=⨯⨯-=7-6 (1))(m 1041.23001038.110325235--⨯=⨯⨯==KT p n (2)(kg)103.51002.61032262330--⨯=⨯⨯==N M μ (3))kg/m (3.1103.51041.232625=⨯⨯⨯==-μρn (4)(m)1046.31041.21193253-⨯=⨯==nl(5)认为氧气分子速率服从麦克斯韦布,故 )(m s 1046.4103230031.86.16.11-23⨯=⨯⨯==-M RT v (6)122ms 1083.43-⨯==MRTv (7)(J)1004.13001038.12522023--⨯=⨯⨯⨯==KT i ε 7-7 3112310m 1006.12371038.1104---⨯=⨯⨯⨯==∴=kT p n nkTp )(cm 1006.135-⨯= 故1cm 3中有51006.1⨯个氮气分子.m101.21006.111d 43113-⨯≈⨯==n7-8 由课本P 257-258例7-4的结论知 )l n (0pp Mg RTh =(m)1096.1)8.01ln(8.9102930031.833⨯=⨯⨯⨯=- 7-9 (1) (J)1021.63001038.123232123--⨯=⨯⨯⨯==KT t (2)看作理想气体,则3132310101030028.16.16.1---⨯⨯⨯==μKTv 12ms 1003.1--⨯=7-10 (J)5.373930031.82323=⨯⨯===RT N E 平动平动ε (J)249330031.8122=⨯⨯===RT N E 转动转动ε内能(J)1023.630031.825253⨯=⨯⨯==RT E7-11 (1)由KTpn nKT p =⇒=∵是等温等压 ∴ 1:1:21=n n (2) MRT v 6.1=是等温,∴4:1322::1221====M M v v7-12317233102.33001038.11033.1---⨯=⨯⨯⨯==m KT P n m)(8.71033.110923001038.1d 2320232=⨯⨯⨯⨯⨯⨯==---ππλpKT7-13 (1)8000021042.56.1d 2⨯=⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫===z M RT v KT p n v n z π(2)由公式MTRK p M RTKT p v n z 222d 26.1d 2d 2πππ===知 z 与T 和P 有关,由于T 不变,故z 只与P 有关.则1854000071.01042.510013.11033.1::--=⨯⨯⨯⨯='='⇒'='s z p p z p p z z 7-14 (1)如图MRT v 32=∴A c A c T T v v ::22=又 C B →等温过程,故C B T T =. 由B A A B V V P P RT Mm pV ===2则A B T T 2= ∴1:2:22=A c V V(2)AAc c A c P T P T pKT ::d 22==λλπλ C B →等温过程 A C A A A C B B C C p p V p V p V p V p =⇒=⨯⇒=221:2:=∴A C7-15 (1)MRTv 73.12= )(ms 100.7102400031.873.1133--⨯=⨯⨯=(2)m 10210)31(2122101021--⨯=⨯+=+=d d d (3)325202210710401042d 2⨯⨯⨯⨯⨯⨯==-ππv n z110s 105-⨯= 7-16 (1)题7-14图MTR k p z KT pn M RT v v n z ππππ8d 28d 222=⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=== ① 又由mREMT RT M m RT M m E 3326=⇒==② 把②代入①知EmkMpKN E m kM pR z ππ3d 43d 4022== EmMpN π3d 402=(2) MRTv P 2=把②代入得mEmR EM M R V P 3232=⨯=(3)平均平动动能 0232323mN EMmR EM k kT t =⨯==ε。
《大学物理》-第二版-课后习题答案--第七章

习题精解7-1一条无限长直导线在一处弯折成半径为R 的圆弧,如图7.6所示,若已知导线中电流强度为I,试利用比奥—萨伐尔定律求:(1)当圆弧为半圆周时,圆心O 处的磁感应强度;(2)当圆弧为1/4圆周时,圆心O 处的磁感应强度。
解(1)如图7.6所示,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于直线电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据比奥—萨伐尔定律,半圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB Rμπ=方向垂直纸面向内。
半圆弧在O 点产生的磁感应强度为 000220444RIIdl I B R R R Rπμμμπππ===⎰方向垂直纸面向里。
(2)如图7.6(b )所示,同理,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据毕奥—萨伐尔定理,1/4圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB R μπ=方向垂直纸面向内,1/4圆弧电流在O 点产生的磁感应强度为00022204428RIIdl I R B R R Rπμμμπππ===⎰方向垂直纸面向里。
7.2 如图7.7所示,有一被折成直角的无限长直导线有20A 电流,P 点在折线的延长线上,设a 为,试求P 点磁感应强度。
解 P 点的磁感应强度可看作由两段载流直导线AB 和BC 所产生的磁场叠加而成。
AB 段在P 点所产生的磁感应强度为零,BC 段在P 点所产生的磁感应强度为 0120(cos cos )4IB r μθθπ=- 式中120,,2r a πθθπ=== 。
所以500(cos cos ) 4.010()42I B T a μπππ=-=⨯ 方向垂直纸面向里。
大学物理第7章真空中的静电场答案

Q 与坐标原点0的距离为ydE方向沿轴正向。
4二;0x (x _ L )(2)如图7— 2图b ,设通过棒的端点与棒垂直上任一点• dx2 4二;°r第七章 真空中的静电场7- 1在边长为a 的正方形的四角,依次放置点电荷 q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为 一^甘4)= 4二;。
(2 a ) 5q 2,方向由q 指向-4q 。
2二;°a 7 — 2如图,均匀带电细棒,长为 L ,电荷线密度为 入。
(1) 求棒的延长线上任一点 P 的场强;(2)求通过棒的端点与棒垂直上 任一点Q 的场强。
解:(1)如图7 — 2图a ,在细棒上任取电荷元 dq ,建立如图坐标, P 与坐标原点0的距离为x ,贝U dq = ■ d ■,设棒的延长线上任一点 dE4二;0(x _ )2 4二;0(x _ )2 则整根细棒在 P 点产生的电场强度的大小为 dq 0 n_(」L 一丄x - L x习题7—2图adE y■ dx 2 4二;0rdE x 亠si n ,4 二;°r因x 二ytg pdxcos2 -习题7—2图b代入上式,则E x 二-dE xPL QE「dE「石石。
込还R S Z= 4jy y2L27— 3 一细棒弯成半径为R的半圆形,均匀分布有电荷q,求半圆中心0处的场强。
解:如图,在半环上任取dl=Rdr的线元,其上所带的电荷为dq=,Rd=对称分析E y=o。
dE x■ Rd v24二0RE = dE x sin -4二0R 02 0Rq2 二2;0R2,如图,方向沿x轴正向。
7 —4如图线电荷密度为入1的无限长均匀带电直线与另一长度为I、线电荷密度为 & 的均匀带电直线在同一平面内,二者互相垂直,求它们间的相互作用力。
大学物理学课后习题7第七章答案

q 6 0
对于边长 a 的正方形,如果它不包含 q
所在的顶点,则 e
q 24 0
,
如果它包含 q 所在顶点则 e 0 .
7.8 均匀带电球壳内半径6cm,外半径10cm,电荷体密度为2×
105 C·m-3求距球心5cm,8cm ,12cm 各点的场强.
解:
高斯定理 当 r 5 cm
均匀分布,其电势U
E
dr
R2
qdr R2 4π 0 r 2
q 4π 0 R
题 7.16 图
(2)外壳接地时,外表面电荷 q 入地,外表面不带电,内表面电荷仍
为 q .所以球壳电势由内球 q 与内表面 q 产生:
U
q 4π 0 R2
q 4π 0 R2
(2)同理
dEQ
1 4π 0
dx
x2
d
2 2
方向如题 7.6 图所示
由于对称性 l dEQx 0 ,即 EQ 只有 y 分量,
∵
dEQy
1 4π 0
dx
x2
d
2 2
d2
x2
d
2 2
EQy
l dEQy
d2 4π 2
l 2
dx
l
3
2
(x2
d
2 2
)
2
l
1由于电荷均匀分布与对称性ab和cd段电荷在o点产生的场强互相抵消取?ddrl?则??ddrq?产生o点e?d如图由于对称性o点场强沿y轴负方向题714图??????cos4dd2220?????rreeyr04???2sin??2sin??r02????2ab电荷在o点产生电势以0??u?????ab200012ln44d4drrxxxxu??????同理cd产生2ln402???u半圆环产生00344??????rru0032142ln2?????????uuuuo715两个平行金属板ab的面积为200cm2a和b之间距离为2cmb板接地如图715所示
(完整版)大学物理学(课后答案)第7章

第七章课后习题解答一、选择题7-1 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,则它们[ ](A) 温度,压强均不相同 (B) 温度相同,但氦气压强大于氮气的压强 (C) 温度,压强都相同 (D) 温度相同,但氦气压强小于氮气的压强分析:理想气体分子的平均平动动能32k kT ε=,仅与温度有关,因此当氦气和氮气的平均平动动能相同时,温度也相同。
又由理想气体的压强公式p nkT =,当两者分子数密度相同时,它们压强也相同。
故选(C )。
7-2 理想气体处于平衡状态,设温度为T ,气体分子的自由度为i ,则每个气体分子所具有的[ ](A) 动能为2i kT (B) 动能为2iRT(C) 平均动能为2i kT (D) 平均平动动能为2iRT分析:由理想气体分子的的平均平动动能32k kT ε=和理想气体分子的的平均动能2ikT ε=,故选择(C )。
7-3 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为()()()1/21/21/222::2A B Cv v v =1:2:4,则其压强之比为A B C p :p :p[ ](A) 1:2:4 (B) 1:4:8 (C) 1:4:16 (D) 4:2:1=,又由物态方程p nkT =,所以当三容器中得分子数密度相同时,得123123::::1:4:16p p p T T T ==。
故选择(C )。
7-4 图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果()2p O v 和()2p H v 分别表示氧气和氢气的最概然速率,则[ ](A) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /4v v =(B) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(C) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(D) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /4v v =分析:在温度相同的情况下,由最概然速率公式p ν=质量22H O M M <,可知氢气的最概然速率大于氧气的最概然速率,故曲线a 对应于氧分子的速率分布曲线。
大学物理习题答案解析第七章

第七章 恒定磁场7 -1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管,两个螺线管的长度相同,R =2r ,螺线管通过的电流相同为I ,螺线管中的磁感强度大小B R 、B r 满足( ) (A ) (B ) (C ) (D )分析与解 在两根通过电流相同的螺线管中,磁感强度大小与螺线管线圈单位长度的匝数成正比.根据题意,用两根长度相同的细导线绕成的线圈单位长度的匝数之比因而正确答案为(C )。
7 -2 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量 为( )(A ) (B ) (C ) (D )分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面,根据磁场的高斯定理,磁感线是闭合曲线,闭合曲面的磁通量为零,即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量;.因而正确答案为(D ). 7 -3 下列说法正确的是( )(A ) 闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过 (B ) 闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零 (C ) 磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D ) 磁感强度沿闭合回路的积分不为零时,回路上任意一点的磁感强度都不可能为零分析与解 由磁场中的安培环路定律,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和必定为零。
因而正确答案为(B ).7 -4 在图(a)和(b)中各有一半径相同的圆形回路L1 、L2 ,圆周内有电流I1 、I2 ,其分布相同,且均在真空中,但在(b)图中L2 回路外有电流I3 ,P 1 、P 2 为两圆形回路上的对应点,则( )r R B B 2=r R B B =r R B B =2r R B B 4=21==R r n n r R B r 2π2B r 2παB r cos π22αB r cos π2S B ⋅=m Φ(A ) ,(B ) ,(C ) ,(D ) ,分析与解 由磁场中的安培环路定律,积分回路外的电流不会影响磁感强度沿回路的积分;但同样会改变回路上各点的磁场分布.因而正确答案为(C ).*7 -5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中,若导体中流过的恒定电流为I ,磁介质的相对磁导率为μr (μr<1),则磁介质内的磁化强度为( ) (A )(B ) (C ) (D )分析与解 利用安培环路定理可先求出磁介质中的磁场强度,再由M =(μr-1)H 求得磁介质内的磁化强度,因而正确答案为(B ).7 -6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道,当环中电子流强度为8 mA 时,在整个环中有多少电子在运行? 已知电子的速率接近光速。
大学物理学 上册 (孙厚谦 著) 清华大学出版社 课后答案 第7章
R
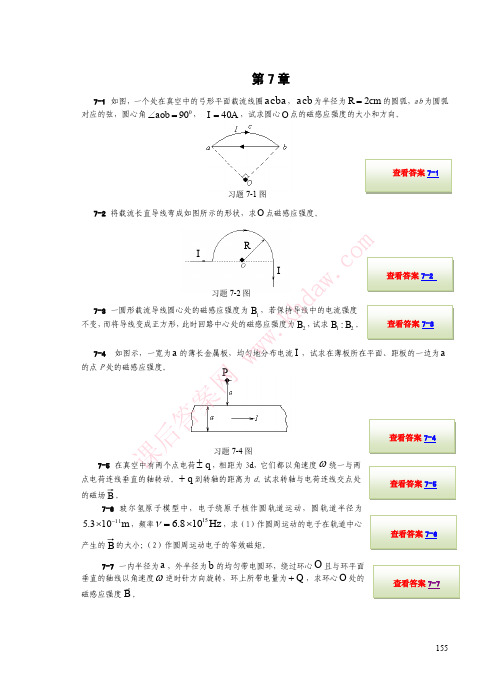
7-8 半径为 R 的薄圆盘均匀带电,总电量为 q 。令此盘绕通过圆盘中心 且垂直盘面的轴线匀速转动,角速度 ,求圆盘中心 O 处的磁感应强度。
查看答案 7-8
7-9 如图所示是一根很长的长直圆管形导体的横截面,内外半径分别为 a 和 b ,导体内载有沿轴线 方向的电流 I ,且电流 I 均匀分布在管的横截面上。试求导体内部( a r
第7章
7-1 如图,一个处在真空中的弓形平面载流线圈 acba , acb 为半径为 R 2cm 的圆弧,ab 为圆弧 对应的弦,圆心角 aob 900 ,
I 40A ,试求圆心 O 点的磁感应强度的大小和方向。
查看答案 7-1 习题 7-1 图 7-2 将载流长直导线弯成如图所示的形状,求 O 点磁感应强度。
B B1 B2 0.86 104 T
方向垂直纸面向外。 7-2
m
返回 7-1
解 如图,将导线分成 1(左侧导线) 、2(半圆导线) 、3(右侧导线)三部分,设各部分在 O 点处产 生的磁感应强度分别为 B1 、 B2 、 B3 。 根据叠加原理可知, O 点处磁感应强度 B
B2
网
利用叠加原理求 P2 点场强
ww
w.
a2 a2 π j πa I 2r 2 a 2 B Bo ( B1 B2 ) 0 ( 4 4 ) 0 a a 2π r π r (4r 2 a 2 ) r r 2 2
kh
2
π
da
r
r r2 a2 4
2πr
2π
r
w. 案
网
答
案
w.
F
co
B 的分布。
大学物理第7章真空中的静电场答案解析

第七章 真空中的静电场7-1 在边长为a 的正方形的四角,依次放置点电荷q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为)41()22(420+=a q F πε=,2520aqπε方向由q 指向-4q 。
7-2 如图,均匀带电细棒,长为L ,电荷线密度为λ。
(1)求棒的延长线上任一点P 的场强;(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解:(1)如图7-2 图a ,在细棒上任取电荷元dq ,建立如图坐标,dq =λd ξ,设棒的延长线上任一点P 与坐标原点0的距离为x ,则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ=)(40L x x L-πελ方向沿ξ轴正向。
(2)如图7-2 图b ,设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y习题7-1图0 dqξd ξ习题7-2 图a204r dxdE πελ=θπελcos 420rdxdE y =, θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===, 代入上式,则)cos 1(400θπελ--=y =)11(4220Ly y+--πελ,方向沿x 轴负向。
θθπελθd ydE E y y ⎰⎰==000cos 4 00sin 4θπελy ==2204Ly y L+πελ7-3 一细棒弯成半径为R 的半圆形,均匀分布有电荷q ,求半圆中心O 处的场强。
解:如图,在半环上任取d l =Rd θ的线元,其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420RRd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ= θθπελθd y dE E x x ⎰⎰-=-=0sin 4xdx习题7-2 图byx习题7-3图2022R q επ=,如图,方向沿x 轴正向。
大学物理课后习题答案第七章 a

第七章 电磁感应选择题7-1 在闭合导线回路的电阻不变的情况下,下述正确的是 ( B ) (A) 穿过闭合回路所围面积的磁通量最大时,回路中的感应电流最大; (B) 穿过闭合回路所围面积的磁通量变化越快,回路中的感应电流越大; (C) 穿过闭合回路所围面积的磁通量变化越大,回路中的感应电流越大; (D) 穿过闭合回路所围面积的磁通量为零时,回路中的感应电流一定为零.7-2 导体细棒ab 与载流长直导线垂直.在如图所示的四种情况中,细棒ab 均以与载流导线平行的速度v 平动,且b 端到长直导线的距离都一样.在(a)、(b)和(c)三种情况中,细棒ab 与光滑金属框保持接触.设四种情况下细棒ab 上的感应电动势分别为a E 、b E 、c E 和d E ,则 ( C )(A) a b c d ==<E E E E ; (B) a b c d ==>E E E >E ; (C) a b c d ===E E E E ;(D) a b c d >>>E E E E .7-3 如图所示,半圆周和直径组成的封闭导线,处在垂直于匀强磁场的平面内.磁场的磁感应强度的大小为B ,直径AB 长为l .如果线圈以速度v 在线圈所在平面内平动, v 与AB 的夹角为θ,则 ( A )(A) 线圈上的感应电动势为零,AB 间的感应电动势sin AB Bl θ=E v ; (B) 线圈上的感应电动势为零,AB 间的感应电动势cos AB Bl θ=E v ;(C) 线圈上的感应电动势为i 2sin Bl θ=E v ,AB 间感应电动势为sin AB Bl θ=E v ; (D) 线圈上的感应电动势为i 2cos Bl θ=E v ,AB 间感应电动势为cos AB Bl θ=E v . 7-4 一个面积210cm S =的圆线圈,其电阻0.10R =Ω,处于垂直于匀强磁场的平面内,若磁感应强度的大小随时间的变化率1d 10T s d Bt-=⋅,则线圈中的感应电流的大小为( D )(A) 3i 1.010A I -=⨯; (B) 2i 1.010A I -=⨯; (C) 2i 1.010A I =⨯; (D) 1i 1.010A I -=⨯.7-5 导线元d l 在磁感应强度为B 的磁场中以速度v 运动时,其上的动生电动势为()i d d =⨯⋅B l E v( D ) (A) 当v 与d l 垂直时,一定有i d d B l =E v ; (B) 当v 与B 垂直时,一定有i d d B l =E v ; (C) 当d l 与B 垂直时,一定有i d d B l =E v ;(D) 只有在v 、B 和d l 三者相互垂直时,才有i d d B l =E v 或i d d B l =-E v .7-6 下述正确的是 ( C )(A) 静电场和感生电场的电场线都不闭合;(B) 静电场的电场线是闭合的,感生电场的电场线不闭合; (C) 感生电场的电场线是闭合的,静电场的电场线不闭合; (D) 静电场和感生电场的电场线都是闭合的.7-7 静止的导体中产生涡电流的原因是 ( C ) (A) 导体处于不均匀的稳恒磁场中; (B) 导体处于不均匀的静电场中; (C) 导体处于随时间变化磁场中; (D) 导体处于通有稳恒电流的线圈内. 7-8 在自感线圈中,电流i 随时间t 的变化曲线如图(a)所示.若以i 的正流向为正方向,则线圈中自感电动势L E 随时间t 的变化曲线应为图(b)中的 ( D )7-9 尺寸相同的铜环和铝环,穿过它们所围面积的磁通量的变化率相同.设铜环上的感应电动势和感应电流分别为1E 和1I ,铝环上的感应电动势和感应电流分别为2E 和2I ,则( C )(A) 12=E E , 12I I =; (B) 12>E E , 12I I >; (C) 12=E E , 12I I >; (D) 12>E E , 12I I =.7-10 如图所示,若一块磁铁沿着一根竖直放置的长铜管的轴线,自管口竖直下落,如果忽略空气阻力,则 ( C )(A) 磁铁越落越快,最后速度趋于无限大; (B) 磁铁越落越慢,最后速度趋于零; (C) 磁铁越落越快,最后达到一恒定速度; (D) 磁铁越落越慢,最后达到一恒定速度;计算题7-11 一个匝数100N =的导线圈,通过每匝线圈的磁通量41510sin10πΦt =⨯,式中1Φ的单为Wb ,t 的单位为s .求:(1) 任意时刻线圈上的感应电动势;(2) 在10s t =时,线圈上的感应电动势的大小.解 (1) 根据法拉第电磁感应定律,任意时刻线圈上的感应电动势为()41i d d100510sin10π0.5πcos10πd d ΦNt t t t-=-=-⨯=-E 式中t 的单位为s ,i E 的单位为V .(2) 10s t =时,线圈上的感应电动势为()i 0.5πcos 10π10 V 1.57 V =-⨯=-i E大小为i 1.57 V =i E7-12 若在一方向不变的磁场中,有一面积为20.03m 的平面线圈,线圈所在平面的法线与磁场的夹角为θ,磁感强度的大小为510B t =+,式中B 的单位为T ,t 的单位为s .求:(1) 当π3θ=时,线圈中的感应电动势的大小; (2) 当π2θ=,2s t =时,线圈中的感应电动势的大小; 解 穿过线圈所围平面的磁通量为()()cos 5100.03cos 0.150.3cos BS t t Φθθθ==+⨯=+线圈中的感应电动势为()i d d0.150.3cos 0.3cos d d t t tΦθθ=-=-+=-E (1) 在π3θ=的情况下,线圈中的感应电动势为 i π0.3cos V 0.15V 3⎛⎫=-=- ⎪⎝⎭E其大小为0.15V(2) 在π2θ=的情况下,2s t =时,线圈中的感应电动势为 i π0.3cos V 02⎛⎫=-= ⎪⎝⎭E7-13 如图所示,一正方形线圈与载流长直导线共面,线圈的匝数为N ,边长为a ,其两边与长直导线平行,与长直导线之间的最小距离为b .长直导线中的电流为I .(1) 求通过线圈的磁通量;(2) 若100N =,20cm a =,10cm b =,当长直导线中的电流I 以12A s -⋅的变化率增长时,求线圈中的感应电动势.解 (1) 坐标选取如图所示.以顺时针为线圈回路的正方向, 则线圈所围平面的法向单位矢量n e 垂直纸面向里.在线圈平面上,长直载流导线的磁感应强度为0n 2πIaxμ=B e .在x 处取面元dS d a x =,则面元矢量为n d d a x =S e .穿过面元的磁通量为0d d d 2πIaΦx xμ=⋅=B S穿过线圈所围平面的磁通量为00d d ln2π2πa bSaIaNIaa bΦN N x xbμμ++=⋅==⎰⎰B S(2) 若100N =,20cm a =,10cm b =,则7064π101000.200.200.10ln ln Wb2π2π0.10 4.4010WbNIaa b I Φb I μ--⎛⎫+⨯⨯⨯⨯+== ⎪⎝⎭=⨯ 线圈中的感应电动势为()666i d d 4.4010 4.40102 V 8.8010 V d d ΦIt t--=-=-⨯=-⨯⨯=-⨯E i 0<E ,表明线圈中的感应电动势沿逆时针方向.7-14 如图所示,矩形导线框ABCD 与载流为I 的长直导线共面,边长分别为b 和l ,AB 与长直导线平行.矩形线框以速度v 在其平面内向右运动,v 与直导线垂直.在时刻t ,AB 与长直导线间的距离为a .求此时线框上的感应电动势.解 在长直导线右侧的线框平面上,到长直导线的距离为r 的点上,载流长直导线的磁场,方向垂直于纸面向里,磁感应强度的大小为02πIB rμ=以顺时针为导线回路的正方向,线圈中的感应电动势为()()()()()i d d d d d ABCDAAB BC CD DA =⨯⋅=⨯⋅+⨯⋅+⨯⋅+⨯⋅⎰⎰⎰⎰⎰B l B l B l B l B lv v v v v E 在BC 和DA 段上,d l v ,()d 0⨯⋅=B l v ,因此积分为零.在时刻t ,AB 处的磁感应强度大小为012πIB aμ=,CD 处的磁感应强度大小为()022πIB a b μ=+.于是()()()i 1200000d d d d d d 11 2π2π2πAB CD AB CD llB l B lI lI l Il a a b a a b μμμ=⨯⋅+⨯⋅=+-⎛⎫=-=- ⎪++⎝⎭⎰⎰⎰⎰⎰⎰B l B l E v v v v v v vi 0>E ,表明线圈中的感应电动势沿顺时针方向.7-15 如图所示,匀强磁场的磁感应强度的大小为B ,方向垂直纸面向外.有一根长为L 的金属棒MN ,可绕点O 在纸面内逆时针旋转,角速度为ω,4LOM =.求金属棒两端之间的电动势.那一端的电势较高?解 如图所示,在棒MN 上,到点O 的距离为l 处,沿径向取位移元d l .d l 的速度v 的方向如图,既垂直于d l ,也垂直于B ,大小为l ω=v .d l 上的动生电动势为()i d d d Bl l ω=⨯⋅=B l dE vMN 上的动生电动势为32441d 4L L MN Bl l BL ωω==⎰E0MN >E ,表明动生电动势的方向为从M 到N ,N 端电势较高.7-16 如图所示,矩形导线框ABCD 与载流长直导线共面,AB 与长直导线平行,相互间的距离为a ,导线框的边长分别为b 和l .如果长直导线上的电流为0πcos 3I I t ω⎛⎫=+ ⎪⎝⎭,式中0I 和ω为常量.求在0t =时,导线框上的感应电动势.解 坐标选取如图所示.以ABCDA ,即顺时针为线框回路的正方向,则平面ABCD 的法向单位矢量n e 垂直纸面向里.在平面ABCD 上,长直载流导线的磁感应强度为0n 2πIx μ=B e .由于0πcos 3I I t ω⎛⎫=+ ⎪⎝⎭,因此B 的具体指向随时间变化.在x 处取面元dS d l x =,则面元矢量为n d d l x =S e .穿过面元的磁通量为0d d d d 2πIlΦB S x xμ=⋅==B S穿过线框所围平面的磁通量为00d d ln2π2πa bSaIlIla bΦx xaμμ++=⋅==⎰⎰B S 矩形线框ABCD 上的感应电动势为0i 0000d d ln d 2πd d ππ ln cos ln sin 2πd 32π3l a b I t a tl I l a b a b I t t a t a μΦμμωωω+=-=-+⎡⎤+⎛⎫⎛⎫=-+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦E0t =时0000i πlnsin ln2π34πI lI l a b a b a aμωω++==E i 0>E ,表明此时线框上的感应电动势沿顺时针方向.7-17 在一个长为0.6m 、直径为5.0cm 的纸筒上,密绕1200匝线圈.求这个长直螺线管的自感.解 长直螺线管的自感为()2220027223π44π101200π 5.010H 5.9210H40.6N SN d L llμμ---==⨯⨯⨯⨯⨯==⨯⨯7-18 一螺线管的自感为21.010H -⨯,流过的电流为2.0A .求其储存的磁场能.解 载流螺线管储存的磁场能为2222m 11 1.010 2.0J 2.010J 22W LI --⎛⎫==⨯⨯⨯=⨯ ⎪⎝⎭7-19 一个直径为0.01m 、长为0.10m 的长直密绕螺线管,共1000匝线圈,总电阻为7.76Ω.若把螺线管接到电动势为2V 的电池上,求电流稳定后,螺线管中储存的磁能和管内的磁能密度.解 长直螺线管的自感为()2220027223π44π101000π 1.010H 9.8710H40.1N SN d L llμμ--==⨯⨯⨯⨯⨯==⨯⨯线圈上稳定电流的强度为2A 0.258A 7.76U I R === 电流稳定后,螺线管中储存的磁能为2325m 119.87100.258J 3.2810J 22W LI --⎛⎫==⨯⨯⨯=⨯ ⎪⎝⎭载流螺线管中磁能密度为()533m m m 22244 3.2810J m 4.18J m ππ1.0100.1W W V d l ---⨯⨯===⋅=⋅⨯⨯w 7-20 在真空中,若一匀强电场中的电场能量密度与一0.5T 的匀强磁场的能量密度相等,求该电场的电场强度.解 设电场强度为E 的匀强电场的能量密度与0.5T B =的匀强磁场的能量密度相等,则有22001122B E εμ=由此可得181m 1.5010 V m E --==⋅=⨯⋅。
大学物理第七章稳恒磁场习题答案

第七章 稳恒磁场习题7-1 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量为多少?解:取平面S ’与半球面S 构成闭合曲面,根据高斯定理有 0m mS mS ΦΦΦ'=+=2cos mS mS r E ΦΦπα'=-=-球面外法线方向为其正方向7-2 如图所示,几种载流导线在平面内分布,电流均为I ,它们在点O 的磁感应强度各为多少?08IR μ垂直画面向外0022II RR μμπ-垂直画面向里 00+42I IR Rμμπ垂直画面向外 7-3 如图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连。
已知圆环的粗细均匀,求环中心O 的磁感应强度。
解: 如图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
且θ-πθ==21221R R I I 电阻电阻 1I 产生1B 方向⊥纸面向外πθπμ2)2(2101-=R I B2I 产生2B 方向⊥纸面向里πθμ22202R I B =∴1)2(2121=-=θθπI I B B 有0210=+=B B B7-4 如图所示,已知地球北极地磁场磁感强度B 的大小为6.0×10-5T 。
如设想此地磁场是由地球赤道上一圆电流所激发的,此电流有多大?流向如何?(已知圆电流轴线上北极点的磁感强度()R IRR IR B 24202/32220μμ=+=)解:9042 1.7310A RBI μ==⨯方向如图所示7-5 有一同轴电缆,其尺寸如题图所示.两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑。
试计算以下各处的磁感应强度:(1)r<R 1;(2)R 1<r<R 2;(3)R 2<r<R 3;(4)r>R 3。
解:同轴电缆的电流分布具有轴对称性在电缆各区域中磁感应线是以电缆轴线为对称轴的同心圆。
大学物理答案第七章

(3)若沿过程曲线从a到c状态,内能改变为
应用热力学第一定律,系统所作的功为
7-3 2mol的氮气从标准状态加热到373 K,如果加热时(1)体积不变;(2)压强不变,问在这两种情况下气体吸热分别是多少?哪个过程吸热较多?为什么?
分析根据热力学第一定律,系统从外界吸收的热量,一部分用于增加系统的内能,另一部分用于对外作功.理想气体的内能是温度的单值函数,在常温和常压下氮气可视为理想气体,无论经过什么样的准静态过程从标准状态加热到373 K,其内能的变化都相同.在等体过程中气体对外不作功,系统从外界吸收的热量,全部用于系统的内能的增加,而在等压过程中,除增加内能外,还要用于系统对外作功,因此吸热量要多些.
分析气体动理论的能量公式表明,气体的温度是气体分子平均平动动能的量度,而且定义了方均根速率 .只要温度不变,无论经历什么样的过程,方均根速率都不变.本题中,可以通过等温过程中系统所作的功的表达式确定该过程中系统的温度.
解等温过程中系统所作的功为
7-92 m3的气体等温地膨胀,压强从 变到 ,求完成的功.
第七章热力学基础
7-1 假设火箭中的气体为单原子理想气体,温度为2000 K,当气体离开喷口时,温度为1000 K,(1)设气体原子质量为4个原子质量单位,求气体分子原来的方均根速率 .已知一个原子质量单位=1.6605×10-27kg;(2)假设气体离开喷口时的流速(即分子定向运动速度)大小相等,均沿同一方向,求这速度的大小,已知气体总的能量不变.
p
p22
p0等温线
1
p1
OV2V1V
图7-12
分析对于双原子理想气体,热容比 .不论经历什么过程,只要初终态气体的温度相同,就可以应用理想气体状态方程,建立类似于等温过程中初态和终态压强和体积之间的关系.
大学物理学(课后答案)第7章

第七章课后习题解答、选择题7-1处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,则它们[](A) 温度,压强均不相同(B)温度相同,但氦气压强大于氮气的压强(C)温度,压强都相同(D)温度相同,但氦气压强小于氮气的压强3分析:理想气体分子的平均平动动能τk= kT,仅与温度有关,因此当氦气和氮2气的平均平动动能相同时,温度也相同。
又由理想气体的压强公式p =nkT ,当两者分子数密度相同时,它们压强也相同。
故选( C)O7-2理想气体处于平衡状态,设温度为T,气体分子的自由度为i ,则每个气体分子所具有的[](A)动能为-kT (B)动能为丄RT2 2(C)平均动能为^kT (D)平均平动动能为^RT分析:由理想气体分子的的平均平动动能3 kT和理想气体分子的的平均动能2T二丄kT ,故选择(C)O27-3三个容器A、B、C中装有同种理想气体,其分子数密度n相同,而方均根1/2 1/2 1/2速率之比为V A : V B : V C 1:2:4 ,则其压强之比为P A : P B : P C[](A) 1:2:4 (B) 1:4:8 (C) 1 : 4 : 16 (D) 4:2:1分析:由分子方均根速率公式= J3RT,又由物态方程p = nkT ,所以当三容器中得分子数密度相同时,得p1: P2: P3 =T1 :T2 :T3 =1:4:16 O故选择(C)O7-4图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果(VP O和(V P 分别表示氧气和氢气的最概然速率,则[](A)图中a表示氧气分子的速率分布曲线且V P O z V P H= 4(B) 图中a表示氧气分子的速率分布曲线且V P O/ V P H? =1/4(C) 图中b表示氧气分子的速率分布曲线且V P O / V P H=1/4(D) 图中b表示氧气分子的速率分布曲线且V P O/ V P H2 =4分析:在温度相同的情况下,由最概然速率公式'..P=I j2RT及氢气与氧气的摩尔质量M H2£M o2,可知氢气的最概然速率大于氧气的最概然速率,故曲线a对应于氧分子的速率分布曲线。
大学物理课后习题答案(上下册全)武汉大学出版社 第7章 热力学基础习题解答

第7章 热力学基础7-1在下列准静态过程中,系统放热且内能减少的过程是[ D ] A .等温膨胀. B .绝热压缩. C .等容升温. D .等压压缩.7-2 如题7-2图所示,一定量的理想气体从体积V 1膨胀到体积V 2分别经历的过程是:A →B 等压过程; A →C 等温过程; A →D 绝热过程 . 其中吸热最多的过程是[ A ] A .A →B 等压过程 B .A →C 等温过程.C .A →D 绝热过程. 题7-2图 D .A →B 和A → C 两过程吸热一样多.7-3 一定量某理想气体所经历的循环过程是:从初态(V 0 ,T 0)开始,先经绝热膨胀使其体积增大1倍,再经等容升温回复到初态温度T 0, 最后经等温过程使其体积回复为V 0 , 则气体在此循环过程中[ B ]A .对外作的净功为正值.B .对外作的净功为负值.C .内能增加了.D .从外界净吸收的热量为正值. 7-4 根据热力学第二定律,判断下列说法正确的是 [ D ] A .功可以全部转化为热量,但热量不能全部转化为功.B .热量可以从高温物体传到低温物体,但不能从低温物体传到高温物体.C .不可逆过程就是不能向相反方向进行的过程.D .一切自发过程都是不可逆的.7-5 关于可逆过程和不可逆过程有以下几种说法,正确的是[ A ] A .可逆过程一定是准静态过程. B .准静态过程一定是可逆过程. C .无摩擦过程一定是可逆过程.D .不可逆过程就是不能向相反方向进行的过程.7-6 理想气体卡诺循环过程的两条绝热线下的面积大小(题7-6图中阴影部分)分别为S 1和S 2 , 则二者的大小关系是[ B ] A .S 1 > S 2 . B .S 1 = S 2 .C .S 1 < S 2 .D .无法确定. 题7-6图 7-7 理想气体进行的下列各种过程,哪些过程可能发生[ D ] A .等容加热时,内能减少,同时压强升高 B . 等温压缩时,压强升高,同时吸热 C .等压压缩时,内能增加,同时吸热 D .绝热压缩时,压强升高,同时内能增加7-8 在题7-8图所示的三个过程中,a →c 为等温过程,则有[ B ] A .a →b 过程 ∆E <0,a →d 过程 ∆E <0. B .a →b 过程 ∆E >0,a →d 过程 ∆E <0. C .a →b 过程 ∆E <0,a →d 过程 ∆E >0.D .a →b 过程 ∆E >0,a →d 过程 ∆E >0. 题7-8图7-9 一定量的理想气体,分别进行如题7-9图所示的两个卡诺循环,若在p V -图上这两个循环过程曲线所围的面积相等,则这两个循环的[ D ] A .效率相等.B .从高温热源吸收的热量相等.C .向低温热源放出的热量相等.D .对外做的净功相等. 题7-9图7-10一定质量的某种理想气体在等压过程中对外作功为 200 J .若此种气体为单原子分子气体,则该过程中需吸热__500__ J ;若为双原子分子气体,则需吸热__700___ J 。
大学物理学第七章参考答案

题7.1:1964年,盖尔曼等人提出基本粒子是由更基本的夸克构成,中子就是由一个带e 32的上夸克和两个带e 31-下夸克构成,若将夸克作为经典粒子处理(夸克线度约为10-20 m ),中子内的两个下夸克之间相距2.60⨯10-15 m 。
求它们之间的斥力。
题7.1解:由于夸克可视为经典点电荷,由库仑定律r r 220r 2210N 78.394141e e e F ===r e r q q πεπεF 与r e 方向相同表明它们之间为斥力。
题7.2:质量为m ,电荷为-e 的电子以圆轨道绕氢核旋转,其动能为E k 。
证明电子的旋转频率满足42k20232me E εν=其中是0ε真空电容率,电子的运动可视为遵守经典力学规律。
题7.2分析:根据题意将电子作为经典粒子处理。
电子、氢核的大小约为10-15 m ,轨道半径约为10-10 m ,故电子、氢核都可视作点电荷。
点电荷间的库仑引力是维持电子沿圆轨道运动的向心力,故有220241r e r v m πε= 由此出发命题可证。
证:由上述分析可得电子的动能为re mv E 202k 8121πε==电子旋转角速度为30224mr e πεω=由上述两式消去r ,得43k 20222324me E επων== 题7.3:在氯化铯晶体中,一价氯离于Cl -与其最邻近的八个一价格离子Cs +构成如图所示的立方晶格结构。
(1)求氯离子所受的库仑力;(2)假设图中箭头所指处缺少一个铯离子(称作品格缺陷),求此时氯离子所受的库仑力。
题7.3分析:铯离子和氯离子均可视作点电荷,可直接将晶格顶角铯离子与氯离子之间的库仑力进行矢量叠加。
为方便计算可以利用晶格的对称性求氯离子所受的合力。
解:(l )由对称性,每条对角线上的一对铯离子与氯离子间的作用合力为零,故01=F (2)除了有缺陷的那条对角线外,其它铯离子与氯离子的作用合力为零,所以氯离子所受的合力2F 的值为N 1092.134920220212-⨯===ae rq q F πεπε2F 方向如图所示。
大学物理习题解答第七章课后习题参考答案

习 题 七7-1 如图所示,O S O S 21=.若在O S 1中放入一折射率为n ,厚度为e 的透明介质片,求O S 1与O S 2之间的光程差.如果1S 和2S 是两个波长为λ的同相位的相干光源,求两光在O 点的相位差.[解] O S1与O S 2的几何路程相等光程差为 ()e n 1-=δ 位相差为 ()e n 122-==∆λπδλπϕ7-2 一束绿光照射到两相距 0.6mm 的双缝上,在距双缝2.5m 处的屏上出现干涉条纹.测得两相邻明条纹中心间的距离为2.27mm ,试求入射光的波长.[解] 由杨氏双缝干涉知 dD x λ=∆ 所以 5448m 10448.55.21060.01027.2733=⨯=⨯⨯⨯=∆=---D xd λÅ7-3 如图所示,在双缝干涉实验中,21SS SS =,用波长为λ的单色光照S ,通过空气后在屏幕E 上形成干涉条纹.已知点P 处为第3级干涉明条纹,求1S 和2S 到点P 的光程差.若整个装置放于某种透明液体中,点P 为第4级干涉明条纹,求该液体的折射率.[解] 1S 和2S 到P 点的光程差满足λλδ312==-=k r r整个装置放置于液体中,1S 和2S 到P 点的光程差满足()λδ412=-=r r nλλ43=n所以得到 33.134==n7-4 如习题7-1图所示,1S 和2S 是两个同相位的相干光源,它们发出波长λ=5000Å的光波,设O 是它们中垂线上的一点,在点1S 与点O 之间插入一折射率n =1.50的薄玻璃,点O 恰为第4级明条纹的中心,求它的厚度e .[解] 在O 点是第4级明条纹的中心光程差 λδ4=-=e ne所以 410414⨯=-=n e λÅ7-5 初位相相同的两相干光源产生的波长为6000Å的光波在空间某点P 相遇产生干涉,其几何路径之差为6102.1-⨯m .如果光线通过的介质分别为空气(11=n )、水(=2n 1.33)或松节油(=3n 1.50)时,点P 的干涉是加强还是减弱.[解] 光在折射率为n 的介质中P 点处光程差为()12r r n -=δ介质为空气时,11=n ,则()λδ2m 102.16121211=⨯=-=-=-r r r r n光程差为半波长的偶数倍,所以P 点处干涉加强. 介质为水时,=2n 1.33,则()m 106.1102.133.1661222--⨯=⨯⨯=-=r r n δ光程差介于两种情况之间,且结果与半波长的奇数倍更接近,所以P 点光强介于明暗条纹中心光强之间,且与暗条纹中心光强更接近.介质为松节油时,=3n 1.50,则()λδ3m 108.1102.15.1661233=⨯=⨯⨯=-=--r r n光程差为半波长的偶数倍,所以P 点处干涉加强.7-6 在双缝干涉实验中,用很薄的云母片(58.1=n )覆盖在双缝的一条上,如图所示.这时屏上零级明纹移到原来第7级明纹位置上.如果入射光波5000Å,试求云母片的厚度(设光线垂直射入云母片).[解] 原来的第7级明纹的位置满足λ721=-r r加上云母片后,光程差满足[]()012121=---=+--e n r r ne e r r所以41003.6158.15000717⨯=-⨯=-=n e λ Å7-7 用单色光源S 照射平行双缝1S 和2S 形成两相干光源.在屏上产生干涉图样,零级明条纹位于点O ,如图所示.若将缝光源S 移到S '位置,问零级明条纹向什么方向移动?若使零级明条纹移回点O ,必须在哪个缝的右边插入一薄云母片才有可能? 若以波长为5890Å的单色光,欲使移动了4个明纹间距的零级明纹移回到点O ,云母片的厚度应为多少? 云母片的折射率为1.58.[解] 零级明纹是光程差为0的位置.移动光源后光线2的光程长了,为仍保持光程差为0,必须让1的光程增加以弥补2的增加,只有在下方1才比2长,所以向下.要回到原点,即通过加片的方法使得1的光程增大,所以在1S 后加.在原点时,两光线的光程差满足()λδ41=-=e n得到 m 1006.4158.1105890414610--⨯=-⨯⨯=-=n e λ7-8 用白光作光源观察杨氏双缝干涉,设缝间距为d ,双缝与屏的距离为D ,试求能观察到的无重叠的可见光(波长范围: 4000~7600Å)光谱的级次.[解] k 级明纹的位置为dD k x λ=k 要使光谱无重叠,必须满足 ()()λm i n 1k λm a x k +≤x x 因此 ()min max 1λλ+≤k k 即 ()140007600+≤k k解得 1.1 ≤k 所以只能看到一级无重叠光谱.7-9 白色平行光垂直照射到间距为m m 0.25=d 的双缝上,在距缝cm 50处放一屏幕,若把白光(4000~7600Å)两极端波长的同级明纹间的距离叫做彩色带的宽度,试求第1级和第5级彩色带的宽度.[解] 每一级的宽度()min max min max λλ-=-=∆dDkx x x 1=k 时,()mm 72.0m 102.710400076001025.010*******21=⨯=⨯-⨯⨯⨯⨯=∆----x 5=k 时,()mm 6.3m 106.310400076001025.010505310325=⨯=⨯-⨯⨯⨯⨯=∆----x7-l0 波长为λ的单色光垂直照射在如图所示的透明薄膜上,薄膜厚度为e .两反射光的光程差是多少?[解]薄膜上下表面的反射光均有半波损失,故没有因半波损失而产生的光程差,因此上下表面反射的光程差为e e n 60.222==δ7-11 白光垂直照射在空气中厚度为71080.3-⨯m 的肥皂膜上,肥皂膜的折射率为1.33,在可见光范围内(4000~7600Å) 哪些波长的光在反射中增强.[解] 光程差 λλδk ne =+=22 所以124-=k neλ 当1=k 时,2021612108.333.1471=-⨯⨯⨯=-λÅ 当2=k 时,同理可得67392=λÅ 当3=k 时,同理可得40433=λÅ所以在可见光范围内波长为4043 Å和6739 Å的光在反射中增强.7-12 在观察肥皂膜的反射光时,表面呈绿色(λ=5000 Å),薄膜表面法线和视线间的夹角为450,试计算薄膜的最小厚度. [解] 两反射光的光程差为λλδk i n n e =+-=2sin 2221221=k 时对应薄膜厚度最小为m 1011.145sin 33.14105000sin 470221022122--⨯=-⨯⨯=-=in n e λ7-13 用波长连续可调的平行光垂直照射覆盖在玻璃板上的油膜,观察到5000 Å和7000 Å这两个波长的光在反射中消失.油的折射率为1.30,玻璃的折射率为1.50.求油膜的厚度.[解] 某一波长的光在反射中消失,表明光在油膜上下表面反射的光干涉相消,故光程差为 ()21222λδ+==k e n对1λ: ()2122112λ+=k e n对2λ: ()2122222λ+=k e n又因1λ与2λ之间没有其他波长的光消失,故1λ与2λ的干涉级数只可能相差一级 故112-=k k 因此575000700012121211===-+λλk k解得 31=k 22=k以31=k 代入得,()m 1073.630.141050007412710211--⨯=⨯⨯⨯=+=n k e λ7-14 波长为5500 Å的黄绿光对人眼和照像底片最敏感,要增大照像机镜头对此光的透射率,可在镜头上镀一层氟化镁 (2MgF )薄膜. 已知氟化镁的折射率为1.38,玻璃的折射率为 1.50,求氟化镁的最小厚度.[解] 要增大波长为λ的光的透射率,则须使反射光干涉减弱.那么,光程差应满足()21222λδ+==k e n当0=k 时,e 最小,为m 1096.938.1410550048102min--⨯=⨯⨯==n e λ7-15 如图所示,用波长为λ的单色光垂直照射折射率为2n 的劈尖.图中各部分折射率的关系是1n <2n <3n ,观察反射光的干涉条纹,从劈尖顶端开始向右数第5条暗纹中心所对应的厚度是多少?[解] 因1n <2n <3n ,故在劈尖上下表面的两反射光无因半波损失引起的附加光程差,干涉暗纹应满足()21222λδ+==k e n因棱边为明纹,故从棱边开始向右数第5条暗纹对应上式中4=k所以()()2225494142412n n n k e λλλ=+⨯=+=7-16 用波长为1λ的单色光垂直照射空气劈尖,从反射光的干涉条纹中观察到劈尖装置的点A 处是暗条纹.若连续改变入射光的波长,直到波长为2λ(2λ>1λ)时,点A 将再变成暗条纹.求点 A 处空气层的厚度. [解] 空气劈尖上暗条纹处满足()21222λλδ+=+=k ne因1=n ,所以()21222λλ+=+k e ,即λk e =2 在A 处 11A 2λk e =,22A 2λk e =同一点,e 相同,又2λ>1λ,故2k <1k ,又因1λ到2λ连续可调,中间无其他波长的光干涉形成暗条纹,故112-=k k因此 122111A 212λλλλλ-==k e7-17 用波长为λ的单色光垂直照射到空气劈尖上,从反射光中观察干涉条纹,距顶点为L 处是暗条纹.使劈尖角θ连续慢慢变大,直到该点再次出现暗条纹为止,劈尖角的改变量θ∆是多少?[解] 空气劈尖干涉暗纹,光程差为 ()21222k λλδ+=+=k e劈尖角为θ时,L 处有 ()212221k 1λλ+=+k e 劈尖角为θθ∆+时,有 ()212222k 2λλ+=+k e因为劈尖角连续改变,即e 连续增大,故2k =1k +1 由上述公式得 ()λ=-12k k 2e e又 θθL L e ==sin 1k ,()()θθθθ∆+=∆+=L L e sin 2k 因此 L2λθ=∆7-18 两块长度为l0cm 的平玻璃片,一端相互接触,另一端用厚度为0.004mm 的纸片隔开形成空气劈尖.以波长为5000Å 的平行光垂直照射,观察反射光的等厚干涉条纹.在全部10cm 长度内呈现多少条明纹?[解] 设平玻璃片长为L ,纸片厚为H ,则形成的空气劈尖角为LH ==θθsin 两相邻明纹间距为 HLl 22sin 2λθλθλ===故总条数为 1610500010004.022103=⨯⨯⨯===--λH l L N7-19 为测量硅片上氧化膜的厚度,常用化学方法将薄膜的一部分腐蚀掉,使之成为劈形(又称为台阶),如图所示.用单色光垂直照射到台阶上,就出现明暗相间的干涉条纹,数出干涉条纹的数目,就可确定氧化硅薄膜的厚度.若用钠光照射,其波长λ=5893Å,在台阶上共看到5条明条纹,求膜的厚度(氧化硅的折射率2n =1.5,硅的折射率为3n =3.42).[解] 因1n <2n < 3n ,故台阶上下表面反射光的光程差为e n 22=δ明条纹满足的条件为 λk e n =22台阶棱边为明纹,因共看到5条明纹,所以4max =k ,由明纹条件得m 1078575.1105893222101022max max--⨯=⨯⨯===n n k e λλ7-20 检查平板的平整度时,在显微镜下观察到的等厚条纹如图所示,条纹的最大畸变量为1.5条纹间距,所用光波波长为546nm ,试描述待测平面的缺陷.[解] 因每一条干涉条纹上对应的空气厚度相同,故在同一条纹上,畸变部分和平行棱边的直线部分所对应的膜厚度相等,本来离棱边越远膜的厚度越大,而现在同一条纹上,远离棱边的畸变部分厚度并不大,这说明畸变部分是凸起的,因最大畸变是为1.5条纹间距,说明最大畸变处膜厚度比非畸变时膜厚度之差e ∆对应的级数差5.1=∆k由劈尖明纹公式 λλk e =+22得 λk e ∆=∆2所以 m 101.421046.55.1277--⨯=⨯⨯=∆=∆λk e7-21 如图所示,A 、B 是两只块规(块规是两端面经过磨平抛光达到相互平行的钢质长方体).A 的长度是标准的,B 是相同规格待校准的.A 、B 放在平台上,用一块样板平玻璃压住.(1)设垂直入射光的波长为λ=5893Å,A 、B 相隔cm 5=d ,T 与A 、 B 间的干涉条纹的间距都是0.55 mm ,试求两块规的长度差.(2)如何判断A 、B 哪一块比较长些?(3)如果T 与A 、B 间的干涉条纹间距分别为0.55 mm 和 0.3 mm ,则说明什么问题?[解] (1) 劈尖干涉,相邻条纹间距l 满足l2sin λα=所以A 、B 两只块规的高度差为m 1068.21055.0210893.51052sin 5372----⨯=⨯⨯⨯⨯⨯===∆l d d h λα (2)因空气劈尖棱边处为暗纹,所以若压平板T ,a 、c 处暗纹位置不变,则B 比A 长,若压T ,b 、d 处暗纹位置不变,则A 比B 长.(3) 设平板T 与A 、B 间形成的劈尖角分别为1α、2α.干涉条纹间距分别为1l 和2l ,则 2sin sin 2211λαα==l l已知1l >2l ,则1α<2α,B 的端面与底面不平行,且d 处向下倾斜.7-22 如图所示的观察牛顿环的装置中,设平球面透镜中心恰好和平玻璃接触,透镜球面的半径cm 400=R ,用某单色光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是cm 30.0(1)求入射光的波长;(2)设图中OA =1.00cm ,求在半径为OA 的范围内可观察到的明环数.[解] (1)牛顿环明环半径公式为()2122k λR k r -=,所以()Rk r 1222k -=λ因中心为暗环,对应第5个明环5=k ,所以()5000104009103.0215222422k =⨯⨯⨯⨯=-⨯=--R r λÅ(2)因为()2122k λR k r -=,所以()5.5010541000.121217222k =⨯⨯⨯+=+≤--λR r k 所以能看到的明环数50个.7-23 用曲率半径为3.00m 的平凸透镜和平板玻璃作牛顿环实验,测得第k 级暗环半径为m m 24.4,第10+k 级暗环的半径为m m 0.6.求所用单色光的波长.[解] 牛顿环暗环半径公式为λkR r =k 故 ()λR k r 1010k +=+因此 ()()323232k 210k 1001.600.3101024.410610⨯=⨯⨯-⨯=-=--+R r r λÅ7-24 用牛顿环实验测单色光的波长.用已知波长为1λ的单色光垂直照射牛顿环装置时,测得第1和第9级暗环的半径之差为1l ;用未知单色光照射时测得第l 和第9级暗环的半径之差为2l .求单色光的波长2λ.[解] 牛顿环暗环半径公式为 λkR r =k对1λ 11λR r = 199λR r = 所以()19119-=-λR r r又 119l r r =-, 故211⨯=λR l 同理得 222⨯=λR l因此 121222λλl l =7-25 一平凸透镜放在平板玻璃上,在反射光中观察牛顿环.当1λ=4500Å时,测得第3级明环的半径为31006.1-⨯m .换用红光,观测到第5级明环的半径为31077.1-⨯m .求透镜曲率半径和红光的波长.[解] 牛顿环明环半径公式为()2122k λR k r -=,对1λ,3=k 时, 25123λR r =对2λ,5=k 时, 29225λR r =由此得 697145001006.191077.15956262123252=⨯⨯⨯⨯⨯==--λλr r Å由25123λR r =得, m 00.110450051006.12521062123=⨯⨯⨯⨯==--λr R7-26 用牛顿环干涉条纹测定凹球面的曲率半径.将已知曲率半径的平凸透镜放在待测的凹球面上,如图所示.在两曲面之间形成空气层,可以观测到环状干涉条纹.测得第4级暗环的半径4r =2.250cm ,已知入射光的波长λ=5893 Å,平凸透镜的曲率半径1R =102.3cm ,求凹球面的曲率半径2R .[解] 牛顿环k 级暗环条件为 ()21222λλ+=+k e 即 λk e =2由几何关系知 ()2111211212k 2e e R e R R r +=--=因为 11R e << ,故 112k 2e R r = 同理 222k 2e R r = 又 21e e e -= 联立上式得2k 1211r k R R λ-= 以 m 023.11=R ,4=k ,m 10589310-⨯=λ,m 10250.224-⨯=r ,代入得cm 8.1022=R7-27 在观察牛顿环干涉条纹的实验中,用图(a )、(b )、(c )所示的装置代替平凸透镜和平玻璃组合.试画出反射光中的干涉条纹(只画暗条纹).[解](a ) (b ) (c )7-28 用波长为λ的单色光源做迈克尔逊干涉仪实验,在移动反光镜2M 的过程中,视场中的干涉条纹移过k 条,求反射镜移动的距离?[解] 设反射镜移过的距离为d ,则光程差改变量为 λδk d ==∆2所以 2λk d =7-29 迈克尔逊干涉仪的一臂中放有长为100.0mm 的玻璃管,其中充有一个大气压空气,用波长为5850Å的光作光源.在把玻璃管抽成真空的过程中,发现视场中有100.0条干涉条纹从某固定点移过.求空气的折射率.[解] 设空气的折射率为n ,在由空气抽成真空的过程中,光程差改变量为()λk e n ∆=-12所以 00029.1100.10021058500.100121310=⨯⨯⨯⨯+=∆+=--e k n λ7-30 在把迈克尔逊干涉仪的可动反射镜移动0.233mm 过程中,数得条纹移动数为792,求所用光的波长.[解] 设反射镜移动距离为d ,则光程差改变 λδk d ∆==∆25884m 10884.579210233.022103=⨯=⨯⨯=∆=--k d λÅ7-31 常用雅敏干涉仪来测定气体在各种温度和压力下的折射率.干涉仪的光路如图所示.S 为光源,L 为正透镜,1G 、2G 为等厚且相互平行的玻璃板.1T 、2T 为等长的两个玻璃管,长度为l .进行测量时,先将1T 、2T 抽空,然后把待测气体徐徐导入一管中,在E123451234512345处观察干涉条纹移动数,即可求得待测气体的折射率.设在测量某气体的折射率时,将气体慢慢放入2T 管中,从开始进气到标准状态时,在E 处共看到有98条干涉条纹移过去.所用的钠光波长λ=5893Å (真空中),l =20cm .求该气体在标准状态下的折射率.[解] 设待测气体在标准状态下的折射率为n ,则在气体导入前后,两条光路中的光程差改变为()λk l n ∆=-1所以00029.110201058939811210=⨯⨯⨯+=∆+=--l k n λ7-32 一单缝宽度4101-⨯=a m ,透镜的焦距m 5.0=f ,若分别用40001=λÅ和76002=λÅ的单色平行光垂直入射,它们的中央明条纹的宽度各是多少?[解] 一级暗纹公式为 λϕ=1sin a 而aλϕϕ==11sin所以 a f f f x λϕϕ===111tan 所以中央明纹的宽度为 af x x λ221==∆对1λ: m 1041011045.02234711---⨯=⨯⨯⨯⨯==∆a f x λ 对2λ: m 106.7101106.75.02234722---⨯=⨯⨯⨯⨯==∆a f x λ7-33 有一单缝宽m m 10.0=a ,在缝后放一焦距cm 50=f 的会聚透镜,用波长λ=5460 Å的平行绿光垂直照射单缝,求位于透镜焦平面处的屏上的中央亮条纹的宽度.如果把此装置浸入水中,并把屏移动到透镜在水中的焦平面上,中央亮条纹的宽度变为多少?设透镜的折射率54.1='n ,水的折射率33.1=n .(提示:透镜在水中的焦距()f nn n n f -'-'=1水) [解] (1) 中央明条纹的宽度为m 1046.51010.01046.51050223372----⨯=⨯⨯⨯⨯⨯==∆a f x λ (2) 在水中,透镜焦距为()f nn n n f -'-'=1水 所以中央明条纹的宽度为()()()()m 1040.1101.033.154.11046.550.0154.12122237---⨯=⨯⨯-⨯⨯⨯-⨯=-'-'==∆a n n f n naf x λλ水7-34 用波长λ=7000Å的平行光垂直照射单缝,缝后放一焦距为70cm 的正透镜,在透镜焦平面处的屏上测得中央亮条纹的宽度为3100.2-⨯m .试计算: (1)单缝的宽度.(2)当用另一单色光照射时,测得中央亮纹的宽度为3105.1-⨯m ,求此光的波长. [解]中央亮条纹宽度为 af x λ2=∆ (1)由上式可得单缝的宽度为 m 109.41021071070224372----⨯=⨯⨯⨯⨯⨯=∆=x f a λ (2)由前式可得光的波长为5250m 1025.510072105.1109.427234=⨯=⨯⨯⨯⨯⨯='∆='----f x a λÅ7-35 用平行光管把某光源发出的单色光变成平行光后垂直照射在宽度为0.308mm 的单缝上.用焦距为12.62cm 的测微目镜测得中央明条纹两侧第5级暗条纹之间的距离为x ∆=2.414mm .求入射光的波长.[解] 单缝衍射暗纹中心到中央亮纹中心距离为 af kx λ= 5=k 时,af x λ55= 两侧第5级暗纹之间的距离为 af x x λ1025==∆ 所以 58921062.121010414.210308.010233=⨯⨯⨯⨯⨯=∆=---f x a λÅ7-36 用波长λ=6328Å的氦-氖激光垂直照射单缝,其夫琅禾费衍射图样的第1级极小的衍射角为50.试求单缝的宽度.[解] 单缝衍射暗纹条件为λϕk a =sin 当 1=k 时,λϕ=sin a所以 ϕλϕλ==sin a 式中 g r a d1805πϕ= 所以 m 1026.7518010328.667--⨯=⨯⨯=πa7-37 在正常照度下,人眼瞳孔的直径约为mm 2,人眼最敏感的波长为5500Å.眼前m m 250 (明视距离)处的点物在视网膜上形成艾里斑的角半径是多少? 明视距离处能够被分辨的两物点的最小距离是多少?(前房液和玻璃状液的折射率33.1=n )[解] (1) 因人眼中玻璃状液体的折射率为n ,所以波长变为nλλ='在视网膜上形成爱里斑的角半径为rad 1052.210233.1105.522.122.122.1437---⨯=⨯⨯⨯⨯=='=nD D λλθ (2) 人眼的最小分辨角 Dλθ22.1min =设在距离L 处能分辨的最小距离为d (l d θ=),则m 104.810250102105.522.122.15337----⨯=⨯⨯⨯⨯⨯==D L d λ7-38 已知天空中两颗星对一望远镜的角距离为61084.4-⨯rad ,设它们发出光的波长为5500Å.望远镜的口径至少要多大才能分辨出这两颗星.[解] 设望远镜孔径为D ,当两星对望远镜的角距离大于其最小分辨角时方可分辨,即Dλ22.11084.46≥⨯-所以 cm 9.131084.4105.522.11084.422.1676=⨯⨯⨯=⨯≥---λD7-39 月球距地面约3.86510⨯km ,设月光按λ=5500Å计算,问月球表面上距离多远的两点才能被直径为5.00m 的天文望远镜所分辨.[解] 设月球上两物点距离为d ,其对望远镜张角大于最小分辨角时,则能分辨该两点即DL d λ22.1≥ 所以 m 8.5100.51086.3105.522.122.187=⨯⨯⨯⨯=≥-D L d λ7-40 用波长为λ=5893Å的钠光垂直照射光栅,测得第2级谱线的衍射角11102'︒=θ,而用待测波长的单色光照射时,测得第一级谱线的衍射角2441'︒=θ.试求光栅常数和待测光的波长.[解] 光栅方程为 ()λϕk b a =+sin 对1λ有 ()11sin λθ=+b a 对2λ有 ()222sin λθ=+b a由上两式得 546410893.51110sin 244sin 2sin sin 27002211=⨯⨯''⨯==-λθθλÅ 将1λ的数值代入得 m 1067.66-⨯=+b a7-4l 一块每毫米刻痕为500条的光栅,用钠黄光正入射,钠黄光中含有两条谱线,其波长分别为5896Å和5890Å.求在第2级光谱中这两条谱线分开的角度.[解] 光栅常数为 m 10250010163--⨯=⨯=+b a 由光栅方程可得 ()122s i nλϕ=+b a ()222sin λϕ='+b a 因此得到 ⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+='-=∆b a b a 21222arcsin 2arcsin λλϕϕϕ6767043.010210890.52arcsin 10210896.52arcsin =⎪⎪⎭⎫⎝⎛⨯⨯⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯⨯=----7-42 一单色平行光投射于衍射光栅,其入射方向与光栅法线夹角为θ,在和法线成︒11和︒53的方向上出现第1级光谱线,并且位于法线的两侧.求θ角的大小.为什么在法线的一侧能观察到第2级谱线,而另一侧却没有?[解](1) 斜入射时,零级主极大在透镜的与入射光线平行的副光轴方向上.530角的衍射光线和入射光线分别在法线两侧,此衍射角应取负值,而110衍射角应取正值,所以两个第一级光谱线对应的方程分别为 ()()λθ-=-+053sin sin b a (1)()()λθ+=++011sin sin b a (2) 因此求得 3039.0sin =θ 07.17=θ(2) 设法线两侧衍射角为900时对应极大的级数分别为k 和k '在与入射光线异侧有 ()()λk b a -=-+0090sin 7.17sin (3) 在与入射光线同侧有 ()()λk b a '=++0090sin 7.17sin (4)由 (1)、(3)式相除,得 4.17.17sin 53sin 7.17sin 90sin 0000≈--=k 由 (2)、(4)式相除,得 64.27.17sin 11sin 7.17sin 90sin 0000≈++='k 由上面结果知,只有与入射光线同侧可观察到第二级谱线.7-43 一衍射光栅,每厘米有200条透光缝,每条透光缝宽为3102-⨯=a cm ,在光栅后放一焦距为m 0.1=f 的凸透镜.现以λ=6000Å单色平行光垂直照射光栅,试求: (1)透光缝的单缝衍射中央明条纹宽度;(2)在该宽度内有哪几个光栅衍射主极大?[解] (1)单缝衍射第一极小满足 λϕ=s i na (1) 中央明纹宽度为m 1061021060.122sin 2tan 2257---⨯=⨯⨯⨯⨯====∆a f f f x λϕϕ (2) 设该范围内主极大最大级数为k ,则()λϕk b a =+sin (2)由 (1)、(2)式有 5.210220010152=⨯⨯⨯=+=--a b a k 所以在此范围内能看到的主极大级数为210±±=,,k ,共5个光栅衍射主极大.7-44 试指出光栅常数()b a +为下述三种情况时,哪些级数的光谱线缺级?(1)光栅常数为狭缝宽度的两倍,即()a b a 2=+; (2)光栅常数为狭缝宽度的三倍,即()a b a 3=+;(3)光栅常数为狭缝宽度的2.5倍,即()a b a 5.2=+.[解] k 级缺级的条件为k aba k '+=() 3,2,1±±±='k (1)()a b a 2=+时,k k '=2,凡2的倍数级都缺级. (2) ()a b a 3=+时,k k '=3,凡3的倍数级都缺级. (3)()a b a 5.2=+时,k k '=5.2,凡5的倍数级都缺级.7-45 波长λ=6000Å的单色光垂直入射到一光栅上,测得第2级主极大的衍射角为︒30,且第3级缺级.(1)光栅常数()b a +是多大?(2)透光缝可能的最小宽度是多少?(3)在屏幕上可能出现的主极大的级次是哪些?[解](1) 由光栅方程得 ()λ230sin 0=+b a所以 m 104.21064430sin 2670--⨯=⨯⨯===+λλb a (2) 当k 级缺级时,满足 k a ba k '+=所以 k kba a '+=当1='k 时,缝宽a 最小,为 m 1083104.276--⨯=⨯=+=k b a a (3) 在屏幕上呈现的主极大的级数由最大级数和缺级情况决定. 因为 ()λφk b a =+sinmax k <4106104.276=⨯⨯=+--λba 因此 m a x k =3又因3=k 缺级,所以在屏上可能出现的级数为 2,1,0±±=k7-46 每厘米刻有400条刻痕的光栅,其透光缝5101-⨯=a m ,用波长为λ=7000Å的光垂直照射在屏幕上可观察到多少条明条纹?[解] 光栅常数 m 105.240010152--⨯=⨯=+b a 因为 ()λϕk b a =+sinmax k <7.35107105.275=⨯⨯=+--λba 因此35max =k 缺级条件 k k k ab a k '='⨯⨯='+=--5.2101105.255所以 凡能被5整除的级数都缺级,共缺级个数为7535=='N 因此,光栅衍射在屏上呈现明条纹总数为 ()5717352=+-⨯=N7-47 以白光(波长范围4000~7600Å)垂直照射光栅,在衍射光谱中,第2级和第3级发生重叠.求第2级被重叠的范围.[解] 最小波长和最大波长分别为4000min =λ Å 7600max =λ Å第3级光谱中,min λ主极大的位置与第2级某一波长λ的主极大位置相同时,开始重叠,由光栅方程可求此波长 ()λϕ2s i n =+b a ()m i n 3s i n λϕ=+b a因此 600040002323min =⨯==λλÅ 故,第2级光谱中被重叠的光谱波长范围为 6000=λÅ~7600 Å7-48 用两米光栅摄谱仪拍摄氢原子光谱,在可见光范围内有四条谱线,如图所示.光栅上每厘米有4000条缝,光栅后的正透镜的焦距为2.00m ,在其焦平面上放一照相底片,求四条谱线在底片上的间距.[解] 光栅常数为 m 105.2400010162--⨯=⨯=+b a ∞对第一条谱线(1=k ),应用光栅方程,为()λϕ=+sin b a 对αH , m 10563.671-⨯=λ,在底片上位置为m 543.0arcsin tan tan 1=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+==b a f f x λϕ 同理可得δγβH H H ,,三条谱线在照像底片上的位置分别为m 396.02=x m 353.03=x m 333.04=x因此 αH 与βH 之间的间距为 7m 14.01=∆x同理可得βH 与γH 之间的间距为 m043.02=∆x γH 与δH 之间的间距为 m 02.03=∆x7-49 用白光照射每毫米50条刻痕的光栅,在距光栅2m 的屏幕上观察到各色光谱,设可见光的上限波长(红光)r λ=7800 Å,下限波长(紫光) v λ=4000 Å,试计算屏幕上第1级光谱的宽度.[解] 第一级谱线满足 ()λϕ=+s i nb a 屏幕上红光谱线的位置为 ba f f x +≈≈r1λϕ 紫光谱线的位置为 ba f f x +≈'≈v2λϕ所以第一级光谱的宽度为()()m 108.310400078001015022103v r 21---⨯=⨯-⨯⨯=-+=-=∆λλb a fx x x7-50 一光源发射红双线在波长λ=6563 Å处,两条谱的波长差λ∆=1.8 Å.有一光栅可以在第1级中把这两条谱线分辨出来,求光栅的最少刻线总数.[解] 光栅的分辨率为 kN R =∆=λλ所以 1.364618.16563=⨯=∆=k N λλ 即光栅最少刻线总数为3647条.7-51 一光栅宽为6cm ,每厘米有6000条刻线,在第三级光谱中,对λ=5000 Å处,可分辨的最小波长间隔是多大?[解] 光栅的总缝数为 3600066000=⨯=N因为光栅的分辨本领为kN =∆λλ046.03600035000=⨯==∆kNλλÅ7-52 一束波长为2.96 Å的X 射线投射到晶体上,所产生的第1级衍射线偏离原入射线方向731'︒,求对应此射线的相邻两原子平面之间的距离.[解] 设掠射角为ϕ,衍射线偏离入射线的角度为θ,则2θϕ=由布拉格方程 λϕk d =sin 2 得相邻两原子平面间距为()52.52731sin296.212sin 2sin 20='⨯⨯===θλϕλk k d Å7-53 以波长为1.10Å的X 射线照射岩盐晶面,测得反射光第1级极大出现在X 射线与晶面的夹角为'3011︒处.问:(1)岩盐晶体的晶格常数d 为多大?(2)当以另一束待测的X 射线照岩盐晶面时,测得反射光第一级极大出现在X 射线与晶面的夹角为'3017︒处,求待测X 射线的波长.[解] (1) 由布拉格方程 λϕk d =sin 2 ,所以 76.25.11sin 210.1sin 20===ϕλk d Å (2) 由布拉格方程得待测X 射线的波长为66.115.17sin 76.22sin 20=⨯⨯==k d ϕλÅ7-54 一束部分偏振光垂直入射于一偏振片上,以入射光为轴旋转偏振片,测得透射光强的最大值是最小值的5倍.求部分偏振光中自然光与线偏振光强度之比.[解] 设该束部分偏振光中自然光光强为0I ,线偏振光光强为I ,透过偏振片后自然光光强变为20I ,因此光强最大时I II +=20max , 光强最小时 20m i n I I =所以22500minmaxI I I I I +== 因此 210=I I7-55 两偏振片A 、B 的透振方向成︒45角,如图所示.入射光是线偏振光,其振动方向和A 的透振方向相同.试求这束光线分别从左边入射和从右边入射时,透射光强之比.[解] 设从左右两边入射时透射光强分别为1I 和2I由马吕斯定律得从左边入射时透射光强为002012145cos I I I == 从右边入射,则00202024145cos 45cos I I I =⋅= 所以入射光从左右两边入射,透射光强之比为1:2:21=I I7-56 三个理想偏振片1P 、2P 、3P 叠放在一起,1P 与3P 的透振方向互相垂直,位于中间的2P 与1P 的透振方向间的夹角为︒30.强度为0I 的自然光垂直入射到1P 上,依次透过1P 、2P 和3P .求通过三个偏振片后的光强.[解] 通过1P 后: 0121I I =通过2P 后: 002128330cos I I I == 通过3P 后: 0022332360cos I I I ==7-57 一束太阳光以某一入射角入射于平面玻璃上,这时反射光为完全偏振光.若透射光的折射角为︒32,试求:(1)太阳光的入射角;(2)这种玻璃的折射率.[解] 因反射光为完全偏振光,所以入射角为布儒斯特角,则 0090=+r i 0000058329090=-=-=r i由布儒斯特定律得 60.158tan tan 00===i n7-58 光从介质1射向介质2时的临界角是︒60.布儒斯特角是多大? [解] 由光的折射定律得 020190sin 60sin n n = 所以2360sin 012==n n 由布儒斯特定律 23tan 120==n n i 由此得 9.400=i7-59 如图所示的各种情况中,以线偏振光或自然光入射于两种介质的界面上.图中0i 为起偏振角, 0i i .试画出折射光线和反射光线并标出它们的偏振状态.[解] 折射光和反射光及其偏振状态如下图7-60 如图(a )所示,一束自然光入射在方解石的表面上,入射光线与光轴成锐角,问有几条光线从方解石透射出来? 如果把方解石切割成等厚的A 、B 两块,并平行地移动一点距离,如图(b )所示,此时光线通过这两块方解石后,有多少条光线射出来? 如果把B 绕入射光线转过一个角度,此时将有几条光线从B 射出来?[答] (1)因入射光不沿光轴方向,也不垂直于光轴,所以在方解石中产生双折射现象,有两条光线透射出来. (2)在A 中为o 光的光线射出来入射到B ,入射面就是B 中o 光的主平面,因此光线通过B 后,只有一条光线射出,同理,在A 中为e 光的光线通过B 后也有一束光线射出,所以从B 中透射出来的仍是两束光.(3)当把B 任意转过一角度时,A 中的o 光和e 透射出来入射到B 中,各自在B 中又发生双折射现象,每条光线在B 中又分为o 光和e 光,因此,总共有四条光线从B 中射出.*7-61 如图所示,一束自然光入射到一方解石晶体上,其光轴垂直于纸面.已知方解石对o 光的折射率o n =1.658,对e 光的折射率为=e n 1.486.(1)如果方解石的厚度为t =1.0 cm ,自然光的入射角︒=45i ,求a ,b 两透射光之间的垂直距离;(2)两透射光的振动方向如何? 哪一束光在晶体中是o 光? 哪一束光在晶体中是e 光?[解](1)由折射定律得:i r n sin sin o o = (1)i r n sin sin e e = (2) 设则,,d BC L AB ==()0e tan tan r r t L -= (3)由于 i ABC =∠,所以 i L d cos = (4)由(1)、(2)、(3)、(4)联立得43.0658.145sin sin sin 000===n i r 002.25=r 48.0486.145sin sin 0e ==r 4.28e =r ()cm 07.02.25tan 4.28tan 0.100=-⨯=Lcm 05.045cos 07.00=⨯=d即a 、b 两光线的垂直距离为cm 05.0.(2)两透射光的振动方向见图.(3)a 为e 光,b 为o 光.*7-62 设方解石对钠黄光 (5893=λÅ)和氦氖激光(63282=λÅ)的主折射率相同,把方解石切割成对上述两光的四分之一波片,其最小厚度各是多少? 6584.1o =n ,4864.1e =n .[解] 设最小厚度分别为1e 和2e ,依题意有()41e o 1λ=-n n e ()42e o 2λ=-n n e所以 ()()m 10565.84864.16584.1410893.5477e 011--⨯=-⨯⨯=-=n n e λ ()()m 10198.94864.16584.1410328.6477e 021--⨯=-⨯⨯=-=n n e λA B C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章课后习题解答一、选择题7-1处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,则它们[ ](A) 温度,压强均不相同 (B) 温度相同,但氦气压强大于氮气的压强(C) 温度,压强都相同 (D) 温度相同,但氦气压强小于氮气的压强分析:理想气体分子的平均平动动能,仅与温度有关,因此当氦气和32k kTε=氮气的平均平动动能相同时,温度也相同。
又由理想气体的压强公式,p nkT =当两者分子数密度相同时,它们压强也相同。
故选(C )。
7-2 理想气体处于平衡状态,设温度为T ,气体分子的自由度为i ,则每个气体分子所具有的[ ](A) 动能为(B) 动能为2ikT 2iRT(C) 平均动能为(D) 平均平动动能为2ikT 2iRT分析:由理想气体分子的的平均平动动能和理想气体分子的的平均动32k kT ε=能,故选择(C )。
2ikT ε=7-3 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为,则其压强之比为 [ ]()()()1/21/21/222::2A B Cvv v =1:2:4A B C p :p :p (A)(B)(C)(D) 1:2:41:4:81:4:164:2:1,又由物态方程,所以当三=p nkT =容器中得分子数密度相同时,得。
故选择(C )。
123123::::1:4:16p p p T T T ==7-4 图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果和分别表示氧气和氢气的最概然速率,则[ ]()2p O v ()2p H vh(A) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /4v v =(B) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(C) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(D) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /4v v =分析:在温度相同的情况下,由最概然速率公式p ν=尔质量,可知氢气的最概然速率大于氧气的最概然速率,故曲线对22H O M M <a 应于氧分子的速率分布曲线。
又因,所以。
故选择(B )。
22116H O M M =22()1()4p H p O νν=7-5 在一个体积不变的容器中,储有一定量的某种理想气体,温度为时,气0T 体分子的平均速率为,分子平均碰撞次数为,平均自由程为,当气体0v 0Z 0λ温度升高为时,气体分子的平均速率,平均碰撞次数和平均自由程分04T v Z λ别为[ ](A) , ,(B) , ,04v v =0Z 4Z =04λλ=02v v =0Z 2Z =0λλ=(C) , ,(D) , ,02v v =0Z 2Z =04λλ=04v v =0Z 2Z =0λλ=分析:由理想气体分子的平均速率公式,所以温度由升至,则ν=0T 04T 平均速率变为原来的2倍;又平均碰撞频率,由于容器容积不变,2Z d n ν=习题7-4图即分子数密度不变,则平均碰撞频率变为;而平均自由程,n 02Z λ=不变,则也不变。
故选择(B )。
n λ二、填空题7-6 在一密闭容器中,装有A 、B 、C 三种理想气体,且处于平衡态。
已知A 种气体的分子数密度为,它产生的压强为,B 种气体的分子数密度为,C1n 1p 12n 种气体的分子数密度为,则混合气体的压强为的________倍。
13n p 1p 答案: 6 分析:由理想气体的压强公式,因在容器容积不发生变化p nkT =的情况下,混合后的气体的总分子数密度,故混合气体的1111236n n n n n =++=压强。
16p p =7-7已知氧气的压强,体积,则其内能2.026 Pa p =233.0010 m V -=⨯________。
E =答案: 0.152 分析:由理想气体的内能公式及理想气体的物态2iE v RT =方程,可知,由因氧气分子是刚性双原子分子,所以,pV vRT =2iE vRT =5i =代入可得。
0.152E J =7-8温度为时,氧气具有的平动动能为________;转动动能为27C ︒ 1 mol ________。
答案: 3739.5J 2493J 分析:由氧气分子的平均平动动能和32kt kT ε=转动动能,可知氧气所具有的平动动能22kr kT ε=1mol ,转动动能,代入数据可3322t A kt A E N kN T RT ε===2222r A kr A E N kN T RT ε===得,。
3739.5t E J =2493r E J =7-9 假定将氧气的热力学温度提高一倍,使氧分子全部离解为氧原子,则氧原子平均速率是氧分子平均速率的________倍。
答案: 2 分析:由理想气体的平均速率,又因分解后、ν=22O O T T =,所以。
212O O M M =22O O νν=7-10 在某平衡状态下,已知理想气体分子的麦克斯韦速率分布函数为,()f v 最概然速率为,试说明式子的物理意义:P v ()Pd v f v v ∞⎰________________________。
答案:速率在区间内的分子数占总分子数的百分比。
p ν∞:三、计算题7-11 在湖面下深处(温度为),有一个体积为的空气50.0m 4.0C ︒531.010m -⨯泡升到湖面上来,若湖面的温度为,求气泡到达湖面的体积(取大气压17.0 C ︒强为)。
50 1.01310Pa p =⨯解 设气泡在湖底和湖面的状态参量分别为和,由分析知气111(,,)p V T 222(,,)p V T 泡位于湖底处时的压强,利用理想气体的物态方程120p p gh p gh ρρ=+=+112212p V p V T T =可得气泡到达湖面时的体积为:。
53122216.1110p T VV m p T -==⨯7-12 试求压强为、质量为、体积为的氧气分子的平均平51.0110 Pa ⨯ 2 g 1.54 L 动动能。
解由理想气体的压强公式,可知,又由理想气体分子p nkT =Ap pVMkT n mN ==的平均平动动能公式32kt kTε=可知。
213 6.201102kt ApVMJ mN ε-==⨯7-13 氢气装在的容器内,当容器内的压强为22.010 kg -⨯334.010 m -⨯时,氢气分子的平均平动动能为多大?53.9010 Pa ⨯解由理想气体的物态方程可知氢气的温度,故氢气分子的平均平动MpVT m R='动能为2233 3.891022k kMpVkT J m Rε-===⨯'7-14 在容积为的容器中,有内能为的刚性双原子分子某332.010 m -⨯26.7510 J ⨯理想气体,求:(1)求气体的压强;(2)若容器中分子总数为个,225.410⨯求分子的平均平动动能及气体的温度。
解 (1)由理想气体的内能公式和理想气体的物态方程,2iE v RT =pV vRT =同时对于双原子分子而言,故可得气体的压强5i =52 1.3510Ep Pa iV==⨯(2)由分子数密度,可得该气体的温度Nn V=23.6210p pV T Knk Nk===⨯气体分子的平均平动动能为2137.49102k kT Jε-==⨯7-15 当温度为时,可将气体分子视为刚性分子,求在此温度下:(1)氧0C ︒分子的平均平动动能和平均转动动能;(2)氧气的内能;(2)34.010 kg -⨯氦气的内能。
34.010 kg -⨯解 根据题意知气体的温度,故273T K =(1)氧分子的平均平动动能为213 5.7102kt kT Jε-==⨯氧分子的平均转动动能为212 3.8102kr kT Jε-==⨯(2)氧气的内能为27.1102m iE RT JM '==⨯(3)氦气的内能为33.4102m iE RT J M '==⨯7-16 假定N 个粒子的速率分布函数为000()0 C v v f v v v >>⎧=⎨>⎩由求:(1)常数;(2)粒子的平均速率。
0v C 解 (1) 因表述的物理意义为气体分子在速率处于附近单位速率区间的()f νν概率,故根据概率密度的归一性知()1f d νν∞=⎰000()()()1f d f d f d C ννννννννν∞∞=+==⎰⎰⎰所以可得1C ν=(2)又因,所以平均速率为()dNf d Nνν=0()2dNf d C d Nννννννννν∞∞====⎰⎰⎰7-17在容积为的容器中,贮有的气体,其压强为333010 m -⨯32010 kg -⨯。
求:该气体分子的最概然速率、平均速率及方均根速率。
350.710 Pa ⨯解由气体分子的最概然速率、理想气体的物态方程和p ν=pV vRT =可得,ANv N =390p m s ν=====同理可得平均速率和方均根速率分别为440m s ν==478rms m s ν==7-18氖分子的有效直径为,求温度为、压强为102.0410 m -⨯600 K 时氖分子的平均碰撞次数。
21.33310 Pa ⨯解由气体分子的平均碰撞次数公式和可得,2Z d n ν=p nkT =612.410Z d s -==⨯7-19在标准状况下,中有多少个氮分子?氮分子的平均速率为多大?平31 cm 均碰撞次数为多少?平均自由程为多大?(氮分子的有效直径。
103.7610 m -=⨯d )解 由题意可知氮分子的分子数密度2532.6910pn m kT-==⨯故其平均速率为454m s ν==则平均碰撞次数为2917.710Z d s ν-==⨯平均自由程为8610m λ-==⨯7-20 在一定的压强下,温度为时,氩气和氮气分子的平均自由程分别为20C ︒和。
求:(1)氩气和氮气分子的有效直径之比;(2)89.910 m -⨯827.510 m -⨯当温度不变且压强为原值的一半时,氮气分子的平均自由程和平均碰撞次数。
解 由气体的平均自由程λ==下平均自由程,在温度不变的情况下,故21dλα1p λα(1)由分析可知2 1.67ArN d d ==(2)当氮气的压强将为原来的一半时,氮气分子的平均自由程2272 5.510NN m λλ-'==⨯而此时的分子平均碰撞频率222818.5610NN N Z s νλ-===⨯'。
